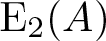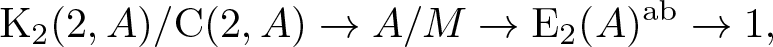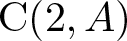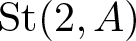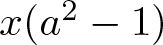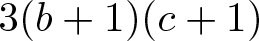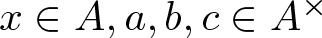Let A be an associative ring with 1. Let 
$\mathit{{\rm E}}_2(A)$ be the elementary subgroup of the general linear group 
$\mathit{{\rm GL}}_2(A)$. In the current paper, we study the abelianization of 
$\mathit{{\rm E}}_2(A)$, i.e. the group
\begin{equation*}
\mathit{{\rm E}}_2(A)^{\rm ab}:=\mathit{{\rm E}}_2(A)/[\mathit{{\rm E}}_2(A),\mathit{{\rm E}}_2(A)].
\end{equation*} This group has been studied in the literature before. The first important result in this direction was proved by P.M. Cohn. In his seminal paper [Reference Cohn5, Theorem 9.3], Cohn showed that if A is quasi-free for GE2 and 
${A^\times}$ is abelian, then
\begin{equation*}
\mathit{{\rm E}}_2(A)^{\rm ab}\simeq A/M,
\end{equation*} where M is the additive subgroup of A generated by axa − x and 
$3(b+1)(c+1)$ with 
$x\in A$ and 
$a,b,c\in {A^\times}$ (see [Reference Cohn5, p. 10] for a definition of quasi-free for GE2). Later Cohn generalized this result to rings that are universal for GE2 [Reference Cohn6, Theorem 2]. In particular, he showed that for any ring A, there is a homomorphism 
$A/M \rightarrow \mathit{{\rm E}}_2(A)^{\rm ab}$.
As the main result of this paper, we show that the homomorphism 
$A/M \rightarrow \mathit{{\rm E}}_2(A)^{\rm ab}$ is a part of an exact sequence with interesting terms. In particular, we show that for any commutative ring A, there is an exact sequence of 
$\mathbb{Z}[{A^\times}/({A^\times})^2]$-modules
\begin{equation*}
H_2(\mathit{{\rm E}}_2(A),\mathbb{Z}) \rightarrow \frac{{\rm K}_2(2,A)}{[{\rm K}_2(2,A), \mathit{{\rm St}}(2,A)]{\rm C}(2,A)} \rightarrow A/M \rightarrow \mathit{{\rm E}}_2(A)^{\rm ab} \rightarrow 0.
\end{equation*} We refer the reader to Theorem 3.1 for a general statement over an arbitrary ring. For the definition of 
$\mathit{{\rm St}}(2,A)$, 
${\rm K}_2(2,A)$ and 
${\rm C}(2,A)$, see § 1.
Many of known results about the structure of 
$\mathit{{\rm E}}_2(A)^{\rm ab}$, that we could find, follow from this exact sequence and we generalize most of them (see for example [Reference Menal11, Theorem], [Reference Cohn5, Theorem 9.3], [Reference Cohn6, Theorem 2], [Reference Stein15, Corollary 4.4]). For example, it follows immediately that if A is universal for GE2, then 
$\mathit{{\rm E}}_2(A)^{\rm ab}\simeq A/M$. Moreover, we show that for any square free integer m, we have
\begin{equation*}
\begin{array}{c}
\mathit{{\rm E}}_2(\mathbb{Z}[\frac{1}{m}])^{\rm ab}\simeq
\end{array}
\begin{cases}
0 & \text{if}\ 2|m,\ 3|m \\
\mathbb{Z}/3 & \text{if}\ 2|m,\ 3\nmid m\\
\mathbb{Z}/4 & \text{if}\ 2\nmid m,\ 3|m\\
\mathbb{Z}/12 & \text{if}\ 2\nmid m,\ 3\nmid m.
\end{cases}
\end{equation*}Some parts of the above isomorphism were known. But during the preparation of this article we could not find this general result in the literature. After that this paper appeared on arXiv, Nyberg-Brodda informed us that he also proved the above isomorphism with a different method. His proof now can be found in [Reference Nyberg-Brodda13].
Finally, we study 
$\mathit{{\rm E}}_2(A)^{\rm ab}$ over the ring of algebraic integers of a quadratic filed 
$\mathbb{Q}(\sqrt{d})$. When d < 0, this group was calculated by Cohn in [Reference Cohn5, Reference Cohn6]. If d > 0, then this group is finite and we give an estimate of its structure.
1. Elementary groups of rank 2 and rings universal for GE2
Let A be a ring (associative with 1). Let 
$\mathit{{\rm E}}_2(A)$ be the subgroup of 
$\mathit{{\rm GL}}_2(A)$ generated by the elementary matrices 
$E_{12}(a):=\begin{pmatrix}
1 & a\\
0 & 1
\end{pmatrix}$ and 
$
E_{21}(a):=\begin{pmatrix}
1 & 0\\
a & 1
\end{pmatrix}$, 
$a\in A$. The group 
$\mathit{{\rm E}}_2(A)$ is generated by the matrices
\begin{equation*}E(a):=\begin{pmatrix}
a & 1\\
-1 & 0
\end{pmatrix},\;\;\;\;a\in A.\end{equation*}In fact
\begin{equation*}
E_{12}(a)=E(-a)E(0)^{-1}, \ \ \ \ \ E_{21}(a)=E(0)^{-1} E(a),
\end{equation*}
\begin{equation*}
E(0)=E_{12}(1)E_{21}(-1)E_{12}(1).
\end{equation*} Let 
${\rm D}_2(A)$ be the subgroup of 
$\mathit{{\rm GL}}_2(A)$ generated by diagonal matrices and let 
${\rm GE}_2(A)$ be the subgroup of 
$\mathit{{\rm GL}}_2(A)$ generated by 
${\rm D}_2(A)$ and 
$\mathit{{\rm E}}_2(A)$. For any 
$a\in {A^\times}$, let
\begin{equation*}
D(a):=\begin{pmatrix}
a & 0\\
0 & a^{-1}
\end{pmatrix}\in {\rm D}_2(A).
\end{equation*}Since
\begin{equation*}
D(-a)=E(a)E(a^{-1})E(a),
\end{equation*} the element D(a) belongs to 
$\mathit{{\rm E}}_2(A)$. It is straightforward to check that
(1)
$E(x)E(0)E(y)=D(-1)E(x+y)$,(2)
$E(x)D(a)=D(a^{-1})E(axa)$,(3)
$\prod_{i=1}^l\! D(a_ib_i)D(a_i^{-1})D(b_i^{-1})\!=\!1$ provided
$\prod_{i=1}^l [a_i,b_i]\!=\!1$,
where 
$x,y\in A$ and 
$a, a_i, b_i\in {A^\times}$. If 
${A^\times}$ is abelian, then (3) just is
(3′)
$D(ab)D(a^{-1})D(b^{-1})=1$ for any
$a,b\in {A^\times}$.
Note that 
$\mathit{{\rm E}}_2(A)$ is normal in 
${\rm GE}_2(A)$ [Reference Cohn5, Theorem 2.2].
Let 
${\rm C}(A)$ be the group generated by symbols 
$\varepsilon(a)$, 
$a\in A$, subject to the relations
(i)
$\varepsilon(x)\varepsilon(0)\varepsilon(y)=h(-1)\varepsilon(x+y)$ for any
$x,y \in A$,(ii)
$\varepsilon(x)h(a)=h(a^{-1})\varepsilon(axa)$, for any
$x\in A$ and
$a\in {A^\times}$,(iii)
$\prod_{i=1}^l\! h(a_ib_i)h(a_i^{-1})h(b_i^{-1})\!=\!1$ for any
$a_i, b_i\!\in\!{A^\times}$ provided
$\prod_{i=1}^l [a_i,b_i]\!=\!1$,
where
\begin{equation*}
h(a):=\varepsilon(-a)\varepsilon(-a^{-1})\varepsilon(-a).
\end{equation*} Note that by (iii), 
$h(1)=1$ and 
$h(-1)^2=1$. Moreover, 
$\varepsilon(-1)^3=h(1)=1$ and 
$\varepsilon(1)^3=h(-1)$. There is a natural surjective map
\begin{equation*}
{\rm C}(A) \rightarrow \mathit{{\rm E}}_2(A), \ \ \ \ \varepsilon(x)\mapsto E(x).
\end{equation*} We denote the kernel of this map by 
${\rm U}(A)$. Thus, we have the extension
\begin{equation*}
1 \rightarrow {\rm U}(A) \rightarrow {\rm C}(A) \rightarrow \mathit{{\rm E}}_2(A) \rightarrow 1.
\end{equation*} A ring A is called universal for GE2 if 
${\rm U}(A)=1$, i.e. the relations (i), (ii) and (iii) form a complete set of defining relations for 
$\mathit{{\rm E}}_2(A)$.
Example 1.1. (i) Any local ring is universal for GE2 [Reference Cohn5, Theorem 4.1]. (ii) Let A be semilocal. Then A is universal for GE2 if and only if none of the rings 
$\mathbb{Z}/2 \times \mathbb{Z}/2$, 
$\mathbb{Z}/6$ and 
${\rm M}_2(\mathbb{Z}/2)$ are a direct factor of 
$A/J(A)$, where J(A) is the Jacobson radical of A [Reference Menal11, Theorem 2.14]. (iii) If A is quasi-free for GE2, then it is universal for GE2 (see [Reference Cohn5, p. 10]). (iv) Any discretely normed ring is quasi-free for GE2 and hence is universal for GE2 [Reference Cohn5, Theorem 5.2] (see [Reference Cohn5, § 5] for the definition of a discretely normed ring). (v) Let 
$\mathcal{O}_d$ be the ring of algebraic integers of an imaginary quadratic field 
$\mathbb{Q}(\sqrt{d})$ (d < 0). Let A be a subring of 
$\mathcal{O}_d$. Then A is discretely normed except for the rings 
$\mathcal{O}_{-1}$, 
$\mathcal{O}_{-2}$, 
$\mathcal{O}_{-3}$, 
$\mathcal{O}_{-7}$, 
$\mathcal{O}_{-11}$ and 
$\mathbb{Z}[\sqrt{-3}]$ (see [Reference Dennis7, Propositions 1, 2] and [Reference Cohn5, § 6]). (vi) Discretely ordered rings are universal for GE2 [Reference Cohn5, Theorem 8.2] (see [Reference Cohn5, § 8] for the definition of a discretely ordered ring). If A is discretely ordered, then 
$A[X]$ is discretely ordered. The most obvious example of a discretely ordered ring is the ring 
$\mathbb{Z}$. Therefore 
$\mathbb{Z}[X_1, \dots, X_n]$ is universal for GE2.
2. Rank-one Steinberg group
The elementary matrices 
$E_{ij}(x)$, 
$i,j\in \{1,2\}$ with i ≠ j, satisfy the following relations
(a)
$E_{ij}(r)E_{ij}(s)=E_{ij}(r+s)$ for any
$r,s \in A$,(b)
$W_{ij}(u)E_{ji}(r)W_{ij}(u)^{-1}=E_{ij}(-uru)$, for any
$u\in {A^\times}$ and
$r\in A$,
where 
$W_{ij}(u):=E_{ij}(u)E_{ji}(-u^{-1})E_{ij}(u)$. Observe that
\begin{equation*}
W_{12}(u)=
\left(\!\!
\begin{array}{cc}
\!\!0 & \!\!u \\
\!\!{-u^{-1}} & \!\!0
\end{array}\!\!
\right), \ \ \ \ \ W_{21}(u)=
\left(\!\!
\begin{array}{cc}
\!\!{0} & \!\!{-u^{-1}} \\
\!\!{u} & \!\!{0}
\end{array}\!\!
\right).
\end{equation*}Set
\begin{equation*}
H_{12}(u):=W_{12}(u)W_{12}(-1)=D(u), \ \ \ \ \ H_{21}(u):=W_{21}(u)W_{21}(-1)=D(u)^{-1}.
\end{equation*} The Steinberg group 
$\mathit{{\rm St}}(2,A)$ is the group with generators 
$x_{12}(r)$ and 
$x_{21}(s)$, 
$r,s\in A$, subject to the Steinberg relations
(α)
$x_{ij}(r)x_{ij}(s)=x_{ij}(r+s)$ for any
$r,s \in A$,(β)
$w_{ij}(u)x_{ji}(r)w_{ij}(u)^{-1}=x_{ij}(-uru)$, for any
$u\in {A^\times}$ and
$r\in A$,
where
\begin{equation*}
w_{ij}(u):=x_{ij}(u)x_{ji}(-u^{-1})x_{ij}(u).
\end{equation*}The natural map
\begin{equation*}
\Theta: \mathit{{\rm St}}(2,A) \rightarrow \mathit{{\rm E}}_2(A), \ \ \ \ \ x_{ij}(r) \mapsto E_{ij}(r)
\end{equation*} is a well-defined homomorphism. The kernel of this map is denoted by 
${\rm K}_2(2,A)$ and is called the unstable K2-group of degree 2. For 
$u\in {A^\times}$, let
\begin{equation*}
h_{ij}(u):=w_{ij}(u)w_{ij}(-1).
\end{equation*} It is not difficult to see that 
$h_{ij}(u)^{-1}=h_{ji}(u)$ [Reference Hutchinson10, Corollary A.5].
Let 
$u,v\in {A^\times}$ commute and let
\begin{equation*}
\{u,v\}_{ij}:=h_{ij}(uv)h_{ij}(u)^{-1}h_{ij}(v)^{-1}.
\end{equation*} Since 
$\Theta(h_{12}(u))=H_{12}(u)=D(u)$ and 
$\Theta(h_{21}(u))=H_{21}(u)=D(u)^{-1}$, we have
\begin{equation*}
\Theta(\{u,v\}_{12})=D(uv)D(u)^{-1}D(v)^{-1}=0, \ \ \ \ \Theta(\{u,v\}_{21})=D(uv)^{-1}D(u)D(v)=0.
\end{equation*} Therefore, 
$\{u,v\}_{i,j}\in {\rm K}_2(2,A)$.
The element 
$\{u,v\}_{ij}$ lies in the centre of 
$\mathit{{\rm St}}(2, A)$ [Reference Dennis and Stein8, § 9]. It is straightforward to check that 
$\{u,v\}_{ji}=\{v,u\}_{ij}^{-1}$. We call 
$\{u,v\}_{ij}$ a Steinberg symbol and set
\begin{equation*}
\{v,u\}:=\{v,u\}_{12}=h_{12}(uv)h_{12}^{-1}(u)h_{12}(v)^{-1}.
\end{equation*} For a commutative ring A, let 
${\rm C}(2,A)$ be the subgroup of 
${\rm K}_2(2, A)$ generated by the Steinberg symbols 
$\{u,v\}$, 
$u,v\in {A^\times}$. Then 
${\rm C}(2, A)$ is a central subgroup of 
${\rm K}_2(2, A)$.
For a ring A let 
${\rm V}_2(A)$ be the subgroup of 
${A^\times}$ generated by all elements 
$a\in {A^\times}$ such that 
${\rm diag}(a,1)$ is in 
$\mathit{{\rm E}}_2(A)$. The following theorem is due to Dennis [Reference Dennis and Stein8, § 9 (d), p. 251].
Theorem 2.1. (Dennis)
A ring A is universal for GE2 if and only if 
${\rm K}_2(2,A)$ is contained in the subgroup of 
$\mathit{{\rm St}}(2,A)$ generated by 
$h_{12}(u)$, 
$h_{21}(u)$, 
$u\in {A^\times}$ and 
${\rm V}_2(A)=[{A^\times},{A^\times}]$ (the commutator subgroup of 
${A^\times}$). If A is commutative, then A is universal for GE2 if and only if 
${\rm K}_2(2, A)$ is generated by the Steinberg symbols.
This result was known to experts of the field but apparently no proof of it exists in the literature. Recently, Hutchinson gave a proof of the second part of the above theorem (see [Reference Hutchinson10, App. A]).
Proposition 2.2. (Hutchinson)
Let A be a commutative ring. Then the natural map 
$\mathit{{\rm St}}(2,A) \rightarrow {\rm C}(A)$ given by 
$x_{12}(a)\mapsto \varepsilon(-a)\varepsilon(0)^3$ and 
$x_{21}(a)\mapsto\varepsilon(0)^3\varepsilon(a)$ induces isomorphisms
\begin{equation*}
\displaystyle \frac{\mathit{{\rm St}}(2,A)}{{\rm C}(2, A)}\simeq {\rm C}(A),\ \ \ \ \displaystyle \frac{{\rm K}_2(2,A)}{{\rm C}(2, A)}\simeq {\rm U}(A).
\end{equation*} In particular, A is universal for GE2 if and only if 
${\rm K}_2(2, A)$ is generated by Steinberg symbols.
Proof. See [Reference Hutchinson10, Theorem A.14, App. A].
Example 2.3. (i) (Morita) Let A be a Dedekind domain, and 
$p \in A$ a non-zero prime element. Suppose that
\begin{equation*}
{A^\times} \rightarrow (A/pA)^\times
\end{equation*} is surjective. If 
${\rm K}_2(2,A)$ is generated by Steinberg symbols, then the same is true for 
${\rm K}_2(2,A{\Big[\frac{1}{p}\Big]})$ [Reference Morita12, Theorem 3.1]. In particular, if A is universal for GE2, then 
$A{\Big[\frac{1}{p}\Big]}$ is universal for GE2. For example, since the natural map 
$\mathbb{Z}^\times \rightarrow (\mathbb{Z}/p)^\times$ is surjective for 
$p=2,3$, 
$\mathbb{Z}\Big[\frac{1}{2}\Big]$ and 
$\mathbb{Z}\Big[\frac{1}{3}\Big]$ are universal for GE2. (ii) (Morita) Let p be a prime number. Then 
${\rm K}_2(2, \mathbb{Z}{\Big[\frac{1}{p}\Big]})$ is generated by Steinberg symbols if and only if 
$p=2,3$ [Reference Morita12, Theorem 5.8]. Thus, 
$\mathbb{Z}{\Big[\frac{1}{p}\Big]}$ is universal for GE2 if and only if 
$p=2,3$. See also [Reference Hutchinson10, Example 6.13, Lemma 6.15].
(iii) Let 
$m=p_1\cdots p_k$ be an integer such that pi are primes and 
$p_1 \lt \cdots \lt p_k$. Then it follows from (i) that 
${\rm K}_2(2, \mathbb{Z}\Big[ \frac{1}{m} \Big])$ is generated by Steinberg symbols whenever 
$(\mathbb{Z}/p_i)^\times$ is generated by the residue classes 
$\{-1, p_1,\dots, p_{i-1}\}$ for all 
$i \leq k$. Observe that the map 
$\mathbb{Z}^\times \rightarrow (\mathbb{Z}/p)^\times$ is surjective only for 
$p=2,3$. Thus p 1 in above chain should be either 2 or 3. For example 
$\mathbb{Z}\Big[\frac{1}{6}\Big]$, 
$\mathbb{Z}\Big[\frac{1}{10}\Big]$, 
$\mathbb{Z}\Big[\frac{1}{15}\Big]$ and 
$\mathbb{Z}\Big[\frac{1}{66}\Big]$ are universal for GE2. (iv) Let k be a field. If A is either 
$k[T]$ or 
$k[T,T^{-1}]$, then 
${\rm K}_2(2,A)$ is generated by Steinberg symbols [Reference Silvester14, Theorem 6], [Reference Alperin and Wright2, Theorem 1].
Let 
$a, b\in A$ be any two elements such that 
$1-ab\in {A^\times}$. We define
\begin{equation*}
\langle a,b\rangle_{ij}:=x_{ji}\bigg(\frac{-b}{1-ab}\bigg)x_{ij}(-a)x_{ji}(b)x_{ij}\bigg(\frac{a}{1-ab}\bigg)h_{ij}(1-ab)^{-1}.
\end{equation*} If a and b commute, then 
$\langle a,b\rangle_{ij}\in {\rm K}_2(2, A)$. We call 
$\langle a,b\rangle_{ij}$ a Dennis–Stein symbol. If 
$u,v\in{A^\times}$ commute, then
\begin{equation*}
\displaystyle\{u,v\}_{ij}=\bigg\langle u, \frac{1-v}{u}\bigg\rangle_{ij}=\bigg\langle \frac{1-u}{v},v\bigg\rangle_{ij}.
\end{equation*}Hence over commutative rings, Dennis–Stein symbols generalize Steinberg symbols.
3. The abelianization of
$\mathit{{\rm E}}_2(A)$
The following theorem is the main result of this paper.
Theorem 3.1. Let A be a ring and let M be the additive subgroup of A generated by axa − x and 
$\sum_{i=1}^l 3(b_i+1)(c_i+1)$, where 
$x\in A$ and 
$a,b_i,c_i \in {A^\times}$ provided that 
$\prod_{i=1}^l [b_i,c_i]=1$. Then there is an exact sequence of abelian groups
\begin{equation*}
H_2(\mathit{{\rm E}}_2(A), \mathbb{Z}) \rightarrow \displaystyle {\rm U}(A)/[{\rm U}(A), {\rm C}(A)]
\overset{\alpha}{\longrightarrow} A/M \overset{\beta}{\longrightarrow} \mathit{{\rm E}}_2(A)^{\rm ab} \rightarrow 0,
\end{equation*} where α is induced by the map 
${\rm C}(A) \rightarrow A/M$, 
$\varepsilon(x)\mapsto x-3$, and β is induced by 
$y\mapsto E_{12}(y)$. Moreover, if A is commutative, then this exact sequence is an exact sequence of 
$\mathbb{Z}[{A^\times}/({A^\times})^2]$-modules.
Proof. From the Lyndon/Hochschild–Serre spectral sequence associated to the extension
\begin{equation*}
1 \rightarrow {\rm U}(A) \rightarrow {\rm C}(A) \rightarrow \mathit{{\rm E}}_2(A) \rightarrow 1,
\end{equation*}we obtain the five-term exact sequence
\begin{equation*}
H_2({\rm C}(A),\mathbb{Z}) \!\rightarrow\! H_2(\mathit{{\rm E}}_2(A),\mathbb{Z})\! \rightarrow\! H_1({\rm U}(A),\mathbb{Z})_{\mathit{{\rm E}}_2(A)}
\!\rightarrow\! H_1({\rm C}(A),\mathbb{Z}) \!\rightarrow\! H_1(\mathit{{\rm E}}_2(A),\mathbb{Z})\!\rightarrow\! 0
\end{equation*}(see [Reference Brown4, Corollary 6.4, Chp. VII]). For the middle term, we have
\begin{equation*}
H_1({\rm U}(A),\mathbb{Z})_{\mathit{{\rm E}}_2(A)}\simeq \displaystyle \bigg(\frac{{\rm U}(A)}{[{\rm U}(A),{\rm U}(A)]}\bigg)_{\mathit{{\rm E}}_2(A)}\simeq
\displaystyle \frac{{\rm U}(A)}{[{\rm U}(A), {\rm C}(A)]}.
\end{equation*} We show that 
$H_1({\rm C}(A),\mathbb{Z})\simeq A/M$. Consider the map
\begin{equation*}
\phi: {\rm C}(A) \rightarrow A/M, \ \ \ \ \ \prod\varepsilon(a_i) \mapsto \sum (a_i-3).
\end{equation*} This map is well-defined. First note that in 
$A/M$ we have 
$a=a^{-1}$ and 
$12=0$. Thus
\begin{equation*}
\phi(h(a))=(-a-3)+(-a^{-1}-3)+(-a-3)=-3a-9=-3a+3=-3(a-1).
\end{equation*}Now we have
\begin{align*}
& \phi(\varepsilon(x)\varepsilon(0)\varepsilon(y))=x-3+0-3+y-3=x+y-9=x+y+3,\\
&\phi(h(-1)\varepsilon(x+y))=-3(-1-1)+x+y-3=x+y+3,\\
&\phi(\varepsilon(x)h(a))=x-3-3(a-1)=x-3a, \\
&\phi(h(a^{-1})\varepsilon(axa))=-3(a^{-1}-1)+axa-3=-3(a-1)+x-3=x-3a.
\end{align*}Moreover,
\begin{align*}
\phi(h(ab)h(a^{-1})h(b^{-1}))&=-3(ab-1)-3(a^{-1}-1)-3(b^{-1}-1)\\
&=-3(ab-1)-3(a-1)-3(b-1)\\
&=-3(ab+a+b+1)\\
&=-3(a+1)(b+1).
\end{align*} These show that the map ϕ is a well-defined homomorphism. Since 
$A/M$ is an abelian group, we have the homomorphism
\begin{equation*}
\bar{\phi}: {\rm C}(A)/[{\rm C}(A), {\rm C}(A)] \rightarrow A/M, \ \ \ \ \varepsilon(x) \mapsto x-3.
\end{equation*}Now we define
\begin{equation*}
\psi: A/M \rightarrow {\rm C}(A)/[{\rm C}(A), {\rm C}(A)], \ \ \ \ \ x\mapsto \varepsilon(x)\varepsilon(0)^{-1}.
\end{equation*} We show that this map is a well-defined homomorphism. Consider the items (i), (ii) and (iii) from the definition of 
${\rm C}(A)$ (§ 1). If in (i) we put 
$y=-x$, then we get
\begin{equation*}
\varepsilon(x)\varepsilon(0)\varepsilon(-x)=h(-1)\varepsilon(0).
\end{equation*} Thus in 
${\rm C}(A)/[{\rm C}(A), {\rm C}(A)]$, we have 
$h(-1)\varepsilon(x)\varepsilon(-x)=1$. From this, we obtain
\begin{align*}
h(a)^2 &=h(-1)h(a)h(-a)\\
&=h(-1)\varepsilon(-a)\varepsilon(-a^{-1})\varepsilon(-a)\varepsilon(a)\varepsilon(a^{-1})\varepsilon(a)\\
&=\Big(h(-1)\varepsilon(a)\varepsilon(-a)\Big)^2 h(-1)\varepsilon(a^{-1})\varepsilon(-a^{-1})=1.
\end{align*}Now we have
\begin{align*}
\psi(axa)&=\varepsilon(axa)\varepsilon(0)^{-1}=h(a)\varepsilon(x)h(a)\varepsilon(0)^{-1}
=h(a)^2\varepsilon(x)\varepsilon(0)^{-1}=\varepsilon(x)\varepsilon(0)^{-1}=\psi(a).
\end{align*} Moreover using (ii) for x = 0 in 
${\rm C}(A)/[{\rm C}(A), {\rm C}(A)]$, we have
\begin{equation*}
\varepsilon(a)=h(a)\varepsilon(a^{-1})h(a)=h(a)^2\varepsilon(a^{-1})=\varepsilon(a^{-1}).
\end{equation*} This implies that 
$h(-a)=\varepsilon(a)\varepsilon(a^{-1})\varepsilon(a)=\varepsilon(a)^3$ and hence
\begin{equation*}
h(a)=h(-1)\varepsilon(a)^3=h(-1)\varepsilon(a^{-1})^3.
\end{equation*} Furthermore by (i), we have 
$\varepsilon(3x)=h(-1)\varepsilon(x)^3$. Using this formula, we obtain
\begin{align*}
\varepsilon(3(a+1)(b+1)) &=\varepsilon(0)\varepsilon(ab)^3\varepsilon(a)^3\varepsilon(b)^3\varepsilon(1)^3\\
&=\varepsilon(0)\varepsilon(ab)^3\varepsilon(a)^3\varepsilon(b)^3h(-1)\\
&=\varepsilon(0)h(-1)\varepsilon(ab)^3h(-1)\varepsilon(a^{-1})^3h(-1)\varepsilon(b^{-1})^3\\
&=\varepsilon(0)h(ab)h(a^{-1})h(b^{-1}).
\end{align*}Thus
\begin{align*}
\psi(3(a+1)(b+1))&=\varepsilon(3(a+1)(b+1))\varepsilon(0)^{-1}
=h(ab)h(a^{-1})h(b^{-1}).
\end{align*}This shows that ψ is well-defined. Since
\begin{equation*}
\psi(x+y)=\varepsilon(x+y)\varepsilon(0)^{-1}=h(-1)\varepsilon(x)\varepsilon(0)\varepsilon(y)\varepsilon(0)^{-1}=h(-1)\varepsilon(x)\varepsilon(y)=\psi(x)\psi(y),
\end{equation*} ψ is a homomorphism of groups. Now it is easy to see that 
$\bar{\phi}$ and ψ are inverses of each other. Thus 
$\bar{\phi}$ is an isomorphism. This shows that the desired sequence is exact.
Now let A be commutative. We know that 
${A^\times}$ acts as follows on 
$\mathit{{\rm E}}_2(A)$:
\begin{equation*}
a.E(x):={\rm diag}(a,1)E(x){\rm diag}(a^{-1},1)=D(a)E(a^{-1}x).
\end{equation*} Now let us define the following action of 
${A^\times}$ on 
${\rm C}(A)$:
\begin{equation*}
a.\varepsilon(x):=h(a)\varepsilon(a^{-1}x),
\end{equation*}
\begin{equation*}
a.(\varepsilon(x)\varepsilon(y)):=\Big(a.\varepsilon(x)\Big)\Big(a.\varepsilon(y)\Big).
\end{equation*}Observe that
\begin{equation*}
a.(\varepsilon(x)\varepsilon(y))=\varepsilon(ax)\varepsilon(a^{-1}y).
\end{equation*} We show that this is in fact an action. Clearly 
$1\cdot \varepsilon(x)=\varepsilon(x)$. Moreover, for any 
$a,b \in {A^\times}$, we have
\begin{align*}
a\cdot(b\cdot \varepsilon(x)) & =a\cdot \Big(h(b)\varepsilon(b^{-1}x)\Big)\\
& =a\cdot \Big(\varepsilon(-b)\varepsilon(-b^{-1})\varepsilon(-b)\varepsilon(b^{-1}x)\Big)\\
& =\Big(a\cdot \varepsilon(-b)\Big) \Big(a\cdot \varepsilon(-b^{-1})\Big)\Big(a\cdot \varepsilon(-b)\Big)\Big(a\cdot \varepsilon(b^{-1}x)\Big)\\
&= \varepsilon(-ab) \varepsilon(-(ab)^{-1})\varepsilon(-ab)\varepsilon((ab)^{-1}x)\\
&=h(ab)\varepsilon((ab)^{-1}x)\\
&=(ab)\cdot \varepsilon(x).
\end{align*}This shows that the above action is well-defined.
Clearly, the natural map 
${\rm C}(A) \rightarrow \mathit{{\rm E}}_2(A)$ respects the above actions. Therefore, the group 
${A^\times}$ acts naturally on the Lyndon/Hochschild–Serre spectral sequence of the extension 
$1 \rightarrow {\rm U}(A) \rightarrow {\rm C}(A) \rightarrow \mathit{{\rm E}}_2(A) \rightarrow 1$:
\begin{equation*}
E_{p,q}^2=H_p(\mathit{{\rm E}}_2(A),H_q({\rm U}(A),\mathbb{Z}))\Rightarrow H_{p+q}({\rm C}(A),\mathbb{Z}).
\end{equation*} This induces an action of 
${A^\times}$ on the five-term exact sequence discussed in the beginning of this proof.
Now we study the action of 
${A^\times}^2$ on the terms of this exact sequence. For 
$\mathit{{\rm E}}_2(A)$, we have
\begin{align*}
a^2.E(x) &:={\rm diag}(a^2,1)E(x){\rm diag}(a^{-2},1)\\
& =D(a)(aI_2)E(x)(a^{-1}I_2) D(a)^{-1}\\
& =D(a)E(x)D(a)^{-1}.
\end{align*} Since 
$D(a)\in \mathit{{\rm E}}_2(A)$ and since the conjugation action induces a trivial action on homology groups [Reference Brown4, Proposition 6.2, Chap. II], the action of 
${A^\times}^2$ on homology groups 
$H_k(\mathit{{\rm E}}_2(A),\mathbb{Z})$ is trivial. The action of 
${A^\times}^2$ on 
${\rm C}(A)$ also is induced by a conjugation:
\begin{align*}
a^2.\varepsilon(x)&=h(a^2)\varepsilon(a^{-2}x)\\
&=h(a^2)h(a^{-1})\varepsilon(x)h(a^{-1})\\
&=h(a)\varepsilon(x)h(a)^{-1}.
\end{align*} This shows that the action of 
${A^\times}^2$ on homology groups 
$H_k({\rm C}(A),\mathbb{Z})$ is trivial. For example through the isomorphism 
$H_1({\rm C}(A),\mathbb{Z})\simeq A/M$, on sees that 
${A^\times}$ acts on 
$A/M$ by the formula 
$a\cdot \overline{x}=\overline{ax}$. Now we have
\begin{equation*}
a^2\cdot \overline{x}=\overline{a^2x}=\overline{x(a^2-1)}+\overline{x}=\overline{x}.
\end{equation*} Finally if 
$\overline{X}\in {\rm U}(A)/[{\rm U}(A), {\rm C}(A)]$, then
\begin{equation*}
a^2\cdot \overline{X}=\overline{h(a)Xh(a)^{-1}}=\overline{h(a)Xh(a)^{-1}X^{-1}}\ \overline{X}=\overline{X}.
\end{equation*} Thus, 
${A^\times}^2$ acts trivially on the terms of the above exact sequence. This implies that the discussed sequence is an exact sequence of 
$\mathbb{Z}[{A^\times}/({A^\times})^2]$-modules. This completes the proof of the theorem.
Remark 3.2. If A is commutative, then by Proposition 2.2, we have the isomorphism
\begin{equation*}
\frac{{\rm U}(A)}{[{\rm U}(A),{\rm C}(A)]}\simeq \frac{{\rm K}_2(2,A)}{[{\rm K}_2(2,A), \mathit{{\rm St}}(2,A)]{\rm C}(2,A)}.
\end{equation*}Corollary 3.3. (Cohn [Reference Cohn6])
Let A be universal for GE2 and M the additive subgroup of A as described in the above theorem. Then 
$\mathit{{\rm E}}_2(A)^{\rm ab}\simeq A/M$.
Proof. Since A is universal for GE2, 
${\rm U}(A)=1$. Thus, the claim follows from the above theorem.
Example 3.4. (i) If 
${A^\times}=\{1,-1\}$, then 
$A/M=A/12\mathbb{Z}$. Thus 
$\mathit{{\rm E}}_2(A)^{\rm ab}$ is a quotient of 
$A/12\mathbb{Z}$. In particular, if A is universal for GE2 and 
${A^\times}=\{1,-1\}$, then 
$\mathit{{\rm E}}_2(A)^{\rm ab}\simeq A/12\mathbb{Z}$. Now by Example 1.1(vi),
\begin{equation*}
\mathit{{\rm E}}_2(\mathbb{Z}[X_1, \dots, X_n])^{\rm ab}\simeq \mathbb{Z}[X_1, \dots, X_n]/12\mathbb{Z} \simeq\mathbb{Z}/12 \oplus \bigoplus_{i\in \mathbb{N}} \mathbb{Z}.
\end{equation*} (ii) Let 
$6\in {A^\times}$. Then for any 
$x\in A$,
\begin{equation*}
x=3(2x2-x)-(3x3-x)\in M.
\end{equation*} This shows that M = A and thus 
$\mathit{{\rm E}}_2(A)^{\rm ab}=1$.
Corollary 3.5. For any commutative ring A, we have the exact sequence
\begin{equation*}
{\rm K}_2(2, A)/{\rm C}(2, A) \rightarrow A/M \rightarrow \mathit{{\rm E}}_2(A)^{\rm ab} \rightarrow 1.
\end{equation*} In particular, if 
${\rm K}_2(2,A)$ is generated by Dennis–Stein symbols, then 
$\mathit{{\rm E}}_2(A)^{\rm ab}\simeq A/N$, where N is the additive subgroup
\begin{equation*}
N:=M+\langle de(d+e-3):d,e\in A \ \text{such that} \ 1-de\in {A^\times}\rangle.
\end{equation*}Proof. The exact sequence follows from Theorem 3.1 and Proposition 2.2. It is straightforward to check that through the composition
\begin{equation*}
\mathit{{\rm St}}(2, A) \rightarrow {\rm C}(A) \rightarrow A/M
\end{equation*}we have
\begin{equation*}
x_{12}(r) \mapsto -r, \ \ \ x_{21}(r)\mapsto r, \ \ \ h_{12}(a)\mapsto -3(a-1).
\end{equation*} Now if 
$\langle d,e\rangle_{12}\in {\rm K}_2(2,A)$ is a Dennis–Stein symbol, then under this composition we have
\begin{align*}
\langle d,e\rangle_{12} &\mapsto -e(1-de)^{-1}+d+e-d(1-de)^{-1}+3(1-de-1)\\
&= -e(1-de)+d+e-d(1-de)+3(1-de-1)\\
&= +de(d+e-3).
\end{align*}This completes the proof.
Corollary 3.6. Let A be a ring such that 
$2\in {A^\times}$. Then we have the exact sequence
\begin{equation*}
H_2(\mathit{{\rm E}}_2(A),\mathbb{Z}) \rightarrow \displaystyle\frac{{\rm U}(A)}{[{\rm U}(A),{\rm C}(A)]} \rightarrow
\displaystyle\frac{A}{\langle axa-x:a\in {A^\times}, x\in A\rangle} \rightarrow \mathit{{\rm E}}_2(A)^{\rm ab} \rightarrow 1.
\end{equation*} In particular, if A is commutative and 
$2\in {A^\times}$, then we have the exact sequence
\begin{equation*}
{\rm K}_2(2,A)/{\rm C}(2,A) \rightarrow A/I\rightarrow \mathit{{\rm E}}_2(A)^{\rm ab} \rightarrow 1,
\end{equation*} where I is the ideal generated by the elements 
$a^2-1$, 
$a\in{A^\times}$.
Proof. Since 
$3=2^2-1$, for any 
$x\in A$, we have
\begin{equation*}
3x=(2^2-1)x=2x2 -x \in \langle axa-x:a\in {A^\times}, x\in A\rangle.
\end{equation*}This implies that
\begin{equation*}
M=\langle axa-x:a\in {A^\times}, x\in A\rangle.
\end{equation*}Thus, the claim follows from Theorem 3.1.
4. The abelianization of
$\mathit{{\rm E}}_2(A)$ for certain rings
Let A be a local ring with maximal ideal 
$\mathfrak{m}_A$. If 
${\rm char}(A/\mathfrak{m}_A)\neq 2, 3$, then 
$6\in {A^\times}$. Thus by Example 3.4(ii), we have 
$\mathit{{\rm E}}_2(A)^{\rm ab}=1$. The following proposition gives the precise structure of 
$\mathit{{\rm E}}_2(A)^{\rm ab}$ over commutative local rings.
Proposition 4.1. Let A be a commutative local ring with maximal ideal 
$\mathfrak{m}_A$. Then
\begin{equation*}
\mathit{{\rm SL}}_2(A)^{\rm ab}=\mathit{{\rm E}}_2(A)^{\rm ab}\simeq
\begin{cases}
A/\mathfrak{m}_A^2 & \text{if}\ |A/\mathfrak{m}_A|=2 \\
A/\mathfrak{m}_A & \text{if}\ |A/\mathfrak{m}_A|=3. \\
0 & \text{if}\ |A/\mathfrak{m}_A|\geq 4 \\
\end{cases}
\end{equation*}Proof. If 
$|A/\mathfrak{m}_A|\geq 4$, then there is 
$a\in {A^\times}$ such that 
$a^2-1\in {A^\times}$. This implies that A = M and thus 
$\mathit{{\rm E}}_2(A)^{\rm ab}=1$. Let 
$A/\mathfrak{m}_A\simeq\mathbb{F}_2$. Then 
$2\in \mathfrak{m}_A, 3\in {A^\times}$. Moreover, for 
$a\in {A^\times}$, 
$a\pm 1\in \mathfrak{m}_A$. Thus 
$M\subseteq \mathfrak{m}_A^2$. Now if 
$a, b\in \mathfrak{m}_A$, then
\begin{equation*}
ab=3(a/3)b=3\Big[((a/3)-1)+1\Big]\Big[((b-1)+1\Big]\in M.
\end{equation*} This implies that 
$\mathfrak{m}_A^2\subseteq M$. Thus 
$M =\mathfrak{m}_A^2$ and we have 
$\mathit{{\rm E}}_2(A)^{\rm ab}\simeq A/\mathfrak{m}_A^2$. Finally let 
$A/\mathfrak{m}_A\simeq\mathbb{F}_3$. If 
$a\in \mathfrak{m}_A$, then 
$a-1, a-2\in {A^\times}$. Since
\begin{equation*}
a=(a-2)^{-1}((a-1)^2-1)\in M,
\end{equation*} we have 
$\mathfrak{m}_A\subseteq M$. Clearly 
$M\subseteq \mathfrak{m}_A$. Therefore 
$\mathit{{\rm E}}_2(A)^{\rm ab}\simeq A/\mathfrak{m}_A\simeq \mathbb{Z}/3$.
Example 4.2. Let A be a commutative local ring such that 
$A/\mathfrak{m}_A\simeq \mathbb{F}_2$. Since 
$\mathfrak{m}_A/\mathfrak{m}_A^2$ is a 
$\mathbb{F}_2$-vector space, from the exact sequence
\begin{equation*}
0 \rightarrow \mathfrak{m}_A/\mathfrak{m}_A^2 \rightarrow A/\mathfrak{m}_A^2 \rightarrow \mathbb{F}_2 \rightarrow 0
\end{equation*}it follows that
\begin{equation*}
|\mathit{{\rm E}}_2(A)^{\rm ab}|=1+\dim_{\mathbb{F}_2} (\mathfrak{m}_A/\mathfrak{m}_A^2).
\end{equation*} Let A be a discrete valuation ring. Then 
$\mathfrak{m}_A$ is generated by a prime element and thus 
$\mathfrak{m}_A/\mathfrak{m}_A^2\simeq \mathbb{F}_2$. Therefore either 
$A/\mathfrak{m}_A^2\simeq \mathbb{Z}/2\times\mathbb{Z}/2$, or 
$A/\mathfrak{m}_A^2\simeq \mathbb{Z}/4$. For example, if 
$A=\mathbb{F}_2[X]/\langle X^2\rangle$, then 
$\mathfrak{m}_A^2=0$ and thus 
$\mathit{{\rm E}}_2(A)^{\rm ab}\simeq A\simeq \mathbb{Z}/2\times \mathbb{Z}/2$. If p is a prime and 
$A=\mathbb{Z}_{(p)}$, then 
$\mathit{{\rm E}}_2(A)^{\rm ab}\simeq \mathbb{Z}/4$.
Example 4.3. Let A be a local ring not necessary commutative. Let 
$A':=Z(A)$ be the centre of A. It is known that Aʹ is a local ring. If 
$|A'/\mathfrak{m}_{A'}|\geq 4$, then as in above proposition we have 
$\mathit{{\rm E}}(A)^{\rm ab}=1$: Let 
$a\in {(A')}^\times$ such that 
$a^2-1\in {(A')}^\times$. If 
$y \in A$ and 
$y':=(a^2-1)^{-1}y$, then 
$y=ay'a-y' \in M$.
Understanding the structure of the homology groups of 
$\mathit{{\rm SL}}_2(\mathbb{Z}[\frac{1}{m}])$ has been topic of many articles, see for example [Reference Adem and Naffah1, Reference Anh Tuan and Ellis3, Reference Williams and Wisner17]. The following result completely calculates the first integral homology of these groups.
Proposition 4.4. Let m be a square free natural number. Then
\begin{equation*}
\begin{array}{c}
\mathit{{\rm SL}}_2(\mathbb{Z}[\frac{1}{m}])^{\rm ab}=\mathit{{\rm E}}_2(\mathbb{Z}[\frac{1}{m}])^{\rm ab}\simeq
\end{array}
\begin{cases}
0 & \text{if}\ 2|m,\ 3|m \\
\mathbb{Z}/3 & \text{if}\ 2|m,\ 3\nmid m\\
\mathbb{Z}/4 & \text{if}\ 2\nmid m,\ 3|m\\
\mathbb{Z}/12 & \text{if}\ 2\nmid m,\ 3\nmid m.
\end{cases}
\end{equation*}Proof. Let 
$A_m:=\mathbb{Z}[\frac{1}{m}]$. Note that 
$A_m^\times=\{\pm n^i: n\mid m, i\in \mathbb{Z}\}$. Since Am is Euclidean, we have 
$\mathit{{\rm E}}_2(A_m)=\mathit{{\rm SL}}_2(A_m)$.
If 
$2|m$ and 
$3|m$, then 
$6\in A_m^\times$. Thus by Example 3.4(ii), we have 
$\mathit{{\rm E}}_2(\mathbb{Z}[\frac{1}{m}])^{\rm ab}=1$.
Let 
$2|m$ and 
$3\nmid m$. Then 
$2\in A_m^\times$ and hence 
$3=2^2-1\in M$. This implies that 
$3A_m\subseteq M$. On the other hand, for any 
$a,b\in A_m^\times$, clearly 
$3(a+1)(b+1)\in 3A_m$. Now consider 
$n^i\in A_m^\times$, 
$i\in \mathbb{Z}$. Since 
$3\nmid n$, we have 
$3|n^2-1$. Therefore 
$3| (n^i)^2-1$ for any 
$i\in \mathbb{Z}$. This implies that 
$M \subseteq 3A_m$. Thus 
$3A_m=M$. Now it is easy to see that 
$A_m/M\simeq \mathbb{Z}/3$. The inclusion 
$A_m\subseteq \mathbb{Z}_{(3)}$ induces the commutative diagram
By Proposition 4.1, the bottom maps are isomorphisms. Thus, the upper right map is injective. This proves that 
$\mathit{{\rm E}}_2(A_m)^{\rm ab}\simeq \mathbb{Z}/3$.
Let 
$2\nmid m$ and 
$3\mid m$. Note that 
$3\in A_m^\times$. We show that 
$M=4A_m$. First note that
\begin{equation*}
4=12-8=3(1+1)(1+1) -(3^2-1)\in M.
\end{equation*} Since for any 
$i\geq 0$,
\begin{equation*}
4m^i=12m^i -m^i(3^2-1),\ \ \ \
4/m^i=4m^i-\frac{4}{m^i}((m^i)^2-1)=12 m'-\frac{4}{m^i}((m^i)^2-1),
\end{equation*} where 
$m'\in\mathbb{Z}$, we have 
$4A_m\in M$. On the other hand, let 
$n\mid m$. Since n is odd, 2 divides n − 1 and n + 1. Thus for any 
$i,j\in\mathbb{Z}$, 
$4\mid (n^i)^2-1$ and 
$4\mid 3(\pm n^i+1)(\pm n^j+1)$. These facts imply that 
$M\subseteq 4A_m$. Therefore 
$M=4A_m$. Now one easily verifies that
\begin{equation*}
A_m/M=A_m/4A_m\simeq \mathbb{Z}/4.
\end{equation*} Since 
$2\nmid m$, 
$A_m \subseteq \mathbb{Z}_{(2)}$. Now with an argument similar to the previous case, using Proposition 4.1 and Example 4.2, one can show that 
$\mathit{{\rm E}}_2(A_m)^{\rm ab}\simeq \mathbb{Z}/4$. Finally let 
$2\nmid m$ and 
$3\nmid m$. As previous cases, we can show that 
$M=12A_m$. Thus
\begin{equation*}
A_m/M=A_m/12A_m\simeq \mathbb{Z}/12.
\end{equation*} Since 
$2\nmid m$ and 
$3\nmid m$, we have 
$A_m\subseteq \mathbb{Z}_{(2)}$ and 
$A_m\subseteq \mathbb{Z}_{(3)}$. Now from the commutative diagram
it follows that the composition
\begin{equation*}
\mathbb{Z}/12 \overset{\simeq}{\longrightarrow} A_m/M \twoheadrightarrow \mathit{{\rm E}}_2(A_m)^{\rm ab}
\end{equation*}is injective. This completes the proof of the proposition.
Corollary 4.5. Let m be a square free natural number. Then
\begin{equation*}
\begin{array}{c}
\mathit{{\rm PSL}}_2(\mathbb{Z}[\frac{1}{m}])^{\rm ab}\simeq
\begin{cases}
0 & \text{if}\ 2\mid m, 3\mid m\\
\mathbb{Z}/3 & \text{if}\ 2\mid m, 3\nmid m\\
\mathbb{Z}/2 & \text{if}\ 2\nmid m, 3\mid m\\
\mathbb{Z}/6 & \text{if}\ 2\nmid m, 3\nmid m.
\end{cases}
\end{array}
\end{equation*}Proof. Let 
$A_m=\mathbb{Z}[\frac{1}{m}]$. From the extension
\begin{equation*}
1 \rightarrow \mu_2(A_m) \rightarrow \mathit{{\rm SL}}_2(A_m) \rightarrow \mathit{{\rm PSL}}_2(A_m) \rightarrow 1,
\end{equation*}we obtain the exact sequence
\begin{equation*}
\mu_2(A_m) \rightarrow \mathit{{\rm SL}}_2(A_m)^{\rm ab} \rightarrow \mathit{{\rm PSL}}_2(A_m)^{\rm ab} \rightarrow 1.
\end{equation*}Now the claim follows from the above proposition and the fact that
\begin{equation*}
\mathit{{\rm PSL}}_2(A_m)^{\rm ab}\simeq H_1(\mathit{{\rm PSL}}_2(A_m),\mathbb{Z})\simeq (\mathbb{Z}/2)^\alpha \oplus (\mathbb{Z}/3)^\beta
\end{equation*}for some α and β by [Reference Williams and Wisner17, Corollary 4.4].
Let 
$\mathcal{O}_d$ be the ring of algebraic integers of the quadratic field 
$\mathbb{Q}(\sqrt{d})$, where d is a square-free integer. It is known that
\begin{equation*}
\mathcal{O}_d=\begin{cases}
\mathbb{Z}[\sqrt{d}] & \text{if}\ d\equiv 2,3\pmod 4\\
\mathbb{Z}[\frac{1+\sqrt{d}}{2}] & \text{if $d\equiv 1\pmod 4$.}\\
\end{cases}
\end{equation*} If d < 0, then 
$\mathcal{O}_d^\times$ has at most six elements. In fact
\begin{equation*}
\mathcal{O}_{-1}^\times=\{\pm 1, \pm i\}, \ \ \ \
\mathcal{O}_{-3}^\times=\{\pm 1, \pm \omega , \pm (\omega - 1)\},
\end{equation*} where 
$i=\sqrt{-1}$, 
$\omega=\displaystyle\frac{1+\sqrt{-3}}{2}$ and for 
$d\neq -1, -3$,
\begin{equation*}
\mathcal{O}_d^\times=\{\pm 1\}.
\end{equation*} It is known that 
$\mathcal{O}_d$ is norm-Euclidean if and only if 
$d = -1,-2,-3,-7,-11$ if and only if
\begin{equation*}
\mathit{{\rm E}}_2(\mathcal{O}_d)=\mathit{{\rm SL}}_2(\mathcal{O}_d)
\end{equation*} (see [Reference Eggleton, Lacampagne and Selfridge9, Theorem 5.1] and [Reference Cohn5, Theorem 6.1]). Observe that for d < 0, 
$\mathcal{O}_d$ is universal for GE2 if and only if 
$d\neq-2,-7,-11$ (see Example 1.1(v) and [Reference Cohn6, Remarks, pp. 162–163]). It is easy to see that
\begin{equation*}
M=\begin{cases}
2\mathcal{O}_{-1} & \text{if}\ d=-1\\
(2\omega-1)\mathcal{O}_{-3} & \text{if}\ d=-3\\
12\mathbb{Z} & \text{otherwise}.
\end{cases}
\end{equation*}It follows from this that
\begin{equation*}
\mathcal{O}_d/M\simeq\begin{cases}
\mathbb{Z}/2 \times\mathbb{Z}/2 & \text{if}\ d=-1\\
\mathbb{Z}/3 & \text{if}\ d=-3\\
\mathbb{Z}/12\times \mathbb{Z} & \text{otherwise}.
\end{cases}
\end{equation*}Example 4.6. If 
$d=-2,-7,-11$, then we have a surjective map
\begin{equation}
\mathbb{Z}/12 \times \mathbb{Z}\simeq \mathcal{O}_d/M \twoheadrightarrow \mathit{{\rm E}}_2(\mathcal{O}_d)^{\rm ab}.
\end{equation} (i) For 
$d=-2$, we have 
$1-(-\sqrt{-2})(\sqrt{-2})\in \mathcal{O}_{-2}^\times$. Thus 
$\langle -\sqrt{-2},\sqrt{-2} \rangle_{12} \in {\rm K}_2(2, \mathcal{O}_{-2})$ is a Dennis–Stein symbol. Hence under the map (4.1), the element
\begin{equation*}
-6=(-\sqrt{-2})(\sqrt{-2})\bigg(-\sqrt{-2}+\sqrt{-2}-3\bigg)=2(-3) \in \mathcal{O}_{-2}/M
\end{equation*} maps to zero (see Corollary 3.5). Thus, we have a surjective map 
$\mathbb{Z}/6 \times \mathbb{Z} \rightarrow \mathit{{\rm E}}_2(\mathcal{O}_{-2})^{\rm ab}$. (ii) For 
$d=-7$, we have 
$\displaystyle 1-\Big(\frac{1+\sqrt{-7}}{2}\Big)\Big(\frac{1-\sqrt{-7}}{2}\Big)\in \mathcal{O}_{-7}^\times$. Thus
\begin{equation*}
\displaystyle\Big\langle \frac{1+\sqrt{-7}}{2}, \frac{1-\sqrt{-7}}{2} \Big\rangle_{12} \in {\rm K}_2(2, \mathcal{O}_{-7})
\end{equation*}is a Dennis–Stein symbol. Again under the map (4.1), the element
\begin{equation*}
4=(\frac{1+\sqrt{-7}}{2})(\frac{1-\sqrt{-7}}{2})\bigg(\frac{1+\sqrt{-7}}{2}+\frac{1-\sqrt{-7}}{2}-3\bigg) \in\mathcal{O}_{-7}/M
\end{equation*} maps to zero. Thus we have a surjective map 
$\mathbb{Z}/4 \times \mathbb{Z} \rightarrow \mathit{{\rm E}}_2(\mathcal{O}_{-7})^{\rm ab}$. (iii) Let 
$d=-11$. It is easy to see that in 
${\rm K}_2(2, \mathcal{O}_{-11})$ any Dennis–Stein symbol is a Steinberg symbol. In fact, there are no 
$x,y \in \mathcal{O}_{-11}$, such that 
$1-xy=-1$ or equivalently xy = 2. But if 
$\displaystyle x=\frac{1+\sqrt{-11}}{2}$, then 
$x\overline{x}=3$. Now we have
\begin{equation*}
(E(x)E(\overline{x}))^3=-I_2.
\end{equation*}From this, we obtain the element
\begin{equation*}
\Theta:=h(-1)(\varepsilon(x)\varepsilon(\overline{x}))^3\in {\rm U}(\mathcal{O}_{-11})\simeq \frac{{\rm K}_2(2, \mathcal{O}_{-11})}{{\rm C}(2, \mathcal{O}_{-11})}.
\end{equation*} Now it is straightforward to see that under the map 
$\displaystyle\frac{{\rm K}_2(2, \mathcal{O}_{-11})}{{\rm C}(2, \mathcal{O}_{-11})} \rightarrow \mathcal{O}_{-11}/M$, we have
\begin{equation*}
\Theta\mapsto -3(-1-1)+3(x-3+ \overline{x}-3)=6-15=-9=3.
\end{equation*} Thus we have a surjective map 
$\mathbb{Z}/3 \times \mathbb{Z} \rightarrow \mathit{{\rm E}}_2(\mathcal{O}_{-11})^{\rm ab}$.
The following theorem is due to P.M. Cohn.
Proposition 4.7. (Cohn [Reference Cohn5, Reference Cohn6])
Let d < 0 be a square free integer. Then
\begin{equation*}
\mathit{{\rm E}}_2(\mathcal{O}_d)^{\rm ab} \simeq
\begin{cases}
\mathbb{Z}/2 \times \mathbb{Z}/2 & \text{if}\ d=-1\\
\mathbb{Z}/6 \times \mathbb{Z} & \text{if}\ d=-2\\
\mathbb{Z}/3 & \text{if $d=-3$}\\
\mathbb{Z}/4 \times \mathbb{Z} & \text{if}\ d=-7\\
\mathbb{Z}/3 \times \mathbb{Z} & \text{if}\ d=-11\\
\mathbb{Z}/12 \times \mathbb{Z} & \text{otherwise}
\end{cases}.
\end{equation*}Proof. We have seen that 
$\mathcal{O}_d$ is universal for GE2 if and only if 
$d\neq -2,-7,-11$ (see Example 1.1 and [Reference Cohn6, Remarks, pp. 162–163]). Thus by Corollary 3.3,
\begin{equation*}
\mathit{{\rm E}}_2(\mathcal{O}_d)^{\rm ab}\simeq \mathcal{O}_d/M.
\end{equation*} This proves the claim for 
$d\neq -2,-7,-11$. For the case 
$d= -2,-7,-11$, see [Reference Cohn6, p. 162].
Now let d > 0. Then 
$\mathcal{O}_d^\times$ has infinitely many units. In fact 
$\mathcal{O}_d^\times=\{\pm u^n:n\in \mathbb{Z}\}$, where u is a particular unit called a fundamental unit. For a fundamental unit u, there are three other fundamental units: 
$\overline{u}$, −u and 
$-\overline {u}$. In fact, one of these four elements which is greater than 1 is called the ‘fundamental unit’. Observe that 
$\mathit{{\rm E}}_2(\mathcal{O}_d)=\mathit{{\rm SL}}_2(\mathcal{O}_d)$ [Reference Vaserstein16, p. 321, Theorem].
Proposition 4.8. Let d > 0 be a square free integer. Let u be the fundamental unit of 
$\mathcal{O}_d^\times$. If 
$d\equiv 2, 3 \pmod 4$ and 
$u=a+b\sqrt{d}$, then
\begin{equation*}
\mathcal{O}_d/M\simeq \begin{cases}
\displaystyle\frac{\mathbb{Z}}{2\gcd(bd, 3a+3, 6)} \times \frac{\mathbb{Z}}{2b} & \text{if}\ N(u)=1\\
\\
\displaystyle\frac{\mathbb{Z}}{2\gcd(a,3)} \times \frac{\mathbb{Z}}{2\gcd(a, 3b)} & \text{if}\ N(u)=-1
\end{cases}
\end{equation*} and if 
$d\equiv 1 \pmod 4$ and 
$u=a+b(1+\sqrt{d})/2$, then
\begin{equation*}
\mathcal{O}_d/M\simeq
\begin{cases}
\displaystyle\frac{\mathbb{Z}}{\gcd(b, 6(a-1), 12)} \times \frac{\mathbb{Z}}{\gcd(bd, 12(a-1)+6b, 24)} & \text{if}\ N(u)=1\\
\\
\displaystyle\frac{\mathbb{Z}}{\gcd(2a+b,6(a-1), 12)} \times \frac{\mathbb{Z}}{\gcd(2a+b, 6b)} & \text{if}\ N(u)=-1.
\end{cases}
\end{equation*} In particular, 
$\mathit{{\rm E}}_2(\mathcal{O}_d)^{\rm ab}$ is a finite group.
Proof. Consider the isomorphism
\begin{equation*}
\mathcal{O}_d/M\simeq \Big(\mathcal{O}_d /\langle u^2-1\rangle\Big) /\Big(M/\langle u^2-1\rangle\big).
\end{equation*}Then
\begin{equation*}
\langle u^2-1\rangle=\langle \overline{u}(u^2-1)\rangle=
\begin{cases}
\langle u- \overline{u} \rangle& \text{if}\ N(u)=1\\
\langle u + \overline{u} \rangle& \text{if}\ N(u)=-1.
\end{cases}
\end{equation*} First let 
$d\equiv 2, 3 \pmod 4$. Then 
$\mathcal{O}_d=\mathbb{Z}[\sqrt{d}]$ and 
$u-\overline{u}=2b\sqrt{d}$ when 
$N(u)=1$ and 
$u+ \overline{u}=2a$ when 
$N(u)=-1$. Hence
\begin{equation*}
\mathcal{O}_d /\langle u^2-1\rangle=\begin{cases}
\mathcal{O}_d/\langle 2b\sqrt{d}\rangle & \text{if}\ N(u)=1\\
\mathcal{O}_d/\langle 2a\rangle & \text{if}\ N(u)=-1
\end{cases}
\simeq
\begin{cases}
\mathbb{Z}/2bd \times \mathbb{Z}/2b & \text{if}\ N(u)=1\\
\mathbb{Z}/2a \times \mathbb{Z}/2a & \text{if}\ N(u)=-1.
\end{cases}
\end{equation*} Since 
$\overline{u}^2=1$ in 
$\mathcal{O}_d /\langle u^2-1\rangle$, we have
\begin{equation*}
M/\langle u^2-1\rangle=\langle \overline{6(u+1)}, \overline{12}\rangle=
\begin{cases}
\langle \overline{6(a+1)},\overline{12}\rangle & \text{if}\ N(u)=1\\
\langle \overline{6(1+b\sqrt{d})}, \overline{12}\rangle & \text{if}\ N(u)=-1.
\end{cases}
\end{equation*}Thus
\begin{equation*}
\mathcal{O}_d/M\simeq \begin{cases}
\mathbb{Z}/\gcd(2bd, 6(a+), 12) \times \mathbb{Z}/2b & \text{if}\ N(u)=1\\
\mathbb{Z}/\gcd(2a,6)\rangle \times \mathbb{Z}/ 2\gcd(2a, 6b) & \text{if}\ N(u)=-1.
\end{cases}
\end{equation*} Now let 
$d\equiv 1 \pmod 4$. Then 
$\mathcal{O}_d=\mathbb{Z}[\omega]$, where 
$\omega=(1+\sqrt{d})/2$. If 
$u=a+b\omega\in \mathcal{O}_d$, then 
$\overline{u}=a+b\overline{\omega}$, where 
$\overline{\omega}=(1-\sqrt{d})/2$. Note that 
$u-\overline{u}=b\sqrt{d}$ if 
$N(u)=1$ and 
$u+ \overline{u}=2a+b$ if 
$N(u)=-1$. Thus, we have
\begin{align*}
\mathcal{O}_d /\langle u^2-1\rangle &=\begin{cases}
\mathcal{O}_d/\langle b\sqrt{d}\rangle & \text{if}\ N(u)=1\\
\mathcal{O}_d/\langle 2a+b\rangle & \text{if}\ N(u)=-1
\end{cases}\\
& \simeq
\begin{cases}
(\mathbb{Z} \times \mathbb{Z})/\langle b(-1,2),b((d-1)/2,1)\rangle & \text{if}\ N(u)=1\\
\mathbb{Z}/(2a+b) \times \mathbb{Z}/(2a+b) & \text{if}\ N(u)=-1
\end{cases}\\
& \simeq
\begin{cases}
\mathbb{Z}/b \times \mathbb{Z}/bd & \text{if}\ N(u)=1\\
\mathbb{Z}/(2a+b) \times \mathbb{Z}/(2a+b) & \text{if}\ N(u)=-1,
\end{cases}
\end{align*}where the isomorphism
\begin{equation*}
(\mathbb{Z} \times \mathbb{Z})/\langle b(-1,2),b((d-1)/2,1)\rangle \rightarrow \mathbb{Z}/b \times \mathbb{Z}/bd
\end{equation*} is given by 
$\overline{(r,s)}\mapsto (\overline{r+s}, \overline{2r+s})$. Moreover, note that
\begin{align*}
M/\langle u^2-1\rangle &=\langle \overline{6(u-1)}, \overline{12}\rangle\\
& =\langle \overline{6(a-1)+6b\omega}, \overline{12}\rangle \\
&\simeq\langle (\overline{6(a-1)},\overline{6b}),\overline{(12,0)}\rangle\\
&\simeq
\begin{cases}
\langle (\overline{6(a-1)},12\overline{(a-1)}+\overline{6b}),\overline{(12,24)}\rangle & \text{if}\ N(u)=1\\
\langle (\overline{6(a-1)},\overline{6b}),\overline{(12,0)}\rangle & \text{if}\ N(u)=-1.
\end{cases}
\end{align*}Thus, we obtain the desired isomorphism.
