Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-11T06:25:22.708Z Has data issue: false hasContentIssue false
  • English
  • Français

TRANSIENT SOLUTION FOR A SIMPLE IMMIGRATION BIRTH–DEATH CATASTROPHE PROCESS

Published online by Cambridge University Press:  16 April 2004

E. G. Kyriakidis
E. G. Kyriakidis
Affiliation:
Department of Statistics and Actuarial Science, University of the Aegean, Karlovassi, 83200 Samos, Greece, E-mail: kyriak@aegean.gr
Rights & Permissions [Opens in a new window]

Abstract

In this note, we consider a simple immigration birth–death process with total catastrophes and we obtain the transient probabilities. Our approach involves a renewal argument. It is comparatively simpler and leads to more elegant expressions than other approaches that appeared in the literature recently.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 18 , Issue 2 , April 2004 , pp. 233 - 236
Copyright
© 2004 Cambridge University Press

1. INTRODUCTION

We consider a simple immigration birth–death process of individuals that is influenced by random total catastrophes which, when they occur, annihilate the entire population. Choosing an appropriate unit of time, it is assumed that when the state of the system is n, the immigration rate is ν, the birth rate is nλ, the death rate is nμ, and the catastrophe rate is one. The process can then be described as having the following transition rates in the time interval (t,t + δt):

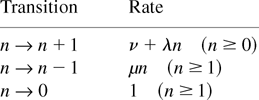
The same process was considered by Kyriakidis [5], Swift [8], and Chao and Zheng [2]. Swift, Chao, and Zheng used the forward Kolmogorov equations to determine the probability pn(t) that the population size N(t) at time t ≥ 0 is equal to n ≥ 0 given that P(N(0) = a) = pa, a ≥ 0. They obtained a partial differential equation for the generating function of pn(t), n ≥ 0. Swift used the symbolic software package Mathematica to solve the partial differential equation and then gave expressions for p0(t) in terms of the hypergeometric function. Chao and Zheng solved the partial differential equation using the method of characteristics and, then, obtained closed-form expressions for pn(t), n ≥ 0. Chao and Zheng also studied the stationary probabilities πn, n ≥ 0, of the process. They solved an ordinary differential equation for the generating function of πn, n ≥ 0, and then obtained expressions for πn, n ≥ 0.

In the next section, we obtain expressions for pn(t), n ≥ 0, in a comparatively simpler manner by applying a renewal argument, which has been used in [5] for the determination of π0. The same renewal argument has also been used for the determination of the transient probabilities of the simple immigration catastrophe process (see [6]) and the transient probabilities of a simple immigration–emigration catastrophe process (see [7]). Economou and Fakinos [4] also utilized this argument to study the transient and limiting distribution of a continuous-time Markov chain influenced by a regulating point process.

2. TRANSIENT SOLUTION

Assume that the catastrophes are introduced at rate 1 even if the process is in state 0. This assumption does not change the behavior of the process and implies that the catastrophes occur as a Poisson process with rate 1. Let Ut, t ≥ 0, be the backward recurrence time (i.e., the length of time measured backward from time t to the last catastrophe at or before t). It is well known (see, e.g., Cox [3, p.31]) that Ut is exponentially distributed with parameter 1, censored at time t (i.e., the distribution of Ut has a continuous part with density e−s in the interval (0,t) and a probability atom of size e−t at t). Therefore, conditioning on Ut, we obtain

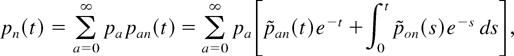
where

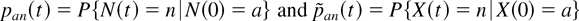
for the simple immigration birth–death process {X(t); t ≥ 0}. Let

the probability generating function of X(t). Clearly,

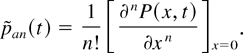
It is well known (see relation (8.71) in Bailey [1]) that

Using the Leibniz rule, we find expressions for the nth derivative of P(x,t) with respect to x, and from (1) and (2), we obtain the following expressions:

If μ ≠ λ ≠ 0,

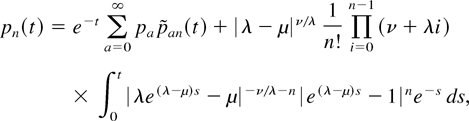
where

If λ = 0 ≠ μ,

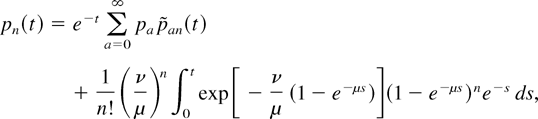
where

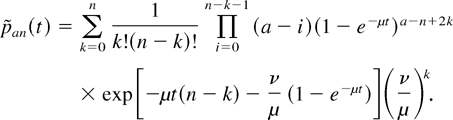
If λ = μ ≠ 0,

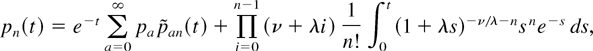
where

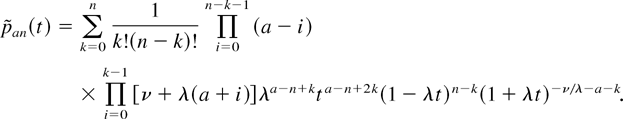
It can be shown that (4) and (5) are equal to the corresponding expressions (19) and (20) in [2].

If t tends to infinity in (3)–(5), the first terms in these expressions vanish. Using the transformation y = e−s in the integrals, we obtain the same expressions for the stationary probabilities that Chao and Zheng obtained (see [2, Thm.3.2]).

Acknowledgment

I would like to thank Dr. A. N. Yannacopoulos for useful discussions.

References

REFERENCES

Bailey, N.T.J. (1964). The elements of stochastic processes. New York: Wiley.
Chao, X. & Zheng, Y. (2003). Transient analysis of immigration birth–death processes with total catastrophes. Probability in the Engineering and Informational Sciences 17: 83–106.Google Scholar
Cox, D.R. (1962). Renewal theory. London: Chapman & Hall.
Economou, A. & Fakinos, D. (2003). A continuous-time Markov chain under the influence of a regulating point process and applications in stochastic models with catastrophes. European Journal of Operational Research 149: 625–640.Google Scholar
Kyriakidis, E.G. (1994). Stationary probabilities for a simple immigration-birth–death process under the influence of total catastrophes. Statistics and Probability Letters 20: 239–240.Google Scholar
Kyriakidis, E.G. (2001). The transient probabilities of the simple immigration–catastrophe process. The Mathematical Scientist 26: 56–58.Google Scholar
Kyriakidis, E.G. (2002). The transient probabilities of a simple immigration–emigration–catastrophe process. The Mathematical Scientist 27: 128–129.Google Scholar
Swift, R.J. (2001). Transient probabilities for a simple birth–death-immigration process under the influence of total catastrophes. International Journal of Mathematics and Mathematical Sciences 25: 689–692.Google Scholar