1. INTRODUCTION
Order statistics have received a great amount of attention from many researchers since they play an important role in reliability, data analysis, goodness-of-fit tests, statistical inference, and other applied probability areas. Please refer to David and Nagaraja [Reference David and Nagaraja5] and Balakrishnan and Rao [Reference Balakrishnan and Rao1, Reference Balakrishnan and Rao2] for more details. Let X 1:n ≤ X 2:n ≤ · · · ≤ X n:n denote the order statistics of random variables X 1, X 2, … , X n. In the reliability context, the lifetimes of parallel and series systems correspond to order statistics, X n:n and X 1:n, respectively, and they have been extensively studied when the components are independent and identically distributed (i.i.d.). However, in practice, usually, the observations are not i.i.d. Due to the complicated nature of the problem, not much work has been done for the non-i.i.d. case.
For ease of reference, let us first recall some stochastic orders that will be used in the sequel. Let X and Y be two nonnegative random variables with distribution functions F and G; survival functions ![]() and
and ![]() ; and density functions f and g, respectively.
; and density functions f and g, respectively.
Definition 1.1
(Shaked and Shanthikumar [Reference Shaked and Shanthikumar17] and Müller and Stoyan [Reference Müller and Stoyan14]): If the ratios below are well defined, X is said to be smaller than Y in the following:
1. likelihood ratio order (denoted by X ≤lrY) if g(x)/f(x) is increasing in x
2. hazard rate order (denoted by X ≤hrY) if
 (x)/
(x)/ (x) is increasing in x
(x) is increasing in x3. reversed hazard rate order (denoted by X ≤rhY) if G(x)/F(x) is increasing in x
4. stochastic order (denoted by X ≤stY) if
 (x) ≤
(x) ≤  (x) for all x.
(x) for all x.
It is well known that
Let {x (1), x (2), … , x (n)} denote the increasing arrangement of the components of the vector x = (x 1, x 2, … , x n).
Definition 1.2
The vector xis said to majorize the vector y(denoted by ![]() ) if
) if

for j = 1, … , n − 1 and ∑i=1nx (i) = ∑i=1ny (i).
For extensive and comprehensive details on the theory of the majorization order and its applications, please refer to Marshall and Olkin [Reference Marshall and Olkin12]. Another interesting order related to the majorization order introduced by Bon and Paltanea [Reference Bon and Paltanea4] is the p-larger order.
Definition 1.3
A vector xin ℝ+nis said to be p-larger than another vector yin ℝ+n(denoted by ![]() ) if
) if

Khaledi and Kochar [Reference Khaledi and Kochar9] proved that, for x, y ∈ ℝ+n,
However, the converse is not true.
Random variables X 1,X 2, … ,X n are said to follow the proportional hazard rates (PHR) model if for i = 1,2, … ,n, the survival function of X i can be expressed as
where ![]() (x) is the survival function of some random variable X. If r(t) is the hazard rate corresponding to the base line distribution F, then the hazard rate of X i is λir(t), i = 1,2, … ,n. We can express (1.1) as
(x) is the survival function of some random variable X. If r(t) is the hazard rate corresponding to the base line distribution F, then the hazard rate of X i is λir(t), i = 1,2, … ,n. We can express (1.1) as
where R(x) = ∫0xr(t)dt, is the cumulative hazard rate of X. Exponential random variables with hazard rates λ1,λ2, … ,λn is a special case of the PHR model with R(x) = x. Many interesting results have been obtained in the literature for the PHR model. Pledger and Proschan [Reference Pledger, Proschan and Rustagi15] proved that if (X 1, … , X n) and (X 1*, … ,X n*) have proportional hazard rate vectors (λ1, … ,λn) and (λ*1, … ,λ*n), respectively, then
implies that, for i = 1, … , n,
Subsequently, Proschan and Sethuraman [Reference Proschan and Sethuraman16] generalized this result from componentwise stochastic ordering to multivariate stochastic ordering. Boland, El-Neweihi, and Proschear [Reference Boland, El-Neweihi and Proschan3] showed by a counterexample that (1.3) cannot be strengthened from stochastic ordering to hazard rate ordering. This topic is followed up by Dykstra, Kochar, and Rojo [Reference Dykstra, Kochar and Rojo6], where they showed that if X 1, … , X n are independent exponential random variables with X i having hazard rate λi, i = 1, … ,n, and if Y 1, … ,Y n is a random sample of size n from an exponential distribution with common hazard rate ![]() = ∑i=1nλi/n, then
= ∑i=1nλi/n, then
Under a weeker condition that if Z 1, … ,Z n are a random sample with common hazard rate λ˜ = (∏i=1nλi)1/n, the geometric mean of the λ's, Khaledi and Kochar [Reference Khaledi and Kochar7] proved that
They also showed there that
which improved the bound given by (1.3). Recently, Khaledi and Kochar [Reference Khaledi, Kochar and Mara10] extended the results (1.5) and (1.6) from the exponential case to the PHR model.
Another interesting topic that has attracted much attention is the sample range, one of the criteria for comparing variabilities among distributions. Kochar and Rojo [Reference Kochar and Rojo11] pointed out that in the case of heterogeneous exponentials,
Later, Khaledi and Kochar [Reference Khaledi and Kochar8] improved upon this result. They proved that
where Z n:n is the maximum of a random sample from exponential distribution with common parameter as the geometric mean of the λi's.
In this article, the above topics are further studied. We prove that if X 1, … ,X n are independent random variables with X i having survival function ![]() λi, i = 1, … ,n, and Y 1, … ,Y n are a random sample with common population survival distribution
λi, i = 1, … ,n, and Y 1, … ,Y n are a random sample with common population survival distribution ![]() , where
, where ![]() = ∑i=1nλi/n, then
= ∑i=1nλi/n, then
and
These two results strengthen and generalize (1.4) and (1.7), respectively.
For the sake of convenience, throughout this article, the term increasing is used for monotone nondecreasing and decreasing is used for monotone nonincreasing.
2. STOCHASTIC COMPARISONS OF PARALLEL SYSTEMS
The following two lemmas will be used to prove our main result.
Lemma 2.1 (Khaledi and Kochar [Reference Khaledi and Kochar7])
For x ≥ 0, the functions
are both decreasing.
Lemma 2.2
Let X 1, … , X nbe independent exponential random variables with X ihaving hazard rate λi, i = 1, … , n. Let Y 1, … , Y nbe a random sample of size n from an exponential distribution with common hazard rate ![]() = ∑i=1nλi/n. Then
= ∑i=1nλi/n. Then
Proof
For x ≥ 0, the distribution function of X n:n is

with density function as

Similarly, the distribution function of Y n:n for x ≥ 0 is
with density function
Note that, for x ≥ 0,
![$$\eqalign{{f_{n:n}\lpar x\rpar \over g_{n:n}\lpar x\rpar }&={{\displaystyle\sum\limits_{i=1}^n}\displaystyle\Bigg[{\lambda_i e^{-\lambda_i x} \over 1-e^{-\lambda_i x}}\Bigg] \over \displaystyle{n \bar \lambda e^{-\bar \lambda x} \over 1-e^{-\bar\lambda x}}} {F_{n:n}\lpar x\rpar \over G_{n:n}\lpar x\rpar }\cr &={{{h_1\lpar x\rpar}\over { n \bar \lambda}} {F_{n:n}\lpar x\rpar \over G_{n:n}\lpar x\rpar },}}$$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022132024594-0921:S0269964807000344_eqnU14.gif?pub-status=live)
Where
![$$\eqalign{h_1\lpar x\rpar &={{\displaystyle\sum\limits_{i=1}^n}\displaystyle \Bigg[{\lambda_i e^{-\lambda_i x} \over 1-e^{-\lambda_i x}}\Bigg] \over \displaystyle{e^{-\bar \lambda x} \over 1-e^{-\bar\lambda x}}}\cr& =\sum_{i=1}^n \lambda_i {e^{\bar\lambda x}-1 \over e^{\lambda_i x}-1}.}$$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022132024594-0921:S0269964807000344_eqnU15.gif?pub-status=live)
Since
it follows from Theorem 3.2 of Dykstra et al. [Reference Dykstra, Kochar and Rojo6] that
is increasing in x ≥ 0. Thus, it is sufficient to prove that h 1(x) is increasing in x ≥ 0.
The derivative of h 1(x) is, for x ≥ 0,

By Lemma 2.1 and Čebyšev's sum inequality (Mitrinović [Reference David and Nagaraja5, Thm. 1, p. 36]), it holds that, for x ≥ 0,

Thus, h′1(x) will be nonnegative if, for x ≥ 0,

holds.
Denote, for x ≥ 0,

Since the derivative of h 2(x) is

and by the arithmetic–geometric mean inequality, for x ≥ 0,

it follows that h′2(x) ≥ 0; for x ≥ 0; that is, h 2(x) is increasing in x ≥ 0. Observing that h 2(0) = 0, we have h 2(x) ≥ 0 for x ≥ 0. Hence, h 1(x) is increasing in x ≥ 0. The required result follows immediately.■
Now, we are ready to extend the above result to the PHR family.
Theorem 2.3
Let X 1, … ,X nbe independent random variables with X ihaving survival function ![]() λi, i = 1, … ,n. Let Y 1, … ,Y nbe a random sample with common population survival distribution
λi, i = 1, … ,n. Let Y 1, … ,Y nbe a random sample with common population survival distribution ![]() , where
, where ![]() = ∑i=1nλi/n. Then
= ∑i=1nλi/n. Then
Proof
Note that the cumulative hazard of F is
Now, for x ≥ 0, i = 1, … ,n,
Where H −1 is the right inverse of H. Denoting X i′ = H(X i), we notice that X i′ is exponential with hazard rate λi for i = 1, … ,n. Similarly, let Y i′ = H(Y i) be exponential with hazard rate ![]() for i = 1, … ,n. It follows from Lemma 2.2 that
for i = 1, … ,n. It follows from Lemma 2.2 that
that is,
Since H −1 is an increasing function, it follows from Theorem 1.C.4 in Shaked and Shanthikumar [Reference Shaked and Shanthikumar17] that
■
One might wonder whether (1.5) of Khaledi and Kochar [Reference Khaledi and Kochar7] can be strengthened from the hazard rate order to the likelihood ratio order. The following example serves as a counterexample.
Example 2.4
Let X 1, … ,X n be independent exponential random variables with X i having hazard rate λi, i = 1, … ,n, and Z 1, … ,Z n be a random sample of size n from an exponential distribution with common hazard rate λ˜ = (∏i=1nλi)1/n. Then the reversed hazard rate of X n:n is

Similarly, the reversed hazard rate of Z n:n is

Let λ1 = λ2 = 1, λ3 = 3, and n = 3; then
Thus,
which implies that
Remark
Remark 2.2 of Khaledi and Kochar [Reference Khaledi and Kochar7] asserted that the stochastic order in (1.6) cannot be extended to the hazard rate order. Example 2.4 also shows that
3. REVERSE HAZARD RATE ORDERING BETWEEN THE SAMPLE RANGES
Theorem 3.2 will strengthen (1.7) from the stochastic order to the reversed hazard rate order and also generalize it to the PHR family. First, let us prove the following lemma.
Lemma 3.1
Let X 1, … ,X nbe independent exponential random variables with X ihaving hazard rate λi, i = 1, … ,n. Let Y 1, … ,Y nbe a random sample of size n from an exponential distribution with common hazard rate ![]() = ∑i=1nλi/n. Then
= ∑i=1nλi/n. Then
Proof
Denote by R X = X n:n − X 1:n and R Y = Y n:n − Y 1:n the sample ranges of X i's and Y i's, respectively. From David and Nagaraja [Reference David and Nagaraja5, p. 26], the distribution function of R X is, for x ≥ 0,

Thus, we have the density function of R X as, for x ≥ 0,
![$$\eqalign{f_{R_X}\lpar x\rpar & ={1 \over {\displaystyle\sum\limits_{i=1}^{n}} \lambda_{i}}\left( \sum_{i=1}^{n} \lambda_{i} \prod_{j=1,j\neq i}^{n}\lpar 1-e^{-\lambda_{j}x}\rpar \right) ^{\!\!\!\prime} \cr & ={1 \over {\displaystyle\sum\limits_{i=1}^{n}} \lambda_{i}}\left[\sum_{i=1}^{n} \lambda_{i}\sum_{j=1,j\neq i}^{n}\lambda_{j}e^{-\lambda_{j}x}\prod_{k=1,k\neq i,j}^{n} \lpar 1-e^{-\lambda_{k}x}\rpar \right] \cr &={1 \over {\displaystyle\sum\limits_{i=1}^{n}} \lambda_{i}}\left[\sum_{i=1}^{n} \lambda_{i}\sum_{j=1,j\neq i}^n{\lambda_{j}e^{-\lambda_{j}x} \over \lpar 1-e^{-\lambda_{i}x}\rpar \lpar 1-e^{-\lambda_{j}x}\rpar }\right]\prod_{i=1}^{n} \lpar 1-e^{-\lambda_{i}x}\rpar \cr &={\prod\limits_{i=1}^{n} \lpar 1-e^{-\lambda_{i}x}\rpar \over {\displaystyle\sum\limits_{i=1}^{n}} \lambda_{i}}\sum_{i=1}^{n}{\lambda_{i} \over 1-e^{-\lambda_{i}x}}\sum_{j=1,j\neq i}^n{\lambda_{j}e^{-\lambda_{j}x} \over 1-e^{-\lambda_{j}x}}.}$$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022132024594-0921:S0269964807000344_eqnU36.gif?pub-status=live)
Hence, the reversed hazard rate of R X is, for x ≥ 0,

The reversed hazard rate of R Y is, for x ≥ 0,
Since, for x ≥ 0,

and

it holds that

Note that, from inequality (2.2),

Combining this with inequality (3.2), we get, for x ≥ 0,

that is, for x ≥ 0,

Observe that
is convex in x ≥ 0. It follows from Jensen's inequality that

that is,

Using inequalities (3.3) and (3.4), it holds that, for x ≥ 0,

Hence, for x ≥ 0,

that is,
The required result follows immediately.■
Now, we extend the above result to the PHR family.
Theorem 3.2
Let X 1, … , X nbe independent random variables with X ihaving survival function ![]() λi, i = 1, … , n. Let Y 1, … , Y nbe a random sample with common population survival distribution
λi, i = 1, … , n. Let Y 1, … , Y nbe a random sample with common population survival distribution ![]() , where
, where ![]() = ∑i=1nλi/n. Then
= ∑i=1nλi/n. Then
Proof
From David and Nagaraja [Reference David and Nagaraja5, p. 26], the distribution function of R X is, for x ≥ 0,
![$$F_{R_X}\lpar x\rpar =\sum_{i=1}^n\vint_0^\infty\lambda_i {\it\bar F}^{\lambda_i-1}\lpar u\rpar\, f\lpar u\rpar \prod_{j=1,j\neq i}^n [{\it\bar F}^{\lambda_j}\lpar u\rpar -{\it\bar F}^{\lambda_j}\lpar u+x\rpar ]du.$$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022132024594-0921:S0269964807000344_eqnU48.gif?pub-status=live)
Hence, the density function is, for x ≥ 0,
![$$\eqalign{f_{R_X}\lpar x\rpar & =\sum_{i=1}^n\vint_0^\infty\lambda_i {\it\bar F}^{\lambda_i-1}\lpar u\rpar f\lpar u\rpar \sum_{j=1,\,j\neq i}^n\lambda_j{\it\bar F}^{\lambda_j-1}\lpar x+u\rpar f\lpar x+u\rpar \cr & \quad \times \prod_{k=1,k\neq i,j}^n[{\it\bar F}^{\lambda_k}\lpar u\rpar -{\it\bar F}^{\lambda_k}\lpar u+x\rpar ]\ du.}$$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022132024594-0921:S0269964807000344_eqnU49.gif?pub-status=live)
Similarly, the distribution function of R Y is, for x ≥ 0,
Hence, the density function is, for x ≥ 0,
From the definition, we need to prove that, for x ≥ 0,
Thus, it is sufficient for us to prove that the following inequality holds:
![$$\eqalign{& \left\{\sum_{i=1}^n\lambda_i {\it\bar F}^{\lambda_i-1}\lpar u\rpar f\lpar u\rpar \sum_{j=1,j\neq i}^n\lambda_j{\it\bar F}^{\lambda_j-1}\lpar x+u\rpar f\lpar x+u\rpar \prod_{k=1,k\neq i,j}^n\left[{\it\bar F}^{\lambda_k}\lpar u\rpar -{\it\bar F}^{\lambda_k}\lpar u+x\rpar \right]\right\} \cr & \quad \times \left\{n\bar \lambda {\it\bar F}^{\bar \lambda-1}\lpar u\rpar f\lpar u\rpar \left[{\it\bar F}^{\bar \lambda}\lpar u\rpar -{\it\bar F}^{\bar \lambda}\lpar u+x\rpar \right]^{n-1}\right\}\cr & \quad \ge \left\{n\lpar n-1\rpar \bar \lambda^2 {\it\bar F}^{\bar\lambda-1}\lpar u\rpar f\lpar u\rpar {\it\bar F}^{\bar\lambda-1}\lpar x+u\rpar f\lpar x+u\rpar \left[{\it\bar F}^{\bar\lambda}\lpar u\rpar -{\it\bar F}^{\bar\lambda}\lpar u+x\rpar \right]^{n-2}\right\} \cr & \quad \times \left\{\sum_{i=1}^n\lambda_i {\it\bar F}^{\lambda_i-1}\lpar u\rpar f\lpar u\rpar \prod_{j=1,j\neq i}^n \left[{\it\bar F}^{\lambda_j}\lpar u\rpar -{\it\bar F}^{\lambda_j}\lpar u+x\rpar \right]\right\}.}$$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022132024594-0921:S0269964807000344_eqnU53.gif?pub-status=live)
After some simplifications, the above inequality is reduced to, for x, u ≥ 0,
![$$\eqalign{& \sum_{i=1}^n {\lambda_i {\it\bar F}^{\lambda_i}\lpar u\rpar \over {\it\bar F}^{\lambda_i}\lpar u\rpar -{\it\bar F}^{\lambda_i}\lpar x+u\rpar }\sum_{j=1,j\neq i}^n {\lambda_j{\it\bar F}^{\lambda_j}\lpar x+u\rpar \over {\it\bar F}^{\lambda_j}\lpar u\rpar -{\it\bar F}^{\lambda_j}\lpar x+u\rpar } \left[{\it\bar F}^{\bar \lambda}\lpar u\rpar -{\it\bar F}^{\bar \lambda}\lpar u+x\rpar \right] \cr & \quad \ge \sum_{i=1}^n {\lambda_i {\it\bar F}^{\lambda_i}\lpar u\rpar \over {\it\bar F}^{\lambda_i}\lpar u\rpar -{\it\bar F}^{\lambda_i}\lpar x+u\rpar } \lpar n-1\rpar \bar \lambda {\it\bar F}^{\bar \lambda} \lpar u+x\rpar ;}$$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022132024594-0921:S0269964807000344_eqnU54.gif?pub-status=live)
that is, for x, u ≥ 0,
![$$\sum_{i=1}^n {\lambda_i \over 1-{\it\bar F}_u^{\lambda_i}\lpar x\rpar }\sum_{j=1,j\neq i}^n {\lambda_j \over {\it\bar F}^{-\lambda_j}_u\lpar x\rpar -1} \left[{\it\bar F}^{-\bar\lambda}_u\lpar x\rpar -1\right] \ge \sum_{i=1}^n {\lambda_i \over 1-{\it\bar F}^{\lambda_i}_u\lpar x\rpar } \lpar n-1\rpar \bar \lambda,$$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022132024594-0921:S0269964807000344_eqn15.gif?pub-status=live)
where
which is the survival function of X u = X − u|X > u, the residual life of X at time u ≥ 0. Now, using the transform
(3.6) is equivalent to
![$$\sum_{i=1}^n {\lambda_i \over 1-e^{-\lambda_i H\lpar x\rpar }}\sum_{j=1,j\neq i}^n {\lambda_j \over e^{\lambda_j H\lpar x\rpar }-1} \left[e^{\bar\lambda \,H\lpar x\rpar }-1\right] \ge\sum_{i=1}^n {\lambda_i \over 1-e^{-\lambda_i H\lpar x\rpar }} \lpar n-1\rpar \bar \lambda;$$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022132024594-0921:S0269964807000344_eqnU57.gif?pub-status=live)
that is, for x ≥ 0,

Thus, the required result follows from inequality (3.5)■
Acknowledgment
The authors are thankful to an anonymous referee for his comments and suggestions, which have led to an improved version of the article.


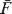
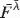 , where
, where 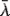 = ∑
= ∑