1. INTRODUCTION
Assume X and Y are two random variables with distribution functions F and G, respectively, and denote by F = 1 − F and G = 1 − G their respective reliability functions. Let Xt = X − t|X > t be the residual life of X at time t ≥ 0 and X(t) = t − X|X ≤ t be the inactivity time (IT) at time t > 0; their corresponding reliability functions can be represented as

The mean inactivity time (MIT) is thus

X or its distribution F is said to be of increasing mean inactivity time (IMIT) if mX(t) is nondecreasing in t > 0.
Having played important roles in survival analysis, reliability theory, maintenance polices, and many other areas of applied probability, both IT and IMIT life distribution received much attention during this decade (see, e.g., Ruiz and Navarro [19], Block, Savits, and Singh [4], Li and Lu [14], Li and Zuo [15], and Ahmad, Kayid, and Pellerey [1]).
In the theory of reliability, X is often regarded as the total life of a component; it is of interest to study XY = X − Y |X > Y, the residual life of X with a random age Y (RLRT) (Stoyan [22]), and X(Y) = Y − X|X ≤ Y, the inactivity time of X at a random time Y (ITRT). The distribution function of XY is
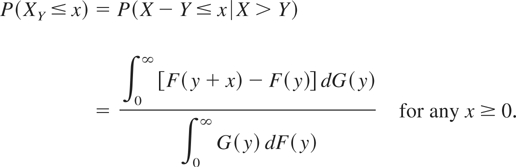
The RLRT represents the actual working time of the standby unit if X is regarded as the total random life of a warm standby unit with its age Y, and the idle time of the server in a GI/G/1 queuing system can also be expressed as a RLRT (see Marshall [16]). For more research conclusions about stochastic comparisons of RLRT and ITRT, refer to Yue and Cao [23] and Li and Zuo [15].
In the current investigation, we further focus on MIT order and IMIT class of life distributions. Section 2 builds some new properties of MIT order and IMIT class of life distributions. Section 3 investigates the preservation property of MIT order under increasing and concave transformations, reversed preservation properties of MIT order, and IMIT class of life distributions under the taking of maximum. Section 4 develops stochastic comparison of a residual life at a random time with certain aging properties. Finally, based on the excess lifetime in a renewal process, the stochastic comparison of IMIT life distribution is conducted in Section 5 as well.
Throughout this article, the term increasing is used instead of monotone nondecreasing and the term decreasing is used instead of monotone nonincreasing. We assume that the random variables under consideration have zero as the common left end point of their supports, and the expectation is assumed to be finite when used.
2. DEFINITIONS AND BASIC PROPERTIES
In this section, we first recall some definitions that will be used in the sequel; then we discuss some basic properties about IMIT class and MIT order.
Definition 2.1:
(a) X is said to be smaller than Y in the hazard rate order (denoted by X ≤hr Y) if G(x)/F(x) is increasing in x for which the ratio is well defined.
(b) X is said to be smaller than Y in the mean residual life order (denoted by X ≤mrl Y) if EXt ≤ EYt for all t ≥ 0 for which the expectations exist.
(c) X is said to be smaller than Y in the mean inactivity time order (denoted by X ≤MIT Y) if EX(t) ≥ EY(t) for all t > 0 for which the expectations exist.
(d) X is said to be smaller than Y in the increasing convex order (denoted by X ≤icx Y) if Eh(X) ≤ Eh(Y) for all increasing and convex h.
For a more comprehensive discussion of the properties as well as other details of those stochastic orderings, readers is referred to Shaked and Shanthikumar [20], Müller and Stoyan [17], Ahmad et al. [1], and Kayid and Ahmad [9].
The following aging properties are closely related to our main theme. For further details on them, refer to Barlow and Proschan [2], Müller and Stoyan [17], and Nanda, Singh, Misra, and Paul [18].
Definition 2.2:
(a) X is of increasing failure rate (IFR) if Xt is stochastically decreasing in t ≥ 0.
(b) X is of decreasing mean residual life (DMRL) if EXt is decreasing in t ≥ 0.
(c) X is of increasing mean inactivity time (IMIT) if mX(t) is increasing in t > 0.
Now let us turn to the following basic properties.
Proposition 2.3: X is IMIT if and only if X ≤MIT X + Y for any Y independent of X.
Proof: Necessity: If mX(t) increases in t > 0, then, by Fubini's theorem, we have, for any t > 0,

Thus, X ≤MIT X + Y.
Sufficiency: In view of the fact that

the desired result follows immediately by putting Y = s ≥ 0. █
According to Theorem 1.D.8 of Shaked and Shanthikumar [20], X is of decreasing mean residual life (DMRL) if and only if Xt ≤mrl X for any t ≥ 0. One may wonder whether IMIT property of X is also equivalent to Xt ≤MIT X for any t ≥ 0. Proposition 2.4 shows that Xt ≤MIT X for any t ≥ 0 implies that X is of IMIT; However, Example 2.5 states that the inverse is not valid.
Proposition 2.4: If Xt ≤MIT X for any t ≥ 0, then X is of IMIT.
Proof: For any t ≥ 0 and s > x ≥ 0,
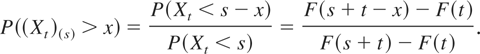
For any t ≥ 0 and s > 0, Xt ≤MIT X is equivalent to

Then for any t ≥ 0 and s > 0,
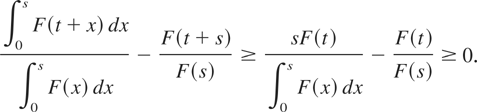
Also,
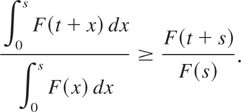
Equivalently, for any t ≥ 0 and s > 0,

which asserts that mX(s) is increasing in s > 0; that is, X is of IMIT. █
Example 2.5: For a random life X with distribution function
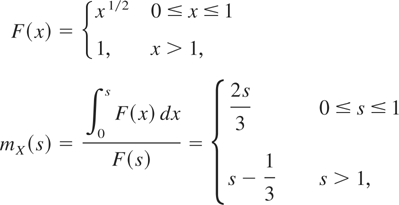
Thus, X is of IMIT.
Put s = t = ½; it can be easily found that
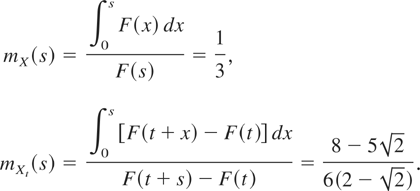
The inequality

tells that Xt ≤MIT X is not true.
3. PRESERVATION PROPERTIES
This section will develop some preservation properties as well as reversed preservation properties of MIT order and IMIT class under both monotonic transformations and the taking of maximum, respectively.
Theorem 3.1: Assume that φ is strictly increasing and concave; φ(0) = 0. If X ≤MIT Y, then φ(X) ≤MIT φ(Y).
Proof: Without loss of generality, assume that φ is differentiable. X ≤MIT Y implies that for any t > 0,

Since φ′(t) is nonnegative and decreasing, by Lemma 7.1(b) of Barlow and Proschan [2] it holds that

Equivalently,
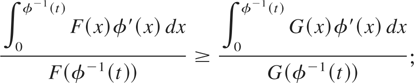
that is, for any t > 0,
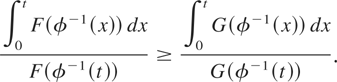
Note that

we have for any t > 0 that

which tells that φ(X) ≤MIT φ(Y). █
Theorem 3.2: Let X1,…, Xn and Y1,…,Yn be independent and identically distributed (i.i.d.) copies of X and Y, respectively. If max{X1,…, Xn} ≤MIT max{Y1,…,Yn}, then X ≤MIT Y.
Proof: max{X1,…, Xn} ≤MIT max{Y1,…,Yn} implies that

that is,
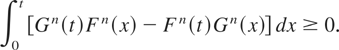
Since, for any t > 0,

is nonnegative and decreasing in x ≥ 0, by Lemma 7.1(b) of Barlow and Proschan [2] we have

which states that X ≤MIT Y. █
Remark: Theorem 3.2 in fact also holds for general variables. Since X ≤MIT Y if and only if −X ≥mrl − Y of Ahmad et al. [1] and

by Theorem 3.2, we immediately reach the following corollary.
Corollary 3.3: Let X1,…, Xn and Y1,…,Yn be i.i.d. copies of X and Y, respectively. If min{X1,…, Xn} ≥mrl min{Y1,…,Yn}, then X ≥mrl Y.
Based on Corollary 3.3 and Lemma 3.4, Theorem 3.5 presents the reversed preservation property of IMIT under the taking of maximum.
Lemma 3.4: X is of IMIT if and only if X(s) ≤mrl X(t) for all 0 < s ≤ t.
Proof: It can be easily established; hence, the proof is omitted. █
Theorem 3.5: Let X,X1,…, Xn be i.i.d. random variables. If max{X1,…, Xn} is of IMIT, then X is also of IMIT.
Proof: For any s > x ≥ 0,

that is, for all s ≥ 0,
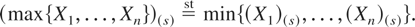
max{X1,…, Xn} is of IMIT and by Lemma 3.4, it holds that
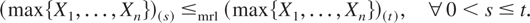
Thus,

Now it follows from Corollary 3.3 that

By Lemma 3.4 again, X is of IMIT. █
4. MEAN RESIDUAL LIFE AT A RANDOM TIME
Stochastic comparison under certain conditions on the concerned total life and random time as well as preservation properties of decreasing reversed hazard rate (DRHR) and IMIT have been conducted by Yue and Cao [23] and Li and Zuo [15]. This section reports some results from further comparisons of RLRT.
Yue and Cao [24, Thm.3(a)] proved that X is NBULt (new better than used in Laplace transform order) if and only if XY is smaller than X in Laplace transform order for all Y independent of X. Recently, Li [11, Thm.4.1(i)] showed that X is NBUMg (new better than used in moment generating function order) if and only if XY is smaller than X in the moment generating function order for all Y independent of X. The following theorem gives a parallel result about the MIT order.
Theorem 4.1: XY ≤MIT X for any Y that is independent of X if and only if Xt ≤MIT X for all t ≥ 0.
Proof: Sufficiency: Since Xt ≤MIT X for all t ≥ 0, it follows from (2) that

In view of (1), this shows XY ≤MIT X.
Necessity: Suppose XY ≤MIT X holds for any nonnegative random variable Y. Then Xt ≤MIT X for all t ≥ 0 follows by taking Y as a degenerate variable. █
Recall that for two subsets Θ and Γ of the real line, a nonnegative function h defined on Θ × Γ is said to be totally positive of order 2 (TP2) on Θ × Γ if

whenever x ≤ x′ and y ≤ y′, and x,x′ ∈ Θ and y, y′ ∈ Γ. The following lemma, which is due to Joag-Dev, Kochar, and Proschan [8], will be utilized to derive Theorem 4.3.
Lemma 4.2: Let ψ(x,y) be any TP2 function (not necessarily a reliability function) in x ∈ Θ and y ∈ Γ and Fi(x) be a distribution function for each i. Denote
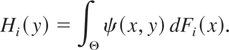
If Fi(x) is TP2 in i ∈ {1,2} and x ∈ Θ and if ψ(x,y) is increasing in x for every y, then Hi(y) is TP2 in y ∈ Γ and i ∈ {1,2}.
Proof of the next result is based on the idea of Theorem 4.2 of Gao, Belzunce, Hu, and Pellerey [7].
Theorem 4.3: Assume that Z is independent of X and Y. If X ≤hr Y and Z is of IMIT, then XZ ≤mrl YZ.
Proof: Denote by F1, F2, and G distribution functions of X, Y, and Z, respectively. Since Z is of IMIT, we have, for all y ≥ 0 and Δ > 0,

that is,
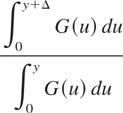
is decreasing in y ≥ 0. Then

for all 0 < t1 ≤ t2 < y1 ≤ y2.
Denote
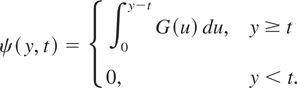
The last inequality states that
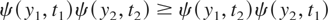
holds for all (t1,t2,y1,y2) ∈ S = {(t1,t2,y1,y2) : 0 < t1 ≤ t2 < y1 ≤ y2}.
It can be easily verified that (3) is also valid for those (t1,t2,y1,y2) ∈ {(t1,t2,y1,y2) : 0 < t1 ≤ t2, 0 < y1 ≤ y2} − S. Thus, ψ(y,t) is TP2 in (y,t) ∈ (0,∞) × (0,∞).
For i = 1,2, let
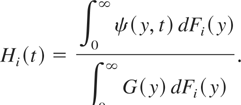
X ≤hr Y implies that Fi(x) is TP2 in (i,x) ∈ {1,2} × (0,∞) and ψ(y,t) is increasing in y for each fixed t. From Lemma 4.2 it follows that Hi(t) is TP2 in (i,t) ∈ {1,2} × (0,∞); that is,

is increasing in t ≥ 0, which is equivalent to
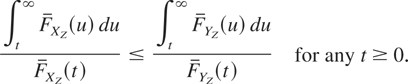
Hence, XZ ≤mrl YZ. █
Remark: Assume X, Y, and Z are three independent nonnegative random variables. Li and Zuo [15, Thm.5] showed that if X ≤hr Y and Z is of IMIT, then Z(X) ≤icx Z(Y). In view of the fact that XZ = Z(X), it is also valid, under the condition of Theorem 4.3, that Z(X) ≤mrl Z(Y). According to Theorem 3.A.13 of Shaked and Shanthikumar [20], X ≤mrl Y implies X ≤icx Y and we in fact develop a stronger conclusion here.
As a direct application of Theorem 4.3, we can get a simple and brief proof of Theorem 6 about DMRL in Li and Zuo [15].
Corollary 4.4: Assume X and Z are independent. If X is of IFR and Z is of IMIT, then XZ is of DMRL.
Proof: According to Theorem 1.B.19 of Shaked and Shanthikumar [20], X is of IFR if and only if Xt ≤hr X for all t ≥ 0. By Theorem 4.3, (Xt)Z ≤mrl XZ for all t ≥ 0. Note that
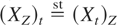
for all t ≥ 0; it holds that (XZ)t ≤mrl XZ for all t ≥ 0. Now, from Theorem 1.D.8 of Shaked and Shanthikumar [20], it follows immediately that XZ is of DMRL. █
5. STOCHASTIC COMPARISON OF RENEWAL EXCESS LIFETIME
Consider a renewal process with i.i.d. interarrival times Xi with common distribution F. For k = 1,2,…, let
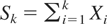
be the time of the kth arrival and S0 = 0. The renewal counting process N(t) = sup{n : Sn ≤ t} gives the number of arrivals until time t ≥ 0, and the excess lifetime γ(t) = SN(t)+1 − t at time t ≥ 0 is the time elapsed from the time t to the first arrival after time t. Of course, it is obvious that
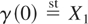
. M(t) = EN(t) is called as renewal function, which satisfies the well-known fundamental renewal equation
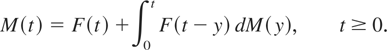
Brown [5] is among the first to survey the stochastic monotonicity of the excess lifetime; afterward, Shaked and Zhu [21] had some further discussions on this line of research. Subsequently, many authors devoted themselves to investigate the behavior of the renewal excess lifetime of a renewal process with interarrivals having certain aging properties, such as NBU, NBUC, NBU(2), NBUE, NBULt and NBUMg, and so forth. Their results in fact assert that various NBU interarrivals can reduce to the corresponding NBU properties of the excess lifetime. For more details, readers are referred to Li [11], Li and Kochar [12], Belzunce, Ortega, and Ruiz [3], Li, Li, and Jing [13], Chen [6], and Barlow and Proschan [2]. In this section, we will investigate the behavior of the excess lifetime of a renewal process with IMIT interarrivals.
Theorem 5.1: If γ(t) is decreasing in the MIT order in t ≥ 0, then X is of IMIT.
Proof: According to Karlin and Taylor [10, p.193], for any t ≥ 0 and x ≥ 0,
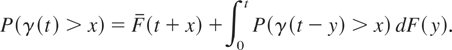
Then
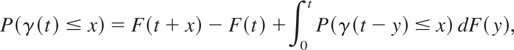
for any t ≥ 0 and x ≥ 0.
Since γ(t) is decreasing in t in the sense of MIT order, we have, for all s > 0 and t ≥ 0,

where the last equality is due to (5).
Note that
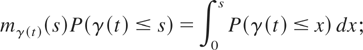
it holds that
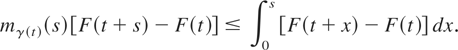
On the other hand,
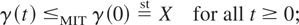
it holds that for all t ≥ 0 and s > 0,

which is equivalent to (2); that is, Xt ≤MIT X for all t ≥ 0. From Proposition 2.4, the desired result follows immediately. █
Theorem 5.2: If Xt ≤MIT X for all t ≥ 0, then γ(t) ≤MIT γ(0) for all t ≥ 0.
Proof: According to Barlow and Proschan [2], it holds that

Thus,
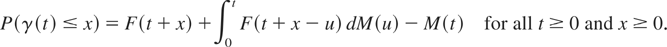
Xt ≤MIT X, by (2), for any t ≥ 0 and s > 0,

Now based on (4) and inequality (6), we have, for any t ≥ 0 and s > 0,

Hence, it holds that for all t ≥ 0 and s > 0,

That is, γ(t) ≤MIT γ(0), for all t ≥ 0. █
Acknowledgments
This research was supported by the National Natural Science Foundations of China (10201010) and the Program for New Century Excellent Talents in University, China.


