Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-11T01:40:45.680Z Has data issue: false hasContentIssue false
  • English
  • Français

RATIO MONOTONICITY FOR TAIL PROBABILITIES IN THE RENEWAL RISK MODEL

Published online by Cambridge University Press:  31 March 2011

Georgios Psarrakos  and
Michael Tsatsomeros
Georgios Psarrakos
Affiliation:
Department of Statistics and Insurance Science, University of Piraeus, Piraeus 18534, Greece E-mail: gpsarr@unipi.gr
Michael Tsatsomeros
Affiliation:
Department of Mathematics, Washington State University, Pullman, WA 99164-3113, E-mail: tsat@wsu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A renewal model in risk theory is considered, where 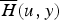is the tail of the distribution of the deficit at ruin with initial surplus u and is the tail of the ladder height distribution. Conditions are derived under which the ratio 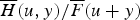is nondecreasing in u for any y≥0. In particular, it is proven that if the ladder height distribution is stable and DFR or phase type, then the above ratio is nondecreasing in u. As a byproduct of this monotonicity, an upper bound and an asymptotic result for 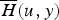are derived. Examples are given to illustrate the monotonicity results.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 25 , Issue 2 , April 2011 , pp. 171 - 185
Copyright
Copyright © Cambridge University Press 2011

References

1.Apostol, T.M. (1974). Mathematical analysis, 2nd ed.Hong Kong: Addison-Wesley.Google Scholar
2.Asmussen, S. (2000). Ruin probabilities. Singapore: World Scientific.CrossRefGoogle Scholar
3.Berman, A. & Plemmons, B. (1994). Nonnegative matrices in the mathematical sciences. Philadelphia: SIAM.CrossRefGoogle Scholar
4.Bingham, N.H., Goldie, C.M. & Teugels, J.L. (1987). Regular variation. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
5.Daley, D.J., Omey, E. & Vesilo, R. (2007). The tail behavior of a random sum of subexponential random variables and vectors. Extremes 10: 21–39.CrossRefGoogle Scholar
6.Dickson, D.C.M. (1998). On a class of renewal risk processes. North American Actuarial Journal 11(3): 128–137.Google Scholar
7.Dickson, D.C.M. & dos Reis, A.E. (1996). On the distribution of the duration of negative surplus. Scandinavian Actuarial Journal 1996: 148–164.CrossRefGoogle Scholar
8.Drekic, S., Dickson, D.C.M., Stanford, D.A. & Willmot, G.E. (2004). On the distribution of the deficit at ruin when claims are phase-type. Scandinavian Actuarial Journal 2004: 105–120.CrossRefGoogle Scholar
9.Embrechts, P. & Veraverbeke, N. (1982). Estimates for the probability of ruin with special emphasis on the possibility of large claims. Insurance: Mathematics and Economics 7: 55–72.Google Scholar
10.Fagiuoli, E. & Pellerey, F. (1994). Preservation of certain classes of life distributions under Poisson shock models. Journal of Applied Probability 31: 458–465.CrossRefGoogle Scholar
11.Gerber, H.U., Goovaerts, M.J. & Kaas, R. (1987). On the probability and severity of ruin. ASTIN Bulletin 17: 152–163.CrossRefGoogle Scholar
12.Horn, R.A. & Johnson, C.R. (1985). Matrix analysis. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
13.Psarrakos, G. (2009). Asymptotic results for heavy-tailed distributions using defective renewal equations. Statistics and Probability Letters 79: 774–779.CrossRefGoogle Scholar
14.Psarrakos, G. & Politis, K. (2009). Monotonicity properties and the deficit at ruin in the Sparre Andersen model. Scandinavian Actuarial Journal 2009: 104–118.CrossRefGoogle Scholar
15.Rolski, T., Schmidli, H., Schmidt, V. & Teugels, J. (1999). Stochastic processes for insurance and finance. New York: Wiley.CrossRefGoogle Scholar
16.Samorodnitsky, G. & Taqqu, M. (1994). Stable non-Gaussian random processes. London: Chapman and Hall.Google Scholar
17.Shanthikumar, J.G. (1988). DFR properties of first-passage times and its preservation under geometric compounding. Annals of Probability 33: 397–406.Google Scholar
18.Willmot, G.E. (2002). Compound geometric residual lifetime distributions and the deficit at ruin. Insurance: Mathematics and Economics 30: 421–438.Google Scholar
19.Willmot, G.E., Dickson, D.C.M., Drekic, S. & Stanford, D.A. (2004). The deficit at ruin in the stationary renewal risk model. Scandinavian Actuarial Journal 2004: 241–255.CrossRefGoogle Scholar
20.Willmot, G.E. & Lin, X.S. (1998). Exact and approximate properties of the distribution of the surplus before and after ruin. Insurance: Mathematics and Economics 23: 91–110.Google Scholar