Published online by Cambridge University Press: 22 January 2004
Supply interruptions resulting from unpredictable events, such as machine breakdowns, order cancellations, unscheduled maintenance, and labor strikes can produce adverse effects on the production/inventory system. In this article, we consider a periodic-review inventory system subject to random demand and unreliable supply. The availability of supply is modeled as an alternating renewal process with general distributions for the durations of the UP and DOWN cycles. We consider the lost-sales case and also discuss the backorder case, for both the discounted and long-run average cost criteria. For the linear cost model, we derive the structural properties and bounds of the optimal policy. We also propose the “end-of-cycle” inventory return contract and show that it may be mutually beneficial to both the firm and the supplier.
We study the effect of random supply interruptions on the performance of a periodic-review inventory system with stochastic demand. Our objective is to develop optimal and near-optimal ordering policies and to understand the impact of supply interruptions on the performance of inventory/production systems.
For “just-in-time” producers, losses from unpredictable events such as machine breakdown, unscheduled maintenance, order cancellations, labor strikes, and fires can be severe. For the small firm, it is painful to undergo cyclic supply interruptions when the supplier chokes off its orders in a period of high demand. Pettit [12] reports that Exar, a NASDAQ-listed small firm, eliminated one of its production lines due to “supply interruptions.” The following are some excerpts from the Wall Street Journal on significant losses resulting from supply interruptions in recent years:
Shortages of injectable or intravenous antibiotics are forcing doctors to scramble to find substitute regimens, and the drug-supply interruptions could put hospital patients at risk, a new survey of infectious-disease experts warns. [1]
Output at the nation's factories, mines and utilities plunged more in June than in any month in the past five years as the General Motors Corp. strikes and the financial crisis in Asia took their toll on the industrial sector. Overall industrial production fell 0.6% in June after a revised 0.3% gain in May, the Federal Reserve reported. [4]
On February 1, 1997, a fire at Aishin Seiki, Co. Ltd., a Toyota subsidiary, incinerated the main source of a crucial brake valve that Toyota buys from Aishin and uses in most of its cars. Most Toyota domestic plants kept only a four-hour supply of this valve and without it, Toyota had to shut down its 20 auto plants in Japan, which build 14,000 cars a day. [13]
In this article, we consider a periodic-review inventory system with random demand and an unreliable supplier whose availability is modeled as an alternating renewal process. The alternating renewal process is said to be UP when supply is available and DOWN otherwise. The durations of the UP and DOWN cycles are generally distributed. The firm is fully informed of the availability of supply at the beginning of each period. At the beginning of an UP period, the firm can replenish inventory up to its target level. However, the firm cannot place any order in a DOWN cycle and must wait until the alternating renewal process returns to the UP state, which is the beginning of the next replenishment cycle. The procurement, holding, and shortage costs are all assumed linear with respect to the quantities. Demands in different periods are independent and identically distributed (i.i.d.) random variables. We consider the lost-sales case and generalize the results to the backorders case. It is worth mentioning that the stationary costs and i.i.d. demand assumptions are not necessary in our models; they can be dependent on the state of the supplier. We imposed them here mainly for notational and expositional simplicity.
The inventory production system with supply interruptions has received increasing attention from researchers in recent years. Parlar and Berkin [9], Parlar and Perry [10], and Moinzadeh and Aggarwal [7] considered continuous-review inventory systems with deterministic demand, where supply availability is modeled as an alternating renewal process, with exponentially distributed ON (available) and OFF (unavailable) cycles. Parlar, Wang, and Gerchak [11], Song and Zipkin [18], and Ozekici and Parlar [8] analyzed periodic-review inventory systems with backorders in a random supply environment modeled as a Markov chain. They showed that, among other things, an environment-dependent base-stock policy is optimal in the linear-cost model. However, unlike these models, here we examine a periodic-review system with stochastic demand and unreliable supply whose availability is observable and modeled as generally distributed UP and DOWN cycles. This setting could be more general than certain Markov environments for supply availability and can be advantageous from the modeling, analysis, and computational aspects. In addition, we focus on the lost-sales case, which has not been thoroughly examined in the literature.
Our model differs from the random yield models (Gerchak, Vickson, and Parlar [3]; Hening and Gerchak [5]), which assume that yields are i.i.d. random variables. The yields in our model are not i.i.d. across different periods, but equal to the target levels that depend on the failure rate of the UP cycle, as we assume that the firm is fully informed of the availability of supply at the beginning of each period.
Our results, which hold for both the lost-sales and backorder cases, can be summarized as follows:
[bull ] We formulate the problem as a dynamic program and show that the optimal ordering policy is a state-dependent base-stock policy whose base-stock level in an UP period depends on the remaining life of the UP cycle and the duration of the DOWN cycle. The optimal base-stock levels increase as the remaining life of the UP cycle becomes stochastically smaller or the life of the DOWN cycle becomes stochastically larger.
[bull ] To overcome the difficulty in computing the optimal base-stock levels for the infinite-cycle model, we define, for given age i in an UP cycle, a cost function for its order period that contains the expected total costs incurred between the current and next order periods. (Recall that we cannot place orders during a DOWN cycle.) We show that the optimal base-stock level for the order period at age i (hereafter referred to as the myopic base-stock level at age i) can be computed in closed form and constitutes an upper bound of the optimal base-stock level at age i. Our numerical examples show that the myopic bound is very tight.
[bull ] We show that the above-described myopic policy is, in fact, optimal when the UP cycle has a nondecreasing failure rate and the firm is protected under the “end-of-cycle” inventory return contract, which specifies that the firm can return to the supplier any unwanted inventory at the purchasing cost at the end of a DOWN cycle. We demonstrate that not only can the return contract assumption lighten the computational burden and shed light on the structure of the optimal policy, but also such a contract can, in fact, be mutually beneficial to both the firm and the supplier.
We gain the following insights from the analysis:
1. Supply interruptions have a significant impact on the inventory/production system. It is better to model such a supply uncertainty than to ignore it. The firm can recover significant cost savings by incorporating supply uncertainty into its inventory planning.
2. A firm facing supply interruptions is well advised to keep higher stock levels than otherwise, which is, of course, intuitive. The effectiveness of such a policy depends on the accurate estimation of the distributions of the UP and DOWN cycles, because it allows the “just-in-time” firm to raise the inventory level at the right time and to the right amount and, hence, balance its needs to keep thin inventory while preventing shortages during the DOWN cycle.
3. The “end-of-cycle” return contract can help the supplier in providing incentives to the buying firm to purchase more of the product in the slack season.
The rest of this article is organized as follows. Section 2 reviews the literature. Section 3 introduces the model and presents a dynamic programming formulation. Section 4 obtains the structural properties of the optimal ordering policy. Section 5 proposes the “end-of-cycle” inventory return contract and studies the myopic policy. Section 6 derives the bounding relationship between the myopic and optimal base-stock levels. Section 7 gives several numerical examples, and Section 8 concludes the article.
We summarize the important articles and discuss them here. Parlar and Berkin [9] developed an EOQ model with exponentially distributed ON and OFF durations based on the renewal reward theorem (see Ross [14, p.52]). Parlar and Perry [10] analyzed the reorder point, order quantity (r,Q) inventory system with deterministic demand, and two sources of supply with ON and OFF durations exponentially distributed. Moinzadeh and Aggarwal [7] studied an unreliable production/inventory system with exponential ON durations, constant OFF durations, fixed setup costs, and constant production and demand rates. They developed a procedure for finding the optimal (s, S) policy as well as a simple heuristic algorithm.
Random yield models are also related to our model. Yano and Lee [22] provided an excellent literature review of lot sizing with random yield. The majority of studies on random yield consider stochastically proportional yield models, which treat the defective rate as a random variable with a differentiable distribution. Gerchak et al. [3] analyzed a periodic-review inventory model with zero setup cost, uncertain demand, and i.i.d. random yield rates. They provided a complete analysis of the final period problem and explored the properties of the penultimate period problem, for which the solution is not myopic. Hening and Gerchak [5] generalized the earlier work of Gerchak et al. [3] and showed that there exists a critical reorder point for each period such that an order should be placed if the on-hand inventory at the beginning of the period is below a critical reorder point. However, the order quantity is a complicated function of the system parameters and the initial inventory levels. In other words, the “order-up-to” type of policy is no longer optimal. Ciarallo, Akella, and Morton [2] modeled the yield as a function of random production capacity and showed that for the single-period model, the optimal order-up-to quantity is independent of the distribution of capacity. They also showed that, for the multiple-period problem, the optimal ordering policy is a modified myopic base-stock policy.
Palar et al. [11] considered a backlogging, periodic-review inventory system with a finite planning horizon, with the UP and DOWN cycles geometrically distributed. A basic setup cost will be incurred whenever an order is placed, and a secondary setup cost will be assessed only when the order is filled. With this ordering structure, they showed that the optimal policy for multiperiod problems is an (s, S) policy. They also showed that for each period, S* is independent of the supply availability of previous periods, but that s* is increasing in the probability that the current order will be supplied. Song and Zipkin [18] developed a backorder model with an exogenous Markovian supply system, where the lead time may depend on the status of the supply system. With zero ordering and linear penalty and holding costs, Song and Zipkin showed that the optimal policy is a base-stock policy and provided the upper and lower bounds of the base-stock level. They also provided the sufficient condition under which the optimal base-stock level is monotonic. Ozekici and Parlar [8] considered a periodic-review backorder model with an unreliable supplier in a Markov environment. The demand–supply availability and cost parameters change with respect to the Markov environment. It is assumed that whereas the firm can observe the state of the environment, it cannot observe the availability of supply. Ozekici and Parlar showed that an environment-dependent base-stock policy is optimal when the order cost is linear in the order quantity.
We consider an infinite horizon, periodic-review inventory system with stochastic demand and a supplier subject to periodic breakdowns. We model supply uncertainty via an alternating renewal process (see Wolff [21, p.62]). The alternating renewal process is said to be UP if supply is available and DOWN otherwise. The durations of UP and DOWN cycles are denoted by independent and integer-valued random variables NU and ND, respectively. A replenishment cycle consists of an UP and a DOWN cycle, with total cycle length NU + ND. We assume that the firm is fully informed of the availability of supply at the beginning of each period. At the beginning of an UP period, the firm replenishes inventory up to its target level (i.e., the lead time is negligible). However, the firm cannot place an order in a DOWN period and must wait until the alternating renewal process returns to the UP state, which is the beginning of the next replenishment cycle.
We define the “age” of an UP cycle as the number of periods that the current UP cycle has continued since the last supply interruption. Let di be the conditional probability that the supply is interrupted at the (i + 1)st period, given that the current UP cycle is at age i. Then,

Thus, {di, i ≥ 1} is the failure rate function of NU (see Ross [16, p.193]). If di ≤ di+1, then the supply availability deteriorates at age i. On the other hand, if di > di+1, it means that the supply can improve its reliability level at age i (e.g., via age-dependent maintenance). When {di, i ≥ 1} is a nondecreasing sequence, we say that the UP cycle has a nondecreasing failure rate function. This notion captures the scenario that the “older” an UP cycle, the larger the likelihood of supply interruption in the following period. Many commonly used distributions, such as the geometric, the uniform, the Erlang, and the binomial, have nondecreasing failure rate functions. We generally do not require {di, i ≥ 1} to be monotone to derive structural properties of the optimal policy.
For expositional simplicity, we assume stationary demand distribution and cost functions, although most of our results still hold if they depend on the states of the UP and DOWN cycles. Denote the demand in period i by Di, i = 1,2,…, and let Di be i.i.d. random variables with cumulative and density functions F(x) and f (x), respectively. There is no economy of scale for replenishment. The purchase procurement cost is a linear function of the quantity ordered (i.e., the setup cost is zero), with a unit purchasing cost c. At the end of each period, a unit holding cost h is incurred for the remaining inventory and a unit penalty cost p is charged for unsatisfied demand. Demand is filled by existing inventory whenever possible, and unmet demand is lost.
Our objective is to determine an optimal ordering policy that minimizes the total discounted or long-run average cost over an infinite horizon, for both the lost-sales and backorder cases. We will mainly discuss the lost-sales case for the discounted-cost criterion. The long-run average cost results follow those of the discounted case after letting the discount factor λ → 1. In Section 6, we show that all of the results can be extended to the backorder case.
Let L(Q) be the expected total holding and penalty cost in an UP period, given that inventory is successfully replenished up to Q. Then,
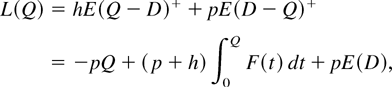
where (x)+ = max(0, x). Let 0 ≤ λ < 1 be the discount factor. If we purchase Q units at the beginning of a period and treat leftover inventory as an asset, then the expected total cost incurred in the single period is
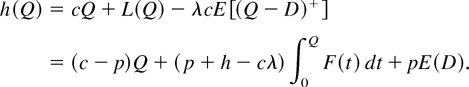
It is well known that h(Q) is convex. Taking the derivative of h(Q) and setting it to zero, we recover the celebrated newsvender solution:
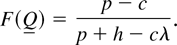
Here, Q is understood as the optimal base-stock level for the lost-sales case over the infinite planning horizon without supply interruptions (see Lee and Nahmias [6, p.26]).
For convenience, let

. The density and cumulative distribution functions of D(k) are denoted by f(k) and F(k), respectively. Let us first develop an expression for the expected discounted cost in a DOWN cycle. Given that the current period is UP (and the firm successfully replenishes the inventory up to Q) and that the next period is DOWN, the starting inventory of the DOWN cycle is (Q − D)+. If a DOWN cycle lasts at least k periods, then the on-hand inventory at the beginning of the kth period of a DOWN cycle is (Q − D(k))+. Thus, the expected total holding plus penalty costs in period k of a DOWN cycle is L((Q − D(k))+), where L is defined in (3.2). Summing up the holding and penalty costs over the DOWN cycle that starts with initial inventory (Q − D)+, we obtain
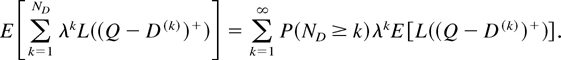
The above expression can be evaluated by conditioning on D(k) = d. If Q > d, then L(Q − d) is evaluated by (3.2). If Q ≤ d, then L(0) = pE(D).
We use (i, x) to describe the system state, where i is the age of the current UP cycle and x is the initial inventory of the current UP period. Let V(i, x) be the minimum expected total discounted cost over the infinite planning horizon starting with state (i, x). From (3.2) and (3.5), the discounted dynamic programming recursion gives us

We interpret (3.6) as follows. The first term is the procurement cost. The second term is the expected penalty and holding costs incurred in the current UP period. The third and fourth terms are the expected DOWN cycle cost and the expected cost from the next UP cycle onward, respectively, given that supply is interrupted in the next period. The fifth term is the cost from the next period onward, given that supply is available in the next period.
Because the term −cx in (3.6) is not affected by the decision variable Q, we let, following Veinott [20],
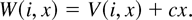
Here, W(i, x) is understood as the minimum expected total discounted cost starting with state (i,0), under the constraint that the inventory level after ordering must be at least x. This is a commonly used, convenient cost accounting scheme that allows us to receive the book value of leftover inventory, x units, at the end of each period, under the constraint that we must procure at least x units at the beginning of the next period. Then,

Using (3.7) and the above expressions, the optimality equation (3.6) becomes

where g(i,Q) is the extended single-period cost that contains the expected discounted cost incurred between the current and next orders, given that we are in state (i,0) and order Q units. Then, we can express g(i,Q) by

where h is the single-period cost as defined by (3.3), D(0) ≡ 0, and P(ND ≥ 0) = P(ND ≥ 1) = 1. Note that the number of periods between two consecutive orders is either one (with probability 1 − di) or ND + 1 (with probability di). In the above expression, we used the accounting scheme that allows the firm to return the leftover inventory at the end of each DOWN period but buying back the same quantity at the same cost at the beginning of the next period, provided that the next period is still DOWN.
In contrast to the conventional dynamic programming formulation for the periodic-review system in which the system transition occurs in each period, in our formulation each transition represents a random number of periods, which corresponds to the periods between two consecutive orders. In other words, we “skip” those DOWN periods during which the firm cannot replenish inventories and use the extended single period (the order period) cost to cover that incurred during a DOWN cycle. This formulation is possible due to the structure of the alternating renewal process and makes the value function more transparent and, as we will see, facilitates easy derivations of the structural properties and closed-form bounds.
To facilitate the analysis, it is useful to truncate W(i, x) to W(n)(i, x), where W(n)(i, x) is the minimum expected discounted cost starting in state (i, x) when there are n orders remaining. Recall that the number of periods between two consecutive orders is either one, if the next period is UP and we can immediately place another order, or ND + 1, if the next period is DOWN and we have to defer the next order until the supply becomes available again. No cost will be incurred after the end of the n orders. For n = 1, we have
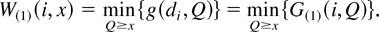
For n ≥ 2, we define, from (3.8), (3.9), and (3.5), that

It is not difficult to show that as n → ∞, G(n)(i,Q) and W(n)(i, x) indeed converge to G(i,Q) and W(i, x), respectively.
For the long-run average-cost criterion with λ = 1, the Bellman optimality equation (the fundamental principle of dynamic programming, stating that the optimal solution to an nth-stage dynamic process must proceed from an optimal solution of the (n − 1)th stage that begins with the optimal outcome of the first stage) becomes

where g is a constant and g(i,Q) is defined in (3.9) with λ = 1. We shall not specifically discuss the long-run average case, except noting that, via standard limiting arguments, our results for the discounted case remain valid for its long-run average counterpart.
Before characterizing the optimal ordering policy for our model, we first explore the properties of the cost function for a single-order period, g(di,Q).
Lemma 1:
1. g(di,Q) is a convex function of Q for any given 0 ≤ di ≤ 1.
2. Let Q and Q be the smallest values that minimize g(0,Q) and g(1,Q), respectively. Then, Q ≤ Q. In addition, g(di,Q) is a subadditive function in 0 ≤ di ≤ 1 and Q < Q ≤ Q.
3. ∂g(di,Q)/∂Q is decreasing in Q if P(ND ≥ k) becomes smaller for each k (i.e., if ND becomes stochastically smaller).
Proof:
1. The expression of g(di,Q) is given in (3.9). Recall that d2f (g(x))/dx2 = f′′(g(x))[g′(x)]2 + f′(g(x))g′′(x). If f is convex in x and g′′(x) = 0 (i.e., linear or piecewise linear), then f (g(x)) is convex in x. Therefore, E [h((Q − D(k))+)] is convex in Q, since h is convex in Q, and ∂2(Q − D)+/∂Q2 = 0. Finally, g(di,Q) is convex in Q, since the weighted sum of convex functions is convex.
2. For di = 0, g(0,Q) = h(Q). Therefore, Q satisfies (3.4). To prove Q ≤ Q, we show that ∂g(1,Q)/∂Q ≤ 0 for Q ≤ Q; then, the result follows from the convexity of g(1,Q). We have

since h is convex, and for Q ≤ Q, dE [h((Q − D(k))+)]/dQ ≤ 0. This implies that Q ≤ Q. Now, from (3.9) and (4.1), for any Q ≤ Q ≤ Q, we have

Due to the convexity of h and g, both terms are nonpositive in Q ≤ Q ≤ Q.
3. The partial derivative of g(di,Q) with respect to Q is

Clearly, ∂g(di,Q)/∂Q decreases as P(ND ≥ k) decreases for each k (i.e., ND becomes stochastically smaller). This also implies that Qi(1), the smallest minimizer of g(di,Q), decreases as ND becomes stochastically smaller. █
For n ≥ 1, define
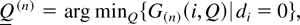
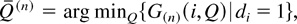
where Q(1) ≡ Q and Q(1) ≡ Q. Using Lemma 1, we now derive the properties associated with the value functions W(n)(i,Q) and G(n)(i,Q), n ≥ 1.
Theorem 1:
1. G(n)(i,Q) is convex in Q for n ≥ 1 and is subadditive in 0 ≤ di ≤ 1 and Q ≤ Q ≤ Q(n).
2. W(n)(i, x) is increasing and convex in x for n ≥ 1 and is subadditive in 0 ≤ di ≤ 1 and 0 ≤ Q ≤ Q(n).
3. For n ≥ 1,

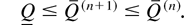
4. Both ∂G(n)(i,Q)/∂Q and ∂W(n)(i,Q)/∂Q decrease in Q if ND stochastically decreases.
Proof: We prove parts 1–4 by induction on n, the total number of order periods. For n = 1, part 1 holds true, since G(1)(i,Q) = g(di,Q), which is convex and subadditive by Lemma 1. To prove part 2 for n = 1, we use (3.10); W(1)(i, x) = minx≤Q{g(di,Q)}. Clearly, W(1)(i, x) is increasing in x. Its convexity and subadditivity follow directly from the same properties of g(di, x). Also, part 4 for n = 1 follows from Lemma 1, part 3. It remains to verify part 3 for n = 1. First, (4.5) holds trivially for n = 1. Also, the left inequality of (4.6) for n = 1 is shown in Lemma 1, part 2. To prove the right inequality of (4.6) for n = 1, we note, for Q ≥ Q(1) ≡ Q,

where the first inequality follows because W(1) is convex and thus has a nonnegative derivative; the second inequality holds because Q ≤ Q and g(1,Q) is minimized at Q. The convexity of g(1,Q) and W(1) then implies Q(2) ≤ Q(1) = Q.
Next, we prove parts 1–4 for n, based on the hypothesis that they are valid for less than n. Consider part 1 first, where G(n)(i, x) is given in (3.11). By Lemma 1, part 1, g(di,Q) is convex in Q. Since ∂(Q − D)+/∂Q ≥ 0 and ∂2(Q − D)+/∂Q2 = 0 and by our hypothesis, both E [W(n−1)(i + 1,(Q − D)+)] and E [W(n−1)(1, (Q − Dk+1)+)] are increasing and convex in Q. This implies that G(n)(i,Q) is a convex function of Q. To prove Gn(i,Q) is subadditive in 0 ≤ di ≤ 1 and Q ≤ Q ≤ Q(n), we have

To derive the inequality here, we used (4.2) and our hypotheses of parts 2 and 3 for n − 1, which state that W(n−1) is subadditive in 0 ≤ di ≤ 1 and Q ≤ Q ≤ Q(n) ≤ Q(n−1). Since both terms of (4.7) are nonpositive for Q ≤ Q ≤ Q(n), it implies that G(n)(i,Q) is subadditive in the specified region. This completes the proof of part 1 for n.
Let Qi(n) be the smallest value that minimizes G(n)(i,Q). From the subadditivity of G(n)(i,Q), we must have Q ≤ Qi(n) ≤ Q(n). Then,

Since G(n)(i,Q) is convex and subadditive, W(n)(i, x) is increasing and also inherits convexity and subadditivity of G(n)(i,Q). This validates part 2.
Next, we prove (4.5) by showing that Q(n) ≤ Q and Q(n) ≥ Q, based on the hypothesis Q(n−1) = Q. From the expression

we observe that (∂G(n)(i,Q)/∂Q)|di=0 is nonnegative for Q ≥ Q, since Q minimizes h(Q) and W(n−1) is increasing in Q. This states that Q(n) ≤ Q. On the other hand, for Q ≤ Q,

where the first inequality is due to part 2 for n − 1, which states that ∂E [W(n−1)(i + 1, (Q − D)+)]/∂Q is decreasing in di+1. The equality follows our hypothesis that for [Q − D]+ ≤ Q(n−1) = Q, the derivative of W(n−1) equals zero. Therefore, Q(n) ≥ Q. This, together with Q(n) ≤ Q, yields (4.5).
To verify the left inequality of (4.6) for n, we use the expression (∂G(n)(i,Q)/∂Q)|di=1 given in (4.6). Since Q(n−1) = Q, then for any Q ≤ Q,
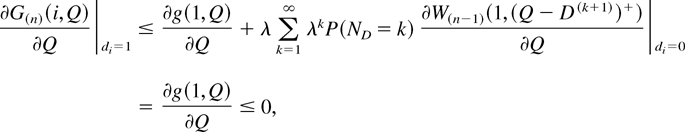
which implies that Q(n) ≥ Q. To prove the right inequality of (4.6) for n, we first realize that both ∂G(n) /∂Q and ∂W(n) /∂Q are increasing functions of n, which can be shown by induction on n. Then, (∂G(n+1)(i,Q))/∂Q|di=1 ≥ (∂G(n)(i,Q))/∂Q|di=1 ≥ 0, for Q ≥ Q(n). We then obtain Q(n+1) ≤ Q(n). This completes the proof of part 3.
Finally, suppose

. We use

to denote the counterpart of g, with the DOWN cycle length

. Let

be similarly defined. From (4.3) and our hypothesis of part 4 for n − 1, we obtain

where the first inequality follows from the hypothesis of part 4 for n − 1 and the second inequality holds because ∂W(n−1)2/∂Q is decreasing as ND is stochastically decreasing. The above expression also means that both ∂W(n) /∂Q and Qi(n) are decreasing if ND is stochastically decreasing. This completes the proof of Theorem 1. █
Theorem 1 allows us to derive the properties associated with the optimal ordering policy, as stated in Theorem 2.
Theorem 2:
1. The optimal ordering policy is an age-dependent base-stock policy; that is, there exist base-stock levels Qi*, i = 1,2,…, such that it is optimal to order up to Qi* units in state (i, x).
2. If {di, i ≥ 1} is nondecreasing in i, then {Qi*, i ≥ 1} is also nondecreasing in i.
3. For each i ≥ 1, Qi* decreases as ND stochastically decreases.
Proof:
1. We have shown in Theorem 1, part 1 that G(n)(i,Q) is convex in Q and is minimized at Qi(n). Letting n → ∞, G(n)(i,Q) converges to G(i,Q). Evidently, G(i,Q) is also a convex function of Q. Let Qi* be the smallest value minimizing G(i,Q). Then, Qi* is the optimal base-stock level in state (i, x), i = 1,2,….
2. Similarly, as in part 1, one can show that G(i,Q) is subadditive in 0 ≤ di ≤ 1 and Q ≤ Q ≤ Q*, where Q minimizes G(i,Q)|di=0 and Q* minimizes G(i,Q)|di=1. Therefore, if di+1 ≥ di,

which means that Qi* ≤ Qi+1*.
3. This is the limiting result of Theorem 1, part 4. █
Observe that Q, defined in (3.4), provides a global lower bound for Qi*, i ≥ 1, and this lower bound is attainable when di = 0. This implies that whereas the firm should keep a higher safety stock level to safeguard itself from random supply breakdowns, it only needs to do so when di is strictly positive. For example, suppose ND has a failure rate function {di, i = 1,2,3,4} = {0,0,0.5,0.5}. Then, in the first two periods, the firm only needs to order up to Q. In other words, the firm does not need to prematurely increase the safety stock levels in the first two periods. It also underscores the importance of an accurate estimate of the failure rate function, because it allows the firm to increase the base-stock level at the right time and to the right level.
Theorem 2 indicates that the optimal ordering policy is a base-stock policy. However, computing the optimal base-stock levels {Qi*, i ≥ 1} is not an easy task (unless di = 0). Therefore, it is desirable to obtain an effective approximation of Qi*, i ≥ 1. In this section, we obtain an explicit expression for the myopic base-stock level, Qi(1), where Qi(1) minimizes the extended single-period cost g(di,Q), i ≥ 1. In the next section, we show that Qi(1) in fact constitutes an upper bound for Qi*, i ≥ 1. From Lemma 1, we see that {Qi(1), i ≥ 1} possesses the structural properties of {Qi*, i ≥ 1}. For example, Qi(1) increases if di increases or ND becomes stochastically larger. Here, we show that if the UP cycle has a nondecreasing failure rate function (i.e., if {di, i ≥ 1} is nondecreasing), then {Qi(1), i ≥ 1} is optimal for the infinite-cycle problem, but under the condition that the firm can return excess inventory at the original purchasing cost at the end of a cycle. We term such a condition “the end-of-cycle inventory return contract” or, simply, “the return contract.” Clearly, with the return contract, the infinite-cycle problem is decomposed into a sequence of identical single-cycle problems. The following lemma derives the closed-form solution for Qi(1), i ≥ 1.
Lemma 2: Let
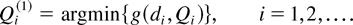
Then, Qi(1), i = 1,2,…, can be explicitly computed as
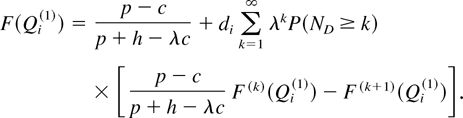
Proof: In Lemma 1, part 1, we have shown that g(di,Q) is a convex function of Q. The first derivative of g(di,Q) with respect to Q satisfies

Applying the Leibniz rule and using the result dh(Q)/dQ = (c − p) + (p + h − λc)F(Q), we obtain

Then, (5.1) and (5.2) follow by setting (5.4) to zero and reorganizing terms. █
Next, we show that the myopic base-stock levels {Qi(1), i ≥ 1}, as given in Lemma 2, are optimal if {di, i ≥ 1} is nondecreasing and the return contract is effective.
Theorem 3: If {di, i ≥ 1} is a nondecreasing sequence, then the optimal policy for the single-cycle model with the return contract is specified by {Qi(1), i ≥ 1}.
Proof: Let Ws(i, x) be the expected cost from period i until the end of the cycle, which can be obtained from (3.8) as
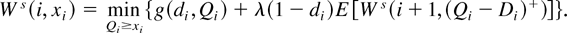
Let Qj represent the base-stock level chosen by the firm in state (j, xj), j ≥ i. Clearly, Qj must satisfy the following constraint:
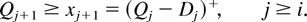
Using the recursive expression given by (5.5), subject to (5.6), we can write (5.5) in the form

where Qj, j ≥ i, are decision variables and subject to constraint (5.6). It is easy to verify that

Hence, (5.7) becomes

subject to constraints

If the sequence {di, i ≥ 1} is nondecreasing, then by Lemma 1, part 2, {Qi(1), i ≥ 1} is a nondecreasing sequence. Thus, {Qi(1), i ≥ 1} satisfy constraints (5.9); here, we assume, without loss of generality that the xi ≤ Qi(1). This implies that the myopic policy {Qi(1), i ≥ 1} is optimal.
The following corollary considers a special case in which the UP cycle has a constant failure rate.
Corollary 1: If the duration of the UP cycle is geometrically distributed with rate d1, the optimal policy for the system with the return contract is identical to that of the system without the contract, which is a stationary myopic base-stock policy whose base-stock level, Q1, can be explicitly computed by (5.2).
Our results in the previous section show that the myopic base-stock level possesses a closed-form solution. In the following theorem, we establish the bounds for the optimal base-stock levels. We show that {Qi(n), n ≥ 1} forms a sequence of upper bounds for Qi*, with Qi(1) as the largest in the sequence.
Theorem 4:
1. (Upper bound) Qi* ≤ Qi(n+1) ≤ Qi(n), n ≥ 1. In particular, Qi* ≤ Qi(1), n ≥ 1.
2. (Lower bound) Let Qi0(1) = min{Qi(1), i ≥ 1}. Then, Qi0(1) ≤ Qi0*. This result, together with part 1, implies Qi0(1) = Qi0*.
Proof:
1. It is intuitively true, and indeed can be proven easily by induction on n, that ∂G(n)(i,Q)/∂Q is increasing in n. As ∂G(n)(i,Q)/∂Q → ∂G(i,Q)/∂Q when n → ∞, it implies that Qi* ≤ Qi(n+1) ≤ Q(n), n ≥ 1.
2. Let Qi0* = min{Qi*, i = 1,2,…} be the smallest optimal base-stock level. We will prove by contradiction that Qi0* < Qi0(1) cannot be true. Suppose Qi0* < Qi0(1), which hypothesizes that the smallest optimal base-stock level is smaller than the myopic base-stock level. Then,

since, from the definition of Qi0*, it holds that (Qi0* − D)+ ≤ Qi0+1* and (Qi0* − D(k+1))+ ≤ Q1* for all k.
Since Qi0* < Qi0(1) and g(di,Q) is convex in Q, the right-hand side of (6.1) must be negative. However, the left-hand side of (6.1) equals zero, since Qi0* minimizes G(i0,Q). This contradiction implies Qi0* ≥ Qi0(1). █
In summary of Theorems 1 and 4, we have the following bounding relations:

In particular, if {di, i ≥ 1} is increasing, then i0 = 1 and we have
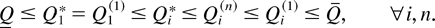
Due to its explicit expression, Qi(1) is an attractive, first-order upper bound of Qi*. However, by Theorem 4, one can tighten the bound by obtaining the nth-order upper bound Qi(n) of Qi*, at the expense of more intensive computations. Because each iteration represents an order period, we expect that this computational procedure is more effective than the conventional successive approximation algorithm in which each iteration represents a single period.
Theorems 3 and 4 also indicate that when {di, i ≥ 1} is increasing, then to ensure the optimality of the myopic policy, the end-of-cycle inventory return contract should be constructed with the critical number Q1* = Q1(1) such that the firm can return the inventory exceeding this value at the end of a DOWN cycle. Notice that the contract is easy to construct, since we have the closed-form solution for the critical value Q1*. It is evident that the minimum expected discounted cost with the contract is less than that without the contract. On the other hand, because the firm's base-stock levels under the myopic policy are higher, the supplier can benefit from selling more products to the firm during the UP cycle so as to offset any loss for providing the end-of-cycle return protection. In our numerical example, when (p − c)/h = 9, under the contract with critical value 7, the firm will purchase 0.91 more units (net of return) per cycle, which is a 5% increase in the total expected purchase cost per cycle. For the pricing issue related to the return contract, readers can refer to the literature about supply chain contracts (Tsay, Nahmias, and Agrawal [19] and the references therein), and we will not pursue the details here.
All of the results stated in Sections 3–6 remain true for the backorder case, with the myopic base-stock level Qi(1) given by
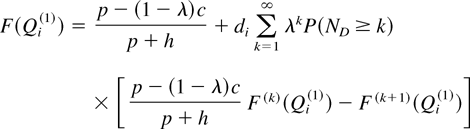
and the global lower bound of Qi(1) for the backorder case given by

Here, Q is the optimal base-stock level for the backorder case over an infinite planning horizon without supply interruptions (see Silver, Pyke, and Peterson [17, p.385]).
We provide numerical examples to illustrate the structures of the optimal and the myopic policies and to quantify the savings the firm can gain by taking supply uncertainty into consideration. The parameters for the numerical examples are the following:
1. Cost ratio: (p − c)/h takes on the values of 3, 9, and 19 and λ = 0.9.
2. Demand: The demand follows a negative binomial distribution with parameter n = 9 and p = 0.5,

; which has a shape similar to the Normal distribution. The mean demand is E(D) = 9 and the variance is Var(D) = 2.25.
3. UP cycle: The distribution and failure rate function of the UP cycle are given as

4. DOWN cycle: We assume that P(ND = 1) = P(ND = 2) = 0.5.
We compute the myopic base-stock levels Qi(1) by (5.2) and apply the value iteration scheme as shown in (3.10) and (3.11) combined with the policy iteration algorithm (Ross [15]) to compute Qi* with the candidate base-stock levels satisfying (6.3). The results are summarized in Table 1. As seen in Table 1, both the myopic and optimal base-stock levels increase as the failure rates increase. For the first UP period, both policies have the same base-stock level, as expected. In this case, since d1 = d2 = 0, Q1* = Q2* = Q.
Comparison of Myopic and Optimal Policies

Next, we compare the optimal and myopic policies with the optimal stationary policy that does not take supply interruptions into consideration. Table 2 summarizes the results. Note that the purchasing cost is set to zero, since a high purchasing cost conceals the savings in implementing the nonstationary policy. As reported in Table 2, the cost reduction could be significant. Also, the performance of the myopic policy is near-optimum.
Percentage Savings by Considering Supply Interruptions

As shown in Table 1, the gap between the myopic and optimal base-stock levels is small. The myopic levels can be easily computed using a commercial software such as EXCEL or MATLAB. Thus, practitioners could consider just using (5.2) or (6.4) as an approximate solution. Also, as we mentioned earlier, the myopic bound can be improved upon by carrying out several iterations of G(n)(i,Q), n ≥ 1.
We investigated the effects of supply interruptions in a periodic review inventory system. We demonstrated that the optimal ordering policy in an UP period is a failure-rate-dependent base-stock policy. The optimal base-stock levels are nondecreasing if the UP cycle has a nondecreasing failure rate. We showed that the myopic base-stock levels can be explicitly and separately solved and can serve as upper bounds for the optimal base-stock policy. We also showed that if the duration of an UP cycle is geometrically distributed, then the optimal and myopic policies coincide, where the optimal base stock level is a constant and can be explicitly computed. If the UP cycle is generally distributed with an increasing failure rate, the myopic policy is near-optimal. In addition, we discussed the benefits of the “end-of-cycle” inventory return contract for the firm and its supplier. Our results contribute to the literature on the periodic-review system with unreliable supplies in which the unmet demand is backlogged.

Comparison of Myopic and Optimal Policies

Percentage Savings by Considering Supply Interruptions