Published online by Cambridge University Press: 01 January 2005
In this article, we study comparison theorems for stochastic
functionals like V(∞;C) =
sup0≤t {M(t) −
C(t)} or V(T;C) =
sup0≤t≤T {M(t)
− C(t)}, where {M(t)} and
{C(t)} are two independent nondecreasing processes
with stationary increments. We will tacitly assume that the considered
stochastic functionals are proper random variables. We prove that
V(T;C′) ≤icxV(T;C) ≤icxV(T;C′′), where
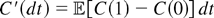 and C′′(dt) = c(0) dt,
provided dC(t) is absolute continuous with density
c(t). Similarly, we show that
V(∞;C′) ≤icxV(∞;C) ≤icxV(∞;C′′). For proofs, we develop
the theory of the ≤idcv ordering defined by increasing
directionally concave functions. We apply the theory to
M/G/1 priority queues and
M/G/1 queues with positive and negative
customers.
and C′′(dt) = c(0) dt,
provided dC(t) is absolute continuous with density
c(t). Similarly, we show that
V(∞;C′) ≤icxV(∞;C) ≤icxV(∞;C′′). For proofs, we develop
the theory of the ≤idcv ordering defined by increasing
directionally concave functions. We apply the theory to
M/G/1 priority queues and
M/G/1 queues with positive and negative
customers.
In this note, we study comparison theorems for stochastic functionals like V(∞;C) = sup0≤t {M(t) − C(t)} or V(T;C) = sup0≤t≤T {M(t) − C(t)}, where {M(t)} and {C(t)} are two independent nondecreasing processes with stationary increments. We will tacitly assume that the considered stochastic functionals are proper random variables. Typically, M(t) is a cumulative service time up to t. For example, in [1,4,6,7,8,9,10,11,13],

, where {N(t)} is a counting Cox process and {Sj} is a sequence of independent random variables, independent of the process {N(t)}, C(t) = t, and the comparisons are made with respect to different Cox processes. The seminal problem was a question by Ross [13] about the optimality of the constant arrival rate in the class of arrival rates with the same asymptotic rate, which was solved in [10]. The worst case among all of the stationary arrival rates with the same asymptotic intensity was detected in [12]. In this article the use of the so-called increasing directionally convex (idcx) functions was proposed to derive the result. In his article, Ross [13] posed a problem on the monotonicity of

with respect to a class {Ma} parameterized by a. This problem has been considered in many articles, and the direct question of Ross for two-state background continuous time Markov chains (CTMCs) was solved in [4]. The case of more states of the background CTMC was addressed in [1]. Recently, quite a general result in terms of a concept based on ≤idcx-ordering was given in [8]. Bonald, Borst, and Proutière [2] addressed how to find insensitive bounds in some wireless data network by the use of ≤idcx-ordering.
The study of ≤idcv-ordering was motivated by two problems from the theory of queues, posed to the author by Borst and Boxma. For these problems, we keep {M(t)} fixed and study comparison theorems with respect to {C(t)}. Whereas in the former studies the orderings ≤sm and ≤idcx were of importance, here we use the dual ordering ≤idcv to the ordering ≤idcx defined by the class of increasing directionally concave functions. These are multivariate extensions of icx and icv orderings of univariate random variables. We also define the notion ≤idcv-regularity, a dual one to ≤idcx-regularity studied in [8]. We apply the theory to M/G/1 with varying instantaneous service speed—in particular, priority queues and M/G/1 queues with positive and negative customers.
We give definitions of needed integral orderings and classes of functions defining these orderings. It is standard to denote by cx and cv respectively the class of convex and concave functions

. For multivariable functions, we have the following fundamental notion.
Definition 2.1: A function

is said to be supermodular (sm) if for any x and

,

where the operators ∧ and ∨ denote respectively coordinatewise minimum and maximum.
A suitable extensions of cx and cv classes for the multivariate case are as follows.
Definition 2.2: A function

is said to be directionally convex (dcx) (directionally concave or [dcv]) if for any

such that for x1 ≤ x2 and y ≥ 0,

We write “i” before “sm,” “dcx,” or “dcv” for restrictions to increasing functions. Note also that the directional convexity is not the same as ordinary convexity. Important properties of dcx and dcv functions are as follows. If f is dcx (dcv) and twice differentiable, then ∂2f (x)/∂xi ∂xj ≥ (≤) 0 for all i and j. Note that for sm, we have only ∂2f (x)/∂xi ∂xj ≥ (≤) 0 for all i ≠ j. More on sm and dcx functions can be found in Müller and Stoyan [9]. Functions dcv and idcv appeared in the doctoral thesis of Meester [6]. It was pointed out there that the composition

of an icv function f with idcv function d on

is also an idcv function of y [6, Lemma2.2.6]. Note that f (x) is idcx if and only if −f (−x) is idcv. We will use the fact that idcx functions form a cone (see, e.g., [9]).
To each class of the above-considered functions we relate the stochastic ordering, which in the terminology of Müller and Stoyan [9] are integral orderings. Let

be a class of functions like cx, icx, cv, icv, sm, ism, dcx, idcx, dcv, and idcv. We say that two random vectors (in the case of cx, icx, cv, and icv random variables) X and Y are

-ordered if E[f (X)] ≤ E[f (Y)] for any function

, such that the expectations are finite. In this way, we define orderings ≤icx, ≤ism, ≤idcx, ≤icv, and ≤idcv used in this note. For ordering of stochastic processes, we have the following definition.
Definition 2.3:
1. For two

-valued stochastic processes

, we say that

is smaller than

in the

-ordering and write

, if for any positive integer k and any

.
2. Let

be two increasing stochastic processes defining random measures dC(t) and dC′(t), respectively. It is said that

, or

, if for any k and 0 ≤ s1 ≤ t1 ≤ s2 ≤ t2 ≤…≤ sk ≤ tk,

where we denote C(a,b] = C(b) − C(a).
3. We say that a stationary stochastic process {Yt}t∈T, where

is ≤idcv-regular (≤idcx-regular) if for each k and all idcv functions

, function φ, defined by

is increasing (decreasing) in t1,t2,…,tk ∈ T.
We first recall that from the Lorenz inequality (see, e.g., [9]), we have the following lemma.
Lemma 2.4: If Z0 =st Z1 =st···=st Zn, then (Z0,…,Zk) ≤sm (Z0,…,Z0).
The notion of ≤idcx-regularity, also called monotonicity in lag, was studied in Miyoshi and Rolski [8]. For later use, we need the following quite obvious lemma.
Lemma 2.5: If a stationary process ξ(t) is ≤idcv-regular, then for a monotone function f, the process f (ξ(t)) is ≤idcv-regular.
Let M(t) and {C(t)} be two increasing processes with stationary increments such that M(0) = 0 and C(0) = 0 and let

. Our aim is to study bounds and comparison theorems for

or

We have the following representations for V:

where Ii,k = ((k − 1)/2i, k/2i] for k = 1,…,i2i and

conventionally. We have

where Ii,kT = ((k − 1)(T/2i),k(T/2i)] for k = 1,…,2i, and X, M, and C are independent.
Let

be icx, which is also assumed to be continuous on the whole

. Similarly to Lemma 1 of [12], we have from the monotone convergence theorem and the continuity of f,


where gk(x) = max{0,x1,…,x1 + ··· + xk} for

. Similarly, we can represent f (VT) by the use of functions x → max{0,y + x1 +···+ xk,x2 +···+ xk,…,x1}. The above functions are idcx.
As in Lemma 2 of [12], gk(x) is idcx (and, moreover, it is a convex function too). Furthermore,

is an idcv function of y. This can be justified as follows. The composition

of an icx function f with an idcx function gk on

is also an idcx function of

[6, Lemma2.2.6]. Therefore,

is idcv. Hence, we have the following lemma.
Lemma 3.1: Let f be icx. Then

is idcv and, hence, −ψk(y1,…,yk) is a decreasing sm function.
Further, to a given process {C(t)}, we now associate two increasing processes {C′(t)} and {C′′(t)} defined as follows:
For further reference, we state the following lemma without proof.
Lemma 3.2: If φ is sm of k variables, then the function

of l1 ×···× lk variables

is sm, provided all cij are positive numbers.
Lemma 3.3: We have for an sm function φ,

where I1,…,Ik are finite intervals. Hence, for an idcv function φ,

Proof: For the proof we have to use the following facts: ≤sm-order is generated by continuous nonnegative sm functions [9, Thm.3.9.13]; hence, for a continuous sm function φ, we have the convergence in distribution of

By Lemma 3.2, φ([sum ]j: j/n∈I1 c(j/n)/n,…,[sum ]j: j/n∈Ik c(j/n)/n) can be considered an sm function of variables c(j/n). From the Lorentz inequality

Hence,

Hence, we can say that −f (V(∞;C)) and −f (V(T;C)) are idcv representable; that is, their expectations are limits of functions, as in Lemma 3.3.
In the next proposition, we consider three stochastic functionals: V(T;C) as defined in (3.1),

and

Similarly, we define V(T;C), V(T;C′), and V(T;C′′).
In point (iv) of Proposition 3.4, we assume that C(dt) = c(t) dt admits an intensity process c(t) and consider a family of random variables V(T;Ca) defined by random measures Ca(dt) = ca(t) dt, where a > 0, admitting an intensity process ca(t) respectively defined by ca(t) = c(at), where {c(t)} is the intensity process of some random measure C. Similarly to [9], we can prove the following a monotonicity of V(T;Ca) with respect to a > 0. In Proposition 3.4, T is finite or infinite and it is tacitly assumed that all stochastic functionals V are proper random variables.
Proposition 3.4:
(i)

(ii) If C is absolute continuous with intensity c(t), then

(iii) If C1 ≤idcv C2, then V(T;C1) ≥icx V(T;C2).
(iv) Suppose that Ca(dt) = ca(t) dt (a > 0) is a family of random measures. If {c(t)} is ≤idcv-regular, then V(T;Ca) is ≤icx-decreasing for a > 0.
Proof:
(i) Assume T infinite. Use (3.6) and the conditional Jensen inequality to obtain

(ii) Use Lemma 3.3 and (3.6).
(iii) In view of (3.6) and Lemma 3.1,

where ψk was defined in (3.7). Since C1 ≤idcv C2, we have

which yields

(iv) In view of (3.6) and Lemma 3.1, it suffices to demonstrate that for an idcv function

is decreasing in a > 0. Without loss of generality, we can assume that intervals I are of forms Ik = [ai,bi), where a1 = 0 and bi = ai+1. Then, for each n = 1,2,…, we define the function

where J = l1 ×···× lk and li is the number j such that j/n ∈ Ii. Now, note that

Hence,

is increasing in a > 0 because c(t) is assumed to be idcv-regular and

is idcv. █
In this section, we show two applications of the theory to single-server queues with Poisson arrivals.
Let {N(t)} be the Poisson process with rate λ > 0, {Si} a sequence of nonnegative independent and identically distributed (i.i.d.) random variables (r.v.'s). We denote by

the cumulative service requirement arriving within interval (s,t] .
Suppose now that the service rate is given by a process c*(t), where 0 ≤ c*(t) ≤ 1 for all t. We assume that c*(t) is stationary (and ergodic) and that {N(t)}, {Si}, and {c*(t)} are independent.
Let V(t) = V(t;C*) be a stochastic process defined by

The solution of (4.1) is

The process {V(t)} represents the workload at time t in the work-conserving single-server queues with varying instantaneous service speed. Since we wish to study the stationary workload, without loss of generality we can assume V(0−) = 0. Otherwise, we have to assume that V(−0) is independent of (M,C). Then

and, hence, the stationary workload

where c(t) = c*(−t). The above is well defined for

. Note that V(∞;C′) is the workload in the standard M/G/1 system, with arrival rate λ/γ and service time distribution B. Under the condition that C(dt) = c(t) dt admits stationary intensity and

a.s., we consider

Note that the above is the workload in the M/G/1 system, with arrival rate λ/c(0) and service time distribution B, of course provided

a.s. Unfortunately, in many cases, the latter assumption is a difficult requirement.
Proposition 4.1: If T is finite or infinite and

, then

and if T is finite or infinite and

a.s., then

Furthermore,

and under the assumption that

a.s.,

Proof: The first part follows directly from Proposition 3.4. For the second part, we use that in the standard M/G/1 queue with arrival rate λ and generic service time S, the mean workload is

. █
Consider now a preemptive resume priority M/G/1 system with two types of customers: low and high priority. Customers of the low (high) priority arrive at the system according to the Poisson process with rate λl (λh) and with i.i.d. service times with distribution Bl (Bh). Then, the workload process for low-priority customers is the workload process in the M/G/1 system with instantaneous service speed

Thus, c*(t) is an on–off process with on and off times being distributed as in the busy and idle periods, respectively, in the M/G/1 system with arrival rate λh and service time distribution Bh. Now, γ is the stationary probability of no high-priority customers. Let Vl be the steady-state workload for the low-priority customers.
Corollary 4.2:

Proof: Use Eq. (4.3) and Proposition 3.4. █
We can also ask for the monotonicity of V(T;Ca) with respect to a > 0. In this case, we must know the answer for the following question.
Question: Is the stationary workload process V(t) in the M/G/1 system ≤idcx-regular or ≤idcv-regular? From this, we would have that

has the same property.
Two types of customer are arriving at the system: according to a Poisson process with rate λ+ i.i.d. customers with service times {Si+} (so-called positive ones), and according to a Poisson process with rate λ− i.i.d. customers with service times {Si−} (so-called negative). The system works as follows. As earlier, we assume a work-conserving discipline. Negative customers require no service, but at their arrival, a stochastic work is instantly removed from the system. Such systems were introduced by Gelenbe [5] and subsequently studied by Boucherie, Boxma, and Sigman [3], among others. In this later system, it was demonstrated the stationary workload is

where

Proposition 4.3:

Proof: From Proposition 3.4. █
To use Proposition 3.4(iii), we have to derive a criterion for an idcv comparison of stochastic processes like (4.4).
Proposition 4.4: If Sj−′ ≤icv Sj−′′ and λ−′ ≤ λ−′′, then dC′ ≤idcv dC′′. Hence, V(C′) ≥icx V(C′′).
Proof: The first part is analogous to the proof of Lemma 4 from Rolski [12]. █
This work was partially supported by KBN grant 2 P03A 020 23 (2002–2004).
I am grateful to Sem Borst, whose question on priority M/G/1 queues prompted this work. Thanks are also due to Ono Boxma, who raised the questions of orderings with respect to negative customers.