Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-05T09:00:24.447Z Has data issue: false hasContentIssue false
  • English
  • Français

NONNEGATIVITY OF COVARIANCES BETWEEN FUNCTIONS OF ORDERED RANDOM VARIABLES

Published online by Cambridge University Press:  22 October 2007

Taizhong Hu ,
Junchao Yao  and
Qingshu Lu
Taizhong Hu
Affiliation:
Department of Statistics and FinanceUniversity of Science and Technology of ChinaHefei, Anhui 230026People's Republic of China E-mail: thu@ustc.edu.cn
Junchao Yao
Affiliation:
Department of Statistics and FinanceUniversity of Science and Technology of ChinaHefei, Anhui 230026People's Republic of China E-mail: thu@ustc.edu.cn
Qingshu Lu
Affiliation:
Department of Statistics and FinanceUniversity of Science and Technology of ChinaHefei, Anhui 230026People's Republic of China E-mail: thu@ustc.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

In this article we investigate conditions by a unified method under which the covariances of functions of two adjacent ordered random variables are nonnegative. The main structural results are applied to several kinds of ordered random variable, such as delayed record values, continuous and discrete ℓ∞⩽-spherical order statistics, epoch times of mixed Poisson processes, generalized order statistics, discrete weak record values, and epoch times of modified geometric processes. These applications extend the main results for ordinary order statistics in Qi [28] and for usual record values in Nagaraja and Nevzorov [25].

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 21 , Issue 4 , October 2007 , pp. 557 - 577
Copyright
Copyright © Cambridge University Press 2007

1. INTRODUCTION

Let X 1, X 2, … , X n be independent and identically distributed (i.i.d.) random variables with a common distribution function F, and let X 1:n ≤ X 2:n ≤ ⋯≤ X n:n be the corresponding order statistics. Qi [Reference Qi28] proved that

(1.1)
$$\hbox{Cov} \lpar \phi \,\lpar X_{i:n}\rpar ,\phi \,\lpar X_{i + 1:n}\rpar \rpar \ge 0, \qquad i = 1,\ldots, n - 1,$$

for all measurable real-valued functions φ such the covariance exists. The result for the case n = 2 is due to Ma [Reference Ma23, Reference Ma24]. Qi [Reference Qi28] and Li [Reference Li22] gave counterexamples to illustrate that (1.1) does not hold for nonadjacent order statistics; that is, for any n > 2 and each pair (i, j), 1 ≤ i, j ≤ n and |i − j| > 1, there exists a function φ such that Cov(φ (X i:n), φ (X j:n)) < 0.

Nagaraja and Nevzorov [Reference Nagaraja and Nevzorov25] established the analogous result of (1.1) for usual record values (the exact definition can be found in the sequel). More precisely, let {X L(n), n ∈ ℕ+} denote the record values of a sequence {X n, n ∈ ℕ+} of i.i.d. random variables with a common distribution function F; here and henceforth ℕ+ = {1, 2, …} and ℕ = {0, 1, 2, …}; They proved that if F is continuous, then

(1.2)
$$\hbox{Cov} \lpar \phi\, \lpar X_{L\lpar n\rpar }\rpar , \phi\,\lpar X_{L\lpar n + 1\rpar }\rpar \rpar \ge 0,\qquad n \in {\open {N}}_+,$$

for all measurable real-valued functions φ such that the covariance exists. Counterexamples were also given in Nagaraja and Nevzorov [Reference Nagaraja and Nevzorov25] to show that (1.2) does not hold when F is discrete and that, for any i, j ∈ ℕ+, |i − j| ≥ 2 and a continuous distribution function F, there exists a function φ such that Cov(φ (X L(i)), φ (X L(j))) < 0.

The purpose of this article is to investigate conditions by a unified method under which the covariances between functions of two adjacent ordered random variables are nonnegative. In Section 2 we give some structural theorems concerning general ordered random variables T 1 ≤ T 2 ≤ ⋯ ≤ T n. These structural results are then applied to continuous and discrete ordered random variables in Sections 3 and 4, respectively. In Section 3 we consider delayed record values, continuous ℓ∞⩽-spherical order statistics, epoch times of mixed Poisson processes, and generalized order statistics. In Section 4 we consider discrete weak record values, discrete ℓ∞⩽-spherical order statistics, and epoch times of modified geometric processes. These applications extend (1.1) and (1.2) to the more general ordered random variables. Some counterexamples are presented in Section 5.

Throughout, “increasing” and “decreasing” mean “nondecreasing” and “nonincreasing”, respectively. When an expectation or a probability is conditioned on an event such as X = x, we assume that x is in the support of X. Also, we denote by [X|A] any random vector (variable) whose distribution is the conditional distribution of X given event A.

2. MAIN RESULTS

Motivated by the idea used in the proof of Theorem 3.1 in Qi [Reference Qi28], we have the following two structural theorems, which give sufficient conditions to ensure nonnegativity of covariances between functions of two ordered random variables.

Theorem 2.1

Let T 1 ≤ T 2 ≤ T 3 ≤ T 4be four random variables such that, for any s ≤ t,

(2.1)
$$ [\lpar T_2, T_3\rpar \vert T_1 = s, T_4 = t] \mathop{=}\limits^{d} \lpar V_{1:2}\lpar s,t\rpar , V_{2:2}\lpar s,t\rpar \rpar ,$$

where $\mathop{=}\limits^{d}$means equality in distribution and V 1:2 (s, t) ≤ V 2:2(s, t) are the order statistics of i.i.d. random variables V 1(s, t) and V 2(s, t). Then

(2.2)
$$\hbox{Cov} \lpar \phi\, \lpar T_2\rpar , \phi \lpar T_3\rpar \rpar \ge 0$$

for all measurable functions φ : ℝ → ℝ such that the covariance exists.

Proof

We use an idea from the proof of Theorem 3.1 in Qi [Reference Qi28]. First, assume that the family {V i(s, t) : i = 1, 2, ∀, s ≤ t} is independent of {T 1, T 4}. For simplicity of notation, let W i = V i(T 1, T 4) and W i:2 = V i:2 (T 1, T 4) for i = 1, 2; that is, W 1:2 and W 2:2 are the order statistics of W 1 and W 2. By conditioning on T 1 and T 4, it follows from (2.1) that

(2.3)
$$\eqalignno{{\ssf E} [\phi\,\lpar T_2\rpar \phi\,\lpar T_3\rpar ] &= {\ssf E} \{{\ssf E} [\phi\,\lpar T_2\rpar\,\phi\,\lpar T_3\rpar \vert T_1, T_4] \} \cr &= {\ssf E} \{{\ssf E} [\phi\,\lpar W_{1:2}\rpar\,\phi\,\lpar W_{2:2}\rpar \vert T_1, T_4] \} \cr &= {\ssf E} \{{\ssf E} [\phi\,\lpar W_1\rpar\,\phi\,\lpar W_2\rpar \vert T_1, T_4] \} \cr &= {\ssf E} \{{\ssf E} [\phi\,\lpar W_1\rpar \vert T_1, T_4] \}^{2}, &}$$

where the last equality follows from the fact that, given (T 1, T 4), W 1 and W 2 are conditionally i.i.d. Similarly,

(2.4)
$${\ssf E} [\phi\, \lpar T_2\rpar ] = {\ssf E}\{ {\ssf E} [\phi\,\lpar T_2\rpar \vert T_1, T_4] \} = {\ssf E} \{ {\ssf E} [\phi\,\lpar W_{1:2}\rpar \vert T_1, T_4] \} = {\ssf E} [\phi\,\lpar W_{1:2}\rpar ] $$

and

(2.5)
$${\ssf E} [\phi\, \lpar T_3\rpar ] = {\ssf E} [\phi\,\lpar W_{2:2}\rpar ]. $$

It is obvious that

$${\ssf E} [\phi\, \lpar W_{1:2}\rpar ] + {\ssf E} [\phi\, \lpar W_{2:2}\rpar ] = 2 {\ssf E} [\phi\, \lpar W_1\rpar ].$$

Therefore, from (2.3)–(2.5), we get that

$$\eqalign{\hbox{Cov} \lpar \phi\, \lpar T_2\rpar , \phi\, \lpar T_3\rpar \rpar &= {\ssf E} \{{\ssf E} [\phi\,\lpar W_1\rpar \vert T_1, T_4] \}^2 - {\ssf E} [\phi\,\lpar W_{1:2}\rpar ]\,{\ssf E}[\phi\,\lpar W_{2:2}\rpar ]\cr &= \hbox{Var} \lpar {\ssf E} [\phi\, \lpar W_1\rpar \vert T_1, T_4]\rpar + \lpar {\ssf E} [\phi\, \lpar W_1\rpar ]\rpar ^2 - {\ssf E} [\phi\, \lpar W_{1:2}\rpar ]\,{\ssf E}[\phi\,\lpar W_{2:2}\rpar ]\cr &= \hbox{Var} \lpar {\ssf E} [\phi\, \lpar W_1\rpar \vert T_1, T_4]\rpar + {1 \over 4}\,\{{\ssf E}\,[\phi\, \lpar W_{1:2}\rpar ] - {\ssf E} [\phi\,\lpar W_{2:2}\rpar ] \}^2 \cr &\quad\ge 0.}$$

This completes the proof of the theorem.■

Theorem 2.2

Let T 1 ≤ T 2 ≤ T 3[resp. T 2 ≤ T 3 ≤ T 4] be three random variables such that, for any s,

(2.6)
$$\eqalignno{[\lpar T_2, T_3\rpar \vert T_1 = s] &\mathop{=}\limits^{d} \lpar V_{1:2}\lpar s\rpar , V_{2:2}\lpar s\rpar \rpar \cr [resp. \;[\lpar T_2, T_3\rpar \vert T_4 = s] &\mathop{=}\limits^{d} \lpar V_{1:2}\lpar s\rpar , V_{2:2}\lpar s\rpar \rpar ], &}$$

where V 1:2(s) ≤ V 2:2(s) are the order statistics of i.i.d. random variables V 1(s) and V 2(s). Then ( 2.2) holds for all measurable functions φ : ℝ → ℝ such that the covariance exists.

Proof

The proof is the same as that of Theorem 2.1 with minor modification and, hence, is omitted.■

Recall from Shaked [Reference Shaked30] and Rinott and Pollak [Reference Rinott and Pollak29] that two random variables X 1 and X 2 are said to positive function dependent (PFD) if

$$\hbox{Cov} \lpar \phi\, \lpar X_1\rpar , \phi\,\lpar\, X_2\rpar \rpar \ge 0$$

for all real-valued function φ such that the covariance exists. It is noted that a number of interchangeable bivariate distributions (i.e., their joint distribution function is symmetric) are PFD. For example, if (X, Y) is conditionally i.i.d., then (X, Y) is PFD. Shaked [Reference Shaked30] proved that the class of PFD distributions is closed under convolution, mixture, and convergence in distribution and also showed that not all PFD distributions are conditionally i.i.d.

Remark 2.3

From the proof of Theorem 2.1, it is seen that the independence property of V 1(s, t) and V 2(s, t) is used in (2.3). If, instead, V 1(s, t) and V 2(s, t)) are PFD and interchangeable, then (2.3) is replaced by

$${\ssf E} [\phi\,\lpar T_2\rpar \phi \, \lpar T_3\rpar ] = {\ssf E} \{{\ssf E} [\phi\, \lpar W_1\rpar \phi\, \lpar W_2\rpar \vert T_1, T_4] \} \ge {\ssf E} \{{\ssf E} [\phi\,\lpar W_1\rpar \vert T_1, T_4] \}^2,$$

and thus the conclusions of Theorems 2.1 and 2.2 are also valid.

We now give two special applications of Theorems 2.1 and 2.2. The corresponding results are stated as the following two theorems (Theorems 2.4 and 2.6), which will be used in Sections 3 and 4, respectively. Further applications of Theorems 2.1 and 2.2 will be given in Sections 3 and 4.

Theorem 2.4

Let W, Z 1, and Z 2be independent random variables such that Z ihas an exponential distribution with failure rate λifor i = 1,2. If

(2.7)
$$2\lambda_2 \ge \lambda_1{\it \comma} $$

then

(2.8)
$$\hbox{Cov}\big( \phi\,\lpar W+Z_1\rpar , \phi\,\lpar W+Z_1+Z_2\rpar \rpar \ge 0 $$

for all measurable functions φ : ℝ → ℝ such that the covariance exists.

Proof

First, assume that 2λ2 > λ1. Let Z 3 be another exponential random variable, independent of everything else, with failure rate λ3 = 2λ2 − λ1 > 0, and set T 1 = W and T j = W + ∑j−1i=1Z i for j = 2, 3, 4. Without loss of generality, assume that W is absolutely continuous with density function f W. Then the joint density function of (T 1, … , T 4) is given by

$$f_{T_1,\ldots, T_4} \lpar t_1, t_2,t_3,t_4\rpar = f_W\lpar t_1\rpar \lambda_1\lambda_2\lambda_3 e^{-\lambda_3 t_4+ \lambda_1 t_1} e^{\delta \lpar t_2+t_3\rpar },\qquad t_1\lt t_2 \lt t_3 \lt t_4,$$

where δ = λ2 − λ1. Hence, the conditional density function of [(T 2,T 3)|T 1 = s, T 4 = t], s < t, is given by

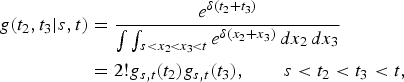
$$\eqalign{g \lpar t_2, t_3 \vert s,t\rpar &= {e^{\delta \lpar t_2+t_3\rpar } \over \vint \vint_{s\lt x_2\!\lt x_3\!\lt t} e^{\delta \lpar x_2 + x_3\rpar }\,dx_2\, dx_3} \cr &= 2! g_{s,t} \lpar t_2\rpar g_{s,t}\lpar t_3\rpar , \qquad s \lt t_2 \lt t_3 \lt t,}$$

where

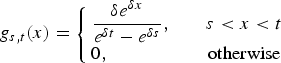
$$\,g_{s,t}\lpar x\rpar =\left\{\matrix{\displaystyle{{\delta e^{\delta x} \over e^{\delta t} -e^{\delta s}}},\hfill & \quad s \lt x \lt t\cr 0,\hfill & \quad \hbox{otherwise}} \right.$$

for δ ≠ 0, and

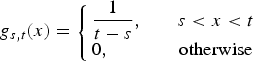
$$\!\!\!\!\!\!\!\!g_{s,t} \lpar x\rpar = \left\{\matrix{\displaystyle{{1 \over t - s}}, & \quad s \lt x \lt t \cr 0,\hfill & \quad \hbox{otherwise}} \right.$$

for δ = 0; that is, condition (2.1) is satisfied where V 1(s, t) and V 2(s, t) are i.i.d. with density function g s,t. Therefore, the desired result for this case now follows from Theorem 2.1.

Next, assume that 2λ2 = λ1. Let δ and T 1, T 2, T 3 be as defined earlier. Then the conditional density function of [(T 2, T 3)|T 1 = s] for any s is given by

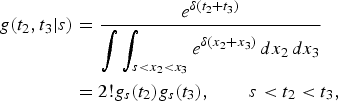
$$\eqalign{g \lpar t_2, t_3\vert s\rpar &= {e^{\delta \lpar t_2 + t_3\rpar } \over \displaystyle{\vint \vint_{s \lt x_2 \lt x_3} e^{\delta \lpar x_2 + x_3\rpar }}\,dx_2\,dx_3} \cr &= 2! g_s \lpar t_2\rpar g_s\lpar t_3\rpar , \qquad s \lt t_2 \lt t_3,}$$

where

$$\,\,\,\,\,\,\,g_s\lpar x\rpar =\left\{\matrix{\lambda_2 e^{-\lambda_2 \lpar x-s\rpar }, & \quad x \gt s \hfill \cr 0,\hfill & \quad \hbox{otherwise};} \right.$$

that is, condition (2.6) is satisfied where V 1(s) and V 2(s) are i.i.d. with density function g s. Therefore, the desired result for this case now follows from Theorem 2.2. This completes the proof of the theorem.■

It is shown by Counterexample 5.1 that (2.8) does not hold if condition (2.7) is violated. To state and prove the next theorem, we need the following lemma.

Lemma 2.5

Let V 1and V 2be two discrete random variables with support 𝒮 and with joint mass function given by

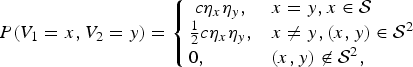
$${\ssf P} \lpar V_1 = x, V_2 = y\rpar = \left \{\matrix{c \eta_x \eta_y, & x =y, x \in {\cal S} \hfill \cr {1\over 2} c \eta_x \eta_y,\hfill & x \ne y, \lpar x,y\rpar \in {\cal S}^2 \cr 0,\hfill & \lpar x,y\rpar \not\in {\cal S}^2{\it \comma}\hfill} \right.$$

where {ηx, x ∈ 𝒮} is a sequence of positive real numbers and c is the normalizing constant given by

$$c = \left[\sum\limits_{x,y \in {\cal S}, x \le y} \eta_x \eta_y \right ]^{-1} \lt +\infty.$$

Then V 1and V 2are conditionally i.i.d. and, hence, PFD.

Proof

Let U 0, U 1, and U 2 be independent discrete random variables with support 𝒮 and with probability mass functions given respectively by

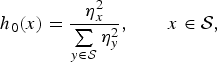
$$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!h_0\lpar x\rpar = {\eta_x^2 \over \sum\limits_{y \in {\cal S}} \eta_y^2}, \qquad x\in {\cal S},$$

and

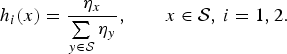
$$h_i \lpar x\rpar = {\eta_x \over \sum\limits_{y\in {\cal S}} \eta_y}, \qquad x \in {\cal S},\, i = 1,2.$$

Let I be a Bernoulli random variable, independent of {U 0, U 1, U 2}, with probability mass function given by

$${\ssf P} \lpar I = 0\rpar ={c \over 2} \left( \sum\limits_{x\in {\cal S}} \eta_x \right) ^2, \qquad {\ssf P} \lpar I = 1\rpar = {c \over 2} \sum\limits_{x \in {\cal S}} \eta_x^2.$$

Straightforward computations yield that

$$\lpar V_1, V_2\rpar \mathop{=}\limits^{d} \lpar I U_0+ \lpar 1 - I\rpar U_1, I U_0 + \lpar 1 - I\rpar U_2\rpar ,$$

which implies that given (U 0, I), (V 1, V 2) is conditionally i.i.d. and, hence, PFD. This completes the proof of the lemma.■

Theorem 2.6

Let W, B 1, and B 2be independent random variables such that B ihas a geometric distribution with parameter p ifor i = 1, 2; that is, ${\ssf P}$(B i = n) = p i(1 − p i)nfor n ∈ ℕ. If

(2.9)
$$\lpar 1 - p_2\rpar ^2 \le 1-p_1{\it\comma} $$

then

$$\hbox{Cov} \lpar \phi\,\lpar W + B_1\rpar , \phi\,\lpar W + B_1 + B_2\rpar \rpar \ge 0$$

holds for all measurable functions φ : ℝ → ℝ such that the covariance exists.

Proof

The proof is similar to that of Theorem 2.4. First, assume that (1 − p 2)2 < 1 − p 1. Let B 3 be another geometric random variable, independent of everything else, with parameter

$$p_3= 1- {\lpar 1-p_2\rpar ^2 \over 1 - p_1} \gt 0.$$

Let T 1 = W and T j = W + ∑j−1i=1B i for j = 2, 3, 4. Without loss of generality, assume that W is discrete with probability mass function f W. Then the joint mass function of (T 1, … , T 4) is given by

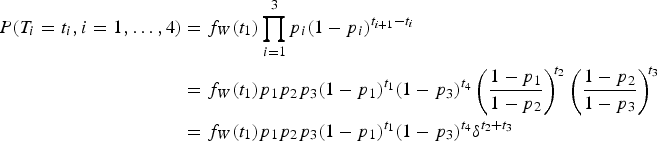
$$\eqalign{{\ssf P} \lpar T_i = t_i, i = 1, \ldots, 4\rpar &= f_W \lpar t_1\rpar \prod\limits^3_{i=1} p_i \lpar 1 - p_i\rpar ^{t_{i + 1} - t_i} \cr &= f_W\lpar t_1\rpar p_1 p_2 p_3 \lpar 1 - p_1\rpar ^{t_1} \lpar 1 - p_3\rpar ^{t_4} \left ( {1 - p_1 \over 1 - p_2} \right)^{\!t_2} \left ( {1 - p_2 \over 1 - p_3} \right) ^{\!t_3}\cr &= f_W\lpar t_1\rpar p_1 p_2 p_3 \lpar 1 - p_1\rpar ^{t_1} \lpar 1 - p_3\rpar ^{t_4} \delta^{t_2 + t_3}}$$

for t 1 ≤ t 2 ≤ t 3 ≤ t 4, where

$$\delta \equiv {1 - p_1 \over 1 - p_2}.$$

Hence, the conditional mass function of [(T 2,T 3)|T 1 = s, T 4 = t], s ≤ t, is given by

(2.10)
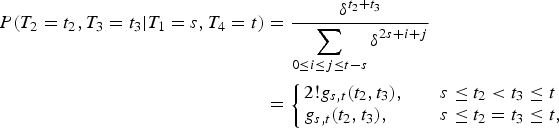
$$\eqalignno{{\ssf P} \lpar T_2 = t_2, T_3 = t_3 \vert T_1 = s, T_4 = t\rpar & = {\delta^{t_2 + t_3} \over \displaystyle{\sum\limits_{0 \le i \le j \le t - s} \delta^{2s + i + j}}} \cr & = \left\{\matrix{2! g_{s,t} \lpar t_2, t_3\rpar ,\hfill & \quad s \le t_2 \lt t_3 \le t\hfill \cr g_{s,t} \lpar t_2, t_3\rpar ,\hfill & \quad s \le t_2 = t_3 \le t,\hfill} \right.&}$$

where

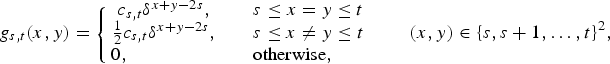
$$g_{s,t}\lpar x, y\rpar = \left\{\matrix{c_{s,t} \delta^{x + y - 2s}, & \quad s \le x = y \le t \cr {1\over 2} c_{s,t} \delta^{x + y - 2s}, & \quad s\le x \ne y\le t \cr 0, \hfill & \quad \hbox{otherwise},\hfill} \right. \qquad \lpar x,y\rpar \in \{s, s+1, \ldots, t\}^2,$$

is the joint mass function of some interchangeable random variables V 1(s, t) and V 2(s, t). Here, c s,t = [∑0 ≤i≤j≤t−sδi+j]−1. Clearly, (2.10) means that condition (2.1) is satisfied. By Lemma 2.5, (V 1(s, t), V 2(s, t)) is conditionally i.i.d. and, hence, PFD. Therefore, the desired result for this case now follows from Remark 2.3.

Next, assume that (1 − p 2)2 = 1 − p 1. Let T 1, T 2, and T 3 be as defined earlier. Then the conditional mass function of [(T 2, T 3)|T 1 = s] is given by

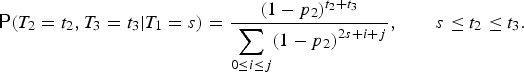
$$\hbox{\ssf P} \lpar T_2 = t_2, T_3 = t_3 \vert T_1 = s\rpar = {\lpar 1 - p_2\rpar ^{t_2 + t_3} \over \displaystyle{\sum\limits_{0\le i \le j} \lpar 1 - p_2\rpar ^{2s + i + j}}}, \qquad s\le t_2\le t_3.$$

A similar argument to the above paragraph yields that (2.6) is satisfied and (V 1(s), V 2(s)) is PFD. Therefore, the desired result for this case now follows from Remark 2.3. This completes the proof of the theorem.■

It is worthwhile to mention that for discrete random variables T i's, if ${\ssf P}$(T 2 < T 3|T 1 = s, T 4 = t) = 1 for s < t, then representation (2.1) does not hold. So, in Theorem 2.6, if the geometric distribution is replaced by the one truncated at zero, then the conclusion of the theorem is in general not true.

3. APPLICATIONS TO ORDERED CONTINUOUS RANDOM VARIABLES

3.1. Delayed Record Values

Let {X n, n ∈ ℕ+} be a sequence of i.i.d. random variables with a continuous distribution F. Let Y be a random variable independent of {X n, n ∈ ℕ+}. The delayed record value sequence is {X L(n)Y, n ∈ ℕ}, where L(0) = 0, X L(0)Y = Y,

$$L\lpar n\rpar = \inf\! \Big\{i \gt L\lpar n - 1\rpar : X_i \gt X_{L\lpar n - 1\rpar }^Y{\Big\}},\qquad n \in {\open {N}}_{+},$$

and X L(n)Y is the first X i in the sequence after X L(n−1)Y to exceed X L(n−1)Y; see Wei and Hu [Reference Wei and Hu38]. The reason for the adjective “delayed” is that record values are not kept until after a value Y has been observed. The usual record value sequence {X L(n), n ∈ ℕ+} is obtained with Y = F −1 (0), where

$$F^{-1} \lpar u\rpar = \sup \{x: F\lpar x\rpar \le u\},\qquad u \in [0, 1\rpar .$$

In this case, the superscript Y is suppressed. The record values have been extensively studied in the literature. For an excellent review, we refer to Ahsanullah [Reference Ahsanullah1, Reference Ahsanullah2] and Arnold, Balakrishnan, and Nagaraja [Reference Arnold, Balakrishnan and Nagaraja4].

The following lemma presents a stochastic representation of delayed record values by partial sums of i.i.d. exponential random variables.

Lemma 3.1 (Wei and Hu [Reference Wei and Hu38])

Let {Z n, n ∈ ℕ+} be a sequence of i.i.d. unit rate exponential random variables, independent of Y. If F is continuous, then

$$\left\{X^Y_{L\lpar 0\rpar }, X^Y_{L\lpar 1\rpar }, X^Y_{L\lpar 2\rpar }, \ldots\right\} \mathop{=}\limits^{d}\, \{H\lpar U\rpar , H\lpar U + Z_1\rpar , H\lpar U + Z_1 + Z_2\rpar , \ldots \},$$

where U = −ln(1 − F(Y)) and H(x) = F −1(1 − e −x) for x ∈ ℝ+.

Theorem 3.2

Let {X L(n)Y, n ∈ ℕ} be a sequence of delayed record values of i.i.d. random variables {X n, n ∈ ℕ+} with a continuous distribution function F. Then

$$\hbox{Cov} \lpar \phi\,\lpar X^Y_{L\lpar n\rpar }\rpar , \phi\,\lpar X^Y_{L\lpar n+1\rpar }\rpar \rpar \ge 0, \qquad n\in {\open N}_+,$$

for all measurable functions φ : ℝ → ℝ such that the covariance exists.

Proof

Let φ be any function such that the covariance exists. and define ψ (x) = φ(H(x)) for x ∈ ℝ+. Denote W = U + ∑i=1n−1Z i, where U and the Z i's are defined in Lemma 3.1. Then by Lemma 3.1 and Theorem 2.4, we have

$$\hbox{Cov} \lpar \phi\,\lpar X^Y_{L\lpar n\rpar }\rpar , \phi\,\lpar X^Y_{L\lpar n+1\rpar }\rpar \rpar = \hbox{Cov} \lpar \psi\,\lpar W + Z_n\rpar , \psi\,\lpar W + Z_n + Z_{n + 1}\rpar \rpar \ge 0.$$

This completes the proof.■

An immediate consequence of Theorem 3.1 is (1.2) (Theorem 1 in Nagaraja and Nevzorov [Reference Nagaraja and Nevzorov25]). They proved it by using the properties of Laguerre polynomials and expanding the function φ(x) into a series in Laguerre polynomials.

3.2. Continuous ℓ∞⩽-Spherical Order Statistics

ℓ∞⩽-Spherical order statistics arise naturally in the Bayesian statistical theory of reliability; see Spizzichino [34, Sects. 1.4 and 4.3]. Nonnegative random variables T 1 ≤ T 2 ≤ … ≤ T n are said to be ℓ∞⩽-spherical order statistics if their joint density function is of the form

(3.1)
$$f_{T_1, \ldots, T_n} \lpar t_1, \ldots, t_n\rpar = \left\{\matrix{\varphi\lpar t_n\rpar , & \quad 0 \le t_1 \le t_2 \le \cdots \le t_n \cr 0,\hfill & \quad \hbox{otherwise},\hfill} \right.$$

for some nonnegative function ϕ. The T i's can be regarded as the order statistics of interchangeable random variables X 1, X 2, … , X n with density function given by

$$f_{X_1,\ldots, X_n}\lpar x_1, \ldots, x_n\rpar = {1 \over n!} \varphi \left ( \max_{i = 1}^n x_i \right) ,\qquad \lpar x_1, x_2, \ldots, x_n\rpar \in {\open {R}}_+^n$$

which is called spherical in ℓ∞-norm. Define

$$Z_1 = T_1, \qquad Z_2 = T_2 - T_1, \qquad \ldots, \qquad Z_n = T_n - T_{n - 1}.$$

Then T 1, … , T n are ℓ∞⩽-spherical order statistics if and only if the density function of (Z 1, … , Z n) is of the form

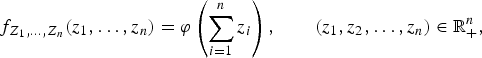
$$f_{Z_1,\ldots, Z_n}\lpar z_1, \ldots, z_n\rpar = \varphi \left ( \sum_{i=1}^n z_i \right) ,\qquad \lpar z_1, z_2, \ldots, z_n\rpar \in {\open {R}}_+^n,$$

which is called Schur constant (see Spizzichino [Reference Spizzichino34]).

Shaked, Spizzichino, and Suter [Reference Shaked, Spizzichino and Suter32, Reference Shaked, Spizzichino and Suter33] characterized, among other things, ℓ∞⩽-spherical distributions by means of epoch times of nonhomogeneous pure birth processes and by means of the uniform and general order statistics property.

Theorem 3.3

Let T 1 ≤ T 2 ≤ … ≤ T nbe ℓ∞⩽-spherical order statistics with density function of the form (3.1), and let φ be any measurable real-valued function such that the covariances below exist. Then

(3.2)
$$\hbox{Cov} \lpar \phi \,\lpar T_r\rpar , \phi\,\lpar T_{r + 1}\rpar \rpar \ge 0$$

for r = 1, … , n − 2. Moreover, if ϕ is differentiable and decreasing, then ( 3.2) holds for r = n − 1.

Proof

Fix r ∈ {1, 2, … , n − 2}. By Proposition 2.4 in Shaked et al. [Reference Shaked, Spizzichino and Suter33] we have

$$ [\lpar T_1, T_2, \ldots, T_{r + 1}\rpar \vert T_{r + 2} = t] \mathop{=}\limits^{d} \lpar V_{1:r + 1}, V_{2:r + 1}, \ldots, V_{r + 1:r + 1}\rpar ,$$

where V 1:r+1 ≤ V 2:r+1 ≤ … ≤ X r+1:r+1 are order statistics of i.i.d. uniform (0, t) random variables V 1, V 2, … , V r+1. It can be checked that

$$\eqalign{[\lpar T_r, T_{r+1}\rpar \vert T_{r - 1} = s, T_{r + 2} = t] &\mathop{=}\limits^{d}\, [\lpar V_{r:r + 1}, V_{r + 1:r + 1}\rpar \vert V_{r - 1:r + 1} = s]\cr &\mathop{=}\limits^{d} \lpar V_{1:2}\lpar s,t\rpar , V_{2:2}\lpar s,t\rpar \rpar ,}$$

where V 1:2(s, t) ≤ V 2:2(s, t) are the order statistics of i.i.d. uniform (s 0, t) random variables V 1(s, t) and V 2(s, t), and the second equality follows from Arnold, Balakrishnan, and Nagaraja [Reference Arnold, Balakrishnan and Nagaraja3, pp. 25–26]. Now, by Theorem 2.1, (3.2) follows.

If ϕ is differentiable and decreasing, Shaked et al. [Reference Shaked, Spizzichino and Suter33] proved that there exists a random variable T n+1 such that T 1 ≤ … ≤ T n ≤ T n+1 have an ℓ∞⩽-spherical density of the form

$$\!f_{T_1,\ldots, T_{n + 1}} \lpar t_1, \ldots, t_{n + 1}\rpar = \left\{\matrix{\widetilde{\varphi} \lpar t_{n + 1}\rpar , & \quad 0 \le t_1\le t_2 \le \cdots \le t_{n + 1}\cr 0,\hfill & \quad \hbox{otherwise},\hfill} \right.$$

where

$$\widetilde{\varphi} \lpar x\rpar = - {d \over dx} \varphi \lpar x\rpar , \qquad x \in {\open {R}}_+.$$

Thus, (3.2) holds for r = n − 1 by the same reasoning as in the above paragraph. This completes the proof.■

Counterexample 5.5 illustrates that (3.2) cannot be true for r = n − 1 if ϕ is differentiable but not decreasing.

Remark 3.4

By applying increasing transformation, the conclusion of Theorem 3.3 also holds for ordered random variables T 1 ≤ T 2 ≤ … ≤ T n with joint density of the form

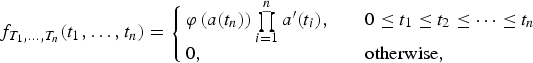
$$f_{T_1,\ldots, T_n} \lpar t_1, \ldots, t_n\rpar = \left\{\matrix{\varphi\,\lpar a\lpar t_n\rpar \rpar \prod\limits_{i=1}^n a^{\prime} \lpar t_i\rpar , & \quad 0\le t_1\le t_2\le \cdots\le t_n \cr 0,\hfill & \quad \hbox{otherwise},\hfill} \right.$$

for some nonnegative function ϕ and some strictly increasing and differentiable function a : ℝ+ → ℝ+.

We now consider epoch times of mixed Poisson processes. A counting process {N(t), t ∈ ℝ+} is said to be a mixed Poisson process if there exist a nonnegative random variable Λ and a unit rate homogeneous Poisson process {N˜(t), t ∈ ℝ+}, independent of each other, such that

(3.3)
$$\{N\lpar t\rpar , t\in {\open {R}}_+\} \mathop{=}\limits^{d} \,\{\widetilde{N} \lpar \Lambda t\rpar , t \in {\open {R}}_+\}.$$

Equivalently, {N(t), t ∈ ℝ+} is a mixed Poisson process if and only if the interepoch intervals {Z i, i ∈ ℕ+} of {N(t), t ∈ ℝ+} are a mixture of i.i.d. exponential random variables; that is, for any n ∈ ℕ+, the joint density of (Z 1, Z 2, … , Z n) is of the form

(3.4)
$$f_{Z_1,\ldots, Z_n} \lpar z_1, \ldots, z_n\rpar = \vint\nolimits_{0-}^{\infty} \lambda^n e^{-\lambda \lpar z_1 + \cdots + z_n\rpar } \hbox{d}\,G \lpar \lambda\rpar ,\qquad \lpar z_1, \ldots, z_n\rpar \in {\open {R}}_+^n,$$

where G is the distribution function of some nonnegative random variable Λ. Mixed Poisson processes play an important role in many branches of applied probability (for instance, in actuarial mathematics and physics). Grandell [Reference Grandell16] provided a detailed coverage of the theory and applications of mixed Poisson processes.

Puri [Reference Puri27] and Hayakawa [Reference Hayakawa17] characterized mixed Poisson processes by using uniform order statistics property (see also Feigin [Reference Feigin15] and Huang and Shoung [Reference Huang and ShoungHuang18]). It is seen from Shaked et al. [Reference Shaked, Spizzichino and Suter33] that a counting process {N(t), t ∈ ℝ+} is a mixed Poisson process if and only if, for all n ∈ ℕ+, the first n epoch times of the process have an ℓ∞⩽-spherical distribution and that not all ℓ∞⩽-spherical order statistics are the epoch times of some mixed Poisson process.

An immediate consequence of Theorem 3.3 is the following corollary.

Corollary 3.5

For epoch times {T n, n ∈ ℕ+} of a mixed Poisson process, we have

(3.5)
$$\hbox{Cov} \lpar \phi\,\lpar T_n\rpar , \phi\, \lpar T_{n + 1}\rpar \rpar \ge 0$$

for n ∈ ℕ+and all measurable functions φ such that the covariance exists.

Recall that a counting process {N(t), t ∈ ℝ+} is said to be a nonhomogeneous pure birth process with intensity functions κn ≥ 0 if the following hold:

  1. 1. {N(t), t ∈ ℜ+} has the Markov property,

  2. 2. ${\ssf P}$(N(t + Δt) = n + 1|N(t) = n) = κn(t)Δt + ○(Δt) for n ∈ ℕ,

  3. 3. ${\ssf P}$(N(t + Δt) > n + 1|N(t) = n) = ○(Δt) for n ∈ ℕ,

where each κn is assumed to satisfy

$$\vint\nolimits_t^{\infty} \kappa_n\lpar u\rpar\, du = + \infty, \qquad t \in {\open {R}}_+;$$

this ensures that, with probability 1, the process has a jump after any time point t. There is a close relationship between mixed Poisson processes and nonhomogeneous pure birth processes; see, for example, Grandell [Reference Grandell16, Sect. 6.1] or Pfeifer and Heller [Reference Pfeifer and Heller26].

Example 3.6

(Pólya process): Let {N(t), t ∈ ℝ+} be a nonhomogeneous pure birth process with intensity functions κn given by

$$\kappa_n \lpar t\rpar = {\gamma +n \over \beta + t},\qquad t \in {\open {R}}_{+}, n \in {\open {N}},$$

where γ ≥ 0 and β > 0 are constants. It is known from Grandell [16, pp. 67] or Shaked et al. [Reference Shaked, Spizzichino and Suter32] that such a process is also a mixed Poisson process with G in (3.4) having Γ(β, γ) distribution, whose density function is given by

$$g \lpar \lambda\rpar ={\beta^{\gamma} \lambda^{\gamma - 1} \over \Gamma \lpar \gamma\rpar } e^{- \beta \lambda}, \qquad \lambda \in {\open {R}}_+.$$

Therefore, Corollary 3.5 can be applied to the epoch times of such a process.

3.3. Generalized Order Statistics

The concept of generalized order statistics was introduced by Kamps [Reference Kamps19, Reference Kamps20] as a unified approach to a variety of models of ordered random variables.

Definition 3.7

Let n ∈ ℕ+, k > 0, and (m 1, … , m n−1) ∈ ℝn−1be parameters such that

(3.6)
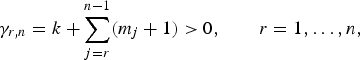
$$\gamma_{r,n} = k + \sum^{n - 1}_{j = r} \lpar m_j + 1\rpar \gt 0, \qquad r = 1, \ldots, n,$$

and let m˜ = (m 1, … , m n−1) if n ≥ 2 (m˜ arbitrary if n = 1). If the random variables U (r,n,m˜,k), r = 1, … , n, possess a joint density of the form

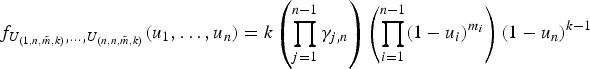
$$f_{U_{\lpar 1,n,{\tilde m},k\rpar },\ldots, U_{\lpar n,n,{\tilde m},k\rpar }}\lpar u_1, \ldots, u_n\rpar = k \left ( \prod\limits_{j = 1}^{n - 1} \gamma_{j,n} \right ) \left ( \prod\limits_{i = 1}^{n - 1} \lpar 1 -u_i\rpar ^{m_i} \right) \lpar 1 - u_n\rpar ^{k - 1}$$

on the cone 0 ≤ u 1 ≤ u 2 ≤ … ≤ u n < 1 of ℝn, then they are called uniform generalized order statistics (GOSs, for short). Now, let F be an arbitrary distribution function. The random variables

$$X_{\lpar r,n, \tilde{m},k\rpar } = F^{-1}\lpar U_{\lpar r,n, \tilde{m},k\rpar }\rpar , \qquad r=1, \ldots, n\,{\it\comma}$$

are called the GOSs based on F.

In the particular case m 1 = … = m n−1 = m, the above random variables are denoted by U (r,n,m,k)and X (r,n,m,k), r = 1, … , n, respectively.

In the past 10 years, there is a vast amount of literature on studying various properties of GOSs. Khaledi and Kochar [Reference Khaledi and Kochar21] and Cramer [Reference Cramer9] investigated the dependence structure of GOSs. The structure of GOSs can be characterized by sums of independent exponential random variables as stated in Lemma 3.8 (see Cramer and Kamps [Reference Cramer and Kamps11]).

Lemma 3.8

Let X (1,n,m˜,k), … , X (n,n,m˜,k)be GOSs based on a continuous distribution function F, and let Z 1, … , Z nbe independent exponential random variables with failure rates γ1,n, … , γn,n, respectively, where γn,n = k. Then

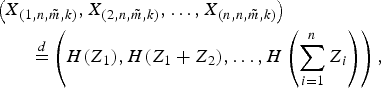
$$\eqalign{&\left( X_{\lpar 1,n, \tilde{m},k\rpar }, X_{\lpar 2,n, \tilde{m},k\rpar }, \ldots, X_{\lpar n,n, \tilde{m},k\rpar } \right) \cr &\qquad \mathop{=}\limits^{d} \left( H\lpar Z_1\rpar , H\lpar Z_1 + Z_2\rpar , \ldots, H \left( \sum^n_{i = 1} Z_i \right) \right) ,}$$

where H(x) = F −1(1 − e −x) for x ∈ ℝ+.

Theorem 3.9

Let X (1,n,m˜,k), … , X (n,n,m˜,k)be GOSs based on a continuous distribution function F. If 2γr,n ≥ γr−1,nfor some r, 2 ≤ r ≤ n; then

$$\hbox{Cov} \lpar \phi\,\lpar X_{\lpar r - 1,n, \tilde{m},k\rpar }\rpar , \phi\,\lpar X_{\lpar r,n, \tilde{m},k\rpar }\rpar \rpar \ge 0$$

for all measurable functions φ : ℝ → ℝ such that the covariance exists.

Proof

The proof is similar to that of Theorem 3.2 by using Lemma 3.8 and Theorem 2.4.■

From (3.6), it follows that

$$\,\,\,2 \gamma_{r,n} - \gamma_{r - 1,n} = \gamma_{r + 1,n} + \lpar m_r-m_{r - 1}\rpar \quad \hbox{for}\,r = 2, \ldots, n - 1$$

and

$$2 \gamma_{n,n} - \gamma_{n - 1,n} = k - \lpar m_{n - 1} + 1\rpar .$$

Thus, a sufficient condition for 2γr,n ≥ γr−1,n is that m r ≥ m r −1 for r = 2, … , n − 1 and k ≥ m n−1 + 1 for r = n. In virtue of this observation, an immediate consequence of Theorem 3.9 is the following corollary.

Corollary 3.10

Let X (1,n,m,k), … , X (n,n,m,k)be GOSs based on a continuous distribution function F, and let φ be any measurable function such that the covariances below exist. Then

$$\hbox{Cov} \lpar \phi\,\lpar X_{\lpar r-1,n,m,k\rpar }\rpar , \phi\,\lpar X_{\lpar r,n,m,k\rpar }\rpar \rpar \ge 0 \quad {for}\,r=2, \ldots, n - 1.$$

Moreover, if k ≥ m + 1, then

$$\hbox{Cov} \lpar \phi\,\lpar X_{\lpar n - 1,n,m,k\rpar }\rpar , \phi\,\lpar X_{\lpar n,n,m,k\rpar }\rpar \rpar \ge 0.$$

It is worthwhile to mention that Theorem 3.9 and Corollary 3.10 do not hold in general for the case of nonadjacent GOSs, as shown by Counterexamples 5.2 and 5.3. Furthermore, Counterexample 5.4 shows that Theorem 3.9 might even not be true for the case of adjacent GOSs if 2γr,n < γr−1,n.

Choosing the parameters appropriately, several other models of ordered random variables are seen to be particular cases. Ordinary order statistics of a random sample from a distribution F are a particular case of GOSs when k = 1 and m r = 0 for r = 1, … , n − 1. When k = 1 and m r = −1 for r = 1, … , n − 1, we get the first n record values from a sequence of i.i.d. random variables with distribution F. Some other models are as follows.

  • • kth record values: Fix k ∈ ℕ+. Let {X n, n ∈ ℕ+} be a sequence of i.i.d. random variables with a continuous distribution F. The random variables L (k)(1) = 1 and

    $$L^{\lpar k\rpar }\lpar n + 1\rpar = \min \left \{ j \gt L^{\lpar k\rpar }\lpar n\rpar : X_{j:j + k - 1} \gt X_{L^{\lpar k\rpar }\lpar n\rpar :L^{\lpar k\rpar }\lpar n\rpar +k-1} \right \},\qquad n \in {\open {N}},$$
    are called k-record times, and
    $$X_{L^{\lpar k\rpar }\lpar n\rpar } = X_{L^{\lpar k\rpar }\lpar n\rpar :L^{\lpar k\rpar }\lpar n\rpar + k - 1}$$
    is called nth k-record values (see Kamps [Reference Kamps20, p. 34] and Arnold et al. [Reference Arnold, Balakrishnan and Nagaraja4]). For k = 1, X L (1)(n) reduces to X L(n). The first n k-records (X L (k)(1), … , X L (k)(n)) are the GOSs (X (1,n,−1,k), … , X (n,n,−1,k)) based on F. By Corollary 3.10, we have
    $$\hbox{Cov} \left( \phi\, \lpar X_{L^{\lpar k\rpar }\lpar n\rpar }\rpar , \phi\,\lpar X_{L^{\lpar k\rpar }\lpar n+1\rpar }\rpar \right) \ge 0, \qquad n\in {\open {N}}_+,$$
    for all measurable real-valued functions φ such that the covariance exists.

  • • Progressive type II censored order statistics: Progressive type II censoring has been suggested in the field of life-testing experiments. Suppose that N units are placed on a lifetime test. The failure times are described by i.i.d. random variables with a common distribution F. A number n (n ≤ N) of units are observed to fail. A predetermined number R i of surviving units at the time of the ith failure are randomly selected and removed from further testing. Thus, ∑i=1nR i units are progressively censored; hence, N = n + ∑i=1nR i. The n observed failure times are called progressive type II censored order statistics based on F, denoted by T 1 ≤ T 2 ≤ … ≤ T n, which correspond to the GOSs based on F with parameters k = R n + 1, m r = R r and γr,n = N − r + 1 − ∑i=1r−1R i for r = 1, … , n − 1. For details on the model of progressive type II censoring, we refer to Balakrishnan and Aggarwala [Reference Balakrishnan and Aggarwala6] and Cramer and Kamps [Reference Cramer, Kamps, Balakrishnan and Rao10]. If R i is decreasing in i and F is continuous, then, by Theorem 3.9 and the comments after Theorem 3.9, we have

    (3.7)
    $$\hbox{Cov} \lpar \phi \,\lpar T_r\rpar , \phi\, \lpar T_{r+1}\rpar \rpar \ge 0$$
    For r = 1, … , n − 1 and for all measurable real-valued functions φ such that the covariance exists.

  • • Order statistics under multivariate imperfect repair Policy(p 1, … , p n): Suppose that n items with i.i.d. random lifetimes, with distribution function F, start to function at the same time 0. Upon failure, an item undergoes a repair and the repair is instantaneous. If i items have already been scrapped, then with probability p i+1, the repair is unsuccessful and the item is scrapped, and with probability 1 − p i+1, the repair is successful and minimal (i.e., the item is restored to a working condition just prior to the failure). When an item fails and is successfully minimally repaired, the other functioning items “do not know” about the failure and repair. The ordered failure times T 1 ≤ T 2 ≤ … ≤ T n are the special case of GOSs based on F with parameters k = p n, m r = (n − r + 1)p r − (n − r)p r+1 − 1 and γr,n = (n − r + 1)p r for r = 1, …, n − 1. For more details, see Shaked and Shanthikumar [Reference Shaked and Shanthikumar31] and Belzunce, Mercader, and Ruiz [Reference Belzunce, Mercader and Ruiz7]. Applying Theorem 3.9 yields that if

    (3.8)
    $$2 \lpar n - r\rpar p_{r + 1} \ge \lpar n - r + 1\rpar p_r$$
    for some r, 1 ≤ r < n, then (3.7) holds for measurable real-valued functions φ such that the covariance exists. A sufficient condition for (3.8) is that p i is increasing in i.

  • • Yule process: A Yule process {N(t), t ∈ ℝ+}, with initial population size θ, is a special homogeneous pure birth process with intensity functions

    $$\kappa_i \lpar t\rpar = i \lambda, \qquad i \in \{\theta, \theta +1, \ldots \},$$
    where λ > 0 is a constant. Let T 1 ≤ T 2 ≤ … ≤ T n be the first n epoch times of the process. Then the T i's can be regarded as the GOSs X (i,n,m,k) based on unit rate exponential distribution, where k = λ(θ + n − 1) and m = −λ −1. Therefore, by Corollary 3.10, (3.7) holds for r ∈ ℕ+ and all measurable functions φ.

4. APPLICATIONS TO ORDERED DISCRETE RANDOM VARIABLES

4.1. Discrete Weak Record Values

In the context of record values, a repetition of a record value can be regarded as a new record, and this makes sense for discrete distributions. This leads to the notion of weak records introduced by Vervaat [Reference Vervaat37]. Recently, a considerable amount of work has been done on weak record statistics; see Stepanov, Balakrishnan, and Hofmann [Reference Stepanov, Balakrishnan and Hofmann36], Wesolowski and López-Blázquez [Reference Wesolowski and López-Blázquez39], Dembińska and López-Blázquez [Reference Dembińska and López-Blázquez13], Bairamov and Stepanov [Reference Bairamov and Stepanov5], Belzunce, Ortega, and Ruiz [Reference Belzunce, Ortega and Ruiz8], Dembińska and Stepanov [Reference Dembińska and Stepanov14], Danielak and Dembińska [Reference Danielak and Dembińska12], and references therein.

Formally, let {X, X n, n ∈ ℕ+} be a sequence of i.i.d. discrete random variables with support being a subset of ℕ. The sequence of weak record times {L w(n), n ∈ ℕ+} is defined by

$$\eqalign{L_w\lpar 1\rpar & = 1, \cr L_w\lpar n + 1\rpar &= \min \{\,j \gt L_w\lpar n\rpar : X_j \ge \max \{X_1, X_2, \ldots, X_{j - 1} \} \}, \qquad n \in {\open {N}}_{+},}$$

and {X L w(n), n ∈ ℕ+} is the sequence of weak records. The discrete weak record values possess the Markov property (see Vervaat [Reference Vervaat37]); that is,

(4.1)
$${\ssf P} \lpar X_{L_w\lpar n + 1\rpar }=j \vert X_{L_w\lpar n\rpar } = i\rpar = { {\ssf P} \lpar X=j\rpar \over {\ssf P} \lpar X\ge i\rpar },\qquad i\le j.$$

Thus, the joint mass function of the first n weak record values is given by

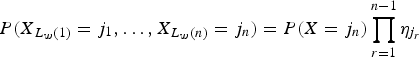
$${\ssf P} \lpar X_{L_w\lpar 1\rpar }=j_1, \ldots, X_{L_w\lpar n\rpar }=j_n\rpar ={\ssf P} \lpar X=j_n\rpar \prod\limits_{r=1}^{n-1} \eta_{j_r}$$

For j 1 ≤ j 2 ≤ … ≤ j n, where

(4.2)
$$\eta_j= {{\ssf P} \lpar X=j\rpar \over {\ssf P} \lpar X\ge j\rpar }$$

is the failure rate function of X.

Theorem 4.1

For the sequence {X L w(n), n ∈ ℕ+} of weak record values, we have

$$\hbox{Cov} \lpar \phi\, \lpar X_{L_w\lpar n\rpar }\rpar , \phi\,\lpar X_{L_w\lpar n+1\rpar }\rpar \rpar \ge 0,\qquad n\in {\open {N}}_+{\it\comma}$$

for all real-valued functions φ such that the expectation exists.

Proof

From (4.1), it follows that the joint mass function of {X L w(r), r = n − 1, …, n + 2} is given by

$${\ssf P} \lpar X_{L_w\lpar r\rpar }=j_r, r=n-1, \ldots, n + 2\rpar ={{\ssf P} \lpar X_{L_w\lpar n-1\rpar }=j_{n-1}\rpar \over {\ssf P}\lpar X\ge j_{n-1}\rpar } {\ssf P}\lpar X=j_{n+2}\rpar \eta_{j_n} \eta_{j_{n+1}}$$

for j n−1 ≤ j n ≤ j n+1 ≤ j n+2 and n ∈ ℕ+, where X L w(0) = 0. Thus,

$$\hbox{\ssf P} \lpar X_{L_w\lpar n\rpar } = x, X_{L_w\lpar n + 1\rpar } = y \vert X_{L_w\lpar n - 1\rpar } = s, X_{L_w\lpar n + 2\rpar } = t\rpar $$
(4.3)
$$\eqalignno{&= {\eta_x \eta_y \over \sum\limits_{s\le i\le j\le t} \eta_i \eta_j} \cr & = \left\{\matrix{2! g_{s,t} \lpar x, y\rpar , & \quad s \le x \lt y \le t \cr g_{s,t} \lpar x, y\rpar ,\hfill &\quad s \le x =y \le t,} \right. &}$$

where

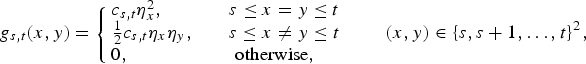
$$g_{s,t}\lpar x, y\rpar =\left\{\matrix{c_{s,t} \eta_x^2,\hfill & \quad s\le x = y\le t \cr {1\over 2} c_{s,t} \eta_x \eta_y, & \quad s\le x \ne y\le t\cr 0,\hfill & \hbox{otherwise},} \right. \qquad \lpar x,y\rpar \in \{s, s+1, \ldots, t\}^2,$$

is the joint mass function of some interchangeable random variable V 1(s,t) and V 2(s,t). Here, c s,t = [∑s≤i≤j≤t ηxηj]−1. Clearly, (4.3) means that condition (2.1) is satisfied. The desired result now follows from Lemma 2.5 and Remark 2.3.■

Now, let B i be the number of weak record values that are equal to i for i ∈ ℕ. Then

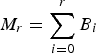
$$M_r = \sum\limits_{i=0}^r B_i$$

is the number of weak record values that are less than or equal to r, r ∈ ℕ. Denote by P i = ${\ssf P}$(X ≥ i) and by u X the right end point of the support of X. Stepanov [Reference Stepanov35] proved that B i, i ∈ ℕ, are independent,

(4.4)
$$\hbox{\ssf P} \lpar B_i = n\rpar = {P_{i + 1} \over P_i} \left ( 1-{P_{i+1}\over P_i} \right) ^n, \qquad n \in {\open {N}},$$

for i = 0, 1, … , u X − 1, and ${\ssf P}$(B u X = +∞) = 1 if u X < ∞.

By Theorem 2.6, we obtain the next result, whose proof is trivial and, hence, is omitted.

Theorem 4.2

Let ηibe the discrete failure rate of X, defined by ( 4.2). If ηr+12 ≤ ηrfor some r ∈ {0, 1, … , u X − 2}, then

(4.5)
$$\hbox{Cov} \lpar \phi\, \lpar M_r\rpar , \phi\, \lpar M_{r + 1}\rpar \rpar \ge 0$$

for all real-valued functions φ such that the expectation exists.

4.2. Discrete ℓ∞⩽-Spherical Order Statistics

Let T 1 ≤ T 2 ≤ … ≤ T n be ℕ-valued random variables. T 1, … , T n are said to be (discrete) ℓ∞⩽-spherical order statistics if their joint mass function of the form

(4.6)
$$p_{T_1,\ldots, T_n}\lpar t_1, \ldots, t_n\rpar =\left\{\matrix{\varphi \lpar t_n\rpar , & \quad 0\le t_1\le t_2\le \cdots \le t_n \cr 0,\hfill & \quad \hbox{otherwise},\hfill} \right.$$

for some nonnegative function ϕ (see Shaked et al. [Reference Shaked, Spizzichino and Suter33]).

The following result is a discrete analogue of Theorem 3.3. Its proof is a straightforward modification of the proof of Theorem 4.1 and, hence, is omitted.

Theorem 4.3

Let T 1 ≤ T 2 ≤ … ≤ T nbe ℓ∞⩽-spherical order statistics on ℕn. Then

(4.7)
$$\hbox{Cov} \lpar \phi\, \lpar T_r\rpar , \phi\,\lpar T_{r+1}\rpar \rpar \ge 0$$

for r = 1, … , n − 2 and for all real-valued functions φ such the covariance exists.

We now modify the definition of a mixed geometric process introduced by Huang and Shoung [Reference Huang and ShoungHuang18].

Definition 4.4

A discrete-time discrete-state process {M t, t ∈ ℕ} is called a modified mixed geometric process if there exists a random variable Θ that takes on values in (0,Reference Ahsanullah1) such that, given Θ = θ, the interepoch intervals Z i, i ∈ ℕ+, of the process are i.i.d. with ${\ssf P}$(Z 1 = z) = θ(1 − θ)zfor z ∈ ℕ.

A modified mixed geometric process can have jumps larger than unity at the jump epochs. Denote by J t the number of jumps occurring at time t; that is, J 0 = M 0 and J t = M t − M t−1 for t ∈ ℕ+. For a modified mixed geometric process, it is seen from Theorem 4.7 in Shaked et al. [Reference Shaked, Spizzichino and Suter33] that the first n epoch times T 1, … , T n are ℓ∞⩽-spherical and that the jump amounts J 0, J 1, … , J n have a Schur-constant mass function on ℕn, which implies that M 0,M 1, … , M n are also ℓ∞⩽-spherical. By Theorem 4.3, we have the following corollary.

Corollary 4.5

Let {T n, n ∈ ℕ+} be the sequence of epoch times of a modified mixed geometric process {M t, t ∈ ℕ}. Then ( 4.5) and ( 4.7) hold for all r ∈ ℕ+and all real-valued functions φ such that the covariances exist.

5. COUNTEREXAMPLES

In this section several counterexamples are presented to illustrate that the conditions of the theorems and corollaries in the previous sections cannot be dropped off and that the nonnegativity property of the covariances do not hold for nonadjacent ordered random variables.

Throughout this section, let Z 1, Z 2, and Z 3 be independent exponential random variables with failure rates λ1, λ2, and λ3, and denote their means by μ1, μ2, and μ3. Choose φ (x) = x 2 − x. Since ${\ssf E}$[Z i2] = 2μi2, ${\ssf E}$[Z i3] = 6μi3 and ${\ssf E}$[Z i4] = 24μi4 for each i, it is easy to see that

$$\hbox{Var} \lpar \phi\, \lpar Z_1\rpar \rpar = {\ssf E} [Z_1^4 - 2 Z_1^3 + Z_1^2] - [{\ssf E} Z_1^2 - {\ssf E} Z_1]^2 = 20 \mu_1^4 - 8 \mu_1^3 +\mu_1^2$$

and

$$\eqalign{\hbox{Cov} \lpar \phi\,\lpar Z_1\rpar , Z_1Z_2\rpar &= \left \{ {\ssf E} [Z_1^3 - Z_1^2] - \lpar {\ssf E} Z_1^2 - {\ssf E} Z_1\rpar {\ssf E} Z_1 \right \} {\ssf E} Z_2 = \mu_2 [4\mu_1^3-\mu_1^2], \cr &\quad \hbox{Cov} \lpar \phi\, \lpar Z_1\rpar , Z_1 Z_3\rpar = \mu_3 [4\mu_1^3 - \mu_1^2].}$$

Then we have

(5.1)
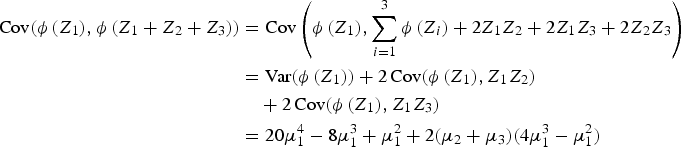
$$\eqalign{\hbox{Cov} \lpar \phi\,\lpar Z_1\rpar , \phi\,\lpar Z_1+Z_2+Z_3\rpar \rpar &= \hbox{Cov}\left( \phi\,\lpar Z_1\rpar , \sum\limits_{i=1}^3 \phi\,\lpar Z_i\rpar + 2 Z_1Z_2 + 2 Z_1 Z_3 + 2 Z_2 Z_3 \right) \cr &= \hbox{Var} \lpar \phi\,\lpar Z_1\rpar \rpar + 2\,\hbox{Cov} \lpar \phi\,\lpar Z_1\rpar , Z_1Z_2\rpar \cr &\quad + 2\,\hbox{Cov} \lpar \phi\,\lpar Z_1\rpar , Z_1Z_3\rpar \cr &= 20 \mu_1^4 - 8\mu_1^3 + \mu_1^2 + 2\lpar \mu_2 + \mu_3\rpar \lpar 4 \mu_1^3 - \mu_1^2\rpar }$$

and

(5.2)
$$\hbox{Cov} \lpar \phi\,\lpar Z_1\rpar , \phi\,\lpar Z_1+Z_2\rpar \rpar = 20 \mu_1^4 -8\mu_1^3 +\mu_1^2 + 2 \mu_2 \lpar 4 \mu_1^3 - \mu_1^2\rpar .$$

Counterexample 5.1

Choose φ(x) = x 2 − x and λ1 = 6, λ2 = 2 such that 2λ2 − λ1 < 0.

From (5.2), it follows that

$$\hbox{Cov} \lpar \phi\,\lpar Z_1\rpar , \phi\,\lpar Z_1 + Z_2\rpar \rpar = -{1\over 324} \lt 0.$$

This shows that Theorem 2.4 does not hold if condition (2.7) is violated.

Counterexample 5.2

Let X (1,3,m˜,4) ≤ X (2,3,m˜,4) ≤ X (3,3,m˜,4) be GOSs based on the standard exponential distribution with m˜ = (2, 1), and choose (λ1, λ2, λ3) = (9, 6, 4) and φ(x) = x 2 − x. By Lemma 3.8, we get

$$\lpar X_{\lpar 1,3,{\tilde m},4\rpar }, X_{\lpar 2,3,{\tilde m},4\rpar }, X_{\lpar 3,3,{\tilde m},4\rpar }\rpar \mathop{=}\limits^{d} \lpar Z_1, Z_1 + Z_2, Z_1 + Z_2 + Z_3\rpar .$$

From (5.1), straightforward computations give

$$\hbox{Cov} \lpar \phi\,\lpar X_{\lpar 1,3, \tilde{m},4\rpar }\rpar , \phi\,\lpar X_{\lpar 3,3, \tilde{m},4\rpar }\rpar \rpar = \hbox{Cov} \lpar \phi\,\lpar Z_1\rpar , \phi\,\lpar Z_1 + Z_2 + Z_3\rpar \rpar = -{51 \over 6\times 9^4} \lt 0.$$

Clearly, 2γr,3 > γr−1,3 for r = 2, 3, satisfying the assumption of Theorem 3.9. This shows that Theorem 3.9 does not hold for the case of nonadjacent GOSs.

Counterexample 5.3

Let X (1,3,1,4) ≤ X (2,3,1,4) ≤ X (3,3,1,4) be GOSs based on the standard exponential distribution, and choose (λ1, λ2, λ3) = (8, 6, 4) and φ (x) = x 2 − x. By Lemma 3.8, we get

$$\lpar X_{\lpar1,3,1,4\rpar }, X_{\lpar 2,3,1,4\rpar }, X_{\lpar 3,3,1,4\rpar }\rpar \mathop{=}\limits^{d} \lpar Z_1, Z_1 + Z_2, Z_1 + Z_2 + Z_3\rpar .$$

Straightforward computations give

$$\hbox{Cov} \lpar \phi\,\lpar X_{\lpar 1,3,1,4\rpar }\rpar , \phi\,\lpar X_{\lpar 3,3,1,4\rpar }\rpar \rpar = \hbox{Cov} \lpar \phi\,\lpar Z_1\rpar , \phi\,\lpar Z_1+Z_2+Z_3\rpar \rpar = -{5\over 3072} \lt 0.$$

This shows that Corollary 3.10 does not hold for the case of nonadjacent GOSs.

Counterexample 5.4

Let X (1,3,m˜,1) ≤ X (2,3,m˜,1) ≤ X (3,3,m˜,1) be GOSs based on the standard exponential distribution with m˜ = (3, 4), and choose (λ1, λ2, λ3) = (10, 6, 1) and φ(x) = x 2 − x. It is easy to see from Lemma 3.8 that

$$\lpar X_{\lpar 1,3, \tilde{m},1\rpar }, X_{\lpar 2,3, \tilde{m},1\rpar }, X_{\lpar 3,3, \tilde{m},1\rpar }\rpar \mathop{=}\limits^{d} \lpar Z_1, Z_1 + Z_2, Z_1 + Z_2 + Z_3\rpar .$$

Straightforward computations give

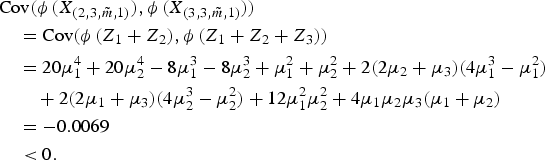
$$\eqalign{&\hbox{Cov} \lpar \phi\,\lpar X_{\lpar 2,3, \tilde{m},1\rpar }\rpar , \phi\,\lpar X_{\lpar 3,3, \tilde{m},1\rpar }\rpar \rpar \cr &\quad = \hbox{Cov} \lpar \phi\,\lpar Z_1 + Z_2\rpar , \phi\, \lpar Z_1 + Z_2 + Z_3\rpar \rpar \cr &\quad = 20 \mu_1^4 + 20 \mu_2^4 - 8\mu_1^3 - 8 \mu_2^3 + \mu_1^2 + \mu_2^2 + 2 \lpar 2\mu_2 + \mu_3\rpar \lpar 4 \mu_1^3 - \mu_1^2\rpar \cr &\qquad + 2 \lpar 2\mu_1 + \mu_3\rpar \lpar 4 \mu_2^3 - \mu_2^2\rpar + 12 \mu_1^2\mu_2^2 + 4 \mu_1\mu_2\mu_3 \lpar \mu_1 + \mu_2\rpar \cr &\quad = -0.0069\cr &\quad \lt 0.}$$

This shows that Theorem 3.9 might even not be true for adjacent GOSs if 2γ3,3 < γ2,3.

Counterexample 5.5

Let (T 1, T 2) have an ℓ∞⩽-spherical density of the form

$$f_{T_1, T_2} \lpar t_1, t_2\rpar =\left \{\matrix{3 t_2, & \quad 0\le t_1\le t_2 \le 1\cr 0,\hfill & \quad \hbox{otherwise}.\hfill} \right.$$

Then the marginal densities of T 1 and T 2 are respectively given by

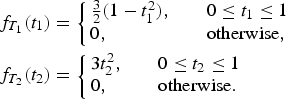
$$\eqalign{& f_{T_1}\lpar t_1\rpar = \left \{\matrix{{3\over 2} \lpar 1 - t_1^2\rpar , & \quad 0\le t_1\le 1\cr 0,\hfill & \quad \hbox{otherwise},\hfill} \right. \cr & f_{T_2}\lpar t_2\rpar = \left \{\matrix{3 t_2^2, & \quad 0\le t_2\le 1\cr 0,\hfill & \quad \hbox{otherwise}.\hfill} \right.}$$

Choose φ (x) = x 2 − x. Then ${\ssf E}$[φ (T 1)] = −7/40, ${\ssf E}$[φ (T 2)] = −3/20, and ${\ssf E}$[φ (T 1)φ (T 2)] = 11/420. Therefore, Cov(φ (T 1), φ (T 2)) = −1/16800 < 0. This shows, by a limiting argument, that (3.2) in Theorem 3.3 cannot be true for r = n − 1 if ϕ is differentiable but not decreasing.

Acknowledgments

This work was supported by the National Natural Science Foundation of China, Program for New Century Excellent Talents in University (No. NCET-04-0569), and by the Knowledge Innovation Program of the Chinese Academy of Sciences (No. KJCX3-SYW-S02).

References

1.Ahsanullah, M. (1988). Introduction to record values. Needham Heights, MA: Ginn Press.Google Scholar
2.Ahsanullah, M. (1995). Record statistics. New York: Nova Science Publishers.Google Scholar
3.Arnold, B.C., Balakrishnan, N., & Nagaraja, H.N. (1992). A first course in order statistics. New York: Wiley.Google Scholar
4.Arnold, B.C., Balakrishnan, N., & Nagaraja, H.N. (1998). Records. New York: Wiley.Google Scholar
5.Bairamov, I. & Stepanov, A. (2006). A note on large deviations for weak records. Statistics and Probability Letters 76: 1449–1453.Google Scholar
6.Balakrishnan, N. & Aggarwala, R. (2000). Progressive censoring. Boston: Birkhauser.CrossRefGoogle Scholar
7.Belzunce, F., Mercader, J.A., & Ruiz, J.M. (2005). Stochastic comparisons of generalized order statistics. Probability in the Engineering and Informational Sciences 19: 99–120.Google Scholar
8.Belzunce, F., Ortega, E.-M., & Ruiz, J.M. (2006). Stochastic orderings of discrete-time processes and discrete record values. Probability in the Engineering and Informational Sciences 20: 447–464.CrossRefGoogle Scholar
9.Cramer, E. (2006). Dependence structure of generalized order statistics. Statistics 40: 409–413.CrossRefGoogle Scholar
10.Cramer, E. & Kamps, U. (2001). Sequential k-out-of-n systems. In Balakrishnan, N. & Rao, C.R. (eds.), Handbook of staistics: Advances in reliability, Vol. 20, Amsterdam: Elsevier, pp. 301–372.Google Scholar
11.Cramer, E. & Kamps, U. (2003). Marginal distributions of sequential and generalized order statistics. Metrika 58: 293–310.CrossRefGoogle Scholar
12.Danielak, K. & Dembińska, A. (2006). On characterizing discrete distributions via conditional expectations of weak record values. Metrika DOI 10.1007/s00184-006-0100-9.Google Scholar
13.Dembińska, A. & López-Blázquez, F. (2005). A characterization of geometric distribution through kth weak records. Communication in Statistics: Theory and Methods 34: 2345–2351.CrossRefGoogle Scholar
14.Dembińska, A. & Stepanov, A. (2006). Limit theorems for the ratio of weak records. Statistics and Probability Letters 76: 1454–1464.CrossRefGoogle Scholar
15.Feigin, P.D. (1979). On the characterization of point processes with the order statistic property. Journal of Applied Probability 16: 297–304.CrossRefGoogle Scholar
16.Grandell, J. (1997). Mixed Poisson processes. London: Chapman & Hall.Google Scholar
17.Hayakawa, Y. (2000). A new characterization property of mixed Poisson process via Berman's theorem. Journal of Applied Probability 37: 261–268.CrossRefGoogle Scholar
18.Huang, W.-J. & ShoungHuang, J.-M. (1994). On a study of some properties of point processes. Sankhyā A 56: 67–76.Google Scholar
19.Kamps, U. (1995). A concept of generalized order statistics. Stuttgard: Teubner.Google Scholar
20.Kamps, U. (1995). A concept of generalized order statistics. Journal of Statistical Planning and Inference 48: 1–23.Google Scholar
21.Khaledi, B.-E. & Kochar, S.C. (2005). Dependence orderings for generalized order statistics. Statistics and Probability Letters 73: 357–367.CrossRefGoogle Scholar
22.Li, L. (1994). A counterexample to a conjecture on order statistics. Statistics and Probability Letters 19: 129–130.CrossRefGoogle Scholar
23.Ma, C. (1992). Variance bound of function of order statistics. Statistics and Probability Letters 13: 25–27.Google Scholar
24.Ma, C. (1992). Moments of functions of order statistics. Statistics and Probability Letters 15: 57–62.Google Scholar
25.Nagaraja, H.N. & Nevzorov, V.B. (1996). Correlations between functions of records can be negative. Statistics and Probability Letters 29: 95–100.CrossRefGoogle Scholar
26.Pfeifer, D. & Heller, U. (1987). A martingale characterization of mixed Poisson processes. Journal of Applied Probability 24: 246–251.Google Scholar
27.Puri, P.S. (1982). On the characterization of point processes with the order statistics property without the moment condition. Journal of Applied Probability 19: 39–51.Google Scholar
28.Qi, Y. (1994). Some results on covariance of function of order statistics. Statistics and Probability Letters 19: 111–114.CrossRefGoogle Scholar
29.Rinott, Y. & Pollak, M. (1980). A strong ordering induced by a concept of positive dependence and monotonicity of asymptotic test sizes. Annals of Statistics 8: 190–198.CrossRefGoogle Scholar
30.Shaked, M. (1979). Some concepts of positive dependence for bivariate interchangeable distributions. Annals of the Institute of Statistical Mathematics 31: 67–84.Google Scholar
31.Shaked, M. & Shanthikumar, J.G. (1986). Multivariate imperfect repair. Operations Research 34: 437–448.CrossRefGoogle Scholar
32.Shaked, M., Spizzichino, F., & Suter, F. (2002). Nonhomogeneous birth processes and l ∞-sperical densities, with applications in reliability theory. Probability in the Engineering and Informational Sciences 16: 271–288.CrossRefGoogle Scholar
33.Shaked, M., Spizzichino, F., & Suter, F. (2004). Uniform order statistics property and l ∞-sperical densities. Probability in the Engineering and Informational Sciences 18: 275–297.Google Scholar
34.Spizzichino, F. (2001). Subjective probability models for lifetimes. New York: Chapman & Hall.CrossRefGoogle Scholar
35.Stepanov, A. (1992). [Limit theorems for weak records.] Theory Probability and Its Applications 38: 762–764.Google Scholar
36.Stepanov, A., Balakrishnan, N., & Hofmann, G. (2003). Exact distributions and Fisher information of weak record values. Statistics and Probability Letters 64: 69–81.CrossRefGoogle Scholar
37.Vervaat, W. (1973). Limit theorems for records from discrete distributions. Stochastic Processes and Their Applications 1: 317–334.Google Scholar
38.Wei, G. & Hu, T. (2006). Characterizations of aging classes in terms of spacings between record values. Technical report, Department of Statistics and Finance, University of Science and Technology of China, Hefei.Google Scholar
39.Wesolowski, J. & López-Blázquez, F. (2004). Linearity of regression for the past weak and ordinary records. Statistics 38: 457–464.CrossRefGoogle Scholar