Published online by Cambridge University Press: 22 June 2005
We study the concept of multivariate dispersion order, defined as the existence of an expansion function that maps a random vector to another one, for multivariate distributions with the same dependence structure. As a particular case, we can order the multivariate t-distribution family in dispersion sense. Finally, we use these results in the problem of detection and characterization of influential observations in regression analysis. This problem can often be used to compare two multivariate t-distributions.
Stochastic orderings arise in statistical decision theory in the comparison of experiments and estimation problems (see [17]). In particular, dispersion has been used to characterize the variability for distributions and it has been extensively studied (see [5,10,13,15,16], among others).
For univariate and multivariate distributions, the concept of dispersion is fundamental; a statistical research is unthinkable for a phenomenon without variability. Unfortunately, there is not a unique definition of dispersion and this problem is much more complicated for distributions on
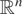
. For univariate distributions, Lewis and Thompson [13] introduced a concept of variability through the definition of the dispersion order (LT sense). Let F and G be two distribution functions; we say that F is less dispersive than G, denoted F [pr ]Disp G, if any pair of quantiles of G are at least as widely separated as the corresponding quantiles of F. Let u be a real value in (0,1); we use the definition of univariate quantile as follows:
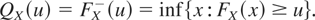
Many useful characterizations of the dispersion order can be found in the literature. An excellent handbook is that by Shaked and Shanthikumar [17]. One of the most interesting characterizations of this univariate order is given in [16]. Let F and G be two strictly increasing and absolutely continuous distribution functions; then X [pr ]Disp Y or F [pr ]Disp G, if and only if there exists a function Φ : SF → SG (where SF and SG are the support of F and G, respectively) such that Y =st Φ(X) and Φ′(x) ≥ 1 for all x in SF. Note that under the last condition, the function Φ is an expansion function; that is, the function Φ verifies Φ(x) − Φ(x′) ≥ x − x′, for all x > x′. Hence, the dispersion ordering in the LT sense is based on the existence of an expansion function that depends on the corresponding distribution functions. Furthermore, in this case, Φ(x) = QY(FX(x)) for all x in SF.
An extension of the univariate dispersion order to the multivariate case was given by Giovagnoli and Wynn [9]. A function
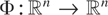
is called an expansion if
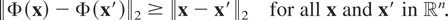
Let X and Y be two n-dimensional random vectors. Suppose that
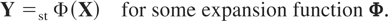
Then we say that X is less than Y in the strong multivariate dispersion order (denoted by X [prcue ]SD Y).
Roughly speaking, the strong multivariate dispersive order is based on the existence of an expansion function that maps stochastically a random vector to another one. Obviously, the ordering in the [prcue ]SD sense is intuitively reasonable and it satisfies many desirable properties. For instance, the strong dispersion ordering implies that ∥X − X′∥2 [pr ]st ∥Y − Y′∥2, where ∥·∥2 corresponds to the Euclidean norm and X′ and Y′ are two independent values for X and Y, respectively. It also implies that Tr(ΣX) ≤ Tr(ΣY), where ΣX and ΣY are the covariance matrices for X and Y, respectively, see Giovagnoli and Wynn [9]. As a consequence of these properties, the [pr ]SD multivariate order has a clear interpretation in dispersion terms.
In the multivariate case, there exist several transformations that map one multidimensional random variable to another one. For this reason, it seems intuitive to define a multivariate dispersion order based on a particular transformation. Note that in the univariate case, the function Φ depends on the corresponding distribution functions, so it has a unique expression. These considerations led Fernández–Ponce and Suárez–Llorens [7] to define a concept of multivariate dispersion order based on the existence of a particular expansion function and, in addition, has a particular interpretation as multivariate quantiles more widely separated.
From this point forward, we assume that X1,…,Xn have an absolutely continuous joint distribution and the corresponding conditioned variables are also absolutely continuous with density functions strictly positive. Let u = (u1,…,un) be a vector in [0,1]n. The multivariate u-quantile for X, denoted as
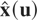
, is defined as follows:
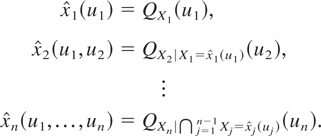
This last construction is widely used in simulation theory, and it is named the standard construction. Obviously, the standard construction depends on the choice of the ordering of the marginal distributions. The notion of the standard construction can be interpreted as a quantile function on
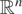
. Fernández-Ponce and Suárez-Llorens [7] provide the notion of corrected orthant associated to the standard construction that interprets the accumulated probability in all orthants.
The definition of the multivariate u-quantile for X led us to define the multivariate x-rate vector, denoted
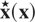
, as
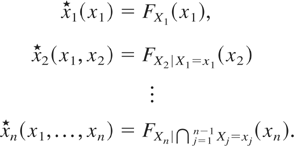
Under the notion of the standard construction and the interpretation as multivariate quantiles, Fernández-Ponce and Suárez-Llorens [7] defined the multivariate dispersive order as a generalization of the univariate dispersive order in the LT sense.
Definition 1: Let X and Y be two random vectors in

. We say that X is less than Y in dispersion sense, denoted as X [pr ]Disp Y, if
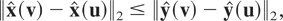
for all u and v in (0,1)n.
Note that this new ordering depends on the chosen permutation (see [7]). Definition 1 defines a multivariate dispersion ordering as quantiles that are more widely separated. Theorem 1 characterizes the multivariate dispersion order by means of a particular expansion function.
Theorem 1: Let X and Y be two random vectors in
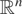
with their distribution functions satisfying the regularity conditions. Then it holds that X [pr ]Disp Y if and only if there exists a function Φ such that
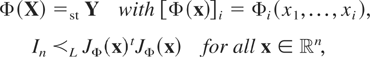
where JΦ(x) is the Jacobian matrix of Φ.

Moreover, in this case,
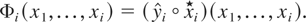
Note that the symbol [pr ]L represents the well-known Loewner ordering of matrices, where A [pr ]L B if and only if the matrix B − A is nonnegative definite. Condition (1) implies that the function Φ is an expansion function; that is, it holds that
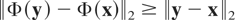
for all x, y in

(see [9]).
To summarize, the multivariate dispersion order can be simplified just by checking whether the multivariate function Φ = (Φ1,…,Φn), defined as
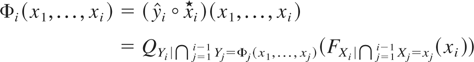
for i = 1,…,n, is an expansion function.
It is apparent that this ordering is a generalization of the dispersive ordering in the LT sense. The multivariate dispersive ordering is characterized through a particular expansion function, so it obviously implies the strong multivariate dispersive ordering. Then we will always consider the multivariate concept of dispersion in the Giovagnoli and Wynn sense. However, when we study the particular case defined by function (2), we will call the strong multivariate dispersion order as the multivariate dispersion order, denoted [pr ]Disp.
The organization in this article is as follows. In Section 2, we will show the multivariate dispersion order between two multivariate random variables, with the same copula, is characterized by the univariate dispersion order for the corresponding marginal distributions. In Section 3, we will use the results from Section 2 to order the multivariate t-Student family in a dispersion sense, [pr ]Disp or [pr ]SD, according to properties of the precision matrix and the degrees of freedom. Finally, in Section 4, we will apply this ordering in the problem of the detection and characterization of influential observations in regression analysis. This problem can be often used to compare two multivariate t-distributions.
Now, we characterize the multivariate dispersion order, [pr ]Disp, for random variables with the same dependence structure in the sense that they have the same copula. A copula C is a cumulative distribution function with uniform margins on [0,1]. Furthermore, it is shown that if H is an n-dimensional distribution function with margins F1,…,Fn, then there exists an n-copula C such that for all x in
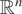
, it holds that

Moreover, if F1,…,Fn are continuous, then C is unique (for more details about copulas, see Nelsen [14]). It follows that if X = (X1,…,Xn) and Y = (Y1,…,Yn) are two n-dimensional random variables, then they have the same copula if and only if

Within this setting, we can formulate the following theorem.
Theorem 2: Let X = (X1,…,Xn) and Y = (Y1,…,Yn) be two n-dimensional random vectors such that they have the same copula, denoted as C. Then X [pr ]Disp Y if and only if Xi [pr ]Disp Yi for all i = 1,…,n.
Proof: In light of Theorem 1, it is only necessary to prove that the component Φi of the function Φ has the following expression:

for i = 1,…,n. In other words, the component Φi of the function Φ, which maps the random vector X to Y, only depends on the ith marginal variable. Note that if (3) holds, the Jacobian matrix of Φ is a diagonal matrix in which the diagonal elements are the functions that map the univariate marginal distribution of X to the corresponding one of Y. Hence, the condition (1) in Theorem 1 is apparent.
The proof of (3) is by mathematical induction. For n = 1, it is trivial. Let us assume that it is true for i = 1,…,j − 1; then we need to show it for i = j. By induction hypothesis, it holds that
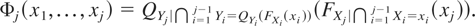
Furthermore, in light of the equality 2.9.1 in Nelsen [14], it is easy to show that
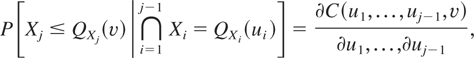
where C is the copula of the distribution function F. By assumption, F and G have the same copula; hence, using (4), it holds that
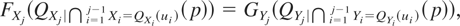
for all 0 ≤ p ≤ 1. Now, if we take ui = FXi(xi) in (5), we obtain that
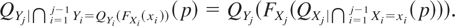
Note that if we now consider
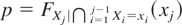
in (6), it is easy to verify that

Therefore, the proof is concluded. █
Corollary 1: Let (X1…,Xn) be a multivariate random vector. Let us consider hi a univariate strictly increasing expansion function for i = 1,…,n. Then it holds that
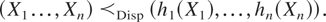
Proof: The corollary follows from the facts that any copula is invariant under monotone increasing transformations (see [14]) and the univariate dispersion order is invariant under strictly increasing expansion functions (see [17]). █
Note that this corollary provides many possible comparisons. In particular, if we take a real number a > 1, then it is easy to show that X [pr ]Disp aX.
Example 1: Let
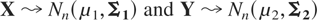
be two multivariate normal distributions. If ρijX = ρijY for all i and j and σiX < σiY, then X [prcue ]Disp Y. It is well known that under the last assumption, X and Y have the same copula. Thus, the proof is apparent using Theorem 2.
In this section, we apply some results obtained in the last section to the particular t-distribution family. For this purpose, we use the corresponding definition of the t-distribution from Bernardo and Smith [2, pp.139,140]. A continuous random vector X has a multivariate t-distribution or a multivariate Student distribution of dimension k, with parameters μ = (μ1,…,μk), Σ, and n, where

, Σ is a symmetric positive-definite k × k matrix and n > 0 if its probability density function, denoted Stk(x|μ, Σ,n), is

where
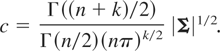
Although not exactly equal to the inverse of the covariance matrix, the parameter Σ is often referred to as the precision matrix of the distribution or, equivalently, the inverse matrix of the dispersion matrix. In the general case, E [X] = μ and Var(X) = Σ−1[n/(n − 2)].
Before introducing the results in this section, we need the definition of a univariate partial order strongly connected with the univariate dispersive ordering. We consider the tail ordering defined by Lawrence [12]. Let X and Y be two univariate random variables symmetric about zero; then we say that X is less in the tail order sense, denoted X [pr ]r Y, if the ratio QY(u)/QX(u) is nondecreasing (nonincreasing) for u ∈ (½,1) (u ∈ (0,½)). In the following theorem, we will use the definition of the tail ordering to order the univariate t-Student family.
Theorem 3: Let St1(0,1,m) and St1(0,1,m) be two univariate t-distributions. Then if n < m, it holds that St1(0,1,m) [pr ]Disp St1(0,1,n).
Proof: To simplify, denote tn as the univariate t-distribution with n degrees of freedom. Capéraà [3] showed that if n ≤ m, then tm [pr ]r tn. In addition, Doksum [6] showed that for univariate absolutely continuous distributions with F(0) = G(0) = 0 such that f (0) ≥ g(0) > 0 and QY(u)/QX(u) nondecreasing for all u ∈ (0,1), it holds that F [pr ]Disp G.
Under the last discussion, we consider the random variable |tn| with the density function given by

A straightforward computation shows that the distribution function of |tn| is F|tn|(x) = 2Ftn(x) − 1 for x ≥ 0. Hence, Q|tn|(u) = Qtn((u + 1)/2) for all u in the interval (0,1). Therefore, it is apparent, using the work of Capéraà [3], that if n ≤ m, then Q|tn|(u)/Q|tm|(u) is nondecreasing for all u ∈ (0,1). Since F|tm|(0) = F|tn|(0) = 0 and, of course f|tm|(0) > f|tn|(0), we obtain, using the result in [5] that |tm| [pr ]Disp |tn|. It is easy to check, using properties of symmetry, that |tm| [pr ]Disp |tn| implies that tm [pr ]Disp tn. █
Note that although in the literature the degrees of freedom of a t-distribution are always associated with the dispersion and the lack of knowledge of the experiment, the previous result provides that the t-distribution family is ordered in a really strict dispersion order. To study in depth the implications of the univariate dispersion order, see Shaked and Shanthikumar [17].
We have ordered two univariate t-distributions pertaining to the degrees of freedom. If we consider the more general class when the precision is different, the following corollary holds.
Corollary 2: Let St1(0,σ1,m) and St1(0,σ2,n) be two univariate t-distributions that satisfy that for n ≤ m and σ2 ≤ σ1, St1(0,σ1,m) [pr ]Disp St1(0,σ2,n).
Proof: The proof is apparent. █
Note that the precision matrix is related to the variance through the expression Var(St1(0,σ1,m)) = σ1−1(m/m − 2).
From this point forward, we will consider two multivariate t-distributions. We generalize the results obtained in Theorem 3 and Corollary 2 to the multivariate case.
Theorem 4: Let Yn ∼ Stk(0, Σ,n) and Ym ∼ Stk(0, Σ,m) be two multivariate t-distributions with the same precision matrix and different degrees of freedom. Then if n ≤ m, it holds that Stk(0, Σ,m) [pr ]Disp Stk(0, Σ,n).
Although, of course, Theorem 4 is more general than Theorem 3, we first need the results of this one to prove the multivariate case.
Proof: Let Ym = (Ym,1,…,Ym,k) and Yn = (Yn,1,…,Yn,k) be the corresponding multivariate t-distributions. First, we need to prove that two multivariate t-distributions with the same precision matrix have the same copula. For this purpose, we define the random vector X such as
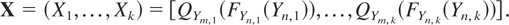
From Exercise 2.15 in Nelsen [14], it holds that the multivariate distributions X and Yn have the same copula. We only have to prove that X =st Ym.
First, from the well-known result that the function QYm,i(FYn,i)(·) for i = 1,…,k, maps the univariate random variable Yn,i to Ym,i, we know that all marginal distributions of X are generalized t-distributions. Hence, using Theorem 1 from Arellano-Valle and Bolfarine [1], we know that X is a multivariate t-distribution with parameters
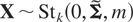
. From the fact that X and Ym have the same degrees of freedom, it is only necessary to show that Var(X) = Var(Ym). Of course, it holds that Var(Xi) = Var(Ym,i) for all i = 1,…,n. Hence, both matrices have the same diagonal elements.
Since X and Yn have the same copula, it is easy to show, using Theorem 5.1.3 in Nelsen [14], that
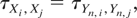
where τX,Y is the population version of Kendall's tau for X and Y. Therefore, using Theorem 3.3 from Frahm, Junker, and Szimayer [8], it holds that they also have the same Pearson's coefficient, ρ, so
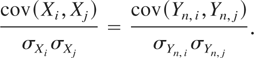
Using the fact that Yn and Ym have the same precision matrix, if we denote Var(Yn) = (σij,n) and Var(Ym) = (σij,m), it holds that
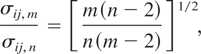
for all i,j = 1,…,k. Hence, it is apparent that cov(Xi,Xj) = cov(Ym,i,Ym,j) and, of course,
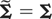
, which implies that Ym =st X.
We have already shown that Ym and Yn have the same copula. Hence, using first Corollary 2 and then Theorem 2, we have that Ym [pr ]Disp Yn. █
At this point, we focus our attention on ordering two multivariate t-distributions with different precision matrices.
Theorem 5: Let Y1 ∼ Stk(0, Σ1,n) and Y2 ∼ Stk(0, Σ2,n) be two multivariate t-distributions with different precision matrices and the same degrees of freedom. Then the following conditions are equivalent:
Proof: It is analogous to Theorem 4 in Giovagnoli and Wynn [9]. █
Note that if both distributions have the same degrees of freedom, it is easy to find several linear transformations that map one t-distribution to the other one. Obviously, this not the case when they have different degrees of freedom; the possible transformations are clearly not linear.
It is necessary to take in account that Theorem 5 does not provide a characterization of the multivariate dispersion order. As we mentioned earlier, the [pr ]Disp ordering is associated to a particular transformation given by the function in (2). Just looking at Example 4.1 in [7] for the multivariate Normal distributions, it is easy to show the linear expression of Φ when we are interested in comparing two multivariate t-distributions. This expression depends on the Cholesky decomposition of the matrices Σ2−1 and Σ1−1.
However, in the conditions of Theorem 5, it holds that Stk(0, Σ1,n) [prcue ]SD Stk(0, Σ2,n). We emphasize that [prcue ]SD is a weaker multivariate dispersion order than the [pr ]Disp ordering. Hence, at least there exists an expansion function that maps one t-distribution to the other one. As we will show in Section 4, we only need to know about the [prcue ]SD order in order to define a new measure of Bayesian influence.
Corollary 3 is needed to compare t-distributions when both degrees of freedom and precision matrices are different.
Corollary 3: Let Y1 ∼ Stk(0, Σ1,m) and Y2 ∼ Stk(0, Σ2,n) be two multivariate t-distributions with different precision matrices and degrees of freedom. Then if it holds that λ(Σ2−1) ≥ λ(Σ1−1) and n < m, then Stk(0, Σ1,m) [prcue ]SD Stk(0, Σ2,n).
Proof: The result follows straightforward from the fact that
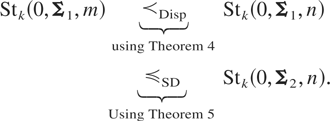
From the well-known result that a composition of two expansion functions is also an expansion function, it easily holds that Stk(0, Σ1,m) [prcue ]SD Stk(0, Σ2,n). █
Note that Corollary 3 provides a sufficient condition for the [prcue ]SD order. It is easy to show that under this condition, it also holds that

However, this last implication cannot be considered a sufficient condition. The reason is that the variance matrix is defined through both the precision matrix and degrees of freedom.
Johnson and Geisser [11] proposed a method of assessing the influence of specified subsets of the data when the goal is to predict future observations using predictive densities. For this purpose, they considered the following model: Y = Xβ + ε, where ε is an N × 1 random vector distributed as MNn(0,θI) (N-dimensional multivariate normal (MN)) with mean vector 0 and covariance matrix θI, θ scalar, β is the p × 1 vector of regression coefficients, X is an N × p matrix of fixed “independent” variables, and Y is the N × 1 vector of responses on the “dependent” variable. Although they noted that a more general model is possible, they assumed the prior density for β and θ to be g(β,θ) ∝ θ−1, which presumes that little prior information is available relative to that information inherent in the data. Assume the case when a particular subset of size k has been deleted; we denote this by (i), and the subset itself is indicated by i. Then the general linear model can then be expressed as
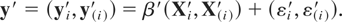
Thus, the predictive densities based on full and subset deleted datasets, when θ is unknown, are two multivariate t-distributions with parameters
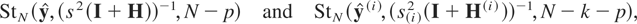
where
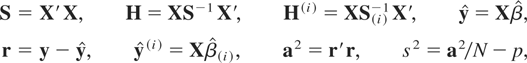
and let S(i), a(i)2, and s(i)2 be similarly defined.
In this case, the problem of detecting influential observations is based on comparing two multivariate t-distributions. If we only study the comparison in terms of variability, it seems logical that if we delete a subset of data, then the obtained predictive density will be expected to be more dispersive than the one based on full data. In other words, it would be expected that f (·) [pr ]SD f(i)(·). This may be interpreted as the added variability, due to deletion of data subset i. However, it is not true that every subset of data with a fixed size k has the same influence. First, using Corollary 3, we checked that f (·) [pr ]SD f(i)(·) for all
subsets, k = 1,2,3. We do not consider it necessary to present these comparisons in this article. After these comparisons, and clearly inspired in Corollary 3, we can define a dispersion Bayesian influence in terms of variability (DBIV) measure to the i subset as

and we will order the subsets from least to most influential according to the magnitude of Qi2. Note that under the assumptions in Corollary 3, if we have the inequality λ(s(i)2(I + H(i))) ≥ λ(s2(I + H)), then it holds that f (·) [pr ]SD f(i)(·).
We consider data from the 1975 Florida Area Cumulus Experiment (FACE) previously discussed in great detail by Cook and Weisberg [4]. This experiment was conducted to determine the merits of using silver iodide to produce rainfall increases and to isolate factors contributing to treatment until additivity. There were 24 observations on 11 variables, including the response rainfall, an indicator variable determining whether clouds were seeded or not seeded, and 8 other variables, including interaction terms that were determined to be related to rainfall.
Initially, we will analyze the full dataset and then delete case 2 (observation 2) and reanalyze in its absence. For an initial analysis, a computer program was written to compute relevant statistics for all
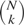
subsets, k = 1,2,3 and N = 23,24 using the Maple 6 package.
A summary of these results for the full dataset, as well as for the full dataset with case 2 deleted, is given in Table 1. It is clear from Table 1 that observations 2, 18, 1, 15, 6, and 3 are most influential in the dispersion sense when k = 1. Moreover, case 2 is clearly an outlier and it significantly affects predictive inferences based in this dataset from the dispersion point of view. Also, it is interesting to note that when case 2 is deleted, the most influential observations in dispersion sense are 18, 1, 15, 5, 6, and 23. Although the order has been changed, we can observe that the differences among the influence measures are not significative. When k = 2 or 3, it is clear from Table 1 that case 2 will be included in most influential subsets. However, we choose to delete case 2 and perform a more careful analysis. Inspection of Table 1 reveals that observations 18 and 1 are not only the most individual influence observations but also the most influential pair. Also, we can observe that case 18 appears jointly with case 1 in the third most influential triple. Also, we note that the pair (1,18) appears in two influential triples. Consequently, the influence for case (1,18) must be taken into account in a dispersion sense.
Top Six Most Influential Subsets k = 1,2,3

Surprisingly, the most influential triple is not composed of the three most influential cases, but the third most influential triple coincides with cases that are most influential individually and in pairs.
With this analysis, we present a way to study the influence of specified subsets of the data in a dispersion sense complementary to the analysis of Johnson and Geisser [10]. This is not obviously an alternative method for studying the divergence between f (·) and f(i)(·). The reason is why the study of the dispersion is, of course, location independent and the location component given by the means of the t-distributions is specially important to study the lack of fit of the model, as Johnson and Geisser [11] showed. However, this study provides an interesting point of view and we would like to emphasize that it was not necessary for the approximation of substituting the multivariate t-distribution for a scaled multivariate Normal density.
We wish to thank the referees whose careful reading and marking in the first version of this manuscript led to a number of corrections.

Top Six Most Influential Subsets k = 1,2,3