Published online by Cambridge University Press: 12 December 2005
Consider a discrete-time insurance risk model with risky investments. Under the assumption that the loss distribution belongs to a certain subclass of the subexponential class, Tang and Tsitsiashvili (Stochastic Processes and Their Applications 108(2): 299–325 (2003)) established a precise estimate for the finite time ruin probability. This article extends the result both to the whole subexponential class and to a nonstandard case with associated discount factors.
Following the works of Nyrhinen [14,15] and Tang and Tsitsiashvili [17,19], we consider the finite time ruin probability of an insurer who invests his wealth into a risky asset. In this stochastic economic environment, the net loss during period n is denoted by a real-valued random variable Xn, n = 1,2,…, and the discount factor from time n to time n − 1 is denoted by another positive random variable Yn, n = 1,2,….
Write An = −Xn and Rn = Yn−1 − 1, n = 1,2,…. Then An denotes the total net income and Rn denotes the total stochastic return rate within period n. We tacitly assume that the income An or the loss Xn is calculated at time n. Let the initial surplus of the insurer be S0 = x ≥ 0. Then the surplus accumulated until time n, denoted by Sn, can be characterized by the recurrence equation
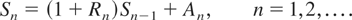
The probability of ruin within time n is defined as
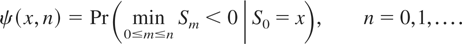
Iterating (1.1) and rewriting the resulting formulas in terms of {Xn : n = 1,2,…} and {Yn : n = 1,2,…}, we obtain that
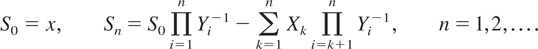
It follows that
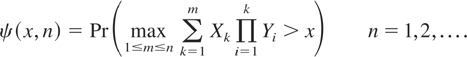
By (1.2), we immediately see that the two-sided inequality
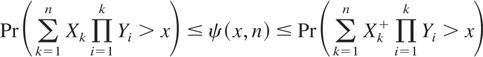
holds for n = 1,2,…, where X+ = X1(X≥0) denotes the positive part of a random variable X and 1A denotes the indicator function of a set A. This inequality will be used below.
Tang and Tsitsiashvili [17,19] made the following standard assumptions:

Under these assumptions, Tang and Tsitsiashvili [17] derived a precise asymptotic estimate for the finite time ruin probability for the case that the loss distribution F belongs to a certain subclass of the subexponential class; see also Tang and Tsitsiashvili [19] for a broader account.
In the present article we aim at extensions of the result of Tang and Tsitsiashvili [17]. In the rest of this article, after a brief review on heavy-tailed distributions in Section 2, we give in Section 3 the first main result in which the loss distribution F ranges over the whole subexponential class, and we give in Section 4 the second main result in which the discount factors {Yn : n = 1,2,…} or, equivalently, the return rates {Rn : n = 1,2,…} are associated.
The most important class of heavy-tailed distributions is the subexponential class. By definition, a distribution F = 1 − F on [0,∞) or its corresponding random variable is said to be subexponential, denoted by
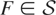
, if the relation
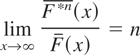
holds for some (or, equivalently, for all) n = 2,3,…, where F*n denotes the n-fold convolution of F. More generally, a distribution F on (−∞,∞) is still said to be subexponential if the distribution F+(x) = F(x)1(x≥0) is subexponential. By Lemma 2.1 and the last inclusion of (2.3) below, it is easy to verify that (2.1) remains valid for the latter general case. The class

contains the Pareto-like, the lognormal-like, and the Weibull-like distributions.
Closely related are the class
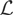
of long-tailed distributions and the class
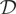
of distributions with dominatedly varying tails. A distribution F on (−∞,∞) belongs to the class
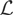
if the relation
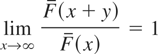
holds for some (or, equivalently, for all) y > 0; F belongs to the class
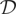
if the relation
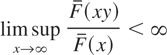
holds for some (or, equivalently, for all) 0 < y < 1.
It is well known that
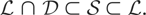
For more details of heavy-tailed distributions, we refer the reader to Embrechts, Klüppelberg, and Mikosch [8] and references therein.
In what follows, all limiting relationships are for x → ∞ unless stated otherwise. For two positive functions a(·) and b(·), we write a(x) = O(b(x)) if lim sup a(x)/b(x) < ∞, a(x) = o(b(x)) if lim a(x)/b(x) = 0, a(x) ∼ b(x) if lim a(x)/b(x) = 1, and a(x) [lsim ] b(x) if lim sup a(x)/b(x) ≤ 1.
The following lemma is well known; see Embrechts and Goldie [7], Cline [5, Cor. 1], and Tang and Tsitsiashvili [17, Lemma3.2].
Lemma 2.1: Let F be the convolution of two distributions F1 and F2. If
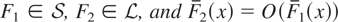
, then

and

The following lemma is from Cline and Samorodnitsky [6, Thm.2.1].
Lemma 2.2: Let X and Y be two independent random variables with distributions F and G, respectively, satisfying

. The distribution H of the product XY is subexponential if there is a positive function a(x) = o(x) such that F(x − a(x)) ∼ F(x) and G(a(x)) = o(H(x)).
Let us go back to the model introduced in Section 1. Hereafter, denote the generic random variable of {Xn : n = 1,2,…} (under assumption P1) by X, the generic random variable of {Yn : n = 1,2,…} (under assumption P2) by Y, and the distribution of XY (under assumptions P1, P2, and P3) by H = F [otimes ] G.
The main result of Tang and Tsitsiashvili [17] is that, under assumptions P1, P2, and P3, the relation
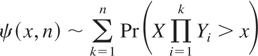
holds for each n = 1,2,… if
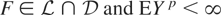
for some large p > 0 (more precisely, for some p larger than the upper Matuszewska index of the distribution F). The estimate given by (3.1) enables us to recursively calculate the ruin probability ψ(x,n). However, an obvious drawback is that the condition
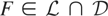
excludes many popular distributions such as the lognormal-like and the Weibull-like distributions; recall (2.2).
The following is our first main result, which extends the scope of the loss distribution to the whole subexponential class
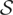
:
Theorem 3.1: Assume P1, P2, and P3. If

and there is some 0 < τ < 1 such that F(x − xτ) ∼ F(x) and G(xτ) = o(H(x)), then (3.1) holds for each n = 1,2,….
Two concrete cases of Theorem 3.1 are listed below without proof.
Corollary 3.1: Assume P1, P2, and P3. Relation (3.1) holds for each n = 1,2,… if one of the following groups of conditions is valid:
(A) F is lognormal-like with a tail satisfying F(x) ∼ cF1(x) for some c > 0, where the distribution F1 has a density function

with −∞ < μ < ∞ and σ > 0, and G(xτ) = o(H(x)) for some 0 < τ < 1.
(B) F is Weibull-like with a tail satisfying F(x) ∼ c exp{−dxν} for some c, d > 0, 0 < ν < 1, and G(xτ) = o(H(x)) for some 0 < τ < 1 − ν.
Clearly, both in Theorem 3.1 and Corollary 3.1, the condition G(xτ) = o(H(x)) is implied by G(xτ) = o(F(x)). More concretely, in Corollary 3.1(A) the G can be every Weibull distribution or every lognormal distribution with a density function
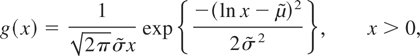
as long as
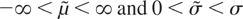
, and in Corollary 3.1(B) the G can be every Weibull-like distribution with a tail
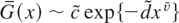
as long as
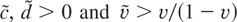
.
In the proof of Theorem 3.1 we will need the following lemma.
Lemma 3.1: Under the conditions of Theorem 3.1, it holds for each k = 1,2,… that
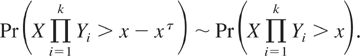
Proof: We only prove the result for k = 1 since the general case extends by induction. Trivially, the condition F(x − xτ) ∼ F(x) implies that F(x − Cxτ) ∼ F(x) holds for every constant C > 0. Choose some 0 < ε < 1 such that G(ε) > 0. Then it holds for all large x > 0 and t ∈ (ε,xτ] that
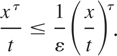
For all large x > 0, we derive

It follows that
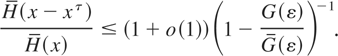
Since G(0) = 0 and ε > 0 can be arbitrarily small, we obtain
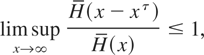
which actually amounts to H(x − xτ) ∼ H(x). █
Proof of Theorem 3.1: Recall the two-sided inequality (1.3). If we can prove the relation
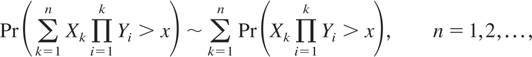
without using F(0−) > 0, then the same proof should also be valid for the relation
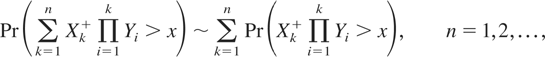
and we immediately obtain (3.1). Write
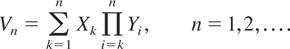
Under assumptions P1, P2, and P3, it is clear that
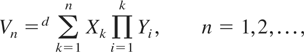
where =d denotes “equal in distribution.” Based on this analysis, it suffices to prove the relation
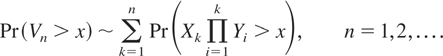
In view of Theorem 4.1 below, we only need to consider the case that Y is unbounded. We prove the asymptotic relation (3.2) by the inductive method.
Trivially, (3.2) holds for n = 1. Applying Lemma 2.2, we also know that V1 is subexponential. Now we assume by induction that (3.2) holds for n = m ≥ 1 and that Vm is subexponential. Clearly, F(x) = O(Pr(Vm > x)) since G(1) > 0. From Lemmas 2.1 and 3.1 and the inductive hypothesis, it follows that the sum Xm+1 + Vm is subexponential and that

Hence, by Lemma 2.2, the random variable Vm+1 is subexponential. By Lemma 2.1 and the inductive hypothesis, we derive that

This proves that (3.2) holds for n = m + 1. By the mathematical inductive method, we conclude that (3.2) holds for each n = 1,2,…. █
Recently, the study on ruin probabilities of nonstandard models has become an important part of risk theory. We refer the reader to Cai [1,2] and Cai and Dickson [4], among many others.
Now we propose a general (positively) dependence structure for the discount factors. We say that a sequence of random variables {Yn : n = 1,2,…} is (positively) associated if the inequality
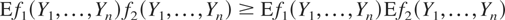
holds for all n = 1,2,… and all coordinatewise (not necessarily strictly) increasing functions f1 and f2 for which the moments involved exist. Since it was introduced by Esary, Proschan, and Walkup [9], this dependence structure has been extensively studied and applied by many researchers in statistics, applied probability, insurance, and finance. Trivially, if in the above definition f1 is coordinatewise increasing but f2 is coordinatewise decreasing, then (4.1) is changed to
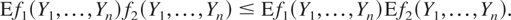
The following is our second main result, which partially extends Theorem 3.1 to the proposed nonstandard case:
Theorem 4.1: Assume P1, P3, and
P2′: The discount factors {Yn : n = 1,2,…} constitute a sequence of bounded, associated, and positive random variables.
If

, then (3.1) holds for each n = 1,2,….
Theorem 4.1 indicates that the association of the bounded discount factors does not influence the asymptotic relation (3.1). Moreover, if we restrict the discussion to the case of Pareto-like loss distributions, then under assumptions P1 and P3, using a result of Resnick and Willekens [16], it is not difficult to prove that (3.1) even holds for arbitrarily dependent discount factors {Yn : n = 1,2,…} as long as they satisfy suitable summability conditions.
We also remark that the boundedness condition of Theorem 4.1 is not so restrictive for application. For example, it allows for a realistic case below (see also Example 4.1 of Tang and Tsitsiashvili [19]).
Suppose that an insurer invests his wealth not only in a risk-free asset (a bank) but also in a risky asset (a stock market). At time n − 1, the insurer has wealth Sn−1, and he keeps a nonrandom fraction, say 0 < an ≤ 1, of his wealth in the bank and invests the remaining part in the stock market. Then, at time n, the first part becomes an(1 + rn)Sn−1 with some deterministic interest rate rn ≥ 0 and the second part becomes (1 − an)(1 + Rn)Sn−1 with some stochastic return rate Rn ∈ [−1,∞). Consequently, the discount factors equal
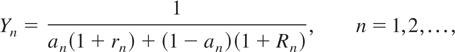
which are obviously bounded from above by positive constants.
For related discussions in continuous-time settings, see Hipp and Plum [12], Gaier and Grandits [10], Gaier, Grandits, and Schachermayer [11], Cai [3], Liu and Yang [13], among others.
Additionally, from (4.3) we see that if 0 < an < 1 for n = 1,2,…, the association of {Yn : n = 1,2,…} is equivalent to that of {Rn : n = 1,2,…}.
In the proof of Theorem 4.1, we will need the following lemma, which is a restatement of Proposition 5.1 of Tang and Tsitsiashvili [18].
Lemma 4.1: Let {X1,…,Xn} be n i.i.d. real-valued random variables with common distribution

. Then, for arbitrarily fixed 0 < a ≤ b < ∞, the relation
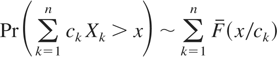
holds uniformly for (c1,…,cn) ∈ [a,b] × ··· × [a,b]; that is,
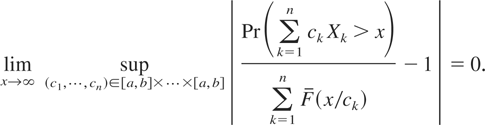
Proof of Theorem 4.1: Choose some constant d = dn > 1 as a common upper bound of the random variables {Y1,…,Yn}. First, we derive an asymptotic upper bound for ψ(x,n). For an arbitrarily fixed 0 < ε < 1 such that Pr(ε < Yj ≤ d) > 0 for each j = 1,…,n, we split the probability on the right-hand side of (1.3) into two parts as

Since the random variables {Y1,…,Yn} are associated and are independent of the nonnegative random variables {X1+,…,Xn+}, by (4.2) it holds that

Substituting (4.6) into (4.5) and rearranging the resulting inequality, we have
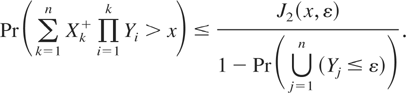
For J2(x,ε), on the event
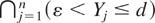
, we have

Hence, by Lemma 4.1 and the independence between {X1,…,Xn} and {Y1,…,Yn},
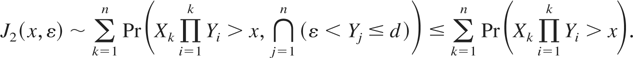
Substituting (4.8) into (4.7) yields
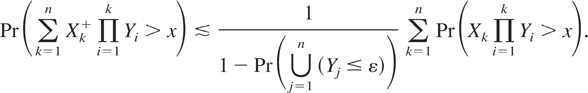
Since the random variables {Y1,…,Yn} are positive and ε > 0 can be arbitrarily small, we prove that
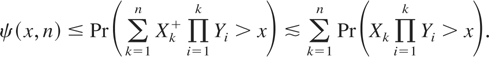
Now we aim at an asymptotic lower bound. From (1.3), Lemma 4.1, and the association of the random variables {Y1,…,Yn}, we derive

As earlier, by letting ε [nearr ] 0, we conclude that
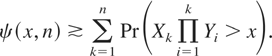
Combining (4.9) and (4.10) leads to the announced result (3.1). █
The author wishes to thank Gurami Tsitsiashvili for his recent joint works and thank the referee for his/her helpful comments. This work was supported by the Natural Science and Engineering Research Council of Canada (project No. 311990).