1. Introduction
Many of the political phenomena we are interested in are outcomes of interactions between units in political systems. These relational systems are complex, featuring interdependence among units that cannot be appreciated when the system is reduced to independent components. Network approaches to modeling provide useful alternatives (Lazer, Reference Lazer2011; Cranmer and Desmarais, Reference Cranmer and Desmarais2016), and recent advancements in inferential network analysis have improved our ability to understand these complex systems (Cranmer et al., Reference Cranmer, Leifeld, McClurg and Rolfe2017). Notably, adoption of the exponential random graph model (ERGM) and its extensions, which allow for statistical inference explicitly on network generating processes, presents us with a way to test relational theories in a theoretically and statistically valid manner (Cranmer and Desmarais, Reference Cranmer and Desmarais2011; Lusher et al., Reference Lusher, Koskinen and Robins2013). At the present, the ERGM family of models has been used to study a variety of political phenomenon.Footnote 1
ERGMs are highly flexible in the features that can be specified as network generating processes, and by extension in the types of networks that can be modeled, but contemporary applications of ERGMs have been largely limited to systems containing relations of a single type. However, political systems often are not as cleanly self-contained as we imply when we treat them as monoplex networks, defined as those with only a single type of tie. Across various commonly studied political systems, researchers have been calling for recognition that there are meaningful interdependencies between them, or to treat these systems as subcomponents of larger processes (e.g., Nye and Keohane, Reference Nye and Keohane1971; Keck and Sikkink, Reference Keck and Sikkink1998; Keohane, Reference Keohane2009; Alter and Meunier, Reference Alter and Meunier2009). For example, in studies of organized conflict, commonly identified mechanisms driving conflict initiation such as diversionary incentives (Downs and Rocke, Reference Downs and Rocke1994; Tir and Jasinski, Reference Tir and Jasinski2008) often imply that different types of belligerent behavior within the global conflict system can be substitutes or complements of each other (Starr, Reference Starr1994). Another example can be found within the broad set of related research agendas on policy-making at different levels of political organization. In these policy networks, information transmission between political actors occurs through a variety of channels (Leifeld and Schneider, Reference Leifeld and Schneider2012; Heaney, Reference Heaney2014; Montgomery and Nyhan, Reference Montgomery and Nyhan2017), and tend to have complementary effects on whether influence is successful (Böhmelt, Reference Böhmelt2010).
Complex interdependent systems such as the the global conflict system can be modeled as multilayer networks, a generalized framework for representing networks that are multimodal, multiplex, temporally dynamic, or characterized by any combination of these complex features (Boccaletti et al., Reference Boccaletti, Bianconi, Criado, Del Genio, Gómez-Gardenes, Romance, Sendina-Nadal, Wang and Zanin2014; Kivelä et al., Reference Kivelä, Arenas, Barthelemy, Gleeson, Moreno and Porter2014). This approach opens important avenues of research, but at the present, the development of methods for studying multilayer networks is a relatively nascent endeavor. In particular, ERGM-based inferential network analysis is highly adaptable to multilayer networks, but aside from methodological illustrations using a specific subtype of multilayer networks (e.g., Wang et al., Reference Wang, Robins, Pattison and Lazega2013, Reference Wang, Robins, Pattison and Lazega2016), fully implemented multilayer applications of ERGMs that model interdependence across subsystems remain limited, especially in the study of politics (Hollway and Koskinen, Reference Hollway and Koskinen2016).
This paper facilitates better understanding of inferential analysis of multilayer networks as an approach for studying complex interdependent systems comprising multiple relational contexts. I draw on developments in network science (Boccaletti et al., Reference Boccaletti, Bianconi, Criado, Del Genio, Gómez-Gardenes, Romance, Sendina-Nadal, Wang and Zanin2014; Kivelä et al., Reference Kivelä, Arenas, Barthelemy, Gleeson, Moreno and Porter2014), in particular the multilayer network as a generalized framework for representing networks comprising differentiated nodes and ties, to improve researchers' ability to better model social and political phenomena as they are intuitively understood. I describe an approach to conducting statistical inference on multilayer networks using the ERGM. There have been previous work on statistical inference of multilayer networks (Wang et al., Reference Wang, Robins, Pattison and Lazega2013, Reference Wang, Robins, Pattison and Lazega2016), but these applications focus on a specific subtype of multilayer networks. My work builds on these studies by describing the approach in terms of the generalized multilayer framework so as to encompass a wider range of social and political phenomena. Finally, this paper has a companion R package, multilayer.ergm, which facilitates the use of the ERGM with multilayer networks.Footnote 2
The multilayer network approach to modeling political systems presents researchers with a tool to more carefully account for the complexity present in political phenomena. In addition to the applications I present in this paper, this approach is applicable to a wide range of topics in political science, including international regimes (Alter and Meunier, Reference Alter and Meunier2009), legislatures (Montgomery and Nyhan, Reference Montgomery and Nyhan2017), and political campaigns (Heaney and Leifeld, Reference Heaney and Leifeld2018). As a network-based approach, it facilitates a systems perspective to understanding politics without sacrificing the granularity that unit-level analysis affords. In the study of international relations, in particular, researchers have consistently presented the global system as one that features qualitatively distinct actors interacting with one another across a multitude of contexts that vary along many dimensions (Keck and Sikkink, Reference Keck and Sikkink1998; Alter and Meunier, Reference Alter and Meunier2009). As I demonstrate in this paper, the multilayer network approach excels at these applications.
The remainder of the paper is organized into two sections. First, using conflict in the post-Cold War Levant as a running example, I describe the process of modeling systems characterized by interdependence that span multiple relational contexts using the ERGM, including how to formally represent these systems as multilayer networks and how to specify appropriate model terms. Second, I describe two types of multilayer networks, the multiplex and the node-colored networks, that are useful for representing a range of different social and political systems. I illustrate each type of multilayer network using a substantive application. For the multiplex network, I use a policy communication network with two types of communication ties; for the node-colored network, I use a global conflict network with three types of conflict ties. Using these applications, I demonstrate that the multilayer network approach produces models that better fit observed reality, and allows researchers to test more complex relational theories.
2. Statistical Inference for Multilayer Networks
Examples of the complex systems introduced above are all characterized by the existence of more than one type of relation existing between one or more groups of actors. These systems can be represented as networks, and as such, modeled using the ERGM. However, as these networks are marked by complexities not present in monoplex networks (i.e., those with a single type of tie), certain extensions are required. In this section, I discuss how multilayer network representations of complex systems afford inferential leverage over monoplex network representations, and show how this can be done through extensions to the monoplex application of ERGMs.
To more clearly illustrate the concepts I am presenting, throughout this section I use a small data set as my running example. Specifically, I use the conflict network between states and nonstate actors in the Levant during the post-Cold War period (1989–1995). This set of conflicts is a subset of the global conflict system which I use as one of my two applications later in the paper. In this system there are three states,12 nonstate actors, and 17 conflict ties of three different types: militarized interstate disputes (MIDs), civil conflicts, and nonstate conflicts. Figure 1 contains two visualization of this network, with the traditional network plot on the left, and the multilayer network representation on the right. The multilayer representation groups nodes by their type into different layers such that the structure of the multilayer network is more easily discerned.
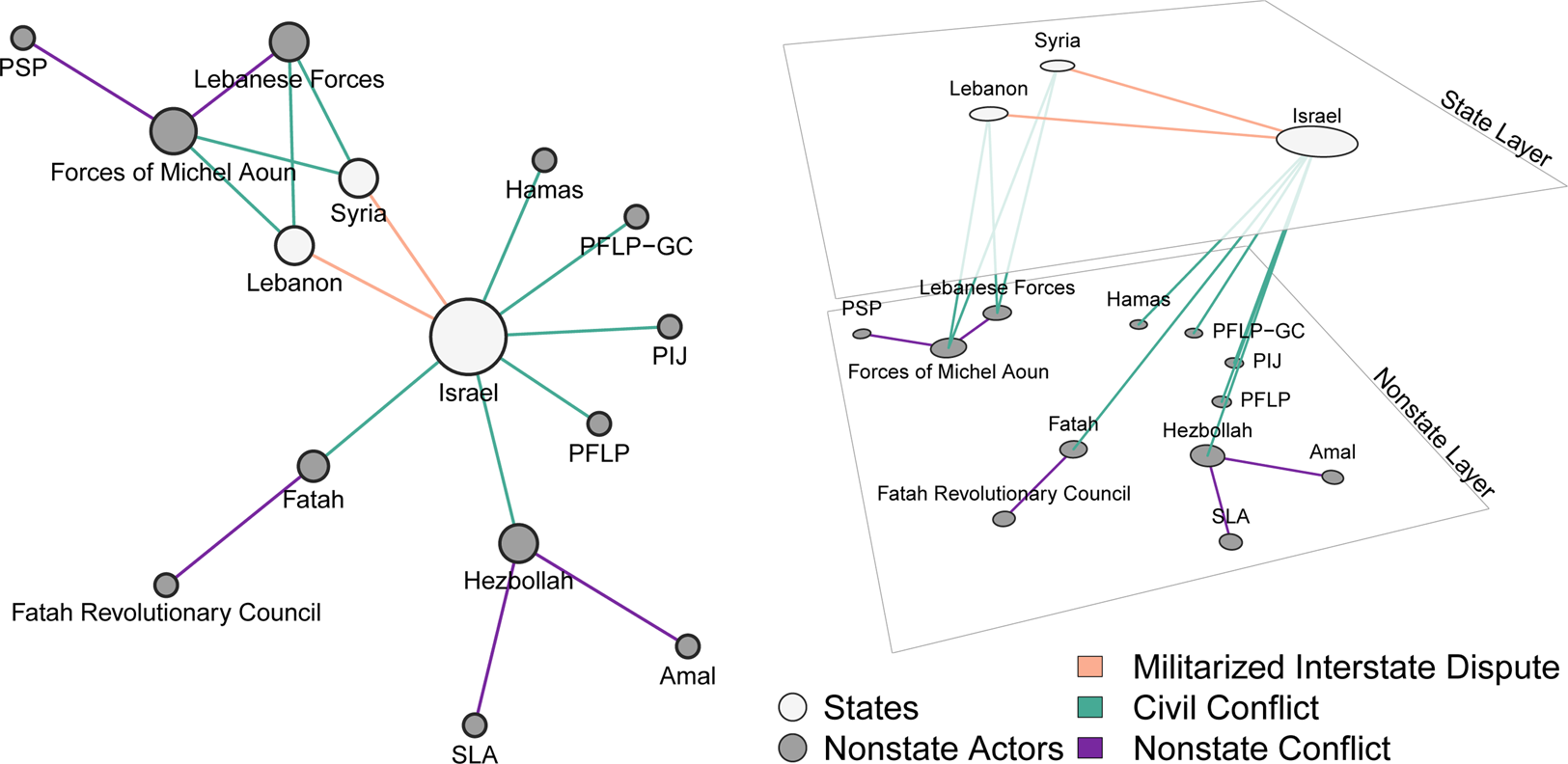
Figure 1. Levantine conflict network, post-Cold War period.
2.1. Modeling Complex Systems Comprising Multiple Relational Contexts
The standard statistical modeling approach in conflict studies, network-based or otherwise, is to examine one set of conflict processes as the outcome variable of interest, while potentially specifying other types of conflicts as exogenous model covariates (e.g., Gleditsch et al., Reference Gleditsch, Salehyan and Schultz2008). In terms of the Levantine conflict network, this means studying, for example, what led to Israel's conflicts with Lebanon and Syria. However, as is apparent from Figure 1, conflict in the region is not limited to these two incidents. Contemporaneous with these MIDs, all three states are engaged in conflicts with nonstate actors, some of whom are also in conflict with other nonstate actors. Isolated examination of these conflicts alone, even controlling for the presence of contemporaneous civil conflicts, misses interdependence that can exist across these processes.
To illustrate the advantage of simultaneously modeling different types of conflict processes, I discuss a set of models for explaining conflict in the Levant that differ in how they model interdependence in the network. To provide context, I first outline the events that led to the Israeli attack on Lebanon in July of 1993 (i.e., the reason for the tie between the two states on the Levantine conflict network). The direct precursor to the 1993 Israeli invasion into Lebanon can be traced to Israel's establishment of a security buffer zone in South Lebanon in 1982 (Luft, Reference Luft2000). The security zone was successful in driving Palestinian Liberation Organization (PLO) member groups out of the region, but the hostile occupation resulted in the birth of the Hezbollah, which began as a movement to expel Israeli occupiers (Jaber, Reference Jaber1997). Conflict persisted between Israel and Hezbollah through the early 1990s. In 1993, after a particularly intense period of Hezbollah aggression, Israel responded by launching a week-long attack into Lebanon.
The highly interdependent nature of the Levantine conflict network should be apparent from this account. To follow convention in the conflict studies literature and specify a model where MIDs are outcomes on interstate dyads and civil and nonstate conflicts are exogenous predictors requires the researcher to be satisfied with claiming that Hezbollah's decision to attack Israel was motivated by some reason completely unrelated to Israel's actions in Lebanon. This is an indefensible position given the wide recognition that the Hezbollah as a militant organization arose primarily in response to the Israeli occupation (Jaber, Reference Jaber1997). This is but one example from the region, with similar types of cross-type interdependence manifesting throughout this conflict network.
It is possible to account for interdependence within the entire conflict system by moving to a joint examination of the three different conflict processes without differentiating between them. In the network analysis context, this is to model the system as a monoplex network. This approach can yield certain insights, as different types of conflicts share similar properties (Cunningham and Lemke, Reference Cunningham and Lemke2013). From the traditional network plot in Figure 1, it is apparent the joint-but-monoplex network possesses features that are generally characteristic of conflict networks, such as high asymmetry in the extent to which conflicts cluster around certain actors, and the apparent lack of triadic closure, both of which are features of the global MID network (Cranmer and Desmarais, Reference Cranmer and Desmarais2011).
However, this is a suboptimal approach. While different types of conflicts reasonably share certain characteristics, there is heterogeneity between strategic considerations of states and nonstate actors facing conflict. This results in nuanced mechanisms across different relational contexts that cannot be captured by models that do not differentiate between different types of actors and conflict processes. Consider for example the most localized form of a conflict cluster, where one actor is simultaneously in conflict with two other actors. In such a scenario, strategic considerations for a state facing two other states (e.g., Israel versus Lebanon and Syria) is likely different than when it faces two nonstate actors (e.g., Israel versus PLO member groups), even after accounting for the usual set of model covariates. For one, despite weakening Westphalian norms, the international community still treats conflict between states differently from state-sanctioned violence within national borders. Because nonstate actors are not embedded in the interstate system, they are both less protected and less constrained. These differences are likely to result in conflict clustering to be driven by different mechanisms. For example, interstate conflict clustering is likely to result from multiparty sanctioning efforts while civil conflict clustering is likely driven by the lack of international pressure on a state's internal behavior.
2.1.1. Presenting Complex Relational Systems as Multilayer Networks
In order to jointly examine these conflict subsystems while differentiating between them so as to be able to identify different cross-type conflict processes, we can utilize the multilayer network, a generalized framework that accounts for networks characterized by differentiated nodes and differentiated ties (Boccaletti et al., Reference Boccaletti, Bianconi, Criado, Del Genio, Gómez-Gardenes, Romance, Sendina-Nadal, Wang and Zanin2014; Kivelä et al., Reference Kivelä, Arenas, Barthelemy, Gleeson, Moreno and Porter2014). The basic organizing principle of multilayer networks are network layers, which group nodes into disjoint subsets, with each layer containing one type of node. These layers and their associated node types are defined by the combination of one or more nodal attributes up to any number d. As presented in Figure 1, the Levantine conflict network has layers defined by one nodal attribute, statehood, which partitions the node set into state and nonstate actor subsets. Generally, layers can be defined as a d-tuple, with each element in the tuple varying along its corresponding attribute, meaning that the set of layers comprises every combination of possible values across all relevant nodal attributes. A multilayer network with d relevant attributes each with k levels has the following layer set where the superscript indexes the attribute and the subscript indexes the attribute level, $\{(attr_1^1,attr_1^2,\ldots ,attr_1^d),(attr_1^1,attr_1^2,\ldots ,attr_2^d),\dots ,(attr_k^1,attr_k^2,\ldots ,attr_k^d)\}$![]() .
.
These network layers are used to define different types of ties in the multilayer network. Specifically, tie types are identified by the combination of types of nodes they are incident to, which can be alternatively referred to by their incident layers. The two layers in the Levantine conflict network yield three types of ties, the militarized interstate dispute incident to two state layers; the nonstate conflict incident to two nonstate layers; and the civil conflict incident to one of each layer. By convention, ties incident to the same layer are referred to as intralayer ties and those incident to different layers are referred to as interlayer ties (Kivelä et al., Reference Kivelä, Arenas, Barthelemy, Gleeson, Moreno and Porter2014).
Represented as a multilayer network, complex interdependent systems such as conflict in post-Cold War Levant can be approached using the variety of methods developed for network analysis. However, as most of these methods were initially developed for monoplex networks, extensions are required so they can account for the complex features of multilayer networks. As my purpose is to examine the generative process that underlies these systems, I focus on extensions to the ERGM.
2.2. Multilayer Extensions to the Exponential Random Graph Model
ERGMs are a class of statistical models that allows for inference on factors contributing to the generative process underlying an observed network, including exogenous node and dyad attributes, and network dependence effects at the dyadic-level and beyond. For example, a “pile-on” effect, whereby ties beget more ties, is a network effect that can manifest in observed conflict clusters (Cranmer and Desmarais, Reference Cranmer and Desmarais2011). Similar to a standard regression model, an ERGM is specified with a set of factors hypothesized to have contributed to the observed outcomes, in this case the set of ties on the network, and results from a fitted ERGM are the estimated sizes of these effects.
In an ERGM, the probability of observing a network Y = {Y ij}, where Y ij = 1 indicates a tie between nodes i and j, is specified as
where θ is a vector of parameters and x is a vector function that yields a vector of observed network statistics computed on Y. $\kappa =\sum _{\bi {Y}^*\in \cal {Y}}\exp \{\bi {\theta } ^ {\,\prime} \bi {x}(\bi {Y}^*)\}$![]() , where $\cal {Y}$
, where $\cal {Y}$![]() is the set of all networks defined on the node set of Y, is the normalizing constant that makes the equation a proper probability distribution.
is the set of all networks defined on the node set of Y, is the normalizing constant that makes the equation a proper probability distribution.
Through the ERGM, researchers can determine whether hypothesized behavioral tendencies beyond node and dyad characteristics systematically contribute to observed relational patterns within a network. This is important because ties in political networks are rarely the result of only node activity and dyadic interaction. Instead, processes operating at the hyperdyadic level such as clustering or transitivity likely play important roles in tie formation among nodes (Cranmer and Desmarais, Reference Cranmer and Desmarais2016). These network effects, along with exogenous node and dyad covariates, which together form the generative model for the observed network, are specified as terms in the vector x(Y), usually in the form of counts of local network structures.
ERGMs are highly flexible in what is a permissible specification, limited only by the requirement that x is finite when evaluated over any binary network (Desmarais and Cranmer, Reference Desmarais and Cranmer2012). Multilayer networks and appropriately specified statistics satisfy this criterion, but despite this flexibility, Y is usually treated as a monoplex network, in turn constraining the statistics specified in x. The key to extending the ERGM to multilayer networks lies in adapting Y and x in ways that account for properties of the multilayer network outlined above. This requires extensions to the matrix representation of Y as a block matrix, which provides a reasonably straightforward way of incorporating layers into local network structures used as network model terms. I discuss these in turn below.
2.2.1. Data Structure
Networks are commonly represented using an adjacency matrix Y = {Y ij} where Y ij indicates the presence of a tie between nodes i and j. For example, the MID network with three nodes {Syria, Lebanon, Israel} indexed from 1 to 3, and two undirected ties {{Syria, Israel}, {Lebanon, Israel}} can be represented as

For the purposes of statistical inference of multilayer networks via the ERGM, the set of ties on a multilayer network with ℓ layers can be grouped by type by partitioning the matrix into ℓ × ℓ blocks:

This procedure places each network layer, with its intralayer ties, into one of the ℓ main diagonal blocks, with the off-diagonal blocks in turn containing interlayer ties. As noted, depending on the specific multilayer network structure, these off-diagonal blocks may be constrained in different ways, discussed in more detail later. The matrix from Equation (2) would therefore occupy the (1, 1) block of the full adjacency matrix of the Levantine conflict network, which is graphically illustrated in Figure 1. In addition to the MID ties on the (1, 1) block, the (2, 2) block represents the nonstate conflict ties, and the off-diagonal blocks (1, 2) and (2, 1), which contain the same information because this network is undirected, represent the interlayer, civil conflict ties.
An additional step in constructing the multilayer adjacency matrix is to specify the constraints appropriate for the overall structure of the network. Applying sampling constraints to the adjacency matrix, usually in the form of disallowing ties to be formed between certain nodes, is a relevant consideration to all ERGM examinations of networks. In any network, contextual characteristics of the system can require that ties never be formed between certain nodes. For example, in a temporally-pooled examination of interstate relations, state entry and exit from the interstate system mean that there are states whose existence do not overlap, such as for Czechoslovakia (exit in 1993) and Palau (entry in 1994). Aside from these contextually idiosyncratic requirements, certain types of multilayer networks require systematic constraints on their off-diagonal blocks. I discuss these in more detail in the application section.
2.2.2. Local Network Structures in Multilayer Networks
The main contribution of the multilayer extension to ERGMs is in the network dependence structures that can be used to account for phenomenon across different types of ties. These cross-layer dependence structures should be specified by the researcher based on appropriate theoretical expectations. In the application section I demonstrate the use of various cross-layer dependence structures, but a full discussion of possible multilayer terms is beyond the scope of this paper. For a detailed description of a broad set of these structures, readers are referred to Wang et al. (Reference Wang, Robins, Pattison and Lazega2013, Reference Wang, Robins, Pattison and Lazega2016). Here, to illustrate the basic construction of a cross-layer network structure, I discuss how clustering structures on a monoplex version of the Levantine conflict network differ from that on multilayer version of the same network.
On a monoplex network, the lowest form of tie-clustering is represented by a two-star, defined as two ties that share a node (Robins et al., Reference Robins, Snijders, Wang, Handcock and Pattison2007). The corresponding network statistic is a count of two-stars on the network. On the multilayer network with three types of conflict ties, there are six different types of two-star clusters, as shown in Figure 3. In order to obtain the size of the desired subset, ties are only counted when they belong to the appropriate blocks. For example, to obtain a count of two-star comprised of a MID and a civil war, instead of computing the statistic over the entire network, only the Y1,1 and Y1,2 blocks from Figure 2 are used. This logic of identifying and limiting counted ties by matrix block remains the same for all cross-layer network structures regardless of their complexity.

Figure 2. Adjacency matrix for post-Cold War levantine conflict network.

Figure 3. Six different types of two-star conflict clustering.
After a complex system has been modeled as a multilayer network and the network represented as an adjacency matrix, statistical inference on the generative process of the system is an exercise in specifying the theoretically appropriate model terms and sampling constraints for the ERGM.
3. Applications
In this section, I outline two substantive applications that are aimed at demonstrating the use of ERGMs with multilayer networks. These applications are selected to show how the general multilayer framework can be structured to encompass different types of multilayer networks to represent a wide range of commonly observed relational systems. Specifically, I describe the multiplex network, which captures systems with multiple types of relations among a single type of actor; and the node-colored network, which captures systems with different types of actors, where ties differ by the combination of interacting actors.
For each application, I discuss the characteristics of the system and introduce the type of multilayer network it fits. I describe characteristics of these multilayer networks including whether actors exist on multiple layers and how the interlayer ties are structured. To make these examples more tractable, I limit the networks discussed to those with only two layers. However, the framework introduced here readily allows multilayer networks with greater than two layers.
3.1. Multiplex Networks: The 1980 ChemG Policy Communication Network
To demonstrate the use of multilayer networks to model multiple relations among a set of actors of a single type, I draw upon a study conducted by Leifeld and Schneider (Reference Leifeld and Schneider2012) on information exchange in policy networks. In this study, Leifeld and Schneider examined the patterns of two types of information exchange, political and scientific, among 30 actors who were relevant to the 1980 German legislation on toxic chemicals regulation (ChemG). This set of observed actors and their interactions can be represented as a directed multiplex network with two layers, where ties indicate flow of one of the two kinds of information. Figure 4 contains the graphical and matrix representations of this network.

Figure 4. Multiplex representation of ChemG policy network.
3.1.1. Multiplex Networks
Multiplex networks are those where different types of ties exist between the same set of real-world actors. Each of these tie types exists on a different network layer. This is a commonly observed network structure, as actors within a system are rarely restricted to only a single type of relation. A policy network where actors share different types of information using different communication channels, or an interstate network of both conflict and trade ties are both examples of multiplex networks. The multiplex network requires constraints placed on the off-diagonal blocks of the adjacency matrix. By definition there is only one set of real-world actors represented by multiple nodes on the network, and interlayer ties are used to couple nodes representing the same actors across layers. These self-coupling interlayer ties are almost always treated as fixed. Specifically, when the relational data is represented as an adjacency matrix, the off-diagonal blocks of the matrix are identity matrices. This data structure is presented in Figure 4 using the German ChemG policy network data from Leifeld and Schneider (Reference Leifeld and Schneider2012). The identity matrices are considered when calculating network statistics but are not modeled as outcomes. Existing approaches to statistical inference on multiplex networks (e.g., Leifeld and Schneider, Reference Leifeld and Schneider2012; Heaney, Reference Heaney2014; Song, Reference Song2014) often treat one layer of the network as the “outcome” network that is allowed to vary, while fixing the other layers as exogenous predictors. Under certain conditions this approach can be reasonable, but elsewhere the underlying assumptions are violated. In these cases, where the two networks are mutually reinforcing, the inferential result will be subject to simultaneity bias on the estimated parameters.
3.1.2. Extensions to Leifeld and Schneider (Reference Leifeld and Schneider2012)
The question Leifeld and Schneider posed is what drives tie formation on these two policy communication networks. They base their argument on a transaction costs approach. As they argue, policy actors send information to each other as attempts at influencing their policy positions. Since establishing contact is costly, actors are more likely to utilize existing channels of communication as opportunity structures to attempt influence at a relatively low cost. Based on this logic, they derive a number of expectations. Here, I limit my multiplex extension to two of these hypotheses, as this is intended as an illustrative exercise.
First, Leifeld and Schneider argue that information exchange is likely to be reciprocated. To test this, they include a term for reciprocal tie formation in both of their political and scientific communication models. For both models, the term was statistically significant with a positive sign, indicating that reciprocal tie formation is as hypothesized a part of the underlying generative process for the observed networks. These monoplex, within-layer examinations, however, cannot account for the potential for more complex forms of reciprocity to occur across network layers. Consider that within a given actor-dyad, where two types of ties are possible for both directions, there are ten different observable combinations of information flow. Figure 5 outlines these combinations with the exception of no information exchange. Of these ten possible information-sharing scenarios between two actors, four include some form of reciprocal tie formation that cannot be modeled without considering cross-layer dependence. For example, when structure F is included as a model term, it captures the tendency for one kind of information exchange to be reciprocated through other means, which is expected in policy networks with actor specialization. The other three structures (G, H, and I) capture complex forms of conditional reciprocity. In the multiplex model I include these cross-layer dependence terms.

Figure 5. Census of dyad configurations in a directed duplex network.
Second, the authors argue that actors who exchange political information are more likely to exchange scientific information and vice versa. For this kind of mutual reinforcement between political and scientific communication, the authors modeled the two networks separately while including the other network as an exogenous predictor. However, specifying edge or node covariates that are simultaneous with the outcome variable in an ERGM as exogenous will result in the same type of simultaneity bias as when endogenous covariates are specified as exogenous in classical regression models. The multiplex approach allows for the inclusion of a dependence term that directly measures cross-layer reinforced tie formation. This term is visualized as structure E in Figure 5, which I include in my multiplex extension.
In this extension, I fit two models of the ChemG multiplex network. The first is a layer independence model that includes both network layers but no cross-layer dependence terms. The model specification here follows exactly those found in Leifeld and Schneider (Reference Leifeld and Schneider2012). The second is a cross-layer dependence model that, in addition to the within-layer terms from the layer independence model, adds cross-layer dependence terms described above. The full reciprocity term captured by structure I is omitted to avoid multicollinearity.
3.1.3. Results
Results from this application are presented in Table 1. The first column contains the two communication networks jointly modeled but without cross-layer dependence terms. To examine this model's ability to capture characteristics of the multilayer network, I conducted a goodness-of-fit test. This is done by simulating 1000 networks using the layer independence model, and comparing the distribution of relevant network statistics to the observed statistics. The results summarized in Table 2 indicate that the layer independence model does not generate the observed cross-layer structures well. Evidently, cross-layer dependence is a feature of the overall multiplex communication network. Table 2 also shows goodness-of-fit results from the cross-layer dependence model, which are a near-perfect match as is expected from a converged model that directly models these structures.
Table 1. Multiplex extension of Leifeld and Schneider (Reference Leifeld and Schneider2012).

*p < 0.05.
Both models were fit in R using the multilayer.ergm package.
Table 2. Goodness-of-fit for cross-layer structures.

Results based on 1000 simulations for each model. All simulations were conducted in R.
The second column of Table 1 contains the cross-layer dependence model. Of the four modeled cross-level dependence terms, two are statistically significant at the 0.05 level. First, the cross-layer reinforcement term is positive and significant, with an estimated log-odds of 3.48. This means that, conditional on all other modeled effects, an actor already sending one type of information to a partner is 32 times as likely to send the other kind of information to the same partner than to someone else. This result supports Leifeld and Schneider's costly influence argument in that if an actor is going to use its resources to attempt influence, it will do so where opportunity structures already exist.
The other statistically significant term is the effect captured by the the presence of reciprocated scientific communication and unreciprocated political communication between a pair of actors (structure H in Figure 5). The negative sign (log-odds of − 3.45) on this term indicates that despite the tendency for reinforcement and reciprocity to facilitate information exchange in this network, these effects are attenuated when the pair of policy actors are reciprocally sharing information that is at least in part scientific. For example, the conditional effect of cross-layer reinforcement on sharing political information is reduced to just 5.4 times as likely (down from 32 times) when the pair of actors are already reciprocating scientific information. One interpretation of this finding is that there are actors who use policy communication for meaningful cooperation as opposed to for attempted influence. In these cases, cross-layer alignment becomes less likely because policy actors specialize, and without the incentive to attempt influence, sending information outside of one's specialization becomes superfluous and not done. These results indicate that while the general transaction cost framework of understanding policy communication still holds, there are additional dynamics governing information exchange that are undetectable using layer independence approaches.
In addition to expanding the types of substantive relational theories that can be examined, inclusion of cross-layer dependence structures can improve model fit to the observed data. To demonstrate this, I simulate 1000 networks from each model and examine the resulting distribution of the cross-layer dyad census presented in Figure 5. The results from these simulations are visualized in Figure 6. In each subfigure, the simulated distribution of counts of the given cross-layer dyad structure for the layer independence and the cross-layer dependence models are respectively shown with darker (dashed outline) and lighter (solid outline) ink. The vertical black line marks the observed value of the given structure. These results indicate that the cross-layer dependence model outperforms the layer independence model in terms of fitting the distribution of types of interactions between pairs of actors.

Figure 6. Comparison of model fit for dyad census.
3.2. Node-colored Networks: The Global Conflict Network
For my second application, I model the global conflict system in the post-Cold War period as an undirected multilayer network. In this application, I focus on the tendency for conflicts to cluster within and across different conflict types, which I discussed above using the Levantine conflict network. As previously noted, researchers are increasingly recognizing that the collective body of organized political conflict, which includes interstate conflict, intrastate conflict, nonstate conflict, and one-sided violence against civilians, are interdependent events within the same system (Starr, Reference Starr1994; Gleditsch et al., Reference Gleditsch, Salehyan and Schultz2008; Allansson et al., Reference Allansson, Melander and Themnér2017). In systems such as these, where we expect strategic interdependence to manifest across subsystems (Tir and Jasinski, Reference Tir and Jasinski2008; Martinez Machain and Rosenberg, Reference Martinez Machain and Rosenberg2018), a monoplex approach requires assumptions about interlayer dependence often not supported by theory, potentially resulting in an incomplete understanding of the set of mechanisms underlying tie generation and in poorly fitting models. My present application is intended to illustrate the advantages of the multilayer approach to modeling these types of systems as node-colored networks.
3.2.1. Node-colored Networks
A node-colored network comprises different types of actors, represented by “colors” that function as categorical labels for actor type (Kivelä et al., Reference Kivelä, Arenas, Barthelemy, Gleeson, Moreno and Porter2014). Nodes are grouped by their colors into different layers, which means that intralayer ties are those that exist between nodes of the same color, and interlayer ties between nodes with different colors. Because actors in node-colored networks never exist on more than one layer, interlayer ties are not used for coupling nodes across layers as they are in multiplex networks. Instead, they represent ties between two different real-world actors and are therefore substantively-meaningful relational outcomes that can be modeled. As such, whereas a multiplex network has as many types of ties as it does layers, a node-colored network with k colors has up to $((_2^k))$![]() types of ties. By this definition, bipartite networks are a specific case of node-colored networks where intralayer ties are assumed away. For example, political contributions modeled as a bipartite network assumes independence between different receivers and between different donors aside from shared cross-type partners (e.g., Heaney and Leifeld, Reference Heaney and Leifeld2018). Unless a node-colored network is truly bipartite, it is desirable to model it as a multilayer network by treating intralayer ties as outcomes.
types of ties. By this definition, bipartite networks are a specific case of node-colored networks where intralayer ties are assumed away. For example, political contributions modeled as a bipartite network assumes independence between different receivers and between different donors aside from shared cross-type partners (e.g., Heaney and Leifeld, Reference Heaney and Leifeld2018). Unless a node-colored network is truly bipartite, it is desirable to model it as a multilayer network by treating intralayer ties as outcomes.
Because the interlayer ties of node-colored networks are usually relational outcomes, systematic constraints are generally not placed on the off-diagonal blocks of node-colored networks. The exception to this is when the interlayer ties represent hierarchical affiliation ties (e.g., employment, citizenship) between nodes in different layers (Wang et al., Reference Wang, Robins, Pattison and Lazega2013). For example, a congressional member network and a congressional staffer network (Montgomery and Nyhan, Reference Montgomery and Nyhan2017) can be represented as a node-colored network with congressional members on one layer and their staffers on another. In these networks, if affiliations are generally stable and not of theoretical interest, the off-diagonal blocks may reasonably be fixed at their observed values.
3.2.2. Modeling Conflict Clustering across conflict Types
In this application I focus on the tendency for conflicts to cluster. I base my model on a study by Gleditsch et al. (Reference Gleditsch, Salehyan and Schultz2008), which examines the relationship between interstate conflict and the presence of civil wars in a country. More specifically, the authors examine MID onset for all politically-relevant dyads during the period of 1948–2000 and find that the presence of civil conflict in at least one state in the dyad predicts MID onset. This relationship should manifest as clustering of interstate and civil conflicts in the system. In their model specification, Gleditsch, Salehyan, and Schultz include the presence of civil conflict in the dyad as an exogenous predictor to MID onset. Specifying one type of conflict as the outcome and the others as exogenous predictors is the current standard in modeling the relationship between different types of conflicts, using the ERGM or otherwise. As illustrated using the Levantine conflict network earlier, what this approach misses is that the presence of different types of intrastate conflict is highly likely to be endogenous to interstate conflict through both simultaneity and confounding.
My multilayer extension departs from Gleditsch et al.'s (Reference Gleditsch, Salehyan and Schultz2008) study in a number of ways. First, using the multilayer approach, I model all potential conflicts in the global system (i.e., interstate, civil, and nonstate conflicts) as outcomes instead of focusing on politically-relevant interstate dyads. Second, to limit the methodological scope of my examination to something that is tractable for this paper, I focus on a single temporal cross-section of the global conflict system instead of a time-series. Specifically, I examine the period immediately following the end of the Cold War, from 1989 to 1995. This period was marked by a drastic change in the balance of power between states and nonstate actors in the periphery in favor of the latter (Kalyvas and Balcells, Reference Kalyvas and Balcells2010). The overall strategic environment at the time, ripe for potential conflict clustering across types, presents an apt opportunity for illustrating the importance of modeling interdependence across different conflict processes.Footnote 3
Similar to the ChemG application, I fit a layer independence and a cross-layer dependence model. The two model specifications are identical except for how dependence across different types of conflicts is modeled. Specifically, both models include within-layer star terms to capture the tendency for within-type conflict clustering, but where the layer independence model approaches cross-type clustering by specifying one type of conflict as an exogenous predictor of another, the cross-layer dependence model uses cross-layer dependence star terms. Further, the cross-layer dependence model also includes a three-way clustering term that captures the tendency for all three types of conflict to cluster at the same time, which is illustrated in Figure 7. This term cannot be modeled in a straightforward manner using conventional approaches. A discussion of the data used, network creation procedure, and modeling steps is included in the online appendix.

Figure 7. Local network structure for three-way clustering: cross-layer three path.
3.2.3. Results
Table 3 contains results from this application. As noted, the models have identical specifications for within-layer terms. The substantive interpretation of these terms do not differ between models, and generally corroborate expectations from the conflict studies literature. Notably, all dyadic terms that are included in Gleditsch et al. (Reference Gleditsch, Salehyan and Schultz2008, Table 2) have the same estimated signs as the original study. The alternating k-star terms for all three types of conflicts are positively signed in both models, indicating tendency for within-type ties to cluster.Footnote 4
Table 3. Models of the post-Cold War global conflict network.

*p < 0.05.
Both models were fit in R using the multilayer.ergm package.
Moving to the cross-conflict clustering terms from the cross-layer dependence model, note that the alternating k-star term for MID-civil conflict clustering is positive, indicating that conditional on involvement in a MID, the state is likely to engage in civil conflict, and vice versa. This result is in line with results from Gleditsch et al. (Reference Gleditsch, Salehyan and Schultz2008). On the other hand, the alternating k-star term for civil-nonstate conflict clustering is negative, meaning that nonstate actors tend to avoid entering into conflicts simultaneously with mixed opponent types. This finding is within theoretical expectations (Fjelde and Nilsson, Reference Fjelde and Nilsson2012), but previously has been shown only with indirect evidence.
The key theoretical contribution from the cross-layer dependence model comes from its three-way clustering term. The estimated coefficient for this term is positively signed, meaning that the odds of a conflict tie forming when it attaches to an existing cluster of the other two types of conflicts is higher than when it is concurrent with only one conflict. Evidence of this kind of interdependence spanning all three types of conflict ties indicates that when states make decisions about their conflict engagements with other states, the neighborhood they consider extends beyond the interstate dyad and its concurrent civil conflict ties, to whether their civil conflict partners are also engaged in conflicts of their own. This finding is intuitive, but prior to the multilayer network approach had not been demonstrated in a straightforward manner.
4. Conclusion
We understand political phenomena as systems of units interacting across multiple relational contexts. The increasing application of ERGMs to modeling these phenomena has yielded theoretical advancements across various areas in the study of politics, but contemporary network approaches still require assumptions about independence of ties across different relational contexts in a manner that does not comport with our understanding of politics. Despite these limitations, relatively little work has been done in adapting network-based modeling approaches for capturing these interdependencies.
In this paper, I illustrated a multilayer network approach that extends the ERGM to account for interdependence in complex systems comprising multiple relations. Through two substantive applications, I demonstrated that the multilayer approach to ERGMs affords us the opportunity to model interdependence across multiple relational contexts using cross-layer dependence terms and to examine these interdependencies as generative features of the system. In the ChemG policy communication application, I showed that reciprocity between actors is more complex than what can be inferred when focusing on only one type of information exchange. Instead, jointly modeling multiple communication networks can yield insights into the conditions under which pairs of actors reciprocate information. In my examination of the global conflict system, I showed that cross-layer dependence terms can be used to model the tendency for different combinations of conflict types to cluster. Results here suggest that when making strategic choices regarding conflict, states assess not only their and their opponent's immediate conflict engagements, but are attentive to the local conflict environment the dyad is situated in, including the extent to which their civil conflict partners are engaged in other conflicts. Just as importantly, I showed using simulation exercises that by accounting for existing cross-layer dependence, the cross-layer dependence models fit observed data better than models constrained be independent across layers.
My present argument for treating multiple systems previously examined independently of one another as components in a larger system comprising multiple relational contexts is an argument for more carefully considering the complexity present in political phenomenon. In addition to the applications presented in my paper, this is a consideration salient to many other commonly studied political systems, such as international regimes (Alter and Meunier, Reference Alter and Meunier2009), legislatures (Montgomery and Nyhan, Reference Montgomery and Nyhan2017), and political campaigns (Heaney and Leifeld, Reference Heaney and Leifeld2018). This argument is not new, but despite the ostensibly wide recognition for these complexities, methods for working with them were lacking. The multilayer extension to the ERGM presented here should afford researchers a useful tool in this endeavor.
Supplementary material
The supplementary material for this article can be found at https://doi:10.1017/psrm.2019.49
Acknowledgments
I would like to thank Bruce Desmarais, Mitch Goist, Boyoon Lee, Douglas Lemke, Fridolin Linder, Kevin Reuning, Xu Xu, participants at the 2018 PolNet Conference and the 2018 PolMeth Meeting, and Daniel Stegmueller and three anonymous reviewers at PSRM for providing valuable feedback at various points in this project. This research is part of the ECANET-consortium (Echo Chambers, Experts and Activists: Networks of Mediated Political Communication), part of the Media and Society Academy Programme (2019-2022), funded by Academy of Finland (SA grant: 32779). Replication materials can be found at the PSRM Dataverse: https://doi.org/10.7910/DVN/X3586I.












