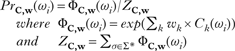2.1 Minimal requirements

A phonotactic grammar is a hypothesised mental component which assesses possible words. This general formulation was already explicit in Chomsky & Halle (Reference Chomsky and Halle1965), who pointed out that English speakers distinguish not only between known words and non-words (e.g. brick vs. blick), but also between non-words which could be English words and those which could not (e.g. blick vs. bnick). As will be shown in this section, what is needed to formalise this concept is an explicit representation of the set of logically possible words and a set of (ordered) well-formedness values. The phonotactic grammar is then defined as a function mapping from possible words to well-formedness values.

One natural property to assume is that the phonotactic grammar must be able to compare any pair of possible words. This assumption is motivated by the fact that human well-formedness judgement tasks often take the form of determining which of two non-words sounds more like a possible word of the listener's language (e.g. Coleman & Pierrehumbert Reference Coleman, Pierrehumbert and Coleman1997, Daland et al. Reference Daland, Hayes, White, Garellek, Davis and Norrmann2011). Furthermore, it is reasonable to assume that relative well-formedness is transitive; for example if a listener indicates that lbick is less well-formed than bnick, and also that bnick is less well-formed than blick, then the listener would agree that lbick is less well-formed than blick. Another property comes from the theory of markedness: it is impossible for a sequence of forms to continually increase in well-formedness. That is, adding a finite amount of material may cause a form to become more well-formed, but one cannot keep increasing well-formedness by adding more and more. Formally, this means that every set of forms must contain a maximally well-formed item. Finally, it is conventional to assume that possible words are strings over an alphabet Σ+. Theorem 1 shows that any grammar which is consistent with these four assumptions can be represented by a score function H : Σ+→ℜ—, where ℜ— is the set of non-positive real numbers. The relative well-formedness of pairs of words is then indicated with the natural order ≤; e.g. H(bnick) ≤ H(blick) means that bnick is equally well-formed as or less well-formed than blick. Under this formulation, the highest possible well-formedness value is 0, and it should be assigned to the maximally well-formed item(s) (see also Smolensky & Legendre Reference Smolensky and Legendre2006: chs 9, 10, 23).

This formulation can be illustrated with reference to Chomsky & Halle's proposal. They envisioned a categorical division between ill-formed and well-formed items. If well-formed items are assigned a score of 0, then ill-formed items should be assigned a score of —1, yielding a mapping H : Σ+→{—1, 0}. Then the relative well-formedness of bnick vs. blick is indicated by the inequality H(bnick) = …1 ≤ 0 = H(blick).Footnote ¹ Note that because this model only allows a binary distinction in well-formedness, it predicts that all ill-formed items are equally ill-formed, and all well-formed items are equally well-formed. For example, it predicts H(lbick) = H(bnick); H(ba) = H(supercalifragilisticexpialidocious).

As Hayes & Wilson (Reference Hayes and Wilson2008) point out, a binary distinction in well-formedness is not adequate for the empirical data:

In principle, it is straightforward to account for gradience by extending the range of possible well-formedness values. For example, one might wish to distinguish three values of well-formedness. In that case, unambiguously ill-formed items like bnick would be mapped to —2, marginal items like bwick or voig would be mapped to —1 and well-formed items like blick would be mapped to 0. Since the scale is unrestricted, in principle it allows for an arbitrary number of distinctions, including countably infinite distinctions.

To recapitulate, the empirical data and standard theoretical assumptions jointly entail that every phonotactic grammar can be represented by a score function H : Σ+→ℜ—. A score function does not intrinsically define a probability distribution, but it does provide the ability to account for gradience up to arbitrary degrees of precision. That is, the need to account for gradience can be met without invoking a probabilistic model of phonotactics.

2.2 Arguments for a probabilistic model of phonotactics

The rationale given by Chomsky & Halle was simply to distinguish well-formed from ill-formed items.Footnote ² However, subsequent research has turned up many other uses for phonotactic knowledge. For example, Coleman & Pierrehumbert (Reference Coleman, Pierrehumbert and Coleman1997) found that a word-form's average well-formedness score (from human judgements) was linearly related to its log probability (according to a probabilistic phonotactic model they proposed in the same paper). A linear relationship between log probability (according to the model) and aggregate well-formedness judgments has since been replicated several times (e.g. Coetzee & Kawahara Reference Coetzee and Kawahara2011, Daland et al. Reference Daland, Hayes, White, Garellek, Davis and Norrmann2011).

Besides the admittedly metalinguistic task of acceptability judgments, phonotactic well-formedness has been implicated in various aspects of speech perception and speech production. For example, Davidson, Wilson and colleagues have made fairly explicit proposals for a Bayesian model of native and non-native speech perception that integrates acoustics and phonotactics (Davidson & Shaw Reference Davidson and Shaw2012, Wilson & Davidson Reference Wilson and Davidson2013, Chodroff & Wilson Reference Chodroff and Wilson2014, Wilson et al. Reference Wilson, Davidson and Martin2014). In Chodroff & Wilson (Reference Chodroff and Wilson2014), the phonotactic grammar plays the role of a ‘prior model’, which calculates the likelihood of encountering e.g. word-initial [bl] vs. word-initial [bəl]; this information is integrated into the acoustic model, which determines how well [bl] matches the observed acoustic sequence vs. how well [bəl] does. As in all Bayesian models, the ability to integrate this information depends on being able to express it in the common language of probability distributions.

The final argument that will be made here for a probabilistic phonotactic grammar comes from word recognition. The need for a probabilistic phonotactic grammar in adults is formally entailed by the following assumptions: (i) word recognition is probabilistic, and (ii) listeners sometimes encounter novel words. The assumption that word recognition is probabilistic represents a consensus position in modern theories of word recognition. For example, Norris & McQueen (Reference Norris and McQueen2008) present a Bayesian model of word recognition called Shortlist B, and model an impressive array of behavioural data. Even models of word recognition which do not use overt probabilities in their update equations, such as the spreading activation model of TRACE (McClelland & Elman Reference McClelland and Elman1986), at least implicitly represent a probabilistic formulation in which the probability of a form is proportional to the exponential of its activation level (1986: 21). It is possible to find either explicit description of lexical probabilities or ‘word-activation level’ equations which correspond very closely to them (usually with activation being linearly related to log probability) in every model of word recognition I am aware of, including MATCHECK (Baayen & Schreuder Reference Baayen and Schreuder2000), automatic speech-recognition systems (e.g. Scharenborg et al. Reference Scharenborg, Norris, Bosch and McQueen2005) and the word-segmentation models pioneered by Goldwater and colleagues (e.g. Elsner et al. Reference Elsner, Goldwater, Feldman and Wood2013).

Something special must occur when a novel word is actually encountered. To see the problem, consider what must occur when a model is presented with a novel word in context, as in (1).

1. (1)

   

The way that these models process normal sentences is by multiplying the probabilities of all the entries. If the model already had a lexical entry tatove, than the probability calculation would be something like (2).

1. (2)

   

(Actually, the calculation would normally be done in the log domain, as a sum over log probabilities, rather than a product over regular probabilities.) However, since the word tatove does not have a preexisting lexical representation, the prior probability assigned to this would normally be 0. In that case, the probability of the parse in (2) would have to be 0 as well, which means it would be literally impossible to recognise the novel form tatove. Norris & McQueen (Reference Norris and McQueen2008: 366) say as much: ‘unknown words require special treatment … The model has to consider the hypothesis that the input is not a known word’.

The problem of unseen items has been extensively studied (e.g. Baayen Reference Baayen2001), and the standard approach is to reserve some probability mass, Pr(ωnew), for previously unseen items. In the case of (2), this would amount to replacing the Pr(tatove) term with a term Pr(ωnew), reflecting the total probability of encountering any new word in this context. However, this value does not faithfully represent the event that occurred: it was not just that some previously unseen word was encountered, but also that the previously unseen word has the form tatove. The probability of the event should be decomposed into two parts: the probability Pr(ωnew) that some previously unseen item has occurred, as well as the probability Pr(ωnew→təˈtov) that an item has the form tatove, given that it is new. The revised computation is given in (3).

1. (3)

   

Note that this latter term is precisely what a probabilistic phonotactic grammar is supposed to calculate. Furthermore, this equation indicates a natural meaning for the probabilities output by a phonotactic grammar: Pr(ωnew→təˈtov) represents the probability that the next nonce word a speaker encounters will have the form [təˈtov]. More generally, then, the formal architecture of word recognition entails a mental component which assigns to each possible word ω a probability, representing the probability that the next novel word the listener encounters will have the form ω. This point has not been forcibly made in the literature on word recognition, presumably because existing models focus mainly on modelling psycholinguistic data pertaining to the recognition of existing words.

In summary, probabilistic phonotactic grammars are needed to link phonotactic well-formedness with observable speech behaviours such as speech perception and speech production. This is particularly clear in the case of word recognition. The consensus position that word recognition is a probabilistic process and the fact that listeners encounter novel words jointly entail the need for a mental component which assigns a probability to every logically possible word. This is exactly what a probabilistic phonotactic grammar is. Formally, a probabilistic phonotactic grammar can be defined as a phonotactic grammar which assigns probabilities. That is, Φ : Σ+→ℜ+ (where ℜ+ is the set of non-negative real numbers) is a probabilistic phonotactic grammar if and only if Φ is a phonotactic grammar, and the sum of the probabilities that Φ assigns over every string in Σ+ totals 1. This definition of probabilistic phonotactic grammars is quite standard in the literature. In fact, the only novel contribution of this section is the argument from the theory of word recognition that a probabilistic phonotactic model is needed – and the interpretation it provides for the probabilities that such a model assigns.

3.1 Desiderata

Within generative phonology, it is standard to regard the core goal of a phonological formalism as computing a mapping from lexical representations to surface representations. For example, one way to account for the pronunciation of English kisses is that the lexical representation is the concatenation of the stem /kIs/ and plural marker /z/, with the grammar computing an epenthesis operation /kIs+z/ → [kIsIz]. Besides the core phenomenon of straightforward categorical mappings like these, there are several properties we might want a phonological formalism to exhibit, as shown in (4).

1. (4)

   

All of these properties either enable a formalism to account for data or enable analysts to use the formalism in order to reason about human linguistic knowledge and behaviour.

3.2 Properties of maximum entropy Harmonic Grammar

Harmonic Grammar (Legendre et al. Reference Legendre, Miyata and Smolensky1990, Smolensky & Legendre Reference Smolensky and Legendre2006) is a constraint-based formalism which was the historical precursor to Optimality Theory (McCarthy & Prince Reference McCarthy and Prince1993, Prince & Smolensky Reference Prince and Smolensky1993), and which crucially differs in having constraints that are weighted rather than strictly ranked. Maxent HG (Goldwater & Johnson Reference Goldwater, Johnson, Spenador, Eriksson and Dahl2003, Jäger Reference Jäger, Zaenen, Simpson, King, Grimshaw, Maling and Manning2007, Hayes & Wilson Reference Hayes and Wilson2008) refers to the natural extension of Harmonic Grammar to a log-linear (maximum entropy) model (Jaynes Reference Jaynes and Rosenkrantz1983, Jelinek Reference Jelinek1997: ch. 13, Manning & Schütze Reference Manning and Schütze1999). Thus maxent HG capitalises on both the theoretically advantageous properties of constraint-based phonology and the statistically sound learning and inference properties of log-linear models.

An HG grammar contains a set of constraints {Ck}k=1…K and an associated set of weights {wk} k=1…K. Each constraint Ck is a function which maps input–output pairs to a violation value. The harmony of an input–output pair (x, y) is defined as the weighted sum of its constraint violations, as in (5).

1. (5)

   

Because violating a constraint is worse than not violating a constraint, more constraint violations should result in a lower harmony. This can be achieved in several notationally distinct but mathematically equivalent ways. This paper will use the convention that constraints assign non-negative values (violation counts), while all weights are non-positive.

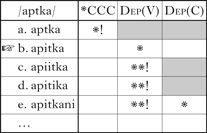
The candidates of an input x consist of all the input–output pairs for which x is the input. Formally, this may be indicated by a relation R (i.e. x R y means that y is an output candidate for input x), though in practice it is most common to simply list the candidates in a tableau, as in (6).

1. (6)

   

Harmonic Grammar tableaux are similar to OT tableaux, but differ in that the constraint weights are explicitly indicated, and include an additional column to indicate the harmony values. The candidate with the greatest harmony is deemed the winner. (6) illustrates a grammar in which ill-formed onset clusters are repaired by vowel epenthesis (rather than cluster simplification).

Maxent HG is a proper extension of Harmonic Grammar. The definition of harmony in (5) remains the same, but in addition, maxent HG defines a function that returns well-formedness values, as in (7).

1. (7)

   

This value represents the well-formedness of the x→y mapping. The well-formedness value is similar to a probability, except that it is not required that the sum over all possible items must add up to 1. The partition function for an input x, Z(x) is defined as the sum of the well-formedness values for the candidates for x, as in (8).

1. (8)

   

As long as the partition function for an input x is finite, it is possible to define the conditional distribution Pr(y|x) as in (9).

1. (9)

   

Thus the probability of a string is directly proportional to its well-formedness value if the partition function is finite, and is not defined if the partition function is not finite. (The well-formedness value is well-defined whether the partition function is finite or not.) Therefore, a key question – the key question addressed in §4 and §5 – is under what circumstances the partition function is finite.

The workings of a maxent HG grammar can also be illustrated by a tableau. (10) repeats tableau (6), augmented with Φ and Pr values.

1. (10)

   

Just as in (6), *Complex and Max(C) have much greater weight than Dep(V). The result is that complex onsets are essentially always repaired by vowel epenthesis. Note that the formalism does assign a marginal degree of probability to other candidates; however these probabilities are so low as to be indistinguishable from the rate of speech errors. In fact, Goldrick & Daland (Reference Goldrick and Daland2009) propose that speech errors can be modelled grammatically in just this way, using the closely related formalism of Noisy Harmonic Grammar. The remainder of this section discusses how maxent HG satisfies the desiderata outlined earlier; the discussion is brief, as many of these points have been covered in more detail by Pater and colleagues in their programme of theory comparison (Pater Reference Pater2008, to appear, Coetzee & Pater Reference Coetzee, Pater, Goldsmith, Riggle and Yu2011, Boersma & Pater to appear).

3.3 Maxent phonotactic grammars

As noted earlier, a phonotactic grammar differs from the normal conception of a phonological grammar. In a ‘normal’ phonological grammar, we find (11).

1. (11)

   

However, in phonotactic grammars, we have (12).

1. (12)

   

Thus a phonotactic grammar is quite different from a ‘normal’ phonological grammar. This section shows that phonotactic grammars fall out as a special type of phonological grammar, if the perspective offered earlier on word recognition is adopted. The class of maxent phonotactic grammars can then be defined by applying this perspective to maxent HG.

Recall that, in order to handle novel words, models of word recognition need a ‘special’ item ωnew (‘<new word>’), and the phonotactic grammar should distribute the probability of this item across all possible strings. This insight allows us to cast a phonotactic grammar as a phonological grammar in which (i) ωnew is the sole lexical representation; (ii) the set of candidates is the set of all possible words Σ+. In the remainder of this section, this perspective is deployed in the context of maxent HG grammars; this is the formal underpinning for what we have been calling maxent phonotactic grammars.

Equation (9) is the fundamental equation by which maxent HG assigns probability to a candidate. In (13), subscripts have been added to explicitly represent a particular set of constraints C and their associated weights w.

1. (13)

   

Since there is only a single, constant lexical representation (ωnew) in phonotactic grammars, it can be suppressed. Moreover, since the candidates are possible words, they are represented as ω. Substituting in this way gives (14), which defines the behaviour of maxent phonotactic grammars.

1. (14)

   

Hayes & Wilson (Reference Hayes and Wilson2008) define phonotactic learning as the process of identifying the markedness constraints that are active in distinguishing possible words from impossible ones, and inferring their weights.Footnote ⁴ They then propose a theory for accomplishing phonotactic learning using maxent phonotactic grammars. The core of the idea is to regard the existing lexicon Λ={ω1, ω2, …, ω _n } as a sample from the phonotactic grammar having constraints C={Ck}k=1…m and weights w={wk}k=1…m. The probability of the lexicon is the product of the probabilities of generating each word in it, where the probability of a word-form ωi is calculated according to (14). Hayes & Wilson (Reference Hayes and Wilson2008) propose that the ‘best’ grammar (C, w) can be found using maximum a posteriori estimation, incorporating a ‘prior’ so that the learned grammar reflects a compromise between making the grammar simple and fitting the data well.

There are two technical obstacles to learning in a completely general way. The first is that the partition function ZC,w is defined over an infinite string set, so it cannot be calculated exactly by brute force. The second obstacle is that there may be billions or even trillions of logically possible markedness constraints, and it is not computationally feasible to include every one. Hayes & Wilson (Reference Hayes and Wilson2008) propose to solve the latter problem with an iterative procedure, in which the learner begins with an ‘empty’ grammar, and then considers constraints one by one, retaining those which increase probability sufficiently. The order in which constraints are tried is governed by heuristics, about which more will be said later. For now, this paper focuses on the first problem, calculating the partition function.

Hayes & Wilson's method for calculating the partition function makes use of finite-state Optimality Theory (Eisner Reference Eisner2002, Riggle Reference Riggle2004, Reference Riggle2009). Each constraint in the grammar is coded as a simple weighted finite-state machine, and the grammar is constructed by ‘intersecting’ all of the constraints (for exposition see Riggle Reference Riggle2004). This results in a very large finite-state machine, each of whose states represents a violation vector corresponding to a (sometimes infinite) class of strings. The expected violation counts for each constraint in the grammar can be summed using Eisner's ‘expectation semi-ring’. From these expected counts it is straightforward to compute the partition function.

As an implementational matter, Hayes & Wilson (Reference Hayes and Wilson2008: 389) choose to impose a finite upper bound on the string set that they sum the partition function over:

In other words, they impose an ‘artificial’ upper limit on how long possible words can be, assigning a probability of 0 by fiat to all strings over this limit. However, careful inspection of the original Eisner (Reference Eisner2002) reference reveals that the string set does not need to be finite. Rather, the requirement is that the partition function have a finite value, or equivalently, that the accumulated weight of all possible paths through the machine be finite. This condition is trivially satisfied when there is a finite upper bound on string length, since the finite sum of finite values is finite. It is also possible to have a finite partition function over an infinite string set. However, it is not guaranteed. This is not just a theoretical problem with maxent phonotactic grammars, but also one that occurs in practice, as the next section demonstrates.

4.1 Precedents

Infinity has beguiled and bedevilled linguists from the earliest days of generative grammar. In an early and influential article, Chomsky (Reference Chomsky1956: 115) addresses the issue of whether sentences are bounded:

Though Chomsky was primarily concerned with the syntactic organisation of sentences rather than the generation and recognition of new words, the issue is essentially the same. In some languages, it is in principle possible to construct an acceptable item that is longer than any given finite bound. Theories which simply stipulate a finite upper bound are insufficiently expressive.

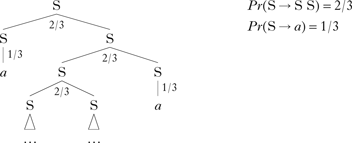
The issues discussed in this paper have a close parallel in the history of the development of probabilistic context-free grammars (PCFGs). Intuitively, a PCFG may be thought of as a grammar that generates trees with probabilities. An example tree and the generating grammar are shown in (15). A PCFG consists of a list of category labels, some terminal labels and a list of rewrite rules with associated probabilities (for in-depth coverage see Chi & Geman Reference Chi and Geman1998, for applications in laboratory phonology Coleman & Pierrehumbert Reference Coleman, Pierrehumbert and Coleman1997 and for a reader-friendly description Daland et al. Reference Daland, Hayes, White, Garellek, Davis and Norrmann2011).

1. (15)

   

The probability of a derivation is simply the product of the probabilities of all the rewrite rules used in the derivation. For example, the probability of the derivation in (15) is 1 × 0·33 × 0·5 × 0·5 × 1 × 1 × 1 × 0·33 × 0·5 × 0·5 × 0·34 = 0·002314125. The probability of a string is the sum of the probabilities of all derivations that yield the string. Since derivation (15) is the only one which can yield Kaeli said that Laura likes goats, the probability the PCFG assigns to this string is also 0·002314125.

As early as 1963, it was noted that probabilistic branching processes might have a non-zero probability of not terminating (Harris Reference Harris1963). An example is given in (16).

1. (16)

   

In the case of (16), it is more likely than not that a given S will expand to more than one S daughter. This means the probability that every S will terminate in a finite number of a's is less than 1. Put another way, some of the probability is ‘wasted’ on infinite trees (which cannot be observed). When the sum over all observable trees is less than 1, the probability distribution is called inconsistent.

More than a decade later, Grenander (Reference Grenander1976) gave a mathematical characterisation of when PCFGs assign a consistent distribution. In essence, every label needs to derive less than one copy of itself (and other self-deriving labels) on average. For example, in the grammar in (16), a given S is expected to give rise to 4/3 immediate S daughters (2×(2/3)+0×(1/3)=4/3), meaning that the number of S's is expected to grow on average with every rule application. More formally, Grenander constructs a matrix whose (i, j) entry indicates the probability that category label j will expand into category label i. The PCFG is consistent if and only if a value called the principal eigenvalue is less than or equal to 1. A very similar condition is shown for maxent phonotactic grammars in Theorem 3.

More than two decades after Grenander's work, Chi & Geman (Reference Chi and Geman1998) proved that if a PCFG is trained on finite (observable) data according to the principle of maximum likelihood, the consistency condition will always be met. The reason for this is relatively simple: in all of the observable data, each symbol eventually leads to less than one copy of a self-deriving symbol (otherwise it would give rise to an infinite tree, which cannot be observed). Maximum-likelihood training causes the estimated likelihood of a rule expansion to match the observed rate of symbol expansion. In other words, the training data does include infinite trees, so the PCFG which is learned approximates this property.

The problem of learning maxent phonotactic grammars is conceptually similar. The first theoretical contribution of this paper is to point out, as Harris (Reference Harris1963) does for PCFGs, that there is at least the potential for an infinity problem with maxent phonotactic grammars. The next theoretical contribution is to give necessary and sufficient conditions for avoiding the infinity problem with maxent phonotactic grammars, as Grenander (Reference Grenander1976) does for PCFGs. The final theoretical contribution is to motivate the conjecture that the infinity problem will not arise when maxent phonotactic grammars are trained on observable samples, provided that they are initialised with a *Struct constraint that is given sufficient weight; this is analogous to the proof that Chi & Geman (Reference Chi and Geman1998) offer for PCFGs.

4.2 Examples

This section gives three examples of maxent phonotactic grammars in which the partition function is not finite, with increasing degrees of phonological realism.

The first example is the simplest one, and is included because it illustrates the nature of the problem so simply. Suppose the alphabet consists of a single segment; Σ={a}. Then Σ+ consists of strings of the form an, where n≥0. Further, let the grammar be ‘empty’ (the initial state that Hayes & Wilson Reference Hayes and Wilson2008 employ in their software implementation). It follows that the weighted sum of the constraint violations of every form an is 0, H[an] = 0 for all n. Then the well-formedness measure of each such an is exp(H[an]) = 1. The partition function is the sum of the well-formedness values over all such strings, Z=Σn≥0 exp(H[an])=Σn≥0 1. Clearly, this sum is not finite.

The reader may rightly protest that no natural phonology includes an inventory with only one phoneme. But adding more phonemes makes the infinity problem worse, not better. To see this, consider an alphabet with just one more symbol, Σ={C, V}, but with the same ‘empty’ grammar as in the previous paragraph. Let us define Zk as the ‘partial’ partition function, summing over all strings of length k or less. Clearly, Zk→Z, as k→∞. Moreover, Zk is equal to the number of such strings (because the well-formedness measure of each such string is 1). Then calculating Zk is a simple matter of counting strings. The number of strings in Zk can be counted by dividing them into sets by their length, i.e. the set of strings of length 0, the set of strings of length 1, the set of strings of length 2, etc. We use the notation Σj for a set of string of length exactly j; |Σj| is the cardinality of this set. For example, Z2 = |Σ0|+|Σ1|+|Σ2|. Because |Σj|=|Σ|j, it follows that Zk is a geometric series with common ratio |Σ|. This makes perfect sense – from every string of length j, we can create exactly |Σ| strings of length j+1, by simply adding one segment from Σ. Thus the total number of strings up to a certain length j should be exponential in j. From this it follows that Zk→∞, so the partition function is not finite.

The reader may think that these artificial examples have little to do with real phonology, so the infinity problem would not occur if a maxent HG were provided with ‘real’ constraints and natural language data. But that is false, as illustrated by the final example, the Wargamay grammar that Hayes & Wilson discuss extensively in their paper. With some careful inspection, it is possible to show that [ˈbamba] is harmonically ‘perfect’ according to this grammar, i.e. is assigned a harmony of 0. Moreover, the possible words [ˈbambaˌbamba] and [ˈbambaˌbambaˌbamba] are also harmonically perfect. The relevant constraints needed to verify this claim are distributed over several pages and tables, each dealing with orthogonal aspects of the grammar (Hayes & Wilson Reference Hayes and Wilson2008: 414, 416, 417, 419, 432–432). First, the ‘onset’ consonant [b] is unpenalised both in absolute word-initial position and intervocalically. Second, [mb] is among the 40 medial consonant clusters described as licit both by Hayes & Wilson and by their reference grammar. Third, the authors explicitly state (2008: 418) that items of the form (ˈσσˌσσˌσσ) incur no pure metrical penalties; they do not list any constraints that penalise longer sequences which satisfy the initial main stress trochaic footing system. Finally, there are numerous constraints regulating the local co-occurrence of [+high], [—back], [+stressed] and [—stressed) vowels, but none specifically or generically targets a stressed [a] followed by [mb] and unstressed [a], or unstressed [a] followed by [b] and stressed [a]. Therefore, every string consisting of initial [ˈbamba] and followed by 0 or more repetitions of [ˌbamba] is unpenalised by this grammar. Then every string of the form ban is assigned a harmony of 0, where b=[ˈbamba] and a=[ˌbamba]. This example is therefore of the same character as the highly idealised one presented above: H[ban] = 0 for all n≥0, and so the partition function is not finite. This is in spite of the fact that the alphabet and the markedness constraints are derived directly from a natural language phonology.

The essential problem in these three examples is underpenalisation. Because Σ+ contains all strings over Σ, it contains some which consist of arbitrary repetitions of relatively well-formed subsequences. In the absence of any specific constraints (the CV example above), all subsequences are well-formed. But even in the presence of many constraints (the Wargamay example above), the infinity problem arises if there is even one well-formed subsequence that may repeat indefinitely. However, the CV example above also provides some indication of a solution. If the number of strings is exponential in their length, perhaps some penalty can be applied which scales with the length. The next section formalises this idea.

5.1 *Struct in maxent phonotactic grammars

Recall that Hayes & Wilson (Reference Hayes and Wilson2008)'s learner includes a constraint-induction procedure, which is distinct from the ‘weight-setting’ procedure. Weight-setting is a learning process in which, given some constraints, the best constraint weights are found (where ‘best’ is defined as maximising the likelihood of observing the lexicon that was actually input to the model). Constraint induction is the process by which the model searches a large space of possible constraints.

In Hayes & Wilson's learner, the constraint-induction process includes two search biases – constraints are searched in order of accuracy, and among constraints that are roughly equivalent in accuracy, more ‘general’ constraints are considered earlier (for details see Hayes & Wilson Reference Hayes and Wilson2008: 394). The default is for the search process to terminate after a certain number of constraints have been included in the grammar (e.g. 100). Clearly, constraints cannot be considered for inclusion in the grammar if the search process terminates before it reaches them. Since the search order is determined by accuracy, the practical effect of the ‘accuracy bias’ is to ensure that constraints with poor accuracy are never considered.

Hayes & Wilson (Reference Hayes and Wilson2008) define accuracy as the ratio of observed violations of the constraint in the training lexicon to the number that is expected according to the preexisting grammar. That is, it favours constraints which do not penalise the training data, rather than ones which distinguish training items from untrained items. Since *Struct penalises every segment in the training data, its accuracy value will be among the worst possible. Therefore, Hayes & Wilson's software will never consider this constraint ‘early’ in the constraint-search process. In practice, the software might examine several thousand constraints from a pool of several hundred millions. The constraint-induction process will always terminate before it even reaches the *Struct constraint, and this fact is independent of whether the *Struct constraint is actually useful. There are numerous reasons to think it is.

Wilson & Obdeyn (Reference Wilson and Obdeyn2009) report on a variant of the Hayes & Wilson software that differs primarily in the constraint-induction process. Rather than searching for constraints according to accuracy, Wilson & Obdeyn's model uses a criterion they call Gain. The Gain of a constraint is defined as the change in the log-likelihood of the training data when the constraint is added to the current grammar. Wilson & Obdeyn's learner induces constraints by checking a pool of constraints, and adding whichever one has the highest Gain. Colin Wilson (personal communication) indicates that he is unable to recall a single instance in which the grammar resulting from running this model did not contain *Struct.

It seems likely that the accuracy-first search bias contributes more generally to an empirical problem with the Hayes & Wilson learner in particular. Hayes & White (Reference Hayes and White2013) document a phenomenon they call ‘accidentally true constraints’. This concerns the tendency of the Hayes & Wilson learner to find constraints that happen to be unviolated in the training data, but which appear not to figure in human grammars of the same language. The authors show this by selecting ten ‘natural’ constraints and ten ‘unnatural’ ones that receive moderate weights (…3 to …5) from an English phonotactic grammar, where naturalness is defined on the basis of phonetic and/or typological support. They then conducted a non-word acceptability judgement task with a set of forms that violate either the ‘natural’ or ‘unnatural’ constraints, finding that the ‘natural’ constraints appear to be much more strongly represented in the English speakers’ judgements. While the article's title suggests that they interpret these results in terms of (phonetic) naturalness, they acknowledge that they may instead be a statistical artefact of the constraint-induction process in the Hayes & Wilson learner. Specifically, Hayes & White's note 23 states:

The *Struct constraint is one example of a ‘more generic’ constraint. It may explain the variation that prompted Hayes & Wilson's search procedure to induce ‘accidentally true’ constraints.

Another situation in which the *Struct constraint is useful is in the generation of artificial lexicons. Daland et al. (Reference Daland, Börschinger and Fourtassi2014) describe a series of simulations in which the phonotactic structure of artificial languages was manipulated to study the effect on word segmentation. Specifically, artificial maxent phonotactic grammars were chosen so as to instantiate varying degrees of restrictiveness in syllable structure (e.g. only CV vs. CV(C)). Artificial lexicons were generated by regarding the lexicon as a sample from the probability distribution generated by the grammar. The *Struct constraint proved necessary for controlling word length during the generation process. More specifically, PhoMEnt, an open source publicly available maxent phonotactic grammar implementation, was used, which currently has a finite upper bound of only six segments on string length.Footnote ⁵ In the absence of *Struct, it turned out that nearly all of the sampled words had six segments, the maximum. The reason for this is very straightforward – the number of phonotactically acceptable words with six segments is many times greater than the number of phonotactically acceptable words of shorter lengths. If all acceptable words are assigned the same well-formedness value, more long words will be chosen, simply because they make up a greater proportion of the pool of candidates. *Struct was therefore included and its weight manipulated in integer steps to control the average length of the sampled lexicons. For most grammars, the best segmentation was found when *Struct was assigned a weight of —3, which is in excellent agreement with Theorem 2: Daland et al. (Reference Daland, Börschinger and Fourtassi2014) use a segmental alphabet Σ consisting of 18 segments, so —ln |Σ|=—ln 18=—2·89.

5.2 Necessary vs. sufficient conditions

Theorem 2 gives sufficient conditions to guarantee a finite partition function (and therefore a proper probability distribution) in maxent phonotactic grammars. That is, if w _*Struct <—ln |Σ|, then a proper probability distribution is guaranteed. However, it is possible for a maxent phonotactic grammar to have a finite partition function even when this condition is not met. For example, the onset grammar that is reported in Hayes & Wilson (Reference Hayes and Wilson2008) has a finite partition function. The key is that the onset grammar strictly penalises plateaus and decreases in sonority. So a sequence like trtrtr contains two rt sonority falls, which are punished by a variety of sonority-regulating constraints (see also Hayes Reference Hayes, Lee and Zee2011). More generally, the sequence (tr)n contains n—1 sonority falls, and is punished for each of them. In this case, the number of violations grows with the sequence length for any sequence in the grammar. The underpenalisation problem does not arise, even though this grammar does not include a *Struct constraint. It would be desirable to be able to characterise not only sufficient, but also necessary, conditions to avoid underpenalisation. Theorem 3 does exactly that. The final result is an eigenvalue condition similar to the one given by Grenander (Reference Grenander1976) for consistency of PCFGs. As the proof is rather technical, its intuition is explained in the online supplementary materials.

5.3 Conjecture: finiteness is guaranteed when training on finite samples

Just as Chi & Geman (Reference Chi and Geman1998) proved that a PCFG derived from maximum likelihood estimation will be consistent, this section offers a rationale for the conjecture that a maxent phonotactic grammar trained on a lexicon will avoid underpenalisation as long as a *Struct constraint is included with sufficient weight in the initial state.

As shown by Della Pietra et al. (Reference Della Pietra, Della Pietra and Lafferty1997), the likelihood of the training data is maximised with respect to a given weight wi when the number of expected violations of Ci (over the entire candidate set) equals the number of observed violations of Ci (over the training set). We can obtain a more intuitive version of this equation by dividing both sides by the number of words in the training set. The total number of violations of *Struct in the training data is the total number of segments in all words; dividing this by the number of such words gives us the average length of a word in the training set. The expected number of violations of *Struct in the candidate set is simply the number of words in the training set multiplied by the average number of *Struct violations over the candidate set; dividing this by the number of words in the training set gives us the expected average length of a word according to the current grammar.

Suppose that the grammar is initialised so that the partition function is finite (or, in other words, the expected length of a word is finite). At this initialisation stage, the weight of *Struct might either be too low or too high. If it is too low, the expected average word length is too long, and the weight-setting procedure will simply increase the weight of *Struct until the expected average word length matches the observed average word length. If it is too high, the expected average word length is too short, and the weight-setting procedure will simply decrease the weight of *Struct until the expected average word length matches the observed average word length. As long as the weight-setting algorithm is initialised with reasonable starting weights, there should be no chance of ‘overshoot’, which would make the weight of *Struct so low that the partition function ceases to be finite. Adding new constraints to the grammar cannot decrease the penalty assigned to any string (since constraints only punish, never reward), so adding a constraint to a grammar with a finite partition function will not cause the partition function to become non-finite.

In short, the training data will always exhibit the property that it has a observable and finite average length. Maximum likelihood estimation with maxent phonotactic grammars will tend to cause the weight of *Struct to settle at whatever value makes the expected average word length match the observed average word length. As long as the prior does not force the weight of *Struct to be too low, underpenalisation should be avoided with the standard maximum a posteriori training.

6.1 Summary of major points

This article considers the properties that a phonotactic grammar should have. It began by discussing the motivations for a phonotactic grammar: the need to assess the well-formedness of potential words is motivated by the fact that humans can do so in well-formedness judgement tasks, and the need to link well-formedness with other cognitive modules, notably speech perception and word recognition. Jointly, these properties call for a probabilistic model of phonotactic knowledge.

An especially promising grammatical formalism is maxent HG, which is a stochastic variant of Optimality Theory, with weighted rather than ranked constraints; it stands out from other stochastic approaches particularly in formal guarantees of optimal learning of languages with variation. Maxent HG can be and has been adapted for modelling phonotactic grammars; the result is called maxent phonotactic grammars here to distinguish them from regular maxent HG grammars.

Like other classes of probabilistic models such as PCFGs, maxent phonotactic grammars require special care when it comes to potentially unbounded sequences. The problem, described here as underpenalisation, is that relatively well-formed subsequences may be concatenated together to form arbitrarily long sequences with no ill-formed subparts. The word supercalifragilisticexpialidocious is an example of just such a possible word. In general, the number of such words may grow exponentially with word length. If these words are all assigned a ‘perfect’ harmony score of 0, the grammar's partition function will not be finite, meaning that the probabilities of individual strings will not be well-defined. One solution to this problem that has been used in the literature is to impose a strict upper limit, such as ten segments, on the length of words to be considered. But this approach is empirically inadequate and theoretically undesirable.

After documenting the underpenalisation issue, this paper has proposed a solution: the *Struct constraint. Formal proofs are given of sufficient and necessary conditions which allow a researcher to steer between a hard upper bound on word length and underpenalisation. Provided that a *Struct constraint is included and initialised with sufficient weight, a maxent phonotactic grammar may allow for possible words of unbounded length, but penalise them enough to avoid an ill-defined probability distribution (by keeping the partition function finite). The practical implications for researchers are as follows: (i) when using the Hayes & Wilson phonotactic learner or other maxent phonotactic grammar software, always include a *Struct constraint and set its initial weight to be greater than ln |Σ|; (ii) if developing one's own maxent phonotactic grammar implementation, either force the grammars to always include a *Struct constraint, or build in the test described in Theorem 3.

The remainder of the discussion briefly considers two issues.

6.2 Comments on arguments against *Struct

Gouskova (Reference Gouskova2003) constitutes a concerted attack upon constraints whose sole purpose is to enforce economy effects, i.e. the general linguistic preference for less structure. The constraint *Struct is a canonical example – without exception, it prefers fewer segments. Gouskova's critique is couched within the framework of what might be called ‘classic OT’ (e.g. Prince & Smolensky Reference Prince and Smolensky1993), in which a categorical grammar regulates input–output mappings with constraints that are totally ranked, rather than weighted. It is argued in this section that Gouskova's critique does not apply to *Struct in the maxent HG phonotactic learning setting.

Gouskova considers two types of argument against this kind of economy constraint. First, she proposes that analyses which include such constraints do not actually need it; in support, she gives an impressive array of examples that have been analysed with a *Struct-like constraint (e.g. *V, which penalises all vowels), and then provides an alternative analysis in which the economy effect falls out from more specific, independently motivated constraints. Gouskova's second argument is that the inclusion of *Struct-like constraints in a grammar leads to improper predictions. The general character of this argument can be illustrated with the most extreme case: if *Struct were the top-ranked constraint in an OT grammar, it would predict the null output to be the winning candidate for every input; in other words, no-one would ever include any overt material in their utterances (i.e. speak). Gouskova considers several less extreme cases that are like this in logical character, and argues that several typologically predicted languages do not occur. She concludes that constraints like *Struct are both unnecessary and actually harmful, so they should be excluded from the theory.

The most fundamental point to make is that Gouskova is working in a different framework, with different properties and assumptions. In classic OT, there is an input–output relationship that is regulated by constraints ranked with a total order. In this framework, faithfulness constraints achieve the work of preventing unboundedly long repetitions of a subsequence in surface forms. High-ranking markedness constraints may require multiple epenthesis operations (e.g. vowel prothesis to repair an onset cluster and glottal stop prothesis to repair the resulting onsetless vowel, as in /ktub/→[ʔuktub]). But in these cases, each application permanently resolves the violation that triggered it (it could not be optimal otherwise). The number of such violations must be finite (because underlying forms are only finitely long, and there are only finitely many constraints that could be violated). Therefore, high-ranking markedness constraints can trigger at most a finite number of epenthetic repairs. In the phonotactic learning setting, there is no underlying representation to be faithful to, as the goal is to spell out the well-formedness of potential words (which have not yet been learned). Therefore, faithfulness constraints cannot eliminate unboundedly long sequences. Since markedness constraints are the only constraints in phonotactic learning, they are the ones which must rule out possible words of an arbitrary length (cf. supercalifragilisticexpialidocious). Gouskova's essential point is that *Struct is not needed in classic OT because faithfulness constraints derive economy effects; this point does not hold for phonotactic learning, where there is no faithfulness.

As the field now possesses a much better theoretical understanding of phonological acquisition than it did at the time of Gouskova's (Reference Gouskova2003) work, it is worth thinking through the acquisition scenario from the child's point of view. It seems reasonable to suppose that the child is initially exposed to a language in which input from caretakers contains segmental content, and moreover that comparatively short words have a higher type frequency, at least during the early stages of phonological acquisition (Hayes Reference Hayes, Kager, Pater and Zonneveld2004). According to the theory described here, it is statistically inappropriate for the child to begin with an ‘empty’ phonotactic grammar, as such a grammar does not assign a well-defined probability distribution over the string-space. However, the child might begin with the next best thing, a phonotactic grammar which merely states that longer words are worse – a prior bias which is empirically supported by the input (specifically, one in which w _*Struct  < …ln |Σ|). As the child begins to recognise, encode and learn word-forms, their phonotactic grammar elaborates. Sequences which systematically fail to occur in the input acquire their own more specific markedness constraints, while sequences which do occur drive down the weight of *Struct and drive up the weight of these more specific constraints. After a large number of word-forms are learned, the grammar will have developed to a considerable extent; the work that was formerly done by *Struct will be mostly replaced by more specific and more accurate constraints. This will presumably leave *Struct with a very low weight relative to inviolable markedness constraints and other constraints that drive active alternations. As the child begins to acquire faithfulness constraints, the weights of remaining markedness constraints may move slightly, but *Struct might be left with a low weight – just enough to match the observed average word length with the expected average word length.

6.3 Implications for maxent HG: the consequences of constraint omission

A reviewer raises the issue of whether the underpenalisation problem potentially arises with all maxent HG grammars, or only with maxent phonotactic grammars. This question is related to the discussion in the preceding section, and the answer is that there may be an underpenalisation problem even with ‘normal’ maxent HG.

As Gouskova (Reference Gouskova2003) points out, economy effects in classical OT are normally derived by faithfulness constraints. For example, a single instance of vowel epenthesis may be motivated by a high-ranking markedness constraint, such as repair of a triconsonantal cluster, illustrated in (17) by the choice of candidate (b) over (a).

1. (17)

   

In general, multiple epentheses will not repair the original markedness violation better than a single epenthesis operation (c)–(e), but they do incur additional Dep violations. Of course, if the Dep constraints were omitted from (17), there would be nothing to stop the speaker from choosing one of the ‘wrong’ candidates (c)–(e). And according to Prince & Smolensky (Reference Prince and Smolensky1993), Gen presents the speaker with an infinite number of wrong candidates. Even if it is at the very bottom of the constraint hierarchy, Dep plays an important role in weeding out uneconomical candidates.

In maxent HG, constraints are weighted rather than strictly ranked. Tableau (18) recapitulates (17), but cast in the framework of maxent HG, with a weight of 0 assigned to both Dep constraints.

1. (18)

   

Since unbounded amounts of epenthesis are unpenalised, there is a countably infinite number of candidates which satisfy the important markedness constraint equally well. Underpenalisation may also occur in this circumstance. Fortunately, the same intuitions which govern underpenalisation in maxent phonotactic grammars apply in this more general setting. Underpenalisation cannot occur if sufficient weight is allocated to Dep and/or Struct constraints. It is straightforward to adapt Theorem 2 to obtain a guaranteed finite partition function over an infinite candidate set in this case (but a formal proof is not given). In effect, this point is merely a formalisation of something that is already conventional wisdom in the field: the candidate set should not contain SRs that both differ from the UR and are underpenalised for being so.

6.4 Conclusion

In summary, it has long been a tenet of constraint-based phonology that the candidate set is infinite (Prince & Smolensky Reference Prince and Smolensky1993). This has not caused practical problems for normal working phonologists, as typical analyses only consider a finite subset of all possible candidates. However, this paper has argued in some detail that the infinite candidate set can and should be considered in the case of phonotactic grammars. The essence of the argument is that speakers can and do produce novel words of arbitrary length, that our speech-processing systems have to be equipped to handle this and that a probabilistic phonotactic grammar plays a central role in doing so. Maximum entropy Harmonic Grammar is a particularly promising phonological formalism, owing to its attractive learning guarantees, and it can be seamlessly adapted for phonotactic grammars, as demonstrated here and in Hayes & Wilson (Reference Hayes and Wilson2008). However, existing implementations of maxent phonotactic grammars have imposed a hard upper limit on the length of possible words, which is undesirably restrictive. Without such a hard upper limit, there is the opposite risk: the infinite candidate set may contain sequences consisting of arbitrarily many relatively well-formed subsequences, which might be underpenalised. In this case, a maxent phonotactic grammar can still characterise the relative well-formedness of words, but it cannot assign a well-defined probability distribution. Besides documenting this problem, this paper has proposed a solution: include the constraint *Struct. Theorems 2 and 3 give necessary and sufficient conditions for maxent phonotactic grammars to avoid underpenalisation. The body of the text gives motivation for the conjecture that an underpenalisation problem will not occur provided that the grammar is initialised with a *Struct constraint of sufficient weight, and the default weight-setting algorithm (maximising the likelihood of the training data) is followed. In plain language, maxent HG is an excellent tool for phonological analysis, but this paper points out there is a subset of the parameter space where the tool does not function as intended; this paper also shows how to avoid that regime, and conjectures that the bad regime will be avoided in normal usage so long as grammars are initialised with a *Struct constraint of sufficient weight.