1

In “Taking Thermodynamics Too Seriously,” Craig Callender (Reference Callender2001) signals the “mistake” of understanding classical thermodynamics (TD) “too literally.”Footnote ¹ He identifies three areas of foundational research in statistical mechanics (SM) where this problem occurs: the analyses of the Second Law, the concept of equilibrium, and the account of a class of physical processes called ‘phase transitions’ (PT). The present work deals with the last issue, which has received surprisingly little attention in the recent literature.Footnote ²

This article is organized as follows. I begin (in Section 2) by spelling out Callender's ‘mistake argument’, as I will call it. This is the argument for the claim that the SM attempt to recover the classical TD treatment of PT is problematic. (By ‘treatment’ I mean, as will become clear shortly, the representation of PT in TD in terms of singularities in the thermodynamic potentials.) In doing this, I focus on the issue raised by the role of infinite idealizations (or ‘infinite models’); the presentation of this problem draws on a number of useful details provided in two earlier related articles by Chuang Liu (Reference Liu1999, Reference Liu2001). Against this backdrop, I argue (in Sections 3 and 4) that while the problem noted by Callender is a genuine puzzle for the relationship between TD and SM, it is less clear what exactly the conceptual origin of the puzzle actually is. My main aim here, however, is not to solve the puzzle but to better grasp its significance. More precisely, I will be making a proposal with regard to its source: I submit that the problem is not so much the mismatch between the mathematical formalisms of TD and SM but that it has a more general methodological nature—and thus transcends these two particular theories. I approach (in Section 5) the PT issue by drawing on Bogen and Woodward's well-known distinction between data and phenomena (Bogen and Woodward Reference Bogen and Woodward1988; Woodward Reference Woodward1989). This distinction was introduced while they were analyzing a series of scientific examples, one of which, interestingly enough, was that of a phase transition.Footnote ³

2

The term ‘phase transition’ refers to a physical process such as vaporizing, melting, liquefying, or sublimating; water's phases—ice, liquid, and vapor—are familiar to everybody. (Perhaps less-familiar PT involve magnetization.) What characterizes this type of behavior in a substance is a marked and quite sudden change of its physical properties. While there can be more than one type of phase transition, from now on I will be discussing only the so-called first-order transitions, a category that still encompasses many of the most interesting natural processes happening around us.

One of the first systematic examinations of phase-change phenomena was carried out by Andrews (Reference Andrews1869). Subsequent attempts to explore them with the conceptual apparatus of classical TD have been remarkably successful, as the standard TD concepts turned out to be appropriate in describing these processes in a very accurate mathematical vocabulary.Footnote ⁴ Consider, for instance, a system evolving along an isotherm, such that the system is ‘near equilibrium’ at every state in the process (see Figure 1, taken from Stanley Reference Stanley1971, 31). After introducing the concept of ‘free energy’, TD represents a (first-order) phase transition as a finite discontinuity in the first derivative of the free energy.Footnote ⁵ Graphically, the curve depicting the Gibbs free energy G (plotted as a function of pressure P for a constant temperature) features a point where the slope of the tangent changes discontinuously (see Figure 1a). This point is also called a ‘singularity’, since G displays singular behavior there (its curvature is infinite).

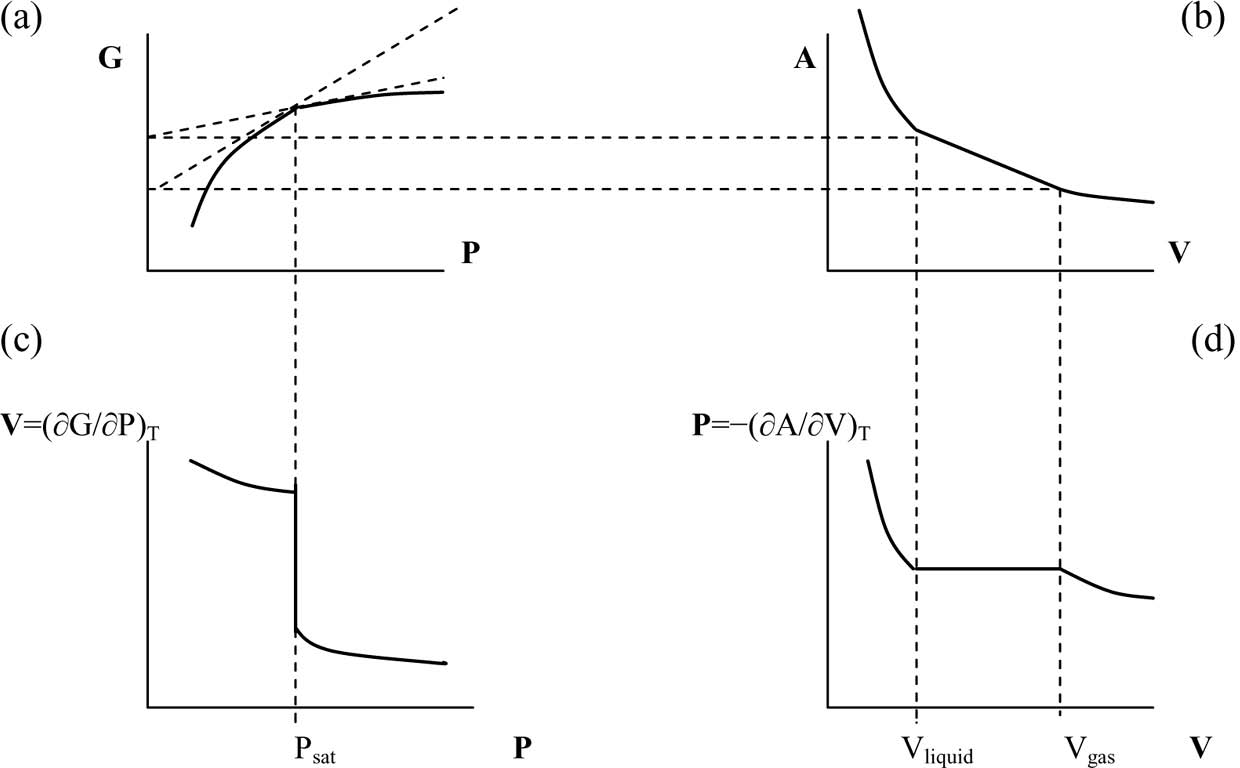
Figure 1. Graphs are drawn for a temperature less than the critical temperature $T_{\mathrm{c}\,}$. Variables G and A are Gibbs and Helmholtz free energies, respectively. The pressure corresponding to the singularities is not the critical pressure $P_{\mathrm{c}\,}$ but the value of the saturated vapor pressure. From Stanley Reference Stanley1971, 31.

The partition function Z plays the essential role in connecting the above macroscopic TD representation of PT to the microscopic SM viewpoint. In SM, the Helmholtz free energy A is given in terms of the partition function Z for the canonical ensemble, as follows:

where

The sum is taken over all microstates having energy $E_{\mathrm{r}\,}$, and $\beta =1/ k_{\mathrm{B}\,}T$, where $k_{\mathrm{B}\,}$ is the Boltzman constant. (Quantization is implicit here; otherwise the expression should be an integral.) Appropriate differentiations of G or A give us all thermodynamic quantities (Reif Reference Reif1965, 164, 213–216; see Figure 1c and 1d). Note that while A is a fundamental TD macrolevel concept, the partition function Z is a genuine SM microlevel concept, since Z is dependent on the number of particles N composing the system (by definition, $k_{\mathrm{B}\,}=R/ N$, where R is the ideal gas constant).

Now the difficulties crop up almost immediately. By following TD, SM states that a phase transition occurs when the free energy has a singular (i.e., nonanalytic) point. Given the above relationship between A and Z, this entails that a phase transition can occur only when the partition function Z has a nonanalytic point. Yet Z is analytic, since it is a finite sum of analytic functions, and such a sum is analytic. (This is a mathematical fact.) Hence, (a nonzero) Z cannot feature any singularities. So the problem is how to show that Z has singularities while keeping it nonzero.

A way around this difficulty was found and essentially consisted in taking what is now called ‘the thermodynamic limit’. This amounts to considering an idealized version of the system—a system having an infinite number of particles N and occupying an infinite volume V, while the ratio $V/ N$ is fixed and finite. It turns out that, as a matter of pure mathematics, a nonanalyticity can actually be identified for such an idealized system in equilibrium (also subject to other stability conditions). In particular, for lattice systems (more specifically, two-dimensional Ising models), the now infinite number of solutions z of the partition function Z ‘pack’ along the circle $\vert z\vert =1$ and, at $T< T_{\mathrm{c}\,}$, the real axis is ‘pinched’. In other words, physicists devised a method to show that Z can harbor singularities (without vanishing); moreover, even an indication where the singularity is located is possible. Thus, SM can show that the infinitely idealized version of the system undergoes a phase transition after all.Footnote ⁶

But this achievement is problematic, since within SM the systems exhibiting PT are finite. As Callender formulates it, the puzzle of the infinite idealizations is this:

Given the failure of finite SM to derive PT, it is natural to conclude that the property ‘undergoing a phase transition’ represents an excellent candidate for an emergent property, one that is not reducible (in a finite model) to its alleged fundamental basis (Humphreys Reference Humphreys1997; Liu Reference Liu1999; Rueger Reference Rueger2000).Footnote ⁷

Callender is not impressed by this conclusion (and this is presumably one of the “strange conclusions” [Reference Callender2001, 547] he thinks one draws when understanding TD [too] literally). He urges a different take on the issue, which would significantly weaken the support for the emergentist position. He notes that central to the derivation of this conclusion is the assumption that the SM definition of PT has to be the same as the TD representation of these phenomena. It is this assumption that he presents as a “mistake.” In other words, he claims that the TD mathematical definition of PT should not be automatically imported into the SM mathematical framework and adopted as a definition of PT there too. To do this would be to take thermodynamics “too seriously” (Reference Callender2001, 550):

Callender thus protests against what he calls “a knee-jerk identification of mathematical definitions across levels” (Reference Callender2001, 550).

It should be clear at this stage in the argument that the serious trouble (the appeal to an infinite model) arises from the attempt to transfer a mathematical representation (or definition) from one domain to another. So before I move on, let me insert a brief remark here about the connection between this aspect of the issue and the positions one can encounter in the recent literature on the applicability of mathematics to physics. What is interesting here is that usually this kind of transfer move has been attended by great successes in the history of science and has led to important physical insight (see, for instance, the idea to model the equations governing the flow of charge or heat on the hydrodynamic equations describing the flow of fluids). Moreover, following the insight offered by the mathematical formalism itself has led to developing and discovering new theories (Steiner Reference Steiner1998, Reference Steiner and Shapiro2005) that explain physical phenomena or even predict new physical entities.Footnote ⁸ Generally speaking, philosophers and physicists reflecting on these issues have thought that what is often called ‘the role of mathematics in natural science’ has been a positive one: mathematics used to solve problems for physicists, not create new ones.Footnote ⁹ Yet this episode seems to show that this enthusiasm needs to be tempered. It shows that the reverse phenomenon is possible, as carrying the formalisms across the board may lead to unwelcome developments.

3

One way to sum up (simplifying a bit) Callender's position is to describe it as a modus tollens: If SM follows the TD representation of PT, then SM must use infinite idealizations. But real systems displaying PT are not infinite, so the consequent should be rejected. Hence, the negation of the antecedent is derived, and thus we are advised that SM should not follow TD. To see the force of this position, just deny the requirement that SM define PT as singularities (like TD). The appeal to the infinite idealization (i.e., taking the thermodynamic limit) is no longer necessary, so the problem dissolves right away.

At this point, let me note that I am in total agreement with this argument so far: it is premature for an SM theorist to worry that SM cannot recover the PT as modeled in TD. (Consequently, it is premature for a philosophically inclined SM theorist to celebrate the discovery of a seemingly indisputable emergent phenomenon.) The correctness of this point granted, the question I ask now is what (if anything) follows from it, especially with regard to the TD treatment of PT. Is this treatment to be dismissed? Is it ‘wrong’ in any of the relevant senses (i.e., grounded in unreasonable assumptions, etc.)? Note also that just dropping this definitional/representational requirement cannot be the end of the matter. If (quantum) SM is meant to be the fundamental theory in this area, then one expects it to be able to represent these familiar phenomena in its own, less problematic, way—that is, without following the TD representation, which leads, as a matter of mathematical necessity, to taking the thermodynamic limit. So, at this point, one might want to learn about the resources of finite SM to deal with PT in a less problematic way.

Unfortunately, Callender is not very forthcoming about what these resources are. And, one suspects, he cannot even be. He first voices his hope (an “article of faith”) that “there are non-singular solutions of the partition function describing real systems that give rise to the macroscopic transitions called phase transitions” (Reference Callender2001, 550). Yet when it comes to the justification of the claim that “physics is hardly impotent in the face of phase transitions in finite N systems” (Reference Callender2001, 551), he mentions mean field theory as the primary tool able to help us. But, as is well known, this is not so straightforward, since all the approximation methods that Callender might have in mind (mean field theory techniques included) bring with them a host of new difficulties because they “introduce considerations not justifiable on grounds of SM” (Liu Reference Liu1999, S97).Footnote ¹⁰ Even a glance at some of the ongoing research in this area reveals that the question ‘Can physicists get around the thermodynamic limit in the SM account of PT?’ (or, equivalently, ‘How do PT arise in “small” systems?’) is actually far from being decided.Footnote ¹¹ For this reason, the appeal to the infinite idealization (i.e., taking the thermodynamic limit) is for the moment essential in proving what physicists call ‘rigorous results’ about PT.Footnote ¹²

When one goes back to Callender's position, it is not hard to see that his modus tollens is vulnerable to the familiar objection raised against any reductio arguments. It is sufficient that one makes the proverbial move and converts his modus tollens into a modus ponens; thus, by accepting the antecedent of the conditional (the idea that the TD treatment of PT is physically well motivated), one derives the standard conclusion—roughly, that ‘SM is able to derive PT only in the thermodynamic limit’. Let me stress that this conversion is not just an academic exercise; it is, as a matter of fact, responsible for the received view among physicists. Voicing this view, the physicist Kadanoff urges that “the existence of a phase transition requires an infinite system. No phase transitions occur in systems with a finite number of degrees of freedom” (Reference Kadanoff2000, 238). In most cases, however, what motivates the physicists’ relaxed attitude in this matter is not a suspect metaphysical easiness with infinities but rather an outright dismissal of the whole finite versus infinite business on the basis of considerations having to do with the limits of experimental accuracy. Since it is virtually impossible to point out observable differences between the behavior of infinite systems and systems featuring a really big number of components (of the order of 10²³ or larger), the philosophers’ worry (do finite systems really undergo PT?) becomes immaterial. As the physicist Baierlein once joked, “It all works because Avogadro's number is closer to infinity than to ten.”Footnote ¹³

4

We have now reached the point where the main task of this article can be formulated. Despite the problems I gestured to above, I concede that Callender is right to maintain that there is no good reason to require SM follow TD; hence, the antecedent of the conditional in the (emergentist's) modus ponens, formulated more imperatively as ‘SM should follow TD’, is untenable. Yet taking the rejection of this antecedent to be the final outcome of this discussion is not entirely satisfactory. One would like to know the deeper reason (if any) for which TD introduces singularities.

In asking for this, my intention is to sketch a way to rethink the puzzle's overall significance. One natural way to react to the claim that ‘SM should not follow TD’ is to construe this assessment as implicitly highlighting a flaw of TD, an intrinsic deficiency of it—after all, we are told not to take it “too seriously.” I claim that while there is an important insight in this urge, this is not the whole story. As I will try to explain in more detail below, we should not think that the puzzle is generated by any intrinsic flaw of TD; instead, I will argue that the singularity puzzle arises from the fact that scientific investigation in thermal physics conforms to a more general methodological requirement common to perhaps all modern mathematized theories. The key element involved in this requirement is the distinction between data (as collected in thermal measurements) on the one hand and their shaping into (thermal) phenomena on the other. In what follows, I will attempt to use, in a way to be explained, Bogen and Woodward's important insight that our understanding of scientific enterprise has to take into account this distinction. The upshot of this discussion, however, will not be the dissolution of the puzzle (recall that this was not my intention) but, I hope, a deeper appreciation of its overall significance. We should be able to see why the ‘mistake’ is not trivial after all, why it has been made, and to what extent it is perhaps unavoidable. Now let me fill in the details needed to substantiate the above proposal.

5

When pointing out his agreement with Liu, Callender notes that “because of the fluctuations we don’t actually measure perfect singularities” (Reference Callender2001, 550; my emphasis). Unpacked, Callender and Liu's position is as follows. The singularities of the thermodynamic functions are, strictly speaking, not observable, or not measurable. From an SM perspective, real systems have a finite number of degrees of freedom; hence, they are subject to fluctuations—which, importantly, disappear when the idealized infinite system is considered within the SM framework.Footnote ¹⁴ Therefore, for a real system, from the perspective of SM, the thermodynamic potentials will not feature any singular points. A graph like the one shown in Figure 2, rather than the one in Figure 1d, offers a most accurate description of the relevant physics. Thus, for a real system, from the viewpoint of SM, “the transition is neither ‘smooth’ nor ‘singular’” (Liu Reference Liu1999, S103). The singularities are in fact posited by TD—added, as it were, to the isotherms. These singularities are “artifacts” (Liu Reference Liu1999, S104), “fictions of TD,” and “do not exist in reality” (Liu Reference Liu2001, S336). So the status of singularities is problematic precisely because they are not observable, or not measurable.

Figure 2. After Liu Reference Liu1999, S102.

To begin applying Bogen and Woodward's terminology, we can say that the graph in Figure 2 displays a set of data collected from experiments. In it, no singularities are shown. As Liu insightfully notes, “No experiments, no matter how finely tuned, can ever determine whether the ‘corners’ which bound PT regions are sharp or round” (Reference Liu2001, S328). The relevance of this observation is supposed to be considerable: realizing that the singularities are artifacts, or posits, would amount to no less than a “conceptual shift” whose effect would be that “the isotherms of systems with multiple phases coming back from the laboratories will no longer have singularities in them” (Liu Reference Liu1999, S105).

Yet, notably, the actual scientific practice (both past and present, both TD and SM) does not quite conform to the ‘conceptual shift’ foresight. A glance at the phase diagrams coming back from the laboratories shows that the scientists are not particularly anxious about the precise geometrical form of the reported phase diagrams. Typically, a phase diagram will display either continuous curves or data points. In some cases the data points are connected, but in other cases they are not, and many phase diagrams feature only continuous curves and what looks like sharp corners.Footnote ¹⁵ While contemporary scientists realize that, strictly speaking, the transitions are neither smooth nor sharp, they continue to talk in terms of and to ‘see’ singularities in the phase diagrams even if, again, strictly speaking, there are none there to be seen. Consequently, a way to make sense of this interesting and rather strange conceptual illusion has to be articulated. As announced, the proposal I shall develop here is that we can better understand the role of singularities by adopting Bogen and Woodward's distinction between data and phenomena. While the distinction is now a classic one, it still draws philosophers’ attention.Footnote ¹⁶ I will begin by presenting a rough sketch of it.

According to Bogen and Woodward, data are constituted by experimental observations performed by instruments (Reference Bogen and Woodward1988, 305) and are, in most cases, reported in quantitative form; in this particular context, they consist of thermometer and/or manometer readings. The record of these observations typically takes the form of a region of scattered individual points on a graph. Yet, essentially, the stage of collecting and recording this raw information constitutes only the starting point of scientific investigations. Bogen and Woodward stress that the role of data is to serve as the basis for the inference of what they call ‘phenomena’ (Reference Bogen and Woodward1988, 309, 311, 313, etc.) While the specific procedures by which phenomena are inferred from data depend on the particular area of scientific research, they all involve statistical techniques and data analysis (Reference Bogen and Woodward1988, 311).

One important feature of the collected data is that they reflect the particular measurement contexts. In our case, it is unavoidable that the data points shown on the P-V diagrams include extraneous factors. They not only contain ‘noise’ from measurement errors but also exhibit the effect of random fluctuations occurring in the particular sample of substance. These elements are distorting insofar as they do not reflect the stable, enduring, characteristic properties of the substance under scrutiny but rather reflect accidental features of it (for one thing, no examined sample is perfectly pure); additional distortions are due to the measurement process itself, since it occurs at a particular time (always further away from perfect equilibrium) and in a particular lab and is carried out using a particular instrument, and so on. Unlike the regions of scattered data points, phenomena are not supposed to be “idiosyncratic to specific experimental contexts” (Bogen and Woodward Reference Bogen and Woodward1988, 317). They are reproducible, and this is so because they do have stable characteristics invariant over various experimental setups (Bogen and Woodward Reference Bogen and Woodward1988, 317, 326; Woodward Reference Woodward2009).

This contrast between the stability of phenomena and the relative variability of the collected data implies a difference in what I will call ‘epistemic relevance’. To be sure, data do have epistemic relevance since they constitute the basis for the inference to phenomena; their relevance, however, is limited to this inferential role. It is what the data are ‘shaped into’, the phenomena, that possess full epistemic relevance, precisely in virtue of their stability. This relevance is epistemic insofar as it is the reproducible, invariant, stable phenomena that are explained and predicted by our theories (Bogen and Woodward Reference Bogen and Woodward1988, 305–306; Woodward Reference Woodward2000, S163); thus, phenomena are the object of scientific knowledge, as embodied in systematic explanations and predictions. Yet it is important to note that Bogen and Woodward's use of the term ‘phenomenon’ departs from the typical meaning one encounters in the philosophical literature. They point out that while data are collected by making observations and measurements, “phenomena for the most part cannot be observed and cannot be reported by observational claims” (Reference Bogen and Woodward1988, 343, 306). And, as Machamer (Reference Machamer2009) remarks, this meaning is different from what most authors (Duhem, for one) take phenomena to be, namely, “observable happenings.” In the philosophical tradition, phenomena to be ‘saved’ included observed planetary positions, the rising of stars, eclipses, and so on.

The idea to use the data versus phenomena framework to illuminate the epistemic status of singularities is prima facie promising, I believe, since a look at the standard modern scientific practice seems to confirm Bogen and Woodward's view. Physicists begin by measuring various thermal quantities and then record them in the form of a region of scattered P-V data points. These records show that transitions are indeed neither smooth nor sharp (see Figure 2). But in light of the data/phenomena distinction, it is crucial to realize that this is true at the level of data collection; however, we should bear in mind that phenomena constitute the real focus of scientific interest. In practice, in both TD and SM, there is always a further step to take after gathering the data points through measurements. This step consists in “transform[ing] the discrete values into mathematical functions,” as the experimental physicist Malanowski (Reference Malanowski, Malanowski and Anderko1988, 281) describes it. What is inferred, through various (usually computerized) techniques of data fitting (polynomial fit, the method of least squares, etc.), is “the algebraic shape of the thermodynamic functions” (Malanowski Reference Malanowski, Malanowski and Anderko1988, 282). Insofar as they are the result of the inferences from data, these functions encode actual information about the thermal processes of interest. More precisely, depending on what kind of thermodynamic properties are measured, different procedures of fitting the data points are used.Footnote ¹⁷ Essentially, then, the singularities are posited at this second, inferential stage. They describe the behavior of these functions (and of their derivatives). Within this framework, we can now say that the role of a singularity is to represent a phase change phenomenon. Note that the term ‘phenomenon’ is used here in the specific sense of Bogen and Woodward. Thus, it is meant to stress the idea that singularities are representative at the phenomenal/unobservable level and not at the data/observable level.

If this framework is to be useful in analyzing PT, it is important to try to clarify the ontological status of phenomena and how this status is connected to the introduction of the singularities.Footnote ¹⁸ Phenomena are what generate, or produce, the data we collect, so they are physically real patterns of behavior ‘out there’ in the world (Bogen and Woodward Reference Bogen and Woodward1988, 321). However, in accepting that, one might still be puzzled by the role of the observable/unobservable distinction. One way to understand this is to note that phenomena are not to be found at the extreme ends of the continuum of difficulty of access by instruments. Thus, in making sense of the claim that phenomena are “detected” (Bogen and Woodward Reference Bogen and Woodward1988, 306), a claim that could prompt the puzzlement hinted at above, we should pay attention to the qualification that they are “detected through the use of data” (306). A better instrument (say, a microscope) would not eventually reveal a phenomenon; instead, it would provide more accurate data, which in turn would be available to be used to reinforce our confidence that a genuine phenomenon exists. What about the thermodynamic singularities, then? As the above characterization of their role suggests, a singularity is not so much a feature of the physical system itself but a feature of its mathematical representation. While phenomena are real, data-producing patterns of physical behavior, their representations—the mathematical singularities—can be said to be theoretical constructs. One might thus suspect that this amounts to maintaining that singularities do not have genuine physical meaning, especially because phenomena were said to be ‘unobservable’.Footnote ¹⁹ Yet if the functions (whose graphs are depicted in the diagrams) describe what is going on within the thermal system under scrutiny, then identifying a singularity of such a function still amounts to characterizing the actual physics: singularities are connected to the actual physics indirectly, via their role in representing (unobservable) phenomena. But, one might ask, aren’t PT observable after all? It turns out that understanding them as phenomena proves appropriate once again, insofar as it reflects the real difficulty to answer this question. The problem is that, on the one hand, it is unquestionable that we witness a physical discontinuity taking place—we all see the condensation of vapors on the walls of the tea kettle every morning; on the other hand, we can’t point out the precise moment when the transition occurs.Footnote ²⁰ Strictly speaking, then, we cannot observe the moment when the physical discontinuity occurs. Hence, insofar as a singularity is supposed to characterize it, a singularity does lack observational significance—while, again, this does not preclude the singularity having physical significance. Thus, singularities do not occur at the level of direct observation (the level of data) but at the next level up, so to speak, the level of phenomena, which are inferred from the data.Footnote ²¹ The significance of a perfectly sharp corner cannot be grasped at the observational, or data, level but only at the phenomenal level. Since scientists’ interest is to “move from claims about data to claims about phenomena” (Bogen and Woodward Reference Bogen and Woodward1988, 314), one sees why and how singularities do legitimately fall under their concern after all.

How does this bear on Callender and Liu's primary worry that singularities are not observable, or not measurable, and thus that they are not (about) data? It is immediate that within this framework this worry lacks the kind of epistemic relevance (in the sense introduced above) assigned to it. Despite misleading appearances (which Bogen and Woodward take great pains to correct), the “claims about data”—such as Liu's, that the isotherms recorded on diagrams of the type in Figure 2 cannot show, even in principle, sharp corners—are not what science (TD and SM in particular) is usually concerned with. Essentially, a dominant feature of scientific inquiry is its interest in phenomena, not data: “Scientific theories are expected to provide systematic explanations of facts about phenomena rather than facts about data” (Bogen and Woodward Reference Bogen and Woodward1988, 322).

To sum up, it is true that no singularity (i.e., perfectly sharp corner) is or can be found on the data-recording graphs such as that in Figure 2. But the mere record of scattered data points is not the right place to look, methodologically speaking, since from neither a TD perspective nor an SM perspective will one find there what one is really interested in—the phenomenon of a phase change. Therefore, that singularities are not measurable (i.e., do not show up on graphs) is of little epistemic import. They retain their central place in the modern treatment of PT via their (representational) connection to PT phenomena, in both TD and SM.

So while I agree that the singularities on isotherms are posits, I emphasize that what really matters is the reason for introducing them. The idea that “phase transitions are characterized as singularities in TD because there is no fluctuation in TD systems, and this is so because TD systems are considered as of continuous matter” (Liu Reference Liu1999, S102; my emphasis) is not wrong but is somewhat misleading. The reason for introducing singularities, I have argued, is scientifically (methodologically) legitimate and transcends the TD and SM perspectives. They occupy center stage not so much because TD, unlike SM, works with an idealized (hence, literally false) ontology but to mark the presence of a phenomenon, the actual concern of scientific investigation for either of those theories. This is why calling them ‘artifacts’, or ‘fictions’, conveys the deceptive suggestion that the definition of PT in TD is somewhat defective and thus should not be taken “too seriously.”

Note, finally, that the data/phenomena distinction proves to be rather rough at this point, and we should perhaps refine it by distinguishing further between TD phenomena and SM phenomena. This distinction allows us to realize that, from the methodological viewpoint adopted here, there is actually no difference between the ways TD and SM construct their phenomena—so, before a case for the contrary view is made, I reject the idea that we should introduce a distinction between what may be called ‘levels of phenomena’. Both theories infer phenomena from the same set of data points (obtained from measurements), and both need (again, in a methodological sense) to shape them into continuous curves that exhibit the sought stability and independence from the vagaries of data collection techniques and thus constitute the proper object of scientific study.Footnote ²²

6

Let me finish by stressing that I have not argued that SM should (must) take thermodynamics seriously full stop (in the matter of PT). Such a requirement is misguided, indeed, together with the hopes that an unquestionable emergent phenomenon has finally been demonstrated (though Liu seems to entertain such hopes; see Liu Reference Liu1999, S92). And, in fact, this is not surprising, as there are many other contexts where we should not follow TD—for instance, in assuming ontological or epistemic views of the world that are literally false (matter is not continuous but granulate, the second law is not absolute but statistical, etc.). Moreover, we should give full credit to the SM theorists’ efforts to account for PT without appealing to the thermodynamic limit. After all, there is no no-go type of theorem claiming that one who begins with a system with a finite number of degrees of freedom and ignores the TD definition of PT as singularities, replacing it with a new and ‘pure’ SM definition, cannot show that PT will occur. Granted that, I emphasize that despite a number of critical points I have raised here, my main aim in this article has been a constructive one, namely, to open up a new way to understand the nature of the infinite idealizations puzzle. I attempted to use Bogen and Woodward's distinction between data and phenomena to elucidate physicists’ reasons to model such systems in terms of singularities and thus to highlight their epistemic significance.Footnote ²³ On this conception, the data do not exhibit singularities; essentially, it is the modeling techniques (fundamentally, statistical data analysis) that introduce them as a way to capture the phenomena, the true object of scientific interest.