1. Introduction
Mean values, or probabilistic averages, are used to define macroquantities in many sciences. In neuroscience, the response of a neuron is characterized in terms of the mean firing rate, or the expected spike frequency within a time window (Rieke et al., Reference Rieke, Warland, Steveninck and Bialek1997). Or in evolutionary theory, “fitness” is the probability of survival.Footnote 1 And then there is the most popular example of all: Temperature defined as the mean kinetic energy of molecules in a gas. We cite these examples in order to suggest that a broader understanding of the role of probabilities, and probabilistic averaging, may be important for a broader understanding of inter-theory relations. Current philosophical work on intertheory relations does not place much emphasis (Batterman Reference Batterman2001b) on probabilistic averaging as a method of “abstracting away from the messy details” (Waters Reference Waters1990) of the underlying microphenomena.
Nagel's (Reference Nagel1961) account of intertheory relations (as deductive relations) highlighted the need for bridge laws to bridge the definitional gap between macroquantities and microquantities. So, the existence of bridge laws is expected. But it could be that the probabilistic nature of bridge laws is unexpected. This is especially so when macroquantities are defined as ensemble averages, where the averages are over possible rather than actual microquantities.
This paper provides a concise survey of the intertheory relations that hold between quantum mechanics (QM) and the deterministic laws of classical physics—in particular, Newton's equations of motion and the ideal gas law in thermodynamics. It may be surprising that deterministic laws can be deduced from a probabilistic theory such as quantum mechanics. Here, curve-fitting examples provide a useful analogy. Suppose that one is interested in predicting the value of some variable y, which is a deterministic function of x, represented by some curve in the x-y plane. The problem is that the observed values of y fluctuate randomly above and below the curve according to a Gaussian (bell-shaped) distribution. Then for any fixed value of x, the value of y on the curve is well estimated by the mean value of the observed y values, and in the large sample limit, the curve emerges out of the noise by plotting the mean values of y as a function of x.
To apply the analogy, consider x and y to be position and momentum, respectively, and the deterministic relation between them to be Newton's laws of motion. Then it may be surprising to learn that Newton's laws of motion emerge from QM as relations between the mean values of QM position and QM momentum. These deterministic relations are known as Ehrenfest's equations. In contrast to curve fitting, the Heisenberg uncertainty relations tell us that the QM variances of position and momentum are not controllable and reducible without limit. Nevertheless, it is possible for both variances to become negligibly small relative to the background noise. This is the standard textbook account of how Newton's laws of motion emerge from QM in the macroscopic limit (e.g., Gillespie Reference Gillespie1970; Messiah Reference Messiah1970; Schwabl Reference Schwabl1993). We review this story in Section 2.
Nevertheless, this is an incomplete account of how the macroworld emerges in QM. For there are other macroscopic laws, such as thermodynamic laws, that do not follow from Ehrenfest's equations. We shall consider the ideal gas law, which relates the pressure, volume, and temperature of a gas.
The ideal gas law appeals to a very simple mechanical model—that of tiny billiard balls bouncing around in a box that have zero potential energy except for the times at which they are in direct contact with each other or the walls of the container. Because the collisions are instantaneous, these times are of measure zero, and can be neglected for some purposes. What is interesting about this idealization is that the assumptions used to derive Ehrenfest's equations are false. Even an appeal to the more fundamental QM equations from which Ehrenfest's equations are derived does not help. The derivation of thermodynamic laws is an independent problem.
We look at how Newtonian mechanics addresses the problem of discontinuous jumps in Section 3. Then, in Section 4, we sketch the QM treatment of a particle in an infinite potential well. Our purpose is not merely to prove the incompleteness of Ehrenfest's equations, but to compare the definitions of pressure in Newtonian mechanics (Section 5), and in statistical mechanics (Section 6), and in QM (Section 7). Our main puzzle is about how pressure can be defined in QM, and we rest content with a solution to the problem in the very simple case of a single particle in a one-dimensional box. More general treatments of the ideal gas law are well documented in other places (e. g., Khinchin Reference Khinchin1960).
In all the cases we examine, the quantities appearing in macrolaws are defined as averages of microquantities. Some possible consequences of this fact for a realist interpretation of theories are mentioned in the final section.
2. Ehrenfest's Equations
We begin with the Hamiltonian operator for a single particle written in the form:
where the ⁁ indicates that it is a Hermitian operator (called an ‘observable’ of quantum mechanics, because all the eigenvalues are real numbers if the operator is Hermitian, and so are their mean values).
![]() $\hat{P}$
and
$\hat{P}$
and
![]() $\hat{X}$
are the momentum and position operators, defined respectively as:
$\hat{X}$
are the momentum and position operators, defined respectively as:
where
![]() $\hat{X}$
operates on a wave function ψ(x) by mapping ψ(x) to xψ(x).
$\hat{X}$
operates on a wave function ψ(x) by mapping ψ(x) to xψ(x).
Using Schrödinger's equation, one may show that the time rate of change of the mean value of any operator is equal to i/ℏ times the mean value of the commutator of that operator with the Hamiltonian (see Gillespie Reference Gillespie1970, 76–77 for a proof). That is, for an arbitrary QM observable, Â,

where the brackets refer to the QM mean, and the subscript t indicates that the mean value depends on the time t.
One of the most famous consequences of this general fact is that any observable that commutes with the Hamiltonian has mean value that is constant in time. In fact, the implications are stronger. Since  2 commutes with
![]() $\hat{H}$
if and only if  computes with
$\hat{H}$
if and only if  computes with
![]() $\hat{H},$
the variance of  is also constant. In fact, the whole probability distribution for  is invariant over time whenever  commutes with
$\hat{H},$
the variance of  is also constant. In fact, the whole probability distribution for  is invariant over time whenever  commutes with
![]() $\hat{H}$
. This applies trivially to the energy itself, for obviously the Hamilitonian commutes with itself. This provides yet another kind of intertheoretic relation of the kind we are discussing: In Newtonian mechanics, the conservation of energy says that E is constant in time. Whereas in QM, this corresponds to the law that the mean value of E, 〈E〉, is constant.
$\hat{H}$
. This applies trivially to the energy itself, for obviously the Hamilitonian commutes with itself. This provides yet another kind of intertheoretic relation of the kind we are discussing: In Newtonian mechanics, the conservation of energy says that E is constant in time. Whereas in QM, this corresponds to the law that the mean value of E, 〈E〉, is constant.
Now choose  to be
![]() $\hat{P}$
, and
$\hat{P}$
, and
![]() $\hat{X}$
. With these choices we derive Ehrenfest's two equations. The time rates of change of
$\hat{X}$
. With these choices we derive Ehrenfest's two equations. The time rates of change of
![]() $\langle \hat{P}\rangle $
and
$\langle \hat{P}\rangle $
and
![]() $\langle \hat{X}\rangle $
are not zero because, in general, neither operator commutes with
$\langle \hat{X}\rangle $
are not zero because, in general, neither operator commutes with
![]() $\hat{H}$
. The exact commutation relations can be derived from (1) and (2). They are (Gillespie Reference Gillespie1970, 110):
$\hat{H}$
. The exact commutation relations can be derived from (1) and (2). They are (Gillespie Reference Gillespie1970, 110):
where
Equation (6) is exactly analogous to how forces are derived from the potential energy function in Newtonian mechanics. For example, if x denote the height of an object above the ground, then
![]() $U(x) =mgx$
is the potential energy of the object, where m is its mass and g is the gravitational field strength. Therefore,
$U(x) =mgx$
is the potential energy of the object, where m is its mass and g is the gravitational field strength. Therefore,
![]() $F(x) \equiv -dU/ dx=-mg$
is the gravitational force (weight) acting on the body, where the minus sign indicates that the force acts in the downward (negative x) direction.
$F(x) \equiv -dU/ dx=-mg$
is the gravitational force (weight) acting on the body, where the minus sign indicates that the force acts in the downward (negative x) direction.
Note that equation (6) assumes that the potential energy function is differentiable with respect to x. This is not true in idealized cases such as an ideal gas modeled in terms of hard wall and hard billiard balls. For then the potential energy changes of 0 to ∞ across a boundary, which is why we shall treat this case separately in later sections.
If we substitute (4) and (5) into (3), we immediately derive Ehrenfest's equations:
Note that these two laws are exact in the sense that no approximation has been used.
If we now differentiate both sides of (7) with respect to t, and make a substitution using (8), we get:
This is also an exact equation of QM. While this looks like Newton's second law, F = ma, it is only functionally equivalent to it if
If (10) does hold, then we need only write down the bridge laws
![]() $\langle \hat{X}\rangle _{t}\equiv q(t) $
and
$\langle \hat{X}\rangle _{t}\equiv q(t) $
and
![]() $\langle \hat{P}\rangle _{t}\,\equiv \,p(t),$
to obtain
$\langle \hat{P}\rangle _{t}\,\equiv \,p(t),$
to obtain
![]() $dq/ dt=p/ m$
, and
$dq/ dt=p/ m$
, and
![]() $F(q) =md^{2}q/ dt^{2}$
. These equations are isomorphic to Newton's laws of motion and therefore have the same solutions.
$F(q) =md^{2}q/ dt^{2}$
. These equations are isomorphic to Newton's laws of motion and therefore have the same solutions.
Equation (10) is true if
![]() $F(x) =const.,$
or if
$F(x) =const.,$
or if
![]() $F(X) =coast\times x$
. But if
$F(X) =coast\times x$
. But if
![]() $F(x) =x^{2}$
, (10) is only approximately true to the extent that the dispersion, or standard deviation, of x is very small. For only then is
$F(x) =x^{2}$
, (10) is only approximately true to the extent that the dispersion, or standard deviation, of x is very small. For only then is
![]() $\langle \hat{X}^{2}\rangle \approx \langle \hat{X}\rangle ^{2}$
. Therefore, in the macroscopic limit, when the dispersion of x is small, Newton's laws of motion hold to a high degree of approximation.
$\langle \hat{X}^{2}\rangle \approx \langle \hat{X}\rangle ^{2}$
. Therefore, in the macroscopic limit, when the dispersion of x is small, Newton's laws of motion hold to a high degree of approximation.
3. The Newtonian ‘Force’ Acting on a Particle in a Box
In Newtonian physics, there are two ways of writing down an expression for the force acting on a particle. The first ‘definition’ is via Newton's second law,
![]() $F=m.a,$
or equivalently,
$F=m.a,$
or equivalently,
![]() $F=dp/ dt$
, where p is the particle's momentum, m is the mass of the particle, and t is time. Or else, in the Hamiltonian formulation of Newtonian mechanics, force is ‘defined’ as minus the space derivative (the x-derivative) of the Hamiltonian, or the potential energy part of the Hamiltonian since the kinetic energy part does not depend explicitly on x. If U(x) denotes the potential energy of the particle at position x, then the force acting on the particle is
$F=dp/ dt$
, where p is the particle's momentum, m is the mass of the particle, and t is time. Or else, in the Hamiltonian formulation of Newtonian mechanics, force is ‘defined’ as minus the space derivative (the x-derivative) of the Hamiltonian, or the potential energy part of the Hamiltonian since the kinetic energy part does not depend explicitly on x. If U(x) denotes the potential energy of the particle at position x, then the force acting on the particle is
![]() $F=-dU/ dx$
. This ‘definition’ works in ‘nice’ cases in which the potential energy function U(x) is everywhere differentiable, but unfortunately an infinitely deep potential well is not so ‘nice’. For here,
$F=-dU/ dx$
. This ‘definition’ works in ‘nice’ cases in which the potential energy function U(x) is everywhere differentiable, but unfortunately an infinitely deep potential well is not so ‘nice’. For here,
where L is the length of the box. U(x) is not differentiable at the points
![]() $x=0$
and
$x=0$
and
![]() $x=L$.
$x=L$.
In loose physical terms, we may say that the particle is subjected to an infinitely large repulsive force when it hits a wall, which causes the particle to instantaneously reverse its momentum along the direction perpendicular to the wall. The details of the interacting forces during the interaction do not matter to the following extent: In any collision, the total momentum is preserved, and if the collision is also elastic (which, by definition, means that the total kinetic energy is conserved), then the final state of the colliding particle after the interaction is fully determined from its initial state by the conservation of total momentum and total energy. This is true irrespective of the exact nature of the forces involved in the interaction itself. The duration of the interaction may vary from case to case, but the duration is small if the repulsive force is very strong.
Still, the force is mathematically undefined at the point at which the particle collides with the wall in the case of an infinitely deep potential well. The only reason why this does not create a technical problem is that the motion of the particle is fully solved from the conservation laws alone. So, the idealization involved in an infinitely deep potential well is harmless in Newtonian mechanics.
4. The Quantum ‘Force’ Acting on a Particle in a Box
By direct analogy, the force operator in quantum mechanics is defined as
![]() $-dU/ dx$
, where U is exactly the same as in the Newtonian potential energy function (except that it is viewed as an operator). So the same problem arises in our example: At
$-dU/ dx$
, where U is exactly the same as in the Newtonian potential energy function (except that it is viewed as an operator). So the same problem arises in our example: At
![]() $x=0$
and
$x=0$
and
![]() $x=L$
,
$x=L$
,
![]() $-dU/ dx=\pm \infty $.
$-dU/ dx=\pm \infty $.
In quantum mechanics, the mean value of a quantum mechanical ‘observable’ (formally represented by a Hermitian operator on the Hilbert space of wave functions) is calculated by applying the operator to the wave function, multiplying the result by the complex conjugate of the wave function, and then integrating the result with respect to x. In the case of an infinite potential well, the wave function is 0 at the boundaries of the box. So, to calculate the mean force, one is faced with the problem of integrating 0 times ∞ at the end points. There are other cases in which one may justifiably assume that 0 times ∞ is equal to 0. For example, to calculate the mean potential energy, one assumes that the infinite potential energy outside the box makes zero contribution because the wave function outside the box is 0. Yet in the case of calculating the mean force, 0 is not the physically correct answer. Common sense tells us that if the mean momentum changes in time, then there must be some mean force responsible for this change. But how is this idea represented in the formalism?
First note that in ‘nice’ cases, in which U(x) is differentiable everywhere,
where
![]() $\hat{H}$
is the Hamiltonian operator,
$\hat{H}$
is the Hamiltonian operator,
![]() $\hat{X}=x$
is the position operator, and
$\hat{X}=x$
is the position operator, and
![]() $\hat{P}=-i\hslash (d/ dx) $
is the momentum operator.Footnote 2 Now, recall the general fact about quantum mechanics that the time-rate of change of the mean value of any operator is equal to i/ℏ times the mean value of the commutator of that operator with the Hamiltonian (see equation [3]). So, if we were to define the quantum mechanical force to be equal to the right-hand side of equation (11), then the mean force would be given by the equation
$\hat{P}=-i\hslash (d/ dx) $
is the momentum operator.Footnote 2 Now, recall the general fact about quantum mechanics that the time-rate of change of the mean value of any operator is equal to i/ℏ times the mean value of the commutator of that operator with the Hamiltonian (see equation [3]). So, if we were to define the quantum mechanical force to be equal to the right-hand side of equation (11), then the mean force would be given by the equation
Denoting the quantum mechanical ‘force’ operator by
![]() $\hat{F},$
we have
$\hat{F},$
we have
where the subscript t reminds us that the means may change with time. Equation 12 is Ehrenfest's second equation.
The interesting fact about QM is that QM solutions exist such that
![]() $\langle \hat{P}\rangle _{t}$
is a continuous differentiable function of time in the case of an infinite potential well. The singularity, which is a universal feature of the classical solution, only emerges in the macroscopic limit. So, the puzzle is this: In the QM case the mean force cannot be calculated from
$\langle \hat{P}\rangle _{t}$
is a continuous differentiable function of time in the case of an infinite potential well. The singularity, which is a universal feature of the classical solution, only emerges in the macroscopic limit. So, the puzzle is this: In the QM case the mean force cannot be calculated from
![]() $\langle -dU/ dx\rangle $
because U is not differentiable. Nevertheless, the mean force does make sense in the QM example if it is defined in terms of equation 12.
$\langle -dU/ dx\rangle $
because U is not differentiable. Nevertheless, the mean force does make sense in the QM example if it is defined in terms of equation 12.
Is this theft or honest toil? In our view, it is not worth struggling over this particular question. The importance of idealization lies in its connection with the model of an ideal gas. So, the important connection is between the changes in momentum of the particle and the pressure exerted on the wall. We compare the classical and quantum mechanical concepts of pressure in the next two sections.
5. Pressure in Newtonian Mechanics
The purpose of this section is to motivate the idea that pressure in Newtonian mechanics is the time average of a kind of generalized force. The generalized force is
![]() $-\partial E/ \partial V,$
where E is the energy and V is the volume. At first sight, this idea seems absurd, since in our simple example
$-\partial E/ \partial V,$
where E is the energy and V is the volume. At first sight, this idea seems absurd, since in our simple example
![]() $E=\frac{1}{2}mv^{2},$
and so E does not depend on the volume V. So how does
$E=\frac{1}{2}mv^{2},$
and so E does not depend on the volume V. So how does
![]() $-\partial E/ \partial V$
make sense, yet alone the time average of such a quantity? Here is must be remembered that
$-\partial E/ \partial V$
make sense, yet alone the time average of such a quantity? Here is must be remembered that
![]() $E=\frac{1}{2}mv^{2}+U(x),$
where the potential energy U(x) does depend on V. Namely, U(x) is 0 for points x inside V and ∞ for points outside V. How does this implicit dependence of U on V enter into the physics?
$E=\frac{1}{2}mv^{2}+U(x),$
where the potential energy U(x) does depend on V. Namely, U(x) is 0 for points x inside V and ∞ for points outside V. How does this implicit dependence of U on V enter into the physics?
The importance of pressure in physics arises from its role in the formula for the work done by a system. In particular, the work done by a system is written as PΔV, where P is the average pressure and ΔV is the change in volume. In our case, the increase in V is due to an increase in L. That is,
![]() $\Delta V=A\Delta L,$
where A is the area of the ends of the cylindrical tube, and ΔL is the increase in the length of tube in some time period ΔT. To ease the calculation, suppose that ΔT is the time that it takes the particle to travel from one end of the tube and back again. Then velocity of the particle is
$\Delta V=A\Delta L,$
where A is the area of the ends of the cylindrical tube, and ΔL is the increase in the length of tube in some time period ΔT. To ease the calculation, suppose that ΔT is the time that it takes the particle to travel from one end of the tube and back again. Then velocity of the particle is
![]() $v=2L/ \Delta T$.
$v=2L/ \Delta T$.
Imagine that a piston at the rightmost end of the cylinder is moving to right at a uniform speed u. Let ΔL be the distance the piston travels during the time ΔT. If the particle is moving just a little faster than the piston, then it will strike the moving piston and reflect off it, while continuing to move to the right with a reduced velocity. Clearly, the particle loses kinetic energy when it strikes a moving wall.
Quantitatively, the change in the energy, ΔE, can be deduced from the fact that the collision is elastic. In the frame of reference in which the moving wall is stationary, the particle approaches the wall with velocity v′ and reflects from the wall with velocity −v′. Clearly, v′ is less than v by the amount u. After some calculation,
When we compare this to the formula
![]() $\Delta E=-P\Delta V,$
we infer that
$\Delta E=-P\Delta V,$
we infer that
That is, pressure is the time average of the change in momentum (2mv′) measured relative to the moving wall, per unit area.
When
![]() $u=0$
, the wall is not moving, and the work done is zero, but the pressure is still well defined. In particular,
$u=0$
, the wall is not moving, and the work done is zero, but the pressure is still well defined. In particular,
The equation
![]() $P=2E/ V$
is a special case of the ideal gas law (for a single particle in one dimension).
$P=2E/ V$
is a special case of the ideal gas law (for a single particle in one dimension).
It is equally clear from the first equation,
![]() $\Delta E=-P\Delta V$
, that
$\Delta E=-P\Delta V$
, that
![]() $P=-\Delta E/ \Delta V$
. So if E were a differentiable function of V, then we could define the instantaneous pressure as
$P=-\Delta E/ \Delta V$
. So if E were a differentiable function of V, then we could define the instantaneous pressure as
![]() $P=-\partial E/ \partial V$
. Then the average pressure could be defined as the average instantaneous pressure. But ‘average pressure’ is well defined far more generally.
$P=-\partial E/ \partial V$
. Then the average pressure could be defined as the average instantaneous pressure. But ‘average pressure’ is well defined far more generally.
6. Pressure in Statistical Mechanics
In classical statistical mechanics, there is a way of defining a generalized force, then calculating the ‘pressure’ by averaging over an ensemble of microstates of the system.Footnote 3 The interesting part of the statistical mechanical story is that generalized force is defined as we should expect from the previous section—as the derivative of the energy function (the Hamiltonian) with respect to the volume, V (see Khinchin Reference Khinchin1949, sections 30 and 31, 139ff.). We shall not discuss the details of this case here, but the analogy with the quantum mechanical case is also striking.
7. Pressure in Quantum Mechanics
In quantum mechanics, the operator ∂
![]() $\hat{H}$
/∂V is no less problematic than the corresponding quantity in classical statistical mechanics (in the case of an infinite well). Surprising the QM mean value of this operator can be calculated, and the calculated value leads directly to the same version of the ideal gas law as before ((P = 2E/V), except that E is replaced by its QM mean value, 〈E〉. That is,
$\hat{H}$
/∂V is no less problematic than the corresponding quantity in classical statistical mechanics (in the case of an infinite well). Surprising the QM mean value of this operator can be calculated, and the calculated value leads directly to the same version of the ideal gas law as before ((P = 2E/V), except that E is replaced by its QM mean value, 〈E〉. That is,
(See the appendix for proof).
Classical statistical mechanics and quantum mechanics have this much in common: Both are able to calculate mean values of a generalized force
![]() $-\partial E/ \partial V$
even for an infinite potential well, and in both cases, the calculation of the mean values leads to an analogous version of the ideal gas law.
$-\partial E/ \partial V$
even for an infinite potential well, and in both cases, the calculation of the mean values leads to an analogous version of the ideal gas law.
8. Philosophical Conclusions
Messiah (Reference Messiah1970, 215) is typical amongst writers of quantum mechanical textbooks in claiming that quantum mechanics explains the success of classical mechanics because “the mean values [of quantum mechanical observables] follow the classical equations of motion to a good approximation” provided that “the dimensions of the wave packet be small with respect to the characteristic dimensions of the problem.” We have extended that story to show how other macroquantities, such as pressure, are also defined in QM as mean values.
There are philosophical puzzles raised. How, for example, can macroscopic quantities be identified with quantum mechanical means when, according to the orthodox interpretation of quantum mechanics, a quantum mechanical observable has no value unless it is in an eigenstate of that observable. For example, Ehrenfest's first equation relates the (rate of change of the) mean position to the mean momentum, but ‘position’ and ‘momentum’ do not commute. So, classical quantities correspond to quantum mechanical observables that have no value! How does this make sense? How does it make sense to say that classical quantities have a value if they correspond to quantum observables that have no value? Why is it okay to make such claims if the uncertainties (the variances) of the observables are small. Why does that make a difference?
Perhaps one should bite the bullet and say that, strictly speaking, Newtonian quantities do not have values? Perhaps this would make sense if we could argue that quantum mechanics really explains the empirical success of classical laws rather than their literal truth. But even the weaker position has a problem. How is ‘empirical success’ defined? How can we say that classical physics is empirically successful if not by saying that the predicted values of macroquantities are close to being the true values?
Perhaps the problem can be resolved by interpreting mean values as real? This would include the orthodox view as a special case, since an eigenstate of an observable is a state in which the mean value of the observable is dispersion free. We need to extend the orthodox view to at least include cases in which the observables are almost dispersion free, but not exactly dispersion free.
We have showed how bridge laws in physics commonly equate macroquantities with ensemble averages, time averages, and QM averages of microquantities. Moreover, neuroscience, evolutionary theory, physics, and many other sciences, appear to follow the same pattern of intertheory relations. Our conclusion is that the philosophy of science needs a probabilistic theory of intertheory relations.
Within such a theory, one could raise new and interesting questions, such as the following. Consider the growing field of econophysics (Mantegna and Stanley Reference Mantegna and Stanley2000; Plerou et al. Reference Plerou, Gopikrishnan and Stanley2003), which is applying the models of statistical mechanics in an attempt to explain how the volatile and unpredictable behavior of the financial markets emerges from a human system with many interacting participants. Do the concepts of temperature and entropy usefully describe the behavior of the financial markets? We have not heard of any such thing. So, why is the analogy with statistical mechanics so influential in econometrics? Perhaps it is the probabilistic methodology that is paying dividends, rather than the physics analogy per se.
Appendix
Here is the QM derivation of the ideal gas law for one particle moving in within a infinite potential well. Consider an arbitrary quantum state
![]() $\psi (x,\,t) =\Sigma \,c_{k}\eta _{k}(x,\,t) $
of a particle in a one-dimensional infinite potential well, where the ηk (x, t) are the energy eigenfunctions, so that for all
$\psi (x,\,t) =\Sigma \,c_{k}\eta _{k}(x,\,t) $
of a particle in a one-dimensional infinite potential well, where the ηk (x, t) are the energy eigenfunctions, so that for all
![]() $k,(\hat{H}-E_{k}) \times \eta _{k}(x,\,t) =0$
. First, differentiate the identity
$k,(\hat{H}-E_{k}) \times \eta _{k}(x,\,t) =0$
. First, differentiate the identity
![]() $\Sigma c_{k}(\hat{H}-E_{k}) \eta _{k}(x,\,t) =0$
with respect to L (the length of the box) to obtain
$\Sigma c_{k}(\hat{H}-E_{k}) \eta _{k}(x,\,t) =0$
with respect to L (the length of the box) to obtain

Now multiply both sides by ψ*(x, t) and integrate with respect to x. We first note that:
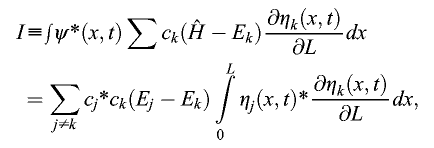
where we have used the Hermicity of
![]() $\hat{H}$
. To evaluate these ‘cross terms’ we need to use the exact expressions for the energy eigenfunctions, which are (see e.g., Gillespie Reference Gillespie1970, 116)
$\hat{H}$
. To evaluate these ‘cross terms’ we need to use the exact expressions for the energy eigenfunctions, which are (see e.g., Gillespie Reference Gillespie1970, 116)
when
![]() $0< x< L$
and 0 otherwise, where
$0< x< L$
and 0 otherwise, where

The calculation is laborious, but the summation is simplified by the fact that

Therefore

where, for all
![]() $k,\,c_{k}=\vert c_{k}\vert e^{i\phi _{k}}$
. Finally,
$k,\,c_{k}=\vert c_{k}\vert e^{i\phi _{k}}$
. Finally,
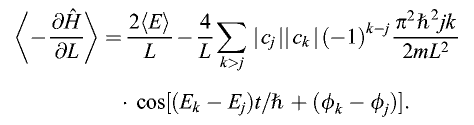
There are three corollaries to this result. The first is obvious: If the state is in an energy eigenstate, then there are no cross terms, and we arrive at a ‘version’ of the ideal gas law:

The second corollary is that if we calculate the time average over a period of time Δt that is sufficiently large, then the cross term will average out to something negligible.
The third corollary considers an ensemble of systems with identical values of ∣c k∣ but with uniform distribution over all the sequences of phases φ1, φ2, φ3,…, so that the cross terms will cancel out in the ensemble average. The ensemble mean now reduces to the same simple law.
The final form of the result is obtained by noting that
![]() $V=L\times A,$
where A is the area of the end walls of the box, from which it follows that:
$V=L\times A,$
where A is the area of the end walls of the box, from which it follows that:

assuming that A is constant. Hence,



