2.1. Boltzmannian Explanations of Time Asymmetry

In the Boltzmannian reasoning, the ultimate goal is to explain within a given system the time asymmetry of some macroscopic processes from the fundamentally time-symmetric microscopic processes that underlie it. The main formal ingredients of this procedure therefore involve a specification of the macro- and microstates of the system, a particular reductive map between them, and a way to describe their behavior. This is usually achieved in the context of the Hamiltonian formalism. In this formalism, the microstates of the systems in question are given in terms of representations of the configurations of the microscopic constituents of the system and their states of motion. These are expressed as generalized position and momentum variables formally represented by a symplectic manifold, Γ, that specifies the phase space of the system. A phase space of this kind has a number of interesting mathematical properties. Of central importance is the existence of a privileged measure, called the Liouville measure μ_L(Σ), that can be used to assign weights to arbitrary regions $\Sigma \in \Gamma$. The Liouville measure is singled out by its rather remarkable symmetry properties that will be discussed in detail below. Concretely, the Liouville measure is the integral over the nth power of the symplectic form, where n is half the dimension of Γ. In Darboux coordinates (q_i, p_i) where $\{q_i,p_j\}={\delta }_{\mathrm{ij}}$, we have ${\mu }_L\left(\Sigma \right)={\int }_{\Sigma }{\prod }_{i=1}^{n}d{p}_{i}d{q}_i$ (i.e., μ_L is the Lebesgue measure on Γ in these coordinates). For systems with infinite degrees of freedom or where the range of positions and momenta is infinite, there may be mathematical difficulties in precisely formulating this measure. The first set of relevant conditions for applying the Boltzmannian logic is therefore that there exists some way of writing a mathematically precise (condition A1) and empirically unambiguous (condition A2) measure μ on Γ. (Note that this does not necessarily have to be the Liouville measure.)

With a suitable measure in hand one can assign weights to arbitrary regions in phase space. These weights can be taken to define different notions of typicality for these regions. For example, one can say that a particular region A is typical on phase space if its weight as determined by μ is sufficiently large with respect to the weight of phase space itself:

(1)$\begin{array}{}\frac{\mu \left(\Gamma \right)-\mu \left(A\right)}{\mu \left(\Gamma \right)}\ll 1.\end{array}$

In general, a set S is said to be typical with respect to some property P and measure μ if its weight according to μ is large as compared with all other sets that possess the property P (Frigg Reference Frigg2009). Clearly, any notion of typicality requires some interpretation for the weights provided by μ in order to have any meaning. For the purposes of Boltzmann’s argument, we will see below that it will be necessary to interpret the weight μ(Σ) as the relative likelihood of finding the system in a particular region Σ (as opposed to somewhere else in Γ) at any given time. We identify this as an additional requirement (condition B) of the formalism.

The next formal step is to define the macrostates of a system. Physically these correspond to macroscopic states of the system, such as temperature, volume, pressure, and so on. Formally they are represented by some macrostate space M that must have a (much) smaller dimension than Γ. Because Boltzmann was usually considering closed systems where the total energy E is preserved, it is customary to consider states restricted to constant energy surfaces ${\Gamma }_E=\Gamma {|}_{E=\text{constant}}$ (i.e., the microcanonical ensemble). In general many microscopic states will be indistinguishable from one another at the macroscopic level. This indistinguishability is modeled as a projection from Γ_E to M. The microstates identified under this projection define a partitioning of Γ_E into the partitions Γ_m, where $m\in M$ ranges over all macrostates in M. These partitions represent equivalence classes of macroscopically indistinguishable microstates. In order for these to be meaningful physically, there must exist some epistemologically motivated coarse-graining procedure that realizes this projection. For example, if the macroscopic variable in question is the temperature, then the temperature must be a well-defined quantity. We identify this requirement with a further condition (condition C). With these ingredients in hand, it is now possible to define the Boltzmann entropy (from now on called the ‘entropy’ unless otherwise stated) of a particular macrostate M as the logarithm of the Liouville weight of the partition Γ_m:

(2)$\begin{array}{}{S}_B=k_B\log \left[{\mu }_L\right({\Gamma }_m\left)\right],\end{array}$

where k_B fixes the units of S _B.

The last formal ingredient describes the behavior of the system. Consider representing a single history of the system by a curve γ in Γ as in figure 1. The dynamics of an entire region can then be understood in terms of a collection of curves, or a flow where each point in the region is mapped to another neighboring point on Γ. For systems where the energy is conserved, this flow can be expressed mathematically in terms of a single phase space function, H, called the Hamiltonian of the system. A theorem of primary importance due to Liouville (Reference Liouville1838) shows that the flow generated by any choice of Hamiltonian function is guaranteed to preserve the Liouville measure. An immediate caveat of this theorem is that, up to a constant, the Liouville measure is the unique (smooth) measure preserved by any choice of Hamiltonian.Footnote ¹ It is this property that mathematically privileges the Liouville measure. Liouville’s theorem is therefore doubly important for Boltzmann’s reasoning. It provides at the same time a possible justification, via uniqueness, for the choice of typicality measure μ and a consistency requirement, via the invariance property under evolution, for being able to use the same measure at different times. The latter point arises as a consequence of a stronger requirement, which we identify as condition A3, that the typicality measure be invariant under all gauge symmetries of the system (in this case time-translational and, crucially, time-reversal invariance). In this context and for the remainder of the article, we will understand a ‘gauge symmetry’ to be a transformation of the representations of a system that relates physically indistinguishable states.

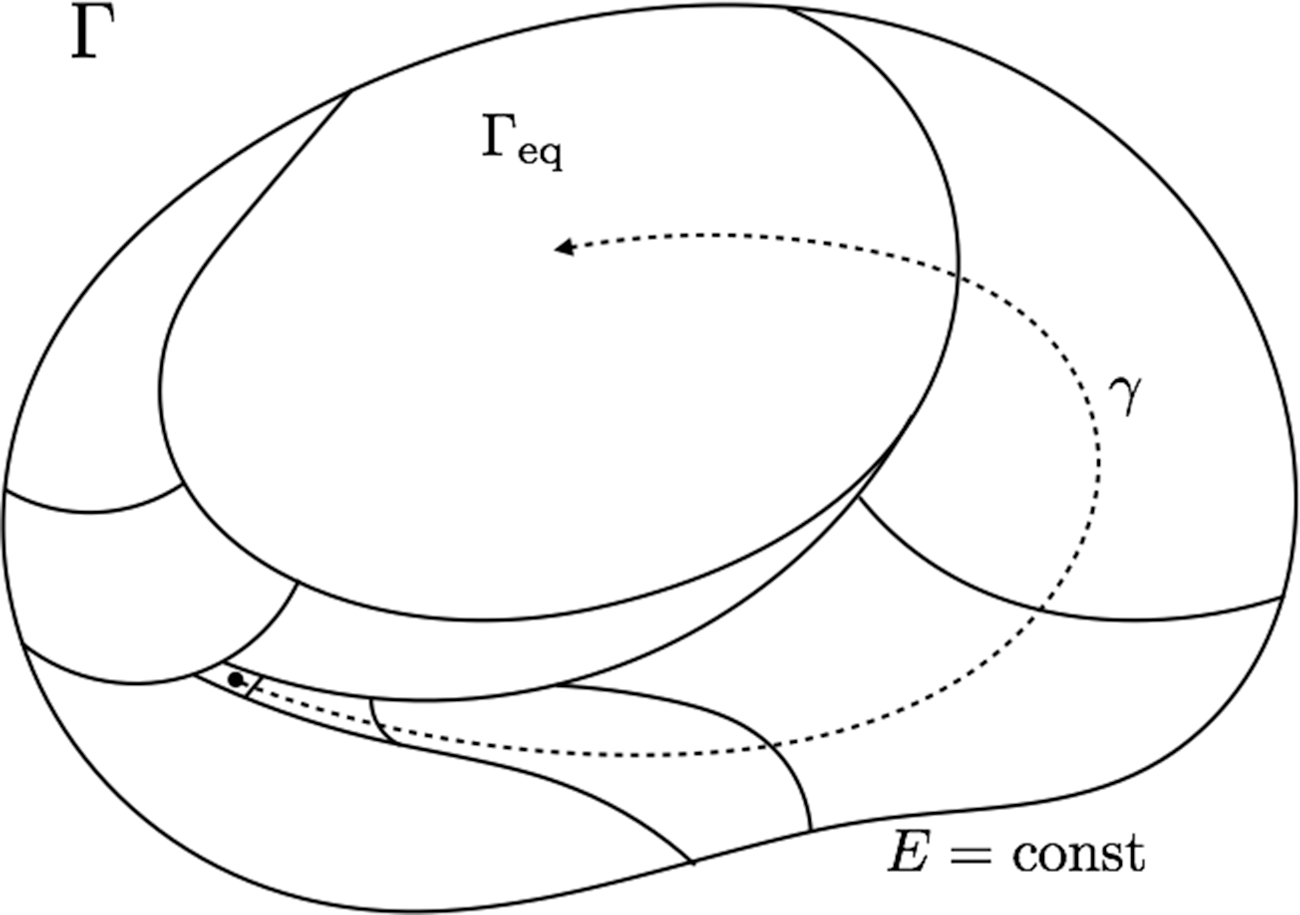
Figure 1. Small, atypical initial state will typically spend most of its future in a large equilibrium state Γ_eq.

We are now equipped to give a modern synthesis of Boltzmann’s reasoning. First one must show that for the system in question there exists an exceptionally large macrostate Γ_eq that takes up most of the phase space volume of the system. We take this to represent a further requirement that Γ_eq be a typical state in Γ_E (condition D). The relevance of condition D can be seen by the interpretation given to the weights of μ given condition B. If μ(Γ_eq) gives the relative likelihood of finding the system in μ(Γ_eq), then for all practical purposes Γ_eq is a steady or equilibrium state of the system because the system will almost always be found there. More significantly, if an equilibrium state exists, then a system that starts in a small macrostate will typically spend most of its future time in Γ_eq. The basic picture is depicted in figure 1. This picture is plausible because the counting suggested by the required interpretation of μ immediately suggests that a system starting outside of Γ_eq has little option but to quickly wander into Γ_eq, where it will remain for a very long time. But now there is a puzzle. Applying the same reasoning backward in time suggests that a state finding itself in a small macrostate will also typically spend of all its past in equilibrium. Because this apparently violates our knowledge that the past entropy of the universe was low, we are faced with the so-called second problem of Boltzmann (see Brown and Uffink Reference Brown and Uffink2001). To solve this problem, one can posit an extremely atypical condition on the earliest relevant state of the system. Under this condition, the system will typically find that it will approach the equilibrium state in the future. Note the temporal significance of the measure (condition B) and its central role in grounding the explanation of time asymmetry.

2.2. The Past Hypothesis

The main idea behind the PH is to evoke the Boltzmann-style reasoning of the previous section to explain time asymmetry in the universe. The system in question is then taken to be the entire universe, and the PH itself translates into a special condition on the earliest relevant state of the universe. All of the mathematical quantities discussed above (phase spaces, measures, macrostates, etc.) are then taken to represent aspects of the universe as a whole. The proposed explanation is given in terms of a typicality argument: universes that obey the appropriate PH, it is claimed, will typically evolve toward an equilibrium state in the future. Time asymmetry arises by asymmetrically applying the special condition to past, rather than future, states. That the Boltzmann reasoning, whose empirical success is traditionally realized in closed subsystems of the universe, can provide explanatory leverage when applied to the universe as a whole is then taken as a further condition (condition E) for the PH. Empirical support for the extreme atypicality of the initial state of our universe is taken to be implied by abundant cosmological evidence for a low-entropy early universe (e.g., the near thermality of the cosmic microwave background [CMB] power spectrum). We take this to be a final condition (condition F) for the viability of the PH.

2.3. Requirements of the Past Hypothesis

We will now state all conditions identified in section 2.1 (this list of conditions is not intended to be sufficient for the PH).

1. (A) There exists a measure, μ_universe, on the phase space of the universe, Γ_universe, that is simultaneously:

   1. (A1) mathematically precise,

   2. (A2) empirically unambiguous, and

   3. (A3) invariant under all gauge symmetries.

2. (B) It is justifiable to interpret the weights given by the chosen measure in terms of the relative likelihood of the system being in a given region at a given time.

3. (C) There is an epistemologically meaningful and mathematically well-defined projection from the microscopic phase space of the universe, Γ_universe, to a macroscopic phase space, M _universe.

4. (D) There exists a unique and exceptionally large state, defined to be the equilibrium state Γ_eq, that is a typical macrostate on the phase space of the universe at any given energy E:

   $\frac{{\mu }_{\text{universe}}\left[{\Gamma }_{E,\text{universe}}\right]-{\mu }_{\text{universe}}\left[{\Gamma }_{\text{eq}}\right]}{{\mu }_{\text{universe}}\left[{\Gamma }_{E,\text{universe}}\right]}\ll 1.$

5. (E) Typicality arguments have explanatory power when applied to the universe.

6. (F) There is cosmological evidence for the PH being true.

3.1. Category I: Mathematical Precision

In this section we will primarily be concerned with issues arising from conditions A due to infinite phase spaces. Such phase spaces entail serious mathematical problems for measure-theoretic approaches to explanation. These problems stem from two distinct sources. The first arises because measures evaluated on an infinite interval can only be defined according to a limiting procedure that typically leads to physically significant regularization ambiguities. These problems are compounded in field theories because of a second source of ambiguity due to the phase space itself being infinite dimensional. In this case, it is a theorem that no Borel measure exists (Curiel Reference Curiel2015), so that the system must be truncated to a finite phase space in order to accommodate any measure. Ambiguities of these two kinds lead to a tension between mathematical precision (condition A1) and empirical uniqueness (condition A2). To make matters worse, the purely mathematical problem of defining any measure on the phase space of general relativity invariant under all space-time symmetries is far from being solved. This open technical problem is in fact one of the main formal obstructions to obtaining a canonical formulation of quantum gravity. With this in mind, it is advisable to explore various approximations to general relativity that render the computations of measures more tractable. But even in this simplified setting, one encounters immediate and troubling difficulties that are emblematic of the more general case.

Pioneering work in Gibbons, Hawking, and Stewart (Reference Gibbons, Hawking and Stewart1987) that was elaborated on by several authors in both the physics (Hawking and Page Reference Hawking and Page1988; Hollands and Wald Reference Hollands and Wald2002; Ashtekar and Sloan Reference Ashtekar and Sloan2011; Corichi and Karami Reference Corichi and Karami2011; Schiffrin and Wald Reference Schiffrin and Wald2012) and philosophy literature (Earman Reference Earman2006; Frigg Reference Frigg2009; Curiel Reference Curiel2015) shows that the natural measure on homogeneous and isotropic cosmologies has infinite phase space volume. In the references listed, different schemes are provided for handling these divergences, and these schemes introduce ambiguities. A particular illustration of this will be outlined in detail in section 4.1. To resolve these mathematical ambiguities (of the first kind discussed above), new inputs, which are often physical in nature, must be introduced. It is thus paramount that the extra inputs needed to resolve these ambiguities neither conflict with other symmetry principles, in accordance with condition A3, nor implicitly assume what is trying to be explained, that is, the time asymmetry of local thermodynamic processes. Otherwise, the explanatory power of the PH is undermined.

To illustrate the extent to which these ambiguities are problematic, consider the concrete results of different authors with different intuitions performing computations of the relative likelihood of cosmic inflation. Advocates for inflation (Kofman, Linde, and Mukhanov Reference Kofman, Linde and Mukhanov2002; Carroll and Tam Reference Carroll and Tam2010) proposed a measure according to which the probability of inflation was found to be infinitesimally close to 1. Inflation skeptics (Gibbons and Turok Reference Gibbons and Turok2008) proposed an alternative measure in which the probability of inflation was found to be 1 part in 10⁸⁵. This remarkably huge discrepancy reflects the extent to which individual beliefs can affect cosmologist’s determinations of the appropriate physical principles used to justify their measure and the difficulties of resolving the tensions between conditions A1 and A2. Any conclusions drawn on the basis of a typicality argument must be assessed in light of such remarkable disagreement between cosmologists.

Ambiguities of this kind are not improved when more realistic models including cosmological inhomogeneities are considered. Any preliminary hopes, such as those alluded to in Callender (Reference Callender, Ernst and Hüttemann2010), that adding an infinite number of degrees of freedom would help resolve these ambiguities can be seen to be in vain when explicit models are considered. This has been done, for example, in Schiffrin and Wald (Reference Schiffrin and Wald2012). What was found there was that the additional degrees of freedom introduce corresponding regularization ambiguities of the second kind discussed above. It is therefore necessary to introduce new physical principles in order to resolve these ambiguities. Given the daunting nature of a full general relativistic treatment, these considerations raises serious doubts regarding the possibility of being able to attribute any meaningful notion of typicality to the universe.

3.2. Category II: Dynamical Considerations

In this section we will consider the unique properties of gravitational dynamics that complicate our entropic intuitions for the universe, assuming that a well-defined truncation of the phase space exists on which a Liouville measure can be defined. Consider the equilibrium state of a free gas. It is smooth, homogeneous, and nothing like the current state of the universe, which is characteristically clumpy and uneven. Those clumps comprise, among other things, star systems—one of which supports the far-from-equilibrium biological system we find ourselves in. Yet, analysis of CMB temperature fluctuations reveals only a small 10⁻⁵ deviation from homogeneity. How can these observations be compatible with a low-entropy past state? The standard response to this is that the gravitational contribution to the entropy should dominate at late times because of the unusual thermodynamic character of the gravitational interactions. This contribution is so great that it more than compensates for the decrease in entropy observed through the clumping of matter. Intuition for this comes from entropic considerations in Newtonian N-body self-gravitating systems, which have been used to model, for example, the dynamics of dust and stars in galaxies and galaxy clusters. But even in this simplified and well-tested setting there are difficulties that are emblematic of the considerations of section 3.1.

Because Liouville volume is a volume on phase space, the inverse square potential due to gravity and the large momenta it can generate flip expectations for what constitutes a high- and low-entropy state. The steep gravitational potential well taps a vast reservoir of entropy allowing for the kind of sizable low-entropy fluctuations we see in biological systems on earth. These features as well as the difficulties they entail are reviewed nicely by Padmanabhan (Reference Padmanabhan1990, Reference Padmanabhan2008), who gives detailed proofs of many of the results referenced below. This flipping of expectations is argued to occur not only for N-body systems but also in a full-fledged general relativistic treatment of entropy. Thus, advocates of the PH (e.g., Goldstein and Lebowitz Reference Goldstein and Lebowitz2004; Albert Reference Albert2009) emphasize the N-body intuition pump as providing an explanation for why the early homogeneous state of the CMB should be thought of as having low entropy and the current clumped state, which contains steadily accumulating stable records, as having high entropy. Moreover, this intuition was a primary motivation for early attempts at formulating an explicit PH such as Penrose’s Weyl Curvature Hypothesis (Reference Penrose, Hawking and Israel1979).

The N-body intuition pump, however, also raises potential concerns. First, if we follow the past state far enough into the early universe, a full general relativistic treatment becomes unavoidable. But as we have already seen in section 3.1, such a treatment suffers from troubling ambiguities, and it is not clear that the simple Newtonian intuition will remain valid. Another significant worry is the definition of equilibrium itself. The notion of equilibrium in gravitational systems is complicated by two sources of divergence (for details, see Padmanabhan Reference Padmanabhan2008): (i) the infinite forces particles exert on one another when they collide and (ii) the infinite distances particles can obtain when ejected from a system. To cure these divergences, it is necessary to render the entropy finite by imposing additional constraints. This involves closing the system at some maximum size, so that particles are not allowed to escape, and forbidding two particles from being able to collide. This requires extra assumptions that must be grounded in physically acceptable principles. It is therefore paramount that these physical idealizations be well motivated. But the fact that these idealizations break down under specified conditions implies difficulties in defining stable equilibrium for the system. Indeed, N-body systems are known to only have local—but no global—maxima (Padmanabhan Reference Padmanabhan2008). Thus, gravitating systems do not have genuine equilibrium states, and condition D cannot be strictly satisfied. In the absence of an equilibrium state, thermodynamic quantities such as macrostates and their entropy cannot be defined, and condition C is strictly violated. While this is not problematic for local meta-stable systems like a galaxy, it can certainly be problematic for globally defined systems like the entire universe. Moreover, even when local equilibria exist, there is still no guarantee that gravitational dynamics will actually steer the system toward these local equilibria in order to satisfy condition B. The crucial role of dynamics in the Boltzmannian argument has been emphasized in Brown and Uffink (Reference Brown and Uffink2001) and Frigg (Reference Frigg2009).

3.3. Category III: Justification and Explanation

This section will first be concerned with the essential need to satisfy condition B by finding a valid justification for using Liouville volume as a typicality measure, assuming all concerns of categories I and II have been resolved. In conventional statistical mechanical systems, this justification proceeds along two traditional routes. The first and oldest route relies on a theorem by Birkhoff (Reference Birkhoff1931), which states that for ergodic systems the average time spent in a particular phase space region becomes roughly proportional to its Liouville volume if the timescales in question are much longer than the Poincaré recurrence time. Unfortunately, for almost all systems—and certainly for the universe—the Poincaré recurrence time is significantly longer than the estimated time since the Big Bang. The second route, usually favored for its practicality, is to argue that the system undergoes a process called mixing. Roughly speaking, a system is mixed when the long-run evolution of the measure of a system becomes approximately homogeneous and therefore Liouvillian. Many systems exhibit this property, and the relevant mixing timescales can be computed explicitly. Unfortunately, Schiffrin and Wald (Reference Schiffrin and Wald2012) argue that the observed expansion of the universe is too rapid to allow the large scale structures of the universe to interact often enough for mixing to occur on these scales. This suggests that it is unreasonable to expect the universe as a whole to undergo mixing. It would seem that in terms of conventional justification schemes for the Liouville measure condition B cannot be made compatible with the observational requirements of condition F.

It is possible to look for justification schemes satisfying condition B that do not originate from conventional statistical mechanical considerations. One proposal made by Penrose (Reference Penrose, Hawking and Israel1979, Reference Penrose1994) and later advocated (either implicitly or explicitly) by Lebowitz (Reference Lebowitz1993), Goldstein (Reference Goldstein2001), and Albert (Reference Albert2009) is a version of the Principle of Insufficient Reason (PIR) as formalized by Laplace. In Penrose’s version, a blind creator must choose initial conditions for the universe among the space of all possibilities. Being indifferent to which conditions to choose, the creator assigns equal likelihood to each possibility according to the Liouville measure. Given the failure of standard justifications schemes, Schiffrin and Wald (Reference Schiffrin and Wald2012) point to Penrose’s proposal as the only available alternative. Unfortunately, the PIR has a troubled history in the philosophy of science and suffers from several well-known difficulties. At least four prominent criticisms are identified in Uffink (Reference Uffink1995). While some of these are addressed implicitly throughout this text, one line of criticism dating back to Bernoulli is noteworthy because it also directly puts into question the validity of condition C. In this line of criticism one derives paradoxes that originate in an incompatibility between the measures obtained when applying the PIR to different choices of partition for the microstates of a system. These paradoxes occur when the partitions correspond to disjunct coarse grainings or refinements of one another (Norton Reference Norton2008). There is nothing in the PIR that tells you which partitioning of the microstates is the “correct” one, precisely because this would require some nontrivial knowledge about how these partitions may have been gerrymandered. Without direct knowledge of the “correct” partitioning of microstates, the PIR loses all explanatory power.

The only remaining justification for the Liouville measure is a uniqueness argument under time symmetry. If one requires a time-symmetric measure, then the uniqueness of the Liouville measure under the requirement of being preserved by arbitrary Hamiltonian evolution does single it out. However, as we will see in section 4, very general symmetry considerations will put into doubt any motivations for using the Liouville measure to establish a notion of typicality for models in the universe.

We end this section by mentioning a prominent dialectic between Price (Reference Price2002, Reference Price and Hitchcock2004) and Callender (Reference Callender2004a, Reference Callender and Hitchcock2004b) on the explanatory power of the PH that questions the validity of condition E. In this dialectic Price argues that the PH itself should require explanation in pain of applying a “temporal double standard” to a past state when an atypical future state would plainly require explanation. Callender responds by stating that contingencies rarely (or never) require explanation, and an initial condition such as a PH is a contingency of this kind.

4.1. Preliminaries: Dynamical Similarity as a Gauge Symmetry of the Universe

Before establishing the horns of the dilemma, it will be convenient to state some results that will be central to the analysis. We will need to give the definition of a particular symmetry of the universe and list some of its core properties. The symmetry that will be central to our argument is called dynamical similarity. The three aspects of dynamical similarity that will be needed for our analysis are, first, that dynamical similarity is a gauge symmetry of any general relativistic formulation of the laws of the universe; second, that the Liouville measure is not invariant under dynamical similarity; and third, that in known theories of the universe dynamically similar measures are badly time asymmetric. To illustrate our first point, we must show that dynamical similarity relates empirically indistinguishable descriptions of a general relativistic system. We will do this first by making a general argument and then by showing that this general argument is consistent with the treatment of particular cosmological theories.

We begin by giving a definition of dynamical similarity.Footnote ² Consider any system whose dynamical possibilities are specified by Hamilton’s principle. For such systems, an action functional S[γ] is given such that the dynamically possible models (DPMs), γ_DPM, of the system are stationary points of S:

(3)$\begin{array}{}\delta S\left[\gamma \right]{|}_{{\gamma }_{\text{DPM}}}=0.\end{array}$

Then any transformation on the state space of such a system that rescales the action functional,

(4)$\begin{array}{}S\to \mathrm{cS},\end{array}$

is defined to be a dynamical similarity. For any system of this kind, a dynamical similarity will map a DPM to another DPM and is therefore a symmetry. This follows straightforwardly from the fact that the stationarity condition (3) is invariant under (4). Dynamical similarities are therefore symmetries of any general relativistic description of the universe because general relativity can be formulated in terms of Hamilton’s principle.

This notion of symmetry, namely, a transformation that maps DPMs to DPMs, is not yet enough for our argument. We will further need to show that dynamically similar DPMs are empirically indistinguishable. To see that this is true, observe that the constant in the transformation (4) can always be set to 1 by a suitable choice of units for the action. Since the unit of action is the unit of angular momentum, we find that dynamical similarities map DPMs to DPMs with different choices of units of angular momentum. Only if these choices can be compared with an external reference scale for angular momentum can the DPMs in question be empirically distinguished. If instead the units of angular momentum are referenced from within the system, then an arbitrary choice of units can have no empirical consequences. Because we are interested in a general relativistic description of the entire universe, there can be no external reference unit to distinguish between dynamically similar descriptions of the system. Thus, dynamical similarities are symmetries of a general relativistic description of the universe that relate empirically indistinguishable models; that is, they are gauge symmetries.

This point is well appreciated by cosmologists. In writing down the equations of cosmological systems, one starts with a general relativistic formulation and then imposes spatial homogeneity and isotropy. The simplest models of inflation can thus be described by a single geometric variable v(t) representing the volume of a comoving patch of the universe and a single massive scale field ϕ(t). The Hamiltonian for this system can be written as

(5)$\begin{array}{}ℍ=\left[-H^2+\frac{{\pi }_{\varphi }^2}{v^2}+{\tilde{m}}^2{\varphi }^2\right],\end{array}$

where H is Hubble red-shift parameter conjugate of v, π_ϕ is the momentum of the scalar field, and $\tilde{m}$ is a dimensionless mass.Footnote ³

This theory inherits a dynamical similarity from its underlying general relativistic description. If we remember that $S=\int dt(\dot{v}H+\dot{\varphi }{\pi }_{\varphi }-ℍ)$, then the transformation

(6)$\begin{array}{}\begin{array}{cc}v\to \mathrm{cv}& \varphi \to \varphi \\ H\to H& {\pi }_{\varphi }\to c{\pi }_{\varphi },\end{array}\end{array}$

is a dynamical similarity when $t\to ct$. The physical significance of the dynamical similarity (6) is straightforward to understand. It represents the freedom to arbitrarily choose the initial volume of a fixed fiducial cell while keeping the red shift fixed. In cosmology, dynamical similarity therefore reflects the well-known property that the scale factor is an unobservable degree of freedom even though its momentum, the Hubble parameter, is observable. This achieves our first objective.

Our second objective is to show that the Liouville measure is not invariant under dynamical similarity. This together with the previous result will be essential for establishing the second horn of the dilemma: the breaking of gauge invariance by the Liouville measure. This can be achieved by expanding on the mismatch between the transformation properties of the volume v and its conjugate momentum H. The Liouville measure is a homogeneous measure on phase space. This means that it gives the same weight to a configuration variable as it does to the corresponding momentum. It is thus impossible for any measure of this kind to be invariant under a symmetry that acts in an unbalanced way on the phase space variables. We can illustrate this explicitly for the cosmological theory given above. A set of canonically conjugate variables for this theory is {v, H, ϕ, π_ϕ}, and therefore the Liouville measure is

(7)$\begin{array}{}{\mu }_L\left(R\right)={\int }_{R}dvdHd\varphi d{\pi }_{\varphi }.\end{array}$

This measure is explicitly not invariant under the symmetry (6). While illustrative and physically relevant, the noninvariance of the Liouville measure in this example is not just a special feature of this particular cosmological theory but a general property of the Liouville measure. In order for a dynamical similarity to rescale the action as in (4) it must rescale the symplectic potential $\theta =pdq\to c\theta$. But since the Liouville measure is just a power of the exterior derivative of the symplectic potential, ${\mu }_L\left(R\right)={\int }_R{\left(d\theta \right)}^n$, the Liouville measure itself will necessarily rescale under a dynamical similarity. Thus, the Liouville measure in general cannot be invariant under dynamical similarity.

The last objective of this section is to show that the lack of invariance of the Liouville measure results in a significant numerical time asymmetry in its projection onto the dynamically similar state space relevant to cosmological theories. This result will be useful in strengthening the case for the loss of explanatory power that leads to the first horn of the dilemma (see sec. 4.2 for details). To achieve the last objective, we will recall the results of well-known derivations.Footnote ⁴ The measure that is relevant to our considerations is a measure not on the space of states but on the space of models. This can be achieved by projecting the Liouville measure onto some initial data surface on phase space. Because the Liouville measure is time independent, the choice of initial data surface is arbitrary. For the cosmological theory presented in this section, a convenient choice of initial data surface that is also empirically meaningful is that of a surface of constant red shift: $H=H^{*}$. This choice leads to the Gibbons-Hawking-Stewart measure (Gibbons et al. Reference Gibbons, Hawking and Stewart1987):

(8)$\begin{array}{}{\mu }_{\text{GHS}}\left(r\right)={\int }_r\sqrt{{\left(H^{*}\right)}^2-{\tilde{m}}^2{\varphi }^2}dv\text{\hspace{0.17em}d}\varphi ,\end{array}$

where r is a region on the surface $H=H^{*}$ that is compact in ϕ but not in v. This measure is not regarded to be physical in part because of its noncompact domain in terms of v but, more importantly, because of the arbitrariness of the value of v in terms of a choice of initial fiducial cell. More recently, Sloan (Reference Sloan2019) has established a direct link between this arbitrariness and dynamical similarity.Footnote ⁵ To obtain a physically significant measure, Hawking and Page (Reference Hawking and Page1988) defined a regularization procedure that takes advantage of the homogeneity of (8) in v to integrate over all possible values of v. The resulting measure

(9)$\begin{array}{}\text{Prob}\left(r_{\varphi }\right)=\underset{v_{\text{max}}\to \infty }{\lim }\frac{{\int }_0^{v_{\text{max}}}dv}{{\int }_0^{v_{\text{max}}}dv}\frac{{\int }_{r_{\varphi }}d\varphi \sqrt{{\left(H^{*}\right)}^2-{\tilde{m}}^2{\varphi }^2}}{{\int }_{r_{{\varphi }_{\text{max}}}}d\varphi \sqrt{{\left(H^{*}\right)}^2-{\tilde{m}}^2{\varphi }^2}}\to \text{finite}\end{array}$

is finite. The result depends only on the ratio of the integrals over the region r _ϕ, which can be used to define inflation, and the finite region r _ϕmax, which is given in terms of the dynamical constraints of the theory. From the perspective of dynamical similarity, the integration over v is motivated by requiring that the physical measure be invariant under symmetries that relate physically indistinguishable models. The integral over v is an integration over the action of the dynamical similarity (6). The physical measure (9) is therefore invariant under (6), while the unphysical measure (8) is not.

The integration over v creates a new problem. The physical measure (9) depends explicitly on the choice of the initial data surface as determined by the choice of initial red-shift factor H*. This dependence on H* is significant. As was shown explicitly in Schiffrin and Wald (Reference Schiffrin and Wald2012), the different choices of H* used by inflation skeptics (Gibbons and Turok Reference Gibbons and Turok2008) compared with inflation advocates (Kofman et al. Reference Kofman, Linde and Mukhanov2002; Carroll and Tam Reference Carroll and Tam2010) leads to a colossal 85 order of magnitude difference between the estimates of the likelihood of inflation. Because a choice of H* corresponds to a choice of initial time, this huge numerical imbalance leads to a significant temporal asymmetry: choosing a more recent value of H* gives a dramatically smaller value for the weight of the same region r _ϕ.

This result is not just a special feature of the particular cosmological theory developed in this section. The Liouville measure is the unique time-independent measure on phase space. But, as we have shown, the Liouville measure is in general not invariant under dynamical similarity. There is therefore no (smooth) time-independent measure invariant under dynamical similarity. This means, in general, that a dynamically similar measure on the space of models will necessarily depend on the choice of the initial data surface (e.g., it will depend on H*). Moreover, the temporal asymmetry introduced by this is significant. For the theory introduced in this section, it leads to an 85 order of magnitude difference between different choices of H*. There are good reasons to believe that this numerical imbalance will persist in any general relativistic description of the universe. The interpretation of dynamical similarity in terms of an arbitrary choice of volume will persist in general relativity. In this context, the red-shift factor H is still the variable conjugate to v. The temporal asymmetry will then always depend on the initial choice of H*, and this varies wildly between now and the empirically accessible past in a monotonic way. The huge monotonic variation of the Hubble parameter over the known history of the universe therefore introduces a significant time asymmetry into the definition of a dynamically similar measure.

4.2. The First Horn: Loss of Explanatory Power

The analysis of section 3 has established that there are many concerns regarding the justification of the choice of typicality measure used to formulate a PH. In section 3.2 it was argued that self-gravitating systems have unusual thermodynamic properties, and in section 3.3 these arguments where combined with known facts about the universe to suggest that conventional statistical mechanical justifications fail when applied to the universe. Justifications that rely on indifference principles were also criticized on epistemological grounds. The analysis of section 3 therefore leads to the conclusion that the only tenable justification for choosing the Liouville measure is an argument from time independence. The Liouville measure is indeed singled out as being the unique measure on phase space that is preserved by an arbitrary choice of dynamics. At first sight this uniqueness appears to be particularly convenient because a time-independent measure is very natural in the context of a PH. But time independence in the measure is more than a question of convenience in the context of a PH. In fact, it is an essential ingredient for the PH independent of any other justificatory considerations.

Following Price (Reference Price2002), the logic of the PH presented in section 2.1 constitutes a contrastive explanation of the form: if A then B rather than C. The explanans A (i.e., the PH itself) is taken to explain the explanandum B (i.e., the fact that typical processes are seen to overwhelmingly occur in a time-asymmetric way). The outcome C is then a typical member of a contrast class of outcomes that would be likely if not for A. The explanatory power of A comes from increasing the likelihood of B relative to C. In the case of a PH, the contrast class is the set of worlds where typical processes overwhelmingly occur in a time-symmetric way. According to this logic, in order for the PH to be a good explanation of time asymmetry, it must be the only significant source of time asymmetry. Clearly this is consistent with the apparent time symmetry of the form of the fundamental laws. This consistency however is not sufficient. When a time-asymmetric measure is introduced into the formalism, the time asymmetry of the measure could itself provide an explanation for the time asymmetry of typical processes. This is especially true if the time asymmetry of the measure introduces a significant numerical temporal gradient as was shown in the previous section for the case of cosmological models. Moreover, the time dependence of the measure introduces an ambiguity in terms of which instant should be used in order to obtain a measure on the space of models. Such an ambiguity can only be resolved by including some additional principle to the PH—thus undermining much of its explanatory appeal. It is therefore essential to the logic of the PH that the measure employed be time independent, and it is especially important that the measure not be badly time asymmetric. Otherwise we would have no reason to believe that processes would not occur in a time-asymmetric way even if the PH were not true. Note that these considerations hold regardless of any other justificatory considerations regarding the measure. This establishes the first horn of the dilemma.

4.3. The Second Horn: Violation of a Gauge Symmetry

In the preliminary section 4.1 we saw that the projection of the Liouville measure onto the space of models, while time independent, is nevertheless considered by cosmologists to be unphysical. Contrastingly, the measure that is considered by cosmologists to be physical was found to be invariant under dynamical similarity. We will now argue that this result is to be expected in any general relativistic description of the universe. To do this, we will show that a measure that is not invariant under symmetries that relate physically indistinguishable descriptions of a system (condition A3) introduces two distinct problems: first, it introduces a distinction without difference, and second, it runs against standard practice in particle and statistic physics.

Consider a region R that lives in the domain 𝒟(μ) of some measure μ and a transformation $T:𝒟\left(\mu \right)\to 𝒟\left(\mu \right)$ that maps this domain onto itself. Our assumptions demand that T map states of a system to empirically indistinguishable states. The set of states in the region R is therefore empirically indistinguishable from the set of states in the transformed region $R^{\prime }=T\left(R\right)$. In general, the noninvariance of μ under T implies that the weight of the transformed region is not necessarily equal to the weight of the original: $\mu \left(R\right)\ne \mu \left(R^{\prime }\right)$. But if this is true then the weights μ(R) and μ(R′) provide a distinction at the representational level between the regions R and R′. Given our original assumptions, this distinction cannot represent any empirical difference. In this sense, the measure μ therefore introduces a representational distinction that cannot be captured by the empirical properties of the world. It is therefore not a valid measure for describing empirical phenomena.

This argument is reinforced by standard practice in particle and statistical physics that requires that physical measures be invariant under all the gauge symmetries of a system. In the standard model of particle physics, the gauge invariance of the path-integral measure is a central foundational principle of the theory. More generally, the Faddeev-Popov determinant, which enforces the gauge invariance of the path-integral measure, is considered a necessary ingredient in gauge theory (see Weinberg [Reference Weinberg2013, chap. 15], for an overview and defense of this standard practice). Similarly in statistical physics, Jaynes (Reference Jaynes1973) has argued influentially that measures should be invariant under transformations that relate indistinguishable states of a system. We therefore conclude that there are strong epistemological and methodological motivations for requiring condition A3.

We are now in a position to state the second horn of our dilemma. As we have shown in the previous section, dynamical similarity is a symmetry that maps states of any general relativistic description of the universe to indistinguishable states. Given the argument above, any measure not invariant under such a symmetry must violate a gauge symmetry and introduce a distinction without difference. Therefore, a measure on the state space of a generally relativistic description of the universe that is not dynamically similar will run into the symmetry-violating horn. But as was shown in section 4.1, the Liouville measure is not dynamically similar. It follows that use of the Liouville measure therefore violates a gauge symmetry of the theory. This is the second horn.

We now recall the first horn of the dilemma. The formulation of the PH must make use of the unique time-independent Liouville measure in order to retain its explanatory power. But the Liouville measure is not dynamically similar and therefore introduces a distinction without difference. An advocate of the PH must therefore face the dilemma stated in the introduction: either lose explanatory power or introduce a distinction without difference.