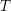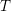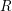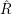1 Introduction
Tilting theory plays an important role in the representation theory of Artin algebras. The classical tilting modules were introduced in the early 1980s by Brenner–Butler [Reference Brenner and Butler6], Bongartz [Reference Bongartz5] and Happel and Ringel [Reference Happel and Ringel19]. Beginning with Miyashita [Reference Miyashita23] and Happel [Reference Happel and Ringel19], the defining conditions for a classical tilting module were relaxed to tilting modules of arbitrary finite projective dimension, and further were relaxed to arbitrary rings and infinitely generated modules by many authors such as Colby and Fuller [Reference Colby and Fuller12], Colpi and Trlifaj [Reference Colpi and Trlifaj14], Angeleri-Hügel and Coelho [Reference Angeleri-Hügel and Coelho1], Bazzoni [Reference Bazzoni4], etc.
One important result in tilting theory is the famous Brenner–Butler Theorem which shows that a classical tilting module induces a torsion theory counter equivalence (later named in [Reference Colby and Fuller11, Reference Colpi, D’Este and Tonolo13]). Precisely, if ![]() $T$ is a classical tilting
$T$ is a classical tilting ![]() $R$-module with the endomorphism algebra
$R$-module with the endomorphism algebra ![]() $S$, then there is a torsion pair
$S$, then there is a torsion pair ![]() $({\mathcal{B}},{\mathcal{A}})$ in the
$({\mathcal{B}},{\mathcal{A}})$ in the ![]() $R$-module category and a torsion pair
$R$-module category and a torsion pair ![]() $({\mathcal{G}},{\mathcal{K}})$ in the
$({\mathcal{G}},{\mathcal{K}})$ in the ![]() $S$-module category such that there is an equivalence between
$S$-module category such that there is an equivalence between ![]() ${\mathcal{A}}$ and
${\mathcal{A}}$ and ![]() ${\mathcal{G}}$ and an equivalence between
${\mathcal{G}}$ and an equivalence between ![]() ${\mathcal{K}}$ and
${\mathcal{K}}$ and ![]() ${\mathcal{B}}$. In this sense, tilting theory may be viewed as a far-reaching way of generalization of the Morita theory of equivalences between module categories. More interesting, when considering the derived category of an algebra, which contains the module category of the algebra as a full subcategory, Happel [Reference Happel18] and later Cline, Parshall and Scott [Reference Cline, Parshall and Scott10] proved that a tilting module of finite projective dimension induces an equivalence between the bounded derived category of the ordinary algebra and the derived category of the endomorphism algebra of the tilting module. This leads to the study of the Morita theory for derived categories, which were completely solved by Rickard [Reference Rickard24] through the notion of tilting complexes and by Keller [Reference Keller21] through dg-categories.
${\mathcal{B}}$. In this sense, tilting theory may be viewed as a far-reaching way of generalization of the Morita theory of equivalences between module categories. More interesting, when considering the derived category of an algebra, which contains the module category of the algebra as a full subcategory, Happel [Reference Happel18] and later Cline, Parshall and Scott [Reference Cline, Parshall and Scott10] proved that a tilting module of finite projective dimension induces an equivalence between the bounded derived category of the ordinary algebra and the derived category of the endomorphism algebra of the tilting module. This leads to the study of the Morita theory for derived categories, which were completely solved by Rickard [Reference Rickard24] through the notion of tilting complexes and by Keller [Reference Keller21] through dg-categories.
A further generalization of tilting modules to tilting modules of possibly infinite projective dimension was given by Wakamatsu [Reference Wakamatsu25]. Following [Reference Green, Reiten and Solberg17], such tilting modules of possibly infinite projective dimension are called Wakamatsu-tilting modules. It is known that Wakamatsu-tilting modules also induce some equivalences between certain subcategories of module categories [Reference Wakamatsu26]. But Wakamatsu-tilting modules do not induce derived equivalences in general.
However, we will show in this paper that Wakamatsu-tilting modules make more sense when we consider a more general category than the derived category of an algebra, namely, the stable module category of the repetitive algebra of an algebra. Let us call the latter category the stable repetitive category of the algebra. The stable repetitive category is a triangulated category. Moreover, by Happel’s result [Reference Happel18], for an Artin algebra ![]() $R$, there is a fully faithful triangle embedding of the bounded derived category of
$R$, there is a fully faithful triangle embedding of the bounded derived category of ![]() $R$ into the stable repetitive category of
$R$ into the stable repetitive category of ![]() $R$. Moreover, this embedding is an equivalence if and only if the global dimension of
$R$. Moreover, this embedding is an equivalence if and only if the global dimension of ![]() $R$ is finite; see [Reference Yamaura28] for a generalization and a simple proof of this result.
$R$ is finite; see [Reference Yamaura28] for a generalization and a simple proof of this result.
We say that two algebras are repetitive equivalent if there is an equivalence between their stable repetitive categories. It should be noted that repetitive equivalences are more general than derived equivalences. In fact, by results in [Reference Asashiba2, Reference Chen7, Reference Rickard24], etc., if two algebras are derived equivalent, then their repetitive algebras are derived equivalent, and hence stably equivalent. Thus, derived equivalences always induce repetitive equivalences. However, repetitive equivalences need not be derived equivalences (see Example 5.3).
The following is the main theorem of this paper.
Theorem 1. Let ![]() $R$ be an Artin algebra. If
$R$ be an Artin algebra. If ![]() $T$ is a good Wakamatsu-tilting
$T$ is a good Wakamatsu-tilting ![]() $R$-module with
$R$-module with ![]() $S=\text{End}(T_{R})^{op}$, that is, bimodules
$S=\text{End}(T_{R})^{op}$, that is, bimodules ![]() $_{S}T_{R}$ and
$_{S}T_{R}$ and ![]() $_{R}DT_{S}$ represent a cotorsion pair counter equivalence between a complete hereditary cotorsion pair
$_{R}DT_{S}$ represent a cotorsion pair counter equivalence between a complete hereditary cotorsion pair ![]() $({\mathcal{B}},{\mathcal{A}})$ in
$({\mathcal{B}},{\mathcal{A}})$ in ![]() $\text{mod}R$ and a complete hereditary cotorsion pair
$\text{mod}R$ and a complete hereditary cotorsion pair ![]() $({\mathcal{G}},{\mathcal{K}})$ in
$({\mathcal{G}},{\mathcal{K}})$ in ![]() $\text{mod}S$, then
$\text{mod}S$, then ![]() $R$ and
$R$ and ![]() $S$ are repetitive equivalent. The equivalence can be chosen to restrict to the equivalence between
$S$ are repetitive equivalent. The equivalence can be chosen to restrict to the equivalence between ![]() ${\mathcal{A}}$ and
${\mathcal{A}}$ and ![]() ${\mathcal{G}}$.
${\mathcal{G}}$.
Remark.
(1) The definition of good Wakamatsu-tilting modules is given in Section 3.2. It is still a question for us whether or not all Wakamatsu-tilting modules are good Wakamatsu-tilting modules in general. For algebras of finite representation type, the answer is affirmative.
(2) In a subsequent paper [Reference Chen and Wei9] collaborated with Chen, we can prove that the equivalence in the main theorem is indeed a triangle equivalence.
(3) The result shows that good Wakamatsu-tilting modules seem to behave in the Morita theory of stable repetitive categories as that tilting modules of finite projective dimension behave in the Morita theory of derived categories. We hope that this paper could give some spark on the study of the Morita theory of stable repetitive categories, which is clearly a new area and far from being solved.
Conversely, we have the following result.
Proposition 2. Let ![]() $R$ and
$R$ and ![]() $S$ be Artin algebras. Assume that there is a triangle equivalence between their stable repetitive categories and that this equivalence restricts to an equivalence between a covariantly finite coresolving subcategory
$S$ be Artin algebras. Assume that there is a triangle equivalence between their stable repetitive categories and that this equivalence restricts to an equivalence between a covariantly finite coresolving subcategory ![]() ${\mathcal{A}}$ in
${\mathcal{A}}$ in ![]() $\text{mod}R$ and a contravariantly finite resolving subcategory
$\text{mod}R$ and a contravariantly finite resolving subcategory ![]() ${\mathcal{G}}$ in
${\mathcal{G}}$ in ![]() $\text{mod}S$. Let
$\text{mod}S$. Let ![]() $T$ be the preimage in
$T$ be the preimage in ![]() $\text{mod}R$ of
$\text{mod}R$ of ![]() $S$. Then
$S$. Then ![]() $T$ is a good Wakamatsu-tilting
$T$ is a good Wakamatsu-tilting ![]() $R$-module with
$R$-module with ![]() $S\simeq \text{End}(T_{R})^{op}$.
$S\simeq \text{End}(T_{R})^{op}$.
The paper is organized as follows. After the introduction, we provide basic knowledge on Wakamatsu-tilting modules and repetitive categories in Section 2. Then in Section 3, we introduce good Wakamatsu-tilting modules through cotorsion pair counter equivalences. Some properties and characterizations of good Wakamatsu-tilting modules are presented. Section 4 is devoted to the proof of the main theorem and the proposition in Section 1. Though the proof of the theorem is a little complicated, the main idea is inspired by constructions in [Reference Happel18, Lemma 4.1 in Chap. 3] and [Reference Wakamatsu26, Section 1]. Finally, we provide some examples in the last section. In particular, it is shown that every Wakamatsu-tilting module over an algebra of finite representation type is a good Wakamatsu-tilting module and hence induces a repetitive equivalence. We also provide an example of repetitive equivalences but not derived equivalences.
Conventions. Throughout this paper, we always work over Artin algebras and finitely generated right modules unless we claim otherwise. For an algebra ![]() $R$, we denote by
$R$, we denote by ![]() $\text{mod}R$ the category of all finitely generated
$\text{mod}R$ the category of all finitely generated ![]() $R$-modules and by
$R$-modules and by ![]() $\text{proj}R$ (resp.,
$\text{proj}R$ (resp., ![]() $\text{inj}R$) the category of finitely generated projective (resp., injective)
$\text{inj}R$) the category of finitely generated projective (resp., injective) ![]() $R$-modules. We denote the usual duality over an Artin algebra
$R$-modules. We denote the usual duality over an Artin algebra ![]() $R$ by
$R$ by ![]() $D$.
$D$.
Let ![]() ${\mathcal{A}}$ be an additive category and
${\mathcal{A}}$ be an additive category and ![]() $T\in {\mathcal{A}}$, we use
$T\in {\mathcal{A}}$, we use ![]() $\text{add}_{{\mathcal{A}}}T$ to denote the additive closure of
$\text{add}_{{\mathcal{A}}}T$ to denote the additive closure of ![]() $T$ in
$T$ in ![]() ${\mathcal{A}}$, that is, the class of all objects in
${\mathcal{A}}$, that is, the class of all objects in ![]() ${\mathcal{A}}$ which is isomorphic to a direct summand of finite direct sums of some copies of
${\mathcal{A}}$ which is isomorphic to a direct summand of finite direct sums of some copies of ![]() $T$.
$T$.
For two functors ![]() $\text{F}:{\mathcal{A}}\rightarrow {\mathcal{B}}$ and
$\text{F}:{\mathcal{A}}\rightarrow {\mathcal{B}}$ and ![]() $\text{G}:{\mathcal{B}}\rightarrow {\mathcal{C}}$, we use
$\text{G}:{\mathcal{B}}\rightarrow {\mathcal{C}}$, we use ![]() $\text{GF}$ to denote their composition. While we use
$\text{GF}$ to denote their composition. While we use ![]() $f\cdot g$, or simply just
$f\cdot g$, or simply just ![]() $fg$, to denote the composition of two homomorphisms
$fg$, to denote the composition of two homomorphisms ![]() $f:A\rightarrow B$ and
$f:A\rightarrow B$ and ![]() $g:B\rightarrow C$.
$g:B\rightarrow C$.
Let ![]() ${\mathcal{A}}$ and
${\mathcal{A}}$ and ![]() ${\mathcal{B}}$ be two additive categories and
${\mathcal{B}}$ be two additive categories and ![]() $\text{F}:{\mathcal{A}}\rightarrow {\mathcal{B}}$ be an additive functor, we use
$\text{F}:{\mathcal{A}}\rightarrow {\mathcal{B}}$ be an additive functor, we use ![]() $\text{KerF}$ to denote the subcategory of
$\text{KerF}$ to denote the subcategory of ![]() $A\in {\mathcal{A}}$ such that
$A\in {\mathcal{A}}$ such that ![]() $\text{F}(A)=0$. Moreover, if
$\text{F}(A)=0$. Moreover, if ![]() $\text{F}_{i}:\text{A}\rightarrow {\mathcal{B}}$,
$\text{F}_{i}:\text{A}\rightarrow {\mathcal{B}}$, ![]() $i\in I$, is a class of functors, we denote
$i\in I$, is a class of functors, we denote ![]() $\text{KerF}_{I}=\bigcap _{i\in I}\text{KerF}_{i}$. For instance,
$\text{KerF}_{I}=\bigcap _{i\in I}\text{KerF}_{i}$. For instance, ![]() $\text{KerExt}_{R}^{{\geqslant}1}(T,-)$ is the subcategory of all
$\text{KerExt}_{R}^{{\geqslant}1}(T,-)$ is the subcategory of all ![]() $M\in \text{mod}R$ such that
$M\in \text{mod}R$ such that ![]() $\text{Ext}_{R}^{i}(T,M)=0$ for all
$\text{Ext}_{R}^{i}(T,M)=0$ for all ![]() $i\geqslant 1$.
$i\geqslant 1$.
We write the elements of direct sums as row vectors.
2 Wakamatsu-tilting modules and repetitive categories
2.1 Wakamatsu-tilting modules
Recall that an ![]() $R$-module
$R$-module ![]() $T\in \text{mod}R$ is Wakamatsu-tilting [Reference Wakamatsu25] provided that
$T\in \text{mod}R$ is Wakamatsu-tilting [Reference Wakamatsu25] provided that
(1)
 $\text{End}(\text{}_{S}T)^{op}\simeq R$, where
$\text{End}(\text{}_{S}T)^{op}\simeq R$, where  $S:=\text{End}(T_{R})^{op}$, and
$S:=\text{End}(T_{R})^{op}$, and(2)
 $\text{Ext}_{R}^{i}(T,T)=0=\text{Ext}_{S}^{i}(T,T)=0$ for all
$\text{Ext}_{R}^{i}(T,T)=0=\text{Ext}_{S}^{i}(T,T)=0$ for all  $i>0$.
$i>0$.
These two conditions are also equivalent to the following two conditions [Reference Wakamatsu25, Proposition 3.5]:
(1)
 $\text{Ext}_{R}^{i}(T,T)=0$ for all
$\text{Ext}_{R}^{i}(T,T)=0$ for all  $i>0$ and
$i>0$ and(2) there is an exact sequence
 $0\rightarrow R\rightarrow T_{0}\rightarrow T_{1}\rightarrow \cdots \,$, where
$0\rightarrow R\rightarrow T_{0}\rightarrow T_{1}\rightarrow \cdots \,$, where  $T_{i}\in \text{add}_{\text{mod}R}T$ for all
$T_{i}\in \text{add}_{\text{mod}R}T$ for all  $i$, which stays exact after applying the functor
$i$, which stays exact after applying the functor  $\text{Hom}_{R}(-,T)$.
$\text{Hom}_{R}(-,T)$.
Note that if ![]() $T$ is Wakamatsu-tilting and
$T$ is Wakamatsu-tilting and ![]() $S=\text{End}(T_{R})^{op}$, then
$S=\text{End}(T_{R})^{op}$, then ![]() $_{S}T$ is a Wakamatsu-tilting left
$_{S}T$ is a Wakamatsu-tilting left ![]() $S$-module. In this case, we say that
$S$-module. In this case, we say that ![]() $T$ is a Wakamatsu-tilting
$T$ is a Wakamatsu-tilting ![]() $S$-
$S$-![]() $R$-bimodule. It is easy to see that
$R$-bimodule. It is easy to see that ![]() $DT$ is a Wakamatsu-tilting
$DT$ is a Wakamatsu-tilting ![]() $R$-
$R$-![]() $S$-bimodule in the mean time.
$S$-bimodule in the mean time.
2.1.1 Auslander–Reiten class and co-Auslander–Reiten class
Let ![]() $T\in \text{mod}R$ be a Wakamatsu-tilting module with
$T\in \text{mod}R$ be a Wakamatsu-tilting module with ![]() $S=\text{End}(T_{R})^{op}$. There are the following two interesting classes associated with Wakamatsu-tilting modules.
$S=\text{End}(T_{R})^{op}$. There are the following two interesting classes associated with Wakamatsu-tilting modules.
The Auslander–Reiten class in ![]() $\text{mod}R$ with respect to the Wakamatsu-tilting module
$\text{mod}R$ with respect to the Wakamatsu-tilting module ![]() $T_{R}$, denoted by
$T_{R}$, denoted by ![]() ${\mathcal{X}}_{T}$, is defined as follows [Reference Auslander and Reiten3].
${\mathcal{X}}_{T}$, is defined as follows [Reference Auslander and Reiten3].
![]() ${\mathcal{X}}_{T}:=\{M\in \text{mod}R|$ there is an infinite exact sequence
${\mathcal{X}}_{T}:=\{M\in \text{mod}R|$ there is an infinite exact sequence ![]() $0\rightarrow M\stackrel{f_{0}}{\longrightarrow }T_{0}\stackrel{f_{1}}{\longrightarrow }T_{1}\stackrel{f_{2}}{\longrightarrow }\cdots \,$ such that
$0\rightarrow M\stackrel{f_{0}}{\longrightarrow }T_{0}\stackrel{f_{1}}{\longrightarrow }T_{1}\stackrel{f_{2}}{\longrightarrow }\cdots \,$ such that ![]() $\text{Im}f_{i}\in \text{KerExt}_{R}^{{\geqslant}1}(-,T)$ for each
$\text{Im}f_{i}\in \text{KerExt}_{R}^{{\geqslant}1}(-,T)$ for each ![]() $i\geqslant 0$, where
$i\geqslant 0$, where ![]() $T_{i}\in \text{add}_{\text{mod}R}T$ for all
$T_{i}\in \text{add}_{\text{mod}R}T$ for all ![]() $i\}$.
$i\}$.
Obviously, it holds that ![]() ${\mathcal{X}}_{T}\subseteq \text{KerExt}_{R}^{{\geqslant}1}(-,T)$. Moreover, these two classes coincide with each other provided that
${\mathcal{X}}_{T}\subseteq \text{KerExt}_{R}^{{\geqslant}1}(-,T)$. Moreover, these two classes coincide with each other provided that ![]() $T$ is a cotilting
$T$ is a cotilting ![]() $R$-module.
$R$-module.
Dually, the co-Auslander–Reiten class in ![]() $\text{mod}R$ with respect to the Wakamatsu-tilting
$\text{mod}R$ with respect to the Wakamatsu-tilting ![]() $R$-module
$R$-module ![]() $T$, denoted by
$T$, denoted by ![]() $_{T}{\mathcal{X}}$, is defined as follows.
$_{T}{\mathcal{X}}$, is defined as follows.
![]() $_{T}{\mathcal{X}}:=\{M\in \text{mod}R|$ there is an infinite exact sequence
$_{T}{\mathcal{X}}:=\{M\in \text{mod}R|$ there is an infinite exact sequence ![]() $\cdots \stackrel{f_{2}}{\longrightarrow }T_{1}\stackrel{f_{1}}{\longrightarrow }T_{0}\stackrel{f_{0}}{\longrightarrow }M\rightarrow 0$ such that
$\cdots \stackrel{f_{2}}{\longrightarrow }T_{1}\stackrel{f_{1}}{\longrightarrow }T_{0}\stackrel{f_{0}}{\longrightarrow }M\rightarrow 0$ such that ![]() $\text{Im}f_{i}\in \text{KerExt}_{R}^{{\geqslant}1}(T,-)$ for each
$\text{Im}f_{i}\in \text{KerExt}_{R}^{{\geqslant}1}(T,-)$ for each ![]() $i\geqslant 0$, where
$i\geqslant 0$, where ![]() $T_{i}\in \text{add}_{\text{mod}R}T$ for all
$T_{i}\in \text{add}_{\text{mod}R}T$ for all ![]() $i\}$.
$i\}$.
Similarly, we have that ![]() $_{T}{\mathcal{X}}\subseteq \text{KerExt}_{R}^{{\geqslant}1}(T,-)$ and they coincide with each other provided that
$_{T}{\mathcal{X}}\subseteq \text{KerExt}_{R}^{{\geqslant}1}(T,-)$ and they coincide with each other provided that ![]() $T$ is a tilting
$T$ is a tilting ![]() $R$-module.
$R$-module.
The following result gives some properties about the Auslander–Reiten class and the co-Auslander–Reiten class for a Wakamatsu-tilting module [Reference Auslander and Reiten3, Reference Mantese and Reiten22, Reference Wakamatsu26, Reference Wakamatsu27].
Proposition.
Let ![]() $T$ be a Wakamatsu-tilting
$T$ be a Wakamatsu-tilting ![]() $R$-module with
$R$-module with ![]() $S=\text{End}(T_{R})^{op}$.
$S=\text{End}(T_{R})^{op}$.
(1) The Auslander–Reiten class
 ${\mathcal{X}}_{T}$ is a resolving subcategory, that is, it contains all projective
${\mathcal{X}}_{T}$ is a resolving subcategory, that is, it contains all projective  $R$-modules and is closed under extensions, kernels of epimorphisms and direct summands.
$R$-modules and is closed under extensions, kernels of epimorphisms and direct summands.(2) The co-Auslander–Reiten class
 $_{T}{\mathcal{X}}$ is a coresolving subcategory, that is, it contains all injective
$_{T}{\mathcal{X}}$ is a coresolving subcategory, that is, it contains all injective  $R$-modules and is closed under extensions, cokernels of monomorphisms and direct summands.
$R$-modules and is closed under extensions, cokernels of monomorphisms and direct summands.(3)
 $\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-)=\text{KerExt}_{R}^{{\geqslant}1}({\mathcal{X}}_{T},-)\subseteq _{T}{\mathcal{X}}$.
$\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-)=\text{KerExt}_{R}^{{\geqslant}1}({\mathcal{X}}_{T},-)\subseteq _{T}{\mathcal{X}}$.(4)
 $\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}})=\text{KerExt}_{R}^{{\geqslant}1}(-,_{T}{\mathcal{X}})\subseteq {\mathcal{X}}_{T}$.
$\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}})=\text{KerExt}_{R}^{{\geqslant}1}(-,_{T}{\mathcal{X}})\subseteq {\mathcal{X}}_{T}$.(5)
 $\text{Hom}_{R}(T,-)$ and
$\text{Hom}_{R}(T,-)$ and  $-\!\otimes _{S}T$ induce an (additive) equivalence between the co-Auslander–Reiten class
$-\!\otimes _{S}T$ induce an (additive) equivalence between the co-Auslander–Reiten class  $_{T}{\mathcal{X}}$ in
$_{T}{\mathcal{X}}$ in  $\text{mod}R$ and the Auslander–Reiten class
$\text{mod}R$ and the Auslander–Reiten class  ${\mathcal{X}}_{DT}$ in
${\mathcal{X}}_{DT}$ in  $\text{mod}S$. The equivalence restricts to an (additive) equivalence between the class
$\text{mod}S$. The equivalence restricts to an (additive) equivalence between the class  $\text{KerExt}_{R}^{{\geqslant}1}({\mathcal{X}}_{T},-)$ and the class
$\text{KerExt}_{R}^{{\geqslant}1}({\mathcal{X}}_{T},-)$ and the class  $\text{KerExt}_{S}^{{\geqslant}1}(-,_{DT}{\mathcal{X}})$.
$\text{KerExt}_{S}^{{\geqslant}1}(-,_{DT}{\mathcal{X}})$.
Proof. (1) and (2) follow from [Reference Auslander and Reiten3, Section 5]; see also [Reference Mantese and Reiten22].
(3) and (4) follow from [Reference Wakamatsu27, Lemma 1.4 and Proposition 1.6].
(5) follows from [Reference Wakamatsu26, Proposition 2.14]. ◻
We remark that in case ![]() $T=R$, the class
$T=R$, the class ![]() ${\mathcal{X}}_{T}={\mathcal{X}}_{R}$ is just the class of all Gorenstein projective
${\mathcal{X}}_{T}={\mathcal{X}}_{R}$ is just the class of all Gorenstein projective ![]() $R$-modules. Dually, in case
$R$-modules. Dually, in case ![]() $T=DR$, the class
$T=DR$, the class ![]() $_{T}{\mathcal{X}}=_{DR}{\mathcal{X}}$ is just the class of all Gorenstein injective modules. We refer to [Reference Enochs and Jenda15] for more on Gorenstein projective and Gorenstein injective modules.
$_{T}{\mathcal{X}}=_{DR}{\mathcal{X}}$ is just the class of all Gorenstein injective modules. We refer to [Reference Enochs and Jenda15] for more on Gorenstein projective and Gorenstein injective modules.
2.1.2
The following is a characterization of the Auslander–Reiten class and the co-Auslander–Reiten class, by [Reference Wakamatsu26, Section 2].
Lemma.
Let ![]() $T$ be a Wakamatsu-tilting
$T$ be a Wakamatsu-tilting ![]() $R$-module with
$R$-module with ![]() $S=\text{End}(T_{R})^{op}$. Assume
$S=\text{End}(T_{R})^{op}$. Assume ![]() $X\in \text{mod}R$.
$X\in \text{mod}R$.
(1)
 $X\in _{T}{\mathcal{X}}$ if and only if
$X\in _{T}{\mathcal{X}}$ if and only if  $X\in \text{KerExt}_{R}^{{>}0}(T,-)$,
$X\in \text{KerExt}_{R}^{{>}0}(T,-)$,  $\text{Hom}_{R}(T,X)\otimes _{S}T\simeq X$ and
$\text{Hom}_{R}(T,X)\otimes _{S}T\simeq X$ and  $\text{Hom}_{R}(T,X)\in \text{KerTor}_{{>}0}^{S}(-,T)$ canonically.
$\text{Hom}_{R}(T,X)\in \text{KerTor}_{{>}0}^{S}(-,T)$ canonically.(2)
 $X\in {\mathcal{X}}_{T}$ if and only if
$X\in {\mathcal{X}}_{T}$ if and only if  $X\in \text{KerExt}_{R}^{{>}0}(-,T)$,
$X\in \text{KerExt}_{R}^{{>}0}(-,T)$,  $\text{Hom}_{S}(\text{Hom}_{R}(X,T),T)$
$\text{Hom}_{S}(\text{Hom}_{R}(X,T),T)$ $\simeq X$ and
$\simeq X$ and  $\text{Hom}_{R}(X,T)\in \text{KerExt}_{S}^{{>}0}(-,T)$ canonically.
$\text{Hom}_{R}(X,T)\in \text{KerExt}_{S}^{{>}0}(-,T)$ canonically.
2.1.3 Useful isomorphisms
Let ![]() $T$ be a Wakamatsu-tilting
$T$ be a Wakamatsu-tilting ![]() $S$-
$S$-![]() $R$-bimodule. Then we have the following isomorphisms of bimodules:
$R$-bimodule. Then we have the following isomorphisms of bimodules:
Given an adjoint pair ![]() $(\text{F},\text{G})$ of functors, we denote by
$(\text{F},\text{G})$ of functors, we denote by ![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}$ the natural adjoint isomorphism
$\boldsymbol{\unicode[STIX]{x1D6E4}}$ the natural adjoint isomorphism
Moreover, for a homomorphism ![]() $f:\text{F}(X)\rightarrow Y$, we denote by
$f:\text{F}(X)\rightarrow Y$, we denote by ![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}(f):X\rightarrow \text{G}(Y)$ the image of
$\boldsymbol{\unicode[STIX]{x1D6E4}}(f):X\rightarrow \text{G}(Y)$ the image of ![]() $f$ under the isomorphism
$f$ under the isomorphism ![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}$. We denote by
$\boldsymbol{\unicode[STIX]{x1D6E4}}$. We denote by ![]() $\unicode[STIX]{x1D702}$ and
$\unicode[STIX]{x1D702}$ and ![]() $\unicode[STIX]{x1D716}$ the unit and counit of this adjoint pair, respectively, that is,
$\unicode[STIX]{x1D716}$ the unit and counit of this adjoint pair, respectively, that is,
In particular, associated with an ![]() $S$-
$S$-![]() $R$-bimodule
$R$-bimodule ![]() $T$, we have the following adjoint isomorphism:
$T$, we have the following adjoint isomorphism:
We denote by ![]() $\unicode[STIX]{x1D702}^{T}$ and
$\unicode[STIX]{x1D702}^{T}$ and ![]() $\unicode[STIX]{x1D716}^{T}$ the unit and counit of this adjoint pair, respectively, that is, for
$\unicode[STIX]{x1D716}^{T}$ the unit and counit of this adjoint pair, respectively, that is, for ![]() $X\in \text{mod}S$ and
$X\in \text{mod}S$ and ![]() $Y\in \text{mod}R$, respectively,
$Y\in \text{mod}R$, respectively,
By the naturality of the isomorphism ![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}$, for all homomorphisms
$\boldsymbol{\unicode[STIX]{x1D6E4}}$, for all homomorphisms ![]() $f:X_{1}\rightarrow X_{2}$,
$f:X_{1}\rightarrow X_{2}$, ![]() $g:\text{F}(X_{2})\rightarrow Y_{1}$ and
$g:\text{F}(X_{2})\rightarrow Y_{1}$ and ![]() $h:Y_{1}\rightarrow Y_{2}$, it holds that
$h:Y_{1}\rightarrow Y_{2}$, it holds that ![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}(\text{F}(f)\cdot g\cdot h)=f\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}(g)\cdot \text{G}(h)$.
$\boldsymbol{\unicode[STIX]{x1D6E4}}(\text{F}(f)\cdot g\cdot h)=f\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}(g)\cdot \text{G}(h)$.
In particular, for a morphism ![]() $g:F(X)\rightarrow Y$, by applying
$g:F(X)\rightarrow Y$, by applying ![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}$ to the composition
$\boldsymbol{\unicode[STIX]{x1D6E4}}$ to the composition ![]() $F(X)\stackrel{1_{F(X)}}{\rightarrow }F(X)\stackrel{g}{\rightarrow }Y$, we have that
$F(X)\stackrel{1_{F(X)}}{\rightarrow }F(X)\stackrel{g}{\rightarrow }Y$, we have that ![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}(g)=\boldsymbol{\unicode[STIX]{x1D6E4}}(1_{F(X)})\cdot \text{G}(g)=\unicode[STIX]{x1D702}_{X}\cdot \text{G}(g)$. Dually, for a morphism
$\boldsymbol{\unicode[STIX]{x1D6E4}}(g)=\boldsymbol{\unicode[STIX]{x1D6E4}}(1_{F(X)})\cdot \text{G}(g)=\unicode[STIX]{x1D702}_{X}\cdot \text{G}(g)$. Dually, for a morphism ![]() $f:X\rightarrow G(Y)$, we have that
$f:X\rightarrow G(Y)$, we have that ![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}^{-1}(f)=F(f)\unicode[STIX]{x1D716}_{Y}$.
$\boldsymbol{\unicode[STIX]{x1D6E4}}^{-1}(f)=F(f)\unicode[STIX]{x1D716}_{Y}$.
2.2 Repetitive algebras and repetitive categories
2.2.1
We recall some basic facts on repetitive algebras mainly from [Reference Happel18].
Let ![]() $R$ be an Artin algebra. The repetitive algebra
$R$ be an Artin algebra. The repetitive algebra ![]() $\widehat{R}$ of
$\widehat{R}$ of ![]() $R$ was first introduced in [Reference Hughes and Waschbüsch20] and is defined to be the direct sum
$R$ was first introduced in [Reference Hughes and Waschbüsch20] and is defined to be the direct sum ![]() $\widehat{R}=\bigoplus _{n\in \mathbb{Z}}R\oplus \bigoplus _{n\in \mathbb{Z}}DR$ with the multiplication given by
$\widehat{R}=\bigoplus _{n\in \mathbb{Z}}R\oplus \bigoplus _{n\in \mathbb{Z}}DR$ with the multiplication given by
The repetitive algebra ![]() $\widehat{R}$ can be interpreted as the following infinite matrix algebra (without the identity):
$\widehat{R}$ can be interpreted as the following infinite matrix algebra (without the identity):
 $$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}\ddots & & & & \\ \ddots & R & & & \\ & DR & R & & \\ & & DR & R & \\ & & & \ddots & \ddots \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}\ddots & & & & \\ \ddots & R & & & \\ & DR & R & & \\ & & DR & R & \\ & & & \ddots & \ddots \end{array}\right).\end{eqnarray}$$2.2.2
Consider the following two categories:
(1)
 ${\mathcal{R}}{\mathcal{C}}^{\otimes }(R):=\{X=\{X_{i},\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\}_{i\in \mathbb{Z}}\mid X_{i}\in \text{mod}R$ such that almost all
${\mathcal{R}}{\mathcal{C}}^{\otimes }(R):=\{X=\{X_{i},\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\}_{i\in \mathbb{Z}}\mid X_{i}\in \text{mod}R$ such that almost all  $X_{i}$ are 0 and
$X_{i}$ are 0 and  $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X):X_{i}\otimes _{R}DR\rightarrow X_{i-1}$ satisfying
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X):X_{i}\otimes _{R}DR\rightarrow X_{i-1}$ satisfying  $(\unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(X)\otimes _{R}DR)\cdot \unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)=0$, for each
$(\unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(X)\otimes _{R}DR)\cdot \unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)=0$, for each  $i\}$, where a morphism between two objects
$i\}$, where a morphism between two objects  $X$ and
$X$ and  $Y$ is given by
$Y$ is given by  $f=\{f_{i}:X_{i}\rightarrow Y_{i}\}$ such that
$f=\{f_{i}:X_{i}\rightarrow Y_{i}\}$ such that  $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot f_{i-1}=f_{i}\otimes _{R}DR\cdot \unicode[STIX]{x1D6FF}_{i}^{\otimes }(Y)$ for all
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot f_{i-1}=f_{i}\otimes _{R}DR\cdot \unicode[STIX]{x1D6FF}_{i}^{\otimes }(Y)$ for all  $i$.
$i$.(2)
 ${\mathcal{R}}{\mathcal{C}}^{\text{H}}(R):=\{X=\{X_{i},\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(X)\}_{i\in \mathbb{Z}}\mid X_{i}\in \text{mod}R$ such that almost all
${\mathcal{R}}{\mathcal{C}}^{\text{H}}(R):=\{X=\{X_{i},\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(X)\}_{i\in \mathbb{Z}}\mid X_{i}\in \text{mod}R$ such that almost all  $X_{i}$ are 0 and
$X_{i}$ are 0 and  $\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(X):X_{i}\rightarrow \text{Hom}_{R}(DR,X_{i-1})$ satisfying
$\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(X):X_{i}\rightarrow \text{Hom}_{R}(DR,X_{i-1})$ satisfying  $\unicode[STIX]{x1D6FF}_{i+1}^{\text{H}}(X)\cdot \text{Hom}_{R}(DR,\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(X))=0$, for each
$\unicode[STIX]{x1D6FF}_{i+1}^{\text{H}}(X)\cdot \text{Hom}_{R}(DR,\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(X))=0$, for each  $i\}$, where a morphism between two objects
$i\}$, where a morphism between two objects  $X$ and
$X$ and  $Y$ is given by
$Y$ is given by  $f=\{f_{i}:X_{i}\rightarrow Y_{i}\}$ such that
$f=\{f_{i}:X_{i}\rightarrow Y_{i}\}$ such that  $\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(X)\cdot \text{Hom}_{R}(DR,f_{i-1})=f_{i}\cdot \unicode[STIX]{x1D6FF}_{i}^{\text{H}}(Y)$ for all
$\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(X)\cdot \text{Hom}_{R}(DR,f_{i-1})=f_{i}\cdot \unicode[STIX]{x1D6FF}_{i}^{\text{H}}(Y)$ for all  $i$.
$i$.
One can check that these two categories ![]() ${\mathcal{R}}{\mathcal{C}}^{\otimes }(R)$ and
${\mathcal{R}}{\mathcal{C}}^{\otimes }(R)$ and ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{H}}(R)$ are both abelian categories. Moreover, they are indeed equivalent to each other as abelian categories, via the adjoint pair
${\mathcal{R}}{\mathcal{C}}^{\text{H}}(R)$ are both abelian categories. Moreover, they are indeed equivalent to each other as abelian categories, via the adjoint pair ![]() $(-\!\otimes _{R}DR,\text{Hom}_{R}(DR,-))$. Indeed, an object
$(-\!\otimes _{R}DR,\text{Hom}_{R}(DR,-))$. Indeed, an object ![]() $X=\{X_{i},\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\}\in {\mathcal{R}}{\mathcal{C}}^{\otimes }(R)$ is equivalent to an object
$X=\{X_{i},\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\}\in {\mathcal{R}}{\mathcal{C}}^{\otimes }(R)$ is equivalent to an object ![]() $X=\{X_{i},\boldsymbol{\unicode[STIX]{x1D6E4}}^{DR}(\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X))\}\in {\mathcal{R}}{\mathcal{C}}^{\text{H}}(R)$. We will freely use this equivalence. In particular, we often view objects
$X=\{X_{i},\boldsymbol{\unicode[STIX]{x1D6E4}}^{DR}(\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X))\}\in {\mathcal{R}}{\mathcal{C}}^{\text{H}}(R)$. We will freely use this equivalence. In particular, we often view objects ![]() $X$ in these two categories being of the following form with almost all terms
$X$ in these two categories being of the following form with almost all terms ![]() $X_{i}=0$
$X_{i}=0$
where ![]() $\unicode[STIX]{x1D6FF}_{i}$ means
$\unicode[STIX]{x1D6FF}_{i}$ means ![]() $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)$ (resp.,
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)$ (resp., ![]() $\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(X)$) if
$\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(X)$) if ![]() $X\in {\mathcal{R}}{\mathcal{C}}^{\otimes }(R)$ (resp.,
$X\in {\mathcal{R}}{\mathcal{C}}^{\otimes }(R)$ (resp., ![]() $X\in {\mathcal{R}}{\mathcal{C}}^{\text{H}}(R)$). We call it a (bounded chain) repe-complex with the repe-difference
$X\in {\mathcal{R}}{\mathcal{C}}^{\text{H}}(R)$). We call it a (bounded chain) repe-complex with the repe-difference ![]() $\unicode[STIX]{x1D6FF}$ and denote by
$\unicode[STIX]{x1D6FF}$ and denote by ![]() ${\mathcal{R}}{\mathcal{C}}(R)$ the category of all such repe-complexes and call it the repetitive category over
${\mathcal{R}}{\mathcal{C}}(R)$ the category of all such repe-complexes and call it the repetitive category over ![]() $R$. Note that there is an obvious automorphism
$R$. Note that there is an obvious automorphism ![]() $[1]:{\mathcal{R}}{\mathcal{C}}(R)\rightarrow {\mathcal{R}}{\mathcal{C}}(R)$ defined by
$[1]:{\mathcal{R}}{\mathcal{C}}(R)\rightarrow {\mathcal{R}}{\mathcal{C}}(R)$ defined by ![]() $(X[1])_{i}=X_{i-1}$ for each
$(X[1])_{i}=X_{i-1}$ for each ![]() $i$.
$i$.
Note that if ![]() $X=\{X_{i}\}$ is a repe-complex, then
$X=\{X_{i}\}$ is a repe-complex, then ![]() $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D6FF}_{i-1}^{\text{H}}(X)=0$ since
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D6FF}_{i-1}^{\text{H}}(X)=0$ since ![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}^{DR}(\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D6FF}_{i-1}^{\text{H}}(X))=\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(X)\cdot \text{Hom}_{R}(DR,\unicode[STIX]{x1D6FF}_{i-1}^{\text{H}}(X))=0$.
$\boldsymbol{\unicode[STIX]{x1D6E4}}^{DR}(\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D6FF}_{i-1}^{\text{H}}(X))=\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(X)\cdot \text{Hom}_{R}(DR,\unicode[STIX]{x1D6FF}_{i-1}^{\text{H}}(X))=0$.
We say that a repe-complex ![]() $X=\{X_{i},\unicode[STIX]{x1D6FF}_{i}\}\in {\mathcal{R}}{\mathcal{C}}(R)$ is trivial if each
$X=\{X_{i},\unicode[STIX]{x1D6FF}_{i}\}\in {\mathcal{R}}{\mathcal{C}}(R)$ is trivial if each ![]() $\unicode[STIX]{x1D6FF}_{i}=0$. The full subcategory of all trivial repe-complexes is denoted by
$\unicode[STIX]{x1D6FF}_{i}=0$. The full subcategory of all trivial repe-complexes is denoted by ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$. Note that there is a natural forgetful functor from
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$. Note that there is a natural forgetful functor from ![]() ${\mathcal{R}}{\mathcal{C}}(R)$ to
${\mathcal{R}}{\mathcal{C}}(R)$ to ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$ by forgetting the repe-difference.
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$ by forgetting the repe-difference.
Let ![]() ${\mathcal{C}}$ be a class of
${\mathcal{C}}$ be a class of ![]() $R$-modules, we denote by
$R$-modules, we denote by ![]() ${\mathcal{R}}{\mathcal{C}}({\mathcal{C}})$ the class of repe-complexes with terms in
${\mathcal{R}}{\mathcal{C}}({\mathcal{C}})$ the class of repe-complexes with terms in ![]() ${\mathcal{C}}$. The notation
${\mathcal{C}}$. The notation ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{C}})$ is defined similarly.
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{C}})$ is defined similarly.
The connection between the repetitive category and the algebra ![]() $\widehat{R}$ is that the repetitive category is equivalent to
$\widehat{R}$ is that the repetitive category is equivalent to ![]() $\text{mod}\widehat{R}$, that is, the module category of the algebra
$\text{mod}\widehat{R}$, that is, the module category of the algebra ![]() $\widehat{R}$, as abelian categories; see [Reference Happel18] for details. Thus, we may identify
$\widehat{R}$, as abelian categories; see [Reference Happel18] for details. Thus, we may identify ![]() ${\mathcal{R}}{\mathcal{C}}(R)=\text{mod}\widehat{R}$.
${\mathcal{R}}{\mathcal{C}}(R)=\text{mod}\widehat{R}$.
2.2.3
As shown in [Reference Happel18], ![]() $\widehat{R}$ is a self-injective algebra and then the category
$\widehat{R}$ is a self-injective algebra and then the category ![]() ${\mathcal{R}}{\mathcal{C}}(R)(=\text{mod}\widehat{R})$ is a Frobenius category, where the projective (and also injective) objects are of the form
${\mathcal{R}}{\mathcal{C}}(R)(=\text{mod}\widehat{R})$ is a Frobenius category, where the projective (and also injective) objects are of the form
where ![]() $P_{i}\in \text{proj}R$,
$P_{i}\in \text{proj}R$, ![]() $I_{i}\in \text{inj}R$ and
$I_{i}\in \text{inj}R$ and ![]() $\unicode[STIX]{x1D6FF}_{i}=\big(\begin{smallmatrix}0 & \unicode[STIX]{x1D6FF}_{i}^{\prime }\\ 0 & 0\end{smallmatrix}\big)$ such that
$\unicode[STIX]{x1D6FF}_{i}=\big(\begin{smallmatrix}0 & \unicode[STIX]{x1D6FF}_{i}^{\prime }\\ 0 & 0\end{smallmatrix}\big)$ such that ![]() $\unicode[STIX]{x1D6FF}_{i}^{\prime }:P_{i}\otimes _{R}DR\rightarrow I_{i-1}$ is an isomorphism (considered in
$\unicode[STIX]{x1D6FF}_{i}^{\prime }:P_{i}\otimes _{R}DR\rightarrow I_{i-1}$ is an isomorphism (considered in ![]() ${\mathcal{R}}{\mathcal{C}}^{\otimes }(R)$) or, equivalently,
${\mathcal{R}}{\mathcal{C}}^{\otimes }(R)$) or, equivalently, ![]() $\unicode[STIX]{x1D6FF}_{i}^{\prime }:P_{i}\rightarrow \text{Hom}_{R}(DR,I_{i-1})$ is an isomorphism (considered in
$\unicode[STIX]{x1D6FF}_{i}^{\prime }:P_{i}\rightarrow \text{Hom}_{R}(DR,I_{i-1})$ is an isomorphism (considered in ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{H}}(R)$). Thus, its stable category
${\mathcal{R}}{\mathcal{C}}^{\text{H}}(R)$). Thus, its stable category ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ is a triangulated category. We will call it the stable repetitive category of
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ is a triangulated category. We will call it the stable repetitive category of ![]() $\text{mod}R$ (or simply, of
$\text{mod}R$ (or simply, of ![]() $R$).
$R$).
It was shown in [Reference Happel18] that there is a fully faithful triangle embedding from the derived category ![]() ${\mathcal{D}}^{b}(\text{mod}R)$ to the stable repetitive category
${\mathcal{D}}^{b}(\text{mod}R)$ to the stable repetitive category ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$. Moreover, there is a triangle equivalence between
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$. Moreover, there is a triangle equivalence between ![]() ${\mathcal{D}}^{b}(\text{mod}R)$ and
${\mathcal{D}}^{b}(\text{mod}R)$ and ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ if and only if
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ if and only if ![]() $R$ has finite global dimension. We note that this result was generalized in [Reference Yamaura28] and also a simple proof of this result was presented there.
$R$ has finite global dimension. We note that this result was generalized in [Reference Yamaura28] and also a simple proof of this result was presented there.
For basic knowledge on triangulated categories, derived categories and the tilting theory, we refer to [Reference Happel18].
3 Cotorsion pairs and good Wakamatsu-tilting modules
3.1 Cotorsion pair counter equivalences
A pair of subcategories ![]() $({\mathcal{B}},{\mathcal{A}})$ in
$({\mathcal{B}},{\mathcal{A}})$ in ![]() $\text{mod}R$ is called a cotorsion pair, if
$\text{mod}R$ is called a cotorsion pair, if ![]() ${\mathcal{B}}=\text{KerExt}_{R}^{1}(-,{\mathcal{A}})$ and
${\mathcal{B}}=\text{KerExt}_{R}^{1}(-,{\mathcal{A}})$ and ![]() ${\mathcal{A}}=\text{KerExt}_{R}^{1}({\mathcal{B}},-)$. A cotorsion pair
${\mathcal{A}}=\text{KerExt}_{R}^{1}({\mathcal{B}},-)$. A cotorsion pair ![]() $({\mathcal{B}},{\mathcal{A}})$ is called hereditary provided that
$({\mathcal{B}},{\mathcal{A}})$ is called hereditary provided that ![]() ${\mathcal{B}}$ is resolving, or equivalently,
${\mathcal{B}}$ is resolving, or equivalently, ![]() ${\mathcal{A}}$ is coresolving. Moreover, a cotorsion pair
${\mathcal{A}}$ is coresolving. Moreover, a cotorsion pair ![]() $({\mathcal{B}},{\mathcal{A}})$ is called complete provided that, for each
$({\mathcal{B}},{\mathcal{A}})$ is called complete provided that, for each ![]() $X\in \text{mod}R$, there exist exact sequences
$X\in \text{mod}R$, there exist exact sequences ![]() $0\rightarrow X\rightarrow A\rightarrow B\rightarrow 0$ and
$0\rightarrow X\rightarrow A\rightarrow B\rightarrow 0$ and ![]() $0\rightarrow A^{\prime }\rightarrow B^{\prime }\rightarrow X\rightarrow 0$ for some
$0\rightarrow A^{\prime }\rightarrow B^{\prime }\rightarrow X\rightarrow 0$ for some ![]() $A,A^{\prime }\in {\mathcal{A}}$ and
$A,A^{\prime }\in {\mathcal{A}}$ and ![]() $B,B^{\prime }\in {\mathcal{B}}$. We refer to the book [Reference Göbel and Trlifaj16] for general results on cotorsion pairs.
$B,B^{\prime }\in {\mathcal{B}}$. We refer to the book [Reference Göbel and Trlifaj16] for general results on cotorsion pairs.
Let ![]() $({\mathcal{B}},{\mathcal{A}})$ be a cotorsion pair in
$({\mathcal{B}},{\mathcal{A}})$ be a cotorsion pair in ![]() $\text{mod}R$ and
$\text{mod}R$ and ![]() $({\mathcal{G}},{\mathcal{K}})$ be a cotorsion pair in
$({\mathcal{G}},{\mathcal{K}})$ be a cotorsion pair in ![]() $\text{mod}S$. Similar to torsion theory counter equivalences in the Brenner–Butler theorem (see [Reference Colby and Fuller11, Reference Colpi, D’Este and Tonolo13]), we say that there is a cotorsion pair counter equivalence between
$\text{mod}S$. Similar to torsion theory counter equivalences in the Brenner–Butler theorem (see [Reference Colby and Fuller11, Reference Colpi, D’Este and Tonolo13]), we say that there is a cotorsion pair counter equivalence between ![]() $({\mathcal{B}},{\mathcal{A}})$ and
$({\mathcal{B}},{\mathcal{A}})$ and ![]() $({\mathcal{G}},{\mathcal{K}})$ provided that there is an equivalence
$({\mathcal{G}},{\mathcal{K}})$ provided that there is an equivalence ![]() $\text{H}:{\mathcal{A}}~_{\longleftarrow }^{\longrightarrow }{\mathcal{G}}:\text{T}$ and an equivalence
$\text{H}:{\mathcal{A}}~_{\longleftarrow }^{\longrightarrow }{\mathcal{G}}:\text{T}$ and an equivalence ![]() $\text{H}^{\prime }:{\mathcal{K}}~_{\longleftarrow }^{\longrightarrow }{\mathcal{B}}:\text{T}^{\prime }$, all as additive categories. Moreover, we say that two bimodules
$\text{H}^{\prime }:{\mathcal{K}}~_{\longleftarrow }^{\longrightarrow }{\mathcal{B}}:\text{T}^{\prime }$, all as additive categories. Moreover, we say that two bimodules ![]() $_{S}V_{R}$ and
$_{S}V_{R}$ and ![]() $_{R}V_{S}^{\prime }$ represent the cotorsion pair counter equivalence if
$_{R}V_{S}^{\prime }$ represent the cotorsion pair counter equivalence if ![]() $\text{H}=\text{Hom}_{R}(V,-)$,
$\text{H}=\text{Hom}_{R}(V,-)$, ![]() $\text{T}=-\!\otimes _{S}V$ and
$\text{T}=-\!\otimes _{S}V$ and ![]() $\text{H}^{\prime }=\text{Hom}_{S}(V^{\prime },-)$,
$\text{H}^{\prime }=\text{Hom}_{S}(V^{\prime },-)$, ![]() $\text{T}^{\prime }=-\!\otimes _{R}V^{\prime }$.
$\text{T}^{\prime }=-\!\otimes _{R}V^{\prime }$.
There are close relations between Wakamatsu-tilting modules and cotorsion pair counter equivalences, as shown in the following proposition.
Proposition.
Let ![]() $T$ be a Wakamatsu-tilting
$T$ be a Wakamatsu-tilting ![]() $R$-module with
$R$-module with ![]() $S=\text{End}(T_{R})^{op}$.
$S=\text{End}(T_{R})^{op}$.
(1) Both pairs
 $(\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}}),_{T}{\mathcal{X}})$ and
$(\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}}),_{T}{\mathcal{X}})$ and  $({\mathcal{X}}_{T},\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-))$ are hereditary cotorsion pairs.
$({\mathcal{X}}_{T},\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-))$ are hereditary cotorsion pairs.(2) The bimodules
 $_{S}T_{R}$ and
$_{S}T_{R}$ and  $_{R}DT_{S}$ represent a cotorsion pair counter equivalence between the cotorsion pair
$_{R}DT_{S}$ represent a cotorsion pair counter equivalence between the cotorsion pair  $(\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}}),_{T}{\mathcal{X}})$ in
$(\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}}),_{T}{\mathcal{X}})$ in  $\text{mod}R$ and the cotorsion pair
$\text{mod}R$ and the cotorsion pair  $({\mathcal{X}}_{DT},\text{KerExt}_{S}^{1}({\mathcal{X}}_{DT},-))$ in
$({\mathcal{X}}_{DT},\text{KerExt}_{S}^{1}({\mathcal{X}}_{DT},-))$ in  $\text{mod}S$.
$\text{mod}S$.(3) The bimodules
 $_{R}DT_{S}$ and
$_{R}DT_{S}$ and  $_{S}T_{R}$ represent a cotorsion pair counter equivalence between the cotorsion pair
$_{S}T_{R}$ represent a cotorsion pair counter equivalence between the cotorsion pair  $(\text{KerExt}_{S}^{1}(-,_{DT}{\mathcal{X}}),_{DT}{\mathcal{X}})$ in
$(\text{KerExt}_{S}^{1}(-,_{DT}{\mathcal{X}}),_{DT}{\mathcal{X}})$ in  $\text{mod}S$ and the cotorsion pair
$\text{mod}S$ and the cotorsion pair  $({\mathcal{X}}_{T},\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-))$ in
$({\mathcal{X}}_{T},\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-))$ in  $\text{mod}R$.
$\text{mod}R$.
(1) follows from [Reference Mantese and Reiten22, Proposition 3.1] and Proposition 2.1.1.
(2) follows from Proposition 2.1.1(5).
(3) is obtained from (2) by replacing
 $_{S}T_{R}$ with
$_{S}T_{R}$ with  $_{R}DT_{S}$. ◻
$_{R}DT_{S}$. ◻
3.2 Good Wakamatsu-tilting modules
3.2.1
In general, the two cotorsion pairs in Proposition 3.1(1) are not complete. For instance, consider the case ![]() $T=R$. Then
$T=R$. Then ![]() ${\mathcal{X}}_{R}$ is the class of all Gorenstein projective modules (note that we only consider finitely generated modules). It is well known that this class is not a precovering class in general; see, for instance, [Reference Yoshino29]. Thus, the cotorsion pair
${\mathcal{X}}_{R}$ is the class of all Gorenstein projective modules (note that we only consider finitely generated modules). It is well known that this class is not a precovering class in general; see, for instance, [Reference Yoshino29]. Thus, the cotorsion pair ![]() $({\mathcal{X}}_{R},\text{KerExt}_{R}^{1}({\mathcal{X}}_{R},-))$ cannot be complete. Dually, the cotorsion pair
$({\mathcal{X}}_{R},\text{KerExt}_{R}^{1}({\mathcal{X}}_{R},-))$ cannot be complete. Dually, the cotorsion pair ![]() $(\text{KerExt}_{R}^{1}(-,_{DR}{\mathcal{X}}),_{DR}{\mathcal{X}})$ in case
$(\text{KerExt}_{R}^{1}(-,_{DR}{\mathcal{X}}),_{DR}{\mathcal{X}})$ in case ![]() $T=DR$ is not complete in general.
$T=DR$ is not complete in general.
However, the other cotorsion pair of the two cotorsion pairs in Proposition 3.1(1), that is, the cotorsion pair
for ![]() $T=R$ and the cotorsion pair
$T=R$ and the cotorsion pair
for ![]() $T=DR$, respectively, is clearly complete. This leads to the following general definition.
$T=DR$, respectively, is clearly complete. This leads to the following general definition.
Definition.
A Wakamatsu-tilting bimodule ![]() $_{S}T_{R}$ is said to be good if the bimodules
$_{S}T_{R}$ is said to be good if the bimodules ![]() $_{S}T_{R}$ and
$_{S}T_{R}$ and ![]() $_{R}DT_{S}$ represent a cotorsion pair counter equivalence between a complete hereditary cotorsion pair
$_{R}DT_{S}$ represent a cotorsion pair counter equivalence between a complete hereditary cotorsion pair ![]() $({\mathcal{B}},{\mathcal{A}})$ in
$({\mathcal{B}},{\mathcal{A}})$ in ![]() $\text{mod}R$ and a complete hereditary cotorsion pair
$\text{mod}R$ and a complete hereditary cotorsion pair ![]() $({\mathcal{G}},{\mathcal{K}})$ in
$({\mathcal{G}},{\mathcal{K}})$ in ![]() $\text{mod}S$. Furthermore, an
$\text{mod}S$. Furthermore, an ![]() $R$-module
$R$-module ![]() $T$ is said to be a good Wakamatsu-tilting module if
$T$ is said to be a good Wakamatsu-tilting module if ![]() $_{S}T_{R}$ is a good Wakamatsu-tilting bimodule with
$_{S}T_{R}$ is a good Wakamatsu-tilting bimodule with ![]() $S=\text{End}(T_{R})^{op}$.
$S=\text{End}(T_{R})^{op}$.
For example, ![]() $R$ and
$R$ and ![]() $DR$ are good Wakamatsu-tilting modules. In general, if
$DR$ are good Wakamatsu-tilting modules. In general, if ![]() $_{S}T_{R}$ is a good Wakamatsu-tilting bimodule, then
$_{S}T_{R}$ is a good Wakamatsu-tilting bimodule, then ![]() $_{R}DT_{S}$ is also a good Wakamatsu-tilting bimodule by the definition and the fact that
$_{R}DT_{S}$ is also a good Wakamatsu-tilting bimodule by the definition and the fact that ![]() $DDT=T$.
$DDT=T$.
In general, we do not know if the following question has an affirmative answer.
Question.
Are all Wakamatsu-tilting modules good Wakamatsu-tilting modules?
However, we will see in Section 5 that the answer to the above question is ‘yes’ for algebras of finite representation type.
3.2.2
By the definition, we have the following property of Wakamatsu-tilting bimodules.
Proposition.
Let ![]() $_{S}T_{R}$ be a Wakamatsu-tilting bimodule. Assume that
$_{S}T_{R}$ be a Wakamatsu-tilting bimodule. Assume that ![]() $({\mathcal{B}},{\mathcal{A}})$ is a hereditary cotorsion pair in
$({\mathcal{B}},{\mathcal{A}})$ is a hereditary cotorsion pair in ![]() $\text{mod}R$ and
$\text{mod}R$ and ![]() $({\mathcal{G}},{\mathcal{K}})$ is a hereditary cotorsion pair in
$({\mathcal{G}},{\mathcal{K}})$ is a hereditary cotorsion pair in ![]() $\text{mod}S$ such that the bimodules
$\text{mod}S$ such that the bimodules ![]() $_{S}T_{R}$ and
$_{S}T_{R}$ and ![]() $_{R}DT_{S}$ represent a cotorsion pair counter equivalence between them. Then
$_{R}DT_{S}$ represent a cotorsion pair counter equivalence between them. Then
(1)
 ${\mathcal{B}}\subseteq {\mathcal{X}}_{T}$,
${\mathcal{B}}\subseteq {\mathcal{X}}_{T}$,  ${\mathcal{A}}\subseteq _{T}{\mathcal{X}}$ and
${\mathcal{A}}\subseteq _{T}{\mathcal{X}}$ and  ${\mathcal{G}}\subseteq {\mathcal{X}}_{DT}$,
${\mathcal{G}}\subseteq {\mathcal{X}}_{DT}$,  ${\mathcal{K}}\subseteq _{DT}{\mathcal{X}}$
${\mathcal{K}}\subseteq _{DT}{\mathcal{X}}$(2)
 $\text{add}_{\text{mod}R}T={\mathcal{B}}\bigcap {\mathcal{A}}$ and
$\text{add}_{\text{mod}R}T={\mathcal{B}}\bigcap {\mathcal{A}}$ and  $\text{add}_{\text{mod}S}DT={\mathcal{G}}\bigcap {\mathcal{K}}$
$\text{add}_{\text{mod}S}DT={\mathcal{G}}\bigcap {\mathcal{K}}$
Proof. (1) First, we show that ![]() $\text{add}_{\text{mod}R}T\subseteq {\mathcal{B}}\bigcap {\mathcal{A}}$ and
$\text{add}_{\text{mod}R}T\subseteq {\mathcal{B}}\bigcap {\mathcal{A}}$ and ![]() $\text{add}_{\text{mod}S}DT\subseteq {\mathcal{G}}\bigcap {\mathcal{K}}$.
$\text{add}_{\text{mod}S}DT\subseteq {\mathcal{G}}\bigcap {\mathcal{K}}$.
Note that all the involved subcategories in (1) are closed under finite direct sums and direct summands. Since ![]() ${\mathcal{G}}$ is resolving, we have that
${\mathcal{G}}$ is resolving, we have that ![]() $S\in {\mathcal{G}}$. By the equivalence between
$S\in {\mathcal{G}}$. By the equivalence between ![]() ${\mathcal{A}}$ and
${\mathcal{A}}$ and ![]() ${\mathcal{G}}$, we obtain that
${\mathcal{G}}$, we obtain that ![]() $T=S\otimes _{S}T\in {\mathcal{A}}$. It follows that
$T=S\otimes _{S}T\in {\mathcal{A}}$. It follows that ![]() $\text{add}_{\text{mod}R}T\subseteq {\mathcal{A}}$. Dually, since
$\text{add}_{\text{mod}R}T\subseteq {\mathcal{A}}$. Dually, since ![]() ${\mathcal{K}}$ is coresolving, we have that
${\mathcal{K}}$ is coresolving, we have that ![]() $DS\in {\mathcal{K}}$. It follows from the equivalence between
$DS\in {\mathcal{K}}$. It follows from the equivalence between ![]() ${\mathcal{B}}$ and
${\mathcal{B}}$ and ![]() ${\mathcal{K}}$ that
${\mathcal{K}}$ that ![]() $T=\text{Hom}_{S}(S,T)=\text{Hom}_{S}(DT,DS)\in {\mathcal{B}}$. Hence,
$T=\text{Hom}_{S}(S,T)=\text{Hom}_{S}(DT,DS)\in {\mathcal{B}}$. Hence, ![]() $\text{add}_{\text{mod}R}T\subseteq {\mathcal{B}}$ too. Thus, we obtain that
$\text{add}_{\text{mod}R}T\subseteq {\mathcal{B}}$ too. Thus, we obtain that ![]() $\text{add}_{\text{mod}R}T\subseteq {\mathcal{B}}\bigcap {\mathcal{A}}$. Dually, one also has
$\text{add}_{\text{mod}R}T\subseteq {\mathcal{B}}\bigcap {\mathcal{A}}$. Dually, one also has ![]() $\text{add}_{\text{mod}S}DT\subseteq {\mathcal{G}}\bigcap {\mathcal{K}}$.
$\text{add}_{\text{mod}S}DT\subseteq {\mathcal{G}}\bigcap {\mathcal{K}}$.
Clearly, ![]() ${\mathcal{B}}=\text{KerExt}_{R}^{1}(-,{\mathcal{A}})=\text{KerExt}_{R}^{{\geqslant}1}(-,{\mathcal{A}})\subseteq \text{KerExt}_{R}^{{\geqslant}1}(-,T)$ follows from
${\mathcal{B}}=\text{KerExt}_{R}^{1}(-,{\mathcal{A}})=\text{KerExt}_{R}^{{\geqslant}1}(-,{\mathcal{A}})\subseteq \text{KerExt}_{R}^{{\geqslant}1}(-,T)$ follows from ![]() $\text{add}_{\text{mod}R}T\subseteq {\mathcal{B}}\bigcap {\mathcal{A}}$ and the fact that
$\text{add}_{\text{mod}R}T\subseteq {\mathcal{B}}\bigcap {\mathcal{A}}$ and the fact that ![]() $({\mathcal{B}},{\mathcal{A}})$ is a hereditary cotorsion pair. Take any
$({\mathcal{B}},{\mathcal{A}})$ is a hereditary cotorsion pair. Take any ![]() $B\in {\mathcal{B}}$, then
$B\in {\mathcal{B}}$, then ![]() $B\otimes _{R}DT\in {\mathcal{K}}$. Take an exact sequence
$B\otimes _{R}DT\in {\mathcal{K}}$. Take an exact sequence ![]() $0\rightarrow B\otimes _{R}DT\rightarrow I\rightarrow Y\rightarrow 0$ with
$0\rightarrow B\otimes _{R}DT\rightarrow I\rightarrow Y\rightarrow 0$ with ![]() $I\in \text{inj}S=\text{add}_{\text{mod}S}DS$. Since
$I\in \text{inj}S=\text{add}_{\text{mod}S}DS$. Since ![]() ${\mathcal{K}}$ is coresolving, we have that
${\mathcal{K}}$ is coresolving, we have that ![]() $I,Y\in {\mathcal{K}}$ too. Applying the functor
$I,Y\in {\mathcal{K}}$ too. Applying the functor ![]() $\text{Hom}_{S}(DT,-)$, we obtain an induced exact sequence
$\text{Hom}_{S}(DT,-)$, we obtain an induced exact sequence ![]() $0\rightarrow \text{Hom}_{S}(DT,B\otimes _{R}DT)\rightarrow \text{Hom}_{S}(DT,I)\rightarrow \text{Hom}_{S}(DT,Y)\rightarrow 0$ since
$0\rightarrow \text{Hom}_{S}(DT,B\otimes _{R}DT)\rightarrow \text{Hom}_{S}(DT,I)\rightarrow \text{Hom}_{S}(DT,Y)\rightarrow 0$ since ![]() ${\mathcal{K}}=\text{KerExt}_{S}^{1}({\mathcal{G}},-)\subseteq \text{KerExt}_{S}^{1}(DT,-)$ by the fact that
${\mathcal{K}}=\text{KerExt}_{S}^{1}({\mathcal{G}},-)\subseteq \text{KerExt}_{S}^{1}(DT,-)$ by the fact that ![]() $DT\in {\mathcal{G}}$. Note that
$DT\in {\mathcal{G}}$. Note that ![]() $B\simeq \text{Hom}_{S}(DT,B\otimes _{R}DT)$,
$B\simeq \text{Hom}_{S}(DT,B\otimes _{R}DT)$, ![]() $\text{Hom}_{S}(DT,I)\in \text{add}_{\text{mod}R}T$ and
$\text{Hom}_{S}(DT,I)\in \text{add}_{\text{mod}R}T$ and ![]() $\text{Hom}_{S}(DT,Y)\in {\mathcal{B}}$, so one can easily see that
$\text{Hom}_{S}(DT,Y)\in {\mathcal{B}}$, so one can easily see that ![]() $B\in {\mathcal{X}}_{T}$. Thus,
$B\in {\mathcal{X}}_{T}$. Thus, ![]() ${\mathcal{B}}\subseteq {\mathcal{X}}_{T}$. By the equivalence in Proposition 3.1(3), we also obtain that
${\mathcal{B}}\subseteq {\mathcal{X}}_{T}$. By the equivalence in Proposition 3.1(3), we also obtain that ![]() ${\mathcal{K}}\subseteq _{DT}{\mathcal{X}}$.
${\mathcal{K}}\subseteq _{DT}{\mathcal{X}}$.
Now considering the Wakamatsu-tilting module ![]() $_{R}DT_{S}$ and applying the above result, we can obtain that
$_{R}DT_{S}$ and applying the above result, we can obtain that ![]() ${\mathcal{G}}\subseteq {\mathcal{X}}_{DT}$ and that
${\mathcal{G}}\subseteq {\mathcal{X}}_{DT}$ and that ![]() ${\mathcal{A}}\subseteq _{T}{\mathcal{X}}$.
${\mathcal{A}}\subseteq _{T}{\mathcal{X}}$.
(2) If ![]() $X\in {\mathcal{B}}\bigcap {\mathcal{A}}$, then
$X\in {\mathcal{B}}\bigcap {\mathcal{A}}$, then ![]() $X\in {\mathcal{B}}$. Following the proof of (1), we obtain that there is an exact sequence
$X\in {\mathcal{B}}$. Following the proof of (1), we obtain that there is an exact sequence ![]() $0\rightarrow X\rightarrow T_{X}\rightarrow X^{\prime }\rightarrow 0$ with
$0\rightarrow X\rightarrow T_{X}\rightarrow X^{\prime }\rightarrow 0$ with ![]() $T_{X}\in \text{add}_{\text{mod}R}T$ and
$T_{X}\in \text{add}_{\text{mod}R}T$ and ![]() $X^{\prime }\in {\mathcal{B}}$. Since
$X^{\prime }\in {\mathcal{B}}$. Since ![]() $X\in {\mathcal{A}}$ too, we have that
$X\in {\mathcal{A}}$ too, we have that ![]() $\text{Ext}_{R}^{1}(X^{\prime },X)=0$. It follows that the exact sequence splits. Hence,
$\text{Ext}_{R}^{1}(X^{\prime },X)=0$. It follows that the exact sequence splits. Hence, ![]() $X\in \text{add}_{\text{mod}R}T$. Together with the first claim in the proof of (1), we obtain that
$X\in \text{add}_{\text{mod}R}T$. Together with the first claim in the proof of (1), we obtain that ![]() $\text{add}_{\text{mod}R}T={\mathcal{B}}\bigcap {\mathcal{A}}$. Dually, we also have that
$\text{add}_{\text{mod}R}T={\mathcal{B}}\bigcap {\mathcal{A}}$. Dually, we also have that ![]() $\text{add}_{\text{mod}S}DT={\mathcal{G}}\bigcap {\mathcal{K}}$.◻
$\text{add}_{\text{mod}S}DT={\mathcal{G}}\bigcap {\mathcal{K}}$.◻
3.2.3
Recall that a subcategory ![]() ${\mathcal{A}}\subseteq \text{mod}R$ is covariantly finite (or a preenveloping class) if for any
${\mathcal{A}}\subseteq \text{mod}R$ is covariantly finite (or a preenveloping class) if for any ![]() $X\in \text{mod}R$, there is an object
$X\in \text{mod}R$, there is an object ![]() $A_{X}\in {\mathcal{A}}$ and a homomorphism
$A_{X}\in {\mathcal{A}}$ and a homomorphism ![]() $u_{_{X}}:X\rightarrow A_{X}$ such that
$u_{_{X}}:X\rightarrow A_{X}$ such that ![]() $\text{Hom}_{R}(u_{_{X}},A)$ is surjective for any object
$\text{Hom}_{R}(u_{_{X}},A)$ is surjective for any object ![]() $A\in {\mathcal{A}}$; see, for instance, [Reference Auslander and Reiten3]. Dually, a subcategory
$A\in {\mathcal{A}}$; see, for instance, [Reference Auslander and Reiten3]. Dually, a subcategory ![]() ${\mathcal{B}}\subseteq \text{mod}R$ is contravariantly finite (or a precovering class) if for any
${\mathcal{B}}\subseteq \text{mod}R$ is contravariantly finite (or a precovering class) if for any ![]() $X\in \text{mod}R$, there is an object
$X\in \text{mod}R$, there is an object ![]() $B_{X}\in {\mathcal{B}}$ and a homomorphism
$B_{X}\in {\mathcal{B}}$ and a homomorphism ![]() $v_{X}:B_{X}\rightarrow X$ such that
$v_{X}:B_{X}\rightarrow X$ such that ![]() $\text{Hom}_{R}(B,v_{X})$ is surjective for any object
$\text{Hom}_{R}(B,v_{X})$ is surjective for any object ![]() $B\in {\mathcal{B}}$.
$B\in {\mathcal{B}}$.
A cotorsion pair ![]() $({\mathcal{B}},{\mathcal{A}})$ is complete if and only if
$({\mathcal{B}},{\mathcal{A}})$ is complete if and only if ![]() ${\mathcal{A}}$ is covariantly finite, if and only if
${\mathcal{A}}$ is covariantly finite, if and only if ![]() ${\mathcal{B}}$ is contravariantly finite; see [Reference Auslander and Reiten3, Proposition 1.9].
${\mathcal{B}}$ is contravariantly finite; see [Reference Auslander and Reiten3, Proposition 1.9].
Let ![]() ${\mathcal{A}}$ be a subcategory of
${\mathcal{A}}$ be a subcategory of ![]() $\text{mod}R$. An
$\text{mod}R$. An ![]() $R$-module
$R$-module ![]() $T$ is said to be Ext-projective in
$T$ is said to be Ext-projective in ![]() ${\mathcal{A}}$ if
${\mathcal{A}}$ if ![]() $T\in {\mathcal{A}}\bigcap \text{KerExt}_{R}^{1}(-,{\mathcal{A}})$. Moreover, it is said to be an Ext-projective generator in
$T\in {\mathcal{A}}\bigcap \text{KerExt}_{R}^{1}(-,{\mathcal{A}})$. Moreover, it is said to be an Ext-projective generator in ![]() ${\mathcal{A}}$ if, for any
${\mathcal{A}}$ if, for any ![]() $A\in {\mathcal{A}}$, there exists an exact sequence
$A\in {\mathcal{A}}$, there exists an exact sequence ![]() $0\rightarrow A^{\prime }\rightarrow T_{A}\rightarrow A\rightarrow 0$ with
$0\rightarrow A^{\prime }\rightarrow T_{A}\rightarrow A\rightarrow 0$ with ![]() $T_{A}\in \text{add}_{\text{mod}R}T$ and
$T_{A}\in \text{add}_{\text{mod}R}T$ and ![]() $A^{\prime }\in {\mathcal{A}}$. Dually, an
$A^{\prime }\in {\mathcal{A}}$. Dually, an ![]() $R$-module
$R$-module ![]() $T$ is said to be an Ext-injective cogenerator in
$T$ is said to be an Ext-injective cogenerator in ![]() ${\mathcal{A}}$ if
${\mathcal{A}}$ if ![]() $T\in {\mathcal{A}}\bigcap \text{KerExt}_{R}^{1}({\mathcal{A}},-)$ and, for any
$T\in {\mathcal{A}}\bigcap \text{KerExt}_{R}^{1}({\mathcal{A}},-)$ and, for any ![]() $A\in {\mathcal{A}}$, there exists an exact sequence
$A\in {\mathcal{A}}$, there exists an exact sequence ![]() $0\rightarrow A\rightarrow T_{A}\rightarrow A^{\prime }\rightarrow 0$ with
$0\rightarrow A\rightarrow T_{A}\rightarrow A^{\prime }\rightarrow 0$ with ![]() $T_{A}\in \text{add}_{\text{mod}R}T$ and
$T_{A}\in \text{add}_{\text{mod}R}T$ and ![]() $A^{\prime }\in {\mathcal{A}}$.
$A^{\prime }\in {\mathcal{A}}$.
Lemma.
Let ![]() ${\mathcal{A}}$ be a subcategory closed under extensions and direct summands.
${\mathcal{A}}$ be a subcategory closed under extensions and direct summands.
(1) Assume that
 ${\mathcal{A}}$ has an Ext-projective generator
${\mathcal{A}}$ has an Ext-projective generator  $T$. If
$T$. If  $0\rightarrow X\rightarrow Y\rightarrow Z\rightarrow 0$ is an exact sequence which stays exact after applying the functor
$0\rightarrow X\rightarrow Y\rightarrow Z\rightarrow 0$ is an exact sequence which stays exact after applying the functor  $\text{Hom}_{R}(T,-)$, where
$\text{Hom}_{R}(T,-)$, where  $Y,Z\in {\mathcal{A}}$, then
$Y,Z\in {\mathcal{A}}$, then  $X\in {\mathcal{A}}$ too.
$X\in {\mathcal{A}}$ too.(2) Assume that
 ${\mathcal{A}}$ has an Ext-injective cogenerator
${\mathcal{A}}$ has an Ext-injective cogenerator  $T$. If
$T$. If  $0\rightarrow X\rightarrow Y\rightarrow Z\rightarrow 0$ is an exact sequence which stays exact after applying the functor
$0\rightarrow X\rightarrow Y\rightarrow Z\rightarrow 0$ is an exact sequence which stays exact after applying the functor  $\text{Hom}_{R}(-,T)$, where
$\text{Hom}_{R}(-,T)$, where  $X,Y\in {\mathcal{A}}$, then
$X,Y\in {\mathcal{A}}$, then  $Z\in {\mathcal{A}}$ too.
$Z\in {\mathcal{A}}$ too.
Proof. (1) By the assumptions, we can construct the following commutative diagram, where ![]() $T_{Z}\in \text{add}_{\text{mod}R}T$ and
$T_{Z}\in \text{add}_{\text{mod}R}T$ and ![]() $Z^{\prime }\in {\mathcal{A}}$:
$Z^{\prime }\in {\mathcal{A}}$:

Since ![]() ${\mathcal{A}}$ is closed under extensions and direct summands, we have that
${\mathcal{A}}$ is closed under extensions and direct summands, we have that ![]() $X\in {\mathcal{A}}$ from the middle column.
$X\in {\mathcal{A}}$ from the middle column.
(2) Dually. ◻
3.2.4
Lemma.
Let ![]() $T$ be a Wakamatsu-tilting
$T$ be a Wakamatsu-tilting ![]() $R$-module,
$R$-module, ![]() $S=\text{End}(T_{R})^{op}$. Assume that
$S=\text{End}(T_{R})^{op}$. Assume that ![]() $\text{Hom}_{R}(T,-):{\mathcal{A}}_{\longleftarrow }^{\longrightarrow }{\mathcal{G}}:-\!\otimes _{S}T$ define an equivalence. Then the following are equivalent:
$\text{Hom}_{R}(T,-):{\mathcal{A}}_{\longleftarrow }^{\longrightarrow }{\mathcal{G}}:-\!\otimes _{S}T$ define an equivalence. Then the following are equivalent:
(1)
 ${\mathcal{A}}$ is coresolving and
${\mathcal{A}}$ is coresolving and  $T$ is an Ext-projective generator in
$T$ is an Ext-projective generator in  ${\mathcal{A}}$.
${\mathcal{A}}$.(2)
 ${\mathcal{G}}$ is resolving and
${\mathcal{G}}$ is resolving and  $DT$ is an Ext-injective cogenerator in
$DT$ is an Ext-injective cogenerator in  ${\mathcal{G}}$.
${\mathcal{G}}$.
Proof. (1) ![]() $\Rightarrow$ (2) The condition that
$\Rightarrow$ (2) The condition that ![]() $T$ is an Ext-projective generator in
$T$ is an Ext-projective generator in ![]() ${\mathcal{A}}$ means that
${\mathcal{A}}$ means that ![]() $T\in {\mathcal{A}}\subseteq \text{KerExt}_{R}^{1}(T,-)$ and that every
$T\in {\mathcal{A}}\subseteq \text{KerExt}_{R}^{1}(T,-)$ and that every ![]() $A\in {\mathcal{A}}$ admits an exact sequence
$A\in {\mathcal{A}}$ admits an exact sequence ![]() $0\rightarrow A^{\prime }\rightarrow T_{A}\rightarrow A\rightarrow 0$ with
$0\rightarrow A^{\prime }\rightarrow T_{A}\rightarrow A\rightarrow 0$ with ![]() $T_{A}\in \text{add}_{\text{mod}R}T$ and
$T_{A}\in \text{add}_{\text{mod}R}T$ and ![]() $A^{\prime }\in {\mathcal{A}}$. This implies that
$A^{\prime }\in {\mathcal{A}}$. This implies that ![]() ${\mathcal{A}}\subseteq \text{KerExt}_{R}^{{\geqslant}1}(T,-)$. In particular,
${\mathcal{A}}\subseteq \text{KerExt}_{R}^{{\geqslant}1}(T,-)$. In particular, ![]() ${\mathcal{A}}\subseteq _{T}{\mathcal{X}}$.
${\mathcal{A}}\subseteq _{T}{\mathcal{X}}$.
Note that, for any ![]() $X\in {\mathcal{A}}$, there is an exact sequence
$X\in {\mathcal{A}}$, there is an exact sequence ![]() $0\rightarrow X\rightarrow I\rightarrow X^{\prime }\rightarrow 0$ with
$0\rightarrow X\rightarrow I\rightarrow X^{\prime }\rightarrow 0$ with ![]() $I\in \text{inj}R\subseteq {\mathcal{A}}$ and
$I\in \text{inj}R\subseteq {\mathcal{A}}$ and ![]() $X^{\prime }\in {\mathcal{A}}$ since
$X^{\prime }\in {\mathcal{A}}$ since ![]() ${\mathcal{A}}$ is coresolving. Applying the functor
${\mathcal{A}}$ is coresolving. Applying the functor ![]() $\text{Hom}_{R}(T,-)$, we have an exact sequence
$\text{Hom}_{R}(T,-)$, we have an exact sequence ![]() $0\rightarrow \text{Hom}_{R}(T,X)\rightarrow \text{Hom}_{R}(T,I)\rightarrow \text{Hom}_{R}(T,X^{\prime })\rightarrow 0$. Since
$0\rightarrow \text{Hom}_{R}(T,X)\rightarrow \text{Hom}_{R}(T,I)\rightarrow \text{Hom}_{R}(T,X^{\prime })\rightarrow 0$. Since ![]() $\text{Hom}_{R}(T,I)\in \text{add}_{\text{mod}S}DT$ and
$\text{Hom}_{R}(T,I)\in \text{add}_{\text{mod}S}DT$ and ![]() $\text{Ext}_{S}^{1}(\text{Hom}_{R}(T,X),DT)\simeq \text{Ext}_{S}^{1}(\text{Hom}_{R}(T,X),\text{Hom}_{R}(T,DR))=0$, we obtain that
$\text{Ext}_{S}^{1}(\text{Hom}_{R}(T,X),DT)\simeq \text{Ext}_{S}^{1}(\text{Hom}_{R}(T,X),\text{Hom}_{R}(T,DR))=0$, we obtain that ![]() $DT$ is an Ext-injective cogenerator in
$DT$ is an Ext-injective cogenerator in ![]() $\text{Hom}_{R}(T,{\mathcal{A}})={\mathcal{G}}$.
$\text{Hom}_{R}(T,{\mathcal{A}})={\mathcal{G}}$.
It is clear that ![]() ${\mathcal{G}}$ is closed under direct summands. Assume now there is an exact sequence
${\mathcal{G}}$ is closed under direct summands. Assume now there is an exact sequence ![]() $(\flat ):0\rightarrow X\rightarrow Y\stackrel{g}{\longrightarrow }Z\rightarrow 0$ with
$(\flat ):0\rightarrow X\rightarrow Y\stackrel{g}{\longrightarrow }Z\rightarrow 0$ with ![]() $Z\in {\mathcal{G}}$, then
$Z\in {\mathcal{G}}$, then ![]() $Z\in \text{Hom}_{R}(T,{\mathcal{A}})\subseteq \text{KerTor}_{1}^{S}(-,T)$. Applying the functor
$Z\in \text{Hom}_{R}(T,{\mathcal{A}})\subseteq \text{KerTor}_{1}^{S}(-,T)$. Applying the functor ![]() $-\!\otimes _{S}T$, we obtain an induced exact sequence
$-\!\otimes _{S}T$, we obtain an induced exact sequence ![]() $(\flat \otimes _{S}T):0\rightarrow X\otimes _{S}T\rightarrow Y\otimes _{S}T\stackrel{g\otimes _{S}T}{\longrightarrow }Z\otimes _{S}T\rightarrow 0$.
$(\flat \otimes _{S}T):0\rightarrow X\otimes _{S}T\rightarrow Y\otimes _{S}T\stackrel{g\otimes _{S}T}{\longrightarrow }Z\otimes _{S}T\rightarrow 0$.
Assume first ![]() $X\in {\mathcal{G}}$ too, then
$X\in {\mathcal{G}}$ too, then ![]() $X\otimes _{S}T\in {\mathcal{A}}$. It follows that
$X\otimes _{S}T\in {\mathcal{A}}$. It follows that ![]() $Y\otimes _{S}T\in {\mathcal{A}}$ too since
$Y\otimes _{S}T\in {\mathcal{A}}$ too since ![]() ${\mathcal{A}}$ is closed under extensions. Note now that there is an exact sequence
${\mathcal{A}}$ is closed under extensions. Note now that there is an exact sequence ![]() $0\rightarrow \text{Hom}_{R}(T,X\otimes _{S}T)\rightarrow \text{Hom}_{R}(T,Y\otimes _{S}T)\rightarrow \text{Hom}_{R}(T,Z\otimes _{S}T)\rightarrow 0$, so we have that
$0\rightarrow \text{Hom}_{R}(T,X\otimes _{S}T)\rightarrow \text{Hom}_{R}(T,Y\otimes _{S}T)\rightarrow \text{Hom}_{R}(T,Z\otimes _{S}T)\rightarrow 0$, so we have that ![]() $\text{Hom}_{R}(T,Y\otimes _{S}T)\simeq Y$ since
$\text{Hom}_{R}(T,Y\otimes _{S}T)\simeq Y$ since ![]() $\text{Hom}_{R}(T,X\otimes _{S}T)\simeq X$ and
$\text{Hom}_{R}(T,X\otimes _{S}T)\simeq X$ and ![]() $\text{Hom}_{R}(T,Z\otimes _{S}T)\simeq Z$. Thus,
$\text{Hom}_{R}(T,Z\otimes _{S}T)\simeq Z$. Thus, ![]() $Y\in \text{Hom}_{R}(T,{\mathcal{A}})={\mathcal{G}}$. This shows that
$Y\in \text{Hom}_{R}(T,{\mathcal{A}})={\mathcal{G}}$. This shows that ![]() ${\mathcal{G}}$ is closed under extensions.
${\mathcal{G}}$ is closed under extensions.
Assume now ![]() $Y\in {\mathcal{G}}$, then
$Y\in {\mathcal{G}}$, then ![]() $\text{Hom}_{R}(T,g\otimes _{S}T)\simeq g$. In particular, we have that
$\text{Hom}_{R}(T,g\otimes _{S}T)\simeq g$. In particular, we have that ![]() $\text{Hom}_{R}(T,X\otimes _{S}T)\simeq X$ and the homomorphism
$\text{Hom}_{R}(T,X\otimes _{S}T)\simeq X$ and the homomorphism ![]() $\text{Hom}_{R}(T,g\otimes _{S}T)$ is surjective. It follows that the exact sequence
$\text{Hom}_{R}(T,g\otimes _{S}T)$ is surjective. It follows that the exact sequence ![]() $(\flat \otimes _{S}T)$ stays exact after applying the functor
$(\flat \otimes _{S}T)$ stays exact after applying the functor ![]() $\text{Hom}_{R}(T,-)$. By Lemma 3.2.3, we obtain that
$\text{Hom}_{R}(T,-)$. By Lemma 3.2.3, we obtain that ![]() $X\otimes _{S}T\in {\mathcal{A}}$. Hence,
$X\otimes _{S}T\in {\mathcal{A}}$. Hence, ![]() $X\in \text{Hom}_{R}(T,{\mathcal{A}})={\mathcal{G}}$. This shows that
$X\in \text{Hom}_{R}(T,{\mathcal{A}})={\mathcal{G}}$. This shows that ![]() ${\mathcal{G}}$ is closed under kernels of epimorphisms. Then we see that
${\mathcal{G}}$ is closed under kernels of epimorphisms. Then we see that ![]() ${\mathcal{G}}$ is resolving.
${\mathcal{G}}$ is resolving.
(2) ![]() $\Rightarrow$ (1) Dually.◻
$\Rightarrow$ (1) Dually.◻
3.2.5
Proposition.
Let ![]() $_{S}T_{R}$ be a Wakamatsu-tilting module. Assume that
$_{S}T_{R}$ be a Wakamatsu-tilting module. Assume that ![]() $({\mathcal{B}},{\mathcal{A}})$ is a hereditary cotorsion pair in
$({\mathcal{B}},{\mathcal{A}})$ is a hereditary cotorsion pair in ![]() $\text{mod}R$ and that
$\text{mod}R$ and that ![]() $T$ is an Ext-projective generator in
$T$ is an Ext-projective generator in ![]() ${\mathcal{A}}$, then
${\mathcal{A}}$, then ![]() $(\text{Hom}_{R}(T,{\mathcal{A}}),{\mathcal{B}}\otimes _{R}DT)$ is a hereditary cotorsion pair in
$(\text{Hom}_{R}(T,{\mathcal{A}}),{\mathcal{B}}\otimes _{R}DT)$ is a hereditary cotorsion pair in ![]() $\text{mod}S$. In particular, the bimodules
$\text{mod}S$. In particular, the bimodules ![]() $_{S}T_{R}$ and
$_{S}T_{R}$ and ![]() $_{R}DT_{S}$ represent a cotorsion pair counter equivalence between
$_{R}DT_{S}$ represent a cotorsion pair counter equivalence between ![]() $({\mathcal{B}},{\mathcal{A}})$ and
$({\mathcal{B}},{\mathcal{A}})$ and ![]() $(\text{Hom}_{R}(T,{\mathcal{A}}),{\mathcal{B}}\otimes _{R}DT)$ in this case.
$(\text{Hom}_{R}(T,{\mathcal{A}}),{\mathcal{B}}\otimes _{R}DT)$ in this case.
Proof. Since ![]() $T$ is an Ext-projective generator in
$T$ is an Ext-projective generator in ![]() ${\mathcal{A}}$, we see that
${\mathcal{A}}$, we see that ![]() $T\in \text{KerExt}_{R}^{1}(-,{\mathcal{A}})\bigcap {\mathcal{A}}={\mathcal{B}}\bigcap {\mathcal{A}}$ and that, for any
$T\in \text{KerExt}_{R}^{1}(-,{\mathcal{A}})\bigcap {\mathcal{A}}={\mathcal{B}}\bigcap {\mathcal{A}}$ and that, for any ![]() $A\in {\mathcal{A}}$, there is an exact sequence
$A\in {\mathcal{A}}$, there is an exact sequence ![]() $0\rightarrow A^{\prime }\rightarrow T_{A}\rightarrow A\rightarrow 0$ with
$0\rightarrow A^{\prime }\rightarrow T_{A}\rightarrow A\rightarrow 0$ with ![]() $T_{A}\in \text{add}_{\text{mod}R}T$ and
$T_{A}\in \text{add}_{\text{mod}R}T$ and ![]() $A^{\prime }\in {\mathcal{A}}$. In particular, for any
$A^{\prime }\in {\mathcal{A}}$. In particular, for any ![]() $X\in {\mathcal{A}}\bigcap {\mathcal{B}}$, there is an exact sequence
$X\in {\mathcal{A}}\bigcap {\mathcal{B}}$, there is an exact sequence ![]() $0\rightarrow X^{\prime }\rightarrow T_{X}\rightarrow X\rightarrow 0$ with
$0\rightarrow X^{\prime }\rightarrow T_{X}\rightarrow X\rightarrow 0$ with ![]() $T_{X}\in \text{add}_{\text{mod}R}T$ and
$T_{X}\in \text{add}_{\text{mod}R}T$ and ![]() $X^{\prime }\in {\mathcal{A}}$, which is clearly split. Hence,
$X^{\prime }\in {\mathcal{A}}$, which is clearly split. Hence, ![]() $X\in \text{add}_{\text{mod}R}T$. It follows that
$X\in \text{add}_{\text{mod}R}T$. It follows that ![]() $\text{add}_{\text{mod}R}T={\mathcal{B}}\bigcap {\mathcal{A}}$. Moreover, by an argument similar to the one used in the proof of [Reference Mantese and Reiten22, Proposition 2.13(b)], we have that
$\text{add}_{\text{mod}R}T={\mathcal{B}}\bigcap {\mathcal{A}}$. Moreover, by an argument similar to the one used in the proof of [Reference Mantese and Reiten22, Proposition 2.13(b)], we have that ![]() $T$ is also an Ext-injective cogenerator in
$T$ is also an Ext-injective cogenerator in ![]() ${\mathcal{B}}$. Note that these facts imply that
${\mathcal{B}}$. Note that these facts imply that ![]() ${\mathcal{A}}\subseteq _{T}{\mathcal{X}}$ and that
${\mathcal{A}}\subseteq _{T}{\mathcal{X}}$ and that ![]() ${\mathcal{B}}\subseteq {\mathcal{X}}_{T}$. In particular,
${\mathcal{B}}\subseteq {\mathcal{X}}_{T}$. In particular, ![]() $\text{Hom}_{R}(T,-):{\mathcal{A}}_{\longleftarrow }^{\longrightarrow }\text{Hom}_{R}(T,{\mathcal{A}}):-\!\otimes _{S}T$ define an equivalence and
$\text{Hom}_{R}(T,-):{\mathcal{A}}_{\longleftarrow }^{\longrightarrow }\text{Hom}_{R}(T,{\mathcal{A}}):-\!\otimes _{S}T$ define an equivalence and ![]() $\text{Hom}_{S}(DT,-):{\mathcal{B}}\otimes _{R}DT_{\longleftarrow }^{\longrightarrow }{\mathcal{B}}:-\!\otimes _{R}DT$ define an equivalence, by Proposition 2.1.1.
$\text{Hom}_{S}(DT,-):{\mathcal{B}}\otimes _{R}DT_{\longleftarrow }^{\longrightarrow }{\mathcal{B}}:-\!\otimes _{R}DT$ define an equivalence, by Proposition 2.1.1.
The above arguments, in particular, show that Lemma 3.2.4 can be applied to ![]() ${\mathcal{A}}$ (considering the Wakamatsu-tilting bimodule
${\mathcal{A}}$ (considering the Wakamatsu-tilting bimodule ![]() $_{S}T_{R}$) and
$_{S}T_{R}$) and ![]() ${\mathcal{B}}$ (considering the Wakamatsu-tilting bimodule
${\mathcal{B}}$ (considering the Wakamatsu-tilting bimodule ![]() $_{R}DT_{S}$); thus, we see that
$_{R}DT_{S}$); thus, we see that ![]() $\text{Hom}_{R}(T,{\mathcal{A}})$ is resolving and that
$\text{Hom}_{R}(T,{\mathcal{A}})$ is resolving and that ![]() ${\mathcal{B}}\otimes _{R}DT$ is coresolving. It is also clear that the bimodules
${\mathcal{B}}\otimes _{R}DT$ is coresolving. It is also clear that the bimodules ![]() $_{S}T_{R}$ and
$_{S}T_{R}$ and ![]() $_{R}DT_{S}$ represent a counter equivalence between two pairs
$_{R}DT_{S}$ represent a counter equivalence between two pairs ![]() $({\mathcal{B}},{\mathcal{A}})$ and
$({\mathcal{B}},{\mathcal{A}})$ and ![]() $(\text{Hom}_{R}(T,{\mathcal{A}}),{\mathcal{B}}\otimes _{R}DT)$, by assumptions. So, it just remains to show that
$(\text{Hom}_{R}(T,{\mathcal{A}}),{\mathcal{B}}\otimes _{R}DT)$, by assumptions. So, it just remains to show that ![]() $(\text{Hom}_{R}(T,{\mathcal{A}}),{\mathcal{B}}\otimes _{R}DT)$ is a cotorsion pair.
$(\text{Hom}_{R}(T,{\mathcal{A}}),{\mathcal{B}}\otimes _{R}DT)$ is a cotorsion pair.
We divide the remaining proof into three steps.
Step 1. ![]() $\text{Ext}_{S}^{i}(\text{Hom}_{R}(T,A),B\otimes _{R}DT)=0$, for any
$\text{Ext}_{S}^{i}(\text{Hom}_{R}(T,A),B\otimes _{R}DT)=0$, for any ![]() $A\in {\mathcal{A}}$ and any
$A\in {\mathcal{A}}$ and any ![]() $B\in {\mathcal{B}}$ and for any
$B\in {\mathcal{B}}$ and for any ![]() $i\geqslant 0$.
$i\geqslant 0$.
Note that there is a natural isomorphism
It induces a natural isomorphism, for any ![]() $S_{i}\in \text{add}_{\text{mod}S}S$,
$S_{i}\in \text{add}_{\text{mod}S}S$,
Now take ![]() $A\in {\mathcal{A}}$; since
$A\in {\mathcal{A}}$; since ![]() $T$ is an Ext-projective generator, there is a long exact sequence
$T$ is an Ext-projective generator, there is a long exact sequence
where each ![]() $T_{i}\in \text{add}_{\text{mod}R}T$ and each image in
$T_{i}\in \text{add}_{\text{mod}R}T$ and each image in ![]() ${\mathcal{A}}$. Here we consider the sequence (†) as a (cochain) complex with the term
${\mathcal{A}}$. Here we consider the sequence (†) as a (cochain) complex with the term ![]() $A$ at the first position.
$A$ at the first position.
Since ![]() $B\in \text{KerExt}_{R}^{1}(-,{\mathcal{A}})$, we have the following induced exact sequence
$B\in \text{KerExt}_{R}^{1}(-,{\mathcal{A}})$, we have the following induced exact sequence ![]() $\text{Hom}_{R}(B,\dagger )$:
$\text{Hom}_{R}(B,\dagger )$:
On the other hand, by applying the functor ![]() $D\text{Hom}_{S}(\text{Hom}_{R}(T,-),B\otimes _{R}DT)$, we have a complex
$D\text{Hom}_{S}(\text{Hom}_{R}(T,-),B\otimes _{R}DT)$, we have a complex ![]() $D\text{Hom}_{S}(\text{Hom}_{R}(T,\dagger ),B\otimes _{R}DT)$:
$D\text{Hom}_{S}(\text{Hom}_{R}(T,\dagger ),B\otimes _{R}DT)$:
Since ![]() $\text{Hom}_{R}(T,\dagger )$ is exact, the functor
$\text{Hom}_{R}(T,\dagger )$ is exact, the functor ![]() $D\text{Hom}_{S}(\text{Hom}_{R}(T,-),B\otimes _{R}DT)$ is right exact. By the above isomorphism (¶), we obtain the following isomorphisms of complexes:
$D\text{Hom}_{S}(\text{Hom}_{R}(T,-),B\otimes _{R}DT)$ is right exact. By the above isomorphism (¶), we obtain the following isomorphisms of complexes:
But the later is exact, so we obtain that, for ![]() $i\geqslant 1$,
$i\geqslant 1$,
Thus, Step 1 is established. In particular, we obtain that ![]() $\text{Hom}_{R}(T,{\mathcal{A}})\subseteq \text{KerExt}_{S}^{1}(-,{\mathcal{B}}\otimes _{R}DT)$ and that
$\text{Hom}_{R}(T,{\mathcal{A}})\subseteq \text{KerExt}_{S}^{1}(-,{\mathcal{B}}\otimes _{R}DT)$ and that ![]() ${\mathcal{B}}\otimes _{R}DT\subseteq \text{KerExt}_{S}^{1}(\text{Hom}_{R}(T,{\mathcal{A}}),-)$ due to the arbitrarity of
${\mathcal{B}}\otimes _{R}DT\subseteq \text{KerExt}_{S}^{1}(\text{Hom}_{R}(T,{\mathcal{A}}),-)$ due to the arbitrarity of ![]() $A\in {\mathcal{A}}$ and
$A\in {\mathcal{A}}$ and ![]() $B\in {\mathcal{B}}$.
$B\in {\mathcal{B}}$.
Step 2. ![]() $\text{KerExt}_{S}^{1}(-,{\mathcal{B}}\otimes _{R}DT)\subseteq \text{Hom}_{R}(T,{\mathcal{A}})$.
$\text{KerExt}_{S}^{1}(-,{\mathcal{B}}\otimes _{R}DT)\subseteq \text{Hom}_{R}(T,{\mathcal{A}})$.
Take any ![]() $Y\in \text{KerExt}_{S}^{1}(-,{\mathcal{B}}\otimes _{R}DT)$ and a projective resolution of
$Y\in \text{KerExt}_{S}^{1}(-,{\mathcal{B}}\otimes _{R}DT)$ and a projective resolution of ![]() $Y$, where we consider as a (cochain) complex with the term
$Y$, where we consider as a (cochain) complex with the term ![]() $Y$ at the zeroth position:
$Y$ at the zeroth position:
Note that ![]() $DT=R\otimes _{R}DT\in {\mathcal{B}}\otimes _{R}DT$ and that
$DT=R\otimes _{R}DT\in {\mathcal{B}}\otimes _{R}DT$ and that ![]() ${\mathcal{B}}\otimes _{R}DT$ is coresolving, so we obtain that
${\mathcal{B}}\otimes _{R}DT$ is coresolving, so we obtain that
Then we have an induced exact sequence:
For any ![]() $B\in {\mathcal{B}}$, applying the left exact functor
$B\in {\mathcal{B}}$, applying the left exact functor ![]() $\text{Hom}_{R}(B,-)$, we obtain a complex
$\text{Hom}_{R}(B,-)$, we obtain a complex ![]() $\text{Hom}_{R}(B,\sharp \otimes _{S}T)$:
$\text{Hom}_{R}(B,\sharp \otimes _{S}T)$:
Applying the right exact functor ![]() $D\text{Hom}_{S}(-,B\otimes _{R}DT)$ to the sequence (♯), we obtain a complex
$D\text{Hom}_{S}(-,B\otimes _{R}DT)$ to the sequence (♯), we obtain a complex ![]() $D\text{Hom}_{S}(\sharp ,B\otimes _{R}DT)$:
$D\text{Hom}_{S}(\sharp ,B\otimes _{R}DT)$:
which is indeed exact since ![]() $S_{i},Y\in \text{KerExt}_{S}^{{>}0}(-,{\mathcal{B}}\otimes _{R}DT)$.
$S_{i},Y\in \text{KerExt}_{S}^{{>}0}(-,{\mathcal{B}}\otimes _{R}DT)$.
By the natural isomorphism (¶) in Step 1 again, we have isomorphisms of truncated complexes
where ![]() $(-)^{{<}0}$ denotes the truncated complex of a complex by replacing the
$(-)^{{<}0}$ denotes the truncated complex of a complex by replacing the ![]() $i$th term with
$i$th term with ![]() $0$ for all
$0$ for all ![]() $i\geqslant 0$.
$i\geqslant 0$.
Since ![]() $B\in \text{KerExt}_{R}^{1}(-,S_{i}\otimes _{S}T)$ and
$B\in \text{KerExt}_{R}^{1}(-,S_{i}\otimes _{S}T)$ and ![]() $\text{Hom}_{R}(B,-)$ is left exact, we obtain that, for
$\text{Hom}_{R}(B,-)$ is left exact, we obtain that, for ![]() $i\geqslant 4$,
$i\geqslant 4$, ![]() $\text{Ext}_{R}^{1}(B,Y_{i}\otimes _{S}T)\simeq \text{H}^{-i+2}(\text{Hom}_{R}(B,\sharp \otimes _{S}T))$, where
$\text{Ext}_{R}^{1}(B,Y_{i}\otimes _{S}T)\simeq \text{H}^{-i+2}(\text{Hom}_{R}(B,\sharp \otimes _{S}T))$, where ![]() $Y_{i}=\text{Im}f_{i}$. But the latter homology is 0 by the above isomorphism of truncated complexes and by the fact that the complex
$Y_{i}=\text{Im}f_{i}$. But the latter homology is 0 by the above isomorphism of truncated complexes and by the fact that the complex ![]() $D\text{Hom}_{S}(\sharp ,B\otimes _{R}DT)$ is exact. This shows that
$D\text{Hom}_{S}(\sharp ,B\otimes _{R}DT)$ is exact. This shows that ![]() $Y_{i}\otimes _{S}T\in \text{KerExt}_{R}^{1}({\mathcal{B}},-)={\mathcal{A}}$, for all
$Y_{i}\otimes _{S}T\in \text{KerExt}_{R}^{1}({\mathcal{B}},-)={\mathcal{A}}$, for all ![]() $i\geqslant 4$.
$i\geqslant 4$.
Now consider the exact sequence obtained from (♯ ⊗ST):
As also each ![]() $S_{i}\otimes _{S}T\in \text{add}_{\text{mod}R}T\subseteq {\mathcal{A}}$ and
$S_{i}\otimes _{S}T\in \text{add}_{\text{mod}R}T\subseteq {\mathcal{A}}$ and ![]() ${\mathcal{A}}$ is coresolving, we obtain that each
${\mathcal{A}}$ is coresolving, we obtain that each ![]() $Y_{i}\otimes _{S}T\in {\mathcal{A}}$, where
$Y_{i}\otimes _{S}T\in {\mathcal{A}}$, where ![]() $Y_{i}=\text{Im}f_{i}$ for
$Y_{i}=\text{Im}f_{i}$ for ![]() $0\leqslant i\leqslant 3$. Thus, the exact sequence
$0\leqslant i\leqslant 3$. Thus, the exact sequence ![]() $\sharp \otimes _{S}T$ is indeed in
$\sharp \otimes _{S}T$ is indeed in ![]() ${\mathcal{A}}$. Then we have an induced exact sequence
${\mathcal{A}}$. Then we have an induced exact sequence ![]() $\text{Hom}_{R}(T,\sharp \otimes _{S}T)$:
$\text{Hom}_{R}(T,\sharp \otimes _{S}T)$:
Since ![]() $S_{i}\simeq \text{Hom}_{R}(T,S_{i}\otimes _{S}T)$ for each
$S_{i}\simeq \text{Hom}_{R}(T,S_{i}\otimes _{S}T)$ for each ![]() $i$, it follows that
$i$, it follows that
This shows that ![]() $\text{KerExt}_{S}^{1}(-,{\mathcal{B}}\otimes _{R}DT)\subseteq \text{Hom}_{R}(T,{\mathcal{A}})$. Together with Step 1, we obtain that
$\text{KerExt}_{S}^{1}(-,{\mathcal{B}}\otimes _{R}DT)\subseteq \text{Hom}_{R}(T,{\mathcal{A}})$. Together with Step 1, we obtain that ![]() $\text{KerExt}_{S}^{1}(-,{\mathcal{B}}\otimes _{R}DT)=\text{Hom}_{R}(T,{\mathcal{A}})$.
$\text{KerExt}_{S}^{1}(-,{\mathcal{B}}\otimes _{R}DT)=\text{Hom}_{R}(T,{\mathcal{A}})$.
Step 3. ![]() $\text{KerExt}_{S}^{1}(\text{Hom}_{R}(T,{\mathcal{A}}),-)\subseteq {\mathcal{B}}\otimes _{R}DT$.
$\text{KerExt}_{S}^{1}(\text{Hom}_{R}(T,{\mathcal{A}}),-)\subseteq {\mathcal{B}}\otimes _{R}DT$.
Note that there is an isomorphism
for any ![]() $A\in \text{mod}R$ and that it induces an isomorphism
$A\in \text{mod}R$ and that it induces an isomorphism
for any ![]() $I_{i}\in \text{add}_{\text{mod}S}DS$.
$I_{i}\in \text{add}_{\text{mod}S}DS$.
Now take any ![]() $X\in \text{KerExt}_{S}^{1}(\text{Hom}_{R}(T,{\mathcal{A}}),-)$ and consider an injective resolution of
$X\in \text{KerExt}_{S}^{1}(\text{Hom}_{R}(T,{\mathcal{A}}),-)$ and consider an injective resolution of ![]() $X$:
$X$:
here, we consider (♮) as a (cochain) complex with the term ![]() $X$ at the zeroth position. Since
$X$ at the zeroth position. Since ![]() $DT\simeq \text{Hom}_{R}(T,DR)\in \text{Hom}_{R}(T,{\mathcal{A}})$ and
$DT\simeq \text{Hom}_{R}(T,DR)\in \text{Hom}_{R}(T,{\mathcal{A}})$ and ![]() $\text{Hom}_{R}(T,{\mathcal{A}})$ is resolving, we obtain that
$\text{Hom}_{R}(T,{\mathcal{A}})$ is resolving, we obtain that
Thus, for any ![]() $A\in {\mathcal{A}}$, applying the functor
$A\in {\mathcal{A}}$, applying the functor ![]() $\text{Hom}_{S}(\text{Hom}_{R}(T,A),-)$, we have an induced exact complex
$\text{Hom}_{S}(\text{Hom}_{R}(T,A),-)$, we have an induced exact complex ![]() $\text{Hom}_{S}(\text{Hom}_{R}(T,A),\natural )$:
$\text{Hom}_{S}(\text{Hom}_{R}(T,A),\natural )$:
On the other hand, by applying the functor ![]() $D\text{Hom}_{R}(\text{Hom}_{S}(DT,-),A)$, we also have the following induced complex
$D\text{Hom}_{R}(\text{Hom}_{S}(DT,-),A)$, we also have the following induced complex ![]() $D\text{Hom}_{R}(\text{Hom}_{S}(DT,\natural ),A)$:
$D\text{Hom}_{R}(\text{Hom}_{S}(DT,\natural ),A)$:
Since ![]() $\text{Hom}_{S}(DT,I_{i})\in \text{add}_{\text{mod}R}\text{Hom}_{S}(DT,DS)=\text{add}_{\text{mod}R}T$ and
$\text{Hom}_{S}(DT,I_{i})\in \text{add}_{\text{mod}R}\text{Hom}_{S}(DT,DS)=\text{add}_{\text{mod}R}T$ and ![]() $A\in \text{KerExt}_{R}^{1}(T,-)$ and since
$A\in \text{KerExt}_{R}^{1}(T,-)$ and since ![]() $\text{Hom}_{S}(DT,\natural )$ is exact and
$\text{Hom}_{S}(DT,\natural )$ is exact and ![]() $\text{Hom}_{R}(-,A)$ is left exact, we can obtain that, for any
$\text{Hom}_{R}(-,A)$ is left exact, we can obtain that, for any ![]() $i\geqslant 2$,
$i\geqslant 2$,
where ![]() $X_{i}:=\text{Im}g_{i}$. However, by the above-mentioned isomorphism
$X_{i}:=\text{Im}g_{i}$. However, by the above-mentioned isomorphism ![]() $(\ast )$ and the fact that
$(\ast )$ and the fact that ![]() $\text{Hom}_{S}(\text{Hom}_{R}(T,A),\natural )$ is exact, we further have that
$\text{Hom}_{S}(\text{Hom}_{R}(T,A),\natural )$ is exact, we further have that
It follows that ![]() $\text{Hom}_{S}(DT,X_{i+1})\in \text{KerExt}_{R}^{1}(-,{\mathcal{A}})={\mathcal{B}}$ for any
$\text{Hom}_{S}(DT,X_{i+1})\in \text{KerExt}_{R}^{1}(-,{\mathcal{A}})={\mathcal{B}}$ for any ![]() $i\geqslant 2$. Since
$i\geqslant 2$. Since ![]() ${\mathcal{B}}$ is resolving and
${\mathcal{B}}$ is resolving and ![]() $\text{Hom}_{S}(DT,I_{i})\in \text{add}_{\text{mod}R}T\subseteq {\mathcal{B}}$, we also obtain that each
$\text{Hom}_{S}(DT,I_{i})\in \text{add}_{\text{mod}R}T\subseteq {\mathcal{B}}$, we also obtain that each ![]() $\text{Hom}_{S}(DT,X_{i})\in {\mathcal{B}}$ for each
$\text{Hom}_{S}(DT,X_{i})\in {\mathcal{B}}$ for each ![]() $0\leqslant i\leqslant 2$, where
$0\leqslant i\leqslant 2$, where ![]() $X_{0}:=X$ and
$X_{0}:=X$ and ![]() $X_{i}:=\text{Im}g_{i}$ for
$X_{i}:=\text{Im}g_{i}$ for ![]() $i=1,2$, from the exact sequence
$i=1,2$, from the exact sequence
The above arguments show that the exact sequence ![]() $\text{Hom}_{S}(DT,\natural )$ is indeed in
$\text{Hom}_{S}(DT,\natural )$ is indeed in ![]() ${\mathcal{B}}$. Then we have an induced exact sequence
${\mathcal{B}}$. Then we have an induced exact sequence ![]() $\text{Hom}_{S}(DT,\natural )\otimes _{R}DT$ as follows since
$\text{Hom}_{S}(DT,\natural )\otimes _{R}DT$ as follows since ![]() ${\mathcal{B}}\subseteq \text{KerExt}_{R}^{1}(-,T)=\text{KerTor}_{1}^{R}(-,DT)$:
${\mathcal{B}}\subseteq \text{KerExt}_{R}^{1}(-,T)=\text{KerTor}_{1}^{R}(-,DT)$:
It follows that
since ![]() $I_{i}\simeq \text{Hom}_{S}(DT,I_{i})\otimes _{R}DT$ for each
$I_{i}\simeq \text{Hom}_{S}(DT,I_{i})\otimes _{R}DT$ for each ![]() $i$. This shows that
$i$. This shows that
Together with Step 1, we obtain that ![]() $\text{KerExt}_{S}^{1}(\text{Hom}_{R}(T,{\mathcal{A}}),-)={\mathcal{B}}\otimes _{R}DT$.
$\text{KerExt}_{S}^{1}(\text{Hom}_{R}(T,{\mathcal{A}}),-)={\mathcal{B}}\otimes _{R}DT$.
Altogether, we obtain that ![]() $(\text{Hom}_{R}(T,{\mathcal{A}}),{\mathcal{B}}\otimes _{R}DT)$ is a hereditary cotorsion pair.◻
$(\text{Hom}_{R}(T,{\mathcal{A}}),{\mathcal{B}}\otimes _{R}DT)$ is a hereditary cotorsion pair.◻
3.2.6
Corollary.
Let ![]() $T\in \text{mod}R$ be Wakamatsu-tilting with
$T\in \text{mod}R$ be Wakamatsu-tilting with ![]() $S=\text{End}(T_{R})^{op}$. Assume that the functor
$S=\text{End}(T_{R})^{op}$. Assume that the functor ![]() $\text{Hom}_{R}(T,-)$ gives an equivalence between a covariantly finite coresolving subcategory
$\text{Hom}_{R}(T,-)$ gives an equivalence between a covariantly finite coresolving subcategory ![]() ${\mathcal{A}}$ in
${\mathcal{A}}$ in ![]() $\text{mod}R$ and a contravariantly finite resolving subcategory
$\text{mod}R$ and a contravariantly finite resolving subcategory ![]() ${\mathcal{G}}$ in
${\mathcal{G}}$ in ![]() $\text{mod}S$. If
$\text{mod}S$. If ![]() $T$ is an Ext-projective generator in
$T$ is an Ext-projective generator in ![]() ${\mathcal{A}}$, then
${\mathcal{A}}$, then ![]() $T$ is a good Wakamatsu-tilting module.
$T$ is a good Wakamatsu-tilting module.
Proof. Since ![]() ${\mathcal{G}}$ is a contravariantly finite resolving subcategory in
${\mathcal{G}}$ is a contravariantly finite resolving subcategory in ![]() $\text{mod}S$, there is a cotorsion pair
$\text{mod}S$, there is a cotorsion pair ![]() $({\mathcal{G}},\text{KerExt}_{S}^{1}({\mathcal{G}},-))$ in
$({\mathcal{G}},\text{KerExt}_{S}^{1}({\mathcal{G}},-))$ in ![]() $\text{mod}S$, by [Reference Auslander and Reiten3, Proposition 1.10]. Dually, there is a cotorsion pair
$\text{mod}S$, by [Reference Auslander and Reiten3, Proposition 1.10]. Dually, there is a cotorsion pair ![]() $(\text{KerExt}_{R}^{1}(-,{\mathcal{A}}),{\mathcal{A}})$ in
$(\text{KerExt}_{R}^{1}(-,{\mathcal{A}}),{\mathcal{A}})$ in ![]() $\text{mod}R$ since
$\text{mod}R$ since ![]() ${\mathcal{A}}$ is a covariantly finite coresolving subcategory in
${\mathcal{A}}$ is a covariantly finite coresolving subcategory in ![]() $\text{mod}R$. Note that both cotorsion pairs are complete and hereditary by [Reference Auslander and Reiten3, Proposition 3.3 and the Remark after Proposition 3.4]. Since
$\text{mod}R$. Note that both cotorsion pairs are complete and hereditary by [Reference Auslander and Reiten3, Proposition 3.3 and the Remark after Proposition 3.4]. Since ![]() $T$ is an Ext-projective generator in
$T$ is an Ext-projective generator in ![]() ${\mathcal{A}}$, by Proposition 3.2.5, the bimodules
${\mathcal{A}}$, by Proposition 3.2.5, the bimodules ![]() $_{S}T_{R}$ and
$_{S}T_{R}$ and ![]() $_{R}DT_{S}$ represent a cotorsion pair counter equivalence between the above two cotorsion pairs. Hence,
$_{R}DT_{S}$ represent a cotorsion pair counter equivalence between the above two cotorsion pairs. Hence, ![]() $T$ is a good Wakamatsu-tilting module by the definition.◻
$T$ is a good Wakamatsu-tilting module by the definition.◻
4 The proof of main results
The whole section will be devoted to the proof of the two results mentioned in Section 1.
Let ![]() $R$ be an Artin algebra and
$R$ be an Artin algebra and ![]() $T$ be a good Wakamatsu-tilting module with
$T$ be a good Wakamatsu-tilting module with ![]() $S=\text{End}(T_{R})^{op}$. Then
$S=\text{End}(T_{R})^{op}$. Then ![]() $_{S}T_{R}$ is a good Wakamatsu-tilting bimodule. Assume that
$_{S}T_{R}$ is a good Wakamatsu-tilting bimodule. Assume that ![]() $({\mathcal{B}},{\mathcal{A}})$ is a complete hereditary cotorsion pair in
$({\mathcal{B}},{\mathcal{A}})$ is a complete hereditary cotorsion pair in ![]() $\text{mod}R$ and
$\text{mod}R$ and ![]() $({\mathcal{G}},{\mathcal{K}})$ is a complete hereditary cotorsion pair in
$({\mathcal{G}},{\mathcal{K}})$ is a complete hereditary cotorsion pair in ![]() $\text{mod}S$ such that the bimodules
$\text{mod}S$ such that the bimodules ![]() $_{S}T_{R}$ and
$_{S}T_{R}$ and ![]() $_{R}DT_{S}$ represent a cotorsion pair counter equivalence between these two cotorsion pairs.
$_{R}DT_{S}$ represent a cotorsion pair counter equivalence between these two cotorsion pairs.
The sketch of our proof of Theorem 1 is as follows.
First, we construct a functor ![]() $\text{L}_{T}:{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)\rightarrow {\mathcal{R}}{\mathcal{C}}(S)$ and a functor
$\text{L}_{T}:{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)\rightarrow {\mathcal{R}}{\mathcal{C}}(S)$ and a functor ![]() $-\hat{\otimes }DT:{\mathcal{R}}{\mathcal{C}}(R)\rightarrow {\mathcal{R}}{\mathcal{C}}(S)$. Then we give a natural homomorphism
$-\hat{\otimes }DT:{\mathcal{R}}{\mathcal{C}}(R)\rightarrow {\mathcal{R}}{\mathcal{C}}(S)$. Then we give a natural homomorphism
which is functorial in both variables. After this, associated with an object ![]() $X\in {\mathcal{R}}{\mathcal{C}}(R)$, we use the condition that
$X\in {\mathcal{R}}{\mathcal{C}}(R)$, we use the condition that ![]() $({\mathcal{B}},{\mathcal{A}})$ is a complete cotorsion pair in
$({\mathcal{B}},{\mathcal{A}})$ is a complete cotorsion pair in ![]() $\text{mod}R$ to obtain an object
$\text{mod}R$ to obtain an object ![]() $A_{X}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{A}})$ and establish a homomorphism
$A_{X}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{A}})$ and establish a homomorphism ![]() $u_{_{X}}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)}(X,A_{X})$. We then show that the assignment
$u_{_{X}}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)}(X,A_{X})$. We then show that the assignment ![]() $X\longmapsto \text{Cok}(l(u_{_{X}}))$ induces our desired functor
$X\longmapsto \text{Cok}(l(u_{_{X}}))$ induces our desired functor ![]() $\mathbf{S}_{T}:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$. We use the dual method to construct another desired functor
$\mathbf{S}_{T}:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$. We use the dual method to construct another desired functor ![]() $\mathbf{Q}_{DT}:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$. Then we prove that there are natural isomorphisms
$\mathbf{Q}_{DT}:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$. Then we prove that there are natural isomorphisms ![]() $\mathbf{Q}_{DT}\mathbf{S}_{T}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)}$ and
$\mathbf{Q}_{DT}\mathbf{S}_{T}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)}$ and ![]() $\mathbf{S}_{T}\mathbf{Q}_{DT}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)}$.
$\mathbf{S}_{T}\mathbf{Q}_{DT}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)}$.
4.1 From  ${\mathcal{R}}{\mathcal{C}}(R)$ to
${\mathcal{R}}{\mathcal{C}}(R)$ to  ${\mathcal{R}}{\mathcal{C}}(S)$: the functor
${\mathcal{R}}{\mathcal{C}}(S)$: the functor  $\mathbf{S}_{T}$
$\mathbf{S}_{T}$
4.1.1 The functor  $\text{L}_{T}:{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)\rightarrow {\mathcal{R}}{\mathcal{C}}(S)$
$\text{L}_{T}:{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)\rightarrow {\mathcal{R}}{\mathcal{C}}(S)$
Let ![]() $X=\{X_{i}\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$. We define
$X=\{X_{i}\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$. We define ![]() $\text{L}_{T}(X)\in {\mathcal{R}}{\mathcal{C}}(S)$ as follows:
$\text{L}_{T}(X)\in {\mathcal{R}}{\mathcal{C}}(S)$ as follows:
(l1) the underlying module
 $\text{L}_{T}(X)_{i}=\text{Hom}_{R}(T,X_{i-1})\oplus X_{i}\otimes _{R}DT$ and
$\text{L}_{T}(X)_{i}=\text{Hom}_{R}(T,X_{i-1})\oplus X_{i}\otimes _{R}DT$ and(l2) the structure map
 $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(\text{L}_{T}(X)):\text{L}_{T}(X)_{i}\otimes _{S}DS\rightarrow \text{L}_{T}(X)_{i-1}$ is given by
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(\text{L}_{T}(X)):\text{L}_{T}(X)_{i}\otimes _{S}DS\rightarrow \text{L}_{T}(X)_{i-1}$ is given by  $\big(\!\begin{smallmatrix}0 & \unicode[STIX]{x1D6FF}_{L_{i}}\\ 0 & 0\end{smallmatrix}\!\big)$, where
$\big(\!\begin{smallmatrix}0 & \unicode[STIX]{x1D6FF}_{L_{i}}\\ 0 & 0\end{smallmatrix}\!\big)$, where  $\unicode[STIX]{x1D6FF}_{L_{i}}$ is the composition:
$\unicode[STIX]{x1D6FF}_{L_{i}}$ is the composition:  $$\begin{eqnarray}\text{Hom}_{R}(T,X_{i-1})\otimes _{S}DS\stackrel{\simeq }{\longrightarrow }\text{Hom}_{R}(T,X_{i-1})\otimes _{S}T\otimes _{R}DT\stackrel{\unicode[STIX]{x1D716}_{X_{i-1}}^{T}\otimes _{R}DT}{\longrightarrow }X_{i-1}\otimes _{R}DT.\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{R}(T,X_{i-1})\otimes _{S}DS\stackrel{\simeq }{\longrightarrow }\text{Hom}_{R}(T,X_{i-1})\otimes _{S}T\otimes _{R}DT\stackrel{\unicode[STIX]{x1D716}_{X_{i-1}}^{T}\otimes _{R}DT}{\longrightarrow }X_{i-1}\otimes _{R}DT.\end{eqnarray}$$
From the functor property of ![]() $\text{Hom}_{R}(T,-)$ and
$\text{Hom}_{R}(T,-)$ and ![]() $-\!\otimes _{R}DT$, one can easily see that
$-\!\otimes _{R}DT$, one can easily see that ![]() $\text{L}_{T}$ is a functor from
$\text{L}_{T}$ is a functor from ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$ to
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$ to ![]() ${\mathcal{R}}{\mathcal{C}}(S)$.
${\mathcal{R}}{\mathcal{C}}(S)$.
Remark.
(1) If
 $X\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(\text{add}_{\text{mod}R}T)$, that is,
$X\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(\text{add}_{\text{mod}R}T)$, that is,  $X=\{X_{i}\}$ with each
$X=\{X_{i}\}$ with each  $X_{i}\in \text{add}_{\text{mod}R}T$, then
$X_{i}\in \text{add}_{\text{mod}R}T$, then  $\text{Hom}_{R}(T,X_{i-1})\in \text{add}_{\text{mod}S}S$ and
$\text{Hom}_{R}(T,X_{i-1})\in \text{add}_{\text{mod}S}S$ and  $\unicode[STIX]{x1D6FF}_{L_{i}}$ defined above is an isomorphism for each
$\unicode[STIX]{x1D6FF}_{L_{i}}$ defined above is an isomorphism for each  $i$. It follows that
$i$. It follows that  $\text{L}_{T}(X)$ is a projective object in
$\text{L}_{T}(X)$ is a projective object in  ${\mathcal{R}}{\mathcal{C}}(S)$ in this case.
${\mathcal{R}}{\mathcal{C}}(S)$ in this case.(2) As a special case, if
 $T=R$, then we obtain the functor
$T=R$, then we obtain the functor  $\text{L}_{R}:{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)\rightarrow {\mathcal{R}}{\mathcal{C}}(R)$ which sends objects in
$\text{L}_{R}:{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)\rightarrow {\mathcal{R}}{\mathcal{C}}(R)$ which sends objects in  ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(\text{add}_{\text{mod}R}R)$ to a projective object in
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(\text{add}_{\text{mod}R}R)$ to a projective object in  ${\mathcal{R}}{\mathcal{C}}(R)$.
${\mathcal{R}}{\mathcal{C}}(R)$.
4.1.2 The functor  $-\hat{\otimes }DT:{\mathcal{R}}{\mathcal{C}}(R)\rightarrow {\mathcal{R}}{\mathcal{C}}(S)$
$-\hat{\otimes }DT:{\mathcal{R}}{\mathcal{C}}(R)\rightarrow {\mathcal{R}}{\mathcal{C}}(S)$
Let ![]() $Y=\{Y_{i},\unicode[STIX]{x1D6FF}_{i}^{\otimes }(Y)\}\in {\mathcal{R}}{\mathcal{C}}(R)$. We define
$Y=\{Y_{i},\unicode[STIX]{x1D6FF}_{i}^{\otimes }(Y)\}\in {\mathcal{R}}{\mathcal{C}}(R)$. We define ![]() $Y\,\hat{\otimes }\,DT\in {\mathcal{R}}{\mathcal{C}}(S)$ by setting
$Y\,\hat{\otimes }\,DT\in {\mathcal{R}}{\mathcal{C}}(S)$ by setting
(t1) the underlying module is
 $(Y\,\hat{\otimes }\,DT)_{i}=Y_{i}\otimes _{R}DT$ and
$(Y\,\hat{\otimes }\,DT)_{i}=Y_{i}\otimes _{R}DT$ and(t2) the structure map
 $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(Y\,\hat{\otimes }\,DT)$ is given by the composition
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(Y\,\hat{\otimes }\,DT)$ is given by the composition  $$\begin{eqnarray}\displaystyle & & \displaystyle Y_{i}\otimes _{R}DT\otimes _{S}DS\stackrel{\simeq }{\longrightarrow }Y_{i}\otimes _{R}DT\otimes _{S}T\otimes _{R}DT\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\simeq }{\longrightarrow }Y_{i}\otimes _{R}DR\otimes _{R}DT\stackrel{\unicode[STIX]{x1D6FF}_{i}^{\otimes }(Y)\otimes _{R}DT}{\longrightarrow }Y_{i-1}\otimes _{R}DT.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle Y_{i}\otimes _{R}DT\otimes _{S}DS\stackrel{\simeq }{\longrightarrow }Y_{i}\otimes _{R}DT\otimes _{S}T\otimes _{R}DT\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\simeq }{\longrightarrow }Y_{i}\otimes _{R}DR\otimes _{R}DT\stackrel{\unicode[STIX]{x1D6FF}_{i}^{\otimes }(Y)\otimes _{R}DT}{\longrightarrow }Y_{i-1}\otimes _{R}DT.\nonumber\end{eqnarray}$$
From the functor property of ![]() $-\!\otimes _{R}DT$, one can see that
$-\!\otimes _{R}DT$, one can see that ![]() $-\hat{\otimes }DT$ is a functor from
$-\hat{\otimes }DT$ is a functor from ![]() ${\mathcal{R}}{\mathcal{C}}(R)$ to
${\mathcal{R}}{\mathcal{C}}(R)$ to ![]() ${\mathcal{R}}{\mathcal{C}}(S)$.
${\mathcal{R}}{\mathcal{C}}(S)$.
4.1.3 The homomorphism  $l_{Y}^{X}:\text{Hom}_{{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)}(X,Y)\rightarrow \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(S)}(X\,\hat{\otimes }\,DT,\text{L}_{T}(Y))$
$l_{Y}^{X}:\text{Hom}_{{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)}(X,Y)\rightarrow \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(S)}(X\,\hat{\otimes }\,DT,\text{L}_{T}(Y))$
Recall that we have a forgetful functor from ![]() ${\mathcal{R}}{\mathcal{C}}(R)$ to
${\mathcal{R}}{\mathcal{C}}(R)$ to ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$. For any
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$. For any ![]() $X\in {\mathcal{R}}{\mathcal{C}}(R)$ and
$X\in {\mathcal{R}}{\mathcal{C}}(R)$ and ![]() $Y\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$, there is a canonical homomorphism
$Y\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$, there is a canonical homomorphism
which is functorial in both variables, defined by
where ![]() $\unicode[STIX]{x1D703}_{l_{i}}$ is given by the composition
$\unicode[STIX]{x1D703}_{l_{i}}$ is given by the composition
 $$\begin{eqnarray}\displaystyle & & \displaystyle X_{i}\otimes _{R}DT\stackrel{\unicode[STIX]{x1D702}_{X_{i}\otimes _{R}DT}^{T}}{\longrightarrow }\text{Hom}_{R}(T,X_{i}\otimes _{R}DT\otimes _{S}T)\stackrel{\simeq }{\longrightarrow }\text{Hom}_{R}(T,X_{i}\otimes _{R}DR)\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\text{Hom}_{R}(T,\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X))}{\longrightarrow }\text{Hom}_{R}(T,X_{i-1})\stackrel{\text{Hom}_{R}(T,u_{i-1})}{\longrightarrow }\text{Hom}_{R}(T,Y_{i-1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle X_{i}\otimes _{R}DT\stackrel{\unicode[STIX]{x1D702}_{X_{i}\otimes _{R}DT}^{T}}{\longrightarrow }\text{Hom}_{R}(T,X_{i}\otimes _{R}DT\otimes _{S}T)\stackrel{\simeq }{\longrightarrow }\text{Hom}_{R}(T,X_{i}\otimes _{R}DR)\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\text{Hom}_{R}(T,\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X))}{\longrightarrow }\text{Hom}_{R}(T,X_{i-1})\stackrel{\text{Hom}_{R}(T,u_{i-1})}{\longrightarrow }\text{Hom}_{R}(T,Y_{i-1}).\nonumber\end{eqnarray}$$Remark.
Using the fact that ![]() $_{R}DR_{R}\simeq _{R}(DT\otimes _{S}T)_{R}$ and the adjoint isomorphism
$_{R}DR_{R}\simeq _{R}(DT\otimes _{S}T)_{R}$ and the adjoint isomorphism
one can easily check that ![]() $\unicode[STIX]{x1D703}_{l_{i}}$ is just the image of the natural homomorphism
$\unicode[STIX]{x1D703}_{l_{i}}$ is just the image of the natural homomorphism ![]() $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot u_{i-1}$ under
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot u_{i-1}$ under ![]() $\unicode[STIX]{x1D6E4}^{T}$, that is,
$\unicode[STIX]{x1D6E4}^{T}$, that is, ![]() $\unicode[STIX]{x1D703}_{l_{i}}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{T}(\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot u_{i-1})$.
$\unicode[STIX]{x1D703}_{l_{i}}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{T}(\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot u_{i-1})$.
In the following, we simply write ![]() $l$ instead of
$l$ instead of ![]() $l_{Y}^{X}$.
$l_{Y}^{X}$.
It is easy to see that, for any commutative diagram in ![]() ${\mathcal{R}}{\mathcal{C}}(R)$
${\mathcal{R}}{\mathcal{C}}(R)$

there is an induced commutative diagram in ![]() ${\mathcal{R}}{\mathcal{C}}(S)$
${\mathcal{R}}{\mathcal{C}}(S)$

4.1.4 A monomorphism  $u_{_{X}}:X\rightarrow A_{X}$ in
$u_{_{X}}:X\rightarrow A_{X}$ in  ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{R}})$ with
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{R}})$ with  $A_{X}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{A}})$, for
$A_{X}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{A}})$, for  $X\in {\mathcal{R}}{\mathcal{C}}(R)$
$X\in {\mathcal{R}}{\mathcal{C}}(R)$
Let ![]() $X=\{X_{i}\}\in {\mathcal{R}}{\mathcal{C}}(R)$. Since
$X=\{X_{i}\}\in {\mathcal{R}}{\mathcal{C}}(R)$. Since ![]() $({\mathcal{B}},{\mathcal{A}})$ is a complete cotorsion pair in
$({\mathcal{B}},{\mathcal{A}})$ is a complete cotorsion pair in ![]() $\text{mod}R$, there are exact sequences
$\text{mod}R$, there are exact sequences ![]() $0\rightarrow X_{i}\stackrel{(u_{_{X}})_{i}}{\longrightarrow }(A_{X})_{i}\stackrel{(\unicode[STIX]{x1D70B}_{_{X}})_{i}}{\longrightarrow }(B_{X})_{i}\rightarrow 0$ with
$0\rightarrow X_{i}\stackrel{(u_{_{X}})_{i}}{\longrightarrow }(A_{X})_{i}\stackrel{(\unicode[STIX]{x1D70B}_{_{X}})_{i}}{\longrightarrow }(B_{X})_{i}\rightarrow 0$ with ![]() $(A_{X})_{i}\in {\mathcal{A}}$ and
$(A_{X})_{i}\in {\mathcal{A}}$ and ![]() $(B_{X})_{i}\in {\mathcal{B}}$, for each
$(B_{X})_{i}\in {\mathcal{B}}$, for each ![]() $i$. This gives an exact sequence
$i$. This gives an exact sequence ![]() $0\rightarrow X\stackrel{u_{_{X}}}{\longrightarrow }A_{X}\stackrel{\unicode[STIX]{x1D70B}_{_{X}}}{\longrightarrow }B_{X}\rightarrow 0$ in
$0\rightarrow X\stackrel{u_{_{X}}}{\longrightarrow }A_{X}\stackrel{\unicode[STIX]{x1D70B}_{_{X}}}{\longrightarrow }B_{X}\rightarrow 0$ in ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$ with
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$ with ![]() $A_{X}=\{(A_{X})_{i}\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{A}})$ and
$A_{X}=\{(A_{X})_{i}\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{A}})$ and ![]() $B_{X}=\{(B_{X})_{i}\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{B}})$.
$B_{X}=\{(B_{X})_{i}\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{B}})$.
Now let ![]() $Y=\{Y_{i}\}\in {\mathcal{R}}{\mathcal{C}}(R)$ and
$Y=\{Y_{i}\}\in {\mathcal{R}}{\mathcal{C}}(R)$ and ![]() $h=\{h_{i}\}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(R)}(X,Y)$. Then we have an exact sequence
$h=\{h_{i}\}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(R)}(X,Y)$. Then we have an exact sequence ![]() $0\rightarrow Y\stackrel{u_{_{Y}}}{\longrightarrow }A_{Y}\stackrel{\unicode[STIX]{x1D70B}_{_{Y}}}{\longrightarrow }B_{Y}\rightarrow 0$ in
$0\rightarrow Y\stackrel{u_{_{Y}}}{\longrightarrow }A_{Y}\stackrel{\unicode[STIX]{x1D70B}_{_{Y}}}{\longrightarrow }B_{Y}\rightarrow 0$ in ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$ with
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$ with ![]() $A_{Y}=\{(A_{Y})_{i}\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{A}})$ and
$A_{Y}=\{(A_{Y})_{i}\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{A}})$ and ![]() $B_{Y}=\{(B_{Y})_{i}\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{B}})$, as above. Using that
$B_{Y}=\{(B_{Y})_{i}\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{B}})$, as above. Using that ![]() ${\mathcal{B}}=\text{KerExt}_{R}^{1}(-,{\mathcal{A}})$, it is easy to see that there is a homomorphism
${\mathcal{B}}=\text{KerExt}_{R}^{1}(-,{\mathcal{A}})$, it is easy to see that there is a homomorphism ![]() $h_{A}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)}(A_{X},A_{Y})$ and further
$h_{A}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)}(A_{X},A_{Y})$ and further ![]() $h_{B}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)}(B_{X},B_{Y})$ such that the following diagram in
$h_{B}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)}(B_{X},B_{Y})$ such that the following diagram in ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$ is commutative with exact rows.
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$ is commutative with exact rows.

4.1.5 The cokernel  $\text{Cok}(l(u_{_{X}}))$
$\text{Cok}(l(u_{_{X}}))$
Applying the functor ![]() $-\!\otimes _{R}DT$ to the exact sequences
$-\!\otimes _{R}DT$ to the exact sequences
above, we obtain induced exact sequences
since ![]() $(B_{X})_{i}\in {\mathcal{B}}\subseteq \text{KerExt}_{R}^{1}(-,T)=\text{KerTor}_{1}^{R}(-,DT)$ for each
$(B_{X})_{i}\in {\mathcal{B}}\subseteq \text{KerExt}_{R}^{1}(-,T)=\text{KerTor}_{1}^{R}(-,DT)$ for each ![]() $i$. It follows that, by applying the homomorphism
$i$. It follows that, by applying the homomorphism ![]() $l$ in 4.1.3 to the homomorphism
$l$ in 4.1.3 to the homomorphism ![]() $u_{_{X}}$ in 4.1.4, there is an induced exact sequence
$u_{_{X}}$ in 4.1.4, there is an induced exact sequence
Remark.
From the definition of ![]() $\text{Cok}(l(u_{_{X}}))$, one sees that, for each
$\text{Cok}(l(u_{_{X}}))$, one sees that, for each ![]() $i$,
$i$, ![]() $\text{Cok}(l(u_{_{X}}))_{i}$ is given by the pushout
$\text{Cok}(l(u_{_{X}}))_{i}$ is given by the pushout

Moreover, for ![]() $Y\in {\mathcal{R}}{\mathcal{C}}(R)$ and
$Y\in {\mathcal{R}}{\mathcal{C}}(R)$ and ![]() $h\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(R)}(X,Y)$, by applying the homomorphism
$h\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(R)}(X,Y)$, by applying the homomorphism ![]() $l$ to the left square in the commutation diagram in 4.1.4, we obtain the following commutative diagram in
$l$ to the left square in the commutation diagram in 4.1.4, we obtain the following commutative diagram in ![]() ${\mathcal{R}}{\mathcal{C}}(S)$, for some
${\mathcal{R}}{\mathcal{C}}(S)$, for some ![]() $h_{\text{Cok}}$:
$h_{\text{Cok}}$:

4.1.6 The assignment  $\mathbf{S}_{T}:{\mathcal{R}}{\mathcal{C}}(R)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$ given by
$\mathbf{S}_{T}:{\mathcal{R}}{\mathcal{C}}(R)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$ given by  $X\longmapsto \text{Cok}(l(u_{_{X}}))$ is a functor
$X\longmapsto \text{Cok}(l(u_{_{X}}))$ is a functor
By 4.1.5, it is sufficient to prove that ![]() $\mathbf{S}_{T}(h):=h_{\text{Cok}}=0$ in
$\mathbf{S}_{T}(h):=h_{\text{Cok}}=0$ in ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$ provided
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$ provided ![]() $h=0$. We divide the proof into two steps.
$h=0$. We divide the proof into two steps.
Step 1: Consider each piece in the commutative diagram in 4.1.4. If ![]() $h=\{h_{i}\}=0$, then
$h=\{h_{i}\}=0$, then ![]() $h_{i}=0$ for each
$h_{i}=0$ for each ![]() $i$. Thus, we have that
$i$. Thus, we have that ![]() $(u_{_{X}})_{i}(h_{A})_{i}=0$ and, consequently,
$(u_{_{X}})_{i}(h_{A})_{i}=0$ and, consequently, ![]() $(h_{A})_{i}=(\unicode[STIX]{x1D70B}_{_{X}})_{i}g_{i}$ for some
$(h_{A})_{i}=(\unicode[STIX]{x1D70B}_{_{X}})_{i}g_{i}$ for some ![]() $g_{i}:(B_{X})_{i}\rightarrow (A_{Y})_{i}$. Since
$g_{i}:(B_{X})_{i}\rightarrow (A_{Y})_{i}$. Since ![]() $(B_{X})_{i}\in {\mathcal{B}}\subseteq {\mathcal{X}}_{T}$ for each
$(B_{X})_{i}\in {\mathcal{B}}\subseteq {\mathcal{X}}_{T}$ for each ![]() $i$ and
$i$ and ![]() $T$ is an Ext-injective cogenerator in
$T$ is an Ext-injective cogenerator in ![]() ${\mathcal{B}}$ (see the first part in the proof of Proposition 3.2.5), there are exact sequences
${\mathcal{B}}$ (see the first part in the proof of Proposition 3.2.5), there are exact sequences ![]() $0\rightarrow (B_{X})_{i}\stackrel{b_{i}}{\longrightarrow }T_{(B_{X})_{i}}\rightarrow (B_{X}^{\prime })_{i}\rightarrow 0$ with
$0\rightarrow (B_{X})_{i}\stackrel{b_{i}}{\longrightarrow }T_{(B_{X})_{i}}\rightarrow (B_{X}^{\prime })_{i}\rightarrow 0$ with ![]() $T_{(B_{X})_{i}}\in \text{add}_{\text{mod}R}T$ and
$T_{(B_{X})_{i}}\in \text{add}_{\text{mod}R}T$ and ![]() $(B_{X}^{\prime })_{i}\in {\mathcal{B}}\subseteq \text{KerExt}_{R}^{1}(-,{\mathcal{A}})$. It follows that there exists
$(B_{X}^{\prime })_{i}\in {\mathcal{B}}\subseteq \text{KerExt}_{R}^{1}(-,{\mathcal{A}})$. It follows that there exists ![]() $t_{i}\in \text{Hom}_{R}(T_{(B_{X})_{i}},(A_{Y})_{i})$ such that
$t_{i}\in \text{Hom}_{R}(T_{(B_{X})_{i}},(A_{Y})_{i})$ such that ![]() $g_{i}=b_{i}t_{i}$. Altogether, we obtain the following commutative diagram:
$g_{i}=b_{i}t_{i}$. Altogether, we obtain the following commutative diagram:

This induces the following commutative diagram in ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$, where
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$, where ![]() $T_{B_{X}}=\{T_{(B_{X})_{i}}\}$:
$T_{B_{X}}=\{T_{(B_{X})_{i}}\}$:

Set ![]() $k:=\unicode[STIX]{x1D70B}_{_{X}}b$. Then
$k:=\unicode[STIX]{x1D70B}_{_{X}}b$. Then ![]() $\text{L}_{T}(h_{A})=\text{L}_{T}(kt)=\text{L}_{T}(k)\text{L}_{T}(t)$.
$\text{L}_{T}(h_{A})=\text{L}_{T}(kt)=\text{L}_{T}(k)\text{L}_{T}(t)$.
Step 2: Consider the commutative diagram in 4.1.5. Since ![]() $(u_{_{X}})_{i}(\unicode[STIX]{x1D70B}_{_{X}})_{i}=0$, it holds that
$(u_{_{X}})_{i}(\unicode[STIX]{x1D70B}_{_{X}})_{i}=0$, it holds that ![]() $\text{Hom}_{R}(T,(u_{_{X}})_{i})\cdot \text{Hom}_{R}(T,(\unicode[STIX]{x1D70B}_{_{X}})_{i})=0$ and
$\text{Hom}_{R}(T,(u_{_{X}})_{i})\cdot \text{Hom}_{R}(T,(\unicode[STIX]{x1D70B}_{_{X}})_{i})=0$ and ![]() $(u_{_{X}})_{i}\otimes _{R}DT\cdot (\unicode[STIX]{x1D70B}_{_{X}})_{i}\otimes _{R}DT=0$. Then we see that
$(u_{_{X}})_{i}\otimes _{R}DT\cdot (\unicode[STIX]{x1D70B}_{_{X}})_{i}\otimes _{R}DT=0$. Then we see that ![]() $l(u_{_{X}})\text{L}_{T}(k)=l(u_{_{X}})\text{L}_{T}(\unicode[STIX]{x1D70B}_{_{X}})\text{L}_{T}(b)=0\cdot \text{L}_{T}(b)=0$ by the definition of the functor
$l(u_{_{X}})\text{L}_{T}(k)=l(u_{_{X}})\text{L}_{T}(\unicode[STIX]{x1D70B}_{_{X}})\text{L}_{T}(b)=0\cdot \text{L}_{T}(b)=0$ by the definition of the functor ![]() $\text{L}_{T}$ in 4.1.1 and the morphism
$\text{L}_{T}$ in 4.1.1 and the morphism ![]() $l(u_{_{X}})$ in 4.1.3. Hence, there is some
$l(u_{_{X}})$ in 4.1.3. Hence, there is some ![]() $\unicode[STIX]{x1D703}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(S)}(\text{Cok}(l(u_{_{X}})),\text{L}_{T}(T_{B_{X}}))$ such that
$\unicode[STIX]{x1D703}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(S)}(\text{Cok}(l(u_{_{X}})),\text{L}_{T}(T_{B_{X}}))$ such that ![]() $\text{L}_{T}(k)=\unicode[STIX]{x1D70B}_{_{l_{X}}}\unicode[STIX]{x1D703}$. Consequently, we have that
$\text{L}_{T}(k)=\unicode[STIX]{x1D70B}_{_{l_{X}}}\unicode[STIX]{x1D703}$. Consequently, we have that ![]() $\text{L}_{T}(h_{A})=\text{L}_{T}(k)L(t)=\unicode[STIX]{x1D70B}_{_{l_{X}}}\unicode[STIX]{x1D703}\text{L}_{T}(t)$. Now we obtain that
$\text{L}_{T}(h_{A})=\text{L}_{T}(k)L(t)=\unicode[STIX]{x1D70B}_{_{l_{X}}}\unicode[STIX]{x1D703}\text{L}_{T}(t)$. Now we obtain that ![]() $\unicode[STIX]{x1D70B}_{_{l_{X}}}h_{\text{Cok}}=\text{L}_{T}(h_{A})\unicode[STIX]{x1D70B}_{_{l_{Y}}}=\unicode[STIX]{x1D70B}_{_{l_{X}}}\unicode[STIX]{x1D703}\text{L}_{T}(t)\unicode[STIX]{x1D70B}_{_{l_{Y}}}$. Since
$\unicode[STIX]{x1D70B}_{_{l_{X}}}h_{\text{Cok}}=\text{L}_{T}(h_{A})\unicode[STIX]{x1D70B}_{_{l_{Y}}}=\unicode[STIX]{x1D70B}_{_{l_{X}}}\unicode[STIX]{x1D703}\text{L}_{T}(t)\unicode[STIX]{x1D70B}_{_{l_{Y}}}$. Since ![]() $\unicode[STIX]{x1D70B}_{l_{X}}$ is epic, we get that
$\unicode[STIX]{x1D70B}_{l_{X}}$ is epic, we get that ![]() $h_{\text{Cok}}=\unicode[STIX]{x1D703}\text{L}_{T}(t)\unicode[STIX]{x1D70B}_{_{l_{Y}}}$. That is, we have the following commutative diagram:
$h_{\text{Cok}}=\unicode[STIX]{x1D703}\text{L}_{T}(t)\unicode[STIX]{x1D70B}_{_{l_{Y}}}$. That is, we have the following commutative diagram:

Note that ![]() $\text{L}_{T}(T_{B_{X}})$ is a projective–injective object in
$\text{L}_{T}(T_{B_{X}})$ is a projective–injective object in ![]() ${\mathcal{R}}{\mathcal{C}}(S)$, so
${\mathcal{R}}{\mathcal{C}}(S)$, so ![]() $h_{\text{Cok}}=0$ in
$h_{\text{Cok}}=0$ in ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$.
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$.
4.1.7 The functor  $\mathbf{S}_{T}:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$
$\mathbf{S}_{T}:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$
We will show that the functor ![]() $\mathbf{S}_{T}$ factors through
$\mathbf{S}_{T}$ factors through ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$.
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$.
To see this, it is enough to show that ![]() $\mathbf{S}_{T}(X)$ is a projective object in
$\mathbf{S}_{T}(X)$ is a projective object in ![]() ${\mathcal{R}}{\mathcal{C}}(S)$ whenever
${\mathcal{R}}{\mathcal{C}}(S)$ whenever ![]() $X$ is a projective object in
$X$ is a projective object in ![]() ${\mathcal{R}}{\mathcal{C}}(R)$.
${\mathcal{R}}{\mathcal{C}}(R)$.
Without loss of generality, we assume that ![]() $X=\{X_{i}\}$ is an indecomposable projective object in
$X=\{X_{i}\}$ is an indecomposable projective object in ![]() ${\mathcal{R}}{\mathcal{C}}(R)$. Thus,
${\mathcal{R}}{\mathcal{C}}(R)$. Thus, ![]() $X$ is of the form
$X$ is of the form
where ![]() $I$ is indecomposable injective and is on the (
$I$ is indecomposable injective and is on the (![]() $k-1$)th position, for some
$k-1$)th position, for some ![]() $k$ [Reference Happel18, 2.2 Lemma].
$k$ [Reference Happel18, 2.2 Lemma].
Note that ![]() $X_{k}=\text{Hom}_{R}(DR,I)\in \text{add}_{\text{mod}R}R\subseteq {\mathcal{B}}$ and
$X_{k}=\text{Hom}_{R}(DR,I)\in \text{add}_{\text{mod}R}R\subseteq {\mathcal{B}}$ and ![]() $X_{k-1}=I\in \text{add}_{\text{mod}R}DR\subseteq {\mathcal{A}}$, so, following 4.1.4, we can choose
$X_{k-1}=I\in \text{add}_{\text{mod}R}DR\subseteq {\mathcal{A}}$, so, following 4.1.4, we can choose ![]() $A_{X}$ to be of the form
$A_{X}$ to be of the form
where ![]() $A_{X_{k}}=T_{k}\in \text{add}_{\text{mod}R}T$. And we have that the homomorphism
$A_{X_{k}}=T_{k}\in \text{add}_{\text{mod}R}T$. And we have that the homomorphism ![]() $u_{_{X}}:X\rightarrow A_{X}$ is of the form
$u_{_{X}}:X\rightarrow A_{X}$ is of the form
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ccccccccccccccc@{}}X: & & \cdots \, & {\rightsquigarrow} & 0 & {\rightsquigarrow} & 0 & {\rightsquigarrow} & \text{Hom}_{R}(DR,I) & {\rightsquigarrow} & I & {\rightsquigarrow} & 0 & {\rightsquigarrow} & \cdots \\ \downarrow u_{_{X}} & & & & & & & & \downarrow u_{k} & & \downarrow 1 & & & & \\ A_{X}: & & \cdots \, & {\rightsquigarrow} & 0 & {\rightsquigarrow} & 0 & {\rightsquigarrow} & T_{k} & {\rightsquigarrow} & I & {\rightsquigarrow} & 0 & {\rightsquigarrow} & \cdots \end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ccccccccccccccc@{}}X: & & \cdots \, & {\rightsquigarrow} & 0 & {\rightsquigarrow} & 0 & {\rightsquigarrow} & \text{Hom}_{R}(DR,I) & {\rightsquigarrow} & I & {\rightsquigarrow} & 0 & {\rightsquigarrow} & \cdots \\ \downarrow u_{_{X}} & & & & & & & & \downarrow u_{k} & & \downarrow 1 & & & & \\ A_{X}: & & \cdots \, & {\rightsquigarrow} & 0 & {\rightsquigarrow} & 0 & {\rightsquigarrow} & T_{k} & {\rightsquigarrow} & I & {\rightsquigarrow} & 0 & {\rightsquigarrow} & \cdots \end{array} & & \displaystyle \nonumber\end{eqnarray}$$ Then, from the structure of ![]() $l(u_{_{X}})$, we can see that
$l(u_{_{X}})$, we can see that ![]() $l(u_{_{X}})$ is of the form
$l(u_{_{X}})$ is of the form
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ccccccccccc@{}}X\,\hat{\otimes }\,DT: & & 0 & {\rightsquigarrow} & 0 & {\rightsquigarrow} & \text{Hom}_{R}(DR,I)\otimes _{R}DT & {\rightsquigarrow} & I\otimes _{R}DT & {\rightsquigarrow} & 0\\ \downarrow l(u_{_{X}}) & & & & \downarrow & & \downarrow (-\unicode[STIX]{x1D703}_{l_{k}},u_{k}\otimes _{R}DT) & & \downarrow 1 & & \\ \text{L}_{T}(A_{X}): & & 0 & {\rightsquigarrow} & \text{Hom}_{R}(T,T_{k}) & \stackrel{(0,\unicode[STIX]{x1D6FF}_{L_{k+1}})}{{\rightsquigarrow}} & \text{Hom}_{R}(T,I)\oplus T_{k}\otimes _{R}DT & {\rightsquigarrow} & I\otimes _{R}DT & {\rightsquigarrow} & 0,\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ccccccccccc@{}}X\,\hat{\otimes }\,DT: & & 0 & {\rightsquigarrow} & 0 & {\rightsquigarrow} & \text{Hom}_{R}(DR,I)\otimes _{R}DT & {\rightsquigarrow} & I\otimes _{R}DT & {\rightsquigarrow} & 0\\ \downarrow l(u_{_{X}}) & & & & \downarrow & & \downarrow (-\unicode[STIX]{x1D703}_{l_{k}},u_{k}\otimes _{R}DT) & & \downarrow 1 & & \\ \text{L}_{T}(A_{X}): & & 0 & {\rightsquigarrow} & \text{Hom}_{R}(T,T_{k}) & \stackrel{(0,\unicode[STIX]{x1D6FF}_{L_{k+1}})}{{\rightsquigarrow}} & \text{Hom}_{R}(T,I)\oplus T_{k}\otimes _{R}DT & {\rightsquigarrow} & I\otimes _{R}DT & {\rightsquigarrow} & 0,\end{array} & & \displaystyle \nonumber\end{eqnarray}$$ where ![]() $\unicode[STIX]{x1D703}_{l_{k}}$ is defined as in 4.1.3 and
$\unicode[STIX]{x1D703}_{l_{k}}$ is defined as in 4.1.3 and ![]() $\unicode[STIX]{x1D6FF}_{L_{k+1}}$ is defined as in 4.1.1, respectively. One checks that both homomorphisms
$\unicode[STIX]{x1D6FF}_{L_{k+1}}$ is defined as in 4.1.1, respectively. One checks that both homomorphisms ![]() $\unicode[STIX]{x1D703}_{l_{k}}$ and
$\unicode[STIX]{x1D703}_{l_{k}}$ and ![]() $\unicode[STIX]{x1D6FF}_{L_{k+1}}$ are, in fact, isomorphisms. So we obtain that
$\unicode[STIX]{x1D6FF}_{L_{k+1}}$ are, in fact, isomorphisms. So we obtain that ![]() $S_{T}(X)=\text{Coker}(l(u_{_{X}}))$ is of the form
$S_{T}(X)=\text{Coker}(l(u_{_{X}}))$ is of the form
where ![]() $\unicode[STIX]{x1D6FF}_{k+1}^{\prime }$ is the induced isomorphism:
$\unicode[STIX]{x1D6FF}_{k+1}^{\prime }$ is the induced isomorphism: ![]() $\text{Hom}_{R}(T,T_{k})\otimes _{S}DS\rightarrow T_{k}\otimes _{R}DT$. Since
$\text{Hom}_{R}(T,T_{k})\otimes _{S}DS\rightarrow T_{k}\otimes _{R}DT$. Since ![]() $T_{k}\otimes _{R}DT\in \text{add}_{\text{mod}S}(T\otimes _{R}DT)=\text{add}_{\text{mod}S}DS$, we see that
$T_{k}\otimes _{R}DT\in \text{add}_{\text{mod}S}(T\otimes _{R}DT)=\text{add}_{\text{mod}S}DS$, we see that ![]() $T_{k}\otimes _{R}DT$ is an injective
$T_{k}\otimes _{R}DT$ is an injective ![]() $S$-module and that
$S$-module and that ![]() $\mathbf{S}_{T}(X)$ is a projective object in
$\mathbf{S}_{T}(X)$ is a projective object in ![]() ${\mathcal{R}}{\mathcal{C}}(S)$.
${\mathcal{R}}{\mathcal{C}}(S)$.
It follows that the functor ![]() $\mathbf{S}_{T}$ factors through
$\mathbf{S}_{T}$ factors through ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$. We still denote by
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$. We still denote by ![]() $\mathbf{S}_{T}$ the induced functor from
$\mathbf{S}_{T}$ the induced functor from ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ to
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ to ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$.
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$.
4.2 From  $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$ to
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$ to  $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$: the functor
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$: the functor  $\mathbf{Q}_{DT}$
$\mathbf{Q}_{DT}$
The functor ![]() $\mathbf{Q}_{DT}$ is indeed defined in a way dual to the construction of
$\mathbf{Q}_{DT}$ is indeed defined in a way dual to the construction of ![]() $\mathbf{S}_{T}$.
$\mathbf{S}_{T}$.
4.2.1 The functor  $\text{R}_{DT}:{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)\rightarrow {\mathcal{R}}{\mathcal{C}}(R)$
$\text{R}_{DT}:{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)\rightarrow {\mathcal{R}}{\mathcal{C}}(R)$
Dually to 4.1.1, for any ![]() $X=\{X_{i}\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)$, we define
$X=\{X_{i}\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)$, we define ![]() $\text{R}_{DT}(X)\in {\mathcal{R}}{\mathcal{C}}(R)$ as follows:
$\text{R}_{DT}(X)\in {\mathcal{R}}{\mathcal{C}}(R)$ as follows:
(r1) the underlying module is
 $\text{R}_{DT}(X)_{i}=\text{Hom}_{S}(DT,X_{i})\oplus X_{i+1}\otimes _{S}T$ and
$\text{R}_{DT}(X)_{i}=\text{Hom}_{S}(DT,X_{i})\oplus X_{i+1}\otimes _{S}T$ and(r2) the structure map
 $\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(\text{R}_{DT}(X))$ is given by
$\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(\text{R}_{DT}(X))$ is given by  $\big(\begin{smallmatrix}0 & \unicode[STIX]{x1D6FF}_{R_{i}}^{\text{H}}0 & 0\end{smallmatrix}\big)$, where
$\big(\begin{smallmatrix}0 & \unicode[STIX]{x1D6FF}_{R_{i}}^{\text{H}}0 & 0\end{smallmatrix}\big)$, where  $\unicode[STIX]{x1D6FF}_{R_{i}}^{\text{H}}$ is the composition
$\unicode[STIX]{x1D6FF}_{R_{i}}^{\text{H}}$ is the composition  $$\begin{eqnarray}\displaystyle & & \displaystyle \text{Hom}_{S}(DT,X_{i})\stackrel{\text{Hom}_{S}(DT,\unicode[STIX]{x1D702}_{X_{i}}^{T})}{\longrightarrow }\text{Hom}_{S}(DT,\text{Hom}_{R}(T,X_{i}\otimes _{S}T))\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \text{Hom}_{R}(DT\otimes _{S}T,X_{i}\otimes _{S}T)\simeq \text{Hom}_{R}(DR,X_{i}\otimes _{S}T).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{Hom}_{S}(DT,X_{i})\stackrel{\text{Hom}_{S}(DT,\unicode[STIX]{x1D702}_{X_{i}}^{T})}{\longrightarrow }\text{Hom}_{S}(DT,\text{Hom}_{R}(T,X_{i}\otimes _{S}T))\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \text{Hom}_{R}(DT\otimes _{S}T,X_{i}\otimes _{S}T)\simeq \text{Hom}_{R}(DR,X_{i}\otimes _{S}T).\nonumber\end{eqnarray}$$
Equivalently, the structure map ![]() $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(\text{R}_{DT}(X))$ is given by
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(\text{R}_{DT}(X))$ is given by ![]() $\big(\!\begin{smallmatrix}0 & \unicode[STIX]{x1D6FF}_{R_{i}}^{\otimes }0 & 0\end{smallmatrix}\!\big)$, where
$\big(\!\begin{smallmatrix}0 & \unicode[STIX]{x1D6FF}_{R_{i}}^{\otimes }0 & 0\end{smallmatrix}\!\big)$, where ![]() $\unicode[STIX]{x1D6FF}_{R_{i}}^{\otimes }$ is the composition
$\unicode[STIX]{x1D6FF}_{R_{i}}^{\otimes }$ is the composition
It is easy to see that ![]() $\text{R}_{DT}$ is a functor.
$\text{R}_{DT}$ is a functor.
Remark.
(1) If
 $X\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(\text{add}_{\text{mod}S}DT)$, that is,
$X\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(\text{add}_{\text{mod}S}DT)$, that is,  $X=\{X_{i}\}$ with each
$X=\{X_{i}\}$ with each  $X_{i}\in \text{add}_{\text{mod}S}DT$, then
$X_{i}\in \text{add}_{\text{mod}S}DT$, then  $\text{Hom}_{S}(DT,X_{i})\in \text{add}_{\text{mod}R}R$ and
$\text{Hom}_{S}(DT,X_{i})\in \text{add}_{\text{mod}R}R$ and  $\unicode[STIX]{x1D6FF}_{R_{i}}$ defined above is an isomorphism for each
$\unicode[STIX]{x1D6FF}_{R_{i}}$ defined above is an isomorphism for each  $i$. It follows that
$i$. It follows that  $\text{R}_{DT}(X)$ is a projective object in
$\text{R}_{DT}(X)$ is a projective object in  ${\mathcal{R}}{\mathcal{C}}(R)$ in this case.
${\mathcal{R}}{\mathcal{C}}(R)$ in this case.(2) As a special case, if
 $T=S$, then we obtain the functor
$T=S$, then we obtain the functor  $\text{R}_{DS}:{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)\rightarrow {\mathcal{R}}{\mathcal{C}}(S)$ which sends objects in
$\text{R}_{DS}:{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)\rightarrow {\mathcal{R}}{\mathcal{C}}(S)$ which sends objects in  ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(\text{add}_{\text{mod}S}DS)$ to a projective object in
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(\text{add}_{\text{mod}S}DS)$ to a projective object in  ${\mathcal{R}}{\mathcal{C}}(S)$.
${\mathcal{R}}{\mathcal{C}}(S)$.
4.2.2 The functor  $\text{Ĥom}(DT,-):{\mathcal{R}}{\mathcal{C}}(S)\rightarrow {\mathcal{R}}{\mathcal{C}}(R)$
$\text{Ĥom}(DT,-):{\mathcal{R}}{\mathcal{C}}(S)\rightarrow {\mathcal{R}}{\mathcal{C}}(R)$
Let ![]() $Y=\{Y_{i},\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(Y)\}\in {\mathcal{R}}{\mathcal{C}}(S)$. We define
$Y=\{Y_{i},\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(Y)\}\in {\mathcal{R}}{\mathcal{C}}(S)$. We define ![]() $\text{Ĥom}(DT,Y)\in {\mathcal{R}}{\mathcal{C}}(R)$ by setting
$\text{Ĥom}(DT,Y)\in {\mathcal{R}}{\mathcal{C}}(R)$ by setting
(h1) the underlying module is
 $\text{Ĥom}(DT,Y)_{i}=\text{Hom}_{S}(DT,Y_{i})$ and
$\text{Ĥom}(DT,Y)_{i}=\text{Hom}_{S}(DT,Y_{i})$ and(h2) the structure map
 $\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(\text{Ĥom}(DT,Y))$ is given by the composition
$\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(\text{Ĥom}(DT,Y))$ is given by the composition  $$\begin{eqnarray}\displaystyle & & \displaystyle \text{Hom}_{S}(DT,Y_{i})\stackrel{\text{Hom}_{S}(DT,\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(Y))}{\longrightarrow }\text{Hom}_{S}(DT,\text{Hom}_{S}(DS,Y_{i-1}))\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \text{Hom}_{R}(DR,\text{Hom}_{S}(DT,Y_{i-1})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{Hom}_{S}(DT,Y_{i})\stackrel{\text{Hom}_{S}(DT,\unicode[STIX]{x1D6FF}_{i}^{\text{H}}(Y))}{\longrightarrow }\text{Hom}_{S}(DT,\text{Hom}_{S}(DS,Y_{i-1}))\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \text{Hom}_{R}(DR,\text{Hom}_{S}(DT,Y_{i-1})).\nonumber\end{eqnarray}$$
Then from the functor property of ![]() $\text{Hom}_{S}(DT,-)$, one can see that
$\text{Hom}_{S}(DT,-)$, one can see that ![]() $\text{Ĥom}(DT,-)$ is a functor from
$\text{Ĥom}(DT,-)$ is a functor from ![]() ${\mathcal{R}}{\mathcal{C}}(S)$ to
${\mathcal{R}}{\mathcal{C}}(S)$ to ![]() ${\mathcal{R}}{\mathcal{C}}(R)$.
${\mathcal{R}}{\mathcal{C}}(R)$.
4.2.3 The homomorphism  $r_{Y}^{X}$
$r_{Y}^{X}$
Dually to the homomorphism ![]() $l_{Y}^{X}$, for any
$l_{Y}^{X}$, for any ![]() $X\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)$ and
$X\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)$ and ![]() $Y\in {\mathcal{R}}{\mathcal{C}}(S)$, we have a canonical homomorphism
$Y\in {\mathcal{R}}{\mathcal{C}}(S)$, we have a canonical homomorphism
which is functorial in both variables, defined by
where ![]() $\unicode[STIX]{x1D701}_{r_{i}}:X_{i+1}\otimes _{S}T\rightarrow \text{Hom}_{S}(DT,Y_{i})$ equals to
$\unicode[STIX]{x1D701}_{r_{i}}:X_{i+1}\otimes _{S}T\rightarrow \text{Hom}_{S}(DT,Y_{i})$ equals to
that is, the composition
 $$\begin{eqnarray}\displaystyle & & \displaystyle X_{i+1}\otimes _{S}T\stackrel{u_{i+1}\otimes _{S}T}{\longrightarrow }Y_{i+1}\otimes _{S}T\stackrel{\unicode[STIX]{x1D6FF}_{i+1}^{H}(Y)\otimes _{S}T}{\longrightarrow }\text{Hom}_{S}(DS,Y_{i})\otimes _{S}T\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \text{Hom}_{S}(T\otimes _{R}DT,Y_{i})\otimes _{S}T\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \text{Hom}_{R}(T,\text{Hom}_{S}(DT,Y_{i}))\otimes _{S}T\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\unicode[STIX]{x1D716}_{\text{Hom}_{S}(DT,Y_{i})}^{T}}{\longrightarrow }\text{Hom}_{S}(DT,Y_{i}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle X_{i+1}\otimes _{S}T\stackrel{u_{i+1}\otimes _{S}T}{\longrightarrow }Y_{i+1}\otimes _{S}T\stackrel{\unicode[STIX]{x1D6FF}_{i+1}^{H}(Y)\otimes _{S}T}{\longrightarrow }\text{Hom}_{S}(DS,Y_{i})\otimes _{S}T\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \text{Hom}_{S}(T\otimes _{R}DT,Y_{i})\otimes _{S}T\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \text{Hom}_{R}(T,\text{Hom}_{S}(DT,Y_{i}))\otimes _{S}T\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\unicode[STIX]{x1D716}_{\text{Hom}_{S}(DT,Y_{i})}^{T}}{\longrightarrow }\text{Hom}_{S}(DT,Y_{i}).\nonumber\end{eqnarray}$$Remark.
Using the fact that ![]() $_{S}DS_{S}\simeq _{S}T\otimes _{R}DT_{S}$ and the adjoint isomorphism
$_{S}DS_{S}\simeq _{S}T\otimes _{R}DT_{S}$ and the adjoint isomorphism
one can easily check that ![]() $\unicode[STIX]{x1D701}_{r_{i}}$ is the image of the natural homomorphism
$\unicode[STIX]{x1D701}_{r_{i}}$ is the image of the natural homomorphism ![]() $(u_{i+1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(Y)$ under
$(u_{i+1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(Y)$ under ![]() $\unicode[STIX]{x1D6E4}^{DT}$, that is,
$\unicode[STIX]{x1D6E4}^{DT}$, that is, ![]() $\unicode[STIX]{x1D701}_{r_{i}}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((u_{i+1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(Y))$.
$\unicode[STIX]{x1D701}_{r_{i}}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((u_{i+1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(Y))$.
In the following, we simply write ![]() $r$ instead of
$r$ instead of ![]() $r_{Y}^{X}$.
$r_{Y}^{X}$.
4.2.4 An epimorphism  $v_{_{Y}}:G_{Y}\rightarrow Y$ in
$v_{_{Y}}:G_{Y}\rightarrow Y$ in  ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{S}})$ with
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{S}})$ with  $G_{Y}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{G}})$, for
$G_{Y}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{G}})$, for  $Y\in {\mathcal{R}}{\mathcal{C}}(S)$
$Y\in {\mathcal{R}}{\mathcal{C}}(S)$
Since ![]() $({\mathcal{G}},{\mathcal{K}})$ is a complete hereditary cotorsion pair in
$({\mathcal{G}},{\mathcal{K}})$ is a complete hereditary cotorsion pair in ![]() $\text{mod}S$, it follows that, for any
$\text{mod}S$, it follows that, for any ![]() $Y=\{Y_{i}\}\in {\mathcal{R}}{\mathcal{C}}(S)$, there is an exact sequence
$Y=\{Y_{i}\}\in {\mathcal{R}}{\mathcal{C}}(S)$, there is an exact sequence ![]() $0\rightarrow K_{Y}\stackrel{k_{_{Y}}}{\longrightarrow }G_{Y}\stackrel{v_{_{Y}}}{\longrightarrow }Y\rightarrow 0$ in
$0\rightarrow K_{Y}\stackrel{k_{_{Y}}}{\longrightarrow }G_{Y}\stackrel{v_{_{Y}}}{\longrightarrow }Y\rightarrow 0$ in ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{S}})$ with
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{S}})$ with ![]() $K_{Y}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{K}})$ and
$K_{Y}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{K}})$ and ![]() $G_{Y}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{G}})$.
$G_{Y}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{G}})$.
Moreover, for any ![]() $h\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(S)}(X,Y)$, there is an induced commutative diagram as follows since
$h\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(S)}(X,Y)$, there is an induced commutative diagram as follows since ![]() $\text{Ext}_{S}^{1}({\mathcal{G}},{\mathcal{K}})=0$:
$\text{Ext}_{S}^{1}({\mathcal{G}},{\mathcal{K}})=0$:

4.2.5 The kernel  $\text{Ker}(r(v_{_{Y}}))$
$\text{Ker}(r(v_{_{Y}}))$
Applying the functor ![]() $\text{Ĥom}(DT,-)$ to the bottom exact sequence in the above diagram, we obtain an induced exact sequence
$\text{Ĥom}(DT,-)$ to the bottom exact sequence in the above diagram, we obtain an induced exact sequence
since ![]() $(K_{Y})_{i}\in {\mathcal{K}}\subseteq \text{KerExt}_{S}^{1}(DT,-)$ for each
$(K_{Y})_{i}\in {\mathcal{K}}\subseteq \text{KerExt}_{S}^{1}(DT,-)$ for each ![]() $i$. Thus, after applying the homomorphism
$i$. Thus, after applying the homomorphism ![]() $r$ in 4.2.3 to the homomorphism
$r$ in 4.2.3 to the homomorphism ![]() $v_{_{Y}}$ in 4.2.4, we obtain the following exact sequence in
$v_{_{Y}}$ in 4.2.4, we obtain the following exact sequence in ![]() ${\mathcal{R}}{\mathcal{C}}(R)$:
${\mathcal{R}}{\mathcal{C}}(R)$:
Moreover, for any ![]() $h\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(S)}(X,Y)$, by applying the homomorphism
$h\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(S)}(X,Y)$, by applying the homomorphism ![]() $r$ to the right part of the commutative diagram in 4.2.4, we obtain the following commutative diagram in
$r$ to the right part of the commutative diagram in 4.2.4, we obtain the following commutative diagram in ![]() ${\mathcal{R}}{\mathcal{C}}(R)$, for some
${\mathcal{R}}{\mathcal{C}}(R)$, for some ![]() $h_{\text{Ker}}$:
$h_{\text{Ker}}$:

4.2.6 The assignment  $\mathbf{Q}_{DT}:{\mathcal{R}}{\mathcal{C}}(S)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ given by
$\mathbf{Q}_{DT}:{\mathcal{R}}{\mathcal{C}}(S)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ given by  $Y\longmapsto \text{Ker}(r(v_{_{Y}}))$ is a functor
$Y\longmapsto \text{Ker}(r(v_{_{Y}}))$ is a functor
By 4.2.5, it is sufficient to prove that ![]() $\mathbf{Q}_{DT}(h):=h_{\text{Ker}}=0$ in
$\mathbf{Q}_{DT}(h):=h_{\text{Ker}}=0$ in ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ provided
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ provided ![]() $h=0$. This is also divided into two steps.
$h=0$. This is also divided into two steps.
Step 1: Consider each piece in the commutative diagram in 4.2.4. If ![]() $h=\{h_{i}\}=0$, then
$h=\{h_{i}\}=0$, then ![]() $h_{i}=0$ for each
$h_{i}=0$ for each ![]() $i$. Thus, we have that
$i$. Thus, we have that ![]() $(h_{G})_{i}(v_{_{Y}})_{i}=0$ and, consequently,
$(h_{G})_{i}(v_{_{Y}})_{i}=0$ and, consequently, ![]() $(h_{G})_{i}=g_{i}(k_{Y})_{i}$ for some
$(h_{G})_{i}=g_{i}(k_{Y})_{i}$ for some ![]() $g_{i}:(G_{X})_{i}\rightarrow (K_{Y})_{i}$. Since
$g_{i}:(G_{X})_{i}\rightarrow (K_{Y})_{i}$. Since ![]() $(K_{Y})_{i}\in {\mathcal{K}}\subseteq _{DT}{\mathcal{X}}$ for all
$(K_{Y})_{i}\in {\mathcal{K}}\subseteq _{DT}{\mathcal{X}}$ for all ![]() $i$, there are exact sequences
$i$, there are exact sequences ![]() $0\rightarrow (K_{Y}^{\prime })_{i}\rightarrow DT_{(K_{Y})_{i}}\stackrel{b_{i}}{\longrightarrow }(K_{Y})_{i}\rightarrow 0$ with
$0\rightarrow (K_{Y}^{\prime })_{i}\rightarrow DT_{(K_{Y})_{i}}\stackrel{b_{i}}{\longrightarrow }(K_{Y})_{i}\rightarrow 0$ with ![]() $DT_{(K_{Y})_{i}}\in \text{add}_{\text{mod}S}DT$ and
$DT_{(K_{Y})_{i}}\in \text{add}_{\text{mod}S}DT$ and ![]() $(K_{Y}^{\prime })_{i}\in {\mathcal{K}}\subseteq \text{KerExt}_{S}^{1}({\mathcal{G}},-)$. It follows that there exists
$(K_{Y}^{\prime })_{i}\in {\mathcal{K}}\subseteq \text{KerExt}_{S}^{1}({\mathcal{G}},-)$. It follows that there exists ![]() $t_{i}\in \text{Hom}_{R}((G_{X})_{i},DT_{(K_{Y})_{i}})$ such that
$t_{i}\in \text{Hom}_{R}((G_{X})_{i},DT_{(K_{Y})_{i}})$ such that ![]() $g_{i}=t_{i}b_{i}$. Altogether, we obtain the following commutative diagram:
$g_{i}=t_{i}b_{i}$. Altogether, we obtain the following commutative diagram:

It follows that there is a commutative diagram in ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)$,
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)$,

where ![]() $DT_{K_{Y}}:=\{DT_{(K_{Y})_{i}}\}$.
$DT_{K_{Y}}:=\{DT_{(K_{Y})_{i}}\}$.
Set ![]() $\unicode[STIX]{x1D6FD}:=bk_{Y}$. Then
$\unicode[STIX]{x1D6FD}:=bk_{Y}$. Then ![]() $\text{R}_{DT}(h_{G})=\text{R}_{DT}(t\unicode[STIX]{x1D6FD})=\text{R}_{DT}(t)\text{R}_{DT}(\unicode[STIX]{x1D6FD})$.
$\text{R}_{DT}(h_{G})=\text{R}_{DT}(t\unicode[STIX]{x1D6FD})=\text{R}_{DT}(t)\text{R}_{DT}(\unicode[STIX]{x1D6FD})$.
Step 2: Consider the commutative diagram in 4.2.5. Since ![]() $(k_{Y})_{i}(v_{_{Y}})_{i}=0$ in 4.2.4, we see that
$(k_{Y})_{i}(v_{_{Y}})_{i}=0$ in 4.2.4, we see that ![]() $\text{R}_{DT}(\unicode[STIX]{x1D6FD})r(v_{_{Y}})=0$ by the definitions. Hence, there is some
$\text{R}_{DT}(\unicode[STIX]{x1D6FD})r(v_{_{Y}})=0$ by the definitions. Hence, there is some ![]() $\unicode[STIX]{x1D703}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(R)}(\text{R}_{DT}(DT_{K_{Y}}),\text{Ker}(r(v_{_{Y}})))$ such that
$\unicode[STIX]{x1D703}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(R)}(\text{R}_{DT}(DT_{K_{Y}}),\text{Ker}(r(v_{_{Y}})))$ such that ![]() $\text{R}_{DT}(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D703}\unicode[STIX]{x1D706}_{r_{Y}}$. Consequently, we have that
$\text{R}_{DT}(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D703}\unicode[STIX]{x1D706}_{r_{Y}}$. Consequently, we have that ![]() $\text{R}_{DT}(h_{G})=\text{R}_{DT}(t)\text{R}_{DT}(\unicode[STIX]{x1D6FD})=\text{R}_{DT}(t)\unicode[STIX]{x1D703}\unicode[STIX]{x1D706}_{r_{Y}}$. Now we obtain that
$\text{R}_{DT}(h_{G})=\text{R}_{DT}(t)\text{R}_{DT}(\unicode[STIX]{x1D6FD})=\text{R}_{DT}(t)\unicode[STIX]{x1D703}\unicode[STIX]{x1D706}_{r_{Y}}$. Now we obtain that ![]() $h_{\text{Ker}}\unicode[STIX]{x1D706}_{r_{Y}}=\unicode[STIX]{x1D706}_{r_{X}}\text{R}_{DT}(h_{G})=\unicode[STIX]{x1D706}_{r_{X}}\text{R}_{DT}(t)\unicode[STIX]{x1D703}\unicode[STIX]{x1D706}_{r_{Y}}$. Since
$h_{\text{Ker}}\unicode[STIX]{x1D706}_{r_{Y}}=\unicode[STIX]{x1D706}_{r_{X}}\text{R}_{DT}(h_{G})=\unicode[STIX]{x1D706}_{r_{X}}\text{R}_{DT}(t)\unicode[STIX]{x1D703}\unicode[STIX]{x1D706}_{r_{Y}}$. Since ![]() $\unicode[STIX]{x1D706}_{r_{Y}}$ is monomorphic, we get that
$\unicode[STIX]{x1D706}_{r_{Y}}$ is monomorphic, we get that ![]() $h_{\text{Ker}}=\unicode[STIX]{x1D706}_{r_{X}}\text{R}_{DT}(t)\unicode[STIX]{x1D703}$, that is, the following diagram is commutative:
$h_{\text{Ker}}=\unicode[STIX]{x1D706}_{r_{X}}\text{R}_{DT}(t)\unicode[STIX]{x1D703}$, that is, the following diagram is commutative:

Note that ![]() $\text{R}_{DT}(DT_{K_{Y}})$ is a projective–injective object in
$\text{R}_{DT}(DT_{K_{Y}})$ is a projective–injective object in ![]() ${\mathcal{R}}{\mathcal{C}}(R)$, so
${\mathcal{R}}{\mathcal{C}}(R)$, so ![]() $h_{\text{Ker}}=0$ in
$h_{\text{Ker}}=0$ in ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$.
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$.
4.2.7 The functor  $\mathbf{Q}_{DT}:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$
$\mathbf{Q}_{DT}:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$
We will show that the functor ![]() $\mathbf{Q}_{DT}$ factors through
$\mathbf{Q}_{DT}$ factors through ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$.
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$.
To see this, it is enough to show that ![]() $\mathbf{Q}_{DT}(X)$ is a projective object in
$\mathbf{Q}_{DT}(X)$ is a projective object in ![]() ${\mathcal{R}}{\mathcal{C}}(R)$, whenever
${\mathcal{R}}{\mathcal{C}}(R)$, whenever ![]() $X$ is a projective object in
$X$ is a projective object in ![]() ${\mathcal{R}}{\mathcal{C}}(S)$.
${\mathcal{R}}{\mathcal{C}}(S)$.
Without loss of generality, we assume that ![]() $X=\{X_{i}\}$ is an indecomposable projective object in
$X=\{X_{i}\}$ is an indecomposable projective object in ![]() ${\mathcal{R}}{\mathcal{C}}(S)$. Thus, we have that
${\mathcal{R}}{\mathcal{C}}(S)$. Thus, we have that ![]() $X$ has the form
$X$ has the form
where ![]() $P$ is indecomposable projective and is on the (
$P$ is indecomposable projective and is on the (![]() $k$+1)th position, for some
$k$+1)th position, for some ![]() $k$; see [Reference Happel18].
$k$; see [Reference Happel18].
Note that ![]() $X_{k+1}=P\in \text{add}_{\text{mod}S}S\subseteq {\mathcal{G}}$ and that
$X_{k+1}=P\in \text{add}_{\text{mod}S}S\subseteq {\mathcal{G}}$ and that ![]() $X_{k}=P\otimes _{S}DS\in \text{add}_{\text{mod}S}DS$
$X_{k}=P\otimes _{S}DS\in \text{add}_{\text{mod}S}DS$![]() $\subseteq {\mathcal{K}}$, so, following 4.2.4, we can choose
$\subseteq {\mathcal{K}}$, so, following 4.2.4, we can choose ![]() $G_{X}$ to be of the form
$G_{X}$ to be of the form
where ![]() $(G_{X})_{k}=DT_{k}\in \text{add}_{\text{mod}S}DT$. And we have an epimorphism
$(G_{X})_{k}=DT_{k}\in \text{add}_{\text{mod}S}DT$. And we have an epimorphism ![]() $v_{_{X}}:G_{X}\rightarrow X$ in
$v_{_{X}}:G_{X}\rightarrow X$ in ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{S}})$ which is of the form
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{S}})$ which is of the form
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ccccccccccccccc@{}}G_{X}: & & \cdots \, & {\rightsquigarrow} & 0 & {\rightsquigarrow} & 0 & {\rightsquigarrow} & P & {\rightsquigarrow} & DT_{k} & {\rightsquigarrow} & 0 & {\rightsquigarrow} & \cdots \\ \downarrow v_{_{X}} & & & & & & & & \downarrow 1 & & \downarrow v_{k} & & & & \\ X: & & \cdots \, & {\rightsquigarrow} & 0 & {\rightsquigarrow} & 0 & {\rightsquigarrow} & P & {\rightsquigarrow} & P\otimes _{S}DS & {\rightsquigarrow} & 0 & {\rightsquigarrow} & \cdots \end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ccccccccccccccc@{}}G_{X}: & & \cdots \, & {\rightsquigarrow} & 0 & {\rightsquigarrow} & 0 & {\rightsquigarrow} & P & {\rightsquigarrow} & DT_{k} & {\rightsquigarrow} & 0 & {\rightsquigarrow} & \cdots \\ \downarrow v_{_{X}} & & & & & & & & \downarrow 1 & & \downarrow v_{k} & & & & \\ X: & & \cdots \, & {\rightsquigarrow} & 0 & {\rightsquigarrow} & 0 & {\rightsquigarrow} & P & {\rightsquigarrow} & P\otimes _{S}DS & {\rightsquigarrow} & 0 & {\rightsquigarrow} & \cdots \end{array} & & \displaystyle \nonumber\end{eqnarray}$$ Then, from the structure of ![]() $r(v_{_{X}})$ in 4.2.3, we can see that
$r(v_{_{X}})$ in 4.2.3, we can see that ![]() $r(v_{_{X}})$ is of the form
$r(v_{_{X}})$ is of the form

where ![]() $\unicode[STIX]{x1D701}_{r_{k}}$ is defined as in 4.2.3 and
$\unicode[STIX]{x1D701}_{r_{k}}$ is defined as in 4.2.3 and ![]() $\unicode[STIX]{x1D6FF}_{R_{k}}$ is defined as in 4.2.1. One checks that both homomorphisms
$\unicode[STIX]{x1D6FF}_{R_{k}}$ is defined as in 4.2.1. One checks that both homomorphisms ![]() $\unicode[STIX]{x1D701}_{r_{k}}$ and
$\unicode[STIX]{x1D701}_{r_{k}}$ and ![]() $\unicode[STIX]{x1D6FF}_{R_{k}}$ are, in fact, isomorphisms. So we obtain that
$\unicode[STIX]{x1D6FF}_{R_{k}}$ are, in fact, isomorphisms. So we obtain that ![]() $\mathbf{Q}_{DT}(X)=\text{Ker}(r(v_{_{X}}))$ is of the form
$\mathbf{Q}_{DT}(X)=\text{Ker}(r(v_{_{X}}))$ is of the form
where ![]() $\unicode[STIX]{x1D6FF}_{k}^{\prime }$ is an induced isomorphism:
$\unicode[STIX]{x1D6FF}_{k}^{\prime }$ is an induced isomorphism: ![]() $\text{Hom}_{S}(DT,DT_{k})\rightarrow \text{Hom}_{R}(DR,DT_{k}\otimes _{S}T)$. Since
$\text{Hom}_{S}(DT,DT_{k})\rightarrow \text{Hom}_{R}(DR,DT_{k}\otimes _{S}T)$. Since ![]() $\text{Hom}_{S}(DT,DT_{k})\in \text{add}_{\text{mod}R}(\text{Hom}_{S}(DT,DT))=\text{add}_{\text{mod}R}R$, we see that
$\text{Hom}_{S}(DT,DT_{k})\in \text{add}_{\text{mod}R}(\text{Hom}_{S}(DT,DT))=\text{add}_{\text{mod}R}R$, we see that ![]() $\text{Hom}_{S}(DT,DT_{k})$ is projective and that
$\text{Hom}_{S}(DT,DT_{k})$ is projective and that ![]() $\mathbf{Q}_{DT}(X)$ is a projective object in
$\mathbf{Q}_{DT}(X)$ is a projective object in ![]() ${\mathcal{R}}{\mathcal{C}}(R)$.
${\mathcal{R}}{\mathcal{C}}(R)$.
It follows that the functor ![]() $\mathbf{Q}_{DT}$ factors through
$\mathbf{Q}_{DT}$ factors through ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$. The induced functor from
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$. The induced functor from ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$ to
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$ to ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ is still denoted by
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ is still denoted by ![]() $\mathbf{Q}_{DT}$.
$\mathbf{Q}_{DT}$.
4.3 The isomorphism  $\mathbf{Q}_{DT}\mathbf{S}_{T}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)}$
$\mathbf{Q}_{DT}\mathbf{S}_{T}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)}$
4.3.1 Computing the composition  $\mathbf{Q}_{DT}\mathbf{S}_{T}$
$\mathbf{Q}_{DT}\mathbf{S}_{T}$
Take any ![]() $X=\{X_{i},\unicode[STIX]{x1D6FF}_{i}^{\otimes }\}\in {\mathcal{R}}{\mathcal{C}}(R)$. From the chosen exact sequence
$X=\{X_{i},\unicode[STIX]{x1D6FF}_{i}^{\otimes }\}\in {\mathcal{R}}{\mathcal{C}}(R)$. From the chosen exact sequence ![]() $0\rightarrow X\stackrel{u_{_{X}}}{\longrightarrow }A_{X}\stackrel{\unicode[STIX]{x1D70B}_{_{_{X}}}}{\longrightarrow }B_{X}\rightarrow 0$ in
$0\rightarrow X\stackrel{u_{_{X}}}{\longrightarrow }A_{X}\stackrel{\unicode[STIX]{x1D70B}_{_{_{X}}}}{\longrightarrow }B_{X}\rightarrow 0$ in ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$ with
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)$ with ![]() $A_{X}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{A}})$ and
$A_{X}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{A}})$ and ![]() $B_{X}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{B}})$, as in 4.1.4, we obtain an exact sequence
$B_{X}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{B}})$, as in 4.1.4, we obtain an exact sequence
by the construction of the functor ![]() $\mathbf{S}_{T}$ in 4.1.5. Note that, for each
$\mathbf{S}_{T}$ in 4.1.5. Note that, for each ![]() $i$,
$i$, ![]() $\mathbf{S}_{T}(X)_{i}$ is given by the pushout diagram
$\mathbf{S}_{T}(X)_{i}$ is given by the pushout diagram

Now we take a projective ![]() $R$-module
$R$-module ![]() $P_{(A_{X})_{i}}$ such that
$P_{(A_{X})_{i}}$ such that ![]() $P_{(A_{X})_{i}}\stackrel{p_{i}}{\longrightarrow }(A_{X})_{i}\rightarrow 0$ is exact. Then we have a pullback diagram
$P_{(A_{X})_{i}}\stackrel{p_{i}}{\longrightarrow }(A_{X})_{i}\rightarrow 0$ is exact. Then we have a pullback diagram

Since ![]() ${\mathcal{B}}$ is closed under kernels of epimorphisms, we see that
${\mathcal{B}}$ is closed under kernels of epimorphisms, we see that ![]() $\overline{X}_{i}\in {\mathcal{B}}$. By applying the functor
$\overline{X}_{i}\in {\mathcal{B}}$. By applying the functor ![]() $-\!\otimes _{R}DT$, the diagram above induces the following commutative diagram with exact rows since
$-\!\otimes _{R}DT$, the diagram above induces the following commutative diagram with exact rows since ![]() ${\mathcal{B}}\subseteq \text{KerTor}_{1}^{R}(-,DT)$:
${\mathcal{B}}\subseteq \text{KerTor}_{1}^{R}(-,DT)$:

Now, one can check that the following diagram is commutative with exact rows, for each ![]() $i$, where the lower row is obtained from the first pushout diagram in this section. Here,
$i$, where the lower row is obtained from the first pushout diagram in this section. Here, ![]() $t_{i}^{P}=(-(q_{i}\otimes _{R}DT)\cdot \unicode[STIX]{x1D703}_{l_{i}},(\overline{u}_{_{X}})_{i}\otimes _{R}DT)$,
$t_{i}^{P}=(-(q_{i}\otimes _{R}DT)\cdot \unicode[STIX]{x1D703}_{l_{i}},(\overline{u}_{_{X}})_{i}\otimes _{R}DT)$, ![]() $t_{i}=(-\unicode[STIX]{x1D703}_{l_{i}},(u_{_{X}})_{i}\otimes _{R}DT)$,
$t_{i}=(-\unicode[STIX]{x1D703}_{l_{i}},(u_{_{X}})_{i}\otimes _{R}DT)$, ![]() $s_{i}^{P}=\big(\!\begin{smallmatrix}s_{i}^{1}\\ (p_{i}\otimes _{R}DT)\cdot s_{i}^{2}\end{smallmatrix}\!\big)$ and
$s_{i}^{P}=\big(\!\begin{smallmatrix}s_{i}^{1}\\ (p_{i}\otimes _{R}DT)\cdot s_{i}^{2}\end{smallmatrix}\!\big)$ and ![]() $s_{i}=\big(\begin{smallmatrix}s_{i}^{1}\\ s_{i}^{2}\end{smallmatrix}\big)$.
$s_{i}=\big(\begin{smallmatrix}s_{i}^{1}\\ s_{i}^{2}\end{smallmatrix}\big)$.

Denote ![]() $\mathfrak{L}_{A_{X}}^{P}:=\{\text{Hom}_{R}(T,(A_{X})_{i-1})\oplus P_{(A_{X})_{i}}\otimes _{R}DT\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)$. Note that
$\mathfrak{L}_{A_{X}}^{P}:=\{\text{Hom}_{R}(T,(A_{X})_{i-1})\oplus P_{(A_{X})_{i}}\otimes _{R}DT\}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)$. Note that ![]() $\overline{X}_{i}\otimes _{R}DT\in {\mathcal{K}}$ and
$\overline{X}_{i}\otimes _{R}DT\in {\mathcal{K}}$ and ![]() $\text{Hom}_{R}(T,(A_{X})_{i-1})\oplus P_{(A_{X})_{i}}\otimes _{R}DT\in {\mathcal{G}}$, so we have an exact sequence in
$\text{Hom}_{R}(T,(A_{X})_{i-1})\oplus P_{(A_{X})_{i}}\otimes _{R}DT\in {\mathcal{G}}$, so we have an exact sequence in ![]() ${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)$ from the first row in the above commutative diagram
${\mathcal{R}}{\mathcal{C}}^{\text{tr}}(S)$ from the first row in the above commutative diagram
with ![]() $\overline{X}\otimes _{R}DT\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{K}})$ and
$\overline{X}\otimes _{R}DT\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{K}})$ and ![]() $\mathfrak{L}_{A_{X}}^{P}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{G}})$, as in 4.2.4. By applying the homomorphism
$\mathfrak{L}_{A_{X}}^{P}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}({\mathcal{G}})$, as in 4.2.4. By applying the homomorphism ![]() $r$ in 4.2.3 to the homomorphism
$r$ in 4.2.3 to the homomorphism ![]() $s^{P}:\mathfrak{L}_{A_{X}}^{P}\rightarrow \mathbf{S}_{T}(X)$, we have an exact sequence in
$s^{P}:\mathfrak{L}_{A_{X}}^{P}\rightarrow \mathbf{S}_{T}(X)$, we have an exact sequence in ![]() ${\mathcal{R}}{\mathcal{C}}(R)$ by the construction of the functor
${\mathcal{R}}{\mathcal{C}}(R)$ by the construction of the functor ![]() $\mathbf{Q}_{DT}$ in 4.2.5
$\mathbf{Q}_{DT}$ in 4.2.5
where ![]() $r(s^{P})$ is defined as in 4.2.3.
$r(s^{P})$ is defined as in 4.2.3.
4.3.2 The object  $X\oplus \text{L}_{R}(P_{A_{X}}^{+})$ in
$X\oplus \text{L}_{R}(P_{A_{X}}^{+})$ in  ${\mathcal{R}}{\mathcal{C}}(R)$
${\mathcal{R}}{\mathcal{C}}(R)$
Denote ![]() $P_{A_{X}}^{+}:=\{P_{(A_{X})_{i+1}}\}$, then
$P_{A_{X}}^{+}:=\{P_{(A_{X})_{i+1}}\}$, then ![]() $P_{A_{X}}^{+}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(\text{add}_{\text{mod}R}R)$. Applying the functor
$P_{A_{X}}^{+}\in {\mathcal{R}}{\mathcal{C}}^{\text{tr}}(\text{add}_{\text{mod}R}R)$. Applying the functor ![]() $\text{L}_{R}$ in the remark in 4.1.1, we obtain that
$\text{L}_{R}$ in the remark in 4.1.1, we obtain that ![]() $\text{L}_{R}(P_{A_{X}}^{+})$ is a projective object in
$\text{L}_{R}(P_{A_{X}}^{+})$ is a projective object in ![]() ${\mathcal{R}}{\mathcal{C}}(R)$. Hence, the object
${\mathcal{R}}{\mathcal{C}}(R)$. Hence, the object ![]() $X\oplus \text{L}_{R}(P_{A_{X}}^{+})$ is isomorphic to
$X\oplus \text{L}_{R}(P_{A_{X}}^{+})$ is isomorphic to ![]() $X$ in
$X$ in ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$.
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$.
We will prove that ![]() $\mathbf{Q}_{DT}\mathbf{S}_{T}(X)\simeq X\oplus \text{L}_{R}(P_{A_{X}}^{+})$ naturally. And then,
$\mathbf{Q}_{DT}\mathbf{S}_{T}(X)\simeq X\oplus \text{L}_{R}(P_{A_{X}}^{+})$ naturally. And then, ![]() $\mathbf{Q}_{DT}\mathbf{S}_{T}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)}$.
$\mathbf{Q}_{DT}\mathbf{S}_{T}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)}$.
The general strategy is as follows. First, we construct a natural homomorphism ![]() $\unicode[STIX]{x1D709}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})$. Second, we show that
$\unicode[STIX]{x1D709}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})$. Second, we show that ![]() $\unicode[STIX]{x1D709}\cdot r(s^{P})=0$, that is, the composition of
$\unicode[STIX]{x1D709}\cdot r(s^{P})=0$, that is, the composition of ![]() $\unicode[STIX]{x1D709}$ and the homomorphism
$\unicode[STIX]{x1D709}$ and the homomorphism ![]() $r(s^{P}):\text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})\rightarrow \hat{\text{H}}\text{om}(DT,\mathbf{S}_{T}(X))$ in the exact sequence above is 0. Thus, we obtain a homomorphism
$r(s^{P}):\text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})\rightarrow \hat{\text{H}}\text{om}(DT,\mathbf{S}_{T}(X))$ in the exact sequence above is 0. Thus, we obtain a homomorphism ![]() $\unicode[STIX]{x1D719}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \mathbf{Q}_{DT}\mathbf{S}_{T}(X)$. Finally, we prove that
$\unicode[STIX]{x1D719}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \mathbf{Q}_{DT}\mathbf{S}_{T}(X)$. Finally, we prove that ![]() $\unicode[STIX]{x1D719}$ is indeed a natural isomorphism.
$\unicode[STIX]{x1D719}$ is indeed a natural isomorphism.
4.3.3 The homomorphism  $\unicode[STIX]{x1D709}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})$
$\unicode[STIX]{x1D709}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})$
Recall from the construction in 4.3.1 that ![]() $X=\{X_{i},\unicode[STIX]{x1D6FF}_{i}^{\otimes }\}$ and,
$X=\{X_{i},\unicode[STIX]{x1D6FF}_{i}^{\otimes }\}$ and,
![]() $\text{L}_{R}(P_{A_{X}}^{+})=\{\text{Hom}_{R}(R,P_{(A_{X})_{i}})\oplus P_{(A_{X})_{i+1}}\otimes _{R}DR\}=\{P_{(A_{X})_{i}}\oplus P_{(A_{X})_{i+1}}\otimes _{R}DR\}$, where the structure map
$\text{L}_{R}(P_{A_{X}}^{+})=\{\text{Hom}_{R}(R,P_{(A_{X})_{i}})\oplus P_{(A_{X})_{i+1}}\otimes _{R}DR\}=\{P_{(A_{X})_{i}}\oplus P_{(A_{X})_{i+1}}\otimes _{R}DR\}$, where the structure map ![]() $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(\text{L}_{R}(P_{A_{X}}^{+})):(\text{L}_{R}(P_{A_{X}}^{+}))_{i}\otimes DR\rightarrow (\text{L}_{R}(P_{A_{X}}^{+}))_{i-1}$ is given by
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(\text{L}_{R}(P_{A_{X}}^{+})):(\text{L}_{R}(P_{A_{X}}^{+}))_{i}\otimes DR\rightarrow (\text{L}_{R}(P_{A_{X}}^{+}))_{i-1}$ is given by ![]() $\big(\begin{smallmatrix}0 & 1_{P_{(A_{X})_{i}}\otimes _{R}DR}\\ 0 & 0\end{smallmatrix}\!\big)$, and that
$\big(\begin{smallmatrix}0 & 1_{P_{(A_{X})_{i}}\otimes _{R}DR}\\ 0 & 0\end{smallmatrix}\!\big)$, and that
 $$\begin{eqnarray}\displaystyle \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P}) & = & \displaystyle \{\text{Hom}_{S}(DT,(\mathfrak{L}_{A_{X}}^{P})_{i})\oplus (\mathfrak{L}_{A_{X}}^{P})_{i+1}\otimes _{S}T\}\nonumber\\ \displaystyle & = & \displaystyle \{\text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1})\oplus P_{(A_{X})_{i}}\otimes _{R}DT)\nonumber\\ \displaystyle & & \displaystyle \oplus \,(\text{Hom}_{R}(T,(A_{X})_{i})\oplus P_{(A_{X})_{i+1}}\otimes _{R}DT)\otimes _{S}T\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P}) & = & \displaystyle \{\text{Hom}_{S}(DT,(\mathfrak{L}_{A_{X}}^{P})_{i})\oplus (\mathfrak{L}_{A_{X}}^{P})_{i+1}\otimes _{S}T\}\nonumber\\ \displaystyle & = & \displaystyle \{\text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1})\oplus P_{(A_{X})_{i}}\otimes _{R}DT)\nonumber\\ \displaystyle & & \displaystyle \oplus \,(\text{Hom}_{R}(T,(A_{X})_{i})\oplus P_{(A_{X})_{i+1}}\otimes _{R}DT)\otimes _{S}T\},\nonumber\end{eqnarray}$$where the structure map
is defined in 4.2.1.
By the definition, we have that ![]() $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(\text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P}))=\bigg(\!\begin{smallmatrix}0 & 0 & \unicode[STIX]{x1D6FE}_{i}^{11} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D6FE}_{i}^{22}\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\end{smallmatrix}\!\bigg)$, where
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(\text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P}))=\bigg(\!\begin{smallmatrix}0 & 0 & \unicode[STIX]{x1D6FE}_{i}^{11} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D6FE}_{i}^{22}\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\end{smallmatrix}\!\bigg)$, where
![]() $\unicode[STIX]{x1D6FE}_{i}^{11}:\text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1}))\otimes _{R}DR\rightarrow \text{Hom}_{R}(T,(A_{X})_{i-1})\otimes _{S}T$ is given by the composition
$\unicode[STIX]{x1D6FE}_{i}^{11}:\text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1}))\otimes _{R}DR\rightarrow \text{Hom}_{R}(T,(A_{X})_{i-1})\otimes _{S}T$ is given by the composition
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FE}_{i}^{11}:\text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1}))\otimes _{R}DR\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1}))\otimes _{R}DT\otimes _{S}T\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\unicode[STIX]{x1D716}_{\text{Hom}_{R}(T,(A_{X})_{i-1})}^{DT}\otimes _{S}T}{\longrightarrow }\text{Hom}_{R}(T,(A_{X})_{i-1})\otimes _{S}T,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FE}_{i}^{11}:\text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1}))\otimes _{R}DR\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1}))\otimes _{R}DT\otimes _{S}T\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\unicode[STIX]{x1D716}_{\text{Hom}_{R}(T,(A_{X})_{i-1})}^{DT}\otimes _{S}T}{\longrightarrow }\text{Hom}_{R}(T,(A_{X})_{i-1})\otimes _{S}T,\nonumber\end{eqnarray}$$ and ![]() $\unicode[STIX]{x1D6FE}_{i}^{22}:\text{Hom}_{S}(DT,P_{(A_{X})_{i}}\otimes _{R}DT)\otimes _{R}DR\rightarrow P_{(A_{X})_{i}}\otimes _{R}DT\otimes _{S}T$ is defined similarly as
$\unicode[STIX]{x1D6FE}_{i}^{22}:\text{Hom}_{S}(DT,P_{(A_{X})_{i}}\otimes _{R}DT)\otimes _{R}DR\rightarrow P_{(A_{X})_{i}}\otimes _{R}DT\otimes _{S}T$ is defined similarly as ![]() $\unicode[STIX]{x1D6FE}_{i}^{11}$ by replacing
$\unicode[STIX]{x1D6FE}_{i}^{11}$ by replacing ![]() $\text{Hom}_{R}(T,(A_{X})_{i-1})$ with
$\text{Hom}_{R}(T,(A_{X})_{i-1})$ with ![]() $P_{(A_{X})_{i}}\otimes _{R}DT$.
$P_{(A_{X})_{i}}\otimes _{R}DT$.
Let ![]() $\unicode[STIX]{x1D709}=\{\unicode[STIX]{x1D709}_{i}\}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})$ be a homomorphism. We may assume that
$\unicode[STIX]{x1D709}=\{\unicode[STIX]{x1D709}_{i}\}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})$ be a homomorphism. We may assume that ![]() $\unicode[STIX]{x1D709}_{i}=(\unicode[STIX]{x1D709}_{i}^{a},\unicode[STIX]{x1D709}_{i}^{b})$, where
$\unicode[STIX]{x1D709}_{i}=(\unicode[STIX]{x1D709}_{i}^{a},\unicode[STIX]{x1D709}_{i}^{b})$, where
and
4.3.3.1 The homomorphism  $\unicode[STIX]{x1D709}_{i}^{a}$ in
$\unicode[STIX]{x1D709}_{i}^{a}$ in  $\text{mod}R$
$\text{mod}R$
We set ![]() $\unicode[STIX]{x1D709}_{i}^{a}=\bigg(\!\begin{smallmatrix}\unicode[STIX]{x1D709}_{i}^{a_{11}} & \unicode[STIX]{x1D709}_{i}^{a_{12}}\\ \unicode[STIX]{x1D709}_{i}^{a_{21}} & \unicode[STIX]{x1D709}_{i}^{a_{22}}\\ \unicode[STIX]{x1D709}_{i}^{a_{31}} & \unicode[STIX]{x1D709}_{i}^{a_{32}}\end{smallmatrix}\!\bigg)$:
$\unicode[STIX]{x1D709}_{i}^{a}=\bigg(\!\begin{smallmatrix}\unicode[STIX]{x1D709}_{i}^{a_{11}} & \unicode[STIX]{x1D709}_{i}^{a_{12}}\\ \unicode[STIX]{x1D709}_{i}^{a_{21}} & \unicode[STIX]{x1D709}_{i}^{a_{22}}\\ \unicode[STIX]{x1D709}_{i}^{a_{31}} & \unicode[STIX]{x1D709}_{i}^{a_{32}}\end{smallmatrix}\!\bigg)$:
Using the isomorphism ![]() $_{S}DS_{S}\simeq _{S}T\otimes _{R}DT_{S}$ and the adjoint isomorphism
$_{S}DS_{S}\simeq _{S}T\otimes _{R}DT_{S}$ and the adjoint isomorphism
we define the components of ![]() $\unicode[STIX]{x1D709}_{i}^{a}$ as follows.
$\unicode[STIX]{x1D709}_{i}^{a}$ as follows.
![]() $\bullet$ The morphism
$\bullet$ The morphism ![]() $\unicode[STIX]{x1D709}_{i}^{a_{11}}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(\unicode[STIX]{x1D703}_{l_{i}}):$
$\unicode[STIX]{x1D709}_{i}^{a_{11}}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(\unicode[STIX]{x1D703}_{l_{i}}):$![]() $X_{i}\rightarrow \text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1}))$, where
$X_{i}\rightarrow \text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1}))$, where ![]() $\unicode[STIX]{x1D703}_{l_{i}}:X_{i}\otimes _{R}DT\rightarrow \text{Hom}_{R}(T,(A_{X})_{i-1})$ is defined in 4.1.3.
$\unicode[STIX]{x1D703}_{l_{i}}:X_{i}\otimes _{R}DT\rightarrow \text{Hom}_{R}(T,(A_{X})_{i-1})$ is defined in 4.1.3.
In other words, the morphism ![]() $\unicode[STIX]{x1D709}_{i}^{a_{11}}$ is given by the composition:
$\unicode[STIX]{x1D709}_{i}^{a_{11}}$ is given by the composition:
and some natural isomorphisms
 $$\begin{eqnarray}\displaystyle & & \displaystyle X_{i}\stackrel{\unicode[STIX]{x1D702}_{_{X_{i}}}^{DR}}{\longrightarrow }\text{Hom}_{R}(DR,X_{i}\otimes _{R}DR)\stackrel{\text{Hom}_{R}(DR,\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X))}{\longrightarrow }\text{Hom}_{R}(DR,X_{i-1})\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\text{Hom}_{R}(DR,(u_{_{X}})_{i-1})}{\longrightarrow }\text{Hom}_{R}(DR,(A_{X})_{i-1})\simeq \text{Hom}_{R}(DT\otimes _{S}T,(A_{X})_{i-1})\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle X_{i}\stackrel{\unicode[STIX]{x1D702}_{_{X_{i}}}^{DR}}{\longrightarrow }\text{Hom}_{R}(DR,X_{i}\otimes _{R}DR)\stackrel{\text{Hom}_{R}(DR,\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X))}{\longrightarrow }\text{Hom}_{R}(DR,X_{i-1})\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\text{Hom}_{R}(DR,(u_{_{X}})_{i-1})}{\longrightarrow }\text{Hom}_{R}(DR,(A_{X})_{i-1})\simeq \text{Hom}_{R}(DT\otimes _{S}T,(A_{X})_{i-1})\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1})).\nonumber\end{eqnarray}$$ ![]() $\bullet$ The morphism
$\bullet$ The morphism
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D709}_{i}^{a_{22}} & = & \displaystyle \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(1_{(P_{(A_{X})_{i}}\otimes _{R}DT)})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D702}_{_{P_{(A_{X})_{i}}}}^{DT}:P_{(A_{X})_{i}}\rightarrow \text{Hom}_{S}(DT,P_{(A_{X})_{i}}\otimes _{R}DT).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D709}_{i}^{a_{22}} & = & \displaystyle \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(1_{(P_{(A_{X})_{i}}\otimes _{R}DT)})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D702}_{_{P_{(A_{X})_{i}}}}^{DT}:P_{(A_{X})_{i}}\rightarrow \text{Hom}_{S}(DT,P_{(A_{X})_{i}}\otimes _{R}DT).\nonumber\end{eqnarray}$$ ![]() $\bullet$ The remaining morphisms
$\bullet$ The remaining morphisms ![]() $\unicode[STIX]{x1D709}_{i}^{a_{12}},\unicode[STIX]{x1D709}_{i}^{a_{21}},\unicode[STIX]{x1D709}_{i}^{a_{31}},\unicode[STIX]{x1D709}_{i}^{a_{32}}$ are all
$\unicode[STIX]{x1D709}_{i}^{a_{12}},\unicode[STIX]{x1D709}_{i}^{a_{21}},\unicode[STIX]{x1D709}_{i}^{a_{31}},\unicode[STIX]{x1D709}_{i}^{a_{32}}$ are all ![]() $0$.
$0$.
So we have that ![]() $\unicode[STIX]{x1D709}_{i}^{a}=\bigg(\!\begin{smallmatrix}\unicode[STIX]{x1D709}_{i}^{a_{11}} & 0\\ 0 & \unicode[STIX]{x1D709}_{i}^{a_{22}}\\ 0 & 0\end{smallmatrix}\!\bigg)$, where
$\unicode[STIX]{x1D709}_{i}^{a}=\bigg(\!\begin{smallmatrix}\unicode[STIX]{x1D709}_{i}^{a_{11}} & 0\\ 0 & \unicode[STIX]{x1D709}_{i}^{a_{22}}\\ 0 & 0\end{smallmatrix}\!\bigg)$, where
4.3.3.2 The homomorphism  $\unicode[STIX]{x1D709}_{i}^{b}$ in
$\unicode[STIX]{x1D709}_{i}^{b}$ in  $\text{mod}R$
$\text{mod}R$
We set  $\unicode[STIX]{x1D709}_{i}^{b}=\bigg(\!\begin{smallmatrix}\unicode[STIX]{x1D709}_{i}^{b_{11}} & \unicode[STIX]{x1D709}_{i}^{b_{12}}\\ \unicode[STIX]{x1D709}_{i}^{b_{21}} & \unicode[STIX]{x1D709}_{i}^{b_{22}}\\ \unicode[STIX]{x1D709}_{i}^{b_{31}} & \unicode[STIX]{x1D709}_{i}^{b_{32}}\end{smallmatrix}\!\bigg)$:
$\unicode[STIX]{x1D709}_{i}^{b}=\bigg(\!\begin{smallmatrix}\unicode[STIX]{x1D709}_{i}^{b_{11}} & \unicode[STIX]{x1D709}_{i}^{b_{12}}\\ \unicode[STIX]{x1D709}_{i}^{b_{21}} & \unicode[STIX]{x1D709}_{i}^{b_{22}}\\ \unicode[STIX]{x1D709}_{i}^{b_{31}} & \unicode[STIX]{x1D709}_{i}^{b_{32}}\end{smallmatrix}\!\bigg)$:
where the components are defined naturally as follows.
∙ The morphism
 $\unicode[STIX]{x1D709}_{i}^{b_{11}}=(u_{_{X}})_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1}:X_{i}\rightarrow \text{Hom}_{R}(T,(A_{X})_{i})\otimes _{S}T$ (note that
$\unicode[STIX]{x1D709}_{i}^{b_{11}}=(u_{_{X}})_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1}:X_{i}\rightarrow \text{Hom}_{R}(T,(A_{X})_{i})\otimes _{S}T$ (note that  $\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T}$ is an isomorphism since
$\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T}$ is an isomorphism since  $(A_{X})_{i}\in {\mathcal{A}}$), that is, is given by the composition
$(A_{X})_{i}\in {\mathcal{A}}$), that is, is given by the composition  $$\begin{eqnarray}X_{i}\stackrel{(u_{_{X}})_{i}}{\longrightarrow }(A_{X})_{i}\stackrel{(\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1}}{\longrightarrow }\text{Hom}_{R}(T,(A_{X})_{i})\otimes _{S}T.\end{eqnarray}$$
$$\begin{eqnarray}X_{i}\stackrel{(u_{_{X}})_{i}}{\longrightarrow }(A_{X})_{i}\stackrel{(\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1}}{\longrightarrow }\text{Hom}_{R}(T,(A_{X})_{i})\otimes _{S}T.\end{eqnarray}$$∙ The morphism
 $\unicode[STIX]{x1D709}_{i}^{b_{21}}=p_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1}:P_{(A_{X})_{i}}\rightarrow \text{Hom}_{R}(T,(A_{X})_{i})\otimes _{S}T$, that is, is given by the composition
$\unicode[STIX]{x1D709}_{i}^{b_{21}}=p_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1}:P_{(A_{X})_{i}}\rightarrow \text{Hom}_{R}(T,(A_{X})_{i})\otimes _{S}T$, that is, is given by the composition  $$\begin{eqnarray}P_{(A_{X})_{i}}\stackrel{p_{i}}{\longrightarrow }(A_{X})_{i}\stackrel{(\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1}}{\longrightarrow }\text{Hom}_{R}(T,(A_{X})_{i})\otimes _{S}T.\end{eqnarray}$$
$$\begin{eqnarray}P_{(A_{X})_{i}}\stackrel{p_{i}}{\longrightarrow }(A_{X})_{i}\stackrel{(\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1}}{\longrightarrow }\text{Hom}_{R}(T,(A_{X})_{i})\otimes _{S}T.\end{eqnarray}$$∙ The morphism
 $\unicode[STIX]{x1D709}_{i}^{b_{32}}:P_{(A_{X})_{i+1}}\otimes _{R}DR\rightarrow P_{(A_{X})_{i+1}}\otimes _{R}DT\otimes _{S}T$ is the natural isomorphism given by
$\unicode[STIX]{x1D709}_{i}^{b_{32}}:P_{(A_{X})_{i+1}}\otimes _{R}DR\rightarrow P_{(A_{X})_{i+1}}\otimes _{R}DT\otimes _{S}T$ is the natural isomorphism given by  $_{R}(DT\otimes _{S}T)_{R}\simeq _{R}DR_{R}$.
$_{R}(DT\otimes _{S}T)_{R}\simeq _{R}DR_{R}$.∙ The remaining morphisms
 $\unicode[STIX]{x1D709}_{i}^{b_{12}},\unicode[STIX]{x1D709}_{i}^{b_{22}},\unicode[STIX]{x1D709}_{i}^{b_{31}}$ are all
$\unicode[STIX]{x1D709}_{i}^{b_{12}},\unicode[STIX]{x1D709}_{i}^{b_{22}},\unicode[STIX]{x1D709}_{i}^{b_{31}}$ are all  $0$.
$0$.
So we have that  $\unicode[STIX]{x1D709}_{i}^{b}=\bigg(\!\begin{smallmatrix}\unicode[STIX]{x1D709}_{i}^{b_{11}} & 0\\ \unicode[STIX]{x1D709}_{i}^{b_{21}} & 0\\ 0 & \unicode[STIX]{x1D709}_{i}^{b_{32}}\end{smallmatrix}\!\bigg)$, where
$\unicode[STIX]{x1D709}_{i}^{b}=\bigg(\!\begin{smallmatrix}\unicode[STIX]{x1D709}_{i}^{b_{11}} & 0\\ \unicode[STIX]{x1D709}_{i}^{b_{21}} & 0\\ 0 & \unicode[STIX]{x1D709}_{i}^{b_{32}}\end{smallmatrix}\!\bigg)$, where ![]() $\unicode[STIX]{x1D709}_{i}^{b_{11}}=(u_{_{X}})_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1}$,
$\unicode[STIX]{x1D709}_{i}^{b_{11}}=(u_{_{X}})_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1}$, ![]() $\unicode[STIX]{x1D709}_{i}^{b_{21}}=p_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1}$, and
$\unicode[STIX]{x1D709}_{i}^{b_{21}}=p_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1}$, and ![]() $\unicode[STIX]{x1D709}_{i}^{b_{32}}$ is the natural isomorphism.
$\unicode[STIX]{x1D709}_{i}^{b_{32}}$ is the natural isomorphism.
4.3.3.3  $\unicode[STIX]{x1D709}$ is a homomorphism in
$\unicode[STIX]{x1D709}$ is a homomorphism in  ${\mathcal{R}}{\mathcal{C}}(R)$
${\mathcal{R}}{\mathcal{C}}(R)$
We now show that the above-defined morphism ![]() $\unicode[STIX]{x1D709}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})$ is compatible with structure maps, that is,
$\unicode[STIX]{x1D709}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})$ is compatible with structure maps, that is,
holds for each ![]() $i$.
$i$.
Indeed, by the involved definitions, we have that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D709}_{i}\otimes _{R}DR\cdot \unicode[STIX]{x1D6FF}_{i}^{\otimes }(\text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})) & = & \displaystyle \left(\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D709}_{i}^{a_{11}} & 0 & \unicode[STIX]{x1D709}_{i}^{b_{11}} & 0\\ 0 & \unicode[STIX]{x1D709}_{i}^{a_{22}} & \unicode[STIX]{x1D709}_{i}^{b_{21}} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D709}_{i}^{b_{32}}\end{array}\right)\otimes _{R}DR\cdot \left(\begin{array}{@{}cccc@{}}0 & 0 & \unicode[STIX]{x1D6FE}_{i}^{11} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D6FE}_{i}^{22}\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\end{array}\right)\nonumber\\ \displaystyle & = & \displaystyle \left(\begin{array}{@{}cccc@{}}0 & 0 & \unicode[STIX]{x1D709}_{i}^{a_{11}}\otimes _{R}DR\cdot \unicode[STIX]{x1D6FE}_{i}^{11} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D709}_{i}^{a_{22}}\otimes _{R}DR\cdot \unicode[STIX]{x1D6FE}_{i}^{22}\\ 0 & 0 & 0 & 0\end{array}\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D709}_{i}\otimes _{R}DR\cdot \unicode[STIX]{x1D6FF}_{i}^{\otimes }(\text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})) & = & \displaystyle \left(\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D709}_{i}^{a_{11}} & 0 & \unicode[STIX]{x1D709}_{i}^{b_{11}} & 0\\ 0 & \unicode[STIX]{x1D709}_{i}^{a_{22}} & \unicode[STIX]{x1D709}_{i}^{b_{21}} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D709}_{i}^{b_{32}}\end{array}\right)\otimes _{R}DR\cdot \left(\begin{array}{@{}cccc@{}}0 & 0 & \unicode[STIX]{x1D6FE}_{i}^{11} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D6FE}_{i}^{22}\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\end{array}\right)\nonumber\\ \displaystyle & = & \displaystyle \left(\begin{array}{@{}cccc@{}}0 & 0 & \unicode[STIX]{x1D709}_{i}^{a_{11}}\otimes _{R}DR\cdot \unicode[STIX]{x1D6FE}_{i}^{11} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D709}_{i}^{a_{22}}\otimes _{R}DR\cdot \unicode[STIX]{x1D6FE}_{i}^{22}\\ 0 & 0 & 0 & 0\end{array}\right)\nonumber\end{eqnarray}$$and that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{i}^{\otimes }(X\oplus \text{L}_{R}(P_{A_{X}}^{+}))\cdot \unicode[STIX]{x1D709}_{i-1} & = & \displaystyle \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X) & 0 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0\end{array}\right)\left(\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D709}_{i-1}^{a_{11}} & 0 & \unicode[STIX]{x1D709}_{i-1}^{b_{11}} & 0\\ 0 & \unicode[STIX]{x1D709}_{i-1}^{a_{22}} & \unicode[STIX]{x1D709}_{i-1}^{b_{21}} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D709}_{i-1}^{b_{32}}\end{array}\right)\nonumber\\ \displaystyle & = & \displaystyle \left(\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D709}_{i-1}^{a_{11}} & 0 & \unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D709}_{i-1}^{b_{11}} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D709}_{i-1}^{b_{32}}\\ 0 & 0 & 0 & 0\end{array}\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{i}^{\otimes }(X\oplus \text{L}_{R}(P_{A_{X}}^{+}))\cdot \unicode[STIX]{x1D709}_{i-1} & = & \displaystyle \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X) & 0 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0\end{array}\right)\left(\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D709}_{i-1}^{a_{11}} & 0 & \unicode[STIX]{x1D709}_{i-1}^{b_{11}} & 0\\ 0 & \unicode[STIX]{x1D709}_{i-1}^{a_{22}} & \unicode[STIX]{x1D709}_{i-1}^{b_{21}} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D709}_{i-1}^{b_{32}}\end{array}\right)\nonumber\\ \displaystyle & = & \displaystyle \left(\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D709}_{i-1}^{a_{11}} & 0 & \unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D709}_{i-1}^{b_{11}} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D709}_{i-1}^{b_{32}}\\ 0 & 0 & 0 & 0\end{array}\right)\nonumber\end{eqnarray}$$∙
 $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D709}_{i-1}^{a_{11}}=0$. In fact, since
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D709}_{i-1}^{a_{11}}=0$. In fact, since  $\unicode[STIX]{x1D709}_{i-1}^{a_{11}}$ is the composition of the morphism
$\unicode[STIX]{x1D709}_{i-1}^{a_{11}}$ is the composition of the morphism  $\unicode[STIX]{x1D6FF}_{i-1}^{\text{H}}(X)\cdot \text{Hom}_{R}(DR,(u_{_{X}})_{i-2})$ and some natural isomorphisms by the construction, we see that
$\unicode[STIX]{x1D6FF}_{i-1}^{\text{H}}(X)\cdot \text{Hom}_{R}(DR,(u_{_{X}})_{i-2})$ and some natural isomorphisms by the construction, we see that  $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D709}_{i-1}^{a_{11}}$ factors through
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D709}_{i-1}^{a_{11}}$ factors through  $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D6FF}_{i-1}^{\text{H}}(X)$. But the latter is 0 as
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D6FF}_{i-1}^{\text{H}}(X)$. But the latter is 0 as  $X$ is a repe-complex. Thus,
$X$ is a repe-complex. Thus,  $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D709}_{i-1}^{a_{11}}=0$.
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D709}_{i-1}^{a_{11}}=0$.∙
 $\unicode[STIX]{x1D709}_{i}^{a_{11}}\otimes _{R}DR\cdot \unicode[STIX]{x1D6FE}_{i}^{11}=\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D709}_{i-1}^{b_{11}}$. This follows from the involved definitions and the following commutative diagram:where
$\unicode[STIX]{x1D709}_{i}^{a_{11}}\otimes _{R}DR\cdot \unicode[STIX]{x1D6FE}_{i}^{11}=\unicode[STIX]{x1D6FF}_{i}^{\otimes }(X)\cdot \unicode[STIX]{x1D709}_{i-1}^{b_{11}}$. This follows from the involved definitions and the following commutative diagram:where
 $\unicode[STIX]{x1D714}:=\unicode[STIX]{x1D716}_{\text{Hom}_{R}(T,(A_{X})_{i-1})}^{DT}\otimes _{S}T$. The last square is commutative since
$\unicode[STIX]{x1D714}:=\unicode[STIX]{x1D716}_{\text{Hom}_{R}(T,(A_{X})_{i-1})}^{DT}\otimes _{S}T$. The last square is commutative since  $\unicode[STIX]{x1D716}_{M}^{DT\otimes _{S}T}=\unicode[STIX]{x1D716}_{\text{Hom}_{R}(T,M)}^{DT}\otimes _{S}T\cdot \unicode[STIX]{x1D716}_{M}^{T}$.
$\unicode[STIX]{x1D716}_{M}^{DT\otimes _{S}T}=\unicode[STIX]{x1D716}_{\text{Hom}_{R}(T,M)}^{DT}\otimes _{S}T\cdot \unicode[STIX]{x1D716}_{M}^{T}$.∙
 $\unicode[STIX]{x1D709}_{i}^{a_{22}}\otimes _{R}DR\cdot \unicode[STIX]{x1D6FE}_{i}^{22}=\unicode[STIX]{x1D709}_{i-1}^{b_{32}}$. This follows from the involved definitions and the equality
$\unicode[STIX]{x1D709}_{i}^{a_{22}}\otimes _{R}DR\cdot \unicode[STIX]{x1D6FE}_{i}^{22}=\unicode[STIX]{x1D709}_{i-1}^{b_{32}}$. This follows from the involved definitions and the equality  $1_{(P_{(A_{X})_{i}}\otimes _{R}DT)}=\unicode[STIX]{x1D702}_{(P_{(A_{X})_{i}})}^{DT}\otimes _{R}DT\cdot \unicode[STIX]{x1D716}_{(P_{(A_{X})_{i}}\otimes _{R}DT)}^{DT}$.
$1_{(P_{(A_{X})_{i}}\otimes _{R}DT)}=\unicode[STIX]{x1D702}_{(P_{(A_{X})_{i}})}^{DT}\otimes _{R}DT\cdot \unicode[STIX]{x1D716}_{(P_{(A_{X})_{i}}\otimes _{R}DT)}^{DT}$.
Then we can easily conclude that the morphism ![]() $\unicode[STIX]{x1D709}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})$ is, in fact, a homomorphism in
$\unicode[STIX]{x1D709}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})$ is, in fact, a homomorphism in ![]() ${\mathcal{R}}{\mathcal{C}}(R)$.
${\mathcal{R}}{\mathcal{C}}(R)$.
4.3.4 The composition  $\unicode[STIX]{x1D709}\cdot r(s^{P})=0$, and so
$\unicode[STIX]{x1D709}\cdot r(s^{P})=0$, and so  $\unicode[STIX]{x1D709}$ factors through a homomorphism
$\unicode[STIX]{x1D709}$ factors through a homomorphism  $\unicode[STIX]{x1D719}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \mathbf{Q}_{DT}\mathbf{S}_{T}(X)$
$\unicode[STIX]{x1D719}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \mathbf{Q}_{DT}\mathbf{S}_{T}(X)$
4.3.4.1 The analysis of the homomorphism  $s:\text{L}_{T}(A_{X})\rightarrow \mathbf{S}_{T}(X)$ in 4.3.1
$s:\text{L}_{T}(A_{X})\rightarrow \mathbf{S}_{T}(X)$ in 4.3.1
Recall from 4.3.1 that ![]() $s=\{s_{i}\}:\text{L}_{T}(A_{X})\rightarrow \mathbf{S}_{T}(X)$ is a homomorphism in
$s=\{s_{i}\}:\text{L}_{T}(A_{X})\rightarrow \mathbf{S}_{T}(X)$ is a homomorphism in ![]() ${\mathcal{R}}{\mathcal{C}}(S)$ which is the cokernel of the homomorphism
${\mathcal{R}}{\mathcal{C}}(S)$ which is the cokernel of the homomorphism ![]() $l(u_{_{X}})$. Note that
$l(u_{_{X}})$. Note that ![]() $(\text{L}_{T}(A_{X}))_{i}=\text{Hom}_{R}(T,(A_{X})_{i-1})\oplus (A_{X})_{i}\otimes _{R}DT$, so we write that
$(\text{L}_{T}(A_{X}))_{i}=\text{Hom}_{R}(T,(A_{X})_{i-1})\oplus (A_{X})_{i}\otimes _{R}DT$, so we write that ![]() $s_{i}=\big(\!\begin{smallmatrix}s_{i}^{1}s_{i}^{2}\end{smallmatrix}\!\big)$ as we have done in the last commutative diagram in 4.3.1. The fact that
$s_{i}=\big(\!\begin{smallmatrix}s_{i}^{1}s_{i}^{2}\end{smallmatrix}\!\big)$ as we have done in the last commutative diagram in 4.3.1. The fact that ![]() $s$ is a homomorphism in
$s$ is a homomorphism in ![]() ${\mathcal{R}}{\mathcal{C}}(S)$ implies that there is the following commutative diagram, for each
${\mathcal{R}}{\mathcal{C}}(S)$ implies that there is the following commutative diagram, for each ![]() $i$:
$i$:

By the definition of ![]() $\unicode[STIX]{x1D6FF}_{i}^{\otimes }(\text{L}_{T}(A_{X}))$ (see 4.1.1) and the above commutative diagram, we obtain that
$\unicode[STIX]{x1D6FF}_{i}^{\otimes }(\text{L}_{T}(A_{X}))$ (see 4.1.1) and the above commutative diagram, we obtain that ![]() $(s_{i}^{2}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i}^{\otimes }(\mathbf{S}_{T}(X))=0$ and that
$(s_{i}^{2}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i}^{\otimes }(\mathbf{S}_{T}(X))=0$ and that ![]() $(s_{i}^{1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i}^{\otimes }(\mathbf{S}_{T}(X))\simeq (\unicode[STIX]{x1D716}_{A_{X_{i-1}}}^{T}\otimes _{R}DT)\cdot s_{i-1}^{2}$.
$(s_{i}^{1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i}^{\otimes }(\mathbf{S}_{T}(X))\simeq (\unicode[STIX]{x1D716}_{A_{X_{i-1}}}^{T}\otimes _{R}DT)\cdot s_{i-1}^{2}$.
4.3.4.2 The homomorphism  $r(s^{P}):\text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})\rightarrow \text{Ĥom}(DT,\mathbf{S}_{T}(X))$
$r(s^{P}):\text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})\rightarrow \text{Ĥom}(DT,\mathbf{S}_{T}(X))$
Recall from 4.3.1 that
By 4.2.3, we know that
and that
where ![]() $\unicode[STIX]{x1D701}_{r_{i}}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((s_{i+1}^{P}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))$.
$\unicode[STIX]{x1D701}_{r_{i}}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((s_{i+1}^{P}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))$.
For convenience, we set ![]() $r(s^{P})_{i}=\big(\!\begin{smallmatrix}r_{i}^{1}r_{i}^{2}\end{smallmatrix}\!\big)$, where
$r(s^{P})_{i}=\big(\!\begin{smallmatrix}r_{i}^{1}r_{i}^{2}\end{smallmatrix}\!\big)$, where
and
4.3.4.3 Checking  $\unicode[STIX]{x1D709}\cdot r(s^{P})=0$
$\unicode[STIX]{x1D709}\cdot r(s^{P})=0$
To check ![]() $\unicode[STIX]{x1D709}\cdot r(s^{P})=0$, we need only to check that
$\unicode[STIX]{x1D709}\cdot r(s^{P})=0$, we need only to check that ![]() $\unicode[STIX]{x1D709}_{i}^{a}r_{i}^{1}+\unicode[STIX]{x1D709}_{i}^{b}r_{i}^{2}=0$ for each
$\unicode[STIX]{x1D709}_{i}^{a}r_{i}^{1}+\unicode[STIX]{x1D709}_{i}^{b}r_{i}^{2}=0$ for each ![]() $i$, since
$i$, since ![]() $\unicode[STIX]{x1D709}_{i}=(\unicode[STIX]{x1D709}_{i}^{a},\unicode[STIX]{x1D709}_{i}^{b})$ and
$\unicode[STIX]{x1D709}_{i}=(\unicode[STIX]{x1D709}_{i}^{a},\unicode[STIX]{x1D709}_{i}^{b})$ and ![]() $r(s^{P})_{i}=\big(\begin{smallmatrix}r_{i}^{1}r_{i}^{2}\end{smallmatrix}\big)$. Note that
$r(s^{P})_{i}=\big(\begin{smallmatrix}r_{i}^{1}r_{i}^{2}\end{smallmatrix}\big)$. Note that ![]() $r_{i}^{1}=\text{Hom}_{S}(DT,s_{i}^{P})$ and
$r_{i}^{1}=\text{Hom}_{S}(DT,s_{i}^{P})$ and ![]() $r_{i}^{2}=-\unicode[STIX]{x1D701}_{r_{i}}$, so it is enough to check that
$r_{i}^{2}=-\unicode[STIX]{x1D701}_{r_{i}}$, so it is enough to check that ![]() $\unicode[STIX]{x1D709}_{i}^{a}\cdot \text{Hom}_{S}(DT,s_{i}^{P})=\unicode[STIX]{x1D709}_{i}^{b}\cdot \unicode[STIX]{x1D701}_{r_{i}}$.
$\unicode[STIX]{x1D709}_{i}^{a}\cdot \text{Hom}_{S}(DT,s_{i}^{P})=\unicode[STIX]{x1D709}_{i}^{b}\cdot \unicode[STIX]{x1D701}_{r_{i}}$.
Since ![]() $\unicode[STIX]{x1D709}_{i}^{a}=\bigg(\begin{smallmatrix}\unicode[STIX]{x1D709}_{11}^{a} & 0\\ 0 & \unicode[STIX]{x1D709}_{22}^{a}\\ 0 & 0\end{smallmatrix}\bigg)$,
$\unicode[STIX]{x1D709}_{i}^{a}=\bigg(\begin{smallmatrix}\unicode[STIX]{x1D709}_{11}^{a} & 0\\ 0 & \unicode[STIX]{x1D709}_{22}^{a}\\ 0 & 0\end{smallmatrix}\bigg)$, ![]() $\unicode[STIX]{x1D709}_{i}^{b}=\bigg(\begin{smallmatrix}\unicode[STIX]{x1D709}_{11}^{b} & 0\\ \unicode[STIX]{x1D709}_{21}^{b} & 0\\ 0 & \unicode[STIX]{x1D709}_{32}^{b}\end{smallmatrix}\bigg)$,
$\unicode[STIX]{x1D709}_{i}^{b}=\bigg(\begin{smallmatrix}\unicode[STIX]{x1D709}_{11}^{b} & 0\\ \unicode[STIX]{x1D709}_{21}^{b} & 0\\ 0 & \unicode[STIX]{x1D709}_{32}^{b}\end{smallmatrix}\bigg)$, ![]() $\unicode[STIX]{x1D701}_{r_{i}}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((s_{i+1}^{P}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))$ and
$\unicode[STIX]{x1D701}_{r_{i}}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((s_{i+1}^{P}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))$ and ![]() $s_{i}^{P}=\big(\begin{smallmatrix}s_{i}^{1}\\ (p_{i}\otimes _{R}DT)\cdot s_{i}^{2}\end{smallmatrix}\big)$, we just check the following.
$s_{i}^{P}=\big(\begin{smallmatrix}s_{i}^{1}\\ (p_{i}\otimes _{R}DT)\cdot s_{i}^{2}\end{smallmatrix}\big)$, we just check the following.
(1)
 $\unicode[STIX]{x1D709}_{11}^{a}\cdot \text{Hom}_{S}(DT,s_{i}^{1})=\unicode[STIX]{x1D709}_{11}^{b}\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((s_{i+1}^{1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))$.
$\unicode[STIX]{x1D709}_{11}^{a}\cdot \text{Hom}_{S}(DT,s_{i}^{1})=\unicode[STIX]{x1D709}_{11}^{b}\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((s_{i+1}^{1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))$.By 4.3.3.1, we have that
where the later equality uses the naturality of $$\begin{eqnarray}\unicode[STIX]{x1D709}_{11}^{a}\cdot \text{Hom}_{S}(DT,s_{i}^{1})=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(\unicode[STIX]{x1D703}_{l_{i}})\cdot \text{Hom}_{S}(DT,s_{i}^{1})=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(\unicode[STIX]{x1D703}_{l_{i}}\cdot s_{i}^{1}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}_{11}^{a}\cdot \text{Hom}_{S}(DT,s_{i}^{1})=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(\unicode[STIX]{x1D703}_{l_{i}})\cdot \text{Hom}_{S}(DT,s_{i}^{1})=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(\unicode[STIX]{x1D703}_{l_{i}}\cdot s_{i}^{1}),\end{eqnarray}$$ $\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}$. On the other hand, by 4.3.3.2 and 4.3.4.1, we obtain that
$\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}$. On the other hand, by 4.3.3.2 and 4.3.4.1, we obtain that  $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D709}_{11}^{b}\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((s_{i+1}^{1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))\nonumber\\ \displaystyle & & \displaystyle \quad =((u_{_{X}})_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1})\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T}\otimes _{R}DT)\cdot s_{i}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((((u_{_{X}})_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1})\otimes _{R}DT)\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T}\otimes _{R}DT)\cdot s_{i}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(((u_{_{X}})_{i}\otimes _{R}DT)\cdot s_{i}^{2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D709}_{11}^{b}\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((s_{i+1}^{1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))\nonumber\\ \displaystyle & & \displaystyle \quad =((u_{_{X}})_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1})\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T}\otimes _{R}DT)\cdot s_{i}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((((u_{_{X}})_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1})\otimes _{R}DT)\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T}\otimes _{R}DT)\cdot s_{i}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(((u_{_{X}})_{i}\otimes _{R}DT)\cdot s_{i}^{2}).\nonumber\end{eqnarray}$$But
 $((u_{_{X}})_{i}\otimes _{R}DT)\cdot s_{i}^{2}=\unicode[STIX]{x1D703}_{l_{i}}\cdot s_{i}^{1}$ by the pushout diagram on
$((u_{_{X}})_{i}\otimes _{R}DT)\cdot s_{i}^{2}=\unicode[STIX]{x1D703}_{l_{i}}\cdot s_{i}^{1}$ by the pushout diagram on  $\mathbf{S}_{T}(X)_{i}$ in 4.3.1. Hence, equality (1) holds.
$\mathbf{S}_{T}(X)_{i}$ in 4.3.1. Hence, equality (1) holds.(2)
 $\unicode[STIX]{x1D709}_{22}^{a}\cdot \text{Hom}_{S}(DT,(p_{i}\otimes _{R}DT)\cdot s_{i}^{2})=\unicode[STIX]{x1D709}_{21}^{b}\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((s_{i+1}^{1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))$.
$\unicode[STIX]{x1D709}_{22}^{a}\cdot \text{Hom}_{S}(DT,(p_{i}\otimes _{R}DT)\cdot s_{i}^{2})=\unicode[STIX]{x1D709}_{21}^{b}\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((s_{i+1}^{1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))$.By 4.3.3.1 and the naturality of
 $\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}$,
$\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}$,  $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D709}_{22}^{a}\cdot \text{Hom}_{S}(DT,(p_{i}\otimes _{R}DT)\cdot s_{i}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(1_{P_{(A_{X})_{i}}\otimes _{R}DT})\cdot \text{Hom}_{S}(DT,(p_{i}\otimes _{R}DT)\cdot s_{i}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(1_{P_{(A_{X})_{i}}\otimes _{R}DT}\cdot ((p_{i}\otimes _{R}DT)\cdot s_{i}^{2}))\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((p_{i}\otimes _{R}DT)\cdot s_{i}^{2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D709}_{22}^{a}\cdot \text{Hom}_{S}(DT,(p_{i}\otimes _{R}DT)\cdot s_{i}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(1_{P_{(A_{X})_{i}}\otimes _{R}DT})\cdot \text{Hom}_{S}(DT,(p_{i}\otimes _{R}DT)\cdot s_{i}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(1_{P_{(A_{X})_{i}}\otimes _{R}DT}\cdot ((p_{i}\otimes _{R}DT)\cdot s_{i}^{2}))\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((p_{i}\otimes _{R}DT)\cdot s_{i}^{2}).\nonumber\end{eqnarray}$$On the other hand, by 4.3.3.2 and 4.3.4.1 and the naturality of
 $\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}$,
$\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}$,  $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D709}_{21}^{b}\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((s_{i+1}^{1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))\nonumber\\ \displaystyle & & \displaystyle \quad =(p_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1})\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T}\otimes _{R}DT)\cdot s_{i}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(((p_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1})\otimes _{R}DT)\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T}\otimes _{R}DT)\cdot s_{i}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((p_{i}\otimes _{R}DT)\cdot s_{i}^{2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D709}_{21}^{b}\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((s_{i+1}^{1}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))\nonumber\\ \displaystyle & & \displaystyle \quad =(p_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1})\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T}\otimes _{R}DT)\cdot s_{i}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(((p_{i}\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T})^{-1})\otimes _{R}DT)\cdot (\unicode[STIX]{x1D716}_{(A_{X})_{i}}^{T}\otimes _{R}DT)\cdot s_{i}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((p_{i}\otimes _{R}DT)\cdot s_{i}^{2}).\nonumber\end{eqnarray}$$Hence, equality (2) holds.
(3)
 $0=\unicode[STIX]{x1D709}_{32}^{b}\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(((p_{i+1}\otimes _{R}DT)\cdot s_{i+1}^{2})\otimes _{S}DS\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))$.
$0=\unicode[STIX]{x1D709}_{32}^{b}\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(((p_{i+1}\otimes _{R}DT)\cdot s_{i+1}^{2})\otimes _{S}DS\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))$.In fact, the equality holds by observing that
since $$\begin{eqnarray}\displaystyle & & \displaystyle \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(((p_{i+1}\otimes _{R}DT)\cdot s_{i+1}^{2})\otimes _{S}DS\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((p_{i+1}\otimes _{R}DT\otimes _{S}DS)\cdot (s_{i+1}^{2}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))\nonumber\\ \displaystyle & & \displaystyle \quad =0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(((p_{i+1}\otimes _{R}DT)\cdot s_{i+1}^{2})\otimes _{S}DS\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))\nonumber\\ \displaystyle & & \displaystyle \quad =\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((p_{i+1}\otimes _{R}DT\otimes _{S}DS)\cdot (s_{i+1}^{2}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X)))\nonumber\\ \displaystyle & & \displaystyle \quad =0\nonumber\end{eqnarray}$$ $(s_{i+1}^{2}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X))=0$ by 4.3.4.1.
$(s_{i+1}^{2}\otimes _{S}DS)\cdot \unicode[STIX]{x1D6FF}_{i+1}^{\otimes }(\mathbf{S}_{T}(X))=0$ by 4.3.4.1.
Altogether, we prove that ![]() $\unicode[STIX]{x1D709}\cdot r(s^{P})=0$ and, therefore,
$\unicode[STIX]{x1D709}\cdot r(s^{P})=0$ and, therefore, ![]() $\unicode[STIX]{x1D709}$ factors through
$\unicode[STIX]{x1D709}$ factors through ![]() $\mathbf{Q}_{DT}\mathbf{S}_{T}(X)=\text{Ker}(r(s^{P}))$ by a homomorphism
$\mathbf{Q}_{DT}\mathbf{S}_{T}(X)=\text{Ker}(r(s^{P}))$ by a homomorphism
in ![]() ${\mathcal{R}}{\mathcal{C}}(R)$, that is,
${\mathcal{R}}{\mathcal{C}}(R)$, that is, ![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D706}$.
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D706}$.
4.3.5 The induced homomorphism  $\unicode[STIX]{x1D719}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \mathbf{Q}_{DT}\mathbf{S}_{T}(X)$ is an isomorphism
$\unicode[STIX]{x1D719}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \mathbf{Q}_{DT}\mathbf{S}_{T}(X)$ is an isomorphism
We now prove that the induced homomorphism ![]() $\unicode[STIX]{x1D719}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \mathbf{Q}_{DT}\mathbf{S}_{T}(X)$ is an isomorphism. Clearly, it is equivalent to show that
$\unicode[STIX]{x1D719}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \mathbf{Q}_{DT}\mathbf{S}_{T}(X)$ is an isomorphism. Clearly, it is equivalent to show that ![]() $\unicode[STIX]{x1D719}_{i}:(X\oplus \text{L}_{R}(P_{A_{X}}^{+}))_{i}\rightarrow \mathbf{Q}_{DT}\mathbf{S}_{T}(X)_{i}$ is an isomorphism, for each
$\unicode[STIX]{x1D719}_{i}:(X\oplus \text{L}_{R}(P_{A_{X}}^{+}))_{i}\rightarrow \mathbf{Q}_{DT}\mathbf{S}_{T}(X)_{i}$ is an isomorphism, for each ![]() $i$.
$i$.
We will show that there is the following commutative diagram (![]() $\ast$) with exact rows, for each
$\ast$) with exact rows, for each ![]() $i$:
$i$:

where
![]() $\overline{X}_{i}\in {\mathcal{B}}$ is obtained in 4.3.1, the morphism
$\overline{X}_{i}\in {\mathcal{B}}$ is obtained in 4.3.1, the morphism ![]() $a_{i}$ is given in 4.3.5.2, the morphism
$a_{i}$ is given in 4.3.5.2, the morphism ![]() $\unicode[STIX]{x1D6FD}_{i}=\bigg(\begin{smallmatrix}(u_{_{X}})_{i} & 0\\ p_{i} & 0\\ 0 & 1\end{smallmatrix}\bigg)$ and the morphism
$\unicode[STIX]{x1D6FD}_{i}=\bigg(\begin{smallmatrix}(u_{_{X}})_{i} & 0\\ p_{i} & 0\\ 0 & 1\end{smallmatrix}\bigg)$ and the morphism ![]() $\unicode[STIX]{x1D70E}_{i}$ is the direct sum of two canonical isomorphisms. Note that
$\unicode[STIX]{x1D70E}_{i}$ is the direct sum of two canonical isomorphisms. Note that ![]() $\text{L}_{R}(P_{A_{X}}^{+})_{i}=P_{(A_{X})_{i}}\oplus P_{(A_{X})_{i+1}}\otimes _{R}DR$.
$\text{L}_{R}(P_{A_{X}}^{+})_{i}=P_{(A_{X})_{i}}\oplus P_{(A_{X})_{i+1}}\otimes _{R}DR$.
Then, since ![]() $\overline{X}_{i}\in {\mathcal{B}}$ implies that
$\overline{X}_{i}\in {\mathcal{B}}$ implies that ![]() $\unicode[STIX]{x1D702}_{\overline{X}_{i}}^{DT}$ is an isomorphism, we obtain that
$\unicode[STIX]{x1D702}_{\overline{X}_{i}}^{DT}$ is an isomorphism, we obtain that ![]() $\unicode[STIX]{x1D719}_{i}$ is also an isomorphism from the above commutative diagram.
$\unicode[STIX]{x1D719}_{i}$ is also an isomorphism from the above commutative diagram.
4.3.5.1 The upper row in the diagram  $(\ast )$ is exact
$(\ast )$ is exact
In fact, the pullback of ![]() $p_{i}:P_{(A_{X})_{i}}\rightarrow (A_{X})_{i}$ and
$p_{i}:P_{(A_{X})_{i}}\rightarrow (A_{X})_{i}$ and ![]() $(u_{_{X}})_{i}:X_{i}\rightarrow (A_{X})_{i}$ in 4.3.1 gives an exact sequence
$(u_{_{X}})_{i}:X_{i}\rightarrow (A_{X})_{i}$ in 4.3.1 gives an exact sequence
 $$\begin{eqnarray}0\rightarrow \overline{X}_{i}\stackrel{(-q_{i},(\overline{u}_{X})_{i})}{\longrightarrow }X_{i}\oplus P_{(A_{X})_{i}}\stackrel{}{\longrightarrow _{}}(A_{X})_{i}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \overline{X}_{i}\stackrel{(-q_{i},(\overline{u}_{X})_{i})}{\longrightarrow }X_{i}\oplus P_{(A_{X})_{i}}\stackrel{}{\longrightarrow _{}}(A_{X})_{i}\rightarrow 0\end{eqnarray}$$ since ![]() $p_{i}$ is surjective. The direct sum of the above exact sequence and the trivial exact sequence
$p_{i}$ is surjective. The direct sum of the above exact sequence and the trivial exact sequence
gives us the exact sequence in the upper row in the diagram ![]() $(\ast )$.
$(\ast )$.
4.3.5.2 The bottom row in the diagram  $(\ast )$ is exact
$(\ast )$ is exact
Note that we have the following exact sequence in 4.3.1
and that
 $$\begin{eqnarray}\displaystyle \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})_{i} & = & \displaystyle \text{Hom}_{S}(DT,(\mathfrak{L}_{A_{X}}^{P})_{i})\oplus (\mathfrak{L}_{A_{X}}^{P})_{i+1}\otimes _{S}T\nonumber\\ \displaystyle & = & \displaystyle \text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1})\oplus P_{(A_{X})_{i}}\otimes _{R}DT)\nonumber\\ \displaystyle & & \displaystyle \oplus \,(\text{Hom}_{R}(T,(A_{X})_{i})\oplus P_{(A_{X})_{i+1}}\otimes _{R}DT)\otimes _{S}T.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P})_{i} & = & \displaystyle \text{Hom}_{S}(DT,(\mathfrak{L}_{A_{X}}^{P})_{i})\oplus (\mathfrak{L}_{A_{X}}^{P})_{i+1}\otimes _{S}T\nonumber\\ \displaystyle & = & \displaystyle \text{Hom}_{S}(DT,\text{Hom}_{R}(T,(A_{X})_{i-1})\oplus P_{(A_{X})_{i}}\otimes _{R}DT)\nonumber\\ \displaystyle & & \displaystyle \oplus \,(\text{Hom}_{R}(T,(A_{X})_{i})\oplus P_{(A_{X})_{i+1}}\otimes _{R}DT)\otimes _{S}T.\nonumber\end{eqnarray}$$So we have the following pullback diagram:

where
![]() $r_{i}^{1},r_{i}^{2}$ and
$r_{i}^{1},r_{i}^{2}$ and ![]() $\unicode[STIX]{x1D706}_{i}^{1},\unicode[STIX]{x1D706}_{i}^{2}$ are the components of the homomorphisms
$\unicode[STIX]{x1D706}_{i}^{1},\unicode[STIX]{x1D706}_{i}^{2}$ are the components of the homomorphisms ![]() $r(s^{P})_{i}$ and
$r(s^{P})_{i}$ and ![]() $\unicode[STIX]{x1D706}_{i}$, respectively, and
$\unicode[STIX]{x1D706}_{i}$, respectively, and ![]() $b_{i}=\text{Hom}_{S}(DT,t_{i})$ with
$b_{i}=\text{Hom}_{S}(DT,t_{i})$ with
is given in 4.3.1.
As the morphism ![]() $\unicode[STIX]{x1D706}_{i}:\mathbf{Q}_{DT}\mathbf{S}_{T}(X)_{i}\rightarrow (\text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P}))_{i}$ is injective, we obtain that the morphism
$\unicode[STIX]{x1D706}_{i}:\mathbf{Q}_{DT}\mathbf{S}_{T}(X)_{i}\rightarrow (\text{R}_{DT}(\mathfrak{L}_{A_{X}}^{P}))_{i}$ is injective, we obtain that the morphism ![]() $q$ in the left column is an isomorphism. Note that
$q$ in the left column is an isomorphism. Note that ![]() $r_{i}^{1}:=\text{Hom}_{S}(DT,s_{i}^{P})$ is surjective since
$r_{i}^{1}:=\text{Hom}_{S}(DT,s_{i}^{P})$ is surjective since ![]() $\overline{X}_{i}\otimes _{R}DT\in {\mathcal{K}}\subseteq \text{KerExt}_{S}^{{>}0}(DT,-)$ by the construction (see 4.3.1), so we can deduce that the upper row in the above diagram is exact. Thus, we get the bottom exact sequence in the diagram
$\overline{X}_{i}\otimes _{R}DT\in {\mathcal{K}}\subseteq \text{KerExt}_{S}^{{>}0}(DT,-)$ by the construction (see 4.3.1), so we can deduce that the upper row in the above diagram is exact. Thus, we get the bottom exact sequence in the diagram ![]() $(\ast )$ by setting
$(\ast )$ by setting ![]() $a_{i}=q^{-1}e$.
$a_{i}=q^{-1}e$.
4.3.5.3 The diagram  $(\ast )$ is commutative
$(\ast )$ is commutative
At first, it is easy to see that the right part of the diagram ![]() $(\ast )$ is commutative from the constructions of the morphisms
$(\ast )$ is commutative from the constructions of the morphisms ![]() $\unicode[STIX]{x1D709}$ in 4.3.3 and
$\unicode[STIX]{x1D709}$ in 4.3.3 and ![]() $\unicode[STIX]{x1D719}$ in 4.3.4, which show that
$\unicode[STIX]{x1D719}$ in 4.3.4, which show that ![]() $\unicode[STIX]{x1D6FD}_{i}\unicode[STIX]{x1D70E}_{i}=\unicode[STIX]{x1D709}_{i}^{b}=\unicode[STIX]{x1D719}_{i}\unicode[STIX]{x1D706}_{i}^{2}$.
$\unicode[STIX]{x1D6FD}_{i}\unicode[STIX]{x1D70E}_{i}=\unicode[STIX]{x1D709}_{i}^{b}=\unicode[STIX]{x1D719}_{i}\unicode[STIX]{x1D706}_{i}^{2}$.
As for the left part of the diagram ![]() $(\ast )$, we first show the following equality of compositions:
$(\ast )$, we first show the following equality of compositions:
Indeed, we have that

and we also have that

Since ![]() $\unicode[STIX]{x1D709}_{11}^{a}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(\unicode[STIX]{x1D703}_{l_{i}})$ and
$\unicode[STIX]{x1D709}_{11}^{a}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(\unicode[STIX]{x1D703}_{l_{i}})$ and ![]() $\unicode[STIX]{x1D709}_{22}^{a}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(1_{(P_{(A_{X})_{i}}\otimes _{R}DT)})$ by the construction in 4.3.3.1, we obtain that
$\unicode[STIX]{x1D709}_{22}^{a}=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(1_{(P_{(A_{X})_{i}}\otimes _{R}DT)})$ by the construction in 4.3.3.1, we obtain that
and that
 $$\begin{eqnarray}\displaystyle (\overline{u}_{X})_{i}\cdot \unicode[STIX]{x1D709}_{22}^{a} & = & \displaystyle (\overline{u}_{X})_{i}\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(1_{(P_{(A_{X})_{i}}\otimes _{R}DT)})\nonumber\\ \displaystyle & = & \displaystyle \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((\overline{u}_{X})_{i}\otimes _{R}DT\cdot 1_{(P_{(A_{X})_{i}}\otimes _{R}DT)})=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((\overline{u}_{X})_{i}\otimes _{R}DT).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\overline{u}_{X})_{i}\cdot \unicode[STIX]{x1D709}_{22}^{a} & = & \displaystyle (\overline{u}_{X})_{i}\cdot \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}(1_{(P_{(A_{X})_{i}}\otimes _{R}DT)})\nonumber\\ \displaystyle & = & \displaystyle \boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((\overline{u}_{X})_{i}\otimes _{R}DT\cdot 1_{(P_{(A_{X})_{i}}\otimes _{R}DT)})=\boldsymbol{\unicode[STIX]{x1D6E4}}^{DT}((\overline{u}_{X})_{i}\otimes _{R}DT).\nonumber\end{eqnarray}$$Hence, we see that the equality (†1) holds.
Since ![]() $a_{i}\cdot \unicode[STIX]{x1D706}_{i}^{2}=0$ and
$a_{i}\cdot \unicode[STIX]{x1D706}_{i}^{2}=0$ and
we also get that
Now, from the property of the pullback in 4.3.5.2, we know that the two equalities (†1) and (†2) together imply that
Thus, the left part of the diagram is also commutative.
4.3.6 The isomorphism  $\unicode[STIX]{x1D719}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \mathbf{Q}_{DT}\mathbf{S}_{T}(X)$ is natural on
$\unicode[STIX]{x1D719}:X\oplus \text{L}_{R}(P_{A_{X}}^{+})\rightarrow \mathbf{Q}_{DT}\mathbf{S}_{T}(X)$ is natural on  $X$
$X$
For any ![]() $X,Y\in {\mathcal{R}}{\mathcal{C}}(R)$ and
$X,Y\in {\mathcal{R}}{\mathcal{C}}(R)$ and ![]() $h\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(R)}(X,Y)$, there is an induced morphism
$h\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}(R)}(X,Y)$, there is an induced morphism ![]() $h_{A}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)}(A_{X},A_{Y})$, following from the construction in 4.1.4. Moreover, following from the construction in 4.3.1 and the definition of
$h_{A}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)}(A_{X},A_{Y})$, following from the construction in 4.1.4. Moreover, following from the construction in 4.3.1 and the definition of ![]() $P_{A_{X}}^{+}$ in 4.3.2, we see that the morphism
$P_{A_{X}}^{+}$ in 4.3.2, we see that the morphism ![]() $h_{A}$ induces a morphism
$h_{A}$ induces a morphism ![]() $p_{h_{A}}^{+}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)}(P_{A_{X}}^{+},P_{A_{Y}}^{+})$. Then, one can prove that
$p_{h_{A}}^{+}\in \text{Hom}_{{\mathcal{R}}{\mathcal{C}}^{\text{tr}}(R)}(P_{A_{X}}^{+},P_{A_{Y}}^{+})$. Then, one can prove that
is a morphism in ![]() ${\mathcal{R}}{\mathcal{C}}(R)$.
${\mathcal{R}}{\mathcal{C}}(R)$.
It is not hard to show that the following diagram is commutative:

Thus, the isomorphism ![]() $\unicode[STIX]{x1D719}$ is natural on
$\unicode[STIX]{x1D719}$ is natural on ![]() $X$. This means that
$X$. This means that ![]() $\mathbf{Q}_{DT}\mathbf{S}_{T}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)}$ naturally.
$\mathbf{Q}_{DT}\mathbf{S}_{T}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)}$ naturally.
4.4 The isomorphism  $\mathbf{S}_{T}\mathbf{Q}_{DT}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)}$
$\mathbf{S}_{T}\mathbf{Q}_{DT}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)}$
Dually to the proof of 4.3, one can show that ![]() $\mathbf{S}_{T}\mathbf{Q}_{DT}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)}$ naturally.
$\mathbf{S}_{T}\mathbf{Q}_{DT}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)}$ naturally.
Namely, for an object ![]() $Y\in {\mathcal{R}}{\mathcal{C}}(S)$, one uses that
$Y\in {\mathcal{R}}{\mathcal{C}}(S)$, one uses that ![]() $({\mathcal{G}},{\mathcal{K}})$ is a complete hereditary cotorsion pair in
$({\mathcal{G}},{\mathcal{K}})$ is a complete hereditary cotorsion pair in ![]() $\text{mod}S$ to obtain exact sequences
$\text{mod}S$ to obtain exact sequences ![]() $0\rightarrow (K_{Y})_{i}\rightarrow (G_{Y})_{i}\rightarrow Y_{i}\rightarrow 0$, for each
$0\rightarrow (K_{Y})_{i}\rightarrow (G_{Y})_{i}\rightarrow Y_{i}\rightarrow 0$, for each ![]() $i$. Then taking an injective
$i$. Then taking an injective ![]() $S$-module
$S$-module ![]() $I_{(G_{Y})_{i}}$ and a monomorphism
$I_{(G_{Y})_{i}}$ and a monomorphism ![]() $(G_{Y})_{i}\rightarrow I_{(G_{Y})_{i}}$, one can show that there is a natural isomorphism
$(G_{Y})_{i}\rightarrow I_{(G_{Y})_{i}}$, one can show that there is a natural isomorphism ![]() $\mathbf{S}_{T}\mathbf{Q}_{DT}(Y)\rightarrow Y\oplus \text{R}_{DS}(I_{G_{Y}}^{-})$, where
$\mathbf{S}_{T}\mathbf{Q}_{DT}(Y)\rightarrow Y\oplus \text{R}_{DS}(I_{G_{Y}}^{-})$, where ![]() $I_{G_{Y}}^{-}=\{I_{(G_{Y})_{i-1}}\}$ and
$I_{G_{Y}}^{-}=\{I_{(G_{Y})_{i-1}}\}$ and ![]() $\text{R}_{DS}(I_{G_{Y}}^{-})$ is a projective object in
$\text{R}_{DS}(I_{G_{Y}}^{-})$ is a projective object in ![]() ${\mathcal{R}}{\mathcal{C}}(S)$ by Remark (2) in 4.2.1. And then one gets that
${\mathcal{R}}{\mathcal{C}}(S)$ by Remark (2) in 4.2.1. And then one gets that ![]() $\mathbf{S}_{T}\mathbf{Q}_{DT}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)}$ naturally.
$\mathbf{S}_{T}\mathbf{Q}_{DT}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)}$ naturally.
4.5 The last proof of Theorem 1
Recall that the natural functor ![]() $[1]$ is an automorphism of repetitive categories, where
$[1]$ is an automorphism of repetitive categories, where ![]() $(X[1])_{i}=X_{i-1}$ for an object in a repetitive category.
$(X[1])_{i}=X_{i-1}$ for an object in a repetitive category.
Define ![]() $\mathbf{F}_{T}:=[-1]\mathbf{S}_{T}:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$ and
$\mathbf{F}_{T}:=[-1]\mathbf{S}_{T}:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$ and ![]() $\mathbf{G}_{T}:=\mathbf{Q}_{DT}[1]:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$. Then we have that
$\mathbf{G}_{T}:=\mathbf{Q}_{DT}[1]:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$. Then we have that ![]() $\mathbf{F}_{T}\mathbf{G}_{T}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)}$ naturally and that
$\mathbf{F}_{T}\mathbf{G}_{T}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)}$ naturally and that ![]() $\mathbf{G}_{T}\mathbf{F}_{T}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)}$ naturally. So
$\mathbf{G}_{T}\mathbf{F}_{T}\simeq 1_{\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)}$ naturally. So ![]() $\mathbf{F}_{T}$ and
$\mathbf{F}_{T}$ and ![]() $\mathbf{G}_{T}$ give a repetitive equivalence between
$\mathbf{G}_{T}$ give a repetitive equivalence between ![]() $R$ and
$R$ and ![]() $S$.
$S$.
It is easy to check that ![]() $\mathbf{F}_{T}|_{{\mathcal{A}}}\simeq \text{Hom}_{R}(T,-)$ and that
$\mathbf{F}_{T}|_{{\mathcal{A}}}\simeq \text{Hom}_{R}(T,-)$ and that ![]() $\mathbf{G}_{T}|_{{\mathcal{G}}}\simeq -\!\otimes _{S}T$ from the definitions of the two functors. Now the proof of the theorem is complete.
$\mathbf{G}_{T}|_{{\mathcal{G}}}\simeq -\!\otimes _{S}T$ from the definitions of the two functors. Now the proof of the theorem is complete.
4.6 The proof of Proposition 2
Assume that the equivalence is given by the functor ![]() $F:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$. By assumptions,
$F:\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)\rightarrow \text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$. By assumptions, ![]() $F$ restricts to an equivalence
$F$ restricts to an equivalence ![]() ${\mathcal{A}}\rightarrow {\mathcal{G}}$. Note that
${\mathcal{A}}\rightarrow {\mathcal{G}}$. Note that ![]() ${\mathcal{G}}$ is resolving and
${\mathcal{G}}$ is resolving and ![]() $S\in {\mathcal{G}}$. Let
$S\in {\mathcal{G}}$. Let ![]() $T=F^{-1}(S)$. Then
$T=F^{-1}(S)$. Then ![]() $T\in {\mathcal{A}}$. By the triangle equivalence, we have that, for any
$T\in {\mathcal{A}}$. By the triangle equivalence, we have that, for any ![]() $A\in {\mathcal{A}}$,
$A\in {\mathcal{A}}$,
where ![]() $\unicode[STIX]{x1D6F4}$ is the translation functor in stable repetitive categories. In particular, we obtain that
$\unicode[STIX]{x1D6F4}$ is the translation functor in stable repetitive categories. In particular, we obtain that ![]() $\text{Hom}_{R}(T,A)\simeq \text{Hom}_{S}(S,F(A))\simeq F(A)$ and that
$\text{Hom}_{R}(T,A)\simeq \text{Hom}_{S}(S,F(A))\simeq F(A)$ and that ![]() $\text{Ext}_{R}^{i}(T,A)=0$ for all
$\text{Ext}_{R}^{i}(T,A)=0$ for all ![]() $i>0$. It follows that
$i>0$. It follows that ![]() $S\simeq \text{End}(T_{R})^{op}$ and that
$S\simeq \text{End}(T_{R})^{op}$ and that ![]() $\text{Ext}_{R}^{i}(T,T)=0$ for all
$\text{Ext}_{R}^{i}(T,T)=0$ for all ![]() $i>0$. Note that
$i>0$. Note that ![]() ${\mathcal{A}}$ is coresolving and
${\mathcal{A}}$ is coresolving and ![]() $DR\in {\mathcal{A}}$, so we also have that
$DR\in {\mathcal{A}}$, so we also have that ![]() $F(DR)\simeq \text{Hom}_{R}(T,DR)\simeq DT$. Thus, we get that
$F(DR)\simeq \text{Hom}_{R}(T,DR)\simeq DT$. Thus, we get that
It follows that ![]() $\text{End}(\text{}_{S}T)^{op}\simeq R$ and that
$\text{End}(\text{}_{S}T)^{op}\simeq R$ and that ![]() $\text{Ext}_{S}^{i}(\text{}_{S}T,_{S}T)=0$ for all
$\text{Ext}_{S}^{i}(\text{}_{S}T,_{S}T)=0$ for all ![]() $i>0$. Thus,
$i>0$. Thus, ![]() $T$ is a Wakamatsu-tilting module.
$T$ is a Wakamatsu-tilting module.
By assumption, ![]() $F|_{{\mathcal{A}}}\simeq \text{Hom}_{R}(T,-)$ gives the equivalence
$F|_{{\mathcal{A}}}\simeq \text{Hom}_{R}(T,-)$ gives the equivalence ![]() ${\mathcal{A}}\rightarrow {\mathcal{G}}$. It follows that
${\mathcal{A}}\rightarrow {\mathcal{G}}$. It follows that ![]() $F^{-1}|_{{\mathcal{G}}}\simeq -\!\otimes _{S}T$ by the uniqueness of the adjoint. Note that
$F^{-1}|_{{\mathcal{G}}}\simeq -\!\otimes _{S}T$ by the uniqueness of the adjoint. Note that ![]() $\text{Hom}_{R}(T,-)$ and
$\text{Hom}_{R}(T,-)$ and ![]() $-\!\otimes _{S}T$ are exact functors on
$-\!\otimes _{S}T$ are exact functors on ![]() ${\mathcal{A}}$ and
${\mathcal{A}}$ and ![]() ${\mathcal{G}}$, respectively, since
${\mathcal{G}}$, respectively, since ![]() $F$ is a triangle functor. As
$F$ is a triangle functor. As ![]() ${\mathcal{A}}$ is coresolving, for any
${\mathcal{A}}$ is coresolving, for any ![]() $A\in {\mathcal{A}}$, the exact sequence
$A\in {\mathcal{A}}$, the exact sequence ![]() $0\rightarrow A\rightarrow I\rightarrow A^{\prime }\rightarrow 0$ with
$0\rightarrow A\rightarrow I\rightarrow A^{\prime }\rightarrow 0$ with ![]() $I\in \text{inj}R$ is a sequence in
$I\in \text{inj}R$ is a sequence in ![]() ${\mathcal{A}}$. Applying the exact functor
${\mathcal{A}}$. Applying the exact functor ![]() $\text{Hom}_{R}(T,-)$, we obtain that
$\text{Hom}_{R}(T,-)$, we obtain that ![]() $\text{Ext}_{R}^{1}(T,A)=0$. It follows that
$\text{Ext}_{R}^{1}(T,A)=0$. It follows that ![]() $T\in {\mathcal{A}}\bigcap \text{KerExt}_{R}^{1}(-,{\mathcal{A}})$, i.e,
$T\in {\mathcal{A}}\bigcap \text{KerExt}_{R}^{1}(-,{\mathcal{A}})$, i.e, ![]() $T$ is Ext-projective in
$T$ is Ext-projective in ![]() ${\mathcal{A}}$. Dually, we have also that
${\mathcal{A}}$. Dually, we have also that ![]() $\text{Tor}_{1}^{S}(X,T)=0$ for any
$\text{Tor}_{1}^{S}(X,T)=0$ for any ![]() $X\in {\mathcal{G}}$. In particular, for any
$X\in {\mathcal{G}}$. In particular, for any ![]() $A\in {\mathcal{A}}$, suppose that
$A\in {\mathcal{A}}$, suppose that ![]() $A=X\otimes _{S}T$ for some
$A=X\otimes _{S}T$ for some ![]() $X\in {\mathcal{G}}$ and take an exact sequence
$X\in {\mathcal{G}}$ and take an exact sequence ![]() $0\rightarrow X^{\prime }\rightarrow P\rightarrow X\rightarrow 0$ with
$0\rightarrow X^{\prime }\rightarrow P\rightarrow X\rightarrow 0$ with ![]() $P\in \text{proj}S$, then the sequence is in
$P\in \text{proj}S$, then the sequence is in ![]() ${\mathcal{G}}$ since
${\mathcal{G}}$ since ![]() ${\mathcal{G}}$ is resolving, and, hence, there is an induced exact sequence
${\mathcal{G}}$ is resolving, and, hence, there is an induced exact sequence ![]() $0\rightarrow X^{\prime }\otimes _{S}T\rightarrow P\otimes _{S}T\rightarrow X\otimes _{S}T\rightarrow 0$ since
$0\rightarrow X^{\prime }\otimes _{S}T\rightarrow P\otimes _{S}T\rightarrow X\otimes _{S}T\rightarrow 0$ since ![]() $-\!\otimes _{S}T$ is exact in
$-\!\otimes _{S}T$ is exact in ![]() ${\mathcal{G}}$. The last sequence gives an exact sequence
${\mathcal{G}}$. The last sequence gives an exact sequence ![]() $0\rightarrow A^{\prime \prime }\rightarrow T_{A}\rightarrow A\rightarrow 0$ with
$0\rightarrow A^{\prime \prime }\rightarrow T_{A}\rightarrow A\rightarrow 0$ with ![]() $T_{A}=P\otimes _{S}T\in \text{add}_{\text{mod}R}T$ and
$T_{A}=P\otimes _{S}T\in \text{add}_{\text{mod}R}T$ and ![]() $A^{\prime \prime }=X^{\prime }\otimes _{S}T\in {\mathcal{A}}$. It follows that
$A^{\prime \prime }=X^{\prime }\otimes _{S}T\in {\mathcal{A}}$. It follows that ![]() $T$ is an Ext-projective generator in
$T$ is an Ext-projective generator in ![]() ${\mathcal{A}}$. Now applying Corollary 3.2.6, we conclude that
${\mathcal{A}}$. Now applying Corollary 3.2.6, we conclude that ![]() $T$ is a good Wakamatsu-tilting module.
$T$ is a good Wakamatsu-tilting module.
5 Examples
5.1 Tilting modules and cotilting modules
Let ![]() $R$ be an Artin algebra. Recall that an
$R$ be an Artin algebra. Recall that an ![]() $R$-module
$R$-module ![]() $T\in \text{mod}R$ is tilting provided the following three conditions are satisfied:
$T\in \text{mod}R$ is tilting provided the following three conditions are satisfied:
(1) the projective dimension of
 $T$ is finite;
$T$ is finite;(2)
 $\text{Ext}_{R}^{i}(T,T)=0$ for all
$\text{Ext}_{R}^{i}(T,T)=0$ for all  $i>0$;
$i>0$;(3) there is an exact sequence
 $0\rightarrow R\rightarrow T_{0}\rightarrow \cdots \rightarrow T_{n}\rightarrow 0$ for some integer
$0\rightarrow R\rightarrow T_{0}\rightarrow \cdots \rightarrow T_{n}\rightarrow 0$ for some integer  $n$, where each
$n$, where each  $T_{i}\in \text{add}_{\text{mod}R}T$.
$T_{i}\in \text{add}_{\text{mod}R}T$.
Dually, an ![]() $R$-module
$R$-module ![]() $T\in \text{mod}R$ is cotilting provided the following three conditions are satisfied:
$T\in \text{mod}R$ is cotilting provided the following three conditions are satisfied:
(1) the injective dimension of
 $T$ is finite;
$T$ is finite;(2)
 $\text{Ext}_{R}^{i}(T,T)=0$ for all
$\text{Ext}_{R}^{i}(T,T)=0$ for all  $i>0$;
$i>0$;(3) there is an exact sequence
 $0\rightarrow T_{n}\rightarrow \cdots \rightarrow T_{0}\rightarrow DR\rightarrow 0$ for some integer
$0\rightarrow T_{n}\rightarrow \cdots \rightarrow T_{0}\rightarrow DR\rightarrow 0$ for some integer  $n$, where each
$n$, where each  $T_{i}\in \text{add}_{\text{mod}R}T$.
$T_{i}\in \text{add}_{\text{mod}R}T$.
An ![]() $R$-module
$R$-module ![]() $T$ is a tilting module if and only if
$T$ is a tilting module if and only if ![]() $DT$ is a cotilting left
$DT$ is a cotilting left ![]() $R$-module if and only if
$R$-module if and only if ![]() $DT$ is a cotilting
$DT$ is a cotilting ![]() $S$-module, where
$S$-module, where ![]() $S=\text{End}(T_{R})^{op}$. Note also that both tilting modules and cotilting modules are Wakamatsu-tilting modules.
$S=\text{End}(T_{R})^{op}$. Note also that both tilting modules and cotilting modules are Wakamatsu-tilting modules.
We need the following well-known results on tilting modules and cotilting modules.
Proposition.
(1) The cotorsion pair
 $(\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}}),_{T}{\mathcal{X}})$ is complete provided that
$(\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}}),_{T}{\mathcal{X}})$ is complete provided that  $T$ is a tilting module.
$T$ is a tilting module.(2) The cotorsion pair
 $({\mathcal{X}}_{T},\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-))$ is complete provided that
$({\mathcal{X}}_{T},\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-))$ is complete provided that  $T$ is a cotilting module.
$T$ is a cotilting module.
Proof. (2) follows from [Reference Auslander and Reiten3, Section 5] and (1) is just the dual of (2). ◻
5.1.1 Tilting modules are good Wakamatsu-tilting
Assume ![]() $T_{R}$ is a tilting module of finite projective dimension. Let
$T_{R}$ is a tilting module of finite projective dimension. Let ![]() $S=\text{End}(T_{R})^{op}$. Then
$S=\text{End}(T_{R})^{op}$. Then ![]() $_{S}T_{R}$ is a good Wakamatsu-tilting module. Hence, there is an equivalence between stable repetitive categories
$_{S}T_{R}$ is a good Wakamatsu-tilting module. Hence, there is an equivalence between stable repetitive categories ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ and
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ and ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$.
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$.
Indeed, if ![]() $_{S}T_{R}$ is a tilting module of finite projective dimension, then
$_{S}T_{R}$ is a tilting module of finite projective dimension, then ![]() $T$ is Wakamatsu-tilting and
$T$ is Wakamatsu-tilting and ![]() $_{R}DT_{S}$ is a cotilting module of finite injective dimension. By Proposition 3.1, we obtain that the bimodules
$_{R}DT_{S}$ is a cotilting module of finite injective dimension. By Proposition 3.1, we obtain that the bimodules ![]() $_{S}T_{R}$ and
$_{S}T_{R}$ and ![]() $_{R}DT_{S}$ represent a cotorsion pair counter equivalence between the complete hereditary cotorsion pair
$_{R}DT_{S}$ represent a cotorsion pair counter equivalence between the complete hereditary cotorsion pair ![]() $(\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}}),_{T}{\mathcal{X}})$ in
$(\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}}),_{T}{\mathcal{X}})$ in ![]() $\text{mod}R$ and the complete hereditary cotorsion pair
$\text{mod}R$ and the complete hereditary cotorsion pair ![]() $({\mathcal{X}}_{DT},\text{KerExt}_{S}^{1}({\mathcal{X}}_{DT},-))$ in
$({\mathcal{X}}_{DT},\text{KerExt}_{S}^{1}({\mathcal{X}}_{DT},-))$ in ![]() $\text{mod}S$. It follows from the definition that
$\text{mod}S$. It follows from the definition that ![]() $_{S}T_{R}$ is a good Wakamatsu-tilting bimodule.
$_{S}T_{R}$ is a good Wakamatsu-tilting bimodule.
5.1.2 Cotilting modules are good Wakamatsu-tilting
Assume now ![]() $T_{R}$ is a cotilting module of finite injective dimension with
$T_{R}$ is a cotilting module of finite injective dimension with ![]() $S=\text{End}(T_{R})^{op}$. Then
$S=\text{End}(T_{R})^{op}$. Then ![]() $_{S}T_{R}$ is also a good Wakamatsu-tilting module. Hence, there is an equivalence between stable repetitive categories
$_{S}T_{R}$ is also a good Wakamatsu-tilting module. Hence, there is an equivalence between stable repetitive categories ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ and
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(R)$ and ![]() $\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$.
$\text{}\underline{{\mathcal{R}}{\mathcal{C}}}(S)$.
Indeed, dually to 5.1.1, if ![]() $_{S}T_{R}$ is a cotilting module of finite injective dimension, then
$_{S}T_{R}$ is a cotilting module of finite injective dimension, then ![]() $_{R}DT_{S}$ is a tilting module of finite projective dimension. By Proposition 3.1 again, we obtain that the bimodules
$_{R}DT_{S}$ is a tilting module of finite projective dimension. By Proposition 3.1 again, we obtain that the bimodules ![]() $_{S}T_{R}$ and
$_{S}T_{R}$ and ![]() $_{R}DT_{S}$ represent a cotorsion pair counter equivalence between the complete hereditary cotorsion pair
$_{R}DT_{S}$ represent a cotorsion pair counter equivalence between the complete hereditary cotorsion pair ![]() $({\mathcal{X}}_{T},\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-))$ in
$({\mathcal{X}}_{T},\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-))$ in ![]() $\text{mod}R$ and the complete hereditary cotorsion pair
$\text{mod}R$ and the complete hereditary cotorsion pair ![]() $(\text{KerExt}_{S}^{1}(-,_{DT}{\mathcal{X}}),_{DT}{\mathcal{X}})$ in
$(\text{KerExt}_{S}^{1}(-,_{DT}{\mathcal{X}}),_{DT}{\mathcal{X}})$ in ![]() $\text{mod}S$. It follows from the definition that
$\text{mod}S$. It follows from the definition that ![]() $_{S}T_{R}$ is also a good Wakamatsu-tilting bimodule.
$_{S}T_{R}$ is also a good Wakamatsu-tilting bimodule.
5.2 Wakamatsu-tilting modules of finite type
5.2.1
We say that a Wakamatsu-tilting ![]() $R$-module
$R$-module ![]() $T$ is of finite type provided that either the subcategory
$T$ is of finite type provided that either the subcategory ![]() $\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}})$ or
$\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}})$ or ![]() $\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-)$ is of finite representation type. In particular, if
$\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-)$ is of finite representation type. In particular, if ![]() $R$ is an algebra of finite representation type, then each subcategory of
$R$ is an algebra of finite representation type, then each subcategory of ![]() $\text{mod}R$ is of finite representation type, and, hence, every Wakamatsu-tilting module in
$\text{mod}R$ is of finite representation type, and, hence, every Wakamatsu-tilting module in ![]() $\text{mod}R$ is of finite type.
$\text{mod}R$ is of finite type.
We note that, if ![]() $T$ is a Wakamatsu-tilting
$T$ is a Wakamatsu-tilting ![]() $R$-module of finite type with
$R$-module of finite type with ![]() $S=\text{End}(T_{R})^{op}$, then
$S=\text{End}(T_{R})^{op}$, then ![]() $DT$ is a Wakamatsu-tilting
$DT$ is a Wakamatsu-tilting ![]() $S$-module of finite type. This follows from the equivalences in Proposition 3.1.
$S$-module of finite type. This follows from the equivalences in Proposition 3.1.
Proposition.
A Wakamatsu-tilting module of finite type is always a good Wakamatsu-tilting module. In particular, every Wakamatsu-tilting module over an algebra of finite representation type is good.
Proof. Let ![]() $T$ be a Wakamatsu-tilting
$T$ be a Wakamatsu-tilting ![]() $R$-module of finite type with
$R$-module of finite type with ![]() $S=\text{End}(T_{R})^{op}$. Assume first that the subcategory
$S=\text{End}(T_{R})^{op}$. Assume first that the subcategory ![]() $\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-)$ is of finite representation type. Then the hereditary cotorsion pair
$\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-)$ is of finite representation type. Then the hereditary cotorsion pair ![]() $({\mathcal{X}}_{T},\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-))$ in
$({\mathcal{X}}_{T},\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-))$ in ![]() $\text{mod}R$ is complete. Moreover, by the equivalence in Proposition 3.1(3), the subcategory
$\text{mod}R$ is complete. Moreover, by the equivalence in Proposition 3.1(3), the subcategory ![]() $\text{KerExt}_{S}^{1}(-,_{DT}{\mathcal{X}})$ is also of finite representation type. Thus, the hereditary cotorsion pair
$\text{KerExt}_{S}^{1}(-,_{DT}{\mathcal{X}})$ is also of finite representation type. Thus, the hereditary cotorsion pair ![]() $(\text{KerExt}_{S}^{1}(-,_{DT}{\mathcal{X}}),_{DT}{\mathcal{X}})$ in
$(\text{KerExt}_{S}^{1}(-,_{DT}{\mathcal{X}}),_{DT}{\mathcal{X}})$ in ![]() $\text{mod}S$ is also complete. It follows that the bimodules
$\text{mod}S$ is also complete. It follows that the bimodules ![]() $_{S}T_{R}$ and
$_{S}T_{R}$ and ![]() $_{R}DT_{S}$ represent a cotorsion pair counter equivalence between the complete hereditary cotorsion pair
$_{R}DT_{S}$ represent a cotorsion pair counter equivalence between the complete hereditary cotorsion pair ![]() $({\mathcal{X}}_{T},\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-))$ in
$({\mathcal{X}}_{T},\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-))$ in ![]() $\text{mod}R$ and the complete hereditary cotorsion pair
$\text{mod}R$ and the complete hereditary cotorsion pair ![]() $(\text{KerExt}_{S}^{1}(-,_{DT}{\mathcal{X}}),_{DT}{\mathcal{X}})$ in
$(\text{KerExt}_{S}^{1}(-,_{DT}{\mathcal{X}}),_{DT}{\mathcal{X}})$ in ![]() $\text{mod}S$. Similarly, in case that
$\text{mod}S$. Similarly, in case that ![]() $\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}})$ is of finite representation type, we have that the bimodules
$\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}})$ is of finite representation type, we have that the bimodules ![]() $_{S}T_{R}$ and
$_{S}T_{R}$ and ![]() $_{R}DT_{S}$ represent a cotorsion pair counter equivalence between the complete hereditary cotorsion pair
$_{R}DT_{S}$ represent a cotorsion pair counter equivalence between the complete hereditary cotorsion pair ![]() $(\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}}),_{T}{\mathcal{X}})$ in
$(\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}}),_{T}{\mathcal{X}})$ in ![]() $\text{mod}R$ and the complete hereditary cotorsion pair
$\text{mod}R$ and the complete hereditary cotorsion pair ![]() $({\mathcal{X}}_{DT},\text{KerExt}_{S}^{1}({\mathcal{X}}_{DT},-))$ in
$({\mathcal{X}}_{DT},\text{KerExt}_{S}^{1}({\mathcal{X}}_{DT},-))$ in ![]() $\text{mod}S$. Altogether, we see that
$\text{mod}S$. Altogether, we see that ![]() $T$ is a good Wakamatsu-tilting module in either case.◻
$T$ is a good Wakamatsu-tilting module in either case.◻
5.2.2
Two trivial examples of Wakamatsu-tilting modules of finite type over an algebra ![]() $R$ are the modules
$R$ are the modules ![]() $R$ and
$R$ and ![]() $DR$. In the first case, the subcategory
$DR$. In the first case, the subcategory ![]() $\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}})=\text{proj}R$ is of finite representation type, while the subcategory
$\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}})=\text{proj}R$ is of finite representation type, while the subcategory ![]() $\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-)=\text{inj}R$ is of finite representation type in the second case.
$\text{KerExt}_{R}^{1}({\mathcal{X}}_{T},-)=\text{inj}R$ is of finite representation type in the second case.
The following is an example of a Wakamatsu-tilting module of finite type over an algebra of infinite representation type.
Example.
Let ![]() $R$ be the bound path algebra given by the following quiver over a field with the relation given by
$R$ be the bound path algebra given by the following quiver over a field with the relation given by ![]() $\text{rad}^{2}R=0$.
$\text{rad}^{2}R=0$.
The following is the preprojective part of the AR-quiver of the algebra:

The algebra is of infinite representation type. Over this algebra, we have a Wakamatsu-tilting module of finite type (and, hence, a good Wakamatsu-tilting module)
Indeed, one can check that the subcategory ![]() $\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}})$ is of finite representation type, while the subcategory
$\text{KerExt}_{R}^{1}(-,_{T}{\mathcal{X}})$ is of finite representation type, while the subcategory ![]() $_{T}{\mathcal{X}}$ is of infinite representation type.
$_{T}{\mathcal{X}}$ is of infinite representation type.
5.3 Repetitive equivalences are not derived equivalences
The following example shows that repetitive equivalences are not derived equivalences.
Example.
[Reference Wakamatsu26] Let ![]() $R$ be the bound path algebra given by the following quiver over a field with the relation given by
$R$ be the bound path algebra given by the following quiver over a field with the relation given by ![]() $\text{rad}^{2}R=0$:
$\text{rad}^{2}R=0$:
The algebra is of finite representative type and the following is the AR-quiver of the algebra:

Over this algebra, we have a Wakamatsu-tilting module of finite type (and, hence, a good Wakamatsu-tilting module)
The endomorphism algebra ![]() $S:=\text{End}(T_{R})^{op}$ is the algebra defined by the following quiver over the field with the relation given by
$S:=\text{End}(T_{R})^{op}$ is the algebra defined by the following quiver over the field with the relation given by ![]() $\text{rad}^{2}R=0$ except the path
$\text{rad}^{2}R=0$ except the path ![]() $2\rightarrow 3\rightarrow 4$.
$2\rightarrow 3\rightarrow 4$.
The algebra is also of finite representative type and the AR-quiver of the algebra is as follows:

Then, ![]() $R$ is repetitive equivalent to
$R$ is repetitive equivalent to ![]() $S$. However,
$S$. However, ![]() $R$ is not derived equivalent to
$R$ is not derived equivalent to ![]() $S$. Indeed, these two algebras are not even singularity equivalent. Recall that the singularity category of the algebra
$S$. Indeed, these two algebras are not even singularity equivalent. Recall that the singularity category of the algebra ![]() $R$, denoted by
$R$, denoted by ![]() $D_{sg}(R)$, is the quotient triangulated category of
$D_{sg}(R)$, is the quotient triangulated category of ![]() $D^{b}(\text{mod}R)$ with respect to the full subcategory formed by perfect complexes (a complex in
$D^{b}(\text{mod}R)$ with respect to the full subcategory formed by perfect complexes (a complex in ![]() $D^{b}(\text{mod}R)$ is perfect provided that it is isomorphic to a bounded complex consisting of finitely generated projective modules). Two algebras
$D^{b}(\text{mod}R)$ is perfect provided that it is isomorphic to a bounded complex consisting of finitely generated projective modules). Two algebras ![]() $R$ and
$R$ and ![]() $S$ are singularity equivalent if there is a triangle equivalence between
$S$ are singularity equivalent if there is a triangle equivalence between ![]() $D_{sg}(R)$ and
$D_{sg}(R)$ and ![]() $D_{sg}(S)$. It is obvious that derived equivalences induce singularity equivalences.
$D_{sg}(S)$. It is obvious that derived equivalences induce singularity equivalences.
In fact, let us consider the simple module ![]() $S_{4}=4$ in
$S_{4}=4$ in ![]() $\text{mod}R$. It is easy to see that, for any natural number
$\text{mod}R$. It is easy to see that, for any natural number ![]() $n$, the
$n$, the ![]() $(2n)$th syzygy
$(2n)$th syzygy ![]() $\unicode[STIX]{x1D6FA}^{2n}(S_{4})=2^{(n)}\oplus 4$ and the
$\unicode[STIX]{x1D6FA}^{2n}(S_{4})=2^{(n)}\oplus 4$ and the ![]() $(2n+1)$th syzygy
$(2n+1)$th syzygy ![]() $\unicode[STIX]{x1D6FA}^{2n+1}(S_{4})=1^{(n)}\oplus 3\oplus 5$. Note that, considered in the singularity category
$\unicode[STIX]{x1D6FA}^{2n+1}(S_{4})=1^{(n)}\oplus 3\oplus 5$. Note that, considered in the singularity category ![]() $D_{sg}(R)$, the endomorphism algebra
$D_{sg}(R)$, the endomorphism algebra ![]() $\text{Hom}_{D_{sg}(R)}(S_{4},S_{4})=\mathop{\lim }_{n\rightarrow \infty }\text{}\underline{\text{Hom}}_{R}(\unicode[STIX]{x1D6FA}^{n}(S_{4}),\unicode[STIX]{x1D6FA}^{n}(S_{4}))$, where
$\text{Hom}_{D_{sg}(R)}(S_{4},S_{4})=\mathop{\lim }_{n\rightarrow \infty }\text{}\underline{\text{Hom}}_{R}(\unicode[STIX]{x1D6FA}^{n}(S_{4}),\unicode[STIX]{x1D6FA}^{n}(S_{4}))$, where ![]() $\text{}\underline{\text{Hom}}_{R}(-,-)$ is defined in the (projectively) stable module category
$\text{}\underline{\text{Hom}}_{R}(-,-)$ is defined in the (projectively) stable module category ![]() $\text{}\underline{\text{mod}}R$; see [Reference Chen8, Proposition 2.3]. Thus, the endomorphism algebra
$\text{}\underline{\text{mod}}R$; see [Reference Chen8, Proposition 2.3]. Thus, the endomorphism algebra ![]() $\text{Hom}_{D_{sg}(R)}(S_{4},S_{4})$ is infinite dimensional.
$\text{Hom}_{D_{sg}(R)}(S_{4},S_{4})$ is infinite dimensional.
Assume that there is an equivalence between ![]() $D_{sg}(R)$ and
$D_{sg}(R)$ and ![]() $D_{sg}(S)$, and denote the image of
$D_{sg}(S)$, and denote the image of ![]() $S_{4}$ to be
$S_{4}$ to be ![]() $S_{4}^{\prime }$. Note that every complex in
$S_{4}^{\prime }$. Note that every complex in ![]() $D_{sg}(S)$ is isomorphic to a finitely generated
$D_{sg}(S)$ is isomorphic to a finitely generated ![]() $S$-module (see [Reference Chen8, Lemma 2.2]), so we may assume that
$S$-module (see [Reference Chen8, Lemma 2.2]), so we may assume that ![]() $S_{4}^{\prime }$ is in
$S_{4}^{\prime }$ is in ![]() $\text{mod}S$. Since every simple module in
$\text{mod}S$. Since every simple module in ![]() $\text{mod}S$ satisfies that all its syzygies have composition length 1 (up to projective direct summands), we see that every module in
$\text{mod}S$ satisfies that all its syzygies have composition length 1 (up to projective direct summands), we see that every module in ![]() $\text{mod}S$ satisfies that all its syzygies have composition length less than a fixed number (up to projective direct summands). Altogether, we have that the endomorphism algebra
$\text{mod}S$ satisfies that all its syzygies have composition length less than a fixed number (up to projective direct summands). Altogether, we have that the endomorphism algebra ![]() $\text{Hom}_{D_{sg}(S)}(S_{4}^{\prime },S_{4}^{\prime })=\mathop{\lim }_{n\rightarrow \infty }\text{}\underline{\text{Hom}}_{S}(\unicode[STIX]{x1D6FA}^{n}(S_{4}^{\prime }),\unicode[STIX]{x1D6FA}^{n}(S_{4}^{\prime }))$ is finite dimensional. However, the singularity equivalence assumption makes
$\text{Hom}_{D_{sg}(S)}(S_{4}^{\prime },S_{4}^{\prime })=\mathop{\lim }_{n\rightarrow \infty }\text{}\underline{\text{Hom}}_{S}(\unicode[STIX]{x1D6FA}^{n}(S_{4}^{\prime }),\unicode[STIX]{x1D6FA}^{n}(S_{4}^{\prime }))$ is finite dimensional. However, the singularity equivalence assumption makes ![]() $\text{Hom}_{D_{sg}(S)}(S_{4}^{\prime },S_{4}^{\prime })$
$\text{Hom}_{D_{sg}(S)}(S_{4}^{\prime },S_{4}^{\prime })$![]() $\simeq \text{Hom}_{D_{sg}(R)}(S_{4},S_{4})$ to be infinite dimensional, which leads to a contradiction. Hence,
$\simeq \text{Hom}_{D_{sg}(R)}(S_{4},S_{4})$ to be infinite dimensional, which leads to a contradiction. Hence, ![]() $R$ and
$R$ and ![]() $S$ are not singularity equivalent. In particular,
$S$ are not singularity equivalent. In particular, ![]() $R$ and
$R$ and ![]() $S$ are not derived equivalent.
$S$ are not derived equivalent.
From the above example, we also see that repetitive equivalences do not imply singularity equivalences. We do not know whether or not singularity equivalences imply repetitive equivalences.
Acknowledgments
The author thanks the referees’ highly valuable comments and helpful suggestions. He also thanks Prof. Xiaowu Chen and Prof. Guodong Zhou for helpful discussions.