1 Introduction
It is interesting to bring some dynamical view points into the category theory. Motivated by the classical theory of dynamical systems, the notion of entropy of categorical dynamical systems (entropy of endofunctors for short) is defined by Dimitrov et al. [Reference Dimitrov, Haiden, Katzarkov and KontsevichDHKK]. The entropy of endofunctors is actually similar to the topological entropy in the sense of sharing many properties (Lemmas 2.7–2.9). Moreover, the entropy of the derived pullback of a surjective endomorphism of a smooth projective variety over  $\mathbb{C}$ is equal to its topological entropy [Reference Kikuta and TakahashiKT]. In other words, the entropy of endofunctors can be thought of as a categorical generalization of the topological entropy.
$\mathbb{C}$ is equal to its topological entropy [Reference Kikuta and TakahashiKT]. In other words, the entropy of endofunctors can be thought of as a categorical generalization of the topological entropy.
In this paper, we add two results on the entropy of endofunctors. The first one is that, for the perfect derived categories  $\text{per}(B)$ of a smooth proper differential graded algebra
$\text{per}(B)$ of a smooth proper differential graded algebra  $B$, the lower bound of the entropy
$B$, the lower bound of the entropy  $h(F)$ of an endofunctor
$h(F)$ of an endofunctor  $F$ is given by the natural logarithm of the spectral radius
$F$ is given by the natural logarithm of the spectral radius  $\unicode[STIX]{x1D70C}({\mathcal{N}}(F))$ on the numerical Grothendieck group, called the (numerical) Gromov–Yomdin type inequality (See also [Reference Kikuta and TakahashiKT, Conjecture 5.3]). It is motivated by the fundamental theorem of the topological entropy for complex dynamics on algebraic varieties due to Gromov–Yomdin [Reference GromovGro1, Reference GromovGro2, Reference YomdinYom]:
$\unicode[STIX]{x1D70C}({\mathcal{N}}(F))$ on the numerical Grothendieck group, called the (numerical) Gromov–Yomdin type inequality (See also [Reference Kikuta and TakahashiKT, Conjecture 5.3]). It is motivated by the fundamental theorem of the topological entropy for complex dynamics on algebraic varieties due to Gromov–Yomdin [Reference GromovGro1, Reference GromovGro2, Reference YomdinYom]:
Theorem (Theorem 2.13). For each endofunctor  $F$ of
$F$ of  $\text{per}(B)$ admitting left or right adjoint functors, such that
$\text{per}(B)$ admitting left or right adjoint functors, such that  $F^{n}B\not \cong 0$ for
$F^{n}B\not \cong 0$ for  $n\geqslant 0$, we have
$n\geqslant 0$, we have
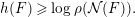 $$\begin{eqnarray}h(F)\geqslant \log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\end{eqnarray}$$
$$\begin{eqnarray}h(F)\geqslant \log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\end{eqnarray}$$For the proof, we use some norm inspired by the theory of dynamical degree and algebraic cycles due to Truong [Reference TruongTru]. Ikeda shows this inequality by the mass growth for Bridgeland’s stability conditions [Reference IkedaIke].
The equality in the Gromov–Yomdin type inequality is now known to hold for elliptic curves [Reference KikutaKik], varieties with the ample (anti-)canonical sheaf [Reference Kikuta and TakahashiKT] and abelian surfaces [Reference YoshiokaYos], which gives some applications to the topological entropy of dynamics on moduli spaces of stable objects in the sense of Bridgeland [Reference OuchiOuc1, Reference YoshiokaYos]. But, in general, it does not hold for some Calabi–Yau varieties [Reference FanFan, Reference OuchiOuc2]. As a corollary of the first main theorem, it is easy to show the equality for derived categories of hereditary finite-dimensional algebras (Proposition 2.14, Corollary 2.15).
The second result of this paper claims the equality for the derived category  ${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ of an orbifold projective line
${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ of an orbifold projective line  $\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}$ introduced by Geigle–Lenzing [Reference Geigle and LenzingGL]. Orbifold projective lines are important and interesting objects since they are not only in the next class to hereditary finite-dimensional algebras but few examples whose homological and classical mirror symmetry are well understood (cf. [Reference Ishibashi, Shiraishi and TakahashiIST, Reference Ishibashi, Shiraishi and TakahashiIST2, Reference Iwaki and TakahashiIT, Reference KeatingKea, Reference RossiRos, Reference Shiraishi and TakahashiST, Reference TakahashiTak1, Reference TakahashiTak2, Reference UedaUed]):
$\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}$ introduced by Geigle–Lenzing [Reference Geigle and LenzingGL]. Orbifold projective lines are important and interesting objects since they are not only in the next class to hereditary finite-dimensional algebras but few examples whose homological and classical mirror symmetry are well understood (cf. [Reference Ishibashi, Shiraishi and TakahashiIST, Reference Ishibashi, Shiraishi and TakahashiIST2, Reference Iwaki and TakahashiIT, Reference KeatingKea, Reference RossiRos, Reference Shiraishi and TakahashiST, Reference TakahashiTak1, Reference TakahashiTak2, Reference UedaUed]):
Theorem (Theorem 3.10). For each auto-equivalence  $F$ of
$F$ of  ${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, we have
${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, we have
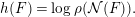 $$\begin{eqnarray}h(F)=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\end{eqnarray}$$
$$\begin{eqnarray}h(F)=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\end{eqnarray}$$ Moreover, the spectral radius  $\unicode[STIX]{x1D70C}({\mathcal{N}}(F))$ is an algebraic integer, and
$\unicode[STIX]{x1D70C}({\mathcal{N}}(F))$ is an algebraic integer, and  $h(F)=0$ if
$h(F)=0$ if  $\unicode[STIX]{x1D712}_{A}\neq 0$.
$\unicode[STIX]{x1D712}_{A}\neq 0$.
It is an important and interesting problem to find a characterization of endofunctors attaining the lower bound of the inequality (1).
2 Preliminaries
2.1 Notations and terminologies
Throughout this paper, we work over the base field  $\mathbb{C}$ and all triangulated categories are
$\mathbb{C}$ and all triangulated categories are  $\mathbb{C}$-linear and not equivalent to the zero category. The translation functor on a triangulated category is denoted by
$\mathbb{C}$-linear and not equivalent to the zero category. The translation functor on a triangulated category is denoted by  $[1]$. All (triangulated) functors are
$[1]$. All (triangulated) functors are  $\mathbb{C}$-linear.
$\mathbb{C}$-linear.
A triangulated category  ${\mathcal{T}}$ is called split-closed if every idempotent in
${\mathcal{T}}$ is called split-closed if every idempotent in  ${\mathcal{T}}$ splits, namely, if it contains all direct summands of its objects, and it is called thick if it is split-closed and closed under isomorphisms. For an object
${\mathcal{T}}$ splits, namely, if it contains all direct summands of its objects, and it is called thick if it is split-closed and closed under isomorphisms. For an object  $M\in {\mathcal{T}}$, we denote
$M\in {\mathcal{T}}$, we denote  $\langle M\rangle$ by the smallest thick triangulated subcategory containing
$\langle M\rangle$ by the smallest thick triangulated subcategory containing  $M$. An object
$M$. An object  $G\in {\mathcal{T}}$ is called a split-generator if
$G\in {\mathcal{T}}$ is called a split-generator if  $\langle G\rangle ={\mathcal{T}}$. A triangulated category
$\langle G\rangle ={\mathcal{T}}$. A triangulated category  ${\mathcal{T}}$ is said to be of finite type if for all
${\mathcal{T}}$ is said to be of finite type if for all  $M,N\in {\mathcal{T}}$ we have
$M,N\in {\mathcal{T}}$ we have  $\sum _{n\in \mathbb{Z}}\dim _{\mathbb{C}}\text{ Hom}_{{\mathcal{T}}}(M,N[n])<\infty$.
$\sum _{n\in \mathbb{Z}}\dim _{\mathbb{C}}\text{ Hom}_{{\mathcal{T}}}(M,N[n])<\infty$.
2.2 Complexity
From now on,  ${\mathcal{T}},{\mathcal{T}}^{\prime }$ denote triangulated categories of finite type.
${\mathcal{T}},{\mathcal{T}}^{\prime }$ denote triangulated categories of finite type.
Definition 2.1. [Reference Dimitrov, Haiden, Katzarkov and KontsevichDHKK, Definition 2.1]
For each  $M,N\in {\mathcal{T}}$, define the function
$M,N\in {\mathcal{T}}$, define the function  $\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M,N):\mathbb{R}\longrightarrow \mathbb{R}_{{\geqslant}0}\cup \{\infty \}$ in
$\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M,N):\mathbb{R}\longrightarrow \mathbb{R}_{{\geqslant}0}\cup \{\infty \}$ in  $t$ by (i)
$t$ by (i)  $\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M,N):=0$ if
$\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M,N):=0$ if  $N\simeq 0$, (ii)
$N\simeq 0$, (ii)

if  $N\in \langle M\rangle$ and (iii)
$N\in \langle M\rangle$ and (iii)  $\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M,N):=\infty$ if
$\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M,N):=\infty$ if  $N\not \in \langle M\rangle$. The function
$N\not \in \langle M\rangle$. The function  $\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M,N)$ is called the complexity of
$\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M,N)$ is called the complexity of  $N$ with respect to
$N$ with respect to  $M$.
$M$.
Remark 2.2. If  ${\mathcal{T}}$ has a split-generator
${\mathcal{T}}$ has a split-generator  $G$ and
$G$ and  $M\in {\mathcal{T}}$ is not isomorphic to a zero object, then an inequality
$M\in {\mathcal{T}}$ is not isomorphic to a zero object, then an inequality  $1\leqslant \unicode[STIX]{x1D6FF}_{{\mathcal{T}},0}(G,M)<\infty$ holds.
$1\leqslant \unicode[STIX]{x1D6FF}_{{\mathcal{T}},0}(G,M)<\infty$ holds.
We recall some basic properties of the complexity.
Lemma 2.3. Let  $M_{1},M_{2},M_{3},M_{4}\in {\mathcal{T}}$.
$M_{1},M_{2},M_{3},M_{4}\in {\mathcal{T}}$.
(i) If
 $M_{2}\in \langle M_{1}\rangle$ and
$M_{2}\in \langle M_{1}\rangle$ and  $M_{2}\not \cong 0$, then
$M_{2}\not \cong 0$, then  $0<\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{2})$.
$0<\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{2})$.(ii) If
 $M_{1}\cong M_{3}$, then
$M_{1}\cong M_{3}$, then  $\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{2})=\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{3},M_{2})$.
$\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{2})=\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{3},M_{2})$.(iii) If
 $M_{2}\cong M_{3}$, then
$M_{2}\cong M_{3}$, then  $\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{2})=\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{3})$.
$\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{2})=\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{3})$.(iv) If
 $M_{2}\not \cong 0$, then
$M_{2}\not \cong 0$, then  $\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{3})\leqslant \unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{2})\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{2},M_{3})$.
$\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{3})\leqslant \unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{2})\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{2},M_{3})$.(v) We have
 $\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{4},M_{2})\leqslant \unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{4},M_{1})+\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{4},M_{3})$ for an exact triangle
$\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{4},M_{2})\leqslant \unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{4},M_{1})+\unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{4},M_{3})$ for an exact triangle  $M_{1}\rightarrow M_{2}\rightarrow M_{3}$.
$M_{1}\rightarrow M_{2}\rightarrow M_{3}$.(vi) We have
 $\unicode[STIX]{x1D6FF}_{{\mathcal{T}}^{\prime },t}(F(M_{1}),F(M_{2}))\leqslant \unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{2})$ for any triangulated functor
$\unicode[STIX]{x1D6FF}_{{\mathcal{T}}^{\prime },t}(F(M_{1}),F(M_{2}))\leqslant \unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(M_{1},M_{2})$ for any triangulated functor  $F:{\mathcal{T}}\longrightarrow {\mathcal{T}}^{\prime }$.
$F:{\mathcal{T}}\longrightarrow {\mathcal{T}}^{\prime }$.
Lemma 2.4. Let  ${\mathcal{D}}^{b}(\mathbb{C})$ be the bounded derived category of finite-dimensional
${\mathcal{D}}^{b}(\mathbb{C})$ be the bounded derived category of finite-dimensional  $\mathbb{C}$-vector spaces. For
$\mathbb{C}$-vector spaces. For  $M\in {\mathcal{D}}^{b}(\mathbb{C})$, we have the following inequality
$M\in {\mathcal{D}}^{b}(\mathbb{C})$, we have the following inequality
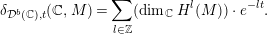 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{C}),t}(\mathbb{C},M)=\mathop{\sum }_{l\in \mathbb{Z}}(\dim _{\mathbb{C}}H^{l}(M))\cdot e^{-lt}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{C}),t}(\mathbb{C},M)=\mathop{\sum }_{l\in \mathbb{Z}}(\dim _{\mathbb{C}}H^{l}(M))\cdot e^{-lt}.\end{eqnarray}$$2.3 Entropy of endofunctors
Endofunctor  $F$ means triangulated functor
$F$ means triangulated functor  $F:{\mathcal{T}}\rightarrow {\mathcal{T}}$. We assume that all endofunctors of
$F:{\mathcal{T}}\rightarrow {\mathcal{T}}$. We assume that all endofunctors of  ${\mathcal{T}}$ satisfy that
${\mathcal{T}}$ satisfy that  $F^{n}G\not \cong 0$ for
$F^{n}G\not \cong 0$ for  $n\geqslant 0$ (if
$n\geqslant 0$ (if  ${\mathcal{T}}$ has a split-generator
${\mathcal{T}}$ has a split-generator  $G$).
$G$).
Definition 2.5. [Reference Dimitrov, Haiden, Katzarkov and KontsevichDHKK, Definition 2.4]
Let  $G$ be a split-generator of
$G$ be a split-generator of  ${\mathcal{T}}$ and
${\mathcal{T}}$ and  $F$ an endofunctor of
$F$ an endofunctor of  ${\mathcal{T}}$. The entropy of
${\mathcal{T}}$. The entropy of  $F$ is the function
$F$ is the function  $h_{t}(F):\mathbb{R}\longrightarrow \{-\infty \}\cup \mathbb{R}$ given by
$h_{t}(F):\mathbb{R}\longrightarrow \{-\infty \}\cup \mathbb{R}$ given by
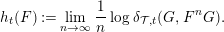 $$\begin{eqnarray}h_{t}(F):=\displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(G,F^{n}G).\end{eqnarray}$$
$$\begin{eqnarray}h_{t}(F):=\displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(G,F^{n}G).\end{eqnarray}$$It follows from [Reference Dimitrov, Haiden, Katzarkov and KontsevichDHKK, Lemma 2.5] that the entropy is well defined and does not depend on the choice of split-generators.
Lemma 2.6. Let  $G,G^{\prime }$ be split-generators of
$G,G^{\prime }$ be split-generators of  ${\mathcal{T}}$ and
${\mathcal{T}}$ and  $F$ an endofunctor of
$F$ an endofunctor of  ${\mathcal{T}}$. The entropy
${\mathcal{T}}$. The entropy  $h_{t}(F)$ of
$h_{t}(F)$ of  $F$ is given by
$F$ is given by
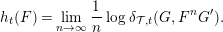 $$\begin{eqnarray}h_{t}(F)=\displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(G,F^{n}G^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}h_{t}(F)=\displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{T}},t}(G,F^{n}G^{\prime }).\end{eqnarray}$$The three lemmas below show that the entropy of endofunctors is similar to the topological entropy.
Lemma 2.7. Let  $G$ be a split-generator of
$G$ be a split-generator of  ${\mathcal{T}}$ and
${\mathcal{T}}$ and  $F_{1},F_{2}$ endofunctors of
$F_{1},F_{2}$ endofunctors of  ${\mathcal{T}}$.
${\mathcal{T}}$.
(i) If
 $F_{1}\cong F_{2}$, then
$F_{1}\cong F_{2}$, then  $h_{t}(F_{1})=h_{t}(F_{2})$.
$h_{t}(F_{1})=h_{t}(F_{2})$.(ii) We have
 $h_{t}(F_{1}^{m})=mh_{t}(F_{1})$ for
$h_{t}(F_{1}^{m})=mh_{t}(F_{1})$ for  $m\geqslant 1$.
$m\geqslant 1$.(iii) We have
 $h_{t}(F_{1}F_{2})=h_{t}(F_{2}F_{1})$.
$h_{t}(F_{1}F_{2})=h_{t}(F_{2}F_{1})$.(iv) If
 $F_{1}F_{2}\cong F_{2}F_{1}$, then
$F_{1}F_{2}\cong F_{2}F_{1}$, then  $h_{t}(F_{1}F_{2})\leqslant h_{t}(F_{1})+h_{t}(F_{2})$.
$h_{t}(F_{1}F_{2})\leqslant h_{t}(F_{1})+h_{t}(F_{2})$.(v) If
 $F_{1}=F_{2}[m]~(m\in \mathbb{Z})$, then
$F_{1}=F_{2}[m]~(m\in \mathbb{Z})$, then  $h_{t}(F_{1})=h_{t}(F_{2})+mt$.
$h_{t}(F_{1})=h_{t}(F_{2})+mt$.
Lemma 2.8. Let  $F_{i}$ be an endofunctor of
$F_{i}$ be an endofunctor of  ${\mathcal{T}}_{i}$ with a split-generator
${\mathcal{T}}_{i}$ with a split-generator  $G_{i}~(i=1,2)$. If there exists a fully faithful functor
$G_{i}~(i=1,2)$. If there exists a fully faithful functor  $F^{\prime }:{\mathcal{T}}_{2}\rightarrow {\mathcal{T}}_{1}$, which has left and right adjoint functors, such that
$F^{\prime }:{\mathcal{T}}_{2}\rightarrow {\mathcal{T}}_{1}$, which has left and right adjoint functors, such that  $F^{\prime }F_{2}\simeq F_{1}F^{\prime }$, then
$F^{\prime }F_{2}\simeq F_{1}F^{\prime }$, then  $h_{t}(F_{2})\leqslant h_{t}(F_{1})$.
$h_{t}(F_{2})\leqslant h_{t}(F_{1})$.
Lemma 2.9. Let  $F_{i}$ be an endofunctor of
$F_{i}$ be an endofunctor of  ${\mathcal{T}}_{i}$ with a split-generator
${\mathcal{T}}_{i}$ with a split-generator  $G_{i}~(i=1,2)$. If there exists an essentially surjective functor
$G_{i}~(i=1,2)$. If there exists an essentially surjective functor  $F^{\prime }:{\mathcal{T}}_{1}\rightarrow {\mathcal{T}}_{2}$ such that
$F^{\prime }:{\mathcal{T}}_{1}\rightarrow {\mathcal{T}}_{2}$ such that  $F^{\prime }F_{1}\simeq F_{2}F^{\prime }$, then
$F^{\prime }F_{1}\simeq F_{2}F^{\prime }$, then  $h_{t}(F_{2})\leqslant h_{t}(F_{1})$.
$h_{t}(F_{2})\leqslant h_{t}(F_{1})$.
As a corollary of Lemma 2.9, we have the following
Corollary 2.10. Let  $F^{\prime }$ an auto-equivalence of
$F^{\prime }$ an auto-equivalence of  ${\mathcal{T}}$. The entropy is a class function, namely,
${\mathcal{T}}$. The entropy is a class function, namely,  $h_{t}(F^{\prime }F{F^{\prime }}^{-1})=h_{t}(F)$.
$h_{t}(F^{\prime }F{F^{\prime }}^{-1})=h_{t}(F)$.
Let  $B$ be a smooth proper differential graded (dg)
$B$ be a smooth proper differential graded (dg)  $\mathbb{C}$-algebra
$\mathbb{C}$-algebra  $B$ and
$B$ and  $\text{per}(B)$ the perfect derived category of dg
$\text{per}(B)$ the perfect derived category of dg  $B$-modules, the full triangulated subcategory of the derived category
$B$-modules, the full triangulated subcategory of the derived category  ${\mathcal{D}}(B)$ of dg
${\mathcal{D}}(B)$ of dg  $B$-modules containing
$B$-modules containing  $B$ closed under isomorphisms and taking direct summands. By definition,
$B$ closed under isomorphisms and taking direct summands. By definition,  $B$ is a split-generator of
$B$ is a split-generator of  $\text{per}(B)$.
$\text{per}(B)$.
The following proposition enables us to compute entropy.
Proposition 2.11. [Reference Dimitrov, Haiden, Katzarkov and KontsevichDHKK, Theorem 2.7]
Let  $G,G^{\prime }$ be split-generators of
$G,G^{\prime }$ be split-generators of  $\text{per}(B)$ and
$\text{per}(B)$ and  $F$ an endofunctor of
$F$ an endofunctor of  $\text{per}(B)$. The entropy
$\text{per}(B)$. The entropy  $h_{t}(F)$ is given by
$h_{t}(F)$ is given by
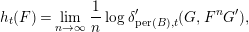 $$\begin{eqnarray}h_{t}(F)=\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B),t}^{\prime }(G,F^{n}G^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}h_{t}(F)=\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B),t}^{\prime }(G,F^{n}G^{\prime }),\end{eqnarray}$$where
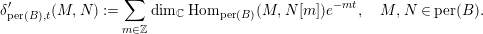 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\text{per}(B),t}^{\prime }(M,N):=\mathop{\sum }_{m\in \mathbb{Z}}\dim _{\mathbb{C}}\text{Hom}_{\text{per}(B)}(M,N[m])e^{-mt},\quad M,N\in \text{per}(B).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\text{per}(B),t}^{\prime }(M,N):=\mathop{\sum }_{m\in \mathbb{Z}}\dim _{\mathbb{C}}\text{Hom}_{\text{per}(B)}(M,N[m])e^{-mt},\quad M,N\in \text{per}(B).\end{eqnarray}$$Proof. The following is proven in the proof of [Reference Dimitrov, Haiden, Katzarkov and KontsevichDHKK, Theorem 2.7].
Lemma 2.12. For each  $M\in \text{per}(B)$, there exist
$M\in \text{per}(B)$, there exist  $C_{1}(t),C_{2}(t)$ for
$C_{1}(t),C_{2}(t)$ for  $t\in \mathbb{R}$ such that
$t\in \mathbb{R}$ such that
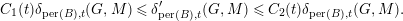 $$\begin{eqnarray}C_{1}(t)\unicode[STIX]{x1D6FF}_{\text{per}(B),t}(G,M)\leqslant \unicode[STIX]{x1D6FF}_{\text{per}(B),t}^{\prime }(G,M)\leqslant C_{2}(t)\unicode[STIX]{x1D6FF}_{\text{per}(B),t}(G,M).\end{eqnarray}$$
$$\begin{eqnarray}C_{1}(t)\unicode[STIX]{x1D6FF}_{\text{per}(B),t}(G,M)\leqslant \unicode[STIX]{x1D6FF}_{\text{per}(B),t}^{\prime }(G,M)\leqslant C_{2}(t)\unicode[STIX]{x1D6FF}_{\text{per}(B),t}(G,M).\end{eqnarray}$$ In particular, for each  $M\in \text{per}(B)$ we have
$M\in \text{per}(B)$ we have
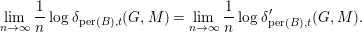 $$\begin{eqnarray}\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B),t}(G,M)=\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B),t}^{\prime }(G,M).\end{eqnarray}$$
$$\begin{eqnarray}\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B),t}(G,M)=\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B),t}^{\prime }(G,M).\end{eqnarray}$$Together with Lemma 2.6, we have
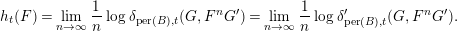 $$\begin{eqnarray}h_{t}(F)=\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B),t}(G,F^{n}G^{\prime })=\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B),t}^{\prime }(G,F^{n}G^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}h_{t}(F)=\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B),t}(G,F^{n}G^{\prime })=\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B),t}^{\prime }(G,F^{n}G^{\prime }).\end{eqnarray}$$We finished the proof of the proposition.◻
In order to state the first main theorem, we prepare some terminologies. For  $M,N\in \text{per}(B)$, set
$M,N\in \text{per}(B)$, set
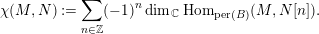 $$\begin{eqnarray}\unicode[STIX]{x1D712}(M,N):=\mathop{\sum }_{n\in \mathbb{Z}}(-1)^{n}\dim _{\mathbb{ C}}\text{Hom}_{\text{per}(B)}(M,N[n]).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(M,N):=\mathop{\sum }_{n\in \mathbb{Z}}(-1)^{n}\dim _{\mathbb{ C}}\text{Hom}_{\text{per}(B)}(M,N[n]).\end{eqnarray}$$ It naturally induces a bilinear form on the Grothendieck group  $K_{0}(\text{per}(B))$ of
$K_{0}(\text{per}(B))$ of  $\text{per}(B)$, called the Euler form, which is denoted by the same letter
$\text{per}(B)$, called the Euler form, which is denoted by the same letter  $\unicode[STIX]{x1D712}$. Then the numerical Grothendieck group
$\unicode[STIX]{x1D712}$. Then the numerical Grothendieck group  ${\mathcal{N}}(\text{per}(B))$ is defined as the quotient of
${\mathcal{N}}(\text{per}(B))$ is defined as the quotient of  $K_{0}(\text{per}(B))$ by the radical of
$K_{0}(\text{per}(B))$ by the radical of  $\unicode[STIX]{x1D712}$ (which is well defined by the Serre duality). It is important to note that
$\unicode[STIX]{x1D712}$ (which is well defined by the Serre duality). It is important to note that  ${\mathcal{N}}(\text{per}(B))$ is a free abelian group of finite rank by Hirzebruch–Riemann–Roch theorem [Reference ShklyarovShk, Reference LuntsLun]. If an endofunctor
${\mathcal{N}}(\text{per}(B))$ is a free abelian group of finite rank by Hirzebruch–Riemann–Roch theorem [Reference ShklyarovShk, Reference LuntsLun]. If an endofunctor  $F$ of
$F$ of  $\text{per}(B)$ admits left or right (hence both by the Serre duality) adjoint functors, it respects the radical of
$\text{per}(B)$ admits left or right (hence both by the Serre duality) adjoint functors, it respects the radical of  $\unicode[STIX]{x1D712}$. Therefore, it induces an endomorphism
$\unicode[STIX]{x1D712}$. Therefore, it induces an endomorphism  ${\mathcal{N}}(F)$ on
${\mathcal{N}}(F)$ on  ${\mathcal{N}}(\text{per}(B))$. Note that an endofunctor lifting to a dg endofunctor of the dg category
${\mathcal{N}}(\text{per}(B))$. Note that an endofunctor lifting to a dg endofunctor of the dg category  $\text{per}_{dg}(B)$ admits adjoint functors. The spectral radius
$\text{per}_{dg}(B)$ admits adjoint functors. The spectral radius  $\unicode[STIX]{x1D70C}({\mathcal{N}}(F))$ of
$\unicode[STIX]{x1D70C}({\mathcal{N}}(F))$ of  ${\mathcal{N}}(F)$ is the maximum of absolute values of eigenvalues of
${\mathcal{N}}(F)$ is the maximum of absolute values of eigenvalues of  $\mathbb{C}$-linear endomorphism
$\mathbb{C}$-linear endomorphism  ${\mathcal{N}}(F)\otimes _{\mathbb{Z}}\mathbb{C}$. Set
${\mathcal{N}}(F)\otimes _{\mathbb{Z}}\mathbb{C}$. Set  $\unicode[STIX]{x1D6FF}_{{\mathcal{T}}}:=\unicode[STIX]{x1D6FF}_{{\mathcal{T}},0},\unicode[STIX]{x1D6FF}_{{\mathcal{T}}}^{\prime }:=\unicode[STIX]{x1D6FF}_{{\mathcal{T}},0}^{\prime },h:=h_{0}$.
$\unicode[STIX]{x1D6FF}_{{\mathcal{T}}}:=\unicode[STIX]{x1D6FF}_{{\mathcal{T}},0},\unicode[STIX]{x1D6FF}_{{\mathcal{T}}}^{\prime }:=\unicode[STIX]{x1D6FF}_{{\mathcal{T}},0}^{\prime },h:=h_{0}$.
Inspired by the theory of dynamical degree and algebraic cycles due to Truong (cf. [Reference TruongTru, eq. (3.2)]), we show the following:
Theorem 2.13. For each endofunctor  $F$ of
$F$ of  $\text{per}(B)$ admitting left or right adjoint functors, we have
$\text{per}(B)$ admitting left or right adjoint functors, we have
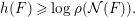 $$\begin{eqnarray}h(F)\geqslant \log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\end{eqnarray}$$
$$\begin{eqnarray}h(F)\geqslant \log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\end{eqnarray}$$Proof. Let  $v_{1},\ldots ,v_{p}~(v_{i}=[M_{i}],M_{i}\in \text{per}(B))$ be a fixed basis of
$v_{1},\ldots ,v_{p}~(v_{i}=[M_{i}],M_{i}\in \text{per}(B))$ be a fixed basis of  ${\mathcal{N}}(\text{per}(B))$. Set
${\mathcal{N}}(\text{per}(B))$. Set  $M_{0}:=\oplus _{i}M_{i},{\mathcal{N}}(\text{per}(B))_{\mathbb{R}}:={\mathcal{N}}(\text{per}(B))\otimes _{\mathbb{Z}}\mathbb{R},{\mathcal{N}}(F)_{\mathbb{R}}:={\mathcal{N}}(F)\otimes _{\mathbb{Z}}\mathbb{R},\unicode[STIX]{x1D712}_{\mathbb{R}}:=\unicode[STIX]{x1D712}\otimes _{\mathbb{Z}}\mathbb{R}$. Define a norm
$M_{0}:=\oplus _{i}M_{i},{\mathcal{N}}(\text{per}(B))_{\mathbb{R}}:={\mathcal{N}}(\text{per}(B))\otimes _{\mathbb{Z}}\mathbb{R},{\mathcal{N}}(F)_{\mathbb{R}}:={\mathcal{N}}(F)\otimes _{\mathbb{Z}}\mathbb{R},\unicode[STIX]{x1D712}_{\mathbb{R}}:=\unicode[STIX]{x1D712}\otimes _{\mathbb{Z}}\mathbb{R}$. Define a norm  $\Vert \cdot \Vert$ on
$\Vert \cdot \Vert$ on  ${\mathcal{N}}(\text{per}(B))_{\mathbb{R}}$ by
${\mathcal{N}}(\text{per}(B))_{\mathbb{R}}$ by
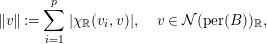 $$\begin{eqnarray}\Vert v\Vert :=\displaystyle \mathop{\sum }_{i=1}^{p}|\unicode[STIX]{x1D712}_{\mathbb{ R}}(v_{i},v)|,\quad v\in {\mathcal{N}}(\text{per}(B))_{\mathbb{R}},\end{eqnarray}$$
$$\begin{eqnarray}\Vert v\Vert :=\displaystyle \mathop{\sum }_{i=1}^{p}|\unicode[STIX]{x1D712}_{\mathbb{ R}}(v_{i},v)|,\quad v\in {\mathcal{N}}(\text{per}(B))_{\mathbb{R}},\end{eqnarray}$$ which induces an operator norm of  ${\mathcal{N}}(F)_{\mathbb{R}}$, that is,
${\mathcal{N}}(F)_{\mathbb{R}}$, that is,
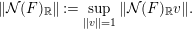 $$\begin{eqnarray}\Vert {\mathcal{N}}(F)_{\mathbb{R}}\Vert :=\displaystyle \sup _{\Vert v\Vert =1}\Vert {\mathcal{N}}(F)_{\mathbb{R}}v\Vert .\end{eqnarray}$$
$$\begin{eqnarray}\Vert {\mathcal{N}}(F)_{\mathbb{R}}\Vert :=\displaystyle \sup _{\Vert v\Vert =1}\Vert {\mathcal{N}}(F)_{\mathbb{R}}v\Vert .\end{eqnarray}$$ By the compactness of the subset  $\{\Vert v\Vert =1\}\subset {\mathcal{N}}(\text{per}(B))_{\mathbb{R}}$, there exists a positive number
$\{\Vert v\Vert =1\}\subset {\mathcal{N}}(\text{per}(B))_{\mathbb{R}}$, there exists a positive number  $C>0$ such that
$C>0$ such that
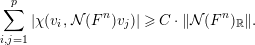 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i,j=1}^{p}|\unicode[STIX]{x1D712}(v_{i},{\mathcal{N}}(F^{n})v_{j})|\geqslant C\cdot \Vert {\mathcal{N}}(F^{n})_{\mathbb{ R}}\Vert .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i,j=1}^{p}|\unicode[STIX]{x1D712}(v_{i},{\mathcal{N}}(F^{n})v_{j})|\geqslant C\cdot \Vert {\mathcal{N}}(F^{n})_{\mathbb{ R}}\Vert .\end{eqnarray}$$ Note that  $B\oplus M_{0}$ is a split-generator of
$B\oplus M_{0}$ is a split-generator of  $\text{per}(B)$. By Proposition 2.11, the statement follows from
$\text{per}(B)$. By Proposition 2.11, the statement follows from
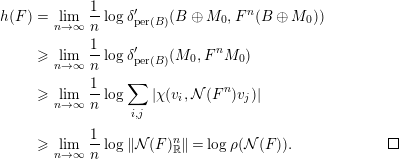 $$\begin{eqnarray}\displaystyle h(F) & = & \displaystyle \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B)}^{\prime }(B\oplus M_{0},F^{n}(B\oplus M_{0}))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B)}^{\prime }(M_{0},F^{n}M_{0})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \mathop{\sum }_{i,j}|\unicode[STIX]{x1D712}(v_{i},{\mathcal{N}}(F^{n})v_{j})|\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \Vert {\mathcal{N}}(F)_{\mathbb{R}}^{n}\Vert =\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(F) & = & \displaystyle \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B)}^{\prime }(B\oplus M_{0},F^{n}(B\oplus M_{0}))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B)}^{\prime }(M_{0},F^{n}M_{0})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \mathop{\sum }_{i,j}|\unicode[STIX]{x1D712}(v_{i},{\mathcal{N}}(F^{n})v_{j})|\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \Vert {\mathcal{N}}(F)_{\mathbb{R}}^{n}\Vert =\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\square\nonumber\end{eqnarray}$$ Let  $\text{Auteq}({\mathcal{T}})$ be the group of (natural isomorphism classes of) auto-equivalences of a triangulated category
$\text{Auteq}({\mathcal{T}})$ be the group of (natural isomorphism classes of) auto-equivalences of a triangulated category  ${\mathcal{T}}$.
${\mathcal{T}}$.
Proposition 2.14. Let  $B$ be a hereditary finite-dimensional
$B$ be a hereditary finite-dimensional  $\mathbb{C}$-algebra. For each auto-equivalence
$\mathbb{C}$-algebra. For each auto-equivalence  $F\in \text{Auteq}(\text{per}(B))$, we have
$F\in \text{Auteq}(\text{per}(B))$, we have
 $$\begin{eqnarray}h(F)=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\end{eqnarray}$$
$$\begin{eqnarray}h(F)=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\end{eqnarray}$$Proof. Due to Theorem 2.13, we only need to show the upper bound. Let  $P_{1},\ldots ,P_{\dim _{\mathbb{C}}B}$ be indecomposable modules. Each auto-equivalence
$P_{1},\ldots ,P_{\dim _{\mathbb{C}}B}$ be indecomposable modules. Each auto-equivalence  $F$ sends an indecomposable object to an indecomposable one. Since
$F$ sends an indecomposable object to an indecomposable one. Since  $B$ is hereditary, there exists
$B$ is hereditary, there exists  $m\in \mathbb{Z}$ such that the indecomposable object
$m\in \mathbb{Z}$ such that the indecomposable object  $F^{n}(P_{i})[m]$ is isomorphic to an object concentrated in degree zero, namely, a
$F^{n}(P_{i})[m]$ is isomorphic to an object concentrated in degree zero, namely, a  $B$-module. By Proposition 2.11, we have
$B$-module. By Proposition 2.11, we have
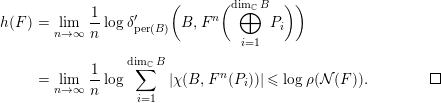 $$\begin{eqnarray}\displaystyle h(F) & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B)}^{\prime }\biggl(B,F^{n}\biggl(\bigoplus _{i=1}^{\dim _{\mathbb{C}}B}P_{i}\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \mathop{\sum }_{i=1}^{\dim _{\mathbb{C}}B}|\unicode[STIX]{x1D712}(B,F^{n}(P_{i}))|\leqslant \log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(F) & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{\text{per}(B)}^{\prime }\biggl(B,F^{n}\biggl(\bigoplus _{i=1}^{\dim _{\mathbb{C}}B}P_{i}\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \mathop{\sum }_{i=1}^{\dim _{\mathbb{C}}B}|\unicode[STIX]{x1D712}(B,F^{n}(P_{i}))|\leqslant \log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\square\nonumber\end{eqnarray}$$Corollary 2.15. Suppose that  $B=\mathbb{C}\vec{\unicode[STIX]{x1D6E5}}$ for some Dynkin quiver
$B=\mathbb{C}\vec{\unicode[STIX]{x1D6E5}}$ for some Dynkin quiver  $\vec{\unicode[STIX]{x1D6E5}}$. Then, we have
$\vec{\unicode[STIX]{x1D6E5}}$. Then, we have
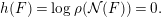 $$\begin{eqnarray}h(F)=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F))=0.\end{eqnarray}$$
$$\begin{eqnarray}h(F)=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F))=0.\end{eqnarray}$$Proof. It is known by [Reference Miyachi and YekutieliMY, Theorem 3.8], that
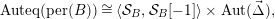 $$\begin{eqnarray}\text{Auteq}(\text{per}(B))\cong \langle {\mathcal{S}}_{B},{\mathcal{S}}_{B}[-1]\rangle \times \text{Aut}(\vec{\unicode[STIX]{x1D6E5}}),\end{eqnarray}$$
$$\begin{eqnarray}\text{Auteq}(\text{per}(B))\cong \langle {\mathcal{S}}_{B},{\mathcal{S}}_{B}[-1]\rangle \times \text{Aut}(\vec{\unicode[STIX]{x1D6E5}}),\end{eqnarray}$$ where  ${\mathcal{S}}_{B}$ is the Serre functor of
${\mathcal{S}}_{B}$ is the Serre functor of  $\text{per}(B)$ and
$\text{per}(B)$ and  $\text{Aut}(\vec{\unicode[STIX]{x1D6E5}})$ is the finite subgroup of
$\text{Aut}(\vec{\unicode[STIX]{x1D6E5}})$ is the finite subgroup of  $\text{Auteq}(\text{per}(B))$ consisting of automorphisms of
$\text{Auteq}(\text{per}(B))$ consisting of automorphisms of  $\vec{\unicode[STIX]{x1D6E5}}$. Again, by [Reference Miyachi and YekutieliMY, Theorem 3.8],
$\vec{\unicode[STIX]{x1D6E5}}$. Again, by [Reference Miyachi and YekutieliMY, Theorem 3.8],  ${\mathcal{S}}_{B}$ is of finite order up to translation. The statement follows from Lemma 2.7(ii), (iv) and (v).◻
${\mathcal{S}}_{B}$ is of finite order up to translation. The statement follows from Lemma 2.7(ii), (iv) and (v).◻
3 Orbifold projective lines
In this section, we shall show the Gromov–Yomdin type theorem for the entropy of an auto-equivalence on the derived category  ${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ of coherent sheaves on an orbifold projective line
${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ of coherent sheaves on an orbifold projective line  $\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}$. We first recall the definition of orbifold projective line in [Reference Geigle and LenzingGL].
$\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}$. We first recall the definition of orbifold projective line in [Reference Geigle and LenzingGL].
Let  $r\geqslant 3$ be a positive integer. Let
$r\geqslant 3$ be a positive integer. Let  $A=(a_{1},\ldots ,a_{r})$ be a multiplet of positive integers and
$A=(a_{1},\ldots ,a_{r})$ be a multiplet of positive integers and  $\unicode[STIX]{x1D6EC}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{r})$ a multiplet of pairwise distinct elements of
$\unicode[STIX]{x1D6EC}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{r})$ a multiplet of pairwise distinct elements of  $\mathbb{P}^{1}(\mathbb{C})$ normalized such that
$\mathbb{P}^{1}(\mathbb{C})$ normalized such that  $\unicode[STIX]{x1D706}_{1}=\infty$,
$\unicode[STIX]{x1D706}_{1}=\infty$,  $\unicode[STIX]{x1D706}_{2}=0$ and
$\unicode[STIX]{x1D706}_{2}=0$ and  $\unicode[STIX]{x1D706}_{3}=1$.
$\unicode[STIX]{x1D706}_{3}=1$.
In order to introduce an orbifold projective line, we prepare some notations.
Definition 3.1. Let  $r$,
$r$,  $A$ and
$A$ and  $\unicode[STIX]{x1D6EC}$ be as above.
$\unicode[STIX]{x1D6EC}$ be as above.
(i) Define a ring
 $R_{A,\unicode[STIX]{x1D6EC}}$ by (15a)where
$R_{A,\unicode[STIX]{x1D6EC}}$ by (15a)where $$\begin{eqnarray}R_{A,\unicode[STIX]{x1D6EC}}:=\mathbb{C}[X_{1},\ldots ,X_{r}]/I_{\unicode[STIX]{x1D6EC}},\end{eqnarray}$$
$$\begin{eqnarray}R_{A,\unicode[STIX]{x1D6EC}}:=\mathbb{C}[X_{1},\ldots ,X_{r}]/I_{\unicode[STIX]{x1D6EC}},\end{eqnarray}$$ $I_{\unicode[STIX]{x1D6EC}}$ is an ideal generated by
$I_{\unicode[STIX]{x1D6EC}}$ is an ideal generated by  $r-2$ homogeneous polynomials (15b)
$r-2$ homogeneous polynomials (15b) $$\begin{eqnarray}X_{i}^{a_{i}}-X_{2}^{a_{2}}+\unicode[STIX]{x1D706}_{i}X_{1}^{a_{1}},\quad i=3,\ldots ,r.\end{eqnarray}$$
$$\begin{eqnarray}X_{i}^{a_{i}}-X_{2}^{a_{2}}+\unicode[STIX]{x1D706}_{i}X_{1}^{a_{1}},\quad i=3,\ldots ,r.\end{eqnarray}$$(ii) Denote by
 $L_{A}$ an abelian group generated by
$L_{A}$ an abelian group generated by  $r$-letters
$r$-letters  $\vec{X_{i}}$,
$\vec{X_{i}}$,  $i=1,\ldots ,r$ defined as the quotient (16a)where
$i=1,\ldots ,r$ defined as the quotient (16a)where $$\begin{eqnarray}L_{A}:=\bigoplus _{i=1}^{r}\mathbb{Z}\vec{X}_{i}/M_{A},\end{eqnarray}$$
$$\begin{eqnarray}L_{A}:=\bigoplus _{i=1}^{r}\mathbb{Z}\vec{X}_{i}/M_{A},\end{eqnarray}$$ $M_{A}$ is the subgroup generated by the elements (16b)
$M_{A}$ is the subgroup generated by the elements (16b) $$\begin{eqnarray}a_{i}\vec{X}_{i}-a_{j}\vec{X}_{j},\quad 1\leqslant i<j\leqslant r.\end{eqnarray}$$
$$\begin{eqnarray}a_{i}\vec{X}_{i}-a_{j}\vec{X}_{j},\quad 1\leqslant i<j\leqslant r.\end{eqnarray}$$(iii) Set
(17) $$\begin{eqnarray}\displaystyle & \displaystyle a:=\text{l.c.m}(a_{1},\ldots ,a_{r}),\qquad \unicode[STIX]{x1D707}_{A}:=2+\mathop{\sum }_{i=1}^{r}(a_{i}-1), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D712}_{A}:=2+\mathop{\sum }_{i=1}^{r}\biggl(\frac{1}{a_{i}}-1\biggr). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle a:=\text{l.c.m}(a_{1},\ldots ,a_{r}),\qquad \unicode[STIX]{x1D707}_{A}:=2+\mathop{\sum }_{i=1}^{r}(a_{i}-1), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D712}_{A}:=2+\mathop{\sum }_{i=1}^{r}\biggl(\frac{1}{a_{i}}-1\biggr). & \displaystyle\end{eqnarray}$$
We then consider the following quotient stack:
Definition 3.2. Let  $r$,
$r$,  $A$ and
$A$ and  $\unicode[STIX]{x1D6EC}$ be as above. Define a stack
$\unicode[STIX]{x1D6EC}$ be as above. Define a stack  $\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}$ by
$\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}$ by
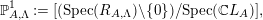 $$\begin{eqnarray}\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}:=[(\text{Spec}(R_{A,\unicode[STIX]{x1D6EC}})\backslash \{0\})/\text{Spec}(\mathbb{C}L_{A})],\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}:=[(\text{Spec}(R_{A,\unicode[STIX]{x1D6EC}})\backslash \{0\})/\text{Spec}(\mathbb{C}L_{A})],\end{eqnarray}$$ which is called the orbifold projective line of type  $(A,\unicode[STIX]{x1D6EC})$.
$(A,\unicode[STIX]{x1D6EC})$.
The orbifold projective line is a Deligne–Mumford stack whose coarse moduli space is a smooth projective line  $\mathbb{P}^{1}$.
$\mathbb{P}^{1}$.
Denote by  $\text{gr}^{L_{A}}(R_{A,\unicode[STIX]{x1D6EC}})$ the abelian category of finitely generated
$\text{gr}^{L_{A}}(R_{A,\unicode[STIX]{x1D6EC}})$ the abelian category of finitely generated  $L_{A}$-graded
$L_{A}$-graded  $R_{A,\unicode[STIX]{x1D6EC}}$-modules and denote by
$R_{A,\unicode[STIX]{x1D6EC}}$-modules and denote by  $\text{tor}^{L_{A}}(R_{A,\unicode[STIX]{x1D6EC}})$ the full subcategory of
$\text{tor}^{L_{A}}(R_{A,\unicode[STIX]{x1D6EC}})$ the full subcategory of  $\text{gr}^{L_{A}}(R_{A,\unicode[STIX]{x1D6EC}})$ whose objects are finite-dimensional
$\text{gr}^{L_{A}}(R_{A,\unicode[STIX]{x1D6EC}})$ whose objects are finite-dimensional  $L_{A}$-graded
$L_{A}$-graded  $R_{A,\unicode[STIX]{x1D6EC}}$-modules. It is known (cf. [Reference Geigle and LenzingGL, Section 1.8]) that the abelian category
$R_{A,\unicode[STIX]{x1D6EC}}$-modules. It is known (cf. [Reference Geigle and LenzingGL, Section 1.8]) that the abelian category  $\text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ of coherent sheaves is given by
$\text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ of coherent sheaves is given by
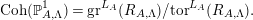 $$\begin{eqnarray}\text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})=\text{gr}^{L_{A}}(R_{A,\unicode[STIX]{x1D6EC}})/\text{tor}^{L_{A}}(R_{A,\unicode[STIX]{x1D6EC}}).\end{eqnarray}$$
$$\begin{eqnarray}\text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})=\text{gr}^{L_{A}}(R_{A,\unicode[STIX]{x1D6EC}})/\text{tor}^{L_{A}}(R_{A,\unicode[STIX]{x1D6EC}}).\end{eqnarray}$$ Denote by  ${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ the bounded derived category
${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ the bounded derived category  ${\mathcal{D}}^{b}(\text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))$.
${\mathcal{D}}^{b}(\text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))$.
For each  $\vec{x}\in L_{A}$, set
$\vec{x}\in L_{A}$, set
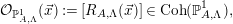 $$\begin{eqnarray}{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}):=[R_{A,\unicode[STIX]{x1D6EC}}(\vec{x})]\in \text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}):=[R_{A,\unicode[STIX]{x1D6EC}}(\vec{x})]\in \text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}),\end{eqnarray}$$ where  $(R_{A,\unicode[STIX]{x1D6EC}}(\vec{x}))_{\vec{y}}:=(R_{A,\unicode[STIX]{x1D6EC}})_{\vec{x}+\vec{y}}$.
$(R_{A,\unicode[STIX]{x1D6EC}}(\vec{x}))_{\vec{y}}:=(R_{A,\unicode[STIX]{x1D6EC}})_{\vec{x}+\vec{y}}$.
Set  $\vec{x}_{i}:=[\vec{X}_{i}]~(i=1,\ldots r)$ and
$\vec{x}_{i}:=[\vec{X}_{i}]~(i=1,\ldots r)$ and  $\vec{c}:=a_{1}\vec{x}_{1}=\cdots =a_{r}\vec{x}_{r}$. An element
$\vec{c}:=a_{1}\vec{x}_{1}=\cdots =a_{r}\vec{x}_{r}$. An element  $\vec{x}\in L_{A}$ has the unique expression of the form
$\vec{x}\in L_{A}$ has the unique expression of the form
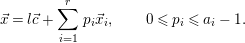 $$\begin{eqnarray}\vec{x}=l\vec{c}+\mathop{\sum }_{i=1}^{r}p_{i}\vec{x}_{i},\qquad 0\leqslant p_{i}\leqslant a_{i}-1.\end{eqnarray}$$
$$\begin{eqnarray}\vec{x}=l\vec{c}+\mathop{\sum }_{i=1}^{r}p_{i}\vec{x}_{i},\qquad 0\leqslant p_{i}\leqslant a_{i}-1.\end{eqnarray}$$ We say that  $\vec{x}$ is positive if
$\vec{x}$ is positive if  $\vec{x}\neq 0$,
$\vec{x}\neq 0$,  $l\geqslant 0$ and
$l\geqslant 0$ and  $p_{i}\geqslant 0$ for
$p_{i}\geqslant 0$ for  $i=1,\ldots ,r$.
$i=1,\ldots ,r$.
For a  $\mathbb{C}$-module
$\mathbb{C}$-module  $M$, set
$M$, set  $M^{\ast }:=\text{Hom}_{\mathbb{C}}(M,\mathbb{C})$.
$M^{\ast }:=\text{Hom}_{\mathbb{C}}(M,\mathbb{C})$.
Proposition 3.3. [Reference Geigle and LenzingGL, Sections 1.8.1 and 2.2]
We have the following:
(i) For
 $\vec{x},\vec{y}\in L_{A}$ with
$\vec{x},\vec{y}\in L_{A}$ with  $\vec{x}-\vec{y}$ positive, (22)
$\vec{x}-\vec{y}$ positive, (22) $$\begin{eqnarray}\text{Hom}({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}),{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{y}))=0.\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}),{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{y}))=0.\end{eqnarray}$$(ii) Set
 $\vec{\unicode[STIX]{x1D714}}:=(r-2)\vec{c}-\sum _{i=1}^{r}\vec{x_{i}}\in L_{A}$. For
$\vec{\unicode[STIX]{x1D714}}:=(r-2)\vec{c}-\sum _{i=1}^{r}\vec{x_{i}}\in L_{A}$. For  $M_{1},M_{2}\in \text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, we have the Serre duality isomorphism: (23)
$M_{1},M_{2}\in \text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, we have the Serre duality isomorphism: (23) $$\begin{eqnarray}\text{Ext}^{1}(M_{2},M_{1})\cong \text{Hom}(M_{1},M_{2}\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{\unicode[STIX]{x1D714}}))^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\text{Ext}^{1}(M_{2},M_{1})\cong \text{Hom}(M_{1},M_{2}\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{\unicode[STIX]{x1D714}}))^{\ast }.\end{eqnarray}$$(iii) The category
 $\text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ is hereditary, namely,
$\text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ is hereditary, namely,  $\text{Ext}^{i}(M_{1},M_{2})=0$ for
$\text{Ext}^{i}(M_{1},M_{2})=0$ for  $M_{1},M_{2}\in \text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ if
$M_{1},M_{2}\in \text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ if  $i\neq 0,1$.
$i\neq 0,1$.
Remark 3.4. It follows from Proposition 3.3(iii) that each indecomposable object of  ${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ is of the form
${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ is of the form  $M[n]$ for some
$M[n]$ for some  $M\in \text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ and
$M\in \text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ and  $n\in \mathbb{Z}$.
$n\in \mathbb{Z}$.
Proposition 3.5. [Reference Geigle and LenzingGL, Sections 1.8.1 and 4.1]
The following sequences are full strongly exceptional collections:
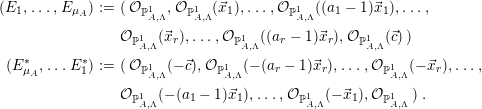 $$\begin{eqnarray}\displaystyle (E_{1},\ldots ,E_{\unicode[STIX]{x1D707}_{A}}) & := & \displaystyle ({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}},{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}_{1}),\ldots ,{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}((a_{1}-1)\vec{x}_{1}),\ldots ,\nonumber\\ \displaystyle & & \displaystyle {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}_{r}),\ldots ,{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}((a_{r}-1)\vec{x}_{r}),{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{c}))\nonumber\\ \displaystyle (E_{\unicode[STIX]{x1D707}_{A}}^{\ast },\ldots E_{1}^{\ast }) & := & \displaystyle ({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{c}),{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-(a_{r}-1)\vec{x}_{r}),\ldots ,{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{x}_{r}),\ldots ,\nonumber\\ \displaystyle & & \displaystyle {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-(a_{1}-1)\vec{x}_{1}),\ldots ,{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{x}_{1}),{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}} ).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (E_{1},\ldots ,E_{\unicode[STIX]{x1D707}_{A}}) & := & \displaystyle ({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}},{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}_{1}),\ldots ,{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}((a_{1}-1)\vec{x}_{1}),\ldots ,\nonumber\\ \displaystyle & & \displaystyle {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}_{r}),\ldots ,{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}((a_{r}-1)\vec{x}_{r}),{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{c}))\nonumber\\ \displaystyle (E_{\unicode[STIX]{x1D707}_{A}}^{\ast },\ldots E_{1}^{\ast }) & := & \displaystyle ({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{c}),{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-(a_{r}-1)\vec{x}_{r}),\ldots ,{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{x}_{r}),\ldots ,\nonumber\\ \displaystyle & & \displaystyle {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-(a_{1}-1)\vec{x}_{1}),\ldots ,{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{x}_{1}),{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}} ).\nonumber\end{eqnarray}$$ In particular,  $G:=\bigoplus _{i=1}^{\unicode[STIX]{x1D707}_{A}}E_{i}$ and
$G:=\bigoplus _{i=1}^{\unicode[STIX]{x1D707}_{A}}E_{i}$ and  $G^{\ast }:=\bigoplus _{i=1}^{\unicode[STIX]{x1D707}_{A}}E_{i}^{\ast }$ are split-generators of
$G^{\ast }:=\bigoplus _{i=1}^{\unicode[STIX]{x1D707}_{A}}E_{i}^{\ast }$ are split-generators of  ${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$.
${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$.
It follows from Proposition 3.5 that  ${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\cong \text{per}(\text{End}(G))$ since the triangulated category
${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\cong \text{per}(\text{End}(G))$ since the triangulated category  ${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ is algebraic. Denote by
${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ is algebraic. Denote by  ${\mathcal{N}}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ its numerical Grothendieck group.
${\mathcal{N}}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ its numerical Grothendieck group.
Definition 3.6. [Reference Geigle and LenzingGL, Section 2.5]
Take  $[1:\unicode[STIX]{x1D706}]\in \mathbb{P}^{1}\setminus \{\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{r}\}$. Define
$[1:\unicode[STIX]{x1D706}]\in \mathbb{P}^{1}\setminus \{\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{r}\}$. Define  $S$ and
$S$ and  $S_{i,j}$ for
$S_{i,j}$ for  $i=1,\ldots ,r$ and
$i=1,\ldots ,r$ and  $j=0,\ldots ,a_{i}-1$ by the following exact sequences:
$j=0,\ldots ,a_{i}-1$ by the following exact sequences:
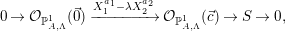 $$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{0})\xrightarrow[{}]{X_{1}^{a_{1}}-\unicode[STIX]{x1D706}X_{2}^{a_{2}}}{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{c})\rightarrow S\rightarrow 0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{0})\xrightarrow[{}]{X_{1}^{a_{1}}-\unicode[STIX]{x1D706}X_{2}^{a_{2}}}{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{c})\rightarrow S\rightarrow 0, & \displaystyle\end{eqnarray}$$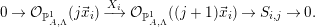 $$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(j\vec{x}_{i})\xrightarrow[{}]{X_{i}}{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}((j+1)\vec{x}_{i})\rightarrow S_{i,j}\rightarrow 0. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(j\vec{x}_{i})\xrightarrow[{}]{X_{i}}{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}((j+1)\vec{x}_{i})\rightarrow S_{i,j}\rightarrow 0. & \displaystyle\end{eqnarray}$$Definition 3.7. [Reference Geigle and LenzingGL, Sections 1.8.2 and 2.8]
The rank and degree are homomorphisms defined as follows:
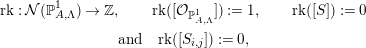 $$\begin{eqnarray}\displaystyle & \displaystyle \text{rk}:{\mathcal{N}}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\rightarrow \mathbb{Z},\qquad \text{rk}([{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}]):=1,\qquad \text{rk}([S]):=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{and}\quad \text{rk}([S_{i,j}]):=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{rk}:{\mathcal{N}}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\rightarrow \mathbb{Z},\qquad \text{rk}([{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}]):=1,\qquad \text{rk}([S]):=0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{and}\quad \text{rk}([S_{i,j}]):=0, & \displaystyle\end{eqnarray}$$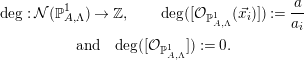 $$\begin{eqnarray}\displaystyle & \displaystyle \text{deg}:{\mathcal{N}}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\rightarrow \mathbb{Z},\qquad \text{deg}([{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x_{i}})]):=\frac{a}{a_{i}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{and}\quad \text{deg}([{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}]):=0. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{deg}:{\mathcal{N}}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\rightarrow \mathbb{Z},\qquad \text{deg}([{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x_{i}})]):=\frac{a}{a_{i}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{and}\quad \text{deg}([{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}]):=0. & \displaystyle\end{eqnarray}$$Definition 3.8. Denote by  $\text{Pic}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ the group consisting of (isomorphism classes of) indecomposable objects in
$\text{Pic}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ the group consisting of (isomorphism classes of) indecomposable objects in  $\text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ of rank one with multiplication induced by the tensor product.
$\text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ of rank one with multiplication induced by the tensor product.
Lemma 3.9. [Reference Geigle and LenzingGL, Section 2.1]
There is an isomorphism of abelian groups
 $$\begin{eqnarray}L_{A}\cong \text{Pic}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}),\qquad \vec{x}_{i}\mapsto {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}_{i}).\end{eqnarray}$$
$$\begin{eqnarray}L_{A}\cong \text{Pic}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}),\qquad \vec{x}_{i}\mapsto {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}_{i}).\end{eqnarray}$$One of our results is the following Gromov–Yomdin type theorem for an orbifold projective line:
Theorem 3.10. For each auto-equivalence  $F$ of
$F$ of  ${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, we have
${\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, we have
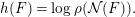 $$\begin{eqnarray}h(F)=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\end{eqnarray}$$
$$\begin{eqnarray}h(F)=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\end{eqnarray}$$ Moreover,  $\unicode[STIX]{x1D70C}({\mathcal{N}}(F))$ is an algebraic integer and
$\unicode[STIX]{x1D70C}({\mathcal{N}}(F))$ is an algebraic integer and  $h(F)=0$ if
$h(F)=0$ if  $\unicode[STIX]{x1D712}_{A}\neq 0$.
$\unicode[STIX]{x1D712}_{A}\neq 0$.
3.1 Proof of Theorem 3.10 for the case  $\unicode[STIX]{x1D712}_{A}\neq 0$
$\unicode[STIX]{x1D712}_{A}\neq 0$
It is important to note that Lenzing–Meltzer [Reference Lenzing and MeltzerLM, Proposition 4.2] shows that, if  $\unicode[STIX]{x1D712}_{A}\neq 0$,
$\unicode[STIX]{x1D712}_{A}\neq 0$,
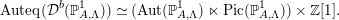 $$\begin{eqnarray}\text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\simeq (\text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\times \mathbb{Z}[1].\end{eqnarray}$$
$$\begin{eqnarray}\text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\simeq (\text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\times \mathbb{Z}[1].\end{eqnarray}$$3.1.1 Case  $\unicode[STIX]{x1D712}_{A}>0$
$\unicode[STIX]{x1D712}_{A}>0$
Geigle–Lenzing (cf. [Reference Geigle and LenzingGL, Section 5.4.1]) gives an equivalence of triangulated categories
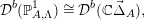 $$\begin{eqnarray}{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\cong {\mathcal{D}}^{b}(\mathbb{C}\vec{\unicode[STIX]{x1D6E5}}_{A}),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\cong {\mathcal{D}}^{b}(\mathbb{C}\vec{\unicode[STIX]{x1D6E5}}_{A}),\end{eqnarray}$$ where  $\vec{\unicode[STIX]{x1D6E5}}_{A}$ is the extended Dynkin quiver below.
$\vec{\unicode[STIX]{x1D6E5}}_{A}$ is the extended Dynkin quiver below.

This equivalence with Proposition 2.14 yields  $h(F)=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F))$. Then, [Reference Miyachi and YekutieliMY, Theorem 4.2, Theorem 4.5] show that
$h(F)=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F))$. Then, [Reference Miyachi and YekutieliMY, Theorem 4.2, Theorem 4.5] show that  $\unicode[STIX]{x1D70C}({\mathcal{N}}(F))=1$. We have finished the proof.◻
$\unicode[STIX]{x1D70C}({\mathcal{N}}(F))=1$. We have finished the proof.◻
3.1.2 Case  $\unicode[STIX]{x1D712}_{A}<0$
$\unicode[STIX]{x1D712}_{A}<0$
We shall prove that  $h(F)=0$ for each
$h(F)=0$ for each  $F\in (\text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\times \mathbb{Z}[1]$ if
$F\in (\text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\times \mathbb{Z}[1]$ if  $\unicode[STIX]{x1D712}_{A}\leqslant 0$.
$\unicode[STIX]{x1D712}_{A}\leqslant 0$.
Choose  $\{[{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}],[S_{1,1}],\ldots ,[S_{i,j}],\ldots ,[S_{r,a_{r}-1}],[S]\}$ as a basis of
$\{[{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}],[S_{1,1}],\ldots ,[S_{i,j}],\ldots ,[S_{r,a_{r}-1}],[S]\}$ as a basis of  ${\mathcal{N}}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$.
${\mathcal{N}}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$.
Lemma 3.11. For  $f\in \text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, the automorphism
$f\in \text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, the automorphism  ${\mathcal{N}}(f^{\ast })$ is a composition of permutations exchanging
${\mathcal{N}}(f^{\ast })$ is a composition of permutations exchanging  $[S_{i,j}]$ and
$[S_{i,j}]$ and  $[S_{i^{\prime },j}]$ for
$[S_{i^{\prime },j}]$ for  $j=1,\ldots a_{i-1}$ if
$j=1,\ldots a_{i-1}$ if  $a_{i}=a_{i^{\prime }}$ and fixing
$a_{i}=a_{i^{\prime }}$ and fixing  $[{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}]$ and
$[{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}]$ and  $[S]$. In particular, we have
$[S]$. In particular, we have  $\unicode[STIX]{x1D70C}({\mathcal{N}}(f^{\ast }))=1$.
$\unicode[STIX]{x1D70C}({\mathcal{N}}(f^{\ast }))=1$.
Proof. This is a direct consequence of [Reference Lenzing and MeltzerLM, Proposition 3.1]. Note also that  $r\geqslant 3$ since
$r\geqslant 3$ since  $\unicode[STIX]{x1D712}_{A}\leqslant 0$ and hence
$\unicode[STIX]{x1D712}_{A}\leqslant 0$ and hence  $\text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ is a finite group.◻
$\text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ is a finite group.◻
Lemma 3.12. For  ${\mathcal{L}}\in \text{Pic}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, we have
${\mathcal{L}}\in \text{Pic}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, we have  $\unicode[STIX]{x1D70C}({\mathcal{N}}(-\otimes {\mathcal{L}}))=1$.
$\unicode[STIX]{x1D70C}({\mathcal{N}}(-\otimes {\mathcal{L}}))=1$.
Proof. Set  ${\mathcal{L}}={\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x})$ for some
${\mathcal{L}}={\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x})$ for some  $\vec{x}\in L_{A}$. By [Reference Geigle and LenzingGL, (2.5.3) and (2.5.4)], for
$\vec{x}\in L_{A}$. By [Reference Geigle and LenzingGL, (2.5.3) and (2.5.4)], for  $i=1,\ldots ,r$ and
$i=1,\ldots ,r$ and  $j=1,\ldots ,a_{i}-1$,
$j=1,\ldots ,a_{i}-1$,
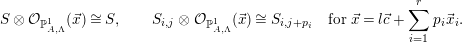 $$\begin{eqnarray}S\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x})\cong S,\qquad S_{i,j}\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x})\cong S_{i,j+p_{i}}\quad \text{for}~\vec{x}=l\vec{c}+\mathop{\sum }_{i=1}^{r}p_{i}\vec{x}_{i}.\end{eqnarray}$$
$$\begin{eqnarray}S\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x})\cong S,\qquad S_{i,j}\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x})\cong S_{i,j+p_{i}}\quad \text{for}~\vec{x}=l\vec{c}+\mathop{\sum }_{i=1}^{r}p_{i}\vec{x}_{i}.\end{eqnarray}$$ It follows from the above isomorphisms that the representation matrix of  ${\mathcal{N}}(-\otimes {\mathcal{L}})$ in the basis becomes an upper triangular matrix whose diagonal entries are all
${\mathcal{N}}(-\otimes {\mathcal{L}})$ in the basis becomes an upper triangular matrix whose diagonal entries are all  $1$. Hence, its spectral radius is equal to
$1$. Hence, its spectral radius is equal to  $1$.◻
$1$.◻
Each auto-equivalence  $F$ is represented as
$F$ is represented as  $F=f^{\ast }(-\otimes {\mathcal{L}})[m]$ (cf. (30)). Since Lemma 2.7(v) gives
$F=f^{\ast }(-\otimes {\mathcal{L}})[m]$ (cf. (30)). Since Lemma 2.7(v) gives  $h(F)=h(f^{\ast }(-\otimes {\mathcal{L}}))$, we may assume
$h(F)=h(f^{\ast }(-\otimes {\mathcal{L}}))$, we may assume  $F=f^{\ast }(-\otimes {\mathcal{L}})$.
$F=f^{\ast }(-\otimes {\mathcal{L}})$.
Proposition 3.13. We have
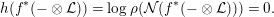 $$\begin{eqnarray}h(f^{\ast }(-\otimes {\mathcal{L}}))=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(f^{\ast }(-\otimes {\mathcal{L}})))=0.\end{eqnarray}$$
$$\begin{eqnarray}h(f^{\ast }(-\otimes {\mathcal{L}}))=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(f^{\ast }(-\otimes {\mathcal{L}})))=0.\end{eqnarray}$$Proof. Take  $G$ and
$G$ and  $G^{\ast }$ as in Proposition 3.5. By Proposition 2.11,
$G^{\ast }$ as in Proposition 3.5. By Proposition 2.11,
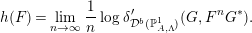 $$\begin{eqnarray}h(F)=\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}^{\prime }(G,F^{n}G^{\ast }).\end{eqnarray}$$
$$\begin{eqnarray}h(F)=\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}^{\prime }(G,F^{n}G^{\ast }).\end{eqnarray}$$By straightforward calculation,
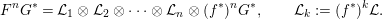 $$\begin{eqnarray}F^{n}G^{\ast }={\mathcal{L}}_{1}\otimes {\mathcal{L}}_{2}\otimes \cdots \otimes {\mathcal{L}}_{n}\otimes (f^{\ast })^{n}G^{\ast },\qquad {\mathcal{L}}_{k}:=(f^{\ast })^{k}{\mathcal{L}}.\end{eqnarray}$$
$$\begin{eqnarray}F^{n}G^{\ast }={\mathcal{L}}_{1}\otimes {\mathcal{L}}_{2}\otimes \cdots \otimes {\mathcal{L}}_{n}\otimes (f^{\ast })^{n}G^{\ast },\qquad {\mathcal{L}}_{k}:=(f^{\ast })^{k}{\mathcal{L}}.\end{eqnarray}$$ Note that  $f^{\ast }(G^{\ast })=G^{\ast }$ and
$f^{\ast }(G^{\ast })=G^{\ast }$ and  $\deg (f^{\ast }{\mathcal{L}})=\deg ({\mathcal{L}})$ by Lemma 3.11.
$\deg (f^{\ast }{\mathcal{L}})=\deg ({\mathcal{L}})$ by Lemma 3.11.
Suppose that  $\text{deg}({\mathcal{L}})>0$. For
$\text{deg}({\mathcal{L}})>0$. For  $n\gg 0$ and
$n\gg 0$ and  $\vec{z}\in L_{A}$, we have
$\vec{z}\in L_{A}$, we have
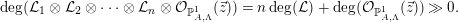 $$\begin{eqnarray}\deg ({\mathcal{L}}_{1}\otimes {\mathcal{L}}_{2}\otimes \cdots \otimes {\mathcal{L}}_{n}\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z}))=n\deg ({\mathcal{L}})+\deg ({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z}))\gg 0.\end{eqnarray}$$
$$\begin{eqnarray}\deg ({\mathcal{L}}_{1}\otimes {\mathcal{L}}_{2}\otimes \cdots \otimes {\mathcal{L}}_{n}\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z}))=n\deg ({\mathcal{L}})+\deg ({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z}))\gg 0.\end{eqnarray}$$Therefore, Proposition 3.3(i) and (ii) yield
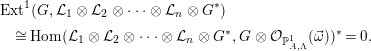 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{Ext}^{1}(G,{\mathcal{L}}_{1}\otimes {\mathcal{L}}_{2}\otimes \cdots \otimes {\mathcal{L}}_{n}\otimes G^{\ast })\nonumber\\ \displaystyle & & \displaystyle \quad \cong \text{Hom}({\mathcal{L}}_{1}\otimes {\mathcal{L}}_{2}\otimes \cdots \otimes {\mathcal{L}}_{n}\otimes G^{\ast },G\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{\unicode[STIX]{x1D714}}))^{\ast }=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{Ext}^{1}(G,{\mathcal{L}}_{1}\otimes {\mathcal{L}}_{2}\otimes \cdots \otimes {\mathcal{L}}_{n}\otimes G^{\ast })\nonumber\\ \displaystyle & & \displaystyle \quad \cong \text{Hom}({\mathcal{L}}_{1}\otimes {\mathcal{L}}_{2}\otimes \cdots \otimes {\mathcal{L}}_{n}\otimes G^{\ast },G\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{\unicode[STIX]{x1D714}}))^{\ast }=0.\nonumber\end{eqnarray}$$ Suppose that  $\deg ({\mathcal{L}})\leqslant 0$. We choose
$\deg ({\mathcal{L}})\leqslant 0$. We choose  $\vec{z}\in L_{A}$ so that
$\vec{z}\in L_{A}$ so that  $\deg ({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z}))\gg 0$. The objects
$\deg ({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z}))\gg 0$. The objects  $G^{\prime }:=G\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z})$ and
$G^{\prime }:=G\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z})$ and  $G^{\prime \prime }:=G^{\ast }\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{z})$ are also split-generators. Therefore, Proposition 3.3(i) yields
$G^{\prime \prime }:=G^{\ast }\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{z})$ are also split-generators. Therefore, Proposition 3.3(i) yields
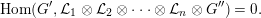 $$\begin{eqnarray}\text{Hom}(G^{\prime },{\mathcal{L}}_{1}\otimes {\mathcal{L}}_{2}\otimes \cdots \otimes {\mathcal{L}}_{n}\otimes G^{\prime \prime })=0.\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}(G^{\prime },{\mathcal{L}}_{1}\otimes {\mathcal{L}}_{2}\otimes \cdots \otimes {\mathcal{L}}_{n}\otimes G^{\prime \prime })=0.\end{eqnarray}$$Hence it follows from Proposition 3.3(iii), Lemmas 3.11 and 3.12 that
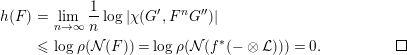 $$\begin{eqnarray}\displaystyle h(F) & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log |\unicode[STIX]{x1D712}(G^{\prime },F^{n}G^{\prime \prime })|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \log \unicode[STIX]{x1D70C}({\mathcal{N}}(F))=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(f^{\ast }(-\otimes {\mathcal{L}})))=0.\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(F) & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log |\unicode[STIX]{x1D712}(G^{\prime },F^{n}G^{\prime \prime })|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \log \unicode[STIX]{x1D70C}({\mathcal{N}}(F))=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(f^{\ast }(-\otimes {\mathcal{L}})))=0.\square\nonumber\end{eqnarray}$$ To summarize, we have finished the proof of Theorem 3.10 for the case  $\unicode[STIX]{x1D712}_{A}<0$.
$\unicode[STIX]{x1D712}_{A}<0$.
3.2 Proof of Theorem 3.10 for the case  $\unicode[STIX]{x1D712}_{A}=0$
$\unicode[STIX]{x1D712}_{A}=0$
Define a homomorphism  $\unicode[STIX]{x1D708}:{\mathcal{N}}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\rightarrow \mathbb{Z}^{2}$ by
$\unicode[STIX]{x1D708}:{\mathcal{N}}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\rightarrow \mathbb{Z}^{2}$ by
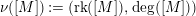 $$\begin{eqnarray}\unicode[STIX]{x1D708}([M]):=(\text{rk}([M]),\text{deg}([M]))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}([M]):=(\text{rk}([M]),\text{deg}([M]))\end{eqnarray}$$ and a skew symmetric bilinear form on  $\mathbb{Z}^{2}$ by
$\mathbb{Z}^{2}$ by
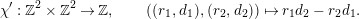 $$\begin{eqnarray}\unicode[STIX]{x1D712}^{\prime }:\mathbb{Z}^{2}\times \mathbb{Z}^{2}\rightarrow \mathbb{Z},\qquad ((r_{1},d_{1}),(r_{2},d_{2}))\mapsto r_{1}d_{2}-r_{2}d_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}^{\prime }:\mathbb{Z}^{2}\times \mathbb{Z}^{2}\rightarrow \mathbb{Z},\qquad ((r_{1},d_{1}),(r_{2},d_{2}))\mapsto r_{1}d_{2}-r_{2}d_{1}.\end{eqnarray}$$Lemma 3.14. For  $M_{1},M_{2}\in {\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, we have
$M_{1},M_{2}\in {\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, we have
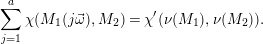 $$\begin{eqnarray}\mathop{\sum }_{j=1}^{a}\unicode[STIX]{x1D712}(M_{1}(j\vec{\unicode[STIX]{x1D714}}),M_{2})=\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D708}(M_{1}),\unicode[STIX]{x1D708}(M_{2})).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{j=1}^{a}\unicode[STIX]{x1D712}(M_{1}(j\vec{\unicode[STIX]{x1D714}}),M_{2})=\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D708}(M_{1}),\unicode[STIX]{x1D708}(M_{2})).\end{eqnarray}$$Proof. It follows from [Reference Geigle and LenzingGL, Section 2.9] with  $\unicode[STIX]{x1D712}_{A}=0$.◻
$\unicode[STIX]{x1D712}_{A}=0$.◻
Lemma 3.14 gives the following natural group homomorphism:
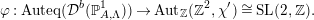 $$\begin{eqnarray}\unicode[STIX]{x1D711}:\text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\rightarrow \text{Aut}_{\mathbb{ Z}}(\mathbb{Z}^{2},\unicode[STIX]{x1D712}^{\prime })\cong \text{SL}(2,\mathbb{Z}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}:\text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\rightarrow \text{Aut}_{\mathbb{ Z}}(\mathbb{Z}^{2},\unicode[STIX]{x1D712}^{\prime })\cong \text{SL}(2,\mathbb{Z}).\end{eqnarray}$$ Denote by  $\text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\subset \text{Pic}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ the subgroup consisting of elements with degree zero.
$\text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\subset \text{Pic}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ the subgroup consisting of elements with degree zero.
Proposition 3.15. There exists the following exact sequence:
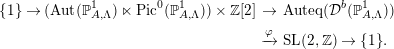 $$\begin{eqnarray}\displaystyle \{1\}\rightarrow (\text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\times \mathbb{Z}[2] & \rightarrow & \displaystyle \text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\nonumber\\ \displaystyle & \xrightarrow[{}]{\unicode[STIX]{x1D711}} & \displaystyle \text{SL}(2,\mathbb{Z})\rightarrow \{1\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \{1\}\rightarrow (\text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\times \mathbb{Z}[2] & \rightarrow & \displaystyle \text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\nonumber\\ \displaystyle & \xrightarrow[{}]{\unicode[STIX]{x1D711}} & \displaystyle \text{SL}(2,\mathbb{Z})\rightarrow \{1\}.\end{eqnarray}$$Proof. This is a direct consequence of [Reference Lenzing and MeltzerLM, Theorem 6.3].◻
Lemma 3.16. The map  $h:\text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\longrightarrow \mathbb{R}_{{\geqslant}0}$,
$h:\text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))\longrightarrow \mathbb{R}_{{\geqslant}0}$,  $F\mapsto h(F)$ factors through
$F\mapsto h(F)$ factors through  $\text{SL}(2,\mathbb{Z})$.
$\text{SL}(2,\mathbb{Z})$.
Proof. Choose  ${\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z})$ so that
${\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z})$ so that  $\deg ({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z}))\gg 0$ and set
$\deg ({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z}))\gg 0$ and set  $G^{\prime }:=G\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z})$,
$G^{\prime }:=G\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{z})$,  $G^{\prime \prime }:=G^{\ast }\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{z})$. By Lemma 2.7(v), we can assume that an element
$G^{\prime \prime }:=G^{\ast }\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{z})$. By Lemma 2.7(v), we can assume that an element  $F\in \text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))$ is of the form
$F\in \text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))$ is of the form  $F=F^{\prime }F_{1}$ with
$F=F^{\prime }F_{1}$ with  $F^{\prime }\in \text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))$ and
$F^{\prime }\in \text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))$ and  $F_{1}\in \text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$. Then there exist
$F_{1}\in \text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$. Then there exist  $F_{2},\ldots ,F_{n}\in \text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ such that
$F_{2},\ldots ,F_{n}\in \text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ such that  $F^{n}=(F^{\prime }F_{1})^{n}={F^{\prime }}^{n}F_{n}\cdots F_{1}$. We have
$F^{n}=(F^{\prime }F_{1})^{n}={F^{\prime }}^{n}F_{n}\cdots F_{1}$. We have
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}(G^{\prime },F^{n}G^{\prime \prime })\leqslant \unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}(G^{\prime },{F^{\prime }}^{n}G^{\prime })\unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime }),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}(G^{\prime },F^{n}G^{\prime \prime })\leqslant \unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}(G^{\prime },{F^{\prime }}^{n}G^{\prime })\unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime }),\end{eqnarray}$$and hence,
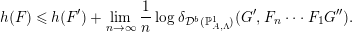 $$\begin{eqnarray}h(F)\leqslant h(F^{\prime })+\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime }).\end{eqnarray}$$
$$\begin{eqnarray}h(F)\leqslant h(F^{\prime })+\lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime }).\end{eqnarray}$$ The functor  $F_{i}$ is of the form
$F_{i}$ is of the form  $f_{i}^{\ast }(-\otimes {\mathcal{L}}_{i})$ for some
$f_{i}^{\ast }(-\otimes {\mathcal{L}}_{i})$ for some  $f_{i}\in \text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ and
$f_{i}\in \text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ and  ${\mathcal{L}}_{i}\in \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$. For arbitrary
${\mathcal{L}}_{i}\in \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$. For arbitrary  $\vec{y}\in L_{A}$, we have
$\vec{y}\in L_{A}$, we have  $\deg (F_{n}\cdots F_{1}({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{y})))=\deg ({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{y}))$. Therefore, it follows from Proposition 3.3(i), (iii) that
$\deg (F_{n}\cdots F_{1}({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{y})))=\deg ({\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{y}))$. Therefore, it follows from Proposition 3.3(i), (iii) that
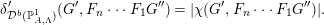 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}^{\prime }(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime })=|\unicode[STIX]{x1D712}(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime })|.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}^{\prime }(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime })=|\unicode[STIX]{x1D712}(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime })|.\end{eqnarray}$$Lemmas 2.12, 3.11 and 3.12 yield
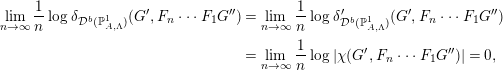 $$\begin{eqnarray}\displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime }) & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}^{\prime }(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime })\nonumber\\ \displaystyle & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log |\unicode[STIX]{x1D712}(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime })|=0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime }) & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}^{\prime }(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime })\nonumber\\ \displaystyle & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log |\unicode[STIX]{x1D712}(G^{\prime },F_{n}\cdots F_{1}G^{\prime \prime })|=0,\nonumber\end{eqnarray}$$ and hence  $h(F)\leqslant h(F^{\prime })$. We also have
$h(F)\leqslant h(F^{\prime })$. We also have  $h(F^{\prime })\leqslant h(F)$ since
$h(F^{\prime })\leqslant h(F)$ since  $F^{\prime }=FF_{1}^{-1}$ and
$F^{\prime }=FF_{1}^{-1}$ and  $F_{1}^{-1}$ belongs to
$F_{1}^{-1}$ belongs to  $\text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$.◻
$\text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$.◻
Proposition 3.17. We have  $h(F)=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F))$.
$h(F)=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F))$.
Proof. Since  $h(F[1])=h(F)$, we may assume that
$h(F[1])=h(F)$, we may assume that  $\text{tr}(\unicode[STIX]{x1D711}(F))\geqslant 0$. It is easy to calculate
$\text{tr}(\unicode[STIX]{x1D711}(F))\geqslant 0$. It is easy to calculate  $h(F)=0$ if
$h(F)=0$ if  $\text{tr}(\unicode[STIX]{x1D711}(F))=0,1$ since
$\text{tr}(\unicode[STIX]{x1D711}(F))=0,1$ since  $\unicode[STIX]{x1D711}(F)$ is of finite order and hence
$\unicode[STIX]{x1D711}(F)$ is of finite order and hence  $F$ is of finite order up to
$F$ is of finite order up to  $\text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$. If
$\text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$. If  $\text{tr}(\unicode[STIX]{x1D711}(F))=2$, then
$\text{tr}(\unicode[STIX]{x1D711}(F))=2$, then  $F=(-\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}))F^{\prime }$ with
$F=(-\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}))F^{\prime }$ with  $F^{\prime }\in \text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ for some
$F^{\prime }\in \text{Aut}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})\ltimes \text{Pic}^{0}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$ for some  $\vec{x}\in L_{A}$. It follows from Proposition 3.13 that
$\vec{x}\in L_{A}$. It follows from Proposition 3.13 that
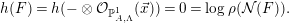 $$\begin{eqnarray}\displaystyle h(F)=h(-\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}))=0=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(F)=h(-\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x}))=0=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)). & & \displaystyle \nonumber\end{eqnarray}$$ Suppose now that  $\text{tr}(\unicode[STIX]{x1D711}(F))>2$.
$\text{tr}(\unicode[STIX]{x1D711}(F))>2$.
Lemma 3.18. For indecomposable objects  $M_{1},M_{2}\in \text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, we have
$M_{1},M_{2}\in \text{Coh}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})$, we have
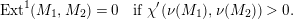 $$\begin{eqnarray}\text{Ext}^{1}(M_{1},M_{2})=0\quad \text{if }\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D708}(M_{1}),\unicode[STIX]{x1D708}(M_{2}))>0.\end{eqnarray}$$
$$\begin{eqnarray}\text{Ext}^{1}(M_{1},M_{2})=0\quad \text{if }\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D708}(M_{1}),\unicode[STIX]{x1D708}(M_{2}))>0.\end{eqnarray}$$Proof. The statement follows from the slope stability for orbifold projective lines [Reference Geigle and LenzingGL, Proposition 5.2] and Proposition 3.3(ii).◻
Lemma 3.19. [Reference KikutaKik, Proposition 4.6]
Assume that  $\text{tr}(\unicode[STIX]{x1D711}(F))>2$.
$\text{tr}(\unicode[STIX]{x1D711}(F))>2$.
There exists a sequence of positive integers  $\mathbf{m}=(m_{2l},\ldots ,m_{1})$ with
$\mathbf{m}=(m_{2l},\ldots ,m_{1})$ with  $l\geqslant 1$ such that
$l\geqslant 1$ such that  $\unicode[STIX]{x1D711}(F)$ is conjugate in
$\unicode[STIX]{x1D711}(F)$ is conjugate in  $\text{SL}(2,\mathbb{Z})$ to
$\text{SL}(2,\mathbb{Z})$ to
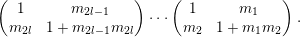 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}1 & m_{2l-1}\\ m_{2l} & 1+m_{2l-1}m_{2l}\end{array}\right)\cdots \left(\begin{array}{@{}cc@{}}1 & m_{1}\\ m_{2} & 1+m_{1}m_{2}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}1 & m_{2l-1}\\ m_{2l} & 1+m_{2l-1}m_{2l}\end{array}\right)\cdots \left(\begin{array}{@{}cc@{}}1 & m_{1}\\ m_{2} & 1+m_{1}m_{2}\end{array}\right).\end{eqnarray}$$ For each sequence of positive integers  $\mathbf{m}=(m_{2l},\ldots ,m_{1})$ with
$\mathbf{m}=(m_{2l},\ldots ,m_{1})$ with  $l\geqslant 1$, take
$l\geqslant 1$, take  $F_{\mathbf{m}}\in \text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))$ so that
$F_{\mathbf{m}}\in \text{Auteq}({\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}))$ so that
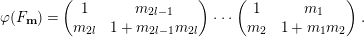 $$\begin{eqnarray}\unicode[STIX]{x1D711}(F_{\mathbf{m}})=\left(\begin{array}{@{}cc@{}}1 & m_{2l-1}\\ m_{2l} & 1+m_{2l-1}m_{2l}\end{array}\right)\cdots \left(\begin{array}{@{}cc@{}}1 & m_{1}\\ m_{2} & 1+m_{1}m_{2}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(F_{\mathbf{m}})=\left(\begin{array}{@{}cc@{}}1 & m_{2l-1}\\ m_{2l} & 1+m_{2l-1}m_{2l}\end{array}\right)\cdots \left(\begin{array}{@{}cc@{}}1 & m_{1}\\ m_{2} & 1+m_{1}m_{2}\end{array}\right).\end{eqnarray}$$ For positive  $\vec{x},\vec{y}\in L_{A}$, an elementary calculation gives
$\vec{x},\vec{y}\in L_{A}$, an elementary calculation gives
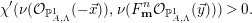 $$\begin{eqnarray}\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D708}({\mathcal{O}}_{\mathbb{ P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{x})),\unicode[STIX]{x1D708}(F_{\mathbf{m}}^{n}{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{y})))>0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D708}({\mathcal{O}}_{\mathbb{ P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{x})),\unicode[STIX]{x1D708}(F_{\mathbf{m}}^{n}{\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{y})))>0.\end{eqnarray}$$ Take  $G,G^{\ast }$ as in Proposition 3.5 and a positive
$G,G^{\ast }$ as in Proposition 3.5 and a positive  $\vec{x}\in L_{A}$. By Proposition 3.3(iii), Lemma 3.18, we obtain
$\vec{x}\in L_{A}$. By Proposition 3.3(iii), Lemma 3.18, we obtain
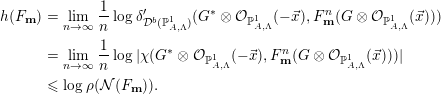 $$\begin{eqnarray}\displaystyle h(F_{\mathbf{m}}) & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}^{\prime }(G^{\ast }\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{x}),F_{\mathbf{m}}^{n}(G\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x})))\nonumber\\ \displaystyle & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log |\unicode[STIX]{x1D712}(G^{\ast }\otimes {\mathcal{O}}_{\mathbb{ P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{x}),F_{\mathbf{m}}^{n}(G\otimes {\mathcal{O}}_{\mathbb{ P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x})))|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \log \unicode[STIX]{x1D70C}({\mathcal{N}}(F_{\mathbf{m}})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(F_{\mathbf{m}}) & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log \unicode[STIX]{x1D6FF}_{{\mathcal{D}}^{b}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1})}^{\prime }(G^{\ast }\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{x}),F_{\mathbf{m}}^{n}(G\otimes {\mathcal{O}}_{\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x})))\nonumber\\ \displaystyle & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{n}\log |\unicode[STIX]{x1D712}(G^{\ast }\otimes {\mathcal{O}}_{\mathbb{ P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(-\vec{x}),F_{\mathbf{m}}^{n}(G\otimes {\mathcal{O}}_{\mathbb{ P}_{A,\unicode[STIX]{x1D6EC}}^{1}}(\vec{x})))|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \log \unicode[STIX]{x1D70C}({\mathcal{N}}(F_{\mathbf{m}})).\nonumber\end{eqnarray}$$Lemma 3.20. We have
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}({\mathcal{N}}(F))=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D711}(F)).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}({\mathcal{N}}(F))=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D711}(F)).\end{eqnarray}$$ In particular,  $\unicode[STIX]{x1D70C}({\mathcal{N}}(F))$ is an algebraic integer.
$\unicode[STIX]{x1D70C}({\mathcal{N}}(F))$ is an algebraic integer.
Proof. The inequality  $\unicode[STIX]{x1D70C}({\mathcal{N}}(F))\geqslant \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D711}(F))$ follows from the commutativity:
$\unicode[STIX]{x1D70C}({\mathcal{N}}(F))\geqslant \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D711}(F))$ follows from the commutativity:  $\unicode[STIX]{x1D711}(F)\circ \unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}\circ {\mathcal{N}}(F)$. The fact that
$\unicode[STIX]{x1D711}(F)\circ \unicode[STIX]{x1D708}=\unicode[STIX]{x1D708}\circ {\mathcal{N}}(F)$. The fact that  $\unicode[STIX]{x1D711}$ factors thorough the surjection
$\unicode[STIX]{x1D711}$ factors thorough the surjection  $\text{Aut}_{\mathbb{Z}}({\mathcal{N}}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}),\unicode[STIX]{x1D712})\rightarrow \text{Aut}_{\mathbb{Z}}(\mathbb{Z}^{2},\unicode[STIX]{x1D712}^{\prime })$ [Reference Lenzing and MeltzerLM, Theorem 7.3] yields the reversed inequality.◻
$\text{Aut}_{\mathbb{Z}}({\mathcal{N}}(\mathbb{P}_{A,\unicode[STIX]{x1D6EC}}^{1}),\unicode[STIX]{x1D712})\rightarrow \text{Aut}_{\mathbb{Z}}(\mathbb{Z}^{2},\unicode[STIX]{x1D712}^{\prime })$ [Reference Lenzing and MeltzerLM, Theorem 7.3] yields the reversed inequality.◻
Since  $\unicode[STIX]{x1D711}(F_{\mathbf{m}})$ is conjugate to
$\unicode[STIX]{x1D711}(F_{\mathbf{m}})$ is conjugate to  $\unicode[STIX]{x1D711}(F)$, it follows from Lemmas 3.16 and 3.20 that
$\unicode[STIX]{x1D711}(F)$, it follows from Lemmas 3.16 and 3.20 that
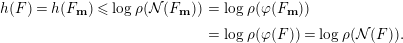 $$\begin{eqnarray}\displaystyle h(F)=h(F_{\mathbf{m}})\leqslant \log \unicode[STIX]{x1D70C}({\mathcal{N}}(F_{\mathbf{m}})) & = & \displaystyle \log \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D711}(F_{\mathbf{m}}))\nonumber\\ \displaystyle & = & \displaystyle \log \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D711}(F))=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(F)=h(F_{\mathbf{m}})\leqslant \log \unicode[STIX]{x1D70C}({\mathcal{N}}(F_{\mathbf{m}})) & = & \displaystyle \log \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D711}(F_{\mathbf{m}}))\nonumber\\ \displaystyle & = & \displaystyle \log \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D711}(F))=\log \unicode[STIX]{x1D70C}({\mathcal{N}}(F)).\nonumber\end{eqnarray}$$By Theorem 2.13, we finished the proof of Proposition 3.17, hence of Theorem 3.10.◻
Acknowledgments
The first author is supported by JSPS KAKENHI Grant Number JP17J00227. The second author is supported by JSPS KAKENHI Grant Number JP15J02913. The third author is supported by JSPS KAKENHI Grant Number JP16H06337, JP26610008.



















































