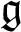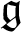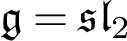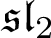1. Introduction and description of the results
Construction and classification of modules are two fundamental problems in representation theory. In most of the cases, the problem of classification of all modules is known to be very hard (i.e., wild), so one is naturally forced to consider special classes of modules, for example, simple modules. Classification of simple modules is also quite hard in most of the cases. For example, for complex semisimple Lie algebras, classification of all simple modules is only known, in some sense, for the algebra
![]() $\mathfrak {sl}_2$
(see Reference Block[8]). At the same time, numerous families of simple modules for semisimple Lie algebras are very well understood, for example, simple highest weight modules (see [Reference Humphreys31], [Reference Verma49]), Whittaker modules (see [Reference Batra and Mazorchuk5], [Reference Kostant37]), weight modules with finite-dimensional weight spaces (see Reference Mathieu[41]), and Gelfand–Zeitlin modules (see Reference Drozd, Ovsienko, Futorny, Bureš and Souček[18], [Reference Early, Mazorchuk and Vishnyakova21], [Reference Webster51] and references therein).
$\mathfrak {sl}_2$
(see Reference Block[8]). At the same time, numerous families of simple modules for semisimple Lie algebras are very well understood, for example, simple highest weight modules (see [Reference Humphreys31], [Reference Verma49]), Whittaker modules (see [Reference Batra and Mazorchuk5], [Reference Kostant37]), weight modules with finite-dimensional weight spaces (see Reference Mathieu[41]), and Gelfand–Zeitlin modules (see Reference Drozd, Ovsienko, Futorny, Bureš and Souček[18], [Reference Early, Mazorchuk and Vishnyakova21], [Reference Webster51] and references therein).
There are two natural generalizations of semisimple Lie algebras: semisimple Lie superalgebras and nonsemisimple Lie algebras. For semisimple Lie superalgebras, a significant progress in classification of simple modules was recently made in [Reference Chen, Coulembier and Mazorchuk13], [Reference Chen and Mazorchuk14]. Basically, for a large class of Lie superalgebras, the results of [Reference Chen, Coulembier and Mazorchuk13], [Reference Chen and Mazorchuk14] reduce the problem of classification of simple modules to a similar problem for the even part of the superalgebra, which is a reductive Lie algebra. In contrast to this situation, for nonsemisimple Lie algebras, very little is known. Apart from the main result of Reference Block[8], which, in addition to
![]() $\mathfrak {sl}_2$
, classifies simple modules over the Borel subalgebra of
$\mathfrak {sl}_2$
, classifies simple modules over the Borel subalgebra of
![]() $\mathfrak {sl}_2$
, several special classes of simple modules were studied for various specific nonsemisimple Lie algebras (see, e.g., [Reference Bavula and Lu6], [Reference Bavula and Lu7], [Reference Cai and Chen10], [Reference Cai, Cheng and Shen11], [Reference Dubsky, Lü, Mazorchuk and Zhao20], [Reference Lau39], [Reference Mazorchuk and Söderberg43], [Reference Wilson52] and references therein). We now look at some of these and some other results in more detail.
$\mathfrak {sl}_2$
, several special classes of simple modules were studied for various specific nonsemisimple Lie algebras (see, e.g., [Reference Bavula and Lu6], [Reference Bavula and Lu7], [Reference Cai and Chen10], [Reference Cai, Cheng and Shen11], [Reference Dubsky, Lü, Mazorchuk and Zhao20], [Reference Lau39], [Reference Mazorchuk and Söderberg43], [Reference Wilson52] and references therein). We now look at some of these and some other results in more detail.
It seems that the so-called current Lie algebras are the ones which are most studied and best understood. These are defined as tensor product of a reductive Lie algebra with a commutative unital associate algebra. For current Lie algebras, there is a full classification of simple weight modules with finite-dimensional weight spaces (see Reference Lau[39]). Moreover, the highest weight theory for the truncated polynomial version of these Lie algebras is developed in Reference Wilson[52]. Moreover, the center of the universal enveloping algebras of such Lie algebras whose semisimple part is of type A is described explicitly in Reference Molev, Doebner, Nattermann and Scherer[45].
A special family of truncated current Lie algebras is formed by the so-called Takiff Lie algebras, studied originally in Reference Takiff[48], which correspond to the case when one tensors a reductive Lie algebra with the associative algebra of dual numbers. The Takiff
![]() $\mathfrak {sl}_2$
is also known as the complexification of the Lie algebra of the Euclidean group
$\mathfrak {sl}_2$
is also known as the complexification of the Lie algebra of the Euclidean group
![]() $E(3)$
, the Lie group of orientation-preserving isometries of the three-dimensional Euclidean space. It belongs to the family of conformal Galilei algebras (see, e.g., Reference Lü, Mazorchuk and Zhao[40]). Category
$E(3)$
, the Lie group of orientation-preserving isometries of the three-dimensional Euclidean space. It belongs to the family of conformal Galilei algebras (see, e.g., Reference Lü, Mazorchuk and Zhao[40]). Category
![]() $\mathcal {O}$
for Takiff
$\mathcal {O}$
for Takiff
![]() $\mathfrak {sl}_2$
was recently studied in Reference Mazorchuk and Söderberg[43], and simple weight modules were classified in Reference Bavula and Lu[6].
$\mathfrak {sl}_2$
was recently studied in Reference Mazorchuk and Söderberg[43], and simple weight modules were classified in Reference Bavula and Lu[6].
The Schrödinger Lie algebra (see Section 5) is also an important and intensively studied example of a nonreductive Lie algebra. Its category
![]() $\mathcal {O}$
was studied in detail in Reference Dubsky, Lü, Mazorchuk and Zhao[20], lowest weight modules were classified in Reference Dobrev, Doebner and Mrugalla[17], and simple weight modules were classified in [Reference Bavula and Lu7], [Reference Dubsky19].
$\mathcal {O}$
was studied in detail in Reference Dubsky, Lü, Mazorchuk and Zhao[20], lowest weight modules were classified in Reference Dobrev, Doebner and Mrugalla[17], and simple weight modules were classified in [Reference Bavula and Lu7], [Reference Dubsky19].
A slight modification of the Schrödinger Lie algebra, called the centerless Schrödinger Lie algebra, belongs to the family of conformal Galilei algebras (see Section 7). As their names suggest, the Schrödinger Lie algebra and conformal Galilei algebras are of great importance in theoretical physics and seem to have originated from there. For example, the Schrödinger Lie algebra comes from the Schrödinger Lie group, the group of symmetries of the free particle Schrödinger equation (see Reference Dobrev, Doebner and Mrugalla[17], [Reference Perroud46]). Conformal Galilei algebras are related to the nonrelativistic version of the AdS/CFT correspondence (see Reference Bagchi and Gopakumar[4]).
Several papers studied a generalization of Whittaker modules (originally defined in Reference Kostant[37] for semisimple Lie algebras), in the setup of conformal Galilei algebras and the Schrödinger Lie algebra (see [Reference Cai and Chen10]–[Reference Cai, Shen and Zhang12], [Reference Lü, Mazorchuk and Zhao40]). Quasi-Whittaker modules are modules on which the radical of the Lie algebra acts locally finitely.
In the present paper, we initiate the study of modules over (nonsemisimple) Lie algebras on which the action of the semisimple part of the Lie algebra is locally finite, that is, which are locally finite over the semisimple part. This condition is, in a sense, the opposite to the condition defining quasi-Whittaker modules. The obvious examples of modules that are locally finite over the semisimple part are simple finite-dimensional modules over the semisimple part on which the radical of our Lie algebra acts trivially. However, we observe that, for many Lie algebras, there exist simple infinite-dimensional modules that are locally finite over the semisimple part. This motivates the problem of classification of such modules, and we show that this problem can be completely answered for the Takiff Lie algebra of
![]() $\mathfrak {sl}_2$
and for the Schrödinger Lie algebra. Moreover, the answer is both nontrivial and interesting. To the best of our knowledge, such modules have not been studied before in the general case (however, for the Schrödinger Lie algebra and the Takiff
$\mathfrak {sl}_2$
and for the Schrödinger Lie algebra. Moreover, the answer is both nontrivial and interesting. To the best of our knowledge, such modules have not been studied before in the general case (however, for the Schrödinger Lie algebra and the Takiff
![]() $\mathfrak {sl}_2$
, they belong to a larger family of weight modules studied in detail in Reference Bavula and Lu[6], [Reference Bavula and Lu7]). Let us now describe the content of the paper in more detail.
$\mathfrak {sl}_2$
, they belong to a larger family of weight modules studied in detail in Reference Bavula and Lu[6], [Reference Bavula and Lu7]). Let us now describe the content of the paper in more detail.
If
![]() $\mathfrak {L}$
is any finite-dimensional Lie algebra and
$\mathfrak {L}$
is any finite-dimensional Lie algebra and
![]() $\mathfrak {g} \subseteq \mathfrak {L}$
its semisimple Levi subalgebra, we study
$\mathfrak {g} \subseteq \mathfrak {L}$
its semisimple Levi subalgebra, we study
![]() $\mathfrak {L}$
-modules whose restriction to
$\mathfrak {L}$
-modules whose restriction to
![]() $\mathfrak {g}$
decomposes into a direct sum of simple finite-dimensional
$\mathfrak {g}$
decomposes into a direct sum of simple finite-dimensional
![]() $\mathfrak {g}$
-modules with finite multiplicities, and call them
$\mathfrak {g}$
-modules with finite multiplicities, and call them
![]() $\mathfrak {g}$
-Harish-Chandra modules. To justify the name, we note that there is an obvious analogy with the classical theory of
$\mathfrak {g}$
-Harish-Chandra modules. To justify the name, we note that there is an obvious analogy with the classical theory of
![]() $(\mathfrak {g},K)$
-modules as in Reference Vogan[50], coming from the setup of real reductive Lie groups. In the classical theory, any
$(\mathfrak {g},K)$
-modules as in Reference Vogan[50], coming from the setup of real reductive Lie groups. In the classical theory, any
![]() $(\mathfrak {g},K)$
-module splits as a direct sum of finite-dimensional modules over the compact group K, and moreover, the multiplicities are finite if the corresponding group representation is irreducible and unitary (a result by Harish-Chandra). In our setup, there is no such automatic splitting, so we pretend that
$(\mathfrak {g},K)$
-module splits as a direct sum of finite-dimensional modules over the compact group K, and moreover, the multiplicities are finite if the corresponding group representation is irreducible and unitary (a result by Harish-Chandra). In our setup, there is no such automatic splitting, so we pretend that
![]() $\mathfrak {g}$
is compact, that is, we consider only those
$\mathfrak {g}$
is compact, that is, we consider only those
![]() $\mathfrak {L}$
-modules that split as
$\mathfrak {L}$
-modules that split as
![]() $\mathfrak {g}$
-modules into a direct sum of finite-dimensional
$\mathfrak {g}$
-modules into a direct sum of finite-dimensional
![]() $\mathfrak {g}$
-modules with finite multiplicities. Hopefully, this analogy could be used to transfer parts of the Langlands classification, or the theory of minimal K-types into our nonreductive algebraic setup. There is another analogy of our setup with integrable modules over a Kac–Moody algebra (see Reference Kac[33]).
$\mathfrak {g}$
-modules with finite multiplicities. Hopefully, this analogy could be used to transfer parts of the Langlands classification, or the theory of minimal K-types into our nonreductive algebraic setup. There is another analogy of our setup with integrable modules over a Kac–Moody algebra (see Reference Kac[33]).
In Section 2, we introduce the basic setup that we work in. In Section 3, we roughly describe universal
![]() $\mathfrak {g}$
-Harish-Chandra modules for Takiff Lie algebras. In particular, we show that such Lie algebras do indeed always have simple infinite-dimensional
$\mathfrak {g}$
-Harish-Chandra modules for Takiff Lie algebras. In particular, we show that such Lie algebras do indeed always have simple infinite-dimensional
![]() $\mathfrak {g}$
-Harish-Chandra modules (see Corollary 9).
$\mathfrak {g}$
-Harish-Chandra modules (see Corollary 9).
In Sections 4 and 5, we prove our most concrete results: Theorem 31 provides a complete classification of simple
![]() $\mathfrak {g}$
-Harish-Chandra modules for the Takiff
$\mathfrak {g}$
-Harish-Chandra modules for the Takiff
![]() $\mathfrak {sl}_2$
, and Theorem 54 gives such a classification for the Schrödinger Lie algebra. These two answers have both clear similarities and differences. In both cases, we crucially use the highest weight theory for corresponding algebras and appropriate analogues of completions functors. Moreover, in both cases, we can consider semisimple
$\mathfrak {sl}_2$
, and Theorem 54 gives such a classification for the Schrödinger Lie algebra. These two answers have both clear similarities and differences. In both cases, we crucially use the highest weight theory for corresponding algebras and appropriate analogues of completions functors. Moreover, in both cases, we can consider semisimple
![]() $\mathfrak {g}$
-Harish-Chandra modules as a monoidal representation of the monoidal category of finite-dimensional
$\mathfrak {g}$
-Harish-Chandra modules as a monoidal representation of the monoidal category of finite-dimensional
![]() $\mathfrak {sl}_2$
-modules. We found it surprising that the combinatorial properties of the corresponding monoidal representation in the Takiff
$\mathfrak {sl}_2$
-modules. We found it surprising that the combinatorial properties of the corresponding monoidal representation in the Takiff
![]() $\mathfrak {sl}_2$
and the Schrödinger cases are rather different.
$\mathfrak {sl}_2$
and the Schrödinger cases are rather different.
In case of the Takiff
![]() $\mathfrak {sl}_2$
, we obtain a family of modules
$\mathfrak {sl}_2$
, we obtain a family of modules
![]() $V(n,\chi )$
which are naturally parameterized by
$V(n,\chi )$
which are naturally parameterized by
![]() $n \in \mathbb {Z}$
and
$n \in \mathbb {Z}$
and
![]() $\chi \in \mathbb {C}\setminus \{0\}$
. However, we show that this family has a redundancy via nontrivial isomorphisms
$\chi \in \mathbb {C}\setminus \{0\}$
. However, we show that this family has a redundancy via nontrivial isomorphisms
![]() $V(n,\chi ) \cong V(-n,-\chi )$
. Roughly speaking,
$V(n,\chi ) \cong V(-n,-\chi )$
. Roughly speaking,
![]() $|n|$
is the minimal
$|n|$
is the minimal
![]() $\mathfrak {g}$
-type, and
$\mathfrak {g}$
-type, and
![]() $\chi ^2$
is the purely radical part of the central character. This classifies all simple infinite-dimensional
$\chi ^2$
is the purely radical part of the central character. This classifies all simple infinite-dimensional
![]() $\mathfrak {g}$
-Harish-Chandra modules.
$\mathfrak {g}$
-Harish-Chandra modules.
In case of the Schrödinger Lie algebra, we obtain a similar family of modules
![]() $V(n,\chi )$
parameterized by
$V(n,\chi )$
parameterized by
![]() $n \in \mathbb {Z}_{\geq 0}$
and
$n \in \mathbb {Z}_{\geq 0}$
and
![]() $\chi \in \mathbb {C}\setminus \{0\}$
, However, in contrast to the Takiff case, this family is irredundant.
$\chi \in \mathbb {C}\setminus \{0\}$
, However, in contrast to the Takiff case, this family is irredundant.
The modules mentioned above are very explicitly described. In both cases, we, moreover, show that all groups of first self-extensions of these modules are one-dimensional (see Theorems 32 and 56). Moreover, we prove that the annihilators of all the above modules in the universal enveloping algebra are centrally generated (see Theorems 38 and Corollary 58). Classification results in Sections 4 and 5 are deducible (with nontrivial effort) from more general results of Reference Bavula and Lu[6], [Reference Bavula and Lu7]; however, we provide a completely different, less computational, and more conceptual approach.
For comparison, it is easy to see that the centerless Schrödinger Lie algebra does not admit simple infinite-dimensional
![]() $\mathfrak {g}$
-Harish-Chandra modules. The reason for this is, roughly speaking, the fact that its purely radical part of the center is trivial (see Remark 55 for details).
$\mathfrak {g}$
-Harish-Chandra modules. The reason for this is, roughly speaking, the fact that its purely radical part of the center is trivial (see Remark 55 for details).
We would like to point out that the methods we utilize for our classification go far beyond direct calculations. We use various functorial constructions, which include, in particular, an appropriate adjustment of Enright’s completion functor (based on Arkhipov’s twisting functor) [Reference Andersen and Stroppel2], [Reference Arkhipov3], Reference Deodhar[15], Reference Enright[22], Reference Khomenko and Mazorchuk[34], Reference König and Mazorchuk[36]. Further development of both, highest weight theory and properties of various Lie theoretic functors as in Reference Mazorchuk and Stroppel[44], for nonsemisimple Lie algebras, should provide an opportunity for generalization of the results of this paper to, in the first step, other Takiff Lie algebras and, further, general finite-dimensional Lie algebras.
In the most general case of an arbitrary finite-dimensional complex Lie algebra
![]() $\mathfrak {L}$
and a nontrivial Levi subalgebra
$\mathfrak {L}$
and a nontrivial Levi subalgebra
![]() $\mathfrak {g}$
, it is clear that simple
$\mathfrak {g}$
, it is clear that simple
![]() $\mathfrak {g}$
-Harish-Chandra modules always exist. Namely, the finite-dimensional
$\mathfrak {g}$
-Harish-Chandra modules always exist. Namely, the finite-dimensional
![]() $\mathfrak {L}$
-modules are, of course,
$\mathfrak {L}$
-modules are, of course,
![]() $\mathfrak {g}$
-Harish-Chandra modules. In Theorem 61 of Section 6, we give a general sufficient condition for existence of infinite-dimensional simple
$\mathfrak {g}$
-Harish-Chandra modules. In Theorem 61 of Section 6, we give a general sufficient condition for existence of infinite-dimensional simple
![]() $\mathfrak {g}$
-Harish-Chandra modules. The sufficient condition, as we formulate it, requires that the nilradical of
$\mathfrak {g}$
-Harish-Chandra modules. The sufficient condition, as we formulate it, requires that the nilradical of
![]() $\mathfrak {L}$
intersects the centralizer in
$\mathfrak {L}$
intersects the centralizer in
![]() $\mathfrak {L}$
of the Cartan subalgebra of
$\mathfrak {L}$
of the Cartan subalgebra of
![]() $\mathfrak {g}$
. In this case, we manage to use highest weight theory for
$\mathfrak {g}$
. In this case, we manage to use highest weight theory for
![]() $\mathfrak {L}$
, combined with various versions of twisting functors, to construct infinite-dimensional simple
$\mathfrak {L}$
, combined with various versions of twisting functors, to construct infinite-dimensional simple
![]() $\mathfrak {g}$
-Harish-Chandra modules. We also provide an example showing that our sufficient condition is not necessary, in general: the semidirect product of
$\mathfrak {g}$
-Harish-Chandra modules. We also provide an example showing that our sufficient condition is not necessary, in general: the semidirect product of
![]() $\mathfrak {sl}_2$
and its four-dimensional simple module does not satisfy our sufficient condition and has trivial highest weight theory in the sense that its simple highest weight modules coincide with simple highest weight
$\mathfrak {sl}_2$
and its four-dimensional simple module does not satisfy our sufficient condition and has trivial highest weight theory in the sense that its simple highest weight modules coincide with simple highest weight
![]() $\mathfrak {sl}_2$
-modules. However, using various combinatorial tricks from Reference Hahn, Huh, Lim and Sohn[27], we show that this Lie algebra does admit simple infinite-dimensional
$\mathfrak {sl}_2$
-modules. However, using various combinatorial tricks from Reference Hahn, Huh, Lim and Sohn[27], we show that this Lie algebra does admit simple infinite-dimensional
![]() $\mathfrak {g}$
-Harish-Chandra modules. This result can be found in Section 7.2.
$\mathfrak {g}$
-Harish-Chandra modules. This result can be found in Section 7.2.
Finally, in Section 7.3, in particular Theorem 68, we classify a class of
![]() $\mathfrak {sl}_2$
-Harish-Chandra modules that are connected to highest weight modules, for the semidirect product of
$\mathfrak {sl}_2$
-Harish-Chandra modules that are connected to highest weight modules, for the semidirect product of
![]() $\mathfrak {sl}_2$
with its simple five-dimensional module. The corresponding category of semisimple
$\mathfrak {sl}_2$
with its simple five-dimensional module. The corresponding category of semisimple
![]() $\mathfrak {g}$
-Harish-Chandra modules is, again, a monoidal representation of the monoidal category of finite-dimensional
$\mathfrak {g}$
-Harish-Chandra modules is, again, a monoidal representation of the monoidal category of finite-dimensional
![]() $\mathfrak {sl}_2$
-modules. But the combinatorics of this monoidal representation is completely different from the ones which we get in the Takiff and the Schrödinger cases (see Remark 75). In particular, contrary to the previous cases, in this case, we obtain an example of two simple
$\mathfrak {sl}_2$
-modules. But the combinatorics of this monoidal representation is completely different from the ones which we get in the Takiff and the Schrödinger cases (see Remark 75). In particular, contrary to the previous cases, in this case, we obtain an example of two simple
![]() $\mathfrak {g}$
-Harish-Chandra modules with different sets of
$\mathfrak {g}$
-Harish-Chandra modules with different sets of
![]() $\mathfrak {g}$
-types, but with the same minimal
$\mathfrak {g}$
-types, but with the same minimal
![]() $\mathfrak {g}$
-type.
$\mathfrak {g}$
-type.
Comparison of the results of Reference Han[28] with Lemmata 11 and 41 suggests a possibility of an interesting connection between
![]() $\mathfrak {g}$
-Harish-Chandra modules and higher-spin algebras from Reference Pope, Romans and Shen[47].
$\mathfrak {g}$
-Harish-Chandra modules and higher-spin algebras from Reference Pope, Romans and Shen[47].
2. Notation and preliminaries
We work over the complex numbers
![]() $\mathbb {C}$
. For a Lie algebra
$\mathbb {C}$
. For a Lie algebra
![]() $\mathfrak {a}$
, we denote by
$\mathfrak {a}$
, we denote by
![]() $U(\mathfrak {a})$
the universal enveloping algebra of
$U(\mathfrak {a})$
the universal enveloping algebra of
![]() $\mathfrak {a}$
.
$\mathfrak {a}$
.
Fix a finite-dimensional Lie algebra
![]() $\mathfrak {L}$
over
$\mathfrak {L}$
over
![]() $\mathbb {C}$
, and fix its Levi decomposition
$\mathbb {C}$
, and fix its Levi decomposition
![]() $\mathfrak {L} \cong \mathfrak {g} \ltimes \mathfrak {r}$
. This is a semidirect product, where
$\mathfrak {L} \cong \mathfrak {g} \ltimes \mathfrak {r}$
. This is a semidirect product, where
![]() $\mathfrak {g}$
is a maximal semisimple Lie subalgebra, unique up to conjugation, and
$\mathfrak {g}$
is a maximal semisimple Lie subalgebra, unique up to conjugation, and
![]() $\mathfrak {r} = \operatorname {\mathrm {Rad}} \mathfrak {L}$
is the radical of
$\mathfrak {r} = \operatorname {\mathrm {Rad}} \mathfrak {L}$
is the radical of
![]() $\mathfrak {L}$
, that is, the unique maximal solvable ideal.
$\mathfrak {L}$
, that is, the unique maximal solvable ideal.
Definition 1. An
![]() $\mathfrak {L}$
-module V is called a
$\mathfrak {L}$
-module V is called a
![]() $\mathfrak {g}$
-Harish-Chandra module, if the restriction of V to
$\mathfrak {g}$
-Harish-Chandra module, if the restriction of V to
![]() $\mathfrak {g}$
decomposes as a direct sum of simple finite-dimensional
$\mathfrak {g}$
decomposes as a direct sum of simple finite-dimensional
![]() $\mathfrak {g}$
-modules, and moreover, each isomorphism class of simple finite-dimensional
$\mathfrak {g}$
-modules, and moreover, each isomorphism class of simple finite-dimensional
![]() $\mathfrak {g}$
-modules occurs with a finite multiplicity in V.
$\mathfrak {g}$
-modules occurs with a finite multiplicity in V.
A simple
![]() $\mathfrak {g}$
-submodule of a
$\mathfrak {g}$
-submodule of a
![]() $\mathfrak {g}$
-Harish-Chandra module V is called a
$\mathfrak {g}$
-Harish-Chandra module V is called a
![]() $\mathfrak {g}$
-type of V. The sum of all
$\mathfrak {g}$
-type of V. The sum of all
![]() $\mathfrak {g}$
-submodules of V isomorphic to a given
$\mathfrak {g}$
-submodules of V isomorphic to a given
![]() $\mathfrak {g}$
-type is called the
$\mathfrak {g}$
-type is called the
![]() $\mathfrak {g}$
-isotypic component of V determined by this
$\mathfrak {g}$
-isotypic component of V determined by this
![]() $\mathfrak {g}$
-type.
$\mathfrak {g}$
-type.
Fix a Cartan subalgebra
![]() $\mathfrak {h} \subseteq \mathfrak {g}$
. Every
$\mathfrak {h} \subseteq \mathfrak {g}$
. Every
![]() $\mathfrak {g}$
-Harish-Chandra module is a weight module with respect to
$\mathfrak {g}$
-Harish-Chandra module is a weight module with respect to
![]() $\mathfrak {h}$
. However, infinite-dimensional
$\mathfrak {h}$
. However, infinite-dimensional
![]() $\mathfrak {g}$
-Harish-Chandra modules might have infinite-dimensional weight spaces.
$\mathfrak {g}$
-Harish-Chandra modules might have infinite-dimensional weight spaces.
Remark 2. Note that the notion of a
![]() $\mathfrak {g}$
-Harish-Chandra module is different from the notion of Harish-Chandra module from Reference Lau[39]. In the latter paper, Harish-Chandra modules are weight modules with finite-dimensional weight spaces. It would be natural to call the modules from Reference Lau[39]
$\mathfrak {g}$
-Harish-Chandra module is different from the notion of Harish-Chandra module from Reference Lau[39]. In the latter paper, Harish-Chandra modules are weight modules with finite-dimensional weight spaces. It would be natural to call the modules from Reference Lau[39]
![]() $\mathfrak {h}$
-Harish-Chandra modules.
$\mathfrak {h}$
-Harish-Chandra modules.
Denote by
![]() $\operatorname {\mathrm {Nrad}}(\mathfrak {L})$
the nilradical of
$\operatorname {\mathrm {Nrad}}(\mathfrak {L})$
the nilradical of
![]() $\mathfrak {L}$
, by which we mean the intersection of kernels of all finite-dimensional simple modules of
$\mathfrak {L}$
, by which we mean the intersection of kernels of all finite-dimensional simple modules of
![]() $\mathfrak {L}$
. It is a nilpotent ideal, but not necessarily equal to the maximal nilpotent ideal. It is well known that
$\mathfrak {L}$
. It is a nilpotent ideal, but not necessarily equal to the maximal nilpotent ideal. It is well known that
![]() $\operatorname {\mathrm {Nrad}}(\mathfrak {L}) = [\mathfrak {L},\mathfrak {L}] \cap \mathfrak {r} = [\mathfrak {L},\mathfrak {r}]$
, and
$\operatorname {\mathrm {Nrad}}(\mathfrak {L}) = [\mathfrak {L},\mathfrak {L}] \cap \mathfrak {r} = [\mathfrak {L},\mathfrak {r}]$
, and
![]() $\mathfrak {L}$
is reductive if and only if
$\mathfrak {L}$
is reductive if and only if
![]() $\operatorname {\mathrm {Nrad}}(\mathfrak {L}) =0$
. Moreover,
$\operatorname {\mathrm {Nrad}}(\mathfrak {L}) =0$
. Moreover,
![]() $\operatorname {\mathrm {Nrad}}(\mathfrak {L})$
is the minimal ideal in
$\operatorname {\mathrm {Nrad}}(\mathfrak {L})$
is the minimal ideal in
![]() $\mathfrak {L}$
for which the quotient
$\mathfrak {L}$
for which the quotient
 is reductive. For proofs, see, for example, [Reference Bourbaki9, Chapter I, Section 5.3].
is reductive. For proofs, see, for example, [Reference Bourbaki9, Chapter I, Section 5.3].
Example 3. If
![]() $\mathfrak {L}=\mathfrak {g} \ltimes \mathfrak {r}$
is a reductive Lie algebra, then
$\mathfrak {L}=\mathfrak {g} \ltimes \mathfrak {r}$
is a reductive Lie algebra, then
![]() $\mathfrak {r}$
is precisely the center of
$\mathfrak {r}$
is precisely the center of
![]() $\mathfrak {L}$
. If V is a simple
$\mathfrak {L}$
. If V is a simple
![]() $\mathfrak {g}$
-Harish-Chandra module for
$\mathfrak {g}$
-Harish-Chandra module for
![]() $\mathfrak {L}$
, then, by Schur’s lemma,
$\mathfrak {L}$
, then, by Schur’s lemma,
![]() $\mathfrak {r}$
acts by scalars on V. It follows that V is just a simple finite-dimensional
$\mathfrak {r}$
acts by scalars on V. It follows that V is just a simple finite-dimensional
![]() $\mathfrak {L}$
-module. So, the notion of
$\mathfrak {L}$
-module. So, the notion of
![]() $\mathfrak {g}$
-Harish-Chandra modules is not very interesting for reductive Lie algebras.
$\mathfrak {g}$
-Harish-Chandra modules is not very interesting for reductive Lie algebras.
Fix a positive part
![]() $\Delta ^+(\mathfrak {g},\mathfrak {h})$
in the root system
$\Delta ^+(\mathfrak {g},\mathfrak {h})$
in the root system
![]() $\Delta (\mathfrak {g},\mathfrak {h})$
, and a nondegenerate invariant symmetric bilinear form
$\Delta (\mathfrak {g},\mathfrak {h})$
, and a nondegenerate invariant symmetric bilinear form
![]() $\langle -, - \rangle $
on
$\langle -, - \rangle $
on
![]() $\mathfrak {h}^\ast $
. We have the classical triangular decomposition
$\mathfrak {h}^\ast $
. We have the classical triangular decomposition
![]() $\mathfrak {g} = \mathfrak {n}_- \oplus \mathfrak {h} \oplus \mathfrak {n}_+$
. Furthermore, fix a weight
$\mathfrak {g} = \mathfrak {n}_- \oplus \mathfrak {h} \oplus \mathfrak {n}_+$
. Furthermore, fix a weight
![]() $\delta \in \mathfrak {h}^\ast $
such that
$\delta \in \mathfrak {h}^\ast $
such that
![]() $\langle \delta , \alpha \rangle>0$
for all
$\langle \delta , \alpha \rangle>0$
for all
![]() $\alpha \in \Delta ^+(\mathfrak {g},\mathfrak {h})$
and such that
$\alpha \in \Delta ^+(\mathfrak {g},\mathfrak {h})$
and such that
![]() $\langle \delta , \alpha \rangle =0$
, for an integral weight
$\langle \delta , \alpha \rangle =0$
, for an integral weight
![]() $\alpha $
, implies
$\alpha $
, implies
![]() $\alpha =0$
. Since
$\alpha =0$
. Since
![]() $\mathfrak {L}$
is a finite-dimensional
$\mathfrak {L}$
is a finite-dimensional
![]() $\mathfrak {g}$
-module with respect to the adjoint action, it decomposes as a direct sum of its weight spaces
$\mathfrak {g}$
-module with respect to the adjoint action, it decomposes as a direct sum of its weight spaces
![]() $\mathfrak {L}_\mu $
, where
$\mathfrak {L}_\mu $
, where
![]() $\mu $
varies over the set of integral weights in
$\mu $
varies over the set of integral weights in
![]() $\mathfrak {h}^\ast $
. Consider the following Lie subalgebras of
$\mathfrak {h}^\ast $
. Consider the following Lie subalgebras of
![]() $\mathfrak {L}$
:
$\mathfrak {L}$
:
 $$ \begin{align} \tilde{\mathfrak{n}}_- := \bigoplus_{\langle\mu ,\delta \rangle < 0} \mathfrak{L}_\mu, \quad \tilde{\mathfrak{h}} := \bigoplus_{\langle\mu ,\delta \rangle = 0} \mathfrak{L}_\mu \quad \tilde{\mathfrak{n}}_+ := \bigoplus_{\langle\mu ,\delta \rangle> 0} \mathfrak{L}_\mu. \end{align} $$
$$ \begin{align} \tilde{\mathfrak{n}}_- := \bigoplus_{\langle\mu ,\delta \rangle < 0} \mathfrak{L}_\mu, \quad \tilde{\mathfrak{h}} := \bigoplus_{\langle\mu ,\delta \rangle = 0} \mathfrak{L}_\mu \quad \tilde{\mathfrak{n}}_+ := \bigoplus_{\langle\mu ,\delta \rangle> 0} \mathfrak{L}_\mu. \end{align} $$
Note that this decomposition heavily depends on the choice of
![]() $\delta $
and not only on the choice of
$\delta $
and not only on the choice of
![]() $\Delta ^+(\mathfrak {g},\mathfrak {h})$
. However, for example, for truncated current Lie algebras (which include Takiff Lie algebras), the Schrödinger Lie algebra and conformal Galilei algebras, the decomposition (1) only depends on the choice of
$\Delta ^+(\mathfrak {g},\mathfrak {h})$
. However, for example, for truncated current Lie algebras (which include Takiff Lie algebras), the Schrödinger Lie algebra and conformal Galilei algebras, the decomposition (1) only depends on the choice of
![]() $\Delta ^+(\mathfrak {g},\mathfrak {h})$
. From the construction, it is clear that
$\Delta ^+(\mathfrak {g},\mathfrak {h})$
. From the construction, it is clear that
![]() $\tilde {\mathfrak {n}}_\pm \cap \mathfrak {g} = \mathfrak {n}_\pm $
, and
$\tilde {\mathfrak {n}}_\pm \cap \mathfrak {g} = \mathfrak {n}_\pm $
, and
 $\tilde {\mathfrak {h}} \cap \mathfrak {g} = \mathfrak {h}$
. Moreover, from the condition prescribed on
$\tilde {\mathfrak {h}} \cap \mathfrak {g} = \mathfrak {h}$
. Moreover, from the condition prescribed on
![]() $\delta $
, it follows that
$\delta $
, it follows that
![]() $\tilde {\mathfrak {h}}$
is precisely the centralizer of
$\tilde {\mathfrak {h}}$
is precisely the centralizer of
![]() $\mathfrak {h}$
in
$\mathfrak {h}$
in
![]() $\mathfrak {L}$
. The decomposition
$\mathfrak {L}$
. The decomposition
 $\mathfrak {L} = \tilde {\mathfrak {n}}_- \oplus \tilde {\mathfrak {h}} \oplus \tilde {\mathfrak {n}}_+$
does not satisfy, in general, all the axioms in [Reference Wilson52, Section 2], since we do not require existence of any analogue of Chevalley involution (and even the dimensions of
$\mathfrak {L} = \tilde {\mathfrak {n}}_- \oplus \tilde {\mathfrak {h}} \oplus \tilde {\mathfrak {n}}_+$
does not satisfy, in general, all the axioms in [Reference Wilson52, Section 2], since we do not require existence of any analogue of Chevalley involution (and even the dimensions of
![]() $\tilde {\mathfrak {n}}_-$
and
$\tilde {\mathfrak {n}}_-$
and
![]() $\tilde {\mathfrak {n}}_+$
might be different). However, it is good enough to define Verma modules with reasonable properties.
$\tilde {\mathfrak {n}}_+$
might be different). However, it is good enough to define Verma modules with reasonable properties.
For an element
 $\lambda \in \tilde {\mathfrak {h}}^\ast $
, denote the one-dimensional
$\lambda \in \tilde {\mathfrak {h}}^\ast $
, denote the one-dimensional
 $\tilde {\mathfrak {b}}:=\tilde {\mathfrak {h}} \oplus \tilde {\mathfrak {n}}_+$
-module where
$\tilde {\mathfrak {b}}:=\tilde {\mathfrak {h}} \oplus \tilde {\mathfrak {n}}_+$
-module where
![]() $\tilde {\mathfrak {h}}$
acts as
$\tilde {\mathfrak {h}}$
acts as
![]() $\lambda $
and
$\lambda $
and
![]() $\tilde {\mathfrak {n}}_+$
acts trivially, by
$\tilde {\mathfrak {n}}_+$
acts trivially, by
![]() $\mathbb {C}_\lambda $
. The Verma module with highest weight
$\mathbb {C}_\lambda $
. The Verma module with highest weight
![]() $\lambda $
is defined as
$\lambda $
is defined as
 $$ \begin{align} \Delta(\lambda) := \operatorname{\mathrm{Ind}}_{\tilde{\mathfrak{b}}}^{\mathfrak{L}} \mathbb{C}_\lambda = U(\mathfrak{L}) \mathbin{\mathop{\otimes}\limits_{U(\tilde{\mathfrak{b}})}} \mathbb{C}_\lambda \cong U(\tilde{\mathfrak{n}}_-) \mathbin{\mathop{\otimes}\limits_{\mathbb{C}}} \mathbb{C}_\lambda. \end{align} $$
$$ \begin{align} \Delta(\lambda) := \operatorname{\mathrm{Ind}}_{\tilde{\mathfrak{b}}}^{\mathfrak{L}} \mathbb{C}_\lambda = U(\mathfrak{L}) \mathbin{\mathop{\otimes}\limits_{U(\tilde{\mathfrak{b}})}} \mathbb{C}_\lambda \cong U(\tilde{\mathfrak{n}}_-) \mathbin{\mathop{\otimes}\limits_{\mathbb{C}}} \mathbb{C}_\lambda. \end{align} $$
Let
 $\Delta ^{\pm }(\mathfrak {L},\mathfrak {h})$
denote the set of all
$\Delta ^{\pm }(\mathfrak {L},\mathfrak {h})$
denote the set of all
![]() $\mu $
such that
$\mu $
such that
![]() $\mathfrak {L}_{\mu }\neq 0$
and
$\mathfrak {L}_{\mu }\neq 0$
and
![]() $\pm \langle \mu , \delta \rangle>0$
. We also set
$\pm \langle \mu , \delta \rangle>0$
. We also set
 $\Gamma ^{\pm }=\mathbb {Z}_{\geq 0}\Delta ^{\pm }(\mathfrak {L},\mathfrak {h})$
. Recall that the support of a weight module is the set of all weights for which the corresponding weight spaces are nonzero. By the standard arguments using PBW theorem (cf. Reference Humphreys[31]), we have:
$\Gamma ^{\pm }=\mathbb {Z}_{\geq 0}\Delta ^{\pm }(\mathfrak {L},\mathfrak {h})$
. Recall that the support of a weight module is the set of all weights for which the corresponding weight spaces are nonzero. By the standard arguments using PBW theorem (cf. Reference Humphreys[31]), we have:
Proposition 4. The Verma module
![]() $\Delta (\lambda )$
is an
$\Delta (\lambda )$
is an
![]() $\mathfrak {h}$
-weight module, whose
$\mathfrak {h}$
-weight module, whose
![]() $\mathfrak {h}$
-support is
$\mathfrak {h}$
-support is
![]() $\lambda |_{\mathfrak {h}}+\Gamma ^{-}$
. The
$\lambda |_{\mathfrak {h}}+\Gamma ^{-}$
. The
![]() $\lambda |_{\mathfrak {h}}$
-weight space is one-dimensional, and
$\lambda |_{\mathfrak {h}}$
-weight space is one-dimensional, and
![]() $\Delta (\lambda )$
is generated by this weight vector, so any nontrivial quotient of
$\Delta (\lambda )$
is generated by this weight vector, so any nontrivial quotient of
![]() $\Delta (\lambda )$
also has one-dimensional
$\Delta (\lambda )$
also has one-dimensional
![]() $\lambda |_{\mathfrak {h}}$
-weight space. Moreover,
$\lambda |_{\mathfrak {h}}$
-weight space. Moreover,
![]() $\Delta (\lambda )$
has a unique simple quotient, which we denote by
$\Delta (\lambda )$
has a unique simple quotient, which we denote by
![]() $\mathbf {L}(\lambda )$
.
$\mathbf {L}(\lambda )$
.
For
![]() $\lambda \in \mathfrak {h}^\ast $
, we denote by
$\lambda \in \mathfrak {h}^\ast $
, we denote by
![]() $\Delta ^{\mathfrak {g}}(\lambda )$
the classical Verma module for
$\Delta ^{\mathfrak {g}}(\lambda )$
the classical Verma module for
![]() $\mathfrak {g}$
with highest weight
$\mathfrak {g}$
with highest weight
![]() $\lambda $
with respect to
$\lambda $
with respect to
![]() $\Delta ^+(\mathfrak {g},\mathfrak {h})$
, and by
$\Delta ^+(\mathfrak {g},\mathfrak {h})$
, and by
![]() $L(\lambda )$
the unique simple quotient of
$L(\lambda )$
the unique simple quotient of
![]() $\Delta ^{\mathfrak {g}}(\lambda )$
.
$\Delta ^{\mathfrak {g}}(\lambda )$
.
3.
 $\mathfrak {g}$
-Harish-Chandra modules for Takiff Lie algebras
$\mathfrak {g}$
-Harish-Chandra modules for Takiff Lie algebras
3.1. Setup
Fix a finite-dimensional semisimple Lie algebra
![]() $\mathfrak {g}$
over
$\mathfrak {g}$
over
![]() $\mathbb {C}$
. Define the associated Takiff Lie algebra
$\mathbb {C}$
. Define the associated Takiff Lie algebra
![]() $\mathfrak {T}$
as
$\mathfrak {T}$
as
where
 $\mathbb {D} = {\mathbb {C}[\mathbf {x}] / (\mathbf {x}^2)}$
is the algebra of dual numbers. The Lie bracket of
$\mathbb {D} = {\mathbb {C}[\mathbf {x}] / (\mathbf {x}^2)}$
is the algebra of dual numbers. The Lie bracket of
![]() $\mathfrak {T}$
is defined in the following way:
$\mathfrak {T}$
is defined in the following way:
 $$ \begin{align*} [v \otimes {\mathbf{x}}^i, w \otimes {\mathbf{x}}^j ] := [v,w] \otimes {\mathbf{x}}^{i+j}. \end{align*} $$
$$ \begin{align*} [v \otimes {\mathbf{x}}^i, w \otimes {\mathbf{x}}^j ] := [v,w] \otimes {\mathbf{x}}^{i+j}. \end{align*} $$
We identify
![]() $\mathfrak {g}$
with the subalgebra
$\mathfrak {g}$
with the subalgebra
![]() $\mathfrak {g} \otimes 1 \subseteq \mathfrak {T}$
, and denote by
$\mathfrak {g} \otimes 1 \subseteq \mathfrak {T}$
, and denote by
![]() $\bar {\mathfrak {g}} = \mathfrak {g} \otimes {\mathbf {x}} \subseteq \mathfrak {T}$
. Then,
$\bar {\mathfrak {g}} = \mathfrak {g} \otimes {\mathbf {x}} \subseteq \mathfrak {T}$
. Then,
![]() $\bar {\mathfrak {g}}$
is a commutative ideal in
$\bar {\mathfrak {g}}$
is a commutative ideal in
![]() $\mathfrak {T}$
, and
$\mathfrak {T}$
, and
![]() $\mathfrak {T} \cong \mathfrak {g} \ltimes \bar {\mathfrak {g}}$
(the semidirect product given by the adjoint action of
$\mathfrak {T} \cong \mathfrak {g} \ltimes \bar {\mathfrak {g}}$
(the semidirect product given by the adjoint action of
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() $\bar {\mathfrak {g}}$
). For
$\bar {\mathfrak {g}}$
). For
![]() $v \in \mathfrak {g}$
, we denote by
$v \in \mathfrak {g}$
, we denote by
![]() $\bar {v} = v \otimes {\mathbf {x}} \in \bar {\mathfrak {g}}$
.
$\bar {v} = v \otimes {\mathbf {x}} \in \bar {\mathfrak {g}}$
.
Observe that the nilradical of
![]() $\mathfrak {T}$
is
$\mathfrak {T}$
is
![]() $\operatorname {\mathrm {Nrad}}(\mathfrak {T}) = [\mathfrak {T},\bar {\mathfrak {g}}]=\bar {\mathfrak {g}}$
. This means that
$\operatorname {\mathrm {Nrad}}(\mathfrak {T}) = [\mathfrak {T},\bar {\mathfrak {g}}]=\bar {\mathfrak {g}}$
. This means that
![]() $\bar {\mathfrak {g}}$
must necessarily annihilate any simple finite-dimensional
$\bar {\mathfrak {g}}$
must necessarily annihilate any simple finite-dimensional
![]() $\mathfrak {T}$
-module.
$\mathfrak {T}$
-module.
In the triangular decomposition (1) for
![]() $\mathfrak {T}$
, we have
$\mathfrak {T}$
, we have
 $\tilde {\mathfrak {h}} = \mathfrak {h} \oplus \bar {\mathfrak {h}}$
and
$\tilde {\mathfrak {h}} = \mathfrak {h} \oplus \bar {\mathfrak {h}}$
and
![]() $\tilde {\mathfrak {n}}_\pm = \mathfrak {n}_\pm \oplus \bar {\mathfrak {n}}_\pm $
. We want to note that this is also a triangular decomposition in the sense of Reference Wilson[52]. A simplicity criterion for Verma modules over
$\tilde {\mathfrak {n}}_\pm = \mathfrak {n}_\pm \oplus \bar {\mathfrak {n}}_\pm $
. We want to note that this is also a triangular decomposition in the sense of Reference Wilson[52]. A simplicity criterion for Verma modules over
![]() $\mathfrak {T}$
can be found in [Reference Wilson52, Theorem 7.1].
$\mathfrak {T}$
can be found in [Reference Wilson52, Theorem 7.1].
3.2. Purely Takiff part of the center
The universal enveloping algebra
![]() $U(\mathfrak {T})$
is free as a module over its center
$U(\mathfrak {T})$
is free as a module over its center
![]() $Z(\mathfrak {T})$
(see [Reference Andersen and Stroppel2
Reference Arkhipov3]–[Reference Geoffriau25]). In case
$Z(\mathfrak {T})$
(see [Reference Andersen and Stroppel2
Reference Arkhipov3]–[Reference Geoffriau25]). In case
![]() $\mathfrak {g}$
is of type A, algebraically independent generators of the center are given explicitly in Reference Molev, Doebner, Nattermann and Scherer[45].
$\mathfrak {g}$
is of type A, algebraically independent generators of the center are given explicitly in Reference Molev, Doebner, Nattermann and Scherer[45].
Proposition 5. There is an isomorphism of algebras
Proof. This is clear since
![]() $U(\mathfrak {g}) \cong U(\bar {\mathfrak {g}})$
as
$U(\mathfrak {g}) \cong U(\bar {\mathfrak {g}})$
as
![]() $\mathfrak {g}$
-modules with respect to the adjoint action. By taking
$\mathfrak {g}$
-modules with respect to the adjoint action. By taking
![]() $\mathfrak {g}$
-invariants, we get (3).
$\mathfrak {g}$
-invariants, we get (3).
It is easy to see that the isomorphism can be obtained by putting bars on all Lie algebra elements that appear in an expression in a fixed PBW-basis of elements from
![]() $Z(\mathfrak {g})$
. Hence, we denote the right-hand side of (3) by
$Z(\mathfrak {g})$
. Hence, we denote the right-hand side of (3) by
 $\overline {Z(\mathfrak {g})}$
. This will be referred to as the purely Takiff part of the center
$\overline {Z(\mathfrak {g})}$
. This will be referred to as the purely Takiff part of the center
![]() $Z(\mathfrak {T})$
. The full center
$Z(\mathfrak {T})$
. The full center
![]() $Z(\mathfrak {T})$
is, in general, bigger than
$Z(\mathfrak {T})$
is, in general, bigger than
 $\overline {Z(\mathfrak {g})}$
(see Reference Molev, Doebner, Nattermann and Scherer[45]).
$\overline {Z(\mathfrak {g})}$
(see Reference Molev, Doebner, Nattermann and Scherer[45]).
3.3. Universal modules
Fix a weight
![]() $\lambda \in \mathfrak {h}^\ast $
which is dominant (i.e.,
$\lambda \in \mathfrak {h}^\ast $
which is dominant (i.e.,
![]() $\langle \lambda ,\alpha \rangle \geq 0$
for all positive roots
$\langle \lambda ,\alpha \rangle \geq 0$
for all positive roots
![]() $\alpha $
) and integral (i.e.,
$\alpha $
) and integral (i.e.,
![]() $\langle \lambda ,\alpha \rangle \in \mathbb {Z}$
for all positive roots
$\langle \lambda ,\alpha \rangle \in \mathbb {Z}$
for all positive roots
![]() $\alpha $
). Note that by these conventions,
$\alpha $
). Note that by these conventions,
![]() $\lambda $
is automatically regular with respect to the dot-action. These conditions are sufficient and necessary for the simple highest weight
$\lambda $
is automatically regular with respect to the dot-action. These conditions are sufficient and necessary for the simple highest weight
![]() $\mathfrak {g}$
-module
$\mathfrak {g}$
-module
![]() $L(\lambda )$
to be finite-dimensional (cf. [Reference Humphreys30, Chapter VI]). Define
$L(\lambda )$
to be finite-dimensional (cf. [Reference Humphreys30, Chapter VI]). Define
 $$ \begin{align*} Q(\lambda) := \operatorname{\mathrm{Ind}}_{\mathfrak{g}}^{\mathfrak{T}} L(\lambda) = U(\mathfrak{T}) \mathbin{\mathop{\otimes}\limits_{U(\mathfrak{g})}} L(\lambda) \cong U(\bar{\mathfrak{g}}) \mathbin{\mathop{\otimes}\limits_{\mathbb{C}}} L(\lambda). \end{align*} $$
$$ \begin{align*} Q(\lambda) := \operatorname{\mathrm{Ind}}_{\mathfrak{g}}^{\mathfrak{T}} L(\lambda) = U(\mathfrak{T}) \mathbin{\mathop{\otimes}\limits_{U(\mathfrak{g})}} L(\lambda) \cong U(\bar{\mathfrak{g}}) \mathbin{\mathop{\otimes}\limits_{\mathbb{C}}} L(\lambda). \end{align*} $$
The following fact is known, but for convenience of the reader, we provide a proof.
Proposition 6 [Reference Knapp35, Proposition 6.5]
We have
 $$ \begin{align} Q(\lambda) \cong Q(0) \mathbin{\mathop{\otimes}\limits_{\mathbb{C}}} L(\lambda), \end{align} $$
$$ \begin{align} Q(\lambda) \cong Q(0) \mathbin{\mathop{\otimes}\limits_{\mathbb{C}}} L(\lambda), \end{align} $$
where we consider
![]() $L(\lambda )$
as a
$L(\lambda )$
as a
![]() $\mathfrak {T}$
-module with the trivial
$\mathfrak {T}$
-module with the trivial
![]() $\bar {\mathfrak {g}}$
-action, and the tensor product is that of
$\bar {\mathfrak {g}}$
-action, and the tensor product is that of
![]() $\mathfrak {T}$
-modules.
$\mathfrak {T}$
-modules.
Proof. For any
![]() $\mathfrak {T}$
-module X, we have
$\mathfrak {T}$
-module X, we have
 $$ \begin{align*} \operatorname{\mathrm{Hom}}_{\mathfrak{T}}\left( Q(\lambda),X \right) &\cong \operatorname{\mathrm{Hom}}_{\mathfrak{T}}\left( \operatorname{\mathrm{Ind}}_{\mathfrak{g}}^{\mathfrak{T}} L(\lambda),X \right) \\ & \cong \operatorname{\mathrm{Hom}}_{\mathfrak{g}}\left( L(\lambda),X \right) \\ & \cong \operatorname{\mathrm{Hom}}_{\mathfrak{g}}\left( L(0) , \operatorname{\mathrm{Hom}}_{\mathbb{C}}\left( L(\lambda),X \right) \right) \\ & \cong \operatorname{\mathrm{Hom}}_{\mathfrak{T}}\left( \operatorname{\mathrm{Ind}}_{\mathfrak{g}}^{\mathfrak{T}} L(0), \operatorname{\mathrm{Hom}}_{\mathbb{C}}\left( L(\lambda),X \right) \right) \\ & \cong \operatorname{\mathrm{Hom}}_{\mathfrak{T}}\left( Q(0) \mathbin{\mathop{\otimes}\limits_{\mathbb{C}}} L(\lambda), X \right), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hom}}_{\mathfrak{T}}\left( Q(\lambda),X \right) &\cong \operatorname{\mathrm{Hom}}_{\mathfrak{T}}\left( \operatorname{\mathrm{Ind}}_{\mathfrak{g}}^{\mathfrak{T}} L(\lambda),X \right) \\ & \cong \operatorname{\mathrm{Hom}}_{\mathfrak{g}}\left( L(\lambda),X \right) \\ & \cong \operatorname{\mathrm{Hom}}_{\mathfrak{g}}\left( L(0) , \operatorname{\mathrm{Hom}}_{\mathbb{C}}\left( L(\lambda),X \right) \right) \\ & \cong \operatorname{\mathrm{Hom}}_{\mathfrak{T}}\left( \operatorname{\mathrm{Ind}}_{\mathfrak{g}}^{\mathfrak{T}} L(0), \operatorname{\mathrm{Hom}}_{\mathbb{C}}\left( L(\lambda),X \right) \right) \\ & \cong \operatorname{\mathrm{Hom}}_{\mathfrak{T}}\left( Q(0) \mathbin{\mathop{\otimes}\limits_{\mathbb{C}}} L(\lambda), X \right), \end{align*} $$
where we have used the fact that the induction is left adjoint to the forgetful functor, as well as the standard hom-tensor duality for Lie algebra modules. This finishes the proof.
Proposition 7. We have the following isomorphism of algebras:
 $$ \begin{align*} \operatorname{\mathrm{End}}(Q(0)) \cong \overline{Z(\mathfrak{g})}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{End}}(Q(0)) \cong \overline{Z(\mathfrak{g})}. \end{align*} $$
Proof. The module
![]() $Q(0)$
is generated by
$Q(0)$
is generated by
![]() $1 \otimes 1$
by construction, so any endomorphism of
$1 \otimes 1$
by construction, so any endomorphism of
![]() $Q(0)$
is uniquely determined by the image of
$Q(0)$
is uniquely determined by the image of
![]() $1 \otimes 1$
. Denote this image by
$1 \otimes 1$
. Denote this image by
![]() $u \otimes 1$
, for some
$u \otimes 1$
, for some
![]() $u \in U(\bar {\mathfrak {g}})$
. The element
$u \in U(\bar {\mathfrak {g}})$
. The element
![]() $u\otimes 1$
generates the trivial
$u\otimes 1$
generates the trivial
![]() $\mathfrak {g}$
-submodule (since
$\mathfrak {g}$
-submodule (since
![]() $1\otimes 1$
does), so u must commute with
$1\otimes 1$
does), so u must commute with
![]() $\mathfrak {g}$
. Of course, u commutes with
$\mathfrak {g}$
. Of course, u commutes with
![]() $\bar {\mathfrak {g}}$
. Hence,
$\bar {\mathfrak {g}}$
. Hence,
 $u \in Z(\mathfrak {T}) \cap U(\bar {\mathfrak {g}}) = \overline {Z(\mathfrak {g})}$
.
$u \in Z(\mathfrak {T}) \cap U(\bar {\mathfrak {g}}) = \overline {Z(\mathfrak {g})}$
.
Conversely, any
 $u \in \overline {Z(\mathfrak {g})}$
, being central, defines an endomorphism of
$u \in \overline {Z(\mathfrak {g})}$
, being central, defines an endomorphism of
![]() $Q(0)$
. This endomorphism maps
$Q(0)$
. This endomorphism maps
![]() $1 \otimes 1$
to
$1 \otimes 1$
to
![]() $u \otimes 1$
. The claim follows.
$u \otimes 1$
. The claim follows.
For an algebra homomorphism
 $\chi \colon \overline {Z(\mathfrak {g})} \to \mathbb {C}$
, consider the corresponding universal module
$\chi \colon \overline {Z(\mathfrak {g})} \to \mathbb {C}$
, consider the corresponding universal module

where
![]() $\mathbf {m}_\chi $
is the maximal ideal in
$\mathbf {m}_\chi $
is the maximal ideal in
 $\overline {Z(\mathfrak {g})}$
corresponding to
$\overline {Z(\mathfrak {g})}$
corresponding to
![]() $\chi $
. On
$\chi $
. On
![]() $Q(\lambda ,\chi )$
, the purely Takiff part of the center acts via the scalars prescribed by
$Q(\lambda ,\chi )$
, the purely Takiff part of the center acts via the scalars prescribed by
![]() $\chi $
. Observe that from (4) and the right exactness of tensor product, we have
$\chi $
. Observe that from (4) and the right exactness of tensor product, we have
For finite-dimensional simple
![]() $\mathfrak {g}$
-modules
$\mathfrak {g}$
-modules
![]() $L(\mu )$
,
$L(\mu )$
,
![]() $L(\nu )$
, and
$L(\nu )$
, and
![]() $L(\lambda )$
, denote by
$L(\lambda )$
, denote by
 $l_{\nu ,\lambda }^\mu $
the Littlewood–Richardson coefficient, that is, the multiplicity of
$l_{\nu ,\lambda }^\mu $
the Littlewood–Richardson coefficient, that is, the multiplicity of
![]() $L(\mu )$
in
$L(\mu )$
in
![]() $L(\nu ) \otimes L(\lambda )$
.
$L(\nu ) \otimes L(\lambda )$
.
Proposition 8.
-
(a) Let
 $\lambda $
,
$\lambda $
,
 $\chi $
be as before. The module
$\chi $
be as before. The module
 $Q(\lambda ,\chi )$
is a
$Q(\lambda ,\chi )$
is a
 $\mathfrak {g}$
-Harish-Chandra module, and the multiplicities are given as follows: (6)
$\mathfrak {g}$
-Harish-Chandra module, and the multiplicities are given as follows: (6) $$ \begin{align} [Q(\lambda,\chi) \colon L(\mu)] = \sum_{\nu} \dim L(\nu)_0 \cdot l_{\nu,\lambda}^\mu < \infty. \end{align} $$
$$ \begin{align} [Q(\lambda,\chi) \colon L(\mu)] = \sum_{\nu} \dim L(\nu)_0 \cdot l_{\nu,\lambda}^\mu < \infty. \end{align} $$
-
(b) Let V be any simple
 $\mathfrak {T}$
-module that has some finite-dimensional
$\mathfrak {T}$
-module that has some finite-dimensional
 $L(\lambda )$
as a simple
$L(\lambda )$
as a simple
 $\mathfrak {g}$
-submodule. Then, V is a quotient of
$\mathfrak {g}$
-submodule. Then, V is a quotient of
 $Q(\lambda ,\chi )$
for a unique
$Q(\lambda ,\chi )$
for a unique
 $\chi $
. In particular, V is a
$\chi $
. In particular, V is a
 $\mathfrak {g}$
-Harish-Chandra module, and (6) gives an upper bound for the multiplicities of its
$\mathfrak {g}$
-Harish-Chandra module, and (6) gives an upper bound for the multiplicities of its
 $\mathfrak {g}$
-types.
$\mathfrak {g}$
-types.
Proof.
-
(a) Suppose first that
 $\lambda =0$
. Then, as a
$\lambda =0$
. Then, as a
 $\mathfrak {g}$
-module,
$\mathfrak {g}$
-module,
 $Q(0)$
is isomorphic to
$Q(0)$
is isomorphic to
 $U(\mathfrak {g})$
with respect to the adjoint action. Taking the
$U(\mathfrak {g})$
with respect to the adjoint action. Taking the
 $\chi $
-component of
$\chi $
-component of
 $Q(0)$
corresponds to factoring
$Q(0)$
corresponds to factoring
 $U(\mathfrak {g})$
by the ideal generated by the corresponding central character of
$U(\mathfrak {g})$
by the ideal generated by the corresponding central character of
 $Z(\mathfrak {g})$
. From Kostant’s theorem (see [Reference Jantzen32, Section 3.1]), it follows that
$Z(\mathfrak {g})$
. From Kostant’s theorem (see [Reference Jantzen32, Section 3.1]), it follows that
 $Q(0)$
decomposes as direct sum of finite-dimensional
$Q(0)$
decomposes as direct sum of finite-dimensional
 $\mathfrak {g}$
-submodules, and that
$\mathfrak {g}$
-submodules, and that
 $[Q(0,\chi ) \colon L(\mu )] = \dim L(\mu )_0$
. The general statement now follows from (5).
$[Q(0,\chi ) \colon L(\mu )] = \dim L(\mu )_0$
. The general statement now follows from (5).Note that the value in (6) is finite, since, for fixed
 $\mu $
and
$\mu $
and
 $\lambda $
, the value
$\lambda $
, the value
 $l^{\mu }_{\nu ,\lambda }$
is nonzero only for finitely many
$l^{\mu }_{\nu ,\lambda }$
is nonzero only for finitely many
 $\nu $
.
$\nu $
. -
(b) This follows from Schur’s Lemma by adjunction.
Corollary 9. Given
![]() $\chi $
, there exists a unique simple
$\chi $
, there exists a unique simple
![]() $\mathfrak {T}$
-module V which contains
$\mathfrak {T}$
-module V which contains
![]() $L(0)$
as a
$L(0)$
as a
![]() $\mathfrak {g}$
-submodule and has the Takiff part of the central character equal to
$\mathfrak {g}$
-submodule and has the Takiff part of the central character equal to
![]() $\chi $
. Moreover, V is a
$\chi $
. Moreover, V is a
![]() $\mathfrak {g}$
-Harish-Chandra module. Furthermore, if
$\mathfrak {g}$
-Harish-Chandra module. Furthermore, if
![]() $\chi $
does not correspond to the trivial
$\chi $
does not correspond to the trivial
![]() $\mathfrak {T}$
-module, then V is infinite-dimensional.
$\mathfrak {T}$
-module, then V is infinite-dimensional.
Proof. By Proposition 8, the module
![]() $Q(0,\chi )$
has a unique occurrence of
$Q(0,\chi )$
has a unique occurrence of
![]() $L(0)$
, and is generated by it. Therefore, the sum all its submodules not containing
$L(0)$
, and is generated by it. Therefore, the sum all its submodules not containing
![]() $L(0)$
as a composition factor is the unique maximal submodule; denote it by N. It follows that
$L(0)$
as a composition factor is the unique maximal submodule; denote it by N. It follows that
 is the unique simple quotient of
is the unique simple quotient of
![]() $Q(0,\chi )$
.
$Q(0,\chi )$
.
Suppose now that V is finite-dimensional. The nilradical
![]() $\bar {\mathfrak {g}}$
must act trivially on it. Because of simplicity, we must have
$\bar {\mathfrak {g}}$
must act trivially on it. Because of simplicity, we must have
![]() $V=L(0)$
, which is a contradiction.
$V=L(0)$
, which is a contradiction.
Conjecture 10. For a generic
![]() $\;\chi $
, the module
$\;\chi $
, the module
![]() $Q(0,\chi )$
is simple.
$Q(0,\chi )$
is simple.
We will prove this conjecture for the Takiff
![]() $\mathfrak {sl}_2$
case in Section 4. We will also prove it for the Schrödinger Lie algebra in Section 5 (but, strictly speaking, it is not a special instance of the above conjecture). This is the starting point in our classification of
$\mathfrak {sl}_2$
case in Section 4. We will also prove it for the Schrödinger Lie algebra in Section 5 (but, strictly speaking, it is not a special instance of the above conjecture). This is the starting point in our classification of
![]() $\mathfrak {g}$
-Harish-Chandra modules for these Lie algebras.
$\mathfrak {g}$
-Harish-Chandra modules for these Lie algebras.
4.
 $\mathfrak {sl}_2$
-Harish-Chandra modules for the Takiff
$\mathfrak {sl}_2$
-Harish-Chandra modules for the Takiff
 $\mathfrak {sl}_2$
$\mathfrak {sl}_2$
4.1. Setup
For this section, we fix the Takiff Lie algebra associated to
![]() $\mathfrak {g} := \mathfrak {sl}_2$
:
$\mathfrak {g} := \mathfrak {sl}_2$
:
We use the usual notation
![]() $f,h,e$
for the standard basis elements of
$f,h,e$
for the standard basis elements of
![]() $\mathfrak {sl}_2$
, and
$\mathfrak {sl}_2$
, and
![]() $\bar {f}, \bar {h}, \bar {e}$
for their counterparts in the ideal
$\bar {f}, \bar {h}, \bar {e}$
for their counterparts in the ideal
![]() $\mathfrak {\overline {sl}}_2$
.
$\mathfrak {\overline {sl}}_2$
.
Our classification of simple
![]() $\mathfrak {g}$
-Harish-Chandra modules for the Takiff
$\mathfrak {g}$
-Harish-Chandra modules for the Takiff
![]() $\mathfrak {sl}_2$
should be, of course, deducible from the classification of all simple weight modules given in Reference Bavula and Lu[6]. However, our approach is completely different and, unlike the approach of Reference Bavula and Lu[6], has clear potential for generalization to other Lie algebras. Moreover, our description of simple
$\mathfrak {sl}_2$
should be, of course, deducible from the classification of all simple weight modules given in Reference Bavula and Lu[6]. However, our approach is completely different and, unlike the approach of Reference Bavula and Lu[6], has clear potential for generalization to other Lie algebras. Moreover, our description of simple
![]() $\mathfrak {g}$
-Harish-Chandra modules is much more explicit, and it provides a connection to highest weight theory for
$\mathfrak {g}$
-Harish-Chandra modules is much more explicit, and it provides a connection to highest weight theory for
![]() $\mathfrak {T}$
and utilizes the use of analogues of projective functors for
$\mathfrak {T}$
and utilizes the use of analogues of projective functors for
![]() $\mathfrak {T}$
.
$\mathfrak {T}$
.
The center
![]() $Z(\mathfrak {T})$
is a polynomial algebra generated by two algebraically independent elements (see Reference Molev, Doebner, Nattermann and Scherer[45]):
$Z(\mathfrak {T})$
is a polynomial algebra generated by two algebraically independent elements (see Reference Molev, Doebner, Nattermann and Scherer[45]):
 $$ \begin{align} & C = \bar{h}h + 2\bar{f}e + 2\bar{e}f, \nonumber\\ & \bar{C} = \bar{h}^2 + 4\bar{f} \bar{e}. \end{align} $$
$$ \begin{align} & C = \bar{h}h + 2\bar{f}e + 2\bar{e}f, \nonumber\\ & \bar{C} = \bar{h}^2 + 4\bar{f} \bar{e}. \end{align} $$
The purely Takiff part of the center is, of course,
 $\overline {Z(\mathfrak {g})} = \mathbb {C}[\bar {C}]$
. So, a homomorphism
$\overline {Z(\mathfrak {g})} = \mathbb {C}[\bar {C}]$
. So, a homomorphism
 $\chi \colon \overline {Z(\mathfrak {g})} \to \mathbb {C}$
is uniquely determined by the value
$\chi \colon \overline {Z(\mathfrak {g})} \to \mathbb {C}$
is uniquely determined by the value
 $\chi (\bar {C})$
, which can be an arbitrary complex number. In the remainder, we write
$\chi (\bar {C})$
, which can be an arbitrary complex number. In the remainder, we write
![]() $\chi $
for
$\chi $
for
 $\chi (\bar {C})$
, for the sake of brevity.
$\chi (\bar {C})$
, for the sake of brevity.
4.2. Universal modules
We can describe
![]() $Q(0,\chi )$
very explicitly.
$Q(0,\chi )$
very explicitly.
Lemma 11.
-
(a) As
 $\mathfrak {T}$
-modules, we have
$\mathfrak {T}$
-modules, we have
 $Q(0) \cong U(\bar {\mathfrak {g}})$
and
$Q(0) \cong U(\bar {\mathfrak {g}})$
and
 , where
, where
 $\mathfrak {g}$
acts by the adjoint action, and
$\mathfrak {g}$
acts by the adjoint action, and
 $\bar {\mathfrak {g}}$
by the left multiplication.
$\bar {\mathfrak {g}}$
by the left multiplication. -
(b) The set
 $\big \{\bar {f}^i \bar {h}^\epsilon \bar {e}^j \colon i,j \geq 0, \ \epsilon \in \{0,1\}\big \}$
is a basis for
$\big \{\bar {f}^i \bar {h}^\epsilon \bar {e}^j \colon i,j \geq 0, \ \epsilon \in \{0,1\}\big \}$
is a basis for
 $Q(0,\chi )$
.
$Q(0,\chi )$
. -
(c) As a
 $\mathfrak {g}$
-module,
$\mathfrak {g}$
-module,
 $Q(0,\chi ) \cong \bigoplus _{k\geq 0} L(2k)$
. Moreover,
$Q(0,\chi ) \cong \bigoplus _{k\geq 0} L(2k)$
. Moreover,
 $\bar {e}^k$
is the highest weight vector in
$\bar {e}^k$
is the highest weight vector in
 $L(2k)$
.
$L(2k)$
. -
(d) C acts as zero on
 $Q(0)$
and on every
$Q(0)$
and on every
 $Q(0,\chi )$
.
$Q(0,\chi )$
.
Proof. The first claim is clear. The second one follows from the PBW basis in
![]() $U(\mathfrak {g})$
and the relation
$U(\mathfrak {g})$
and the relation
![]() $\bar {h}^2 = -4\bar {f} \bar {e} + \chi $
in the quotient.
$\bar {h}^2 = -4\bar {f} \bar {e} + \chi $
in the quotient.
The decomposition in the third claim is given by Kostant’s theorem (see [Reference Jantzen32, Section 3.1]). Since
![]() $\bar {e}^k$
is of weight
$\bar {e}^k$
is of weight
![]() $2k$
and annihilated by e, it must be a highest weight vector of a
$2k$
and annihilated by e, it must be a highest weight vector of a
![]() $\mathfrak {g}$
-submodule isomorphic to
$\mathfrak {g}$
-submodule isomorphic to
![]() $L(2k)$
, which, we know, occurs uniquely in
$L(2k)$
, which, we know, occurs uniquely in
![]() $Q(0,\chi )$
.
$Q(0,\chi )$
.
The last claim follows from the definitions by a direct calculation.
The action of
![]() $\mathfrak {T}$
on
$\mathfrak {T}$
on
![]() $U(\bar {\mathfrak {g}})$
and its quotients will be denoted by
$U(\bar {\mathfrak {g}})$
and its quotients will be denoted by
![]() $\circ $
, in order not to confuse it with the multiplication
$\circ $
, in order not to confuse it with the multiplication
![]() $\cdot $
in the enveloping algebra. These coincide for
$\cdot $
in the enveloping algebra. These coincide for
![]() $\bar {\mathfrak {g}}$
but not for
$\bar {\mathfrak {g}}$
but not for
![]() $\mathfrak {g}$
, where the action is adjoint. Note that
$\mathfrak {g}$
, where the action is adjoint. Note that
![]() $U(\bar {\mathfrak {g}})$
is not closed under the left multiplication with the whole
$U(\bar {\mathfrak {g}})$
is not closed under the left multiplication with the whole
![]() $\mathfrak {T}$
.
$\mathfrak {T}$
.
Theorem 12. The module
![]() $Q(0,\chi )$
is simple if and only if
$Q(0,\chi )$
is simple if and only if
![]() $\chi \neq 0$
.
$\chi \neq 0$
.
The module
![]() $Q(0,0)$
has infinite length, and a
$Q(0,0)$
has infinite length, and a
![]() $\mathfrak {T}$
-filtration whose composition factors are
$\mathfrak {T}$
-filtration whose composition factors are
![]() $L(0), L(2), L(4) \ldots $
with the trivial action of
$L(0), L(2), L(4) \ldots $
with the trivial action of
![]() $\bar {\mathfrak {g}}$
.
$\bar {\mathfrak {g}}$
.
Proof. Assume
![]() $\chi \neq 0$
, and let
$\chi \neq 0$
, and let
![]() $V \subseteq Q(0,\chi )$
be nonzero submodule. Take k to be the smallest nonnegative integer such that
$V \subseteq Q(0,\chi )$
be nonzero submodule. Take k to be the smallest nonnegative integer such that
![]() $L(2k) \subseteq V$
. If
$L(2k) \subseteq V$
. If
![]() $k=0$
, then
$k=0$
, then
![]() $V = Q(0,\chi )$
, since
$V = Q(0,\chi )$
, since
![]() $L(0)$
generates
$L(0)$
generates
![]() $Q(0,\chi )$
, and we are done. So, let us assume now
$Q(0,\chi )$
, and we are done. So, let us assume now
![]() $k \geq 1$
. We have
$k \geq 1$
. We have
![]() $\bar {e}^k \in V$
, so if we find an element from
$\bar {e}^k \in V$
, so if we find an element from
![]() $U(\mathfrak {T})$
that maps
$U(\mathfrak {T})$
that maps
![]() $\bar {e}^k \in V$
to
$\bar {e}^k \in V$
to
![]() $\bar {e}^{k-1}$
, we will get a contradiction. That element can be taken as
$\bar {e}^{k-1}$
, we will get a contradiction. That element can be taken as
 $\frac {1}{k\chi }(4k \bar {f} - \bar {h}f)$
, namely:
$\frac {1}{k\chi }(4k \bar {f} - \bar {h}f)$
, namely:
 $$ \begin{align*} (4k \bar{f} - \bar{h}f) \circ \bar{e}^k &= 4k\bar{f}\bar{e}^k - \bar{h}[f,\bar{e}^k] \\ &= 4k\bar{f}\bar{e}^k + k \bar{h}^2\bar{e}^{k-1} \\ &= 4k\bar{f}\bar{e}^k + k (-4\bar{f} \bar{e} + \chi)\bar{e}^{k-1} \\ &= k\chi \bar{e}^{k-1}. \end{align*} $$
$$ \begin{align*} (4k \bar{f} - \bar{h}f) \circ \bar{e}^k &= 4k\bar{f}\bar{e}^k - \bar{h}[f,\bar{e}^k] \\ &= 4k\bar{f}\bar{e}^k + k \bar{h}^2\bar{e}^{k-1} \\ &= 4k\bar{f}\bar{e}^k + k (-4\bar{f} \bar{e} + \chi)\bar{e}^{k-1} \\ &= k\chi \bar{e}^{k-1}. \end{align*} $$
We conclude that
![]() $Q(0,\chi )$
is simple.
$Q(0,\chi )$
is simple.
For the converse, assume
![]() $\chi = 0$
. We will show that for any
$\chi = 0$
. We will show that for any
![]() $k \geq 0$
, the subspace
$k \geq 0$
, the subspace
![]() $Q_k := \oplus _{t \geq k} L(2t)$
is a submodule. From this, the theorem will follow.
$Q_k := \oplus _{t \geq k} L(2t)$
is a submodule. From this, the theorem will follow.
Let us first prove that
![]() $L(2k)$
is equal to the span of
$L(2k)$
is equal to the span of
 $\big \{\bar {f}^i \bar {h}^\epsilon \bar {e}^j \colon \epsilon \in \{0,1\}, i+\epsilon + j = k \big \}$
. This set contains
$\big \{\bar {f}^i \bar {h}^\epsilon \bar {e}^j \colon \epsilon \in \{0,1\}, i+\epsilon + j = k \big \}$
. This set contains
![]() $\bar {e}^k$
, so it is enough to see that it is stable under f. We calculate the two cases whether
$\bar {e}^k$
, so it is enough to see that it is stable under f. We calculate the two cases whether
![]() $\epsilon $
is
$\epsilon $
is
![]() $0$
or
$0$
or
![]() $1$
separately:
$1$
separately:
 $$ \begin{align*} f \circ \bar{f}^i \bar{e}^j &= \bar{f}^i [f,\bar{e}^j] = - j \bar{f}^i \bar{h} \bar{e}^{j-1}, \\[.5em] f \circ \bar{f}^i \bar{h} \bar{e}^j &= \bar{f}^i [f,\bar{h}]\bar{e}^j + \bar{f}^i \bar{h} [f,\bar{e}^j] \\ &= 2\bar{f}^{i+1} \bar{e}^j -j \bar{f}^i \bar{h}^2 \bar{e}^{j-1} \\ &= 2\bar{f}^{i+1} \bar{e}^j +4j \bar{f}^{i+1} \bar{e}^{j} \\ &= (4j+2)\bar{f}^{i+1} \bar{e}^j. \end{align*} $$
$$ \begin{align*} f \circ \bar{f}^i \bar{e}^j &= \bar{f}^i [f,\bar{e}^j] = - j \bar{f}^i \bar{h} \bar{e}^{j-1}, \\[.5em] f \circ \bar{f}^i \bar{h} \bar{e}^j &= \bar{f}^i [f,\bar{h}]\bar{e}^j + \bar{f}^i \bar{h} [f,\bar{e}^j] \\ &= 2\bar{f}^{i+1} \bar{e}^j -j \bar{f}^i \bar{h}^2 \bar{e}^{j-1} \\ &= 2\bar{f}^{i+1} \bar{e}^j +4j \bar{f}^{i+1} \bar{e}^{j} \\ &= (4j+2)\bar{f}^{i+1} \bar{e}^j. \end{align*} $$
From this description of
![]() $L(2k)$
, one easily checks that
$L(2k)$
, one easily checks that
![]() $\bar {f}, \bar {h},\bar {e}$
map
$\bar {f}, \bar {h},\bar {e}$
map
![]() $L(2k)$
to
$L(2k)$
to
![]() $L(2k+2)$
. From this, it follows that
$L(2k+2)$
. From this, it follows that
![]() $Q_k$
is a submodule.
$Q_k$
is a submodule.
Remark 13 (Sketch of an alternative proof of simplicity of
 $Q(0,\chi )$
)
$Q(0,\chi )$
)
Assume
![]() $\chi \neq 0$
, and suppose V is a
$\chi \neq 0$
, and suppose V is a
![]() $\mathfrak {T}$
-submodule of
$\mathfrak {T}$
-submodule of
![]() $Q(0,\chi )$
containing
$Q(0,\chi )$
containing
![]() $L(2k)$
, with
$L(2k)$
, with
![]() $k>0$
minimal. By applying
$k>0$
minimal. By applying
![]() $\bar {e}$
, we see that, as a
$\bar {e}$
, we see that, as a
![]() $\mathfrak {g}$
-module,
$\mathfrak {g}$
-module,
![]() $V \cong L(2k) \oplus L(2k+2) \oplus \ldots $
. This implies that the quotient
$V \cong L(2k) \oplus L(2k+2) \oplus \ldots $
. This implies that the quotient

is simple as a
![]() $\mathfrak {T}$
-module and is finite-dimensional. Since
$\mathfrak {T}$
-module and is finite-dimensional. Since
![]() $\bar {C}$
consists of elements from the nilradical of
$\bar {C}$
consists of elements from the nilradical of
![]() $\mathfrak {T}$
, it must act as zero on this quotient. This is a contradiction with
$\mathfrak {T}$
, it must act as zero on this quotient. This is a contradiction with
![]() $\chi \neq 0$
.
$\chi \neq 0$
.
To classify simple
![]() $\mathfrak {g}$
-Harish-Chandra modules, by (5) and Proposition 8(b), we should find all simple quotients of all tensor products of
$\mathfrak {g}$
-Harish-Chandra modules, by (5) and Proposition 8(b), we should find all simple quotients of all tensor products of
![]() $Q(0,\chi )$
with finite-dimensional
$Q(0,\chi )$
with finite-dimensional
![]() $\mathfrak {g}$
-modules. It is not easy to do this directly, so we establish a connection with Verma modules, and perform calculations there.
$\mathfrak {g}$
-modules. It is not easy to do this directly, so we establish a connection with Verma modules, and perform calculations there.
4.3. Verma modules
Verma modules for the Takiff
![]() $\mathfrak {sl}_2$
are studied in detail in Reference Mazorchuk and Söderberg[43]. Recall (2) and Proposition 4. Moreover, recall that
$\mathfrak {sl}_2$
are studied in detail in Reference Mazorchuk and Söderberg[43]. Recall (2) and Proposition 4. Moreover, recall that
 $\tilde {\mathfrak {h}} = \mathfrak {h} \oplus \bar {\mathfrak {h}}$
and
$\tilde {\mathfrak {h}} = \mathfrak {h} \oplus \bar {\mathfrak {h}}$
and
![]() $\tilde {\mathfrak {n}}_\pm = \mathfrak {n}_\pm \oplus \bar {\mathfrak {n}}_\pm $
. For a weight
$\tilde {\mathfrak {n}}_\pm = \mathfrak {n}_\pm \oplus \bar {\mathfrak {n}}_\pm $
. For a weight
 $\lambda \in \tilde {\mathfrak {h}}^\ast = \mathfrak {h}^\ast \oplus \bar {\mathfrak {h}}^\ast $
, we denote
$\lambda \in \tilde {\mathfrak {h}}^\ast = \mathfrak {h}^\ast \oplus \bar {\mathfrak {h}}^\ast $
, we denote
![]() $\lambda _1 := \lambda (h)$
and
$\lambda _1 := \lambda (h)$
and
 $\lambda _2 := \lambda (\bar {h})$
.
$\lambda _2 := \lambda (\bar {h})$
.
Proposition 14 ([Reference Mazorchuk and Söderberg43, Proposition 1] or [Reference Wilson52, Theorem 7.1])
The Verma module
![]() $\Delta (\lambda )$
is simple if and only if
$\Delta (\lambda )$
is simple if and only if
![]() $\lambda _2 \neq 0$
.
$\lambda _2 \neq 0$
.
The generators of the center C and
![]() $\bar {C}$
act on the Verma module
$\bar {C}$
act on the Verma module
![]() $\Delta (\lambda )$
as the scalars
$\Delta (\lambda )$
as the scalars
![]() $\lambda _2(\lambda _1+2)$
and
$\lambda _2(\lambda _1+2)$
and
![]() $\lambda _2^2$
, respectively (see (7)). Therefore, with our convection,
$\lambda _2^2$
, respectively (see (7)). Therefore, with our convection,
 $\chi = \lambda _2^2$
.
$\chi = \lambda _2^2$
.
Lemma 15. Nonisomorphic Verma modules
![]() $\Delta (\lambda )$
and
$\Delta (\lambda )$
and
![]() $\Delta (\lambda ')$
have the same central character if and only if either
$\Delta (\lambda ')$
have the same central character if and only if either
![]() $\lambda ^{\prime }_2=\lambda _2=0$
, or
$\lambda ^{\prime }_2=\lambda _2=0$
, or
![]() $\lambda ^{\prime }_2=-\lambda _2 \neq 0$
and
$\lambda ^{\prime }_2=-\lambda _2 \neq 0$
and
![]() $\lambda ^{\prime }_1 = -\lambda _1-4$
.
$\lambda ^{\prime }_1 = -\lambda _1-4$
.
Proof. From the explicit description of generators of the center, we get a system of equations
 $$ \begin{align*} \begin{cases} \lambda_2(\lambda_1+2)=\lambda_2'(\lambda_1'+2) \\ \lambda_2^2 = (\lambda_2')^2 \end{cases}\!\!, \end{align*} $$
$$ \begin{align*} \begin{cases} \lambda_2(\lambda_1+2)=\lambda_2'(\lambda_1'+2) \\ \lambda_2^2 = (\lambda_2')^2 \end{cases}\!\!, \end{align*} $$
which is easily solved.
Denote by
 $\Delta ^{\mathfrak {g}}(\mu ) = U(\mathfrak {g}) \mathbin {\mathop {\otimes }_{U(\mathfrak {b})}} \mathbb {C}_\mu $
the classical Verma module for
$\Delta ^{\mathfrak {g}}(\mu ) = U(\mathfrak {g}) \mathbin {\mathop {\otimes }_{U(\mathfrak {b})}} \mathbb {C}_\mu $
the classical Verma module for
![]() $\mathfrak {g}$
with highest weight
$\mathfrak {g}$
with highest weight
![]() $\mu \in \mathbb {C}$
, and by
$\mu \in \mathbb {C}$
, and by
![]() $P^{\mathfrak {g}}(\mu )$
its indecomposable projective cover in the category
$P^{\mathfrak {g}}(\mu )$
its indecomposable projective cover in the category
![]() $\mathcal {O}$
for
$\mathcal {O}$
for
![]() $\mathfrak {g}$
. Recall that, if
$\mathfrak {g}$
. Recall that, if
![]() $\mu \in \mathbb {Z}_{\geq 0}$
,
$\mu \in \mathbb {Z}_{\geq 0}$
,
![]() $P^{\mathfrak {g}}(-\mu -2)$
is the unique nontrivial extension of
$P^{\mathfrak {g}}(-\mu -2)$
is the unique nontrivial extension of
![]() $\Delta ^{\mathfrak {g}}(-\mu -2)$
by
$\Delta ^{\mathfrak {g}}(-\mu -2)$
by
![]() $\Delta ^{\mathfrak {g}}(\mu )$
, and that there are no extensions between other
$\Delta ^{\mathfrak {g}}(\mu )$
, and that there are no extensions between other
![]() $\Delta ^{\mathfrak {g}}$
’s (inside category
$\Delta ^{\mathfrak {g}}$
’s (inside category
![]() $\mathcal {O}$
).
$\mathcal {O}$
).
Lemma 16. As a
![]() $\mathfrak {g}$
-module,
$\mathfrak {g}$
-module,
![]() $\Delta (\lambda )$
has a filtration with subquotients isomorphic to the
$\Delta (\lambda )$
has a filtration with subquotients isomorphic to the
![]() $\mathfrak {g}$
-Verma modules
$\mathfrak {g}$
-Verma modules
![]() $\Delta ^{\mathfrak {g}}(\lambda _1 - 2k)$
,
$\Delta ^{\mathfrak {g}}(\lambda _1 - 2k)$
,
![]() $k = 0, 1, 2, \ldots $
.
$k = 0, 1, 2, \ldots $
.
If
![]() $\lambda _2 = 0$
or
$\lambda _2 = 0$
or
![]() $\lambda _1 \not \in \mathbb {Z}_{\geq 0}$
, then, as a
$\lambda _1 \not \in \mathbb {Z}_{\geq 0}$
, then, as a
![]() $\mathfrak {g}$
-module, we have
$\mathfrak {g}$
-module, we have
 $$ \begin{align*} \Delta(\lambda) \cong \bigoplus_{k \geq 0} \Delta^{\mathfrak{g}}(\lambda_1 - 2k). \end{align*} $$
$$ \begin{align*} \Delta(\lambda) \cong \bigoplus_{k \geq 0} \Delta^{\mathfrak{g}}(\lambda_1 - 2k). \end{align*} $$
Otherwise (i.e., if
![]() $\lambda _2 \neq 0$
and
$\lambda _2 \neq 0$
and
![]() $\lambda _1 \in \mathbb {Z}_{\geq 0}$
), we have, as
$\lambda _1 \in \mathbb {Z}_{\geq 0}$
), we have, as
![]() $\mathfrak {g}$
-modules,
$\mathfrak {g}$
-modules,
 $$ \begin{align*} \Delta(\lambda) \cong \begin{cases} \displaystyle \bigoplus_{k =1}^{\frac{\lambda_1}{2}+1} P^{\mathfrak{g}}(-2k) \oplus \bigoplus_{k \geq 2} \Delta^{\mathfrak{g}}(-\lambda_1 - 2k) &\colon \lambda_1 \text{ even}, \\ \displaystyle \Delta^{\mathfrak{g}}(-1)\oplus \bigoplus_{k =1}^{\frac{\lambda_1+1}{2}} P^{\mathfrak{g}}(-2k-1) \oplus \bigoplus_{k \geq 2} \Delta^{\mathfrak{g}}(-\lambda_1 - 2k) &\colon \lambda_1 \text{ odd}. \end{cases} \end{align*} $$
$$ \begin{align*} \Delta(\lambda) \cong \begin{cases} \displaystyle \bigoplus_{k =1}^{\frac{\lambda_1}{2}+1} P^{\mathfrak{g}}(-2k) \oplus \bigoplus_{k \geq 2} \Delta^{\mathfrak{g}}(-\lambda_1 - 2k) &\colon \lambda_1 \text{ even}, \\ \displaystyle \Delta^{\mathfrak{g}}(-1)\oplus \bigoplus_{k =1}^{\frac{\lambda_1+1}{2}} P^{\mathfrak{g}}(-2k-1) \oplus \bigoplus_{k \geq 2} \Delta^{\mathfrak{g}}(-\lambda_1 - 2k) &\colon \lambda_1 \text{ odd}. \end{cases} \end{align*} $$
Proof. Denote by
![]() $v_\lambda $
a basis element of
$v_\lambda $
a basis element of
![]() $\mathbb {C}_\lambda $
. Then,
$\mathbb {C}_\lambda $
. Then,
![]() $\Delta (\lambda )$
has a basis of weight vectors
$\Delta (\lambda )$
has a basis of weight vectors
 $\{ f^i \bar {f}^j v_\lambda \colon i,j \geq 0\}$
. A direct computation (with help of [Reference Humphreys30, Lemma 21.2] and its Takiff analogue, alternatively use [Reference Cai, Shen and Zhang12, Lemma 2.1]) shows that
$\{ f^i \bar {f}^j v_\lambda \colon i,j \geq 0\}$
. A direct computation (with help of [Reference Humphreys30, Lemma 21.2] and its Takiff analogue, alternatively use [Reference Cai, Shen and Zhang12, Lemma 2.1]) shows that
 $$ \begin{align} e \cdot f^i \bar{f}^j v_\lambda &= [e , f^i] \bar{f}^j v_\lambda + f^i [e,\bar{f}^j ] v_\lambda \\ \nonumber &= i(\lambda_1 - i -2j +1) f^{i-1} \bar{f}^j v_\lambda + j \lambda_2 f^i \bar{f}^{j-1} v_\lambda. \end{align} $$
$$ \begin{align} e \cdot f^i \bar{f}^j v_\lambda &= [e , f^i] \bar{f}^j v_\lambda + f^i [e,\bar{f}^j ] v_\lambda \\ \nonumber &= i(\lambda_1 - i -2j +1) f^{i-1} \bar{f}^j v_\lambda + j \lambda_2 f^i \bar{f}^{j-1} v_\lambda. \end{align} $$
This implies that the required filtration is given by the degree of
![]() $\bar {f}$
. The subquotients are given by the span of
$\bar {f}$
. The subquotients are given by the span of
 $\{ f^i \bar {f}^k v_\lambda \colon i \geq 0\}$
, which is clearly isomorphic to
$\{ f^i \bar {f}^k v_\lambda \colon i \geq 0\}$
, which is clearly isomorphic to
![]() $\Delta ^{\mathfrak {g}}(\lambda _1 - 2k)$
.
$\Delta ^{\mathfrak {g}}(\lambda _1 - 2k)$
.
If
![]() $\lambda _2 =0$
, it is clear that the span of
$\lambda _2 =0$
, it is clear that the span of
 $\{ f^i \bar {f}^k v_\lambda \colon i \geq 0\}$
, k fixed, is a
$\{ f^i \bar {f}^k v_\lambda \colon i \geq 0\}$
, k fixed, is a
![]() $\mathfrak {g}$
-submodule. If
$\mathfrak {g}$
-submodule. If
![]() $\lambda _1 \not \in \mathbb {Z}_{\geq 0}$
, then there are no possible nontrivial extensions between
$\lambda _1 \not \in \mathbb {Z}_{\geq 0}$
, then there are no possible nontrivial extensions between
![]() $\Delta ^{\mathfrak {g}}(\lambda _1 - 2k)$
,
$\Delta ^{\mathfrak {g}}(\lambda _1 - 2k)$
,
![]() $k \geq 0$
; hence
$k \geq 0$
; hence
![]() $\Delta (\lambda )$
splits as a direct sum of these.
$\Delta (\lambda )$
splits as a direct sum of these.
Suppose now
![]() $\lambda _2 \neq 0$
and
$\lambda _2 \neq 0$
and
![]() $\lambda _1 \in \mathbb {Z}_{\geq 0}$
. Fix
$\lambda _1 \in \mathbb {Z}_{\geq 0}$
. Fix
![]() $\mu \in \{0,1,\ldots ,\lambda _1\}$
of the same parity as
$\mu \in \{0,1,\ldots ,\lambda _1\}$
of the same parity as
![]() $\lambda _1$
. It is enough to show that
$\lambda _1$
. It is enough to show that
![]() $\Delta ^{\mathfrak {g}}(-\mu - 2)$
is not a
$\Delta ^{\mathfrak {g}}(-\mu - 2)$
is not a
![]() $\mathfrak {g}$
-submodule of
$\mathfrak {g}$
-submodule of
![]() $\Delta (\lambda )$
. Suppose it is. Its highest weight vector
$\Delta (\lambda )$
. Suppose it is. Its highest weight vector
![]() $v_{-\mu -2}$
must be a nontrivial linear combination of
$v_{-\mu -2}$
must be a nontrivial linear combination of
![]() $f^i \bar {f}^j v_\lambda $
with
$f^i \bar {f}^j v_\lambda $
with
 $i+ j = \frac {\lambda _1+\mu }{2}+1 =:t$
, with a nonzero coefficient by
$i+ j = \frac {\lambda _1+\mu }{2}+1 =:t$
, with a nonzero coefficient by
![]() $\bar {f}^{t} v_\lambda $
.
$\bar {f}^{t} v_\lambda $
.
From (8), it follows that the matrix of e in bases
![]() $f^{i} \bar {f}^{t-i} v_\lambda $
,
$f^{i} \bar {f}^{t-i} v_\lambda $
,
![]() $i=0,\ldots ,t$
, and
$i=0,\ldots ,t$
, and
![]() $f^{i} \bar {f}^{t-1-i} v_\lambda $
,
$f^{i} \bar {f}^{t-1-i} v_\lambda $
,
![]() $i=0,\ldots ,t-1$
, has the form
$i=0,\ldots ,t-1$
, has the form
 $$ \begin{align*} \begin{pmatrix} \ast & \ast & 0 & \ldots & 0 & 0 & 0 \\ 0 & \ast & \ast & \ldots & 0 & 0 & 0 \\ 0 & 0 & \ast & \ddots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \vdots & \ddots & \ast & 0 & 0 \\ 0 & 0 & 0 & \ldots & \ast & \ast & 0 \\ 0 & 0 & 0 & \ldots & 0 & \ast & \ast \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} \ast & \ast & 0 & \ldots & 0 & 0 & 0 \\ 0 & \ast & \ast & \ldots & 0 & 0 & 0 \\ 0 & 0 & \ast & \ddots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \vdots & \ddots & \ast & 0 & 0 \\ 0 & 0 & 0 & \ldots & \ast & \ast & 0 \\ 0 & 0 & 0 & \ldots & 0 & \ast & \ast \end{pmatrix}, \end{align*} $$
with all
![]() $\ast $
nonzero, except the one on the position
$\ast $
nonzero, except the one on the position
![]() $(\mu +1,\mu +2)$
, where we have zero (because the bracket in (8) is zero for
$(\mu +1,\mu +2)$
, where we have zero (because the bracket in (8) is zero for
 $f^{\mu +1} \bar {f}^{\left (\frac {\lambda _1-\mu }{2} \right )} v_\lambda $
). From this, it follows that e cannot annihilate
$f^{\mu +1} \bar {f}^{\left (\frac {\lambda _1-\mu }{2} \right )} v_\lambda $
). From this, it follows that e cannot annihilate
![]() $v_{-\mu -2}$
, a contradiction.
$v_{-\mu -2}$
, a contradiction.
Lemma 17. For
![]() $\lambda _2 \neq 0$
and
$\lambda _2 \neq 0$
and
![]() $\mu \in \mathbb {Z}_{\geq 0}$
, there is an isomorphism of
$\mu \in \mathbb {Z}_{\geq 0}$
, there is an isomorphism of
![]() $\mathfrak {T}$
-modules
$\mathfrak {T}$
-modules
Proof. In the same way as for the semisimple case (see, e.g., [Reference Humphreys31, Section 6.3]), one sees that the left-hand side has a filtration with subquotients equal to the summands on the right-hand side. But these subquotients have different central characters, which follows from Lemma 15, so they split.
4.4. Enright–Arkhipov completion
Here, we show that
![]() $\mathfrak {g}$
-Harish-Chandra modules naturally occur in a certain completion (or localization) of Verma modules. We consider a combination of two of such constructions, originally given by Enright in Reference Enright[22], and Arkhipov in Reference Arkhipov[3]. See also [Reference Andersen and Stroppel2], [Reference Deodhar15], [Reference Khomenko and Mazorchuk34], [Reference König and Mazorchuk36]. To ease the notation a little bit, we will write U instead of
$\mathfrak {g}$
-Harish-Chandra modules naturally occur in a certain completion (or localization) of Verma modules. We consider a combination of two of such constructions, originally given by Enright in Reference Enright[22], and Arkhipov in Reference Arkhipov[3]. See also [Reference Andersen and Stroppel2], [Reference Deodhar15], [Reference Khomenko and Mazorchuk34], [Reference König and Mazorchuk36]. To ease the notation a little bit, we will write U instead of
![]() $U(\mathfrak {T})$
for the rest of this section.
$U(\mathfrak {T})$
for the rest of this section.
Fix an
![]() $\operatorname {\mathrm {ad}}$
-nilpotent element
$\operatorname {\mathrm {ad}}$
-nilpotent element
![]() $x \in \mathfrak {T}$
(e.g., f, e, or
$x \in \mathfrak {T}$
(e.g., f, e, or
![]() $\bar {e}$
, which we will use), and denote by
$\bar {e}$
, which we will use), and denote by
![]() $U_{(x)}$
the localization of the algebra U by the multiplicative set generated by x. This localization satisfies the Ore conditions by [Reference Mathieu41, Lemma 4.2], but this is also visible from the proof of Lemma 33. Since U has no zero divisors, the canonical map
$U_{(x)}$
the localization of the algebra U by the multiplicative set generated by x. This localization satisfies the Ore conditions by [Reference Mathieu41, Lemma 4.2], but this is also visible from the proof of Lemma 33. Since U has no zero divisors, the canonical map
![]() $U \to U_{(x)}$
is injective. Hence, we may consider the U–U-bimodule
$U \to U_{(x)}$
is injective. Hence, we may consider the U–U-bimodule

Lemma 18.
-
(a) Suppose
 $\{x, x_1, \ldots , x_{5}\}$
is a basis for
$\{x, x_1, \ldots , x_{5}\}$
is a basis for
 $\mathfrak {T}$
. The set of all monomials is a basis for
$\mathfrak {T}$
. The set of all monomials is a basis for $$ \begin{align*} \{ x^{k} x_1^{k_1} \ldots x_5^{k_5} \colon k \in \mathbb{Z}, \ k_1,\ldots, k_5 \in \mathbb{Z}_{\geq 0} \} \end{align*} $$
$$ \begin{align*} \{ x^{k} x_1^{k_1} \ldots x_5^{k_5} \colon k \in \mathbb{Z}, \ k_1,\ldots, k_5 \in \mathbb{Z}_{\geq 0} \} \end{align*} $$
 $U_{(x)}$
.
$U_{(x)}$
.
-
(b) The analogous set, but with
 $k\in \mathbb {Z}_{<0}$
, is a basis for the quotient
$k\in \mathbb {Z}_{<0}$
, is a basis for the quotient
 $S_x$
.
$S_x$
.
Proof. The set in the first claim is a generating set for
![]() $U_{(x)}$
, which follows from PBW and the properties of Ore localization. But this set is also linearly independent, since for its any finite subset, the multiplication from the left by
$U_{(x)}$
, which follows from PBW and the properties of Ore localization. But this set is also linearly independent, since for its any finite subset, the multiplication from the left by
![]() $x^m$
for some large m produces a linearly independent set in
$x^m$
for some large m produces a linearly independent set in
![]() $U \leq U_{(x)}$
. This proves the first claim, and the second claim follows from it.
$U \leq U_{(x)}$
. This proves the first claim, and the second claim follows from it.
Denote by
![]() $j \colon M \to U_{(x)} \mathbin {\mathop {\otimes }_{U}} M$
the canonical map. By using the right exactness of the tensor product, we can identify
$j \colon M \to U_{(x)} \mathbin {\mathop {\otimes }_{U}} M$
the canonical map. By using the right exactness of the tensor product, we can identify

Moreover, if M is a
![]() $\mathfrak {T}$
-module on which x acts injectively, then the canonical map j is injective. In particular, this is true if M is a Verma module
$\mathfrak {T}$
-module on which x acts injectively, then the canonical map j is injective. In particular, this is true if M is a Verma module
![]() $\Delta (\lambda )$
and
$\Delta (\lambda )$
and
![]() $x=f$
.
$x=f$
.
Lemma 19 ([Reference Andersen and Stroppel2], [Reference Deodhar15])
Fix
 $x \in \{f,e,\bar {f},\bar {e}\}$
, and let M be
$x \in \{f,e,\bar {f},\bar {e}\}$
, and let M be
![]() $\mathfrak {T}$
-module and L a finite-dimensional
$\mathfrak {T}$
-module and L a finite-dimensional
![]() $\mathfrak {T}$
-module. Then, there is a natural isomorphism of
$\mathfrak {T}$
-module. Then, there is a natural isomorphism of
![]() $\mathfrak {T}$
-modules
$\mathfrak {T}$
-modules
 $$ \begin{align*} S_x \mathbin{\mathop{\otimes}\limits_{U}} \left(M \otimes L \right) \cong \left(S_x \mathbin{\mathop{\otimes}\limits_{U}} M\right) \mathbin{\mathop{\otimes}\limits_{}} L. \end{align*} $$
$$ \begin{align*} S_x \mathbin{\mathop{\otimes}\limits_{U}} \left(M \otimes L \right) \cong \left(S_x \mathbin{\mathop{\otimes}\limits_{U}} M\right) \mathbin{\mathop{\otimes}\limits_{}} L. \end{align*} $$
Proof. There is an isomorphism
 $U_{(x)} \otimes _{U} (M \otimes L) \to (U_{(x)} \otimes _{U} M) \otimes L$
given by
$U_{(x)} \otimes _{U} (M \otimes L) \to (U_{(x)} \otimes _{U} M) \otimes L$
given by
 $$ \begin{align*} x^{-n} \otimes (m \otimes v) \mapsto \sum_{k\geq 0} (-1)^k {n+k-1 \choose k} (x^{-n-k} \otimes m) \otimes x^k v, \end{align*} $$
$$ \begin{align*} x^{-n} \otimes (m \otimes v) \mapsto \sum_{k\geq 0} (-1)^k {n+k-1 \choose k} (x^{-n-k} \otimes m) \otimes x^k v, \end{align*} $$
with the inverse given by
 $(x^{-n} \otimes m) \otimes v \mapsto x^{-ar} \otimes \sum _{k \geq 0} {ar \choose k}( x^{ar-n-k} m \otimes x^kv)$
, where
$(x^{-n} \otimes m) \otimes v \mapsto x^{-ar} \otimes \sum _{k \geq 0} {ar \choose k}( x^{ar-n-k} m \otimes x^kv)$
, where
![]() $r,a \in \mathbb {Z}_{>0}$
are chosen, so that
$r,a \in \mathbb {Z}_{>0}$
are chosen, so that
![]() $x^r$
annihilates L and
$x^r$
annihilates L and
![]() $(r-1)a \geq n$
. This is proved in [Reference Deodhar15, Theorem 3.1] and [Reference Andersen and Stroppel2, Theorem 3.2] for the semisimple case, but the proof is analogous in general. In proving that these maps compose to the identity, the following combinatorial formula is helpful:
$(r-1)a \geq n$
. This is proved in [Reference Deodhar15, Theorem 3.1] and [Reference Andersen and Stroppel2, Theorem 3.2] for the semisimple case, but the proof is analogous in general. In proving that these maps compose to the identity, the following combinatorial formula is helpful:
 $\sum _{k=0}^n (-1)^k{a \choose n-k} {b+k \choose k} = {a-b-1 \choose n}$
.
$\sum _{k=0}^n (-1)^k{a \choose n-k} {b+k \choose k} = {a-b-1 \choose n}$
.
One can check that these isomorphisms preserve the canonical images of
![]() $M \otimes L$
in both sides (see (9)), so they induce the required isomorphisms on the quotients.
$M \otimes L$
in both sides (see (9)), so they induce the required isomorphisms on the quotients.
For a
![]() $\mathfrak {T}$
-module M, we write
$\mathfrak {T}$
-module M, we write
![]() ${}^{x}\!M$
for the set of all elements
${}^{x}\!M$
for the set of all elements
![]() $m \in M$
for which the action of x is locally finite, in the sense that
$m \in M$
for which the action of x is locally finite, in the sense that
![]() $\dim \mathbb {C}[x]m<\infty $
. Note that this is a variant of the Zuckerman functor.
$\dim \mathbb {C}[x]m<\infty $
. Note that this is a variant of the Zuckerman functor.
Lemma 20. For a
![]() $\mathfrak {T}$
-module M,
$\mathfrak {T}$
-module M,
![]() ${}^{x}\!M$
is a
${}^{x}\!M$
is a
![]() $\mathfrak {T}$
-submodule. Moreover, the assignment
$\mathfrak {T}$
-submodule. Moreover, the assignment
![]() $M \mapsto {}^{x}\!M$
is a left-exact functor in the obvious way.
$M \mapsto {}^{x}\!M$
is a left-exact functor in the obvious way.
Proof. Since x is assumed to be
![]() $\operatorname {\mathrm {ad}}$
-nilpotent, the claim follows from the formula in [Reference Humphreys30, Lemma 21.4].
$\operatorname {\mathrm {ad}}$
-nilpotent, the claim follows from the formula in [Reference Humphreys30, Lemma 21.4].
Definition 21. For a
![]() $\mathfrak {T}$
-module M, define
$\mathfrak {T}$
-module M, define
 $$ \begin{align} \operatorname{\mathrm{\mathbf{EA}}}(M) := {}^{e}{\left( S_f \mathbin{\mathop{\otimes}\limits_{U}} M \right)}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{\mathbf{EA}}}(M) := {}^{e}{\left( S_f \mathbin{\mathop{\otimes}\limits_{U}} M \right)}. \end{align} $$
This is a functor on the category of
![]() $\mathfrak {T}$
-modules in the obvious way, which we call Enright–Arkhipov’s completion functor.
$\mathfrak {T}$
-modules in the obvious way, which we call Enright–Arkhipov’s completion functor.
Proposition 22. The functor
![]() $\operatorname {\mathrm {\mathbf {EA}}}$
commutes with tensoring with a finite-dimensional
$\operatorname {\mathrm {\mathbf {EA}}}$
commutes with tensoring with a finite-dimensional
![]() $\mathfrak {T}$
-module. More precisely, let M be a
$\mathfrak {T}$
-module. More precisely, let M be a
![]() $\mathfrak {T}$
-module and L a finite-dimensional
$\mathfrak {T}$
-module and L a finite-dimensional
![]() $\mathfrak {T}$
-module. Then, there is a natural isomorphism of
$\mathfrak {T}$
-module. Then, there is a natural isomorphism of
![]() $\mathfrak {T}$
-modules
$\mathfrak {T}$
-modules
Proof. Because of Lemma 19, it is enough to show that
![]() ${}^{e}(M \otimes L) = ({}^{e}\!M) \otimes L$
for
${}^{e}(M \otimes L) = ({}^{e}\!M) \otimes L$
for
![]() $\mathfrak {g}$
-modules M and L with
$\mathfrak {g}$
-modules M and L with
![]() $L=L(\mu )$
simple finite-dimensional. This is proved in [Reference Deodhar15, Corollary 3.2], but we also give a proof for the sake of completeness.
$L=L(\mu )$
simple finite-dimensional. This is proved in [Reference Deodhar15, Corollary 3.2], but we also give a proof for the sake of completeness.
The inclusion
![]() $({}^{e}\!M) \otimes L \subseteq {}^{e}(M \otimes L)$
is trivial. For the converse, denote by v the lowest weight vector of L. Then,
$({}^{e}\!M) \otimes L \subseteq {}^{e}(M \otimes L)$
is trivial. For the converse, denote by v the lowest weight vector of L. Then,
![]() $v, e v, \ldots , e^{\mu } v$
is a basis for L. Take a general element
$v, e v, \ldots , e^{\mu } v$
is a basis for L. Take a general element
 $m = \sum _{i=0}^\mu m_i \otimes e^i v \in {}^{e}(M \otimes L)$
, and observe that for
$m = \sum _{i=0}^\mu m_i \otimes e^i v \in {}^{e}(M \otimes L)$
, and observe that for
![]() $n> \mu $
, we have
$n> \mu $
, we have
 $$ \begin{align*} e^n \cdot m &= \sum_{i=0}^\mu \sum_{j=0}^{\mu-i} {n \choose j}e^{n-j} m_i \otimes e^{i+j} v \\ &= \sum_{i=0}^\mu \left( e^n m_i + \sum_{j=0}^{i-1} {n \choose i-j}e^{n+j-i} m_j \right) \otimes e^{i} v. \end{align*} $$
$$ \begin{align*} e^n \cdot m &= \sum_{i=0}^\mu \sum_{j=0}^{\mu-i} {n \choose j}e^{n-j} m_i \otimes e^{i+j} v \\ &= \sum_{i=0}^\mu \left( e^n m_i + \sum_{j=0}^{i-1} {n \choose i-j}e^{n+j-i} m_j \right) \otimes e^{i} v. \end{align*} $$
For a fixed i, the vectors inside the big brackets must span a finite-dimensional space when n varies. From this, and an induction on i, it follows that
![]() $e^n m_i$
span a finite-dimensional space, hence
$e^n m_i$
span a finite-dimensional space, hence
![]() $m \in ({}^{e}\!M) \otimes L$
.
$m \in ({}^{e}\!M) \otimes L$
.
Example 23. Let us consider
![]() $\Delta ^{\mathfrak {g}}(\mu )$
, with
$\Delta ^{\mathfrak {g}}(\mu )$
, with
![]() $\mu \in \mathbb {C}$
. From Lemma 18, it follows that the set
$\mu \in \mathbb {C}$
. From Lemma 18, it follows that the set
 $\{ f^{-k} v_\mu \colon k>0\}$
is a basis for
$\{ f^{-k} v_\mu \colon k>0\}$
is a basis for
![]() $S_f \mathbin {\mathop {\otimes }_{U}} \Delta ^{\mathfrak {g}}(\mu )$
(and from an argument for linear independence very similar to the one in the proof of Lemma 18). One can easily prove by induction the following commutation relations (similar to [Reference Mazorchuk42, Section 3.5]):
$S_f \mathbin {\mathop {\otimes }_{U}} \Delta ^{\mathfrak {g}}(\mu )$
(and from an argument for linear independence very similar to the one in the proof of Lemma 18). One can easily prove by induction the following commutation relations (similar to [Reference Mazorchuk42, Section 3.5]):
 $$ \begin{align} &[h,f^{-k}] = 2k f^{-k}, \\ \nonumber & [e,f^{-k}] = -k f^{-k-1}(h+k+1). \end{align} $$
$$ \begin{align} &[h,f^{-k}] = 2k f^{-k}, \\ \nonumber & [e,f^{-k}] = -k f^{-k-1}(h+k+1). \end{align} $$
From this, it is not hard to see that
 $$ \begin{align*} \operatorname{\mathrm{\mathbf{EA}}}(\Delta^{\mathfrak{g}}(\mu)) \cong \begin{cases} L(-\mu-2) &\colon \mu \in \mathbb{Z} \text{ and } \mu \leq -2, \\ 0 &\colon \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{\mathbf{EA}}}(\Delta^{\mathfrak{g}}(\mu)) \cong \begin{cases} L(-\mu-2) &\colon \mu \in \mathbb{Z} \text{ and } \mu \leq -2, \\ 0 &\colon \text{otherwise}. \end{cases} \end{align*} $$
Similarly, one sees that
![]() $\operatorname {\mathrm {\mathbf {EA}}}(P^{\mathfrak {g}}(\mu ))=0$
for
$\operatorname {\mathrm {\mathbf {EA}}}(P^{\mathfrak {g}}(\mu ))=0$
for
![]() $\mu \in \mathbb {Z}$
and
$\mu \in \mathbb {Z}$
and
![]() $\mu \leq -2$
(or using the fact that big projective modules can be obtained by tensoring dominant Verma modules with finite-dimensional modules, together with Proposition 22).
$\mu \leq -2$
(or using the fact that big projective modules can be obtained by tensoring dominant Verma modules with finite-dimensional modules, together with Proposition 22).
Recall that we use notation
 $\lambda =(\lambda _1,\lambda _2) \in \tilde {\mathfrak {h}}^\ast $
, with
$\lambda =(\lambda _1,\lambda _2) \in \tilde {\mathfrak {h}}^\ast $
, with
![]() $\lambda _1 = \lambda (h)$
and
$\lambda _1 = \lambda (h)$
and
 $\lambda _2 = \lambda (\bar {h})$
.
$\lambda _2 = \lambda (\bar {h})$
.
Theorem 24. Take
![]() $\lambda $
with
$\lambda $
with
![]() $\lambda _1 \in \mathbb {Z}$
and
$\lambda _1 \in \mathbb {Z}$
and
![]() $\lambda _2 \neq 0$
. Then,
$\lambda _2 \neq 0$
. Then,
![]() $\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
is a simple
$\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
is a simple
![]() $\mathfrak {g}$
-Harish-Chandra module. As a
$\mathfrak {g}$
-Harish-Chandra module. As a
![]() $\mathfrak {g}$
-module, it decomposes as follows:
$\mathfrak {g}$
-module, it decomposes as follows:
 $$ \begin{align} \operatorname{\mathrm{\mathbf{EA}}}(\Delta(\lambda)) \cong \bigoplus_{k \geq 0} L(|\lambda_1 + 2| +2k). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{\mathbf{EA}}}(\Delta(\lambda)) \cong \bigoplus_{k \geq 0} L(|\lambda_1 + 2| +2k). \end{align} $$
Proof. Lemma 16, the fact that the functor
![]() $\operatorname {\mathrm {\mathbf {EA}}}$
commutes with the forgetful functor from
$\operatorname {\mathrm {\mathbf {EA}}}$
commutes with the forgetful functor from
![]() $\mathfrak {T}$
-modules to
$\mathfrak {T}$
-modules to
![]() $\mathfrak {g}$
-modules, and Example 23 imply (12).
$\mathfrak {g}$
-modules, and Example 23 imply (12).
From Lemma 18, we have a basis for
 $S_f \mathbin {\mathop {\otimes }\limits _{U}} \Delta (\lambda )$
consisting of
$S_f \mathbin {\mathop {\otimes }\limits _{U}} \Delta (\lambda )$
consisting of
![]() $f^{-i} \bar {f}^j v_\lambda $
, for
$f^{-i} \bar {f}^j v_\lambda $
, for
![]() $i \geq 1$
and
$i \geq 1$
and
![]() $j \geq 0$
. Since the lowest weight vector of a
$j \geq 0$
. Since the lowest weight vector of a
![]() $\mathfrak {g}$
-type
$\mathfrak {g}$
-type
![]() $L(\mu )$
(
$L(\mu )$
(
![]() $\mu $
of the same parity as
$\mu $
of the same parity as
![]() $\lambda _1$
) inside
$\lambda _1$
) inside
![]() $\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
must be annihilated by f, it must be (up to scalar) equal to
$\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
must be annihilated by f, it must be (up to scalar) equal to
![]() $f^{-1} \bar {f}^t v_\lambda $
, where
$f^{-1} \bar {f}^t v_\lambda $
, where
 $t = \frac {\mu +\lambda _1}{2}+1$
.
$t = \frac {\mu +\lambda _1}{2}+1$
.
Now, we will prove that
![]() $\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
is simple. Let V be its nonzero submodule, and suppose it contains
$\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
is simple. Let V be its nonzero submodule, and suppose it contains
![]() $L(\mu )$
for some
$L(\mu )$
for some
![]() $\mu $
from (12). By applying
$\mu $
from (12). By applying
![]() $\bar {f}$
on
$\bar {f}$
on
![]() $f^{-1} \bar {f}^t v_\lambda $
, we get that
$f^{-1} \bar {f}^t v_\lambda $
, we get that
![]() $L(\mu +2k) \subseteq V$
, for all
$L(\mu +2k) \subseteq V$
, for all
![]() $k \geq 0$
.
$k \geq 0$
.
To prove that
![]() $V=\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
, it is enough to assume
$V=\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
, it is enough to assume
![]() $\mu> |\lambda _1+2|$
and to find an element in
$\mu> |\lambda _1+2|$
and to find an element in
![]() $U(\mathfrak {T})$
that maps
$U(\mathfrak {T})$
that maps
![]() $f^{-1} \bar {f}^t v_\lambda $
to
$f^{-1} \bar {f}^t v_\lambda $
to
![]() $f^{-1} \bar {f}^{t-1} v_\lambda $
.
$f^{-1} \bar {f}^{t-1} v_\lambda $
.
In addition to (11), we will use the following commutation relations, whose proofs are analogous to the ones for (11):
 $$ \begin{align} &[\bar{h},f^{-k}] = 2k f^{-k-1} \bar{f}, \\ \nonumber &[\bar{e},f^{-k}] = - kf^{-k-1} \bar{h} - k(k+1)f^{-k-2} \bar{f}. \end{align} $$
$$ \begin{align} &[\bar{h},f^{-k}] = 2k f^{-k-1} \bar{f}, \\ \nonumber &[\bar{e},f^{-k}] = - kf^{-k-1} \bar{h} - k(k+1)f^{-k-2} \bar{f}. \end{align} $$
From this, we have:
 $$ \begin{align*} e \cdot f^{-1} \bar{f}^t v_\lambda &= [e,f^{-1}] \bar{f}^t v_\lambda + f^{-1} [e,\bar{f}^t] v_\lambda \\ &= - f^{-2} (h+2) \bar{f}^t v_\lambda + t \lambda_2 f^{-1} \bar{f}^{t-1} v_\lambda \\ &= \mu f^{-2} \bar{f}^t v_\lambda + t \lambda_2 f^{-1} \bar{f}^{t-1} v_\lambda, \\[.5em] \bar{h}e \cdot f^{-1} \bar{f}^t v_\lambda &= \mu \bar{h} f^{-2} \bar{f}^t v_\lambda + t \lambda_2 \bar{h} f^{-1} \bar{f}^{t-1} v_\lambda \\ &= \mu [\bar{h}, f^{-2}] \bar{f}^t v_\lambda + \mu \lambda_2 f^{-2} \bar{f}^t v_\lambda + t\lambda_2 [\bar{h},f^{-1}] \bar{f}^{t-1} v_\lambda + t\lambda_2^2 f^{-1} \bar{f}^{t-1} v_\lambda \\ &= 4\mu f^{-3} \bar{f}^{t+1} v_\lambda + (\lambda_1 + 2\mu + 2)\lambda_2 f^{-2} \bar{f}^{t} v_\lambda + t\lambda_2^2 f^{-1} \bar{f}^{t-1} v_\lambda, \\[.5em] 2\mu \bar{e} \cdot f^{-1} \bar{f}^t v_\lambda &= 2\mu[\bar{e}, f^{-1}] \bar{f}^t v_\lambda \\ &= -4\mu f^{-3} \bar{f}^{t+1} v_\lambda - 2\mu\lambda_2 f^{-2} \bar{f}^t v_\lambda. \end{align*} $$
$$ \begin{align*} e \cdot f^{-1} \bar{f}^t v_\lambda &= [e,f^{-1}] \bar{f}^t v_\lambda + f^{-1} [e,\bar{f}^t] v_\lambda \\ &= - f^{-2} (h+2) \bar{f}^t v_\lambda + t \lambda_2 f^{-1} \bar{f}^{t-1} v_\lambda \\ &= \mu f^{-2} \bar{f}^t v_\lambda + t \lambda_2 f^{-1} \bar{f}^{t-1} v_\lambda, \\[.5em] \bar{h}e \cdot f^{-1} \bar{f}^t v_\lambda &= \mu \bar{h} f^{-2} \bar{f}^t v_\lambda + t \lambda_2 \bar{h} f^{-1} \bar{f}^{t-1} v_\lambda \\ &= \mu [\bar{h}, f^{-2}] \bar{f}^t v_\lambda + \mu \lambda_2 f^{-2} \bar{f}^t v_\lambda + t\lambda_2 [\bar{h},f^{-1}] \bar{f}^{t-1} v_\lambda + t\lambda_2^2 f^{-1} \bar{f}^{t-1} v_\lambda \\ &= 4\mu f^{-3} \bar{f}^{t+1} v_\lambda + (\lambda_1 + 2\mu + 2)\lambda_2 f^{-2} \bar{f}^{t} v_\lambda + t\lambda_2^2 f^{-1} \bar{f}^{t-1} v_\lambda, \\[.5em] 2\mu \bar{e} \cdot f^{-1} \bar{f}^t v_\lambda &= 2\mu[\bar{e}, f^{-1}] \bar{f}^t v_\lambda \\ &= -4\mu f^{-3} \bar{f}^{t+1} v_\lambda - 2\mu\lambda_2 f^{-2} \bar{f}^t v_\lambda. \end{align*} $$
From this, it follows that
 $$ \begin{align*} (\bar{h}e - 2\mu \bar{e}) \cdot f^{-1} \bar{f}^t v_\lambda = (\lambda_1 + 2)\lambda_2 f^{-2} \bar{f}^{t} v_\lambda + t\lambda_2^2 f^{-1} \bar{f}^{t-1} v_\lambda. \end{align*} $$
$$ \begin{align*} (\bar{h}e - 2\mu \bar{e}) \cdot f^{-1} \bar{f}^t v_\lambda = (\lambda_1 + 2)\lambda_2 f^{-2} \bar{f}^{t} v_\lambda + t\lambda_2^2 f^{-1} \bar{f}^{t-1} v_\lambda. \end{align*} $$
Now, we claim that a nontrivial linear combination of e and
 $(\bar {h}e - 2\mu \bar {e})$
will map
$(\bar {h}e - 2\mu \bar {e})$
will map
![]() $f^{-1} \bar {f}^t v_\lambda $
to
$f^{-1} \bar {f}^t v_\lambda $
to
![]() $f^{-1} \bar {f}^{t-1} v_\lambda $
. This is true, because the determinant
$f^{-1} \bar {f}^{t-1} v_\lambda $
. This is true, because the determinant
 $$ \begin{align*} \begin{vmatrix} \mu & (\lambda_1+2)\lambda_2 \\ t\lambda_2 & t\lambda_2^2 \end{vmatrix} = \lambda_2^2(\mu+\lambda_1+2)(\mu-\lambda_1-2) \neq 0. \end{align*} $$
$$ \begin{align*} \begin{vmatrix} \mu & (\lambda_1+2)\lambda_2 \\ t\lambda_2 & t\lambda_2^2 \end{vmatrix} = \lambda_2^2(\mu+\lambda_1+2)(\mu-\lambda_1-2) \neq 0. \end{align*} $$
This finishes the proof of simplicity.
Remark 25 (Sketch of an alternative proof of simplicity of
 $\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
)
$\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
)
Assume
![]() $\lambda _1 \in \mathbb {Z}$
and
$\lambda _1 \in \mathbb {Z}$
and
![]() $\lambda _2\neq 0$
, and suppose that V is a submodule of
$\lambda _2\neq 0$
, and suppose that V is a submodule of
![]() $\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
having
$\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
having
![]() $L(\mu )$
,
$L(\mu )$
,
![]() $\mu>|\lambda _1+2|$
minimal. By applying
$\mu>|\lambda _1+2|$
minimal. By applying
![]() $\bar {f}$
, we see that as a
$\bar {f}$
, we see that as a
![]() $\mathfrak {g}$
-module,
$\mathfrak {g}$
-module,
![]() $V \cong L(\mu ) \oplus L(\mu +2) \oplus \ldots $
. This implies that the quotient
$V \cong L(\mu ) \oplus L(\mu +2) \oplus \ldots $
. This implies that the quotient
![]() ${\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))}/{V} \cong L(|\lambda _1+2|) \oplus L(|\lambda _1+2|+2) \oplus \cdots \oplus L(\mu -2)$
is simple as a
${\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))}/{V} \cong L(|\lambda _1+2|) \oplus L(|\lambda _1+2|+2) \oplus \cdots \oplus L(\mu -2)$
is simple as a
![]() $\mathfrak {T}$
-module and finite-dimensional. Since
$\mathfrak {T}$
-module and finite-dimensional. Since
![]() $\bar {C}$
consists of elements from the nilradical of
$\bar {C}$
consists of elements from the nilradical of
![]() $\mathfrak {T}$
, it must act as zero on this quotient. But
$\mathfrak {T}$
, it must act as zero on this quotient. But
![]() $\bar {C}$
is central, so it still acts as
$\bar {C}$
is central, so it still acts as
![]() $\lambda ^2_2$
on the localization, a contradiction.
$\lambda ^2_2$
on the localization, a contradiction.
4.5. Classification
In this subsection, we use the relation with highest weight theory established above to classify all simple
![]() $\mathfrak {g}$
-Harish-Chandra modules for
$\mathfrak {g}$
-Harish-Chandra modules for
![]() $\mathfrak {T}$
. It will be more convenient to shift the notation for the first parameter in our modules by
$\mathfrak {T}$
. It will be more convenient to shift the notation for the first parameter in our modules by
![]() $-2$
.
$-2$
.
Definition 26. For
![]() $n \in \mathbb {Z}$
and
$n \in \mathbb {Z}$
and
![]() $\lambda _2 \neq 0$
, denote
$\lambda _2 \neq 0$
, denote
Corollary 27. The module
![]() $V(n,\lambda _2)$
is a simple
$V(n,\lambda _2)$
is a simple
![]() $\mathfrak {g}$
-Harish-Chandra module, it has
$\mathfrak {g}$
-Harish-Chandra module, it has
![]() $\mathfrak {g}$
-types
$\mathfrak {g}$
-types
![]() $L(|n|), L(|n|+2), L(|n|+4) \ldots $
, and each of these occurs with multiplicity 1.
$L(|n|), L(|n|+2), L(|n|+4) \ldots $
, and each of these occurs with multiplicity 1.
If
![]() $V(n,\lambda _2) \cong V(n',\lambda _2')$
, then
$V(n,\lambda _2) \cong V(n',\lambda _2')$
, then
![]() $(n',\lambda _2') = (n,\lambda _2)$
or
$(n',\lambda _2') = (n,\lambda _2)$
or
![]() $(-n,-\lambda _2)$
.
$(-n,-\lambda _2)$
.
Proof. The first statement follows from Theorem 24.
It is clear that the functor
![]() $\operatorname {\mathrm {\mathbf {EA}}}$
preserves central character. So, the generators of the center C and
$\operatorname {\mathrm {\mathbf {EA}}}$
preserves central character. So, the generators of the center C and
![]() $\bar {C}$
act as the scalars
$\bar {C}$
act as the scalars
![]() $n\lambda _2$
and
$n\lambda _2$
and
![]() $\lambda _2^2$
, respectively. From this, the second statement follows.
$\lambda _2^2$
, respectively. From this, the second statement follows.
We are going to see later in this subsection that the modules
![]() $V(n,\lambda _2)$
exhaust all infinite-dimensional simple
$V(n,\lambda _2)$
exhaust all infinite-dimensional simple
![]() $\mathfrak {g}$
-Harish-Chandra modules.
$\mathfrak {g}$
-Harish-Chandra modules.
On Figure 1, we present several
![]() $V(n,\lambda _2)$
’s, and how they are constructed. The gray area on the left-hand side is the Verma module, decomposed into rows according to Lemma 16, and furthermore, into weight spaces. The remaining bullets represent
$V(n,\lambda _2)$
’s, and how they are constructed. The gray area on the left-hand side is the Verma module, decomposed into rows according to Lemma 16, and furthermore, into weight spaces. The remaining bullets represent
![]() $S_f$
tensored with the Verma module. The arrows represent nonzero action of e, and the light-gray area on the right-hand side contains vectors not having a finite e-orbit. The remaining (not shaded) part is our
$S_f$
tensored with the Verma module. The arrows represent nonzero action of e, and the light-gray area on the right-hand side contains vectors not having a finite e-orbit. The remaining (not shaded) part is our
![]() $V(n,\lambda _2)$
, with its
$V(n,\lambda _2)$
, with its
![]() $\mathfrak {g}$
-types clearly visible.
$\mathfrak {g}$
-types clearly visible.

Figure 1 Construction of simple
![]() $\mathfrak {g}$
-Harish Chandra modules for the Takiff
$\mathfrak {g}$
-Harish Chandra modules for the Takiff
![]() $\mathfrak {sl}_2$
.
$\mathfrak {sl}_2$
.
From Corollary 9, Theorem 12, and Corollary 27, we have the following consequence:
Corollary 28. For
![]() $\lambda _2 \neq 0$
, we have
$\lambda _2 \neq 0$
, we have
 $V(0,\lambda _2) \cong V(0,-\lambda _2) \cong Q(0,\lambda _2^2)$
.
$V(0,\lambda _2) \cong V(0,-\lambda _2) \cong Q(0,\lambda _2^2)$
.
From Lemma 17, Proposition 22, and the definition of
![]() $V(n,\lambda _2)$
, we have:
$V(n,\lambda _2)$
, we have:
Proposition 29. For
![]() $n \in \mathbb {Z}$
,
$n \in \mathbb {Z}$
,
![]() $\lambda _2 \neq 0$
, and
$\lambda _2 \neq 0$
, and
![]() $\mu \in \mathbb {Z}_{\geq 0}$
, we have the following isomorphism of
$\mu \in \mathbb {Z}_{\geq 0}$
, we have the following isomorphism of
![]() $\mathfrak {T}$
-modules:
$\mathfrak {T}$
-modules:
Now, we can completely describe the universal modules:
Proposition 30. For
![]() $n \in \mathbb {Z}_{\geq 0}$
and
$n \in \mathbb {Z}_{\geq 0}$
and
![]() $\chi \neq 0$
, choose any square root
$\chi \neq 0$
, choose any square root
![]() $\lambda _2$
of
$\lambda _2$
of
![]() $\chi $
. Then,
$\chi $
. Then,
Moreover,
![]() $V(n,\lambda _2) \cong V(-n,-\lambda _2)$
.
$V(n,\lambda _2) \cong V(-n,-\lambda _2)$
.
Proof. The first claim follows from Proposition 29, Corollary 28, and (5). The second claim follows from the first one by comparing both choices
![]() $\pm \lambda _2$
and central characters of the summands.
$\pm \lambda _2$
and central characters of the summands.
Theorem 31. Let V be a simple
![]() $\mathfrak {g}$
-Harish-Chandra module for
$\mathfrak {g}$
-Harish-Chandra module for
![]() $\mathfrak {T}$
. Denote by
$\mathfrak {T}$
. Denote by
 $\chi = \chi (\bar {C})$
the purely Takiff part of the central character, and suppose
$\chi = \chi (\bar {C})$
the purely Takiff part of the central character, and suppose
![]() $L(n)$
,
$L(n)$
,
![]() $n \in \mathbb {Z}_{\geq 0}$
, is the minimal
$n \in \mathbb {Z}_{\geq 0}$
, is the minimal
![]() $\mathfrak {g}$
-type of V.
$\mathfrak {g}$
-type of V.
-
• If
 $\chi \neq 0$
, then
$\chi \neq 0$
, then
 $V \cong V(n,\lambda _2)$
, for a square root
$V \cong V(n,\lambda _2)$
, for a square root
 $\lambda _2$
of
$\lambda _2$
of
 $\chi $
.
$\chi $
. -
• If
 $\chi = 0$
, then
$\chi = 0$
, then
 $V \cong L(n)$
with the trivial
$V \cong L(n)$
with the trivial
 $\bar {\mathfrak {g}}$
-action.
$\bar {\mathfrak {g}}$
-action.
In other words,
![]() $V(n,\lambda _2)$
,
$V(n,\lambda _2)$
,
![]() $n \in \mathbb {Z}$
,
$n \in \mathbb {Z}$
,
![]() $\lambda _2 \in \mathbb {C}\setminus \{0\}$
, together with the finite-dimensional simple
$\lambda _2 \in \mathbb {C}\setminus \{0\}$
, together with the finite-dimensional simple
![]() $\mathfrak {g}$
-modules constitute a complete list of simple
$\mathfrak {g}$
-modules constitute a complete list of simple
![]() $\mathfrak {g}$
-Harish-Chandra modules for
$\mathfrak {g}$
-Harish-Chandra modules for
![]() $\mathfrak {T}$
. The only isomorphisms between different members of the list are
$\mathfrak {T}$
. The only isomorphisms between different members of the list are
![]() $V(n,\lambda _2) \cong V(-n,-\lambda _2)$
.
$V(n,\lambda _2) \cong V(-n,-\lambda _2)$
.
Proof. By Proposition 8(b), V is a quotient of
![]() $Q(n,\chi )$
.
$Q(n,\chi )$
.
If
![]() $\chi \neq 0$
, from Proposition 30 and Corollary 27, we see that the only possible choices with the correct minimal
$\chi \neq 0$
, from Proposition 30 and Corollary 27, we see that the only possible choices with the correct minimal
![]() $\mathfrak {g}$
-type are
$\mathfrak {g}$
-type are
![]() $V(n,\lambda _2)$
or
$V(n,\lambda _2)$
or
![]() $V(n,-\lambda _2)$
.
$V(n,-\lambda _2)$
.
If
![]() $\chi = 0$
, by the second part of Theorem 12, we see that the only possible simple quotients of
$\chi = 0$
, by the second part of Theorem 12, we see that the only possible simple quotients of
![]() $Q(n,0) \cong Q(0,0) \otimes L(n)$
are just finite-dimensional simple
$Q(n,0) \cong Q(0,0) \otimes L(n)$
are just finite-dimensional simple
![]() $\mathfrak {g}$
-modules with the trivial
$\mathfrak {g}$
-modules with the trivial
![]() $\bar {\mathfrak {g}}$
-action.
$\bar {\mathfrak {g}}$
-action.
4.6. Extensions
Here, we calculate the first extension groups of simple
![]() $\mathfrak {g}$
-Harish-Chandra modules, restricting to the infinite-dimensional cases, that is, a nontrivial central character. Since in that case nonisomorphic
$\mathfrak {g}$
-Harish-Chandra modules, restricting to the infinite-dimensional cases, that is, a nontrivial central character. Since in that case nonisomorphic
![]() $\mathfrak {g}$
-Harish-Chandra modules have different central characters, there are no nontrivial extensions between them. So, it only makes sense to calculate the self-extensions.
$\mathfrak {g}$
-Harish-Chandra modules have different central characters, there are no nontrivial extensions between them. So, it only makes sense to calculate the self-extensions.
Theorem 32. For an infinite-dimensional simple
![]() $\mathfrak {g}$
-Harish-Chandra module V, we have
$\mathfrak {g}$
-Harish-Chandra module V, we have
 $$ \begin{align*} \operatorname{\mathrm{Ext}}^1(V,V) \cong \mathbb{C}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ext}}^1(V,V) \cong \mathbb{C}. \end{align*} $$
Proof. Assume first that
![]() $V= Q(0,\chi )$
for
$V= Q(0,\chi )$
for
![]() $\chi \neq 0$
, and suppose we have a nonsplit short exact sequence
$\chi \neq 0$
, and suppose we have a nonsplit short exact sequence
 $0 \to V \stackrel {i}{\hookrightarrow } M \stackrel {p}{\twoheadrightarrow } V \to 0$
. Denote by
$0 \to V \stackrel {i}{\hookrightarrow } M \stackrel {p}{\twoheadrightarrow } V \to 0$
. Denote by
![]() $1 \in V$
the generator from
$1 \in V$
the generator from
![]() $L(0)$
and set
$L(0)$
and set
![]() $w=i(1) \in M$
. We can find
$w=i(1) \in M$
. We can find
![]() $v \in M$
such that
$v \in M$
such that
![]() $p(v)=1$
and, in addition, such that v generates a trivial
$p(v)=1$
and, in addition, such that v generates a trivial
![]() $\mathfrak {g}$
-submodule in M (note that the sequence must split in the category of
$\mathfrak {g}$
-submodule in M (note that the sequence must split in the category of
![]() $\mathfrak {g}$
-modules). By the universal property, there is a
$\mathfrak {g}$
-modules). By the universal property, there is a
![]() $\mathfrak {T}$
-homomorphism
$\mathfrak {T}$
-homomorphism
![]() $f \colon Q(0) \to M$
, and the triangle below commutes:
$f \colon Q(0) \to M$
, and the triangle below commutes:

The map f must be surjective, since otherwise its image would define a splitting of the short exact sequence. So, there is an element in
![]() $Q(0)$
that maps to w via f; by Lemma 11 and Proposition 7, such an element is necessarily of the form
$Q(0)$
that maps to w via f; by Lemma 11 and Proposition 7, such an element is necessarily of the form
 $p(\bar {C})$
for some polynomial p. Since the triangle above commutes, we must have
$p(\bar {C})$
for some polynomial p. Since the triangle above commutes, we must have
![]() $p(\chi )=0$
. Since
$p(\chi )=0$
. Since
![]() $[M \colon L(0)] =2$
, we can take
$[M \colon L(0)] =2$
, we can take
 $p(\bar {C})=\bar {C}-\chi $
. From this, one can see that
$p(\bar {C})=\bar {C}-\chi $
. From this, one can see that
![]() $\operatorname {\mathrm {Ker}} f$
is generated by
$\operatorname {\mathrm {Ker}} f$
is generated by
 $(\bar {C} - \chi )^2$
, that is,
$(\bar {C} - \chi )^2$
, that is,
 . This uniquely determines M. Conversely, one sees directly that such M defines a nonsplit self-extension of
. This uniquely determines M. Conversely, one sees directly that such M defines a nonsplit self-extension of
![]() $Q(0,\chi )$
.
$Q(0,\chi )$
.
The general statement is obtained from this by translation functors, that is, tensoring extensions of
![]() $Q(0,\chi )$
by
$Q(0,\chi )$
by
![]() $L(n)$
and then taking the component with the correct central character (see Proposition 29). This functor defines a homomorphism of abelian groups
$L(n)$
and then taking the component with the correct central character (see Proposition 29). This functor defines a homomorphism of abelian groups
 $$ \begin{align*}\operatorname{\mathrm{Ext}}^1(V(0,\lambda_2),V(0,\lambda_2)) \to \operatorname{\mathrm{Ext}}^1(V(n,\lambda_2),V(n,\lambda_2)). \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Ext}}^1(V(0,\lambda_2),V(0,\lambda_2)) \to \operatorname{\mathrm{Ext}}^1(V(n,\lambda_2),V(n,\lambda_2)). \end{align*} $$
In the same way, we get a homomorphism in the other direction. The fact that these homomorphisms compose to the identities on the
![]() $\operatorname {\mathrm {Ext}}^1$
groups is an easy application of the
$\operatorname {\mathrm {Ext}}^1$
groups is an easy application of the
![]() $5$
-lemma.
$5$
-lemma.
4.7. Annihilators
We will prove here that the infinite-dimensional simple
![]() $\mathfrak {g}$
-Harish-Chandra modules have the same annihilators in
$\mathfrak {g}$
-Harish-Chandra modules have the same annihilators in
![]() $U=U(\mathfrak {T})$
as the corresponding Verma modules. We start by showing that, in the cases we are interested in, the localization does not decrease the annihilator. Then, we construct a certain inverse of the functor
$U=U(\mathfrak {T})$
as the corresponding Verma modules. We start by showing that, in the cases we are interested in, the localization does not decrease the annihilator. Then, we construct a certain inverse of the functor
![]() $\operatorname {\mathrm {\mathbf {EA}}}$
, which will produce Verma modules out of
$\operatorname {\mathrm {\mathbf {EA}}}$
, which will produce Verma modules out of
![]() $\mathfrak {g}$
-Harish-Chandra modules. This will be given by the localization by
$\mathfrak {g}$
-Harish-Chandra modules. This will be given by the localization by
![]() $\bar {e}$
, that is, tensoring with
$\bar {e}$
, that is, tensoring with
![]() $S_{\bar {e}}$
over U.
$S_{\bar {e}}$
over U.
Lemma 33. Let x be an
![]() $\operatorname {\mathrm {ad}}$
-nilpotent element in
$\operatorname {\mathrm {ad}}$
-nilpotent element in
![]() $\mathfrak {T}$
, and M a
$\mathfrak {T}$
, and M a
![]() $\mathfrak {T}$
-module on which x acts injectively. Then, in U, we have
$\mathfrak {T}$
-module on which x acts injectively. Then, in U, we have
 $$ \begin{align*} \operatorname{\mathrm{Ann}}(M) = \operatorname{\mathrm{Ann}} \left(U_{(x)} \mathbin{\mathop{\otimes}\limits_{U}} M \right) \subseteq \operatorname{\mathrm{Ann}} \left(S_x \mathbin{\mathop{\otimes}\limits_{U}} M \right). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ann}}(M) = \operatorname{\mathrm{Ann}} \left(U_{(x)} \mathbin{\mathop{\otimes}\limits_{U}} M \right) \subseteq \operatorname{\mathrm{Ann}} \left(S_x \mathbin{\mathop{\otimes}\limits_{U}} M \right). \end{align*} $$
Proof. The only nonobvious thing to prove is if
![]() $u \in \operatorname {\mathrm {Ann}}(M)$
, then
$u \in \operatorname {\mathrm {Ann}}(M)$
, then
![]() $u x^{-n} \otimes m =0$
, for all
$u x^{-n} \otimes m =0$
, for all
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $m\in M$
.
$m\in M$
.
By assumption, for any
![]() $u \in U$
, there exists
$u \in U$
, there exists
![]() $k_1>0$
such that
$k_1>0$
such that
 $$ \begin{align*} 0 = \left(\operatorname{\mathrm{ad}}(x)\right)^{k_1}(u) = \sum_{i=0}^{k_1} (-1)^{i}{k_1 \choose i} x^i u x^{k_1-i}, \end{align*} $$
$$ \begin{align*} 0 = \left(\operatorname{\mathrm{ad}}(x)\right)^{k_1}(u) = \sum_{i=0}^{k_1} (-1)^{i}{k_1 \choose i} x^i u x^{k_1-i}, \end{align*} $$
so
![]() $x^{k_1} u = u_1 x$
for
$x^{k_1} u = u_1 x$
for
 $u_1 := \sum _{i=0}^{k_1-1} (-1)^{k_1+i}{k_1 \choose i} x^i u x^{k_1-i-1}$
. If
$u_1 := \sum _{i=0}^{k_1-1} (-1)^{k_1+i}{k_1 \choose i} x^i u x^{k_1-i-1}$
. If
![]() $u \in \operatorname {\mathrm {Ann}}(M)$
, then so is
$u \in \operatorname {\mathrm {Ann}}(M)$
, then so is
![]() $u_1$
, since
$u_1$
, since
![]() $\operatorname {\mathrm {Ann}}(M)$
is a two-sided ideal. We can inductively apply the same procedure on
$\operatorname {\mathrm {Ann}}(M)$
is a two-sided ideal. We can inductively apply the same procedure on
![]() $u_1$
to get
$u_1$
to get
![]() $k_2$
such that
$k_2$
such that
![]() $x^{k_2} u_1 = u_2 x$
, and so on. Repeating this n times, we get
$x^{k_2} u_1 = u_2 x$
, and so on. Repeating this n times, we get
![]() $x^{k_{n}} u_{n-1} = u_n$
for some
$x^{k_{n}} u_{n-1} = u_n$
for some
![]() $u_n \in \operatorname {\mathrm {Ann}}(M)$
. From the construction, it follows that
$u_n \in \operatorname {\mathrm {Ann}}(M)$
. From the construction, it follows that
Since x acts injectively on M, the same is true for
 $U_{(x)} \mathbin {\mathop {\otimes }\limits _{U}} M$
. From this, it follows that
$U_{(x)} \mathbin {\mathop {\otimes }\limits _{U}} M$
. From this, it follows that
![]() $ux^{-n} \otimes m =0$
.
$ux^{-n} \otimes m =0$
.
Proposition 34. Suppose
![]() $n \in \mathbb {Z}$
and
$n \in \mathbb {Z}$
and
![]() $\lambda _2 \neq 0$
.
$\lambda _2 \neq 0$
.
-
(a) The element
 $\bar {e}$
acts injectively on
$\bar {e}$
acts injectively on
 $V(n,\lambda _2)$
.
$V(n,\lambda _2)$
. -
(b) The module
 $S_{\bar {e}} \mathbin {\mathop {\otimes }\limits _{U}} V(n,\lambda _2)$
is isomorphic to the direct sum of Verma modules
$S_{\bar {e}} \mathbin {\mathop {\otimes }\limits _{U}} V(n,\lambda _2)$
is isomorphic to the direct sum of Verma modules
 $\Delta (n-2,\lambda _2) \oplus \Delta (-n-2,-\lambda _2)$
.
$\Delta (n-2,\lambda _2) \oplus \Delta (-n-2,-\lambda _2)$
.
Proof. The first claim follows from Lemma 11(b) for
 $V(0,\lambda _2) \cong Q(0,\lambda _2^2)$
, and from Proposition 30 for general
$V(0,\lambda _2) \cong Q(0,\lambda _2^2)$
, and from Proposition 30 for general
![]() $V(n,\lambda _2)$
.
$V(n,\lambda _2)$
.
We prove the second claim also for
![]() $n=0$
, and again translate the result to the other cases. From Lemma 11(b), we get a basis for
$n=0$
, and again translate the result to the other cases. From Lemma 11(b), we get a basis for
 $W:=S_{\bar {e}} \mathbin {\mathop {\otimes }\limits _{U}} Q(0,\lambda _2^2)$
consisting of
$W:=S_{\bar {e}} \mathbin {\mathop {\otimes }\limits _{U}} Q(0,\lambda _2^2)$
consisting of
 $$ \begin{align*} (\bar{e})^{-k} \bar{f}^l \bar{h}^\epsilon, \text{ for } k>0, \ l \geq 0, \ \epsilon \in \{0,1\}, \end{align*} $$
$$ \begin{align*} (\bar{e})^{-k} \bar{f}^l \bar{h}^\epsilon, \text{ for } k>0, \ l \geq 0, \ \epsilon \in \{0,1\}, \end{align*} $$
where
![]() $\mathfrak {g}$
acts by the adjoint action, and
$\mathfrak {g}$
acts by the adjoint action, and
![]() $\bar {\mathfrak {g}}$
by the (commutative) multiplication. We denote this action of
$\bar {\mathfrak {g}}$
by the (commutative) multiplication. We denote this action of
![]() $\mathfrak {T}$
by
$\mathfrak {T}$
by
![]() $\circ $
.
$\circ $
.
Consider the following two elements in W:
 $$ \begin{align*} w_\pm := (\bar{e})^{-1} \pm \frac{1}{\lambda_2}(\bar{e})^{-1}\bar{h}.\end{align*} $$
$$ \begin{align*} w_\pm := (\bar{e})^{-1} \pm \frac{1}{\lambda_2}(\bar{e})^{-1}\bar{h}.\end{align*} $$
It is an easy calculation to see that
![]() $e \circ w_{\pm } = \bar {e} \circ w_{\pm } = 0$
,
$e \circ w_{\pm } = \bar {e} \circ w_{\pm } = 0$
,
![]() $h \circ w_{\pm } = -2 w_\pm $
, and
$h \circ w_{\pm } = -2 w_\pm $
, and
![]() $\bar {h} \circ w_\pm = \pm \lambda _2 w_{\pm }$
, from which it follows by the universal property of Verma modules that each
$\bar {h} \circ w_\pm = \pm \lambda _2 w_{\pm }$
, from which it follows by the universal property of Verma modules that each
![]() $w_\pm $
generates a copy of
$w_\pm $
generates a copy of
![]() $\Delta (-2,\pm \lambda _2)$
in W. Because of their simplicity, these submodules can only intersect trivially. By comparing the dimensions of weight spaces, we conclude that W cannot have any other composition factor, that is,
$\Delta (-2,\pm \lambda _2)$
in W. Because of their simplicity, these submodules can only intersect trivially. By comparing the dimensions of weight spaces, we conclude that W cannot have any other composition factor, that is,
In general, we calculate
 $S_{\bar {e}} \mathbin {\mathop {\otimes }\limits _{U}} Q(n,\lambda _2^2)$
in two ways and compare the results:
$S_{\bar {e}} \mathbin {\mathop {\otimes }\limits _{U}} Q(n,\lambda _2^2)$
in two ways and compare the results:
 $$ \begin{align} \nonumber S_{\bar{e}} {}\mathbin{\mathop{\otimes}\limits_{U}}{} & Q(n,\lambda_2^2) \cong S_{\bar{e}} \mathbin{\mathop{\otimes}\limits_{U}} \left( Q(0,\lambda_2^2) \mathbin{\mathop{\otimes}\limits_{}} L(n) \right) && \text{by (5)}, \\ \nonumber\cong & \left( S_{\bar{e}} \mathbin{\mathop{\otimes}\limits_{U}} Q(0,\lambda_2^2) \right) \mathbin{\mathop{\otimes}\limits_{}} L(n) && \text{by Lemma 19}, \\ \nonumber\cong & \, \big( \Delta(-2,\lambda_2) \oplus \Delta(-2,-\lambda_2) \big) \mathbin{\mathop{\otimes}\limits_{}} L(n) && \text{by (14)}, \\ \cong & \bigoplus_{k=0}^n \Delta(n-2-2k,\lambda_2) \oplus \bigoplus_{k=0}^n \Delta(n-2-2k,-\lambda_2) && \text{by Lemma 17}. \end{align} $$
$$ \begin{align} \nonumber S_{\bar{e}} {}\mathbin{\mathop{\otimes}\limits_{U}}{} & Q(n,\lambda_2^2) \cong S_{\bar{e}} \mathbin{\mathop{\otimes}\limits_{U}} \left( Q(0,\lambda_2^2) \mathbin{\mathop{\otimes}\limits_{}} L(n) \right) && \text{by (5)}, \\ \nonumber\cong & \left( S_{\bar{e}} \mathbin{\mathop{\otimes}\limits_{U}} Q(0,\lambda_2^2) \right) \mathbin{\mathop{\otimes}\limits_{}} L(n) && \text{by Lemma 19}, \\ \nonumber\cong & \, \big( \Delta(-2,\lambda_2) \oplus \Delta(-2,-\lambda_2) \big) \mathbin{\mathop{\otimes}\limits_{}} L(n) && \text{by (14)}, \\ \cong & \bigoplus_{k=0}^n \Delta(n-2-2k,\lambda_2) \oplus \bigoplus_{k=0}^n \Delta(n-2-2k,-\lambda_2) && \text{by Lemma 17}. \end{align} $$
On the other hand, by Proposition 30, we have
 $$ \begin{align} S_{\bar{e}} \mathbin{\mathop{\otimes}\limits_{U}} Q(n,\lambda_2^2) \cong \bigoplus_{k=0}^n S_{\bar{e}} \mathbin{\mathop{\otimes}\limits_{U}} V(n-2k,\lambda_2). \end{align} $$
$$ \begin{align} S_{\bar{e}} \mathbin{\mathop{\otimes}\limits_{U}} Q(n,\lambda_2^2) \cong \bigoplus_{k=0}^n S_{\bar{e}} \mathbin{\mathop{\otimes}\limits_{U}} V(n-2k,\lambda_2). \end{align} $$
By comparing the central characters (which are preserved under the localization) of the direct summands in (15) and (16), the claim (b) follows.
From Lemma 33, Proposition 34, and the definition of
![]() $V(n,\lambda _2)$
, we have:
$V(n,\lambda _2)$
, we have:
Corollary 35. Suppose
![]() $n \in \mathbb {Z}$
and
$n \in \mathbb {Z}$
and
![]() $\lambda _2 \neq 0$
. Then,
$\lambda _2 \neq 0$
. Then,
We want to prove that these annihilators are centrally generated. It is easier to do this for Verma modules. This has already been proved in [Reference Bavula and Lu6, Proposition 6.1]. We present a different and a more direct proof, and along the way reveal some structure of the quotients of U by the centrally generated ideals.
For this, we need to express elements of U modulo a maximal ideal in the center in a convenient way. We describe this in the next two lemmas. We denote by
![]() $U_0 := U(\mathfrak {T})_0$
, the zero-weight space of
$U_0 := U(\mathfrak {T})_0$
, the zero-weight space of
![]() $\mathfrak {h}$
in U.
$\mathfrak {h}$
in U.
Lemma 36. The subalgebra
![]() $U_0$
of U is generated by
$U_0$
of U is generated by
 $S=\{h, \bar {h}, fe, \bar {f}e, f\bar {e}, \bar {f}\bar {e}\}$
.
$S=\{h, \bar {h}, fe, \bar {f}e, f\bar {e}, \bar {f}\bar {e}\}$
.
Proof. We need to prove that any product
![]() $x = x_1 x_2 \ldots x_k$
, where each
$x = x_1 x_2 \ldots x_k$
, where each
![]() $x_i$
belongs to the standard basis of
$x_i$
belongs to the standard basis of
![]() $\mathfrak {T}$
, with the property that the number of i’s for which
$\mathfrak {T}$
, with the property that the number of i’s for which
 $x_i \in \{f,\bar {f}\}$
is equal to the number of j’s for which
$x_i \in \{f,\bar {f}\}$
is equal to the number of j’s for which
![]() $x_j \in \{e,\bar {e}\}$
, can be generated by elements in S. We prove this by induction on k. If
$x_j \in \{e,\bar {e}\}$
, can be generated by elements in S. We prove this by induction on k. If
![]() $x_1 x_2 \ldots x_k$
consists only of h and
$x_1 x_2 \ldots x_k$
consists only of h and
![]() $\bar {h}$
, we are done. If not, chose some
$\bar {h}$
, we are done. If not, chose some
 $x_i \in \{f,\bar {f}\}$
and
$x_i \in \{f,\bar {f}\}$
and
![]() $x_j \in \{e,\bar {e}\}$
, and assume without loss of generality
$x_j \in \{e,\bar {e}\}$
, and assume without loss of generality
![]() $i<j$
. We commute them to the rightmost place:
$i<j$
. We commute them to the rightmost place:
 $$ \begin{align*} x = (\underbrace{x_1 \ldots \hat{x_i} \ldots \hat{x_j} \ldots x_k}_{x'})(\underbrace{x_i x_j}_{\in S}) + \sum_t y_t,\end{align*} $$
$$ \begin{align*} x = (\underbrace{x_1 \ldots \hat{x_i} \ldots \hat{x_j} \ldots x_k}_{x'})(\underbrace{x_i x_j}_{\in S}) + \sum_t y_t,\end{align*} $$
where the factors with hat are omitted. It is clear from the commutation relations that
![]() $x'$
and all
$x'$
and all
![]() $y_t$
are products of the basis elements with the same property, but shorter. We are done by induction.
$y_t$
are products of the basis elements with the same property, but shorter. We are done by induction.
Lemma 37. Fix an algebra homomorphism
![]() $\chi \colon Z(\mathfrak {T}) \to \mathbb {C}$
. For any
$\chi \colon Z(\mathfrak {T}) \to \mathbb {C}$
. For any
 , there exists
, there exists
![]() $n \in \mathbb {Z}_{\geq 0}$
such that
$n \in \mathbb {Z}_{\geq 0}$
such that
 $(\bar {f}\bar {e})^n \cdot u$
is equal to a linear combination of monomials of the form
$(\bar {f}\bar {e})^n \cdot u$
is equal to a linear combination of monomials of the form
 $h^k \left (f \bar {e}\right )^l \left (\bar {h}\right )^m$
for
$h^k \left (f \bar {e}\right )^l \left (\bar {h}\right )^m$
for
![]() $k,l,m \in \mathbb {Z}_{\geq 0}$
, modulo
$k,l,m \in \mathbb {Z}_{\geq 0}$
, modulo
![]() $U_0 \cdot \operatorname {\mathrm {Ker}} \chi $
.
$U_0 \cdot \operatorname {\mathrm {Ker}} \chi $
.
Proof. In the quotient above, by using (7), we can express
![]() $\bar {f}\bar {e}$
as a linear combination of
$\bar {f}\bar {e}$
as a linear combination of
![]() $\bar {h}^2$
and
$\bar {h}^2$
and
![]() $1$
, and also
$1$
, and also
![]() $\bar {f}e$
as a linear combination of
$\bar {f}e$
as a linear combination of
![]() $\bar {h}h$
,
$\bar {h}h$
,
![]() $\bar {h}$
,
$\bar {h}$
,
![]() $f\bar {e}$
, and
$f\bar {e}$
, and
![]() $1$
. Using this with Lemma 36, we see that the generators in the quotient are just h,
$1$
. Using this with Lemma 36, we see that the generators in the quotient are just h,
![]() $\bar {h}$
,
$\bar {h}$
,
![]() $fe$
, and
$fe$
, and
![]() $f\bar {e}$
.
$f\bar {e}$
.
First, let us assume that
![]() $u=x_1 x_2 \ldots x_r$
, a product of these four generators in any order. Since h commutes with everything here, we can ignore it. Denote by
$u=x_1 x_2 \ldots x_r$
, a product of these four generators in any order. Since h commutes with everything here, we can ignore it. Denote by
![]() $a=fe$
,
$a=fe$
,
![]() $b=f\bar {e}$
, and
$b=f\bar {e}$
, and
![]() $c=\bar {h}$
,
$c=\bar {h}$
,
![]() $\chi _1 = \chi (C)$
and
$\chi _1 = \chi (C)$
and
 $\chi _2=\chi (\bar {C})$
. One can check that we have the following relations in the quotient:
$\chi _2=\chi (\bar {C})$
. One can check that we have the following relations in the quotient:
 $$ \begin{align} [c,b] &= \frac{1}{2}c^2 -\frac{1}{2}\chi_2, \end{align} $$
$$ \begin{align} [c,b] &= \frac{1}{2}c^2 -\frac{1}{2}\chi_2, \end{align} $$
 $$ \begin{align} \bar{f}\bar{e} \cdot a &= -b^2 - hc^2 - \frac{3}{2}c^2 - hbc - 2bc + \frac{\chi_1}{2}b + \frac{\chi_1}{2}c + \frac{\chi_2}{2}. \end{align} $$
$$ \begin{align} \bar{f}\bar{e} \cdot a &= -b^2 - hc^2 - \frac{3}{2}c^2 - hbc - 2bc + \frac{\chi_1}{2}b + \frac{\chi_1}{2}c + \frac{\chi_2}{2}. \end{align} $$
Suppose that
![]() $x_1 \neq a$
, but some
$x_1 \neq a$
, but some
![]() $x_i =a$
, and assume i is minimal. Using the relations (17) and (18), we commute
$x_i =a$
, and assume i is minimal. Using the relations (17) and (18), we commute
![]() $x_{i-1}x_i = x_i x_{i-1} + [x_{i-1},x_i]$
. In this way, u becomes a sum of several monomials, each of which has either one a less, or have their most-left a one place closer to the most-left position. It follows that we can move this a to the most left part in a finite number of steps, that is, we can express u as a finite sum
$x_{i-1}x_i = x_i x_{i-1} + [x_{i-1},x_i]$
. In this way, u becomes a sum of several monomials, each of which has either one a less, or have their most-left a one place closer to the most-left position. It follows that we can move this a to the most left part in a finite number of steps, that is, we can express u as a finite sum
![]() $u =\sum a y_t + \sum w_t$
, where
$u =\sum a y_t + \sum w_t$
, where
![]() $y_t$
is a finite product of a’s, b’s, and c’s, but has at least one a less than the original expression of u had, and
$y_t$
is a finite product of a’s, b’s, and c’s, but has at least one a less than the original expression of u had, and
![]() $w_t$
is a finite product of b’s and c’s.
$w_t$
is a finite product of b’s and c’s.
From (20) and the relation
![]() $4\bar {f}\bar {e} = \chi _2 - c^2$
, it follows that
$4\bar {f}\bar {e} = \chi _2 - c^2$
, it follows that
![]() $\bar {f}\bar {e} \cdot u$
is a finite sum
$\bar {f}\bar {e} \cdot u$
is a finite sum
![]() $\sum z_t$
, where each
$\sum z_t$
, where each
![]() $z_t$
is a product of a’s, b’s, and c’s, but has at least one a less than the original expression of u had. By induction, for some k, we get that
$z_t$
is a product of a’s, b’s, and c’s, but has at least one a less than the original expression of u had. By induction, for some k, we get that
 $(\bar {f}\bar {e})^k \cdot u$
is a finite sum of products of b’s and c’s.
$(\bar {f}\bar {e})^k \cdot u$
is a finite sum of products of b’s and c’s.
Now, observe that any product of b’s and c’s can be expressed as a linear combination of standard monomials
![]() $b^i c^j$
, using the relation (19) and a very similar reasoning as before. The point is that a does not appear in
$b^i c^j$
, using the relation (19) and a very similar reasoning as before. The point is that a does not appear in
![]() $[c,b]$
in (19), so we will not end up in an infinite loop.
$[c,b]$
in (19), so we will not end up in an infinite loop.
Finally, note that the argument is essentially the same if we started from u equal to a linear combination of products of the generators, instead of just one monomial.
Theorem 38. Suppose
![]() $n \in \mathbb {Z}$
and
$n \in \mathbb {Z}$
and
![]() $\lambda _2 \neq 0$
. The annihilators in Corollary 35 are centrally generated. More precisely, they are equal to the ideal
$\lambda _2 \neq 0$
. The annihilators in Corollary 35 are centrally generated. More precisely, they are equal to the ideal
![]() $U \cdot \operatorname {\mathrm {Ker}} \chi $
, where
$U \cdot \operatorname {\mathrm {Ker}} \chi $
, where
 $$ \begin{align*} \chi \colon Z(\mathfrak{T})=\mathbb{C}[C,\bar{C}] \to \mathbb{C} \end{align*} $$
$$ \begin{align*} \chi \colon Z(\mathfrak{T})=\mathbb{C}[C,\bar{C}] \to \mathbb{C} \end{align*} $$
is a homomorphism of algebras defined on the generators by
![]() $C \mapsto n\lambda _2$
and
$C \mapsto n\lambda _2$
and
 $\bar {C} \mapsto \lambda _2^2$
.
$\bar {C} \mapsto \lambda _2^2$
.
Proof. We prove this for the annihilator of the Verma module
![]() $\Delta := \Delta (n-2,\lambda _2)$
. This is known from [Reference Bavula and Lu6, Proposition 6.1], but we present here a different and a more direct proof.
$\Delta := \Delta (n-2,\lambda _2)$
. This is known from [Reference Bavula and Lu6, Proposition 6.1], but we present here a different and a more direct proof.
The inclusion
![]() $U \cdot \operatorname {\mathrm {Ker}} \chi \subseteq \operatorname {\mathrm {Ann}}(\Delta )$
is trivial. For the converse, recall that
$U \cdot \operatorname {\mathrm {Ker}} \chi \subseteq \operatorname {\mathrm {Ann}}(\Delta )$
is trivial. For the converse, recall that
![]() $\operatorname {\mathrm {Ann}}(\Delta )$
is stable under the adjoint action, so it is generated by its
$\operatorname {\mathrm {Ann}}(\Delta )$
is stable under the adjoint action, so it is generated by its
![]() $U_0$
part. So, it is enough to prove
$U_0$
part. So, it is enough to prove
To prove this, for any nonzero element
 , we want to find an element from
, we want to find an element from
![]() $\Delta $
which is not annihilated by u. Because of Lemma 37, we can assume without loss of generality that
$\Delta $
which is not annihilated by u. Because of Lemma 37, we can assume without loss of generality that
 $$ \begin{align*} u = \sum_{k,l,m \geq 0} \alpha_{klm} h^k \left(f \bar{e}\right)^l \left(\bar{h}\right)^m, \end{align*} $$
$$ \begin{align*} u = \sum_{k,l,m \geq 0} \alpha_{klm} h^k \left(f \bar{e}\right)^l \left(\bar{h}\right)^m, \end{align*} $$
with
![]() $\alpha _{klm} \in \mathbb {C}$
and only finitely many nonzero. Define a polynomial (with commutative variables) by the same scalars:
$\alpha _{klm} \in \mathbb {C}$
and only finitely many nonzero. Define a polynomial (with commutative variables) by the same scalars:
 $p(x,y,z)= \sum _{k,l,m \geq 0} \alpha _{klm} x^k y^l z^m \in \mathbb {C}[x,y,z]$
.
$p(x,y,z)= \sum _{k,l,m \geq 0} \alpha _{klm} x^k y^l z^m \in \mathbb {C}[x,y,z]$
.
Denote by v the highest weight vector in
![]() $\Delta $
, by
$\Delta $
, by
![]() $\Delta _{q}$
the weight space in
$\Delta _{q}$
the weight space in
![]() $\Delta $
of weight
$\Delta $
of weight
![]() $n-2-2q$
,
$n-2-2q$
,
![]() $q \geq 0$
, and recall that it has basis
$q \geq 0$
, and recall that it has basis
![]() $f^i \bar {f}^{q-i} v$
, for
$f^i \bar {f}^{q-i} v$
, for
![]() $i=0,1,\ldots ,q$
. Similarly to (8), one can prove the following formulas for the action on
$i=0,1,\ldots ,q$
. Similarly to (8), one can prove the following formulas for the action on
![]() $\Delta $
:
$\Delta $
:
 $$ \begin{align} \nonumber h \cdot f^i \bar{f}^{q-i} v &= (n-2-2q) f^i \bar{f}^{q-i} v, \\ \nonumber f\bar{e} \cdot f^i \bar{f}^{q-i} v &= i \lambda_2 f^i \bar{f}^{q-i} v -i(i-1) f^{i-1} \bar{f}^{q-i+1} v, \\ \bar{h} \cdot f^i \bar{f}^{q-i} v &= \lambda_2 f^i \bar{f}^{q-i} v -2i f^{i-1} \bar{f}^{q-i+1} v. \end{align} $$
$$ \begin{align} \nonumber h \cdot f^i \bar{f}^{q-i} v &= (n-2-2q) f^i \bar{f}^{q-i} v, \\ \nonumber f\bar{e} \cdot f^i \bar{f}^{q-i} v &= i \lambda_2 f^i \bar{f}^{q-i} v -i(i-1) f^{i-1} \bar{f}^{q-i+1} v, \\ \bar{h} \cdot f^i \bar{f}^{q-i} v &= \lambda_2 f^i \bar{f}^{q-i} v -2i f^{i-1} \bar{f}^{q-i+1} v. \end{align} $$
It follows that in this basis of
![]() $\Delta _q$
, the operator representing u is upper triangular, with the diagonal entries
$\Delta _q$
, the operator representing u is upper triangular, with the diagonal entries
![]() $p(n-2-2q,i \lambda _2,\lambda _2)$
,
$p(n-2-2q,i \lambda _2,\lambda _2)$
,
![]() $i=0,\ldots ,q$
. We would like to find a basis element
$i=0,\ldots ,q$
. We would like to find a basis element
![]() $f^i \bar {f}^{q-i} v$
, for which
$f^i \bar {f}^{q-i} v$
, for which
![]() $p(n-2-2q,i \lambda _2,\lambda _2) \neq 0$
. However, a problem arises if
$p(n-2-2q,i \lambda _2,\lambda _2) \neq 0$
. However, a problem arises if
![]() $p(x,y,z)$
is divisible by
$p(x,y,z)$
is divisible by
![]() $(z-\lambda _2)$
.
$(z-\lambda _2)$
.
We claim that we can decompose
for some
![]() $r \geq 0$
, such that
$r \geq 0$
, such that
![]() $\tilde {p}(n-2-2q,i \lambda _2,\lambda _2)$
is not identically zero for
$\tilde {p}(n-2-2q,i \lambda _2,\lambda _2)$
is not identically zero for
![]() $(q,i) \in D$
, where
$(q,i) \in D$
, where
![]() $D \subseteq \mathbb {C}^2$
is any Zariski dense subset.
$D \subseteq \mathbb {C}^2$
is any Zariski dense subset.
To prove this claim, write
 $p(x,y,z)= \sum _{j=0}^m p_j(x,y)(z-\lambda _2)^j$
. Suppose that this is zero when evaluated on
$p(x,y,z)= \sum _{j=0}^m p_j(x,y)(z-\lambda _2)^j$
. Suppose that this is zero when evaluated on
![]() $D \times \{\lambda _2\}$
for a Zariski dense set
$D \times \{\lambda _2\}$
for a Zariski dense set
![]() $D \subseteq \mathbb {C}^2$
. It follows that
$D \subseteq \mathbb {C}^2$
. It follows that
![]() $p_0(x,y)=0$
(on
$p_0(x,y)=0$
(on
![]() $\mathbb {C}^2$
), so
$\mathbb {C}^2$
), so
 $p(x,y,z)= p^{(1)}(x,y,z)(z-\lambda _2)$
, for a polynomial
$p(x,y,z)= p^{(1)}(x,y,z)(z-\lambda _2)$
, for a polynomial
 $p^{(1)}(x,y,z)$
of a strictly smaller total degree. If necessary, we continue to apply the same argument inductively on
$p^{(1)}(x,y,z)$
of a strictly smaller total degree. If necessary, we continue to apply the same argument inductively on
 $p^{(1)}(x,y,z)$
, and so on, until we reach (22) with
$p^{(1)}(x,y,z)$
, and so on, until we reach (22) with
![]() $\tilde {p}(x,y,\lambda _2)$
nonzero on some point in
$\tilde {p}(x,y,\lambda _2)$
nonzero on some point in
![]() $(x,y) \in D$
. The number r is independent of D, since the set
$(x,y) \in D$
. The number r is independent of D, since the set
![]() $\{(x,y) \colon \tilde {p}(x,y,\lambda _2) \neq 0\}$
is nonempty and Zariski open, hence intersects any Zariski dense set in
$\{(x,y) \colon \tilde {p}(x,y,\lambda _2) \neq 0\}$
is nonempty and Zariski open, hence intersects any Zariski dense set in
![]() $\mathbb {C}^2$
.
$\mathbb {C}^2$
.
The claim is now proved, because the map
![]() $(q,i) \mapsto (n-2-2q,i \lambda _2)$
is an algebraic isomorphism
$(q,i) \mapsto (n-2-2q,i \lambda _2)$
is an algebraic isomorphism
![]() $\mathbb {C}^2 \to \mathbb {C}^2$
. Here, it is crucial that
$\mathbb {C}^2 \to \mathbb {C}^2$
. Here, it is crucial that
![]() $\lambda _2 \neq 0$
.
$\lambda _2 \neq 0$
.
Write
 $\tilde {p}(x,y,z)= \sum _{k,l,m \geq 0} \tilde {\alpha }_{klm} x^k y^l z^m$
, and define
$\tilde {p}(x,y,z)= \sum _{k,l,m \geq 0} \tilde {\alpha }_{klm} x^k y^l z^m$
, and define
 $\tilde {u}= \sum _{k,l,m \geq 0} \tilde {\alpha }_{klm} h^k \left (f \bar {e}\right )^l \left (\bar {h}\right )^m$
. Then, it is also true that
$\tilde {u}= \sum _{k,l,m \geq 0} \tilde {\alpha }_{klm} h^k \left (f \bar {e}\right )^l \left (\bar {h}\right )^m$
. Then, it is also true that
 $$ \begin{align*} u = \tilde{u} \cdot (\bar{h}-\lambda_2)^r, \end{align*} $$
$$ \begin{align*} u = \tilde{u} \cdot (\bar{h}-\lambda_2)^r, \end{align*} $$
since the monomials in u and
![]() $\tilde {u}$
have
$\tilde {u}$
have
![]() $\bar {h}$
on the most-right position, so no commuting of the variables is necessary.
$\bar {h}$
on the most-right position, so no commuting of the variables is necessary.
There exists a pair
![]() $(q,i)$
from the cone
$(q,i)$
from the cone
![]() $\{(q,i) \in \mathbb {Z}\times \mathbb {Z} \colon q\geq r, \ 0 \leq i \leq q-r \}$
(which is Zariski dense in
$\{(q,i) \in \mathbb {Z}\times \mathbb {Z} \colon q\geq r, \ 0 \leq i \leq q-r \}$
(which is Zariski dense in
![]() $\mathbb {C}^2$
), such that
$\mathbb {C}^2$
), such that
![]() $\tilde {p}(n-2-2q,i \lambda _2,\lambda _2) \neq 0$
. Put
$\tilde {p}(n-2-2q,i \lambda _2,\lambda _2) \neq 0$
. Put
 $w:=f^{i+r} \bar {f}^{q-i-r}v \in \Delta _q$
. It follows from (21) that
$w:=f^{i+r} \bar {f}^{q-i-r}v \in \Delta _q$
. It follows from (21) that
 $(\bar {h}-\lambda _2)^r \cdot w = c \cdot f^{i} \bar {f}^{q-i}$
, for some constant
$(\bar {h}-\lambda _2)^r \cdot w = c \cdot f^{i} \bar {f}^{q-i}$
, for some constant
![]() $c \neq 0$
. From this, we have that
$c \neq 0$
. From this, we have that
 $$ \begin{align*} u \cdot w &= c \cdot \tilde{u} \cdot f^{i} \bar{f}^{q-i}v \\ &= c \cdot \tilde{p}(n-2-2q,i \lambda_2,\lambda_2) \cdot f^{i} \bar{f}^{q-i}v + \sum_{j=0}^{i-1} c_j f^{j} \bar{f}^{q-j}v \neq 0. \end{align*} $$
$$ \begin{align*} u \cdot w &= c \cdot \tilde{u} \cdot f^{i} \bar{f}^{q-i}v \\ &= c \cdot \tilde{p}(n-2-2q,i \lambda_2,\lambda_2) \cdot f^{i} \bar{f}^{q-i}v + \sum_{j=0}^{i-1} c_j f^{j} \bar{f}^{q-j}v \neq 0. \end{align*} $$
This finishes the proof of the theorem.
4.8. The action of finite-dimensional
 $\mathfrak {sl}_2$
-modules
$\mathfrak {sl}_2$
-modules
Denote by
![]() $\mathscr {F}$
the monoidal category of finite-dimensional
$\mathscr {F}$
the monoidal category of finite-dimensional
![]() $\mathfrak {sl}_2$
-modules. For a fixed nonzero
$\mathfrak {sl}_2$
-modules. For a fixed nonzero
![]() $\chi \in \mathbb {C}$
, denote by
$\chi \in \mathbb {C}$
, denote by
![]() $\mathcal {H}_{\chi }$
the category of semisimple
$\mathcal {H}_{\chi }$
the category of semisimple
![]() $\mathfrak {g}$
-Harish-Chandra
$\mathfrak {g}$
-Harish-Chandra
![]() $\mathfrak {T}$
-modules on which the action of the purely Takiff part of the center is given by
$\mathfrak {T}$
-modules on which the action of the purely Takiff part of the center is given by
![]() $\chi $
.
$\chi $
.
Proposition 39. For each nonzero
![]() $\chi $
, the category
$\chi $
, the category
![]() $\mathcal {H}_{\chi }$
is a simple module category over the monoidal category
$\mathcal {H}_{\chi }$
is a simple module category over the monoidal category
![]() $\mathscr {F}$
.
$\mathscr {F}$
.
Proof. The fact that
![]() $\mathcal {H}_{\chi }$
is a module category over
$\mathcal {H}_{\chi }$
is a module category over
![]() $\mathscr {F}$
follows directly from Proposition 29. Since
$\mathscr {F}$
follows directly from Proposition 29. Since
![]() $\mathcal {H}_{\chi }$
is semisimple by definition, to show that it is a simple module category over
$\mathcal {H}_{\chi }$
is semisimple by definition, to show that it is a simple module category over
![]() $\mathscr {F}$
, it is enough to show that, starting from any simple object of
$\mathscr {F}$
, it is enough to show that, starting from any simple object of
![]() $\mathcal {H}_{\chi }$
and tensoring it with finite-dimensional
$\mathcal {H}_{\chi }$
and tensoring it with finite-dimensional
![]() $\mathfrak {sl}_2$
-modules, we can obtain any other simple object of
$\mathfrak {sl}_2$
-modules, we can obtain any other simple object of
![]() $\mathcal {H}_{\chi }$
as a direct summand, up to isomorphism. This claim follows by combining Proposition 29 with Theorem 31.
$\mathcal {H}_{\chi }$
as a direct summand, up to isomorphism. This claim follows by combining Proposition 29 with Theorem 31.
We note that, by Proposition 29, the combinatorics of the
![]() $\mathscr {F}$
-module category
$\mathscr {F}$
-module category
![]() $\mathcal {H}_{\chi }$
does not depend on
$\mathcal {H}_{\chi }$
does not depend on
![]() $\chi $
.
$\chi $
.
5.
 $\mathfrak {sl}_2$
-Harish-Chandra modules for the Schrödinger Lie algebra
$\mathfrak {sl}_2$
-Harish-Chandra modules for the Schrödinger Lie algebra
5.1. Setup
The Schrödinger Lie algebra
![]() $\mathfrak {s}$
can be defined by basis
$\mathfrak {s}$
can be defined by basis
![]() $\{e,h,f,p,q,z\}$
and the following relations: in addition to the usual
$\{e,h,f,p,q,z\}$
and the following relations: in addition to the usual
![]() $\mathfrak {g} :=\mathfrak {sl}_2$
relations on
$\mathfrak {g} :=\mathfrak {sl}_2$
relations on
![]() $e,h,f$
, we also have
$e,h,f$
, we also have
 $$ \begin{align*} &[e,p] = 0, & &[h,p] = p, & &[f,p] = q, && \\ &[e,q] = p, & &[h,q] = -q, & &[f,q] = 0, && [p,q]=z, \end{align*} $$
$$ \begin{align*} &[e,p] = 0, & &[h,p] = p, & &[f,p] = q, && \\ &[e,q] = p, & &[h,q] = -q, & &[f,q] = 0, && [p,q]=z, \end{align*} $$
and z is declared to commute with all
![]() $\mathfrak {s}$
. It is clear that
$\mathfrak {s}$
. It is clear that
![]() $\mathfrak {s} = \mathfrak {g} \ltimes \mathfrak {H}$
, where
$\mathfrak {s} = \mathfrak {g} \ltimes \mathfrak {H}$
, where
![]() $\mathfrak {H}$
is the ideal spanned by
$\mathfrak {H}$
is the ideal spanned by
![]() $p,q,z$
, and is isomorphic to the three-dimensional Heisenberg Lie algebra. As a
$p,q,z$
, and is isomorphic to the three-dimensional Heisenberg Lie algebra. As a
![]() $\mathfrak {g}$
-module,
$\mathfrak {g}$
-module,
![]() $\mathfrak {H}$
is isomorphic to
$\mathfrak {H}$
is isomorphic to
![]() $L(1) \oplus L(0)$
.
$L(1) \oplus L(0)$
.
The nilradical of
![]() $\mathfrak {s}$
is
$\mathfrak {s}$
is
![]() $\operatorname {\mathrm {Nrad}}(\mathfrak {s})=[\mathfrak {s},\mathfrak {H}]=\mathfrak {H}$
. Recall that this means that
$\operatorname {\mathrm {Nrad}}(\mathfrak {s})=[\mathfrak {s},\mathfrak {H}]=\mathfrak {H}$
. Recall that this means that
![]() $\mathfrak {H}$
must necessarily annihilate any simple finite-dimensional
$\mathfrak {H}$
must necessarily annihilate any simple finite-dimensional
![]() $\mathfrak {s}$
-module.
$\mathfrak {s}$
-module.
There is also the centerless Schrödinger Lie algebra
![]() , which is isomorphic to the semidirect product
, which is isomorphic to the semidirect product
![]() $\mathfrak {g} \ltimes L(1)$
.
$\mathfrak {g} \ltimes L(1)$
.
The disclaimer from the previous section related to Reference Bavula and Lu[6] applies to the present section with respect to Reference Bavula and Lu[7].
The algebra
![]() $U(\mathfrak {s})$
is free as a module over its center
$U(\mathfrak {s})$
is free as a module over its center
![]() $Z(\mathfrak {s})$
, and
$Z(\mathfrak {s})$
, and
![]() $Z(\mathfrak {s})$
is generated by two algebraically independent generators (see, e.g., Reference Dubsky, Lü, Mazorchuk and Zhao[20]):
$Z(\mathfrak {s})$
is generated by two algebraically independent generators (see, e.g., Reference Dubsky, Lü, Mazorchuk and Zhao[20]):
 $$ \begin{align} C := (h^2+h+4fe)z - 2(fp^2 -eq^2-hpq), \text{ and } z. \end{align} $$
$$ \begin{align} C := (h^2+h+4fe)z - 2(fp^2 -eq^2-hpq), \text{ and } z. \end{align} $$
It is also clear that
![]() $Z(\mathfrak {s}) \cap U(\mathfrak {H}) = \mathbb {C}[z]$
, which we will refer to as the purely Schrödinger part of the center. For a module with central character, the scalar by which z acts is usually called the central charge of the module.
$Z(\mathfrak {s}) \cap U(\mathfrak {H}) = \mathbb {C}[z]$
, which we will refer to as the purely Schrödinger part of the center. For a module with central character, the scalar by which z acts is usually called the central charge of the module.
The theory we develop here for the Schrödinger Lie algebra is very similar to the Takiff
![]() $\mathfrak {sl}_2$
case. So we will omit most of the details, as they are usually analogous, but easier. One reason for this is that the purely Schrödinger part of the center is generated by a degree
$\mathfrak {sl}_2$
case. So we will omit most of the details, as they are usually analogous, but easier. One reason for this is that the purely Schrödinger part of the center is generated by a degree
![]() $1$
element, and for the Takiff
$1$
element, and for the Takiff
![]() $\mathfrak {sl}_2$
, we had a degree
$\mathfrak {sl}_2$
, we had a degree
![]() $2$
element. However, a small complication now is that the radical of
$2$
element. However, a small complication now is that the radical of
![]() $\mathfrak {s}$
is not abelian anymore.
$\mathfrak {s}$
is not abelian anymore.
5.2. Universal modules
As before, the universal modules are induced from
![]() $\mathfrak {g}$
, that is, for
$\mathfrak {g}$
, that is, for
![]() $n \in \mathbb {Z}_{\geq 0}$
, set
$n \in \mathbb {Z}_{\geq 0}$
, set
 $Q(n) := \operatorname {\mathrm {Ind}}_{\mathfrak {g}}^{\mathfrak {s}} L(n) = U(\mathfrak {s}) \mathbin {\mathop {\otimes }\limits _{U(\mathfrak {g})}} L(n) \cong U(\mathfrak {H}) \mathbin {\mathop {\otimes }\limits _{\mathbb {C}}} L(n)$
. Recall that
$Q(n) := \operatorname {\mathrm {Ind}}_{\mathfrak {g}}^{\mathfrak {s}} L(n) = U(\mathfrak {s}) \mathbin {\mathop {\otimes }\limits _{U(\mathfrak {g})}} L(n) \cong U(\mathfrak {H}) \mathbin {\mathop {\otimes }\limits _{\mathbb {C}}} L(n)$
. Recall that
![]() $Q(n) \cong Q(0) \mathbin {\mathop {\otimes }\limits _{}} L(n)$
, where we consider
$Q(n) \cong Q(0) \mathbin {\mathop {\otimes }\limits _{}} L(n)$
, where we consider
![]() $L(n)$
as an
$L(n)$
as an
![]() $\mathfrak {s}$
-module with the trivial
$\mathfrak {s}$
-module with the trivial
![]() $\mathfrak {H}$
-action.
$\mathfrak {H}$
-action.
Proposition 40. We have the following isomorphisms of algebras:
where
![]() $U(\mathfrak {H})^{\mathfrak {g}}$
denotes the invariants of the adjoint action of
$U(\mathfrak {H})^{\mathfrak {g}}$
denotes the invariants of the adjoint action of
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() $U(\mathfrak {H})$
.
$U(\mathfrak {H})$
.
Proof. The isomorphism
![]() $\operatorname {\mathrm {End}}(Q(0))^{\text {op}} \cong U(\mathfrak {H})^{\mathfrak {g}}$
follows from the same argument as in the proof of Proposition 7. The inclusion
$\operatorname {\mathrm {End}}(Q(0))^{\text {op}} \cong U(\mathfrak {H})^{\mathfrak {g}}$
follows from the same argument as in the proof of Proposition 7. The inclusion
![]() $U(\mathfrak {H})^{\mathfrak {g}} \supseteq \mathbb {C}[z]$
is obvious. The converse follows easily from the following commutation relations:
$U(\mathfrak {H})^{\mathfrak {g}} \supseteq \mathbb {C}[z]$
is obvious. The converse follows easily from the following commutation relations:
 $$ \begin{align} [h,p^mq^n] &= (m-n) p^mq^n, \\ \nonumber [e,p^mq^n] &= n p^{m+1} q^{n-1} - \frac{n(n-1)}{2} p^{m} q^{n-2}z, \\ \nonumber [f,p^mq^n] &= m p^{m-1} q^{n+1} - \frac{m(m-1)}{2} p^{m-2} q^{n}z, \end{align} $$
$$ \begin{align} [h,p^mq^n] &= (m-n) p^mq^n, \\ \nonumber [e,p^mq^n] &= n p^{m+1} q^{n-1} - \frac{n(n-1)}{2} p^{m} q^{n-2}z, \\ \nonumber [f,p^mq^n] &= m p^{m-1} q^{n+1} - \frac{m(m-1)}{2} p^{m-2} q^{n}z, \end{align} $$
which can be proved, for example, by induction.
Fix
![]() $\chi \in \mathbb {C}$
, and denote by
$\chi \in \mathbb {C}$
, and denote by
![]() $\mathbf {m}_\chi $
the maximal ideal
$\mathbf {m}_\chi $
the maximal ideal
![]() $(z-\chi ) \subseteq \mathbb {C}[z]$
. As before, we define the universal module as
$(z-\chi ) \subseteq \mathbb {C}[z]$
. As before, we define the universal module as
 . It clearly has central charge
. It clearly has central charge
![]() $\chi $
. As before, we have
$\chi $
. As before, we have
![]() $Q(n,\chi ) \cong Q(0,\chi ) \otimes L(n)$
.
$Q(n,\chi ) \cong Q(0,\chi ) \otimes L(n)$
.
Lemma 41.
-
(a) As
 $\mathfrak {s}$
-modules,
$\mathfrak {s}$
-modules,
 $Q(0) \cong U(\mathfrak {H})$
and
$Q(0) \cong U(\mathfrak {H})$
and
 , where
, where
 $\mathfrak {g}$
acts by the adjoint action, and
$\mathfrak {g}$
acts by the adjoint action, and
 $\mathfrak {H}$
by the left multiplication. The set
$\mathfrak {H}$
by the left multiplication. The set
 $\big \{p^i q^j \colon i,j \geq 0\big \}$
is a basis for
$\big \{p^i q^j \colon i,j \geq 0\big \}$
is a basis for
 $Q(0,\chi )$
.
$Q(0,\chi )$
. -
(b) As a
 $\mathfrak {g}$
-module,
$\mathfrak {g}$
-module,
 $Q(0,\chi ) \cong \bigoplus _{k\geq 0} L(k)$
. Moreover,
$Q(0,\chi ) \cong \bigoplus _{k\geq 0} L(k)$
. Moreover,
 $p^k$
is the highest weight vector in
$p^k$
is the highest weight vector in
 $L(k)$
.
$L(k)$
. -
(c) C acts as zero on
 $Q(0)$
and every
$Q(0)$
and every
 $Q(0,\chi )$
.
$Q(0,\chi )$
.
Proof. The first claim is clear. We use it to prove the others.
For the second claim, note that
![]() $p^k$
generates a
$p^k$
generates a
![]() $\mathfrak {g}$
-submodule isomorphic to
$\mathfrak {g}$
-submodule isomorphic to
![]() $L(k)$
. Since the action of
$L(k)$
. Since the action of
![]() $\mathfrak {g}$
preserves
$\mathfrak {g}$
preserves
![]() $Q^n :=\operatorname {span}\{p^i q^j \colon i+j \leq n\}$
, by counting dimensions, we see that
$Q^n :=\operatorname {span}\{p^i q^j \colon i+j \leq n\}$
, by counting dimensions, we see that
![]() $Q^n \cong \oplus _{k=0}^n L(k)$
. The claim now follows by taking colimits.
$Q^n \cong \oplus _{k=0}^n L(k)$
. The claim now follows by taking colimits.
The last claim can be checked directly (enough on the generator of
![]() $Q(0)$
).
$Q(0)$
).
From the previous lemma, the Clebsch–Gordan coefficients for
![]() $\mathfrak {sl}_2$
, and the adjunction, the following is not hard to deduce:
$\mathfrak {sl}_2$
, and the adjunction, the following is not hard to deduce:
Proposition 42.
-
(a)
 $Q(n,\chi )$
is a
$Q(n,\chi )$
is a
 $\mathfrak {g}$
-Harish-Chandra module, and for
$\mathfrak {g}$
-Harish-Chandra module, and for
 $k \geq 0$
: (25)
$k \geq 0$
: (25) $$ \begin{align} [Q(n,\chi) \colon L(k)] = \min\{k+1,n+1\}. \end{align} $$
$$ \begin{align} [Q(n,\chi) \colon L(k)] = \min\{k+1,n+1\}. \end{align} $$
-
(b) Let V be any simple
 $\mathfrak {s}$
-module that has some
$\mathfrak {s}$
-module that has some
 $L(n)$
as a simple
$L(n)$
as a simple
 $\mathfrak {g}$
-submodule. Then, V is a quotient of
$\mathfrak {g}$
-submodule. Then, V is a quotient of
 $Q(n,\chi )$
for a unique
$Q(n,\chi )$
for a unique
 $\chi $
. In particular, V is a
$\chi $
. In particular, V is a
 $\mathfrak {g}$
-Harish-Chandra module, and (25) gives an upper bound for the multiplicities of its
$\mathfrak {g}$
-Harish-Chandra module, and (25) gives an upper bound for the multiplicities of its
 $\mathfrak {g}$
-types.
$\mathfrak {g}$
-types. -
(c) For a fixed
 $\chi $
, there exists a unique simple
$\chi $
, there exists a unique simple
 $\mathfrak {s}$
-module which contains
$\mathfrak {s}$
-module which contains
 $L(0)$
as a
$L(0)$
as a
 $\mathfrak {g}$
-submodule and has central charge
$\mathfrak {g}$
-submodule and has central charge
 $\chi $
. Moreover, it is a
$\chi $
. Moreover, it is a
 $\mathfrak {g}$
-Harish-Chandra module.
$\mathfrak {g}$
-Harish-Chandra module.
Theorem 43. The module
![]() $Q(0,\chi )$
is simple if and only if
$Q(0,\chi )$
is simple if and only if
![]() $\chi \neq 0$
.
$\chi \neq 0$
.
The module
![]() $Q(0,0)$
has infinite length, and an
$Q(0,0)$
has infinite length, and an
![]() $\mathfrak {s}$
-filtration whose composition factors are
$\mathfrak {s}$
-filtration whose composition factors are
![]() $L(0), L(1), L(2) \ldots $
with the trivial action of
$L(0), L(1), L(2) \ldots $
with the trivial action of
![]() $\mathfrak {H}$
.
$\mathfrak {H}$
.
Proof. As before, the
![]() $\mathfrak {s}$
-action on
$\mathfrak {s}$
-action on
![]() $Q(0)$
and
$Q(0)$
and
![]() $Q(0,\chi )$
will be denoted by
$Q(0,\chi )$
will be denoted by
![]() $\circ $
.
$\circ $
.
Note that
 $[q,p^n] = -n p^{n-1}z$
and
$[q,p^n] = -n p^{n-1}z$
and
 $[p,q^n] = n q^{n-1}z$
. Using this and the equations (24), one can check that
$[p,q^n] = n q^{n-1}z$
. Using this and the equations (24), one can check that
 $$ \begin{align*} (pf - nq) \circ p^n = \frac{n(n+1)}{2}\chi \cdot p^{n-1}. \end{align*} $$
$$ \begin{align*} (pf - nq) \circ p^n = \frac{n(n+1)}{2}\chi \cdot p^{n-1}. \end{align*} $$
So, if
![]() $\chi \neq 0$
, the module
$\chi \neq 0$
, the module
![]() $Q(0,\chi )$
is simple.
$Q(0,\chi )$
is simple.
Alternatively, one can use a nilradical argument analogous to the one in Remark 13.
If
![]() $\chi =0$
, then p and q commute in
$\chi =0$
, then p and q commute in
![]() $Q(0,\chi )$
, and
$Q(0,\chi )$
, and
![]() $\mathfrak {g}$
preserves the total degree of monomials
$\mathfrak {g}$
preserves the total degree of monomials
![]() $p^iq^j$
. The rest of the proof is obvious.
$p^iq^j$
. The rest of the proof is obvious.
5.3. Verma modules
Verma modules for the Schrödinger Lie algebra are studied in detail in Reference Dubsky, Lü, Mazorchuk and Zhao[20].
In the triangular decomposition (1), we have
 $$ \begin{align*} \tilde{\mathfrak{n}}_- = \operatorname{span}\{f,q\}, \ \tilde{\mathfrak{h}} = \operatorname{span}\{h,z\}, \ \text{and} \ \tilde{\mathfrak{n}}_+ = \operatorname{span}\{e,p\}. \end{align*} $$
$$ \begin{align*} \tilde{\mathfrak{n}}_- = \operatorname{span}\{f,q\}, \ \tilde{\mathfrak{h}} = \operatorname{span}\{h,z\}, \ \text{and} \ \tilde{\mathfrak{n}}_+ = \operatorname{span}\{e,p\}. \end{align*} $$
For an element
 $\lambda \in \tilde {\mathfrak {h}}^\ast $
, denote
$\lambda \in \tilde {\mathfrak {h}}^\ast $
, denote
![]() $\lambda _1 := \lambda (h)$
and
$\lambda _1 := \lambda (h)$
and
![]() $\lambda _2 := \lambda (z)$
.
$\lambda _2 := \lambda (z)$
.
Proposition 44 [Reference Dubsky, Lü, Mazorchuk and Zhao20, Proposition 5]
If
![]() $\lambda _2 \neq 0$
, then the Verma module
$\lambda _2 \neq 0$
, then the Verma module
![]() $\Delta (\lambda )$
is simple for any
$\Delta (\lambda )$
is simple for any
![]() $\lambda _1 \in \mathbb {Z}$
.
$\lambda _1 \in \mathbb {Z}$
.
It is easy to see that the central element C acts on the Verma module
![]() $\Delta (\lambda )$
as the scalar
$\Delta (\lambda )$
as the scalar
![]() $(\lambda _1+1)(\lambda _1+2)\lambda _2$
, and the central charge is
$(\lambda _1+1)(\lambda _1+2)\lambda _2$
, and the central charge is
![]() $\chi := \lambda _2$
(see (23)). We will be concerned mostly with nonzero central charge cases.
$\chi := \lambda _2$
(see (23)). We will be concerned mostly with nonzero central charge cases.
Lemma 45. Nonisomorphic Verma modules
![]() $\Delta (\lambda )$
and
$\Delta (\lambda )$
and
![]() $\Delta (\lambda ')$
with the same nonzero central charge have the same central character if and only if
$\Delta (\lambda ')$
with the same nonzero central charge have the same central character if and only if
![]() $\lambda ^{\prime }_1 = -\lambda _1-3$
.
$\lambda ^{\prime }_1 = -\lambda _1-3$
.
Proof. This reduces to solving the equation
![]() $(\lambda _1+1)(\lambda _1+2) = (\lambda ^{\prime }_1+1)(\lambda ^{\prime }_1+2)$
.
$(\lambda _1+1)(\lambda _1+2) = (\lambda ^{\prime }_1+1)(\lambda ^{\prime }_1+2)$
.
Lemma 46. As a
![]() $\mathfrak {g}$
-module,
$\mathfrak {g}$
-module,
![]() $\Delta (\lambda )$
has a filtration with subquotients isomorphic to the
$\Delta (\lambda )$
has a filtration with subquotients isomorphic to the
![]() $\mathfrak {g}$
-Verma modules
$\mathfrak {g}$
-Verma modules
![]() $\Delta ^{\mathfrak {g}}(\lambda _1 - k)$
,
$\Delta ^{\mathfrak {g}}(\lambda _1 - k)$
,
![]() $k = 0, 1, 2, \ldots $
.
$k = 0, 1, 2, \ldots $
.
If
![]() $\lambda _2 = 0$
or
$\lambda _2 = 0$
or
![]() $\lambda _1 \not \in \mathbb {Z}_{\geq 0}$
, then as a
$\lambda _1 \not \in \mathbb {Z}_{\geq 0}$
, then as a
![]() $\mathfrak {g}$
-module, we have
$\mathfrak {g}$
-module, we have
 $\Delta (\lambda ) \cong \bigoplus _{k \geq 0} \Delta ^{\mathfrak {g}}(\lambda _1 - k)$
. Otherwise (
$\Delta (\lambda ) \cong \bigoplus _{k \geq 0} \Delta ^{\mathfrak {g}}(\lambda _1 - k)$
. Otherwise (
![]() $\lambda _2 \neq 0$
and
$\lambda _2 \neq 0$
and
![]() $\lambda _1 \in \mathbb {Z}_{\geq 0}$
), we have as
$\lambda _1 \in \mathbb {Z}_{\geq 0}$
), we have as
![]() $\mathfrak {g}$
-modules
$\mathfrak {g}$
-modules
 $$ \begin{align*} \Delta(\lambda) \cong \Delta^{\mathfrak{g}}(-1)\oplus \bigoplus_{k =2}^{\lambda_1+2} P^{\mathfrak{g}}(-k) \oplus \bigoplus_{k \geq 3} \Delta^{\mathfrak{g}}(-\lambda_1 - k). \end{align*} $$
$$ \begin{align*} \Delta(\lambda) \cong \Delta^{\mathfrak{g}}(-1)\oplus \bigoplus_{k =2}^{\lambda_1+2} P^{\mathfrak{g}}(-k) \oplus \bigoplus_{k \geq 3} \Delta^{\mathfrak{g}}(-\lambda_1 - k). \end{align*} $$
Proof. Denote by
![]() $v_\lambda $
a basis element of
$v_\lambda $
a basis element of
![]() $\mathbb {C}_\lambda $
. Then,
$\mathbb {C}_\lambda $
. Then,
![]() $\Delta (\lambda )$
has a basis of weight vectors
$\Delta (\lambda )$
has a basis of weight vectors
![]() $\{ f^i q^j v_\lambda \colon i,j \geq 0\}$
. A direct computation shows that
$\{ f^i q^j v_\lambda \colon i,j \geq 0\}$
. A direct computation shows that
 $$ \begin{align*} e \cdot f^i q^j v_\lambda = i(\lambda_1 - i -j +1) f^{i-1} q^j v_\lambda + \lambda_2 \frac{j(j-1)}{2} f^i q^{j-2} v_\lambda. \end{align*} $$
$$ \begin{align*} e \cdot f^i q^j v_\lambda = i(\lambda_1 - i -j +1) f^{i-1} q^j v_\lambda + \lambda_2 \frac{j(j-1)}{2} f^i q^{j-2} v_\lambda. \end{align*} $$
This implies that the required filtration is given by the degree of q. The subquotients are given by the span of
 $\{ f^i q^k v_\lambda \colon i \geq 0\}$
, which is clearly isomorphic to
$\{ f^i q^k v_\lambda \colon i \geq 0\}$
, which is clearly isomorphic to
![]() $\Delta ^{\mathfrak {g}}(\lambda _1 - k)$
. The rest can be proved in the same way as for Lemma 16.
$\Delta ^{\mathfrak {g}}(\lambda _1 - k)$
. The rest can be proved in the same way as for Lemma 16.
Lemma 47. For
![]() $\lambda _1 \in \mathbb {Z}$
,
$\lambda _1 \in \mathbb {Z}$
,
![]() $\lambda _2 \neq 0$
, and
$\lambda _2 \neq 0$
, and
![]() $\mu \in \mathbb {Z}_{\geq 0}$
, there is an isomorphism of
$\mu \in \mathbb {Z}_{\geq 0}$
, there is an isomorphism of
![]() $\mathfrak {s}$
-modules
$\mathfrak {s}$
-modules
Proof. The left-hand side has a filtration with subquotients equal to the summands on the right-hand side. But these subquotients have different central characters by Lemma 45, since the first components of their highest weights have the same parity, so they must split.
5.4. Enright–Arkhipov completion
Fix an
![]() $\operatorname {\mathrm {ad}}$
-nilpotent element
$\operatorname {\mathrm {ad}}$
-nilpotent element
![]() $x \in \mathfrak {s}$
(e.g., f or p, which we will use), and denote by
$x \in \mathfrak {s}$
(e.g., f or p, which we will use), and denote by
 the localization of the algebra
the localization of the algebra
![]() $U(\mathfrak {s})$
by x, modulo the canonical copy of
$U(\mathfrak {s})$
by x, modulo the canonical copy of
![]() $U(\mathfrak {s})$
inside it. This is a
$U(\mathfrak {s})$
inside it. This is a
![]() $U(\mathfrak {s})$
-bimodule. For an
$U(\mathfrak {s})$
-bimodule. For an
![]() $\mathfrak {s}$
-module M, write
$\mathfrak {s}$
-module M, write
 $$ \begin{align*} \operatorname{\mathrm{\mathbf{EA}}}(M) := {}^{e}{\left( S_f \mathbin{\mathop{\otimes}\limits_{U(\mathfrak{s})}} M \right)}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{\mathbf{EA}}}(M) := {}^{e}{\left( S_f \mathbin{\mathop{\otimes}\limits_{U(\mathfrak{s})}} M \right)}. \end{align*} $$
As before, one can check that this is a well-defined functor on the category of
![]() $\mathfrak {s}$
-modules. Moreover, Proposition 22 is valid here, with the same proof.
$\mathfrak {s}$
-modules. Moreover, Proposition 22 is valid here, with the same proof.
Theorem 48. Take
![]() $\lambda $
with
$\lambda $
with
![]() $\lambda _1 \in \mathbb {Z}$
and
$\lambda _1 \in \mathbb {Z}$
and
![]() $\lambda _2 \neq 0$
. Then,
$\lambda _2 \neq 0$
. Then,
![]() $\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
is a simple
$\operatorname {\mathrm {\mathbf {EA}}}(\Delta (\lambda ))$
is a simple
![]() $\mathfrak {g}$
-Harish-Chandra module, and decomposes as a
$\mathfrak {g}$
-Harish-Chandra module, and decomposes as a
![]() $\mathfrak {g}$
-module as
$\mathfrak {g}$
-module as
 $$ \begin{align} \operatorname{\mathrm{\mathbf{EA}}}(\Delta(\lambda)) \cong \bigoplus_{k \geq 0} L\left(\left|\lambda_1 + \frac{3}{2}\right| - \frac{1}{2} +k \right). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{\mathbf{EA}}}(\Delta(\lambda)) \cong \bigoplus_{k \geq 0} L\left(\left|\lambda_1 + \frac{3}{2}\right| - \frac{1}{2} +k \right). \end{align} $$
Proof. Lemma 46, the fact that the functor
![]() $\operatorname {\mathrm {\mathbf {EA}}}$
commutes with the forgetful functor from
$\operatorname {\mathrm {\mathbf {EA}}}$
commutes with the forgetful functor from
![]() $\mathfrak {s}$
-modules to
$\mathfrak {s}$
-modules to
![]() $\mathfrak {g}$
-modules, and (the Schrödinger analogue of) Example 23 imply the decomposition (26).
$\mathfrak {g}$
-modules, and (the Schrödinger analogue of) Example 23 imply the decomposition (26).
Note that the lowest weight vector of a
![]() $L(\mu )$
in (26) is
$L(\mu )$
in (26) is
![]() $f^{-1} q^t v_\lambda $
, where
$f^{-1} q^t v_\lambda $
, where
![]() $t:=2+\lambda _1+\mu $
. To prove simplicity, it is enough for
$t:=2+\lambda _1+\mu $
. To prove simplicity, it is enough for
 $\mu \geq \left | \lambda _1 + \frac {3}{2}\right | + \frac {1}{2}$
to find an element in
$\mu \geq \left | \lambda _1 + \frac {3}{2}\right | + \frac {1}{2}$
to find an element in
![]() $U(\mathfrak {s})$
that maps
$U(\mathfrak {s})$
that maps
![]() $f^{-1} q^t v_\lambda $
to
$f^{-1} q^t v_\lambda $
to
![]() $f^{-1} q^{t-1} v_\lambda $
. One can check by direct calculation that
$f^{-1} q^{t-1} v_\lambda $
. One can check by direct calculation that
 $$ \begin{align*} \left( p - \frac{1}{\mu} qe \right) \cdot f^{-1} q^t v_\lambda = \frac{\lambda_2 t}{2 \mu}(\mu-\lambda_1-1) f^{-1} q^{t-1} v_\lambda. \end{align*} $$
$$ \begin{align*} \left( p - \frac{1}{\mu} qe \right) \cdot f^{-1} q^t v_\lambda = \frac{\lambda_2 t}{2 \mu}(\mu-\lambda_1-1) f^{-1} q^{t-1} v_\lambda. \end{align*} $$
The scalar on the right-hand side is nonzero because of the assumption on
![]() $\mu $
.
$\mu $
.
Alternatively, one can use a nilradical argument analogous to the one in Remark 25.
Theorem 48, Proposition 42(c), and Theorem 43 together give:
Corollary 49. For
![]() $\lambda _2 \neq 0$
, we have
$\lambda _2 \neq 0$
, we have
5.5. Classification
The Enright–Arkhipov completion of Verma modules again gives us a family of
![]() $\mathfrak {g}$
-Harish-Chandra modules. This construction gives all infinite-dimensional
$\mathfrak {g}$
-Harish-Chandra modules. This construction gives all infinite-dimensional
![]() $\mathfrak {g}$
-Harish-Chandra modules, as we will see in this subsection.
$\mathfrak {g}$
-Harish-Chandra modules, as we will see in this subsection.
Definition 50. For
![]() $n \in \mathbb {Z}$
and
$n \in \mathbb {Z}$
and
![]() $\lambda _2 \neq 0$
, denote
$\lambda _2 \neq 0$
, denote
 $$ \begin{align*} V(n,\lambda_2) := \begin{cases} \operatorname{\mathrm{\mathbf{EA}}}(\Delta(n-1, \lambda_2)) &\colon n \geq 0, \\ \operatorname{\mathrm{\mathbf{EA}}}(\Delta(n-2, \lambda_2)) &\colon n \leq 0. \end{cases} \end{align*} $$
$$ \begin{align*} V(n,\lambda_2) := \begin{cases} \operatorname{\mathrm{\mathbf{EA}}}(\Delta(n-1, \lambda_2)) &\colon n \geq 0, \\ \operatorname{\mathrm{\mathbf{EA}}}(\Delta(n-2, \lambda_2)) &\colon n \leq 0. \end{cases} \end{align*} $$
From Corollary 49, we have that
![]() $V(0,\lambda _2)$
is well defined, and moreover isomorphic to
$V(0,\lambda _2)$
is well defined, and moreover isomorphic to
![]() $Q(0,\lambda _2)$
. Note that the central element C acts on
$Q(0,\lambda _2)$
. Note that the central element C acts on
![]() $V(n,\lambda _2)$
as
$V(n,\lambda _2)$
as
![]() $n(n+1)\lambda _2$
if
$n(n+1)\lambda _2$
if
![]() $n \geq 0$
, and as
$n \geq 0$
, and as
![]() $n(n-1)\lambda _2$
if
$n(n-1)\lambda _2$
if
![]() $n \leq 0 $
.
$n \leq 0 $
.
Theorem 48 and Lemma 45 easily give:
Corollary 51. The module
![]() $V(n,\lambda _2)$
is a simple
$V(n,\lambda _2)$
is a simple
![]() $\mathfrak {g}$
-Harish-Chandra module, and has
$\mathfrak {g}$
-Harish-Chandra module, and has
![]() $\mathfrak {g}$
-types
$\mathfrak {g}$
-types
![]() $L(|n|), L(|n|+1), L(|n|+2) \ldots $
with multiplicity 1.
$L(|n|), L(|n|+1), L(|n|+2) \ldots $
with multiplicity 1.
If
![]() $V(n,\lambda _2) \cong V(n',\lambda _2')$
, then
$V(n,\lambda _2) \cong V(n',\lambda _2')$
, then
![]() $\lambda _2'=\lambda _2$
and
$\lambda _2'=\lambda _2$
and
![]() $n' \in \{n,-n\}$
.
$n' \in \{n,-n\}$
.
On Figure 2, we present several
![]() $V(n,\lambda _2)$
’s, and how they are constructed. It is interesting to compare this to the Takiff
$V(n,\lambda _2)$
’s, and how they are constructed. It is interesting to compare this to the Takiff
![]() $\mathfrak {sl}_2$
case (cf. Figure 1).
$\mathfrak {sl}_2$
case (cf. Figure 1).

Figure 2 Construction of simple
![]() $\mathfrak {g}$
-Harish Chandra modules for the Schrödinger Lie algebra.
$\mathfrak {g}$
-Harish Chandra modules for the Schrödinger Lie algebra.
Proposition 52. For
![]() $n \in \mathbb {Z}_{\geq 0}$
and
$n \in \mathbb {Z}_{\geq 0}$
and
![]() $\lambda _2 \neq 0$
, we have
$\lambda _2 \neq 0$
, we have
![]() $V(-n,\lambda _2) \cong V(n,\lambda _2)$
. Moreover,
$V(-n,\lambda _2) \cong V(n,\lambda _2)$
. Moreover,
Proof. We use induction over n. The basis is given in Corollary 49. Suppose the proposition is true for all
![]() $k=0,\ldots ,n-1$
, where
$k=0,\ldots ,n-1$
, where
![]() $n\geq 1$
is fixed. Observe that, using (the Schrödinger version of) Proposition 22 and Lemma 47, we have
$n\geq 1$
is fixed. Observe that, using (the Schrödinger version of) Proposition 22 and Lemma 47, we have
 $$ \begin{align} Q(n,\lambda_2) \cong & \, Q(0,\lambda_2) \otimes L(n) \cong \operatorname{\mathrm{\mathbf{EA}}}(\Delta(-1,\lambda_2)) \otimes L(n) \\ \nonumber \cong & \operatorname{\mathrm{\mathbf{EA}}}(\Delta(n-1,\lambda_2)) \oplus \operatorname{\mathrm{\mathbf{EA}}}(\Delta(n-3,\lambda_2)) \oplus \cdots \oplus \operatorname{\mathrm{\mathbf{EA}}}(\Delta(-n-1,\lambda_2)) \\ \nonumber \cong & \, V(n,\lambda_2) \oplus V(n-2,\lambda_2) \oplus \cdots \oplus V(\epsilon,\lambda_2) \oplus{} \\ \nonumber & \oplus V(\epsilon-1,\lambda_2) \oplus V(\epsilon-3,\lambda_2) \oplus \cdots \oplus V(-n+1,\lambda_2), \end{align} $$
$$ \begin{align} Q(n,\lambda_2) \cong & \, Q(0,\lambda_2) \otimes L(n) \cong \operatorname{\mathrm{\mathbf{EA}}}(\Delta(-1,\lambda_2)) \otimes L(n) \\ \nonumber \cong & \operatorname{\mathrm{\mathbf{EA}}}(\Delta(n-1,\lambda_2)) \oplus \operatorname{\mathrm{\mathbf{EA}}}(\Delta(n-3,\lambda_2)) \oplus \cdots \oplus \operatorname{\mathrm{\mathbf{EA}}}(\Delta(-n-1,\lambda_2)) \\ \nonumber \cong & \, V(n,\lambda_2) \oplus V(n-2,\lambda_2) \oplus \cdots \oplus V(\epsilon,\lambda_2) \oplus{} \\ \nonumber & \oplus V(\epsilon-1,\lambda_2) \oplus V(\epsilon-3,\lambda_2) \oplus \cdots \oplus V(-n+1,\lambda_2), \end{align} $$
where
![]() $\epsilon \in \{0,1\}$
is of the same parity as n. By inductive assumption, it follows that
$\epsilon \in \{0,1\}$
is of the same parity as n. By inductive assumption, it follows that
 $$\begin{align*}\nonumber Q(n,\lambda_2) \cong & \, V(n,\lambda_2) \oplus V(n-1,\lambda_2) \oplus \cdots \oplus V(1,\lambda_2) \oplus V(0,\lambda_2) \\ \nonumber \cong & \, V(n,\lambda_2) \oplus Q(n-1,\lambda_2). \end{align*}$$
$$\begin{align*}\nonumber Q(n,\lambda_2) \cong & \, V(n,\lambda_2) \oplus V(n-1,\lambda_2) \oplus \cdots \oplus V(1,\lambda_2) \oplus V(0,\lambda_2) \\ \nonumber \cong & \, V(n,\lambda_2) \oplus Q(n-1,\lambda_2). \end{align*}$$
In the same way, but using
![]() $Q(0,\lambda _2) \cong \operatorname {\mathrm {\mathbf {EA}}}(\Delta (-2,\lambda _2))$
in the first line (27), we can get that
$Q(0,\lambda _2) \cong \operatorname {\mathrm {\mathbf {EA}}}(\Delta (-2,\lambda _2))$
in the first line (27), we can get that
![]() $Q(n,\lambda _2) \cong V(-n,\lambda _2) \oplus Q(n-1,\lambda _2)$
. It follows that
$Q(n,\lambda _2) \cong V(-n,\lambda _2) \oplus Q(n-1,\lambda _2)$
. It follows that
![]() $V(n,\lambda _2) \cong V(-n,\lambda _2)$
.
$V(n,\lambda _2) \cong V(-n,\lambda _2)$
.
Similarly, one can prove the following analogue of Proposition 29:
Proposition 53. Let
![]() $n,k \in \mathbb {Z}_{\geq 0}$
and
$n,k \in \mathbb {Z}_{\geq 0}$
and
![]() $\lambda _2 \neq 0$
. If
$\lambda _2 \neq 0$
. If
![]() $k \leq n$
, then
$k \leq n$
, then
If
![]() $k>n$
, then
$k>n$
, then
 $$ \begin{align*} &V(n,\lambda_2) \mathbin{\mathop{\otimes}\limits_{}} L(k) = V(0,\lambda_2) \oplus V(1,\lambda_2) \oplus \cdots \oplus V(k-n-1,\lambda_2) \oplus {} \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad{} \oplus V(k-n,\lambda_2) \oplus V(k-n+2,\lambda_2) \oplus \cdots \oplus V(k+n,\lambda_2). \end{align*} $$
$$ \begin{align*} &V(n,\lambda_2) \mathbin{\mathop{\otimes}\limits_{}} L(k) = V(0,\lambda_2) \oplus V(1,\lambda_2) \oplus \cdots \oplus V(k-n-1,\lambda_2) \oplus {} \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad{} \oplus V(k-n,\lambda_2) \oplus V(k-n+2,\lambda_2) \oplus \cdots \oplus V(k+n,\lambda_2). \end{align*} $$
Since any simple
![]() $\mathfrak {g}$
-Harish-Chandra module is a quotient of some
$\mathfrak {g}$
-Harish-Chandra module is a quotient of some
![]() $Q(n,\lambda _2)$
, we have proved the following theorem:
$Q(n,\lambda _2)$
, we have proved the following theorem:
Theorem 54. Let V be a simple
![]() $\mathfrak {g}$
-Harish-Chandra module for
$\mathfrak {g}$
-Harish-Chandra module for
![]() $\mathfrak {s}$
. Denote by
$\mathfrak {s}$
. Denote by
![]() $\lambda _2$
its central charge, and suppose
$\lambda _2$
its central charge, and suppose
![]() $L(n)$
,
$L(n)$
,
![]() $n \in \mathbb {Z}_{\geq 0}$
, is the minimal
$n \in \mathbb {Z}_{\geq 0}$
, is the minimal
![]() $\mathfrak {g}$
-type of V.
$\mathfrak {g}$
-type of V.
-
• If
 $\lambda _2 \neq 0$
, then
$\lambda _2 \neq 0$
, then
 $V \cong V(n,\lambda _2) \cong V(-n,\lambda _2)$
.
$V \cong V(n,\lambda _2) \cong V(-n,\lambda _2)$
. -
• If
 $\lambda _2 = 0$
, then
$\lambda _2 = 0$
, then
 $V \cong L(n)$
with the trivial
$V \cong L(n)$
with the trivial
 $\mathfrak {H}$
-action.
$\mathfrak {H}$
-action.
In other words,
![]() $V(n,\lambda _2)$
,
$V(n,\lambda _2)$
,
![]() $n \in \mathbb {Z}_{\geq 0}$
, and
$n \in \mathbb {Z}_{\geq 0}$
, and
![]() $\lambda _2 \in \mathbb {C}\setminus \{0\}$
, together with the finite-dimensional simple
$\lambda _2 \in \mathbb {C}\setminus \{0\}$
, together with the finite-dimensional simple
![]() $\mathfrak {g}$
-modules, constitute a complete list of pairwise nonisomorphic simple
$\mathfrak {g}$
-modules, constitute a complete list of pairwise nonisomorphic simple
![]() $\mathfrak {g}$
-Harish-Chandra modules for
$\mathfrak {g}$
-Harish-Chandra modules for
![]() $\mathfrak {s}$
.
$\mathfrak {s}$
.
Remark 55. For the centerless Schrödinger Lie algebra
![]() $\bar {\mathfrak {s}}$
, infinite-dimensional simple
$\bar {\mathfrak {s}}$
, infinite-dimensional simple
![]() $\mathfrak {g}$
-Harish-Chandra modules do not exist. All simple
$\mathfrak {g}$
-Harish-Chandra modules do not exist. All simple
![]() $\mathfrak {g}$
-Harish-Chandra modules are given by
$\mathfrak {g}$
-Harish-Chandra modules are given by
![]() $L(n)$
,
$L(n)$
,
![]() $n \in \mathbb {Z}_{\geq 0}$
, with the trivial action of
$n \in \mathbb {Z}_{\geq 0}$
, with the trivial action of
 .
.
This follows from observing that the endomorphism ring of
 $\operatorname {\mathrm {Ind}}_{\mathfrak {g}}^{\bar {\mathfrak {s}}}(L(0))$
is only
$\operatorname {\mathrm {Ind}}_{\mathfrak {g}}^{\bar {\mathfrak {s}}}(L(0))$
is only
![]() $\mathbb {C}$
(similarly as in Proposition 40), and so all the universal modules have
$\mathbb {C}$
(similarly as in Proposition 40), and so all the universal modules have
![]() $\bar {\mathfrak {s}}$
-filtrations by simple finite-dimensional modules (similarly as in Theorem 43 for
$\bar {\mathfrak {s}}$
-filtrations by simple finite-dimensional modules (similarly as in Theorem 43 for
![]() $\chi =0$
).
$\chi =0$
).
5.6. Extensions
Self-extensions of infinite-dimensional simple
![]() $\mathfrak {g}$
-Harish-Chandra modules (i.e., the ones having nonzero central charge) can be calculated in the same way as for the Takiff
$\mathfrak {g}$
-Harish-Chandra modules (i.e., the ones having nonzero central charge) can be calculated in the same way as for the Takiff
![]() $\mathfrak {sl}_2$
case (Section 4.6):
$\mathfrak {sl}_2$
case (Section 4.6):
Theorem 56. Let V be a simple infinite-dimensional
![]() $\mathfrak {g}$
-Harish-Chandra module for
$\mathfrak {g}$
-Harish-Chandra module for
![]() $\mathfrak {s}$
. Then,
$\mathfrak {s}$
. Then,
 $\operatorname {\mathrm {Ext}}^1(V,V) \cong \mathbb {C}$
.
$\operatorname {\mathrm {Ext}}^1(V,V) \cong \mathbb {C}$
.
5.7. Annihilators
We show that simple infinite-dimensional
![]() $\mathfrak {g}$
-Harish-Chandra modules again have the same annihilators as the corresponding Verma modules. The fact that annihilators of Verma modules for
$\mathfrak {g}$
-Harish-Chandra modules again have the same annihilators as the corresponding Verma modules. The fact that annihilators of Verma modules for
![]() $\mathfrak {s}$
are centrally generated is already known (see [Reference Dubsky, Lü, Mazorchuk and Zhao20, Theorem 21]).
$\mathfrak {s}$
are centrally generated is already known (see [Reference Dubsky, Lü, Mazorchuk and Zhao20, Theorem 21]).
Proposition 57. Suppose
![]() $n \in \mathbb {Z}_{\geq 0}$
and
$n \in \mathbb {Z}_{\geq 0}$
and
![]() $\lambda _2 \neq 0$
.
$\lambda _2 \neq 0$
.
-
(a) The element p acts injectively on
 $V(n,\lambda _2)$
.
$V(n,\lambda _2)$
. -
(b) The module
 $S_{p} \mathbin {\mathop {\otimes }\limits _{U(\mathfrak {s})}} V(n,\lambda _2)$
is isomorphic to the direct sum of Verma modules
$S_{p} \mathbin {\mathop {\otimes }\limits _{U(\mathfrak {s})}} V(n,\lambda _2)$
is isomorphic to the direct sum of Verma modules
 $\Delta (n-1,\lambda _2) \oplus \Delta (-n-2,\lambda _2)$
.
$\Delta (n-1,\lambda _2) \oplus \Delta (-n-2,\lambda _2)$
.
Proof. The proof is analogous to the proof of Proposition 34, but easier. So we will omit it.
From (the Schrödinger version of) Lemma 33, Proposition 57, the definition of
![]() $V(n,\lambda _2)$
, and [Reference Dubsky, Lü, Mazorchuk and Zhao20, Theorem 21], we have:
$V(n,\lambda _2)$
, and [Reference Dubsky, Lü, Mazorchuk and Zhao20, Theorem 21], we have:
Corollary 58. Suppose
![]() $n \in \mathbb {Z}_{\geq 0}$
and
$n \in \mathbb {Z}_{\geq 0}$
and
![]() $\lambda _2 \neq 0$
. Then,
$\lambda _2 \neq 0$
. Then,
and these annihilators are centrally generated.
5.8. The action of finite-dimensional
 $\mathfrak {sl}_2$
-modules
$\mathfrak {sl}_2$
-modules
Denote by
![]() $\mathscr {F}$
the monoidal category of finite-dimensional
$\mathscr {F}$
the monoidal category of finite-dimensional
![]() $\mathfrak {sl}_2$
-modules. For a fixed nonzero
$\mathfrak {sl}_2$
-modules. For a fixed nonzero
![]() $\chi \in \mathbb {C}$
, denote by
$\chi \in \mathbb {C}$
, denote by
![]() $\mathcal {K}_{\chi }$
the category of semisimple
$\mathcal {K}_{\chi }$
the category of semisimple
![]() $\mathfrak {g}$
-Harish-Chandra
$\mathfrak {g}$
-Harish-Chandra
![]() $\mathfrak {s}$
-modules of central charge
$\mathfrak {s}$
-modules of central charge
![]() $\chi $
.
$\chi $
.
Proposition 59. For each nonero
![]() $\chi $
, the category
$\chi $
, the category
![]() $\mathcal {K}_{\chi }$
is a simple module category over the monoidal category
$\mathcal {K}_{\chi }$
is a simple module category over the monoidal category
![]() $\mathscr {F}$
.
$\mathscr {F}$
.
Proof. The fact that
![]() $\mathcal {K}_{\chi }$
is a module category over
$\mathcal {K}_{\chi }$
is a module category over
![]() $\mathscr {F}$
follows directly from Proposition 53. Since
$\mathscr {F}$
follows directly from Proposition 53. Since
![]() $\mathcal {K}_{\chi }$
is semisimple by definition, to show that it is a simple module category over
$\mathcal {K}_{\chi }$
is semisimple by definition, to show that it is a simple module category over
![]() $\mathscr {F}$
, it is enough to show that, starting from any simple object of
$\mathscr {F}$
, it is enough to show that, starting from any simple object of
![]() $\mathcal {K}_{\chi }$
and tensoring it with finite-dimensional
$\mathcal {K}_{\chi }$
and tensoring it with finite-dimensional
![]() $\mathfrak {sl}_2$
-modules, we can obtain any other simple object of
$\mathfrak {sl}_2$
-modules, we can obtain any other simple object of
![]() $\mathcal {K}_{\chi }$
as a direct summand, up to isomorphism. This claim follows by combining Proposition 53 with Theorem 54.
$\mathcal {K}_{\chi }$
as a direct summand, up to isomorphism. This claim follows by combining Proposition 53 with Theorem 54.
We note that, by Proposition 53, the combinatorics of the
![]() $\mathscr {F}$
-module category
$\mathscr {F}$
-module category
![]() $\mathcal {K}_{\chi }$
does not depend on
$\mathcal {K}_{\chi }$
does not depend on
![]() $\chi $
. Furthermore, by comparing Propositions 29 and 53, we see that the combinatorics of the
$\chi $
. Furthermore, by comparing Propositions 29 and 53, we see that the combinatorics of the
![]() $\mathscr {F}$
-module category
$\mathscr {F}$
-module category
![]() $\mathcal {H}_{\chi }$
is different from the combinatorics of the
$\mathcal {H}_{\chi }$
is different from the combinatorics of the
![]() $\mathscr {F}$
-module category
$\mathscr {F}$
-module category
![]() $\mathcal {K}_{\chi }$
.
$\mathcal {K}_{\chi }$
.
6. Some general results on
 $\mathfrak {g}$
-Harish-Chandra modules
$\mathfrak {g}$
-Harish-Chandra modules
6.1. A sufficient condition for existence of simple infinite-dimensional
 $\mathfrak {g}$
-Harish-Chandra modules
$\mathfrak {g}$
-Harish-Chandra modules
Recall our general setup from Section 2, where
![]() $\mathfrak {L} \cong \mathfrak {g} \ltimes \mathfrak {r}$
was arbitrary finite-dimensional Lie algebra. Assume that a triangular decomposition (1) is fixed. Denote by
$\mathfrak {L} \cong \mathfrak {g} \ltimes \mathfrak {r}$
was arbitrary finite-dimensional Lie algebra. Assume that a triangular decomposition (1) is fixed. Denote by
![]() $\mathfrak {r}_0$
the zero-weight space of
$\mathfrak {r}_0$
the zero-weight space of
![]() $\mathfrak {r}$
. Obviously, we have
$\mathfrak {r}$
. Obviously, we have
 $\tilde {\mathfrak {h}} = \mathfrak {h} \oplus \mathfrak {r}_0$
.
$\tilde {\mathfrak {h}} = \mathfrak {h} \oplus \mathfrak {r}_0$
.
To prove the main theorem in this section, we need to use another variant of Enright’s and Arkhipov’s functors. It will be the same as
![]() $\operatorname {\mathrm {\mathbf {EA}}}$
from before, but without taking the locally finite for the positive root vector. Fix a simple reflection s, and the corresponding
$\operatorname {\mathrm {\mathbf {EA}}}$
from before, but without taking the locally finite for the positive root vector. Fix a simple reflection s, and the corresponding
![]() $\mathfrak {sl}_2$
-triple
$\mathfrak {sl}_2$
-triple
![]() $\{f,h,e\} \subseteq \mathfrak {g}$
. For an
$\{f,h,e\} \subseteq \mathfrak {g}$
. For an
![]() $\mathfrak {L}$
-module M, set
$\mathfrak {L}$
-module M, set
 $$ \begin{align*} \operatorname{\mathrm{\mathbf{C}}}_s(M) := S_f \mathbin{\mathop{\otimes}\limits_{U(\mathfrak{L})}} M , \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{\mathbf{C}}}_s(M) := S_f \mathbin{\mathop{\otimes}\limits_{U(\mathfrak{L})}} M , \end{align*} $$
where, as before,
![]() $S_f$
denotes the localized algebra
$S_f$
denotes the localized algebra
 $U(\mathfrak {L})_{(f)}$
modulo
$U(\mathfrak {L})_{(f)}$
modulo
![]() $U(\mathfrak {L})$
. This functor commutes with the forgetful functor that forgets the
$U(\mathfrak {L})$
. This functor commutes with the forgetful functor that forgets the
![]() $\mathfrak {r}$
-action. Moreover, it preserves
$\mathfrak {r}$
-action. Moreover, it preserves
![]() $\mathfrak {g}$
-central characters.
$\mathfrak {g}$
-central characters.
Remark 60. Note that if we would twist the action on
![]() $\operatorname {\mathrm {\mathbf {C}}}_s(M)$
by the inner automorphism of
$\operatorname {\mathrm {\mathbf {C}}}_s(M)$
by the inner automorphism of
![]() $\mathfrak {L}$
that corresponds to the simple reflection s, we would get exactly the twisting functor
$\mathfrak {L}$
that corresponds to the simple reflection s, we would get exactly the twisting functor
![]() $T_s(M)$
from [Reference Andersen and Stroppel2], [Reference Arkhipov3]. We conclude that if M is from the category
$T_s(M)$
from [Reference Andersen and Stroppel2], [Reference Arkhipov3]. We conclude that if M is from the category
![]() $\mathcal {O}$
for
$\mathcal {O}$
for
![]() $\mathfrak {g}$
, then
$\mathfrak {g}$
, then
![]() $\operatorname {\mathrm {\mathbf {C}}}_s(M)$
is also from the category
$\operatorname {\mathrm {\mathbf {C}}}_s(M)$
is also from the category
![]() $\mathcal {O}$
for
$\mathcal {O}$
for
![]() $\mathfrak {g}$
, but for another choice of Borel subalgebra.
$\mathfrak {g}$
, but for another choice of Borel subalgebra.
Theorem 61. Suppose that
![]() $[\mathfrak {L},\mathfrak {r}] \cap \mathfrak {r}_0 \neq 0$
. Then, there exists an infinite-dimensional simple
$[\mathfrak {L},\mathfrak {r}] \cap \mathfrak {r}_0 \neq 0$
. Then, there exists an infinite-dimensional simple
![]() $\mathfrak {g}$
-Harish-Chandra module for
$\mathfrak {g}$
-Harish-Chandra module for
![]() $\mathfrak {L}$
.
$\mathfrak {L}$
.
Proof. Fix an element
![]() $c \in [\mathfrak {L},\mathfrak {r}] \cap \mathfrak {r}_0$
. Then,
$c \in [\mathfrak {L},\mathfrak {r}] \cap \mathfrak {r}_0$
. Then,
![]() $c \in \operatorname {\mathrm {Nrad}}(\mathfrak {L})$
, so c must annihilate any simple finite-dimensional
$c \in \operatorname {\mathrm {Nrad}}(\mathfrak {L})$
, so c must annihilate any simple finite-dimensional
![]() $\mathfrak {L}$
-module.
$\mathfrak {L}$
-module.
The idea is to start with the simple quotient of a Verma module for
![]() $\mathfrak {L}$
, which has finite multiplicities of its
$\mathfrak {L}$
, which has finite multiplicities of its
![]() $\mathfrak {g}$
-submodules (but possibly infinite-dimensional), and then use the functors
$\mathfrak {g}$
-submodules (but possibly infinite-dimensional), and then use the functors
![]() $\operatorname {\mathrm {\mathbf {C}}}_s$
to obtain an
$\operatorname {\mathrm {\mathbf {C}}}_s$
to obtain an
![]() $\mathfrak {L}$
-module that should have a finite-dimensional
$\mathfrak {L}$
-module that should have a finite-dimensional
![]() $\mathfrak {g}$
-submodule. Then, the image of the universal
$\mathfrak {g}$
-submodule. Then, the image of the universal
![]() $\mathfrak {L}$
-module in the constructed module should have only finite-dimensional
$\mathfrak {L}$
-module in the constructed module should have only finite-dimensional
![]() $\mathfrak {g}$
-submodules with finite multiplicities. The element c will insure infinite-dimensionality.
$\mathfrak {g}$
-submodules with finite multiplicities. The element c will insure infinite-dimensionality.
Fix an antidominant, regular, and integral
![]() $\lambda \in \mathfrak {h}^\ast $
, and extend it to
$\lambda \in \mathfrak {h}^\ast $
, and extend it to
 $\tilde {\lambda } \in \tilde {\mathfrak {h}}^\ast $
such that
$\tilde {\lambda } \in \tilde {\mathfrak {h}}^\ast $
such that
 $\tilde {\lambda }(c) \neq 0$
. Consider the Verma module
$\tilde {\lambda }(c) \neq 0$
. Consider the Verma module
 $\Delta (\tilde {\lambda })$
as in (2), and its simple quotient
$\Delta (\tilde {\lambda })$
as in (2), and its simple quotient
 $\mathbf {L}(\tilde {\lambda })$
.
$\mathbf {L}(\tilde {\lambda })$
.
By considering the
![]() $\mathfrak {h}$
-weight spaces of
$\mathfrak {h}$
-weight spaces of
 $\Delta (\tilde {\lambda })$
(Proposition 4), it follows that as a
$\Delta (\tilde {\lambda })$
(Proposition 4), it follows that as a
![]() $\mathfrak {g}$
-module,
$\mathfrak {g}$
-module,
 $\mathbf {L}(\tilde {\lambda })$
has a
$\mathbf {L}(\tilde {\lambda })$
has a
![]() $\mathfrak {g}$
-direct summand
$\mathfrak {g}$
-direct summand
![]() $\Delta ^{\mathfrak {g}}(\lambda )$
generated by the highest weight vector
$\Delta ^{\mathfrak {g}}(\lambda )$
generated by the highest weight vector
 $\mathbf {v} \in \mathbf {L}(\tilde {\lambda })$
, and this is the only
$\mathbf {v} \in \mathbf {L}(\tilde {\lambda })$
, and this is the only
![]() $\mathfrak {g}$
-composition factor of
$\mathfrak {g}$
-composition factor of
 $\mathbf {L}(\tilde {\lambda })$
of this
$\mathbf {L}(\tilde {\lambda })$
of this
![]() $\mathfrak {g}$
-central character.
$\mathfrak {g}$
-central character.
From the fact that
 $\Delta (\tilde {\lambda })$
and
$\Delta (\tilde {\lambda })$
and
 $\mathbf {L}(\tilde {\lambda })$
have finite-dimensional weight spaces, it follows that, when considered as
$\mathbf {L}(\tilde {\lambda })$
have finite-dimensional weight spaces, it follows that, when considered as
![]() $\mathfrak {g}$
-modules, they contain any simple
$\mathfrak {g}$
-modules, they contain any simple
![]() $\mathfrak {g}$
-composition factor with at most finite multiplicity. Moreover, from this, it follows that their components in any fixed
$\mathfrak {g}$
-composition factor with at most finite multiplicity. Moreover, from this, it follows that their components in any fixed
![]() $\mathfrak {g}$
-central character lie in the category
$\mathfrak {g}$
-central character lie in the category
![]() $\mathcal {O}$
for
$\mathcal {O}$
for
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
The element c acts on
 $\mathbf {v} \in \Delta ^{\mathfrak {g}}(\lambda ) \subseteq \mathbf {L}(\tilde {\lambda })$
by the scalar
$\mathbf {v} \in \Delta ^{\mathfrak {g}}(\lambda ) \subseteq \mathbf {L}(\tilde {\lambda })$
by the scalar
 $\tilde {\lambda }(c) \neq 0$
.
$\tilde {\lambda }(c) \neq 0$
.
Choose a reduced expression
![]() $w_0 = s_1 s_2 \ldots s_k$
of the longest element in the Weyl group for
$w_0 = s_1 s_2 \ldots s_k$
of the longest element in the Weyl group for
![]() $\mathfrak {g}$
, and set
$\mathfrak {g}$
, and set
![]() $\operatorname {\mathrm {\mathbf {C}}}_{w_0} = \operatorname {\mathrm {\mathbf {C}}}_{s_1} \circ \operatorname {\mathrm {\mathbf {C}}}_{s_2} \circ \cdots \circ \operatorname {\mathrm {\mathbf {C}}}_{s_k}$
.
$\operatorname {\mathrm {\mathbf {C}}}_{w_0} = \operatorname {\mathrm {\mathbf {C}}}_{s_1} \circ \operatorname {\mathrm {\mathbf {C}}}_{s_2} \circ \cdots \circ \operatorname {\mathrm {\mathbf {C}}}_{s_k}$
.
Consider for a moment
![]() $\Delta ^{\mathfrak {g}}(\lambda )$
as an
$\Delta ^{\mathfrak {g}}(\lambda )$
as an
![]() $\mathfrak {L}$
-module, by declaring that
$\mathfrak {L}$
-module, by declaring that
![]() $\mathfrak {r}$
acts trivially on it. From Remark 60 and [Reference Andersen and Stroppel2, Theorem 2.3], it follows that
$\mathfrak {r}$
acts trivially on it. From Remark 60 and [Reference Andersen and Stroppel2, Theorem 2.3], it follows that
![]() $\operatorname {\mathrm {\mathbf {C}}}_{w_0}(\Delta ^{\mathfrak {g}}(\lambda ))$
is isomorphic to the dual dominant
$\operatorname {\mathrm {\mathbf {C}}}_{w_0}(\Delta ^{\mathfrak {g}}(\lambda ))$
is isomorphic to the dual dominant
![]() $\mathfrak {g}$
-Verma module for the opposite Borel subalgebra. From this, we can conclude
$\mathfrak {g}$
-Verma module for the opposite Borel subalgebra. From this, we can conclude
![]() $\operatorname {\mathrm {\mathbf {C}}}_{w_0}(\Delta ^{\mathfrak {g}}(\lambda ))$
contains the finite-dimensional
$\operatorname {\mathrm {\mathbf {C}}}_{w_0}(\Delta ^{\mathfrak {g}}(\lambda ))$
contains the finite-dimensional
![]() $\mathfrak {g}$
-submodule
$\mathfrak {g}$
-submodule
![]() $L(\mu )$
, where
$L(\mu )$
, where
![]() $\mu := w_0 \cdot \lambda $
is dominant and integral. Moreover, by observing what is happening on the
$\mu := w_0 \cdot \lambda $
is dominant and integral. Moreover, by observing what is happening on the
![]() $\mathfrak {sl}_2$
-subalgebras of
$\mathfrak {sl}_2$
-subalgebras of
![]() $\mathfrak {g}$
, one can conclude that the lowest weight vector in
$\mathfrak {g}$
, one can conclude that the lowest weight vector in
![]() $L(\mu )$
is given by
$L(\mu )$
is given by
 $$ \begin{align} f_1^{-1} f_2^{-1} \ldots f_k^{-1} \mathbf{v}, \end{align} $$
$$ \begin{align} f_1^{-1} f_2^{-1} \ldots f_k^{-1} \mathbf{v}, \end{align} $$
where
![]() $f_i$
is the negative root vector corresponding to
$f_i$
is the negative root vector corresponding to
![]() $s_i$
.
$s_i$
.
It follows that
 $M:=\operatorname {\mathrm {\mathbf {C}}}_{w_0}(\mathbf {L}(\tilde {\lambda }))$
as a
$M:=\operatorname {\mathrm {\mathbf {C}}}_{w_0}(\mathbf {L}(\tilde {\lambda }))$
as a
![]() $\mathfrak {g}$
-module has also
$\mathfrak {g}$
-module has also
![]() $L(\mu )$
as a
$L(\mu )$
as a
![]() $\mathfrak {g}$
-direct summand. Moreover, from Remark 60, it follows that
$\mathfrak {g}$
-direct summand. Moreover, from Remark 60, it follows that
![]() $L(\mu )$
appears in M precisely once, and that each simple
$L(\mu )$
appears in M precisely once, and that each simple
![]() $\mathfrak {g}$
-module appears with at most finite multiplicity.
$\mathfrak {g}$
-module appears with at most finite multiplicity.
Consider the
![]() $\mathfrak {L}$
-module
$\mathfrak {L}$
-module
 $Q(\mu ) := \operatorname {\mathrm {Ind}}_{\mathfrak {g}}^{\mathfrak {L}}(L(\mu )) \cong U(\mathfrak {L}) \mathbin {\mathop {\otimes } _{U(\mathfrak {g})}} L(\mu )$
. It has only finite-dimensional
$Q(\mu ) := \operatorname {\mathrm {Ind}}_{\mathfrak {g}}^{\mathfrak {L}}(L(\mu )) \cong U(\mathfrak {L}) \mathbin {\mathop {\otimes } _{U(\mathfrak {g})}} L(\mu )$
. It has only finite-dimensional
![]() $\mathfrak {g}$
-composition factors, but possibly with infinite multiplicities.
$\mathfrak {g}$
-composition factors, but possibly with infinite multiplicities.
By the universal property of the induction functor, we get a nonzero
![]() $\mathfrak {L}$
-homomorphism
$\mathfrak {L}$
-homomorphism
![]() $\varphi \colon Q(\mu ) \to M$
, hitting the
$\varphi \colon Q(\mu ) \to M$
, hitting the
![]() $\mathfrak {g}$
-submodule
$\mathfrak {g}$
-submodule
![]() $L(\mu )$
in M. Denote by N the image of this map. It follows from the construction N is a
$L(\mu )$
in M. Denote by N the image of this map. It follows from the construction N is a
![]() $\mathfrak {g}$
-Harish-Chandra module, generated by its unique occurrence of the
$\mathfrak {g}$
-Harish-Chandra module, generated by its unique occurrence of the
![]() $\mathfrak {g}$
-type
$\mathfrak {g}$
-type
![]() $L(\mu )$
.
$L(\mu )$
.
Furthermore, N has a unique simple quotient V, which contains this
![]() $\mathfrak {g}$
-type
$\mathfrak {g}$
-type
![]() $L(\mu )$
. Clearly, V is a simple
$L(\mu )$
. Clearly, V is a simple
![]() $\mathfrak {g}$
-Harish-Chandra
$\mathfrak {g}$
-Harish-Chandra
![]() $\mathfrak {L}$
-module.
$\mathfrak {L}$
-module.
But also, V is infinite-dimensional. To see this, it is enough to check that c does not annihilate the vector (28). Observe that
 $$ \begin{align*} c \cdot f_1^{-1} f_2^{-1} \ldots f_k^{-1} \mathbf{v} &= \tilde{\lambda}(c) \cdot f_1^{-1} f_2^{-1} \ldots f_k^{-1} \mathbf{v} + \sum_{i=1}^k f_1^{-1} \ldots [c,f_i^{-1}] \ldots f_k^{-1} \mathbf{v}. \end{align*} $$
$$ \begin{align*} c \cdot f_1^{-1} f_2^{-1} \ldots f_k^{-1} \mathbf{v} &= \tilde{\lambda}(c) \cdot f_1^{-1} f_2^{-1} \ldots f_k^{-1} \mathbf{v} + \sum_{i=1}^k f_1^{-1} \ldots [c,f_i^{-1}] \ldots f_k^{-1} \mathbf{v}. \end{align*} $$
Since
 $[c,f_i^{-1}] = f_i^{-1}[f_i,c]f_i^{-1}$
, each summand with
$[c,f_i^{-1}] = f_i^{-1}[f_i,c]f_i^{-1}$
, each summand with
 $[c,f_i^{-1}]\neq 0$
will contain a factor from
$[c,f_i^{-1}]\neq 0$
will contain a factor from
![]() $\operatorname {\mathrm {Nrad}}(\mathfrak {L})$
. Therefore, these terms cannot cancel with
$\operatorname {\mathrm {Nrad}}(\mathfrak {L})$
. Therefore, these terms cannot cancel with
 $\tilde {\lambda }(c) \cdot f_1^{-1} f_2^{-1} \ldots f_k^{-1} \mathbf {v}$
, and so the total result is nonzero.
$\tilde {\lambda }(c) \cdot f_1^{-1} f_2^{-1} \ldots f_k^{-1} \mathbf {v}$
, and so the total result is nonzero.
We believe that the connection to the highest weight theory could be established in a more general setup, at least for the Takiff Lie algebras. Using the notation from Section 3, we formulate:
Conjecture 62. Let
![]() $\mathfrak {T}$
be a Takiff Lie algebra attached to a semisimple Lie algebra
$\mathfrak {T}$
be a Takiff Lie algebra attached to a semisimple Lie algebra
![]() $\mathfrak {g}$
. For a generic
$\mathfrak {g}$
. For a generic
 $\;\chi \colon \overline {Z(\mathfrak {g})} \to \mathbb {C}$
, there is
$\;\chi \colon \overline {Z(\mathfrak {g})} \to \mathbb {C}$
, there is
![]() $\lambda \in \bar {\mathfrak {h}}^\ast $
such that
$\lambda \in \bar {\mathfrak {h}}^\ast $
such that
![]() $\operatorname {\mathrm {\mathbf {EA}}}_{w_0}(\Delta (-2\rho ,\lambda )) \cong Q(0,\chi )$
.
$\operatorname {\mathrm {\mathbf {EA}}}_{w_0}(\Delta (-2\rho ,\lambda )) \cong Q(0,\chi )$
.
Here,
![]() $\rho $
is the half-sum of all elements in
$\rho $
is the half-sum of all elements in
![]() $\Delta ^+(\mathfrak {g},\mathfrak {h})$
, and
$\Delta ^+(\mathfrak {g},\mathfrak {h})$
, and
![]() $\operatorname {\mathrm {\mathbf {EA}}}_{w_0}$
should be defined as the composition
$\operatorname {\mathrm {\mathbf {EA}}}_{w_0}$
should be defined as the composition
![]() $\operatorname {\mathrm {\mathbf {EA}}}_{s_1} \circ \operatorname {\mathrm {\mathbf {EA}}}_{s_2} \circ \cdots \circ \operatorname {\mathrm {\mathbf {EA}}}_{s_k}$
, where
$\operatorname {\mathrm {\mathbf {EA}}}_{s_1} \circ \operatorname {\mathrm {\mathbf {EA}}}_{s_2} \circ \cdots \circ \operatorname {\mathrm {\mathbf {EA}}}_{s_k}$
, where
![]() $w_0 = s_1 s_2 \ldots s_k$
is a fixed a reduced expression of the longest element in the Weyl group for
$w_0 = s_1 s_2 \ldots s_k$
is a fixed a reduced expression of the longest element in the Weyl group for
![]() $\mathfrak {g}$
. Each
$\mathfrak {g}$
. Each
![]() $\operatorname {\mathrm {\mathbf {EA}}}_s$
should be defined as in Definition 21, that is, as
$\operatorname {\mathrm {\mathbf {EA}}}_s$
should be defined as in Definition 21, that is, as
![]() $\operatorname {\mathrm {\mathbf {EA}}}_s := {}^{e}{\left (\operatorname {\mathrm {\mathbf {C}}}_s(-)\right )}$
for the
$\operatorname {\mathrm {\mathbf {EA}}}_s := {}^{e}{\left (\operatorname {\mathrm {\mathbf {C}}}_s(-)\right )}$
for the
![]() $\mathfrak {sl}_2$
-triple
$\mathfrak {sl}_2$
-triple
![]() $\{f,h,e\}$
corresponding to s. It is not a priori clear that such
$\{f,h,e\}$
corresponding to s. It is not a priori clear that such
![]() $\operatorname {\mathrm {\mathbf {EA}}}_{w_0}$
does not depend on the choice of a reduced expression.
$\operatorname {\mathrm {\mathbf {EA}}}_{w_0}$
does not depend on the choice of a reduced expression.
Conjecture 62 was already proved for the Takiff
![]() $\mathfrak {sl}_2$
case in Section 4. Analogous statement is proved also for the Schrödinger Lie algebra in Section 5.
$\mathfrak {sl}_2$
case in Section 4. Analogous statement is proved also for the Schrödinger Lie algebra in Section 5.
6.2. On classification of simple
 $\mathfrak {g}$
-Harish-Chandra modules for generalized Takiff Lie algebras
$\mathfrak {g}$
-Harish-Chandra modules for generalized Takiff Lie algebras
In this subsection, we consider a finite-dimensional Lie algebra
![]() $\mathfrak {L}$
with a fixed Levi decomposition
$\mathfrak {L}$
with a fixed Levi decomposition
![]() $\mathfrak {L} \cong \mathfrak {g} \ltimes \mathfrak {r}$
and assume that:
$\mathfrak {L} \cong \mathfrak {g} \ltimes \mathfrak {r}$
and assume that:
It is reasonable to call such algebras generalized Takiff Lie algebras. In analogy to Section 3.2, we consider the purely radical part
 $\overline {Z(\mathfrak {L})}:=Z(\mathfrak {L})\cap U(\mathfrak {r})$
of the center
$\overline {Z(\mathfrak {L})}:=Z(\mathfrak {L})\cap U(\mathfrak {r})$
of the center
![]() $Z(\mathfrak {L})$
of
$Z(\mathfrak {L})$
of
![]() $U(\mathfrak {L})$
. Since
$U(\mathfrak {L})$
. Since
![]() $\mathfrak {r}$
is assumed to be abelian, it is obvious that
$\mathfrak {r}$
is assumed to be abelian, it is obvious that
 $\overline {Z(\mathfrak {L})} = U(\mathfrak {r})^{\mathfrak {g}}$
, the
$\overline {Z(\mathfrak {L})} = U(\mathfrak {r})^{\mathfrak {g}}$
, the
![]() $\mathfrak {g}$
-invariants in
$\mathfrak {g}$
-invariants in
![]() $U(\mathfrak {r}) \cong \operatorname {\mathrm {Sym}}(\mathfrak {r})$
with respect to the adjoint action. For brevity, algebra homomorphisms
$U(\mathfrak {r}) \cong \operatorname {\mathrm {Sym}}(\mathfrak {r})$
with respect to the adjoint action. For brevity, algebra homomorphisms
 $\chi :\overline {Z(\mathfrak {L})}\to \mathbb {C}$
will be loosely called radical central characters.
$\chi :\overline {Z(\mathfrak {L})}\to \mathbb {C}$
will be loosely called radical central characters.
For
![]() $\lambda \in \mathfrak {h}^\ast $
dominant and integral, we have the universal module
$\lambda \in \mathfrak {h}^\ast $
dominant and integral, we have the universal module
 $$ \begin{align*} Q(\lambda) := \operatorname{\mathrm{Ind}}_{\mathfrak{g}}^{\mathfrak{L}} L(\lambda) = U(\mathfrak{L}) \mathbin{\mathop{\otimes}\limits_{U(\mathfrak{g})}} L(\lambda) \cong U(\mathfrak{r}) \mathbin{\mathop{\otimes}\limits_{\mathbb{C}}} L(\lambda) \cong \operatorname{\mathrm{Sym}}(\mathfrak{r}) \mathbin{\mathop{\otimes}\limits_{\mathbb{C}}} L(\lambda). \end{align*} $$
$$ \begin{align*} Q(\lambda) := \operatorname{\mathrm{Ind}}_{\mathfrak{g}}^{\mathfrak{L}} L(\lambda) = U(\mathfrak{L}) \mathbin{\mathop{\otimes}\limits_{U(\mathfrak{g})}} L(\lambda) \cong U(\mathfrak{r}) \mathbin{\mathop{\otimes}\limits_{\mathbb{C}}} L(\lambda) \cong \operatorname{\mathrm{Sym}}(\mathfrak{r}) \mathbin{\mathop{\otimes}\limits_{\mathbb{C}}} L(\lambda). \end{align*} $$
Clearly, it is
![]() $\mathfrak {g}$
-locally finite. Completely analogously to Proposition 7, one can show that
$\mathfrak {g}$
-locally finite. Completely analogously to Proposition 7, one can show that
 $\operatorname {\mathrm {End}} Q(0) \cong \overline {Z(\mathfrak {L})}$
. Given also a radical central character
$\operatorname {\mathrm {End}} Q(0) \cong \overline {Z(\mathfrak {L})}$
. Given also a radical central character
 $\chi \colon \overline {Z(\mathfrak {L})} \to \mathbb {C}$
, we define
$\chi \colon \overline {Z(\mathfrak {L})} \to \mathbb {C}$
, we define

where
![]() $\mathbf {m}_\chi := \operatorname {\mathrm {Ker}} \chi $
is the maximal ideal in
$\mathbf {m}_\chi := \operatorname {\mathrm {Ker}} \chi $
is the maximal ideal in
 $\overline {Z(\mathfrak {L})}$
corresponding to
$\overline {Z(\mathfrak {L})}$
corresponding to
![]() $\chi $
.
$\chi $
.
From [Reference Knapp35, Proposition 6.5], we have
![]() $Q(\lambda ) \cong Q(0) \otimes L(\lambda )$
, and from this and right exactness of tensor product, we conclude
$Q(\lambda ) \cong Q(0) \otimes L(\lambda )$
, and from this and right exactness of tensor product, we conclude
![]() $Q(\lambda ,\chi ) \cong Q(0,\chi ) \otimes L(\lambda )$
. In these formulas,
$Q(\lambda ,\chi ) \cong Q(0,\chi ) \otimes L(\lambda )$
. In these formulas,
![]() $L(\lambda )$
is considered to be an
$L(\lambda )$
is considered to be an
![]() $\mathfrak {L}$
-module with the trivial action of
$\mathfrak {L}$
-module with the trivial action of
![]() $\mathfrak {r}$
.
$\mathfrak {r}$
.
By construction, the action of
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() $Q(0,\chi )$
is locally finite, with the trivial module
$Q(0,\chi )$
is locally finite, with the trivial module
![]() $L(0)$
having multiplicity exactly
$L(0)$
having multiplicity exactly
![]() $1$
in
$1$
in
![]() $Q(0,\chi )$
. Since
$Q(0,\chi )$
. Since
![]() $Q(0,\chi )$
is generated by this unique copy of
$Q(0,\chi )$
is generated by this unique copy of
![]() $L(0)$
, it follows that
$L(0)$
, it follows that
![]() $Q(0,\chi )$
has a unique simple quotient, which we denote by
$Q(0,\chi )$
has a unique simple quotient, which we denote by
![]() $V(0,\chi )$
.
$V(0,\chi )$
.
From Theorem 12, we know that
![]() $Q(0,\chi )=V(0,\chi )$
when
$Q(0,\chi )=V(0,\chi )$
when
![]() $\mathfrak {L}$
is the Takiff
$\mathfrak {L}$
is the Takiff
![]() $\mathfrak {sl}_2$
and
$\mathfrak {sl}_2$
and
![]() $\chi $
is not the radical central character of the trivial module, but generally this fails, for example, when
$\chi $
is not the radical central character of the trivial module, but generally this fails, for example, when
![]() $\mathfrak {r} \cong L(4)$
as a
$\mathfrak {r} \cong L(4)$
as a
![]() $\mathfrak {g}$
-module, as we will see in Section 7.3.
$\mathfrak {g}$
-module, as we will see in Section 7.3.
We will use the notion of Gelfand–Kirillov dimension, for the definition and basic properties (see [Reference Chen, Coulembier and Mazorchuk13, Subsection 2.3] or Reference Krause and Lenagan[38]). The Gelfand–Kirillov dimension of a finitely generated module M will be denoted by
![]() $\operatorname {\mathrm {GK}}(M)$
and the Bernstein number by
$\operatorname {\mathrm {GK}}(M)$
and the Bernstein number by
![]() $\operatorname {\mathrm {e}}(M)$
.
$\operatorname {\mathrm {e}}(M)$
.
Proposition 63. Fix a radical central character
![]() $\chi $
.
$\chi $
.
-
•
 $V(0,\chi )$
is the unique simple
$V(0,\chi )$
is the unique simple
 $\mathfrak {L}$
-module having both radical central character
$\mathfrak {L}$
-module having both radical central character
 $\chi $
and the trivial
$\chi $
and the trivial
 $\mathfrak {g}$
-module as one of
$\mathfrak {g}$
-module as one of
 $\mathfrak {g}$
-types.
$\mathfrak {g}$
-types. -
• If
 $[\mathfrak {g},\mathfrak {r}]=\mathfrak {r}$
, then
$[\mathfrak {g},\mathfrak {r}]=\mathfrak {r}$
, then
 $V(0,\chi )$
is either the trivial
$V(0,\chi )$
is either the trivial
 $\mathfrak {L}$
-module (precisely when
$\mathfrak {L}$
-module (precisely when
 $\chi $
is the radical central character of the trivial
$\chi $
is the radical central character of the trivial
 $\mathfrak {L}$
-module), or infinite-dimensional.
$\mathfrak {L}$
-module), or infinite-dimensional. -
•
 $V(0,\chi )$
is a
$V(0,\chi )$
is a
 $\mathfrak {g}$
-Harish-Chandra module.
$\mathfrak {g}$
-Harish-Chandra module.
Proof. The first claim follows from universal property of the induction functor.
For the second claim, recall that
![]() $[\mathfrak {g},\mathfrak {r}]=\operatorname {\mathrm {Nrad}} \mathfrak {L}$
is the intersection of all kernels of simple finite-dimensional
$[\mathfrak {g},\mathfrak {r}]=\operatorname {\mathrm {Nrad}} \mathfrak {L}$
is the intersection of all kernels of simple finite-dimensional
![]() $\mathfrak {L}$
-modules (see Section 2). Therefore, any simple finite-dimensional
$\mathfrak {L}$
-modules (see Section 2). Therefore, any simple finite-dimensional
![]() $\mathfrak {L}$
-module necessarily has the same radical central character as the trivial
$\mathfrak {L}$
-module necessarily has the same radical central character as the trivial
![]() $\mathfrak {L}$
-module. From the uniqueness in the first part, it follows that
$\mathfrak {L}$
-module. From the uniqueness in the first part, it follows that
![]() $V(0,\chi )$
is either trivial or infinite-dimensional.
$V(0,\chi )$
is either trivial or infinite-dimensional.
It remains to prove that
![]() $V(0,\chi )$
is a
$V(0,\chi )$
is a
![]() $\mathfrak {g}$
-Harish-Chandra module. It is
$\mathfrak {g}$
-Harish-Chandra module. It is
![]() $\mathfrak {g}$
-locally finite by construction. Assume that
$\mathfrak {g}$
-locally finite by construction. Assume that
![]() $[V(0,\chi ) \colon L] = \infty $
for some simple finite-dimensional
$[V(0,\chi ) \colon L] = \infty $
for some simple finite-dimensional
![]() $\mathfrak {g}$
-module L. The module
$\mathfrak {g}$
-module L. The module
![]() $V(0,\chi ) \otimes L^\ast $
is also
$V(0,\chi ) \otimes L^\ast $
is also
![]() $\mathfrak {g}$
-locally finite and finitely generated. By [Reference Jantzen32, Lemma 8.8], we have
$\mathfrak {g}$
-locally finite and finitely generated. By [Reference Jantzen32, Lemma 8.8], we have
Moreover,
 $$ \begin{align*} &[ V(0,\chi) \otimes L^\ast \colon L(0) ] = {\dim} \operatorname{\mathrm{Hom}}_{\mathfrak{g}} \left(L(0),V(0,\chi) \otimes L^\ast\right)) = \\ &\qquad\qquad\qquad\qquad\qquad\qquad= {\dim} \operatorname{\mathrm{Hom}}_{\mathfrak{g}} \left(L(0)\otimes L ,V(0,\chi)\right) = [V(0,\chi) \colon L] = \infty. \end{align*} $$
$$ \begin{align*} &[ V(0,\chi) \otimes L^\ast \colon L(0) ] = {\dim} \operatorname{\mathrm{Hom}}_{\mathfrak{g}} \left(L(0),V(0,\chi) \otimes L^\ast\right)) = \\ &\qquad\qquad\qquad\qquad\qquad\qquad= {\dim} \operatorname{\mathrm{Hom}}_{\mathfrak{g}} \left(L(0)\otimes L ,V(0,\chi)\right) = [V(0,\chi) \colon L] = \infty. \end{align*} $$
By uniqueness in the first part, it follows that
![]() $V(0,\chi )$
appears in
$V(0,\chi )$
appears in
![]() $V(0,\chi ) \otimes L^\ast $
infinitely many times. This is a contradiction with (29) and [Reference Chen, Coulembier and Mazorchuk13, Lemma 8].
$V(0,\chi ) \otimes L^\ast $
infinitely many times. This is a contradiction with (29) and [Reference Chen, Coulembier and Mazorchuk13, Lemma 8].
Remark 64. One can check that Gelfand–Kirillov dimensions of all infinite-dimensional simple
![]() $\mathfrak {g}$
-Harish-Chandra modules for the Takiff
$\mathfrak {g}$
-Harish-Chandra modules for the Takiff
![]() $\mathfrak {sl}_2$
(Section 4) as well for the Schrödinger Lie algebra (Section 5) are
$\mathfrak {sl}_2$
(Section 4) as well for the Schrödinger Lie algebra (Section 5) are
![]() $2$
.
$2$
.
Proposition 65. Let
![]() $\chi $
be a radical central character and L a simple finite-dimensional
$\chi $
be a radical central character and L a simple finite-dimensional
![]() $\mathfrak {g}$
-module. Then,
$\mathfrak {g}$
-module. Then,
![]() $\mathfrak {L}$
has a simple
$\mathfrak {L}$
has a simple
![]() $\mathfrak {g}$
-Harish-Chandra module with the radical central character
$\mathfrak {g}$
-Harish-Chandra module with the radical central character
![]() $\chi $
and having L as one of
$\chi $
and having L as one of
![]() $\mathfrak {g}$
-types.
$\mathfrak {g}$
-types.
Moreover, the number of (isomorphism classes of) simple
![]() $\mathfrak {g}$
-Harish-Chandra modules with the radical central character
$\mathfrak {g}$
-Harish-Chandra modules with the radical central character
![]() $\chi $
and having L as one of its
$\chi $
and having L as one of its
![]() $\mathfrak {g}$
-types is at most
$\mathfrak {g}$
-types is at most
 $$ \begin{align} \sum_{M} l_{M,L}^L [V(0,\chi):M] < \infty, \end{align} $$
$$ \begin{align} \sum_{M} l_{M,L}^L [V(0,\chi):M] < \infty, \end{align} $$
where M runs through the set of isomorphism classes of simple finite-dimensional
![]() $\mathfrak {g}$
-modules and
$\mathfrak {g}$
-modules and
 $l_{M,L}^L$
is the Littlewood–Richardson coefficient, that is, the multiplicity of L in
$l_{M,L}^L$
is the Littlewood–Richardson coefficient, that is, the multiplicity of L in
![]() $M\otimes L$
.
$M\otimes L$
.
We note that only finitely many summands in (30) are nonzero, as
 $l_{M,V}^V\neq 0$
if and only if M appears as a summand of
$l_{M,V}^V\neq 0$
if and only if M appears as a summand of
![]() $V\otimes V^{*}$
.
$V\otimes V^{*}$
.
Proof. Since we know from Proposition 63 that
![]() $V(0,\chi )$
is a
$V(0,\chi )$
is a
![]() $\mathfrak {g}$
-Harish-Chandra module having
$\mathfrak {g}$
-Harish-Chandra module having
![]() $L(0)$
as a
$L(0)$
as a
![]() $\mathfrak {g}$
-type, it follows that
$\mathfrak {g}$
-type, it follows that
![]() $L\otimes V(0,\chi )$
is also a
$L\otimes V(0,\chi )$
is also a
![]() $\mathfrak {g}$
-Harish-Chandra module, having L as one of
$\mathfrak {g}$
-Harish-Chandra module, having L as one of
![]() $\mathfrak {g}$
-types. This implies the first part of the proposition.
$\mathfrak {g}$
-types. This implies the first part of the proposition.
Conversely, let N be a simple
![]() $\mathfrak {g}$
-Harish-Chandra module with the radical central character
$\mathfrak {g}$
-Harish-Chandra module with the radical central character
![]() $\chi $
and having L as one of
$\chi $
and having L as one of
![]() $\mathfrak {g}$
-types. Then,
$\mathfrak {g}$
-types. Then,
![]() $L^{*} \otimes N$
is a
$L^{*} \otimes N$
is a
![]() $\mathfrak {g}$
-Harish-Chandra module with the radical central character
$\mathfrak {g}$
-Harish-Chandra module with the radical central character
![]() $\chi $
and having
$\chi $
and having
![]() $L(0)$
as one of
$L(0)$
as one of
![]() $\mathfrak {g}$
-types, and therefore contains
$\mathfrak {g}$
-types, and therefore contains
![]() $V(0,\chi )$
as a subquotient.
$V(0,\chi )$
as a subquotient.
The above arguments, combined with the biadjunction
![]() $(L\otimes {}-,L^{*}\otimes {}-)$
, imply that any simple
$(L\otimes {}-,L^{*}\otimes {}-)$
, imply that any simple
![]() $\mathfrak {g}$
-Harish-Chandra module with the radical central character
$\mathfrak {g}$
-Harish-Chandra module with the radical central character
![]() $\chi $
and having L as one of
$\chi $
and having L as one of
![]() $\mathfrak {g}$
-types is a subquotient of
$\mathfrak {g}$
-types is a subquotient of
![]() $L \otimes V(0,\chi )$
. The latter is a
$L \otimes V(0,\chi )$
. The latter is a
![]() $\mathfrak {g}$
-Harish-Chandra module in which the multiplicity of L is bounded by the expression in (30) (see the proof of Proposition 8). This implies the second part of the proposition.
$\mathfrak {g}$
-Harish-Chandra module in which the multiplicity of L is bounded by the expression in (30) (see the proof of Proposition 8). This implies the second part of the proposition.
7. On
 $\mathfrak {sl}_2$
-Harish-Chandra modules for other conformal Galilei algebras
$\mathfrak {sl}_2$
-Harish-Chandra modules for other conformal Galilei algebras
7.1. Conformal Galilei algebras
By a conformal Galilei algebra, we mean a semidirect product
![]() $\mathfrak {L}^n := \mathfrak {sl}_2 \ltimes L(n)$
, where
$\mathfrak {L}^n := \mathfrak {sl}_2 \ltimes L(n)$
, where
![]() $n \in \mathbb {Z}_{\geq 0}$
. Here,
$n \in \mathbb {Z}_{\geq 0}$
. Here,
![]() $L(n)$
is an abelian ideal on which
$L(n)$
is an abelian ideal on which
![]() $\mathfrak {g} := \mathfrak {sl}_2$
acts in the obvious way. For a more general definition and various central extensions, see [Reference Alshammari, Isaac and Marquette1], [Reference Gomis and Kamimura26], [Reference Lü, Mazorchuk and Zhao40].
$\mathfrak {g} := \mathfrak {sl}_2$
acts in the obvious way. For a more general definition and various central extensions, see [Reference Alshammari, Isaac and Marquette1], [Reference Gomis and Kamimura26], [Reference Lü, Mazorchuk and Zhao40].
Note that we have
![]() $\mathfrak {L}^0 \cong \mathfrak {gl}_2$
,
$\mathfrak {L}^0 \cong \mathfrak {gl}_2$
,
![]() $\mathfrak {L}^1$
is the centerless Schrödinger Lie algebra, and
$\mathfrak {L}^1$
is the centerless Schrödinger Lie algebra, and
![]() $\mathfrak {L}^2$
is the Takiff
$\mathfrak {L}^2$
is the Takiff
![]() $\mathfrak {sl}_2$
.
$\mathfrak {sl}_2$
.
We have
![]() $\operatorname {\mathrm {Nrad}}(\mathfrak {L}^n) = \mathfrak {r} = L(n)$
, and so
$\operatorname {\mathrm {Nrad}}(\mathfrak {L}^n) = \mathfrak {r} = L(n)$
, and so
![]() $[\mathfrak {L}^n,\mathfrak {r}] \cap \mathfrak {r}_0 \cong \mathbb {C}$
if and only if n is even (i.e.,
$[\mathfrak {L}^n,\mathfrak {r}] \cap \mathfrak {r}_0 \cong \mathbb {C}$
if and only if n is even (i.e.,
![]() $L(n)$
is odd-dimensional), otherwise
$L(n)$
is odd-dimensional), otherwise
![]() $[\mathfrak {L}^n,\mathfrak {r}] \cap \mathfrak {r}_0 = 0$
.
$[\mathfrak {L}^n,\mathfrak {r}] \cap \mathfrak {r}_0 = 0$
.
Denote by
![]() $v_n, v_{n-2}, \ldots , v_{-n}$
a basis of
$v_n, v_{n-2}, \ldots , v_{-n}$
a basis of
![]() $L(n)$
such that each
$L(n)$
such that each
![]() $v_i$
is a weight vector of weight i, and
$v_i$
is a weight vector of weight i, and
![]() $[e,v_{n-2i}] = (n-i+1) v_{n-2i+2}$
, for
$[e,v_{n-2i}] = (n-i+1) v_{n-2i+2}$
, for
![]() $i \in \{1,2,\ldots ,n\}$
.
$i \in \{1,2,\ldots ,n\}$
.
7.2. The Lie algebra
 $\mathfrak {L}^3 = \mathfrak {sl}_2 \ltimes L(3)$
$\mathfrak {L}^3 = \mathfrak {sl}_2 \ltimes L(3)$
Since
![]() $\mathfrak {r} = L(3)$
has trivial zero-weight space, the assumption in Theorem 61 is not satisfied. Nevertheless, we will show that simple infinite-dimensional
$\mathfrak {r} = L(3)$
has trivial zero-weight space, the assumption in Theorem 61 is not satisfied. Nevertheless, we will show that simple infinite-dimensional
![]() $\mathfrak {g}$
-Harish-Chandra modules exist. So, the converse of Theorem 61 is not true. This suggest that the highest weight theory is not enough to obtain and classify
$\mathfrak {g}$
-Harish-Chandra modules exist. So, the converse of Theorem 61 is not true. This suggest that the highest weight theory is not enough to obtain and classify
![]() $\mathfrak {g}$
-Harish-Chandra modules for any Lie algebra.
$\mathfrak {g}$
-Harish-Chandra modules for any Lie algebra.
From the classical invariant theory, it is well known that
![]() $\operatorname {\mathrm {Sym}}(\mathfrak {r})^{\mathfrak {g}}$
is generated by only one element C, homogeneous of degree
$\operatorname {\mathrm {Sym}}(\mathfrak {r})^{\mathfrak {g}}$
is generated by only one element C, homogeneous of degree
![]() $4$
, the so-called cubic discriminant (see, e.g., [Reference Hilbert29, Lecture XVII]):
$4$
, the so-called cubic discriminant (see, e.g., [Reference Hilbert29, Lecture XVII]):
 $$ \begin{align*} C= v_{-1}^2 v_{1}^2 - 27 v_{-3}^2 v_{3}^2 - 4 v_{-1}^3v_3 - 4 v_{-1}v_3^3 + 18v_{-3}v_{-1}v_1 v_3. \end{align*} $$
$$ \begin{align*} C= v_{-1}^2 v_{1}^2 - 27 v_{-3}^2 v_{3}^2 - 4 v_{-1}^3v_3 - 4 v_{-1}v_3^3 + 18v_{-3}v_{-1}v_1 v_3. \end{align*} $$
This expression of C is just for the record; we will not use it in the computations. We identify radical central characters with their value on C.
For
![]() $\chi \in \mathbb {C}$
, we have the universal
$\chi \in \mathbb {C}$
, we have the universal
![]() $\mathfrak {L}^3$
-module
$\mathfrak {L}^3$
-module
 .
.
Proposition 66. For
![]() $\chi \neq 0$
, the module
$\chi \neq 0$
, the module
![]() $Q(0,\chi )$
is
$Q(0,\chi )$
is
![]() $\mathfrak {g}$
-Harish-Chandra. The multiplicities of its
$\mathfrak {g}$
-Harish-Chandra. The multiplicities of its
![]() $\mathfrak {g}$
-types are given by
$\mathfrak {g}$
-types are given by
 $[ Q(0,\chi ) \colon L(k)] = k - 2 \left \lfloor {\frac {k+2}{3}}\right \rfloor +1$
.
$[ Q(0,\chi ) \colon L(k)] = k - 2 \left \lfloor {\frac {k+2}{3}}\right \rfloor +1$
.
Proof. From the main result of Reference Futorny and Ovsienko[23], it follows easily that
![]() $\operatorname {\mathrm {Sym}}(\mathfrak {r})$
is free as a module over
$\operatorname {\mathrm {Sym}}(\mathfrak {r})$
is free as a module over
![]() $\operatorname {\mathrm {Sym}}(\mathfrak {r})^{\mathfrak {g}} = \mathbb {C}[C]$
. This implies that the
$\operatorname {\mathrm {Sym}}(\mathfrak {r})^{\mathfrak {g}} = \mathbb {C}[C]$
. This implies that the
![]() $\mathfrak {g}$
-structure of
$\mathfrak {g}$
-structure of
![]() $Q(0,\chi )$
does not depend on the choice of
$Q(0,\chi )$
does not depend on the choice of
![]() $\chi $
. So, in particular, it is enough to prove the multiplicity statement for
$\chi $
. So, in particular, it is enough to prove the multiplicity statement for
![]() $Q(0,0)$
, which is as a
$Q(0,0)$
, which is as a
![]() $\mathfrak {g}$
-module isomorphic to
$\mathfrak {g}$
-module isomorphic to
 .
.
But these are now graded modules, so we can subtract their graded characters. More precisely, for
![]() $d \geq 4$
and
$d \geq 4$
and
![]() $k \geq 0$
, we have
$k \geq 0$
, we have
 $$ \begin{align} [Q(0,0)^d \colon L(k)] = [\operatorname{\mathrm{Sym}}^d(\mathfrak{r}) \colon L(k)] - [\operatorname{\mathrm{Sym}}^{d-4}(\mathfrak{r}) \colon L(k)], \end{align} $$
$$ \begin{align} [Q(0,0)^d \colon L(k)] = [\operatorname{\mathrm{Sym}}^d(\mathfrak{r}) \colon L(k)] - [\operatorname{\mathrm{Sym}}^{d-4}(\mathfrak{r}) \colon L(k)], \end{align} $$
where
 $(-)^d$
denotes the homogeneous part of degree d.
$(-)^d$
denotes the homogeneous part of degree d.
Using Reference Hahn, Huh, Lim and Sohn[27], one can calculate the right-hand side of (31). For nonnegative integers
![]() $a,b,c$
, let
$a,b,c$
, let
![]() $p(a,b,c)$
denote the number of partitions of c into at most b parts, and each part bounded above by a. Denote
$p(a,b,c)$
denote the number of partitions of c into at most b parts, and each part bounded above by a. Denote
![]() $N(a,b,c) := p(a,b,c) - p(a,b,c-1)$
if
$N(a,b,c) := p(a,b,c) - p(a,b,c-1)$
if
![]() $c \geq 1$
, and set
$c \geq 1$
, and set
![]() $N(a,b,0) := 1$
. By [Reference Hahn, Huh, Lim and Sohn27, Theorem 3.1], the multiplicity (31) is equal to
$N(a,b,0) := 1$
. By [Reference Hahn, Huh, Lim and Sohn27, Theorem 3.1], the multiplicity (31) is equal to
![]() $0$
if
$0$
if
![]() $k \not \in \{3d,3d-2,3d-4,\ldots \}$
, and to
$k \not \in \{3d,3d-2,3d-4,\ldots \}$
, and to
 $$ \begin{align} N \left(d,3,\frac{3d-k}{2}\right) - N\left(d-4,3,\frac{3d-k}{2}-6\right) \end{align} $$
$$ \begin{align} N \left(d,3,\frac{3d-k}{2}\right) - N\left(d-4,3,\frac{3d-k}{2}-6\right) \end{align} $$
otherwise. But the latter is also equal to
![]() $0$
whenever
$0$
whenever
![]() $k<d-4$
, by using the formulas in [Reference Hahn, Huh, Lim and Sohn27, Corollary 3.2]. It follows that any
$k<d-4$
, by using the formulas in [Reference Hahn, Huh, Lim and Sohn27, Corollary 3.2]. It follows that any
![]() $L(k)$
can appear in
$L(k)$
can appear in
![]() $Q(0,0)$
in at most degree
$Q(0,0)$
in at most degree
![]() $k+4$
, hence only finitely many times.
$k+4$
, hence only finitely many times.
Note that
![]() $[Q(0,0) \colon L(k)]$
is equal to the sum of the expressions (32), where d ranges from
$[Q(0,0) \colon L(k)]$
is equal to the sum of the expressions (32), where d ranges from
![]() $0$
to
$0$
to
![]() $k+4$
. Now, using the same formulas in [Reference Hahn, Huh, Lim and Sohn27, Corollary 3.2], one can derive the multiplicity formula from the statement of the proposition. We omit the details.
$k+4$
. Now, using the same formulas in [Reference Hahn, Huh, Lim and Sohn27, Corollary 3.2], one can derive the multiplicity formula from the statement of the proposition. We omit the details.
Either from Proposition 63, or from Proposition 66, we have:
Corollary 67. The unique simple quotient
![]() $V(0,\chi )$
of
$V(0,\chi )$
of
![]() $Q(0,\chi )$
is
$Q(0,\chi )$
is
![]() $\mathfrak {g}$
-Harish-Chandra. It is infinite-dimensional if
$\mathfrak {g}$
-Harish-Chandra. It is infinite-dimensional if
![]() $\chi \neq 0$
.
$\chi \neq 0$
.
We do not know whether
![]() $Q(0,\chi )=V(0,\chi )$
, that is, whether
$Q(0,\chi )=V(0,\chi )$
, that is, whether
![]() $Q(0,\chi )$
is already simple (for
$Q(0,\chi )$
is already simple (for
![]() $\chi \neq 0$
), as was in the Takiff
$\chi \neq 0$
), as was in the Takiff
![]() $\mathfrak {sl}_2$
and the Schrödinger cases.
$\mathfrak {sl}_2$
and the Schrödinger cases.
7.3. The Lie algebra
 $\mathfrak {L}^4 = \mathfrak {sl}_2 \ltimes L(4)$
$\mathfrak {L}^4 = \mathfrak {sl}_2 \ltimes L(4)$
Consider now the algebra
![]() $\mathfrak {L}^4$
. In this subsection, we classify simple
$\mathfrak {L}^4$
. In this subsection, we classify simple
![]() $\mathfrak {g}$
-Harish-Chandra modules for
$\mathfrak {g}$
-Harish-Chandra modules for
![]() $\mathfrak {L}^4$
which appear in Enright–Arkhipov completions of simple highest weight modules.
$\mathfrak {L}^4$
which appear in Enright–Arkhipov completions of simple highest weight modules.
The algebra
![]() $\operatorname {\mathrm {Sym}}(\mathfrak {r})^{\mathfrak {g}}$
is generated by two algebraically independent elements, homogeneous of degrees
$\operatorname {\mathrm {Sym}}(\mathfrak {r})^{\mathfrak {g}}$
is generated by two algebraically independent elements, homogeneous of degrees
![]() $2$
and
$2$
and
![]() $3$
(see, e.g., [Reference Hilbert29, Lecture XVIII]):
$3$
(see, e.g., [Reference Hilbert29, Lecture XVIII]):
 $$ \begin{align*} C_2 &= v_0^2 -3 v_{-2} v_2 + 12 v_{-4} v_4, \\ C_3 &= v_0^3 - \frac{9}{2} v_{-2} v_0 v_2 + \frac{27}{2} v_{-2}^2 v_4 + \frac{27}{2} v_{-4} v_2^2 - 36 v_{-4} v_0 v_4. \end{align*} $$
$$ \begin{align*} C_2 &= v_0^2 -3 v_{-2} v_2 + 12 v_{-4} v_4, \\ C_3 &= v_0^3 - \frac{9}{2} v_{-2} v_0 v_2 + \frac{27}{2} v_{-2}^2 v_4 + \frac{27}{2} v_{-4} v_2^2 - 36 v_{-4} v_0 v_4. \end{align*} $$
Recall also, from [Reference Lü, Mazorchuk and Zhao40, Theorem 4], the structure of simple highest weight
![]() $\mathfrak {L}^4$
-modules. Let
$\mathfrak {L}^4$
-modules. Let
![]() $\tilde {\mathfrak {h}}$
denote the (generalized) Cartan subalgebra of
$\tilde {\mathfrak {h}}$
denote the (generalized) Cartan subalgebra of
![]() $\mathfrak {L}^4$
spanned by h and
$\mathfrak {L}^4$
spanned by h and
![]() $v_0$
. If
$v_0$
. If
 $\lambda \in \tilde {\mathfrak {h}}^\ast $
is such that
$\lambda \in \tilde {\mathfrak {h}}^\ast $
is such that
![]() $\lambda (v_0)=0$
, then
$\lambda (v_0)=0$
, then
![]() $\mathfrak {r}$
annihilates the corresponding simple highest weight module
$\mathfrak {r}$
annihilates the corresponding simple highest weight module
![]() $\mathbf {L}(\lambda )$
. If
$\mathbf {L}(\lambda )$
. If
 $\lambda \in \tilde {\mathfrak {h}}^\ast $
is such that
$\lambda \in \tilde {\mathfrak {h}}^\ast $
is such that
![]() $\lambda (v_0)\neq 0$
, then the restriction of
$\lambda (v_0)\neq 0$
, then the restriction of
![]() $\mathbf {L}(\lambda )$
to
$\mathbf {L}(\lambda )$
to
![]() $\mathfrak {g}$
has a multiplicity free Verma filtration with subquotients of the form
$\mathfrak {g}$
has a multiplicity free Verma filtration with subquotients of the form
![]() $\Delta ^{\mathfrak {g}}(\lambda -n\alpha )$
, where
$\Delta ^{\mathfrak {g}}(\lambda -n\alpha )$
, where
![]() $n\in \mathbb {Z}_{\geq 0}$
and
$n\in \mathbb {Z}_{\geq 0}$
and
![]() $\alpha $
is the root corresponding to
$\alpha $
is the root corresponding to
![]() $e\in \mathfrak {g}$
. Note that the elements
$e\in \mathfrak {g}$
. Note that the elements
![]() $C_2$
and
$C_2$
and
![]() $C_3$
act on
$C_3$
act on
![]() $\mathbf {L}(\lambda )$
as the scalars
$\mathbf {L}(\lambda )$
as the scalars
 $\lambda (v_0)^2$
and
$\lambda (v_0)^2$
and
 $\lambda (v_0)^3$
, respectively.
$\lambda (v_0)^3$
, respectively.
Denote by
![]() $\mathcal {F}$
the semisimple additive category generated by simple subquotients of Enright–Arkhipov completions of simple highest weight
$\mathcal {F}$
the semisimple additive category generated by simple subquotients of Enright–Arkhipov completions of simple highest weight
![]() $\mathfrak {L}^4$
-modules. Note that all modules in
$\mathfrak {L}^4$
-modules. Note that all modules in
![]() $\mathcal {F}$
are
$\mathcal {F}$
are
![]() $\mathfrak {g}$
-Harish-Chandra modules for
$\mathfrak {g}$
-Harish-Chandra modules for
![]() $\mathfrak {L}^4$
. Our main result of this subsection is the following theorem.
$\mathfrak {L}^4$
. Our main result of this subsection is the following theorem.
Theorem 68.
-
(a) For each
 $\tilde {\lambda }\in \mathbb {C}\setminus \{0\}$
and for each
$\tilde {\lambda }\in \mathbb {C}\setminus \{0\}$
and for each
 $i\in \mathbb {Z}_{>0}$
, there is a unique, up to isomorphism, simple object
$i\in \mathbb {Z}_{>0}$
, there is a unique, up to isomorphism, simple object
 $V(i,\tilde {\lambda })$
in
$V(i,\tilde {\lambda })$
in
 $\mathcal {F}$
on which
$\mathcal {F}$
on which
 $C_j$
, where
$C_j$
, where
 $j=2,3$
, acts via
$j=2,3$
, acts via
 $\tilde {\lambda }^j$
and which has
$\tilde {\lambda }^j$
and which has
 $\mathfrak {g}$
-types
$\mathfrak {g}$
-types
 $L(i)$
,
$L(i)$
,
 $L(i+2)$
,
$L(i+2)$
,
 $L(i+4),\dots $
, all multiplicity free.
$L(i+4),\dots $
, all multiplicity free. -
(b) For each
 $\tilde {\lambda }\in \mathbb {C}\setminus \{0\}$
, there is a unique, up to isomorphism, simple object
$\tilde {\lambda }\in \mathbb {C}\setminus \{0\}$
, there is a unique, up to isomorphism, simple object
 $V'(0,\tilde {\lambda })$
in
$V'(0,\tilde {\lambda })$
in
 $\mathcal {F}$
on which
$\mathcal {F}$
on which
 $C_j$
, where
$C_j$
, where
 $j=2,3$
, acts via
$j=2,3$
, acts via
 $\tilde {\lambda }^j$
and which has
$\tilde {\lambda }^j$
and which has
 $\mathfrak {g}$
-types
$\mathfrak {g}$
-types
 $L(0)$
,
$L(0)$
,
 $L(4)$
,
$L(4)$
,
 $L(8),\dots $
, all multiplicity free.
$L(8),\dots $
, all multiplicity free. -
(c) For each
 $\tilde {\lambda }\in \mathbb {C}\setminus \{0\}$
, there is a unique, up to isomorphism, simple object
$\tilde {\lambda }\in \mathbb {C}\setminus \{0\}$
, there is a unique, up to isomorphism, simple object
 $V'(2,\tilde {\lambda })$
in
$V'(2,\tilde {\lambda })$
in
 $\mathcal {F}$
on which
$\mathcal {F}$
on which
 $C_j$
, where
$C_j$
, where
 $j=2,3$
, acts via
$j=2,3$
, acts via
 $\tilde {\lambda }^j$
and which has
$\tilde {\lambda }^j$
and which has
 $\mathfrak {g}$
-types
$\mathfrak {g}$
-types
 $L(2)$
,
$L(2)$
,
 $L(6)$
,
$L(6)$
,
 $L(10),\dots $
, all multiplicity free.
$L(10),\dots $
, all multiplicity free. -
(d) The modules above provide a complete and irredundant list of representatives of isomorphism classes of simple objects in
 $\mathcal {F}$
.
$\mathcal {F}$
. -
(e) Let V be a simple
 $\mathfrak {g}$
-Harish-Chandra module on which
$\mathfrak {g}$
-Harish-Chandra module on which
 $C_j$
, where
$C_j$
, where
 $j=2,3$
, acts via
$j=2,3$
, acts via
 $\tilde {\lambda }^j$
, for some
$\tilde {\lambda }^j$
, for some
 $\tilde {\lambda }\in \mathbb {C}\setminus \{0\}$
. Then, V belongs to
$\tilde {\lambda }\in \mathbb {C}\setminus \{0\}$
. Then, V belongs to
 $\mathcal {F}$
.
$\mathcal {F}$
.
To prove this result, we will need some preparation. The following lemma extends [Reference Hahn, Huh, Lim and Sohn27, Corollary 3.5] (note that the case treated in the lemma below is referred to as complicated in Reference Hahn, Huh, Lim and Sohn[27]).
Lemma 69. For every nonnegative integer k, we have
 $$ \begin{align*} \sum_{s=0}^{\lfloor\frac{2k-1}{4}\rfloor} \left( \left\lfloor\frac{2k-4s-1}{2}\right\rfloor- \left\lfloor\frac{2k-4s-2}{3}\right\rfloor \right) -\sum_{s=0}^{k-2} \left( \left\lfloor\frac{s}{2}\right\rfloor- \left\lfloor\frac{s-1}{3}\right\rfloor \right) =0. \end{align*} $$
$$ \begin{align*} \sum_{s=0}^{\lfloor\frac{2k-1}{4}\rfloor} \left( \left\lfloor\frac{2k-4s-1}{2}\right\rfloor- \left\lfloor\frac{2k-4s-2}{3}\right\rfloor \right) -\sum_{s=0}^{k-2} \left( \left\lfloor\frac{s}{2}\right\rfloor- \left\lfloor\frac{s-1}{3}\right\rfloor \right) =0. \end{align*} $$
Proof. Using computer, it is easy to check that the claim of the lemma is true for small values of k (we checked this independently and by different methods using Scilab and SageMath up to
![]() $k=200$
). After that, one can do induction on k with induction step
$k=200$
). After that, one can do induction on k with induction step
![]() $12$
. So, we write
$12$
. So, we write
![]() $k=12a+r$
and consider each r separately. Let
$k=12a+r$
and consider each r separately. Let
![]() $S(k)$
denote the left-hand side of the formula. For
$S(k)$
denote the left-hand side of the formula. For
![]() $k>12$
, the value
$k>12$
, the value
![]() $S(k)-S(k-12)$
can be written as a polynomial in a (the polynomial itself depends on r) of degree at most 2.
$S(k)-S(k-12)$
can be written as a polynomial in a (the polynomial itself depends on r) of degree at most 2.
From the original computation, it follows that
![]() $S(k)-S(k-12)$
vanishes for enough values of a to conclude that
$S(k)-S(k-12)$
vanishes for enough values of a to conclude that
![]() $S(k)-S(k-12)$
is identically
$S(k)-S(k-12)$
is identically
![]() $0$
. The claim follows.
$0$
. The claim follows.
Remark 70. The results of Reference Hahn, Huh, Lim and Sohn[27] say that Lemma 69 is equivalent to the fact that, for each
![]() $k\geq 0$
, the set
$k\geq 0$
, the set
![]() $\Lambda _1$
of all vectors
$\Lambda _1$
of all vectors
![]() $(a,b,c,d,e)$
with nonnegative integer coefficients satisfying
$(a,b,c,d,e)$
with nonnegative integer coefficients satisfying
![]() $a+b+c+d+e=k$
and
$a+b+c+d+e=k$
and
![]() $2a+b-d-2e=1$
has the same cardinality as the set
$2a+b-d-2e=1$
has the same cardinality as the set
![]() $\Lambda _2$
of all vectors
$\Lambda _2$
of all vectors
![]() $(a,b,c,d,e)$
with nonnegative integer coefficients satisfying
$(a,b,c,d,e)$
with nonnegative integer coefficients satisfying
![]() $a+b+c+d+e=k$
and
$a+b+c+d+e=k$
and
![]() $2a+b-d-2e=2$
. We give here explicitly a bijection between these sets. First, note that
$2a+b-d-2e=2$
. We give here explicitly a bijection between these sets. First, note that
![]() $\{ (a,b,c,d,e) \in \Lambda _1 \colon e \neq 0 \}$
maps bijectively to
$\{ (a,b,c,d,e) \in \Lambda _1 \colon e \neq 0 \}$
maps bijectively to
![]() $\{ (a',b',c',d',e') \in \Lambda _2 \colon d' \neq 0 \}$
by
$\{ (a',b',c',d',e') \in \Lambda _2 \colon d' \neq 0 \}$
by
The remainder
![]() $\{ (a,b,c,d,0) \in \Lambda _1\}$
maps bijectively to
$\{ (a,b,c,d,0) \in \Lambda _1\}$
maps bijectively to
![]() $\{ (a',b',c',0,e') \in \Lambda _2\}$
by the formula
$\{ (a',b',c',0,e') \in \Lambda _2\}$
by the formula
Lemma 71. Let V be a simple infinite-dimensional
![]() $\mathfrak {g}$
-Harish-Chandra module for
$\mathfrak {g}$
-Harish-Chandra module for
![]() $\mathfrak {L}^4$
. Then, each
$\mathfrak {L}^4$
. Then, each
![]() $v_i$
acts injectively on V.
$v_i$
acts injectively on V.
Proof. Since the adjoint action of
![]() $v_i$
on
$v_i$
on
![]() $\mathfrak {L}^4$
is locally nilpotent, the action of
$\mathfrak {L}^4$
is locally nilpotent, the action of
![]() $v_i$
on each simple
$v_i$
on each simple
![]() $\mathfrak {L}^4$
-module is either injective or locally nilpotent (cf. [Reference Dimitrov, Mathieu and Penkov16, Section 3]). Note that the action of both e and f on V is locally nilpotent by definition. Let
$\mathfrak {L}^4$
-module is either injective or locally nilpotent (cf. [Reference Dimitrov, Mathieu and Penkov16, Section 3]). Note that the action of both e and f on V is locally nilpotent by definition. Let
![]() $x\in V$
be such that
$x\in V$
be such that
![]() $v_i\cdot x=0$
, for some
$v_i\cdot x=0$
, for some
![]() $i\neq 4$
, and
$i\neq 4$
, and
![]() $e^m\cdot v=0$
. Then,
$e^m\cdot v=0$
. Then,
![]() $\mathrm {ad}^m(v_i)(e^m)\cdot x=0$
, and it is easy to check that this implies that
$\mathrm {ad}^m(v_i)(e^m)\cdot x=0$
, and it is easy to check that this implies that
![]() $v_{i+2}^m\cdot x=0$
. That is, the action of
$v_{i+2}^m\cdot x=0$
. That is, the action of
![]() $v_{i+2}$
is locally nilpotent. Applying similar arguments using e and f, we get that the action of all
$v_{i+2}$
is locally nilpotent. Applying similar arguments using e and f, we get that the action of all
![]() $v_{j}$
’s is locally nilpotent.
$v_{j}$
’s is locally nilpotent.
As all
![]() $v_{j}$
’s commute, V must contain some nonzero x which is killed by all the
$v_{j}$
’s commute, V must contain some nonzero x which is killed by all the
![]() $v_{j}$
’s. Since the adjoint action of e preserves the set of the
$v_{j}$
’s. Since the adjoint action of e preserves the set of the
![]() $v_{j}$
’s, we can even assume that e kills x. But then, this means that V is a highest weight module. Being also a
$v_{j}$
’s, we can even assume that e kills x. But then, this means that V is a highest weight module. Being also a
![]() $\mathfrak {g}$
-Harish-Chandra module, this implies that V must be finite-dimensional, a contradiction.
$\mathfrak {g}$
-Harish-Chandra module, this implies that V must be finite-dimensional, a contradiction.
For
![]() $\chi _2, \chi _3 \in \mathbb {C}$
, we recall the universal
$\chi _2, \chi _3 \in \mathbb {C}$
, we recall the universal
![]() $\mathfrak {L}^4$
-module
$\mathfrak {L}^4$
-module

and its unique simple quotient
![]() $V(0,\chi _2, \chi _3)$
containing
$V(0,\chi _2, \chi _3)$
containing
![]() $L(0)$
.
$L(0)$
.
Proposition 72. Fix
 $\tilde {\lambda } \in \mathbb {C}\setminus \{0\}$
. The module
$\tilde {\lambda } \in \mathbb {C}\setminus \{0\}$
. The module
 $V(0,\tilde {\lambda }^2, \tilde {\lambda }^3)$
is a simple infinite-dimensional
$V(0,\tilde {\lambda }^2, \tilde {\lambda }^3)$
is a simple infinite-dimensional
![]() $\mathfrak {g}$
-Harish-Chandra module. Its
$\mathfrak {g}$
-Harish-Chandra module. Its
![]() $\mathfrak {g}$
-types are
$\mathfrak {g}$
-types are
![]() $L(0), L(4), L(8) \ldots $
, each occurring with multiplicity 1.
$L(0), L(4), L(8) \ldots $
, each occurring with multiplicity 1.
Proof. By [Reference Hahn, Huh, Lim and Sohn27, Theorem 3.1 and Corollary 3.4], the multiplicity of
![]() $L(2)$
in
$L(2)$
in
![]() $Q(0)$
is given by the left-hand side of the formula from Lemma 69. Therefore, by Lemma 69,
$Q(0)$
is given by the left-hand side of the formula from Lemma 69. Therefore, by Lemma 69,
![]() $L(2)$
does not appear in
$L(2)$
does not appear in
![]() $Q(0)$
.
$Q(0)$
.
Now, take
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lambda (h)=-2$
and
$\lambda (h)=-2$
and
 $\lambda (v_0)=\tilde {\lambda }$
. Then,
$\lambda (v_0)=\tilde {\lambda }$
. Then,
![]() $\mathbf {EA}(\mathbf {L}(\lambda ))$
is a
$\mathbf {EA}(\mathbf {L}(\lambda ))$
is a
![]() $\mathfrak {g}$
-Harish-Chandra module having multiplicity-free
$\mathfrak {g}$
-Harish-Chandra module having multiplicity-free
![]() $\mathfrak {g}$
-types
$\mathfrak {g}$
-types
![]() $L(0)$
,
$L(0)$
,
![]() $L(2)$
,
$L(2)$
,
![]() $L(4),\dots $
. As
$L(4),\dots $
. As
![]() $v_4$
commutes with e, from Lemma 71, it follows that
$v_4$
commutes with e, from Lemma 71, it follows that
![]() $v_4$
sends each nonzero highest weight vector of
$v_4$
sends each nonzero highest weight vector of
![]() $L(i)$
inside
$L(i)$
inside
![]() $\mathbf {EA}(\mathbf {L}(\lambda ))$
to a nonzero highest weight vector of
$\mathbf {EA}(\mathbf {L}(\lambda ))$
to a nonzero highest weight vector of
![]() $L(i+4)$
inside
$L(i+4)$
inside
![]() $\mathbf {EA}(\mathbf {L}(\lambda ))$
. Note that all simple subquotients of
$\mathbf {EA}(\mathbf {L}(\lambda ))$
. Note that all simple subquotients of
![]() $\mathbf {EA}(\mathbf {L}(\lambda ))$
must be infinite-dimensional as the central characters of
$\mathbf {EA}(\mathbf {L}(\lambda ))$
must be infinite-dimensional as the central characters of
![]() $\mathbf {EA}(\mathbf {L}(\lambda ))$
is different, by construction, from the central characters of simple finite-dimensional
$\mathbf {EA}(\mathbf {L}(\lambda ))$
is different, by construction, from the central characters of simple finite-dimensional
![]() $\mathfrak {L}^4$
-modules.
$\mathfrak {L}^4$
-modules.
By the universal property of
![]() $Q(0)$
, the inclusion of
$Q(0)$
, the inclusion of
![]() $L(0)$
in
$L(0)$
in
![]() $\mathbf {EA}(\mathbf {L}(\lambda ))$
gives rise to a nonzero homomorphism from
$\mathbf {EA}(\mathbf {L}(\lambda ))$
gives rise to a nonzero homomorphism from
![]() $Q(0)$
to
$Q(0)$
to
![]() $\mathbf {EA}(\mathbf {L}(\lambda ))$
. The image V of this homomorphism does not contain
$\mathbf {EA}(\mathbf {L}(\lambda ))$
. The image V of this homomorphism does not contain
![]() $L(2)$
, as was established in the first paragraph of the proof. Therefore, from Lemma 71, it follows that V has
$L(2)$
, as was established in the first paragraph of the proof. Therefore, from Lemma 71, it follows that V has
![]() $\mathfrak {g}$
-types
$\mathfrak {g}$
-types
![]() $L(0)$
,
$L(0)$
,
![]() $L(4)$
,
$L(4)$
,
![]() $L(8),\dots $
, and the quotient
$L(8),\dots $
, and the quotient
![]() $\mathbf {EA}(\mathbf {L}(\lambda ))/V$
has
$\mathbf {EA}(\mathbf {L}(\lambda ))/V$
has
![]() $\mathfrak {g}$
-types
$\mathfrak {g}$
-types
![]() $L(2)$
,
$L(2)$
,
![]() $L(6)$
,
$L(6)$
,
![]() $L(10),\dots $
. In fact, from Lemma 71 and the above remark that all simple subquotients of
$L(10),\dots $
. In fact, from Lemma 71 and the above remark that all simple subquotients of
![]() $\mathbf {EA}(\mathbf {L}(\lambda ))$
must be infinite-dimensional, it follows that both V and
$\mathbf {EA}(\mathbf {L}(\lambda ))$
must be infinite-dimensional, it follows that both V and
![]() $\mathbf {EA}(\mathbf {L}(\lambda ))/V$
are simple modules.
$\mathbf {EA}(\mathbf {L}(\lambda ))/V$
are simple modules.
This implies that
 $V\cong V(0,\tilde {\lambda }^2, \tilde {\lambda }^3)$
, and the claim of the lemma follows.
$V\cong V(0,\tilde {\lambda }^2, \tilde {\lambda }^3)$
, and the claim of the lemma follows.
Lemma 73. If
![]() $\lambda (v_0)\neq 0$
, then, in the category of h-weight
$\lambda (v_0)\neq 0$
, then, in the category of h-weight
![]() $\mathfrak {L}^4$
-modules, we have the vanishing
$\mathfrak {L}^4$
-modules, we have the vanishing
 $\mathrm {Ext}^1(\mathbf {L}(\lambda -\alpha ),\mathbf {L}(\lambda ))=0$
.
$\mathrm {Ext}^1(\mathbf {L}(\lambda -\alpha ),\mathbf {L}(\lambda ))=0$
.
Proof. Let
![]() $\mathbf {L}(\lambda )\hookrightarrow M\twoheadrightarrow \mathbf {L}(\lambda -\alpha )$
be a short exact sequence in the category of h-weight
$\mathbf {L}(\lambda )\hookrightarrow M\twoheadrightarrow \mathbf {L}(\lambda -\alpha )$
be a short exact sequence in the category of h-weight
![]() $\mathfrak {L}^4$
-modules. Consider the vector space
$\mathfrak {L}^4$
-modules. Consider the vector space
![]() $X:=M_{\lambda }\oplus M_{\lambda -\alpha }$
, and note that it is killed by
$X:=M_{\lambda }\oplus M_{\lambda -\alpha }$
, and note that it is killed by
![]() $v_4$
. Therefore, this vector space is a module over the polynomial algebra A in e and
$v_4$
. Therefore, this vector space is a module over the polynomial algebra A in e and
![]() $v_2$
. The space of first self-extensions for each simple A-module is two-dimensional. Since
$v_2$
. The space of first self-extensions for each simple A-module is two-dimensional. Since
![]() $\mathbf {L}(\lambda )$
is simple, the submodule
$\mathbf {L}(\lambda )$
is simple, the submodule
![]() $Y:=\mathbf {L}(\lambda )_{\lambda }\oplus \mathbf {L}(\lambda )_{\lambda -\alpha }$
of X is indecomposable. Since
$Y:=\mathbf {L}(\lambda )_{\lambda }\oplus \mathbf {L}(\lambda )_{\lambda -\alpha }$
of X is indecomposable. Since
![]() $\mathbf {L}(\lambda )_{\lambda -\alpha }$
has dimension
$\mathbf {L}(\lambda )_{\lambda -\alpha }$
has dimension
![]() $2$
, Y is the universal self-extension of the trivial A-module. This implies that, in the category of A-modules, the first extension from
$2$
, Y is the universal self-extension of the trivial A-module. This implies that, in the category of A-modules, the first extension from
![]() $\mathbf {L}(\lambda -\alpha )_{\lambda -\alpha }$
to Y coming from the socle of Y vanishes. Consequently, M must have a nonzero vector of weight
$\mathbf {L}(\lambda -\alpha )_{\lambda -\alpha }$
to Y coming from the socle of Y vanishes. Consequently, M must have a nonzero vector of weight
![]() $\lambda -\alpha $
which is killed by both e and
$\lambda -\alpha $
which is killed by both e and
![]() $v_2$
. As the adjoint action of
$v_2$
. As the adjoint action of
![]() $v_0$
leaves the span of e and
$v_0$
leaves the span of e and
![]() $v_2$
invariant, it follows that M contains a highest weight vector of weight
$v_2$
invariant, it follows that M contains a highest weight vector of weight
![]() $\lambda -\alpha $
. Consequently, M splits, proving the claim.
$\lambda -\alpha $
. Consequently, M splits, proving the claim.
Now, we are ready to prove Theorem 68.
Proof Proof of Theorem 68
We take
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lambda (h)=-2$
and
$\lambda (h)=-2$
and
 $\lambda (v_0)=\tilde {\lambda }$
.
$\lambda (v_0)=\tilde {\lambda }$
.
The
![]() $\mathfrak {L}^4$
-module
$\mathfrak {L}^4$
-module
 $V'(0,\tilde {\lambda }):=V(0,\tilde {\lambda }^2, \tilde {\lambda }^3)$
and the module
$V'(0,\tilde {\lambda }):=V(0,\tilde {\lambda }^2, \tilde {\lambda }^3)$
and the module
 $V'(2,\tilde {\lambda }):=\mathbf {EA}(L(\lambda ))/V$
(cf. the proof of Proposition 72) are already constructed. Note that the proof of Proposition 72 implies
$V'(2,\tilde {\lambda }):=\mathbf {EA}(L(\lambda ))/V$
(cf. the proof of Proposition 72) are already constructed. Note that the proof of Proposition 72 implies
 $$ \begin{align*} \mathrm{Ext}^1(V'(0,\tilde{\lambda}),V'(2,\tilde{\lambda})) =0 \end{align*} $$
$$ \begin{align*} \mathrm{Ext}^1(V'(0,\tilde{\lambda}),V'(2,\tilde{\lambda})) =0 \end{align*} $$
in the category of
![]() $\mathfrak {g}$
-Harish-Chandra modules. As usual, on the category of
$\mathfrak {g}$
-Harish-Chandra modules. As usual, on the category of
![]() $\mathfrak {g}$
-Harish-Chandra modules, we have the restricted duality, which we denote by
$\mathfrak {g}$
-Harish-Chandra modules, we have the restricted duality, which we denote by
![]() $\star $
. This duality maps
$\star $
. This duality maps
 $ \bigoplus _i L(i)^{\oplus m_i}$
to
$ \bigoplus _i L(i)^{\oplus m_i}$
to
 $\bigoplus _i (L(i)^*)^{\oplus m_i}$
. The fact that
$\bigoplus _i (L(i)^*)^{\oplus m_i}$
. The fact that
 $V'(0,\tilde {\lambda })$
is self-dual follows directly from its uniqueness given by construction. Applying
$V'(0,\tilde {\lambda })$
is self-dual follows directly from its uniqueness given by construction. Applying
![]() $\star $
, we obtain
$\star $
, we obtain
 $$ \begin{align*} \mathrm{Ext}^1(V'(2,\tilde{\lambda})^{\star},V'(0,\tilde{\lambda})) =0, \end{align*} $$
$$ \begin{align*} \mathrm{Ext}^1(V'(2,\tilde{\lambda})^{\star},V'(0,\tilde{\lambda})) =0, \end{align*} $$
where the modules
 $V'(2,\tilde {\lambda })$
and
$V'(2,\tilde {\lambda })$
and
 $V'(2,\tilde {\lambda })^{\star }$
have the same
$V'(2,\tilde {\lambda })^{\star }$
have the same
![]() $\mathfrak {g}$
-types. If we assume that
$\mathfrak {g}$
-types. If we assume that
 $V'(2,\tilde {\lambda })\not \cong V'(2,\tilde {\lambda })^{\star }$
, then, from Proposition 65, it follows that these are the only simple
$V'(2,\tilde {\lambda })\not \cong V'(2,\tilde {\lambda })^{\star }$
, then, from Proposition 65, it follows that these are the only simple
![]() $\mathfrak {g}$
-Harish-Chandra modules having
$\mathfrak {g}$
-Harish-Chandra modules having
![]() $L(2)$
as a
$L(2)$
as a
![]() $\mathfrak {g}$
-type.
$\mathfrak {g}$
-type.
Consider now the module
 $L(2)\otimes V'(0,\tilde {\lambda })$
. By adjunction, this must have both
$L(2)\otimes V'(0,\tilde {\lambda })$
. By adjunction, this must have both
 $V'(2,\tilde {\lambda })$
and
$V'(2,\tilde {\lambda })$
and
 $V'(2,\tilde {\lambda })^{\star }$
as simple subquotients, both with multiplicity 1. The remaining
$V'(2,\tilde {\lambda })^{\star }$
as simple subquotients, both with multiplicity 1. The remaining
![]() $\mathfrak {g}$
-types are
$\mathfrak {g}$
-types are
![]() $L(4)$
,
$L(4)$
,
![]() $L(8)$
,
$L(8)$
,
![]() $L(10).\dots $
. If V is a subquotient of
$L(10).\dots $
. If V is a subquotient of
 $L(2)\otimes V'(0,\tilde {\lambda })$
whose
$L(2)\otimes V'(0,\tilde {\lambda })$
whose
![]() $\mathfrak {g}$
-types form a subset of these remaining
$\mathfrak {g}$
-types form a subset of these remaining
![]() $\mathfrak {g}$
-types, then V, by adjunction, cannot be in the top or socle of
$\mathfrak {g}$
-types, then V, by adjunction, cannot be in the top or socle of
 $L(2)\otimes V'(0,\tilde {\lambda })$
as
$L(2)\otimes V'(0,\tilde {\lambda })$
as
![]() $L(2)\otimes V$
does not have
$L(2)\otimes V$
does not have
![]() $L(0)$
as a simple subquotient. This implies that
$L(0)$
as a simple subquotient. This implies that
 $L(2)\otimes V'(0,\tilde {\lambda })$
must have socle
$L(2)\otimes V'(0,\tilde {\lambda })$
must have socle
 $V'(2,\tilde {\lambda })$
and top
$V'(2,\tilde {\lambda })$
and top
 $V'(2,\tilde {\lambda })^{\star }$
or vice versa. However, since both
$V'(2,\tilde {\lambda })^{\star }$
or vice versa. However, since both
 $V'(0,\tilde {\lambda })$
and
$V'(0,\tilde {\lambda })$
and
![]() $L(2)$
are self-dual, so is
$L(2)$
are self-dual, so is
 $L(2)\otimes V'(0,\tilde {\lambda })$
, a contradiction. Therefore,
$L(2)\otimes V'(0,\tilde {\lambda })$
, a contradiction. Therefore,
 $V'(2,\tilde {\lambda })\cong V'(2,\tilde {\lambda })^{\star }$
, and thus
$V'(2,\tilde {\lambda })\cong V'(2,\tilde {\lambda })^{\star }$
, and thus
 $$ \begin{align} \mathbf{EA}(\mathbf{L}(\lambda))\cong V'(0,\tilde{\lambda})\oplus V'(2,\tilde{\lambda}). \end{align} $$
$$ \begin{align} \mathbf{EA}(\mathbf{L}(\lambda))\cong V'(0,\tilde{\lambda})\oplus V'(2,\tilde{\lambda}). \end{align} $$
Consider now the module
 $L(1)\otimes V'(0,\tilde {\lambda })$
. It has
$L(1)\otimes V'(0,\tilde {\lambda })$
. It has
![]() $\mathfrak {g}$
-types
$\mathfrak {g}$
-types
![]() $L(1)$
,
$L(1)$
,
![]() $L(3)$
,
$L(3)$
,
![]() $L(5),\dots $
, all with multiplicity 1. We claim that
$L(5),\dots $
, all with multiplicity 1. We claim that
 $L(1)\otimes V'(0,\tilde {\lambda })$
is a simple
$L(1)\otimes V'(0,\tilde {\lambda })$
is a simple
![]() $\mathfrak {g}$
-module which we can declare to be
$\mathfrak {g}$
-module which we can declare to be
 $V(1,\tilde {\lambda })$
. Assume that
$V(1,\tilde {\lambda })$
. Assume that
 $L(1)\otimes V'(0,\tilde {\lambda })$
is not simple, and let V be a submodule or a quotient of
$L(1)\otimes V'(0,\tilde {\lambda })$
is not simple, and let V be a submodule or a quotient of
 $L(1)\otimes V'(0,\tilde {\lambda })$
which does not have
$L(1)\otimes V'(0,\tilde {\lambda })$
which does not have
![]() $L(1)$
as its
$L(1)$
as its
![]() $\mathfrak {g}$
-type. Using the self-adjointness of
$\mathfrak {g}$
-type. Using the self-adjointness of
![]() $L(1)\otimes -$
, by adjunction, we have a nonzero homomorphism between
$L(1)\otimes -$
, by adjunction, we have a nonzero homomorphism between
 $V'(0,\tilde {\lambda })$
and
$V'(0,\tilde {\lambda })$
and
![]() $L(1)\otimes V$
. However, the latter is not possible as
$L(1)\otimes V$
. However, the latter is not possible as
![]() $L(0)$
is not a
$L(0)$
is not a
![]() $\mathfrak {g}$
-type of
$\mathfrak {g}$
-type of
![]() $L(1)\otimes V$
due to our definition of V. This shows that
$L(1)\otimes V$
due to our definition of V. This shows that
 $L(1)\otimes V'(0,\tilde {\lambda })$
is simple.
$L(1)\otimes V'(0,\tilde {\lambda })$
is simple.
From Lemma 73, it follows that
 $L(1)\otimes \mathbf {L}(\lambda )\cong \mathbf {L}(\lambda -\frac {1}{2}\alpha )\oplus \mathbf {L}(\lambda +\frac {1}{2}\alpha )$
. As
$L(1)\otimes \mathbf {L}(\lambda )\cong \mathbf {L}(\lambda -\frac {1}{2}\alpha )\oplus \mathbf {L}(\lambda +\frac {1}{2}\alpha )$
. As
![]() $\mathbf {EA}$
commutes with
$\mathbf {EA}$
commutes with
![]() $L(1)\otimes -$
, it follows that
$L(1)\otimes -$
, it follows that
 $$ \begin{align*} L(1)\otimes \mathbf{EA}(\mathbf{L}(\lambda))\cong \mathbf{EA}(\mathbf{L}(\lambda-\frac{1}{2}\alpha))\oplus \mathbf{EA}(\mathbf{L}(\lambda+\frac{1}{2}\alpha)). \end{align*} $$
$$ \begin{align*} L(1)\otimes \mathbf{EA}(\mathbf{L}(\lambda))\cong \mathbf{EA}(\mathbf{L}(\lambda-\frac{1}{2}\alpha))\oplus \mathbf{EA}(\mathbf{L}(\lambda+\frac{1}{2}\alpha)). \end{align*} $$
By comparing the
![]() $\mathfrak {g}$
-types, we see that
$\mathfrak {g}$
-types, we see that
 $$ \begin{align*} \mathbf{EA}(\mathbf{L}(\lambda-\frac{1}{2}\alpha))\cong V(1,\tilde{\lambda})\quad\text{ or }\quad \mathbf{EA}(\mathbf{L}(\lambda+\frac{1}{2}\alpha))\cong V(1,\tilde{\lambda}). \end{align*} $$
$$ \begin{align*} \mathbf{EA}(\mathbf{L}(\lambda-\frac{1}{2}\alpha))\cong V(1,\tilde{\lambda})\quad\text{ or }\quad \mathbf{EA}(\mathbf{L}(\lambda+\frac{1}{2}\alpha))\cong V(1,\tilde{\lambda}). \end{align*} $$
Consider the first case, the second one is similar. By adjunction, we have
 $$ \begin{align*} \mathrm{Hom}(V(1,\tilde{\lambda}),L(1)\otimes \mathbf{EA}(\mathbf{L}(\lambda)))\cong \mathrm{Hom}(L(1)\otimes V(1,\tilde{\lambda}),\mathbf{EA}(\mathbf{L}(\lambda))). \end{align*} $$
$$ \begin{align*} \mathrm{Hom}(V(1,\tilde{\lambda}),L(1)\otimes \mathbf{EA}(\mathbf{L}(\lambda)))\cong \mathrm{Hom}(L(1)\otimes V(1,\tilde{\lambda}),\mathbf{EA}(\mathbf{L}(\lambda))). \end{align*} $$
By the above,
 $L(1)\otimes V(1,\tilde {\lambda })$
has
$L(1)\otimes V(1,\tilde {\lambda })$
has
![]() $\mathbf {EA}(\mathbf {L}(\lambda ))$
as a direct summand, and the endomorphism of
$\mathbf {EA}(\mathbf {L}(\lambda ))$
as a direct summand, and the endomorphism of
![]() $\mathbf {EA}(\mathbf {L}(\lambda ))$
has dimension 2. Consequently,
$\mathbf {EA}(\mathbf {L}(\lambda ))$
has dimension 2. Consequently,
 $\mathrm {Hom}(V(1,\tilde {\lambda }),\mathbf {L}(\lambda +\frac {1}{2}\alpha ))$
must be nonzero, which implies
$\mathrm {Hom}(V(1,\tilde {\lambda }),\mathbf {L}(\lambda +\frac {1}{2}\alpha ))$
must be nonzero, which implies
 $$ \begin{align*} \operatorname{\mathrm{\mathbf{EA}}} (\mathbf{L}(\lambda+\frac{1}{2}\alpha)) \cong V(1,\tilde{\lambda}) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{\mathbf{EA}}} (\mathbf{L}(\lambda+\frac{1}{2}\alpha)) \cong V(1,\tilde{\lambda}) \end{align*} $$
by comparing the
![]() $\mathfrak {g}$
-types of these modules.
$\mathfrak {g}$
-types of these modules.
Using, inductively, arguments similar to the ones used above, we construct modules
 $$ \begin{align*} V(i,\tilde{\lambda})\cong \operatorname{\mathrm{\mathbf{EA}}}(\mathbf{L}(\lambda+\frac{i}{2}\alpha)), \end{align*} $$
$$ \begin{align*} V(i,\tilde{\lambda})\cong \operatorname{\mathrm{\mathbf{EA}}}(\mathbf{L}(\lambda+\frac{i}{2}\alpha)), \end{align*} $$
for
![]() $i>1$
. The proof of Theorem 68 is now completed easily using construction and adjunction.
$i>1$
. The proof of Theorem 68 is now completed easily using construction and adjunction.
Remark 74 (Sketch of an alternative proof of the splitting (33))
Denote by
![]() $\mathfrak {b}$
the span of h and e, and consider the polynomials
$\mathfrak {b}$
the span of h and e, and consider the polynomials
![]() $\mathbb {C}[x]$
as
$\mathbb {C}[x]$
as
![]() $(\mathfrak {b} \ltimes L(4))$
-module by declaring:
$(\mathfrak {b} \ltimes L(4))$
-module by declaring:
 $h \cdot x^k = (-2-2k)x^k$
, e acts as
$h \cdot x^k = (-2-2k)x^k$
, e acts as
![]() $\frac {\partial }{\partial x}$
,
$\frac {\partial }{\partial x}$
,
![]() $v_4$
and
$v_4$
and
![]() $v_2$
annihilate everything,
$v_2$
annihilate everything,
![]() $v_0$
multiplies by
$v_0$
multiplies by
![]() $3 \tilde {\lambda }$
,
$3 \tilde {\lambda }$
,
![]() $v_{-2}$
multiplies by
$v_{-2}$
multiplies by
![]() $6 \tilde {\lambda } x$
, and
$6 \tilde {\lambda } x$
, and
![]() $v_{-2}$
multiplies by
$v_{-2}$
multiplies by
![]() $3 \tilde {\lambda } x^2$
(this is known as the Fock module). From [Reference Lü, Mazorchuk and Zhao40, Theorem 4(ii)], it follows that
$3 \tilde {\lambda } x^2$
(this is known as the Fock module). From [Reference Lü, Mazorchuk and Zhao40, Theorem 4(ii)], it follows that
 $\mathbf {L}(\lambda ) \cong \operatorname {\mathrm {Ind}}_{\mathfrak {b} \ltimes L(4)}^{\mathfrak {L}^4} \mathbb {C}[x]$
(recall that
$\mathbf {L}(\lambda ) \cong \operatorname {\mathrm {Ind}}_{\mathfrak {b} \ltimes L(4)}^{\mathfrak {L}^4} \mathbb {C}[x]$
(recall that
![]() $\lambda (h)=-2$
and
$\lambda (h)=-2$
and
 $\lambda (v_0)=\tilde {\lambda }$
). From this, we have that
$\lambda (v_0)=\tilde {\lambda }$
). From this, we have that
![]() $\operatorname {\mathrm {\mathbf {EA}}}(\mathbf {L}(\lambda ))$
has
$\operatorname {\mathrm {\mathbf {EA}}}(\mathbf {L}(\lambda ))$
has
![]() $\mathfrak {g}$
-types
$\mathfrak {g}$
-types
![]() $L(0), L(2), L(4), \dots $
, and the lowest weight vector in each
$L(0), L(2), L(4), \dots $
, and the lowest weight vector in each
![]() $L(2k)$
is
$L(2k)$
is
![]() $f^{-1} \otimes x^k$
. By a long and tedious, but straightforward computation, one can see that
$f^{-1} \otimes x^k$
. By a long and tedious, but straightforward computation, one can see that
 $$ \begin{align*} v_4 f^{-1} \otimes x^k = \frac{3 \tilde{\lambda}}{4(k+1)(k+2)(2k+1)(2k+3)} {}\cdot{} & e^4 f^{-1} \otimes x^{k+2} \\ - \frac{3 \tilde{\lambda}}{2(2k+3)(2k-1)} {}\cdot{} & e^2 f^{-1} \otimes x^k \\ + \frac{3 \tilde{\lambda} k (k-1)}{4(2k+1)(2k-1)} {}\cdot{} & f^{-1} \otimes x^{k-2} .\end{align*} $$
$$ \begin{align*} v_4 f^{-1} \otimes x^k = \frac{3 \tilde{\lambda}}{4(k+1)(k+2)(2k+1)(2k+3)} {}\cdot{} & e^4 f^{-1} \otimes x^{k+2} \\ - \frac{3 \tilde{\lambda}}{2(2k+3)(2k-1)} {}\cdot{} & e^2 f^{-1} \otimes x^k \\ + \frac{3 \tilde{\lambda} k (k-1)}{4(2k+1)(2k-1)} {}\cdot{} & f^{-1} \otimes x^{k-2} .\end{align*} $$
From this formula, it follows easily that
![]() $\mathfrak {L}^4$
maps
$\mathfrak {L}^4$
maps
![]() $L(k)$
to
$L(k)$
to
![]() $L(k+4) \oplus L(k) \oplus L(k-4)$
if
$L(k+4) \oplus L(k) \oplus L(k-4)$
if
![]() $k \geq 2$
, and to
$k \geq 2$
, and to
![]() $L(k+2) \oplus L(k)$
, for
$L(k+2) \oplus L(k)$
, for
![]() $k=0,1$
, with nonzero projections to each summand. This proves the claim.
$k=0,1$
, with nonzero projections to each summand. This proves the claim.
Remark 75. From the proof of Theorem 68, the combinatorics of tensoring with
![]() $L(1)$
can be recorded as follows:
$L(1)$
can be recorded as follows:
 $$ \begin{align*} \begin{array}{ccll} L(1)\otimes V'(0,\tilde{\lambda})&\cong& V(1,\tilde{\lambda});\\ L(1)\otimes V'(2,\tilde{\lambda})&\cong& V(1,\tilde{\lambda});\\ L(1)\otimes V(1,\tilde{\lambda})&\cong& V'(0,\tilde{\lambda})\oplus V'(2,\tilde{\lambda})\oplus V(2,\tilde{\lambda});\\ L(1)\otimes V(i,\tilde{\lambda})&\cong& V(i-1,\tilde{\lambda})\oplus V(i+1,\tilde{\lambda}), &i>1.\\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ccll} L(1)\otimes V'(0,\tilde{\lambda})&\cong& V(1,\tilde{\lambda});\\ L(1)\otimes V'(2,\tilde{\lambda})&\cong& V(1,\tilde{\lambda});\\ L(1)\otimes V(1,\tilde{\lambda})&\cong& V'(0,\tilde{\lambda})\oplus V'(2,\tilde{\lambda})\oplus V(2,\tilde{\lambda});\\ L(1)\otimes V(i,\tilde{\lambda})&\cong& V(i-1,\tilde{\lambda})\oplus V(i+1,\tilde{\lambda}), &i>1.\\ \end{array} \end{align*} $$
In particular, the additive closure of
 $V'(0,\tilde {\lambda })$
,
$V'(0,\tilde {\lambda })$
,
 $V'(2,\tilde {\lambda })$
, and all
$V'(2,\tilde {\lambda })$
, and all
 $V(i,\tilde {\lambda })$
forms a simple
$V(i,\tilde {\lambda })$
forms a simple
![]() $\mathscr {F}$
-module category (cf. Propositions 39 and 59). From the above formulae, we see that the combinatorics of this
$\mathscr {F}$
-module category (cf. Propositions 39 and 59). From the above formulae, we see that the combinatorics of this
![]() $\mathscr {F}$
-module category is different from the combinatorics of the
$\mathscr {F}$
-module category is different from the combinatorics of the
![]() $\mathscr {F}$
-module categories described in Propositions 39 and 59.
$\mathscr {F}$
-module categories described in Propositions 39 and 59.
We note that there might exist, potentially, other simple
![]() $\mathfrak {g}$
-Harish-Chandra modules for
$\mathfrak {g}$
-Harish-Chandra modules for
![]() $\mathfrak {L}^4$
which correspond to characters of
$\mathfrak {L}^4$
which correspond to characters of
![]() $\operatorname {\mathrm {Sym}}(\mathfrak {r})^{\mathfrak {g}}$
that do not occur in simple highest weight modules. The problem here seems to be the absence, in case of
$\operatorname {\mathrm {Sym}}(\mathfrak {r})^{\mathfrak {g}}$
that do not occur in simple highest weight modules. The problem here seems to be the absence, in case of
![]() $\mathfrak {L}^4$
, of an analogue of the classical theorem by Harish-Chandra that, in case of reductive Lie algebras, any central character is realizable on some highest weight module.
$\mathfrak {L}^4$
, of an analogue of the classical theorem by Harish-Chandra that, in case of reductive Lie algebras, any central character is realizable on some highest weight module.
7.4. Some speculations in case of the Lie algebras
 $\mathfrak {L}^n = \mathfrak {sl}_2\ltimes L(n)$
with n even
$\mathfrak {L}^n = \mathfrak {sl}_2\ltimes L(n)$
with n even
For an even nonnegative integer n, consider the Lie algebra
![]() $\mathfrak {L}^n = \mathfrak {sl}_2 \ltimes L(n)$
. The algebra
$\mathfrak {L}^n = \mathfrak {sl}_2 \ltimes L(n)$
. The algebra
![]() $\mathfrak {L}^0$
is reductive, and hence all its
$\mathfrak {L}^0$
is reductive, and hence all its
![]() $\mathfrak {sl}_2$
-Harish-Chandra modules are finite-dimensional. Classification of all
$\mathfrak {sl}_2$
-Harish-Chandra modules are finite-dimensional. Classification of all
![]() $\mathfrak {sl}_2$
-Harish-Chandra modules for the Takiff Lie algebra
$\mathfrak {sl}_2$
-Harish-Chandra modules for the Takiff Lie algebra
![]() $\mathfrak {L}^2$
is given in Section 4. Note that all simple
$\mathfrak {L}^2$
is given in Section 4. Note that all simple
![]() $\mathfrak {sl}_2$
-Harish-Chandra modules for
$\mathfrak {sl}_2$
-Harish-Chandra modules for
![]() $\mathfrak {L}^2$
are connected to highest weight
$\mathfrak {L}^2$
are connected to highest weight
![]() $\mathfrak {L}^2$
-modules. For the Lie algebra
$\mathfrak {L}^2$
-modules. For the Lie algebra
![]() $\mathfrak {L}^4$
, all
$\mathfrak {L}^4$
, all
![]() $\mathfrak {sl}_2$
-Harish-Chandra modules that are connected to highest weight
$\mathfrak {sl}_2$
-Harish-Chandra modules that are connected to highest weight
![]() $\mathfrak {L}^4$
-modules are classified in the previous subsection. Potentially, these are not all
$\mathfrak {L}^4$
-modules are classified in the previous subsection. Potentially, these are not all
![]() $\mathfrak {sl}_2$
-Harish-Chandra modules for
$\mathfrak {sl}_2$
-Harish-Chandra modules for
![]() $\mathfrak {L}^4$
. As we see, the level of difficulty of the problem increases drastically with n.
$\mathfrak {L}^4$
. As we see, the level of difficulty of the problem increases drastically with n.
The highest weight theory for
![]() $\mathfrak {L}^n$
is described in [Reference Lü, Mazorchuk and Zhao40, Theorem 4]. As vector space, simple highest weight
$\mathfrak {L}^n$
is described in [Reference Lü, Mazorchuk and Zhao40, Theorem 4]. As vector space, simple highest weight
![]() $\mathfrak {L}^n$
-modules look the same, independently of n. Therefore, we expect that the problem of classification of simple
$\mathfrak {L}^n$
-modules look the same, independently of n. Therefore, we expect that the problem of classification of simple
![]() $\mathfrak {sl}_2$
-Harish-Chandra modules for
$\mathfrak {sl}_2$
-Harish-Chandra modules for
![]() $\mathfrak {L}^n$
that are connected to highest weight
$\mathfrak {L}^n$
that are connected to highest weight
![]() $\mathfrak {L}^n$
-modules via Enright–Arkhipov functor should be solvable. One of the crucial missing ingredients, at the moment, seems to be an analogue of [Reference Hahn, Huh, Lim and Sohn27, Corollary 3.4] for general n (i.e., for general k in the notation of Reference Hahn, Huh, Lim and Sohn[27]).
$\mathfrak {L}^n$
-modules via Enright–Arkhipov functor should be solvable. One of the crucial missing ingredients, at the moment, seems to be an analogue of [Reference Hahn, Huh, Lim and Sohn27, Corollary 3.4] for general n (i.e., for general k in the notation of Reference Hahn, Huh, Lim and Sohn[27]).
Of special interest is the question of what kind of a monoidal representation of the monoidal category of finite-dimensional
![]() $\mathfrak {sl}_2$
-modules do the
$\mathfrak {sl}_2$
-modules do the
![]() $\mathfrak {L}^n$
-modules from the previous paragraph form.
$\mathfrak {L}^n$
-modules from the previous paragraph form.