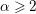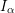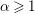1 Introduction
Let ![]() $K$ be a field of characteristic zero and let
$K$ be a field of characteristic zero and let ![]() $A=K[x_{1},\ldots ,x_{d}]$ be the graded polynomial ring with
$A=K[x_{1},\ldots ,x_{d}]$ be the graded polynomial ring with ![]() $\deg (x_{i})=a_{i}>0$ (
$\deg (x_{i})=a_{i}>0$ (![]() $i=1,\ldots ,d$) and homogeneous maximal ideal
$i=1,\ldots ,d$) and homogeneous maximal ideal ![]() $M$. Introduced by Herzog and Huneke in [Reference Herzog and Huneke3], the strongly Golod ideals in
$M$. Introduced by Herzog and Huneke in [Reference Herzog and Huneke3], the strongly Golod ideals in ![]() $A$ are the proper homogeneous ideals
$A$ are the proper homogeneous ideals ![]() $I$ that satisfy the condition
$I$ that satisfy the condition ![]() $\unicode[STIX]{x2202}(I)^{2}\subseteq I$, where
$\unicode[STIX]{x2202}(I)^{2}\subseteq I$, where ![]() $\unicode[STIX]{x2202}(I)$ is the ideal generated by the partial derivatives of all the elements of
$\unicode[STIX]{x2202}(I)$ is the ideal generated by the partial derivatives of all the elements of ![]() $I$. The motivation for the introduction of this notion comes from a result proved in the same paper [Reference Herzog and Huneke3, Theorem 1.1] which shows that if
$I$. The motivation for the introduction of this notion comes from a result proved in the same paper [Reference Herzog and Huneke3, Theorem 1.1] which shows that if ![]() $I$ is strongly Golod, then the ring
$I$ is strongly Golod, then the ring ![]() $A/I$ is Golod, that is, the Poincaré series of
$A/I$ is Golod, that is, the Poincaré series of ![]() $A/I$
$A/I$
coincides with the rational series
where ![]() $\operatorname{H}_{i}(\mathbf{y};A/I)$ is the
$\operatorname{H}_{i}(\mathbf{y};A/I)$ is the ![]() $i$th Koszul homology of
$i$th Koszul homology of ![]() $A/I$ with respect to a minimal homogeneous set of generators
$A/I$ with respect to a minimal homogeneous set of generators ![]() $\mathbf{y}=y_{1},\ldots ,y_{n}$ of the maximal homogeneous ideal of
$\mathbf{y}=y_{1},\ldots ,y_{n}$ of the maximal homogeneous ideal of ![]() $A/I$. As proved by Serre,
$A/I$. As proved by Serre, ![]() $P_{A/I}(t)$ is coefficientwise bounded above by
$P_{A/I}(t)$ is coefficientwise bounded above by ![]() $H_{A/I}(t)$, and the ring
$H_{A/I}(t)$, and the ring ![]() $A/I$ is called Golod if
$A/I$ is called Golod if ![]() $P_{A/I}(t)=H_{A/I}(t)$.
$P_{A/I}(t)=H_{A/I}(t)$.
Herzog and Huneke further studied the properties of the strongly Golod ideals. For every homogeneous ideal ![]() $I$ of
$I$ of ![]() $A$, among other things, they proved that the powers
$A$, among other things, they proved that the powers ![]() $I^{s}$, the symbolic powers
$I^{s}$, the symbolic powers ![]() $I^{(s)}$, and the saturations
$I^{(s)}$, and the saturations ![]() $(I^{s}:M^{\infty })$ are strongly Golod for all
$(I^{s}:M^{\infty })$ are strongly Golod for all ![]() $s\geqslant 2$ [Reference Herzog and Huneke3, Theorem 2.3]. Moreover, if
$s\geqslant 2$ [Reference Herzog and Huneke3, Theorem 2.3]. Moreover, if ![]() $I$ is strongly Golod, then the Ratliff–Rush ideal
$I$ is strongly Golod, then the Ratliff–Rush ideal ![]() $\tilde{I} =\bigcup _{i\geqslant 1}(I^{i+1}:I^{i})$ is strongly Golod [Reference Herzog and Huneke3, Proposition 2.1] and the integral closures
$\tilde{I} =\bigcup _{i\geqslant 1}(I^{i+1}:I^{i})$ is strongly Golod [Reference Herzog and Huneke3, Proposition 2.1] and the integral closures ![]() $\overline{I^{s}}$ are strongly Golod for
$\overline{I^{s}}$ are strongly Golod for ![]() $s\geqslant d+1$ [Reference Herzog and Huneke3, Theorem 2.11].
$s\geqslant d+1$ [Reference Herzog and Huneke3, Theorem 2.11].
For monomial ideals, Herzog and Huneke improved the previous result by showing that if ![]() $I$ is a monomial strongly Golod ideal, then the integral closure
$I$ is a monomial strongly Golod ideal, then the integral closure ![]() $\overline{I}$ is also strongly Golod [Reference Herzog and Huneke3, Proposition 3.1]. In particular, for an arbitrary monomial ideal
$\overline{I}$ is also strongly Golod [Reference Herzog and Huneke3, Proposition 3.1]. In particular, for an arbitrary monomial ideal ![]() $I$, the integral closures
$I$, the integral closures ![]() $\overline{I^{s}}$ are strongly Golod for
$\overline{I^{s}}$ are strongly Golod for ![]() $s\geqslant 2$. More generally, De Stefani later proved that the rational powers
$s\geqslant 2$. More generally, De Stefani later proved that the rational powers ![]() $I_{\unicode[STIX]{x1D6FC}}$ of a monomial ideal
$I_{\unicode[STIX]{x1D6FC}}$ of a monomial ideal ![]() $I$ are strongly Golod for every rational
$I$ are strongly Golod for every rational ![]() $\unicode[STIX]{x1D6FC}\geqslant 2$ [Reference De Stefani1, Proposition 3.7], and if
$\unicode[STIX]{x1D6FC}\geqslant 2$ [Reference De Stefani1, Proposition 3.7], and if ![]() $I$ is a monomial strongly Golod ideal, then
$I$ is a monomial strongly Golod ideal, then ![]() $I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for every rational
$I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for every rational ![]() $\unicode[STIX]{x1D6FC}\geqslant 1$ [Reference De Stefani1, Theorem 3.5].
$\unicode[STIX]{x1D6FC}\geqslant 1$ [Reference De Stefani1, Theorem 3.5].
In this article we show that the above results, which had been proved for monomial ideals, are actually valid for all homogeneous ideals. More precisely, we prove that if ![]() $I$ is a homogeneous strongly Golod ideal, then the integral closure
$I$ is a homogeneous strongly Golod ideal, then the integral closure ![]() $\overline{I}$ is strongly Golod (Corollary 3.5), positively answering a question of Huneke [Reference McCullough and Peeva6, Problem 6.19]. More generally, if
$\overline{I}$ is strongly Golod (Corollary 3.5), positively answering a question of Huneke [Reference McCullough and Peeva6, Problem 6.19]. More generally, if ![]() $I$ is a homogeneous strongly Golod ideal, then the rational power
$I$ is a homogeneous strongly Golod ideal, then the rational power ![]() $I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for every
$I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for every ![]() $\unicode[STIX]{x1D6FC}\geqslant 1$ (Corollary 4.6). Moreover, if
$\unicode[STIX]{x1D6FC}\geqslant 1$ (Corollary 4.6). Moreover, if ![]() $I$ is an arbitrary homogeneous ideal, then all the rational powers
$I$ is an arbitrary homogeneous ideal, then all the rational powers ![]() $I_{\unicode[STIX]{x1D6FC}}$ are strongly Golod for
$I_{\unicode[STIX]{x1D6FC}}$ are strongly Golod for ![]() $\unicode[STIX]{x1D6FC}\geqslant 2$ (Corollary 4.4).
$\unicode[STIX]{x1D6FC}\geqslant 2$ (Corollary 4.4).
Our techniques are very different from those of Herzog and Huneke [Reference Herzog and Huneke3] and De Stefani [Reference De Stefani1], which can only be used in the monomial case. The main ingredient in our arguments is the Rees-like algebra ![]() $A[\unicode[STIX]{x2202}(I)t^{a},It^{2a},t^{-1}]$ with
$A[\unicode[STIX]{x2202}(I)t^{a},It^{2a},t^{-1}]$ with ![]() $a\in \mathbb{N}^{\ast }$ and the main tool used is a result of Seidenberg [Reference Seidenberg7, Section 3] showing that a derivation on a noetherian domain
$a\in \mathbb{N}^{\ast }$ and the main tool used is a result of Seidenberg [Reference Seidenberg7, Section 3] showing that a derivation on a noetherian domain ![]() $R$ containing a field of characteristic zero, when extended to its quotient field, will map every element of the integral closure
$R$ containing a field of characteristic zero, when extended to its quotient field, will map every element of the integral closure ![]() $\overline{R}$ to an element of
$\overline{R}$ to an element of ![]() $\overline{R}$ (see (2.5)). Using this approach, we prove that if
$\overline{R}$ (see (2.5)). Using this approach, we prove that if ![]() $I$ is a homogeneous strongly Golod ideal, then
$I$ is a homogeneous strongly Golod ideal, then ![]() $\unicode[STIX]{x2202}(\overline{I^{m}})\unicode[STIX]{x2202}(\overline{I^{n}})\subseteq \overline{I^{m+n-1}}$ for all positive integers
$\unicode[STIX]{x2202}(\overline{I^{m}})\unicode[STIX]{x2202}(\overline{I^{n}})\subseteq \overline{I^{m+n-1}}$ for all positive integers ![]() $m,n$ (Theorem 3.4). More generally, for rational powers of ideals, if
$m,n$ (Theorem 3.4). More generally, for rational powers of ideals, if ![]() $I$ is a homogeneous strongly Golod ideal, then
$I$ is a homogeneous strongly Golod ideal, then ![]() $\unicode[STIX]{x2202}(I_{\unicode[STIX]{x1D6FC}})\subseteq I_{\unicode[STIX]{x1D6FC}-(1/2)}$ for every rational
$\unicode[STIX]{x2202}(I_{\unicode[STIX]{x1D6FC}})\subseteq I_{\unicode[STIX]{x1D6FC}-(1/2)}$ for every rational ![]() $\unicode[STIX]{x1D6FC}\geqslant \frac{1}{2}$ (Theorem 4.5). For arbitrary ideals, we also prove that
$\unicode[STIX]{x1D6FC}\geqslant \frac{1}{2}$ (Theorem 4.5). For arbitrary ideals, we also prove that ![]() $\unicode[STIX]{x2202}(I_{\unicode[STIX]{x1D6FC}})\subseteq I_{\unicode[STIX]{x1D6FC}-1}$ for every rational
$\unicode[STIX]{x2202}(I_{\unicode[STIX]{x1D6FC}})\subseteq I_{\unicode[STIX]{x1D6FC}-1}$ for every rational ![]() $\unicode[STIX]{x1D6FC}\geqslant 1$ (Theorem 4.3). The main results of the paper regarding the strongly Golod property of the integral closure and the rational powers of a homogeneous ideal are then obtained as immediate consequences.
$\unicode[STIX]{x1D6FC}\geqslant 1$ (Theorem 4.3). The main results of the paper regarding the strongly Golod property of the integral closure and the rational powers of a homogeneous ideal are then obtained as immediate consequences.
Finally, as already mentioned above, Herzog and Huneke proved that the Ratliff–Rush ideal of a strongly Golod ideal is strongly Golod as well. In the last section of the paper, we extend this result by showing that all the coefficient ideals ![]() $I_{\{k\}}$ (
$I_{\{k\}}$ (![]() $1\leqslant k\leqslant d$) of a strongly Golod ideal
$1\leqslant k\leqslant d$) of a strongly Golod ideal ![]() $I$ of finite colength are strongly Golod (Theorem 5.4), answering a question raised by De Stefani [Reference De Stefani1, Question 5.9]. (The coefficient ideal
$I$ of finite colength are strongly Golod (Theorem 5.4), answering a question raised by De Stefani [Reference De Stefani1, Question 5.9]. (The coefficient ideal ![]() $I_{\{d\}}$ of an ideal of finite colength is the Ratliff–Rush ideal
$I_{\{d\}}$ of an ideal of finite colength is the Ratliff–Rush ideal ![]() $\tilde{I}$.)
$\tilde{I}$.)
2 Preliminaries
Let ![]() $K$ be a field of characteristic zero and
$K$ be a field of characteristic zero and ![]() $A=K[x_{1},\ldots ,x_{d}]$ a graded polynomial ring with
$A=K[x_{1},\ldots ,x_{d}]$ a graded polynomial ring with ![]() $\deg (x_{i})=a_{i}>0$.
$\deg (x_{i})=a_{i}>0$.
2.1. For an ideal ![]() $I$ of
$I$ of ![]() $A$ and
$A$ and ![]() $i\in \{1,\ldots ,d\}$, we denote by
$i\in \{1,\ldots ,d\}$, we denote by ![]() $\unicode[STIX]{x2202}_{i}(I)$ the ideal generated by the partial derivatives
$\unicode[STIX]{x2202}_{i}(I)$ the ideal generated by the partial derivatives ![]() $\unicode[STIX]{x2202}_{i}f=\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{i}$ with
$\unicode[STIX]{x2202}_{i}f=\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{i}$ with ![]() $f\in I$, and by
$f\in I$, and by ![]() $\unicode[STIX]{x2202}(I)$ the ideal generated by
$\unicode[STIX]{x2202}(I)$ the ideal generated by ![]() $\{\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{i}\mid f\in I,1\leqslant i\leqslant d\}$, that is,
$\{\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{i}\mid f\in I,1\leqslant i\leqslant d\}$, that is, ![]() $\unicode[STIX]{x2202}(I)=\unicode[STIX]{x2202}_{1}(I)+\cdots +\unicode[STIX]{x2202}_{d}(I)$.
$\unicode[STIX]{x2202}(I)=\unicode[STIX]{x2202}_{1}(I)+\cdots +\unicode[STIX]{x2202}_{d}(I)$.
Note that for an arbitrary ideal ![]() $I$ we always have
$I$ we always have ![]() $I\subseteq \unicode[STIX]{x2202}(I)$. Indeed, if
$I\subseteq \unicode[STIX]{x2202}(I)$. Indeed, if ![]() $f\in I$, then
$f\in I$, then ![]() $x_{1}f\in I$, so
$x_{1}f\in I$, so ![]() $f=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{1})(x_{1}f)-x_{1}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{1})(f)\in \unicode[STIX]{x2202}(I)$.
$f=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{1})(x_{1}f)-x_{1}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{1})(f)\in \unicode[STIX]{x2202}(I)$.
2.2. If ![]() $f\in A$ is a homogeneous polynomial, then
$f\in A$ is a homogeneous polynomial, then
and since the characteristic of ![]() $K$ is zero, it follows that
$K$ is zero, it follows that ![]() $f\in (\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{1},\ldots ,\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{d})$.
$f\in (\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{1},\ldots ,\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{d})$.
Assume that ![]() $I=(f_{1},\ldots ,f_{s})$ with
$I=(f_{1},\ldots ,f_{s})$ with ![]() $f_{i}$ homogeneous polynomials in
$f_{i}$ homogeneous polynomials in ![]() $A$. If
$A$. If ![]() $f=g_{1}f_{1}+\cdots +g_{s}f_{s}$ with
$f=g_{1}f_{1}+\cdots +g_{s}f_{s}$ with ![]() $g_{i}\in A$, from the previous observation it follows that for each
$g_{i}\in A$, from the previous observation it follows that for each ![]() $\ell =1,\ldots ,d$ we have
$\ell =1,\ldots ,d$ we have
and therefore ![]() $\unicode[STIX]{x2202}(I)=(\unicode[STIX]{x2202}f_{i}/\unicode[STIX]{x2202}x_{j}\mid 1\leqslant i\leqslant s,1\leqslant j\leqslant d)$.
$\unicode[STIX]{x2202}(I)=(\unicode[STIX]{x2202}f_{i}/\unicode[STIX]{x2202}x_{j}\mid 1\leqslant i\leqslant s,1\leqslant j\leqslant d)$.
Definition 2.3. [Reference Herzog and Huneke3]
A proper homogeneous ideal ![]() $I$ of
$I$ of ![]() $A$ is said to be strongly Golod if
$A$ is said to be strongly Golod if ![]() $\unicode[STIX]{x2202}(I)^{2}\subseteq I$.
$\unicode[STIX]{x2202}(I)^{2}\subseteq I$.
Remark 2.4. As noted in [Reference Herzog and Huneke3, Remark 2.1], if ![]() $A$ is standard graded and
$A$ is standard graded and ![]() $I$ is an ideal of
$I$ is an ideal of ![]() $A$, the condition
$A$, the condition ![]() $\unicode[STIX]{x2202}(I)^{2}\subseteq I$ does not depend on the chosen coordinates in
$\unicode[STIX]{x2202}(I)^{2}\subseteq I$ does not depend on the chosen coordinates in ![]() $A$. More precisely, if
$A$. More precisely, if ![]() $y_{1},\ldots ,y_{d}$ are linear forms in
$y_{1},\ldots ,y_{d}$ are linear forms in ![]() $A$ such that
$A$ such that ![]() $K[x_{1},\ldots ,x_{d}]=K[y_{1},\ldots ,y_{d}]$ and
$K[x_{1},\ldots ,x_{d}]=K[y_{1},\ldots ,y_{d}]$ and ![]() $\unicode[STIX]{x2202}^{\prime }(I)$ is the ideal of
$\unicode[STIX]{x2202}^{\prime }(I)$ is the ideal of ![]() $A$ generated by all the partial derivatives
$A$ generated by all the partial derivatives ![]() $\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}y_{j}$ with
$\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}y_{j}$ with ![]() $f\in I$ and
$f\in I$ and ![]() $j=1,\ldots ,d$, then
$j=1,\ldots ,d$, then ![]() $\unicode[STIX]{x2202}(I)^{2}\subseteq I$ if and only if
$\unicode[STIX]{x2202}(I)^{2}\subseteq I$ if and only if ![]() $\unicode[STIX]{x2202}^{\prime }(I)^{2}\subseteq I$.
$\unicode[STIX]{x2202}^{\prime }(I)^{2}\subseteq I$.
2.5. (Derivations and integral closure)
Let ![]() $R$ be a noetherian integral domain containing a field of characteristic zero, and let
$R$ be a noetherian integral domain containing a field of characteristic zero, and let ![]() $D$ be a derivation of its quotient field
$D$ be a derivation of its quotient field ![]() $Q(R)$. Seidenberg [Reference Seidenberg7, Section 3] proved that if
$Q(R)$. Seidenberg [Reference Seidenberg7, Section 3] proved that if ![]() $D(R)\subseteq R$, then
$D(R)\subseteq R$, then ![]() $D(\overline{R})\subseteq \overline{R}$, where
$D(\overline{R})\subseteq \overline{R}$, where ![]() $\overline{R}$ is the integral closure of
$\overline{R}$ is the integral closure of ![]() $R$ in
$R$ in ![]() $Q(R)$. In fact, as Seidenberg shows, the result holds even without the noetherian assumption if the integral closure
$Q(R)$. In fact, as Seidenberg shows, the result holds even without the noetherian assumption if the integral closure ![]() $\overline{R}$ is replaced by the quasi-integral closure of
$\overline{R}$ is replaced by the quasi-integral closure of ![]() $R$, that is, the ring consisting of all the elements
$R$, that is, the ring consisting of all the elements ![]() $\unicode[STIX]{x1D6FC}\in Q(R)$ for which there exists
$\unicode[STIX]{x1D6FC}\in Q(R)$ for which there exists ![]() $c\in R\setminus \{0\}$ such that
$c\in R\setminus \{0\}$ such that ![]() $c\unicode[STIX]{x1D6FC}^{n}\in R$ for all
$c\unicode[STIX]{x1D6FC}^{n}\in R$ for all ![]() $n\geqslant 0$. In the literature, this is also referred to as the complete integral closure of
$n\geqslant 0$. In the literature, this is also referred to as the complete integral closure of ![]() $R$.
$R$.
3 Integral closure of strongly Golod ideals
Throughout this section ![]() $K$ is a field of characteristic zero and
$K$ is a field of characteristic zero and ![]() $A=K[x_{1},\ldots ,x_{d}]$ is a polynomial ring with
$A=K[x_{1},\ldots ,x_{d}]$ is a polynomial ring with ![]() $\deg (x_{i})=a_{i}>0$. We show that the integral closure of a strongly Golod ideal is also strongly Golod. The results of this section are further extended to rational powers of ideals in the next section, and technically can be obtained as particular cases of them. However, for the sake of clarity, we prefer to present the main technique applied to the case of the integral closure of an ideal in this separate section.
$\deg (x_{i})=a_{i}>0$. We show that the integral closure of a strongly Golod ideal is also strongly Golod. The results of this section are further extended to rational powers of ideals in the next section, and technically can be obtained as particular cases of them. However, for the sake of clarity, we prefer to present the main technique applied to the case of the integral closure of an ideal in this separate section.
Theorem 3.1. Let ![]() $I$ be an arbitrary ideal of
$I$ be an arbitrary ideal of ![]() $A$. Then for every positive integer
$A$. Then for every positive integer ![]() $n$,
$n$,
Proof. Consider the (extended) Rees algebra ![]() ${\mathcal{R}}=A[It,t^{-1}]$ with quotient field
${\mathcal{R}}=A[It,t^{-1}]$ with quotient field ![]() $Q({\mathcal{R}})$. Since
$Q({\mathcal{R}})$. Since ![]() $A$ is normal, the integral closure of
$A$ is normal, the integral closure of ![]() ${\mathcal{R}}$ in its quotient field is
${\mathcal{R}}$ in its quotient field is ![]() $\overline{{\mathcal{R}}}=\bigoplus _{n\in \mathbb{Z}}\overline{I^{n}}t^{n}$, where
$\overline{{\mathcal{R}}}=\bigoplus _{n\in \mathbb{Z}}\overline{I^{n}}t^{n}$, where ![]() $\overline{I^{n}}=A$ for
$\overline{I^{n}}=A$ for ![]() $n\leqslant 0$. For every
$n\leqslant 0$. For every ![]() $i\in \{1,\ldots ,d\}$, since
$i\in \{1,\ldots ,d\}$, since ![]() $\unicode[STIX]{x2202}_{i}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{i}$ is a derivation on
$\unicode[STIX]{x2202}_{i}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{i}$ is a derivation on ![]() $Q({\mathcal{R}})=Q(A)(t)=K(x_{1},\ldots ,x_{d},t)$, it follows that
$Q({\mathcal{R}})=Q(A)(t)=K(x_{1},\ldots ,x_{d},t)$, it follows that
is also an additive group homomorphism that satisfies the Leibniz’s rule, and hence ![]() $D_{i}$ is a derivation on
$D_{i}$ is a derivation on ![]() $Q({\mathcal{R}})$.
$Q({\mathcal{R}})$.
Since ![]() $\unicode[STIX]{x2202}_{i}(I^{n})\subseteq I^{n-1}$, we have
$\unicode[STIX]{x2202}_{i}(I^{n})\subseteq I^{n-1}$, we have ![]() $D_{i}({\mathcal{R}})\subseteq {\mathcal{R}}$ and by Seidenberg’s theorem (2.5) it follows that
$D_{i}({\mathcal{R}})\subseteq {\mathcal{R}}$ and by Seidenberg’s theorem (2.5) it follows that ![]() $D_{i}(\overline{{\mathcal{R}}})\subseteq \overline{{\mathcal{R}}}$, or equivalently,
$D_{i}(\overline{{\mathcal{R}}})\subseteq \overline{{\mathcal{R}}}$, or equivalently, ![]() $\unicode[STIX]{x2202}_{i}(\overline{I^{n}})\subseteq \overline{I^{n-1}}$ for every positive
$\unicode[STIX]{x2202}_{i}(\overline{I^{n}})\subseteq \overline{I^{n-1}}$ for every positive ![]() $n$. Since this holds for all
$n$. Since this holds for all ![]() $i$, we obtain
$i$, we obtain ![]() $\unicode[STIX]{x2202}(\overline{I^{n}})\subseteq \overline{I^{n-1}}$.◻
$\unicode[STIX]{x2202}(\overline{I^{n}})\subseteq \overline{I^{n-1}}$.◻
As an immediate consequence, we show that ![]() $\overline{I^{n}}$ is strongly Golod for every homogeneous ideal
$\overline{I^{n}}$ is strongly Golod for every homogeneous ideal ![]() $I$ and every
$I$ and every ![]() $n\geqslant 2$. This result was already known to be true for monomial ideals [Reference Herzog and Huneke3, Proposition 3.1]. In the case of homogeneous ideals, it was only known for
$n\geqslant 2$. This result was already known to be true for monomial ideals [Reference Herzog and Huneke3, Proposition 3.1]. In the case of homogeneous ideals, it was only known for ![]() $n\geqslant d+1$ [Reference Herzog and Huneke3, Theorem 2.11].
$n\geqslant d+1$ [Reference Herzog and Huneke3, Theorem 2.11].
Corollary 3.2. Let ![]() $I$ be a homogeneous ideal of
$I$ be a homogeneous ideal of ![]() $A$. Then
$A$. Then ![]() $\overline{I^{n}}$ is strongly Golod for every integer
$\overline{I^{n}}$ is strongly Golod for every integer ![]() $n\geqslant 2$.
$n\geqslant 2$.
Proof. Using the previous theorem we have ![]() $\unicode[STIX]{x2202}(\overline{I^{n}})^{2}\subseteq (\overline{I^{n-1}})^{2}\subseteq \overline{I^{2n-2}}\subseteq \overline{I^{n}}$ for
$\unicode[STIX]{x2202}(\overline{I^{n}})^{2}\subseteq (\overline{I^{n-1}})^{2}\subseteq \overline{I^{2n-2}}\subseteq \overline{I^{n}}$ for ![]() $n\geqslant 2$.◻
$n\geqslant 2$.◻
In order to be able to prove that the integral closure ![]() $\overline{I}$ of a strongly Golod ideal
$\overline{I}$ of a strongly Golod ideal ![]() $I$ is strongly Golod, we need a refinement of the first inclusion in the proof of Corollary 3.2. We obtain this by considering the Rees-like algebra
$I$ is strongly Golod, we need a refinement of the first inclusion in the proof of Corollary 3.2. We obtain this by considering the Rees-like algebra ![]() $A[\unicode[STIX]{x2202}(I)t,It^{2},t^{-1}]$ instead of the classical Rees algebra
$A[\unicode[STIX]{x2202}(I)t,It^{2},t^{-1}]$ instead of the classical Rees algebra ![]() $A[It,t^{-1}]$. We begin by identifying the homogeneous components of this new algebra.
$A[It,t^{-1}]$. We begin by identifying the homogeneous components of this new algebra.
Lemma 3.3. Let ![]() $I$ be a strongly Golod ideal of
$I$ be a strongly Golod ideal of ![]() $A$ and let
$A$ and let
Then
Proof. We start by observing that ![]() $J_{2}=\unicode[STIX]{x2202}(I)^{2}+I=I$, since
$J_{2}=\unicode[STIX]{x2202}(I)^{2}+I=I$, since ![]() $I$ is strongly Golod. From the
$I$ is strongly Golod. From the ![]() $t$-graded structure on
$t$-graded structure on ![]() ${\mathcal{S}}$, it is clear that
${\mathcal{S}}$, it is clear that ![]() $I^{n}\subseteq J_{2n}$ and
$I^{n}\subseteq J_{2n}$ and ![]() $\unicode[STIX]{x2202}(I)I^{n}\subseteq J_{2n+1}$ for
$\unicode[STIX]{x2202}(I)I^{n}\subseteq J_{2n+1}$ for ![]() $n\geqslant 0$. On the other hand, since
$n\geqslant 0$. On the other hand, since ![]() $\unicode[STIX]{x2202}(I)^{2}\subseteq I$, we also have
$\unicode[STIX]{x2202}(I)^{2}\subseteq I$, we also have ![]() $J_{2n}=\sum _{k=0}^{n}I^{k}\unicode[STIX]{x2202}(I)^{2n-2k}\subseteq \sum _{k=0}^{n}I^{k}I^{n-k}=I^{n}$ and
$J_{2n}=\sum _{k=0}^{n}I^{k}\unicode[STIX]{x2202}(I)^{2n-2k}\subseteq \sum _{k=0}^{n}I^{k}I^{n-k}=I^{n}$ and ![]() $J_{2n+1}=\sum _{k=0}^{n}I^{k}\unicode[STIX]{x2202}(I)^{2n+1-2k}\subseteq \sum _{k=0}^{n}I^{k}I^{n-k}\unicode[STIX]{x2202}(I)=I^{n}\unicode[STIX]{x2202}(I)$, finishing the proof.◻
$J_{2n+1}=\sum _{k=0}^{n}I^{k}\unicode[STIX]{x2202}(I)^{2n+1-2k}\subseteq \sum _{k=0}^{n}I^{k}I^{n-k}\unicode[STIX]{x2202}(I)=I^{n}\unicode[STIX]{x2202}(I)$, finishing the proof.◻
Theorem 3.4. Let ![]() $I$ be a homogeneous ideal of
$I$ be a homogeneous ideal of ![]() $A$. If
$A$. If ![]() $I$ is strongly Golod, then for every positive integers
$I$ is strongly Golod, then for every positive integers ![]() $m,n$,
$m,n$,
Proof. We consider the Rees-like ![]() $A$-algebra from the previous lemma
$A$-algebra from the previous lemma ![]() ${\mathcal{S}}=A[\unicode[STIX]{x2202}(I)t,It^{2}]=\bigoplus _{n\geqslant 0}J_{n}t^{n}$. As noted in Section 2.1, we have
${\mathcal{S}}=A[\unicode[STIX]{x2202}(I)t,It^{2}]=\bigoplus _{n\geqslant 0}J_{n}t^{n}$. As noted in Section 2.1, we have ![]() $I\subseteq \unicode[STIX]{x2202}(I)$, and therefore
$I\subseteq \unicode[STIX]{x2202}(I)$, and therefore ![]() $J_{n+1}\subseteq J_{n}$ for all
$J_{n+1}\subseteq J_{n}$ for all ![]() $n\geqslant 0$. If we set
$n\geqslant 0$. If we set ![]() ${\mathcal{U}}:={\mathcal{S}}[t^{-1}]$, this implies that
${\mathcal{U}}:={\mathcal{S}}[t^{-1}]$, this implies that ![]() ${\mathcal{U}}=\bigoplus _{n\in \mathbb{Z}}J_{n}t^{n}$ with
${\mathcal{U}}=\bigoplus _{n\in \mathbb{Z}}J_{n}t^{n}$ with ![]() $J_{n}=A$ for
$J_{n}=A$ for ![]() $n<0$. On the quotient field
$n<0$. On the quotient field ![]() $Q({\mathcal{U}})=Q(A)(t)$, for each
$Q({\mathcal{U}})=Q(A)(t)$, for each ![]() $i=1,\ldots ,d$, we consider again the derivation
$i=1,\ldots ,d$, we consider again the derivation
We claim that ![]() $D_{i}({\mathcal{U}})\subseteq {\mathcal{U}}$ for every
$D_{i}({\mathcal{U}})\subseteq {\mathcal{U}}$ for every ![]() $i=1,\ldots ,d$. Indeed, for
$i=1,\ldots ,d$. Indeed, for ![]() $n\geqslant 1$,
$n\geqslant 1$,
Similarly, for ![]() $n\geqslant 1$,
$n\geqslant 1$,
 $$\begin{eqnarray}\displaystyle D_{i}(J_{2n+1}t^{2n+1}) & = & \displaystyle \frac{1}{t}t^{2n+1}\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x2202}(I)I^{n})\subseteq t^{2n}[\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x2202}(I))I^{n}+\unicode[STIX]{x2202}_{i}(I^{n})\unicode[STIX]{x2202}(I)]\nonumber\\ \displaystyle & \subseteq & \displaystyle t^{2n}(I^{n}+I^{n-1}\unicode[STIX]{x2202}(I)^{2})\subseteq I^{n}t^{2n}=J_{2n}t^{2n}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D_{i}(J_{2n+1}t^{2n+1}) & = & \displaystyle \frac{1}{t}t^{2n+1}\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x2202}(I)I^{n})\subseteq t^{2n}[\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x2202}(I))I^{n}+\unicode[STIX]{x2202}_{i}(I^{n})\unicode[STIX]{x2202}(I)]\nonumber\\ \displaystyle & \subseteq & \displaystyle t^{2n}(I^{n}+I^{n-1}\unicode[STIX]{x2202}(I)^{2})\subseteq I^{n}t^{2n}=J_{2n}t^{2n}.\nonumber\end{eqnarray}$$ Since we also clearly have ![]() $D_{i}(J_{n}t^{n})\subseteq J_{n-1}t^{n-1}$ for
$D_{i}(J_{n}t^{n})\subseteq J_{n-1}t^{n-1}$ for ![]() $n\leqslant 1$, it follows that
$n\leqslant 1$, it follows that ![]() $D_{i}({\mathcal{U}})\subseteq {\mathcal{U}}$. By Seidenberg’s theorem applied to the noetherian
$D_{i}({\mathcal{U}})\subseteq {\mathcal{U}}$. By Seidenberg’s theorem applied to the noetherian ![]() $A$-algebra
$A$-algebra ![]() ${\mathcal{U}}$, we then obtain
${\mathcal{U}}$, we then obtain ![]() $D_{i}(\overline{{\mathcal{U}}})\subseteq \overline{{\mathcal{U}}}$ for all
$D_{i}(\overline{{\mathcal{U}}})\subseteq \overline{{\mathcal{U}}}$ for all ![]() $i$. On the other hand, since
$i$. On the other hand, since ![]() $A$ is a normal domain, we have
$A$ is a normal domain, we have ![]() $\overline{{\mathcal{U}}}=\bigoplus _{n\in \mathbb{Z}}L_{n}t^{n}\subseteq A[t,t^{-1}]$ with
$\overline{{\mathcal{U}}}=\bigoplus _{n\in \mathbb{Z}}L_{n}t^{n}\subseteq A[t,t^{-1}]$ with ![]() $L_{n}$ ideals of
$L_{n}$ ideals of ![]() $A$ and
$A$ and ![]() $L_{n}=A$ for
$L_{n}=A$ for ![]() $n\leqslant 0$. Therefore
$n\leqslant 0$. Therefore
We now claim that ![]() $L_{2n}=\overline{I^{n}}$ for
$L_{2n}=\overline{I^{n}}$ for ![]() $n\geqslant 1$. First, if
$n\geqslant 1$. First, if ![]() $f\in \overline{I^{n}}$, then
$f\in \overline{I^{n}}$, then ![]() $ft^{2n}\in \overline{I^{n}}t^{2n}$, so
$ft^{2n}\in \overline{I^{n}}t^{2n}$, so ![]() $ft^{2n}$ belongs to the integral closure of
$ft^{2n}$ belongs to the integral closure of ![]() $A[It^{2}]$ in
$A[It^{2}]$ in ![]() $A[t^{2}]$. Then
$A[t^{2}]$. Then ![]() $ft^{2n}$ is also integral over
$ft^{2n}$ is also integral over ![]() ${\mathcal{U}}=A[\unicode[STIX]{x2202}(I)t,It^{2},t^{-1}]$, hence
${\mathcal{U}}=A[\unicode[STIX]{x2202}(I)t,It^{2},t^{-1}]$, hence ![]() $f\in L_{2n}$. For the opposite inclusion, let
$f\in L_{2n}$. For the opposite inclusion, let ![]() $f\in L_{2n}$. As
$f\in L_{2n}$. As ![]() $ft^{2n}$ belongs to
$ft^{2n}$ belongs to ![]() $\overline{{\mathcal{U}}}$, it satisfies an equation of integral dependence
$\overline{{\mathcal{U}}}$, it satisfies an equation of integral dependence ![]() $(ft^{2n})^{k}+a_{1}(ft^{2n})^{k-1}+\cdots +a_{k-1}(ft^{2n})+a_{k}=0$ with
$(ft^{2n})^{k}+a_{1}(ft^{2n})^{k-1}+\cdots +a_{k-1}(ft^{2n})+a_{k}=0$ with ![]() $a_{1},\ldots ,a_{k}\in {\mathcal{U}}$. By considering the homogeneous part of
$a_{1},\ldots ,a_{k}\in {\mathcal{U}}$. By considering the homogeneous part of ![]() $t$-degree
$t$-degree ![]() $2nk$ in this equation, we may assume that
$2nk$ in this equation, we may assume that ![]() $a_{j}\in I^{nj}t^{2nj}$ for
$a_{j}\in I^{nj}t^{2nj}$ for ![]() $j=1,\ldots ,k.$ If we write
$j=1,\ldots ,k.$ If we write ![]() $a_{j}=b_{j}t^{2nj}$ with
$a_{j}=b_{j}t^{2nj}$ with ![]() $b_{j}\in I^{nj}$ we then obtain
$b_{j}\in I^{nj}$ we then obtain
showing that ![]() $f\in \overline{I^{n}}$.
$f\in \overline{I^{n}}$.
From (3.4.1) we now obtain ![]() $\unicode[STIX]{x2202}_{i}(\overline{I^{n}})t^{2n-1}=D_{i}(L_{2n}t^{2n})\subseteq L_{2n-1}t^{2n-1}$, that is,
$\unicode[STIX]{x2202}_{i}(\overline{I^{n}})t^{2n-1}=D_{i}(L_{2n}t^{2n})\subseteq L_{2n-1}t^{2n-1}$, that is, ![]() $\unicode[STIX]{x2202}_{i}(\overline{I^{n}})\subseteq L_{2n-1}$ for
$\unicode[STIX]{x2202}_{i}(\overline{I^{n}})\subseteq L_{2n-1}$ for ![]() $n\geqslant 1$. Since this holds for every
$n\geqslant 1$. Since this holds for every ![]() $i=1,\ldots ,d$, it follows that
$i=1,\ldots ,d$, it follows that ![]() $\unicode[STIX]{x2202}(\overline{I^{n}})\subseteq L_{2n-1}$. Therefore, for
$\unicode[STIX]{x2202}(\overline{I^{n}})\subseteq L_{2n-1}$. Therefore, for ![]() $m,n\geqslant 1$, we have
$m,n\geqslant 1$, we have
where the second inclusion follows from the ![]() $t$-graded structure of
$t$-graded structure of ![]() $\overline{{\mathcal{U}}}$.◻
$\overline{{\mathcal{U}}}$.◻
Corollary 3.5. Let ![]() $I$ be a homogeneous ideal of
$I$ be a homogeneous ideal of ![]() $A$. If
$A$. If ![]() $I$ is strongly Golod, then the integral closure
$I$ is strongly Golod, then the integral closure ![]() $\overline{I}$ is strongly Golod, too.
$\overline{I}$ is strongly Golod, too.
Proof. From the previous theorem, ![]() $\unicode[STIX]{x2202}(\overline{I})\unicode[STIX]{x2202}(\overline{I})\subseteq \overline{I}$, so
$\unicode[STIX]{x2202}(\overline{I})\unicode[STIX]{x2202}(\overline{I})\subseteq \overline{I}$, so ![]() $\overline{I}$ is strongly Golod.◻
$\overline{I}$ is strongly Golod.◻
Note that the above result also recovers Corollary 3.2, for the power ![]() $I^{n}$ is strongly Golod for every
$I^{n}$ is strongly Golod for every ![]() $n\geqslant 2$ [Reference Herzog and Huneke3, Theorem 2.3].
$n\geqslant 2$ [Reference Herzog and Huneke3, Theorem 2.3].
4 Rational powers of ideals
As before, ![]() $K$ is a field of characteristic zero and
$K$ is a field of characteristic zero and ![]() $A=K[x_{1},\ldots ,x_{d}]$ is a polynomial ring with
$A=K[x_{1},\ldots ,x_{d}]$ is a polynomial ring with ![]() $\deg (x_{i})=a_{i}>0$.
$\deg (x_{i})=a_{i}>0$.
The strongly Golod property for rational powers of ideals in ![]() $A$ was studied by De Stefani in [Reference De Stefani1]. If
$A$ was studied by De Stefani in [Reference De Stefani1]. If ![]() $I$ is a monomial ideal and
$I$ is a monomial ideal and ![]() $\unicode[STIX]{x1D6FC}\in \mathbb{Q}$, De Stefani proved that the rational power
$\unicode[STIX]{x1D6FC}\in \mathbb{Q}$, De Stefani proved that the rational power ![]() $I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for
$I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for ![]() $\unicode[STIX]{x1D6FC}\geqslant 2$. Moreover, if
$\unicode[STIX]{x1D6FC}\geqslant 2$. Moreover, if ![]() $I$ is a monomial strongly Golod ideal, then
$I$ is a monomial strongly Golod ideal, then ![]() $I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for
$I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for ![]() $\unicode[STIX]{x1D6FC}\geqslant 1$. Using techniques similar to those employed in the previous section, we extend these results to homogeneous ideals.
$\unicode[STIX]{x1D6FC}\geqslant 1$. Using techniques similar to those employed in the previous section, we extend these results to homogeneous ideals.
We begin with a brief overview of the rational powers of ideals.
Definition 4.1. Let ![]() $I$ be an ideal in a noetherian ring
$I$ be an ideal in a noetherian ring ![]() $R$ and
$R$ and ![]() $\unicode[STIX]{x1D6FC}=p/q\in \mathbb{Q}$ with
$\unicode[STIX]{x1D6FC}=p/q\in \mathbb{Q}$ with ![]() $p,q$ positive integers. The
$p,q$ positive integers. The ![]() $\unicode[STIX]{x1D6FC}$th rational power of the ideal
$\unicode[STIX]{x1D6FC}$th rational power of the ideal ![]() $I$ is defined by
$I$ is defined by ![]() $I_{\unicode[STIX]{x1D6FC}}:=\{x\in R\mid x^{q}\in \overline{I^{p}}\}$.
$I_{\unicode[STIX]{x1D6FC}}:=\{x\in R\mid x^{q}\in \overline{I^{p}}\}$.
The definition is independent of the representation of ![]() $\unicode[STIX]{x1D6FC}$ as a quotient of integers. Moreover,
$\unicode[STIX]{x1D6FC}$ as a quotient of integers. Moreover, ![]() $I_{\unicode[STIX]{x1D6FC}}$ is an integrally closed ideal of
$I_{\unicode[STIX]{x1D6FC}}$ is an integrally closed ideal of ![]() $R$ for every positive rational
$R$ for every positive rational ![]() $\unicode[STIX]{x1D6FC}$. (If
$\unicode[STIX]{x1D6FC}$. (If ![]() $m$ is a positive integer, the
$m$ is a positive integer, the ![]() $m$th rational power
$m$th rational power ![]() $I_{m}$ of
$I_{m}$ of ![]() $I$ is the integral closure
$I$ is the integral closure ![]() $\overline{I^{m}}$.) For every positive rationals
$\overline{I^{m}}$.) For every positive rationals ![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$, we have
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$, we have ![]() $I_{\unicode[STIX]{x1D6FC}}I_{\unicode[STIX]{x1D6FD}}\subseteq I_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}$, and if
$I_{\unicode[STIX]{x1D6FC}}I_{\unicode[STIX]{x1D6FD}}\subseteq I_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}$, and if ![]() $\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FD}$, then
$\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FD}$, then ![]() $I_{\unicode[STIX]{x1D6FC}}\subseteq I_{\unicode[STIX]{x1D6FD}}$. For these facts and other properties of the rational powers of ideals we refer the reader to [Reference Huneke and Swanson4, 10.5].
$I_{\unicode[STIX]{x1D6FC}}\subseteq I_{\unicode[STIX]{x1D6FD}}$. For these facts and other properties of the rational powers of ideals we refer the reader to [Reference Huneke and Swanson4, 10.5].
Remark 4.2. Like the integral closures ![]() $\overline{I^{m}}$ (
$\overline{I^{m}}$ (![]() $m\geqslant 1$), the rational powers can be obtained as homogeneous components of the integral closure of a Rees-like algebra. Let
$m\geqslant 1$), the rational powers can be obtained as homogeneous components of the integral closure of a Rees-like algebra. Let ![]() $I$ be an ideal in a noetherian ring
$I$ be an ideal in a noetherian ring ![]() $R$ and
$R$ and ![]() $a\geqslant 1$ an integer. Let
$a\geqslant 1$ an integer. Let ![]() $T=R[It^{a},t^{-1}]$ and let
$T=R[It^{a},t^{-1}]$ and let ![]() $\overline{T}=\bigoplus _{n\in \mathbb{Z}}J_{n}t^{n}$ be the integral closure of
$\overline{T}=\bigoplus _{n\in \mathbb{Z}}J_{n}t^{n}$ be the integral closure of ![]() $T$ in
$T$ in ![]() $R[t,t^{-1}]$. Then
$R[t,t^{-1}]$. Then ![]() $J_{n}=I_{n/a}$ for
$J_{n}=I_{n/a}$ for ![]() $n\geqslant 1$.
$n\geqslant 1$.
To see this we first note that ![]() $J_{na}=\overline{I^{n}}$ for all integers
$J_{na}=\overline{I^{n}}$ for all integers ![]() $n\geqslant 1$. Indeed, if
$n\geqslant 1$. Indeed, if ![]() $f\in \overline{I^{n}}$, then
$f\in \overline{I^{n}}$, then ![]() $ft^{na}\in \overline{I^{n}}t^{na}$, so
$ft^{na}\in \overline{I^{n}}t^{na}$, so ![]() $ft^{na}$ belongs to the integral closure of
$ft^{na}$ belongs to the integral closure of ![]() $R[It^{a}]$ in
$R[It^{a}]$ in ![]() $R[t^{a}]$. Then
$R[t^{a}]$. Then ![]() $ft^{na}$ is integral over
$ft^{na}$ is integral over ![]() $T=R[It^{a},t^{-1}]$, hence
$T=R[It^{a},t^{-1}]$, hence ![]() $f\in J_{na}$. For the other inclusion, let
$f\in J_{na}$. For the other inclusion, let ![]() $f\in J_{na}$. Since
$f\in J_{na}$. Since ![]() $ft^{na}\in \overline{T}$, we have an equation of integral dependence
$ft^{na}\in \overline{T}$, we have an equation of integral dependence ![]() $(ft^{na})^{k}+a_{1}(ft^{na})^{k-1}+\cdots +a_{k-1}(ft^{na})+a_{k}=0$ with
$(ft^{na})^{k}+a_{1}(ft^{na})^{k-1}+\cdots +a_{k-1}(ft^{na})+a_{k}=0$ with ![]() $a_{1},\ldots ,a_{k}\in T$. Moreover, by taking the homogeneous part of
$a_{1},\ldots ,a_{k}\in T$. Moreover, by taking the homogeneous part of ![]() $t$-degree
$t$-degree ![]() $nak$ in this equation, we may assume that
$nak$ in this equation, we may assume that ![]() $a_{j}\in I^{nj}t^{naj}$ for
$a_{j}\in I^{nj}t^{naj}$ for ![]() $j=1,\ldots ,k,$ and if we write
$j=1,\ldots ,k,$ and if we write ![]() $a_{j}=b_{j}t^{naj}$ with
$a_{j}=b_{j}t^{naj}$ with ![]() $b_{j}\in I^{nj}$, we obtain an equation of integral dependence of
$b_{j}\in I^{nj}$, we obtain an equation of integral dependence of ![]() $f$ over
$f$ over ![]() $I^{n}$.
$I^{n}$.
For the general case, if ![]() $f\in J_{n}$, then
$f\in J_{n}$, then ![]() $f^{a}\in J_{na}=\overline{I^{n}}$, so
$f^{a}\in J_{na}=\overline{I^{n}}$, so ![]() $f\in I_{n/a}$. Conversely, if
$f\in I_{n/a}$. Conversely, if ![]() $f\in I_{n/a}$, then
$f\in I_{n/a}$, then ![]() $f^{a}\in \overline{I^{n}}$, so
$f^{a}\in \overline{I^{n}}$, so ![]() $(ft^{n})^{a}\in \overline{I^{n}}t^{na}=J_{na}t^{na}\subseteq \overline{T}$. This implies that
$(ft^{n})^{a}\in \overline{I^{n}}t^{na}=J_{na}t^{na}\subseteq \overline{T}$. This implies that ![]() $ft^{n}$ is also integral over
$ft^{n}$ is also integral over ![]() $T$, so
$T$, so ![]() $f\in J_{n}$.
$f\in J_{n}$.
Theorem 4.3. Let ![]() $I$ be an arbitrary ideal of
$I$ be an arbitrary ideal of ![]() $A$ and
$A$ and ![]() $\unicode[STIX]{x1D6FC}\in \mathbb{Q}$ with
$\unicode[STIX]{x1D6FC}\in \mathbb{Q}$ with ![]() $\unicode[STIX]{x1D6FC}\geqslant 1$. Then
$\unicode[STIX]{x1D6FC}\geqslant 1$. Then
Proof. Write ![]() $\unicode[STIX]{x1D6FC}=N/a$ with
$\unicode[STIX]{x1D6FC}=N/a$ with ![]() $a,N$ positive integers and consider the
$a,N$ positive integers and consider the ![]() $A$-algebra
$A$-algebra ![]() $T=A[It^{a},t^{-1}]$. Since
$T=A[It^{a},t^{-1}]$. Since ![]() $A$ is a normal domain, the integral closure of
$A$ is a normal domain, the integral closure of ![]() $T$ in its quotient field
$T$ in its quotient field ![]() $Q(A)(t)$ coincides with the integral closure
$Q(A)(t)$ coincides with the integral closure ![]() $\overline{T}=\bigoplus _{n\in \mathbb{Z}}J_{n}t^{n}$ of
$\overline{T}=\bigoplus _{n\in \mathbb{Z}}J_{n}t^{n}$ of ![]() $T$ in
$T$ in ![]() $A[t,t^{-1}]$. For every
$A[t,t^{-1}]$. For every ![]() $i\in \{1,\ldots ,d\}$, let
$i\in \{1,\ldots ,d\}$, let
This map is a derivation, and since ![]() $\unicode[STIX]{x2202}_{i}(I^{n})\subseteq I^{n-1}$, we have
$\unicode[STIX]{x2202}_{i}(I^{n})\subseteq I^{n-1}$, we have ![]() $D_{i}(I^{n}t^{na})\subseteq I^{n-1}t^{(n-1)a}$ for all
$D_{i}(I^{n}t^{na})\subseteq I^{n-1}t^{(n-1)a}$ for all ![]() $n$, that is,
$n$, that is, ![]() $D_{i}(T)\subseteq T$. By Seidenberg’s theorem, we then obtain
$D_{i}(T)\subseteq T$. By Seidenberg’s theorem, we then obtain ![]() $D_{i}(\overline{T})\subseteq \overline{T}$, or equivalently,
$D_{i}(\overline{T})\subseteq \overline{T}$, or equivalently, ![]() $\unicode[STIX]{x2202}_{i}(J_{n})\subseteq J_{n-a}$ for every integer
$\unicode[STIX]{x2202}_{i}(J_{n})\subseteq J_{n-a}$ for every integer ![]() $n$. Therefore
$n$. Therefore ![]() $\unicode[STIX]{x2202}(J_{n})\subseteq J_{n-a}$ for all integers
$\unicode[STIX]{x2202}(J_{n})\subseteq J_{n-a}$ for all integers ![]() $n$. However, as explained in Remark 4.2,
$n$. However, as explained in Remark 4.2, ![]() $J_{N}=I_{N/a}=I_{\unicode[STIX]{x1D6FC}}$ and
$J_{N}=I_{N/a}=I_{\unicode[STIX]{x1D6FC}}$ and ![]() $J_{N-a}=I_{(N-a)/a}=I_{\unicode[STIX]{x1D6FC}-1}$, so
$J_{N-a}=I_{(N-a)/a}=I_{\unicode[STIX]{x1D6FC}-1}$, so ![]() $\unicode[STIX]{x2202}(I_{\unicode[STIX]{x1D6FC}})\subseteq I_{\unicode[STIX]{x1D6FC}-1}$.◻
$\unicode[STIX]{x2202}(I_{\unicode[STIX]{x1D6FC}})\subseteq I_{\unicode[STIX]{x1D6FC}-1}$.◻
Corollary 4.4. Let ![]() $I$ be a homogeneous ideal of
$I$ be a homogeneous ideal of ![]() $A$. Then
$A$. Then ![]() $I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for every
$I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for every ![]() $\unicode[STIX]{x1D6FC}\in \mathbb{Q}$ with
$\unicode[STIX]{x1D6FC}\in \mathbb{Q}$ with ![]() $\unicode[STIX]{x1D6FC}\geqslant 2$.
$\unicode[STIX]{x1D6FC}\geqslant 2$.
Proof. From the previous theorem, ![]() $\unicode[STIX]{x2202}(I_{\unicode[STIX]{x1D6FC}})^{2}\subseteq I_{\unicode[STIX]{x1D6FC}-1}I_{\unicode[STIX]{x1D6FC}-1}\subseteq I_{2\unicode[STIX]{x1D6FC}-2}\subseteq I_{\unicode[STIX]{x1D6FC}}$ for
$\unicode[STIX]{x2202}(I_{\unicode[STIX]{x1D6FC}})^{2}\subseteq I_{\unicode[STIX]{x1D6FC}-1}I_{\unicode[STIX]{x1D6FC}-1}\subseteq I_{2\unicode[STIX]{x1D6FC}-2}\subseteq I_{\unicode[STIX]{x1D6FC}}$ for ![]() $\unicode[STIX]{x1D6FC}\geqslant 2$.◻
$\unicode[STIX]{x1D6FC}\geqslant 2$.◻
If the ideal ![]() $I$ is strongly Golod, the inclusion proved in Theorem 4.3 can be improved.
$I$ is strongly Golod, the inclusion proved in Theorem 4.3 can be improved.
Theorem 4.5. Let ![]() $I$ be a homogeneous ideal of
$I$ be a homogeneous ideal of ![]() $A$. If
$A$. If ![]() $I$ is strongly Golod, then for every
$I$ is strongly Golod, then for every ![]() $\unicode[STIX]{x1D6FC}\in \mathbb{Q}$ with
$\unicode[STIX]{x1D6FC}\in \mathbb{Q}$ with ![]() $\unicode[STIX]{x1D6FC}\geqslant \frac{1}{2}$,
$\unicode[STIX]{x1D6FC}\geqslant \frac{1}{2}$,
Proof. Write ![]() $\unicode[STIX]{x1D6FC}=N/2a$ with
$\unicode[STIX]{x1D6FC}=N/2a$ with ![]() $N,a$ positive integers. (It will become clear later that it is important to represent
$N,a$ positive integers. (It will become clear later that it is important to represent ![]() $\unicode[STIX]{x1D6FC}$ with an even denominator.) Let
$\unicode[STIX]{x1D6FC}$ with an even denominator.) Let ![]() ${\mathcal{C}}=A[\unicode[STIX]{x2202}(I)t^{a},It^{2a}]=\bigoplus _{n\geqslant 0}C_{na}t^{na}$. From Lemma 3.3, it follows that
${\mathcal{C}}=A[\unicode[STIX]{x2202}(I)t^{a},It^{2a}]=\bigoplus _{n\geqslant 0}C_{na}t^{na}$. From Lemma 3.3, it follows that ![]() $C_{2na}=I^{n}$ and
$C_{2na}=I^{n}$ and ![]() $C_{(2n+1)a}=\unicode[STIX]{x2202}(I)I^{n}$ for
$C_{(2n+1)a}=\unicode[STIX]{x2202}(I)I^{n}$ for ![]() $n\geqslant 0$. Moreover, as noted in Section 2.1,
$n\geqslant 0$. Moreover, as noted in Section 2.1, ![]() $I\subseteq \unicode[STIX]{x2202}(I)$, so
$I\subseteq \unicode[STIX]{x2202}(I)$, so ![]() $C_{(n+1)a}\subseteq C_{na}$ for every
$C_{(n+1)a}\subseteq C_{na}$ for every ![]() $n\geqslant 0$.
$n\geqslant 0$.
Now let
From the description of the graded components ![]() $C_{na}$ given above and the fact that
$C_{na}$ given above and the fact that ![]() $C_{(n+1)a}\subseteq C_{na}$ for every
$C_{(n+1)a}\subseteq C_{na}$ for every ![]() $n\geqslant 0$, it follows that
$n\geqslant 0$, it follows that
 $$\begin{eqnarray}\displaystyle {\mathcal{V}}=A[t^{-1}] & \oplus & \displaystyle \unicode[STIX]{x2202}(I)t\oplus \unicode[STIX]{x2202}(I)t^{2}\oplus \cdots \oplus \unicode[STIX]{x2202}(I)t^{a}\nonumber\\ \displaystyle & \oplus & \displaystyle It^{a+1}\oplus It^{a+2}\oplus \cdots \oplus It^{2a}\nonumber\\ \displaystyle & \oplus & \displaystyle I\unicode[STIX]{x2202}(I)t^{2a+1}\oplus I\unicode[STIX]{x2202}(I)t^{2a+2}\oplus \cdots \oplus I\unicode[STIX]{x2202}(I)t^{3a}\nonumber\\ \displaystyle & \oplus & \displaystyle I^{2}t^{3a+1}\oplus I^{2}t^{3a+2}\oplus \cdots \oplus I^{2}t^{4a}\nonumber\\ \displaystyle & \oplus & \displaystyle I^{2}\unicode[STIX]{x2202}(I)t^{4a+1}\oplus I^{2}\unicode[STIX]{x2202}(I)t^{4a+2}\oplus \cdots \oplus I^{2}\unicode[STIX]{x2202}(I)t^{5a}\nonumber\\ \displaystyle & \oplus & \displaystyle \cdots \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{V}}=A[t^{-1}] & \oplus & \displaystyle \unicode[STIX]{x2202}(I)t\oplus \unicode[STIX]{x2202}(I)t^{2}\oplus \cdots \oplus \unicode[STIX]{x2202}(I)t^{a}\nonumber\\ \displaystyle & \oplus & \displaystyle It^{a+1}\oplus It^{a+2}\oplus \cdots \oplus It^{2a}\nonumber\\ \displaystyle & \oplus & \displaystyle I\unicode[STIX]{x2202}(I)t^{2a+1}\oplus I\unicode[STIX]{x2202}(I)t^{2a+2}\oplus \cdots \oplus I\unicode[STIX]{x2202}(I)t^{3a}\nonumber\\ \displaystyle & \oplus & \displaystyle I^{2}t^{3a+1}\oplus I^{2}t^{3a+2}\oplus \cdots \oplus I^{2}t^{4a}\nonumber\\ \displaystyle & \oplus & \displaystyle I^{2}\unicode[STIX]{x2202}(I)t^{4a+1}\oplus I^{2}\unicode[STIX]{x2202}(I)t^{4a+2}\oplus \cdots \oplus I^{2}\unicode[STIX]{x2202}(I)t^{5a}\nonumber\\ \displaystyle & \oplus & \displaystyle \cdots \nonumber\end{eqnarray}$$ More precisely, if ![]() ${\mathcal{V}}=\bigoplus _{n\in \mathbb{Z}}V_{n}t^{n}$ (with
${\mathcal{V}}=\bigoplus _{n\in \mathbb{Z}}V_{n}t^{n}$ (with ![]() $V_{n}=A$ for
$V_{n}=A$ for ![]() $n\leqslant 0$), for each
$n\leqslant 0$), for each ![]() $n\geqslant 1$ let
$n\geqslant 1$ let ![]() $b=\left\lfloor (n-1)/a\right\rfloor$ so that we can write
$b=\left\lfloor (n-1)/a\right\rfloor$ so that we can write ![]() $n=ab+r$ with
$n=ab+r$ with ![]() $b,r\in \mathbb{N}$ and
$b,r\in \mathbb{N}$ and ![]() $1\leqslant r\leqslant a$. Then
$1\leqslant r\leqslant a$. Then ![]() $V_{n}=I^{(b+1)/2}$ if
$V_{n}=I^{(b+1)/2}$ if ![]() $b$ is odd and
$b$ is odd and ![]() $V_{n}=I^{b/2}\unicode[STIX]{x2202}(I)$ if
$V_{n}=I^{b/2}\unicode[STIX]{x2202}(I)$ if ![]() $b$ is even.
$b$ is even.
We now consider ![]() $\overline{{\mathcal{V}}}$ the integral closure of
$\overline{{\mathcal{V}}}$ the integral closure of ![]() ${\mathcal{V}}$ in its quotient field
${\mathcal{V}}$ in its quotient field ![]() $Q(A)(t)$. Since
$Q(A)(t)$. Since ![]() $A$ is integrally closed,
$A$ is integrally closed, ![]() $\overline{{\mathcal{V}}}=\bigoplus _{n\in \mathbb{Z}}W_{n}t^{n}$ is a graded subalgebra of
$\overline{{\mathcal{V}}}=\bigoplus _{n\in \mathbb{Z}}W_{n}t^{n}$ is a graded subalgebra of ![]() $A[t,t^{-1}]$ with
$A[t,t^{-1}]$ with ![]() $W_{n}=A$ for
$W_{n}=A$ for ![]() $n\leqslant 0$.
$n\leqslant 0$.
We first claim that ![]() $W_{2na}=\overline{I^{n}}$ for all
$W_{2na}=\overline{I^{n}}$ for all ![]() $n\geqslant 1$. Indeed, for
$n\geqslant 1$. Indeed, for ![]() $f\in \overline{I^{n}}$ we have
$f\in \overline{I^{n}}$ we have ![]() $ft^{2an}\in \overline{I^{n}}t^{2an}$, so
$ft^{2an}\in \overline{I^{n}}t^{2an}$, so ![]() $ft^{2an}$ belongs to the integral closure of
$ft^{2an}$ belongs to the integral closure of ![]() $A[It^{2a}]$ in
$A[It^{2a}]$ in ![]() $A[t^{2a}]$. Then
$A[t^{2a}]$. Then ![]() $ft^{2an}$ is also integral over
$ft^{2an}$ is also integral over ![]() ${\mathcal{V}}$, so
${\mathcal{V}}$, so ![]() $f\in W_{2an}$. Conversely, if
$f\in W_{2an}$. Conversely, if ![]() $f\in W_{2an}$, then
$f\in W_{2an}$, then ![]() $ft^{2an}$ satisfies an equation of integral dependence over
$ft^{2an}$ satisfies an equation of integral dependence over ![]() ${\mathcal{V}}$,
${\mathcal{V}}$, ![]() $(ft^{2na})^{k}+a_{1}(ft^{2na})^{k-1}+\cdots +a_{k-1}(ft^{2na})+a_{k}=0$, with
$(ft^{2na})^{k}+a_{1}(ft^{2na})^{k-1}+\cdots +a_{k-1}(ft^{2na})+a_{k}=0$, with ![]() $a_{1},\ldots ,a_{k}\in {\mathcal{V}}$. By considering the homogeneous part of
$a_{1},\ldots ,a_{k}\in {\mathcal{V}}$. By considering the homogeneous part of ![]() $t$-degree
$t$-degree ![]() $2nak$ in this equation, we may assume that
$2nak$ in this equation, we may assume that ![]() $a_{j}\in I^{nj}t^{2naj}$ for
$a_{j}\in I^{nj}t^{2naj}$ for ![]() $j=1,\ldots ,k.$ This becomes an equation of integral dependence over
$j=1,\ldots ,k.$ This becomes an equation of integral dependence over ![]() $A[It^{2a}]$, so
$A[It^{2a}]$, so ![]() $f\in \overline{I^{n}}$.
$f\in \overline{I^{n}}$.
We now claim that ![]() $W_{n}=I_{n/2a}$ for all
$W_{n}=I_{n/2a}$ for all ![]() $n\geqslant 1$. For
$n\geqslant 1$. For ![]() $f\in I_{n/2a}$ we have
$f\in I_{n/2a}$ we have ![]() $f^{2a}t^{2na}\in \overline{I^{n}}t^{2na}=W_{2na}t^{2na}\subseteq \overline{{\mathcal{V}}}$, so
$f^{2a}t^{2na}\in \overline{I^{n}}t^{2na}=W_{2na}t^{2na}\subseteq \overline{{\mathcal{V}}}$, so ![]() $(ft^{n})^{2a}$ is integral over
$(ft^{n})^{2a}$ is integral over ![]() ${\mathcal{V}}$. Then
${\mathcal{V}}$. Then ![]() $ft^{n}$ is integral over
$ft^{n}$ is integral over ![]() ${\mathcal{V}}$ as well, so
${\mathcal{V}}$ as well, so ![]() $f\in W_{n}$. Conversely, if
$f\in W_{n}$. Conversely, if ![]() $f\in W_{n}$, then
$f\in W_{n}$, then ![]() $f^{2a}\in W_{2na}=\overline{I^{n}}$, so
$f^{2a}\in W_{2na}=\overline{I^{n}}$, so ![]() $f\in I_{n/2a}$.
$f\in I_{n/2a}$.
For ![]() $i=1,\ldots ,d$, consider again the derivation
$i=1,\ldots ,d$, consider again the derivation
We now show that ![]() $D_{i}({\mathcal{V}})\subseteq {\mathcal{V}}$, or equivalently,
$D_{i}({\mathcal{V}})\subseteq {\mathcal{V}}$, or equivalently, ![]() $\unicode[STIX]{x2202}_{i}(V_{n})\subseteq V_{n-a}$ for all integers
$\unicode[STIX]{x2202}_{i}(V_{n})\subseteq V_{n-a}$ for all integers ![]() $n$. This is clear for
$n$. This is clear for ![]() $n\leqslant a$, so we may assume
$n\leqslant a$, so we may assume ![]() $n\geqslant a+1$. If
$n\geqslant a+1$. If ![]() $n=(2k+1)a+r$ with integers
$n=(2k+1)a+r$ with integers ![]() $k\geqslant 0$ and
$k\geqslant 0$ and ![]() $1\leqslant r\leqslant a$, then
$1\leqslant r\leqslant a$, then ![]() $V_{n}=I^{k+1}$,
$V_{n}=I^{k+1}$, ![]() $V_{n-a}=I^{k}\unicode[STIX]{x2202}(I)$, and
$V_{n-a}=I^{k}\unicode[STIX]{x2202}(I)$, and ![]() $\unicode[STIX]{x2202}_{i}(I^{k+1})\subseteq I^{k}\unicode[STIX]{x2202}(I)$. In the other case, if
$\unicode[STIX]{x2202}_{i}(I^{k+1})\subseteq I^{k}\unicode[STIX]{x2202}(I)$. In the other case, if ![]() $n=2ka+r$ with integers
$n=2ka+r$ with integers ![]() $k\geqslant 1$ and
$k\geqslant 1$ and ![]() $1\leqslant r\leqslant a$, we have
$1\leqslant r\leqslant a$, we have ![]() $V_{n}=I^{k}\unicode[STIX]{x2202}(I)$,
$V_{n}=I^{k}\unicode[STIX]{x2202}(I)$, ![]() $V_{n-a}=I^{k}$, and
$V_{n-a}=I^{k}$, and ![]() $\unicode[STIX]{x2202}_{i}(I^{k}\unicode[STIX]{x2202}(I))\subseteq I^{k}\unicode[STIX]{x2202}(\unicode[STIX]{x2202}(I))+I^{k-1}\unicode[STIX]{x2202}(I)\unicode[STIX]{x2202}(I)\subseteq I^{k}$ since
$\unicode[STIX]{x2202}_{i}(I^{k}\unicode[STIX]{x2202}(I))\subseteq I^{k}\unicode[STIX]{x2202}(\unicode[STIX]{x2202}(I))+I^{k-1}\unicode[STIX]{x2202}(I)\unicode[STIX]{x2202}(I)\subseteq I^{k}$ since ![]() $I$ is strongly Golod.
$I$ is strongly Golod.
We can now apply Seidenberg’s theorem. From ![]() $D_{i}(\overline{{\mathcal{V}}})\subseteq \overline{{\mathcal{V}}}$ we obtain
$D_{i}(\overline{{\mathcal{V}}})\subseteq \overline{{\mathcal{V}}}$ we obtain ![]() $D_{i}(W_{n}t^{n})\subseteq W_{n-a}t^{n-a}$ for all
$D_{i}(W_{n}t^{n})\subseteq W_{n-a}t^{n-a}$ for all ![]() $n$, or equivalently,
$n$, or equivalently, ![]() $\unicode[STIX]{x2202}_{i}(W_{n})\subseteq W_{n-a}$. On the other hand, we know that
$\unicode[STIX]{x2202}_{i}(W_{n})\subseteq W_{n-a}$. On the other hand, we know that ![]() $W_{N}=I_{N/2a}=I_{\unicode[STIX]{x1D6FC}}$, so
$W_{N}=I_{N/2a}=I_{\unicode[STIX]{x1D6FC}}$, so ![]() $\unicode[STIX]{x2202}_{i}(I_{\unicode[STIX]{x1D6FC}})=\unicode[STIX]{x2202}_{i}(I_{N/2a})\subseteq I_{(N-a)/2a}=I_{\unicode[STIX]{x1D6FC}-(1/2)}$. As this holds for every
$\unicode[STIX]{x2202}_{i}(I_{\unicode[STIX]{x1D6FC}})=\unicode[STIX]{x2202}_{i}(I_{N/2a})\subseteq I_{(N-a)/2a}=I_{\unicode[STIX]{x1D6FC}-(1/2)}$. As this holds for every ![]() $i$, we obtain
$i$, we obtain ![]() $\unicode[STIX]{x2202}(I_{\unicode[STIX]{x1D6FC}})\subseteq I_{\unicode[STIX]{x1D6FC}-(1/2)}$.◻
$\unicode[STIX]{x2202}(I_{\unicode[STIX]{x1D6FC}})\subseteq I_{\unicode[STIX]{x1D6FC}-(1/2)}$.◻
Corollary 4.6. Let ![]() $I$ be a homogeneous ideal of
$I$ be a homogeneous ideal of ![]() $A$. If
$A$. If ![]() $I$ is strongly Golod, then
$I$ is strongly Golod, then ![]() $I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for every
$I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for every ![]() $\unicode[STIX]{x1D6FC}\in \mathbb{Q}$ with
$\unicode[STIX]{x1D6FC}\in \mathbb{Q}$ with ![]() $\unicode[STIX]{x1D6FC}\geqslant 1$.
$\unicode[STIX]{x1D6FC}\geqslant 1$.
Proof. By the previous theorem, ![]() $\unicode[STIX]{x2202}(I_{\unicode[STIX]{x1D6FC}})^{2}\subseteq I_{\unicode[STIX]{x1D6FC}-(1/2)}I_{\unicode[STIX]{x1D6FC}-(1/2)}\subseteq I_{2\unicode[STIX]{x1D6FC}-1}\subseteq I_{\unicode[STIX]{x1D6FC}}$ for
$\unicode[STIX]{x2202}(I_{\unicode[STIX]{x1D6FC}})^{2}\subseteq I_{\unicode[STIX]{x1D6FC}-(1/2)}I_{\unicode[STIX]{x1D6FC}-(1/2)}\subseteq I_{2\unicode[STIX]{x1D6FC}-1}\subseteq I_{\unicode[STIX]{x1D6FC}}$ for ![]() $\unicode[STIX]{x1D6FC}\geqslant 1$.◻
$\unicode[STIX]{x1D6FC}\geqslant 1$.◻
5 Coefficient ideals
Let ![]() $M$ denote the maximal homogeneous ideal of the polynomial ring
$M$ denote the maximal homogeneous ideal of the polynomial ring ![]() $A=K[x_{1},\ldots ,x_{d}]$ with
$A=K[x_{1},\ldots ,x_{d}]$ with ![]() $\deg x_{i}=a_{i}$ and
$\deg x_{i}=a_{i}$ and ![]() $K$ an infinite field. If
$K$ an infinite field. If ![]() $I$ is an
$I$ is an ![]() $M$-primary ideal, for
$M$-primary ideal, for ![]() $n\gg 0$ the length
$n\gg 0$ the length ![]() $\unicode[STIX]{x1D706}(A/I^{n})$ becomes a polynomial function
$\unicode[STIX]{x1D706}(A/I^{n})$ becomes a polynomial function ![]() $P_{I}(n)$ of degree
$P_{I}(n)$ of degree ![]() $d$, the Hilbert–Samuel polynomial of
$d$, the Hilbert–Samuel polynomial of ![]() $I$. We write this polynomial
$I$. We write this polynomial
with integer coefficients ![]() $\operatorname{e}_{i}(I)$, subsequently referred to as the Hilbert coefficients of
$\operatorname{e}_{i}(I)$, subsequently referred to as the Hilbert coefficients of ![]() $I$. The coefficient
$I$. The coefficient ![]() $\operatorname{e}_{0}(I)$ (the multiplicity of
$\operatorname{e}_{0}(I)$ (the multiplicity of ![]() $I$) is positive and a well-known result of Rees shows that the integral closure
$I$) is positive and a well-known result of Rees shows that the integral closure ![]() $\overline{I}$ is the largest ideal containing
$\overline{I}$ is the largest ideal containing ![]() $I$ having the same coefficient
$I$ having the same coefficient ![]() $\operatorname{e}_{0}$. Similarly, the Ratliff–Rush ideal
$\operatorname{e}_{0}$. Similarly, the Ratliff–Rush ideal ![]() $\tilde{I} =\bigcup _{i\geqslant 0}(I^{i+1}:I^{i})$ is the unique largest ideal containing
$\tilde{I} =\bigcup _{i\geqslant 0}(I^{i+1}:I^{i})$ is the unique largest ideal containing ![]() $I$ having the same Hilbert coefficients
$I$ having the same Hilbert coefficients ![]() $\operatorname{e}_{0},\operatorname{e}_{1},\ldots ,\operatorname{e}_{d}$. In fact, Shah [Reference Shah8] proved that there exists a chain of ideals
$\operatorname{e}_{0},\operatorname{e}_{1},\ldots ,\operatorname{e}_{d}$. In fact, Shah [Reference Shah8] proved that there exists a chain of ideals
where ![]() $I_{\{k\}}$ is the unique ideal containing
$I_{\{k\}}$ is the unique ideal containing ![]() $I$ maximal with respect to the property of having the same coefficients
$I$ maximal with respect to the property of having the same coefficients ![]() $\operatorname{e}_{0},\ldots ,\operatorname{e}_{k}$ as those of
$\operatorname{e}_{0},\ldots ,\operatorname{e}_{k}$ as those of ![]() $I$. The ideal
$I$. The ideal ![]() $I_{\{k\}}$ is called the
$I_{\{k\}}$ is called the ![]() $k$th coefficient ideal of
$k$th coefficient ideal of ![]() $I$.
$I$.
Remark 5.1. Shah proved the existence of this chain for an ideal primary to the maximal ideal in a formally equidimensional local ring with infinite residue field. However, since ![]() $\unicode[STIX]{x1D706}(A/I^{n})=\unicode[STIX]{x1D706}(A_{M}/I^{n}A_{M})$, Shah’s result is valid in the polynomial setting as well and
$\unicode[STIX]{x1D706}(A/I^{n})=\unicode[STIX]{x1D706}(A_{M}/I^{n}A_{M})$, Shah’s result is valid in the polynomial setting as well and ![]() $I_{\{k\}}=(IA_{M})_{\{k\}}\cap A$.
$I_{\{k\}}=(IA_{M})_{\{k\}}\cap A$.
Remark 5.2. Coefficient ideals in polynomial rings have been studied by Heinzer and Lantz in [Reference Heinzer and Lantz2]. They observed that if ![]() $I$ is monomial, then its coefficient ideals are monomial, too [Reference Heinzer and Lantz2, Observation 3.3]. In fact, with a modification of their of argument, one can prove that if
$I$ is monomial, then its coefficient ideals are monomial, too [Reference Heinzer and Lantz2, Observation 3.3]. In fact, with a modification of their of argument, one can prove that if ![]() $I$ is a homogeneous ideal, then all the coefficient ideals of
$I$ is a homogeneous ideal, then all the coefficient ideals of ![]() $I$ are homogeneous as well. To see this, for each
$I$ are homogeneous as well. To see this, for each ![]() $u\in K\setminus \{0\}$, let
$u\in K\setminus \{0\}$, let ![]() $\unicode[STIX]{x1D719}_{u}:A\rightarrow A$ be the
$\unicode[STIX]{x1D719}_{u}:A\rightarrow A$ be the ![]() $K$-algebra automorphism of
$K$-algebra automorphism of ![]() $A$ defined by
$A$ defined by ![]() $\unicode[STIX]{x1D719}_{u}(x_{i})=u^{a_{i}}x_{i}$ for
$\unicode[STIX]{x1D719}_{u}(x_{i})=u^{a_{i}}x_{i}$ for ![]() $i=1,\ldots ,d$. If
$i=1,\ldots ,d$. If ![]() $K$ is infinite, it is known that
$K$ is infinite, it is known that ![]() $I$ is a homogeneous ideal of
$I$ is a homogeneous ideal of ![]() $A$ if and only if
$A$ if and only if ![]() $\unicode[STIX]{x1D719}_{u}(I)=I$ for every
$\unicode[STIX]{x1D719}_{u}(I)=I$ for every ![]() $u\in K\setminus \{0\}$; see [Reference Matsumura5, Exercise 13.1] for a more general statement. With this automorphism, the argument detailed in [Reference Heinzer and Lantz2, Observation 3.3] shows that
$u\in K\setminus \{0\}$; see [Reference Matsumura5, Exercise 13.1] for a more general statement. With this automorphism, the argument detailed in [Reference Heinzer and Lantz2, Observation 3.3] shows that ![]() $\unicode[STIX]{x1D719}_{u}(I_{\{k\}})=I_{\{k\}}$ for every
$\unicode[STIX]{x1D719}_{u}(I_{\{k\}})=I_{\{k\}}$ for every ![]() $u\in K\setminus \{0\}$ and
$u\in K\setminus \{0\}$ and ![]() $k\geqslant 1$, and therefore the coefficient ideals
$k\geqslant 1$, and therefore the coefficient ideals ![]() $I_{\{k\}}$ are homogeneous for
$I_{\{k\}}$ are homogeneous for ![]() $k\geqslant 1$. For
$k\geqslant 1$. For ![]() $k=0$, it is also well known that the integral closure
$k=0$, it is also well known that the integral closure ![]() $\overline{I}=I_{\{0\}}$ is homogeneous.
$\overline{I}=I_{\{0\}}$ is homogeneous.
We now consider a homogeneous strongly Golod ideal ![]() $I$ in the polynomial ring
$I$ in the polynomial ring ![]() $A=K[x_{1},\ldots ,x_{d}]$ over a field
$A=K[x_{1},\ldots ,x_{d}]$ over a field ![]() $K$ of characteristic zero. Herzog and Huneke proved that the Ratliff–Rush ideal
$K$ of characteristic zero. Herzog and Huneke proved that the Ratliff–Rush ideal ![]() $\tilde{I}$ is strongly Golod [Reference Herzog and Huneke3, Proposition 2.12]. Moreover, we proved in Corollary 3.5 that the integral closure
$\tilde{I}$ is strongly Golod [Reference Herzog and Huneke3, Proposition 2.12]. Moreover, we proved in Corollary 3.5 that the integral closure ![]() $\overline{I}$ is also strongly Golod. Assuming that
$\overline{I}$ is also strongly Golod. Assuming that ![]() $I$ is
$I$ is ![]() $M$-primary, we prove that all the other coefficient ideals of
$M$-primary, we prove that all the other coefficient ideals of ![]() $I$ are strongly Golod as well, answering a question raised in [Reference De Stefani1, Question 5.9].
$I$ are strongly Golod as well, answering a question raised in [Reference De Stefani1, Question 5.9].
5.3. We first recall the following structure theorem for coefficient ideals [Reference Shah8, Theorem 2]. If ![]() $I$ is an ideal primary to the maximal ideal of a formally equidimensional local ring with infinite residue field and
$I$ is an ideal primary to the maximal ideal of a formally equidimensional local ring with infinite residue field and ![]() $1\leqslant k\leqslant d$, then
$1\leqslant k\leqslant d$, then
where the union is taken over all ![]() $n\geqslant 1$ and all length
$n\geqslant 1$ and all length ![]() $k$ sequences
$k$ sequences ![]() $a_{1},\ldots ,a_{k}$ extendable to some minimal reduction of
$a_{1},\ldots ,a_{k}$ extendable to some minimal reduction of ![]() $I^{n}$. Moreover, this union can be replaced by a single quotient ideal [Reference Shah8, Theorem 3], that is, there exist
$I^{n}$. Moreover, this union can be replaced by a single quotient ideal [Reference Shah8, Theorem 3], that is, there exist ![]() $m\geqslant 1$ and
$m\geqslant 1$ and ![]() $a_{1},\ldots ,a_{k}\in I^{m}$ extendable to some minimal reduction of
$a_{1},\ldots ,a_{k}\in I^{m}$ extendable to some minimal reduction of ![]() $I^{m}$ such that
$I^{m}$ such that
Note that this description is only valid for ![]() $k\geqslant 1$, hence excluding the integral closure of
$k\geqslant 1$, hence excluding the integral closure of ![]() $I$.
$I$.
In the polynomial setting with ![]() $I$ primary to the maximal homogeneous ideal
$I$ primary to the maximal homogeneous ideal ![]() $M$ of
$M$ of ![]() $A=K[x_{1},\ldots ,x_{d}]$, after localizing at
$A=K[x_{1},\ldots ,x_{d}]$, after localizing at ![]() $M$ as in Remark 5.1, this means that there exist
$M$ as in Remark 5.1, this means that there exist ![]() $m\geqslant 1$ and
$m\geqslant 1$ and ![]() $a_{1},\ldots ,a_{k}\in I^{m}$ extendable to some minimal reduction of
$a_{1},\ldots ,a_{k}\in I^{m}$ extendable to some minimal reduction of ![]() $I^{m}A_{M}$ such that (5.3.2) holds.
$I^{m}A_{M}$ such that (5.3.2) holds.
Theorem 5.4. Let ![]() $I$ be an
$I$ be an ![]() $M$-primary strongly Golod ideal of a polynomial ring
$M$-primary strongly Golod ideal of a polynomial ring ![]() $A=K[x_{1},\ldots ,x_{d}]$ over a field
$A=K[x_{1},\ldots ,x_{d}]$ over a field ![]() $K$ of characteristic zero. Then the coefficient ideals
$K$ of characteristic zero. Then the coefficient ideals ![]() $I_{\{k\}}$ are strongly Golod for all
$I_{\{k\}}$ are strongly Golod for all ![]() $k\in \{1,\ldots ,d\}$.
$k\in \{1,\ldots ,d\}$.
Proof. As in (5.3.2), choose ![]() $m\geqslant 1$ and
$m\geqslant 1$ and ![]() $a_{1},\ldots ,a_{k}\in I^{m}$ extendable to some minimal reduction
$a_{1},\ldots ,a_{k}\in I^{m}$ extendable to some minimal reduction ![]() $(a_{1},\ldots ,a_{k},a_{k+1},\ldots ,a_{d})$ of
$(a_{1},\ldots ,a_{k},a_{k+1},\ldots ,a_{d})$ of ![]() $I^{m}A_{M}$ such that
$I^{m}A_{M}$ such that ![]() $I_{\{k\}}=(I^{m+1}:(a_{1},\ldots ,a_{k}))$. Let
$I_{\{k\}}=(I^{m+1}:(a_{1},\ldots ,a_{k}))$. Let ![]() $f\in I_{\{k\}}$ and
$f\in I_{\{k\}}$ and ![]() $s\in \{1,\ldots ,k\}$. Since
$s\in \{1,\ldots ,k\}$. Since ![]() $fa_{s}\in I^{m+1}$, for every
$fa_{s}\in I^{m+1}$, for every ![]() $i\in \{1,\ldots ,d\}$ we have
$i\in \{1,\ldots ,d\}$ we have ![]() $\unicode[STIX]{x2202}_{i}(f)a_{s}+f\unicode[STIX]{x2202}_{i}(a_{s})\in I^{m}\unicode[STIX]{x2202}(I)$. However, since
$\unicode[STIX]{x2202}_{i}(f)a_{s}+f\unicode[STIX]{x2202}_{i}(a_{s})\in I^{m}\unicode[STIX]{x2202}(I)$. However, since ![]() $a_{s}\in I^{m}$, we have
$a_{s}\in I^{m}$, we have ![]() $\unicode[STIX]{x2202}_{i}(a_{s})\in I^{m-1}\unicode[STIX]{x2202}(I)$, and therefore
$\unicode[STIX]{x2202}_{i}(a_{s})\in I^{m-1}\unicode[STIX]{x2202}(I)$, and therefore ![]() $\unicode[STIX]{x2202}_{i}(f)a_{s}\in fI^{m-1}\unicode[STIX]{x2202}(I)+I^{m}\unicode[STIX]{x2202}(I)$. Since
$\unicode[STIX]{x2202}_{i}(f)a_{s}\in fI^{m-1}\unicode[STIX]{x2202}(I)+I^{m}\unicode[STIX]{x2202}(I)$. Since ![]() $fa_{s}\in I^{m+1}$ and
$fa_{s}\in I^{m+1}$ and ![]() $a_{s}\in I^{m}$ we then obtain
$a_{s}\in I^{m}$ we then obtain ![]() $\unicode[STIX]{x2202}_{i}(f)a_{s}^{2}\in I^{2m}\unicode[STIX]{x2202}(I)+a_{s}I^{m}\unicode[STIX]{x2202}(I)\subseteq I^{2m}\unicode[STIX]{x2202}(I)$. This holds for every
$\unicode[STIX]{x2202}_{i}(f)a_{s}^{2}\in I^{2m}\unicode[STIX]{x2202}(I)+a_{s}I^{m}\unicode[STIX]{x2202}(I)\subseteq I^{2m}\unicode[STIX]{x2202}(I)$. This holds for every ![]() $f\in I_{\{k\}}$ and all
$f\in I_{\{k\}}$ and all ![]() $i=1,\ldots ,d$, and therefore
$i=1,\ldots ,d$, and therefore ![]() $\unicode[STIX]{x2202}(I_{\{k\}})a_{s}^{2}\subseteq I^{2m}\unicode[STIX]{x2202}(I).$ Since
$\unicode[STIX]{x2202}(I_{\{k\}})a_{s}^{2}\subseteq I^{2m}\unicode[STIX]{x2202}(I).$ Since ![]() $I$ is strongly Golod, this implies that
$I$ is strongly Golod, this implies that
As this holds for all ![]() $s\in \{1,\ldots ,k\}$, we get
$s\in \{1,\ldots ,k\}$, we get
Finally, ![]() $a_{1}^{4},\ldots ,a_{k}^{4}$ is part of the minimal reduction (
$a_{1}^{4},\ldots ,a_{k}^{4}$ is part of the minimal reduction (![]() $a_{1}^{4},\ldots ,a_{k}^{4}$,
$a_{1}^{4},\ldots ,a_{k}^{4}$, ![]() $a_{k+1}^{4},\ldots ,a_{d}^{4}$) of
$a_{k+1}^{4},\ldots ,a_{d}^{4}$) of ![]() $I^{4m}A_{M}$, and from (5.3.1) it follows that
$I^{4m}A_{M}$, and from (5.3.1) it follows that ![]() $\unicode[STIX]{x2202}(I_{\{k\}})^{2}\subseteq (IA_{M})_{\{k\}}\cap A=I_{\{k\}}$, and therefore
$\unicode[STIX]{x2202}(I_{\{k\}})^{2}\subseteq (IA_{M})_{\{k\}}\cap A=I_{\{k\}}$, and therefore ![]() $I_{\{k\}}$ is strongly Golod.◻
$I_{\{k\}}$ is strongly Golod.◻