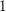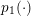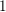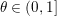1 Introduction
Let 
$\mathbf{R}^{N}$ denote the 
$N$-dimensional Euclidean space. We denote by 
$B(x,r)$ the open ball centered at 
$x$ of radius 
$r$. For a locally integrable function 
$f$ on an open set 
$G\subset \mathbf{R}^{N}$, we consider the maximal function
$$\begin{eqnarray}Mf(x)=\sup _{r>0}\frac{1}{|B(x,r)|}\int _{G\cap B(x,r)}|f(y)|\,dy.\end{eqnarray}$$ Following Kováčik and Rákosník [Reference Kováčik and Rákosník19], we consider a positive continuous function 
$p_{1}(\cdot )$ on 
$\mathbf{B}=B(0,1)$ and a measurable function 
$f$ satisfying
$$\begin{eqnarray}\int _{\mathbf{B}}|f(y)|^{p_{1}(y)}dy<\infty .\end{eqnarray}$$ In this paper we are concerned with 
$p_{1}(\cdot )$ such that
$$\begin{eqnarray}p_{1}(x)=1+\frac{a}{\log (e+1/|x|)}+\frac{b\log (\log (e+1/|x|))}{\log (e+1/|x|)}\end{eqnarray}$$ for 
$x\in \mathbf{B}$, where 
$a\geqslant 0$ and 
$b\geqslant 0$.
Cruz-Uribe et al. [Reference Cruz-Uribe, Fiorenza and Neugebauer8] proved the maximal operator 
$M$ is not bounded on 
$L^{p(\cdot )}(G)$ if 
$\inf _{G}p(x)=1$, where 
$G$ is a bounded set. Hästö [Reference Hästö17] proved that the maximal operator 
$M$ is bounded from 
$L^{p(\cdot )}(G)$ with variable exponent approaching 
$1$ to 
$L^{1}(G)$ when 
$G$ satisfies a certain regular condition. As an extension of Hästö [Reference Hästö17], Futamura and Mizuta [Reference Futamura and Mizuta13] proved the following:
Theorem A. Let 
$p_{1}(\cdot )$ be as in (1.1). If 
$b\geqslant 1/N$, then there exists a constant 
$C>0$ such that
$$\begin{eqnarray}\int _{\mathbf{B}}Mf(x)\,dx<\infty\end{eqnarray}$$ for all 
$f\in L^{p_{1}(\cdot )}(\mathbf{B})$.
We also refer to [Reference Mizuta, Ohno and Shimomura23, Reference Mizuta, Ohno and Shimomura24] for integrability of maximal functions for generalized Lebesgue spaces with variable exponent approaching 
$1$.
For 
$0<\unicode[STIX]{x1D6FC}<N$, we define the Riesz potential of order 
$\unicode[STIX]{x1D6FC}$ of a locally integrable function 
$f$ on an open set 
$G\subset \mathbf{R}^{N}$ by
$$\begin{eqnarray}I_{\unicode[STIX]{x1D6FC}}f(x)=\int _{G}|x-y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy.\end{eqnarray}$$ Our first aim in this paper is to deal with integrability of 
$I_{\unicode[STIX]{x1D6FC}}f$ for generalized Lebesgue spaces 
$L^{p_{1}(\cdot )}(\mathbf{B})$ on the unit ball with variable exponent approaching 
$1$ (Theorem 3.2). To do so, we use the boundedness of the maximal operator (Lemma 2.4). The sharpness of Theorem 3.2 will be discussed in Remarks 3.3 and 3.4.
Regarding regularity theory of differential equations, Baroni et al. [Reference Baroni, Colombo and Mingione3, Reference Colombo and Mingione9] studied a double phase functional
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(x,t)=t^{p}+a(x)t^{q},\quad x\in \mathbf{R}^{N},t\geqslant 0,\end{eqnarray}$$ where 
$1<p<q$, 
$a(\cdot )$ is nonnegative, bounded and Hölder continuous of order 
$\unicode[STIX]{x1D703}\in (0,1]$ (see also [Reference Esposito, Leonetti and Mingione11, Reference Fonseca, Malý and Mingione12]). In [Reference Colombo and Mingione9], Colombo and Mingione showed the boundedness of the maximal operator on 
$L^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FA})$ when 
$\unicode[STIX]{x1D6F7}(x,t)=t^{p}+a(x)t^{q}$, 
$q>p>1$, 
$\unicode[STIX]{x1D6FA}\subset \mathbf{R}^{N}$ is bounded, 
$a\in C^{\unicode[STIX]{x1D703}}(\bar{\unicode[STIX]{x1D6FA}})$ is nonnegative and 
$q<(1+\unicode[STIX]{x1D703}/N)p$. Further, in [Reference Hästö18], Hästö showed the boundedness of the maximal operator on 
$L^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FA})$ in case 
$q\leqslant (1+\unicode[STIX]{x1D703}/N)p$.
As an application of integrability of 
$I_{\unicode[STIX]{x1D6FC}}f$ (Theorem 3.2), we shall study integrability of maximal functions for the double phase functional given by
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{d}(x,t)=t^{p_{1}(x)}+a(x)t^{p_{2}} & & \displaystyle \nonumber\end{eqnarray}$$ for 
$x\in \mathbf{B}$ and 
$t\geqslant 0$, where 
$a(x)^{1/p_{2}}$ is nonnegative, bounded and Hölder continuous of order 
$\unicode[STIX]{x1D703}\in (0,1]$ and 
$1/p_{2}=1-\unicode[STIX]{x1D703}/N>0$ (Theorem 3.7). In fact, we shall give 
$\Vert Mf\Vert _{L^{\unicode[STIX]{x1D6F7}_{1,d}}(\mathbf{B})}\leqslant C\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})}$. Our result extends Theorem A and [Reference Hästö18, Theorem 4.7]. See also [Reference Colasuonno and Squassina7, Reference Harjulehto, Hästö and Karppinen16]. For the sharpness of Theorem 3.7, see Remark 3.8. We also discuss integrability of 
$I_{\unicode[STIX]{x1D6FC}}f$ for the double phase functional 
$\unicode[STIX]{x1D6F7}_{d}$ (Theorem 3.11). In fact, we shall show 
$\Vert I_{\unicode[STIX]{x1D6FC}}f\Vert _{L^{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC},d}}(\mathbf{B})}\leqslant C\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})}$. See Section 3 for the definitions of 
$\unicode[STIX]{x1D6F7}_{1,d}$ and 
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC},d}$.
Let 
$A(r)\,=\,\mathbf{B}\,\cap \,[B(0,2r)\setminus B(0,r)]$ and let 
$\unicode[STIX]{x1D714}(r):(0,\infty )\,\rightarrow \,(0,\infty )$ be almost monotone on 
$(0,\infty )$ satisfying the doubling condition. For 
$0\,<\,q\,\leqslant \,\infty$, we define Herz–Morrey spaces 
${\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D714}}(\mathbf{B})$ of all measurable functions 
$f$ on the unit ball 
$\mathbf{B}$ such that
$$\begin{eqnarray}\Vert f\Vert _{{\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D714}}(\mathbf{B})}=\left(\int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(r))}\right)^{q}\,\frac{dr}{r}\right)^{1/q}<\infty\end{eqnarray}$$ when 
$q<\infty$ and
$$\begin{eqnarray}\Vert f\Vert _{{\mathcal{H}}^{p_{1}(\cdot ),\infty ,\unicode[STIX]{x1D714}}(\mathbf{B})}=\sup _{0<r<1}~\unicode[STIX]{x1D714}(r)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(r))}<\infty\end{eqnarray}$$ when 
$q=\infty$. In [Reference Mizuta and Ohno21, Reference Mizuta and Ohno22], the boundedness of the maximal and Riesz potential operators were studied for Herz–Morrey spaces with variable exponents in a way different from Almeida and Drihem [Reference Almeida and Drihem2]. See also Samko [Reference Samko26]. There are several Morrey type spaces related to our nonhomogeneous central Morrey type spaces; for example, Morrey spaces by Adams and Xiao [Reference Adams and Xiao1], local Morrey type spaces by Burenkov et al. [Reference Burenkov, Gogatishvili, Guliyev and Mustafayev4–Reference Burenkov and Guliyev6, Reference Guliyev, Hasanov and Samko14, Reference Guliyev, Hasanov and Sawano15].
Next we deal with integrability of maximal functions for Herz–Morrey spaces 
${\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D714}}(\mathbf{B})$ on the unit ball with variable exponent approaching 
$1$ (Theorem 4.4), as an extension of Theorem A and [Reference Hästö18, Theorem 4.7]. The sharpness of Theorem 4.4 will be discussed in Remark 4.8. We also establish norm inequalities for the Riesz potential operator 
$f\rightarrow I_{\unicode[STIX]{x1D6FC}}f$ from 
${\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D714}}(\mathbf{B})$ to the Herz–Morrey–Orlicz space 
${\mathcal{H}}^{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}},q,\unicode[STIX]{x1D714}}(\mathbf{B})$ (Theorem 4.14). See Section 3 for the definition of 
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}$.
Our final goal is to study norm inequalities for the maximal operator in the frame of double phase functionals, as well as the Riesz potential operators (see Theorems 4.12 and 4.15).
Throughout this paper, let 
$C$ denote various constants independent of the variables in question. The symbol 
$g\sim h$ means that 
$C^{-1}h\leqslant g\leqslant Ch$ for some constant 
$C>0$.
2 Integrability of maximal functions
For a positive continuous nonincreasing function 
$k$ on 
$(0,\infty )$, assume that there exists a constant 
$\unicode[STIX]{x1D700}_{0}>0$ such that:
- (k1)
$(\log (e+1/r))^{-\unicode[STIX]{x1D700}_{0}}k(r)$ is nondecreasing on $(0,1)$;- (k2)
- $k(1)\geqslant e^{\unicode[STIX]{x1D700}_{0}}$.
By (k1), we see that
$$\begin{eqnarray}k(r)\leqslant k(r^{2})\leqslant Ck(r)\quad \text{whenever }0<r<1,\end{eqnarray}$$ which implies the doubling condition on 
$k$, that is, there exists a constant 
$C\geqslant 1$ such that 
$k(r)\leqslant Ck(2r)$ for all 
$0<r<1$. Further, (k1) and (k2) imply that 
$\log k(r)/(\log (e+1/r))$ is nondecreasing on 
$(0,1)$ [Reference Mizuta, Ohno and Shimomura23, Lemma 2.1].
Our typical example of 
$k$ is
$$\begin{eqnarray}k(r)=a(\log (e+1/r))^{b}\end{eqnarray}$$ for 
$0<r<1$, where 
$a\geqslant e^{b}(\log (e+1))^{-b}$ and 
$b>0$.
Lemma 2.1. (Cf. [Reference Mizuta and Shimomura25, Lemmas 2.1 and 2.2])
(1) For
$a>0$, there exists a constant $C\geqslant 1$ such that for all$$\begin{eqnarray}C^{-1}k(r)\leqslant k(r^{a})\leqslant Ck(r)\end{eqnarray}$$$0<r<1$.(2) For
$b>0$, there exists a constant $C\geqslant 1$ such that for all$$\begin{eqnarray}r_{1}^{b}k(r_{1})\leqslant Cr_{2}^{b}k(r_{2})\end{eqnarray}$$$0<r_{1}<r_{2}<1$.
We consider a positive convex function 
$\unicode[STIX]{x1D6F7}$ on 
$(0,\infty )$ satisfying:
- $(\unicode[STIX]{x1D6F7}0)$
- $\unicode[STIX]{x1D6F7}(0)=\lim _{r\rightarrow 0}\unicode[STIX]{x1D6F7}(r)=0$;
- $(\unicode[STIX]{x1D6F7}1)$
- $\unicode[STIX]{x1D6F7}$ is doubling on $(0,\infty )$; namely there exists a constant $C\geqslant 1$ such that $$\begin{eqnarray}\unicode[STIX]{x1D6F7}(2r)\leqslant C\unicode[STIX]{x1D6F7}(r)\quad \text{for all }r>0.\end{eqnarray}$$
For an open set 
$G\subset \mathbf{R}^{N}$ and 
$f\in L_{\text{loc}}^{1}(G)$, we define the norm
$$\begin{eqnarray}\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}}(G)}=\inf \left\{\unicode[STIX]{x1D706}>0:\int _{G}\unicode[STIX]{x1D6F7}\left(\frac{|f(y)|}{\unicode[STIX]{x1D706}}\right)\,dy\leqslant 1\right\}.\end{eqnarray}$$ For a locally integrable function 
$f$ on 
$\mathbf{B}$, we consider the maximal function
$$\begin{eqnarray}Mf(x)=\sup _{r>0}\frac{1}{|B(x,r)|}\int _{\mathbf{B}\cap B(x,r)}|f(y)|\,dy.\end{eqnarray}$$The following lemma is an extension of Stein [Reference Stein27].
Lemma 2.2. (Cf. [Reference Mizuta, Ohno and Shimomura23, Theorem 3.1])
Let 
$\unicode[STIX]{x1D6F7}\in C^{1}((0,\infty ))$ be a nondecreasing positive function on 
$(0,\infty )$ satisfying 
$(\unicode[STIX]{x1D6F7}0)$, 
$(\unicode[STIX]{x1D6F7}1)$ and
- $(\unicode[STIX]{x1D6F7};k)$
there exists a constant
$C>0$ such that $$\begin{eqnarray}\int _{1}^{t}\frac{\unicode[STIX]{x1D6F7}^{\prime }(s)}{s}\,ds\leqslant Ck(t^{-1})\end{eqnarray}$$for all
$t>1$.
If 
$f$ is a locally integrable function on 
$\mathbf{B}$ such that
$$\begin{eqnarray}\int _{\mathbf{B}}|f(x)|k(|f(x)|^{-1})\,dx\leqslant 1,\end{eqnarray}$$ then there exists a constant 
$C>0$ such that
$$\begin{eqnarray}\int _{\mathbf{B}}\unicode[STIX]{x1D6F7}(Mf(x))\,dx\leqslant C.\end{eqnarray}$$ Consider a function 
$p_{1}(\cdot )$ such that 
$p_{1}(0)=1$ and
$$\begin{eqnarray}p_{1}(x)=1+\frac{\log k(|x|)}{\log (e+1/|x|)}\end{eqnarray}$$ for 
$x\in \mathbf{B}\setminus \{0\}$. Here note that 
$\lim _{|x|\rightarrow 0}p_{1}(x)=p_{1}(0)$. For an open set
$G\subset \mathbf{R}^{N}$, we define the 
$L^{p_{1}(\cdot )}$-norm of a function 
$f\in L_{\text{loc}}^{1}(G)$ by
$$\begin{eqnarray}\Vert f\Vert _{L^{p_{1}(\cdot )}(G)}=\inf \left\{\unicode[STIX]{x1D706}>0:\int _{G}\left(\frac{|f(y)|}{\unicode[STIX]{x1D706}}\right)^{p_{1}(y)}\,dy\leqslant 1\right\};\end{eqnarray}$$see [Reference Diening, Harjulehto, Hästö and Růžička10].
In view of [Reference Mizuta, Ohno and Shimomura23, Lemma 2.4], we know the following result.
Lemma 2.3. Let 
$f$ be a measurable function on 
$\mathbf{B}$ with 
$\Vert f\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})}\leqslant 1$. Then there exists a constant 
$C>0$ such that
$$\begin{eqnarray}\int _{\mathbf{B}}|f(x)|k(|f(x)|^{-1})^{N}\,dx\leqslant C.\end{eqnarray}$$By Lemmas 2.2 and 2.3, we have the following result.
Lemma 2.4. Let 
$\unicode[STIX]{x1D6F7}\in C^{1}((0,\infty ))$ be a positive convex function on 
$(0,\infty )$ satisfying 
$(\unicode[STIX]{x1D6F7}0)$, 
$(\unicode[STIX]{x1D6F7}1)$ and 
$(\unicode[STIX]{x1D6F7};k^{N})$. Then there exists a constant 
$C>0$ such that
$$\begin{eqnarray}\Vert Mf\Vert _{L^{\unicode[STIX]{x1D6F7}}(\mathbf{B})}\leqslant C\Vert f\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})}\end{eqnarray}$$ for all 
$f\in L^{p_{1}(\cdot )}(\mathbf{B})$.
3 Integrability of Riesz potentials
For 
$0<\unicode[STIX]{x1D6FC}<N$, we define the Riesz potential of order 
$\unicode[STIX]{x1D6FC}$ of a locally integrable function 
$f$ on 
$\mathbf{B}$ by
$$\begin{eqnarray}I_{\unicode[STIX]{x1D6FC}}f(x)=\int _{\mathbf{B}}|x-y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy.\end{eqnarray}$$Lemma 3.1. There is a constant 
$C>0$ such that
$$\begin{eqnarray}\int _{B(x,r)}|f(y)|\,dy\leqslant Ck(r)^{-N}\Vert f\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})}\end{eqnarray}$$ for all 
$x\in \mathbf{B}$, 
$0<r<1$ and 
$f\in L^{p_{1}(\cdot )}(\mathbf{B})$.
Proof. Let 
$x\in \mathbf{B}$ and 
$0<r<1$. Let 
$f$ be a measurable function on 
$\mathbf{B}$ satisfying 
$\Vert f\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})}\leqslant 1$. We find by Lemmas 2.1 and 2.3
$$\begin{eqnarray}\displaystyle \int _{B(x,r)}|f(y)|\,dy & {\leqslant} & \displaystyle Cr^{N}\left(rk(r)\right)^{-N}+\int _{B(x,r)}|f(y)|\left(\frac{k(|f(y)|^{-1})}{k\left(\left(rk(r)\right)^{N}\right)}\right)^{N}\,dy\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\left\{k(r)^{-N}+k(r)^{-N}\int _{\mathbf{B}}|f(y)|k(|f(y)|^{-1})^{N}\,dy\right\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle Ck(r)^{-N},\nonumber\end{eqnarray}$$which proves the result. ◻
In what follows, let us assume that 
$\unicode[STIX]{x1D6F7}$ is a positive convex function in 
$C^{1}((0,\infty ))$ satisfying 
$(\unicode[STIX]{x1D6F7}0)$, 
$(\unicode[STIX]{x1D6F7}1)$ and 
$(\unicode[STIX]{x1D6F7};k^{N})$ when it is not specially mentioned. Set
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}(t)=\unicode[STIX]{x1D6F7}\left(\left(tk(t^{-1})^{\unicode[STIX]{x1D6FC}}\right)^{N/(N-\unicode[STIX]{x1D6FC})}\right).\end{eqnarray}$$Theorem 3.2. There exists a constant 
$C>0$ such that
$$\begin{eqnarray}\int _{\mathbf{B}}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}(|I_{\unicode[STIX]{x1D6FC}}f(x)|)\,dx\leqslant C\end{eqnarray}$$ for all measurable functions 
$f$ on 
$\mathbf{B}$ such that 
$\Vert f\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})}\leqslant 1$.
Proof. Let 
$f$ be a measurable function on 
$\mathbf{B}$ such that 
$\Vert f\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})}\leqslant 1$. For 
$x\in \mathbf{B}$ and 
$0<r\leqslant 1$, write
$$\begin{eqnarray}\displaystyle I_{\unicode[STIX]{x1D6FC}}f(x) & = & \displaystyle \int _{B(x,r)}|x-y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy+\int _{\mathbf{B}\setminus B(x,r)}|x-y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy\nonumber\\ \displaystyle & = & \displaystyle I_{1}(x)+I_{2}(x).\nonumber\end{eqnarray}$$Then note that
$$\begin{eqnarray}\displaystyle |I_{1}(x)|\leqslant Cr^{\unicode[STIX]{x1D6FC}}Mf(x). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |I_{2}(x)| & {\leqslant} & \displaystyle C\int _{r}^{2}\left(\int _{B(x,t)}|f(y)|\,dy\right)t^{\unicode[STIX]{x1D6FC}-N}\,\frac{dt}{t}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\int _{r}^{2}t^{\unicode[STIX]{x1D6FC}-N}k(t)^{-N}\,\frac{dt}{t}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle Cr^{\unicode[STIX]{x1D6FC}-N}k(r)^{-N}.\nonumber\end{eqnarray}$$Now we establish
$$\begin{eqnarray}\displaystyle |I_{\unicode[STIX]{x1D6FC}}f(x)|\leqslant C\left\{r^{\unicode[STIX]{x1D6FC}}Mf(x)+r^{\unicode[STIX]{x1D6FC}-N}k(r)^{-N}\right\}. & & \displaystyle \nonumber\end{eqnarray}$$ If 
$Mf(x)\leqslant 1$, then, taking 
$r=1$, we have
$$\begin{eqnarray}|I_{\unicode[STIX]{x1D6FC}}f(x)|\leqslant C.\end{eqnarray}$$ Next consider the case 
$Mf(x)>1$. Since 
$\sup _{t>1}t^{-1/N}k(t^{-1})^{-1}\leqslant c_{1}$ for some constant 
$c_{1}>0$, taking 
$r=c_{1}^{-1}Mf(x)^{-1/N}k(Mf(x)^{-1})^{-1}\leqslant 1$, we find
$$\begin{eqnarray}\displaystyle |I_{\unicode[STIX]{x1D6FC}}f(x)|\leqslant CMf(x)^{1-\unicode[STIX]{x1D6FC}/N}k(Mf(x)^{-1})^{-\unicode[STIX]{x1D6FC}}. & & \displaystyle \nonumber\end{eqnarray}$$Therefore we obtain
$$\begin{eqnarray}\displaystyle \left(|I_{\unicode[STIX]{x1D6FC}}f(x)|k(|I_{\unicode[STIX]{x1D6FC}}f(x)|^{-1})^{\unicode[STIX]{x1D6FC}}\right)^{N/(N-\unicode[STIX]{x1D6FC})}\leqslant C\left\{Mf(x)+1\right\}. & & \displaystyle \nonumber\end{eqnarray}$$ In view of 
$(\unicode[STIX]{x1D6F7}1)$ and Lemma 2.4, we have
$$\begin{eqnarray}\displaystyle \int _{\mathbf{B}}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}(|I_{\unicode[STIX]{x1D6FC}}f(x)|)\,dx\leqslant C\left\{\int _{\mathbf{B}}\unicode[STIX]{x1D6F7}(Mf(x))\,dx+1\right\}\leqslant C, & & \displaystyle \nonumber\end{eqnarray}$$which proves the result. ◻
Remark 3.3. For 
$\unicode[STIX]{x1D6FD}<-1$, consider the function
$$\begin{eqnarray}f(y)=|y|^{-N}(\log (e+1/|y|))^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D712}_{\boldsymbol{ B}}(y),\end{eqnarray}$$ where 
$\unicode[STIX]{x1D712}_{E}$ the characteristic function of a measurable set 
$E\subset \mathbf{R}^{N}$. Then we have the following:
(1) there exists a constant
$C>0$ such that $$\begin{eqnarray}\int _{\mathbf{B}}f(y)\,dy\leqslant C;\end{eqnarray}$$(2) there exists a constant
$C>0$ such that for all$$\begin{eqnarray}Mf(x)\geqslant C|x|^{-N}(\log (e+1/|x|))^{\unicode[STIX]{x1D6FD}+1}\end{eqnarray}$$$x\in \mathbf{B}$;(3) there exists a constant
$C>0$ such that for all$$\begin{eqnarray}I_{\unicode[STIX]{x1D6FC}}f(x)\geqslant C|x|^{\unicode[STIX]{x1D6FC}-N}(\log (e+1/|x|))^{\unicode[STIX]{x1D6FD}+1}\end{eqnarray}$$$x\in \mathbf{B}$.
Let 
$\unicode[STIX]{x1D6FE}>-1$. If 
$-\unicode[STIX]{x1D6FE}-2<\unicode[STIX]{x1D6FD}<-1$, then (2) implies
$$\begin{eqnarray}Mf(x)(\log (e+Mf(x)))^{\unicode[STIX]{x1D6FE}}\geqslant C|x|^{-N}(\log (e+1/|x|))^{\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}+1}\quad \text{for }x\in \mathbf{B},\end{eqnarray}$$so that
$$\begin{eqnarray}\int _{\mathbf{B}}Mf(x)(\log (e+Mf(x)))^{\unicode[STIX]{x1D6FE}}\,dx=\infty .\end{eqnarray}$$ Thus the maximal operator 
$M:f\mapsto Mf$ is not bounded from 
$L^{1}(\mathbf{B})$ to 
$L^{\widetilde{\unicode[STIX]{x1D6F7}}}(\mathbf{B})$, where 
$\widetilde{\unicode[STIX]{x1D6F7}}(t)=t(\log (e+t))^{\unicode[STIX]{x1D6FE}}$ with 
$\unicode[STIX]{x1D6FE}>-1$.
If 
$-(\unicode[STIX]{x1D6FE}+1)(N-\unicode[STIX]{x1D6FC})/N-1<\unicode[STIX]{x1D6FD}<-1$, then (3) implies
$$\begin{eqnarray}I_{\unicode[STIX]{x1D6FC}}f(x)^{N/(N-\unicode[STIX]{x1D6FC})}(\log (e+I_{\unicode[STIX]{x1D6FC}}f(x)))^{\unicode[STIX]{x1D6FE}}\geqslant C|x|^{-N}(\log (e+1/|x|))^{(\unicode[STIX]{x1D6FD}+1)N/(N-\unicode[STIX]{x1D6FC})+\unicode[STIX]{x1D6FE}}\end{eqnarray}$$ for 
$x\in \mathbf{B}$, so that
$$\begin{eqnarray}\int _{\mathbf{B}}I_{\unicode[STIX]{x1D6FC}}f(x)^{N/(N-\unicode[STIX]{x1D6FC})}(\log (e+I_{\unicode[STIX]{x1D6FC}}f(x)))^{\unicode[STIX]{x1D6FE}}\,dx=\infty .\end{eqnarray}$$ Thus the Riesz potential operator 
$I_{\unicode[STIX]{x1D6FC}}:f\mapsto I_{\unicode[STIX]{x1D6FC}}f$ is not bounded from 
$L^{1}(\mathbf{B})$ to 
$L^{\widetilde{\unicode[STIX]{x1D6F9}}_{\unicode[STIX]{x1D6FC}}}(\mathbf{B})$, where 
$\widetilde{\unicode[STIX]{x1D6F9}}_{\unicode[STIX]{x1D6FC}}(t)=t^{N/(N-\unicode[STIX]{x1D6FC})}(\log (e+t))^{\unicode[STIX]{x1D6FE}}$ with 
$\unicode[STIX]{x1D6FE}>-1$.
Remark 3.4. Let 
$k(r)=a(\log (e+1/r))^{b}$ with 
$a\geqslant e^{b}(\log (e+1))^{-b}$ and 
$b\geqslant 1/N$. Then
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(r)=r(\log (e+r))^{bN-1}\end{eqnarray}$$ satisfies 
$(\unicode[STIX]{x1D6F7};k^{N})$ and
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}(r)\sim r^{N/(N-\unicode[STIX]{x1D6FC})}(\log (e+r))^{b\unicode[STIX]{x1D6FC}N/(N-\unicode[STIX]{x1D6FC})+bN-1}\end{eqnarray}$$ for 
$0<r<1$. Then Lemma 2.2 and Theorem 3.2 hold for the above 
$\unicode[STIX]{x1D6F7}$ and 
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}$.
Consider the function
$$\begin{eqnarray}f(y)=|y|^{-N}(\log (e+1/|y|))^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D712}_{\boldsymbol{ B}}(y).\end{eqnarray}$$Then we have the following:
(1) if
$\unicode[STIX]{x1D6FD}+bN+1<0$, then there exists a constant $C>0$ such that $$\begin{eqnarray}\int _{\mathbf{B}}f(y)^{p_{1}(y)}\,dy\leqslant C;\end{eqnarray}$$(2) if
$\unicode[STIX]{x1D6FD}+1<0$, then there exists a constant $C>0$ such that for all$$\begin{eqnarray}Mf(x)\geqslant C|x|^{-N}(\log (e+1/|x|))^{\unicode[STIX]{x1D6FD}+1}\end{eqnarray}$$$x\in \mathbf{B}$;(3) if
$\unicode[STIX]{x1D6FD}+1<0$, then there exists a constant $C>0$ such that for all$$\begin{eqnarray}I_{\unicode[STIX]{x1D6FC}}f(x)\geqslant C|x|^{\unicode[STIX]{x1D6FC}-N}(\log (e+1/|x|))^{\unicode[STIX]{x1D6FD}+1}\end{eqnarray}$$$x\in \mathbf{B}$.
Hence, for 
$\unicode[STIX]{x1D6FD}=-b^{\prime }N-1$ and 
$b^{\prime }>b$, (2) implies
$$\begin{eqnarray}Mf(x)(\log (e+Mf(x)))^{b^{\prime }N-1}\geqslant C|x|^{-N}(\log (e+1/|x|))^{\unicode[STIX]{x1D6FD}+b^{\prime }N}\quad \text{for }x\in \mathbf{B},\end{eqnarray}$$so that
$$\begin{eqnarray}\int _{\mathbf{B}}Mf(x)(\log (e+Mf(x)))^{b^{\prime }N-1}\,dx=\infty .\end{eqnarray}$$ For 
$\unicode[STIX]{x1D6FD}=-bN-\unicode[STIX]{x1D6FC}(b^{\prime }-b)-1$ and 
$b^{\prime }>b$, (3) implies
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(I_{\unicode[STIX]{x1D6FC}}f(x)(\log (e+I_{\unicode[STIX]{x1D6FC}}f(x)))^{\unicode[STIX]{x1D6FC}b^{\prime }}\right)^{N/(N-\unicode[STIX]{x1D6FC})}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \,C|x|^{-N}(\log (e+1/|x|))^{(\unicode[STIX]{x1D6FD}+1+\unicode[STIX]{x1D6FC}b^{\prime })N/(N-\unicode[STIX]{x1D6FC})}\nonumber\end{eqnarray}$$ for 
$x\in \mathbf{B}$, so that
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbf{B}}\unicode[STIX]{x1D6F7}\left(\left(I_{\unicode[STIX]{x1D6FC}}f(x)(\log (e+I_{\unicode[STIX]{x1D6FC}}f(x)))^{\unicode[STIX]{x1D6FC}b^{\prime }}\right)^{N/(N-\unicode[STIX]{x1D6FC})}\right)\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \,C\int _{\mathbf{B}}|x|^{-N}(\log (e+1/|x|))^{-1}\,dx=\infty .\nonumber\end{eqnarray}$$ Thus the exponents of the log terms of 
$\unicode[STIX]{x1D6F7}$ and 
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}$ are sharp.
Let us consider a double phase functional given by
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{d}(x,t)=t^{p_{1}(x)}+a(x)t^{p_{2}}=t^{p_{1}(x)}+(b(x)t)^{p_{2}} & & \displaystyle \nonumber\end{eqnarray}$$ for 
$x\in \mathbf{B}$ and 
$t\geqslant 0$, where:
∙
$b(x)$ is nonnegative, bounded and Hölder continuous of order $\unicode[STIX]{x1D703}\in (0,1]$;∙
$1/p_{2}=1-\unicode[STIX]{x1D703}/N>0$;∙
$b(x)=a(x)^{1/p_{2}}$;
(cf. [Reference Colombo and Mingione9, Reference Hästö18]). For an open set 
$G\subset \mathbf{R}^{N}$ and 
$f\in L_{\text{loc}}^{1}(G)$, we define the norm
$$\begin{eqnarray}\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(G)}=\inf \left\{\unicode[STIX]{x1D706}>0:\int _{G}\unicode[STIX]{x1D6F7}_{d}\left(y,\frac{|f(y)|}{\unicode[STIX]{x1D706}}\right)\,dy\leqslant 1\right\}.\end{eqnarray}$$ For a locally integrable function 
$f$ on 
$\mathbf{B}$ and 
$0\leqslant \unicode[STIX]{x1D70E}<N$, we consider the fractional maximal function
$$\begin{eqnarray}M_{\unicode[STIX]{x1D70E}}f(x)=\sup _{r>0}\frac{r^{\unicode[STIX]{x1D70E}}}{|B(x,r)|}\int _{\mathbf{B}\cap B(x,r)}|f(y)|\,dy.\end{eqnarray}$$In view of Theorem 3.2 we find the following:
Lemma 3.5. There exists a constant 
$C>0$ such that
$$\begin{eqnarray}\displaystyle \Vert M_{\unicode[STIX]{x1D703}}f\Vert _{L^{p_{2}}(\mathbf{B})}\leqslant C\Vert f\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})} & & \displaystyle \nonumber\end{eqnarray}$$ for all 
$f\in L^{p_{1}(\cdot )}(\mathbf{B})$.
In fact, it suffices to note
$$\begin{eqnarray}M_{\unicode[STIX]{x1D703}}f(x)\leqslant C(I_{\unicode[STIX]{x1D703}}|f|)(x)\end{eqnarray}$$and
$$\begin{eqnarray}t^{p_{2}}\leqslant C\left(tk(t^{-1})^{\unicode[STIX]{x1D703}}\right)^{p_{2}}\leqslant C\unicode[STIX]{x1D6F7}\left(\left(tk(t^{-1})^{\unicode[STIX]{x1D703}}\right)^{N/(N-\unicode[STIX]{x1D703})}\right)=C\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D703}}(t)\end{eqnarray}$$ for all 
$t\geqslant 1$. Now we apply Theorem 3.2.
Lemma 3.6. There exists a constant 
$C>0$ such that
$$\begin{eqnarray}\displaystyle \Vert bMf\Vert _{L^{p_{2}}(\mathbf{B})}\leqslant C\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})} & & \displaystyle \nonumber\end{eqnarray}$$ for all 
$f\in L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})$.
Proof. Let 
$f\in L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})$. Note that
$$\begin{eqnarray}\displaystyle & & \displaystyle b(x)\frac{1}{|B(x,r)|}\int _{B(x,r)}|f(y)|\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{|B(x,r)|}\int _{B(x,r)}[b(x)-b(y)]|f(y)|\,dy+\frac{1}{|B(x,r)|}\int _{B(x,r)}b(y)|f(y)|\,dy\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,Cr^{\unicode[STIX]{x1D703}}\frac{1}{|B(x,r)|}\int _{B(x,r)}|f(y)|\,dy+\frac{1}{|B(x,r)|}\int _{B(x,r)}b(y)|f(y)|\,dy,\nonumber\end{eqnarray}$$so that
$$\begin{eqnarray}b(x)Mf(x)\leqslant CM_{\unicode[STIX]{x1D703}}f(x)+M[bf](x).\end{eqnarray}$$ Hence, by Lemma 3.5 and the boundedness of maximal operator on 
$L^{p_{2}}(\mathbf{B})$, we give
$$\begin{eqnarray}\displaystyle \Vert bMf\Vert _{L^{p_{2}}(\mathbf{B})} & {\leqslant} & \displaystyle C\{\Vert M_{\unicode[STIX]{x1D703}}f\Vert _{L^{p_{2}}(\mathbf{B})}+\Vert M[bf]\Vert _{L^{p_{2}}(\mathbf{B})}\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\{\Vert f\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})}+\Vert bf\Vert _{L^{p_{2}}(\mathbf{B})}\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})},\nonumber\end{eqnarray}$$as required. ◻
Set
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{1,d}(x,t)=\unicode[STIX]{x1D6F7}(t)+(b(x)t)^{p_{2}}.\end{eqnarray}$$By Lemmas 2.4 and 3.6, we establish the following result.
Theorem 3.7. There exists a constant 
$C>0$ such that
$$\begin{eqnarray}\displaystyle \Vert Mf\Vert _{L^{\unicode[STIX]{x1D6F7}_{1,d}}(\mathbf{B})}\leqslant C\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})} & & \displaystyle \nonumber\end{eqnarray}$$ for all 
$f\in L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})$.
Remark 3.8. Consider 
$b_{\unicode[STIX]{x1D703}}(x)=\min \{\max \{x_{N}^{\unicode[STIX]{x1D703}},0\},1\}$ for 
$x=(x^{\prime },x_{N})\in \mathbf{B}$. In Remark 3.3, if 
$0<\unicode[STIX]{x1D703}_{1}<\unicode[STIX]{x1D703}$, then
$$\begin{eqnarray}\displaystyle \int _{\mathbf{B}}|b_{\unicode[STIX]{x1D703}_{1}}(x)Mf_{1}(x)|^{p_{2}}\,dx=\infty , & & \displaystyle \nonumber\end{eqnarray}$$ where 
$f_{1}(y)=f(y)$ when 
$y_{N}<0$ and 
$f_{1}(y)=0$ when 
$y_{N}\geqslant 0$ with 
$y=(y^{\prime },y_{N})\in \mathbf{B}$.
The optimality of 
$\unicode[STIX]{x1D703}$ and 
$p_{2}$ is also considered in [Reference Esposito, Leonetti and Mingione11, Reference Fonseca, Malý and Mingione12].
Set
$$\begin{eqnarray}\frac{1}{p_{2}^{\ast }}=\frac{1}{p_{2}}-\frac{\unicode[STIX]{x1D6FC}}{N}=1-\frac{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}}{N}.\end{eqnarray}$$Lemma 3.9. If 
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}<N$, then there exists a constant 
$C>0$ such that
$$\begin{eqnarray}\displaystyle \Vert I_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}}f\Vert _{L^{p_{2}^{\ast }}(\mathbf{B})}\leqslant C\Vert f\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})} & & \displaystyle \nonumber\end{eqnarray}$$ for all 
$f\in L^{p_{1}(\cdot )}(\mathbf{B})$.
In fact, it suffices to note
$$\begin{eqnarray}t^{p_{2}^{\ast }}\leqslant C\left(tk(t^{-1})^{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}}\right)^{p_{2}^{\ast }}\leqslant C\unicode[STIX]{x1D6F7}\left(\left(tk(t^{-1})^{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}}\right)^{p_{2}^{\ast }}\right)=C\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}}(t)\end{eqnarray}$$ for all 
$t\geqslant 1$. Now we apply Theorem 3.2.
Lemma 3.10. If 
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}<N$, then there exists a constant 
$C>0$ such that
$$\begin{eqnarray}\displaystyle \Vert bI_{\unicode[STIX]{x1D6FC}}f\Vert _{L^{p_{2}^{\ast }}(\mathbf{B})}\leqslant C\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})} & & \displaystyle \nonumber\end{eqnarray}$$ for all 
$f\in L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})$.
Proof. Let 
$f\in L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})$ be a nonnegative function. Note that
$$\begin{eqnarray}\displaystyle & & \displaystyle b(x)\int _{\mathbf{B}}|x-y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\mathbf{B}}[b(x)-b(y)]|x-y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy+\int _{\mathbf{B}}|x-y|^{\unicode[STIX]{x1D6FC}-N}b(y)f(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{\mathbf{B}}|x-y|^{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}-N}f(y)\,dy+\int _{\mathbf{B}}|x-y|^{\unicode[STIX]{x1D6FC}-N}b(y)f(y)\,dy,\nonumber\end{eqnarray}$$so that
$$\begin{eqnarray}\displaystyle b(x)I_{\unicode[STIX]{x1D6FC}}f(x)\leqslant CI_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}}f(x)+I_{\unicode[STIX]{x1D6FC}}[bf](x). & & \displaystyle \nonumber\end{eqnarray}$$ Hence, by Lemma 3.9 and the Sobolev inequality on 
$L^{p_{2}}(\mathbf{B})$, we give
$$\begin{eqnarray}\displaystyle \Vert bI_{\unicode[STIX]{x1D6FC}}f\Vert _{L^{p_{2}^{\ast }}(\mathbf{B})} & {\leqslant} & \displaystyle C\{\Vert I_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}}f\Vert _{L^{p_{2}^{\ast }}(\mathbf{B})}+\Vert I_{\unicode[STIX]{x1D6FC}}[bf]\Vert _{L^{p_{2}^{\ast }}(\mathbf{B})}\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\{\Vert f\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})}+\Vert bf\Vert _{L^{p_{2}}(\mathbf{B})}\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})},\nonumber\end{eqnarray}$$as required. ◻
Set
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC},d}(x,t)=\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}(t)+(b(x)t)^{p_{2}^{\ast }}.\end{eqnarray}$$Theorem 3.2 and Lemma 3.10, we establish the following result.
Theorem 3.11. If 
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}<N$, then there exists a constant 
$C>0$ such that
$$\begin{eqnarray}\displaystyle \Vert I_{\unicode[STIX]{x1D6FC}}f\Vert _{L^{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC},d}}(\mathbf{B})}\leqslant C\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})} & & \displaystyle \nonumber\end{eqnarray}$$ for all 
$f\in L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})$.
4 Herz–Morrey spaces
We consider a measurable function 
$\unicode[STIX]{x1D714}(r):(0,\infty )\rightarrow (0,\infty )$ satisfying the following conditions (
$\unicode[STIX]{x1D714}1$) and (
$\unicode[STIX]{x1D714}2$):
- ($\unicode[STIX]{x1D714}1$)
- $\unicode[STIX]{x1D714}(\cdot )$ is almost monotone on $(0,\infty )$; that is, $\unicode[STIX]{x1D714}(\cdot )$ is almost increasing on $(0,\infty )$ or $\unicode[STIX]{x1D714}(\cdot )$ is almost decreasing on $(0,\infty )$; namely there exists a constant $c_{1}>0$ such that $$\begin{eqnarray}\unicode[STIX]{x1D714}(r)\leqslant c_{1}\unicode[STIX]{x1D714}(s)\quad \text{for all }0<r<s\end{eqnarray}$$
or
$$\begin{eqnarray}\unicode[STIX]{x1D714}(s)\leqslant c_{1}\unicode[STIX]{x1D714}(r)\quad \text{for all }0<r<s,\end{eqnarray}$$respectively;
- ($\unicode[STIX]{x1D714}2$)
- $\unicode[STIX]{x1D714}(\cdot )$ is doubling on $(0,\infty )$; that is, there exists a constant $C>1$ such that $$\begin{eqnarray}C^{-1}\unicode[STIX]{x1D714}(r)\leqslant \unicode[STIX]{x1D714}(2r)\leqslant C\unicode[STIX]{x1D714}(r)\quad \text{for all }r>0.\end{eqnarray}$$
For 
$0<q\leqslant \infty$, we define Herz–Morrey spaces 
${\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D714}}(\mathbf{B})$ of all measurable functions 
$f$ on 
$\mathbf{B}$ such that
$$\begin{eqnarray}\Vert f\Vert _{{\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D714}}(\mathbf{B})}=\left(\int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(r))}\right)^{q}\,\frac{dr}{r}\right)^{1/q}<\infty\end{eqnarray}$$ when 
$q<\infty$ and
$$\begin{eqnarray}\Vert f\Vert _{{\mathcal{H}}^{p_{1}(\cdot ),\infty ,\unicode[STIX]{x1D714}}(\mathbf{B})}=\sup _{0<r<1}~\unicode[STIX]{x1D714}(r)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(r))}<\infty\end{eqnarray}$$ when 
$q=\infty$, where 
$A(r)=\mathbf{B}\cap [B(0,2r)\setminus B(0,r)]$. We refer the reader to [Reference Adams and Xiao1] for Morrey spaces. When 
$\unicode[STIX]{x1D714}(r)=r^{\unicode[STIX]{x1D708}}$, we simply write 
${\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D708}}(\mathbf{B})$ for 
${\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D714}}(\mathbf{B})$.
Further, for 
$0<q\leqslant \infty$, we define Herz–Morrey–Orlicz spaces 
${\mathcal{H}}^{\unicode[STIX]{x1D6F7},q,\unicode[STIX]{x1D714}}(\mathbf{B})$ of all measurable functions 
$f$ on 
$\mathbf{B}$ such that
$$\begin{eqnarray}\Vert f\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7},q,\unicode[STIX]{x1D714}}(\mathbf{B})}=\left(\int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}}(A(r))}\right)^{q}\,\frac{dr}{r}\right)^{1/q}<\infty\end{eqnarray}$$ when 
$q<\infty$ and
$$\begin{eqnarray}\Vert f\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7},\infty ,\unicode[STIX]{x1D714}}(\mathbf{B})}=\sup _{0<r<1}~\unicode[STIX]{x1D714}(r)\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}}(A(r))}<\infty\end{eqnarray}$$ when 
$q=\infty$.
For fundamental properties of Herz–Morrey spaces, we have the following.
Lemma 4.1. For 
$0<q_{1}<q_{2}<\infty$,
$$\begin{eqnarray}{\mathcal{H}}^{p_{1}(\cdot ),q_{1},\unicode[STIX]{x1D714}}(\mathbf{R}^{N})\subset {\mathcal{H}}^{p_{1}(\cdot ),q_{2},\unicode[STIX]{x1D714}}(\mathbf{R}^{N})\subset {\mathcal{H}}^{p_{1}(\cdot ),\infty ,\unicode[STIX]{x1D714}}(\mathbf{R}^{N}).\end{eqnarray}$$For later use we prepare the following result.
Lemma 4.2. Let 
$\unicode[STIX]{x1D6F7}(r)$ be a positive convex function on 
$(0,\infty )$ satisfying 
$(\unicode[STIX]{x1D6F7}0)$ and 
$(\unicode[STIX]{x1D6F7}1)$. Then there is a constant 
$C>0$ such that
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D712}_{A(r)}\Vert _{L^{\unicode[STIX]{x1D6F7}}(\mathbf{B})}\leqslant C\{\unicode[STIX]{x1D6F7}^{-1}(r^{-N})\}^{-1}\end{eqnarray}$$ for all 
$0<r<1$.
We consider the following two types of conditions for 
$\unicode[STIX]{x1D714}(r)$:
- ($\unicode[STIX]{x1D714}1;\unicode[STIX]{x1D709}$)
- $r\mapsto r^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}(r)$ is almost decreasing on $(0,1]$ for some $\unicode[STIX]{x1D700}_{1}>0$;
- ($\unicode[STIX]{x1D714}2;\unicode[STIX]{x1D707}$)
- $r\mapsto r^{-\unicode[STIX]{x1D700}_{2}+\unicode[STIX]{x1D707}}\unicode[STIX]{x1D714}(r)$ is almost increasing on $(0,1]$ for some $\unicode[STIX]{x1D700}_{2}>0$.
Remark 4.3. (
$\unicode[STIX]{x1D714}1;\unicode[STIX]{x1D709}$) implies that there exists a constant 
$0<\unicode[STIX]{x1D700}_{1}^{\prime }<\unicode[STIX]{x1D700}_{1}$ such that 
$r\mapsto r^{\unicode[STIX]{x1D700}_{1}^{\prime }+\unicode[STIX]{x1D709}}k(r)^{N}\unicode[STIX]{x1D714}(r)$ is almost decreasing on 
$(0,1]$. Similarly, (
$\unicode[STIX]{x1D714}2;\unicode[STIX]{x1D707}$) implies that there exists a constant 
$0<\unicode[STIX]{x1D700}_{2}^{\prime }<\unicode[STIX]{x1D700}_{2}$ such that 
$r\mapsto r^{-\unicode[STIX]{x1D700}_{2}^{\prime }+\unicode[STIX]{x1D707}}k(r)^{N}\unicode[STIX]{x1D714}(r)$ is almost increasing on 
$(0,1]$.
In view of Almeida and Drihem [Reference Almeida and Drihem2], we know that the maximal operator 
$M:f\rightarrow Mf$ is bounded in 
${\mathcal{H}}^{p,q,\unicode[STIX]{x1D708}}(\mathbf{R}^{N})$, when 
$1<p<\infty$. The case 
$p=1$ is treated in the following.
Theorem 4.4. Assume that 
$\unicode[STIX]{x1D714}(r)$ satisfies 
$(\unicode[STIX]{x1D714}1;0)$ and 
$(\unicode[STIX]{x1D714}2;N)$. Suppose further:
- $(\unicode[STIX]{x1D6F7}k1)$
there exist constants
$0<\tilde{\unicode[STIX]{x1D700}}_{1}<\unicode[STIX]{x1D700}_{1}$ and $C>0$ such that $$\begin{eqnarray}\left(\int _{t}^{1}\left(\left\{\unicode[STIX]{x1D6F7}^{-1}(r^{-N})\right\}^{-1}r^{-\tilde{\unicode[STIX]{x1D700}}_{1}-N}k(r)^{-N}\right)^{q}\frac{dr}{r}\right)^{1/q}\leqslant Ct^{-\tilde{\unicode[STIX]{x1D700}}_{1}}\end{eqnarray}$$for all
$0<t<1$ when $0<q<\infty$ and $$\begin{eqnarray}\sup _{0<r<1}\left(\left\{\unicode[STIX]{x1D6F7}^{-1}(r^{-N})\right\}^{-1}r^{-N}k(r)^{-N}\right)\leqslant C\end{eqnarray}$$when
$q=\infty$;- $(\unicode[STIX]{x1D6F7}k2)$
there exist constants
$0<\tilde{\unicode[STIX]{x1D700}}_{2}<\unicode[STIX]{x1D700}_{2}$ and $C>0$ such that $$\begin{eqnarray}\left(\int _{0}^{t}\left(\left\{\unicode[STIX]{x1D6F7}^{-1}(r^{-N})\right\}^{-1}r^{\tilde{\unicode[STIX]{x1D700}}_{2}-N}k(r)^{-N}\right)^{q}\frac{dr}{r}\right)^{1/q}\leqslant Ct^{\tilde{\unicode[STIX]{x1D700}}_{2}}\end{eqnarray}$$for
$0<t<1$ when $0<q<\infty$ and $$\begin{eqnarray}\sup _{0<r<1}\left(\left\{\unicode[STIX]{x1D6F7}^{-1}(r^{-N})\right\}^{-1}r^{-N}k(r)^{-N}\right)\leqslant C\end{eqnarray}$$when
$q=\infty$.
Then there exists a constant 
$C>0$ such that
$$\begin{eqnarray}\Vert Mf\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7},q,\unicode[STIX]{x1D714}}(\mathbf{B})}\leqslant C\Vert f\Vert _{{\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D714}}(\mathbf{B})}\end{eqnarray}$$ for all 
$f\in {\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D714}}(\mathbf{B})$.
Remark 4.5. Let 
$k(r)=a(\log (e+1/r))^{b}$ with 
$a\geqslant e^{b}(\log (e+1))^{-b}$ and 
$b\geqslant 1/N$. Then we can take
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(r)=r(\log (e+r))^{bN-1}.\end{eqnarray}$$In this case,
$$\begin{eqnarray}\left\{\unicode[STIX]{x1D6F7}^{-1}(r^{-N})\right\}^{-1}\sim r^{N}(\log (e+1/r))^{bN-1}\quad \text{when }0<r<1.\end{eqnarray}$$To show Theorem 4.4, we prepare the estimates of Hardy type operators:
Lemma 4.6. (Cf. [Reference Maeda, Mizuta and Shimomura20, Lemma 3.4])
Let 
$\unicode[STIX]{x1D6FD}\in \mathbf{R}$. If 
$\unicode[STIX]{x1D714}(r)$ satisfies 
$(\unicode[STIX]{x1D714}1;N-\unicode[STIX]{x1D6FD})$ and 
$0<\unicode[STIX]{x1D700}<\unicode[STIX]{x1D700}_{1}$, then
$$\begin{eqnarray}\displaystyle H_{\unicode[STIX]{x1D6FD}}^{-}f(r) & \equiv & \displaystyle r^{-\unicode[STIX]{x1D6FD}}\int _{B(0,r)}|y|^{\unicode[STIX]{x1D6FD}-N}|f(y)|\,dy\nonumber\\ \displaystyle & {\leqslant} & \displaystyle Cr^{-\unicode[STIX]{x1D700}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\left(\int _{0}^{r}\left(t^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)^{1/q}\nonumber\end{eqnarray}$$ for all 
$0<r<1$ and 
$f\in L_{\text{loc}}^{1}(\mathbf{B})$ when 
$0<q<\infty$ and
$$\begin{eqnarray}\displaystyle H_{\unicode[STIX]{x1D6FD}}^{-}f(r)\leqslant Cr^{-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\sup _{0<t<r}\left(\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p(\cdot )}(A(t))}\right) & & \displaystyle \nonumber\end{eqnarray}$$ for all 
$0<r<1$ and 
$f\in L_{\text{loc}}^{1}(\mathbf{B})$ when 
$q=\infty$.
Proof. Let 
$0<r<1$, 
$0<\unicode[STIX]{x1D700}<\unicode[STIX]{x1D700}_{1}$ and 
$f\in L_{\text{loc}}^{1}(\mathbf{B})$. Then we have by Lemma 3.1,
$$\begin{eqnarray}\displaystyle \int _{B(0,r)}|y|^{\unicode[STIX]{x1D6FD}-N}|f(y)|\,dy & {\leqslant} & \displaystyle C\int _{B(0,r)}\left(\int _{|y|/2}^{|y|}t^{\unicode[STIX]{x1D6FD}-N}\,\frac{dt}{t}\right)|f(y)|\,dy\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\int _{0}^{r}t^{\unicode[STIX]{x1D6FD}-N}\left(\int _{A(t)}|f(y)|\,dy\right)\,\frac{dt}{t}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\int _{0}^{r}t^{\unicode[STIX]{x1D6FD}-N}k(t)^{-N}\Vert f\Vert _{L^{p(\cdot )}(A(t))}\,\frac{dt}{t}.\nonumber\end{eqnarray}$$ In case 
$1<q<\infty$, by Hölder’s inequality and 
$(\unicode[STIX]{x1D714}1;N-\unicode[STIX]{x1D6FD})$, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{B(0,r)}|y|^{\unicode[STIX]{x1D6FD}-N}|f(y)|\,dy\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\left(\int _{0}^{r}\left(t^{-\unicode[STIX]{x1D700}+\unicode[STIX]{x1D6FD}-N}k(t)^{-N}\unicode[STIX]{x1D714}(t)^{-1}\right)^{q^{\prime }}\,\frac{dt}{t}\right)^{1/q^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{0}^{r}\left(t^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)^{1/q}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,Cr^{-\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D6FD}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\left(\int _{0}^{r}(t^{-\unicode[STIX]{x1D700}+\unicode[STIX]{x1D700}_{1}})^{q^{\prime }}\,\frac{dt}{t}\right)^{1/q^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{0}^{r}\left(t^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)^{1/q}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,Cr^{-\unicode[STIX]{x1D700}+\unicode[STIX]{x1D6FD}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\left(\int _{0}^{r}\left(t^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)^{1/q}.\nonumber\end{eqnarray}$$ In case 
$0<q\leqslant 1$, by 
$(\unicode[STIX]{x1D714}1;N-\unicode[STIX]{x1D6FD})$ and Minkowski’s inequality, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{B(0,r)}|y|^{\unicode[STIX]{x1D6FD}-N}|f(y)|\,dy\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,Cr^{-\unicode[STIX]{x1D700}+\unicode[STIX]{x1D6FD}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\int _{0}^{r}t^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p(\cdot )}(A(t)\cap B(0,r))}\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,Cr^{-\unicode[STIX]{x1D700}+\unicode[STIX]{x1D6FD}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{0}^{r}\left(\int _{t/\sqrt{2}}^{t\sqrt{2}}\left(s^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(s)\Vert f\Vert _{L^{p(\cdot )}(A(s)\cap B(0,r))}\right)^{q}\frac{ds}{s}\right)^{1/q}\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,Cr^{-\unicode[STIX]{x1D700}+\unicode[STIX]{x1D6FD}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{0}^{r\sqrt{2}}\left(s^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(s)\Vert f\Vert _{L^{p(\cdot )}(A(s)\cap B(0,r))}\right)^{q}\left(\int _{s/\sqrt{2}}^{s\sqrt{2}}\frac{dt}{t}\right)^{q}\frac{ds}{s}\right)^{1/q}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,Cr^{-\unicode[STIX]{x1D700}+\unicode[STIX]{x1D6FD}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\left(\int _{0}^{r}\left(s^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(s)\Vert f\Vert _{L^{p(\cdot )}(A(s))}\right)^{q}\frac{ds}{s}\right)^{1/q}.\nonumber\end{eqnarray}$$ In case 
$q=\infty$, by 
$(\unicode[STIX]{x1D714}1;N-\unicode[STIX]{x1D6FD})$, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{B(0,r)}|y|^{\unicode[STIX]{x1D6FD}-N}|f(y)|\,dy\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\left(\int _{0}^{r}t^{-\unicode[STIX]{x1D700}+\unicode[STIX]{x1D6FD}-N}k(t)^{-N}\unicode[STIX]{x1D714}(t)^{-1}\,\frac{dt}{t}\right)\sup _{0<t<r}\left(t^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p(\cdot )}(A(t))}\right)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,Cr^{-\unicode[STIX]{x1D700}+\unicode[STIX]{x1D6FD}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\sup _{0<t<r}\left(t^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p(\cdot )}(A(t))}\right)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,Cr^{\unicode[STIX]{x1D6FD}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\sup _{0<t<r}\left(\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p(\cdot )}(A(t))}\right).\nonumber\end{eqnarray}$$Therefore, we obtain the required result. ◻
Lemma 4.7. (Cf. [Reference Maeda, Mizuta and Shimomura20, Lemma 3.5])
Let 
$\unicode[STIX]{x1D6FD}\in \mathbf{R}$. If 
$\unicode[STIX]{x1D714}(r)$ satisfies 
$(\unicode[STIX]{x1D714}2;N-\unicode[STIX]{x1D6FD})$ and 
$0<\unicode[STIX]{x1D700}<\unicode[STIX]{x1D700}_{2}$, then
$$\begin{eqnarray}\displaystyle H_{\unicode[STIX]{x1D6FD}}^{+}f(r) & \equiv & \displaystyle r^{-\unicode[STIX]{x1D6FD}}\int _{\mathbf{B}\setminus B(0,r)}|y|^{\unicode[STIX]{x1D6FD}-N}|f(y)|\,dy\nonumber\\ \displaystyle & {\leqslant} & \displaystyle Cr^{\unicode[STIX]{x1D700}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\left(\int _{r/2}^{1}\left(t^{-\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\frac{dt}{t}\,\right)^{1/q}\nonumber\end{eqnarray}$$ for all 
$0<r<1$ and 
$f\in L_{\text{loc}}^{1}(\mathbf{B})$ when 
$0<q<\infty$ and
$$\begin{eqnarray}\displaystyle H_{\unicode[STIX]{x1D6FD}}^{+}f(r)\leqslant Cr^{-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\sup _{r/2<t<1}\left(\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p(\cdot )}(A(t))}\right) & & \displaystyle \nonumber\end{eqnarray}$$ for all 
$0<r<1$ and 
$f\in L_{\text{loc}}^{1}(\mathbf{B})$ when 
$q=\infty$.
Proof. We show only the case when 
$1<q<\infty$. Let 
$0<r<1$, 
$0<\unicode[STIX]{x1D700}<\unicode[STIX]{x1D700}_{2}$ and 
$f\in L_{\text{loc}}^{1}(\mathbf{B})$. By Lemma 3.1,
$$\begin{eqnarray}\displaystyle \int _{\mathbf{B}\setminus B(0,r)}|y|^{\unicode[STIX]{x1D6FD}-N}|f(y)|\,dy & {\leqslant} & \displaystyle C\int _{\mathbf{B}\setminus B(0,r)}\left(\int _{|y|/2}^{|y|}t^{\unicode[STIX]{x1D6FD}-N}\,\frac{dt}{t}\right)|f(y)|\,dy\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\int _{r/2}^{1}t^{\unicode[STIX]{x1D6FD}-N}\left(\int _{A(t)}|f(y)|\,dy\right)\frac{dt}{t}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\int _{r/2}^{1}t^{\unicode[STIX]{x1D6FD}-N}k(t)^{-N}\Vert f\Vert _{L^{p(\cdot )}(A(t))}\,\frac{dt}{t}.\nonumber\end{eqnarray}$$ By Hölder’s inequality and 
$(\unicode[STIX]{x1D714}2;N-\unicode[STIX]{x1D6FD})$, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{r/2}^{1}t^{\unicode[STIX]{x1D6FD}-N}k(t)^{-N}\Vert f\Vert _{L^{p(\cdot )}(A(t))}\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\left(\int _{r/2}^{1}\left(t^{\unicode[STIX]{x1D700}+\unicode[STIX]{x1D6FD}-N}k(t)^{-N}\unicode[STIX]{x1D714}(t)^{-1}\right)^{q^{\prime }}\,\frac{dt}{t}\right)^{1/q^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{r/2}^{1}\left(t^{-\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)^{1/q}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,Cr^{\unicode[STIX]{x1D700}_{2}+\unicode[STIX]{x1D6FD}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\left(\int _{r/2}^{1}(t^{\unicode[STIX]{x1D700}-\unicode[STIX]{x1D700}_{2}})^{q^{\prime }}\,\frac{dt}{t}\right)^{1/q^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{r/2}^{1}\left(t^{-\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)^{1/q}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,Cr^{\unicode[STIX]{x1D700}+\unicode[STIX]{x1D6FD}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\left(\int _{r/2}^{1}\left(t^{-\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)^{1/q},\nonumber\end{eqnarray}$$which gives the required result. ◻
Now we are ready to prove Theorem 4.4.
Proof of Theorem 4.4.
We show only the case when 
$0<q<\infty$, because the remaining case is easily obtained. Let 
$f$ be a measurable function on 
$\mathbf{B}$ such that 
$\Vert f\Vert _{{\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D714}}(\mathbf{B})}\leqslant 1$. For 
$0<r<1$, write
$$\begin{eqnarray}f=f\unicode[STIX]{x1D712}_{B(0,r/2)}+f\unicode[STIX]{x1D712}_{\tilde{A}(r)}+f\unicode[STIX]{x1D712}_{\mathbf{B}\setminus B(0,4r)}=f_{1}+f_{2}+f_{3},\end{eqnarray}$$ where 
$\tilde{A}(r)=A(r/2)\cup A(r)\cup A(2r)$. Note here that
$$\begin{eqnarray}\displaystyle Mf_{1}(x) & {\leqslant} & \displaystyle \sup _{t\geqslant r/2}\frac{1}{|B(x,t)|}\int _{B(x,t)\cap B(0,r/2)}|f(y)|\,dy\nonumber\\ \displaystyle & {\leqslant} & \displaystyle Cr^{-N}\int _{B(0,r/2)}|f(y)|\,dy\nonumber\\ \displaystyle & {\leqslant} & \displaystyle CH_{N}^{-}f(r)\nonumber\end{eqnarray}$$ for 
$x\in A(r)$. Hence we obtain by Lemmas 4.2 and 4.6, 
$(\unicode[STIX]{x1D6F7}k1)$ and Fubini’s theorem
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert Mf_{1}\Vert _{L^{\unicode[STIX]{x1D6F7}}(A(r))}\right)^{q}\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(\left\{\unicode[STIX]{x1D6F7}^{-1}(r^{-N})\right\}^{-1}r^{-\tilde{\unicode[STIX]{x1D700}}_{1}-N}k(r)^{-N}\right)^{q}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{0}^{r}\left(t^{\tilde{\unicode[STIX]{x1D700}}_{1}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(t^{\tilde{\unicode[STIX]{x1D700}}_{1}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{t}^{1}\left(\left\{\unicode[STIX]{x1D6F7}^{-1}(r^{-N})\right\}^{-1}r^{-\tilde{\unicode[STIX]{x1D700}}_{1}-N}k(r)^{-N}\right)^{q}\,\frac{dr}{r}\right)\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C.\end{eqnarray}$$ Since 
$f_{3}=0$ in case 
$1/4\leqslant r<1$ and
$$\begin{eqnarray}\displaystyle Mf_{3}(x)\leqslant C\int _{\mathbf{B}\setminus B(0,4r)}|y|^{-N}|f(y)|\,dy\leqslant CH_{0}^{+}f(4r) & & \displaystyle \nonumber\end{eqnarray}$$ for 
$x\in A(r)$ in case 
$0<r<1/4$, we obtain by Lemmas 4.2 and 4.7, 
$(\unicode[STIX]{x1D6F7}k2)$ and Fubini’s theorem
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert Mf_{3}\Vert _{L^{\unicode[STIX]{x1D6F7}}(A(r))}\right)^{q}\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(\left\{\unicode[STIX]{x1D6F7}^{-1}(r^{-N})\right\}^{-1}r^{\tilde{\unicode[STIX]{x1D700}}_{2}-N}k(r)^{-N}\right)^{q}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{r}^{1}\left(t^{-\tilde{\unicode[STIX]{x1D700}}_{2}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(t^{-\tilde{\unicode[STIX]{x1D700}}_{2}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{0}^{t}\left(\left\{\unicode[STIX]{x1D6F7}^{-1}(r^{-N})\right\}^{-1}r^{\tilde{\unicode[STIX]{x1D700}}_{2}-N}k(r)^{-N}\right)^{q}\,\frac{dr}{r}\right)\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C.\end{eqnarray}$$ For 
$f_{2}$, by Lemma 2.4
$$\begin{eqnarray}\Vert Mf_{2}\Vert _{L^{\unicode[STIX]{x1D6F7}}(A(r))}\leqslant C\Vert f_{2}\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})}=C\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}}(\tilde{A}(r))},\end{eqnarray}$$so that
$$\begin{eqnarray}\int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert Mf_{2}\Vert _{L^{\unicode[STIX]{x1D6F7}}(A(r))}\right)^{q}\,\frac{dr}{r}\leqslant C.\end{eqnarray}$$
$$\begin{eqnarray}\hspace{74.50008pt}\int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert Mf\Vert _{L^{\unicode[STIX]{x1D6F7}}(A(r))}\right)^{q}\,\frac{dr}{r}\leqslant C.\hspace{74.50008pt}\square\end{eqnarray}$$Remark 4.8. Let 
$k(r)=a(\log (e+1/r))^{b}$ with 
$a\geqslant e^{b}(\log (e+1))^{-b}$ and 
$b\geqslant 1/N$ and 
$\unicode[STIX]{x1D714}(r)=r^{\unicode[STIX]{x1D708}}$ with 
$-N<\unicode[STIX]{x1D708}<0$. Then note that 
$\unicode[STIX]{x1D6F7}(r)=r(\log (e+r))^{bN-1}$ by Remark 3.4. Let 
$b_{1}>b$ and 
$0<r<1/2$. We choose 
$0<\unicode[STIX]{x1D706}_{2}<\unicode[STIX]{x1D706}_{1}<1$ such that 
$b_{1}>(1+\unicode[STIX]{x1D706}_{1})b$. For 
$|x_{0}|=r$, consider
$$\begin{eqnarray}f(y)=|x_{0}-y|^{-N}\unicode[STIX]{x1D712}_{C(x_{0},r,\unicode[STIX]{x1D706}_{1})},\end{eqnarray}$$ where 
$C(x_{0},r,\unicode[STIX]{x1D706}_{1})=\{y\in A(r):r^{1+\unicode[STIX]{x1D706}_{1}}<|x_{0}-y|<r\}$. Note that
$$\begin{eqnarray}\displaystyle \frac{\log k(|y|)}{\log (e+1/|y|)}\log f(y) & {\leqslant} & \displaystyle \frac{\log k(|y|)}{\log (e+1/|y|)}\log \left(\left(|y|/2\right)^{-(1+\unicode[STIX]{x1D706}_{1})N}\right)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{\log k(|y|)}{\log (e+1/|y|)}\left((1+\unicode[STIX]{x1D706}_{1})N\log (1/|y|)+C\right)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \log \left(k(|y|)^{(1+\unicode[STIX]{x1D706}_{1})N}\right)+C\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \log \left(k(|x_{0}-y|)^{(1+\unicode[STIX]{x1D706}_{1})N}\right)+C\nonumber\end{eqnarray}$$ for 
$y\in C(x_{0},r,\unicode[STIX]{x1D706}_{1})$ since
$$\begin{eqnarray}|x_{0}-y|<r<|y|<2r<2|x_{0}-y|^{1/(1+\unicode[STIX]{x1D706}_{1})}.\end{eqnarray}$$Then we have
$$\begin{eqnarray}\displaystyle \int _{\mathbf{B}}f(y)^{p_{1}(y)}\,dy & = & \displaystyle \int _{C(x_{0},r,\unicode[STIX]{x1D706}_{1})}|x_{0}-y|^{-N}\exp \left(\frac{\log k(|y|)}{\log (e+1/|y|)}\log f(y)\right)\,dy\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\int _{C(x_{0},r,\unicode[STIX]{x1D706}_{1})}|x_{0}-y|^{-N}(\log (e+1/|x_{0}-y|))^{(1+\unicode[STIX]{x1D706}_{1})bN}\,dy\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\int _{r^{1+\unicode[STIX]{x1D706}_{1}}}^{r}(\log (e+1/t))^{(1+\unicode[STIX]{x1D706}_{1})bN}\,\frac{dt}{t}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(\log (e+1/r))^{(1+\unicode[STIX]{x1D706}_{1})bN+1}.\nonumber\end{eqnarray}$$Set
$$\begin{eqnarray}f_{r}(y)=r^{-\unicode[STIX]{x1D708}}(\log (e+1/r))^{-(1+\unicode[STIX]{x1D706}_{1})bN-1}f(y).\end{eqnarray}$$We see that
$$\begin{eqnarray}\Vert f_{r}\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})}\leqslant Cr^{-\unicode[STIX]{x1D708}},\end{eqnarray}$$so that
$$\begin{eqnarray}\displaystyle \int _{0}^{1}\left(t^{\unicode[STIX]{x1D708}}\Vert f_{r}\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t} & {\leqslant} & \displaystyle \int _{r/2}^{2r}\left(t^{\unicode[STIX]{x1D708}}\Vert f_{r}\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\left(r^{\unicode[STIX]{x1D708}}\Vert f_{r}\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})}\right)^{q}\leqslant C\nonumber\end{eqnarray}$$ when 
$0<q<\infty$ and
$$\begin{eqnarray}\displaystyle \sup _{0<t<1}\left(t^{\unicode[STIX]{x1D708}}\Vert f_{r}\Vert _{L^{p_{1}(\cdot )}(A(t))}\right) & {\leqslant} & \displaystyle \sup _{r/2<t<2r}\left(t^{\unicode[STIX]{x1D708}}\Vert f_{r}\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle Cr^{\unicode[STIX]{x1D708}}\Vert f_{r}\Vert _{L^{p_{1}(\cdot )}(\mathbf{B})}\leqslant C\nonumber\end{eqnarray}$$ when 
$q=\infty$. Therefore 
$\Vert f_{r}\Vert _{{\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D708}}(\mathbf{B})}\leqslant C$ for all 
$0<r<1/2$.
On the other hand, for 
$x\in C(x_{0},r,\unicode[STIX]{x1D706}_{2})$ we find
$$\begin{eqnarray}\displaystyle Mf(x) & {\geqslant} & \displaystyle \frac{C}{|B(x_{0},|x_{0}-x|)|}\int _{B(x_{0},|x_{0}-x|)}f(y)\,dy\nonumber\\ \displaystyle & {\geqslant} & \displaystyle C|x_{0}-x|^{-N}\int _{r^{1+\unicode[STIX]{x1D706}_{1}}}^{|x_{0}-x|}\,\frac{dt}{t}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle C|x_{0}-x|^{-N}\int _{|x_{0}-x|^{(1+\unicode[STIX]{x1D706}_{1})/(1+\unicode[STIX]{x1D706}_{2})}}^{|x_{0}-x|}\,\frac{dt}{t}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle C|x_{0}-x|^{-N}\log (e+1/|x_{0}-x|).\nonumber\end{eqnarray}$$Then we obtain
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{A(r)}Mf_{r}(x)/\left(r^{-\unicode[STIX]{x1D708}}(\log (e+1/r))^{(b_{1}-(1+\unicode[STIX]{x1D706}_{1})b)N}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\log \left(e+Mf_{r}(x)/\left(r^{-\unicode[STIX]{x1D708}}(\log (e+1/r))^{(b_{1}-(1+\unicode[STIX]{x1D706}_{1})b)N}\right)\right)\right)^{b_{1}N-1}\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{A(r)}(\log (e+1/r))^{-(b_{1}N+1)}Mf(x)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\log \left(e+(\log (e+1/r))^{-(b_{1}N+1)}Mf(x)\right)\right)^{b_{1}N-1}\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \,C(\log (e+1/r))^{-(b_{1}N+1)}\int _{C(x_{0},r,\unicode[STIX]{x1D706}_{2})}|x_{0}-x|^{-N}\log (e+1/|x_{0}-x|)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\log \left(e+|x_{0}-x|^{-N}\left(\log (e+1/|x_{0}-x|)\right)^{-b_{1}N}\right)\right)^{b_{1}N-1}\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \,C(\log (e+1/r))^{-(b_{1}N+1)}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{C(x_{0},r,\unicode[STIX]{x1D706}_{2})}|x_{0}-x|^{-N}(\log (e+1/|x_{0}-x|))^{b_{1}N}\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \,C.\nonumber\end{eqnarray}$$It follows that
$$\begin{eqnarray}\displaystyle \Vert Mf_{r}\Vert _{L^{\unicode[STIX]{x1D6F7}_{1}}(A(r))}\geqslant Cr^{-\unicode[STIX]{x1D708}}(\log (e+1/r))^{(b_{1}-(1+\unicode[STIX]{x1D706}_{1})b)N}, & & \displaystyle \nonumber\end{eqnarray}$$ where 
$\unicode[STIX]{x1D6F7}_{1}(r)=r(\log (e+r))^{b_{1}N-1}$. Hence
$$\begin{eqnarray}\displaystyle \int _{0}^{1}\left(t^{\unicode[STIX]{x1D708}}\Vert Mf_{r}\Vert _{L^{\unicode[STIX]{x1D6F7}_{1}}(A(t))}\right)^{q}\,\frac{dt}{t} & {\geqslant} & \displaystyle \int _{3r/4}^{3r/2}\left(t^{\unicode[STIX]{x1D708}}\Vert Mf_{r}\Vert _{L^{\unicode[STIX]{x1D6F7}_{1}}(A(t))}\right)^{q}\,\frac{dt}{t}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle C\left(r^{\unicode[STIX]{x1D708}}\Vert Mf_{r}\Vert _{L^{\unicode[STIX]{x1D6F7}_{1}}(A(r))}\right)^{q}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle C(\log (e+1/r))^{(b_{1}-(1+\unicode[STIX]{x1D706}_{1})b)Nq}\nonumber\end{eqnarray}$$ when 
$0<q<\infty$ and
$$\begin{eqnarray}\displaystyle \sup _{0<t<1}\left(t^{\unicode[STIX]{x1D708}}\Vert Mf_{r}\Vert _{L^{\unicode[STIX]{x1D6F7}_{1}}(A(t))}\right) & {\geqslant} & \displaystyle Cr^{\unicode[STIX]{x1D708}}\Vert Mf_{r}\Vert _{L^{\unicode[STIX]{x1D6F7}_{1}}(A(r))}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle C(\log (e+1/r))^{(b_{1}-(1+\unicode[STIX]{x1D706}_{1})b)N}\nonumber\end{eqnarray}$$ when 
$q=\infty$, so that 
$\Vert Mf_{r}\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7}_{1},q,\unicode[STIX]{x1D708}}(\mathbf{B})}\rightarrow \infty$ as 
$r\rightarrow 0$.
Thus Theorem 4.4 is the best possible.
Remark 4.9. Let 
$k(r)=a(\log (e+1/r))^{b}$ with 
$a\geqslant e^{b}(\log (e+1))^{-b}$ and 
$b\geqslant 1/N$ and 
$\unicode[STIX]{x1D6F7}(r)=r(\log (e+r))^{bN-1}$ as in Remark 3.4 . If 
$\Vert f\Vert _{{\mathcal{H}}^{p_{1}(\cdot ),1,\unicode[STIX]{x1D708}}(\mathbf{B})}\leqslant 1$ and 
$-N<\unicode[STIX]{x1D708}<0$, then we can find a constant 
$C>0$ such that
$$\begin{eqnarray}\int _{\mathbf{B}}|x|^{\unicode[STIX]{x1D708}}Mf(x)(\log (e+Mf(x)))^{bN-1}\,dx\leqslant C.\end{eqnarray}$$ We shall show this. We may assume that 
$\Vert Mf\Vert _{L^{\unicode[STIX]{x1D6F7}}(A(r))}\leqslant 1$ for all
$0<r<1$ by Lemma 4.1 and Theorem 4.4. Then note that
$$\begin{eqnarray}\displaystyle 1 & = & \displaystyle \int _{A(r)}\unicode[STIX]{x1D6F7}\left(Mf(x)/\Vert Mf\Vert _{L^{\unicode[STIX]{x1D6F7}}(A(r))}\right)\,dx\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (\Vert Mf\Vert _{L^{\unicode[STIX]{x1D6F7}}(A(r))})^{-1}\int _{A(r)}\unicode[STIX]{x1D6F7}(Mf(x))\,dx.\nonumber\end{eqnarray}$$Therefore, by Fubini’s theorem and Theorem 4.4
$$\begin{eqnarray}\displaystyle \int _{\mathbf{B}}|x|^{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D6F7}(Mf(x))\,dx & {\leqslant} & \displaystyle C\int _{\mathbf{B}}\unicode[STIX]{x1D6F7}(Mf(x))\left(\int _{|x|/2}^{|x|}t^{\unicode[STIX]{x1D708}}\,\frac{dt}{t}\right)\,dx\nonumber\\ \displaystyle & = & \displaystyle C\int _{0}^{1}t^{\unicode[STIX]{x1D708}}\left(\int _{A(t)}\unicode[STIX]{x1D6F7}(Mf(x))\,dx\right)\,\frac{dt}{t}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\int _{0}^{1}t^{\unicode[STIX]{x1D708}}\Vert Mf\Vert _{L^{\unicode[STIX]{x1D6F7}}(A(t))}\,\frac{dt}{t}\nonumber\\ \displaystyle & = & \displaystyle C\Vert Mf\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7},1,\unicode[STIX]{x1D708}}(\mathbf{B})}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C,\nonumber\end{eqnarray}$$which proves the result.
As in the proof of Lemmas 4.6 and 4.7, we have the following results by using
$$\begin{eqnarray}t^{-N}\int _{A(t)}|f(y)|\,dy\leqslant Ct^{-N/p}\Vert f\Vert _{L^{p}(A(t))}\end{eqnarray}$$ for 
$t>0$ and 
$p\geqslant 1$.
Lemma 4.10. (Cf. [Reference Maeda, Mizuta and Shimomura20, Lemma 3.4])
Let 
$\unicode[STIX]{x1D6FD}\in \mathbf{R}$ and 
$p\geqslant 1$. If 
$\unicode[STIX]{x1D714}(r)$ satisfies 
$(\unicode[STIX]{x1D714}1;N/p-\unicode[STIX]{x1D6FD})$ and 
$0<\unicode[STIX]{x1D700}<\unicode[STIX]{x1D700}_{1}$, then
$$\begin{eqnarray}\displaystyle H_{\unicode[STIX]{x1D6FD}}^{-}f(r)\leqslant Cr^{-\unicode[STIX]{x1D700}-N/p}\unicode[STIX]{x1D714}(r)^{-1}\left(\int _{0}^{r}\left(t^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p}(A(t))}\right)^{q}\,\frac{dt}{t}\right)^{1/q} & & \displaystyle \nonumber\end{eqnarray}$$ for all 
$0<r<1$ and 
$f\in L_{\text{loc}}^{1}(\mathbf{B})$ when 
$0<q<\infty$ and
$$\begin{eqnarray}\displaystyle H_{\unicode[STIX]{x1D6FD}}^{-}f(r)\leqslant Cr^{-N/p}\unicode[STIX]{x1D714}(r)^{-1}\sup _{0<t<r}\left(\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p}(A(t))}\right) & & \displaystyle \nonumber\end{eqnarray}$$ for all 
$0<r<1$ and 
$f\in L_{\text{loc}}^{1}(\mathbf{B})$ when 
$q=\infty$.
Lemma 4.11. (Cf. [Reference Maeda, Mizuta and Shimomura20, Lemma 3.5])
Let 
$\unicode[STIX]{x1D6FD}\in \mathbf{R}$ and let 
$p\geqslant 1$. If 
$\unicode[STIX]{x1D714}(r)$ satisfies 
$(\unicode[STIX]{x1D714}2;N/p-\unicode[STIX]{x1D6FD})$ and 
$0<\unicode[STIX]{x1D700}<\unicode[STIX]{x1D700}_{2}$, then
$$\begin{eqnarray}\displaystyle H_{\unicode[STIX]{x1D6FD}}^{+}f(r)\leqslant Cr^{\unicode[STIX]{x1D700}-N/p}\unicode[STIX]{x1D714}(r)^{-1}\left(\int _{r/2}^{1}\left(t^{-\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p}(A(t))}\right)^{q}\frac{dt}{t}\,\right)^{1/q} & & \displaystyle \nonumber\end{eqnarray}$$ for all 
$0<r<1$ and 
$f\in L_{\text{loc}}^{1}(\mathbf{B})$ when 
$0<q<\infty$ and
$$\begin{eqnarray}\displaystyle H_{\unicode[STIX]{x1D6FD}}^{+}f(r)\leqslant Cr^{-N/p}\unicode[STIX]{x1D714}(r)^{-1}\sup _{r/2<t<1}\left(\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p}(A(t))}\right) & & \displaystyle \nonumber\end{eqnarray}$$ for all 
$0<r<1$ and 
$f\in L_{\text{loc}}^{1}(\mathbf{B})$ when 
$q=\infty$.
For 
$0<q\leqslant \infty$, we define Herz–Morrey–Musielak–Orlicz spaces 
${\mathcal{H}}^{\unicode[STIX]{x1D6F7}_{d},q,\unicode[STIX]{x1D714}}(\mathbf{B})$ of all measurable functions 
$f$ on 
$\mathbf{B}$ such that
$$\begin{eqnarray}\Vert f\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7}_{d},q,\unicode[STIX]{x1D714}}(\mathbf{B})}=\left(\int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(A(r))}\right)^{q}\,\frac{dr}{r}\right)^{1/q}<\infty\end{eqnarray}$$ when 
$q<\infty$ and
$$\begin{eqnarray}\Vert f\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7}_{d},\infty ,\unicode[STIX]{x1D714}}(\mathbf{B})}=\sup _{0<r<1}~\unicode[STIX]{x1D714}(r)\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(A(r))}<\infty\end{eqnarray}$$ when 
$q=\infty$.
Theorem 4.12. Assume that 
$\unicode[STIX]{x1D714}(r)$ satisfies 
$(\unicode[STIX]{x1D714}1;0)$ and 
$(\unicode[STIX]{x1D714}2;N-\unicode[STIX]{x1D703})$. Suppose further 
$(\unicode[STIX]{x1D6F7}k1)$ and 
$(\unicode[STIX]{x1D6F7}k2)$ hold. Then there exists a constant 
$C>0$ such that
$$\begin{eqnarray}\Vert Mf\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7}_{1,d},q,\unicode[STIX]{x1D714}}(\mathbf{B})}\leqslant C\Vert f\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7}_{d},q,\unicode[STIX]{x1D714}}(\mathbf{B})}\end{eqnarray}$$ for all 
$f\in {\mathcal{H}}^{\unicode[STIX]{x1D6F7}_{d},q,\unicode[STIX]{x1D714}}(\mathbf{B})$.
Proof. We show only the case when 
$0<q<\infty$, because the remaining case is easily obtained. Let 
$f$ be a measurable function on 
$\mathbf{B}$ such that 
$\Vert f\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7}_{d},q,\unicode[STIX]{x1D714}}(\mathbf{B})}\leqslant 1$. Note that 
$(\unicode[STIX]{x1D714}1;0)$ and 
$(\unicode[STIX]{x1D714}2;N-\unicode[STIX]{x1D703})$ imply 
$(\unicode[STIX]{x1D714}1;N/p_{2}-N)$ and 
$(\unicode[STIX]{x1D714}2;N)$, respectively.
By Theorem 4.4, we have
$$\begin{eqnarray}\int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert Mf\Vert _{L^{\unicode[STIX]{x1D6F7}}(A(r))}\right)^{q}\,\frac{dr}{r}\leqslant C.\end{eqnarray}$$ For 
$0<r<1$, write
$$\begin{eqnarray}f=f\unicode[STIX]{x1D712}_{B(0,r/2)}+f\unicode[STIX]{x1D712}_{\tilde{A}(r)}+f\unicode[STIX]{x1D712}_{\mathbf{B}\setminus B(0,4r)}=f_{1}+f_{2}+f_{3},\end{eqnarray}$$ where 
$\tilde{A}(r)=A(r/2)\cup A(r)\cup A(2r)$. Here note from (3.1) that
$$\begin{eqnarray}\displaystyle b(x)Mf_{1}(x) & {\leqslant} & \displaystyle CM_{\unicode[STIX]{x1D703}}f_{1}(x)+M[bf_{1}](x)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\left\{\sup _{t\geqslant r/2}\frac{t^{\unicode[STIX]{x1D703}}}{|B(x,t)|}\int _{B(x,t)\cap B(0,r/2)}|f(y)|\,dy+H_{N}^{-}[bf](r)\right\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\left\{r^{-N+\unicode[STIX]{x1D703}}\int _{B(0,r/2)}|f(y)|\,dy+H_{N}^{-}[bf](r)\right\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\left\{r^{\unicode[STIX]{x1D703}}H_{N}^{-}f(r)+H_{N}^{-}[bf](r)\right\}\nonumber\end{eqnarray}$$ for 
$x\in A(r)$. Let 
$0<\tilde{\unicode[STIX]{x1D700}}_{1}<\unicode[STIX]{x1D700}_{1}$ and 
$0<\tilde{\unicode[STIX]{x1D700}}_{2}<\unicode[STIX]{x1D700}_{2}$. Hence we obtain by Lemmas 4.2, 4.6 and 4.10 and Fubini’s theorem
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert bMf_{1}\Vert _{L^{p_{2}}(A(r))}\right)^{q}\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\bigg\{\int _{0}^{1}\left(r^{-\tilde{\unicode[STIX]{x1D700}}_{1}-N+N/p_{2}+\unicode[STIX]{x1D703}}k(r)^{-N}\right)^{q}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{0}^{r}\left(t^{\tilde{\unicode[STIX]{x1D700}}_{1}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{0}^{1}\left(r^{-\tilde{\unicode[STIX]{x1D700}}_{1}-N/p_{2}+N/p_{2}}\right)^{q}\left(\int _{0}^{r}\left(t^{\tilde{\unicode[STIX]{x1D700}}_{1}}\unicode[STIX]{x1D714}(t)\Vert bf\Vert _{L^{p_{2}}(A(t))}\right)^{q}\,\frac{dt}{t}\right)\,\frac{dr}{r}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\bigg\{\int _{0}^{1}\left(t^{\tilde{\unicode[STIX]{x1D700}}_{1}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\left(\int _{t}^{1}r^{-\tilde{\unicode[STIX]{x1D700}}_{1}q}\,\frac{dr}{r}\right)\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{0}^{1}\left(t^{\tilde{\unicode[STIX]{x1D700}}_{1}}\unicode[STIX]{x1D714}(t)\Vert bf\Vert _{L^{p_{2}}(A(t))}\right)^{q}\left(\int _{t}^{1}r^{-\tilde{\unicode[STIX]{x1D700}}_{1}q}\,\frac{dr}{r}\right)\,\frac{dt}{t}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(A(t))}\right)^{q}\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C.\end{eqnarray}$$ Since 
$f_{3}=0$ in case 
$1/4\leqslant r<1$ and
$$\begin{eqnarray}\displaystyle & & \displaystyle b(x)Mf_{3}(x)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\left\{\sup _{t>0}\frac{1}{|B(x,t)|}\int _{B(x,t)\cap B(0,4r)}|x-y|^{\unicode[STIX]{x1D703}}|f(y)|\,dy+H_{0}^{+}[bf](4r)\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\left\{\int _{\mathbf{B}\cap B(0,4r)}|y|^{\unicode[STIX]{x1D703}-N}|f(y)|\,dy+H_{0}^{+}[bf](4r)\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\left\{r^{\unicode[STIX]{x1D703}}H_{\unicode[STIX]{x1D703}}^{+}f(4r)+H_{0}^{+}[bf](4r)\right\}\nonumber\end{eqnarray}$$ for 
$x\in A(r)$ in case 
$0<r<1/4$, we obtain by Lemmas 4.2, 4.7 and 4.11 and Fubini’s theorem
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert bMf_{3}\Vert _{L^{p_{2}}(A(r))}\right)^{q}\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\bigg\{\int _{0}^{1}\left(r^{\tilde{\unicode[STIX]{x1D700}}_{2}}k(r)^{-N}\right)^{q}\left(\int _{r}^{1}\left(t^{-\tilde{\unicode[STIX]{x1D700}}_{2}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{0}^{1}r^{\tilde{\unicode[STIX]{x1D700}}_{2}q}\left(\int _{r}^{1}\left(t^{-\tilde{\unicode[STIX]{x1D700}}_{2}}\unicode[STIX]{x1D714}(t)\Vert bf\Vert _{L^{p_{2}}(A(t))}\right)^{q}\,\frac{dt}{t}\right)\,\frac{dr}{r}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(A(t))}\right)^{q}\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C.\end{eqnarray}$$ For 
$f_{2}$, by Lemma 3.6
$$\begin{eqnarray}\Vert bMf_{2}\Vert _{L^{p_{2}}(A(r))}\leqslant C\Vert f_{2}\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(\mathbf{B})}=C\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(\tilde{A}(r))},\end{eqnarray}$$so that
$$\begin{eqnarray}\int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert bMf_{2}\Vert _{L^{p_{2}}(A(r))}\right)^{q}\,\frac{dr}{r}\leqslant C.\end{eqnarray}$$
$$\begin{eqnarray}\hspace{72.5001pt}\int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert bMf\Vert _{L^{p_{2}}(A(r))}\right)^{q}\,\frac{dr}{r}\leqslant C.\hspace{72.5001pt}\square\end{eqnarray}$$Remark 4.13. Let 
$k(r)=a(\log (e+1/r))^{b}$ with 
$a\geqslant e^{b}(\log (e+1))^{-b}$ and 
$b\geqslant 1/N$ and 
$\unicode[STIX]{x1D6F7}(r)=r(\log (e+r))^{bN-1}$ as in Remark 3.4. If 
$\Vert f\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7}_{d},1,\unicode[STIX]{x1D708}}(\mathbf{B})}\leqslant 1$ and 
$-N+\unicode[STIX]{x1D703}<\unicode[STIX]{x1D708}<0$, then we can find a constant 
$C>0$ such that
$$\begin{eqnarray}\int _{\mathbf{B}}|x|^{\unicode[STIX]{x1D708}}\left\{Mf(x)(\log (e+Mf(x)))^{bN-1}+\left(b(x)Mf(x)\right)^{p_{2}}\right\}\,dx\leqslant C.\end{eqnarray}$$Theorem 4.14. Assume that 
$\unicode[STIX]{x1D714}(r)$ satisfies 
$(\unicode[STIX]{x1D714}1;0)$ and 
$(\unicode[STIX]{x1D714}2;N-\unicode[STIX]{x1D6FC})$. Suppose:
- $(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}k1)$
there exist constants
$0<\tilde{\unicode[STIX]{x1D700}}_{1}<\unicode[STIX]{x1D700}_{1}$ and $C>0$ such that$$\begin{eqnarray}\left(\int _{t}^{1}\left(\left\{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}^{-1}(r^{-N})\right\}^{-1}r^{-\tilde{\unicode[STIX]{x1D700}}_{1}+\unicode[STIX]{x1D6FC}-N}k(r)^{-N}\right)^{q}\frac{dr}{r}\right)^{1/q}\leqslant Ct^{-\tilde{\unicode[STIX]{x1D700}}_{1}}\end{eqnarray}$$for all
$0<t<1$ when $0<q<\infty$ and $$\begin{eqnarray}\sup _{0<r<1}\left(\left\{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}^{-1}(r^{-N})\right\}^{-1}r^{\unicode[STIX]{x1D6FC}-N}k(r)^{-N}\right)\leqslant C\end{eqnarray}$$when
$q=\infty$;- $(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}k2)$
there exist constants
$0<\tilde{\unicode[STIX]{x1D700}}_{2}<\unicode[STIX]{x1D700}_{2}$ and $C>0$ such that $$\begin{eqnarray}\left(\int _{0}^{t}\left(\left\{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}^{-1}(r^{-N})\right\}^{-1}r^{\tilde{\unicode[STIX]{x1D700}}_{2}+\unicode[STIX]{x1D6FC}-N}k(r)^{-N}\right)^{q}\frac{dr}{r}\right)^{1/q}\leqslant Ct^{\tilde{\unicode[STIX]{x1D700}}_{2}}\end{eqnarray}$$for
$0<t<1$ when $0<q<\infty$ and $$\begin{eqnarray}\sup _{0<r<1}\left(\left\{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}^{-1}(r^{-N})\right\}^{-1}r^{\unicode[STIX]{x1D6FC}-N}k(r)^{-N}\right)\leqslant C\end{eqnarray}$$when
$q=\infty$.
Then there exists a constant 
$C>0$ such that
$$\begin{eqnarray}\Vert I_{\unicode[STIX]{x1D6FC}}f\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}},q,\unicode[STIX]{x1D714}}(\mathbf{B})}\leqslant C\Vert f\Vert _{{\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D714}}(\mathbf{B})}\end{eqnarray}$$ for all 
$f\in {\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D714}}(\mathbf{B})$.
Proof. Let 
$f$ be a nonnegative measurable function on 
$\mathbf{B}$ such that 
$\Vert f\Vert _{{\mathcal{H}}^{p_{1}(\cdot ),q,\unicode[STIX]{x1D714}}(\mathbf{B})}\leqslant 1$. For 
$x\in \mathbf{B}$, set
$$\begin{eqnarray}\displaystyle I_{\unicode[STIX]{x1D6FC}}f(x) & = & \displaystyle \int _{B(0,|x|/2)}|x-y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy\nonumber\\ \displaystyle & & \displaystyle +\,\int _{(B(0,2|x|)\cap \mathbf{B})\setminus B(0,|x|/2)}|x-y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy\nonumber\\ \displaystyle & & \displaystyle +\,\int _{\mathbf{B}\setminus B(0,2|x|)}|x-y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy\nonumber\\ \displaystyle & = & \displaystyle u_{1}(x)+u_{2}(x)+u_{3}(x).\nonumber\end{eqnarray}$$ Let 
$0<r<1$. Since
$$\begin{eqnarray}\displaystyle u_{1}(x) & {\leqslant} & \displaystyle C|x|^{\unicode[STIX]{x1D6FC}-N}\int _{B(0,|x|/2)}f(y)\,dy\nonumber\\ \displaystyle & {\leqslant} & \displaystyle Cr^{\unicode[STIX]{x1D6FC}}H_{N}^{-}f(r)\nonumber\end{eqnarray}$$ for 
$x\in A(r)$, using Lemma 4.6 we have
$$\begin{eqnarray}u_{1}(x)\leqslant Cr^{-\tilde{\unicode[STIX]{x1D700}}_{1}+\unicode[STIX]{x1D6FC}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\left(\int _{0}^{r}\left(t^{\tilde{\unicode[STIX]{x1D700}}_{1}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)^{1/q}.\end{eqnarray}$$ Hence we obtain by Lemma 4.2, 
$(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}k1)$ and Fubini’s theorem
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert u_{1}\Vert _{L^{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}}(A(r))}\right)^{q}\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(\left\{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}^{-1}(r^{-N})\right\}^{-1}r^{-\tilde{\unicode[STIX]{x1D700}}_{1}+\unicode[STIX]{x1D6FC}-N}k(r)^{-N}\right)^{q}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{0}^{r}\left(t^{\tilde{\unicode[STIX]{x1D700}}_{1}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(t^{\tilde{\unicode[STIX]{x1D700}}_{1}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{t}^{1}\left(\left\{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}^{-1}(r^{-N})\right\}^{-1}r^{-\tilde{\unicode[STIX]{x1D700}}_{1}+\unicode[STIX]{x1D6FC}-N}k(r)^{-N}\right)^{q}\,\frac{dr}{r}\right)\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C.\end{eqnarray}$$Similarly, since
$$\begin{eqnarray}\displaystyle u_{3}(x) & {\leqslant} & \displaystyle C\int _{\mathbf{B}\setminus B(0,2|x|)}|y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy\nonumber\\ \displaystyle & {\leqslant} & \displaystyle Cr^{\unicode[STIX]{x1D6FC}}H_{\unicode[STIX]{x1D6FC}}^{+}f(2r)\nonumber\end{eqnarray}$$ for 
$x\in A(r)$, we see by Lemma 4.7,
$$\begin{eqnarray}u_{3}(x)\leqslant Cr^{\tilde{\unicode[STIX]{x1D700}}_{2}+\unicode[STIX]{x1D6FC}-N}k(r)^{-N}\unicode[STIX]{x1D714}(r)^{-1}\left(\int _{r}^{1}\left(t^{-\tilde{\unicode[STIX]{x1D700}}_{2}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)^{1/q}.\end{eqnarray}$$ Hence we obtain by Lemma 4.2, 
$(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}k2)$ and Fubini’s theorem
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert u_{3}\Vert _{L^{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}}(A(r))}\right)^{q}\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(\left\{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}^{-1}(r^{-N})\right\}^{-1}r^{\tilde{\unicode[STIX]{x1D700}}_{2}+\unicode[STIX]{x1D6FC}-N}k(r)^{-N}\right)^{q}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{r}^{1}\left(t^{-\tilde{\unicode[STIX]{x1D700}}_{2}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(t^{-\tilde{\unicode[STIX]{x1D700}}_{2}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{0}^{t}\left(\left\{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}^{-1}(r^{-N})\right\}^{-1}r^{\tilde{\unicode[STIX]{x1D700}}_{2}+\unicode[STIX]{x1D6FC}-N}k(r)^{-N}\right)^{q}\,\frac{dr}{r}\right)\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C.\end{eqnarray}$$ Let 
$\tilde{A}(r)=A(r/2)\cup A(r)\cup A(2r)$. Since 
$|u_{2}(x)|\leqslant CI_{\unicode[STIX]{x1D6FC}}(f\unicode[STIX]{x1D712}_{(B(0,4r)\cap \mathbf{B})\setminus B(0,r/2)})(x)$ for 
$x\in A(r)$, we have by Theorem 3.2
$$\begin{eqnarray}\Vert u_{2}\Vert _{L^{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}}(A(r))}\leqslant C\Vert f\Vert _{L^{p_{1}(\cdot )}(\tilde{A}(r))},\end{eqnarray}$$so that
$$\begin{eqnarray}\int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert u_{2}\Vert _{L^{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}}(A(r))}\right)^{q}\,\frac{dr}{r}\leqslant C.\end{eqnarray}$$Thus, by (4.7), (4.8) and (4.9), we obtain the required result.◻
Theorem 4.15. Suppose 
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}<N$. Assume that 
$\unicode[STIX]{x1D714}(r)$ satisfies 
$(\unicode[STIX]{x1D714}1;0)$ and 
$(\unicode[STIX]{x1D714}2;N-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D703})$. Suppose further 
$(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}k1)$ and 
$(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}k2)$ hold. Then there exists a constant 
$C>0$ such that
$$\begin{eqnarray}\Vert I_{\unicode[STIX]{x1D6FC}}f\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC},d},q,\unicode[STIX]{x1D714}}(\mathbf{B})}\leqslant C\Vert f\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7}_{d},q,\unicode[STIX]{x1D714}}(\mathbf{B})}\end{eqnarray}$$ for all 
$f\in {\mathcal{H}}^{\unicode[STIX]{x1D6F7}_{d},q,\unicode[STIX]{x1D714}}(\mathbf{B})$.
Proof. We show only the case when 
$0<q<\infty$, because the remaining case is easily obtained. Let 
$f$ be a nonnegative measurable function on 
$\mathbf{B}$ such that 
$\Vert f\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7}_{d},q,\unicode[STIX]{x1D714}}(\mathbf{B})}\leqslant 1$. Note that 
$(\unicode[STIX]{x1D714}1;0)$ and 
$(\unicode[STIX]{x1D714}2;N-\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D703})$ imply 
$(\unicode[STIX]{x1D714}1;-\unicode[STIX]{x1D703})$ and 
$(\unicode[STIX]{x1D714}2;N-\unicode[STIX]{x1D6FC})$, respectively.
By Theorem 4.14, we have
$$\begin{eqnarray}\int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert I_{\unicode[STIX]{x1D6FC}}f\Vert _{L^{\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}}(A(r))}\right)^{q}\,\frac{dr}{r}\leqslant C.\end{eqnarray}$$ For 
$x\in \mathbf{B}$, set
$$\begin{eqnarray}\displaystyle I_{\unicode[STIX]{x1D6FC}}f(x) & = & \displaystyle \int _{B(0,|x|/2)}|x-y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy\nonumber\\ \displaystyle & & \displaystyle +\,\int _{(B(0,2|x|)\cap \mathbf{B})\setminus B(0,|x|/2)}|x-y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy\nonumber\\ \displaystyle & & \displaystyle +\,\int _{\mathbf{B}\setminus B(0,2|x|)}|x-y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy\nonumber\\ \displaystyle & = & \displaystyle u_{1}(x)+u_{2}(x)+u_{3}(x).\nonumber\end{eqnarray}$$ Let 
$0<r<1$. Let 
$0<\tilde{\unicode[STIX]{x1D700}}_{1}<\unicode[STIX]{x1D700}_{1}$ and 
$0<\tilde{\unicode[STIX]{x1D700}}_{2}<\unicode[STIX]{x1D700}_{2}$. Since
$$\begin{eqnarray}\displaystyle & & \displaystyle b(x)u_{1}(x)\leqslant Cb(x)|x|^{\unicode[STIX]{x1D6FC}-N}\int _{B(0,|x|/2)}f(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\left\{|x|^{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}-N}\int _{B(0,|x|/2)}f(y)\,dy+|x|^{\unicode[STIX]{x1D6FC}-N}\int _{B(0,|x|/2)}b(y)f(y)\,dy\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\left\{r^{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}}H_{N}^{-}f(r)+r^{\unicode[STIX]{x1D6FC}}H_{N}^{-}[bf](r)\right\}\nonumber\end{eqnarray}$$ for 
$x\in A(r)$, we obtain by Lemmas 4.2, 4.6 and 4.10 and Fubini’s theorem
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert bu_{1}\Vert _{L^{p_{2}^{\ast }}(A(r))}\right)^{q}\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\bigg\{\int _{0}^{1}\left(r^{-\tilde{\unicode[STIX]{x1D700}}_{1}+N/p_{2}^{\ast }+\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}-N}k(r)^{-N}\right)^{q}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{0}^{r}\left(t^{\tilde{\unicode[STIX]{x1D700}}_{1}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{0}^{1}\left(r^{-\tilde{\unicode[STIX]{x1D700}}_{1}+N/p_{2}^{\ast }+\unicode[STIX]{x1D6FC}-N/p_{2}}\right)^{q}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left(\int _{0}^{r}\left(t^{\tilde{\unicode[STIX]{x1D700}}_{1}}\unicode[STIX]{x1D714}(t)\Vert bf\Vert _{L^{p_{2}}(A(t))}\right)^{q}\,\frac{dt}{t}\right)\,\frac{dr}{r}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\bigg\{\int _{0}^{1}\left(t^{\tilde{\unicode[STIX]{x1D700}}_{1}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\left(\int _{t}^{1}r^{-\tilde{\unicode[STIX]{x1D700}}_{1}q}\,\frac{dr}{r}\right)\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{0}^{1}\left(t^{\tilde{\unicode[STIX]{x1D700}}_{1}}\unicode[STIX]{x1D714}(t)\Vert bf\Vert _{L^{p_{2}}(A(t))}\right)^{q}\left(\int _{t}^{1}r^{-\tilde{\unicode[STIX]{x1D700}}_{1}q}\,\frac{dr}{r}\right)\,\frac{dt}{t}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(A(t))}\right)^{q}\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C.\end{eqnarray}$$Similarly
$$\begin{eqnarray}\displaystyle & & \displaystyle b(x)u_{3}(x)\leqslant Cb(x)\int _{\mathbf{B}\setminus B(0,2|x|)}|y|^{\unicode[STIX]{x1D6FC}-N}f(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\left\{\int _{\mathbf{B}\setminus B(0,2|x|)}|y|^{\unicode[STIX]{x1D6FC}-N+\unicode[STIX]{x1D703}}f(y)\,dy+\int _{\mathbf{B}\setminus B(0,2|x|)}|y|^{\unicode[STIX]{x1D6FC}-N}b(y)f(y)\,dy\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\left\{r^{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}}H_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}}^{+}f(2r)+r^{\unicode[STIX]{x1D6FC}}H_{\unicode[STIX]{x1D6FC}}^{+}[bf](2r)\right\}\nonumber\end{eqnarray}$$ for 
$x\in A(r)$, we obtain by Lemmas 4.2, 4.7 and 4.11 and Fubini’s theorem
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert bu_{3}\Vert _{L^{p_{2}^{\ast }}(A(r))}\right)^{q}\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\bigg\{\int _{0}^{1}\left(r^{\tilde{\unicode[STIX]{x1D700}}_{2}}k(r)^{-N}\right)^{q}\left(\int _{r}^{1}\left(t^{-\tilde{\unicode[STIX]{x1D700}}_{2}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\,\frac{dt}{t}\right)\,\frac{dr}{r}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{0}^{1}r^{\tilde{\unicode[STIX]{x1D700}}_{2}q}\left(\int _{r}^{1}\left(t^{-\tilde{\unicode[STIX]{x1D700}}_{2}}\unicode[STIX]{x1D714}(t)\Vert bf\Vert _{L^{p_{2}}(A(t))}\right)^{q}\,\frac{dt}{t}\right)\,\frac{dr}{r}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\bigg\{\int _{0}^{1}\left(t^{-\tilde{\unicode[STIX]{x1D700}}_{2}}\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{p_{1}(\cdot )}(A(t))}\right)^{q}\left(\int _{0}^{t}r^{\tilde{\unicode[STIX]{x1D700}}_{2}q}\,\frac{dr}{r}\right)\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{0}^{1}\left(t^{-\tilde{\unicode[STIX]{x1D700}}_{2}}\unicode[STIX]{x1D714}(t)\Vert bf\Vert _{L^{p_{2}}(A(t))}\right)^{q}\left(\int _{0}^{t}r^{\tilde{\unicode[STIX]{x1D700}}_{2}q}\,\frac{dr}{r}\right)\,\frac{dt}{t}\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C\int _{0}^{1}\left(\unicode[STIX]{x1D714}(t)\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(A(t))}\right)^{q}\,\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C.\end{eqnarray}$$ Let 
$\tilde{A}(r)=A(r/2)\cup A(r)\cup A(2r)$. Since 
$u_{2}(x)\leqslant CI_{\unicode[STIX]{x1D6FC}}(f\unicode[STIX]{x1D712}_{(B(0,4r)\cap \mathbf{B})\setminus B(0,r/2)})(x)$ for 
$x\in A(r)$, we have by Lemma 3.10
$$\begin{eqnarray}\Vert bu_{2}\Vert _{L^{p_{2}^{\ast }}(A(r))}\leqslant C\Vert f\Vert _{L^{\unicode[STIX]{x1D6F7}_{d}}(\tilde{A}(r))},\end{eqnarray}$$so that
$$\begin{eqnarray}\int _{0}^{1}\left(\unicode[STIX]{x1D714}(r)\Vert bu_{2}\Vert _{L^{p_{2}^{\ast }}(A(r))}\right)^{q}\,\frac{dr}{r}\leqslant C.\end{eqnarray}$$Thus, by (4.10), (4.11) and (4.12), we obtain the required result.◻
Remark 4.16. Let 
$k(r)=a(\log (e+1/r))^{b}$ with 
$a\geqslant e^{b}(\log (e+1))^{-b}$ and 
$b\geqslant 1/N$. Then
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6FC}}(r)\sim r^{N/(N-\unicode[STIX]{x1D6FC})}(\log (e+r))^{b\unicode[STIX]{x1D6FC}N/(N-\unicode[STIX]{x1D6FC})+bN-1}\end{eqnarray}$$ as in Remark 3.4. Let 
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}<N$. If 
$\Vert f\Vert _{{\mathcal{H}}^{\unicode[STIX]{x1D6F7}_{d},1,\unicode[STIX]{x1D708}}(\mathbf{B})}\leqslant 1$ and 
$-N+\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D703}<\unicode[STIX]{x1D708}<0$, then we can find a constant 
$C>0$ such that
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbf{B}}|x|^{\unicode[STIX]{x1D708}}\left\{I_{\unicode[STIX]{x1D6FC}}f(x)^{N/(N-\unicode[STIX]{x1D6FC})}(\log (e+I_{\unicode[STIX]{x1D6FC}}f(x)))^{b\unicode[STIX]{x1D6FC}N/(N-\unicode[STIX]{x1D6FC})+bN-1}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\left(b(x)I_{\unicode[STIX]{x1D6FC}}f(x)\right)^{p_{2}^{\ast }}\right\}\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C.\nonumber\end{eqnarray}$$
