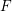1 Introduction
Let ![]() $X$ be a projective variety over a field
$X$ be a projective variety over a field ![]() $k$. When
$k$. When ![]() $k$ is the field of complex numbers, results from the minimal model program can be used to understand the birational geometry of
$k$ is the field of complex numbers, results from the minimal model program can be used to understand the birational geometry of ![]() $X$. However, when
$X$. However, when ![]() $k$ is an arbitrary field, many of these results and the tools used to prove them are unavailable. The most problematic situation is when
$k$ is an arbitrary field, many of these results and the tools used to prove them are unavailable. The most problematic situation is when ![]() $k$ is an imperfect field of characteristic
$k$ is an imperfect field of characteristic ![]() $p>0$, in which case there are three major difficulties. To begin with, since
$p>0$, in which case there are three major difficulties. To begin with, since ![]() $k$ is of characteristic
$k$ is of characteristic ![]() $p>0$,
$p>0$,
(I) Resolutions of singularities are not known to exist (see [Reference Hauser32]), and
(II) Vanishing theorems are false (Raynaud [Reference Raynaud56]).
A common workaround for (I) is to use de Jong’s theory of alterations [Reference de Jong38]. Circumventing (II), on the other hand, is more difficult. One useful approach is to exploit the Frobenius morphism ![]() $F:X\rightarrow X$ and its Grothendieck trace
$F:X\rightarrow X$ and its Grothendieck trace ![]() $F_{\ast }\unicode[STIX]{x1D714}_{X}^{\bullet }\rightarrow \unicode[STIX]{x1D714}_{X}^{\bullet }$; see [Reference Patakfalvi, Schwede and Tucker54]. However, for imperfect fields, this approach runs into another problem:
$F_{\ast }\unicode[STIX]{x1D714}_{X}^{\bullet }\rightarrow \unicode[STIX]{x1D714}_{X}^{\bullet }$; see [Reference Patakfalvi, Schwede and Tucker54]. However, for imperfect fields, this approach runs into another problem:
(III) Most applications of Frobenius techniques require
 $k$ to be
$k$ to be  $F$-finite, that is, satisfy
$F$-finite, that is, satisfy  $[k:k^{p}]<\infty$.
$[k:k^{p}]<\infty$.
This last issue arises since Grothendieck duality cannot be applied to the Frobenius if it is not finite. Recent advances in the minimal model program over imperfect fields due to Tanaka [Reference Tanaka64; Reference Tanaka65] suggest that it would be worthwhile to develop a systematic way to deal with (III).
Our first goal is to provide such a systematic way to reduce to the case when ![]() $k$ is
$k$ is ![]() $F$-finite. While passing to a perfect closure of
$F$-finite. While passing to a perfect closure of ![]() $k$ fixes the
$k$ fixes the ![]() $F$-finiteness issue, this operation can change the singularities of
$F$-finiteness issue, this operation can change the singularities of ![]() $X$ drastically. To preserve singularities, we prove the following scheme-theoretic version of the gamma construction of Hochster and Huneke [Reference Hochster and Huneke34].
$X$ drastically. To preserve singularities, we prove the following scheme-theoretic version of the gamma construction of Hochster and Huneke [Reference Hochster and Huneke34].
Theorem A. Let ![]() $X$ be a scheme essentially of finite type over a field
$X$ be a scheme essentially of finite type over a field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$, and let
$p>0$, and let ![]() ${\mathcal{Q}}$ be a set of properties in the following list: local complete intersection, Gorenstein, Cohen–Macaulay,
${\mathcal{Q}}$ be a set of properties in the following list: local complete intersection, Gorenstein, Cohen–Macaulay, ![]() $(S_{n})$, regular,
$(S_{n})$, regular, ![]() $(R_{n})$, normal, weakly normal, reduced, strongly
$(R_{n})$, normal, weakly normal, reduced, strongly ![]() $F$-regular,
$F$-regular, ![]() $F$-pure,
$F$-pure, ![]() $F$-rational,
$F$-rational, ![]() $F$-injective. Then, there exists a purely inseparable field extension
$F$-injective. Then, there exists a purely inseparable field extension ![]() $k\subseteq k^{\unicode[STIX]{x1D6E4}}$ such that
$k\subseteq k^{\unicode[STIX]{x1D6E4}}$ such that ![]() $k^{\unicode[STIX]{x1D6E4}}$ is
$k^{\unicode[STIX]{x1D6E4}}$ is ![]() $F$-finite and such that the projection morphism
$F$-finite and such that the projection morphism
is a homeomorphism that identifies ![]() ${\mathcal{P}}$ loci for every
${\mathcal{P}}$ loci for every ![]() ${\mathcal{P}}\in {\mathcal{Q}}$.
${\mathcal{P}}\in {\mathcal{Q}}$.
See Section 2.4 for definitions of ![]() $F$-singularities in the non-
$F$-singularities in the non-![]() $F$-finite setting. We in fact prove a slightly stronger version of Theorem A that allows
$F$-finite setting. We in fact prove a slightly stronger version of Theorem A that allows ![]() $k$ to be replaced by a complete local ring and allows finitely many schemes instead of just one; see Theorem 3.4. We use this added flexibility to prove that klt and log canonical pairs can be preserved under the gamma construction for surfaces and threefolds (Corollary 3.7), providing alternative proofs for the reduction steps in [Reference Tanaka64, Theorem 3.8] and [Reference Tanaka65, Theorem 4.12].
$k$ to be replaced by a complete local ring and allows finitely many schemes instead of just one; see Theorem 3.4. We use this added flexibility to prove that klt and log canonical pairs can be preserved under the gamma construction for surfaces and threefolds (Corollary 3.7), providing alternative proofs for the reduction steps in [Reference Tanaka64, Theorem 3.8] and [Reference Tanaka65, Theorem 4.12].
We note that parts of Theorems A and 3.4 are new even if ![]() $X$ is affine. Namely, the statements for weak normality are completely new, and the statements for
$X$ is affine. Namely, the statements for weak normality are completely new, and the statements for ![]() $F$-purity and
$F$-purity and ![]() $F$-injectivity in Theorem 3.4 were previously only known when the scheme
$F$-injectivity in Theorem 3.4 were previously only known when the scheme ![]() $X$ is the spectrum of a complete local ring [Reference Enescu and Hochster17, Lemma 2.9; Reference Ma45, Proposition 5.6].
$X$ is the spectrum of a complete local ring [Reference Enescu and Hochster17, Lemma 2.9; Reference Ma45, Proposition 5.6].
In the remainder of this paper, we give applications of the gamma construction (Theorem A) to the theory of asymptotic invariants of line bundles over arbitrary fields, in the spirit of recent work of Cutkosky [Reference Cutkosky8], Fulger–Kollár–Lehmann [Reference Fulger, Kollár and Lehmann21], Birkar [Reference Birkar4], and Burgos Gil–Gubler–Jell–Künnemann–Martin [Reference Burgos Gil, Gubler, Jell, Künnemann and Martin6]. See [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa14] for a survey of the theory for smooth complex varieties. While the main difficulty lies in positive characteristic, we also prove statements over fields of characteristic zero that are not necessarily algebraically closed.
Our first application provides a characterization of ampleness based on the asymptotic growth of higher cohomology groups. It is well known that if ![]() $X$ is a projective variety of dimension
$X$ is a projective variety of dimension ![]() $n>0$, then
$n>0$, then ![]() $h^{i}(X,{\mathcal{O}}_{X}(mL))=O(m^{n})$ for every Cartier divisor
$h^{i}(X,{\mathcal{O}}_{X}(mL))=O(m^{n})$ for every Cartier divisor ![]() $L$; see [Reference Lazarsfeld43, Example 1.2.20]. It is natural to ask when cohomology groups have submaximal growth. The following result says that ample Cartier divisors
$L$; see [Reference Lazarsfeld43, Example 1.2.20]. It is natural to ask when cohomology groups have submaximal growth. The following result says that ample Cartier divisors ![]() $L$ are characterized by having submaximal growth of higher cohomology groups for small perturbations of
$L$ are characterized by having submaximal growth of higher cohomology groups for small perturbations of ![]() $L$.
$L$.
Theorem B. Let ![]() $X$ be a projective variety of dimension
$X$ be a projective variety of dimension ![]() $n>0$ over a field
$n>0$ over a field ![]() $k$. Let
$k$. Let ![]() $L$ be an
$L$ be an ![]() $\mathbf{R}$-Cartier divisor on
$\mathbf{R}$-Cartier divisor on ![]() $X$, and consider the following property:
$X$, and consider the following property:
(⋆) There exists a very ample Cartier divisor
 $A$ on
$A$ on  $X$ and a real number
$X$ and a real number  $\unicode[STIX]{x1D700}>0$ such that for all
$\unicode[STIX]{x1D700}>0$ such that for all $$\begin{eqnarray}\widehat{h}^{i}(X,L-tA):=\limsup _{m\rightarrow \infty }\frac{h^{i}(X,{\mathcal{O}}_{X}(\lceil m(L-tA)\rceil ))}{m^{n}/n!}=0\end{eqnarray}$$
$$\begin{eqnarray}\widehat{h}^{i}(X,L-tA):=\limsup _{m\rightarrow \infty }\frac{h^{i}(X,{\mathcal{O}}_{X}(\lceil m(L-tA)\rceil ))}{m^{n}/n!}=0\end{eqnarray}$$ $i>0$ and for all
$i>0$ and for all  $t\in [0,\unicode[STIX]{x1D700})$.
$t\in [0,\unicode[STIX]{x1D700})$.
Then, ![]() $L$ is ample if and only if
$L$ is ample if and only if ![]() $L$ satisfies
$L$ satisfies ![]() $(\star )$ for some pair
$(\star )$ for some pair ![]() $(A,\unicode[STIX]{x1D700})$.
$(A,\unicode[STIX]{x1D700})$.
Here, the functions ![]() $\widehat{h}^{i}(X,-)$ are the asymptotic higher cohomological functions introduced by Küronya [Reference Küronya41]. Theorem B was first proved by de Fernex, Küronya, and Lazarsfeld over the complex numbers [Reference de Fernex, Küronya and Lazarsfeld12, Theorem 4.1]. In positive characteristic, an interesting aspect of our proof is that it requires the gamma construction (Theorem A) to reduce to the case when
$\widehat{h}^{i}(X,-)$ are the asymptotic higher cohomological functions introduced by Küronya [Reference Küronya41]. Theorem B was first proved by de Fernex, Küronya, and Lazarsfeld over the complex numbers [Reference de Fernex, Küronya and Lazarsfeld12, Theorem 4.1]. In positive characteristic, an interesting aspect of our proof is that it requires the gamma construction (Theorem A) to reduce to the case when ![]() $k$ is
$k$ is ![]() $F$-finite. The main outline of the proof follows that in [Reference de Fernex, Küronya and Lazarsfeld12], although overcoming the three problems described above requires care.
$F$-finite. The main outline of the proof follows that in [Reference de Fernex, Küronya and Lazarsfeld12], although overcoming the three problems described above requires care.
We note that our motivation for Theorem B comes from studying Seshadri constants, where Theorem B can be used to show that Seshadri constants and moving Seshadri constants of ![]() $\mathbf{Q}$-Cartier divisors can be described via jet separation on projective varieties over arbitrary fields, without smoothness assumptions [Reference Murayama50, Proposition 7.2.10]. As a result, one can extend [Reference Murayama49, Theorem A] to varieties with either singularities of dense
$\mathbf{Q}$-Cartier divisors can be described via jet separation on projective varieties over arbitrary fields, without smoothness assumptions [Reference Murayama50, Proposition 7.2.10]. As a result, one can extend [Reference Murayama49, Theorem A] to varieties with either singularities of dense ![]() $F$-injective type in characteristic zero, or varieties with
$F$-injective type in characteristic zero, or varieties with ![]() $F$-injective singularities in characteristic
$F$-injective singularities in characteristic ![]() $p>0$, without any assumptions on the ground field [Reference Murayama50, Theorem 7.3.1]. In [Reference Murayama50, Theorem D], we use a similar argument to prove a new, local version of the Angehrn–Siu theorem [Reference Angehrn and Siu1, Theorem 0.1] in characteristic zero without the use of Kodaira-type vanishing theorems.
$p>0$, without any assumptions on the ground field [Reference Murayama50, Theorem 7.3.1]. In [Reference Murayama50, Theorem D], we use a similar argument to prove a new, local version of the Angehrn–Siu theorem [Reference Angehrn and Siu1, Theorem 0.1] in characteristic zero without the use of Kodaira-type vanishing theorems.
Our second application is a special case of a conjecture of Boucksom, Broustet, and Pacienza [Reference Boucksom, Broustet and Pacienza5]. If ![]() $D$ is a pseudoeffective
$D$ is a pseudoeffective ![]() $\mathbf{R}$-Cartier divisor on a projective variety
$\mathbf{R}$-Cartier divisor on a projective variety ![]() $X$, then both the restricted base locus
$X$, then both the restricted base locus ![]() of
of ![]() $D$, which is a lower approximation of the stable base locus
$D$, which is a lower approximation of the stable base locus ![]() $\mathbf{B}(D)$ of
$\mathbf{B}(D)$ of ![]() $D$, and the non-nef locus
$D$, and the non-nef locus ![]() $\operatorname{NNef}(D)$ of
$\operatorname{NNef}(D)$ of ![]() $D$, which is defined in terms of divisorial valuations, are empty if and only if
$D$, which is defined in terms of divisorial valuations, are empty if and only if ![]() $D$ is nef. See Section 5.1 for definitions of both invariants. Boucksom, Broustet, and Pacienza conjectured that these two invariants of
$D$ is nef. See Section 5.1 for definitions of both invariants. Boucksom, Broustet, and Pacienza conjectured that these two invariants of ![]() $D$ are equal for all pseudoeffective
$D$ are equal for all pseudoeffective ![]() $\mathbf{R}$-Cartier divisors on normal projective varieties [Reference Boucksom, Broustet and Pacienza5, Conjecture 2.7]. We extend the known cases of their conjecture to projective varieties over arbitrary fields.
$\mathbf{R}$-Cartier divisors on normal projective varieties [Reference Boucksom, Broustet and Pacienza5, Conjecture 2.7]. We extend the known cases of their conjecture to projective varieties over arbitrary fields.
Theorem C. Let ![]() $X$ be a normal projective variety over a field
$X$ be a normal projective variety over a field ![]() $k$, and let
$k$, and let ![]() $D$ be a pseudoeffective
$D$ be a pseudoeffective ![]() $\mathbf{R}$-Cartier divisor on
$\mathbf{R}$-Cartier divisor on ![]() $X$. If
$X$. If ![]() $\operatorname{char}k=0$ and the non-klt locus of
$\operatorname{char}k=0$ and the non-klt locus of ![]() $X$ is at most zero-dimensional, or if
$X$ is at most zero-dimensional, or if ![]() $\operatorname{char}k=p>0$ and the non-strongly
$\operatorname{char}k=p>0$ and the non-strongly ![]() $F$-regular locus of
$F$-regular locus of ![]() $X$ is at most zero-dimensional, then
$X$ is at most zero-dimensional, then
This extends theorems of Nakayama [Reference Nakayama52, Lemma V.1.9(1)] (in the smooth case) and Cacciola–Di Biagio [Reference Cacciola and Di Biagio7, Corollary 4.9] over the complex numbers, and of Mustaţă [Reference Mustaţă51, Theorem 7.2] (in the regular case) and Sato [Reference Sato57, Corollary 4.8] over ![]() $F$-finite fields of characteristic
$F$-finite fields of characteristic ![]() $p>0$.
$p>0$.
Outline
This paper is structured as follows: in Section 2, we review some basic material, including the necessary background on ![]() $F$-finiteness,
$F$-finiteness, ![]() $F$-singularities, and test ideals. In Section 3, we prove Theorem 3.4, which is a stronger version of Theorem A. We use this stronger version in some applications to the minimal model program over imperfect fields in Section 3.2. The last two sections are devoted to our applications of the gamma construction. In Section 4, we prove Theorem B after reviewing some background on asymptotic cohomological functions. An important ingredient is a lemma on base loci (Proposition 4.6) analogous to [Reference de Fernex, Küronya and Lazarsfeld12, Proposition 3.1]. In Section 5, we prove Theorem C after giving some background on restricted base loci and non-nef loci. Finally, in Appendix A, we prove some results on
$F$-singularities, and test ideals. In Section 3, we prove Theorem 3.4, which is a stronger version of Theorem A. We use this stronger version in some applications to the minimal model program over imperfect fields in Section 3.2. The last two sections are devoted to our applications of the gamma construction. In Section 4, we prove Theorem B after reviewing some background on asymptotic cohomological functions. An important ingredient is a lemma on base loci (Proposition 4.6) analogous to [Reference de Fernex, Küronya and Lazarsfeld12, Proposition 3.1]. In Section 5, we prove Theorem C after giving some background on restricted base loci and non-nef loci. Finally, in Appendix A, we prove some results on ![]() $F$-injective rings for which we could not find a suitable reference, and in Appendix B, we describe different notions of strong
$F$-injective rings for which we could not find a suitable reference, and in Appendix B, we describe different notions of strong ![]() $F$-regularity for non-
$F$-regularity for non-![]() $F$-finite rings.
$F$-finite rings.
Notation
All rings will be commutative with identity. If ![]() $R$ is a ring, then
$R$ is a ring, then ![]() $R^{\circ }$ denotes the complement of the union of the minimal primes of
$R^{\circ }$ denotes the complement of the union of the minimal primes of ![]() $R$. A variety is a reduced and irreducible scheme that is separated and of finite type over a field. A complete scheme is a scheme that is proper over a field. Intersection products are defined using Euler characteristics; see [Reference Kleiman40, Appendix B].
$R$. A variety is a reduced and irreducible scheme that is separated and of finite type over a field. A complete scheme is a scheme that is proper over a field. Intersection products are defined using Euler characteristics; see [Reference Kleiman40, Appendix B].
Let ![]() $\mathbf{k}\in \{\mathbf{Q},\mathbf{R}\}$. A
$\mathbf{k}\in \{\mathbf{Q},\mathbf{R}\}$. A ![]() $\mathbf{k}$-Cartier divisor (resp.
$\mathbf{k}$-Cartier divisor (resp. ![]() $\mathbf{k}$-Weil divisor) is an element of
$\mathbf{k}$-Weil divisor) is an element of ![]() $\operatorname{Div}_{\mathbf{k}}(X):=\operatorname{Div}(X)\otimes _{\mathbf{Z}}\mathbf{k}$ (resp.
$\operatorname{Div}_{\mathbf{k}}(X):=\operatorname{Div}(X)\otimes _{\mathbf{Z}}\mathbf{k}$ (resp. ![]() $\operatorname{WDiv}_{\mathbf{k}}(X):=\operatorname{WDiv}(X)\otimes _{\mathbf{Z}}\mathbf{k}$). We denote
$\operatorname{WDiv}_{\mathbf{k}}(X):=\operatorname{WDiv}(X)\otimes _{\mathbf{Z}}\mathbf{k}$). We denote ![]() $\mathbf{k}$-linear equivalence (resp.
$\mathbf{k}$-linear equivalence (resp. ![]() $\mathbf{k}$-numerical equivalence) by
$\mathbf{k}$-numerical equivalence) by ![]() ${\sim}_{\mathbf{k}}$ (resp.
${\sim}_{\mathbf{k}}$ (resp. ![]() $\equiv _{\mathbf{k}}$). We then set
$\equiv _{\mathbf{k}}$). We then set ![]() $N_{\mathbf{k}}^{1}(X):=\operatorname{Div}_{\mathbf{k}}(X)/\equiv _{\mathbf{k}}$, which is a finite-dimensional
$N_{\mathbf{k}}^{1}(X):=\operatorname{Div}_{\mathbf{k}}(X)/\equiv _{\mathbf{k}}$, which is a finite-dimensional ![]() $\mathbf{k}$-vector space if
$\mathbf{k}$-vector space if ![]() $X$ is a complete scheme [Reference Cutkosky8, Proposition 2.3]. We fix compatible norms
$X$ is a complete scheme [Reference Cutkosky8, Proposition 2.3]. We fix compatible norms ![]() $\Vert \cdot \Vert$ on
$\Vert \cdot \Vert$ on ![]() $N_{\mathbf{k}}^{1}(X)$ for
$N_{\mathbf{k}}^{1}(X)$ for ![]() $\mathbf{k}\in \{\mathbf{Q},\mathbf{R}\}$.
$\mathbf{k}\in \{\mathbf{Q},\mathbf{R}\}$.
If ![]() $X$ is a scheme of prime characteristic
$X$ is a scheme of prime characteristic ![]() $p>0$, then we denote by
$p>0$, then we denote by ![]() $F:X\rightarrow X$ the (absolute) Frobenius morphism, which is given by the identity map on points, and the
$F:X\rightarrow X$ the (absolute) Frobenius morphism, which is given by the identity map on points, and the ![]() $p$-power map
$p$-power map

on structure sheaves, where ![]() $U\subseteq X$ is an open subset. If
$U\subseteq X$ is an open subset. If ![]() $R$ is a ring of prime characteristic
$R$ is a ring of prime characteristic ![]() $p>0$, we denote the corresponding ring homomorphism by
$p>0$, we denote the corresponding ring homomorphism by ![]() $F:R\rightarrow F_{\ast }R$. For every integer
$F:R\rightarrow F_{\ast }R$. For every integer ![]() $e\geqslant 0$, the
$e\geqslant 0$, the ![]() $e$th iterate of the Frobenius morphisms for schemes or rings is denoted by
$e$th iterate of the Frobenius morphisms for schemes or rings is denoted by ![]() $F^{e}$.
$F^{e}$.
2 Definitions and preliminaries
2.1 Morphisms essentially of finite type
Recall that a ring homomorphism ![]() $A\rightarrow B$ is essentially of finite type if
$A\rightarrow B$ is essentially of finite type if ![]() $B$ is isomorphic (as an
$B$ is isomorphic (as an ![]() $A$-algebra) to a localization of an
$A$-algebra) to a localization of an ![]() $A$-algebra of finite type. The corresponding scheme-theoretic notion is the following:
$A$-algebra of finite type. The corresponding scheme-theoretic notion is the following:
Definition 2.1. [Reference Nayak53, Definition 2.1(a)]
Let ![]() $f:X\rightarrow Y$ be a morphism of schemes. We say that
$f:X\rightarrow Y$ be a morphism of schemes. We say that ![]() $f$ is locally essentially of finite type if there is an affine open covering
$f$ is locally essentially of finite type if there is an affine open covering ![]() $Y=\bigcup _{i}\operatorname{Spec}A_{i}$ such that for every
$Y=\bigcup _{i}\operatorname{Spec}A_{i}$ such that for every ![]() $i$, there is an affine open covering
$i$, there is an affine open covering
for which the corresponding ring homomorphisms ![]() $A_{i}\rightarrow B_{ij}$ are essentially of finite type. We say that
$A_{i}\rightarrow B_{ij}$ are essentially of finite type. We say that ![]() $f$ is essentially of finite type if it is locally essentially of finite type and quasicompact.
$f$ is essentially of finite type if it is locally essentially of finite type and quasicompact.
The class of morphisms (locally) essentially of finite type is closed under composition and base change [Reference Nayak53, (2.2)].
2.2 Base loci
In this subsection, we define the base ideal of a Cartier divisor and related objects.
Definition 2.2. (see [Reference Lazarsfeld43, Definition 1.1.8])
Let ![]() $X$ be a complete scheme over a field
$X$ be a complete scheme over a field ![]() $k$, and let
$k$, and let ![]() $D$ be a Cartier divisor. The complete linear series associated to
$D$ be a Cartier divisor. The complete linear series associated to ![]() $D$ is the projective space
$D$ is the projective space ![]() $|D|:=\mathbf{P}(H^{0}(X,{\mathcal{O}}_{X}(D))^{\vee })$ of one-dimensional subspaces of
$|D|:=\mathbf{P}(H^{0}(X,{\mathcal{O}}_{X}(D))^{\vee })$ of one-dimensional subspaces of ![]() $H^{0}(X,{\mathcal{O}}_{X}(D))$. The base ideal of
$H^{0}(X,{\mathcal{O}}_{X}(D))$. The base ideal of ![]() $D$ is
$D$ is
The base scheme ![]() $\operatorname{Bs}(|D|)$ of
$\operatorname{Bs}(|D|)$ of ![]() $D$ is the closed subscheme of
$D$ is the closed subscheme of ![]() $X$ defined by
$X$ defined by ![]() $\mathfrak{b}(|D|)$, and the base locus of
$\mathfrak{b}(|D|)$, and the base locus of ![]() $D$ is the underlying closed subset
$D$ is the underlying closed subset ![]() $\operatorname{Bs}(|D|)_{\text{red}}$.
$\operatorname{Bs}(|D|)_{\text{red}}$.
We need the following description for how base ideals transform under birational morphisms.
Lemma 2.3. Let ![]() $f:X^{\prime }\rightarrow X$ be a birational morphism between complete varieties, where
$f:X^{\prime }\rightarrow X$ be a birational morphism between complete varieties, where ![]() $X$ is normal. Then, for every Cartier divisor
$X$ is normal. Then, for every Cartier divisor ![]() $D$ on
$D$ on ![]() $X$, we have
$X$, we have ![]() $f^{-1}\mathfrak{b}(|D|)\cdot {\mathcal{O}}_{X^{\prime }}=\mathfrak{b}(|f^{\ast }D|)$.
$f^{-1}\mathfrak{b}(|D|)\cdot {\mathcal{O}}_{X^{\prime }}=\mathfrak{b}(|f^{\ast }D|)$.
Proof. Since ![]() $X$ is normal, we have
$X$ is normal, we have ![]() $f_{\ast }{\mathcal{O}}_{X^{\prime }}\simeq {\mathcal{O}}_{X}$ [Reference Hartshorne29, Proof of Corollary III.11.4]. By the projection formula, we then have
$f_{\ast }{\mathcal{O}}_{X^{\prime }}\simeq {\mathcal{O}}_{X}$ [Reference Hartshorne29, Proof of Corollary III.11.4]. By the projection formula, we then have
and the lemma then follows by pulling back the evaluation map (1).◻
Next, we define a stable version of the base locus.
Definition 2.4. (see [Reference Lazarsfeld43, Definition 2.1.20])
Let ![]() $X$ be a complete scheme over a field, and let
$X$ be a complete scheme over a field, and let ![]() $D$ be a Cartier divisor on
$D$ be a Cartier divisor on ![]() $X$. The stable base locus of
$X$. The stable base locus of ![]() $D$ is the closed subset
$D$ is the closed subset
of ![]() $X$, where the intersection runs over every integer
$X$, where the intersection runs over every integer ![]() $m>0$. The Noetherian property implies
$m>0$. The Noetherian property implies ![]() $\mathbf{B}(D)=\mathbf{B}(nD)$ for every integer
$\mathbf{B}(D)=\mathbf{B}(nD)$ for every integer ![]() $n>0$ [Reference Lazarsfeld43, Example 2.1.23], hence the formula (2) can be used for
$n>0$ [Reference Lazarsfeld43, Example 2.1.23], hence the formula (2) can be used for ![]() $\mathbf{Q}$-Cartier divisors
$\mathbf{Q}$-Cartier divisors ![]() $D$ by taking the intersection over every integer
$D$ by taking the intersection over every integer ![]() $m>0$ such that
$m>0$ such that ![]() $mD$ is integral.
$mD$ is integral.
The stable base locus is not a numerical invariant of ![]() $D$ [Reference Lazarsfeld44, Example 10.3.3]. In Section 5.1, we define the restricted base locus
$D$ [Reference Lazarsfeld44, Example 10.3.3]. In Section 5.1, we define the restricted base locus ![]() , which is a numerically invariant approximation of
, which is a numerically invariant approximation of ![]() $\mathbf{B}(D)$.
$\mathbf{B}(D)$.
2.3  $F$-finite schemes
$F$-finite schemes
As mentioned in Section 1, in positive characteristic, one often needs to restrict or reduce to the case when the Frobenius morphism is finite. We isolate this class of schemes.
Definition 2.5. Let ![]() $X$ be a scheme of prime characteristic
$X$ be a scheme of prime characteristic ![]() $p>0$. We say that
$p>0$. We say that ![]() $X$ is
$X$ is ![]() $F$-finite if the (absolute) Frobenius morphism
$F$-finite if the (absolute) Frobenius morphism ![]() $F:X\rightarrow X$ is finite. We say that a ring
$F:X\rightarrow X$ is finite. We say that a ring ![]() $R$ of prime characteristic
$R$ of prime characteristic ![]() $p>0$ is
$p>0$ is ![]() $F$-finite if
$F$-finite if ![]() $\operatorname{Spec}R$ is
$\operatorname{Spec}R$ is ![]() $F$-finite, or equivalently if
$F$-finite, or equivalently if ![]() $F:R\rightarrow F_{\ast }R$ is module-finite.
$F:R\rightarrow F_{\ast }R$ is module-finite.
Note that a field ![]() $k$ is
$k$ is ![]() $F$-finite if and only if
$F$-finite if and only if ![]() $[k:k^{p}]<\infty$.
$[k:k^{p}]<\infty$. ![]() $F$-finite schemes are ubiquitous in geometric contexts because of the following:
$F$-finite schemes are ubiquitous in geometric contexts because of the following:
Example 2.6. (see [Reference Kunz42, p. 999])
If ![]() $X$ is a scheme that is locally essentially of finite type over an
$X$ is a scheme that is locally essentially of finite type over an ![]() $F$-finite scheme of prime characteristic
$F$-finite scheme of prime characteristic ![]() $p>0$, then
$p>0$, then ![]() $X$ is
$X$ is ![]() $F$-finite. In particular, schemes essentially of finite type over perfect or
$F$-finite. In particular, schemes essentially of finite type over perfect or ![]() $F$-finite fields are
$F$-finite fields are ![]() $F$-finite.
$F$-finite.
If a scheme ![]() $X$ of prime characteristic
$X$ of prime characteristic ![]() $p>0$ is
$p>0$ is ![]() $F$-finite, then Grothendieck duality can be applied to the Frobenius morphism since it is finite [Reference Hartshorne28, III.6]. The
$F$-finite, then Grothendieck duality can be applied to the Frobenius morphism since it is finite [Reference Hartshorne28, III.6]. The ![]() $F$-finiteness condition implies other desirable conditions as well.
$F$-finiteness condition implies other desirable conditions as well.
Theorem 2.7. [Reference Kunz42, Theorem 2.5; Reference Gabber22, Remark 13.6]
Let ![]() $R$ be a Noetherian
$R$ be a Noetherian ![]() $F$-finite ring of prime characteristic
$F$-finite ring of prime characteristic ![]() $p>0$. Then,
$p>0$. Then, ![]() $R$ is excellent and is isomorphic to a quotient of a regular ring of finite Krull dimension. In particular,
$R$ is excellent and is isomorphic to a quotient of a regular ring of finite Krull dimension. In particular, ![]() $R$ admits a dualizing complex
$R$ admits a dualizing complex ![]() $\unicode[STIX]{x1D714}_{R}^{\bullet }$.
$\unicode[STIX]{x1D714}_{R}^{\bullet }$.
2.4  $F$-singularities
$F$-singularities
We review some classes of singularities defined using the Frobenius morphism. See [Reference Takagi and Watanabe62] for a survey, and see Appendix B for more material on strong ![]() $F$-regularity for non-
$F$-regularity for non-![]() $F$-finite rings. Recall that a ring homomorphism
$F$-finite rings. Recall that a ring homomorphism ![]() $R\rightarrow S$ is pure if the homomorphism
$R\rightarrow S$ is pure if the homomorphism ![]() $R\otimes _{R}M\rightarrow S\otimes _{R}M$ is injective for every
$R\otimes _{R}M\rightarrow S\otimes _{R}M$ is injective for every ![]() $R$-module
$R$-module ![]() $M$.
$M$.
Definition 2.8. [Reference Hashimoto30, Definition 3.3; Reference Hochster and Roberts36, p. 121]
Let ![]() $R$ be a Noetherian ring of prime characteristic
$R$ be a Noetherian ring of prime characteristic ![]() $p>0$. For every
$p>0$. For every ![]() $c\in R$ and every integer
$c\in R$ and every integer ![]() $e>0$, we denote by
$e>0$, we denote by ![]() $\unicode[STIX]{x1D706}_{c}^{e}$ the composition
$\unicode[STIX]{x1D706}_{c}^{e}$ the composition
If ![]() $c\in R$, then following [Reference Datta and Smith10, Definition 6.1.1] we say that
$c\in R$, then following [Reference Datta and Smith10, Definition 6.1.1] we say that ![]() $R$ is
$R$ is ![]() $F$-pure along
$F$-pure along ![]() $c$ if
$c$ if ![]() $\unicode[STIX]{x1D706}_{c}^{e}$ is pure for some
$\unicode[STIX]{x1D706}_{c}^{e}$ is pure for some ![]() $e>0$, and that
$e>0$, and that
(a)
 $R$ is strongly
$R$ is strongly  $F$-regular if every localization
$F$-regular if every localization  $R_{\mathfrak{p}}$ of
$R_{\mathfrak{p}}$ of  $R$ is
$R$ is  $F$-pure along every
$F$-pure along every  $c\in R_{\mathfrak{p}}^{\circ }$; and
$c\in R_{\mathfrak{p}}^{\circ }$; and(b)
 $R$ is
$R$ is  $F$-pure if
$F$-pure if  $R$ is
$R$ is  $F$-pure along
$F$-pure along  $1\in R$.
$1\in R$.
Note that (a) is not the usual definition (Definition B.1(a)) for strong ![]() $F$-regularity, which coincides with ours for
$F$-regularity, which coincides with ours for ![]() $F$-finite rings. See Appendix B for a description of the relationship between different notions of strong
$F$-finite rings. See Appendix B for a description of the relationship between different notions of strong ![]() $F$-regularity for non-
$F$-regularity for non-![]() $F$-finite rings.
$F$-finite rings.
To define ![]() $F$-rationality, we recall that if
$F$-rationality, we recall that if ![]() $R$ is a Noetherian ring, then a sequence of elements
$R$ is a Noetherian ring, then a sequence of elements ![]() $x_{1},x_{2},\ldots ,x_{n}\in R$ is a sequence of parameters if for every prime ideal
$x_{1},x_{2},\ldots ,x_{n}\in R$ is a sequence of parameters if for every prime ideal ![]() $\mathfrak{p}$ containing
$\mathfrak{p}$ containing ![]() $(x_{1},x_{2},\ldots ,x_{n})$, the images of
$(x_{1},x_{2},\ldots ,x_{n})$, the images of ![]() $x_{1},x_{2},\ldots ,x_{n}$ in
$x_{1},x_{2},\ldots ,x_{n}$ in ![]() $R_{\mathfrak{p}}$ are part of a system of parameters in
$R_{\mathfrak{p}}$ are part of a system of parameters in ![]() $R_{\mathfrak{p}}$ [Reference Hochster and Huneke33, Definition 2.1].
$R_{\mathfrak{p}}$ [Reference Hochster and Huneke33, Definition 2.1].
Definition 2.9. [Reference Fedder and Watanabe19, Definition 1.10]
A Noetherian ring of prime characteristic ![]() $p>0$ is
$p>0$ is ![]() $F$-rational if every ideal generated by a sequence of parameters in
$F$-rational if every ideal generated by a sequence of parameters in ![]() $R$ is tightly closed in
$R$ is tightly closed in ![]() $R$.
$R$.
See [Reference Hochster and Huneke33, Definition 3.1] for the definition of tight closure. Finally, we define ![]() $F$-injective singularities.
$F$-injective singularities.
Definition 2.10. [Reference Fedder18, Definition on p. 473]
A Noetherian ring ![]() $R$ of prime characteristic
$R$ of prime characteristic ![]() $p>0$ is
$p>0$ is ![]() $F$-injective if, for every maximal ideal
$F$-injective if, for every maximal ideal ![]() $\mathfrak{m}\subseteq R$, the
$\mathfrak{m}\subseteq R$, the ![]() $R_{\mathfrak{m}}$-module homomorphism
$R_{\mathfrak{m}}$-module homomorphism ![]() $H_{\mathfrak{m}}^{i}(F):H_{\mathfrak{m}}^{i}(R_{\mathfrak{m}})\rightarrow H_{\mathfrak{m}}^{i}(F_{\ast }R_{\mathfrak{m}})$ induced by Frobenius is injective for all
$H_{\mathfrak{m}}^{i}(F):H_{\mathfrak{m}}^{i}(R_{\mathfrak{m}})\rightarrow H_{\mathfrak{m}}^{i}(F_{\ast }R_{\mathfrak{m}})$ induced by Frobenius is injective for all ![]() $i$.
$i$.
We prove some basic results about ![]() $F$-injective rings in Appendix A.
$F$-injective rings in Appendix A.
The relationship between these classes of singularities can be summarized as follows:

2.5 Test ideals
We review the theory of test ideals, which are the positive characteristic analogues of multiplier ideals. We recall that following [Reference Lazarsfeld43, Definition 2.4.14], a collection ![]() $\mathfrak{a}_{\bullet }:=\{\mathfrak{a}_{m}\}_{m=1}^{\infty }$ of coherent ideal sheaves
$\mathfrak{a}_{\bullet }:=\{\mathfrak{a}_{m}\}_{m=1}^{\infty }$ of coherent ideal sheaves ![]() $\mathfrak{a}_{m}\subseteq {\mathcal{O}}_{X}$ on a locally Noetherian scheme
$\mathfrak{a}_{m}\subseteq {\mathcal{O}}_{X}$ on a locally Noetherian scheme ![]() $X$ is a graded family of ideals if
$X$ is a graded family of ideals if ![]() $\mathfrak{a}_{m}\cdot \mathfrak{a}_{n}\subseteq \mathfrak{a}_{m+n}$ for all
$\mathfrak{a}_{m}\cdot \mathfrak{a}_{n}\subseteq \mathfrak{a}_{m+n}$ for all ![]() $m,n\geqslant 1$. We now fix the following notational conventions for pairs.
$m,n\geqslant 1$. We now fix the following notational conventions for pairs.
Definition 2.11. (cf. [Reference Schwede59, Definition 2.3])
A pair ![]() $(X,\mathfrak{a}_{\bullet }^{\unicode[STIX]{x1D706}})$ consists of
$(X,\mathfrak{a}_{\bullet }^{\unicode[STIX]{x1D706}})$ consists of
(i) an excellent reduced Noetherian scheme
 $X$; and
$X$; and(ii) a symbol
 $\mathfrak{a}_{\bullet }^{\unicode[STIX]{x1D706}}$ where
$\mathfrak{a}_{\bullet }^{\unicode[STIX]{x1D706}}$ where  $\mathfrak{a}_{\bullet }$ is a graded family of ideals on
$\mathfrak{a}_{\bullet }$ is a graded family of ideals on  $X$ such that for every open affine subset
$X$ such that for every open affine subset  $U=\operatorname{Spec}R\subseteq X$, we have
$U=\operatorname{Spec}R\subseteq X$, we have  $\mathfrak{a}_{m}(U)\cap R^{\circ }\neq \emptyset$ for some
$\mathfrak{a}_{m}(U)\cap R^{\circ }\neq \emptyset$ for some  $m>0$, and where
$m>0$, and where  $\unicode[STIX]{x1D706}$ is a positive real number.
$\unicode[STIX]{x1D706}$ is a positive real number.
We drop ![]() $\unicode[STIX]{x1D706}$ from our notation if
$\unicode[STIX]{x1D706}$ from our notation if ![]() $\unicode[STIX]{x1D706}=1$. If
$\unicode[STIX]{x1D706}=1$. If ![]() $\mathfrak{a}_{\bullet }=\{\mathfrak{a}^{m}\}_{m=1}^{\infty }$ for some fixed ideal sheaf
$\mathfrak{a}_{\bullet }=\{\mathfrak{a}^{m}\}_{m=1}^{\infty }$ for some fixed ideal sheaf ![]() $\mathfrak{a}$, then we denote the pair by
$\mathfrak{a}$, then we denote the pair by ![]() $(X,\mathfrak{a}^{t})$. If
$(X,\mathfrak{a}^{t})$. If ![]() $X=\operatorname{Spec}R$ for a ring
$X=\operatorname{Spec}R$ for a ring ![]() $R$, then we denote the pair by
$R$, then we denote the pair by ![]() $(R,\mathfrak{a}_{\bullet }^{\unicode[STIX]{x1D706}})$.
$(R,\mathfrak{a}_{\bullet }^{\unicode[STIX]{x1D706}})$.
We now define test ideals for ![]() $F$-finite schemes of prime characteristic
$F$-finite schemes of prime characteristic ![]() $p>0$. See [Reference Schwede and Tucker61] and [Reference Takagi and Watanabe62, Section 5] for overviews of the theory. We take Schwede’s characterization of test ideals via
$p>0$. See [Reference Schwede and Tucker61] and [Reference Takagi and Watanabe62, Section 5] for overviews of the theory. We take Schwede’s characterization of test ideals via ![]() $F$-compatibility [Reference Schwede59] as our definition.
$F$-compatibility [Reference Schwede59] as our definition.
Definition 2.12. [Reference Schwede59, Definition 3.1 and Theorem 6.3]
Let ![]() $(R,\mathfrak{a}^{t})$ be a pair such that
$(R,\mathfrak{a}^{t})$ be a pair such that ![]() $R$ is an
$R$ is an ![]() $F$-finite ring of prime characteristic
$F$-finite ring of prime characteristic ![]() $p>0$. An ideal
$p>0$. An ideal ![]() $J\subseteq R$ is uniformly
$J\subseteq R$ is uniformly ![]() $(\mathfrak{a}^{t},F)$-compatible if for every integer
$(\mathfrak{a}^{t},F)$-compatible if for every integer ![]() $e>0$ and every
$e>0$ and every ![]() $\unicode[STIX]{x1D711}\in \operatorname{Hom}_{R}(F_{\ast }^{e}R,R)$, we have
$\unicode[STIX]{x1D711}\in \operatorname{Hom}_{R}(F_{\ast }^{e}R,R)$, we have
Now let ![]() $(X,\mathfrak{a}^{t})$ be a pair such that
$(X,\mathfrak{a}^{t})$ be a pair such that ![]() $X$ is an
$X$ is an ![]() $F$-finite scheme of prime characteristic
$F$-finite scheme of prime characteristic ![]() $p>0$. The test ideal
$p>0$. The test ideal ![]() $\unicode[STIX]{x1D70F}(X,\mathfrak{a}^{t})$ is defined locally on each affine open subset
$\unicode[STIX]{x1D70F}(X,\mathfrak{a}^{t})$ is defined locally on each affine open subset ![]() $U=\operatorname{Spec}R\subseteq X$ as the smallest ideal that is uniformly
$U=\operatorname{Spec}R\subseteq X$ as the smallest ideal that is uniformly ![]() $(\mathfrak{a}^{t},F)$-compatible and intersects
$(\mathfrak{a}^{t},F)$-compatible and intersects ![]() $R^{\circ }$.
$R^{\circ }$.
The test ideal is well defined by [Reference Schwede60, Proposition 3.23(ii)], and exists by [Reference Schwede60, Theorem 3.18]. Formal properties analogous to those for multiplier ideals hold for test ideals; see [Reference Takagi and Watanabe62, Proposition 5.6]. We can therefore define the following asymptotic version of test ideals:
Definition 2.13. [Reference Sato57, Proposition-Definition 2.16]
Let ![]() $(X,\mathfrak{a}_{\bullet }^{\unicode[STIX]{x1D706}})$ be a pair such that
$(X,\mathfrak{a}_{\bullet }^{\unicode[STIX]{x1D706}})$ be a pair such that ![]() $X$ is
$X$ is ![]() $F$-finite of prime characteristic
$F$-finite of prime characteristic ![]() $p>0$. The asymptotic test ideal
$p>0$. The asymptotic test ideal ![]() $\unicode[STIX]{x1D70F}(X,\mathfrak{a}_{\bullet }^{\unicode[STIX]{x1D706}})$ is defined to be
$\unicode[STIX]{x1D70F}(X,\mathfrak{a}_{\bullet }^{\unicode[STIX]{x1D706}})$ is defined to be ![]() $\unicode[STIX]{x1D70F}(X,\mathfrak{a}_{m}^{\unicode[STIX]{x1D706}/m})$ for sufficiently large and divisible
$\unicode[STIX]{x1D70F}(X,\mathfrak{a}_{m}^{\unicode[STIX]{x1D706}/m})$ for sufficiently large and divisible ![]() $m$.
$m$.
We often drop ![]() $X$ from our notation if it is clear from context. Similarly, we drop
$X$ from our notation if it is clear from context. Similarly, we drop ![]() $\mathfrak{a}^{t}$ or
$\mathfrak{a}^{t}$ or ![]() $\mathfrak{a}_{\bullet }^{\unicode[STIX]{x1D706}}$ from our notation when working with the scheme itself.
$\mathfrak{a}_{\bullet }^{\unicode[STIX]{x1D706}}$ from our notation when working with the scheme itself.
The subadditivity theorem holds for both test ideals and asymptotic test ideals on regular complete local rings [Reference Hara and Yoshida27, Theorem 6.10(2)], and therefore also holds on all regular ![]() $F$-finite schemes
$F$-finite schemes ![]() $X$, since for
$X$, since for ![]() $F$-finite schemes, the formation of test ideals is compatible with localization and completion [Reference Hara and Takagi26, Propositions 3.1 and 3.2].
$F$-finite schemes, the formation of test ideals is compatible with localization and completion [Reference Hara and Takagi26, Propositions 3.1 and 3.2].
The following example will be the most important in our applications.
Example 2.14. (see [Reference Sato57, Definition 2.36])
Let ![]() $X$ be a complete reduced scheme over an
$X$ be a complete reduced scheme over an ![]() $F$-finite field of characteristic
$F$-finite field of characteristic ![]() $p>0$. If
$p>0$. If ![]() $D$ is a Cartier divisor such that
$D$ is a Cartier divisor such that ![]() $H^{0}(X,{\mathcal{O}}_{X}(mD))\neq 0$ for some positive integer
$H^{0}(X,{\mathcal{O}}_{X}(mD))\neq 0$ for some positive integer ![]() $m$, then for every real number
$m$, then for every real number ![]() $t>0$, we set
$t>0$, we set
If ![]() $D$ is a
$D$ is a ![]() $\mathbf{Q}$-Cartier divisor such that
$\mathbf{Q}$-Cartier divisor such that ![]() $H^{0}(X,{\mathcal{O}}_{X}(mD))\neq 0$ for some sufficiently divisible
$H^{0}(X,{\mathcal{O}}_{X}(mD))\neq 0$ for some sufficiently divisible ![]() $m>0$, then for every real number
$m>0$, then for every real number ![]() $\unicode[STIX]{x1D706}>0$, we set
$\unicode[STIX]{x1D706}>0$, we set
where ![]() $\mathfrak{a}_{m}(D)=\mathfrak{b}(|mD|)$ if
$\mathfrak{a}_{m}(D)=\mathfrak{b}(|mD|)$ if ![]() $mD$ is integral, and
$mD$ is integral, and ![]() $0$ otherwise. See [Reference Lazarsfeld43, Example 2.4.16(ii)].
$0$ otherwise. See [Reference Lazarsfeld43, Example 2.4.16(ii)].
3 The gamma construction of Hochster–Huneke
Our goal in this section is to prove Theorem A, which is a scheme-theoretic version of the gamma construction of Hochster and Huneke [Reference Hochster and Huneke34]. Hochster and Huneke first introduced the gamma construction in order to prove that test elements (in the sense of tight closure) exist for rings that are essentially of finite type over an excellent local ring of prime characteristic ![]() $p>0$. However, to the best of our knowledge, their construction has not been applied explicitly in a geometric context.
$p>0$. However, to the best of our knowledge, their construction has not been applied explicitly in a geometric context.
As mentioned in Section 1, Theorem A provides a systematic way to reduce to the case when the ground field ![]() $k$ is
$k$ is ![]() $F$-finite. We in fact show a more general result (Theorem 3.4), which allows for the ground field
$F$-finite. We in fact show a more general result (Theorem 3.4), which allows for the ground field ![]() $k$ to be replaced by a complete local ring, and allows finitely many schemes instead of just one. After proving Theorems A and 3.4 in Section 3.1, we prove that the
$k$ to be replaced by a complete local ring, and allows finitely many schemes instead of just one. After proving Theorems A and 3.4 in Section 3.1, we prove that the ![]() $F$-pure locus is open in schemes essentially of finite type over excellent local rings (Corollary 3.5). We then give some basic applications of Theorem 3.4 to the minimal model program over imperfect fields in Section 3.2.
$F$-pure locus is open in schemes essentially of finite type over excellent local rings (Corollary 3.5). We then give some basic applications of Theorem 3.4 to the minimal model program over imperfect fields in Section 3.2.
3.1 The construction and proof of Theorem A
We start with the following account of Hochster and Huneke’s construction.
Construction 3.1. [Reference Hochster and Huneke34, (6.7) and (6.11)]
Let ![]() $(A,\mathfrak{m},k)$ be a Noetherian complete local ring of prime characteristic
$(A,\mathfrak{m},k)$ be a Noetherian complete local ring of prime characteristic ![]() $p>0$. By the Cohen structure theorem, we may identify
$p>0$. By the Cohen structure theorem, we may identify ![]() $k$ with a coefficient field
$k$ with a coefficient field ![]() $k\subseteq A$. Moreover, by Zorn’s lemma (see [Reference Matsumura48, p. 202]), we may choose a
$k\subseteq A$. Moreover, by Zorn’s lemma (see [Reference Matsumura48, p. 202]), we may choose a ![]() $p$-basis
$p$-basis ![]() $\unicode[STIX]{x1D6EC}$ for
$\unicode[STIX]{x1D6EC}$ for ![]() $k$, which is a subset
$k$, which is a subset ![]() $\unicode[STIX]{x1D6EC}\subseteq k$ such that
$\unicode[STIX]{x1D6EC}\subseteq k$ such that ![]() $k=k^{p}(\unicode[STIX]{x1D6EC})$, and such that for every finite subset
$k=k^{p}(\unicode[STIX]{x1D6EC})$, and such that for every finite subset ![]() $\unicode[STIX]{x1D6F4}\subseteq \unicode[STIX]{x1D6EC}$ with
$\unicode[STIX]{x1D6F4}\subseteq \unicode[STIX]{x1D6EC}$ with ![]() $s$ elements, we have
$s$ elements, we have ![]() $[k^{p}(\unicode[STIX]{x1D6F4}):k^{p}]=p^{s}$.
$[k^{p}(\unicode[STIX]{x1D6F4}):k^{p}]=p^{s}$.
Now let ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$ be a cofinite subset, that is, a subset
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$ be a cofinite subset, that is, a subset ![]() $\unicode[STIX]{x1D6E4}$ of
$\unicode[STIX]{x1D6E4}$ of ![]() $\unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6EC}$ such that ![]() $\unicode[STIX]{x1D6EC}\smallsetminus \unicode[STIX]{x1D6E4}$ is a finite set. For each integer
$\unicode[STIX]{x1D6EC}\smallsetminus \unicode[STIX]{x1D6E4}$ is a finite set. For each integer ![]() $e\geqslant 0$, consider the subfield
$e\geqslant 0$, consider the subfield
of a perfect closure ![]() $k_{\text{perf}}$ of
$k_{\text{perf}}$ of ![]() $k$. These form an ascending chain, and we then set
$k$. These form an ascending chain, and we then set
where ![]() $k_{e}^{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x27E6}A\unicode[STIX]{x27E7}$ is the completion of
$k_{e}^{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x27E6}A\unicode[STIX]{x27E7}$ is the completion of ![]() $k_{e}^{\unicode[STIX]{x1D6E4}}\otimes _{k}A$ at the extended ideal
$k_{e}^{\unicode[STIX]{x1D6E4}}\otimes _{k}A$ at the extended ideal ![]() $\mathfrak{m}\cdot (k_{e}^{\unicode[STIX]{x1D6E4}}\otimes _{k}A)$. Note that if
$\mathfrak{m}\cdot (k_{e}^{\unicode[STIX]{x1D6E4}}\otimes _{k}A)$. Note that if ![]() $A=k$ is a field, then
$A=k$ is a field, then ![]() $A^{\unicode[STIX]{x1D6E4}}=k^{\unicode[STIX]{x1D6E4}}$ is a field by construction.
$A^{\unicode[STIX]{x1D6E4}}=k^{\unicode[STIX]{x1D6E4}}$ is a field by construction.
Finally, let ![]() $X$ be a scheme essentially of finite type over
$X$ be a scheme essentially of finite type over ![]() $A$, and consider two cofinite subsets
$A$, and consider two cofinite subsets ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$ and
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$ and ![]() $\unicode[STIX]{x1D6E4}^{\prime }\subseteq \unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6E4}^{\prime }\subseteq \unicode[STIX]{x1D6EC}$ such that ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}^{\prime }$. We then have the following commutative diagram whose vertical faces are cartesian:
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}^{\prime }$. We then have the following commutative diagram whose vertical faces are cartesian:

We list some elementary properties of the gamma construction.
Lemma 3.2. Fix notation as in Construction 3.1, and let ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$ be a cofinite subset.
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$ be a cofinite subset.
(i) The ring
 $A^{\unicode[STIX]{x1D6E4}}$ and the scheme
$A^{\unicode[STIX]{x1D6E4}}$ and the scheme  $X^{\unicode[STIX]{x1D6E4}}$ are Noetherian and
$X^{\unicode[STIX]{x1D6E4}}$ are Noetherian and  $F$-finite.
$F$-finite.(ii) The morphism
 $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ is a faithfully flat universal homeomorphism with local complete intersection fibers.
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ is a faithfully flat universal homeomorphism with local complete intersection fibers.(iii) Given a cofinite subset
 $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}^{\prime }$, the morphism
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}^{\prime }$, the morphism  $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D6E4}^{\prime }}$ is a faithfully flat universal homeomorphism.
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D6E4}^{\prime }}$ is a faithfully flat universal homeomorphism.
Proof. The ring ![]() $A^{\unicode[STIX]{x1D6E4}}$ is Noetherian and
$A^{\unicode[STIX]{x1D6E4}}$ is Noetherian and ![]() $F$-finite [Reference Hochster and Huneke34, (6.11)], hence
$F$-finite [Reference Hochster and Huneke34, (6.11)], hence ![]() $X^{\unicode[STIX]{x1D6E4}}$ is also by Example 2.6 and the fact that morphisms essentially of finite type are preserved under base change [Reference Nayak53, (2.2)]. The ring extensions
$X^{\unicode[STIX]{x1D6E4}}$ is also by Example 2.6 and the fact that morphisms essentially of finite type are preserved under base change [Reference Nayak53, (2.2)]. The ring extensions ![]() $A\subseteq A^{\unicode[STIX]{x1D6E4}}$ and
$A\subseteq A^{\unicode[STIX]{x1D6E4}}$ and ![]() $A^{\unicode[STIX]{x1D6E4}}\subseteq A^{\unicode[STIX]{x1D6E4}^{\prime }}$ are purely inseparable and faithfully flat [Reference Hochster and Huneke34, (6.11)], hence induce faithfully flat universal homeomorphisms on spectra [Reference Grothendieck and Dieudonné24, Proposition 2.4.5(i)]. Thus, the morphisms
$A^{\unicode[STIX]{x1D6E4}}\subseteq A^{\unicode[STIX]{x1D6E4}^{\prime }}$ are purely inseparable and faithfully flat [Reference Hochster and Huneke34, (6.11)], hence induce faithfully flat universal homeomorphisms on spectra [Reference Grothendieck and Dieudonné24, Proposition 2.4.5(i)]. Thus, the morphisms ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ and
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ and ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D6E4}^{\prime }}$ are faithfully flat universal homeomorphisms by base change. Finally, the ring extension
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D6E4}^{\prime }}$ are faithfully flat universal homeomorphisms by base change. Finally, the ring extension ![]() $A\subseteq A^{\unicode[STIX]{x1D6E4}}$ is flat with local complete intersection fibers [Reference Hashimoto30, Lemma 3.19], hence
$A\subseteq A^{\unicode[STIX]{x1D6E4}}$ is flat with local complete intersection fibers [Reference Hashimoto30, Lemma 3.19], hence ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ is also by base change [Reference Avramov2, Corollary 4].◻
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ is also by base change [Reference Avramov2, Corollary 4].◻
Our goal now is to prove that if a local property of schemes satisfies certain conditions, then the property is preserved when passing from ![]() $X$ to
$X$ to ![]() $X^{\unicode[STIX]{x1D6E4}}$ for “small enough”
$X^{\unicode[STIX]{x1D6E4}}$ for “small enough” ![]() $\unicode[STIX]{x1D6E4}$. For a scheme
$\unicode[STIX]{x1D6E4}$. For a scheme ![]() $X$ and a property
$X$ and a property ![]() ${\mathcal{P}}$ of local rings on
${\mathcal{P}}$ of local rings on ![]() $X$, the
$X$, the ![]() ${\mathcal{P}}$locus of
${\mathcal{P}}$locus of ![]() $X$ is
$X$ is ![]() ${\mathcal{P}}(X):=\{x\in X\mid {\mathcal{O}}_{X,x}\text{ is }{\mathcal{P}}\}$.
${\mathcal{P}}(X):=\{x\in X\mid {\mathcal{O}}_{X,x}\text{ is }{\mathcal{P}}\}$.
Proposition 3.3. Fix notation as in Construction 3.1, and let ![]() ${\mathcal{P}}$ be a property of local rings of prime characteristic
${\mathcal{P}}$ be a property of local rings of prime characteristic ![]() $p>0$.
$p>0$.
(i) Suppose that for every flat local homomorphism
 $B\rightarrow C$ of Noetherian local rings with local complete intersection fibers, if
$B\rightarrow C$ of Noetherian local rings with local complete intersection fibers, if  $B$ is
$B$ is  ${\mathcal{P}}$, then
${\mathcal{P}}$, then  $C$ is
$C$ is  ${\mathcal{P}}$. Then,
${\mathcal{P}}$. Then,  $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}}))={\mathcal{P}}(X)$ for every cofinite subset
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}}))={\mathcal{P}}(X)$ for every cofinite subset  $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$.
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$.(ii) Consider the following conditions:
(Γ1) If
 $B$ is a Noetherian
$B$ is a Noetherian  $F$-finite ring of prime characteristic
$F$-finite ring of prime characteristic  $p>0$, then
$p>0$, then  ${\mathcal{P}}(\operatorname{Spec}B)$ is open.
${\mathcal{P}}(\operatorname{Spec}B)$ is open.(Γ2) For every flat local homomorphism
 $B\rightarrow C$ of Noetherian local rings of prime characteristic
$B\rightarrow C$ of Noetherian local rings of prime characteristic  $p>0$ with zero-dimensional fibers, if
$p>0$ with zero-dimensional fibers, if  $C$ is
$C$ is  ${\mathcal{P}}$, then
${\mathcal{P}}$, then  $B$ is
$B$ is  ${\mathcal{P}}$.
${\mathcal{P}}$.(Γ3) For every local ring
 $B$ essentially of finite type over
$B$ essentially of finite type over  $A$, if
$A$, if  $B$ is
$B$ is  ${\mathcal{P}}$, then there exists a cofinite subset
${\mathcal{P}}$, then there exists a cofinite subset  $\unicode[STIX]{x1D6E4}_{1}\subseteq \unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6E4}_{1}\subseteq \unicode[STIX]{x1D6EC}$ such that  $B^{\unicode[STIX]{x1D6E4}}$ is
$B^{\unicode[STIX]{x1D6E4}}$ is  ${\mathcal{P}}$ for every cofinite subset
${\mathcal{P}}$ for every cofinite subset  $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{1}$.
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{1}$.
(Γ3′) For every flat local homomorphism
 $B\rightarrow C$ of Noetherian local rings of prime characteristic
$B\rightarrow C$ of Noetherian local rings of prime characteristic  $p>0$ such that the closed fiber is a field, if
$p>0$ such that the closed fiber is a field, if  $B$ is
$B$ is  ${\mathcal{P}}$, then
${\mathcal{P}}$, then  $C$ is
$C$ is  ${\mathcal{P}}$.
${\mathcal{P}}$.
If
 ${\mathcal{P}}$ satisfies (
${\mathcal{P}}$ satisfies ( $\unicode[STIX]{x1D6E4}1$ ), (
$\unicode[STIX]{x1D6E4}1$ ), ( $\unicode[STIX]{x1D6E4}2$ ), and one of either (
$\unicode[STIX]{x1D6E4}2$ ), and one of either ( $\unicode[STIX]{x1D6E4}3$ ) or (
$\unicode[STIX]{x1D6E4}3$ ) or ( $\unicode[STIX]{x1D6E4}3^{\prime }$ ), then there exists a cofinite subset
$\unicode[STIX]{x1D6E4}3^{\prime }$ ), then there exists a cofinite subset  $\unicode[STIX]{x1D6E4}_{0}\subseteq \unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6E4}_{0}\subseteq \unicode[STIX]{x1D6EC}$ such that  $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}}))={\mathcal{P}}(X)$ for every cofinite subset
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}}))={\mathcal{P}}(X)$ for every cofinite subset  $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$.
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$.
Proof. For (i), it suffices to note that ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ is faithfully flat with local complete intersection fibers by Lemma 3.2(ii).
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ is faithfully flat with local complete intersection fibers by Lemma 3.2(ii).
For (ii), we first note that (![]() $\unicode[STIX]{x1D6E4}3^{\prime }$) implies (
$\unicode[STIX]{x1D6E4}3^{\prime }$) implies (![]() $\unicode[STIX]{x1D6E4}3$), since there exists a cofinite subset
$\unicode[STIX]{x1D6E4}3$), since there exists a cofinite subset ![]() $\unicode[STIX]{x1D6E4}_{1}\subseteq \unicode[STIX]{x1D6EC}$ such that the closed fiber is a field for every cofinite subset
$\unicode[STIX]{x1D6E4}_{1}\subseteq \unicode[STIX]{x1D6EC}$ such that the closed fiber is a field for every cofinite subset ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{1}$ by [Reference Hochster and Huneke34, Lemma 6.13(b)]. From now on, we therefore assume that
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{1}$ by [Reference Hochster and Huneke34, Lemma 6.13(b)]. From now on, we therefore assume that ![]() ${\mathcal{P}}$ satisfies (
${\mathcal{P}}$ satisfies (![]() $\unicode[STIX]{x1D6E4}1$), (
$\unicode[STIX]{x1D6E4}1$), (![]() $\unicode[STIX]{x1D6E4}2$), and (
$\unicode[STIX]{x1D6E4}2$), and (![]() $\unicode[STIX]{x1D6E4}3$).
$\unicode[STIX]{x1D6E4}3$).
For every cofinite subset ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$, the set
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$, the set ![]() ${\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}})$ is open by (
${\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}})$ is open by (![]() $\unicode[STIX]{x1D6E4}1$) since
$\unicode[STIX]{x1D6E4}1$) since ![]() $X^{\unicode[STIX]{x1D6E4}}$ is Noetherian and
$X^{\unicode[STIX]{x1D6E4}}$ is Noetherian and ![]() $F$-finite by Lemma 3.2(i). Moreover, the morphisms
$F$-finite by Lemma 3.2(i). Moreover, the morphisms ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ and
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ and ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D6E4}^{\prime }}$ are faithfully flat universal homeomorphisms for every cofinite subset
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D6E4}^{\prime }}$ are faithfully flat universal homeomorphisms for every cofinite subset ![]() $\unicode[STIX]{x1D6E4}^{\prime }\subseteq \unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6E4}^{\prime }\subseteq \unicode[STIX]{x1D6EC}$ such that ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}^{\prime }$ by Lemmas 3.2(ii) and 3.2(iii), hence by (
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}^{\prime }$ by Lemmas 3.2(ii) and 3.2(iii), hence by (![]() $\unicode[STIX]{x1D6E4}2$), we have the inclusions
$\unicode[STIX]{x1D6E4}2$), we have the inclusions
in ![]() $X$, where
$X$, where ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}}))$ and
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}}))$ and ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}^{\prime }}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}^{\prime }}))$ are open. Since
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}^{\prime }}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}^{\prime }}))$ are open. Since ![]() $X$ is Noetherian, it satisfies the ascending chain condition on the open sets
$X$ is Noetherian, it satisfies the ascending chain condition on the open sets ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}}))$, hence we can choose a cofinite subset
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}}))$, hence we can choose a cofinite subset ![]() $\unicode[STIX]{x1D6E4}_{0}\subseteq \unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6E4}_{0}\subseteq \unicode[STIX]{x1D6EC}$ such that ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}_{0}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}_{0}}))$ is maximal with respect to inclusion.
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}_{0}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}_{0}}))$ is maximal with respect to inclusion.
We claim that ![]() ${\mathcal{P}}(X)=\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}_{0}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}_{0}}))$ for every cofinite subset
${\mathcal{P}}(X)=\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}_{0}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}_{0}}))$ for every cofinite subset ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$. By (3), it suffices to show the inclusion
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$. By (3), it suffices to show the inclusion ![]() $\subseteq$. Suppose there exists
$\subseteq$. Suppose there exists ![]() $x\in {\mathcal{P}}(X)\smallsetminus \unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}_{0}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}_{0}}))$. By (
$x\in {\mathcal{P}}(X)\smallsetminus \unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}_{0}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}_{0}}))$. By (![]() $\unicode[STIX]{x1D6E4}3$), there exists a cofinite subset
$\unicode[STIX]{x1D6E4}3$), there exists a cofinite subset ![]() $\unicode[STIX]{x1D6E4}_{1}\subseteq \unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6E4}_{1}\subseteq \unicode[STIX]{x1D6EC}$ such that ![]() $(\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}})^{-1}(x)\in {\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}})$ for every cofinite subset
$(\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}})^{-1}(x)\in {\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}})$ for every cofinite subset ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{1}$. Choosing
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{1}$. Choosing ![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{0}\cap \unicode[STIX]{x1D6E4}_{1}$, we have
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{0}\cap \unicode[STIX]{x1D6E4}_{1}$, we have ![]() $x\in \unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}}))\smallsetminus \unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}_{0}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}_{0}}))$, contradicting the maximality of
$x\in \unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}}))\smallsetminus \unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}_{0}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}_{0}}))$, contradicting the maximality of ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}_{0}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}_{0}}))$.◻
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}_{0}}({\mathcal{P}}(X^{\unicode[STIX]{x1D6E4}_{0}}))$.◻
We now prove that the properties in Theorem A are preserved when passing to ![]() $X^{\unicode[STIX]{x1D6E4}}$. Special cases of the following result appear in [Reference Hochster and Huneke34, Lemma 6.13], [Reference Vélez66, Theorem 2.2], [Reference Enescu and Hochster17, Lemma 2.9], [Reference Hashimoto30, Lemmas 3.23 and 3.30], and [Reference Ma45, Proposition 5.6].
$X^{\unicode[STIX]{x1D6E4}}$. Special cases of the following result appear in [Reference Hochster and Huneke34, Lemma 6.13], [Reference Vélez66, Theorem 2.2], [Reference Enescu and Hochster17, Lemma 2.9], [Reference Hashimoto30, Lemmas 3.23 and 3.30], and [Reference Ma45, Proposition 5.6].
Theorem 3.4. Fix notation as in Construction 3.1.
(i) For every cofinite subset
 $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$, the map
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$, the map  $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ identifies local complete intersection, Gorenstein, Cohen–Macaulay, and
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ identifies local complete intersection, Gorenstein, Cohen–Macaulay, and  $(S_{n})$ loci.
$(S_{n})$ loci.(ii) There exists a cofinite subset
 $\unicode[STIX]{x1D6E4}_{0}\subseteq \unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6E4}_{0}\subseteq \unicode[STIX]{x1D6EC}$ such that  $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ identifies regular (resp.
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ identifies regular (resp.  $(R_{n})$, normal, weakly normal, reduced, strongly
$(R_{n})$, normal, weakly normal, reduced, strongly  $F$-regular,
$F$-regular,  $F$-pure,
$F$-pure,  $F$-rational,
$F$-rational,  $F$-injective) loci for every cofinite subset
$F$-injective) loci for every cofinite subset  $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$.
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$.
Note that Theorem 3.4 implies Theorem A since if ![]() $A$ is a field, then
$A$ is a field, then ![]() $A^{\unicode[STIX]{x1D6E4}}$ is also by Construction 3.1, and moreover if one wants to preserve more than one property at once, then it suffices to intersect the various
$A^{\unicode[STIX]{x1D6E4}}$ is also by Construction 3.1, and moreover if one wants to preserve more than one property at once, then it suffices to intersect the various ![]() $\unicode[STIX]{x1D6E4}_{0}$ for the different properties.
$\unicode[STIX]{x1D6E4}_{0}$ for the different properties.
Proof. For (i), it suffices to note that these properties satisfy the condition in Proposition 3.3(i) by [Reference Avramov2, Corollary 2] and [Reference Matsumura48, Theorem 23.4, Corollary to Theorem 23.3, and Theorem 23.9(iii)], respectively.
We now prove (ii). We first note that (ii) holds for regularity since (![]() $\unicode[STIX]{x1D6E4}1$) holds by the excellence of
$\unicode[STIX]{x1D6E4}1$) holds by the excellence of ![]() $X^{\unicode[STIX]{x1D6E4}}$, and (
$X^{\unicode[STIX]{x1D6E4}}$, and (![]() $\unicode[STIX]{x1D6E4}2$) and (
$\unicode[STIX]{x1D6E4}2$) and (![]() $\unicode[STIX]{x1D6E4}3^{\prime }$) hold by [Reference Matsumura48, Theorem 23.7]. Since
$\unicode[STIX]{x1D6E4}3^{\prime }$) hold by [Reference Matsumura48, Theorem 23.7]. Since ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ preserves the dimension of local rings, we therefore see that (ii) holds for
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ preserves the dimension of local rings, we therefore see that (ii) holds for ![]() $(R_{n})$. (ii) for normality and reducedness then follows from (i) since they are equivalent to
$(R_{n})$. (ii) for normality and reducedness then follows from (i) since they are equivalent to ![]() $(R_{1})+(S_{2})$ and
$(R_{1})+(S_{2})$ and ![]() $(R_{0})+(S_{1})$, respectively.
$(R_{0})+(S_{1})$, respectively.
To prove (ii) holds in the remaining cases, we check the conditions in Proposition 3.3(ii). For weak normality, (![]() $\unicode[STIX]{x1D6E4}1$) holds by [Reference Bingener and Flenner3, Theorem 7.1.3], and (
$\unicode[STIX]{x1D6E4}1$) holds by [Reference Bingener and Flenner3, Theorem 7.1.3], and (![]() $\unicode[STIX]{x1D6E4}2$) holds by [Reference Manaresi47, Corollary II.2]. To show that (
$\unicode[STIX]{x1D6E4}2$) holds by [Reference Manaresi47, Corollary II.2]. To show that (![]() $\unicode[STIX]{x1D6E4}3$) holds, recall by [Reference Manaresi47, Theorem I.6] that a reduced ring
$\unicode[STIX]{x1D6E4}3$) holds, recall by [Reference Manaresi47, Theorem I.6] that a reduced ring ![]() $B$ is weakly normal if and only if
$B$ is weakly normal if and only if
is an equalizer diagram, where ![]() $B^{\unicode[STIX]{x1D708}}$ is the normalization of
$B^{\unicode[STIX]{x1D708}}$ is the normalization of ![]() $B$. Now suppose
$B$. Now suppose ![]() $B$ is weakly normal, and let
$B$ is weakly normal, and let ![]() $\unicode[STIX]{x1D6E4}_{1}\subseteq \unicode[STIX]{x1D6EC}$ be a cofinite subset such that
$\unicode[STIX]{x1D6E4}_{1}\subseteq \unicode[STIX]{x1D6EC}$ be a cofinite subset such that ![]() $B^{\unicode[STIX]{x1D6E4}}$ is reduced,
$B^{\unicode[STIX]{x1D6E4}}$ is reduced, ![]() $(B^{\unicode[STIX]{x1D708}})^{\unicode[STIX]{x1D6E4}}$ is normal, and
$(B^{\unicode[STIX]{x1D708}})^{\unicode[STIX]{x1D6E4}}$ is normal, and ![]() $((B^{\unicode[STIX]{x1D708}}\otimes _{B}B^{\unicode[STIX]{x1D708}})_{\text{red}})^{\unicode[STIX]{x1D6E4}}$ is reduced for every cofinite subset
$((B^{\unicode[STIX]{x1D708}}\otimes _{B}B^{\unicode[STIX]{x1D708}})_{\text{red}})^{\unicode[STIX]{x1D6E4}}$ is reduced for every cofinite subset ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{1}$; such a
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{1}$; such a ![]() $\unicode[STIX]{x1D6E4}_{1}$ exists by the previous paragraph. We claim that
$\unicode[STIX]{x1D6E4}_{1}$ exists by the previous paragraph. We claim that ![]() $B^{\unicode[STIX]{x1D6E4}}$ is weakly normal for every
$B^{\unicode[STIX]{x1D6E4}}$ is weakly normal for every ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{1}$ cofinite in
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{1}$ cofinite in ![]() $\unicode[STIX]{x1D6EC}$. Since (
$\unicode[STIX]{x1D6EC}$. Since (
) is an equalizer diagram and ![]() $A\subseteq A^{\unicode[STIX]{x1D6E4}}$ is flat, the diagram
$A\subseteq A^{\unicode[STIX]{x1D6E4}}$ is flat, the diagram
is an equalizer diagram. Moreover, since ![]() $B^{\unicode[STIX]{x1D6E4}}\subseteq (B^{\unicode[STIX]{x1D708}})^{\unicode[STIX]{x1D6E4}}$ is an integral extension of rings with the same total ring of fractions, and
$B^{\unicode[STIX]{x1D6E4}}\subseteq (B^{\unicode[STIX]{x1D708}})^{\unicode[STIX]{x1D6E4}}$ is an integral extension of rings with the same total ring of fractions, and ![]() $(B^{\unicode[STIX]{x1D708}})^{\unicode[STIX]{x1D6E4}}$ is normal, we see that
$(B^{\unicode[STIX]{x1D708}})^{\unicode[STIX]{x1D6E4}}$ is normal, we see that ![]() $(B^{\unicode[STIX]{x1D708}})^{\unicode[STIX]{x1D6E4}}=(B^{\unicode[STIX]{x1D6E4}})^{\unicode[STIX]{x1D708}}$. Finally,
$(B^{\unicode[STIX]{x1D708}})^{\unicode[STIX]{x1D6E4}}=(B^{\unicode[STIX]{x1D6E4}})^{\unicode[STIX]{x1D708}}$. Finally, ![]() $((B^{\unicode[STIX]{x1D708}}\otimes _{B}B^{\unicode[STIX]{x1D708}})_{\text{red}})^{\unicode[STIX]{x1D6E4}}$ is reduced, hence we have the natural isomorphism
$((B^{\unicode[STIX]{x1D708}}\otimes _{B}B^{\unicode[STIX]{x1D708}})_{\text{red}})^{\unicode[STIX]{x1D6E4}}$ is reduced, hence we have the natural isomorphism
Thus, since the analogue of (
4) with ![]() $B$ replaced by
$B$ replaced by ![]() $B^{\unicode[STIX]{x1D6E4}}$ is an equalizer diagram, we see that
$B^{\unicode[STIX]{x1D6E4}}$ is an equalizer diagram, we see that ![]() $B^{\unicode[STIX]{x1D6E4}}$ is weakly normal for every
$B^{\unicode[STIX]{x1D6E4}}$ is weakly normal for every ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{1}$ cofinite in
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{1}$ cofinite in ![]() $\unicode[STIX]{x1D6EC}$, hence (
$\unicode[STIX]{x1D6EC}$, hence (![]() $\unicode[STIX]{x1D6E4}3$) holds for weak normality.
$\unicode[STIX]{x1D6E4}3$) holds for weak normality.
We now prove (ii) for strong ![]() $F$-regularity,
$F$-regularity, ![]() $F$-purity, and
$F$-purity, and ![]() $F$-rationality. First, (
$F$-rationality. First, (![]() $\unicode[STIX]{x1D6E4}1$) holds for strong
$\unicode[STIX]{x1D6E4}1$) holds for strong ![]() $F$-regularity by [Reference Hashimoto30, Lemma 3.29], and the same argument shows that (
$F$-regularity by [Reference Hashimoto30, Lemma 3.29], and the same argument shows that (![]() $\unicode[STIX]{x1D6E4}1$) holds for
$\unicode[STIX]{x1D6E4}1$) holds for ![]() $F$-purity since the
$F$-purity since the ![]() $F$-pure and
$F$-pure and ![]() $F$-split loci coincide for
$F$-split loci coincide for ![]() $F$-finite rings [Reference Hochster and Roberts36, Corollary 5.3]. Next, (
$F$-finite rings [Reference Hochster and Roberts36, Corollary 5.3]. Next, (![]() $\unicode[STIX]{x1D6E4}1$) for
$\unicode[STIX]{x1D6E4}1$) for ![]() $F$-rationality holds by [Reference Vélez66, Theorem 1.11] since the reduced locus is open and reduced
$F$-rationality holds by [Reference Vélez66, Theorem 1.11] since the reduced locus is open and reduced ![]() $F$-finite rings are admissible in the sense of [Reference Vélez66, Definition 1.5] by Theorem 2.7. It then suffices to note that (
$F$-finite rings are admissible in the sense of [Reference Vélez66, Definition 1.5] by Theorem 2.7. It then suffices to note that (![]() $\unicode[STIX]{x1D6E4}2$) holds by [Reference Hashimoto30, Lemma 3.17], [Reference Hochster and Roberts36, Proposition 5.13], and [Reference Vélez66, (6) on p. 440], respectively, and (
$\unicode[STIX]{x1D6E4}2$) holds by [Reference Hashimoto30, Lemma 3.17], [Reference Hochster and Roberts36, Proposition 5.13], and [Reference Vélez66, (6) on p. 440], respectively, and (![]() $\unicode[STIX]{x1D6E4}3$) holds by [Reference Hashimoto30, Corollary 3.31], [Reference Ma45, Proposition 5.4], and [Reference Vélez66, Lemma 2.3], respectively.
$\unicode[STIX]{x1D6E4}3$) holds by [Reference Hashimoto30, Corollary 3.31], [Reference Ma45, Proposition 5.4], and [Reference Vélez66, Lemma 2.3], respectively.
Finally, we prove (ii) for ![]() $F$-injectivity. First, (
$F$-injectivity. First, (![]() $\unicode[STIX]{x1D6E4}1$) and (
$\unicode[STIX]{x1D6E4}1$) and (![]() $\unicode[STIX]{x1D6E4}2$) hold by Lemmas A.2 and A.3, respectively. The proof of [Reference Enescu and Hochster17, Lemma 2.9(b)] implies (
$\unicode[STIX]{x1D6E4}2$) hold by Lemmas A.2 and A.3, respectively. The proof of [Reference Enescu and Hochster17, Lemma 2.9(b)] implies (![]() $\unicode[STIX]{x1D6E4}3$), since the residue field of
$\unicode[STIX]{x1D6E4}3$), since the residue field of ![]() $B$ is a finite extension of
$B$ is a finite extension of ![]() $k$, hence socles of Artinian
$k$, hence socles of Artinian ![]() $B$-modules are finite-dimensional
$B$-modules are finite-dimensional ![]() $k$-vector spaces.◻
$k$-vector spaces.◻
We have the following consequence of Theorem 3.4, which was first attributed to Hoshi in [Reference Hashimoto31, Theorem 3.2]. Note that the analogous statements for strong ![]() $F$-regularity and
$F$-regularity and ![]() $F$-rationality appear in [Reference Hashimoto30, Proposition 3.33] and [Reference Vélez66, Theorem 3.5], respectively.
$F$-rationality appear in [Reference Hashimoto30, Proposition 3.33] and [Reference Vélez66, Theorem 3.5], respectively.
Corollary 3.5. Let ![]() $X$ be a scheme essentially of finite type over a local
$X$ be a scheme essentially of finite type over a local ![]() $G$-ring
$G$-ring ![]() $(A,\mathfrak{m})$ of prime characteristic
$(A,\mathfrak{m})$ of prime characteristic ![]() $p>0$. Then, the
$p>0$. Then, the ![]() $F$-pure locus is open in
$F$-pure locus is open in ![]() $X$.
$X$.
Recall that a Noetherian ring ![]() $R$ is a
$R$ is a ![]() $G$-ring if, for every prime ideal
$G$-ring if, for every prime ideal ![]() $\mathfrak{p}\subseteq R$, the completion homomorphism
$\mathfrak{p}\subseteq R$, the completion homomorphism ![]() $R_{\mathfrak{p}}\rightarrow \widehat{R_{\mathfrak{p}}}$ is regular; see [Reference Matsumura48, pp. 255–256] for the definitions of
$R_{\mathfrak{p}}\rightarrow \widehat{R_{\mathfrak{p}}}$ is regular; see [Reference Matsumura48, pp. 255–256] for the definitions of ![]() $G$-rings and of regular homomorphisms. Excellent rings are
$G$-rings and of regular homomorphisms. Excellent rings are ![]() $G$-rings by definition; see [Reference Matsumura48, Definition on p. 260].
$G$-rings by definition; see [Reference Matsumura48, Definition on p. 260].
Proof. Let ![]() $A\rightarrow \widehat{A}$ be the completion of
$A\rightarrow \widehat{A}$ be the completion of ![]() $A$ at
$A$ at ![]() $\mathfrak{m}$, and let
$\mathfrak{m}$, and let ![]() $\unicode[STIX]{x1D6EC}$ be a
$\unicode[STIX]{x1D6EC}$ be a ![]() $p$-basis for
$p$-basis for ![]() $\widehat{A}/\mathfrak{m}\widehat{A}$ as in Construction 3.1. For every cofinite subset
$\widehat{A}/\mathfrak{m}\widehat{A}$ as in Construction 3.1. For every cofinite subset ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$, consider the commutative diagram
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$, consider the commutative diagram

where the squares are cartesian. By Theorem 3.4, there exists a cofinite subset ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6EC}$ such that ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ is a homeomorphism identifying
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}$ is a homeomorphism identifying ![]() $F$-pure loci. Since
$F$-pure loci. Since ![]() $X\times _{A}\widehat{A}^{\unicode[STIX]{x1D6E4}}$ is
$X\times _{A}\widehat{A}^{\unicode[STIX]{x1D6E4}}$ is ![]() $F$-finite, the
$F$-finite, the ![]() $F$-pure locus in
$F$-pure locus in ![]() $X\times _{A}\widehat{A}$ is therefore open by the fact that (
$X\times _{A}\widehat{A}$ is therefore open by the fact that (![]() $\unicode[STIX]{x1D6E4}1$) holds for
$\unicode[STIX]{x1D6E4}1$) holds for ![]() $F$-purity (see the proof of Theorem 3.4(ii)).
$F$-purity (see the proof of Theorem 3.4(ii)).
Now let ![]() $x\in X\times _{A}\widehat{A}$. Since
$x\in X\times _{A}\widehat{A}$. Since ![]() $A\rightarrow \widehat{A}$ is a regular homomorphism, the morphism
$A\rightarrow \widehat{A}$ is a regular homomorphism, the morphism ![]() $\unicode[STIX]{x1D70B}$ is also regular by base change [Reference Grothendieck and Dieudonné24, Proposition 6.8.3(iii)]. Thus,
$\unicode[STIX]{x1D70B}$ is also regular by base change [Reference Grothendieck and Dieudonné24, Proposition 6.8.3(iii)]. Thus, ![]() ${\mathcal{O}}_{X\times _{A}\widehat{A},x}$ is
${\mathcal{O}}_{X\times _{A}\widehat{A},x}$ is ![]() $F$-pure if and only if
$F$-pure if and only if ![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D70B}(x)}$ is
${\mathcal{O}}_{X,\unicode[STIX]{x1D70B}(x)}$ is ![]() $F$-pure by [Reference Hochster and Roberts36, Proposition 5.13] and [Reference Hashimoto30, Propositions 2.4(4) and 2.4(6)]. Denoting the
$F$-pure by [Reference Hochster and Roberts36, Proposition 5.13] and [Reference Hashimoto30, Propositions 2.4(4) and 2.4(6)]. Denoting the ![]() $F$-pure locus in
$F$-pure locus in ![]() $X$ by
$X$ by ![]() $W$, we see that
$W$, we see that ![]() $\unicode[STIX]{x1D70B}^{-1}(W)$ is the
$\unicode[STIX]{x1D70B}^{-1}(W)$ is the ![]() $F$-pure locus in
$F$-pure locus in ![]() $X\times _{A}\widehat{A}$. Since
$X\times _{A}\widehat{A}$. Since ![]() $\unicode[STIX]{x1D70B}^{-1}(W)$ is open and
$\unicode[STIX]{x1D70B}^{-1}(W)$ is open and ![]() $\unicode[STIX]{x1D70B}$ is quasicompact and faithfully flat by base change, the
$\unicode[STIX]{x1D70B}$ is quasicompact and faithfully flat by base change, the ![]() $F$-pure locus
$F$-pure locus ![]() $W\subseteq X$ is open by [Reference Grothendieck and Dieudonné24, Corollaire 2.3.12].◻
$W\subseteq X$ is open by [Reference Grothendieck and Dieudonné24, Corollaire 2.3.12].◻
Remark 3.6. Although Lemma A.2 shows that the ![]() $F$-injective locus is open under
$F$-injective locus is open under ![]() $F$-finiteness hypotheses, and the gamma construction (Theorem 3.4) implies that the
$F$-finiteness hypotheses, and the gamma construction (Theorem 3.4) implies that the ![]() $F$-injective locus is open for schemes essentially of finite type over complete local rings, the fact that the
$F$-injective locus is open for schemes essentially of finite type over complete local rings, the fact that the ![]() $F$-injective locus is open under the hypotheses of Corollary 3.5 is a recent result due to Rankeya Datta and the author [Reference Datta and Murayama9, Theorem B].
$F$-injective locus is open under the hypotheses of Corollary 3.5 is a recent result due to Rankeya Datta and the author [Reference Datta and Murayama9, Theorem B].
3.2 Application to the minimal model program over imperfect fields
With notation as in Construction 3.1, let ![]() $\{X_{i}\}$ be a finite set of schemes essentially of finite type over
$\{X_{i}\}$ be a finite set of schemes essentially of finite type over ![]() $A$. For each
$A$. For each ![]() $i$, Theorem 3.4 produces a cofinite subset
$i$, Theorem 3.4 produces a cofinite subset ![]() $\unicode[STIX]{x1D6E4}_{0}^{i}\subseteq \unicode[STIX]{x1D6EC}$ such that properties of
$\unicode[STIX]{x1D6E4}_{0}^{i}\subseteq \unicode[STIX]{x1D6EC}$ such that properties of ![]() $X_{i}$ are inherited by
$X_{i}$ are inherited by ![]() $X_{i}^{\unicode[STIX]{x1D6E4}}$ for every
$X_{i}^{\unicode[STIX]{x1D6E4}}$ for every ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}^{i}$ cofinite in
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}^{i}$ cofinite in ![]() $\unicode[STIX]{x1D6EC}$. Setting
$\unicode[STIX]{x1D6EC}$. Setting ![]() $\unicode[STIX]{x1D6E4}_{0}=\bigcap _{i}\unicode[STIX]{x1D6E4}_{0}^{i}$ gives a cofinite subset of
$\unicode[STIX]{x1D6E4}_{0}=\bigcap _{i}\unicode[STIX]{x1D6E4}_{0}^{i}$ gives a cofinite subset of ![]() $\unicode[STIX]{x1D6EC}$ which works for every scheme in the set
$\unicode[STIX]{x1D6EC}$ which works for every scheme in the set ![]() $\{X_{i}\}$ at once. We illustrate this strategy with the following:
$\{X_{i}\}$ at once. We illustrate this strategy with the following:
Corollary 3.7. Let ![]() $(X,\unicode[STIX]{x1D6E5})$ be a pair consisting of a normal variety
$(X,\unicode[STIX]{x1D6E5})$ be a pair consisting of a normal variety ![]() $X$ over a field
$X$ over a field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$ and an
$p>0$ and an ![]() $\mathbf{R}$-Weil divisor
$\mathbf{R}$-Weil divisor ![]() $\unicode[STIX]{x1D6E5}$ on
$\unicode[STIX]{x1D6E5}$ on ![]() $X$. Fix notation as in Construction 3.1, where we set
$X$. Fix notation as in Construction 3.1, where we set ![]() $A=k$.
$A=k$.
(i) If
 $X$ is a regular variety and
$X$ is a regular variety and  $\unicode[STIX]{x1D6E5}$ has simple normal crossing support, then there exists a cofinite subset
$\unicode[STIX]{x1D6E5}$ has simple normal crossing support, then there exists a cofinite subset  $\unicode[STIX]{x1D6E4}_{0}\subseteq \unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6E4}_{0}\subseteq \unicode[STIX]{x1D6EC}$ such that  $X^{\unicode[STIX]{x1D6E4}}$ is a regular variety and
$X^{\unicode[STIX]{x1D6E4}}$ is a regular variety and  $(\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}})^{\ast }\unicode[STIX]{x1D6E5}$ has simple normal crossing support for every cofinite subset
$(\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}})^{\ast }\unicode[STIX]{x1D6E5}$ has simple normal crossing support for every cofinite subset  $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$.
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$.(ii) If
 $\dim X\leqslant 3$ and
$\dim X\leqslant 3$ and  $(X,\unicode[STIX]{x1D6E5})$ is klt (resp. log canonical), then there exists a cofinite subset
$(X,\unicode[STIX]{x1D6E5})$ is klt (resp. log canonical), then there exists a cofinite subset  $\unicode[STIX]{x1D6E4}_{0}\subseteq \unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6E4}_{0}\subseteq \unicode[STIX]{x1D6EC}$ such that  $(X^{\unicode[STIX]{x1D6E4}},(\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}})^{\ast }\unicode[STIX]{x1D6E5})$ is klt (resp. log canonical) for every cofinite subset
$(X^{\unicode[STIX]{x1D6E4}},(\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}})^{\ast }\unicode[STIX]{x1D6E5})$ is klt (resp. log canonical) for every cofinite subset  $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$.
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$.
Proof. For (i), first write ![]() $\unicode[STIX]{x1D6E5}=\sum a_{i}D_{i}$, where
$\unicode[STIX]{x1D6E5}=\sum a_{i}D_{i}$, where ![]() $a_{i}\in \mathbf{R}$ and
$a_{i}\in \mathbf{R}$ and ![]() $D_{i}$ are prime divisors. By Theorem 3.4 applied to the regular locus of
$D_{i}$ are prime divisors. By Theorem 3.4 applied to the regular locus of ![]() $X$ and of every set of intersections of the
$X$ and of every set of intersections of the ![]() $D_{i}$, we see that there exists a cofinite subset
$D_{i}$, we see that there exists a cofinite subset ![]() $\unicode[STIX]{x1D6E4}_{0}\subseteq \unicode[STIX]{x1D6EC}$ such that
$\unicode[STIX]{x1D6E4}_{0}\subseteq \unicode[STIX]{x1D6EC}$ such that ![]() $X^{\unicode[STIX]{x1D6E4}}$ is a regular variety and
$X^{\unicode[STIX]{x1D6E4}}$ is a regular variety and ![]() $(\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}})^{\ast }\unicode[STIX]{x1D6E5}=\sum a_{i}(\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}})^{\ast }D_{i}$ has simple normal crossing support for every
$(\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}})^{\ast }\unicode[STIX]{x1D6E5}=\sum a_{i}(\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}})^{\ast }D_{i}$ has simple normal crossing support for every ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$ cofinite in
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$ cofinite in ![]() $\unicode[STIX]{x1D6EC}$. (ii) then follows by applying (i) to a log resolution of
$\unicode[STIX]{x1D6EC}$. (ii) then follows by applying (i) to a log resolution of ![]() $(X,\unicode[STIX]{x1D6E5})$ while simultaneously choosing
$(X,\unicode[STIX]{x1D6E5})$ while simultaneously choosing ![]() $\unicode[STIX]{x1D6E4}_{0}$ such that
$\unicode[STIX]{x1D6E4}_{0}$ such that ![]() $X^{\unicode[STIX]{x1D6E4}}$ is normal for every cofinite subset
$X^{\unicode[STIX]{x1D6E4}}$ is normal for every cofinite subset ![]() $\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$.◻
$\unicode[STIX]{x1D6E4}\subseteq \unicode[STIX]{x1D6E4}_{0}$.◻
Corollary 3.7(ii) easily provides another method for proving the reduction step in [Reference Tanaka64, Theorem 3.8]. It can also be used to prove the more subtle reduction step in the following result of Tanaka.
Theorem 3.8. [Reference Tanaka65, Theorem 4.12]
Let ![]() $k$ be a field of characteristic
$k$ be a field of characteristic![]() $p>0$. Let
$p>0$. Let ![]() $(X,\unicode[STIX]{x1D6E5})$ be a log canonical surface over
$(X,\unicode[STIX]{x1D6E5})$ be a log canonical surface over ![]() $k$, where
$k$, where ![]() $\unicode[STIX]{x1D6E5}$ is a
$\unicode[STIX]{x1D6E5}$ is a ![]() $\mathbf{Q}$-Weil divisor. Let
$\mathbf{Q}$-Weil divisor. Let ![]() $f:X\rightarrow S$ be a projective morphism to a separated scheme
$f:X\rightarrow S$ be a projective morphism to a separated scheme ![]() $S$ of finite type over
$S$ of finite type over ![]() $k$. If
$k$. If ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is
$K_{X}+\unicode[STIX]{x1D6E5}$ is ![]() $f$-nef, then
$f$-nef, then ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is
$K_{X}+\unicode[STIX]{x1D6E5}$ is ![]() $f$-semi-ample.
$f$-semi-ample.
The first step of the proof in [Reference Tanaka65] is to reduce to the case where ![]() $k$ is
$k$ is ![]() $F$-finite and contains an infinite perfect field in order to apply [Reference Tanaka63, Theorem 1]. We illustrate how one can use the gamma construction (Theorem 3.4) to make this reduction.
$F$-finite and contains an infinite perfect field in order to apply [Reference Tanaka63, Theorem 1]. We illustrate how one can use the gamma construction (Theorem 3.4) to make this reduction.
Proof of reduction.
Note that the formation of ![]() $K_{X}$ is compatible with ground field extensions [Reference Hartshorne28, Corollary V.3.4(a)], and that
$K_{X}$ is compatible with ground field extensions [Reference Hartshorne28, Corollary V.3.4(a)], and that ![]() $f$-nefness is preserved under base change since
$f$-nefness is preserved under base change since ![]() $f$-ampleness is. By flat base change and the fact that field extensions are faithfully flat,
$f$-ampleness is. By flat base change and the fact that field extensions are faithfully flat, ![]() $f$-semi-ampleness can be checked after a ground field extension. Since
$f$-semi-ampleness can be checked after a ground field extension. Since ![]() $k(x^{1/p^{\infty }})$ contains the infinite perfect field
$k(x^{1/p^{\infty }})$ contains the infinite perfect field ![]() $\mathbf{F}_{p}(x^{1/p^{\infty }})$ and applying the gamma construction to
$\mathbf{F}_{p}(x^{1/p^{\infty }})$ and applying the gamma construction to ![]() $k(x^{1/p^{\infty }})$ results in an
$k(x^{1/p^{\infty }})$ results in an ![]() $F$-finite field (Construction 3.1 and Lemma 3.2(i)), it therefore suffices to show that for some choice of
$F$-finite field (Construction 3.1 and Lemma 3.2(i)), it therefore suffices to show that for some choice of ![]() $\unicode[STIX]{x1D6E4}$, the base change of
$\unicode[STIX]{x1D6E4}$, the base change of ![]() $(X,\unicode[STIX]{x1D6E5})$ under the sequence of ground field extensions
$(X,\unicode[STIX]{x1D6E5})$ under the sequence of ground field extensions
is a log canonical surface. Moreover, Corollary 3.7(ii) implies it suffices to prove that the base change of ![]() $(X,\unicode[STIX]{x1D6E5})$ to
$(X,\unicode[STIX]{x1D6E5})$ to ![]() $k(x^{1/p^{\infty }})$ is a log canonical surface.
$k(x^{1/p^{\infty }})$ is a log canonical surface.
Fix a log resolution ![]() $\unicode[STIX]{x1D707}:Y\rightarrow X$ for
$\unicode[STIX]{x1D707}:Y\rightarrow X$ for ![]() $(X,\unicode[STIX]{x1D6E5})$, and write
$(X,\unicode[STIX]{x1D6E5})$, and write ![]() $K_{Y}-\unicode[STIX]{x1D707}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})=\sum _{i}a_{i}E_{i}$. Note that
$K_{Y}-\unicode[STIX]{x1D707}^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})=\sum _{i}a_{i}E_{i}$. Note that ![]() $k(x^{1/p^{\infty }})=\bigcup _{e}k(x^{1/p^{e}})$, and that each field
$k(x^{1/p^{\infty }})=\bigcup _{e}k(x^{1/p^{e}})$, and that each field ![]() $k(x^{1/p^{e}})$ is isomorphic to
$k(x^{1/p^{e}})$ is isomorphic to ![]() $k(x)$. Since integrality, normality, and regularity are preserved under limits of schemes with affine and flat transition morphisms [Reference Grothendieck and Dieudonné24, Corollaire 5.13.4 and Proposition 5.13.7], it suffices to show that
$k(x)$. Since integrality, normality, and regularity are preserved under limits of schemes with affine and flat transition morphisms [Reference Grothendieck and Dieudonné24, Corollaire 5.13.4 and Proposition 5.13.7], it suffices to show that ![]() $X\times _{k}k(x)$ is a normal variety,
$X\times _{k}k(x)$ is a normal variety, ![]() $Y\times _{k}k(x)$ is a regular variety, and each
$Y\times _{k}k(x)$ is a regular variety, and each ![]() $E_{i}\times _{k}k(x)$ is a regular variety such that every intersection of the
$E_{i}\times _{k}k(x)$ is a regular variety such that every intersection of the ![]() $E_{i}\times _{k}k(x)$’s is regular. This follows for
$E_{i}\times _{k}k(x)$’s is regular. This follows for ![]() $X\times _{k}k(x)$, since if
$X\times _{k}k(x)$, since if ![]() $\bigcup _{j}U_{j}$ is an affine open covering of
$\bigcup _{j}U_{j}$ is an affine open covering of ![]() $X$, then
$X$, then ![]() $X\times _{k}k(x)$ is covered by affine open subsets that are localizations of the normal varieties
$X\times _{k}k(x)$ is covered by affine open subsets that are localizations of the normal varieties ![]() $U_{j}\times _{k}\mathbf{A}_{k}^{1}$, which pairwise intersect. A similar argument works for
$U_{j}\times _{k}\mathbf{A}_{k}^{1}$, which pairwise intersect. A similar argument works for ![]() $Y$, the
$Y$, the ![]() $E_{i}$’s, and the intersections of the
$E_{i}$’s, and the intersections of the ![]() $E_{i}$’s.◻
$E_{i}$’s.◻
4 The ampleness criterion of de Fernex–Küronya–Lazarsfeld
We now come to our first application of the gamma construction, Theorem B. Let ![]() $X$ be a projective variety of dimension
$X$ be a projective variety of dimension ![]() $n>0$. For every Cartier divisor
$n>0$. For every Cartier divisor ![]() $L$ on
$L$ on ![]() $X$, we have
$X$, we have
for every ![]() $i$; see [Reference Lazarsfeld43, Example 1.2.20]. In [Reference de Fernex, Küronya and Lazarsfeld12, Theorem 4.1], de Fernex, Küronya, and Lazarsfeld asked when the higher cohomology groups have submaximal growth, that is, when
$i$; see [Reference Lazarsfeld43, Example 1.2.20]. In [Reference de Fernex, Küronya and Lazarsfeld12, Theorem 4.1], de Fernex, Küronya, and Lazarsfeld asked when the higher cohomology groups have submaximal growth, that is, when ![]() $h^{i}(X,{\mathcal{O}}_{X}(mL))=o(m^{n})$. They proved that over the complex numbers, ample Cartier divisors
$h^{i}(X,{\mathcal{O}}_{X}(mL))=o(m^{n})$. They proved that over the complex numbers, ample Cartier divisors ![]() $L$ are characterized by having submaximal growth of higher cohomology groups for small perturbations of
$L$ are characterized by having submaximal growth of higher cohomology groups for small perturbations of ![]() $L$. The content of Theorem B is that their characterization holds for projective varieties over arbitrary fields. Note that one can have
$L$. The content of Theorem B is that their characterization holds for projective varieties over arbitrary fields. Note that one can have ![]() $\widehat{h}^{i}(X,L)=0$ for all
$\widehat{h}^{i}(X,L)=0$ for all ![]() $i>0$ without
$i>0$ without ![]() $L$ being ample, or even pseudoeffective, hence the perturbation by
$L$ being ample, or even pseudoeffective, hence the perturbation by ![]() $A$ is necessary; see [Reference Küronya41, Section 3.1] or [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa14, Example 4.4].
$A$ is necessary; see [Reference Küronya41, Section 3.1] or [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa14, Example 4.4].
After reviewing some background material on asymptotic cohomological functions in Section 4.1 following [Reference Küronya41, Section 2; Reference Burgos Gil, Gubler, Jell, Künnemann and Martin6, Section 3], we prove an analogue of a lemma on base loci [Reference de Fernex, Küronya and Lazarsfeld12, Proposition 3.1] in Section 4.2. This latter subsection is where asymptotic test ideals are used. Finally, we prove Theorem B in Section 4.3 using the gamma construction and alterations.
Before getting into the details of the proof, we briefly describe the main difficulties in adapting the proof of [Reference de Fernex, Küronya and Lazarsfeld12, Theorem 4.1] to positive characteristic. First, the proof of [Reference de Fernex, Küronya and Lazarsfeld12, Proposition 3.1] requires resolutions of singularities, and because of this, we can only prove a version of this lemma (Proposition 4.6) under the additional hypothesis that a specific pair has (a weak version of) a log resolution. This weaker result suffices for Theorem B since we can reduce to this situation by taking the Stein factorization of an alteration. Second, [Reference de Fernex, Küronya and Lazarsfeld12] uses the assumption that the ground field is uncountable to choose countably many very general divisors that facilitate an inductive argument. We reduce to the setting where the ground field is uncountable by adjoining uncountably many indeterminates to our ground field and then applying the gamma construction (Theorem A) to reduce to the ![]() $F$-finite case; see Lemma 4.9.
$F$-finite case; see Lemma 4.9.
4.1 Background on asymptotic cohomological functions
We first review Küronya’s asymptotic cohomological functions with suitable modifications to work over arbitrary fields, following [Reference Küronya41, Section 2; Reference Burgos Gil, Gubler, Jell, Künnemann and Martin6, Section 3]. Asymptotic cohomological functions are defined as follows:
Definition 4.1. [Reference Burgos Gil, Gubler, Jell, Künnemann and Martin6, Definition 3.4.6]
Let ![]() $X$ be a projective scheme of dimension
$X$ be a projective scheme of dimension ![]() $n$ over a field. For every integer
$n$ over a field. For every integer ![]() $i\geqslant 0$, the ith asymptotic cohomological function on
$i\geqslant 0$, the ith asymptotic cohomological function on ![]() $X$ is the function defined by setting
$X$ is the function defined by setting
for an ![]() $\mathbf{R}$-Cartier divisor
$\mathbf{R}$-Cartier divisor ![]() $D$ on
$D$ on ![]() $X$, where the round-up is defined by writing
$X$, where the round-up is defined by writing ![]() $D=\sum _{i}a_{i}D_{i}$ as an
$D=\sum _{i}a_{i}D_{i}$ as an ![]() $\mathbf{R}$-linear combination of Cartier divisors and setting
$\mathbf{R}$-linear combination of Cartier divisors and setting ![]() $\lceil mD\rceil :=\sum _{i}\lceil ma_{i}\rceil D_{i}$; see [Reference Burgos Gil, Gubler, Jell, Künnemann and Martin6, Definition 3.4.1]. The numbers
$\lceil mD\rceil :=\sum _{i}\lceil ma_{i}\rceil D_{i}$; see [Reference Burgos Gil, Gubler, Jell, Künnemann and Martin6, Definition 3.4.1]. The numbers ![]() $\widehat{h}^{i}(X,D)$ only depend on the
$\widehat{h}^{i}(X,D)$ only depend on the ![]() $\mathbf{R}$-linear equivalence class of
$\mathbf{R}$-linear equivalence class of ![]() $D$ and are independent of the decomposition
$D$ and are independent of the decomposition ![]() $D=\sum _{i}a_{i}D_{i}$ by [Reference Burgos Gil, Gubler, Jell, Künnemann and Martin6, Remark 3.4.5], hence
$D=\sum _{i}a_{i}D_{i}$ by [Reference Burgos Gil, Gubler, Jell, Künnemann and Martin6, Remark 3.4.5], hence ![]() $\widehat{h}^{i}(X,-)$ gives rise to well-defined functions
$\widehat{h}^{i}(X,-)$ gives rise to well-defined functions ![]() $\operatorname{Div}_{\mathbf{R}}(X)\rightarrow \mathbf{R}$ and
$\operatorname{Div}_{\mathbf{R}}(X)\rightarrow \mathbf{R}$ and ![]() $\operatorname{Div}_{\mathbf{R}}(X)/{\sim}_{\mathbf{R}}\rightarrow \mathbf{R}$.
$\operatorname{Div}_{\mathbf{R}}(X)/{\sim}_{\mathbf{R}}\rightarrow \mathbf{R}$.
A key property of asymptotic cohomological functions is the following:
Proposition 4.2. [Reference Burgos Gil, Gubler, Jell, Künnemann and Martin6, Proposition 3.4.8]
Let ![]() $X$ be a projective scheme of dimension
$X$ be a projective scheme of dimension ![]() $n$ over a field. For every
$n$ over a field. For every ![]() $i\geqslant 0$, the function
$i\geqslant 0$, the function ![]() $\widehat{h}^{i}(X,-)$ on
$\widehat{h}^{i}(X,-)$ on ![]() $\operatorname{Div}_{\mathbf{R}}(X)$ is homogeneous of degree
$\operatorname{Div}_{\mathbf{R}}(X)$ is homogeneous of degree ![]() $n$, and is continuous on every finite-dimensional
$n$, and is continuous on every finite-dimensional ![]() $\mathbf{R}$-subspace of
$\mathbf{R}$-subspace of ![]() $\operatorname{Div}_{\mathbf{R}}(X)$ with respect to every norm.
$\operatorname{Div}_{\mathbf{R}}(X)$ with respect to every norm.
Proposition 4.2 shows that Definition 4.1 is equivalent to Küronya’s original definition in [Reference Küronya41], and allows us to prove that asymptotic cohomological functions behave well with respect to generically finite morphisms.
Proposition 4.3. (cf. [Reference Küronya41, Proposition 2.9(1)])
Let ![]() $f:Y\rightarrow X$ be a surjective morphism of projective varieties, and consider an
$f:Y\rightarrow X$ be a surjective morphism of projective varieties, and consider an ![]() $\mathbf{R}$-Cartier divisor
$\mathbf{R}$-Cartier divisor ![]() $D$ on
$D$ on ![]() $X$. Suppose
$X$. Suppose ![]() $f$ is generically finite of degree
$f$ is generically finite of degree ![]() $d$. Then, for every
$d$. Then, for every ![]() $i$, we have
$i$, we have
Proof. The proof of [Reference Küronya41, Proposition 2.9(1)] works in our setting with the additional hypothesis that ![]() $D$ is a Cartier divisor. It therefore suffices to reduce to this case. If the statement holds for integral
$D$ is a Cartier divisor. It therefore suffices to reduce to this case. If the statement holds for integral ![]() $D$, then it also holds for
$D$, then it also holds for ![]() $D\in \operatorname{Div}_{\mathbf{Q}}(X)$ by homogeneity of
$D\in \operatorname{Div}_{\mathbf{Q}}(X)$ by homogeneity of ![]() $\widehat{h}^{i}$ (Proposition 4.2). Moreover, the subspace of
$\widehat{h}^{i}$ (Proposition 4.2). Moreover, the subspace of ![]() $\operatorname{Div}_{\mathbf{R}}(X)$ spanned by the Cartier divisors appearing in
$\operatorname{Div}_{\mathbf{R}}(X)$ spanned by the Cartier divisors appearing in ![]() $D$ is finite-dimensional, hence by approximating each coefficient in
$D$ is finite-dimensional, hence by approximating each coefficient in ![]() $D$ by rational numbers, Proposition 4.2 implies the statement for
$D$ by rational numbers, Proposition 4.2 implies the statement for ![]() $D\in \operatorname{Div}_{\mathbf{R}}(X)$ by continuity.◻
$D\in \operatorname{Div}_{\mathbf{R}}(X)$ by continuity.◻
Remark 4.4. We repeatedly use the same steps as in the proof of Proposition 4.3 to prove statements about ![]() $\widehat{h}^{i}(X,D)$ for arbitrary
$\widehat{h}^{i}(X,D)$ for arbitrary ![]() $\mathbf{R}$-Cartier divisors by reducing to the case when
$\mathbf{R}$-Cartier divisors by reducing to the case when ![]() $D$ is a Cartier divisor. If
$D$ is a Cartier divisor. If ![]() $D$ is an
$D$ is an ![]() $\mathbf{R}$-Cartier divisor, we can write
$\mathbf{R}$-Cartier divisor, we can write ![]() $D$ as the limit of
$D$ as the limit of ![]() $\mathbf{Q}$-Cartier divisors by approximating each coefficient in a decomposition of
$\mathbf{Q}$-Cartier divisors by approximating each coefficient in a decomposition of ![]() $D$ by rational numbers, and continuity of asymptotic cohomological functions (Proposition 4.2) then allows us to reduce to the case when
$D$ by rational numbers, and continuity of asymptotic cohomological functions (Proposition 4.2) then allows us to reduce to the case when ![]() $D$ is a
$D$ is a ![]() $\mathbf{Q}$-Cartier divisor. By homogeneity of asymptotic cohomology functions (Proposition 4.2), one can then reduce to the case when
$\mathbf{Q}$-Cartier divisor. By homogeneity of asymptotic cohomology functions (Proposition 4.2), one can then reduce to the case when ![]() $D$ is a Cartier divisor.
$D$ is a Cartier divisor.
We also need the following:
Proposition 4.5. (Asymptotic Serre duality; cf. [Reference Küronya41, Corollary 2.11])
Let ![]() $X$ be a projective variety of dimension
$X$ be a projective variety of dimension ![]() $n$, and let
$n$, and let ![]() $D$ be an
$D$ be an ![]() $\mathbf{R}$-Cartier divisor on
$\mathbf{R}$-Cartier divisor on ![]() $X$. Then, for every
$X$. Then, for every ![]() $0\leqslant i\leqslant n$, we have
$0\leqslant i\leqslant n$, we have
Proof. By Remark 4.4, it suffices to consider the case when ![]() $D$ is integral. Let
$D$ is integral. Let ![]() $f:Y\rightarrow X$ be a regular alteration of degree
$f:Y\rightarrow X$ be a regular alteration of degree ![]() $d$ [Reference de Jong38, Theorem 4.1]. We then have
$d$ [Reference de Jong38, Theorem 4.1]. We then have
by Serre duality and [Reference Burgos Gil, Gubler, Jell, Künnemann and Martin6, Lemma 3.2.1], respectively. By Proposition 4.3, the left-hand side is equal to ![]() $d\cdot \widehat{h}^{i}(X,D)$ and the right-hand side is equal to
$d\cdot \widehat{h}^{i}(X,D)$ and the right-hand side is equal to ![]() $d\cdot \widehat{h}^{n-i}(X,-D)$, hence the statement follows after dividing by
$d\cdot \widehat{h}^{n-i}(X,-D)$, hence the statement follows after dividing by ![]() $d$.◻
$d$.◻
4.2 A lemma on base loci
A key ingredient in our proof of Theorem B is the following result on base loci, which is an analogue of [Reference de Fernex, Küronya and Lazarsfeld12, Proposition 3.1] over more general fields. In positive characteristic, we use asymptotic test ideals instead of asymptotic multiplier ideals, which requires working over an ![]() $F$-finite field.
$F$-finite field.
Proposition 4.6. Let ![]() $V$ be a normal projective variety of dimension at least two over an infinite field
$V$ be a normal projective variety of dimension at least two over an infinite field ![]() $k$, where if
$k$, where if ![]() $\operatorname{char}k=p>0$, then we also assume that
$\operatorname{char}k=p>0$, then we also assume that ![]() $k$ is
$k$ is ![]() $F$-finite. Let
$F$-finite. Let ![]() $D$ be a Cartier divisor on
$D$ be a Cartier divisor on ![]() $V$. Assume there exists a closed subscheme
$V$. Assume there exists a closed subscheme ![]() $Z\subseteq V$ of pure dimension
$Z\subseteq V$ of pure dimension ![]() $1$ such that
$1$ such that
(i)
 $D\cdot Z_{\unicode[STIX]{x1D6FC}}<0$ for every irreducible component
$D\cdot Z_{\unicode[STIX]{x1D6FC}}<0$ for every irreducible component  $Z_{\unicode[STIX]{x1D6FC}}$ of
$Z_{\unicode[STIX]{x1D6FC}}$ of  $Z$, and
$Z$, and(ii) There exists a projective birational morphism
 $\unicode[STIX]{x1D707}:V^{\prime }\rightarrow V$ such that
$\unicode[STIX]{x1D707}:V^{\prime }\rightarrow V$ such that  $V^{\prime }$ is regular and
$V^{\prime }$ is regular and  $(\unicode[STIX]{x1D707}^{-1}(Z))_{\text{red}}$ is a simple normal crossing divisor.
$(\unicode[STIX]{x1D707}^{-1}(Z))_{\text{red}}$ is a simple normal crossing divisor.
Let ![]() $\mathfrak{a}\subseteq {\mathcal{O}}_{V}$ be the ideal sheaf of
$\mathfrak{a}\subseteq {\mathcal{O}}_{V}$ be the ideal sheaf of ![]() $Z$. Then, there exist positive integers
$Z$. Then, there exist positive integers ![]() $q$ and
$q$ and ![]() $c$ such that for every integer
$c$ such that for every integer ![]() $m\geqslant c$, we have
$m\geqslant c$, we have
Here, ![]() $\mathfrak{b}(|D|)$ denotes the base ideal of the Cartier divisor
$\mathfrak{b}(|D|)$ denotes the base ideal of the Cartier divisor ![]() $D$; see Definition 2.2. We note that the
$D$; see Definition 2.2. We note that the ![]() $Z_{\unicode[STIX]{x1D6FC}}$ can possibly be nonreduced.
$Z_{\unicode[STIX]{x1D6FC}}$ can possibly be nonreduced.
In the proof below, we use the fact [Reference Kleiman40, Lemma B.12] that if ![]() $W$ is a one-dimensional subscheme of a complete scheme
$W$ is a one-dimensional subscheme of a complete scheme ![]() $X$ over a field, and if
$X$ over a field, and if ![]() $D$ is a Cartier divisor on
$D$ is a Cartier divisor on ![]() $X$, then
$X$, then
where the ![]() $W_{\unicode[STIX]{x1D6FC}}$ are the one-dimensional components of
$W_{\unicode[STIX]{x1D6FC}}$ are the one-dimensional components of ![]() $W$ with generic points
$W$ with generic points ![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}\in W_{\unicode[STIX]{x1D6FC}}$.
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FC}}\in W_{\unicode[STIX]{x1D6FC}}$.
Proof. The statement is trivial if ![]() $H^{0}(V,{\mathcal{O}}_{V}(mD))=0$ for every integer
$H^{0}(V,{\mathcal{O}}_{V}(mD))=0$ for every integer ![]() $m>0$, since in this case
$m>0$, since in this case ![]() $\mathfrak{b}(|mqD|)=0$ for all positive integers
$\mathfrak{b}(|mqD|)=0$ for all positive integers ![]() $m,q$. We therefore assume
$m,q$. We therefore assume ![]() $H^{0}(V,{\mathcal{O}}_{V}(mD))\neq 0$ for some integer
$H^{0}(V,{\mathcal{O}}_{V}(mD))\neq 0$ for some integer ![]() $m>0$. We prove the statement in positive characteristic; see Remark 4.7 for the characteristic zero case.
$m>0$. We prove the statement in positive characteristic; see Remark 4.7 for the characteristic zero case.
We fix some notation. Set ![]() $D^{\prime }=\unicode[STIX]{x1D707}^{\ast }D$ and set
$D^{\prime }=\unicode[STIX]{x1D707}^{\ast }D$ and set ![]() $E=(\unicode[STIX]{x1D707}^{-1}(Z))_{\text{red}}$. We fix a very ample Cartier divisor
$E=(\unicode[STIX]{x1D707}^{-1}(Z))_{\text{red}}$. We fix a very ample Cartier divisor ![]() $H$ on
$H$ on ![]() $V^{\prime }$, and set
$V^{\prime }$, and set ![]() $A=K_{V^{\prime }}+(\dim V^{\prime }+1)H$. For every subvariety
$A=K_{V^{\prime }}+(\dim V^{\prime }+1)H$. For every subvariety ![]() $W\subseteq V^{\prime }$, a complete intersection curve is a curve formed by taking the intersection of
$W\subseteq V^{\prime }$, a complete intersection curve is a curve formed by taking the intersection of ![]() $\dim W-1$ hyperplane sections in
$\dim W-1$ hyperplane sections in ![]() $|H|_{W}|$, and a general complete intersection curve is one formed by taking these hyperplane sections to be general in
$|H|_{W}|$, and a general complete intersection curve is one formed by taking these hyperplane sections to be general in ![]() $|H|_{W}|$. For each positive integer
$|H|_{W}|$. For each positive integer ![]() $q$, we consider the asymptotic test ideal
$q$, we consider the asymptotic test ideal
By uniform global generation for test ideals [Reference Sato57, Proposition 4.1], the sheaf
is globally generated for every integer ![]() $q>0$.
$q>0$.
Step 1. There exists an integer ![]() $\ell _{0}>0$ such that for every integer
$\ell _{0}>0$ such that for every integer ![]() $\ell >\ell _{0}$ and for every irreducible component
$\ell >\ell _{0}$ and for every irreducible component ![]() $F$ of
$F$ of ![]() $E$ that dominates
$E$ that dominates ![]() $(Z_{\unicode[STIX]{x1D6FC}})_{\text{red}}$ for some
$(Z_{\unicode[STIX]{x1D6FC}})_{\text{red}}$ for some ![]() $\unicode[STIX]{x1D6FC}$, we have
$\unicode[STIX]{x1D6FC}$, we have
Let ![]() $C\subseteq F$ be a general complete intersection curve; note that
$C\subseteq F$ be a general complete intersection curve; note that ![]() $C$ is integral by Bertini’s theorem [Reference Flenner, O’Carroll and Vogel20, Theorem 3.4.10 and Corollary 3.4.14] and dominates
$C$ is integral by Bertini’s theorem [Reference Flenner, O’Carroll and Vogel20, Theorem 3.4.10 and Corollary 3.4.14] and dominates ![]() $(Z_{\unicode[STIX]{x1D6FC}})_{\text{red}}$ for some
$(Z_{\unicode[STIX]{x1D6FC}})_{\text{red}}$ for some ![]() $\unicode[STIX]{x1D6FC}$, hence
$\unicode[STIX]{x1D6FC}$, hence ![]() $(D^{\prime }\cdot C)<0$ by the projection formula and (5). If for some integer
$(D^{\prime }\cdot C)<0$ by the projection formula and (5). If for some integer ![]() $q>0$, the curve
$q>0$, the curve ![]() $C$ is not contained in the zero locus of
$C$ is not contained in the zero locus of ![]() $\unicode[STIX]{x1D70F}(\Vert qD^{\prime }\Vert )$, then the fact that the sheaf (6) is globally generated implies
$\unicode[STIX]{x1D70F}(\Vert qD^{\prime }\Vert )$, then the fact that the sheaf (6) is globally generated implies
Letting ![]() $\ell _{0F}=-(A\cdot C)/(D^{\prime }\cdot C)$, we see that the ideal
$\ell _{0F}=-(A\cdot C)/(D^{\prime }\cdot C)$, we see that the ideal ![]() $\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )$ vanishes everywhere along
$\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )$ vanishes everywhere along ![]() $C$ for every integer
$C$ for every integer ![]() $\ell >\ell _{0F}$. By varying
$\ell >\ell _{0F}$. By varying ![]() $C$, the ideal
$C$, the ideal ![]() $\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )$ must vanish everywhere along
$\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )$ must vanish everywhere along ![]() $F$ for every integer
$F$ for every integer ![]() $\ell >\ell _{0F}$, hence we can set
$\ell >\ell _{0F}$, hence we can set ![]() $\ell _{0}=\max _{F}\{\ell _{0F}\}$.
$\ell _{0}=\max _{F}\{\ell _{0F}\}$.
Step 2. Let ![]() $E_{i}$ be an irreducible component of
$E_{i}$ be an irreducible component of ![]() $E$ not dominating
$E$ not dominating ![]() $Z_{\unicode[STIX]{x1D6FC}}$ for every
$Z_{\unicode[STIX]{x1D6FC}}$ for every ![]() $\unicode[STIX]{x1D6FC}$. Suppose
$\unicode[STIX]{x1D6FC}$. Suppose ![]() $E_{j}$ is another irreducible component of
$E_{j}$ is another irreducible component of ![]() $E$ such that
$E$ such that ![]() $E_{i}\cap E_{j}\neq \emptyset$ and for which there exists an integer
$E_{i}\cap E_{j}\neq \emptyset$ and for which there exists an integer ![]() $\ell _{j}$ such that for every integer
$\ell _{j}$ such that for every integer ![]() $\ell >\ell _{j}$, we have
$\ell >\ell _{j}$, we have
Then, there is an integer ![]() $\ell _{i}\geqslant \ell _{j}$ such that for every integer
$\ell _{i}\geqslant \ell _{j}$ such that for every integer ![]() $\ell >\ell _{i}$, we have
$\ell >\ell _{i}$, we have
Let ![]() $C\subseteq E_{i}$ be a complete intersection curve. By the assumption that
$C\subseteq E_{i}$ be a complete intersection curve. By the assumption that ![]() $E$ is a simple normal crossing divisor, there exists at least one closed point
$E$ is a simple normal crossing divisor, there exists at least one closed point ![]() $P\in C\cap E_{j}$. For every
$P\in C\cap E_{j}$. For every ![]() $\ell >\ell _{j}$ and every
$\ell >\ell _{j}$ and every ![]() $m>0$, we have the sequence of inclusions
$m>0$, we have the sequence of inclusions
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}} & & (\unicode[STIX]{x1D70F}(\Vert m\ell D^{\prime }\Vert )\otimes {\mathcal{O}}_{V^{\prime }}(m\ell D^{\prime }+A))\cdot {\mathcal{O}}_{C}\\ & & \qquad \subseteq (\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )^{m}\otimes {\mathcal{O}}_{V^{\prime }}(m\ell D^{\prime }+A))\cdot {\mathcal{O}}_{C}\\ & & \qquad \subseteq ({\mathcal{O}}_{V^{\prime }}(-mE_{j})\otimes {\mathcal{O}}_{V^{\prime }}(m\ell D^{\prime }+A))\cdot {\mathcal{O}}_{C}\\ & & \qquad \subseteq {\mathcal{O}}_{C}(A|_{C}-mP),\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}} & & (\unicode[STIX]{x1D70F}(\Vert m\ell D^{\prime }\Vert )\otimes {\mathcal{O}}_{V^{\prime }}(m\ell D^{\prime }+A))\cdot {\mathcal{O}}_{C}\\ & & \qquad \subseteq (\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )^{m}\otimes {\mathcal{O}}_{V^{\prime }}(m\ell D^{\prime }+A))\cdot {\mathcal{O}}_{C}\\ & & \qquad \subseteq ({\mathcal{O}}_{V^{\prime }}(-mE_{j})\otimes {\mathcal{O}}_{V^{\prime }}(m\ell D^{\prime }+A))\cdot {\mathcal{O}}_{C}\\ & & \qquad \subseteq {\mathcal{O}}_{C}(A|_{C}-mP),\end{array} & & \displaystyle\end{eqnarray}$$ where the first two inclusions follow from subadditivity [Reference Hara and Yoshida27, Theorem 6.10(2)] and by assumption, respectively. The last inclusion holds since ![]() $C$ maps to a closed point in
$C$ maps to a closed point in ![]() $V$, hence
$V$, hence ![]() ${\mathcal{O}}_{C}(D^{\prime })={\mathcal{O}}_{C}$. By the global generation of the sheaf in (6) for
${\mathcal{O}}_{C}(D^{\prime })={\mathcal{O}}_{C}$. By the global generation of the sheaf in (6) for ![]() $q=m\ell$, the inclusion (7) implies that for every integer
$q=m\ell$, the inclusion (7) implies that for every integer ![]() $\ell >\ell _{j}$, if
$\ell >\ell _{j}$, if ![]() $\unicode[STIX]{x1D70F}(\Vert m\ell D^{\prime }\Vert )$ does not vanish everywhere along
$\unicode[STIX]{x1D70F}(\Vert m\ell D^{\prime }\Vert )$ does not vanish everywhere along ![]() $C$, then
$C$, then ![]() $(A\cdot C)\geqslant m$. Choosing
$(A\cdot C)\geqslant m$. Choosing ![]() $\ell _{i}=\ell _{j}\cdot ((A\cdot C)+1)$, we see that
$\ell _{i}=\ell _{j}\cdot ((A\cdot C)+1)$, we see that ![]() $\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )$ vanishes everywhere along
$\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )$ vanishes everywhere along ![]() $C$ for every integer
$C$ for every integer ![]() $\ell >\ell _{i}$. By varying
$\ell >\ell _{i}$. By varying ![]() $C$, we have
$C$, we have ![]() $\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )\subseteq {\mathcal{O}}_{V^{\prime }}(-E_{i})$ for every integer
$\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )\subseteq {\mathcal{O}}_{V^{\prime }}(-E_{i})$ for every integer ![]() $\ell >\ell _{i}$.
$\ell >\ell _{i}$.
Step 3. There exists an integer ![]() $a>0$ such that
$a>0$ such that
for every integer ![]() $m>0$.
$m>0$.
Write
where the ![]() $E_{ij}$ are the irreducible components of
$E_{ij}$ are the irreducible components of ![]() $E$, and the
$E$, and the ![]() $\bigcup _{i\in I_{j}}E_{ij}$ are the connected components of
$\bigcup _{i\in I_{j}}E_{ij}$ are the connected components of ![]() $E$. Since
$E$. Since ![]() $V$ is normal, each preimage
$V$ is normal, each preimage ![]() $\unicode[STIX]{x1D707}^{-1}(Z_{\unicode[STIX]{x1D6FC}})$ is connected by Zariski’s main theorem [Reference Hartshorne29, Corollary III.11.4], hence each connected component
$\unicode[STIX]{x1D707}^{-1}(Z_{\unicode[STIX]{x1D6FC}})$ is connected by Zariski’s main theorem [Reference Hartshorne29, Corollary III.11.4], hence each connected component ![]() $\bigcup _{i\in I_{j}}E_{ij}$ of
$\bigcup _{i\in I_{j}}E_{ij}$ of ![]() $E$ contains an irreducible component
$E$ contains an irreducible component ![]() $E_{i_{0}j}$ that dominates
$E_{i_{0}j}$ that dominates ![]() $(Z_{\unicode[STIX]{x1D6FC}})_{\text{red}}$ for some
$(Z_{\unicode[STIX]{x1D6FC}})_{\text{red}}$ for some ![]() $\unicode[STIX]{x1D6FC}$. By Step 1, there exists an integer
$\unicode[STIX]{x1D6FC}$. By Step 1, there exists an integer ![]() $\ell _{0}$ such that for every
$\ell _{0}$ such that for every ![]() $j$, we have
$j$, we have ![]() $\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )\subseteq {\mathcal{O}}_{V^{\prime }}(-E_{i_{0}j})$ for every integer
$\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )\subseteq {\mathcal{O}}_{V^{\prime }}(-E_{i_{0}j})$ for every integer ![]() $\ell >\ell _{0}$. For each
$\ell >\ell _{0}$. For each ![]() $j$, by applying Step 2
$j$, by applying Step 2 ![]() $(|I_{j}|-1)$ times to the
$(|I_{j}|-1)$ times to the ![]() $j$th connected component
$j$th connected component ![]() $\bigcup _{i\in I_{j}}E_{ij}$ of
$\bigcup _{i\in I_{j}}E_{ij}$ of ![]() $E$, we can find
$E$, we can find ![]() $\ell _{j}$ such that
$\ell _{j}$ such that ![]() $\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )\subseteq {\mathcal{O}}_{V^{\prime }}(-E_{ij})$ for every
$\unicode[STIX]{x1D70F}(\Vert \ell D^{\prime }\Vert )\subseteq {\mathcal{O}}_{V^{\prime }}(-E_{ij})$ for every ![]() $i\in I_{j}$ and for every integer
$i\in I_{j}$ and for every integer ![]() $\ell >\ell _{j}$. Setting
$\ell >\ell _{j}$. Setting ![]() $a=\max _{j}\{\ell _{j}\}+1$, we have
$a=\max _{j}\{\ell _{j}\}+1$, we have ![]() $\unicode[STIX]{x1D70F}(\Vert aD^{\prime }\Vert )\subseteq {\mathcal{O}}_{V^{\prime }}(-E)$. Thus, for every integer
$\unicode[STIX]{x1D70F}(\Vert aD^{\prime }\Vert )\subseteq {\mathcal{O}}_{V^{\prime }}(-E)$. Thus, for every integer ![]() $m>0$, we have
$m>0$, we have
where the first inclusion follows by the fact that ![]() $V^{\prime }$ is regular hence strongly
$V^{\prime }$ is regular hence strongly ![]() $F$-regular [Reference Takagi and Watanabe62, Propositions 5.6(1) and 5.6(5)], the second inclusion is by definition of the asymptotic test ideal, and the third inclusion is by subadditivity [Reference Hara and Yoshida27, Theorem 6.10(2)].
$F$-regular [Reference Takagi and Watanabe62, Propositions 5.6(1) and 5.6(5)], the second inclusion is by definition of the asymptotic test ideal, and the third inclusion is by subadditivity [Reference Hara and Yoshida27, Theorem 6.10(2)].
Step 4. Conclusion of proof of Proposition 4.6.
Let ![]() $\unicode[STIX]{x1D70B}:V^{\prime \prime }\rightarrow V^{\prime }$ be the normalized blowup of the ideal
$\unicode[STIX]{x1D70B}:V^{\prime \prime }\rightarrow V^{\prime }$ be the normalized blowup of the ideal ![]() $\unicode[STIX]{x1D707}^{-1}\mathfrak{a}\cdot {\mathcal{O}}_{V^{\prime }}$, and write
$\unicode[STIX]{x1D707}^{-1}\mathfrak{a}\cdot {\mathcal{O}}_{V^{\prime }}$, and write ![]() $(\unicode[STIX]{x1D707}\circ \unicode[STIX]{x1D70B})^{-1}\mathfrak{a}\cdot {\mathcal{O}}_{V^{\prime \prime }}={\mathcal{O}}_{V^{\prime \prime }}(-E^{\prime \prime })$ for a Cartier divisor
$(\unicode[STIX]{x1D707}\circ \unicode[STIX]{x1D70B})^{-1}\mathfrak{a}\cdot {\mathcal{O}}_{V^{\prime \prime }}={\mathcal{O}}_{V^{\prime \prime }}(-E^{\prime \prime })$ for a Cartier divisor ![]() $E^{\prime \prime }$ on
$E^{\prime \prime }$ on ![]() $V^{\prime \prime }$. Note that since
$V^{\prime \prime }$. Note that since ![]() ${\mathcal{O}}_{V^{\prime \prime }}(-(\unicode[STIX]{x1D70B}^{\ast }E)_{\text{red}})$ is the radical of
${\mathcal{O}}_{V^{\prime \prime }}(-(\unicode[STIX]{x1D70B}^{\ast }E)_{\text{red}})$ is the radical of ![]() ${\mathcal{O}}_{V^{\prime \prime }}(-E^{\prime \prime })$, there exists an integer
${\mathcal{O}}_{V^{\prime \prime }}(-E^{\prime \prime })$, there exists an integer ![]() $b>0$ such that
$b>0$ such that ![]() ${\mathcal{O}}_{V^{\prime \prime }}(-b(\unicode[STIX]{x1D70B}^{\ast }E)_{\text{red}})\subseteq {\mathcal{O}}_{V^{\prime \prime }}(-E^{\prime \prime })$. We then have
${\mathcal{O}}_{V^{\prime \prime }}(-b(\unicode[STIX]{x1D70B}^{\ast }E)_{\text{red}})\subseteq {\mathcal{O}}_{V^{\prime \prime }}(-E^{\prime \prime })$. We then have
 $$\begin{eqnarray}\displaystyle \mathfrak{b}(|mab\,\unicode[STIX]{x1D70B}^{\ast }D^{\prime }|) & = & \displaystyle \unicode[STIX]{x1D70B}^{-1}\mathfrak{b}(|mabD^{\prime }|)\cdot {\mathcal{O}}_{V^{\prime \prime }}\nonumber\\ \displaystyle & \subseteq & \displaystyle {\mathcal{O}}_{V^{\prime \prime }}(-mb\,\unicode[STIX]{x1D70B}^{\ast }E)\nonumber\\ \displaystyle & \subseteq & \displaystyle {\mathcal{O}}_{V^{\prime \prime }}(-mb(\unicode[STIX]{x1D70B}^{\ast }E)_{\text{red}})\nonumber\\ \displaystyle & \subseteq & \displaystyle {\mathcal{O}}_{V^{\prime \prime }}(-mE^{\prime \prime })\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{b}(|mab\,\unicode[STIX]{x1D70B}^{\ast }D^{\prime }|) & = & \displaystyle \unicode[STIX]{x1D70B}^{-1}\mathfrak{b}(|mabD^{\prime }|)\cdot {\mathcal{O}}_{V^{\prime \prime }}\nonumber\\ \displaystyle & \subseteq & \displaystyle {\mathcal{O}}_{V^{\prime \prime }}(-mb\,\unicode[STIX]{x1D70B}^{\ast }E)\nonumber\\ \displaystyle & \subseteq & \displaystyle {\mathcal{O}}_{V^{\prime \prime }}(-mb(\unicode[STIX]{x1D70B}^{\ast }E)_{\text{red}})\nonumber\\ \displaystyle & \subseteq & \displaystyle {\mathcal{O}}_{V^{\prime \prime }}(-mE^{\prime \prime })\nonumber\end{eqnarray}$$ by Step 3, where the first equality holds by Lemma 2.3. Setting ![]() $q=ab$ and pushing forward by
$q=ab$ and pushing forward by ![]() $\unicode[STIX]{x1D707}\circ \unicode[STIX]{x1D70B}$, we have
$\unicode[STIX]{x1D707}\circ \unicode[STIX]{x1D70B}$, we have
where the first inclusion follows from Lemma 2.3, and where ![]() $\overline{\mathfrak{a}^{m}}$ is the integral closure of
$\overline{\mathfrak{a}^{m}}$ is the integral closure of ![]() $\mathfrak{a}^{m}$ [Reference Lazarsfeld44, Remark 9.6.4]. Finally, given any ideal
$\mathfrak{a}^{m}$ [Reference Lazarsfeld44, Remark 9.6.4]. Finally, given any ideal ![]() $\mathfrak{a}\subseteq {\mathcal{O}}_{V}$, there exists an integer
$\mathfrak{a}\subseteq {\mathcal{O}}_{V}$, there exists an integer ![]() $c$ such that
$c$ such that ![]() $\overline{\mathfrak{a}^{\ell +1}}=\mathfrak{a}\cdot \overline{\mathfrak{a}^{\ell }}$ for all
$\overline{\mathfrak{a}^{\ell +1}}=\mathfrak{a}\cdot \overline{\mathfrak{a}^{\ell }}$ for all ![]() $\ell \geqslant c$ [Reference Lazarsfeld44, Proof of Proposition 9.6.6], hence
$\ell \geqslant c$ [Reference Lazarsfeld44, Proof of Proposition 9.6.6], hence ![]() $\overline{\mathfrak{a}^{m}}\subseteq \mathfrak{a}^{m-c}$ for all
$\overline{\mathfrak{a}^{m}}\subseteq \mathfrak{a}^{m-c}$ for all ![]() $m\geqslant c$.◻
$m\geqslant c$.◻
Remark 4.7. When ![]() $\operatorname{char}k=0$, one can prove the stronger statement of [Reference de Fernex, Küronya and Lazarsfeld12, Proposition 3.1] using resolutions of singularities and the asymptotic multiplier ideals
$\operatorname{char}k=0$, one can prove the stronger statement of [Reference de Fernex, Küronya and Lazarsfeld12, Proposition 3.1] using resolutions of singularities and the asymptotic multiplier ideals ![]() ${\mathcal{J}}(\Vert D\Vert )$ defined in [Reference Lazarsfeld44, Definition 11.1.2] by replacing [Reference Takagi and Watanabe62, Proposition 5.6] and [Reference Hara and Yoshida27, Theorem 6.10(2)] with [Reference de Fernex and Mustaţă13, Proposition 2.3] and [Reference Jonsson and Mustaţă39, Theorem A.2], respectively. To replace [Reference Sato57, Proposition 4.1], one can pass to the algebraic closure (since the formation of multiplier ideals is compatible with ground field extensions [Reference Jonsson and Mustaţă39, Proposition 1.9]) to deduce uniform global generation from the algebraically closed case [Reference Lazarsfeld44, Corollary 11.2.13].
${\mathcal{J}}(\Vert D\Vert )$ defined in [Reference Lazarsfeld44, Definition 11.1.2] by replacing [Reference Takagi and Watanabe62, Proposition 5.6] and [Reference Hara and Yoshida27, Theorem 6.10(2)] with [Reference de Fernex and Mustaţă13, Proposition 2.3] and [Reference Jonsson and Mustaţă39, Theorem A.2], respectively. To replace [Reference Sato57, Proposition 4.1], one can pass to the algebraic closure (since the formation of multiplier ideals is compatible with ground field extensions [Reference Jonsson and Mustaţă39, Proposition 1.9]) to deduce uniform global generation from the algebraically closed case [Reference Lazarsfeld44, Corollary 11.2.13].
Before moving on to the proof of Theorem B, we note that after a preprint of this paper was posted, the authors of [Reference Ma, Polstra, Schwede and Tucker46] informed us that they had proved an asymptotic nonvanishing statement [Reference Ma, Polstra, Schwede and Tucker46, Lemma 4.2] using techniques similar to ours in Proposition 4.6 and Theorem B. By combining the methods in this paper and in [Reference Ma, Polstra, Schwede and Tucker46, Lemmas 4.3 and 4.4], one can prove the full analogue of [Reference de Fernex, Küronya and Lazarsfeld12, Proposition 3.1], namely:
Proposition 4.8. Let ![]() $V$ be a normal projective variety of dimension at least two over a field
$V$ be a normal projective variety of dimension at least two over a field ![]() $k$. Let
$k$. Let ![]() $D$ be a Cartier divisor on
$D$ be a Cartier divisor on ![]() $V$, and suppose there exists an integral curve
$V$, and suppose there exists an integral curve ![]() $Z\subseteq V$ such that
$Z\subseteq V$ such that ![]() $(D\cdot Z)<0$. Denote by
$(D\cdot Z)<0$. Denote by ![]() $\mathfrak{a}\subseteq {\mathcal{O}}_{V}$ the ideal sheaf defining
$\mathfrak{a}\subseteq {\mathcal{O}}_{V}$ the ideal sheaf defining ![]() $Z$. Then, there exist positive integers
$Z$. Then, there exist positive integers ![]() $q$ and
$q$ and ![]() $c$ such that for every integer
$c$ such that for every integer ![]() $m\geqslant c$, we have
$m\geqslant c$, we have
We will not use Proposition 4.8 in the sequel. See [Reference Murayama50, Proposition 6.2.1] for a proof.
4.3 Proof of Theorem B
We now prove Theorem B. We first note that the direction ![]() $\Rightarrow$ in Theorem B follows from existing results.
$\Rightarrow$ in Theorem B follows from existing results.
Proof of  $\Rightarrow$ in Theorem B.
$\Rightarrow$ in Theorem B.
Let ![]() $A$ be a very ample Cartier divisor. Then, for all
$A$ be a very ample Cartier divisor. Then, for all ![]() $t$ such that
$t$ such that ![]() $L-tA$ is ample, we have
$L-tA$ is ample, we have ![]() $\widehat{h}^{i}(X,L-tA)=0$ by Serre vanishing and by homogeneity and continuity; see Remark 4.4.◻
$\widehat{h}^{i}(X,L-tA)=0$ by Serre vanishing and by homogeneity and continuity; see Remark 4.4.◻
For the direction ![]() $\Leftarrow$, it suffices to show Theorem B for Cartier divisors
$\Leftarrow$, it suffices to show Theorem B for Cartier divisors ![]() $L$ by continuity and homogeneity; see Remark 4.4. We also make the following two reductions. Recall that an
$L$ by continuity and homogeneity; see Remark 4.4. We also make the following two reductions. Recall that an ![]() $\mathbf{R}$-Cartier divisor
$\mathbf{R}$-Cartier divisor ![]() $L$ on
$L$ on ![]() $X$satisfies (
$X$satisfies (![]() $\star$ ) for a pair
$\star$ ) for a pair ![]() $(A,\unicode[STIX]{x1D700})$ consisting of a very ample Cartier divisor
$(A,\unicode[STIX]{x1D700})$ consisting of a very ample Cartier divisor ![]() $A$ on
$A$ on ![]() $X$ and a real number
$X$ and a real number ![]() $\unicode[STIX]{x1D700}>0$ if
$\unicode[STIX]{x1D700}>0$ if ![]() $\widehat{h}^{i}(X,L-tA)=0$ for all
$\widehat{h}^{i}(X,L-tA)=0$ for all ![]() $i>0$ and all
$i>0$ and all ![]() $t\in [0,\unicode[STIX]{x1D700})$.
$t\in [0,\unicode[STIX]{x1D700})$.
Lemma 4.9. To prove the direction ![]() $\Leftarrow$ in Theorem B, we may assume that the ground field
$\Leftarrow$ in Theorem B, we may assume that the ground field ![]() $k$ is uncountable. In positive characteristic, we may also assume that
$k$ is uncountable. In positive characteristic, we may also assume that ![]() $k$ is
$k$ is ![]() $F$-finite.
$F$-finite.
Proof. We first construct a sequence
of two field extensions such that ![]() $X\times _{k}K$ is integral, where
$X\times _{k}K$ is integral, where ![]() $k^{\prime }$ is uncountable and
$k^{\prime }$ is uncountable and ![]() $K$ is
$K$ is ![]() $F$-finite in positive characteristic. If
$F$-finite in positive characteristic. If ![]() $k$ is already uncountable, then let
$k$ is already uncountable, then let ![]() $k^{\prime }=k$. Otherwise, consider a purely transcendental extension
$k^{\prime }=k$. Otherwise, consider a purely transcendental extension
where ![]() $\{{x_{\unicode[STIX]{x1D6FC}}\}}_{\unicode[STIX]{x1D6FC}\in A}$ is an uncountable set of indeterminates; note that
$\{{x_{\unicode[STIX]{x1D6FC}}\}}_{\unicode[STIX]{x1D6FC}\in A}$ is an uncountable set of indeterminates; note that ![]() $k^{\prime }$ is uncountable by construction. To show that
$k^{\prime }$ is uncountable by construction. To show that ![]() $X\times _{k}k^{\prime }$ is integral, let
$X\times _{k}k^{\prime }$ is integral, let ![]() $\bigcup _{j}U_{j}$ be an affine open covering of
$\bigcup _{j}U_{j}$ be an affine open covering of ![]() $X$. Then,
$X$. Then, ![]() $X\times _{k}k^{\prime }$ is covered by affine open subsets that are localizations of the integral varieties
$X\times _{k}k^{\prime }$ is covered by affine open subsets that are localizations of the integral varieties ![]() $U_{j}\times _{k}\operatorname{Spec}(k[x_{\unicode[STIX]{x1D6FC}}]_{\unicode[STIX]{x1D6FC}\in A})$, which pairwise intersect, hence
$U_{j}\times _{k}\operatorname{Spec}(k[x_{\unicode[STIX]{x1D6FC}}]_{\unicode[STIX]{x1D6FC}\in A})$, which pairwise intersect, hence ![]() $X\times _{k}k^{\prime }$ is integral. We set
$X\times _{k}k^{\prime }$ is integral. We set ![]() $K=k^{\prime }$ in characteristic zero, and in positive characteristic, the gamma construction (Theorem A) shows that there is a field extension
$K=k^{\prime }$ in characteristic zero, and in positive characteristic, the gamma construction (Theorem A) shows that there is a field extension ![]() $k^{\prime }\subseteq K$ such that
$k^{\prime }\subseteq K$ such that ![]() $K$ is
$K$ is ![]() $F$-finite and the scheme
$F$-finite and the scheme ![]() $X\times _{k}K$ is integral. Note that
$X\times _{k}K$ is integral. Note that ![]() $K$ is uncountable since it contains the uncountable field
$K$ is uncountable since it contains the uncountable field ![]() $k^{\prime }$.
$k^{\prime }$.
Now suppose ![]() $X$ is a projective variety over
$X$ is a projective variety over ![]() $k$, and let
$k$, and let ![]() $L$ be an Cartier divisor satisfying (
$L$ be an Cartier divisor satisfying (![]() $\star$ ) for some pair
$\star$ ) for some pair ![]() $(A,\unicode[STIX]{x1D700})$. Let
$(A,\unicode[STIX]{x1D700})$. Let
be the first projection map, which we note is faithfully flat by base change. Then, the pullback ![]() $\unicode[STIX]{x1D70B}^{\ast }A$ of
$\unicode[STIX]{x1D70B}^{\ast }A$ of ![]() $A$ is very ample, and to show that
$A$ is very ample, and to show that ![]() $L$ is ample, it suffices to show that
$L$ is ample, it suffices to show that ![]() $\unicode[STIX]{x1D70B}^{\ast }L$ is ample by flat base change and Serre’s criterion for ampleness. By the special case of Theorem B over the ground field
$\unicode[STIX]{x1D70B}^{\ast }L$ is ample by flat base change and Serre’s criterion for ampleness. By the special case of Theorem B over the ground field ![]() $K$, it therefore suffices to show that
$K$, it therefore suffices to show that ![]() $\unicode[STIX]{x1D70B}^{\ast }L$ satisfies (
$\unicode[STIX]{x1D70B}^{\ast }L$ satisfies (![]() $\star$ ) for the pair
$\star$ ) for the pair ![]() $(\unicode[STIX]{x1D70B}^{\ast }A,\unicode[STIX]{x1D700})$.
$(\unicode[STIX]{x1D70B}^{\ast }A,\unicode[STIX]{x1D700})$.
We want to show that for every ![]() $i>0$ and for all
$i>0$ and for all ![]() $t\in [0,\unicode[STIX]{x1D700})$, we have
$t\in [0,\unicode[STIX]{x1D700})$, we have
For every ![]() $D\in \operatorname{Div}(X)$ and every
$D\in \operatorname{Div}(X)$ and every ![]() $i\geqslant 0$, the number
$i\geqslant 0$, the number ![]() $h^{i}(X,{\mathcal{O}}_{X}(D))$ is invariant under ground field extensions by flat base change, hence
$h^{i}(X,{\mathcal{O}}_{X}(D))$ is invariant under ground field extensions by flat base change, hence ![]() $\widehat{h}^{i}(X,D)$ is also. By homogeneity and continuity (see Remark 4.4), the number
$\widehat{h}^{i}(X,D)$ is also. By homogeneity and continuity (see Remark 4.4), the number ![]() $\widehat{h}^{i}(X,D)$ is also invariant under ground field extensions for
$\widehat{h}^{i}(X,D)$ is also invariant under ground field extensions for ![]() $D\in \operatorname{Div}_{\mathbf{R}}(X)$, hence (8) holds.◻
$D\in \operatorname{Div}_{\mathbf{R}}(X)$, hence (8) holds.◻
Remark 4.10. We note that if ![]() $k$ is
$k$ is ![]() $F$-finite or perfect, then one can construct a field extension
$F$-finite or perfect, then one can construct a field extension ![]() $k\subseteq K$ as in Lemma 4.9 in a more elementary manner. When
$k\subseteq K$ as in Lemma 4.9 in a more elementary manner. When ![]() $k$ is
$k$ is ![]() $F$-finite of characteristic
$F$-finite of characteristic ![]() $p>0$, then one can set
$p>0$, then one can set ![]() $K$ to be
$K$ to be ![]() $k(x_{\unicode[STIX]{x1D6FC}}^{1/p^{\infty }})_{\unicode[STIX]{x1D6FC}\in A}$ for an uncountable set of indeterminates
$k(x_{\unicode[STIX]{x1D6FC}}^{1/p^{\infty }})_{\unicode[STIX]{x1D6FC}\in A}$ for an uncountable set of indeterminates ![]() $\{{x_{\unicode[STIX]{x1D6FC}}\}}_{\unicode[STIX]{x1D6FC}\in A}$, since integrality and normality are preserved under limits of schemes with affine and flat transition morphisms [Reference Grothendieck and Dieudonné24, Corollaire 5.13.4]. When
$\{{x_{\unicode[STIX]{x1D6FC}}\}}_{\unicode[STIX]{x1D6FC}\in A}$, since integrality and normality are preserved under limits of schemes with affine and flat transition morphisms [Reference Grothendieck and Dieudonné24, Corollaire 5.13.4]. When ![]() $k$ is perfect, then one can set
$k$ is perfect, then one can set ![]() $K$ to be a perfect closure of
$K$ to be a perfect closure of ![]() $k(x_{\unicode[STIX]{x1D6FC}})_{\unicode[STIX]{x1D6FC}\in A}$. In this case,
$k(x_{\unicode[STIX]{x1D6FC}})_{\unicode[STIX]{x1D6FC}\in A}$. In this case, ![]() $X$ is geometrically reduced, and the morphism
$X$ is geometrically reduced, and the morphism ![]() $X\times _{k}K\rightarrow X\times _{k}k(x_{\unicode[STIX]{x1D6FC}})_{\unicode[STIX]{x1D6FC}\in A}$ is a homeomorphism since
$X\times _{k}K\rightarrow X\times _{k}k(x_{\unicode[STIX]{x1D6FC}})_{\unicode[STIX]{x1D6FC}\in A}$ is a homeomorphism since ![]() $k(x_{\unicode[STIX]{x1D6FC}})_{\unicode[STIX]{x1D6FC}\in A}\subseteq K$ is purely inseparable [Reference Grothendieck and Dieudonné24, Proposition 2.4.5(i)]. Thus, the base extension
$k(x_{\unicode[STIX]{x1D6FC}})_{\unicode[STIX]{x1D6FC}\in A}\subseteq K$ is purely inseparable [Reference Grothendieck and Dieudonné24, Proposition 2.4.5(i)]. Thus, the base extension ![]() $X\times _{k}K$ is integral.
$X\times _{k}K$ is integral.
Lemma 4.11. To prove the direction ![]() $\Leftarrow$ in Theorem B, it suffices to show that every Cartier divisor satisfying (
$\Leftarrow$ in Theorem B, it suffices to show that every Cartier divisor satisfying (![]() $\star$ ) is nef.
$\star$ ) is nef.
Proof. Suppose ![]() $L$ is a Cartier divisor satisfying (
$L$ is a Cartier divisor satisfying (![]() $\star$ ) for a pair
$\star$ ) for a pair ![]() $(A,\unicode[STIX]{x1D700})$. Choose
$(A,\unicode[STIX]{x1D700})$. Choose ![]() $\unicode[STIX]{x1D6FF}\in (0,\unicode[STIX]{x1D700})\cap \mathbf{Q}$ and let
$\unicode[STIX]{x1D6FF}\in (0,\unicode[STIX]{x1D700})\cap \mathbf{Q}$ and let ![]() $m$ be a positive integer such that
$m$ be a positive integer such that ![]() $m\unicode[STIX]{x1D6FF}$ is an integer. Then, the Cartier divisor
$m\unicode[STIX]{x1D6FF}$ is an integer. Then, the Cartier divisor ![]() $m(L-\unicode[STIX]{x1D6FF}A)$ is nef since
$m(L-\unicode[STIX]{x1D6FF}A)$ is nef since
 $$\begin{eqnarray}\displaystyle \widehat{h}^{i}(X,m(L-\unicode[STIX]{x1D6FF}A)-tA) & = & \displaystyle \widehat{h}^{i}(X,mL-(t+m\unicode[STIX]{x1D6FF})A)\nonumber\\ \displaystyle & = & \displaystyle m\cdot \widehat{h}^{i}\biggl(X,L-\biggl(\frac{t}{m}+\unicode[STIX]{x1D6FF}\biggr)A\biggr)=0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{h}^{i}(X,m(L-\unicode[STIX]{x1D6FF}A)-tA) & = & \displaystyle \widehat{h}^{i}(X,mL-(t+m\unicode[STIX]{x1D6FF})A)\nonumber\\ \displaystyle & = & \displaystyle m\cdot \widehat{h}^{i}\biggl(X,L-\biggl(\frac{t}{m}+\unicode[STIX]{x1D6FF}\biggr)A\biggr)=0\nonumber\end{eqnarray}$$ for all ![]() $t\in [0,m\unicode[STIX]{x1D700}-\unicode[STIX]{x1D6FF})$ by homogeneity (Proposition 4.2). Thus, the Cartier divisor
$t\in [0,m\unicode[STIX]{x1D700}-\unicode[STIX]{x1D6FF})$ by homogeneity (Proposition 4.2). Thus, the Cartier divisor ![]() $L=(L-\unicode[STIX]{x1D6FF}A)+\unicode[STIX]{x1D6FF}A$ is ample by [Reference Lazarsfeld43, Corollary 1.4.10].◻
$L=(L-\unicode[STIX]{x1D6FF}A)+\unicode[STIX]{x1D6FF}A$ is ample by [Reference Lazarsfeld43, Corollary 1.4.10].◻
We also need the following result to allow for an inductive proof. Note that the proof in [Reference de Fernex, Küronya and Lazarsfeld12] works in our setting.
Lemma 4.12. [Reference de Fernex, Küronya and Lazarsfeld12, Lemma 4.3]
Let ![]() $X$ be a projective variety of dimension
$X$ be a projective variety of dimension ![]() $n>0$ over an uncountable field, and let
$n>0$ over an uncountable field, and let ![]() $L$ be a Cartier divisor on
$L$ be a Cartier divisor on ![]() $X$. Suppose
$X$. Suppose ![]() $L$ satisfies (
$L$ satisfies (![]() $\star$ ) for a pair
$\star$ ) for a pair ![]() $(A,\unicode[STIX]{x1D700})$, and let
$(A,\unicode[STIX]{x1D700})$, and let ![]() $E\in |A|$ be a very general divisor. Then, the restriction
$E\in |A|$ be a very general divisor. Then, the restriction ![]() $L|_{E}$ satisfies (
$L|_{E}$ satisfies (![]() $\star$ ) for the pair
$\star$ ) for the pair ![]() $(A|_{E},\unicode[STIX]{x1D700})$.
$(A|_{E},\unicode[STIX]{x1D700})$.
We can now show the direction ![]() $\Leftarrow$ in Theorem B; by Lemma 4.11, we need to show that every Cartier divisor satisfying (
$\Leftarrow$ in Theorem B; by Lemma 4.11, we need to show that every Cartier divisor satisfying (![]() $\star$ ) is nef. Recall that by Lemma 4.9, we may assume that the ground field
$\star$ ) is nef. Recall that by Lemma 4.9, we may assume that the ground field ![]() $k$ is uncountable, and in positive characteristic, we may assume that
$k$ is uncountable, and in positive characteristic, we may assume that ![]() $k$ is
$k$ is ![]() $F$-finite as well. Our proof follows that in [Reference de Fernex, Küronya and Lazarsfeld12, pp. 450–454] after reducing to a setting where Proposition 4.6 applies, although we have to be more careful in positive characteristic.
$F$-finite as well. Our proof follows that in [Reference de Fernex, Küronya and Lazarsfeld12, pp. 450–454] after reducing to a setting where Proposition 4.6 applies, although we have to be more careful in positive characteristic.
Proof of  $\Leftarrow$ in Theorem B.
$\Leftarrow$ in Theorem B.
We proceed by induction on ![]() $\dim X$. Suppose
$\dim X$. Suppose ![]() $\dim X=1$; we show the contrapositive. If
$\dim X=1$; we show the contrapositive. If ![]() $L$ is not nef, then
$L$ is not nef, then ![]() $\deg L<0$ and
$\deg L<0$ and ![]() $-L$ is ample. Thus, by asymptotic Serre duality (Proposition 4.5), we have
$-L$ is ample. Thus, by asymptotic Serre duality (Proposition 4.5), we have ![]() $\widehat{h}^{1}(X,L)=\widehat{h}^{0}(X,-L)\neq 0$, hence (
$\widehat{h}^{1}(X,L)=\widehat{h}^{0}(X,-L)\neq 0$, hence (![]() $\star$ ) does not hold for every choice of
$\star$ ) does not hold for every choice of ![]() $(A,\unicode[STIX]{x1D700})$.
$(A,\unicode[STIX]{x1D700})$.
We now assume ![]() $\dim X\geqslant 2$. Suppose by way of contradiction that there is a non-nef Cartier divisor
$\dim X\geqslant 2$. Suppose by way of contradiction that there is a non-nef Cartier divisor ![]() $L$ satisfying (
$L$ satisfying (![]() $\star$ ). We first claim that there exists a finite morphism
$\star$ ). We first claim that there exists a finite morphism ![]() $\unicode[STIX]{x1D708}:\widetilde{X}\rightarrow X$ such that
$\unicode[STIX]{x1D708}:\widetilde{X}\rightarrow X$ such that ![]() $\unicode[STIX]{x1D708}^{\ast }L$ satisfies (
$\unicode[STIX]{x1D708}^{\ast }L$ satisfies (![]() $\star$ ), and such that
$\star$ ), and such that ![]() $\widetilde{X}$ satisfies the hypotheses of Proposition 4.6 for
$\widetilde{X}$ satisfies the hypotheses of Proposition 4.6 for ![]() $D=\unicode[STIX]{x1D708}^{\ast }L$. Choose an integral curve
$D=\unicode[STIX]{x1D708}^{\ast }L$. Choose an integral curve ![]() $Z\subset X$ such that
$Z\subset X$ such that ![]() $L\cdot Z<0$, and let
$L\cdot Z<0$, and let ![]() $\unicode[STIX]{x1D711}:X^{\prime }\rightarrow X$ be a regular alteration for the pair
$\unicode[STIX]{x1D711}:X^{\prime }\rightarrow X$ be a regular alteration for the pair ![]() $(X,Z)$ [Reference de Jong38, Theorem 4.1], in which case
$(X,Z)$ [Reference de Jong38, Theorem 4.1], in which case ![]() $(\unicode[STIX]{x1D711}^{-1}(Z))_{\text{red}}$ is a simple normal crossing divisor. Consider the Stein factorization [Reference Hartshorne29, Corollary III.11.5]
$(\unicode[STIX]{x1D711}^{-1}(Z))_{\text{red}}$ is a simple normal crossing divisor. Consider the Stein factorization [Reference Hartshorne29, Corollary III.11.5]

for the morphism ![]() $\unicode[STIX]{x1D711}$, in which case
$\unicode[STIX]{x1D711}$, in which case ![]() $\widetilde{X}$ is a normal projective variety. Now let
$\widetilde{X}$ is a normal projective variety. Now let ![]() $\widetilde{Z}$ be the scheme-theoretic inverse image of
$\widetilde{Z}$ be the scheme-theoretic inverse image of ![]() $Z$ under
$Z$ under ![]() $\unicode[STIX]{x1D708}$, and write
$\unicode[STIX]{x1D708}$, and write
where ![]() $\widetilde{Z}_{\unicode[STIX]{x1D6FC}}$ are the irreducible components of
$\widetilde{Z}_{\unicode[STIX]{x1D6FC}}$ are the irreducible components of ![]() $\widetilde{Z}$. Since
$\widetilde{Z}$. Since ![]() $\unicode[STIX]{x1D708}$ is finite, every
$\unicode[STIX]{x1D708}$ is finite, every ![]() $\widetilde{Z}_{\unicode[STIX]{x1D6FC}}$ is one-dimensional and dominates
$\widetilde{Z}_{\unicode[STIX]{x1D6FC}}$ is one-dimensional and dominates ![]() $Z$, hence the projection formula and (5) imply
$Z$, hence the projection formula and (5) imply ![]() $\unicode[STIX]{x1D708}^{\ast }L\cdot \widetilde{Z}_{\unicode[STIX]{x1D6FC}}<0$. Finally,
$\unicode[STIX]{x1D708}^{\ast }L\cdot \widetilde{Z}_{\unicode[STIX]{x1D6FC}}<0$. Finally, ![]() $(\unicode[STIX]{x1D711}^{-1}(Z))_{\text{red}}=(\unicode[STIX]{x1D707}^{-1}(\widetilde{Z}))_{\text{red}}$ is a simple normal crossing divisor by the factorization (
$(\unicode[STIX]{x1D711}^{-1}(Z))_{\text{red}}=(\unicode[STIX]{x1D707}^{-1}(\widetilde{Z}))_{\text{red}}$ is a simple normal crossing divisor by the factorization (
).
We now show that ![]() $\unicode[STIX]{x1D708}^{\ast }L$ satisfies (
$\unicode[STIX]{x1D708}^{\ast }L$ satisfies (![]() $\star$ ). Since
$\star$ ). Since ![]() $\unicode[STIX]{x1D708}^{\ast }A$ is ample [Reference Lazarsfeld43, Proposition 1.2.13], we can choose a positive integer
$\unicode[STIX]{x1D708}^{\ast }A$ is ample [Reference Lazarsfeld43, Proposition 1.2.13], we can choose a positive integer ![]() $a$ such that
$a$ such that ![]() $a\,\unicode[STIX]{x1D708}^{\ast }A$ is very ample. Then, Proposition 4.3 implies
$a\,\unicode[STIX]{x1D708}^{\ast }A$ is very ample. Then, Proposition 4.3 implies
for all ![]() $i>0$ and for all
$i>0$ and for all ![]() $t\in [0,\unicode[STIX]{x1D700}/a)$. Replacing
$t\in [0,\unicode[STIX]{x1D700}/a)$. Replacing ![]() $A$ by
$A$ by ![]() $aA$, we assume that
$aA$, we assume that ![]() $\unicode[STIX]{x1D708}^{\ast }A$ is very ample.
$\unicode[STIX]{x1D708}^{\ast }A$ is very ample.
For the rest of the proof, our goal is to show that
for ![]() $0<\unicode[STIX]{x1D6FF}\ll 1$, contradicting (10). Let
$0<\unicode[STIX]{x1D6FF}\ll 1$, contradicting (10). Let ![]() $F\in |\unicode[STIX]{x1D708}^{\ast }A|$ be a very general divisor. By Bertini’s theorem [Reference Flenner, O’Carroll and Vogel20, Theorem 3.4.10 and Corollary 3.4.14], we may assume that
$F\in |\unicode[STIX]{x1D708}^{\ast }A|$ be a very general divisor. By Bertini’s theorem [Reference Flenner, O’Carroll and Vogel20, Theorem 3.4.10 and Corollary 3.4.14], we may assume that ![]() $F$ is a subvariety of
$F$ is a subvariety of ![]() $\widetilde{X}$, in which case by inductive hypothesis and Lemma 4.12, we have that
$\widetilde{X}$, in which case by inductive hypothesis and Lemma 4.12, we have that ![]() $\unicode[STIX]{x1D708}^{\ast }L|_{F}$ is ample. Since ampleness is an open condition in families [Reference Grothendieck and Dieudonné25, Corollaire 9.6.4], there exists an integer
$\unicode[STIX]{x1D708}^{\ast }L|_{F}$ is ample. Since ampleness is an open condition in families [Reference Grothendieck and Dieudonné25, Corollaire 9.6.4], there exists an integer ![]() $b>0$ such that
$b>0$ such that ![]() $b\,\unicode[STIX]{x1D708}^{\ast }L$ is very ample along the generic divisor
$b\,\unicode[STIX]{x1D708}^{\ast }L$ is very ample along the generic divisor ![]() $F_{\unicode[STIX]{x1D702}}\in |\unicode[STIX]{x1D708}^{\ast }A|$. By possibly replacing
$F_{\unicode[STIX]{x1D702}}\in |\unicode[STIX]{x1D708}^{\ast }A|$. By possibly replacing ![]() $b$ with a multiple, we may also assume that
$b$ with a multiple, we may also assume that ![]() $mb\,\unicode[STIX]{x1D708}^{\ast }L|_{F_{\unicode[STIX]{x1D702}}}$ has vanishing higher cohomology for every integer
$mb\,\unicode[STIX]{x1D708}^{\ast }L|_{F_{\unicode[STIX]{x1D702}}}$ has vanishing higher cohomology for every integer ![]() $m>0$. Since the ground field
$m>0$. Since the ground field ![]() $k$ is uncountable, we can then choose a sequence of very general Cartier divisors
$k$ is uncountable, we can then choose a sequence of very general Cartier divisors ![]() $\{E_{\unicode[STIX]{x1D6FD}}\}_{\unicode[STIX]{x1D6FD}=1}^{\infty }\subseteq |\unicode[STIX]{x1D708}^{\ast }A|$ such that the following properties hold:
$\{E_{\unicode[STIX]{x1D6FD}}\}_{\unicode[STIX]{x1D6FD}=1}^{\infty }\subseteq |\unicode[STIX]{x1D708}^{\ast }A|$ such that the following properties hold:
(a)
 $E_{\unicode[STIX]{x1D6FD}}$ is a subvariety of
$E_{\unicode[STIX]{x1D6FD}}$ is a subvariety of  $\widetilde{X}$ for all
$\widetilde{X}$ for all  $\unicode[STIX]{x1D6FD}$ (by Bertini’s theorem [Reference Flenner, O’Carroll and Vogel20, Theorem 3.4.10 and Corollary 3.4.14]);
$\unicode[STIX]{x1D6FD}$ (by Bertini’s theorem [Reference Flenner, O’Carroll and Vogel20, Theorem 3.4.10 and Corollary 3.4.14]);(b) for all
 $\unicode[STIX]{x1D6FD}$,
$\unicode[STIX]{x1D6FD}$,  $b\,\unicode[STIX]{x1D708}^{\ast }L|_{E_{\unicode[STIX]{x1D6FD}}}$ is very ample and
$b\,\unicode[STIX]{x1D708}^{\ast }L|_{E_{\unicode[STIX]{x1D6FD}}}$ is very ample and  $mb\,\unicode[STIX]{x1D708}^{\ast }L|_{E_{\unicode[STIX]{x1D6FD}}}$ has vanishing higher cohomology for every integer
$mb\,\unicode[STIX]{x1D708}^{\ast }L|_{E_{\unicode[STIX]{x1D6FD}}}$ has vanishing higher cohomology for every integer  $m>0$ (by the constructibility of very ampleness in families [Reference Grothendieck and Dieudonné25, Proposition 9.6.3] and by semicontinuity); and
$m>0$ (by the constructibility of very ampleness in families [Reference Grothendieck and Dieudonné25, Proposition 9.6.3] and by semicontinuity); and(c) for every positive integer
 $r$ and for all nonnegative integers
$r$ and for all nonnegative integers  $j$ and
$j$ and  $m$, the
$m$, the  $k$-dimension of cohomology groups of the form (12)is independent of the
$k$-dimension of cohomology groups of the form (12)is independent of the $$\begin{eqnarray}H^{j}(E_{\unicode[STIX]{x1D6FD}_{1}}\cap E_{\unicode[STIX]{x1D6FD}_{2}}\cap \cdots \cap E_{\unicode[STIX]{x1D6FD}_{r}},{\mathcal{O}}_{E_{\unicode[STIX]{x1D6FD}_{1}}\cap E_{\unicode[STIX]{x1D6FD}_{2}}\cap \cdots \cap E_{\unicode[STIX]{x1D6FD}_{r}}}(mL))\end{eqnarray}$$
$$\begin{eqnarray}H^{j}(E_{\unicode[STIX]{x1D6FD}_{1}}\cap E_{\unicode[STIX]{x1D6FD}_{2}}\cap \cdots \cap E_{\unicode[STIX]{x1D6FD}_{r}},{\mathcal{O}}_{E_{\unicode[STIX]{x1D6FD}_{1}}\cap E_{\unicode[STIX]{x1D6FD}_{2}}\cap \cdots \cap E_{\unicode[STIX]{x1D6FD}_{r}}}(mL))\end{eqnarray}$$ $r$-tuple
$r$-tuple  $(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2},\ldots ,\unicode[STIX]{x1D6FD}_{r})$ (by semicontinuity; see [Reference Küronya41, Proposition 5.5]).
$(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2},\ldots ,\unicode[STIX]{x1D6FD}_{r})$ (by semicontinuity; see [Reference Küronya41, Proposition 5.5]).
We denote by ![]() $h^{j}({\mathcal{O}}_{E_{1}\cap E_{2}\cap \cdots \cap E_{r}}(mL))$ the dimensions of the cohomology groups (12). By homogeneity (Proposition 4.2), we can replace
$h^{j}({\mathcal{O}}_{E_{1}\cap E_{2}\cap \cdots \cap E_{r}}(mL))$ the dimensions of the cohomology groups (12). By homogeneity (Proposition 4.2), we can replace ![]() $L$ by
$L$ by ![]() $bL$ so that
$bL$ so that ![]() $\unicode[STIX]{x1D708}^{\ast }L|_{E_{\unicode[STIX]{x1D6FD}}}$ is very ample with vanishing higher cohomology for all
$\unicode[STIX]{x1D708}^{\ast }L|_{E_{\unicode[STIX]{x1D6FD}}}$ is very ample with vanishing higher cohomology for all ![]() $\unicode[STIX]{x1D6FD}$.
$\unicode[STIX]{x1D6FD}$.
To show (11), we now follow the proof in [Reference de Fernex, Küronya and Lazarsfeld12, pp. 453–454] with appropriate modifications. Given positive integers ![]() $m$ and
$m$ and ![]() $r$, consider the complex
$r$, consider the complex
 $$\begin{eqnarray}\displaystyle K_{m,r}^{\bullet } & := & \displaystyle \biggl(\bigotimes _{\unicode[STIX]{x1D6FD}=1}^{r}({\mathcal{O}}_{\widetilde{X}}\longrightarrow {\mathcal{O}}_{E_{\unicode[STIX]{x1D6FD}}})\biggr)\otimes {\mathcal{O}}_{\widetilde{X}}(m\,\unicode[STIX]{x1D708}^{\ast }L)\nonumber\\ \displaystyle & = & \displaystyle \left\{\begin{array}{@{}lcl@{}}{\mathcal{O}}_{\widetilde{X}}(m\,\unicode[STIX]{x1D708}^{\ast }L)\, & \longrightarrow \, & \displaystyle \bigoplus _{\unicode[STIX]{x1D6FD}=1}^{r}{\mathcal{O}}_{E_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D708}^{\ast }L)\\ \, & \longrightarrow \, & \displaystyle \bigoplus _{1\leqslant \unicode[STIX]{x1D6FD}_{1}<\unicode[STIX]{x1D6FD}_{2}\leqslant r}{\mathcal{O}}_{E_{\unicode[STIX]{x1D6FD}_{1}}\cap E_{\unicode[STIX]{x1D6FD}_{2}}}(m\,\unicode[STIX]{x1D708}^{\ast }L)\longrightarrow \cdots \end{array}\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{m,r}^{\bullet } & := & \displaystyle \biggl(\bigotimes _{\unicode[STIX]{x1D6FD}=1}^{r}({\mathcal{O}}_{\widetilde{X}}\longrightarrow {\mathcal{O}}_{E_{\unicode[STIX]{x1D6FD}}})\biggr)\otimes {\mathcal{O}}_{\widetilde{X}}(m\,\unicode[STIX]{x1D708}^{\ast }L)\nonumber\\ \displaystyle & = & \displaystyle \left\{\begin{array}{@{}lcl@{}}{\mathcal{O}}_{\widetilde{X}}(m\,\unicode[STIX]{x1D708}^{\ast }L)\, & \longrightarrow \, & \displaystyle \bigoplus _{\unicode[STIX]{x1D6FD}=1}^{r}{\mathcal{O}}_{E_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D708}^{\ast }L)\\ \, & \longrightarrow \, & \displaystyle \bigoplus _{1\leqslant \unicode[STIX]{x1D6FD}_{1}<\unicode[STIX]{x1D6FD}_{2}\leqslant r}{\mathcal{O}}_{E_{\unicode[STIX]{x1D6FD}_{1}}\cap E_{\unicode[STIX]{x1D6FD}_{2}}}(m\,\unicode[STIX]{x1D708}^{\ast }L)\longrightarrow \cdots \end{array}\right\}.\nonumber\end{eqnarray}$$ By [Reference Küronya41, Corollary 4.2], this complex is acyclic away from ![]() ${\mathcal{O}}_{\widetilde{X}}(m\,\unicode[STIX]{x1D708}^{\ast }L)$, hence is a resolution for
${\mathcal{O}}_{\widetilde{X}}(m\,\unicode[STIX]{x1D708}^{\ast }L)$, hence is a resolution for ![]() ${\mathcal{O}}_{\widetilde{X}}(m\,\unicode[STIX]{x1D708}^{\ast }L-r\,\unicode[STIX]{x1D708}^{\ast }A)$. In particular, we have
${\mathcal{O}}_{\widetilde{X}}(m\,\unicode[STIX]{x1D708}^{\ast }L-r\,\unicode[STIX]{x1D708}^{\ast }A)$. In particular, we have
The right-hand side is computed by an ![]() $E_{1}$-spectral sequence whose first page is
$E_{1}$-spectral sequence whose first page is

hence there is a natural inclusion
We want to bound the left-hand side of (13) from below. First, there exists a constant ![]() $C_{1}>0$ such that
$C_{1}>0$ such that ![]() $h^{0}({\mathcal{O}}_{E_{1}\cap E_{2}}(m\,\unicode[STIX]{x1D708}^{\ast }L))\leqslant C_{1}\cdot m^{n-2}$ for all
$h^{0}({\mathcal{O}}_{E_{1}\cap E_{2}}(m\,\unicode[STIX]{x1D708}^{\ast }L))\leqslant C_{1}\cdot m^{n-2}$ for all ![]() $m\gg 0$ [Reference Lazarsfeld43, Example 1.2.20]. Thus, we have
$m\gg 0$ [Reference Lazarsfeld43, Example 1.2.20]. Thus, we have
for some ![]() $C_{2}$ and for all
$C_{2}$ and for all ![]() $m\gg 0$. Now by Proposition 4.6, there are positive integers
$m\gg 0$. Now by Proposition 4.6, there are positive integers ![]() $q$ and
$q$ and ![]() $c$ such that
$c$ such that ![]() $\mathfrak{b}(|mq\,\unicode[STIX]{x1D708}^{\ast }L|)\subseteq \mathfrak{a}^{m-c}$ for all
$\mathfrak{b}(|mq\,\unicode[STIX]{x1D708}^{\ast }L|)\subseteq \mathfrak{a}^{m-c}$ for all ![]() $m>c$, where
$m>c$, where ![]() $\mathfrak{a}$ is the ideal sheaf of
$\mathfrak{a}$ is the ideal sheaf of ![]() $\widetilde{Z}$. By replacing
$\widetilde{Z}$. By replacing ![]() $L$ by
$L$ by ![]() $qL$, we can assume that this inclusion holds for
$qL$, we can assume that this inclusion holds for ![]() $q=1$. The morphism
$q=1$. The morphism ![]() $v_{m,r}$ therefore fits into the following commutative diagram:
$v_{m,r}$ therefore fits into the following commutative diagram:

We claim that there exists a constant ![]() $C_{3}>0$ such that for all
$C_{3}>0$ such that for all ![]() $m\gg 0$,
$m\gg 0$,
Granted this, we have
for some constant ![]() $C_{4}>0$ and for all
$C_{4}>0$ and for all ![]() $m\gg 0$. Fixing a rational number
$m\gg 0$. Fixing a rational number ![]() $0<\unicode[STIX]{x1D6FF}\ll 1$ and setting
$0<\unicode[STIX]{x1D6FF}\ll 1$ and setting ![]() $r=m\unicode[STIX]{x1D6FF}$ for an integer
$r=m\unicode[STIX]{x1D6FF}$ for an integer ![]() $m>0$ such that
$m>0$ such that ![]() $m\unicode[STIX]{x1D6FF}$ is an integer, we then see that there exists a constant
$m\unicode[STIX]{x1D6FF}$ is an integer, we then see that there exists a constant ![]() $C_{5}>0$ such that
$C_{5}>0$ such that
for all ![]() $m\gg 0$, contradicting (10).
$m\gg 0$, contradicting (10).
It remains to show (14). Since the vanishing locus of ![]() $\mathfrak{a}$ may have no
$\mathfrak{a}$ may have no ![]() $k$-rational points, we pass to the algebraic closure of
$k$-rational points, we pass to the algebraic closure of ![]() $k$ to bound the codimension on the left-hand side of (14) from below. Let
$k$ to bound the codimension on the left-hand side of (14) from below. Let ![]() $\overline{E}_{\unicode[STIX]{x1D6FD}}:=E_{\unicode[STIX]{x1D6FD}}\times _{k}\overline{k}$, and denote by
$\overline{E}_{\unicode[STIX]{x1D6FD}}:=E_{\unicode[STIX]{x1D6FD}}\times _{k}\overline{k}$, and denote by ![]() $\unicode[STIX]{x1D70B}:\overline{E}_{\unicode[STIX]{x1D6FD}}\rightarrow E_{\unicode[STIX]{x1D6FD}}$ the projection morphism. Note that
$\unicode[STIX]{x1D70B}:\overline{E}_{\unicode[STIX]{x1D6FD}}\rightarrow E_{\unicode[STIX]{x1D6FD}}$ the projection morphism. Note that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{codim}(H^{0}({\mathcal{O}}_{E_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D708}^{\ast }L)\otimes \mathfrak{a}^{m-c})\subseteq H^{0}({\mathcal{O}}_{E_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D708}^{\ast }L)))\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{codim}(H^{0}({\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)\otimes \unicode[STIX]{x1D70B}^{-1}\mathfrak{a}^{m-c}\cdot {\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}})\subseteq H^{0}({\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{codim}(H^{0}({\mathcal{O}}_{E_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D708}^{\ast }L)\otimes \mathfrak{a}^{m-c})\subseteq H^{0}({\mathcal{O}}_{E_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D708}^{\ast }L)))\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{codim}(H^{0}({\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)\otimes \unicode[STIX]{x1D70B}^{-1}\mathfrak{a}^{m-c}\cdot {\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}})\subseteq H^{0}({\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)))\nonumber\end{eqnarray}$$ by the flatness of ![]() $k\subseteq \overline{k}$. Since
$k\subseteq \overline{k}$. Since ![]() ${\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)$ is very ample by base change, we can choose a closed point
${\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)$ is very ample by base change, we can choose a closed point ![]() $x\in Z(\unicode[STIX]{x1D70B}^{-1}\mathfrak{a}\cdot {\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}})\cap \overline{E}_{\unicode[STIX]{x1D6FD}}$, in which case
$x\in Z(\unicode[STIX]{x1D70B}^{-1}\mathfrak{a}\cdot {\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}})\cap \overline{E}_{\unicode[STIX]{x1D6FD}}$, in which case ![]() $m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L$ separates
$m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L$ separates ![]() $(m-c)$-jets at
$(m-c)$-jets at ![]() $x$ by [Reference Ito37, Proof of Lemma 3.7]. Finally, the dimension of the space of
$x$ by [Reference Ito37, Proof of Lemma 3.7]. Finally, the dimension of the space of ![]() $(m-c)$-jets at
$(m-c)$-jets at ![]() $x$ is at least that for a regular point of a variety of dimension
$x$ is at least that for a regular point of a variety of dimension ![]() $n$, hence
$n$, hence
 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{codim}(H^{0}({\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)\otimes \unicode[STIX]{x1D70B}^{-1}\mathfrak{a}^{m-c}\cdot {\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}})\subseteq H^{0}({\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)))\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \operatorname{codim}(H^{0}({\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)\otimes \mathfrak{m}_{x}^{m-c})\subseteq H^{0}({\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)))\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \binom{m-c+n}{n-1}\geqslant C_{3}\cdot m^{n-1}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{codim}(H^{0}({\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)\otimes \unicode[STIX]{x1D70B}^{-1}\mathfrak{a}^{m-c}\cdot {\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}})\subseteq H^{0}({\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)))\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \operatorname{codim}(H^{0}({\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)\otimes \mathfrak{m}_{x}^{m-c})\subseteq H^{0}({\mathcal{O}}_{\overline{E}_{\unicode[STIX]{x1D6FD}}}(m\,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D708}^{\ast }L)))\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant \binom{m-c+n}{n-1}\geqslant C_{3}\cdot m^{n-1}\nonumber\end{eqnarray}$$ for some constant ![]() $C_{3}>0$ and all
$C_{3}>0$ and all ![]() $m\gg 0$, as required.◻
$m\gg 0$, as required.◻
5 Nakayama’s theorem on restricted base loci
We now come to our second application of the gamma construction, Theorem C. This result extends known cases of the following conjecture due to Boucksom, Broustet, and Pacienza.
Conjecture 5.1. [Reference Boucksom, Broustet and Pacienza5, Conjecture 2.7]
Let ![]() $X$ be a normal projective variety, and let
$X$ be a normal projective variety, and let ![]() $D$ be a pseudoeffective
$D$ be a pseudoeffective ![]() $\mathbf{R}$-divisor on
$\mathbf{R}$-divisor on ![]() $X$. Then, we have
$X$. Then, we have
In Section 5.1, we define the restricted base locus ![]() and the non-nef locus
and the non-nef locus ![]() $\operatorname{NNef}(D)$. We then prove Theorem C in Section 5.2 using the gamma construction (Theorem 3.4) to reduce to the
$\operatorname{NNef}(D)$. We then prove Theorem C in Section 5.2 using the gamma construction (Theorem 3.4) to reduce to the ![]() $F$-finite case, in which case it suffices to apply results in [Reference Sato57]. We recall that
$F$-finite case, in which case it suffices to apply results in [Reference Sato57]. We recall that ![]() $\Vert \cdot \Vert$ denotes a compatible choice of Euclidean norms on the vector spaces
$\Vert \cdot \Vert$ denotes a compatible choice of Euclidean norms on the vector spaces ![]() $N_{\mathbf{Q}}^{1}(X)$ and
$N_{\mathbf{Q}}^{1}(X)$ and ![]() $N_{\mathbf{R}}^{1}(X)$, which are finite-dimensional for complete schemes
$N_{\mathbf{R}}^{1}(X)$, which are finite-dimensional for complete schemes ![]() $X$ by [Reference Cutkosky8, Proposition 2.3].
$X$ by [Reference Cutkosky8, Proposition 2.3].
5.1 Background on restricted base loci and non-nef loci
We start by defining the following numerically invariant approximation of the stable base locus defined in Definition 2.4.
Definition 5.2. [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa15, Definition 1.12]
Let ![]() $X$ be a projective scheme over a field, and let
$X$ be a projective scheme over a field, and let ![]() $D$ be an
$D$ be an ![]() $\mathbf{R}$-Cartier divisor on
$\mathbf{R}$-Cartier divisor on ![]() $X$. The restricted base locus of
$X$. The restricted base locus of ![]() $D$ is the subset
$D$ is the subset
of ![]() $X$, where the union runs over all ample
$X$, where the union runs over all ample ![]() $\mathbf{R}$-Cartier divisors
$\mathbf{R}$-Cartier divisors ![]() $A$ such that
$A$ such that ![]() $D+A$ is a
$D+A$ is a ![]() $\mathbf{Q}$-Cartier divisor. Note that
$\mathbf{Q}$-Cartier divisor. Note that ![]() if and only if
if and only if ![]() $D$ is nef [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa15, Example 1.18].
$D$ is nef [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa15, Example 1.18].
We need the following result, which says that the formation of restricted base loci is compatible with ground field extensions.
Lemma 5.3. Let ![]() $X$ be a projective scheme over a field
$X$ be a projective scheme over a field ![]() $k$, and let
$k$, and let ![]() $D$ be an
$D$ be an ![]() $\mathbf{R}$-Cartier divisor on
$\mathbf{R}$-Cartier divisor on ![]() $X$. Let
$X$. Let ![]() $k\subseteq k^{\prime }$ be a field extension with corresponding projection morphism
$k\subseteq k^{\prime }$ be a field extension with corresponding projection morphism ![]() $\unicode[STIX]{x1D70B}:X\times _{k}k^{\prime }\rightarrow X$. Then,
$\unicode[STIX]{x1D70B}:X\times _{k}k^{\prime }\rightarrow X$. Then,
Proof. Let ![]() $\{{A_{n}\}}_{n\geqslant 1}$ be a sequence of ample
$\{{A_{n}\}}_{n\geqslant 1}$ be a sequence of ample ![]() $\mathbf{R}$-Cartier divisors such that
$\mathbf{R}$-Cartier divisors such that ![]() $\lim _{n\rightarrow \infty }\Vert A_{n}\Vert =0$ and such that
$\lim _{n\rightarrow \infty }\Vert A_{n}\Vert =0$ and such that ![]() $D+A_{n}$ is a
$D+A_{n}$ is a ![]() $\mathbf{Q}$-Cartier divisor for every
$\mathbf{Q}$-Cartier divisor for every ![]() $n$. By [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa15, Proposition 1.19], we have
$n$. By [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa15, Proposition 1.19], we have
By flat base change, we have ![]() $\unicode[STIX]{x1D70B}^{-1}(\mathbf{B}(D+A_{n}))=\mathbf{B}(\unicode[STIX]{x1D70B}^{\ast }(D+A_{n}))$, hence
$\unicode[STIX]{x1D70B}^{-1}(\mathbf{B}(D+A_{n}))=\mathbf{B}(\unicode[STIX]{x1D70B}^{\ast }(D+A_{n}))$, hence
where the second equality follows from applying [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa15, Proposition 1.19] again to the sequence ![]() $\{\unicode[STIX]{x1D70B}^{\ast }{A_{n}\}}_{n\geqslant 1}$ of ample
$\{\unicode[STIX]{x1D70B}^{\ast }{A_{n}\}}_{n\geqslant 1}$ of ample ![]() $\mathbf{R}$-Cartier divisors on
$\mathbf{R}$-Cartier divisors on ![]() $X\times _{k}k^{\prime }$.◻
$X\times _{k}k^{\prime }$.◻
Next, we want to define the non-nef locus.
Definition 5.4. [Reference Nakayama52, Definition III.2.2; Reference Cacciola and Di Biagio7, Definition 2.11]
Let ![]() $X$ be a normal projective variety, and let
$X$ be a normal projective variety, and let ![]() $D$ be a big
$D$ be a big ![]() $\mathbf{R}$-Cartier divisor. Consider a divisorial valuation
$\mathbf{R}$-Cartier divisor. Consider a divisorial valuation ![]() $v$ on
$v$ on ![]() $X$. The numerical vanishing order of
$X$. The numerical vanishing order of ![]() $D$ along
$D$ along ![]() $v$ is
$v$ is
where the infimum runs over all effective ![]() $\mathbf{R}$-Cartier divisors
$\mathbf{R}$-Cartier divisors ![]() $\mathbf{R}$-numerically equivalent to
$\mathbf{R}$-numerically equivalent to ![]() $D$. When
$D$. When ![]() $D$ is a pseudoeffective
$D$ is a pseudoeffective ![]() $\mathbf{R}$-Cartier divisor, we set
$\mathbf{R}$-Cartier divisor, we set
where the supremum runs over all ample ![]() $\mathbf{R}$-Cartier divisors
$\mathbf{R}$-Cartier divisors ![]() $A$ on
$A$ on ![]() $X$, and where we note that
$X$, and where we note that ![]() $D+A$ is a big
$D+A$ is a big ![]() $\mathbf{R}$-Cartier divisor by [Reference Lazarsfeld43, Theorem 2.2.26]. The non-nef locus of a pseudoeffective
$\mathbf{R}$-Cartier divisor by [Reference Lazarsfeld43, Theorem 2.2.26]. The non-nef locus of a pseudoeffective ![]() $\mathbf{R}$-Cartier divisor
$\mathbf{R}$-Cartier divisor ![]() $D$ is
$D$ is
where the union runs over all divisorial valuations such that ![]() $v_{\text{num}}(D)>0$, and
$v_{\text{num}}(D)>0$, and ![]() $c_{X}(v)$ is the center of the divisorial valuation
$c_{X}(v)$ is the center of the divisorial valuation ![]() $v$. Note that
$v$. Note that ![]() $\operatorname{NNef}(D)=\emptyset$ if and only if
$\operatorname{NNef}(D)=\emptyset$ if and only if ![]() $D$ is nef [Reference Nakayama52, Remark III.2.8].
$D$ is nef [Reference Nakayama52, Remark III.2.8].
To prove Theorem C, we also use the following:
Definition 5.5. [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa15, Definition 2.2 and Remark 2.3]
Let ![]() $X$ be a normal projective variety, and let
$X$ be a normal projective variety, and let ![]() $D$ be a
$D$ be a ![]() $\mathbf{Q}$-Cartier divisor. Consider a divisorial valuation
$\mathbf{Q}$-Cartier divisor. Consider a divisorial valuation ![]() $v$ on
$v$ on ![]() $X$. The asymptotic order of vanishing of
$X$. The asymptotic order of vanishing of ![]() $D$ along
$D$ along ![]() $v$ is
$v$ is
where the infimum runs over all effective ![]() $\mathbf{Q}$-Cartier divisors
$\mathbf{Q}$-Cartier divisors ![]() $\mathbf{Q}$-linearly equivalent to
$\mathbf{Q}$-linearly equivalent to ![]() $D$.
$D$.
5.2 Proof of Theorem C
We start by proving a version of Theorem C for arbitrary normal projective varieties. We fix some notation. Let ![]() $X$ be a normal projective variety over a field
$X$ be a normal projective variety over a field ![]() $k$. If
$k$. If ![]() $\operatorname{char}k=0$ and
$\operatorname{char}k=0$ and ![]() $\unicode[STIX]{x1D6E5}$ is an effective
$\unicode[STIX]{x1D6E5}$ is an effective ![]() $\mathbf{Q}$-Weil divisor on
$\mathbf{Q}$-Weil divisor on ![]() $X$ such that
$X$ such that ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is
$K_{X}+\unicode[STIX]{x1D6E5}$ is ![]() $\mathbf{Q}$-Cartier, then the non-klt locus of the pair
$\mathbf{Q}$-Cartier, then the non-klt locus of the pair ![]() $(X,\unicode[STIX]{x1D6E5})$ is
$(X,\unicode[STIX]{x1D6E5})$ is ![]() $\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}):=Z({\mathcal{J}}(X,\unicode[STIX]{x1D6E5}))$, where
$\operatorname{Nklt}(X,\unicode[STIX]{x1D6E5}):=Z({\mathcal{J}}(X,\unicode[STIX]{x1D6E5}))$, where ![]() ${\mathcal{J}}(X,\unicode[STIX]{x1D6E5})$ is the multiplier ideal [Reference Lazarsfeld44, Definition 9.3.56], and the non-klt locus of
${\mathcal{J}}(X,\unicode[STIX]{x1D6E5})$ is the multiplier ideal [Reference Lazarsfeld44, Definition 9.3.56], and the non-klt locus of ![]() $X$ is
$X$ is
where the intersection runs over all effective ![]() $\mathbf{Q}$-Weil divisors
$\mathbf{Q}$-Weil divisors ![]() $\unicode[STIX]{x1D6E5}$ such that
$\unicode[STIX]{x1D6E5}$ such that ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is
$K_{X}+\unicode[STIX]{x1D6E5}$ is ![]() $\mathbf{Q}$-Cartier. If
$\mathbf{Q}$-Cartier. If ![]() $\operatorname{char}k=p>0$, then the non-strongly
$\operatorname{char}k=p>0$, then the non-strongly ![]() $F$-regular locus of
$F$-regular locus of ![]() $X$ is
$X$ is
If ![]() $X$ is
$X$ is ![]() $F$-finite, then
$F$-finite, then ![]() $\operatorname{NSFR}(X)=Z(\unicode[STIX]{x1D70F}(X))$, since test ideals localize [Reference Schwede60, Proposition 3.23(ii)], and since
$\operatorname{NSFR}(X)=Z(\unicode[STIX]{x1D70F}(X))$, since test ideals localize [Reference Schwede60, Proposition 3.23(ii)], and since ![]() $\unicode[STIX]{x1D70F}(R)=R$ for an
$\unicode[STIX]{x1D70F}(R)=R$ for an ![]() $F$-finite ring
$F$-finite ring ![]() $R$ if and only if
$R$ if and only if ![]() $R$ is strongly
$R$ is strongly ![]() $F$-regular [Reference Takagi and Watanabe62, Proposition 5.6(5)].
$F$-regular [Reference Takagi and Watanabe62, Proposition 5.6(5)].
Theorem 5.6. (cf. [Reference Cacciola and Di Biagio7, Corollary 4.7; Reference Sato57, Corollary 4.7])
Let ![]() $X$ be a normal projective variety over a field
$X$ be a normal projective variety over a field ![]() $k$, and let
$k$, and let ![]() $D$ be a pseudoeffective
$D$ be a pseudoeffective ![]() $\mathbf{R}$-Cartier divisor on
$\mathbf{R}$-Cartier divisor on ![]() $X$. If
$X$. If ![]() $\operatorname{char}k=0$, then
$\operatorname{char}k=0$, then
and if ![]() $\operatorname{char}k=p>0$, then
$\operatorname{char}k=p>0$, then
Proof. We first prove that ![]() for every pseudoeffective
for every pseudoeffective ![]() $\mathbf{R}$-Cartier divisor
$\mathbf{R}$-Cartier divisor ![]() $D$, following [Reference Boucksom, Broustet and Pacienza5, Lemma 2.6]. Let
$D$, following [Reference Boucksom, Broustet and Pacienza5, Lemma 2.6]. Let ![]() , and let
, and let ![]() $v$ be a divisorial valuation such that
$v$ be a divisorial valuation such that ![]() $x\in c_{X}(v)$. By definition of
$x\in c_{X}(v)$. By definition of ![]() , there exists an ample
, there exists an ample ![]() $\mathbf{R}$-Cartier divisor
$\mathbf{R}$-Cartier divisor ![]() $A$ such that
$A$ such that ![]() $D+A$ is
$D+A$ is ![]() $\mathbf{Q}$-Cartier divisor for which
$\mathbf{Q}$-Cartier divisor for which ![]() $x\notin \mathbf{B}(D+A)$. Thus, there exists an effective
$x\notin \mathbf{B}(D+A)$. Thus, there exists an effective ![]() $\mathbf{Q}$-Cartier divisor
$\mathbf{Q}$-Cartier divisor ![]() $E$ such that
$E$ such that ![]() $E{\sim}_{\mathbf{Q}}D+A$ and such that
$E{\sim}_{\mathbf{Q}}D+A$ and such that ![]() $x\notin \operatorname{Supp}E$. We therefore have
$x\notin \operatorname{Supp}E$. We therefore have ![]() $v_{\text{num}}(D+A)\leqslant v(E)=0$.
$v_{\text{num}}(D+A)\leqslant v(E)=0$.
It remains to show the inclusions ![]() $\subseteq$. We first consider the case when
$\subseteq$. We first consider the case when ![]() $\operatorname{char}k=0$. Let
$\operatorname{char}k=0$. Let ![]() $\unicode[STIX]{x1D6E5}$ be an effective
$\unicode[STIX]{x1D6E5}$ be an effective ![]() $\mathbf{Q}$-Weil divisor such that
$\mathbf{Q}$-Weil divisor such that ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is
$K_{X}+\unicode[STIX]{x1D6E5}$ is ![]() $\mathbf{Q}$-Cartier. The proof of [Reference Cacciola and Di Biagio7, Theorem 4.5] holds in this setting after replacing the application of Nadel vanishing and Castelnuovo–Mumford regularity in the proof of [Reference Cacciola and Di Biagio7, Lemma 4.1] with the uniform global generation statement mentioned in Remark 4.7, hence
$\mathbf{Q}$-Cartier. The proof of [Reference Cacciola and Di Biagio7, Theorem 4.5] holds in this setting after replacing the application of Nadel vanishing and Castelnuovo–Mumford regularity in the proof of [Reference Cacciola and Di Biagio7, Lemma 4.1] with the uniform global generation statement mentioned in Remark 4.7, hence ![]() . Taking the union over all
. Taking the union over all ![]() $\mathbf{Q}$-Weil divisors
$\mathbf{Q}$-Weil divisors ![]() $\unicode[STIX]{x1D6E5}$ such that
$\unicode[STIX]{x1D6E5}$ such that ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is
$K_{X}+\unicode[STIX]{x1D6E5}$ is ![]() $\mathbf{Q}$-Cartier, we then see that the inclusion
$\mathbf{Q}$-Cartier, we then see that the inclusion ![]() $\subseteq$ holds in (15).
$\subseteq$ holds in (15).
We now consider the characteristic ![]() $p>0$ case. By [Reference Cacciola and Di Biagio7, Lemmas 2.12 and 2.13], there exists a sequence
$p>0$ case. By [Reference Cacciola and Di Biagio7, Lemmas 2.12 and 2.13], there exists a sequence ![]() $\{{A_{n}\}}_{n\geqslant 0}$ of ample
$\{{A_{n}\}}_{n\geqslant 0}$ of ample ![]() $\mathbf{R}$-Cartier divisors on
$\mathbf{R}$-Cartier divisors on ![]() $X$ such that
$X$ such that ![]() $D+A_{n}$ is a
$D+A_{n}$ is a ![]() $\mathbf{Q}$-Cartier divisor for every
$\mathbf{Q}$-Cartier divisor for every ![]() $n$,
$n$, ![]() $\lim _{n\rightarrow \infty }\Vert A_{n}\Vert \rightarrow 0$, and
$\lim _{n\rightarrow \infty }\Vert A_{n}\Vert \rightarrow 0$, and
By proving the inclusion ![]() $\subseteq$ in (16) for
$\subseteq$ in (16) for ![]() $D+A_{n}$, it therefore suffices to consider the case when
$D+A_{n}$, it therefore suffices to consider the case when ![]() $D$ is a big
$D$ is a big ![]() $\mathbf{Q}$-Cartier divisor. Let
$\mathbf{Q}$-Cartier divisor. Let ![]() , and consider a divisorial valuation
, and consider a divisorial valuation ![]() $v$ on
$v$ on ![]() $X$ such that
$X$ such that ![]() $c_{X}(v)=\overline{\{x\}}$, which is given by the order of vanishing along a prime Cartier divisor
$c_{X}(v)=\overline{\{x\}}$, which is given by the order of vanishing along a prime Cartier divisor ![]() $E$ on a normal birational model
$E$ on a normal birational model ![]() $X^{\prime }$ of
$X^{\prime }$ of ![]() $X$. By applying the gamma construction (Theorem 3.4) to
$X$. By applying the gamma construction (Theorem 3.4) to ![]() $X$,
$X$, ![]() $X^{\prime }$, and
$X^{\prime }$, and ![]() $E$, there exists a field extension
$E$, there exists a field extension ![]() $k\subseteq k^{\unicode[STIX]{x1D6E4}}$ such that
$k\subseteq k^{\unicode[STIX]{x1D6E4}}$ such that ![]() $X\times _{k}k^{\unicode[STIX]{x1D6E4}}$ and
$X\times _{k}k^{\unicode[STIX]{x1D6E4}}$ and ![]() $X^{\prime }\times _{k}k^{\unicode[STIX]{x1D6E4}}$ are normal varieties,
$X^{\prime }\times _{k}k^{\unicode[STIX]{x1D6E4}}$ are normal varieties, ![]() $E\times _{k}k^{\unicode[STIX]{x1D6E4}}$ is a prime divisor, and
$E\times _{k}k^{\unicode[STIX]{x1D6E4}}$ is a prime divisor, and ![]() $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}(\operatorname{NSFR}(X^{\unicode[STIX]{x1D6E4}}))=\operatorname{NSFR}(X)$. Note that the order of vanishing along
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}}(\operatorname{NSFR}(X^{\unicode[STIX]{x1D6E4}}))=\operatorname{NSFR}(X)$. Note that the order of vanishing along ![]() $E\times _{k}k^{\unicode[STIX]{x1D6E4}}$ defines a divisorial valuation
$E\times _{k}k^{\unicode[STIX]{x1D6E4}}$ defines a divisorial valuation ![]() $v^{\unicode[STIX]{x1D6E4}}$ on
$v^{\unicode[STIX]{x1D6E4}}$ on ![]() $X^{\unicode[STIX]{x1D6E4}}$ extending
$X^{\unicode[STIX]{x1D6E4}}$ extending ![]() $v$. Since
$v$. Since ![]() by Lemma 5.3, we have
by Lemma 5.3, we have ![]() , hence [Reference Sato57, Corollary 4.6] implies
, hence [Reference Sato57, Corollary 4.6] implies
By the proof of the implication ![]() $(2)\Rightarrow (5)$ in [Reference Sato57, Proposition 3.17] (which does not use the assumption that
$(2)\Rightarrow (5)$ in [Reference Sato57, Proposition 3.17] (which does not use the assumption that ![]() $K_{X}$ is
$K_{X}$ is ![]() $\mathbf{Q}$-Cartier), we see that
$\mathbf{Q}$-Cartier), we see that ![]() $v^{\unicode[STIX]{x1D6E4}}(\Vert (\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}})^{\ast }D\Vert )>0$, and by pulling back Cartier divisors in
$v^{\unicode[STIX]{x1D6E4}}(\Vert (\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D6E4}})^{\ast }D\Vert )>0$, and by pulling back Cartier divisors in ![]() $|D|$ to
$|D|$ to ![]() $X^{\unicode[STIX]{x1D6E4}}$, we have
$X^{\unicode[STIX]{x1D6E4}}$, we have ![]() $v(\Vert D\Vert )>0$ as well. Finally, since
$v(\Vert D\Vert )>0$ as well. Finally, since ![]() $D$ is big, [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa15, Lemma 3.3] implies
$D$ is big, [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa15, Lemma 3.3] implies ![]() $v_{\text{num}}(D)=v(\Vert D\Vert )>0$, hence
$v_{\text{num}}(D)=v(\Vert D\Vert )>0$, hence ![]() $x\in \operatorname{NNef}(D)$, and the inclusion
$x\in \operatorname{NNef}(D)$, and the inclusion ![]() $\subseteq$ holds in (16).◻
$\subseteq$ holds in (16).◻
We now prove Theorem C.
Proof of Theorem C.
As in the proof of Theorem 5.6, the inclusion ![]() holds, hence it suffices to show the reverse inclusion. By Theorem 5.6, we have
holds, hence it suffices to show the reverse inclusion. By Theorem 5.6, we have ![]() (resp.
(resp. ![]() ). Now let
). Now let![]() $\{{A_{n}\}}_{n\geqslant 1}$ be a sequence of ample
$\{{A_{n}\}}_{n\geqslant 1}$ be a sequence of ample ![]() $\mathbf{R}$-Cartier divisors such that
$\mathbf{R}$-Cartier divisors such that ![]() $\lim _{n\rightarrow \infty }\Vert A_{n}\Vert \rightarrow 0$ and such that
$\lim _{n\rightarrow \infty }\Vert A_{n}\Vert \rightarrow 0$ and such that ![]() $D+A_{n}$ is a
$D+A_{n}$ is a ![]() $\mathbf{Q}$-Cartier divisor for every
$\mathbf{Q}$-Cartier divisor for every ![]() $n$. By [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa15, Proposition 1.19], we have
$n$. By [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa15, Proposition 1.19], we have
Since each ![]() $\mathbf{B}(D+A_{n})$ does not contain any isolated points [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa16, Proposition 1.1], we see that
$\mathbf{B}(D+A_{n})$ does not contain any isolated points [Reference Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa16, Proposition 1.1], we see that ![]() does not contain any isolated points. Finally, since
does not contain any isolated points. Finally, since ![]() $\operatorname{Nklt}(X)$ (resp.
$\operatorname{Nklt}(X)$ (resp. ![]() $\operatorname{NSFR}(X)$) is a discrete set of isolated closed points by assumption, we have
$\operatorname{NSFR}(X)$) is a discrete set of isolated closed points by assumption, we have ![]() by Theorem 5.6.◻
by Theorem 5.6.◻
Acknowledgments
I am grateful to my advisor Mircea Mustaţă for his constant support and for several illuminating conversations, and to Mitsuyasu Hashimoto, Melvin Hochster, Emanuel Reinecke, Karen E. Smith, Daniel Smolkin, Matthew Stevenson, Shunsuke Takagi, and Farrah Yhee for helpful discussions. I am particularly grateful to Harold Blum for pointing out applications of [Reference de Fernex, Küronya and Lazarsfeld12], to Rankeya Datta for clarifications on strong ![]() $F$-regularity for non-
$F$-regularity for non-![]() $F$-finite rings, to Alex Küronya for talking to me about his results in [Reference Küronya41] and [Reference de Fernex, Küronya and Lazarsfeld12], and to Linquan Ma, Thomas Polstra, Karl Schwede, and Kevin Tucker for sharing a preliminary draft of [Reference Ma, Polstra, Schwede and Tucker46] with me. I first proved Theorem B in order to prove some results in joint work with Mihai Fulger, and I would especially like to thank him for allowing me to write this standalone paper. Finally, I am indebted to the anonymous referee for useful suggestions that improved the quality of this paper.
$F$-finite rings, to Alex Küronya for talking to me about his results in [Reference Küronya41] and [Reference de Fernex, Küronya and Lazarsfeld12], and to Linquan Ma, Thomas Polstra, Karl Schwede, and Kevin Tucker for sharing a preliminary draft of [Reference Ma, Polstra, Schwede and Tucker46] with me. I first proved Theorem B in order to prove some results in joint work with Mihai Fulger, and I would especially like to thank him for allowing me to write this standalone paper. Finally, I am indebted to the anonymous referee for useful suggestions that improved the quality of this paper.
Appendix A. Some results on  $F$-injective rings
$F$-injective rings
Let ![]() $R$ be a Noetherian ring of prime characteristic
$R$ be a Noetherian ring of prime characteristic ![]() $p>0$. Recall from Definition 2.10 that
$p>0$. Recall from Definition 2.10 that ![]() $R$ is
$R$ is ![]() $F$-injective if for every maximal ideal
$F$-injective if for every maximal ideal ![]() $\mathfrak{m}\subseteq R$, the
$\mathfrak{m}\subseteq R$, the ![]() $R$-module homomorphism
$R$-module homomorphism ![]() $H_{\mathfrak{m}}^{i}(F):H_{\mathfrak{m}}^{i}(R_{\mathfrak{m}})\rightarrow H_{\mathfrak{m}}^{i}(F_{\ast }R_{\mathfrak{m}})$ induced by Frobenius is injective for all
$H_{\mathfrak{m}}^{i}(F):H_{\mathfrak{m}}^{i}(R_{\mathfrak{m}})\rightarrow H_{\mathfrak{m}}^{i}(F_{\ast }R_{\mathfrak{m}})$ induced by Frobenius is injective for all ![]() $i$.
$i$.
In this appendix, we prove some facts about ![]() $F$-injective rings for which we could not find a reference. First, we characterize
$F$-injective rings for which we could not find a reference. First, we characterize ![]() $F$-finite rings that are
$F$-finite rings that are ![]() $F$-injective using Grothendieck duality. This characterization is already implicit in [Reference Fedder18, Remark on p. 473] and the proof of [Reference Schwede58, Proposition 4.3]. Note that if
$F$-injective using Grothendieck duality. This characterization is already implicit in [Reference Fedder18, Remark on p. 473] and the proof of [Reference Schwede58, Proposition 4.3]. Note that if ![]() $R$ is an
$R$ is an ![]() $F$-finite ring, then the exceptional pullback
$F$-finite ring, then the exceptional pullback ![]() $F^{!}$ from Grothendieck duality exists [Reference Hartshorne28, III.6], and
$F^{!}$ from Grothendieck duality exists [Reference Hartshorne28, III.6], and ![]() $R$ has a normalized dualizing complex
$R$ has a normalized dualizing complex ![]() $\unicode[STIX]{x1D714}_{R}^{\bullet }$ by Theorem 2.7.
$\unicode[STIX]{x1D714}_{R}^{\bullet }$ by Theorem 2.7.
Lemma A.1. (cf. [Reference Fedder18, Remark on p. 473])
Let ![]() $R$ be an
$R$ be an ![]() $F$-finite Noetherian ring of prime characteristic
$F$-finite Noetherian ring of prime characteristic ![]() $p>0$. Then,
$p>0$. Then, ![]() $R$ is
$R$ is ![]() $F$-injective if and only if the
$F$-injective if and only if the ![]() $R$-module homomorphisms
$R$-module homomorphisms
induced by the Grothendieck trace of Frobenius are surjective for all ![]() $i$.
$i$.
Lemma A.1 is most useful when ![]() $R$ is essentially of finite type over an
$R$ is essentially of finite type over an ![]() $F$-finite field, in which case
$F$-finite field, in which case ![]() $F^{!}\unicode[STIX]{x1D714}_{R}^{\bullet }\simeq \unicode[STIX]{x1D714}_{R}^{\bullet }$ in the derived category
$F^{!}\unicode[STIX]{x1D714}_{R}^{\bullet }\simeq \unicode[STIX]{x1D714}_{R}^{\bullet }$ in the derived category ![]() $\mathbf{D}_{\text{qc}}^{+}(R)$ [Reference Nayak53, Theorem 5.3], hence the homomorphisms in (A1) can be written as
$\mathbf{D}_{\text{qc}}^{+}(R)$ [Reference Nayak53, Theorem 5.3], hence the homomorphisms in (A1) can be written as ![]() $\mathbf{h}^{-i}F_{\ast }\unicode[STIX]{x1D714}_{R}^{\bullet }\rightarrow \mathbf{h}^{-i}\unicode[STIX]{x1D714}_{R}^{\bullet }$.
$\mathbf{h}^{-i}F_{\ast }\unicode[STIX]{x1D714}_{R}^{\bullet }\rightarrow \mathbf{h}^{-i}\unicode[STIX]{x1D714}_{R}^{\bullet }$.
Proof. By Grothendieck local duality [Reference Hartshorne28, Corollary V.6.3], ![]() $R$ is
$R$ is ![]() $F$-injective if and only if
$F$-injective if and only if
is surjective for all ![]() $i$. By Grothendieck duality for finite morphisms [Reference Hartshorne28, Theorem III.6.7], this occurs if and only if
$i$. By Grothendieck duality for finite morphisms [Reference Hartshorne28, Theorem III.6.7], this occurs if and only if
is surjective for all ![]() $i$. Since
$i$. Since ![]() $\operatorname{Ext}_{R}^{-i}(R,-)=\mathbf{h}^{-i}(-)$ and by the description of the Grothendieck duality isomorphism [Reference Hartshorne28, Theorem III.6.7], this is equivalent to the surjectivity of (A1) for all
$\operatorname{Ext}_{R}^{-i}(R,-)=\mathbf{h}^{-i}(-)$ and by the description of the Grothendieck duality isomorphism [Reference Hartshorne28, Theorem III.6.7], this is equivalent to the surjectivity of (A1) for all ![]() $i$.◻
$i$.◻
Next, we prove that ![]() $F$-injectivity is an open condition on
$F$-injectivity is an open condition on ![]() $F$-finite schemes. This extends [Reference Quy and Shimomoto55, Proposition 3.12] to the nonlocal case.
$F$-finite schemes. This extends [Reference Quy and Shimomoto55, Proposition 3.12] to the nonlocal case.
Lemma A.2. (cf. [Reference Quy and Shimomoto55, Proposition 3.12; Reference Schwede58, Proposition 4.3])
If ![]() $R$ is an
$R$ is an ![]() $F$-finite Noetherian ring of prime characteristic
$F$-finite Noetherian ring of prime characteristic ![]() $p>0$, then the locus
$p>0$, then the locus
is open. In particular, ![]() $R$ is
$R$ is ![]() $F$-injective if and only if
$F$-injective if and only if ![]() $R_{\mathfrak{p}}$ is
$R_{\mathfrak{p}}$ is ![]() $F$-injective for every prime ideal
$F$-injective for every prime ideal ![]() $\mathfrak{p}\subseteq R$.
$\mathfrak{p}\subseteq R$.
Proof. For each integer ![]() $i$, let
$i$, let ![]() $M_{i}$ be the cokernel of the
$M_{i}$ be the cokernel of the ![]() $R$-module homomorphism in (A1). Since the Grothendieck trace is compatible with flat base change [Reference Hartshorne28, Proposition III.6.6(2)] and Frobenius is compatible with localizations, the support of
$R$-module homomorphism in (A1). Since the Grothendieck trace is compatible with flat base change [Reference Hartshorne28, Proposition III.6.6(2)] and Frobenius is compatible with localizations, the support of ![]() $M_{i}$ is the locus where
$M_{i}$ is the locus where ![]() $R$ is not
$R$ is not ![]() $F$-injective by Lemma A.1. Now
$F$-injective by Lemma A.1. Now ![]() $\unicode[STIX]{x1D714}_{R}^{\bullet }$ and
$\unicode[STIX]{x1D714}_{R}^{\bullet }$ and ![]() $F_{\ast }F^{!}\unicode[STIX]{x1D714}_{R}^{\bullet }$ have coherent cohomology that is nonzero in only finitely many degrees by definition of
$F_{\ast }F^{!}\unicode[STIX]{x1D714}_{R}^{\bullet }$ have coherent cohomology that is nonzero in only finitely many degrees by definition of ![]() $\unicode[STIX]{x1D714}_{R}^{\bullet }$ and [Reference Hartshorne28, Proposition III.6.1], hence each
$\unicode[STIX]{x1D714}_{R}^{\bullet }$ and [Reference Hartshorne28, Proposition III.6.1], hence each ![]() $M_{i}$ is finitely generated over
$M_{i}$ is finitely generated over ![]() $R$, has closed support, and is nonzero for only finitely many
$R$, has closed support, and is nonzero for only finitely many ![]() $i$. The locus
$i$. The locus
is therefore open, proving the first statement. The locus (A2) is in particular closed under generization, hence ![]() $R$ is
$R$ is ![]() $F$-injective only if
$F$-injective only if ![]() $R_{\mathfrak{p}}$ is
$R_{\mathfrak{p}}$ is ![]() $F$-injective for every prime ideal
$F$-injective for every prime ideal ![]() $\mathfrak{p}\subseteq R$. The converse implication holds by definition, proving the second statement.◻
$\mathfrak{p}\subseteq R$. The converse implication holds by definition, proving the second statement.◻
Finally, to prove Theorem 3.4, we used the following descent property for ![]() $F$-injectivity.
$F$-injectivity.
Lemma A.3. (cf. [Reference Hashimoto30, Lemma 4.6])
Let ![]() $\unicode[STIX]{x1D711}:R\rightarrow S$ be a pure homomorphism of rings of prime characteristic
$\unicode[STIX]{x1D711}:R\rightarrow S$ be a pure homomorphism of rings of prime characteristic ![]() $p>0$. If
$p>0$. If ![]() $I\subseteq R$ is a finitely generated ideal such that the Frobenius action
$I\subseteq R$ is a finitely generated ideal such that the Frobenius action
is injective for some ![]() $i$, then the Frobenius action
$i$, then the Frobenius action
is also injective.
In particular, suppose that ![]() $(R,\mathfrak{m})$ and
$(R,\mathfrak{m})$ and ![]() $(S,\mathfrak{n})$ are Noetherian local rings and that
$(S,\mathfrak{n})$ are Noetherian local rings and that ![]() $\unicode[STIX]{x1D711}$ is a local homomorphism with zero-dimensional closed fiber. If
$\unicode[STIX]{x1D711}$ is a local homomorphism with zero-dimensional closed fiber. If ![]() $S$ is
$S$ is ![]() $F$-injective, then
$F$-injective, then ![]() $R$ is
$R$ is ![]() $F$-injective.
$F$-injective.
In the non-Noetherian case, we define local cohomology modules by taking injective resolutions in the category of sheaves of abelian groups on spectra, as is done in [Reference Grothendieck23, Exposé I, Définition 2.1].
Proof. For each ![]() $i$, we have the following commutative square:
$i$, we have the following commutative square:

Since ![]() $\unicode[STIX]{x1D711}$ is pure, the map
$\unicode[STIX]{x1D711}$ is pure, the map ![]() $H_{I}^{i}(R){\hookrightarrow}H_{IS}^{i}(S)$ is injective by applying [Reference Hochster and Roberts35, Corollary 6.6] to the Čech complex, which computes local cohomology by [Reference Grothendieck23, Exposé II, Proposition 5]. The bottom horizontal arrow in (
$H_{I}^{i}(R){\hookrightarrow}H_{IS}^{i}(S)$ is injective by applying [Reference Hochster and Roberts35, Corollary 6.6] to the Čech complex, which computes local cohomology by [Reference Grothendieck23, Exposé II, Proposition 5]. The bottom horizontal arrow in (
) is injective by assumption, hence the top horizontal arrow ![]() $H_{I}^{i}(F_{R})$ in (
$H_{I}^{i}(F_{R})$ in (
) is also injective by the commutativity of the diagram. The second statement in the lemma is a special case of the first, since under the given assumptions, we have ![]() $\sqrt{\mathfrak{m}S}=\mathfrak{n}$, hence
$\sqrt{\mathfrak{m}S}=\mathfrak{n}$, hence ![]() $H_{\mathfrak{m}S}^{i}(S)\simeq H_{\mathfrak{n}}^{i}(S)$.◻
$H_{\mathfrak{m}S}^{i}(S)\simeq H_{\mathfrak{n}}^{i}(S)$.◻
Appendix B. Strong  $F$-regularity for non-
$F$-regularity for non- $F$-finite rings
$F$-finite rings
In this appendix, we describe the relationship between different notions of strong ![]() $F$-regularity in the non-
$F$-regularity in the non-![]() $F$-finite setting. This material is based on [Reference Hashimoto30, Section 3] and [Reference Datta and Smith10, Section 6].
$F$-finite setting. This material is based on [Reference Hashimoto30, Section 3] and [Reference Datta and Smith10, Section 6].
Definition B.1. Let ![]() $R$ be a Noetherian ring of prime characteristic
$R$ be a Noetherian ring of prime characteristic ![]() $p>0$. We follow the notation in Definition 2.8. For every
$p>0$. We follow the notation in Definition 2.8. For every ![]() $c\in R$, we also say that
$c\in R$, we also say that ![]() $R$ is
$R$ is ![]() $F$-split along
$F$-split along ![]() $c$ if
$c$ if ![]() $\unicode[STIX]{x1D706}_{c}^{e}$ splits as an
$\unicode[STIX]{x1D706}_{c}^{e}$ splits as an ![]() $R$-module homomorphism for some
$R$-module homomorphism for some ![]() $e>0$. We then say that
$e>0$. We then say that
(a)
 $R$ is split
$R$ is split  $F$-regular if
$F$-regular if  $R$ is
$R$ is  $F$-split along every
$F$-split along every  $c\in R^{\circ }$ [Reference Hochster and Huneke34, Definition 5.1];
$c\in R^{\circ }$ [Reference Hochster and Huneke34, Definition 5.1];(b)
 $R$ is
$R$ is  $F$-pure regular if
$F$-pure regular if  $R$ is
$R$ is  $F$-pure along every
$F$-pure along every  $c\in R^{\circ }$ [Reference Hochster and Huneke34, Remark 5.3]; and
$c\in R^{\circ }$ [Reference Hochster and Huneke34, Remark 5.3]; and(c)
 $R$ is strongly
$R$ is strongly  $F$-regular if every inclusion of
$F$-regular if every inclusion of  $R$-modules is tightly closed [Reference Hashimoto30, Definition 3.3].
$R$-modules is tightly closed [Reference Hashimoto30, Definition 3.3].
The definition in (c) is due to Hochster; see [Reference Hochster and Huneke33, Definition 8.2] for the definition of tight closure for modules. While (c) is not the definition used in the rest of this paper (Definition 2.8(a)), these two definitions are equivalent by [Reference Hashimoto30, Lemma 3.6].
Note that (a) is the usual definition of strong ![]() $F$-regularity in the
$F$-regularity in the ![]() $F$-finite setting. The terminology in (a) and (b) is from [Reference Datta and Smith10, Definitions 6.6.1 and 6.1.1].
$F$-finite setting. The terminology in (a) and (b) is from [Reference Datta and Smith10, Definitions 6.6.1 and 6.1.1]. ![]() $F$-pure regular rings are called very strongly
$F$-pure regular rings are called very strongly ![]() $F$-regular in [Reference Hashimoto30, Definition 3.4].
$F$-regular in [Reference Hashimoto30, Definition 3.4].
The relationship between these notions of strong ![]() $F$-regularity can be summarized as follows:
$F$-regularity can be summarized as follows: