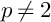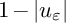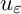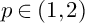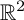1 Introduction
Let
![]() $G \subset \mathbb {R}^2$
be a bounded and simply connected domain with smooth boundary
$G \subset \mathbb {R}^2$
be a bounded and simply connected domain with smooth boundary
![]() $\partial G$
, and g be a smooth map from
$\partial G$
, and g be a smooth map from
![]() $\partial G$
to
$\partial G$
to
![]() $S^1$
satisfying
$S^1$
satisfying
![]() $d:=\deg (g,\partial G) \neq 0$
. Without loss of generality, we assume
$d:=\deg (g,\partial G) \neq 0$
. Without loss of generality, we assume
![]() $d>0$
. Bethuel et al. [Reference Bethuel, Brezis and Helein3] and Struwe [Reference Struwe21] well studied the asymptotic behavior of the Ginzburg–Landau functional
$d>0$
. Bethuel et al. [Reference Bethuel, Brezis and Helein3] and Struwe [Reference Struwe21] well studied the asymptotic behavior of the Ginzburg–Landau functional
 $$ \begin{align*}E(u)=\frac{1}{2}\int_G|\nabla u|^2 +\frac{1}{4\varepsilon^2}\int_G(1-|u|^2)^2 \end{align*} $$
$$ \begin{align*}E(u)=\frac{1}{2}\int_G|\nabla u|^2 +\frac{1}{4\varepsilon^2}\int_G(1-|u|^2)^2 \end{align*} $$
as
![]() $\varepsilon \to 0^+$
, and established the
$\varepsilon \to 0^+$
, and established the
![]() $C^k$
-convergence relation between the minimizer and some harmonic map
$C^k$
-convergence relation between the minimizer and some harmonic map
![]() $u_*$
on G. Namely, if
$u_*$
on G. Namely, if
![]() $u_\varepsilon $
is the minimizer of
$u_\varepsilon $
is the minimizer of
![]() $E(u)$
in
$E(u)$
in
![]() $H_g^1(G,\mathbb {R}^2)$
, then there exists a subsequence
$H_g^1(G,\mathbb {R}^2)$
, then there exists a subsequence
![]() $u_{\varepsilon _k}$
such that when
$u_{\varepsilon _k}$
such that when
![]() $k \to \infty $
,
$k \to \infty $
,
for any
![]() $l \geq 1$
. Here,
$l \geq 1$
. Here,
![]() $a_1,a_2,\ldots ,a_d$
are the singularities of
$a_1,a_2,\ldots ,a_d$
are the singularities of
![]() $u_*$
in G. In particular, [Reference Bethuel, Brezis and Helein3, Theorem VII.2] shows the following property of the energy concentration
$u_*$
in G. In particular, [Reference Bethuel, Brezis and Helein3, Theorem VII.2] shows the following property of the energy concentration
 $$ \begin{align} \lim_{\varepsilon_k \to 0} \frac{(1-|u_{\varepsilon_k}|^2)^2}{4\varepsilon_k^2}=\frac{\pi}{2} \sum_{j=1}^d\delta_{a_j},\quad \mbox{in the weak star topology of}\quad C(\overline{G}). \end{align} $$
$$ \begin{align} \lim_{\varepsilon_k \to 0} \frac{(1-|u_{\varepsilon_k}|^2)^2}{4\varepsilon_k^2}=\frac{\pi}{2} \sum_{j=1}^d\delta_{a_j},\quad \mbox{in the weak star topology of}\quad C(\overline{G}). \end{align} $$
These results come into play when studying the location of the vortices in phase transition problems occurring in superconductivity and superfluids. In addition, these results are also helpful to understand the regularity of harmonic maps and the distribution of the singularities.
In addition, 19 open problems were posed in [Reference Bethuel, Brezis and Helein3]. Comte and Mironescu gave positive answers to the 7th problem (cf. [Reference Comte and Mironescu8], [Reference Comte and Mironescu9], and [Reference Mironescu20]) on the global analysis of the Ginzburg–Landau energy. In particular, there exists
![]() $C>0$
such that as
$C>0$
such that as
![]() $\varepsilon \to 0$
,
$\varepsilon \to 0$
,
 $$ \begin{align} \int_G(1-|u_\varepsilon|^2)^\alpha |\nabla u_\varepsilon|^2 \leq C\alpha^{-1}, \quad \forall \alpha>0, \end{align} $$
$$ \begin{align} \int_G(1-|u_\varepsilon|^2)^\alpha |\nabla u_\varepsilon|^2 \leq C\alpha^{-1}, \quad \forall \alpha>0, \end{align} $$
 $$ \begin{align} \int_G|\det(\nabla u_\varepsilon)| \leq C. \end{align} $$
$$ \begin{align} \int_G|\det(\nabla u_\varepsilon)| \leq C. \end{align} $$
In this paper, we are concerned with the asymptotic behavior of the minimizer
![]() $u_{\varepsilon }$
of the p-Ginzburg-Landau-type functional
$u_{\varepsilon }$
of the p-Ginzburg-Landau-type functional
 $$ \begin{align*}E_\varepsilon(u,G)= \frac{1}{p}\int_G|\nabla u|^p +\frac{1}{4\varepsilon^p}\int_G(1-|u|^2)^2 \quad (p>1 \ \mbox{and} \ p\neq 2) \end{align*} $$
$$ \begin{align*}E_\varepsilon(u,G)= \frac{1}{p}\int_G|\nabla u|^p +\frac{1}{4\varepsilon^p}\int_G(1-|u|^2)^2 \quad (p>1 \ \mbox{and} \ p\neq 2) \end{align*} $$
in the space
![]() $W=\{v \in W^{1,p}(G,\mathbb {R}^2) \cap L^4(G,\mathbb {R}^2); v|_{\partial G}=g\}$
.
$W=\{v \in W^{1,p}(G,\mathbb {R}^2) \cap L^4(G,\mathbb {R}^2); v|_{\partial G}=g\}$
.
Functional
![]() $E_\varepsilon (u,G)$
can be used to study the partial regularity of p-harmonic maps and the location of the singularities when
$E_\varepsilon (u,G)$
can be used to study the partial regularity of p-harmonic maps and the location of the singularities when
![]() $p \in (1,2)$
and p approaches the dimension 2 (cf. [Reference Hardt and Lin14], [Reference Wang24]). Different from the case
$p \in (1,2)$
and p approaches the dimension 2 (cf. [Reference Hardt and Lin14], [Reference Wang24]). Different from the case
![]() $p \in (1,2)$
,
$p \in (1,2)$
,
![]() $W_g^{1,p}(G, S^1)=\emptyset $
when
$W_g^{1,p}(G, S^1)=\emptyset $
when
![]() $p>2$
and
$p>2$
and
![]() $d \neq 0$
. Therefore, there does not exist p-harmonic map from G to
$d \neq 0$
. Therefore, there does not exist p-harmonic map from G to
![]() $S^1$
. Thus, functional
$S^1$
. Thus, functional
![]() $E_\varepsilon (u,G)$
is naturally used by the idea of penalization which is analogous to researching harmonic maps in [Reference Bethuel, Brezis and Helein3]. In fact, the same idea had been used in studying flow of p-harmonic maps (cf. [Reference Chen, Hong and Hungerbuhler6]).
$E_\varepsilon (u,G)$
is naturally used by the idea of penalization which is analogous to researching harmonic maps in [Reference Bethuel, Brezis and Helein3]. In fact, the same idea had been used in studying flow of p-harmonic maps (cf. [Reference Chen, Hong and Hungerbuhler6]).
In this paper, we investigate the global properties of functional
![]() $E_\varepsilon (u,G)$
. In addition, the singularity properties of the functional is also interesting. When
$E_\varepsilon (u,G)$
. In addition, the singularity properties of the functional is also interesting. When
![]() $p=2$
, the results (1.1)–(1.3) describe the singularity and the global properties. We expect to generalize them to the case of
$p=2$
, the results (1.1)–(1.3) describe the singularity and the global properties. We expect to generalize them to the case of
![]() $p \neq 2$
.
$p \neq 2$
.
By the direct methods, we know the existence of the minimizer
![]() $u_\varepsilon $
of
$u_\varepsilon $
of
![]() $E_\varepsilon (u,B)$
in the space W. Clearly, the minimizer is a weak solution to the following system
$E_\varepsilon (u,B)$
in the space W. Clearly, the minimizer is a weak solution to the following system
By the regularity theory (cf. [Reference Tolksdorf22]),
![]() $u_\varepsilon \in C^{\alpha }(\overline {G}) \cap C_{loc}^{1,\alpha }(G)$
for each
$u_\varepsilon \in C^{\alpha }(\overline {G}) \cap C_{loc}^{1,\alpha }(G)$
for each
![]() $\varepsilon $
. In addition, by [Reference Hong15, analogous proof of Theorem 2.2], we also have
$\varepsilon $
. In addition, by [Reference Hong15, analogous proof of Theorem 2.2], we also have
There may be several minimizers of
![]() $E_\varepsilon (u,G)$
. One of them, denoted by
$E_\varepsilon (u,G)$
. One of them, denoted by
![]() $\tilde {u}_{\varepsilon }$
, can be obtained as the limit of a subsequence
$\tilde {u}_{\varepsilon }$
, can be obtained as the limit of a subsequence
![]() $u_{\varepsilon }^{\eta _k}$
of the minimizers
$u_{\varepsilon }^{\eta _k}$
of the minimizers
![]() $u_{\varepsilon }^{\eta }$
of the regularized functional (if we follow Uhlenbeck’s idea in [Reference Uhlenbeck23])
$u_{\varepsilon }^{\eta }$
of the regularized functional (if we follow Uhlenbeck’s idea in [Reference Uhlenbeck23])
 $$ \begin{align*}E_{\varepsilon}^{\eta}(u,G):= \frac{1}{p}\displaystyle\int_G(|\nabla u|^2+\eta)^{\frac{p}{2}} +\frac{1}{4\varepsilon^{p}}\displaystyle\int_{G}(1-|u|^2)^2 \ \ (\eta>0, \ \varepsilon>0) \end{align*} $$
$$ \begin{align*}E_{\varepsilon}^{\eta}(u,G):= \frac{1}{p}\displaystyle\int_G(|\nabla u|^2+\eta)^{\frac{p}{2}} +\frac{1}{4\varepsilon^{p}}\displaystyle\int_{G}(1-|u|^2)^2 \ \ (\eta>0, \ \varepsilon>0) \end{align*} $$
in W (see also [Reference Giaquinta and Modica13] and [Reference Hong15]). Namely, there exists a subsequence
![]() $\eta _k$
of
$\eta _k$
of
![]() $\eta $
such that
$\eta $
such that
where
![]() $\tilde {u}_\varepsilon $
is also a minimizer of
$\tilde {u}_\varepsilon $
is also a minimizer of
![]() $E_\varepsilon (u,G)$
in W. Here,
$E_\varepsilon (u,G)$
in W. Here,
![]() $\tilde {u}_\varepsilon $
is called the regularized minimizer.
$\tilde {u}_\varepsilon $
is called the regularized minimizer.
When
![]() $p>2$
, [Reference Lei17, Theorem 6.3] shows a convergence result of the minimizer
$p>2$
, [Reference Lei17, Theorem 6.3] shows a convergence result of the minimizer
![]() $u_\varepsilon $
of
$u_\varepsilon $
of
![]() $E_\varepsilon (u,G)$
in W. Namely, there exists a subsequence
$E_\varepsilon (u,G)$
in W. Namely, there exists a subsequence
![]() $u_{\varepsilon _k}$
of
$u_{\varepsilon _k}$
of
![]() $u_\varepsilon $
, such that when
$u_\varepsilon $
, such that when
![]() $k \to \infty $
,
$k \to \infty $
,
where
![]() $u_p$
is a p-harmonic map on
$u_p$
is a p-harmonic map on
![]() $G \setminus \{a_1,a_2,\cdots ,a_N\}$
. In addition, [Reference Lei18, Theorem 1.1] shows that
$G \setminus \{a_1,a_2,\cdots ,a_N\}$
. In addition, [Reference Lei18, Theorem 1.1] shows that
 $$ \begin{align} \lim_{\varepsilon_k \to 0} \frac{(1-|\tilde{u}_{\varepsilon_k}|^2)^2}{4\varepsilon_k^2}= \sum_{j=1}^N m_j\delta_{a_j},\quad \mbox{in the weak star topology of}\quad C(\overline{G}), \end{align} $$
$$ \begin{align} \lim_{\varepsilon_k \to 0} \frac{(1-|\tilde{u}_{\varepsilon_k}|^2)^2}{4\varepsilon_k^2}= \sum_{j=1}^N m_j\delta_{a_j},\quad \mbox{in the weak star topology of}\quad C(\overline{G}), \end{align} $$
where
![]() $m_j>0$
for
$m_j>0$
for
![]() $j=1,2,\ldots ,N$
.
$j=1,2,\ldots ,N$
.
The following theorem presents results similar to (1.2) and (1.3) when
![]() $p> 2$
, which will be proved in Section 3.
$p> 2$
, which will be proved in Section 3.
Theorem 1.1. Assume
![]() $p>2$
,
$p>2$
,
![]() $u_\varepsilon $
is a minimizer of
$u_\varepsilon $
is a minimizer of
![]() $E_\varepsilon (u,G)$
in W. Then we can find a subsequence
$E_\varepsilon (u,G)$
in W. Then we can find a subsequence
![]() $\varepsilon _k$
of
$\varepsilon _k$
of
![]() $\varepsilon $
, and
$\varepsilon $
, and
![]() $P_j\geq 0$
which is independent of
$P_j\geq 0$
which is independent of
![]() $\varepsilon _k$
(
$\varepsilon _k$
(
![]() $j=1,2,\ldots ,N$
), such that
$j=1,2,\ldots ,N$
), such that
 $$ \begin{align} \lim_{\varepsilon_k \to 0} \varepsilon_k^{p-2} |\det(\nabla u_{\varepsilon_k})|^{p/2} = \sum_{j=1}^N P_j\delta_{a_j},\ \mbox{weakly* in} \ C(\overline{G}), \end{align} $$
$$ \begin{align} \lim_{\varepsilon_k \to 0} \varepsilon_k^{p-2} |\det(\nabla u_{\varepsilon_k})|^{p/2} = \sum_{j=1}^N P_j\delta_{a_j},\ \mbox{weakly* in} \ C(\overline{G}), \end{align} $$
where
![]() $\delta _{a_j}$
is the Dirac mass at
$\delta _{a_j}$
is the Dirac mass at
![]() $a_j$
. In addition, for any
$a_j$
. In addition, for any
![]() $\alpha \geq 2-\frac {4}{p}$
, there exists
$\alpha \geq 2-\frac {4}{p}$
, there exists
![]() $L_j> 0$
which is independent of
$L_j> 0$
which is independent of
![]() $\varepsilon _k$
(
$\varepsilon _k$
(
![]() $j=1,2,\ldots ,N$
), such that
$j=1,2,\ldots ,N$
), such that
 $$ \begin{align} \lim_{\varepsilon_k \to 0}(1-|u_{\varepsilon_k}|^2)^{\alpha}|\nabla u_{\varepsilon_k}|^2 = \sum_{j=1}^N L_j\delta_{a_j},\ \mbox{weakly* in} \ C(\overline{G}). \end{align} $$
$$ \begin{align} \lim_{\varepsilon_k \to 0}(1-|u_{\varepsilon_k}|^2)^{\alpha}|\nabla u_{\varepsilon_k}|^2 = \sum_{j=1}^N L_j\delta_{a_j},\ \mbox{weakly* in} \ C(\overline{G}). \end{align} $$
When
![]() $p \in (1,2)$
, [Reference Lei16, Theorem 1.3] implies a convergence result of the regularized minimizer. Namely,
$p \in (1,2)$
, [Reference Lei16, Theorem 1.3] implies a convergence result of the regularized minimizer. Namely,
![]() $\tilde {u}_\varepsilon $
is a regularized minimizer. When
$\tilde {u}_\varepsilon $
is a regularized minimizer. When
![]() $p \in (2-t,2)$
for some
$p \in (2-t,2)$
for some
![]() $t \in (0,1/2)$
, there is a subsequence
$t \in (0,1/2)$
, there is a subsequence
![]() $\tilde {u}_k$
of
$\tilde {u}_k$
of
![]() $\tilde {u}_\varepsilon $
such that
$\tilde {u}_\varepsilon $
such that
where
![]() $u_p$
is a p-harmonic map on G and
$u_p$
is a p-harmonic map on G and
![]() $a_1,a_2,\ldots ,a_N \in \overline {G}$
are singularities of
$a_1,a_2,\ldots ,a_N \in \overline {G}$
are singularities of
![]() $u_p$
.
$u_p$
.
The following theorem shows a result similar to (1.1)–(1.3) in the case of
![]() $p \in (1,2)$
, which will be proved in Section 5.
$p \in (1,2)$
, which will be proved in Section 5.
Theorem 1.2. Assume that
![]() $p \in (1,2)$
approaches the dimension
$p \in (1,2)$
approaches the dimension
![]() $2$
, and
$2$
, and
![]() ${u}_\varepsilon $
is a minimizer in W. Then we can find a subsequence
${u}_\varepsilon $
is a minimizer in W. Then we can find a subsequence
![]() $\varepsilon _k$
of
$\varepsilon _k$
of
![]() $\varepsilon $
, and
$\varepsilon $
, and
![]() $Q_j \geq 0$
which is independent of
$Q_j \geq 0$
which is independent of
![]() $\varepsilon $
(
$\varepsilon $
(
![]() $j=1,2,\ldots ,N$
), such that
$j=1,2,\ldots ,N$
), such that
 $$ \begin{align} \lim_{\varepsilon_k \to 0} |\det(\nabla {u}_{\varepsilon_k})|^{p/2} = \sum_{j=1}^N Q_j\delta_{a_j},\ \mbox{weakly* in} \ C(\overline{G}). \end{align} $$
$$ \begin{align} \lim_{\varepsilon_k \to 0} |\det(\nabla {u}_{\varepsilon_k})|^{p/2} = \sum_{j=1}^N Q_j\delta_{a_j},\ \mbox{weakly* in} \ C(\overline{G}). \end{align} $$
Moreover, if
![]() $\tilde {u}_\varepsilon $
is a regularized minimizer, then we can find
$\tilde {u}_\varepsilon $
is a regularized minimizer, then we can find
![]() $K_j>0$
which is independent of
$K_j>0$
which is independent of
![]() $\varepsilon $
(
$\varepsilon $
(
![]() $j=1,2,\ldots ,N$
), such that
$j=1,2,\ldots ,N$
), such that
 $$ \begin{align} \lim_{\varepsilon_k \to 0} \frac{(1-|\tilde{u}_{\varepsilon_k}|^2)^2}{4\varepsilon_k^2}= \sum_{j=1}^N K_j \delta_{a_j},\ \mbox{weakly* in} \ C(\overline{G}). \end{align} $$
$$ \begin{align} \lim_{\varepsilon_k \to 0} \frac{(1-|\tilde{u}_{\varepsilon_k}|^2)^2}{4\varepsilon_k^2}= \sum_{j=1}^N K_j \delta_{a_j},\ \mbox{weakly* in} \ C(\overline{G}). \end{align} $$
In addition, for any
![]() $\alpha \geq 2-p$
, there exist
$\alpha \geq 2-p$
, there exist
![]() $M_j \geq 0$
which are independent of
$M_j \geq 0$
which are independent of
![]() $\varepsilon $
(
$\varepsilon $
(
![]() $j=1,2,\ldots ,N$
), such that
$j=1,2,\ldots ,N$
), such that
 $$ \begin{align} \lim_{\varepsilon_k \to 0}(1-|\tilde{u}_{\varepsilon_k}|^2)^{\alpha}|\nabla \tilde{u}_{\varepsilon_k}|^2 = \sum_{j=1}^N M_j\delta_{a_j}, \ \mbox{weakly* in} \ C(\overline{G}). \end{align} $$
$$ \begin{align} \lim_{\varepsilon_k \to 0}(1-|\tilde{u}_{\varepsilon_k}|^2)^{\alpha}|\nabla \tilde{u}_{\varepsilon_k}|^2 = \sum_{j=1}^N M_j\delta_{a_j}, \ \mbox{weakly* in} \ C(\overline{G}). \end{align} $$
Here,
![]() $M_j>0$
when
$M_j>0$
when
![]() $a_j \in G$
, and
$a_j \in G$
, and
![]() $M_j=0$
when
$M_j=0$
when
![]() $a_j \in \partial G$
.
$a_j \in \partial G$
.
Remark 1.1. When
![]() $p \neq 2$
, if
$p \neq 2$
, if
![]() $u_\varepsilon $
has radial structure, that is,
$u_\varepsilon $
has radial structure, that is,
![]() $G=B_1(0)$
and
$G=B_1(0)$
and
![]() $u_\varepsilon (x) \in \{u \in W; u(x)=f(r)(\cos d\theta , \sin d\theta ), r=|x|, x=(\cos \theta , \sin \theta )$
}, then
$u_\varepsilon (x) \in \{u \in W; u(x)=f(r)(\cos d\theta , \sin d\theta ), r=|x|, x=(\cos \theta , \sin \theta )$
}, then
![]() $N=1$
. According to [Reference Lei and Xu19, Theorems 1.1 and 1.2],
$N=1$
. According to [Reference Lei and Xu19, Theorems 1.1 and 1.2],
![]() $P_1$
in Theorem 1.1 and
$P_1$
in Theorem 1.1 and
![]() $Q_1$
in Theorem 1.2 are positive. For a general minimizer
$Q_1$
in Theorem 1.2 are positive. For a general minimizer
![]() $u_\varepsilon $
(i.e.,
$u_\varepsilon $
(i.e.,
![]() $u_\varepsilon $
without the radial structure), it seems difficult to determine the values of
$u_\varepsilon $
without the radial structure), it seems difficult to determine the values of
![]() $P_j$
and
$P_j$
and
![]() $Q_j$
even if
$Q_j$
even if
![]() $p=2$
(cf. [Reference Comte and Mironescu9]).
$p=2$
(cf. [Reference Comte and Mironescu9]).
Remark 1.2. (i) Equations (1.8)–(1.10) and (1.12)–(1.14) generalize (1.1)–(1.3) in the cases of
![]() $p>2$
and
$p>2$
and
![]() $p \in (1,2)$
, respectively. Different from the case of
$p \in (1,2)$
, respectively. Different from the case of
![]() $p=2$
, the conformal invariant of the functional with
$p=2$
, the conformal invariant of the functional with
![]() $p \neq 2$
is lost. So the results does not look concise. Namely, we need balance the energy functional by some proper weights to ensure the new energy integrals are globally bounded.
$p \neq 2$
is lost. So the results does not look concise. Namely, we need balance the energy functional by some proper weights to ensure the new energy integrals are globally bounded.
(ii) When
![]() $p>2$
, (1.8) and (1.9) show the concentration properties of
$p>2$
, (1.8) and (1.9) show the concentration properties of
![]() $\varepsilon ^{p-2}E_\varepsilon (u_\varepsilon ,G)$
. For the regularized minimizer
$\varepsilon ^{p-2}E_\varepsilon (u_\varepsilon ,G)$
. For the regularized minimizer
![]() $\tilde {u}_{\varepsilon }$
, [Reference Lei18, Theorem 1.1] shows that the first and the second terms of
$\tilde {u}_{\varepsilon }$
, [Reference Lei18, Theorem 1.1] shows that the first and the second terms of
![]() $\varepsilon ^{p-2}E_\varepsilon (u_\varepsilon ,G)$
have the same convergence orders, and
$\varepsilon ^{p-2}E_\varepsilon (u_\varepsilon ,G)$
have the same convergence orders, and
![]() $\varepsilon _k^{p-2}E_\varepsilon (\tilde {u}_{\varepsilon _k},G) \to \frac {p}{p-2} \Sigma _{j=1}^N m_j\delta _{a_j}$
when
$\varepsilon _k^{p-2}E_\varepsilon (\tilde {u}_{\varepsilon _k},G) \to \frac {p}{p-2} \Sigma _{j=1}^N m_j\delta _{a_j}$
when
![]() $k \to \infty $
, where
$k \to \infty $
, where
![]() $m_j$
is the positive coefficients in (1.8).
$m_j$
is the positive coefficients in (1.8).
(iii) When
![]() $p \in (1,2)$
, (1.13) shows the concentration property of the second term of
$p \in (1,2)$
, (1.13) shows the concentration property of the second term of
![]() $\varepsilon ^{p-2}E_\varepsilon (\tilde {u}_\varepsilon ,G)$
. Moreover, when
$\varepsilon ^{p-2}E_\varepsilon (\tilde {u}_\varepsilon ,G)$
. Moreover, when
![]() $p \in ((\sqrt {17}-1)/2,2)$
, the first term of
$p \in ((\sqrt {17}-1)/2,2)$
, the first term of
![]() $\varepsilon ^{p-2}E_\varepsilon (\tilde {u}_{\varepsilon },G)$
is blow-up if
$\varepsilon ^{p-2}E_\varepsilon (\tilde {u}_{\varepsilon },G)$
is blow-up if
![]() $\tilde {u}_{\varepsilon }$
is radial (cf. [Reference Lei and Xu19, (1.20)]). So the convergence orders of the first and the second terms of
$\tilde {u}_{\varepsilon }$
is radial (cf. [Reference Lei and Xu19, (1.20)]). So the convergence orders of the first and the second terms of
![]() $\varepsilon ^{p-2}E_\varepsilon (\tilde {u}_{\varepsilon },G)$
are different.
$\varepsilon ^{p-2}E_\varepsilon (\tilde {u}_{\varepsilon },G)$
are different.
To prove (1.12), we need the decay result of the gradient of
![]() $|u_\varepsilon |-1$
in arbitrary compact subset of
$|u_\varepsilon |-1$
in arbitrary compact subset of
![]() $G\setminus (\cup _j\{a_j\})$
. For the regularized minimizer
$G\setminus (\cup _j\{a_j\})$
. For the regularized minimizer
![]() $\tilde {u}_\varepsilon $
, it is clear in view of (1.11). For the general minimizer
$\tilde {u}_\varepsilon $
, it is clear in view of (1.11). For the general minimizer
![]() $u_\varepsilon $
it is not easy to be obtained.
$u_\varepsilon $
it is not easy to be obtained.
In Section 4, we will prove the following decay result, which does not only come into play to deduce (1.12), but also has its own meaning of independence.
Theorem 1.3. Let
![]() $p \in (1,2)$
. Assume
$p \in (1,2)$
. Assume
![]() ${u}_\varepsilon $
is a minimizer in W. Then for any compact subset
${u}_\varepsilon $
is a minimizer in W. Then for any compact subset
![]() $K \subset G \setminus \{a_j\}_{j=1}^N$
, there holds
$K \subset G \setminus \{a_j\}_{j=1}^N$
, there holds
 $$ \begin{align} \int_K [|\nabla (1-|u_\varepsilon|)|^p+\frac{1}{\varepsilon^p} (1-|u_\varepsilon|)^2] \to 0, \quad when \ \varepsilon \to 0. \end{align} $$
$$ \begin{align} \int_K [|\nabla (1-|u_\varepsilon|)|^p+\frac{1}{\varepsilon^p} (1-|u_\varepsilon|)^2] \to 0, \quad when \ \varepsilon \to 0. \end{align} $$
Finally, we consider the finite energy solutions of
When
![]() $p=2$
, Brezis et al. [Reference Brezis, Merle and Riviere5] gave a Liouville theorem by an idea of Cazenave. Namely, if
$p=2$
, Brezis et al. [Reference Brezis, Merle and Riviere5] gave a Liouville theorem by an idea of Cazenave. Namely, if
![]() $\nabla u \in L^2(\mathbb {R}^2)$
, then either
$\nabla u \in L^2(\mathbb {R}^2)$
, then either
![]() $u(x) \equiv 0$
, or
$u(x) \equiv 0$
, or
![]() $u(x) \equiv C$
with
$u(x) \equiv C$
with
![]() $|C| =1$
. When
$|C| =1$
. When
![]() $p \neq 2$
, we have the following result which will be proved in Section 6.
$p \neq 2$
, we have the following result which will be proved in Section 6.
Theorem 1.4. Let u be a classical solution of (1.16) with
![]() $p>1$
and
$p>1$
and
![]() $p \neq 2$
. If
$p \neq 2$
. If
then
where C is a constant vector satisfying
![]() $|C| \in \{0,1\}$
.
$|C| \in \{0,1\}$
.
Remark 1.3. The Liouville theorem of the critical points of p-Ginzburg–Landau energy on the Riemannian manifold can be seen in [Reference Chong, Cheng, Dong and Zhang7]. In addition, the p-Ginzburg–Laudan functional on
![]() $\mathbb {R}^2$
was well studied in [Reference Almog, Berlyand, Golovaty and Shafrir1] and [Reference Almog, Berlyand, Golovaty and Shafrir2].
$\mathbb {R}^2$
was well studied in [Reference Almog, Berlyand, Golovaty and Shafrir1] and [Reference Almog, Berlyand, Golovaty and Shafrir2].
2 Preliminaries
Besides (1.7), (1.8), and (1.11), we recall several results of the case
![]() $p \neq 2$
.
$p \neq 2$
.
Assume
![]() $u_{\varepsilon }$
is a minimizer of
$u_{\varepsilon }$
is a minimizer of
![]() $E_{\varepsilon }(u,G)$
in W. Denote the disc with x as center and r as radius by
$E_{\varepsilon }(u,G)$
in W. Denote the disc with x as center and r as radius by
![]() $B(x,r)$
or
$B(x,r)$
or
![]() $B_r(x)$
. Let
$B_r(x)$
. Let
![]() $\lambda , \mu $
be two positive constants which are independent of
$\lambda , \mu $
be two positive constants which are independent of
![]() $\varepsilon $
. If
$\varepsilon $
. If
 $$ \begin{align*}\int_{G\cap B(x^{\varepsilon}, 2\lambda \varepsilon)}(1-|u_{\varepsilon}|^2)^2 \leq \mu\varepsilon^2, \end{align*} $$
$$ \begin{align*}\int_{G\cap B(x^{\varepsilon}, 2\lambda \varepsilon)}(1-|u_{\varepsilon}|^2)^2 \leq \mu\varepsilon^2, \end{align*} $$
then
![]() $B(x^{\varepsilon },\lambda \varepsilon )$
is called a good disc. Otherwise
$B(x^{\varepsilon },\lambda \varepsilon )$
is called a good disc. Otherwise
![]() $B(x^{\varepsilon },\lambda \varepsilon )$
is called a bad disc. When
$B(x^{\varepsilon },\lambda \varepsilon )$
is called a bad disc. When
![]() $p>2$
, [Reference Lei17, Remark 2.7] shows that the zeros of
$p>2$
, [Reference Lei17, Remark 2.7] shows that the zeros of
![]() $u_{\varepsilon }$
are included in finite nonintersecting bad discs
$u_{\varepsilon }$
are included in finite nonintersecting bad discs
![]() $B(x_i^{\varepsilon },h\varepsilon )$
(
$B(x_i^{\varepsilon },h\varepsilon )$
(
![]() $i=1,2,...,N_1$
), where
$i=1,2,...,N_1$
), where
![]() $N_1$
and
$N_1$
and
![]() $h>0$
are independent of
$h>0$
are independent of
![]() $\varepsilon $
. As
$\varepsilon $
. As
![]() $\varepsilon \to 0$
, there exists a subsequence
$\varepsilon \to 0$
, there exists a subsequence
![]() $x_i^{\varepsilon _k}$
of the center
$x_i^{\varepsilon _k}$
of the center
![]() $x_i^{\varepsilon }$
of bad discs such that
$x_i^{\varepsilon }$
of bad discs such that
![]() $x_i^{\varepsilon _k} \to a_i \in \overline {G} (i=1,2,...,N_1).$
Since there may be at least two subsequences that converge to the same point, we denote the limit points by
$x_i^{\varepsilon _k} \to a_i \in \overline {G} (i=1,2,...,N_1).$
Since there may be at least two subsequences that converge to the same point, we denote the limit points by
![]() $a_1,a_2,...,a_N (N \leq N_1)$
. Write
$a_1,a_2,...,a_N (N \leq N_1)$
. Write
![]() $\Lambda _j:=\{i; x_i^{\varepsilon _k} \to a_j$
when
$\Lambda _j:=\{i; x_i^{\varepsilon _k} \to a_j$
when
![]() $k \to \infty \}$
for each j. We can choose
$k \to \infty \}$
for each j. We can choose
![]() $\sigma>0$
suitably small such that
$\sigma>0$
suitably small such that
![]() $B_\sigma (a_j) \subset G$
when
$B_\sigma (a_j) \subset G$
when
![]() $a_j \in G$
, and
$a_j \in G$
, and
![]() $B_\sigma (a_j) \cap B_\sigma (a_m) = \emptyset $
for
$B_\sigma (a_j) \cap B_\sigma (a_m) = \emptyset $
for
![]() $j \neq m$
. When
$j \neq m$
. When
![]() $p \in (1,2)$
, [Reference Lei16, Section 3] also presents the same conclusions above. Clearly, these results still hold for the regularized minimizers.
$p \in (1,2)$
, [Reference Lei16, Section 3] also presents the same conclusions above. Clearly, these results still hold for the regularized minimizers.
2.1 Case of
 $p>2$
$p>2$
We now introduce several results in [Reference Lei17] and [Reference Lei18] which will be used later.
Proposition 2.1. [Reference Lei17, Proposition 2.1]
Let
![]() $u_{\varepsilon }$
be a minimizer of
$u_{\varepsilon }$
be a minimizer of
![]() $E_{\varepsilon }(u,G)$
in W. Then, there exists a constant
$E_{\varepsilon }(u,G)$
in W. Then, there exists a constant
![]() $C>0$
which is independent of
$C>0$
which is independent of
![]() $\varepsilon \in (0,1)$
, such that
$\varepsilon \in (0,1)$
, such that
![]() $E_{\varepsilon }(u_{\varepsilon },G) \leq C\varepsilon ^{2-p}$
.
$E_{\varepsilon }(u_{\varepsilon },G) \leq C\varepsilon ^{2-p}$
.
Proposition 2.2. [Reference Lei17, Proposition 2.2]
There exists a constant
![]() $C_0>0$
which is independent of
$C_0>0$
which is independent of
![]() $\varepsilon \in (0,1)$
, such that for any
$\varepsilon \in (0,1)$
, such that for any
![]() $x,y \in \overline {G}$
,
$x,y \in \overline {G}$
,
Proposition 2.3. [Reference Lei17, Theorem 2.6]
All the zeros of
![]() $u_{\varepsilon }$
are contained in finite, disjointed bad discs
$u_{\varepsilon }$
are contained in finite, disjointed bad discs
![]() $\{B(x_j^{\varepsilon },h\varepsilon );j=1,2,\ldots ,N_1\}$
. In addition,
$\{B(x_j^{\varepsilon },h\varepsilon );j=1,2,\ldots ,N_1\}$
. In addition,
Proposition 2.4. [Reference Lei18, Proposition 2.4]
Write
![]() $d_i:= \deg (u_\varepsilon , \partial B(x_i^{\varepsilon },h\varepsilon ))$
. Then for each i, there exists a subsequence
$d_i:= \deg (u_\varepsilon , \partial B(x_i^{\varepsilon },h\varepsilon ))$
. Then for each i, there exists a subsequence
![]() $\varepsilon _k$
of
$\varepsilon _k$
of
![]() $\varepsilon $
such that
$\varepsilon $
such that
![]() $d_i$
is independent of
$d_i$
is independent of
![]() $\varepsilon _k$
as long as k is sufficiently large.
$\varepsilon _k$
as long as k is sufficiently large.
Proposition 2.5. [Reference Lei17, Theorem 3.1]
Let
![]() $u_\varepsilon $
be a minimizer of
$u_\varepsilon $
be a minimizer of
![]() $E_{\varepsilon }(u,G)$
in W. Then for any compact subset K of
$E_{\varepsilon }(u,G)$
in W. Then for any compact subset K of
![]() $G\setminus \{a_1,a_2,...,a_N\}$
, there exists a constant
$G\setminus \{a_1,a_2,...,a_N\}$
, there exists a constant
![]() $C>0$
which does not depend on
$C>0$
which does not depend on
![]() $\varepsilon $
, such that
$\varepsilon $
, such that
![]() $E_{\varepsilon }(u_{\varepsilon },K)\leq C$
.
$E_{\varepsilon }(u_{\varepsilon },K)\leq C$
.
2.2 Case of
 $p \in (1,2)$
$p \in (1,2)$
In [Reference Lei16], the following free energy functional was studied
 $$ \begin{align*}E_{\varepsilon,\varrho}(u)= \frac{1}{2}\int_{B_1}|\nabla u|^2 +\frac{1}{4\varepsilon^2}\int_{B_1\setminus B_{\varrho}}(1-|u|^2)^2 +\frac{1}{2\varepsilon^2}\int_{B_{\varrho}}|u|^2, \end{align*} $$
$$ \begin{align*}E_{\varepsilon,\varrho}(u)= \frac{1}{2}\int_{B_1}|\nabla u|^2 +\frac{1}{4\varepsilon^2}\int_{B_1\setminus B_{\varrho}}(1-|u|^2)^2 +\frac{1}{2\varepsilon^2}\int_{B_{\varrho}}|u|^2, \end{align*} $$
where
![]() $B_r=\{x \in \mathbb {R}^2;|x|<r\}$
,
$B_r=\{x \in \mathbb {R}^2;|x|<r\}$
,
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\varrho $
are small positive parameters. It is associated with the model of superconductivity with normal impurity inclusion such as superconducting-normal junctions. There are two major differences between
$\varrho $
are small positive parameters. It is associated with the model of superconductivity with normal impurity inclusion such as superconducting-normal junctions. There are two major differences between
![]() $E_{\varepsilon ,\varrho }(u)$
and
$E_{\varepsilon ,\varrho }(u)$
and
![]() $E_\varepsilon (u,G)$
. The former models an heterogenous superconductor and the latter models the homogenous case. In addition, the domain considered in [Reference Lei16] is the unit disk.
$E_\varepsilon (u,G)$
. The former models an heterogenous superconductor and the latter models the homogenous case. In addition, the domain considered in [Reference Lei16] is the unit disk.
In fact, the domain considered in [Reference Lei16] can be replaced by the more general G and the purpose of using
![]() $B_1$
there is for convenience (see also [Reference Ding, Liu and Yu10]). In addition, if
$B_1$
there is for convenience (see also [Reference Ding, Liu and Yu10]). In addition, if
![]() $\varrho =0$
, then
$\varrho =0$
, then
![]() $E_{\varepsilon ,\varrho }(u)$
becomes
$E_{\varepsilon ,\varrho }(u)$
becomes
![]() $E_\varepsilon (u,G)$
, and we can see the results from the corresponding conclusions of Case I (i.e.,
$E_\varepsilon (u,G)$
, and we can see the results from the corresponding conclusions of Case I (i.e.,
![]() $\varrho =O(\varepsilon )$
) in [Reference Lei16], as long as we replace
$\varrho =O(\varepsilon )$
) in [Reference Lei16], as long as we replace
![]() $B_1$
by G and p approaches the dimension
$B_1$
by G and p approaches the dimension
![]() $2$
.
$2$
.
First, by [Reference Lei16, (1–6) in Theorem 1.2], we have
Proposition 2.6. Let
![]() $p\in(1,2),\; u_\varepsilon $
be a minimizer of
$p\in(1,2),\; u_\varepsilon $
be a minimizer of
![]() $E_\varepsilon (u,G)$
in W. Then there exists a constant
$E_\varepsilon (u,G)$
in W. Then there exists a constant
![]() $C>0$
which is independent of
$C>0$
which is independent of
![]() $\varepsilon $
, such that
$\varepsilon $
, such that
![]() $E_\varepsilon (u_\varepsilon ,G)\leq C.$
$E_\varepsilon (u_\varepsilon ,G)\leq C.$
Next, by [Reference Lei16, Theorem 3.1 and Proposition 2.2], we have
Proposition 2.7. Assume that
![]() $p\in(1,2),\;u_{\varepsilon }\in W$
satisfies the (1.4) in the weak sense. Then there is a constant
$p\in(1,2),\;u_{\varepsilon }\in W$
satisfies the (1.4) in the weak sense. Then there is a constant
![]() $\rho _0>0$
, such that for
$\rho _0>0$
, such that for
![]() $\rho \in (0,\rho _0)$
,
$\rho \in (0,\rho _0)$
,
Here,
![]() $G^{\rho \varepsilon }:=\{x \in G; dist(x,\partial G)> \rho \varepsilon \}$
. In addition, for any
$G^{\rho \varepsilon }:=\{x \in G; dist(x,\partial G)> \rho \varepsilon \}$
. In addition, for any
![]() $\rho>0$
, there exists a positive constant
$\rho>0$
, there exists a positive constant
![]() $C_1$
which is independent of
$C_1$
which is independent of
![]() $\varepsilon $
, such that
$\varepsilon $
, such that
By [Reference Lei16, (3-1) in Proposition 3.2], we have
Proposition 2.8. Let
![]() $p\in(1,2),\;u_\varepsilon $
be a minimizer of
$p\in(1,2),\;u_\varepsilon $
be a minimizer of
![]() $E_\varepsilon (u,G)$
in W. Then, there exists a constant
$E_\varepsilon (u,G)$
in W. Then, there exists a constant
![]() $C>0$
which is independent of
$C>0$
which is independent of
![]() $\varepsilon \in (0,\varepsilon _0)$
with
$\varepsilon \in (0,\varepsilon _0)$
with
![]() $\varepsilon _0$
sufficiently small, such that,
$\varepsilon _0$
sufficiently small, such that,
 $$ \begin{align*}\frac{1}{\varepsilon^2} \int_{G}(1-|u_\varepsilon|^2)^2 \leq C. \end{align*} $$
$$ \begin{align*}\frac{1}{\varepsilon^2} \int_{G}(1-|u_\varepsilon|^2)^2 \leq C. \end{align*} $$
By [Reference Lei16, (3-10)], we have
Proposition 2.9. Let
![]() $p\in(1,2),\;u_\varepsilon $
be a minimizer of
$p\in(1,2),\;u_\varepsilon $
be a minimizer of
![]() $E_\varepsilon (u,G)$
in W. For any given
$E_\varepsilon (u,G)$
in W. For any given
![]() $\sigma>0$
, and
$\sigma>0$
, and
![]() $0<\varepsilon \ll \sigma $
, there holds
$0<\varepsilon \ll \sigma $
, there holds
The next proposition shows the reversed Hölder inequality, which is crucial in the proofs of (1.14) and (1.15). We now use the same ideas in [Reference Giaquinta11, Chapter 5] to prove this reversed Hölder inequality.
Proposition 2.10. Assume
![]() $p \in [3/2,2)$
,
$p \in [3/2,2)$
,
![]() $u_{\varepsilon }$
is a minimizer of
$u_{\varepsilon }$
is a minimizer of
![]() $E_{\varepsilon }(u,G)$
in W. Then there exists a constant
$E_{\varepsilon }(u,G)$
in W. Then there exists a constant
![]() $R_0 \in (0,1/2)$
which is independent of
$R_0 \in (0,1/2)$
which is independent of
![]() $\varepsilon $
, such that for any
$\varepsilon $
, such that for any
![]() $B_R \subset G (2R<R_0)$
, we have
$B_R \subset G (2R<R_0)$
, we have
 $$ \begin{align*}\left(\int_{B_R}|\nabla u_{\varepsilon}|^{\tilde{q}}\right)^{1/\tilde{q}} \leq C\left(\int_{B_{2R}}(|\nabla u_{\varepsilon}|^2+1) ^{p/2}\right)^{1/p}, \quad \forall \tilde{q} \in [p,p(1+t)), \end{align*} $$
$$ \begin{align*}\left(\int_{B_R}|\nabla u_{\varepsilon}|^{\tilde{q}}\right)^{1/\tilde{q}} \leq C\left(\int_{B_{2R}}(|\nabla u_{\varepsilon}|^2+1) ^{p/2}\right)^{1/p}, \quad \forall \tilde{q} \in [p,p(1+t)), \end{align*} $$
where
![]() $C>0$
depends on
$C>0$
depends on
![]() $R_0,p,\tilde {q}$
, and
$R_0,p,\tilde {q}$
, and
![]() $t \in (0,1/2)$
only depends on
$t \in (0,1/2)$
only depends on
![]() $R_0$
.
$R_0$
.
Proof .
Step 1. Let
![]() $Q \subset \mathbb {R}^2$
be a square and
$Q \subset \mathbb {R}^2$
be a square and
![]() $m \in [3/2,2)$
. Suppose
$m \in [3/2,2)$
. Suppose
 $$ \begin{align} \frac{1}{|Q_R|}\int_{Q_R(x_0)}g^m \leq b \left( \frac{1}{|Q_{2R}|} \int_{Q_{2R}(x_0)}g \right)^m \end{align} $$
$$ \begin{align} \frac{1}{|Q_R|}\int_{Q_R(x_0)}g^m \leq b \left( \frac{1}{|Q_{2R}|} \int_{Q_{2R}(x_0)}g \right)^m \end{align} $$
for each
![]() $x_0 \in Q$
and each
$x_0 \in Q$
and each
![]() $0<R<\frac {1}{3}\min \{dist(x_0,\partial Q), R_0\}$
, where
$0<R<\frac {1}{3}\min \{dist(x_0,\partial Q), R_0\}$
, where
![]() $b>1$
and
$b>1$
and
![]() $R_0>0$
are absolute constants. By the same argument of [Reference Giaquinta11, proof of Theorem 1.2], we claim that
$R_0>0$
are absolute constants. By the same argument of [Reference Giaquinta11, proof of Theorem 1.2], we claim that
![]() $g \in L_{loc}^q(Q)$
for
$g \in L_{loc}^q(Q)$
for
![]() $q \in [m,m(1+t))$
and
$q \in [m,m(1+t))$
and
 $$ \begin{align} \left(\frac{1}{|Q_R|}\int_{Q_R}g^q \right)^{\frac{1}{q}} \leq C\left(\frac{1}{|Q_{2R}|}\int_{Q_{2R}}g^m\right)^{\frac{1}{m}} \end{align} $$
$$ \begin{align} \left(\frac{1}{|Q_R|}\int_{Q_R}g^q \right)^{\frac{1}{q}} \leq C\left(\frac{1}{|Q_{2R}|}\int_{Q_{2R}}g^m\right)^{\frac{1}{m}} \end{align} $$
for
![]() $Q_{2R} \subset Q$
,
$Q_{2R} \subset Q$
,
![]() $0<R<R_0$
, where t is a positive constant only depending on b, and
$0<R<R_0$
, where t is a positive constant only depending on b, and
![]() $C>0$
depends on
$C>0$
depends on
![]() $b,m,q$
. In particular, C is blowing up when q approaches
$b,m,q$
. In particular, C is blowing up when q approaches
![]() $m(1+t)$
.
$m(1+t)$
.
In fact, when we check [Reference Giaquinta and Modica12, Proposition 5.1], (2.3) implies
![]() $\theta =0$
and
$\theta =0$
and
![]() $f(x) \equiv 0$
. Set
$f(x) \equiv 0$
. Set
As in [Reference Giaquinta and Modica12, proof of (5.4)], by the Calderon–Zygmund subdivision argument and an iteration, we still obtain
 $$ \begin{align} \int_{E(\Phi,T)}\Phi^m \leq aT^{m-1}\int_{E(\Phi,T)}\Phi \end{align} $$
$$ \begin{align} \int_{E(\Phi,T)}\Phi^m \leq aT^{m-1}\int_{E(\Phi,T)}\Phi \end{align} $$
for
![]() $T \geq 1$
. According to the result of [Reference Giaquinta and Modica12] (see line 7 in page 167), a in (2.5) can be chosen as
$T \geq 1$
. According to the result of [Reference Giaquinta and Modica12] (see line 7 in page 167), a in (2.5) can be chosen as
 $$ \begin{align*} a=b\left(\frac{5m}{m-1}\right)^{m-1}(30^2\cdot 5m+2^2). \end{align*} $$
$$ \begin{align*} a=b\left(\frac{5m}{m-1}\right)^{m-1}(30^2\cdot 5m+2^2). \end{align*} $$
In view of
![]() $m \in [3/2,2)$
, a can be bounded by an absolute constant
$m \in [3/2,2)$
, a can be bounded by an absolute constant
![]() $\tilde {a}$
(which is independent of m). Now, (2.5) with
$\tilde {a}$
(which is independent of m). Now, (2.5) with
![]() $a=\tilde {a}$
is (1.6) in Chapter 5 of [Reference Giaquinta11], which implies that the conditions of [Reference Giaquinta11, Lemma 1.2 in Chapter 5] are satisfied if we write
$a=\tilde {a}$
is (1.6) in Chapter 5 of [Reference Giaquinta11], which implies that the conditions of [Reference Giaquinta11, Lemma 1.2 in Chapter 5] are satisfied if we write
![]() $h(T)=\int _{E(\Phi ,T)}\Phi $
and
$h(T)=\int _{E(\Phi ,T)}\Phi $
and
![]() $H(T) \equiv 0$
. By applying Lemma 1.2 in Chapter 5 of [Reference Giaquinta11], we can deduce (2.4) for
$H(T) \equiv 0$
. By applying Lemma 1.2 in Chapter 5 of [Reference Giaquinta11], we can deduce (2.4) for
![]() $q \in [m,\frac {\tilde {a}}{\tilde {a}-1}m)$
. Set
$q \in [m,\frac {\tilde {a}}{\tilde {a}-1}m)$
. Set
![]() $\frac {\tilde {a}}{\tilde {a}-1}=1+t$
, then
$\frac {\tilde {a}}{\tilde {a}-1}=1+t$
, then
This implies that t is independent of m. In addition, C in (2.4) depends on
![]() $m[\tilde {a}m- (\tilde {a}-1)q]^{-1}$
, which implies that C is blowing up when q approaches
$m[\tilde {a}m- (\tilde {a}-1)q]^{-1}$
, which implies that C is blowing up when q approaches
![]() $m(1+t)$
.
$m(1+t)$
.
Step 2. Let
![]() $y=x\varepsilon ^{-1}$
in
$y=x\varepsilon ^{-1}$
in
![]() $E_{\varepsilon }(u,G)$
and denote
$E_{\varepsilon }(u,G)$
and denote
![]() $ v_{\varepsilon }(y)=u_{\varepsilon }(x)$
,
$ v_{\varepsilon }(y)=u_{\varepsilon }(x)$
,
![]() $G_{\varepsilon }=\{y=x\varepsilon ^{-1};x \in G\}$
. Then
$G_{\varepsilon }=\{y=x\varepsilon ^{-1};x \in G\}$
. Then
 $$ \begin{align*}\begin{array}{ll} E_{\varepsilon}(u_{\varepsilon},G) &\displaystyle =\varepsilon^{2-p}\left(\frac{1}{p} \int_{G_{\varepsilon}} |\nabla v_{\varepsilon}|^p dy+ \frac{1}{4} \int_{G_{\varepsilon}}(1-|v_{\varepsilon}|^2)^2dy \right)\\[3mm] & :=\varepsilon^{2-p}E(v_{\varepsilon},G_{\varepsilon}). \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ll} E_{\varepsilon}(u_{\varepsilon},G) &\displaystyle =\varepsilon^{2-p}\left(\frac{1}{p} \int_{G_{\varepsilon}} |\nabla v_{\varepsilon}|^p dy+ \frac{1}{4} \int_{G_{\varepsilon}}(1-|v_{\varepsilon}|^2)^2dy \right)\\[3mm] & :=\varepsilon^{2-p}E(v_{\varepsilon},G_{\varepsilon}). \end{array} \end{align*} $$
It is clear that
![]() $v_{\varepsilon }$
is also a minimizer of
$v_{\varepsilon }$
is also a minimizer of
![]() $E(v,G_{\varepsilon })$
.
$E(v,G_{\varepsilon })$
.
Let
![]() $m=(p+2)/2$
, then
$m=(p+2)/2$
, then
![]() $m \in [3/2,2)$
when
$m \in [3/2,2)$
when
![]() $p \in [3/2,2)$
. Clearly,
$p \in [3/2,2)$
. Clearly,
![]() $(A+B)^m \leq (2\max \{A,B\})^m \leq 2^m(A^m+B^m)$
as long as
$(A+B)^m \leq (2\max \{A,B\})^m \leq 2^m(A^m+B^m)$
as long as
![]() $A,B$
are positive. Checking the proof of Theorem 3.1 in Chapter 5 of [Reference Giaquinta11], we find that
$A,B$
are positive. Checking the proof of Theorem 3.1 in Chapter 5 of [Reference Giaquinta11], we find that
![]() $c(m)$
in lines 13–14 of page 160 satisfies
$c(m)$
in lines 13–14 of page 160 satisfies
![]() $c(m) = 2^m \leq 4$
for
$c(m) = 2^m \leq 4$
for
![]() $p \in [3/2,2)$
. Therefore,
$p \in [3/2,2)$
. Therefore,
![]() $c_4$
in (3.5) (see line 5 of page 161) is independent of p after an iteration (by Lemma 3.1). Next, the Sobolev–Poincare inequality shows that
$c_4$
in (3.5) (see line 5 of page 161) is independent of p after an iteration (by Lemma 3.1). Next, the Sobolev–Poincare inequality shows that
![]() $c_5$
can be chosen as a suitably large absolute constant in view of
$c_5$
can be chosen as a suitably large absolute constant in view of
![]() $p \in [3/2,2)$
. Thus, we also derive a condition which satisfies (2.3) with
$p \in [3/2,2)$
. Thus, we also derive a condition which satisfies (2.3) with
![]() $b=c_5$
. Using the reversed Hölder inequality (2.4) with
$b=c_5$
. Using the reversed Hölder inequality (2.4) with
![]() $g=(\varepsilon +|\nabla v_\varepsilon |)^{\frac {2p}{2+p}}$
, we know that there exist constants
$g=(\varepsilon +|\nabla v_\varepsilon |)^{\frac {2p}{2+p}}$
, we know that there exist constants
![]() $t, R_0 \in (0,1/2)$
and
$t, R_0 \in (0,1/2)$
and
![]() $C>0$
, such that for any
$C>0$
, such that for any
![]() $B_R \subset B_{R_0/2} \subset G$
and
$B_R \subset B_{R_0/2} \subset G$
and
![]() $q \in [m,m(1+t))$
, the inequality
$q \in [m,m(1+t))$
, the inequality
 $$ \begin{align*}&\displaystyle \left(\frac{1}{|B_{R/\varepsilon}|} \int_{B_{R/\varepsilon}} |\nabla v_{\varepsilon}|^{\frac{2pq}{2+p}}dy \right)^{1/q}\\&\quad\displaystyle \leq \left(\frac{1}{|B_{R/\varepsilon}|} \int_{B_{R/\varepsilon}} (|\nabla v_{\varepsilon}|+\varepsilon)^{\frac{2pq}{2+p}}dy\right)^{1/q}\\&\quad\displaystyle \leq C\left(\frac{1}{|B_{2R/\varepsilon}|} \int_{B_{2R/\varepsilon}} (|\nabla v_{\varepsilon}|+ \varepsilon)^{p}dy\right)^{\frac{2}{p+2}}\end{align*} $$
$$ \begin{align*}&\displaystyle \left(\frac{1}{|B_{R/\varepsilon}|} \int_{B_{R/\varepsilon}} |\nabla v_{\varepsilon}|^{\frac{2pq}{2+p}}dy \right)^{1/q}\\&\quad\displaystyle \leq \left(\frac{1}{|B_{R/\varepsilon}|} \int_{B_{R/\varepsilon}} (|\nabla v_{\varepsilon}|+\varepsilon)^{\frac{2pq}{2+p}}dy\right)^{1/q}\\&\quad\displaystyle \leq C\left(\frac{1}{|B_{2R/\varepsilon}|} \int_{B_{2R/\varepsilon}} (|\nabla v_{\varepsilon}|+ \varepsilon)^{p}dy\right)^{\frac{2}{p+2}}\end{align*} $$
holds, where
![]() $B_{R/\varepsilon }=\{y=x\varepsilon ^{-1};x \in B_R\}$
. Letting
$B_{R/\varepsilon }=\{y=x\varepsilon ^{-1};x \in B_R\}$
. Letting
![]() $x=y\varepsilon $
and multiplying by
$x=y\varepsilon $
and multiplying by
![]() $\varepsilon ^{-\frac {2p}{p+2}}$
, we obtain
$\varepsilon ^{-\frac {2p}{p+2}}$
, we obtain
 $$ \begin{align*}\left(\int_{B_R}|\nabla u_{\varepsilon}|^{\frac{2pq}{2+p}}dx\right)^{\frac{p+2}{2pq}} \leq C\left(\int_{B_{2R}} (|\nabla u_{\varepsilon}|^2+1)^{p}dx\right)^{1/p}. \end{align*} $$
$$ \begin{align*}\left(\int_{B_R}|\nabla u_{\varepsilon}|^{\frac{2pq}{2+p}}dx\right)^{\frac{p+2}{2pq}} \leq C\left(\int_{B_{2R}} (|\nabla u_{\varepsilon}|^2+1)^{p}dx\right)^{1/p}. \end{align*} $$
Let
![]() $\tilde {q}=\frac {2pq}{p+2}$
. Noticing
$\tilde {q}=\frac {2pq}{p+2}$
. Noticing
![]() $q \in [m,m(1+t))$
, we can see
$q \in [m,m(1+t))$
, we can see
![]() $\tilde {q} \in [p,p(1+t))$
. And hence the proposition holds.
$\tilde {q} \in [p,p(1+t))$
. And hence the proposition holds.
Clearly, the results above (Propositions 2.6–2.10) still hold for the regularized minimizers.
By [Reference Lei16, Proposition 5.3], we have
Proposition 2.11. Assume
![]() $p \in (1, 2)$
approaches the dimension
$p \in (1, 2)$
approaches the dimension
![]() $2$
, and
$2$
, and
![]() $\tilde {u}_\varepsilon $
is a regularized minimizer. Then, for any compact subset
$\tilde {u}_\varepsilon $
is a regularized minimizer. Then, for any compact subset
![]() $K \subset G \setminus (\cup _{j=1}^N\{a_j\})$
, there exists a positive constant
$K \subset G \setminus (\cup _{j=1}^N\{a_j\})$
, there exists a positive constant
![]() $C=C(K)$
which is independent of
$C=C(K)$
which is independent of
![]() $\varepsilon $
, such that
$\varepsilon $
, such that
3 Proof of Theorem 1.1
In this section, we assume
![]() $p> 2$
, and
$p> 2$
, and
![]() $u_\varepsilon $
is the minimizer of
$u_\varepsilon $
is the minimizer of
![]() $E_\varepsilon (u,G)$
in W.
$E_\varepsilon (u,G)$
in W.
Proof of (1.10).
Noting
![]() $\alpha \geq 2-\frac {4}{p}$
, using (1.5), the Hölder inequality and Proposition 2.1, we deduce that
$\alpha \geq 2-\frac {4}{p}$
, using (1.5), the Hölder inequality and Proposition 2.1, we deduce that
 $$ \begin{align*}&\displaystyle\int_{G} |\nabla u_\varepsilon|^2(1-|u_\varepsilon|^2)^{\alpha}\\&\quad\leq C\displaystyle\int_{G} |\nabla u_\varepsilon|^2(1-|u_\varepsilon|^2)^{2-\frac{4}{p}}\\&\quad\leq C \left(\displaystyle\int_{G} (1-|u_\varepsilon|^2)^2\right)^{1-\frac{2}{p}} \left(\displaystyle\int_{G} |\nabla u_\varepsilon|^p\right)^{\frac{2}{p}}\\&\quad\leq C\varepsilon^{2(1-\frac{2}{p})+\frac{2}{p}(2-p)} = C.\end{align*} $$
$$ \begin{align*}&\displaystyle\int_{G} |\nabla u_\varepsilon|^2(1-|u_\varepsilon|^2)^{\alpha}\\&\quad\leq C\displaystyle\int_{G} |\nabla u_\varepsilon|^2(1-|u_\varepsilon|^2)^{2-\frac{4}{p}}\\&\quad\leq C \left(\displaystyle\int_{G} (1-|u_\varepsilon|^2)^2\right)^{1-\frac{2}{p}} \left(\displaystyle\int_{G} |\nabla u_\varepsilon|^p\right)^{\frac{2}{p}}\\&\quad\leq C\varepsilon^{2(1-\frac{2}{p})+\frac{2}{p}(2-p)} = C.\end{align*} $$
Namely,
![]() $|\nabla u_\varepsilon |^2(1-|u_\varepsilon |^2)^{\alpha }$
is bounded in
$|\nabla u_\varepsilon |^2(1-|u_\varepsilon |^2)^{\alpha }$
is bounded in
![]() $L^1(G)$
. Thus, there exists a Radon measure
$L^1(G)$
. Thus, there exists a Radon measure
![]() $\omega _1$
such that
$\omega _1$
such that
Next, using the Hölder inequality and Proposition 2.5, we see that as
![]() $\varepsilon \to 0$
,
$\varepsilon \to 0$
,
 $$ \begin{align}\begin{split}&\displaystyle \int_{G\setminus \cup_{j=1}^N B(a_j,\sigma)}|\nabla u_\varepsilon|^2(1-|u_\varepsilon|^2)^{\alpha}\\&\quad \leq \left[\displaystyle\int_{G\setminus \cup_j B(a_j,\sigma)}|\nabla u_\varepsilon|^p\right]^{\frac{2}{p}} \\&\qquad \cdot\left[\displaystyle\int_{G\setminus \cup_jB(a_j,\sigma)} (1-|u_\varepsilon|^2)^{\frac{p\alpha}{p-2}} \right]^{\frac{p-2}{p}} \to 0.\end{split}\end{align} $$
$$ \begin{align}\begin{split}&\displaystyle \int_{G\setminus \cup_{j=1}^N B(a_j,\sigma)}|\nabla u_\varepsilon|^2(1-|u_\varepsilon|^2)^{\alpha}\\&\quad \leq \left[\displaystyle\int_{G\setminus \cup_j B(a_j,\sigma)}|\nabla u_\varepsilon|^p\right]^{\frac{2}{p}} \\&\qquad \cdot\left[\displaystyle\int_{G\setminus \cup_jB(a_j,\sigma)} (1-|u_\varepsilon|^2)^{\frac{p\alpha}{p-2}} \right]^{\frac{p-2}{p}} \to 0.\end{split}\end{align} $$
Thus,
![]() $supp(\omega _1) \subset \{a_j\}_{j=1}^N$
. Therefore, we can find
$supp(\omega _1) \subset \{a_j\}_{j=1}^N$
. Therefore, we can find
![]() $L_j\geq 0$
such that
$L_j\geq 0$
such that
 $$ \begin{align*}\omega_1=\sum_{j=1}^N L_j\delta_{a_j}. \end{align*} $$
$$ \begin{align*}\omega_1=\sum_{j=1}^N L_j\delta_{a_j}. \end{align*} $$
We claim
![]() $L_j>0$
for each j (and hence
$L_j>0$
for each j (and hence
![]() $supp(\omega _1) = \{a_j\}_{j=1}^N$
). For convenience, we here drop k from
$supp(\omega _1) = \{a_j\}_{j=1}^N$
). For convenience, we here drop k from
![]() $\varepsilon _k$
.
$\varepsilon _k$
.
Noting
![]() $B_{h\varepsilon }(x_i)$
contains zeros of
$B_{h\varepsilon }(x_i)$
contains zeros of
![]() $u_\varepsilon $
, by Propositions 2.3 we have
$u_\varepsilon $
, by Propositions 2.3 we have
as long as
![]() $h\varepsilon $
is suitably small. For each
$h\varepsilon $
is suitably small. For each
![]() $x_1 \in \partial B_{h\varepsilon }(x_i)$
, by Proposition 2.2, we get
$x_1 \in \partial B_{h\varepsilon }(x_i)$
, by Proposition 2.2, we get
Here,
![]() $\hat {l}:=\min \{(8C_0)^{\frac {p}{2-p}},h\}$
. Therefore,
$\hat {l}:=\min \{(8C_0)^{\frac {p}{2-p}},h\}$
. Therefore,
As in [Reference Hong15, Theorem 3.9], by (3.2) we can write
and hence
Thus, by the Hölder inequality, there holds
 $$ \begin{align*}&\displaystyle \int_{B_{h\varepsilon}(x_i) \setminus B_{(h-\hat{l}/2)\varepsilon}(x_i)} (1-|u_\varepsilon|^2)^{\alpha}|\nabla u_\varepsilon|^2 \\&\quad\displaystyle \geq \left(1-\frac{7}{8}\right)^{\alpha} \int_{B_{h\varepsilon}(x_i) \setminus B_{(h-\hat{l}/2)\varepsilon}(x_i)} |u_\varepsilon|^2 r^{-2}|\nabla _{\tau}\phi(r,\tau)|^2 \\&\quad\displaystyle \geq \left(\frac{1}{8}\right)^\alpha \left(\frac{3}{8}\right)^2 \int_{(h-\hat{l}/2)\varepsilon}^{h\varepsilon} \left(\int_{S^1}|\nabla_{\tau}\phi|^2ds\right)\frac{dr}{r}\\&\quad\displaystyle \geq \left(\frac{1}{8}\right)^\alpha \left(\frac{3}{8}\right)^2 \int_{(h-\hat{l}/2)\varepsilon}^{h\varepsilon}\frac{1}{2\pi} \left(\int_{S^1}|\nabla_{\tau}\phi|ds\right)^2\frac{dr}{r}.\end{align*} $$
$$ \begin{align*}&\displaystyle \int_{B_{h\varepsilon}(x_i) \setminus B_{(h-\hat{l}/2)\varepsilon}(x_i)} (1-|u_\varepsilon|^2)^{\alpha}|\nabla u_\varepsilon|^2 \\&\quad\displaystyle \geq \left(1-\frac{7}{8}\right)^{\alpha} \int_{B_{h\varepsilon}(x_i) \setminus B_{(h-\hat{l}/2)\varepsilon}(x_i)} |u_\varepsilon|^2 r^{-2}|\nabla _{\tau}\phi(r,\tau)|^2 \\&\quad\displaystyle \geq \left(\frac{1}{8}\right)^\alpha \left(\frac{3}{8}\right)^2 \int_{(h-\hat{l}/2)\varepsilon}^{h\varepsilon} \left(\int_{S^1}|\nabla_{\tau}\phi|^2ds\right)\frac{dr}{r}\\&\quad\displaystyle \geq \left(\frac{1}{8}\right)^\alpha \left(\frac{3}{8}\right)^2 \int_{(h-\hat{l}/2)\varepsilon}^{h\varepsilon}\frac{1}{2\pi} \left(\int_{S^1}|\nabla_{\tau}\phi|ds\right)^2\frac{dr}{r}.\end{align*} $$
Theorem 8.2 in [Reference Brezis, Coron and Lieb4] shows that
 $$ \begin{align*}\int_{S^1}|\nabla_{\tau}\phi|ds \geq 2\pi|d_i|, \end{align*} $$
$$ \begin{align*}\int_{S^1}|\nabla_{\tau}\phi|ds \geq 2\pi|d_i|, \end{align*} $$
where
![]() $d_i=\deg (u_\varepsilon ,\partial B_{h\varepsilon }(x_i))$
is independent of
$d_i=\deg (u_\varepsilon ,\partial B_{h\varepsilon }(x_i))$
is independent of
![]() $\varepsilon $
(see Proposition 2.4). Therefore,
$\varepsilon $
(see Proposition 2.4). Therefore,
 $$ \begin{align*}\int_{B_{h\varepsilon}(x_i) \setminus B_{(h-\hat{l}/2)\varepsilon}(x_i)} (1-|u_\varepsilon|^2)^{\alpha}|\nabla u_\varepsilon|^2 \geq \left(\frac{1}{8}\right)^\alpha \left(\frac{3}{8}\right)^2 (2\pi d_i^2) \cdot \left(\log \frac{h}{h-\hat{l}/2}\right). \end{align*} $$
$$ \begin{align*}\int_{B_{h\varepsilon}(x_i) \setminus B_{(h-\hat{l}/2)\varepsilon}(x_i)} (1-|u_\varepsilon|^2)^{\alpha}|\nabla u_\varepsilon|^2 \geq \left(\frac{1}{8}\right)^\alpha \left(\frac{3}{8}\right)^2 (2\pi d_i^2) \cdot \left(\log \frac{h}{h-\hat{l}/2}\right). \end{align*} $$
This implies
![]() $L_j>0$
, and hence (1.10) is proved.
$L_j>0$
, and hence (1.10) is proved.
Proof of (1.9).
Denote
![]() $u_\varepsilon $
by u. Clearly, by the Cauchy inequality,
$u_\varepsilon $
by u. Clearly, by the Cauchy inequality,
By Proposition 2.1, we obtain that for each j,
 $$ \begin{align} \varepsilon^{p-2}\int_{G\cap B(a_j,\sigma)}|\det(\nabla u)|^{p/2} \leq \frac{\varepsilon^{p-2}}{2}\int_{G}|\nabla u|^p \leq C. \end{align} $$
$$ \begin{align} \varepsilon^{p-2}\int_{G\cap B(a_j,\sigma)}|\det(\nabla u)|^{p/2} \leq \frac{\varepsilon^{p-2}}{2}\int_{G}|\nabla u|^p \leq C. \end{align} $$
Using Proposition 2.5, we get
 $$ \begin{align} \varepsilon^{p-2}\int_{G \setminus \cup_j B(a_j,\sigma)}|\det(\nabla u)|^{p/2} \leq \frac{\varepsilon^{p-2}}{2}\int_{G \setminus \cup_j B(a_j,\sigma)}|\nabla u|^p \leq C\varepsilon^{p-2}. \end{align} $$
$$ \begin{align} \varepsilon^{p-2}\int_{G \setminus \cup_j B(a_j,\sigma)}|\det(\nabla u)|^{p/2} \leq \frac{\varepsilon^{p-2}}{2}\int_{G \setminus \cup_j B(a_j,\sigma)}|\nabla u|^p \leq C\varepsilon^{p-2}. \end{align} $$
Combining (3.4) and (3.5), we see that
![]() $\varepsilon ^{p-2}|\det (\nabla u)|^{p/2}$
is bounded in
$\varepsilon ^{p-2}|\det (\nabla u)|^{p/2}$
is bounded in
![]() $L^1(G)$
. Thus, there exists a Radon measure
$L^1(G)$
. Thus, there exists a Radon measure
![]() $\omega _2$
such that
$\omega _2$
such that
By virtue of (3.5),
![]() $supp(\omega _2) \subset \{a_j\}_{j=1}^N$
. Thus, we can find
$supp(\omega _2) \subset \{a_j\}_{j=1}^N$
. Thus, we can find
![]() $P_j\geq 0$
such that
$P_j\geq 0$
such that
 $$ \begin{align*}\omega_2=\sum_{j=1}^N P_j\delta_{a_j}. \end{align*} $$
$$ \begin{align*}\omega_2=\sum_{j=1}^N P_j\delta_{a_j}. \end{align*} $$
Equation (1.9) is proved.
4 Convergence rate of
 $|u_\varepsilon |-1$
when
$|u_\varepsilon |-1$
when
 $p \in (1,2)$
$p \in (1,2)$
In this section, we consider the case of
![]() $p \in (1,2)$
. Proposition 2.8 implies that
$p \in (1,2)$
. Proposition 2.8 implies that
![]() $|{u}_{\varepsilon }|-1$
tends to zero and the decay rate is presented. Here, we will give a decay rate of the gradient of
$|{u}_{\varepsilon }|-1$
tends to zero and the decay rate is presented. Here, we will give a decay rate of the gradient of
![]() $|{u}_{\varepsilon }|-1$
.
$|{u}_{\varepsilon }|-1$
.
Proof of Theorem 1.3
Proof.
Step 1. Let
![]() $R>0$
be a small constant such that
$R>0$
be a small constant such that
![]() $B(x,2R) \subset \subset G\setminus \cup _{i=1}^N\{a_i\}$
. Applying (1.5) and Proposition 2.9, we have
$B(x,2R) \subset \subset G\setminus \cup _{i=1}^N\{a_i\}$
. Applying (1.5) and Proposition 2.9, we have
By the integral mean value theorem and Proposition 2.6, there is
![]() $r \in [R,2R]$
such that
$r \in [R,2R]$
such that
 $$ \begin{align} \int_{\partial B(x,r)}|\nabla |{u}_\varepsilon||^pd\xi +\frac{1}{\varepsilon^p} \int_{\partial B(x,r)}(1-|{u}_{\varepsilon}|^2)^2d\xi \leq C \end{align} $$
$$ \begin{align} \int_{\partial B(x,r)}|\nabla |{u}_\varepsilon||^pd\xi +\frac{1}{\varepsilon^p} \int_{\partial B(x,r)}(1-|{u}_{\varepsilon}|^2)^2d\xi \leq C \end{align} $$
with
![]() $C=C(r)>0$
independent of
$C=C(r)>0$
independent of
![]() $\varepsilon $
. Denote
$\varepsilon $
. Denote
![]() $B(x,r)$
by B. If
$B(x,r)$
by B. If
![]() $\rho _1$
is a minimizer of the functional
$\rho _1$
is a minimizer of the functional
 $$ \begin{align*}E(\rho,B)=\frac{1}{p} \int_B(|\nabla \rho|^2+1)^{p/2} +\frac{1}{2\varepsilon^p} \int_B(1-\rho)^2 \end{align*} $$
$$ \begin{align*}E(\rho,B)=\frac{1}{p} \int_B(|\nabla \rho|^2+1)^{p/2} +\frac{1}{2\varepsilon^p} \int_B(1-\rho)^2 \end{align*} $$
in
![]() $W_{|{u}_{\varepsilon }|}^{1,p}(B,\mathbb {R}^+\cup \{0\})$
, then it solves
$W_{|{u}_{\varepsilon }|}^{1,p}(B,\mathbb {R}^+\cup \{0\})$
, then it solves
By the maximum principle, it follows from (4.1) that
Applying Proposition 2.6 we see easily that
Step 2. Multiplying (4.3) with
![]() $\rho =\rho _1$
by
$\rho =\rho _1$
by
![]() $(\nu \cdot \nabla \rho _1)$
, we have
$(\nu \cdot \nabla \rho _1)$
, we have
 $$ \begin{align} \begin{array}{ll} -\displaystyle\int_{\partial B}v^{(p-2)/2}|\partial_\nu\rho_1|^2d\xi &+\displaystyle\int_Bv^{(p-2)/2}\nabla \rho_1 \cdot \nabla (\nu \cdot \nabla \rho_1)\\[3mm] &=\displaystyle\frac{1}{\varepsilon^p} \int_B(1-\rho_1)(\nu \cdot \nabla \rho_1), \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll} -\displaystyle\int_{\partial B}v^{(p-2)/2}|\partial_\nu\rho_1|^2d\xi &+\displaystyle\int_Bv^{(p-2)/2}\nabla \rho_1 \cdot \nabla (\nu \cdot \nabla \rho_1)\\[3mm] &=\displaystyle\frac{1}{\varepsilon^p} \int_B(1-\rho_1)(\nu \cdot \nabla \rho_1), \end{array} \end{align} $$
where
![]() $\nu $
denotes the unit outside norm vector on
$\nu $
denotes the unit outside norm vector on
![]() $\partial B$
and
$\partial B$
and
![]() $v=|\nabla \rho _1|^2+1$
. Integrating by parts yields
$v=|\nabla \rho _1|^2+1$
. Integrating by parts yields
 $$ \begin{align} \begin{split}& \displaystyle\int_Bv^{(p-2)/2}\nabla \rho_1 \cdot \nabla (\nu \cdot \nabla \rho_1)\\&\quad= \displaystyle\int_Bv^{(p-2)/2}|\nabla \rho_1|^2 +\frac{1}{p}\int_B \nu \cdot \nabla (v^{p/2})\\&\quad= \displaystyle\int_Bv^{(p-2)/2}|\nabla \rho_1|^2 +\frac{1}{p}\int_{\partial B}v^{p/2}d\xi -\frac{1}{p}\int_B v^{p/2} ({\textrm{div}} \nu), \end{split} \end{align} $$
$$ \begin{align} \begin{split}& \displaystyle\int_Bv^{(p-2)/2}\nabla \rho_1 \cdot \nabla (\nu \cdot \nabla \rho_1)\\&\quad= \displaystyle\int_Bv^{(p-2)/2}|\nabla \rho_1|^2 +\frac{1}{p}\int_B \nu \cdot \nabla (v^{p/2})\\&\quad= \displaystyle\int_Bv^{(p-2)/2}|\nabla \rho_1|^2 +\frac{1}{p}\int_{\partial B}v^{p/2}d\xi -\frac{1}{p}\int_B v^{p/2} ({\textrm{div}} \nu), \end{split} \end{align} $$
and
 $$ \begin{align*}\displaystyle\frac{1}{\varepsilon^p} \int_B(1-\rho_1)(\nu \cdot \nabla \rho_1) = \frac{1}{2\varepsilon^p} \int_B(1-\rho_1)^2({\textrm{div}}\nu) -\frac{1}{2\varepsilon^p} \int_{\partial B}(1-\rho_1)^2d\xi. \end{align*} $$
$$ \begin{align*}\displaystyle\frac{1}{\varepsilon^p} \int_B(1-\rho_1)(\nu \cdot \nabla \rho_1) = \frac{1}{2\varepsilon^p} \int_B(1-\rho_1)^2({\textrm{div}}\nu) -\frac{1}{2\varepsilon^p} \int_{\partial B}(1-\rho_1)^2d\xi. \end{align*} $$
Substitute this result and (4.8) into (4.7). Noting div
![]() $\nu =r^{-1}>0$
, we can use (4.5), (4.6), (4.4), and (4.2) to obtain
$\nu =r^{-1}>0$
, we can use (4.5), (4.6), (4.4), and (4.2) to obtain
 $$ \begin{align} \int_{\partial B}v^{(p-2)/2}|\partial_\nu\rho_1|^2d\xi \leq C+\frac{1}{p}\int_{\partial B}v^{p/2}d\xi. \end{align} $$
$$ \begin{align} \int_{\partial B}v^{(p-2)/2}|\partial_\nu\rho_1|^2d\xi \leq C+\frac{1}{p}\int_{\partial B}v^{p/2}d\xi. \end{align} $$
Step 3. By the Jensen inequality
![]() $(1+a^2+b^2)^{1/2} \leq 1+|a|+|b|$
and (4.4), there holds
$(1+a^2+b^2)^{1/2} \leq 1+|a|+|b|$
and (4.4), there holds
 $$ \begin{align*}\int_{\partial B} v^{p/2}d\xi \leq \int_{\partial B}v^{(p-1)/2} [(1+|\partial_\tau |u_\varepsilon||) +|\partial_\nu \rho_1|]d\xi, \end{align*} $$
$$ \begin{align*}\int_{\partial B} v^{p/2}d\xi \leq \int_{\partial B}v^{(p-1)/2} [(1+|\partial_\tau |u_\varepsilon||) +|\partial_\nu \rho_1|]d\xi, \end{align*} $$
where
![]() $\tau $
denotes the unit tangent vector on
$\tau $
denotes the unit tangent vector on
![]() $\partial B$
. Using the Hölder inequality and (4.2), we deduce from the result above that
$\partial B$
. Using the Hölder inequality and (4.2), we deduce from the result above that
 $$ \begin{align*}\int_{\partial B} v^{p/2}d\xi \leq C\left(\int_{\partial B} v^{\frac{p}{2}}d\xi\right)^{\frac{p-1}{p}} +\left(\int_{\partial B}v^{\frac{p-2}{2}}|\partial_\nu \rho_1|^2d\xi\right)^{\frac{1}{2}} \left(\int_{\partial B} v^{\frac{p}{2}}d\xi\right)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*}\int_{\partial B} v^{p/2}d\xi \leq C\left(\int_{\partial B} v^{\frac{p}{2}}d\xi\right)^{\frac{p-1}{p}} +\left(\int_{\partial B}v^{\frac{p-2}{2}}|\partial_\nu \rho_1|^2d\xi\right)^{\frac{1}{2}} \left(\int_{\partial B} v^{\frac{p}{2}}d\xi\right)^{\frac{1}{2}}. \end{align*} $$
Inserting (4.9) into this result and using the Young inequality, we obtain that for any
![]() $\delta \in (0,1)$
,
$\delta \in (0,1)$
,
 $$ \begin{align*}\int_{\partial B} v^{p/2}d\xi \leq C(\delta)+\left(\delta+\displaystyle\frac{1}{2p} +\frac{1}{2}\right)\int_{\partial B}v^{p/2}d\xi, \end{align*} $$
$$ \begin{align*}\int_{\partial B} v^{p/2}d\xi \leq C(\delta)+\left(\delta+\displaystyle\frac{1}{2p} +\frac{1}{2}\right)\int_{\partial B}v^{p/2}d\xi, \end{align*} $$
Therefore, by choosing
![]() $\delta>0$
sufficiently small we get
$\delta>0$
sufficiently small we get
 $$ \begin{align} \int_{\partial B}(|\nabla \rho_1|^2+1)^{p/2}d\xi \leq C. \end{align} $$
$$ \begin{align} \int_{\partial B}(|\nabla \rho_1|^2+1)^{p/2}d\xi \leq C. \end{align} $$
Multiply (4.3) by
![]() $(1-\rho _1)$
. In view of (4.4), applying the Hölder inequality, and using (4.2) and (4.10), we get
$(1-\rho _1)$
. In view of (4.4), applying the Hölder inequality, and using (4.2) and (4.10), we get
 $$ \begin{align} \begin{split}&\displaystyle\int_B[(|\nabla\rho_1|^2+1)^{(p-2)/2}|\nabla\rho_1|^2 +\frac{1}{\varepsilon^p}(1-\rho_1)^2]\\&\quad\leq \left\vert\displaystyle\int_{\partial B}(1-\rho_1)(|\nabla\rho_1|^2+1)^{(p-2)/2} (\nu\cdot\nabla\rho_1)d\xi\right\vert \leq C\varepsilon. \end{split} \end{align} $$
$$ \begin{align} \begin{split}&\displaystyle\int_B[(|\nabla\rho_1|^2+1)^{(p-2)/2}|\nabla\rho_1|^2 +\frac{1}{\varepsilon^p}(1-\rho_1)^2]\\&\quad\leq \left\vert\displaystyle\int_{\partial B}(1-\rho_1)(|\nabla\rho_1|^2+1)^{(p-2)/2} (\nu\cdot\nabla\rho_1)d\xi\right\vert \leq C\varepsilon. \end{split} \end{align} $$
Step 4. Set
![]() $U=\rho _1w$
on B;
$U=\rho _1w$
on B;
![]() $U={u}_{\varepsilon }$
on
$U={u}_{\varepsilon }$
on
![]() $G\setminus B$
, where
$G\setminus B$
, where
![]() $w={u}_{\varepsilon }/|{u}_{\varepsilon }|$
. Then
$w={u}_{\varepsilon }/|{u}_{\varepsilon }|$
. Then
![]() $U \in W$
. Since
$U \in W$
. Since
![]() ${u}_{\varepsilon }$
is a minimizer of
${u}_{\varepsilon }$
is a minimizer of
![]() $E_{\varepsilon }(u,G)$
, we have
$E_{\varepsilon }(u,G)$
, we have
In view of
![]() $p \in (1,2)$
, we get
$p \in (1,2)$
, we get
 $$ \begin{align*}&\displaystyle\int_B(|\nabla \rho_1|^2 +\rho_1^2|\nabla w|^2)^{p/2} -\int_B(\rho_1^2|\nabla w|^2)^{p/2}\\&\quad=\displaystyle\frac{p}{2}\int_B \int_0^1(s|\nabla \rho_1|^2 +\rho_1^2|\nabla w|^2)^{(p-2)/2} |\nabla \rho_1|^2dsdx\\&\quad\leq \displaystyle\frac{p}{2}\int_B|\nabla \rho_1|^pdx \cdot \int_0^1s^{(p-2)/2}ds =\int_B|\nabla \rho_1|^p.\end{align*} $$
$$ \begin{align*}&\displaystyle\int_B(|\nabla \rho_1|^2 +\rho_1^2|\nabla w|^2)^{p/2} -\int_B(\rho_1^2|\nabla w|^2)^{p/2}\\&\quad=\displaystyle\frac{p}{2}\int_B \int_0^1(s|\nabla \rho_1|^2 +\rho_1^2|\nabla w|^2)^{(p-2)/2} |\nabla \rho_1|^2dsdx\\&\quad\leq \displaystyle\frac{p}{2}\int_B|\nabla \rho_1|^pdx \cdot \int_0^1s^{(p-2)/2}ds =\int_B|\nabla \rho_1|^p.\end{align*} $$
Here, we use the fact
![]() $\int _0^1s^{(p-2)/2}ds=2/p$
. Combining this with (4.12) leads to
$\int _0^1s^{(p-2)/2}ds=2/p$
. Combining this with (4.12) leads to
 $$ \begin{align*}E_{\varepsilon}(u_{\varepsilon},B) \leq E_{\varepsilon}(\rho_1 w,B) \leq \frac{1}{p} \int_B(\rho_1^2|\nabla w|^2)^{p/2} +E_\varepsilon(\rho_1,B). \end{align*} $$
$$ \begin{align*}E_{\varepsilon}(u_{\varepsilon},B) \leq E_{\varepsilon}(\rho_1 w,B) \leq \frac{1}{p} \int_B(\rho_1^2|\nabla w|^2)^{p/2} +E_\varepsilon(\rho_1,B). \end{align*} $$
Using (4.5) and (4.11), we can see from the result above that
 $$ \begin{align} E_{\varepsilon}(u_{\varepsilon},B) \leq \frac{1}{p} \int_B |\nabla w|^p+C\varepsilon. \end{align} $$
$$ \begin{align} E_{\varepsilon}(u_{\varepsilon},B) \leq \frac{1}{p} \int_B |\nabla w|^p+C\varepsilon. \end{align} $$
Step 5. Here, we denote
![]() $|u_\varepsilon |$
by
$|u_\varepsilon |$
by
![]() $h_\varepsilon $
.
$h_\varepsilon $
.
Clearly,
![]() $(sa^2+b^2)^{(p-2)/2} \geq (a^2+b^2)^{(p-2)/2}$
when
$(sa^2+b^2)^{(p-2)/2} \geq (a^2+b^2)^{(p-2)/2}$
when
![]() $s \in (0,1)$
and
$s \in (0,1)$
and
![]() $p \in (1,2)$
. Therefore, according to the mean value theorem, it follows that
$p \in (1,2)$
. Therefore, according to the mean value theorem, it follows that
 $$ \begin{align*}&\displaystyle(|\nabla h_\varepsilon|^2 +h_\varepsilon^2|\nabla w|^2)^{p/2} -(h_\varepsilon|\nabla w|^2)^{p/2}\\[3mm]&\quad=\displaystyle\frac{p}{2}\left(\int_0^1[s(|\nabla h_\varepsilon|^2 +h_\varepsilon^2|\nabla w|^2) +(1-s)(h_\varepsilon^2|\nabla w|^2)]^{\frac{p-2}{2}}ds\right) \cdot |\nabla h_\varepsilon|^2\\[3mm]&\quad\geq \displaystyle\frac{p}{2}|\nabla u_\varepsilon|^{p-2}|\nabla h_\varepsilon|^2. \end{align*} $$
$$ \begin{align*}&\displaystyle(|\nabla h_\varepsilon|^2 +h_\varepsilon^2|\nabla w|^2)^{p/2} -(h_\varepsilon|\nabla w|^2)^{p/2}\\[3mm]&\quad=\displaystyle\frac{p}{2}\left(\int_0^1[s(|\nabla h_\varepsilon|^2 +h_\varepsilon^2|\nabla w|^2) +(1-s)(h_\varepsilon^2|\nabla w|^2)]^{\frac{p-2}{2}}ds\right) \cdot |\nabla h_\varepsilon|^2\\[3mm]&\quad\geq \displaystyle\frac{p}{2}|\nabla u_\varepsilon|^{p-2}|\nabla h_\varepsilon|^2. \end{align*} $$
This and (4.13) imply
 $$ \begin{align}&\displaystyle\frac{1}{2}\int_B|\nabla u_\varepsilon|^{p-2}|\nabla h_\varepsilon|^2 +\frac{1}{p}\int_B(h_\varepsilon^p-1)|\nabla w|^p +\frac{1}{4\varepsilon^p}\int_B(1-h_\varepsilon^2)^2\notag\\[3mm]&\quad\leq E_{\varepsilon}(u_{\varepsilon},B) -\displaystyle\frac{1}{p}\int_B|\nabla w|^p \leq C\varepsilon. \end{align} $$
$$ \begin{align}&\displaystyle\frac{1}{2}\int_B|\nabla u_\varepsilon|^{p-2}|\nabla h_\varepsilon|^2 +\frac{1}{p}\int_B(h_\varepsilon^p-1)|\nabla w|^p +\frac{1}{4\varepsilon^p}\int_B(1-h_\varepsilon^2)^2\notag\\[3mm]&\quad\leq E_{\varepsilon}(u_{\varepsilon},B) -\displaystyle\frac{1}{p}\int_B|\nabla w|^p \leq C\varepsilon. \end{align} $$
In view of (4.1), there holds
 $$ \begin{align*}\frac{1}{p} \int_B(1-h_\varepsilon^p)|\nabla w|^p \leq \frac{2^p}{p}\int_B(1-h_\varepsilon^2)|\nabla u_\varepsilon|^p. \end{align*} $$
$$ \begin{align*}\frac{1}{p} \int_B(1-h_\varepsilon^p)|\nabla w|^p \leq \frac{2^p}{p}\int_B(1-h_\varepsilon^2)|\nabla u_\varepsilon|^p. \end{align*} $$
Applying the Hölder inequality and Propositions 2.10 and 2.6, we can obtain
 $$ \begin{align*}\frac{1}{p} \int_B(1-h_\varepsilon^p)|\nabla w|^p \leq C\varepsilon^{2t_0/(1+t_0)} \end{align*} $$
$$ \begin{align*}\frac{1}{p} \int_B(1-h_\varepsilon^p)|\nabla w|^p \leq C\varepsilon^{2t_0/(1+t_0)} \end{align*} $$
with
![]() $t_0 \in (0,t)$
is suitably small. Combining this with (4.14), we can see
$t_0 \in (0,t)$
is suitably small. Combining this with (4.14), we can see
 $$ \begin{align} \frac{1}{2}\int_B|\nabla u_\varepsilon|^{p-2}|\nabla h_\varepsilon|^2 +\frac{1}{4\varepsilon^p}\int_B(1-h_\varepsilon^2)^2 \leq C\varepsilon^{2t_0/(1+t_0)}. \end{align} $$
$$ \begin{align} \frac{1}{2}\int_B|\nabla u_\varepsilon|^{p-2}|\nabla h_\varepsilon|^2 +\frac{1}{4\varepsilon^p}\int_B(1-h_\varepsilon^2)^2 \leq C\varepsilon^{2t_0/(1+t_0)}. \end{align} $$
Using the Hölder inequality, by (4.15) and Proposition 2.6, we see that
 $$ \begin{align*}\int_B|\nabla h|^p \leq \left(\int_B|\nabla u_\varepsilon|^{p-2}|\nabla h_\varepsilon|^2\right)^{\frac{p}{2}} \left(\int_B|\nabla u_\varepsilon|^p\right)^{\frac{2-p}{2}} \leq C\varepsilon^{pt_0/(1+t_0)}. \end{align*} $$
$$ \begin{align*}\int_B|\nabla h|^p \leq \left(\int_B|\nabla u_\varepsilon|^{p-2}|\nabla h_\varepsilon|^2\right)^{\frac{p}{2}} \left(\int_B|\nabla u_\varepsilon|^p\right)^{\frac{2-p}{2}} \leq C\varepsilon^{pt_0/(1+t_0)}. \end{align*} $$
Combining with (4.15) and by an argument of finite coverings, we can see (1.15).
5 Proof of Theorem 1.2
Proof of (1.12).
By (3.3) and Proposition 2.6, we get
 $$ \begin{align} \int_{G}|\det(\nabla u_\varepsilon)|^{p/2} \leq \int_G|\nabla u_\varepsilon|^p \leq C. \end{align} $$
$$ \begin{align} \int_{G}|\det(\nabla u_\varepsilon)|^{p/2} \leq \int_G|\nabla u_\varepsilon|^p \leq C. \end{align} $$
Therefore, we can find a Radon measure
![]() $\omega _3$
and a subsequence
$\omega _3$
and a subsequence
![]() $\varepsilon _k$
of
$\varepsilon _k$
of
![]() $\varepsilon $
such that
$\varepsilon $
such that
Proposition 2.9 implies that there exists
![]() $\phi _\varepsilon $
such that when
$\phi _\varepsilon $
such that when
![]() $x \in G \setminus \cup _jB_\sigma (a_j)$
,
$x \in G \setminus \cup _jB_\sigma (a_j)$
,
where
![]() $h_\varepsilon (x)=|u_\varepsilon (x)|$
. Thus, on
$h_\varepsilon (x)=|u_\varepsilon (x)|$
. Thus, on
![]() $G \setminus \cup _jB_\sigma (a_j)$
,
$G \setminus \cup _jB_\sigma (a_j)$
,
Therefore, by the Hölder inequality, there holds
 $$ \begin{align}\begin{split}&\displaystyle\int_{G \setminus \cup_jB_\sigma(a_j)}|\det(\nabla u_\varepsilon)|^{p/2}\\&\quad \leq \left(\int_{G \setminus \cup_jB_\sigma(a_j)}|\nabla h_\varepsilon|^p\right)^{\frac{1}{2}} \left(\int_{G \setminus \cup_jB_\sigma(a_j)}|h_\varepsilon\nabla \phi_\varepsilon|^p\right)^{\frac{1}{2}}. \end{split} \end{align} $$
$$ \begin{align}\begin{split}&\displaystyle\int_{G \setminus \cup_jB_\sigma(a_j)}|\det(\nabla u_\varepsilon)|^{p/2}\\&\quad \leq \left(\int_{G \setminus \cup_jB_\sigma(a_j)}|\nabla h_\varepsilon|^p\right)^{\frac{1}{2}} \left(\int_{G \setminus \cup_jB_\sigma(a_j)}|h_\varepsilon\nabla \phi_\varepsilon|^p\right)^{\frac{1}{2}}. \end{split} \end{align} $$
In view of Proposition 2.6 and (1.15),
 $$ \begin{align*}\int_{G \setminus \cup_jB_\sigma(a_j)}|\det(\nabla u_\varepsilon)|^{p/2} \leq C\left(\int_{G \setminus \cup_jB_\sigma(a_j)}|\nabla h_\varepsilon|^p\right)^{\frac{1}{2}} \to 0 \end{align*} $$
$$ \begin{align*}\int_{G \setminus \cup_jB_\sigma(a_j)}|\det(\nabla u_\varepsilon)|^{p/2} \leq C\left(\int_{G \setminus \cup_jB_\sigma(a_j)}|\nabla h_\varepsilon|^p\right)^{\frac{1}{2}} \to 0 \end{align*} $$
when
![]() $\varepsilon \to 0$
. Therefore,
$\varepsilon \to 0$
. Therefore,
![]() $supp(\omega _3) \subset \{a_j\}_{j=1}^N$
. Thus, there exists constants
$supp(\omega _3) \subset \{a_j\}_{j=1}^N$
. Thus, there exists constants
![]() $Q_j \geq 0$
such that
$Q_j \geq 0$
such that
 $$ \begin{align*}\omega_3=\sum_{j=1}^N Q_j\delta_{a_j}. \end{align*} $$
$$ \begin{align*}\omega_3=\sum_{j=1}^N Q_j\delta_{a_j}. \end{align*} $$
Equation (1.12) is proved.
Proof of (1.14).
First we observe that
![]() $2-p<pt$
since p is sufficiently close to
$2-p<pt$
since p is sufficiently close to
![]() $2$
, where t is the constant in Proposition 2.10 (which implies that t is independent of p). Thus we can choose
$2$
, where t is the constant in Proposition 2.10 (which implies that t is independent of p). Thus we can choose
![]() $\gamma \in (2-p,pt)$
. By (1.5), the Hölder inequality and Propositions 2.10 and 2.6, we have
$\gamma \in (2-p,pt)$
. By (1.5), the Hölder inequality and Propositions 2.10 and 2.6, we have
 $$ \begin{align} \int_{G\setminus G^{2\rho\varepsilon}} (1-|\tilde{u}_\varepsilon|^2)^{\alpha} |\nabla \tilde{u}_\varepsilon|^2 \leq \left(\int_{G\setminus G^{2\rho\varepsilon}} |\nabla \tilde{u}_\varepsilon|^{p+\gamma}\right)^{\frac{2}{p+\gamma}} |G\setminus G^{2\rho\varepsilon}|^{1-\frac{2}{p+\gamma}} \to 0 \end{align} $$
$$ \begin{align} \int_{G\setminus G^{2\rho\varepsilon}} (1-|\tilde{u}_\varepsilon|^2)^{\alpha} |\nabla \tilde{u}_\varepsilon|^2 \leq \left(\int_{G\setminus G^{2\rho\varepsilon}} |\nabla \tilde{u}_\varepsilon|^{p+\gamma}\right)^{\frac{2}{p+\gamma}} |G\setminus G^{2\rho\varepsilon}|^{1-\frac{2}{p+\gamma}} \to 0 \end{align} $$
when
![]() $\varepsilon \to 0$
.
$\varepsilon \to 0$
.
In view of (1.5), the right hand side of (1.4) with
![]() $u=\tilde {u}_\varepsilon $
is bounded by
$u=\tilde {u}_\varepsilon $
is bounded by
![]() $\varepsilon ^{-p}$
. Thus, checking the proof of Proposition 5.1 in [Reference Tolksdorf22], and applying Proposition 2.6 we get
$\varepsilon ^{-p}$
. Thus, checking the proof of Proposition 5.1 in [Reference Tolksdorf22], and applying Proposition 2.6 we get
 $$ \begin{align*}\|\nabla \tilde{u}_\varepsilon\|_{L^{\infty}(G^{\rho\varepsilon} \cap B_\sigma(a_j))}^p \leq C\sigma^{-2}\varepsilon^{-p} \int_G(1+|\nabla \tilde{u}_\varepsilon|^p) \leq C\varepsilon^{-p}. \end{align*} $$
$$ \begin{align*}\|\nabla \tilde{u}_\varepsilon\|_{L^{\infty}(G^{\rho\varepsilon} \cap B_\sigma(a_j))}^p \leq C\sigma^{-2}\varepsilon^{-p} \int_G(1+|\nabla \tilde{u}_\varepsilon|^p) \leq C\varepsilon^{-p}. \end{align*} $$
Therefore, by the Hölder inequality, we obtain that for any
![]() $\gamma>0$
,
$\gamma>0$
,
 $$ \begin{align}\begin{split}&\displaystyle\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} (1-|\tilde{u}_\varepsilon|^2)^{\alpha} |\nabla \tilde{u}_\varepsilon|^2 \\&\quad\leq C\varepsilon^{p-2}\displaystyle\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} (1-|\tilde{u}_\varepsilon|^2)^{\alpha} |\nabla \tilde{u}_\varepsilon|^p \\&\quad\leq C\varepsilon^{p-2} \left(\displaystyle\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} |\nabla \tilde{u}_\varepsilon|^{p+\gamma}\right)^{\frac{p}{p+\gamma}}\\&\qquad \cdot\left(\displaystyle\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} (1-|\tilde{u}_\varepsilon|^2)^{(p+\gamma)\alpha/\gamma}\right)^{\frac{\gamma}{p+\gamma}}. \end{split}\end{align} $$
$$ \begin{align}\begin{split}&\displaystyle\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} (1-|\tilde{u}_\varepsilon|^2)^{\alpha} |\nabla \tilde{u}_\varepsilon|^2 \\&\quad\leq C\varepsilon^{p-2}\displaystyle\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} (1-|\tilde{u}_\varepsilon|^2)^{\alpha} |\nabla \tilde{u}_\varepsilon|^p \\&\quad\leq C\varepsilon^{p-2} \left(\displaystyle\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} |\nabla \tilde{u}_\varepsilon|^{p+\gamma}\right)^{\frac{p}{p+\gamma}}\\&\qquad \cdot\left(\displaystyle\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} (1-|\tilde{u}_\varepsilon|^2)^{(p+\gamma)\alpha/\gamma}\right)^{\frac{\gamma}{p+\gamma}}. \end{split}\end{align} $$
We set
Then for any
![]() $\alpha \geq 2-p$
,
$\alpha \geq 2-p$
,
 $$ \begin{align} \frac{(p+\gamma_0)\alpha}{\gamma_0} \geq 2. \end{align} $$
$$ \begin{align} \frac{(p+\gamma_0)\alpha}{\gamma_0} \geq 2. \end{align} $$
In addition,
![]() $\gamma _0 \in (0,pt)$
since p is sufficiently close to
$\gamma _0 \in (0,pt)$
since p is sufficiently close to
![]() $2$
. Here, t is the constant in Proposition 2.10.
$2$
. Here, t is the constant in Proposition 2.10.
According to Proposition 2.10, and by Proposition 2.6, it follows that
 $$ \begin{align*}\left(\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} |\nabla \tilde{u}_\varepsilon|^{p+\gamma_0}\right)^{\frac{p}{p+\gamma_0}} \leq C\int_G(|\nabla \tilde{u}_\varepsilon|^2+1)^{p/2} \leq C. \end{align*} $$
$$ \begin{align*}\left(\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} |\nabla \tilde{u}_\varepsilon|^{p+\gamma_0}\right)^{\frac{p}{p+\gamma_0}} \leq C\int_G(|\nabla \tilde{u}_\varepsilon|^2+1)^{p/2} \leq C. \end{align*} $$
Inserting this result into (5.5) with
![]() $\gamma =\gamma _0$
yields
$\gamma =\gamma _0$
yields
 $$ \begin{align}\begin{split}&\displaystyle\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} (1-|u_\varepsilon|^2)^{\alpha} |\nabla \tilde{u}_\varepsilon|^2\\&\quad\leq C\varepsilon^{p-2} \displaystyle \left(\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} (1-|\tilde{u}_\varepsilon|^2)^{(p+\gamma_0)\alpha/\gamma_0} \right)^{\frac{\gamma_0}{p+\gamma_0}}.\end{split}\end{align} $$
$$ \begin{align}\begin{split}&\displaystyle\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} (1-|u_\varepsilon|^2)^{\alpha} |\nabla \tilde{u}_\varepsilon|^2\\&\quad\leq C\varepsilon^{p-2} \displaystyle \left(\int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} (1-|\tilde{u}_\varepsilon|^2)^{(p+\gamma_0)\alpha/\gamma_0} \right)^{\frac{\gamma_0}{p+\gamma_0}}.\end{split}\end{align} $$
Using (5.6), Proposition 2.8, we can deduce from (5.7) that
 $$ \begin{align} \int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} (1-|\tilde{u}_\varepsilon|^2)^{\alpha} |\nabla \tilde{u}_\varepsilon|^2 \leq C\varepsilon^{p-2+\frac{2\gamma_0}{p+\gamma_0}}=C. \end{align} $$
$$ \begin{align} \int_{G^{\rho\varepsilon}\cap B(a_j,\sigma)} (1-|\tilde{u}_\varepsilon|^2)^{\alpha} |\nabla \tilde{u}_\varepsilon|^2 \leq C\varepsilon^{p-2+\frac{2\gamma_0}{p+\gamma_0}}=C. \end{align} $$
Next, using
and
which are implied by (1.11), we derive that when
![]() $\varepsilon \to 0$
,
$\varepsilon \to 0$
,
 $$ \begin{align}\begin{split}&\displaystyle\int_{G^{\rho\varepsilon}\setminus \cup_jB(a_j,\sigma)}(1-|\tilde{u}_\varepsilon|^2)^{\alpha} |\nabla \tilde{u}_\varepsilon|^2 \\&\quad\leq \displaystyle\left(\mathop{\mathrm{sup}}\limits_{G\setminus \cup_jB(a_j,\sigma)}(1-|\tilde{u}_\varepsilon|^2)^{\alpha}\right) \left(\mathop{\mathrm{sup}}\limits_{G\setminus \cup_jB(a_j,\sigma)}|\nabla \tilde{u}_\varepsilon|^2\right) |G\setminus \cup_jB_\sigma(a_j)|\\&\quad \to 0. \end{split} \end{align} $$
$$ \begin{align}\begin{split}&\displaystyle\int_{G^{\rho\varepsilon}\setminus \cup_jB(a_j,\sigma)}(1-|\tilde{u}_\varepsilon|^2)^{\alpha} |\nabla \tilde{u}_\varepsilon|^2 \\&\quad\leq \displaystyle\left(\mathop{\mathrm{sup}}\limits_{G\setminus \cup_jB(a_j,\sigma)}(1-|\tilde{u}_\varepsilon|^2)^{\alpha}\right) \left(\mathop{\mathrm{sup}}\limits_{G\setminus \cup_jB(a_j,\sigma)}|\nabla \tilde{u}_\varepsilon|^2\right) |G\setminus \cup_jB_\sigma(a_j)|\\&\quad \to 0. \end{split} \end{align} $$
Combining (5.4), (5.8) with (5.9), we obtain that
![]() $(1-|\tilde {u}_\varepsilon |^2)^{\alpha } |\nabla \tilde {u}_\varepsilon |^2$
is bounded in
$(1-|\tilde {u}_\varepsilon |^2)^{\alpha } |\nabla \tilde {u}_\varepsilon |^2$
is bounded in
![]() $L^1(G)$
, and hence
$L^1(G)$
, and hence
where
![]() $\omega _4$
is a Radon measure. In addition, (5.9) implies
$\omega _4$
is a Radon measure. In addition, (5.9) implies
![]() $supp(\omega _4) \subset \{a_j\}_{j=1}^N$
. Thus, there exists constants
$supp(\omega _4) \subset \{a_j\}_{j=1}^N$
. Thus, there exists constants
![]() $M_j \geq 0$
such that
$M_j \geq 0$
such that
 $$ \begin{align*}\omega_4=\sum_{j=1}^N M_j\delta_{a_j}. \end{align*} $$
$$ \begin{align*}\omega_4=\sum_{j=1}^N M_j\delta_{a_j}. \end{align*} $$
By (5.4), we see that
![]() $M_j=0$
when
$M_j=0$
when
![]() $a_j \in \partial G$
.
$a_j \in \partial G$
.
For the other
![]() $a_j$
which are contained in G, using (2.2) instead of Proposition 2.2 in the proof of
$a_j$
which are contained in G, using (2.2) instead of Proposition 2.2 in the proof of
![]() $L_j>0$
, we also get
$L_j>0$
, we also get
![]() $M_j>0$
. Equation (1.14) is proved.
$M_j>0$
. Equation (1.14) is proved.
Proof of (1.13).
By Proposition 2.8,
![]() $\frac {(1-|\tilde {u}_\varepsilon |^2)^2}{\varepsilon ^2}$
is bounded in
$\frac {(1-|\tilde {u}_\varepsilon |^2)^2}{\varepsilon ^2}$
is bounded in
![]() $L^1(G)$
. Thus, there exist a subsequence
$L^1(G)$
. Thus, there exist a subsequence
![]() $\varepsilon _k$
of
$\varepsilon _k$
of
![]() $\varepsilon $
and a Radon measure
$\varepsilon $
and a Radon measure
![]() $\omega _5$
, such that
$\omega _5$
, such that
 $$ \begin{align*}\lim_{k \to 0}\frac{(1-|\tilde{u}_{\varepsilon_k}|^2)^2}{\varepsilon_k^2} =\omega_5, \quad \mbox{weakly star in}\quad C(\overline{G}). \end{align*} $$
$$ \begin{align*}\lim_{k \to 0}\frac{(1-|\tilde{u}_{\varepsilon_k}|^2)^2}{\varepsilon_k^2} =\omega_5, \quad \mbox{weakly star in}\quad C(\overline{G}). \end{align*} $$
In addition, according to Proposition 2.11,
 $$ \begin{align*}\frac{1}{\varepsilon_k^2}\int_{G \setminus \cup_j B_\sigma(a_j)} (1-|\tilde{u}_{\varepsilon_k}|^2)^2 \leq C\varepsilon_k^{2(p-1)} \to 0 \end{align*} $$
$$ \begin{align*}\frac{1}{\varepsilon_k^2}\int_{G \setminus \cup_j B_\sigma(a_j)} (1-|\tilde{u}_{\varepsilon_k}|^2)^2 \leq C\varepsilon_k^{2(p-1)} \to 0 \end{align*} $$
when
![]() $\varepsilon _k \to 0$
. Therefore, we can see that
$\varepsilon _k \to 0$
. Therefore, we can see that
![]() $supp(\omega _5) \subset \{a_j\}_{j=1}^N$
, and hence
$supp(\omega _5) \subset \{a_j\}_{j=1}^N$
, and hence
 $$ \begin{align*}\omega_5=\sum_{j=1}^N K_j\delta_{a_j}, \end{align*} $$
$$ \begin{align*}\omega_5=\sum_{j=1}^N K_j\delta_{a_j}, \end{align*} $$
where
![]() $K_j \geq 0$
.
$K_j \geq 0$
.
We claim
![]() $K_j>0$
for each j. In fact, there exists
$K_j>0$
for each j. In fact, there exists
![]() $x_j^\varepsilon $
which is the center of the bad disc tends to
$x_j^\varepsilon $
which is the center of the bad disc tends to
![]() $a_j$
when
$a_j$
when
![]() $\varepsilon \to 0$
. Recalling the definition of the bad disc in Section 2, we have
$\varepsilon \to 0$
. Recalling the definition of the bad disc in Section 2, we have
 $$ \begin{align*}\frac{1}{\varepsilon^2}\int_{B(x_j^\varepsilon,h\varepsilon)}(1-|\tilde{u}_\varepsilon|^2)^2 \geq \mu>0. \end{align*} $$
$$ \begin{align*}\frac{1}{\varepsilon^2}\int_{B(x_j^\varepsilon,h\varepsilon)}(1-|\tilde{u}_\varepsilon|^2)^2 \geq \mu>0. \end{align*} $$
for each j. This implies
![]() $K_j>0$
(and hence
$K_j>0$
(and hence
![]() $supp(\omega _5) = \{a_j\}_{j=1}^N$
). Equation (1.13) is proved.
$supp(\omega _5) = \{a_j\}_{j=1}^N$
). Equation (1.13) is proved.
6 Proof of Theorem 1.4
Step 1. First we claim
For convenience, sometimes we denote
![]() $B_R(0)$
by
$B_R(0)$
by
![]() $B_R$
.
$B_R$
.
From (1.17), it follows that
 $$ \begin{align*} 0 & =\lim_{R \to \infty} \int_{B_{2R}\setminus B_R} |\nabla u|^p dx \\ & =\lim_{R \to \infty} \int_R^{2R}\left[r\int_{\partial B_r} |\nabla u|^p d\xi\right] \frac{dr}{r} \\ & \geq \lim_{R \to \infty} \inf_{r \in [R,2R]}\left[r\int_{\partial B_r} |\nabla u|^p d\xi\right] \cdot (\log 2). \end{align*} $$
$$ \begin{align*} 0 & =\lim_{R \to \infty} \int_{B_{2R}\setminus B_R} |\nabla u|^p dx \\ & =\lim_{R \to \infty} \int_R^{2R}\left[r\int_{\partial B_r} |\nabla u|^p d\xi\right] \frac{dr}{r} \\ & \geq \lim_{R \to \infty} \inf_{r \in [R,2R]}\left[r\int_{\partial B_r} |\nabla u|^p d\xi\right] \cdot (\log 2). \end{align*} $$
Therefore, we can find a subsequence
![]() $R_k$
of R such that
$R_k$
of R such that
 $$ \begin{align} \lim_{R_k \to \infty}R_k\int_{\partial B_{R_k}(0)}|\nabla u|^pd\xi=0. \end{align} $$
$$ \begin{align} \lim_{R_k \to \infty}R_k\int_{\partial B_{R_k}(0)}|\nabla u|^pd\xi=0. \end{align} $$
When
![]() $p \in (1,2)$
, the Sobolev inequality implies
$p \in (1,2)$
, the Sobolev inequality implies
![]() $u \in L^{\frac {2p}{2-p}}(\mathbb {R}^2)$
. By the same proof of (6.2), there also holds that
$u \in L^{\frac {2p}{2-p}}(\mathbb {R}^2)$
. By the same proof of (6.2), there also holds that
 $$ \begin{align} \lim_{R_k \to \infty}R_k\int_{\partial B_{R_k}(0)}|u|^{\frac{2p}{2-p}}d\xi=0. \end{align} $$
$$ \begin{align} \lim_{R_k \to \infty}R_k\int_{\partial B_{R_k}(0)}|u|^{\frac{2p}{2-p}}d\xi=0. \end{align} $$
Here,
![]() $R_k$
is also a subsequence of R.
$R_k$
is also a subsequence of R.
Set
![]() $\Phi =u-u\min \{1,|u|\}/|u|$
and
$\Phi =u-u\min \{1,|u|\}/|u|$
and
![]() $B_+=\{x \in \mathbb {R}^2; |u(x)|>1\}$
, then
$B_+=\{x \in \mathbb {R}^2; |u(x)|>1\}$
, then
 $$ \begin{align*}\left\{\!\begin{array}{ll}\nabla \Phi=\nabla u-|u|^{-1}\nabla u+(u\cdot\nabla u)u/|u|^3, \quad &on \ B_+;\\[3mm]\nabla \Phi=0 &on \ \mathbb{R}^2 \setminus B_+. \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{\!\begin{array}{ll}\nabla \Phi=\nabla u-|u|^{-1}\nabla u+(u\cdot\nabla u)u/|u|^3, \quad &on \ B_+;\\[3mm]\nabla \Phi=0 &on \ \mathbb{R}^2 \setminus B_+. \end{array} \right. \end{align*} $$
Multiplying (1.16) by
![]() $\Phi $
and integrating on
$\Phi $
and integrating on
![]() $B_{R_k}$
and then letting
$B_{R_k}$
and then letting
![]() $R_k \to \infty $
, we get
$R_k \to \infty $
, we get
 $$ \begin{align} \begin{array}{ll} &-\displaystyle\lim_{R_k \to \infty}\int_{\partial B_{R_k}(0)} u|\nabla u|^{p-2}\partial_{\nu}ud\xi\\[3mm] &+\displaystyle\lim_{R_k \to \infty}\int_{\partial B_{R_k}(0)} \frac{u}{|u|}\min\{1,|u|\}|\nabla u|^{p-2}\partial_{\nu}u d\xi\\[3mm] &+\displaystyle\int_{B_+}(1-1/|u|)|\nabla u|^p +\int_{B_+}|\nabla u|^{p-2}(u \cdot \nabla u)^2/|u|^3\\[3mm] &+\displaystyle\int_{B_+}|u|(|u|+1)(|u|-1)^2=0. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll} &-\displaystyle\lim_{R_k \to \infty}\int_{\partial B_{R_k}(0)} u|\nabla u|^{p-2}\partial_{\nu}ud\xi\\[3mm] &+\displaystyle\lim_{R_k \to \infty}\int_{\partial B_{R_k}(0)} \frac{u}{|u|}\min\{1,|u|\}|\nabla u|^{p-2}\partial_{\nu}u d\xi\\[3mm] &+\displaystyle\int_{B_+}(1-1/|u|)|\nabla u|^p +\int_{B_+}|\nabla u|^{p-2}(u \cdot \nabla u)^2/|u|^3\\[3mm] &+\displaystyle\int_{B_+}|u|(|u|+1)(|u|-1)^2=0. \end{array} \end{align} $$
When
![]() $R_k \to \infty $
, by the Hölder inequality and (6.2) and (6.3), there holds
$R_k \to \infty $
, by the Hölder inequality and (6.2) and (6.3), there holds
 $$ \begin{align} \begin{split}&\displaystyle \int_{\partial B_{R_k}} |u||\nabla u|^{p-1} d\xi\\&\quad\leq \displaystyle R_k^{-\frac{1}{2}} \left(R_k\int_{\partial B_{R_k}}|\nabla u|^pd\xi\right)^{1-\frac{1}{p}} \left(R_k\int_{\partial B_{R_k}}|u|^{\frac{2p}{2-p}}d\xi\right)^{\frac{2-p}{2p}} |\partial B_{R_k}|^{\frac{1}{2}}\\&\quad\to 0, \end{split}\end{align} $$
$$ \begin{align} \begin{split}&\displaystyle \int_{\partial B_{R_k}} |u||\nabla u|^{p-1} d\xi\\&\quad\leq \displaystyle R_k^{-\frac{1}{2}} \left(R_k\int_{\partial B_{R_k}}|\nabla u|^pd\xi\right)^{1-\frac{1}{p}} \left(R_k\int_{\partial B_{R_k}}|u|^{\frac{2p}{2-p}}d\xi\right)^{\frac{2-p}{2p}} |\partial B_{R_k}|^{\frac{1}{2}}\\&\quad\to 0, \end{split}\end{align} $$
which implies both the first and the second terms of the left hand side of (6.4) are equal to zero. This shows
![]() $|B_+|=0$
and hence (6.1) is proved when
$|B_+|=0$
and hence (6.1) is proved when
![]() $p \in (1.2)$
.
$p \in (1.2)$
.
When
![]() $p>2$
, set
$p>2$
, set
![]() $\Phi :=(|u|-1)_+$
. Then,
$\Phi :=(|u|-1)_+$
. Then,
 $$ \begin{align*}\left\{\!\begin{array}{l}\nabla\Phi=0,\quad on \quad \mathbb{R}^2\setminus B_+;\\[3mm]\nabla\Phi=\frac{u \cdot \nabla u}{|u|},\quad on \quad B_+. \end{array}\right. \end{align*} $$
$$ \begin{align*}\left\{\!\begin{array}{l}\nabla\Phi=0,\quad on \quad \mathbb{R}^2\setminus B_+;\\[3mm]\nabla\Phi=\frac{u \cdot \nabla u}{|u|},\quad on \quad B_+. \end{array}\right. \end{align*} $$
Obviously, (1.17) implies
Let
![]() $\zeta \in C^{\infty }(\mathbb {R}^2,[0,1])$
be a cut-off function satisfying
$\zeta \in C^{\infty }(\mathbb {R}^2,[0,1])$
be a cut-off function satisfying
![]() $\zeta (y)=1$
for
$\zeta (y)=1$
for
![]() $|y|\leq 1$
, and
$|y|\leq 1$
, and
![]() $\zeta (y)=0$
for
$\zeta (y)=0$
for
![]() $|y|\geq 2$
. Set
$|y|\geq 2$
. Set
![]() $\zeta _t(y)=\zeta (\frac {y}{t})$
. Multiply (1.16) by
$\zeta _t(y)=\zeta (\frac {y}{t})$
. Multiply (1.16) by
![]() $\xi $
, where
$\xi $
, where
 $$ \begin{align*}\left\{\!\begin{array}{l} \xi=0,\quad on \quad \mathbb{R}^2\setminus B_+;\\[3mm]\xi=\frac{u}{|u|}\zeta_t,\quad on \quad B_+. \end{array}\right. \end{align*} $$
$$ \begin{align*}\left\{\!\begin{array}{l} \xi=0,\quad on \quad \mathbb{R}^2\setminus B_+;\\[3mm]\xi=\frac{u}{|u|}\zeta_t,\quad on \quad B_+. \end{array}\right. \end{align*} $$
Then,
 $$ \begin{align*}\int_{B_+}|\nabla u|^{p-2}\nabla u\nabla(\frac{u}{|u|}\zeta_t) =-\int_{B_+}|u|(1+|u|)\Phi\zeta_t. \end{align*} $$
$$ \begin{align*}\int_{B_+}|\nabla u|^{p-2}\nabla u\nabla(\frac{u}{|u|}\zeta_t) =-\int_{B_+}|u|(1+|u|)\Phi\zeta_t. \end{align*} $$
By calculating the left hand side, we can obtain that
 $$ \begin{align} \begin{split}&\displaystyle\int_{B_+}|u|^{-1}|\nabla u|^p\zeta_t -\int_{B_+}|u|^{-3}|\nabla u|^{p-2}(u \cdot \nabla u)^2\zeta_t\\&\quad+\displaystyle\int_{B_+}|u|(1+|u|)\Phi\zeta_t +\int_{B_+}|\nabla u|^{p-2}\nabla \Phi\nabla\zeta_t=0. \end{split} \end{align} $$
$$ \begin{align} \begin{split}&\displaystyle\int_{B_+}|u|^{-1}|\nabla u|^p\zeta_t -\int_{B_+}|u|^{-3}|\nabla u|^{p-2}(u \cdot \nabla u)^2\zeta_t\\&\quad+\displaystyle\int_{B_+}|u|(1+|u|)\Phi\zeta_t +\int_{B_+}|\nabla u|^{p-2}\nabla \Phi\nabla\zeta_t=0. \end{split} \end{align} $$
In view of
![]() $|\nabla u|^2 \geq (u \cdot \nabla u)^2/|u|^2$
, the first and the second terms in the left hand side of (6.7) is nonnegative. Therefore, using (1.17) and (6.6), we can deduce that
$|\nabla u|^2 \geq (u \cdot \nabla u)^2/|u|^2$
, the first and the second terms in the left hand side of (6.7) is nonnegative. Therefore, using (1.17) and (6.6), we can deduce that
 $$ \begin{align*}&\displaystyle\int_{B_+}|u|(1+|u|)\Phi\zeta_t \leq |\int_{B_+}|\nabla u|^{p-2}\nabla \Phi\nabla\zeta_t|\\&\quad\leq \displaystyle\frac{1}{t}\int_{{B_+}\cap\{y;t\leq|y|\leq2t\}} |\nabla u|^{p-2}|\nabla \Phi| \leq \frac{1}{t}\|\nabla u\|_p^{p-2}\|\nabla\Phi\|_p t^{2/p}.\end{align*} $$
$$ \begin{align*}&\displaystyle\int_{B_+}|u|(1+|u|)\Phi\zeta_t \leq |\int_{B_+}|\nabla u|^{p-2}\nabla \Phi\nabla\zeta_t|\\&\quad\leq \displaystyle\frac{1}{t}\int_{{B_+}\cap\{y;t\leq|y|\leq2t\}} |\nabla u|^{p-2}|\nabla \Phi| \leq \frac{1}{t}\|\nabla u\|_p^{p-2}\|\nabla\Phi\|_p t^{2/p}.\end{align*} $$
When
![]() $t \to \infty $
, the right hand side converges to zero by virtue of
$t \to \infty $
, the right hand side converges to zero by virtue of
![]() $p>2$
. And hence so is the left hand side. This means
$p>2$
. And hence so is the left hand side. This means
![]() $|B_+|=0$
or
$|B_+|=0$
or
![]() $\Phi =0$
a.e. on
$\Phi =0$
a.e. on
![]() $\mathbb {R}^2$
. Thus, (6.1) is proved when
$\mathbb {R}^2$
. Thus, (6.1) is proved when
![]() $p>2$
.
$p>2$
.
Step 2. Multiplying (1.16) by u and integrating on
![]() $B_R(0)$
yield
$B_R(0)$
yield
 $$ \begin{align} \int_{B_R(0)}|u|^2(1-|u|^2) =\int_{B_R(0)} |\nabla u|^p - \int_{\partial B_R(0)}u|\nabla u|^{p-2}\partial_{\nu}ud\xi. \end{align} $$
$$ \begin{align} \int_{B_R(0)}|u|^2(1-|u|^2) =\int_{B_R(0)} |\nabla u|^p - \int_{\partial B_R(0)}u|\nabla u|^{p-2}\partial_{\nu}ud\xi. \end{align} $$
When
![]() $p \in (1,2)$
, we use (6.5) and (1.17) to get
$p \in (1,2)$
, we use (6.5) and (1.17) to get
 $$ \begin{align} \int_{\mathbb{R}^2}|u|^2(1-|u|^2) =\int_{\mathbb{R}^2} |\nabla u|^p <\infty. \end{align} $$
$$ \begin{align} \int_{\mathbb{R}^2}|u|^2(1-|u|^2) =\int_{\mathbb{R}^2} |\nabla u|^p <\infty. \end{align} $$
When
![]() $p>2$
, by (6.1) and (6.2), there holds
$p>2$
, by (6.1) and (6.2), there holds
 $$ \begin{align*}\left\vert\int_{\partial B_{R_k}}u|\nabla u|^{p-2}\partial_{\nu}ud\xi\right\vert \leq CR_k^{\frac{1}{p}-1}\left(R_k\int_{\partial B_{R_k}}|\nabla u|^pd\xi\right)^{1-\frac{1}{p}} |\partial B_{R_k}|^{\frac{1}{p}} \to 0 \end{align*} $$
$$ \begin{align*}\left\vert\int_{\partial B_{R_k}}u|\nabla u|^{p-2}\partial_{\nu}ud\xi\right\vert \leq CR_k^{\frac{1}{p}-1}\left(R_k\int_{\partial B_{R_k}}|\nabla u|^pd\xi\right)^{1-\frac{1}{p}} |\partial B_{R_k}|^{\frac{1}{p}} \to 0 \end{align*} $$
when
![]() $R_k \to \infty $
. From (6.8) with
$R_k \to \infty $
. From (6.8) with
![]() $R=R_k$
, we also deduce (6.9).
$R=R_k$
, we also deduce (6.9).
Multiply (1.16) by
![]() $(x \cdot \nabla u)$
and integrate on
$(x \cdot \nabla u)$
and integrate on
![]() $B_R(0)$
. Integrating by parts, we can see the left hand side
$B_R(0)$
. Integrating by parts, we can see the left hand side
 $$ \begin{align*}&-\displaystyle\int_{B_R}{\textrm{div}}(|\nabla u|^{p-2}\nabla u)(x \cdot \nabla u)\\&\quad=-R\displaystyle\int_{\partial B_R}|\nabla u|^{p-2}|\partial_{\nu}u|^2d\xi +\int_{B_R}|\nabla u|^p+\frac{1}{p}\int_{B_R} x\cdot \nabla (|\nabla u|^p)\\&\quad=-R\displaystyle\int_{\partial B_R}|\nabla u|^{p-2}|\partial_{\nu}u|^2d\xi +(1-\frac{2}{p})\int_{B_R}|\nabla u|^p+\frac{R}{p}\int_{\partial B_R} |\nabla u|^pd\xi.\end{align*} $$
$$ \begin{align*}&-\displaystyle\int_{B_R}{\textrm{div}}(|\nabla u|^{p-2}\nabla u)(x \cdot \nabla u)\\&\quad=-R\displaystyle\int_{\partial B_R}|\nabla u|^{p-2}|\partial_{\nu}u|^2d\xi +\int_{B_R}|\nabla u|^p+\frac{1}{p}\int_{B_R} x\cdot \nabla (|\nabla u|^p)\\&\quad=-R\displaystyle\int_{\partial B_R}|\nabla u|^{p-2}|\partial_{\nu}u|^2d\xi +(1-\frac{2}{p})\int_{B_R}|\nabla u|^p+\frac{R}{p}\int_{\partial B_R} |\nabla u|^pd\xi.\end{align*} $$
Therefore,
 $$ \begin{align} \begin{split}&\displaystyle\left(\frac{2}{p}-1\right)\int_{B_R}|\nabla u|^p +\frac{1}{2}\int_{B_R}(1-|u|^2)^2\\&\quad=\displaystyle\frac{R}{4}\int_{\partial B_R}(1-|u|^2)^2 d\xi -R\int_{\partial B_R}|\nabla u|^{p-2}|\partial_{\nu}u|^2d\xi\\&\qquad +\displaystyle\frac{R}{p}\int_{\partial B_R} |\nabla u|^pd\xi, \end{split} \end{align} $$
$$ \begin{align} \begin{split}&\displaystyle\left(\frac{2}{p}-1\right)\int_{B_R}|\nabla u|^p +\frac{1}{2}\int_{B_R}(1-|u|^2)^2\\&\quad=\displaystyle\frac{R}{4}\int_{\partial B_R}(1-|u|^2)^2 d\xi -R\int_{\partial B_R}|\nabla u|^{p-2}|\partial_{\nu}u|^2d\xi\\&\qquad +\displaystyle\frac{R}{p}\int_{\partial B_R} |\nabla u|^pd\xi, \end{split} \end{align} $$
and
 $$ \begin{align} \begin{split}&\displaystyle \left(1-\frac{2}{p}\right)\int_{B_R}|\nabla u|^p +\int_{B_R}(|u|^2-\frac{1}{2}|u|^4)\\&\quad=\displaystyle\frac{R}{2}\int_{\partial B_R}(|u|^2-\frac{1}{2}|u|^4) d\xi +R\int_{\partial B_R}|\nabla u|^{p-2}|\partial_{\nu}u|^2d\xi\\&\qquad -\displaystyle\frac{R}{p}\int_{\partial B_R} |\nabla u|^pd\xi. \end{split} \end{align} $$
$$ \begin{align} \begin{split}&\displaystyle \left(1-\frac{2}{p}\right)\int_{B_R}|\nabla u|^p +\int_{B_R}(|u|^2-\frac{1}{2}|u|^4)\\&\quad=\displaystyle\frac{R}{2}\int_{\partial B_R}(|u|^2-\frac{1}{2}|u|^4) d\xi +R\int_{\partial B_R}|\nabla u|^{p-2}|\partial_{\nu}u|^2d\xi\\&\qquad -\displaystyle\frac{R}{p}\int_{\partial B_R} |\nabla u|^pd\xi. \end{split} \end{align} $$
Step 3. We claim that there exists
![]() $R_0>0$
such that either
$R_0>0$
such that either
![]() $|u|<\frac {1}{4}$
or
$|u|<\frac {1}{4}$
or
![]() $|u|>T$
on
$|u|>T$
on
![]() $\mathbb {R}^2 \setminus B_{R_0}$
, where
$\mathbb {R}^2 \setminus B_{R_0}$
, where
 $$ \begin{align*}T:=\left \{\! \begin{array}{ll} 3/4, \quad & when \ p \in (1,2);\\ \sqrt{p/(3p-4)}, \quad & when \ p>2. \end{array}\right. \end{align*} $$
$$ \begin{align*}T:=\left \{\! \begin{array}{ll} 3/4, \quad & when \ p \in (1,2);\\ \sqrt{p/(3p-4)}, \quad & when \ p>2. \end{array}\right. \end{align*} $$
In fact, the following set is bounded
 $$ \begin{align*}S:=\left\{x \in \mathbb{R}^2; \frac{1}{4} \leq |u(x)| \leq T\right\}. \end{align*} $$
$$ \begin{align*}S:=\left\{x \in \mathbb{R}^2; \frac{1}{4} \leq |u(x)| \leq T\right\}. \end{align*} $$
Otherwise, there exists a sequence
![]() $x_m \to \infty $
(when
$x_m \to \infty $
(when
![]() $m \to \infty $
) such that
$m \to \infty $
) such that
![]() $\frac {1}{4} \leq |u(x_m)| \leq T$
. In view of (1.17) and (6.1), by the Tolksdorf theorem (cf. [Reference Tolksdorf22]), we have
$\frac {1}{4} \leq |u(x_m)| \leq T$
. In view of (1.17) and (6.1), by the Tolksdorf theorem (cf. [Reference Tolksdorf22]), we have
![]() $|\nabla u(x)| \leq C$
for each
$|\nabla u(x)| \leq C$
for each
![]() $x \in \mathbb {R}^2$
. Therefore, for
$x \in \mathbb {R}^2$
. Therefore, for
![]() $\sigma \in (0,1-T)$
, we can find
$\sigma \in (0,1-T)$
, we can find
![]() $\delta \in (0,1)$
which is independent of m such that
$\delta \in (0,1)$
which is independent of m such that
Therefore,
 $$ \begin{align} \int_{B(x_m,\delta)}|u|^2(1-|u|^2) \geq \left(\frac{1}{8}\right)^2 (1-(T+\sigma)^2)\pi\delta^2:=M_*. \end{align} $$
$$ \begin{align} \int_{B(x_m,\delta)}|u|^2(1-|u|^2) \geq \left(\frac{1}{8}\right)^2 (1-(T+\sigma)^2)\pi\delta^2:=M_*. \end{align} $$
Clearly,
![]() $M_*$
is independent of m. On the other hand, by (6.9), we can find
$M_*$
is independent of m. On the other hand, by (6.9), we can find
![]() $R_*>0$
such that
$R_*>0$
such that
 $$ \begin{align} \int_{|x|>R_*}|u|^2(1-|u|^2)<M_*. \end{align} $$
$$ \begin{align} \int_{|x|>R_*}|u|^2(1-|u|^2)<M_*. \end{align} $$
Noting
![]() $B(x_m,\delta ) \subset \mathbb {R}^2 \setminus B_{R_*}$
for sufficiently large m, (6.13) contradicts with (6.12). This implies S is bounded. Namely, there exists
$B(x_m,\delta ) \subset \mathbb {R}^2 \setminus B_{R_*}$
for sufficiently large m, (6.13) contradicts with (6.12). This implies S is bounded. Namely, there exists
![]() $R_0>0$
such that
$R_0>0$
such that
![]() $S \subset B_{R_0}$
. Since
$S \subset B_{R_0}$
. Since
![]() $\mathbb {R}^2 \setminus B_{R_0}$
is connected and u is continuous, then either
$\mathbb {R}^2 \setminus B_{R_0}$
is connected and u is continuous, then either
![]() $|u|<\frac {1}{4}$
or
$|u|<\frac {1}{4}$
or
![]() $|u|>T$
on
$|u|>T$
on
![]() $\mathbb {R}^2 \setminus B_{R_0}$
in view of the definition of S.
$\mathbb {R}^2 \setminus B_{R_0}$
in view of the definition of S.
Step 4. When
![]() $p \in (1,2)$
, we will prove Theorem 1.4.
$p \in (1,2)$
, we will prove Theorem 1.4.
When
![]() $|u|<\frac {1}{4}$
on
$|u|<\frac {1}{4}$
on
![]() $\mathbb {R}^2 \setminus B_{R_0}$
, (6.9) and (6.1) lead to
$\mathbb {R}^2 \setminus B_{R_0}$
, (6.9) and (6.1) lead to
This implies
 $$ \begin{align*}\frac{R_k}{2}\int_{\partial B_{R_k}}(|u|^2-\frac{1}{2}|u|^4) d\xi \to 0 \end{align*} $$
$$ \begin{align*}\frac{R_k}{2}\int_{\partial B_{R_k}}(|u|^2-\frac{1}{2}|u|^4) d\xi \to 0 \end{align*} $$
when
![]() $R_k \to \infty $
. Inserting this and (6.2) into (6.11) with
$R_k \to \infty $
. Inserting this and (6.2) into (6.11) with
![]() $R=R_k$
, we get
$R=R_k$
, we get
 $$ \begin{align} \left(1-\frac{2}{p}\right)\int_{\mathbb{R}^2}|\nabla u|^p +\int_{\mathbb{R}^2}(|u|^2-\frac{1}{2}|u|^4)=0. \end{align} $$
$$ \begin{align} \left(1-\frac{2}{p}\right)\int_{\mathbb{R}^2}|\nabla u|^p +\int_{\mathbb{R}^2}(|u|^2-\frac{1}{2}|u|^4)=0. \end{align} $$
Inserting (6.9) into (6.15) yields
 $$ \begin{align*}\left(\frac{3}{2}-\frac{2}{p}\right)\int_{\mathbb{R}^2}|u|^4=\left(2-\frac{2}{p}\right)\int_{\mathbb{R}^2}|u|^2 \geq \left(2-\frac{2}{p}\right)\int_{\mathbb{R}^2}|u|^4. \end{align*} $$
$$ \begin{align*}\left(\frac{3}{2}-\frac{2}{p}\right)\int_{\mathbb{R}^2}|u|^4=\left(2-\frac{2}{p}\right)\int_{\mathbb{R}^2}|u|^2 \geq \left(2-\frac{2}{p}\right)\int_{\mathbb{R}^2}|u|^4. \end{align*} $$
This implies
![]() $|u| \equiv 0$
.
$|u| \equiv 0$
.
When
![]() $|u|>3/4$
on
$|u|>3/4$
on
![]() $\mathbb {R}^2 \setminus B_{R_0}$
, (6.9) and (6.1) lead to
$\mathbb {R}^2 \setminus B_{R_0}$
, (6.9) and (6.1) lead to
This implies
 $$ \begin{align*}\frac{R_k}{4}\int_{\partial B_{R_k}}(1-|u|^2)^2 d\xi \to 0 \end{align*} $$
$$ \begin{align*}\frac{R_k}{4}\int_{\partial B_{R_k}}(1-|u|^2)^2 d\xi \to 0 \end{align*} $$
when
![]() $R_k \to \infty $
. Inserting this and (6.2) into (6.10), we get
$R_k \to \infty $
. Inserting this and (6.2) into (6.10), we get
 $$ \begin{align} \left(\frac{2}{p}-1\right)\int_{\mathbb{R}^2}|\nabla u|^p +\frac{1}{2}\int_{\mathbb{R}^2}(1-|u|^2)^2 =0. \end{align} $$
$$ \begin{align} \left(\frac{2}{p}-1\right)\int_{\mathbb{R}^2}|\nabla u|^p +\frac{1}{2}\int_{\mathbb{R}^2}(1-|u|^2)^2 =0. \end{align} $$
In view of
![]() $p \in (1,2)$
, (6.17) implies
$p \in (1,2)$
, (6.17) implies
![]() $|\nabla u|=1-|u|^2=0$
on
$|\nabla u|=1-|u|^2=0$
on
![]() $\mathbb {R}^2$
. Therefore,
$\mathbb {R}^2$
. Therefore,
![]() $u \equiv C$
with
$u \equiv C$
with
![]() $|C|=1$
.
$|C|=1$
.
Step 5. When
![]() $p>2$
, we will prove Theorem 1.4.
$p>2$
, we will prove Theorem 1.4.
When
![]() $|u|<\frac {1}{4}$
on
$|u|<\frac {1}{4}$
on
![]() $\mathbb {R}^2 \setminus B_{R_0}$
, by (6.1) and (6.15) we get
$\mathbb {R}^2 \setminus B_{R_0}$
, by (6.1) and (6.15) we get
![]() $u \equiv 0$
.
$u \equiv 0$
.
When
![]() $|u|>T$
on
$|u|>T$
on
![]() $\mathbb {R}^2 \setminus B_{R_0}$
, (6.17) still holds. Combining with (6.9) leads to
$\mathbb {R}^2 \setminus B_{R_0}$
, (6.17) still holds. Combining with (6.9) leads to
 $$ \begin{align*}\left(2-\frac{4}{p}\right)\int_{\mathbb{R}^2}|u|^2(1-|u|^2)=\int_{\mathbb{R}^2}(1-|u|^2)^2. \end{align*} $$
$$ \begin{align*}\left(2-\frac{4}{p}\right)\int_{\mathbb{R}^2}|u|^2(1-|u|^2)=\int_{\mathbb{R}^2}(1-|u|^2)^2. \end{align*} $$
Namely,
 $$ \begin{align*}\int_{\mathbb{R}^2}(1-|u|^2)[(3-\frac{4}{p})|u|^2-1]=0. \end{align*} $$
$$ \begin{align*}\int_{\mathbb{R}^2}(1-|u|^2)[(3-\frac{4}{p})|u|^2-1]=0. \end{align*} $$
By (6.1) and
![]() $|u|>T=\sqrt {p/(3p-4)}$
, we have
$|u|>T=\sqrt {p/(3p-4)}$
, we have
![]() $|u| \equiv 1$
on
$|u| \equiv 1$
on
![]() $\mathbb {R}^2$
. Inserting this into (6.9) we see that
$\mathbb {R}^2$
. Inserting this into (6.9) we see that
![]() $u \equiv C$
with
$u \equiv C$
with
![]() $|C|=1$
.
$|C|=1$
.
Acknowledgements
The author thanks the unknown referees very much for useful suggestions. Those suggestions have greatly improved this article. This research was supported by NNSF (11871278) of China.