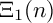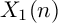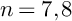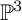1 Introduction
A line arrangement
![]() $\mathcal {C}=\ell _{1}+\dots +\ell _{k}$
is a finite union of lines
$\mathcal {C}=\ell _{1}+\dots +\ell _{k}$
is a finite union of lines
![]() $\ell _{j}$
in the projective plane
$\ell _{j}$
in the projective plane
![]() $\mathbb {P}^{2}$
. Line arrangements are ubiquitous objects studied in various fields such as topology, algebra, algebraic geometry, see, for instance, [Reference Suciu12], [Reference Yoshinaga16] for two surveys. In [Reference Roulleau9], the second author described a number of operators acting on line arrangements: if
$\mathbb {P}^{2}$
. Line arrangements are ubiquitous objects studied in various fields such as topology, algebra, algebraic geometry, see, for instance, [Reference Suciu12], [Reference Yoshinaga16] for two surveys. In [Reference Roulleau9], the second author described a number of operators acting on line arrangements: if
![]() $\mathfrak {n,m}$
are sets of integers at least
$\mathfrak {n,m}$
are sets of integers at least
![]() $2$
, the operator
$2$
, the operator ![]() associates to a line arrangement
associates to a line arrangement
![]() $\mathcal {C}$
the line arrangement
$\mathcal {C}$
the line arrangement ![]() which is the union of the lines that contain
which is the union of the lines that contain
![]() $n\in \mathfrak {n}$
points among the m-points of
$n\in \mathfrak {n}$
points among the m-points of
![]() $\mathcal {C}$
, for
$\mathcal {C}$
, for
![]() $m\in \mathfrak {m}$
(recall that an m-point of
$m\in \mathfrak {m}$
(recall that an m-point of
![]() $\mathcal {C}$
is a point where exactly m lines of
$\mathcal {C}$
is a point where exactly m lines of
![]() $\mathcal {C}$
meet). For example
$\mathcal {C}$
meet). For example ![]() is the union of the lines that contain exactly three double points of
is the union of the lines that contain exactly three double points of
![]() $\mathcal {C}$
(that line arrangement might be empty).
$\mathcal {C}$
(that line arrangement might be empty).
A labeled line arrangement
![]() $\mathcal {C}=(\ell _{1},\dots ,\ell _{k})$
is a line arrangement for which one fixes the order of the lines. The configuration of a labeled line arrangement
$\mathcal {C}=(\ell _{1},\dots ,\ell _{k})$
is a line arrangement for which one fixes the order of the lines. The configuration of a labeled line arrangement
![]() $\mathcal {C}$
is described by its associated matroid
$\mathcal {C}$
is described by its associated matroid
![]() $M=M(\mathcal {C})$
. Conversely, given a matroid M (a combinatorial object), one can look at line arrangements
$M=M(\mathcal {C})$
. Conversely, given a matroid M (a combinatorial object), one can look at line arrangements
![]() $\mathcal {C}$
for which
$\mathcal {C}$
for which
![]() $M(\mathcal {C})=M$
. When such a
$M(\mathcal {C})=M$
. When such a
![]() $\mathcal {C}$
exists, one says that
$\mathcal {C}$
exists, one says that
![]() $\mathcal {C}$
is a realization of M. Let us denote by
$\mathcal {C}$
is a realization of M. Let us denote by
![]() $\mathcal {R}=\mathcal {R}(M)$
the moduli space of realizations of M: a point of
$\mathcal {R}=\mathcal {R}(M)$
the moduli space of realizations of M: a point of
![]() $\mathcal {R}$
is the orbit under the action of the projective general linear group
$\mathcal {R}$
is the orbit under the action of the projective general linear group
![]() $\text {PGL}_{3}$
of a realization of M. The space of all realizations of M is denoted by
$\text {PGL}_{3}$
of a realization of M. The space of all realizations of M is denoted by
![]() $\mathfrak {U}=\mathfrak {U}(M)$
and there is a natural quotient map
$\mathfrak {U}=\mathfrak {U}(M)$
and there is a natural quotient map
![]() $\mathfrak {U}\to \mathcal {R}$
.
$\mathfrak {U}\to \mathcal {R}$
.
In [Reference Kühne and Roulleau5], we constructed a realizable matroid
![]() $M_{n}$
for any
$M_{n}$
for any
![]() $n\geq 7$
that is based on the regular n-gon. Interestingly, there exists an operator
$n\geq 7$
that is based on the regular n-gon. Interestingly, there exists an operator ![]() among the ones we described above (for example if
among the ones we described above (for example if
![]() $n=2k+1$
is odd, then
$n=2k+1$
is odd, then ![]() ) which acts non-trivially on
) which acts non-trivially on
![]() $\mathfrak {U}(M_n)$
: if
$\mathfrak {U}(M_n)$
: if
![]() $\mathcal {C}$
is a (generic) realization of
$\mathcal {C}$
is a (generic) realization of
![]() $M_{n},$
then
$M_{n},$
then ![]() is also a realization of
is also a realization of
![]() $M_{n}$
. We obtain in that way a dominant self-rational map
$M_{n}$
. We obtain in that way a dominant self-rational map
![]() $\unicode{x0142} $
on the realization space
$\unicode{x0142} $
on the realization space
![]() $\mathcal {R}_{n}=\mathcal {R}(M_{n})$
.
$\mathcal {R}_{n}=\mathcal {R}(M_{n})$
.
The main result of [Reference Kühne and Roulleau5] establishes that the realization space
![]() $\mathcal {R}_{n}$
is an open dense sub-scheme of the elliptic modular surface
$\mathcal {R}_{n}$
is an open dense sub-scheme of the elliptic modular surface
![]() $\Xi _{1}(n)$
, a well-studied surface, see, for example, Shioda’s paper [Reference Shioda11]. Recall that this surface
$\Xi _{1}(n)$
, a well-studied surface, see, for example, Shioda’s paper [Reference Shioda11]. Recall that this surface
![]() $\Xi _{1}(n)$
parametrizes (up to isomorphisms) triples
$\Xi _{1}(n)$
parametrizes (up to isomorphisms) triples
![]() $(E,t,p)$
of an elliptic curve and points
$(E,t,p)$
of an elliptic curve and points
![]() $t,p$
on E such that t has order n. The modular curve
$t,p$
on E such that t has order n. The modular curve
![]() $X_{1}(n)$
parametrizes (up to isomorphisms) pairs
$X_{1}(n)$
parametrizes (up to isomorphisms) pairs
![]() $(E,t)$
, where
$(E,t)$
, where
![]() $E,t$
are as above. The map
$E,t$
are as above. The map
![]() $(E,t,p)\to (E,t)$
defines an elliptic fibration on
$(E,t,p)\to (E,t)$
defines an elliptic fibration on
![]() $\Xi _{1}(n)$
, with fiber over the point
$\Xi _{1}(n)$
, with fiber over the point
![]() $(E,t)$
isomorphic to E. For any integer m, there is a natural multiplication by m rational map of the elliptic surface
$(E,t)$
isomorphic to E. For any integer m, there is a natural multiplication by m rational map of the elliptic surface
![]() $\Xi _{1}(n)$
. We obtain in [Reference Kühne and Roulleau5] that, through the identification of
$\Xi _{1}(n)$
. We obtain in [Reference Kühne and Roulleau5] that, through the identification of
![]() $\mathcal {R}_{n}$
as an open subscheme of
$\mathcal {R}_{n}$
as an open subscheme of
![]() $\Xi _{1}(n)$
, the rational self map
$\Xi _{1}(n)$
, the rational self map ![]() induced by
induced by ![]() is the multiplication by
is the multiplication by
![]() $-2$
map acting on
$-2$
map acting on
![]() $\Xi _{1}(n)$
, in particular
$\Xi _{1}(n)$
, in particular
![]() $\unicode{x0142} $
has degree
$\unicode{x0142} $
has degree
![]() $4$
.
$4$
.
The aim of the present paper is to study the peculiar cases when
![]() $n=7,8$
in more detail. In particular, we give another proof that the surface
$n=7,8$
in more detail. In particular, we give another proof that the surface
![]() $\mathcal {R}_{n}$
is an open dense subscheme of
$\mathcal {R}_{n}$
is an open dense subscheme of
![]() $\Xi _{1}(n),$
and the degree of
$\Xi _{1}(n),$
and the degree of ![]() is
is
![]() $4$
in these cases. From now on assume
$4$
in these cases. From now on assume
![]() $n\in \{7,8\}$
; in those cases, we obtain (singular) models of
$n\in \{7,8\}$
; in those cases, we obtain (singular) models of
![]() $\Xi _{1}(n)$
as quartic surfaces in
$\Xi _{1}(n)$
as quartic surfaces in
![]() $\mathbb {P}^{3}$
. There is a natural section
$\mathbb {P}^{3}$
. There is a natural section
![]() $\mathcal {R}_{n}\to \mathfrak {U}_{n}=\mathfrak {U}(M_{n})$
of the quotient map
$\mathcal {R}_{n}\to \mathfrak {U}_{n}=\mathfrak {U}(M_{n})$
of the quotient map
![]() $\mathfrak {U}_{n}\to \mathcal {R}_{n}$
, so that one may consider
$\mathfrak {U}_{n}\to \mathcal {R}_{n}$
, so that one may consider
![]() $\mathcal {R}_{n}$
as contained in
$\mathcal {R}_{n}$
as contained in
![]() $\mathfrak {U}_{n}$
, and therefore one may consider a class as a realization of
$\mathfrak {U}_{n}$
, and therefore one may consider a class as a realization of
![]() $M_{n}$
. Using that fact, we are able to give explicit polynomials for the action
$M_{n}$
. Using that fact, we are able to give explicit polynomials for the action ![]() of
of ![]() on
on
![]() $\mathcal {R}_n\subset \mathbb {P}^{3}$
.
$\mathcal {R}_n\subset \mathbb {P}^{3}$
.
Recall that a dynamical system is a pair ![]() of a variety X and a dominant rational map
of a variety X and a dominant rational map ![]() . A dynamical system
. A dynamical system ![]() is called semi-conjugated to a dynamical system
is called semi-conjugated to a dynamical system
![]() $(Y,\mu )$
if there exists a generically finite rational dominant map
$(Y,\mu )$
if there exists a generically finite rational dominant map
![]() $\pi :X\to Y$
such that
$\pi :X\to Y$
such that ![]() . A principal result of this article is the following.
. A principal result of this article is the following.
Theorem 1.1. For
![]() $n\in \{7,8\}$
, the dynamical system
$n\in \{7,8\}$
, the dynamical system ![]() is semi-conjugated to
is semi-conjugated to
![]() $(\mathbb {P}^{2},F)$
where
$(\mathbb {P}^{2},F)$
where
![]() $F:\mathbb {P}^{2}\dashrightarrow \mathbb {P}^{2}$
is an explicitly described rational self map; the dominant rational map
$F:\mathbb {P}^{2}\dashrightarrow \mathbb {P}^{2}$
is an explicitly described rational self map; the dominant rational map
![]() $\pi :\mathcal {R}_{n}\to \mathbb {P}^{2}$
such that
$\pi :\mathcal {R}_{n}\to \mathbb {P}^{2}$
such that ![]() is a double cover of
is a double cover of
![]() $\mathbb {P}^{2}$
branched along a sextic curve.
$\mathbb {P}^{2}$
branched along a sextic curve.
The surfaces
![]() $\Xi _{1}(7),\,\Xi _{1}(8)$
are K3 surfaces; to our knowledge these are the first examples of a degree
$\Xi _{1}(7),\,\Xi _{1}(8)$
are K3 surfaces; to our knowledge these are the first examples of a degree
![]() $>1$
dynamical system on a K3 surfaces that is semi-conjugated to the plane.
$>1$
dynamical system on a K3 surfaces that is semi-conjugated to the plane.
Let us describe the structure of this paper and some further results. In §2, we start by describing the line operators ![]() and general results on matroids. In §2.3, we study under which conditions a K3 surface which is the double cover of the
and general results on matroids. In §2.3, we study under which conditions a K3 surface which is the double cover of the
![]() $\mathbb {P}^2$
may be semi-conjugated to
$\mathbb {P}^2$
may be semi-conjugated to
![]() $\mathbb {P}^2$
. Subsequently, we study the case
$\mathbb {P}^2$
. Subsequently, we study the case
![]() $n=7$
in §3: we start by recalling the definition of the matroid
$n=7$
in §3: we start by recalling the definition of the matroid
![]() $M_{7}$
and then show that
$M_{7}$
and then show that ![]() induces a rational self map
induces a rational self map ![]() on the quartic surface
on the quartic surface
![]() $\mathcal {R}_{7}\subset \mathbb {P}^{3}$
. We then compute the degree of
$\mathcal {R}_{7}\subset \mathbb {P}^{3}$
. We then compute the degree of ![]() and prove that
and prove that
![]() $\mathcal {R}_{7}$
is an open subset of the elliptic modular surface
$\mathcal {R}_{7}$
is an open subset of the elliptic modular surface
![]() $\Xi _{1}(7)$
. The automorphism group of the matroid
$\Xi _{1}(7)$
. The automorphism group of the matroid
![]() $M_{7}$
is the order
$M_{7}$
is the order
![]() $42$
Frobenius group. There is a natural action of that group on the surface
$42$
Frobenius group. There is a natural action of that group on the surface
![]() $\mathcal {R}_{7}$
. We show that this action is faithful. The quotient surface
$\mathcal {R}_{7}$
. We show that this action is faithful. The quotient surface ![]() is the moduli space for unlabeled line arrangements coming from realizations of
is the moduli space for unlabeled line arrangements coming from realizations of
![]() $M_{7}$
: we obtain that this is a rational surface. In §3.6, we describe explicitly the semi-conjugacy of
$M_{7}$
: we obtain that this is a rational surface. In §3.6, we describe explicitly the semi-conjugacy of
![]() $\mathcal {R}_{7}$
(or equivalently
$\mathcal {R}_{7}$
(or equivalently
![]() $\Xi _1(7)$
) with
$\Xi _1(7)$
) with
![]() $\mathbb {P}^{2}$
. The branch loci of the double cover
$\mathbb {P}^{2}$
. The branch loci of the double cover
![]() $\Xi _1(7)\to \mathbb {P}^2$
is the union of a line and a singular quintic curve which we describe. §4 follows a similar pattern for the case
$\Xi _1(7)\to \mathbb {P}^2$
is the union of a line and a singular quintic curve which we describe. §4 follows a similar pattern for the case
![]() $n=8$
. In that case, the branch loci of the double cover
$n=8$
. In that case, the branch loci of the double cover
![]() $\Xi _1(8)\to \mathbb {P}^2$
is union of a conic and a singular quartic curve. We moreover describe some
$\Xi _1(8)\to \mathbb {P}^2$
is union of a conic and a singular quartic curve. We moreover describe some
![]() $3$
-periodic line arrangements for
$3$
-periodic line arrangements for ![]() ; their classes are fixed points for the action of
; their classes are fixed points for the action of ![]() on
on
![]() $\mathcal {R}_8$
.
$\mathcal {R}_8$
.
We remark that for
![]() $n=9$
, one may similarly obtain that
$n=9$
, one may similarly obtain that
![]() $\mathcal {R}_9$
(contained as a sextic surface in
$\mathcal {R}_9$
(contained as a sextic surface in
![]() $\mathbb {P}^3$
) is birational to
$\mathbb {P}^3$
) is birational to
![]() $\Xi _1(9)$
. That elliptic surface is no longer a K3 surface and we could not find a semi-conjugacy with the plane.
$\Xi _1(9)$
. That elliptic surface is no longer a K3 surface and we could not find a semi-conjugacy with the plane.
Computations in this paper are based on Magma [Reference Bosma, Cannon and Playoust1] and OSCAR [Reference Corey, Kühne and Schröter3]. The arXiv ancillary file of this paper contains some data related to these computations.
2 Notations and definitions.
Throughout this article we assume to be working over the field
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
2.1 Line arrangements and the operator 
A line arrangement
![]() $\mathcal {C}=\ell _{1}+\dots +\ell _{n}$
is a union of finitely many distinct lines in
$\mathcal {C}=\ell _{1}+\dots +\ell _{n}$
is a union of finitely many distinct lines in
![]() $\mathbb {P}^{2}$
. A labeled line arrangement
$\mathbb {P}^{2}$
. A labeled line arrangement
![]() $\mathcal {C}=(\ell _{1},\dots ,\ell _{n})$
is a line arrangement with a numbering of the lines. We sometime put a superscript
$\mathcal {C}=(\ell _{1},\dots ,\ell _{n})$
is a line arrangement with a numbering of the lines. We sometime put a superscript
![]() $^{\ell }$
(resp.
$^{\ell }$
(resp.
![]() $^{u}$
) when we want to emphasize that an arrangement or related objects has (resp. does not have) a labeling.
$^{u}$
) when we want to emphasize that an arrangement or related objects has (resp. does not have) a labeling.
For an integer
![]() $k\geq 2$
, a k-point of the line arrangement
$k\geq 2$
, a k-point of the line arrangement
![]() $\mathcal {C}$
is a point where exactly k lines of
$\mathcal {C}$
is a point where exactly k lines of
![]() $\mathcal {C}$
meet. As in [Reference Roulleau9], for a subset
$\mathcal {C}$
meet. As in [Reference Roulleau9], for a subset
![]() $\mathfrak {n}$
of integers at least
$\mathfrak {n}$
of integers at least
![]() $2$
, let us denote by
$2$
, let us denote by
![]() $\mathcal {P}_{\mathfrak {n}}(\mathcal {C})$
the set of k-points of
$\mathcal {P}_{\mathfrak {n}}(\mathcal {C})$
the set of k-points of
![]() $\mathcal {C}$
for all
$\mathcal {C}$
for all
![]() $k\in \mathfrak {n}$
. We denote by
$k\in \mathfrak {n}$
. We denote by
![]() $t_{k}=t_{k}(\mathcal {C})=|\mathcal {P}_{\{k\}}(\mathcal {C})|$
the number of k-points of
$t_{k}=t_{k}(\mathcal {C})=|\mathcal {P}_{\{k\}}(\mathcal {C})|$
the number of k-points of
![]() $\mathcal {C}$
. For a finite set of point
$\mathcal {C}$
. For a finite set of point
![]() $\mathcal {P}$
in
$\mathcal {P}$
in
![]() $\mathbb {P}^{2}$
and
$\mathbb {P}^{2}$
and
![]() $\mathfrak {n}$
as above, we denote by
$\mathfrak {n}$
as above, we denote by
![]() $\mathcal {L}_{\mathfrak {n}}(\mathcal {P})$
the set of lines which contain exactly n points in
$\mathcal {L}_{\mathfrak {n}}(\mathcal {P})$
the set of lines which contain exactly n points in
![]() $\mathcal {P}$
for some
$\mathcal {P}$
for some
![]() $n\in \mathfrak {n}$
.
$n\in \mathfrak {n}$
.
For subsets
![]() $\mathfrak {n,m}$
of integers at least
$\mathfrak {n,m}$
of integers at least
![]() $2$
, let us denote by
$2$
, let us denote by ![]() the line arrangement that contains all lines of
the line arrangement that contains all lines of
![]() $\mathbb {P}^{2}$
containing exactly m points of
$\mathbb {P}^{2}$
containing exactly m points of
![]() $\mathcal {P}_{\mathfrak {n}}(\mathcal {C})$
for
$\mathcal {P}_{\mathfrak {n}}(\mathcal {C})$
for
![]() $m\in \mathfrak {m}$
. For example
$m\in \mathfrak {m}$
. For example ![]() is the union of the lines that contain three or four double points of
is the union of the lines that contain three or four double points of
![]() $\mathcal {C}$
. The arrangement could be the empty arrangement if no such lines exists.
$\mathcal {C}$
. The arrangement could be the empty arrangement if no such lines exists.
2.2 Matroids and the period map of the moduli of a matroid.
A matroid is a fundamental and actively studied object in combinatorics. Matroids generalize linear dependency in vector spaces as well as forests in graphs. See, for example, [Reference Oxley8] for a comprehensive treatment of matroids. We just briefly mention a few concepts about matroids that are relevant for this article.
A matroid is a pair
![]() $M=(E,\mathcal {B})$
, where E is a finite ground set of elements called atoms and
$M=(E,\mathcal {B})$
, where E is a finite ground set of elements called atoms and
![]() $\mathcal {B}$
is a nonempty collection of subsets of E, called bases, satisfying an exchange property reminiscent from linear algebra.
$\mathcal {B}$
is a nonempty collection of subsets of E, called bases, satisfying an exchange property reminiscent from linear algebra.
The prime examples of matroids arise by choosing a finite set E of vectors in a vector space and declaring the maximal linearly independent subsets of E as bases. In our case we obtain matroids through line arrangements: If
![]() $\mathcal {C}=(\ell _{1},\dots ,\ell _{m})$
is a labeled line arrangement, the subsets
$\mathcal {C}=(\ell _{1},\dots ,\ell _{m})$
is a labeled line arrangement, the subsets
![]() $\{i,j,k\}\subseteq \{1,\dots ,m\}$
such that the lines
$\{i,j,k\}\subseteq \{1,\dots ,m\}$
such that the lines
![]() $\ell _{i},\ell _{j},\ell _{k}$
meet in three distinct points are the bases of a matroid
$\ell _{i},\ell _{j},\ell _{k}$
meet in three distinct points are the bases of a matroid
![]() $M(\mathcal {C})$
over the set
$M(\mathcal {C})$
over the set
![]() $\{1,\dots ,m\}$
. We say that
$\{1,\dots ,m\}$
. We say that
![]() $M(\mathcal {C})$
is the matroid associated to
$M(\mathcal {C})$
is the matroid associated to
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
We denote by ![]() the automorphism group of the matroid M, that is, the set of isomorphisms from M to M.
the automorphism group of the matroid M, that is, the set of isomorphisms from M to M.
A realization (over some field) of a matroid
![]() $M=(E,\mathcal {B})$
is a converse operation to the association
$M=(E,\mathcal {B})$
is a converse operation to the association
![]() $\mathcal {C}\to M(\mathcal {C})$
: it is a
$\mathcal {C}\to M(\mathcal {C})$
: it is a
![]() $3\times m$
-matrix with non-zero columns
$3\times m$
-matrix with non-zero columns
![]() $C_{1},\dots ,C_{m}$
, which are considered up to a multiplication by a scalar (thus as point in the projective plane) such that a subset
$C_{1},\dots ,C_{m}$
, which are considered up to a multiplication by a scalar (thus as point in the projective plane) such that a subset
![]() $\{i_{1},i_{2},i_{3}\}$
of E of size
$\{i_{1},i_{2},i_{3}\}$
of E of size
![]() $3$
is a basis if and only if the
$3$
is a basis if and only if the
![]() $3\times 3$
minor
$3\times 3$
minor
![]() $|C_{i_{1}},C_{i_{2}},C_{i_{3}}|$
is nonzero. We denote by
$|C_{i_{1}},C_{i_{2}},C_{i_{3}}|$
is nonzero. We denote by
![]() $\ell _{i}$
the line with normal vector the point
$\ell _{i}$
the line with normal vector the point
![]() $C_{i}\in \mathbb {P}^{2}$
.
$C_{i}\in \mathbb {P}^{2}$
.
If
![]() $\mathcal {C}=(\ell _{1},\dots ,\ell _{m})$
is a realization of M and
$\mathcal {C}=(\ell _{1},\dots ,\ell _{m})$
is a realization of M and
![]() $\gamma \in PGL_{3}$
, then
$\gamma \in PGL_{3}$
, then
![]() $(\gamma \ell _{1},\dots ,\gamma \ell _{m})$
is another realization of M; we denote by
$(\gamma \ell _{1},\dots ,\gamma \ell _{m})$
is another realization of M; we denote by
![]() $[\mathcal {C}]$
the orbit of
$[\mathcal {C}]$
the orbit of
![]() $\mathcal {C}$
under that action of
$\mathcal {C}$
under that action of
![]() $PGL_{3}$
. The moduli space
$PGL_{3}$
. The moduli space
![]() $\mathcal {R}(M)$
of realizations of M parametrizes the orbits
$\mathcal {R}(M)$
of realizations of M parametrizes the orbits
![]() $[\mathcal {C}]$
of realizations. A more detailed introduction to these moduli spaces together with a description of a software package in OSCAR that can compute these spaces is given in [Reference Corey, Kühne and Schröter3].
$[\mathcal {C}]$
of realizations. A more detailed introduction to these moduli spaces together with a description of a software package in OSCAR that can compute these spaces is given in [Reference Corey, Kühne and Schröter3].
In this article, we always assume that each subset of three elements of the first four atoms is a basis (otherwise, we replace M by a matroid isomorphic to it). Then in the moduli space
![]() $\mathcal {R}(M)$
, one can always map the first four vectors of
$\mathcal {R}(M)$
, one can always map the first four vectors of
![]() $\mathcal {C}\in [\mathcal {C}]$
to a fixed projective basis, so that each element
$\mathcal {C}\in [\mathcal {C}]$
to a fixed projective basis, so that each element
![]() $[\mathcal {C}]$
of
$[\mathcal {C}]$
of
![]() $\mathcal {R}(M)$
has a canonical representative, which we will identify with
$\mathcal {R}(M)$
has a canonical representative, which we will identify with
![]() $[\mathcal {C}]$
.
$[\mathcal {C}]$
.
A useful tool for the computations related to the moduli space
![]() $\mathcal {R}=\mathcal {R}(M)$
of realizations of a matroid M is what we call the period map: Let us denote by
$\mathcal {R}=\mathcal {R}(M)$
of realizations of a matroid M is what we call the period map: Let us denote by
![]() $\mathfrak {U}=\mathfrak {U}(M)$
the scheme of all realizations of M in
$\mathfrak {U}=\mathfrak {U}(M)$
the scheme of all realizations of M in
![]() $\mathbb {P}^{2}$
. By analogy with similar objects, we call the quotient map
$\mathbb {P}^{2}$
. By analogy with similar objects, we call the quotient map
the period map; a point c of
![]() $\mathcal {R}=\mathcal {R}(M)$
is the class
$\mathcal {R}=\mathcal {R}(M)$
is the class
![]() $c=[\mathcal {C}]$
of a realization
$c=[\mathcal {C}]$
of a realization
![]() $\mathcal {C}$
. Once a basis is fixed, each class c has a unique representative
$\mathcal {C}$
. Once a basis is fixed, each class c has a unique representative
![]() $\mathcal {C}_{0}$
and we can (and we will) identify c with that representative.
$\mathcal {C}_{0}$
and we can (and we will) identify c with that representative.
It often occurs that
![]() $\mathcal {R}$
is embedded in a space
$\mathcal {R}$
is embedded in a space
![]() $\mathbb {S}=\mathbb {S}(y_{1},\dots ,y_{k})$
(affine or projective) of small dimension, like
$\mathbb {S}=\mathbb {S}(y_{1},\dots ,y_{k})$
(affine or projective) of small dimension, like
![]() $\mathbb {P}^{3}$
. The coordinates of the normal vectors
$\mathbb {P}^{3}$
. The coordinates of the normal vectors
![]() $n^{(j)}=(n_{1}^{(j)}:n_{2}^{(j)}:n_{3}^{(j)})$
of
$n^{(j)}=(n_{1}^{(j)}:n_{2}^{(j)}:n_{3}^{(j)})$
of
![]() $\mathcal {C}_{0}$
are then polynomials
$\mathcal {C}_{0}$
are then polynomials
![]() $n_{1}^{(j)}=P_{1}^{(j)}(y),\dots ,n_{3}^{(j)}=P_{3}^{(j)}(y)$
in the coordinates
$n_{1}^{(j)}=P_{1}^{(j)}(y),\dots ,n_{3}^{(j)}=P_{3}^{(j)}(y)$
in the coordinates
![]() $y_{1},\dots ,y_{k}$
of
$y_{1},\dots ,y_{k}$
of
![]() $\mathcal {R}$
in
$\mathcal {R}$
in
![]() $\mathbb {S}$
.
$\mathbb {S}$
.
One often arrives at the natural question on computing the point
![]() $y=(y_{1},\dots ,y_{k})$
in
$y=(y_{1},\dots ,y_{k})$
in
![]() $\mathcal {R}$
from the knowledge of the normal vectors n. In other words, we need an explicit form of the period map
$\mathcal {R}$
from the knowledge of the normal vectors n. In other words, we need an explicit form of the period map
![]() $\mathfrak {q}$
as a map from
$\mathfrak {q}$
as a map from
![]() $\mathfrak {U}$
to the scheme
$\mathfrak {U}$
to the scheme
![]() $\mathcal {R}$
embedded in the space
$\mathcal {R}$
embedded in the space
![]() $\mathbb {S}$
. The answer to that problem are polynomials (or rational functions)
$\mathbb {S}$
. The answer to that problem are polynomials (or rational functions)
![]() $Q_{1},\dots ,Q_{k}$
in the coordinates of the normal vectors
$Q_{1},\dots ,Q_{k}$
in the coordinates of the normal vectors
![]() $n^{(1)},\dots ,n^{(m)}$
etc.; here m is the number of lines in an arrangement.
$n^{(1)},\dots ,n^{(m)}$
etc.; here m is the number of lines in an arrangement.
2.3 Degree two K3 surfaces semi-conjugated to the plane.
Let
![]() $C_{1}:Q_{1}=0$
be a sextic curve with at most ADE singularities, so that the desingularization
$C_{1}:Q_{1}=0$
be a sextic curve with at most ADE singularities, so that the desingularization
![]() $X^{s}$
of the associated double cover
$X^{s}$
of the associated double cover
is a K3 surface. Let
![]() $F:\mathbb {P}^{2}\to \mathbb {P}^{2}$
be a rational self-map defined by coprime homogeneous polynomials
$F:\mathbb {P}^{2}\to \mathbb {P}^{2}$
be a rational self-map defined by coprime homogeneous polynomials
![]() $(F_{1},F_{2},F_{3})$
of degree m. Suppose that
$(F_{1},F_{2},F_{3})$
of degree m. Suppose that
![]() $F^{*}C_{1}=C_{1}+2D$
, for an effective divisor D; in algebraic terms, that means that we assume that
$F^{*}C_{1}=C_{1}+2D$
, for an effective divisor D; in algebraic terms, that means that we assume that
for some polynomial R. Then the following relation holds
where
![]() $z=(z_{1}:z_{2}:z_{3})\in \mathbb {P}^{2}$
. Hence, the rational map
$z=(z_{1}:z_{2}:z_{3})\in \mathbb {P}^{2}$
. Hence, the rational map
is a rational self-map acting on the K3 surface
![]() $X^{s}$
. Let
$X^{s}$
. Let
![]() $\pi :X\to \mathbb {P}^{2}$
be the double cover map. The following diagram
$\pi :X\to \mathbb {P}^{2}$
be the double cover map. The following diagram
 $$ \begin{align} \begin{array}{ccc} X & \stackrel{\tilde{F}}{\dashrightarrow} & X\\ \pi\downarrow & & \pi\downarrow\\ \mathbb{P}^{2} & \stackrel{F}{\dashrightarrow} & \mathbb{P}^{2,} \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ccc} X & \stackrel{\tilde{F}}{\dashrightarrow} & X\\ \pi\downarrow & & \pi\downarrow\\ \mathbb{P}^{2} & \stackrel{F}{\dashrightarrow} & \mathbb{P}^{2,} \end{array} \end{align} $$
is commutative and, by analogy with other dynamical systems, we say that the dynamical system
![]() $(X,\tilde {F})$
is semi-conjugated to
$(X,\tilde {F})$
is semi-conjugated to
![]() $(\mathbb {P}^{2},F)$
.
$(\mathbb {P}^{2},F)$
.
Example 2.1. Let C be an irreducible curve of degree
![]() $6$
with
$6$
with
![]() $10$
nodes. A Coble surface Y is the blow-up of
$10$
nodes. A Coble surface Y is the blow-up of
![]() $\mathbb {P}^{2}$
at the
$\mathbb {P}^{2}$
at the
![]() $10$
nodal singularities of C. The group of birational transformations G preserving C is infinite, it is generated by Bertini involutions centered at the nodal points of C. When C is generic, the group G lifts to Y and the elements of G become automorphisms of Y. The automorphism group
$10$
nodal singularities of C. The group of birational transformations G preserving C is infinite, it is generated by Bertini involutions centered at the nodal points of C. When C is generic, the group G lifts to Y and the elements of G become automorphisms of Y. The automorphism group ![]() preserves the pull-back
preserves the pull-back
![]() $C'$
of C, thus taking the double cover of Y branched over
$C'$
of C, thus taking the double cover of Y branched over
![]() $C'$
, one gets a smooth K3 surface X and the group G is in fact the automorphism group of X (see, e.g., [Reference Cantat and Dolgachev2]). The surface X is also the minimal desingularization of the double cover branched over C and the diagram (2.1) is commutative.
$C'$
, one gets a smooth K3 surface X and the group G is in fact the automorphism group of X (see, e.g., [Reference Cantat and Dolgachev2]). The surface X is also the minimal desingularization of the double cover branched over C and the diagram (2.1) is commutative.
3 The heptagon.
3.1
 is a rational self-map on
is a rational self-map on
 $ \mathcal {R}_{7}$
and
$ \mathcal {R}_{7}$
and
 $ \mathfrak {U}_7.$
$ \mathfrak {U}_7.$
3.1.1 Definition of the matroid
 $M_{7}.$
$M_{7}.$
The matroid
![]() $M_{7}$
has
$M_{7}$
has
![]() $14$
atoms
$14$
atoms
![]() $1,\dots ,7,1',\dots ,7'$
and the bases are the triples
$1,\dots ,7,1',\dots ,7'$
and the bases are the triples
![]() $\{a,b,c\}$
with
$\{a,b,c\}$
with
![]() $\{a,b\}\subset \{1,\dots ,7\}$
and
$\{a,b\}\subset \{1,\dots ,7\}$
and
![]() $c\in \{1',\dots ,7'\}$
such that
$c\in \{1',\dots ,7'\}$
such that
![]() $a+b\neq 2c\ \mod 7$
. A sketch of
$a+b\neq 2c\ \mod 7$
. A sketch of
![]() $M_7$
is described in Figure 1, where the atoms
$M_7$
is described in Figure 1, where the atoms
![]() $i\in \{1,\dots ,7\}$
and
$i\in \{1,\dots ,7\}$
and
![]() $j\in \{1',\dots ,7'\}$
correspond to the lines
$j\in \{1',\dots ,7'\}$
correspond to the lines
![]() $\ell _i$
and
$\ell _i$
and
![]() $\ell _j'$
, resp., and three lines form a basis if they do not meet in one point. Note that the central singularity of arrangement in Figure 1 is not part of the matroid and therefore removed.
$\ell _j'$
, resp., and three lines form a basis if they do not meet in one point. Note that the central singularity of arrangement in Figure 1 is not part of the matroid and therefore removed.

Figure 1 The matroid
![]() $M_{7}$
whose construction is based on the regular heptagon.
$M_{7}$
whose construction is based on the regular heptagon.
Let
![]() $\mathcal {A}_{1}$
be a generic line arrangement realizing the matroid
$\mathcal {A}_{1}$
be a generic line arrangement realizing the matroid
![]() $M_{7}$
. We write
$M_{7}$
. We write
![]() $\mathcal {A}_{1}=\mathcal {C}_{0}\cup \mathcal {C}_{1}$
where
$\mathcal {A}_{1}=\mathcal {C}_{0}\cup \mathcal {C}_{1}$
where
![]() $\mathcal {C}_{0}$
are the first seven lines and
$\mathcal {C}_{0}$
are the first seven lines and
![]() $\mathcal {C}_{1}$
are the seven last ones. By the combinatorics of the matroid
$\mathcal {C}_{1}$
are the seven last ones. By the combinatorics of the matroid
![]() $M_{7}$
and the genericity assumption, the property
$M_{7}$
and the genericity assumption, the property ![]() holds, and – that will be important for us – the image of
holds, and – that will be important for us – the image of
![]() $\mathcal {C}_{0}$
by the operator
$\mathcal {C}_{0}$
by the operator ![]() has a natural labeling: for any
has a natural labeling: for any
![]() $j\in \{1,\dots ,7\}$
, the six line arrangement
$j\in \{1,\dots ,7\}$
, the six line arrangement
 $$ \begin{align} H_{j}=\sum_{k\in\{1,\dots,7\},\,k\neq j}\ell_{k{,}} \end{align} $$
$$ \begin{align} H_{j}=\sum_{k\in\{1,\dots,7\},\,k\neq j}\ell_{k{,}} \end{align} $$
is such that the line arrangement ![]() is a unique line
is a unique line
![]() $\ell _{j}'$
, moreover:
$\ell _{j}'$
, moreover:
Since ![]() , to shorten our notations, we will often speak of
, to shorten our notations, we will often speak of
![]() $\mathcal {C}_{0}$
as a realization of
$\mathcal {C}_{0}$
as a realization of
![]() $M_{7}$
instead of
$M_{7}$
instead of
![]() $\mathcal {C}_{0}\cup \mathcal {C}_{1}$
.
$\mathcal {C}_{0}\cup \mathcal {C}_{1}$
.
The singularities of
![]() $\mathcal {C}_{0}$
(resp.
$\mathcal {C}_{0}$
(resp.
![]() $\mathcal {C}_{1}$
) are
$\mathcal {C}_{1}$
) are
![]() $21$
double points. The
$21$
double points. The
![]() $21$
singularities on
$21$
singularities on
![]() $\mathcal {C}_{0}$
become the triple points on
$\mathcal {C}_{0}$
become the triple points on
![]() $\mathcal {C}_{0}\cup \mathcal {C}_{1}$
, moreover
$\mathcal {C}_{0}\cup \mathcal {C}_{1}$
, moreover
![]() $t_{2}(\mathcal {C}_{0}\cup \mathcal {C}_{1})=28$
.
$t_{2}(\mathcal {C}_{0}\cup \mathcal {C}_{1})=28$
.
3.1.2 Equation of the quartic surface
 $Z_7$
and realization space of
$Z_7$
and realization space of
 $M_{7.}$
$M_{7.}$
Consider
![]() $Z_7$
, the quartic surface in
$Z_7$
, the quartic surface in
![]() $\mathbb {P}^{3}$
given by the equation
$\mathbb {P}^{3}$
given by the equation
The eight singularities of
![]() $Z_7$
are of type
$Z_7$
are of type
![]() $4A_{1}+A_{2}+3A_{3},$
at the points respectively
$4A_{1}+A_{2}+3A_{3},$
at the points respectively
 $$\begin{align*}\begin{array}{c} s_{1}=(0:0:0:1),s_{2}=(1:0:0:1),s_{3}=(0:0:1:0),s_{4}=(1:0:1:0),\\ s_{5}=(0:1:0:0),s_{6}=(0:1:0:1),s_{7}=(1:-1:1:0),s_{8}=(1:0:0:0). \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{c} s_{1}=(0:0:0:1),s_{2}=(1:0:0:1),s_{3}=(0:0:1:0),s_{4}=(1:0:1:0),\\ s_{5}=(0:1:0:0),s_{6}=(0:1:0:1),s_{7}=(1:-1:1:0),s_{8}=(1:0:0:0). \end{array} \end{align*}$$
The minimal desingularization of
![]() $Z_7$
is a K3 surface which we denote by
$Z_7$
is a K3 surface which we denote by
![]() $Z_7^{s}$
. Let
$Z_7^{s}$
. Let
![]() $x_{1},x_{2},x_{3}$
be the coordinates on the affine chart
$x_{1},x_{2},x_{3}$
be the coordinates on the affine chart
![]() $y_{4}\neq 0$
. For a generic point
$y_{4}\neq 0$
. For a generic point
![]() $x=(x_{1},x_{2},x_{3})$
on the surface
$x=(x_{1},x_{2},x_{3})$
on the surface
![]() $Z_7$
in the chart
$Z_7$
in the chart
![]() $y_{4}\neq 0$
, let us define the labeled arrangement of seven lines
$y_{4}\neq 0$
, let us define the labeled arrangement of seven lines
![]() $\mathfrak {\mathcal {C}}_{0}=\mathfrak {\mathcal {C}}_{0}(x)$
with normal vectors the points
$\mathfrak {\mathcal {C}}_{0}=\mathfrak {\mathcal {C}}_{0}(x)$
with normal vectors the points
![]() $p_{1},\dots ,p_{7}$
respectively defined by
$p_{1},\dots ,p_{7}$
respectively defined by
 $$ \begin{align} \begin{array}{c} (1:0:0),(0:1:0),(0:0:1),(-1:1:1)\\ (-x_{1}x_{2}^{2}-x_{1}x_{2}x_{3}+x_{1}x_{2}-x_{2}x_{3}+x_{3}\,:\,x_{1}x_{2}+x_{1}x_{3}-x_{1}\,:\,x_{2}-1)\\ (-x_{1}x_{2}^{2}-x_{1}x_{2}x_{3}+x_{1}x_{2}-x_{2}x_{3}+x_{3}\,:\,x_{1}x_{2}+x_{1}x_{3}-x_{1}+x_{2}^{2}\\ +x_{2}x_{3}-2x_{2}-x_{3}+1\,:\,x_{2}^{2}+x_{2}x_{3}-x_{2}-x_{3})\\ (-x_{1}x_{2}^{2}-x_{1}x_{2}x_{3}+x_{1}x_{2}+x_{3}^{2}\,:\,x_{1}x_{2}+x_{1}x_{3}-x_{1}-x_{2}x_{3}\\ -x_{3}^{2}+x_{3}\,:\,x_{2}^{2}+x_{2}x_{3}-x_{2}-x_{3}). \end{array} \end{align} $$
$$ \begin{align} \begin{array}{c} (1:0:0),(0:1:0),(0:0:1),(-1:1:1)\\ (-x_{1}x_{2}^{2}-x_{1}x_{2}x_{3}+x_{1}x_{2}-x_{2}x_{3}+x_{3}\,:\,x_{1}x_{2}+x_{1}x_{3}-x_{1}\,:\,x_{2}-1)\\ (-x_{1}x_{2}^{2}-x_{1}x_{2}x_{3}+x_{1}x_{2}-x_{2}x_{3}+x_{3}\,:\,x_{1}x_{2}+x_{1}x_{3}-x_{1}+x_{2}^{2}\\ +x_{2}x_{3}-2x_{2}-x_{3}+1\,:\,x_{2}^{2}+x_{2}x_{3}-x_{2}-x_{3})\\ (-x_{1}x_{2}^{2}-x_{1}x_{2}x_{3}+x_{1}x_{2}+x_{3}^{2}\,:\,x_{1}x_{2}+x_{1}x_{3}-x_{1}-x_{2}x_{3}\\ -x_{3}^{2}+x_{3}\,:\,x_{2}^{2}+x_{2}x_{3}-x_{2}-x_{3}). \end{array} \end{align} $$
Let us also define the lines arrangement
![]() $\mathcal {C}_{1}=\mathcal {C}_{1}(x)$
with normal vectors
$\mathcal {C}_{1}=\mathcal {C}_{1}(x)$
with normal vectors
 $$ \begin{align} \begin{array}{c} (-x_{1}x_{2}^{2}-x_{1}x_{2}x_{3}+x_{1}x_{2}+x_{3}^{2}\,:\,x_{1}x_{2}^{2}+2x_{1}x_{2}x_{3}-x_{1}x_{2}+x_{1}x_{3}^{2}\\ -x_{1}x_{3}-x_{2}^{2}x_{3}-2x_{2}x_{3}^{2}+x_{2}x_{3}-x_{3}^{3}+x_{3}^{2}\,:\,x_{2}^{2}+x_{2}x_{3}-x_{2}-x_{3}),\\ (-x_{1}x_{2}-x_{1}x_{3}+x_{1}\,:\,x_{1}x_{2}+x_{1}x_{3}-x_{1}\,:\,x_{2}-1),(-x_{2}:1:0),\\ (-x_{1}x_{2}^{3}-2x_{1}x_{2}^{2}x_{3}+x_{1}x_{2}^{2}-x_{1}x_{2}x_{3}^{2}+x_{1}x_{2}x_{3}-x_{2}^{2}x_{3}-x_{2}x_{3}^{2}+x_{2}x_{3}\\ +x_{3}^{2}\,:\,x_{1}x_{2}+x_{1}x_{3}-x_{1}+x_{2}^{2}+x_{2}x_{3}-2x_{2}-x_{3}+1\,:\,x_{2}^{2}+x_{2}x_{3}-x_{2}-x_{3}),\\ (-x_{1}x_{2}^{2}-x_{1}x_{2}x_{3}+x_{1}x_{2}-x_{2}x_{3}+x_{3}\,:\,0\,:\,x_{2}^{2}+x_{2}x_{3}-x_{2}-x_{3}),\\ (-x_{2}^{2}-x_{2}x_{3}+x_{2}+x_{3}\,:\,x_{1}x_{2}+x_{1}x_{3}-x_{1}-x_{2}x_{3}-x_{3}^{2}+x_{3}\,:\,x_{2}^{2}+x_{2}x_{3}\\ -x_{2}-x_{3}),(0:1:1). \end{array} \end{align} $$
$$ \begin{align} \begin{array}{c} (-x_{1}x_{2}^{2}-x_{1}x_{2}x_{3}+x_{1}x_{2}+x_{3}^{2}\,:\,x_{1}x_{2}^{2}+2x_{1}x_{2}x_{3}-x_{1}x_{2}+x_{1}x_{3}^{2}\\ -x_{1}x_{3}-x_{2}^{2}x_{3}-2x_{2}x_{3}^{2}+x_{2}x_{3}-x_{3}^{3}+x_{3}^{2}\,:\,x_{2}^{2}+x_{2}x_{3}-x_{2}-x_{3}),\\ (-x_{1}x_{2}-x_{1}x_{3}+x_{1}\,:\,x_{1}x_{2}+x_{1}x_{3}-x_{1}\,:\,x_{2}-1),(-x_{2}:1:0),\\ (-x_{1}x_{2}^{3}-2x_{1}x_{2}^{2}x_{3}+x_{1}x_{2}^{2}-x_{1}x_{2}x_{3}^{2}+x_{1}x_{2}x_{3}-x_{2}^{2}x_{3}-x_{2}x_{3}^{2}+x_{2}x_{3}\\ +x_{3}^{2}\,:\,x_{1}x_{2}+x_{1}x_{3}-x_{1}+x_{2}^{2}+x_{2}x_{3}-2x_{2}-x_{3}+1\,:\,x_{2}^{2}+x_{2}x_{3}-x_{2}-x_{3}),\\ (-x_{1}x_{2}^{2}-x_{1}x_{2}x_{3}+x_{1}x_{2}-x_{2}x_{3}+x_{3}\,:\,0\,:\,x_{2}^{2}+x_{2}x_{3}-x_{2}-x_{3}),\\ (-x_{2}^{2}-x_{2}x_{3}+x_{2}+x_{3}\,:\,x_{1}x_{2}+x_{1}x_{3}-x_{1}-x_{2}x_{3}-x_{3}^{2}+x_{3}\,:\,x_{2}^{2}+x_{2}x_{3}\\ -x_{2}-x_{3}),(0:1:1). \end{array} \end{align} $$
A computation in OSCAR yields the following concrete description of the moduli space
![]() $\mathcal {R}_{7}=\mathcal {R}(M_7)$
.
$\mathcal {R}_{7}=\mathcal {R}(M_7)$
.
Proposition 3.1. The moduli space
![]() $\mathcal {R}_{7}$
is an open sub-scheme of
$\mathcal {R}_{7}$
is an open sub-scheme of
![]() $Z_7$
: for
$Z_7$
: for
![]() $x\in \mathcal {R}_{7}$
, the line arrangement
$x\in \mathcal {R}_{7}$
, the line arrangement
![]() $\mathcal {A}=\mathcal {C}_{0}(x)\cup \mathcal {C}_{1}(x)$
is a realization of
$\mathcal {A}=\mathcal {C}_{0}(x)\cup \mathcal {C}_{1}(x)$
is a realization of
![]() $M_{7}$
, and conversely any realization of
$M_{7}$
, and conversely any realization of
![]() $M_{7}$
is projectively equivalent to a unique such line arrangement.
$M_{7}$
is projectively equivalent to a unique such line arrangement.
The complement of
![]() $\mathcal {R}_{7}$
in
$\mathcal {R}_{7}$
in
![]() $Z_7$
is the union of
$Z_7$
is the union of
![]() $20$
irreducible curves described in §3.2.
$20$
irreducible curves described in §3.2.
From the definition of the matroid
![]() $M_{7},$
if
$M_{7},$
if
![]() $\mathcal {A}=\mathcal {C}_{0}\cup \mathcal {C}_{1}$
is a realization of
$\mathcal {A}=\mathcal {C}_{0}\cup \mathcal {C}_{1}$
is a realization of
![]() $M_{7}$
, one has
$M_{7}$
, one has ![]() , but the following result on
, but the following result on ![]() is unexpected
is unexpected
Theorem 3.2. Let
![]() $\mathcal {A}_{0}=\mathcal {C}_{0}\cup \mathcal {C}_{1}$
be a generic realization of
$\mathcal {A}_{0}=\mathcal {C}_{0}\cup \mathcal {C}_{1}$
be a generic realization of
![]() $M_{7}$
and define
$M_{7}$
and define ![]() . The labeled line arrangement
. The labeled line arrangement
![]() $\mathcal {A}_{1}=\mathcal {C}_{1}\cup \mathcal {C}_{2}$
is again a realization of
$\mathcal {A}_{1}=\mathcal {C}_{1}\cup \mathcal {C}_{2}$
is again a realization of
![]() $M_{7}$
. The operator
$M_{7}$
. The operator ![]() induces a rational self-map on the schemes
induces a rational self-map on the schemes
![]() $\mathfrak {U}_7$
of all realizations of
$\mathfrak {U}_7$
of all realizations of
![]() $M_{7}$
and its moduli space
$M_{7}$
and its moduli space
![]() $\mathcal {R}_{7}$
.
$\mathcal {R}_{7}$
.
We denote by ![]() the rational self-map on
the rational self-map on
![]() $Z_7$
induced by
$Z_7$
induced by ![]() .
.
Proof. Up to projective automorphism, one can suppose that the line arrangement
![]() $\mathcal {A}_{0}$
is of the form
$\mathcal {A}_{0}$
is of the form
![]() $\mathcal {A}_{0}=\mathcal {C}_{0}(x)\cup \mathcal {C}_{1}(x)$
for x generic in
$\mathcal {A}_{0}=\mathcal {C}_{0}(x)\cup \mathcal {C}_{1}(x)$
for x generic in
![]() $Z_7$
: concretely, we use
$Z_7$
: concretely, we use
![]() $x=(x_{1},x_{2},x_{3})$
, where
$x=(x_{1},x_{2},x_{3})$
, where
![]() $x_{1},x_{2},x_{3}\in \mathbb {C}(Z_7)$
are considered as rational functions. A direct computation (with Magma) then shows that
$x_{1},x_{2},x_{3}\in \mathbb {C}(Z_7)$
are considered as rational functions. A direct computation (with Magma) then shows that ![]() is a line arrangement of seven lines. It has a canonical labeling as described in the previous Subsection and we then check that the matroid associated to
is a line arrangement of seven lines. It has a canonical labeling as described in the previous Subsection and we then check that the matroid associated to
![]() $\mathcal {C}_{1}\cup \mathcal {C}_{2}$
is equal to
$\mathcal {C}_{1}\cup \mathcal {C}_{2}$
is equal to
![]() $M_{7}$
, so that
$M_{7}$
, so that
![]() $\mathcal {C}_{1}\cup \mathcal {C}_{2}$
is a realization of
$\mathcal {C}_{1}\cup \mathcal {C}_{2}$
is a realization of
![]() $M_{7}$
. Using the period map, one computes
$M_{7}$
. Using the period map, one computes ![]() and obtain that it is a dominant rational map. The reader can find the polynomials defining
and obtain that it is a dominant rational map. The reader can find the polynomials defining ![]() in an ancillary file of this paper on arXiv; it can be also retrieved from the polynomials given in §3.6. That describes action of
in an ancillary file of this paper on arXiv; it can be also retrieved from the polynomials given in §3.6. That describes action of ![]() on the space of realization
on the space of realization
![]() $\mathfrak {U}_7$
and on the moduli space
$\mathfrak {U}_7$
and on the moduli space
![]() $\mathcal {R}_{7}$
.
$\mathcal {R}_{7}$
.
3.2 The open surface
 $ \mathcal {R}_{7}$
inside
$ \mathcal {R}_{7}$
inside
 $Z_7.$
$Z_7.$
The scheme
![]() $Z_7\setminus \mathcal {R}_{7}$
is the union of the following curves:
$Z_7\setminus \mathcal {R}_{7}$
is the union of the following curves:
-
• The
 $12$
lines These lines are also the lines contained in the quartic surface
$12$
lines These lines are also the lines contained in the quartic surface $$\begin{equation*}\begin{array}{lll} L_{1}: y_{2}=y_{3}=0, &L_{2}:y_{1}=y_{3}=0, &L_{3}:y_{2}=y_{4}=0,\\ L_{4}:y_{1}-y_{3}=y_{4}=0, &L_{5}: y_{1}=y_{4}=0, &L_{6}:y_{2}-y_{4}=y_{3}=0,\\ L_{7}:y_{1}-y_{3}-y_{4}=y_{2}+y_{3}=0,\, &L_{8}: y_{1}-y_{3}=y_{2}+y_{3}=0, &L_{9}:y_{2}+y_{3}=y_{4}=0,\\ L_{10}:y_{1}-y_{4}=y_{3}=0, &L_{11}: y_{1}-y_{3}=y_{2}-y_{4}=0,\, &L_{12}:y_{1}=y_{2}-y_{4}=0. \end{array} \end{equation*}$$
$$\begin{equation*}\begin{array}{lll} L_{1}: y_{2}=y_{3}=0, &L_{2}:y_{1}=y_{3}=0, &L_{3}:y_{2}=y_{4}=0,\\ L_{4}:y_{1}-y_{3}=y_{4}=0, &L_{5}: y_{1}=y_{4}=0, &L_{6}:y_{2}-y_{4}=y_{3}=0,\\ L_{7}:y_{1}-y_{3}-y_{4}=y_{2}+y_{3}=0,\, &L_{8}: y_{1}-y_{3}=y_{2}+y_{3}=0, &L_{9}:y_{2}+y_{3}=y_{4}=0,\\ L_{10}:y_{1}-y_{4}=y_{3}=0, &L_{11}: y_{1}-y_{3}=y_{2}-y_{4}=0,\, &L_{12}:y_{1}=y_{2}-y_{4}=0. \end{array} \end{equation*}$$
 $Z_7$
that contain at least two double points of
$Z_7$
that contain at least two double points of
 $Z_7$
.
$Z_7$
.
-
• The conic
 $C_{o}$
defined by
$C_{o}$
defined by
 $y_{1}y_{3}-y_{3}^{2}-y_{1}y_{4}=y_{2}+y_{3}-y_{4}=0$
.
$y_{1}y_{3}-y_{3}^{2}-y_{1}y_{4}=y_{2}+y_{3}-y_{4}=0$
. -
• Seven curves
 $E_{1},\dots ,E_{7}$
of geometric genus one. For example, one of these curves is given by
$E_{1},\dots ,E_{7}$
of geometric genus one. For example, one of these curves is given by  $$\begin{align*}y_{1}^{2}-2y_{1}y_{3}+y_{3}^{2}-y_{1}y_{4}=y_{2}^{2}+y_{2}y_{3}+y_{1}y_{4}-y_{3}y_{4}-y_{4}^{2}=0. \end{align*}$$
$$\begin{align*}y_{1}^{2}-2y_{1}y_{3}+y_{3}^{2}-y_{1}y_{4}=y_{2}^{2}+y_{2}y_{3}+y_{1}y_{4}-y_{3}y_{4}-y_{4}^{2}=0. \end{align*}$$
The j-invariant of the normalizations of the curves
![]() $E_{i}$
is equal to
$E_{i}$
is equal to
![]() $-5^{6}/28$
. The elliptic curve with this j-invariant is known as the modular curve
$-5^{6}/28$
. The elliptic curve with this j-invariant is known as the modular curve
![]() $X_{1}(14)$
parameterizing pairs
$X_{1}(14)$
parameterizing pairs
![]() $(E,t)$
where E is an elliptic curve and t is an order
$(E,t)$
where E is an elliptic curve and t is an order
![]() $14$
torsion element of E. For a generic point p on the curves
$14$
torsion element of E. For a generic point p on the curves
![]() $E_{1},\dots ,E_{7}$
, the line arrangement
$E_{1},\dots ,E_{7}$
, the line arrangement
![]() $\mathcal {C}_{0}(p)$
with normal vectors as in (3.3) is well-defined. The line arrangement
$\mathcal {C}_{0}(p)$
with normal vectors as in (3.3) is well-defined. The line arrangement ![]() has seven lines, but its singularities are
has seven lines, but its singularities are
![]() $t_{2}=6,t_{3}=5$
, and one has
$t_{2}=6,t_{3}=5$
, and one has ![]() . Moreover, the singularities of
. Moreover, the singularities of
![]() $\mathcal {C}_{0}\cup \mathcal {C}_{1}$
are
$\mathcal {C}_{0}\cup \mathcal {C}_{1}$
are
![]() $t_{2}=13,t_{3}=26$
.
$t_{2}=13,t_{3}=26$
.
The image of the curves
![]() $C_{o},E_{1},\dots ,E_{7}$
under the map
$C_{o},E_{1},\dots ,E_{7}$
under the map ![]() are lines
are lines
![]() $L_{k}$
; when defined, the image of the lines
$L_{k}$
; when defined, the image of the lines
![]() $L_{k}$
are lines
$L_{k}$
are lines
![]() $L_{k'}$
or points.
$L_{k'}$
or points.
3.3 The degree of 
Recall that ![]() denotes the action of the operator
denotes the action of the operator ![]() on the K3 surface
on the K3 surface
![]() $Z_7$
. One has:
$Z_7$
. One has:
Theorem 3.3. The operator ![]() acts on
acts on
![]() $Z_7$
as a degree
$Z_7$
as a degree
![]() $4$
rational self-map.
$4$
rational self-map.
In order to prove Theorem 3.3, let us describe the period map: Let
![]() $\ell _{1},...,\ell _{7}$
be the lines of
$\ell _{1},...,\ell _{7}$
be the lines of
![]() $\mathcal {C}_{0}$
with normal vectors as in Equation (3.3). Let us denote by
$\mathcal {C}_{0}$
with normal vectors as in Equation (3.3). Let us denote by
![]() $p_{i,j}$
the intersection point of the lines
$p_{i,j}$
the intersection point of the lines
![]() $\ell _{i}$
and
$\ell _{i}$
and
![]() $\ell _{j}$
. The point
$\ell _{j}$
. The point
![]() $p_{5,7}$
is
$p_{5,7}$
is
![]() $(1:x_{2}:x_{3})$
, so that one may recover
$(1:x_{2}:x_{3})$
, so that one may recover
![]() $x_{2},x_{3}$
from the knowledge of that point. Also the point
$x_{2},x_{3}$
from the knowledge of that point. Also the point
![]() $p_{1,7}$
is
$p_{1,7}$
is
this is linear in
![]() $x_{1}$
, so that from the knowledge of
$x_{1}$
, so that from the knowledge of
![]() $p_{5,7}$
and
$p_{5,7}$
and
![]() $p_{1,7}$
, one may recover the point
$p_{1,7}$
, one may recover the point
![]() $(x_{1},x_{2},x_{3})\in Z_7$
.
$(x_{1},x_{2},x_{3})\in Z_7$
.
Proof of Theorem 3.3
Let
![]() $A\in PGL_{3}(\mathbb {C})$
be the projective transformation that sends the first four lines of
$A\in PGL_{3}(\mathbb {C})$
be the projective transformation that sends the first four lines of
![]() $\mathcal {C}_{1}$
to the four lines having the same normal vectors as the one of
$\mathcal {C}_{1}$
to the four lines having the same normal vectors as the one of
![]() $\mathcal {C}_{0}$
. Let
$\mathcal {C}_{0}$
. Let
![]() $\mathcal {C}_{1}'=(\ell _{1}',\dots ,\ell _{7}')$
be the image of
$\mathcal {C}_{1}'=(\ell _{1}',\dots ,\ell _{7}')$
be the image of
![]() $\mathcal {C}_{1}$
by A. Using the period map, one can determine the points
$\mathcal {C}_{1}$
by A. Using the period map, one can determine the points
![]() $p_{5,7}'$
and
$p_{5,7}'$
and
![]() $p_{1,7}'$
and we obtain a point
$p_{1,7}'$
and we obtain a point
![]() $x'=(x_{1}',x_{2}',x_{3}')$
(in the function field of
$x'=(x_{1}',x_{2}',x_{3}')$
(in the function field of
![]() $Z_7$
). The line arrangements
$Z_7$
). The line arrangements
![]() $\mathcal {C}_{0}(x_{1}',x_{2}',x_{3}')$
and
$\mathcal {C}_{0}(x_{1}',x_{2}',x_{3}')$
and
![]() $\mathcal {C}_{1}'$
are equal, and the action of
$\mathcal {C}_{1}'$
are equal, and the action of ![]() on
on
![]() $Z_7$
is through the map
$Z_7$
is through the map
The rational self-map ![]() is studied in §3.6.
is studied in §3.6.
Let us compute the degree of ![]() ; we apply the method from [Reference Voisin15]. Let
; we apply the method from [Reference Voisin15]. Let
![]() $f(x_{1},x_{2},x_{3})$
be the equation of the quartic
$f(x_{1},x_{2},x_{3})$
be the equation of the quartic
![]() $Z_7$
in the chart
$Z_7$
in the chart
![]() $U_{4}:y_{4}\neq 0$
. The space of global non-vanishing differential
$U_{4}:y_{4}\neq 0$
. The space of global non-vanishing differential
![]() $2$
-forms is generated by a form
$2$
-forms is generated by a form
![]() $\unicode{xf8} $
, which one can choose so that on an open set of
$\unicode{xf8} $
, which one can choose so that on an open set of
![]() $U_{4}$
one has:
$U_{4}$
one has:

The rational self-map ![]() preserves
preserves
![]() $U_{4}$
, and by a direct computation one obtains that
$U_{4}$
, and by a direct computation one obtains that
The above expression shows that when applying ![]() , the volume form
, the volume form ![]() is multiplied by
is multiplied by
![]() $4$
, which gives the degree of
$4$
, which gives the degree of ![]() .
.
3.4 Action of  on the K3 surface
on the K3 surface
 $Z_7^{s}.$
$Z_7^{s}.$
The automorphism group of
![]() $M_{7}$
is generated by the order
$M_{7}$
is generated by the order
![]() $7$
and
$7$
and
![]() $6$
permutations
$6$
permutations
with
![]() $1'=8,\dots ,7'=14$
. This group is isomorphic to the the Frobenius group
$1'=8,\dots ,7'=14$
. This group is isomorphic to the the Frobenius group
![]() $F_{7}=\mathbb {Z}/6\mathbb {Z}\rtimes \mathbb {Z}/7\mathbb {Z}$
. These automorphisms act on the K3 surface Z.
$F_{7}=\mathbb {Z}/6\mathbb {Z}\rtimes \mathbb {Z}/7\mathbb {Z}$
. These automorphisms act on the K3 surface Z.
Proposition 3.4. The action of ![]() on
on
![]() $Z_7$
is faithful.
$Z_7$
is faithful.
Proof. As in the proof of Theorem 3.3, let
![]() $\mathcal {C}_{0}=\mathcal {C}_{0}(x_{1},x_{2},x_{3})$
be the generic line arrangement in
$\mathcal {C}_{0}=\mathcal {C}_{0}(x_{1},x_{2},x_{3})$
be the generic line arrangement in
![]() $\mathcal {R}_{7}$
, where
$\mathcal {R}_{7}$
, where
![]() $x_{1},x_{2},x_{3}\in \mathbb {C}(Z_7)$
are considered as rational functions.
$x_{1},x_{2},x_{3}\in \mathbb {C}(Z_7)$
are considered as rational functions.
For ![]() let
let
![]() $\mathcal {C}_{0}^{\sigma }$
be the image of
$\mathcal {C}_{0}^{\sigma }$
be the image of
![]() $\mathcal {C}_{0}$
under the action of
$\mathcal {C}_{0}$
under the action of
![]() $\sigma $
(that is just the permutation of the lines under
$\sigma $
(that is just the permutation of the lines under
![]() $\sigma $
). We apply the period map to the line arrangement
$\sigma $
). We apply the period map to the line arrangement
![]() $\mathcal {C}_{0}^{\sigma }$
, where
$\mathcal {C}_{0}^{\sigma }$
, where
![]() $\mathcal {C}_{0}=\mathcal {C}_{0}(x)$
. Using the period map, we obtain the point
$\mathcal {C}_{0}=\mathcal {C}_{0}(x)$
. Using the period map, we obtain the point
![]() $\sigma (x)=(x_{1}',x_{2}',x_{3}')$
which is a zero of the equation of
$\sigma (x)=(x_{1}',x_{2}',x_{3}')$
which is a zero of the equation of
![]() $Z_7$
and such that
$Z_7$
and such that
![]() $\mathcal {C}_{0}(\sigma (x))$
is projectively equivalent to
$\mathcal {C}_{0}(\sigma (x))$
is projectively equivalent to
![]() $\mathcal {C}_{0}^{\sigma }$
.
$\mathcal {C}_{0}^{\sigma }$
.
When
![]() $\sigma =\sigma _{1}$
, the automorphism
$\sigma =\sigma _{1}$
, the automorphism
![]() $\sigma _{1}$
acts on
$\sigma _{1}$
acts on
![]() $Z_7$
through the map in
$Z_7$
through the map in
![]() $\mathbb {P}^{3}$
given by the ring homomorphism which to
$\mathbb {P}^{3}$
given by the ring homomorphism which to
![]() $(y_{1},y_{2},y_{3},y_{4})$
associates
$(y_{1},y_{2},y_{3},y_{4})$
associates
 $$\begin{align*}\begin{array}{c} (y_{1}y_{2}^{2}y_{3}+y_{1}y_{2}y_{3}^{2}-y_{2}^{2}y_{3}^{2}-y_{2}y_{3}^{3}-y_{1}y_{2}y_{3}y_{4}-y_{2}^{2}y_{3}y_{4}+y_{2}y_{3}y_{4}^{2}+y_{3}^{2}y_{4}^{2},\\ y_{1}y_{2}^{3}+y_{1}y_{2}^{2}y_{3}+y_{2}^{2}y_{3}^{2}+y_{2}y_{3}^{3}-2y_{1}y_{2}^{2}y_{4}-y_{1}y_{2}y_{3}y_{4}-2y_{2}y_{3}^{2}y_{4}-y_{3}^{3}y_{4}+y_{1}y_{2}y_{4}^{2}+y_{3}^{2}y_{4}^{2},\\ y_{1}y_{2}^{2}y_{3}+y_{1}y_{2}y_{3}^{2}-y_{2}^{2}y_{3}^{2}-y_{2}y_{3}^{3}-y_{1}y_{2}y_{3}y_{4}+y_{2}y_{3}^{2}y_{4},\\ y_{2}^{3}y_{3}+2y_{2}^{2}y_{3}^{2}+y_{2}y_{3}^{3}-2y_{2}^{2}y_{3}y_{4}-3y_{2}y_{3}^{2}y_{4}-y_{3}^{3}y_{4}+y_{2}y_{3}y_{4}^{2}+y_{3}^{2}y_{4}^{2}). \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{c} (y_{1}y_{2}^{2}y_{3}+y_{1}y_{2}y_{3}^{2}-y_{2}^{2}y_{3}^{2}-y_{2}y_{3}^{3}-y_{1}y_{2}y_{3}y_{4}-y_{2}^{2}y_{3}y_{4}+y_{2}y_{3}y_{4}^{2}+y_{3}^{2}y_{4}^{2},\\ y_{1}y_{2}^{3}+y_{1}y_{2}^{2}y_{3}+y_{2}^{2}y_{3}^{2}+y_{2}y_{3}^{3}-2y_{1}y_{2}^{2}y_{4}-y_{1}y_{2}y_{3}y_{4}-2y_{2}y_{3}^{2}y_{4}-y_{3}^{3}y_{4}+y_{1}y_{2}y_{4}^{2}+y_{3}^{2}y_{4}^{2},\\ y_{1}y_{2}^{2}y_{3}+y_{1}y_{2}y_{3}^{2}-y_{2}^{2}y_{3}^{2}-y_{2}y_{3}^{3}-y_{1}y_{2}y_{3}y_{4}+y_{2}y_{3}^{2}y_{4},\\ y_{2}^{3}y_{3}+2y_{2}^{2}y_{3}^{2}+y_{2}y_{3}^{3}-2y_{2}^{2}y_{3}y_{4}-3y_{2}y_{3}^{2}y_{4}-y_{3}^{3}y_{4}+y_{2}y_{3}y_{4}^{2}+y_{3}^{2}y_{4}^{2}). \end{array} \end{align*}$$
For
![]() $\sigma _{2}$
, we obtain that it acts on the surface
$\sigma _{2}$
, we obtain that it acts on the surface
![]() $Z_7$
through the map which to
$Z_7$
through the map which to
![]() $(y_{1},y_{2},y_{3},y_{4})$
associates
$(y_{1},y_{2},y_{3},y_{4})$
associates
 $$\begin{align*}\begin{array}{c} (-y_{2}^{2}y_{3}-y_{2}y_{3}^{2}+y_{2}y_{3}y_{4},-y_{1}y_{2}y_{3}+y_{2}y_{3}^{2}+y_{2}y_{3}y_{4}-y_{3}y_{4}^{2},\\ y_{1}y_{2}^{2}+y_{1}y_{2}y_{3}-y_{2}^{2}y_{3}-y_{2}y_{3}^{2}-y_{1}y_{2}y_{4}+y_{2}y_{3}y_{4},y_{2}y_{3}y_{4}-y_{3}y_{4}^{2}); \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{c} (-y_{2}^{2}y_{3}-y_{2}y_{3}^{2}+y_{2}y_{3}y_{4},-y_{1}y_{2}y_{3}+y_{2}y_{3}^{2}+y_{2}y_{3}y_{4}-y_{3}y_{4}^{2},\\ y_{1}y_{2}^{2}+y_{1}y_{2}y_{3}-y_{2}^{2}y_{3}-y_{2}y_{3}^{2}-y_{1}y_{2}y_{4}+y_{2}y_{3}y_{4},y_{2}y_{3}y_{4}-y_{3}y_{4}^{2}); \end{array} \end{align*}$$
this map is a birational transformation of
![]() $\mathbb {P}^{3}$
. In order to check that the action of
$\mathbb {P}^{3}$
. In order to check that the action of ![]() is faithful on
is faithful on
![]() $Z_7$
, it is then enough to check that the orbit of one point (for example the point
$Z_7$
, it is then enough to check that the orbit of one point (for example the point
![]() $(-6:-25/8:5:1)$
in
$(-6:-25/8:5:1)$
in
![]() $Z_7$
) has
$Z_7$
) has
![]() $42$
elements, which is a direct computation.
$42$
elements, which is a direct computation.
The fixed points under the order seven element
![]() $\sigma _{1}$
are the singularities
$\sigma _{1}$
are the singularities
![]() $s_{5},s_{7},s_{8}$
; (there is a unique conjugacy class of elements of order
$s_{5},s_{7},s_{8}$
; (there is a unique conjugacy class of elements of order
![]() $7$
in
$7$
in
![]() $F_{7}$
).
$F_{7}$
).
The fixed points locus of
![]() $\sigma _{2}$
and the order
$\sigma _{2}$
and the order
![]() $3$
automorphism
$3$
automorphism
![]() $\sigma _{2}^{2}$
acting on
$\sigma _{2}^{2}$
acting on
![]() $Z_7$
are:
$Z_7$
are:
-
1. The
 $A_{3}$
singularity
$A_{3}$
singularity
 $(0:1:0:1)$
,
$(0:1:0:1)$
, -
2. The four points
 $p=(r^{2}+1:r{}^{2}-r+2:r:1)$
where r is any complex root of
$p=(r^{2}+1:r{}^{2}-r+2:r:1)$
where r is any complex root of
 $X^{4}-X^{3}+3X^{2}-X+1$
. These points are in
$X^{4}-X^{3}+3X^{2}-X+1$
. These points are in
 $Z_7\setminus \mathcal {R}_{7}$
; they are periodic of period
$Z_7\setminus \mathcal {R}_{7}$
; they are periodic of period
 $2$
for the rational self-map
$2$
for the rational self-map  , moreover the (unlabeled) line arrangements
, moreover the (unlabeled) line arrangements  have
have
 $7,10,$
and
$7,10,$
and
 $37$
lines, respectively. It seems likely that the number of lines of the sequence
$37$
lines, respectively. It seems likely that the number of lines of the sequence  goes to infinity.
goes to infinity. -
3. The points
 $(w+1:-w:w:1)$
where
$(w+1:-w:w:1)$
where
 $w^{2}+w+1=0$
, which are fixed by the rational self-map
$w^{2}+w+1=0$
, which are fixed by the rational self-map  ; these two points are in
; these two points are in
 $Z_7\setminus \mathcal {R}_{7}$
.
$Z_7\setminus \mathcal {R}_{7}$
.
The fixed-point locus of the involution
![]() $\sigma _{2}^{3}$
acting on
$\sigma _{2}^{3}$
acting on
![]() $Z_7$
is the union of the line
$Z_7$
is the union of the line
![]() $L_{7}$
and a curve
$L_{7}$
and a curve
![]() $E_{j}$
, which is in
$E_{j}$
, which is in
![]() $Z_7\setminus \mathcal {R}_{7}$
(see §3.2). There is a unique conjugacy class of involutions in
$Z_7\setminus \mathcal {R}_{7}$
(see §3.2). There is a unique conjugacy class of involutions in
![]() $F_{7}$
, so that similarly, any involution from
$F_{7}$
, so that similarly, any involution from ![]() fixes a curve and a line.
fixes a curve and a line.
There is an open set in the quotient surface ![]() which parametrizes unlabeled line arrangements
which parametrizes unlabeled line arrangements
![]() $\mathcal {C}_{0}^{o}$
associated to
$\mathcal {C}_{0}^{o}$
associated to
![]() $\mathcal {C}_{0}$
in
$\mathcal {C}_{0}$
in
![]() $\mathcal {R}_{7}$
. One has:
$\mathcal {R}_{7}$
. One has:
Corollary 3.5. The surface ![]() is rational.
is rational.
Proof. Since an involution of ![]() fixes a one dimensional curve, it is non-symplectic (see [Reference Huybrechts4]), thus
fixes a one dimensional curve, it is non-symplectic (see [Reference Huybrechts4]), thus ![]() is rational.
is rational.
For a labeled line arrangement
![]() $\mathcal {C}_{0}=(\ell _{1},\dots ,\ell _{k})\in \mathfrak {U}_7$
and
$\mathcal {C}_{0}=(\ell _{1},\dots ,\ell _{k})\in \mathfrak {U}_7$
and
![]() $j\in \{1,\dots ,7\}$
, let us denote by
$j\in \{1,\dots ,7\}$
, let us denote by
![]() $H_{j}(\mathcal {C}_{0})$
the line arrangement
$H_{j}(\mathcal {C}_{0})$
the line arrangement
![]() $H_{j}=\sum _{k\neq j}\ell _{k}$
. The labeled line arrangement
$H_{j}=\sum _{k\neq j}\ell _{k}$
. The labeled line arrangement ![]() is
is
An element ![]() permutes the lines of
permutes the lines of
![]() $\mathcal {C}_{0}$
: it can also be seen as a permutation of
$\mathcal {C}_{0}$
: it can also be seen as a permutation of
![]() $\{1,\dots ,7\}$
. The
$\{1,\dots ,7\}$
. The
![]() $\sigma (j)^{th}$
line of
$\sigma (j)^{th}$
line of
![]() $\sigma .\mathcal {C}_{1}$
is
$\sigma .\mathcal {C}_{1}$
is ![]() . Since
. Since
 $$\begin{align*}H_{\sigma(j)}(\mathcal{C}_{0})=\sum_{k\neq j}\ell_{\sigma(k)}=H_{j}(\sigma.\mathcal{C}_{0}), \end{align*}$$
$$\begin{align*}H_{\sigma(j)}(\mathcal{C}_{0})=\sum_{k\neq j}\ell_{\sigma(k)}=H_{j}(\sigma.\mathcal{C}_{0}), \end{align*}$$
the
![]() $\sigma (j)^{th}$
line of
$\sigma (j)^{th}$
line of
![]() $\sigma .\mathcal {C}_{1}$
is
$\sigma .\mathcal {C}_{1}$
is ![]() . Thus
. Thus
and we obtain that:
Proposition 3.6. The action of ![]() commutes with the action of
commutes with the action of ![]() , that is for all
, that is for all ![]() it holds that
it holds that
Remark 3.7. The group ![]() acts faithfully on the surface
acts faithfully on the surface
![]() $Z_7\subset \mathbb {P}^{3}$
, but does not extend canonically to a well-defined action on the ambient space
$Z_7\subset \mathbb {P}^{3}$
, but does not extend canonically to a well-defined action on the ambient space
![]() $\mathbb {P}^{3}$
. For example, the action of
$\mathbb {P}^{3}$
. For example, the action of
![]() $\sigma _{2}$
we computed is the restriction of an order
$\sigma _{2}$
we computed is the restriction of an order
![]() $6$
birational map
$6$
birational map
![]() $\tilde {\sigma _{2}}$
of
$\tilde {\sigma _{2}}$
of
![]() $\mathbb {P}^{3}$
; in particular
$\mathbb {P}^{3}$
; in particular
![]() $\tilde {\sigma _{2}}^{3}$
is a birational involution of
$\tilde {\sigma _{2}}^{3}$
is a birational involution of
![]() $\mathbb {P}^{3}$
defined by degree
$\mathbb {P}^{3}$
defined by degree
![]() $5$
coprime polynomials. If instead one starts with
$5$
coprime polynomials. If instead one starts with
![]() $\sigma _{2}^{3}=(1,6)(2,5)(3,7)(8,13)(9,12)(10,14)$
and computes the action of
$\sigma _{2}^{3}=(1,6)(2,5)(3,7)(8,13)(9,12)(10,14)$
and computes the action of
![]() $\widetilde {\sigma _{2}^{3}}$
on
$\widetilde {\sigma _{2}^{3}}$
on
![]() $Z_7$
as we did above for
$Z_7$
as we did above for
![]() $\sigma _{1}$
and
$\sigma _{1}$
and
![]() $\sigma _{2}$
, one obtains that, surprisingly, the defining coprime polynomials of the rational map
$\sigma _{2}$
, one obtains that, surprisingly, the defining coprime polynomials of the rational map
![]() $\widetilde {\sigma _{2}^{3}}:\mathbb {P}^{3}\dashrightarrow \mathbb {P}^{3}$
have degree
$\widetilde {\sigma _{2}^{3}}:\mathbb {P}^{3}\dashrightarrow \mathbb {P}^{3}$
have degree
![]() $4$
, although the maps
$4$
, although the maps
![]() $\widetilde {\sigma _{2}^{3}}$
and
$\widetilde {\sigma _{2}^{3}}$
and
![]() $\tilde {\sigma _{2}}^{3}$
have the same effect on
$\tilde {\sigma _{2}}^{3}$
have the same effect on
![]() $Z_7$
. Moreover although
$Z_7$
. Moreover although
![]() $(\widetilde {\sigma _{2}^{3}})^{2}$
is the identity on the surface
$(\widetilde {\sigma _{2}^{3}})^{2}$
is the identity on the surface
![]() $Z_7$
, it is not the identity on
$Z_7$
, it is not the identity on
![]() $\mathbb {P}^{3}$
(it is defined by degree
$\mathbb {P}^{3}$
(it is defined by degree
![]() $6$
coprime polynomials). Moreover, one can compute that the rational map
$6$
coprime polynomials). Moreover, one can compute that the rational map
![]() $(\widetilde {\sigma _{2}^{3}})^{4}$
is defined by degree
$(\widetilde {\sigma _{2}^{3}})^{4}$
is defined by degree
![]() $21$
coprime polynomials.
$21$
coprime polynomials.
3.5 Fibration preserved by  and the elliptic modular surface
and the elliptic modular surface
 $\Xi _{1}(7).$
$\Xi _{1}(7).$
The line
![]() $L_{6}:\,y_{2}-y_{4}=y_{3}=0$
is contained in the surface
$L_{6}:\,y_{2}-y_{4}=y_{3}=0$
is contained in the surface
![]() $Z_7$
. Let
$Z_7$
. Let
![]() $\gamma :Z_{7}\to \mathbb {P}^{1}$
be the elliptic fibration induced by the projection from that line. One obtains a smooth cubic affine model A in
$\gamma :Z_{7}\to \mathbb {P}^{1}$
be the elliptic fibration induced by the projection from that line. One obtains a smooth cubic affine model A in ![]() of that elliptic fibration by substituting
of that elliptic fibration by substituting
![]() $(x,1+ty,y,1)$
in the equation of
$(x,1+ty,y,1)$
in the equation of
![]() $Z_{7}$
. A computation shows that
$Z_{7}$
. A computation shows that
![]() $Z_{7}^{s}\to \mathbb {P}^{1}$
is (isomorphic to) the elliptic surface Y associated to the elliptic curve
$Z_{7}^{s}\to \mathbb {P}^{1}$
is (isomorphic to) the elliptic surface Y associated to the elliptic curve
![]() $E_{/\mathbb {Q}(t)}$
with Weierstrass model
$E_{/\mathbb {Q}(t)}$
with Weierstrass model
The map between A and Y sends
![]() $(0,0)$
to the zero section. The elliptic fibration
$(0,0)$
to the zero section. The elliptic fibration
![]() $Y\to \mathbb {P}^{1}$
has singular fibers
$Y\to \mathbb {P}^{1}$
has singular fibers
![]() $3I_{7}+3I_{1}$
at the points
$3I_{7}+3I_{1}$
at the points
respectively.
We recall that the curve
![]() $X_{1}(7)$
parametrizes (up to isomorphisms) the pairs
$X_{1}(7)$
parametrizes (up to isomorphisms) the pairs
![]() $(E,p)$
where E is an elliptic curve and p is a torsion point of order
$(E,p)$
where E is an elliptic curve and p is a torsion point of order
![]() $7$
on E. A Weierstrass model
$7$
on E. A Weierstrass model
![]() $E'$
of the elliptic modular surface
$E'$
of the elliptic modular surface
![]() $\Xi _{1}(7)$
over the curve
$\Xi _{1}(7)$
over the curve
![]() $X_{1}(7)\simeq \mathbb {P}^{1}$
is computed in [Reference Top and Yui13]. The j-invariant maps
$X_{1}(7)\simeq \mathbb {P}^{1}$
is computed in [Reference Top and Yui13]. The j-invariant maps
![]() $j_{E}(t),j_{E'}(t)\in \mathbb {Q}$
of E and
$j_{E}(t),j_{E'}(t)\in \mathbb {Q}$
of E and
![]() $E'$
are related by the equality
$E'$
are related by the equality
![]() $j_{E'}(t)=j_{E}(-\tfrac {1}{t})$
, which shows that E is isomorphic to
$j_{E'}(t)=j_{E}(-\tfrac {1}{t})$
, which shows that E is isomorphic to
![]() $E'$
and
$E'$
and
![]() $Z_7^{s}$
is isomorphic to the elliptic modular surface
$Z_7^{s}$
is isomorphic to the elliptic modular surface
![]() $X_{1}(7)$
.
$X_{1}(7)$
.
The Mordell–Weil group of E is isomorphic to
![]() $\mathbb {Z}/7\mathbb {Z}$
; it is generated by the point
$\mathbb {Z}/7\mathbb {Z}$
; it is generated by the point
We thus obtained the first part of the following theorem
Theorem 3.8.
-
1. The K3 surface
 $Z_7^{s}$
is isomorphic to the modular elliptic surface
$Z_7^{s}$
is isomorphic to the modular elliptic surface
 $\Xi _{1}(7)$
.
$\Xi _{1}(7)$
. -
2. The rational self-map
 preserves the elliptic fibration
preserves the elliptic fibration
 $\gamma :Z_{7}\to \mathbb {P}^{1}$
and acts on the base curve
$\gamma :Z_{7}\to \mathbb {P}^{1}$
and acts on the base curve
 $\mathbb {P}^{1}$
through the order
$\mathbb {P}^{1}$
through the order
 $3$
map
$3$
map
 $t\to -1/(t+1)$
. There exists an automorphism
$t\to -1/(t+1)$
. There exists an automorphism
 $\sigma _{0}$
coming from
$\sigma _{0}$
coming from  such that
such that  preserves the fibration
preserves the fibration
 $\gamma $
and acts on E as the multiplication by
$\gamma $
and acts on E as the multiplication by
 $2$
map.
$2$
map.
The last property implies that the operator ![]() preserves the moduli interpretation of
preserves the moduli interpretation of
![]() $X_{1}(7)$
.
$X_{1}(7)$
.
Proof. Using the period map and the function field of A, one computes that the action of ![]() on the base
on the base
![]() $\mathbb {P}^{1}$
of the fibration
$\mathbb {P}^{1}$
of the fibration
![]() $A\to \mathbb {P}^{1}$
is through the map
$A\to \mathbb {P}^{1}$
is through the map
![]() $t\to -1/(t+1)$
.
$t\to -1/(t+1)$
.
An automorphism ![]() acts on the surface
acts on the surface
![]() $Z_7\cap \{y_{4}\neq 0\}$
and on the affine model A. Using the period map and again the generic point of A, one computes the action of the rational self-maps
$Z_7\cap \{y_{4}\neq 0\}$
and on the affine model A. Using the period map and again the generic point of A, one computes the action of the rational self-maps ![]() (
(![]() ) on A. For
) on A. For
![]() $14$
of these maps, the action on the base curve
$14$
of these maps, the action on the base curve
![]() $\mathbb {P}^{1}$
is trivial. This is the case for example for
$\mathbb {P}^{1}$
is trivial. This is the case for example for
The map ![]() also acts on E, one can thus compute its action on the generic point of E. Knowing that action, we are now able to compute the pull-back of a non-zero holomorphic one-form
also acts on E, one can thus compute its action on the generic point of E. Knowing that action, we are now able to compute the pull-back of a non-zero holomorphic one-form ![]() by
by
![]() $\mu $
, which is:
$\mu $
, which is: ![]() . Using the seven torsion points, one computes that
. Using the seven torsion points, one computes that
![]() $\mu $
fixes the origin, thus
$\mu $
fixes the origin, thus
![]() $\mu =[2]$
.
$\mu =[2]$
.
Among the
![]() $12$
lines contained in
$12$
lines contained in
![]() $Z_7$
, in the complement of
$Z_7$
, in the complement of
![]() $\mathcal {R}_{7}$
, eight are contained in the singular fibers of the fibration
$\mathcal {R}_{7}$
, eight are contained in the singular fibers of the fibration
![]() $\gamma $
, and
$\gamma $
, and
![]() $4$
are sections.
$4$
are sections.
Using the pull-back to
![]() $Z_7^{s}$
of the lines contained in
$Z_7^{s}$
of the lines contained in
![]() $Z_7$
and the
$Z_7$
and the
![]() $(-2)$
-curves of the desingularization, one may compute the Néron–Severi lattice of
$(-2)$
-curves of the desingularization, one may compute the Néron–Severi lattice of
![]() $Z_7^{s}$
, and obtain that it has discriminant
$Z_7^{s}$
, and obtain that it has discriminant
![]() $-7$
and rank
$-7$
and rank
![]() $20$
. The modular elliptic surface
$20$
. The modular elliptic surface
![]() $\Xi _{1}(7)$
is well-known and studied; it is known as the unique K3 surface with Néron–Severi lattice of rank
$\Xi _{1}(7)$
is well-known and studied; it is known as the unique K3 surface with Néron–Severi lattice of rank
![]() $20$
and discriminant
$20$
and discriminant
![]() $-7$
: we obtain that way another proof that
$-7$
: we obtain that way another proof that
![]() $Z^s$
is isomorphic to
$Z^s$
is isomorphic to
![]() $\Xi _1(7)$
. The inequivalent fibrations of
$\Xi _1(7)$
. The inequivalent fibrations of
![]() $\Xi _{1}(7)$
have been classified (see [Reference Lecacheux6]). Another remarkable fact is that
$\Xi _{1}(7)$
have been classified (see [Reference Lecacheux6]). Another remarkable fact is that
![]() $\Xi _{1}(7)$
is a ball-quotient surface: there exists a co-compact lattice
$\Xi _{1}(7)$
is a ball-quotient surface: there exists a co-compact lattice
![]() $\Gamma $
in the automorphism group of the unit ball
$\Gamma $
in the automorphism group of the unit ball
![]() $\mathbb {B}_{2}$
such that
$\mathbb {B}_{2}$
such that
![]() $\Xi _{1}(7)\simeq \mathbb {B}_{2}/\Gamma $
[Reference Naruki7]. The automorphism group of
$\Xi _{1}(7)\simeq \mathbb {B}_{2}/\Gamma $
[Reference Naruki7]. The automorphism group of
![]() $\Xi _{1}(7)$
is studied in [Reference Ujikawa14].
$\Xi _{1}(7)$
is studied in [Reference Ujikawa14].
3.6 The K3 surface
 $Z_7^{s}$
is semi-conjugated to the plane.
$Z_7^{s}$
is semi-conjugated to the plane.
The rational self-map ![]() acting on the quartic
acting on the quartic
![]() $Z_7\hookrightarrow \mathbb {P}^{3}(y_{1},\dots ,y_{4})$
is defined by
$Z_7\hookrightarrow \mathbb {P}^{3}(y_{1},\dots ,y_{4})$
is defined by
where
![]() $P_{1},\dots ,P_{4}$
are four homogeneous degree
$P_{1},\dots ,P_{4}$
are four homogeneous degree
![]() $11$
polynomials computed via the period map. These polynomials are given in the ancillary file in the arXiv version of this paper; they also may be obtained from the polynomials
$11$
polynomials computed via the period map. These polynomials are given in the ancillary file in the arXiv version of this paper; they also may be obtained from the polynomials
![]() $Q_{1},Q_{2},Q_{3}$
and R below. A remarkable fact about the polynomials
$Q_{1},Q_{2},Q_{3}$
and R below. A remarkable fact about the polynomials
![]() $P_{1},\dots ,P_{4}$
is that
$P_{1},\dots ,P_{4}$
is that
where
![]() $\deg _{y_{1}}$
denote the degree relative to the variable
$\deg _{y_{1}}$
denote the degree relative to the variable
![]() $y_{1}$
.
$y_{1}$
.
Let us define the polynomials
![]() $\tilde {P_{k}}=P_{k+1}(0,z_{1},z_{2},z_{3})$
for
$\tilde {P_{k}}=P_{k+1}(0,z_{1},z_{2},z_{3})$
for
![]() $k\in \{1,2,3\}$
(where
$k\in \{1,2,3\}$
(where
![]() $z_{1},z_{2},z_{3}$
are the three coordinates on the plane
$z_{1},z_{2},z_{3}$
are the three coordinates on the plane
![]() $\mathbb {P}^{2}:y_{1}=0$
). The polynomials
$\mathbb {P}^{2}:y_{1}=0$
). The polynomials
![]() $\tilde {P}_{k}$
,
$\tilde {P}_{k}$
,
![]() $k\in \{1,2,3\}$
define a rational self-map
$k\in \{1,2,3\}$
define a rational self-map
![]() $F:\mathbb {P}^{2}\dashrightarrow \mathbb {P}^{2}$
; the base locus of the linear system generated by
$F:\mathbb {P}^{2}\dashrightarrow \mathbb {P}^{2}$
; the base locus of the linear system generated by
![]() $\tilde {P_{1}},\tilde {P_{2}},\tilde {P_{3}}$
is the quintic curve B defined by
$\tilde {P_{1}},\tilde {P_{2}},\tilde {P_{3}}$
is the quintic curve B defined by
 $$\begin{align*} Q&=z_{1}^{3}z_{2}^{2}+2z_{1}^{2}z_{2}^{3}+z_{1}z_{2}^{4}+2z_{1}^{3}z_{2}z_{3}+4z_{1}^{2}z_{2}^{2}z_{3}+2z_{1}z_{2}^{3}z_{3}+z_{1}^{3}z_{3}^{2}\\ &\quad-4z_{1}^{2}z_{2}z_{3}^{2}-9z_{1}z_{2}^{2}z_{3}^{2}-4z_{2}^{3}z_{3}^{2}-2z_{1}^{2}z_{3}^{3}+2z_{1}z_{2}z_{3}^{3}+4z_{2}^{2}z_{3}^{3}+z_{1}z_{3}^{4}. \end{align*}$$
$$\begin{align*} Q&=z_{1}^{3}z_{2}^{2}+2z_{1}^{2}z_{2}^{3}+z_{1}z_{2}^{4}+2z_{1}^{3}z_{2}z_{3}+4z_{1}^{2}z_{2}^{2}z_{3}+2z_{1}z_{2}^{3}z_{3}+z_{1}^{3}z_{3}^{2}\\ &\quad-4z_{1}^{2}z_{2}z_{3}^{2}-9z_{1}z_{2}^{2}z_{3}^{2}-4z_{2}^{3}z_{3}^{2}-2z_{1}^{2}z_{3}^{3}+2z_{1}z_{2}z_{3}^{3}+4z_{2}^{2}z_{3}^{3}+z_{1}z_{3}^{4}. \end{align*}$$
That curve is irreducible, has geometric genus
![]() $1$
and its normalization has j-invariant
$1$
and its normalization has j-invariant
![]() $-5^{6}/28$
. By removing the base locus B, one obtains that the rational self-map F is defined by the following degree
$-5^{6}/28$
. By removing the base locus B, one obtains that the rational self-map F is defined by the following degree
![]() $6$
polynomials
$6$
polynomials
 $$ \begin{align*} Q_{1}=&z_{1}Q,\\ Q_{2}=&-z_{1}^{5}z_{2}-3z_{1}^{4}z_{2}^{2}-3z_{1}^{3}z_{2}^{3}-z_{1}^{2}z_{2}^{4}+z_{1}^{4}z_{2}z_{3}+2z_{1}^{3}z_{2}^{2}z_{3}+z_{1}^{2}z_{2}^{3}z_{3}\\ &+z_{1}^{3}z_{2}z_{3}^{2}+2z_{1}^{2}z_{2}^{2}z_{3}^{2}+z_{1}z_{2}^{3}z_{3}^{2}-z_{1}^{2}z_{2}z_{3}^{3}+z_{2}^{3}z_{3}^{3}-z_{2}^{2}z_{3}^{4},\\ Q_{3}=&2z_{1}^{4}z_{2}z_{3}+4z_{1}^{3}z_{2}^{2}z_{3}+2z_{1}^{2}z_{2}^{3}z_{3}+z_{1}^{4}z_{3}^{2}-4z_{1}^{3}z_{2}z_{3}^{2}-8z_{1}^{2}z_{2}^{2}z_{3}^{2}-3z_{1}z_{2}^{3}z_{3}^{2}\\ &-2z_{1}^{3}z_{3}^{3}+2z_{1}^{2}z_{2}z_{3}^{3}+4z_{1}z_{2}^{2}z_{3}^{3}+z_{2}^{3}z_{3}^{3}+z_{1}^{2}z_{3}^{4}, \end{align*} $$
$$ \begin{align*} Q_{1}=&z_{1}Q,\\ Q_{2}=&-z_{1}^{5}z_{2}-3z_{1}^{4}z_{2}^{2}-3z_{1}^{3}z_{2}^{3}-z_{1}^{2}z_{2}^{4}+z_{1}^{4}z_{2}z_{3}+2z_{1}^{3}z_{2}^{2}z_{3}+z_{1}^{2}z_{2}^{3}z_{3}\\ &+z_{1}^{3}z_{2}z_{3}^{2}+2z_{1}^{2}z_{2}^{2}z_{3}^{2}+z_{1}z_{2}^{3}z_{3}^{2}-z_{1}^{2}z_{2}z_{3}^{3}+z_{2}^{3}z_{3}^{3}-z_{2}^{2}z_{3}^{4},\\ Q_{3}=&2z_{1}^{4}z_{2}z_{3}+4z_{1}^{3}z_{2}^{2}z_{3}+2z_{1}^{2}z_{2}^{3}z_{3}+z_{1}^{4}z_{3}^{2}-4z_{1}^{3}z_{2}z_{3}^{2}-8z_{1}^{2}z_{2}^{2}z_{3}^{2}-3z_{1}z_{2}^{3}z_{3}^{2}\\ &-2z_{1}^{3}z_{3}^{3}+2z_{1}^{2}z_{2}z_{3}^{3}+4z_{1}z_{2}^{2}z_{3}^{3}+z_{2}^{3}z_{3}^{3}+z_{1}^{2}z_{3}^{4}, \end{align*} $$
and the indeterminacy locus of
![]() $F=(Q_{1}:Q_{2}:Q_{3})$
are the
$F=(Q_{1}:Q_{2}:Q_{3})$
are the
![]() $8$
points
$8$
points
 $$\begin{align*}q_{1}&=(0:0:1),q_{2}=(1:0:1),q_{3}=(0:1:0),q_{4}=(-1:1:0),\\q_{5}&=(1:0:0),\,q_{r}=(-r{}^{2}+2r:r:1) \end{align*}$$
$$\begin{align*}q_{1}&=(0:0:1),q_{2}=(1:0:1),q_{3}=(0:1:0),q_{4}=(-1:1:0),\\q_{5}&=(1:0:0),\,q_{r}=(-r{}^{2}+2r:r:1) \end{align*}$$
where r is any root of
![]() $X^{3}-4X^{2}+3X+1$
(the field
$X^{3}-4X^{2}+3X+1$
(the field
![]() $\mathbb {Q}(r)$
is the degree
$\mathbb {Q}(r)$
is the degree
![]() $3$
real subfield of
$3$
real subfield of
![]() $\mathbb {Q}(\zeta _{7})$
).
$\mathbb {Q}(\zeta _{7})$
).
Let us define the projection map
![]() $\pi _{1}:Z_7\to \mathbb {P}^{2}(z_{1},z_{2},z_{3})$
from the point
$\pi _{1}:Z_7\to \mathbb {P}^{2}(z_{1},z_{2},z_{3})$
from the point
![]() $s_{8}:y_{2}=y_{3}=y_{4}=0$
contained in surface
$s_{8}:y_{2}=y_{3}=y_{4}=0$
contained in surface
![]() $Z_7$
. This point is an
$Z_7$
. This point is an
![]() $A_{3}$
singularity on
$A_{3}$
singularity on
![]() $Z_7$
, in particular it has multiplicity
$Z_7$
, in particular it has multiplicity
![]() $2$
, thus the map
$2$
, thus the map
![]() $\pi _{1}$
from the quartic to the plane has degree
$\pi _{1}$
from the quartic to the plane has degree
![]() $2$
. One has:
$2$
. One has:
Lemma 3.9. The branch loci of
![]() $\pi _{1}$
is the union of the quintic curve
$\pi _{1}$
is the union of the quintic curve
![]() $B=\{Q=0\}$
and the line
$B=\{Q=0\}$
and the line
![]() $L:z_{1}=0$
.
$L:z_{1}=0$
.
Proof. The ramification locus of
![]() $\pi _{1}$
is the discriminant of the equation of
$\pi _{1}$
is the discriminant of the equation of
![]() $Z_7$
(given in (3.2)) with respect to the variable
$Z_7$
(given in (3.2)) with respect to the variable
![]() $y_{1}$
. The image of the ramification curve by
$y_{1}$
. The image of the ramification curve by
![]() $\pi _{1}$
is the curve
$\pi _{1}$
is the curve
![]() $B+L$
.
$B+L$
.
The curve B has singularities of type
![]() $A_{4},A_{4},A_{2}$
at the points
$A_{4},A_{4},A_{2}$
at the points
![]() $q_{2},q_{4},q_{5}$
, respectively. The union
$q_{2},q_{4},q_{5}$
, respectively. The union
![]() $L+B$
has singularities of type
$L+B$
has singularities of type
![]() $A_{1},A_{3},A_{4},A_{3},A_{4},A_{2}$
at the points
$A_{1},A_{3},A_{4},A_{3},A_{4},A_{2}$
at the points
![]() $q_{0}=(0:1:1),q_{1},q_{2},q_{3},q_{4},q_{5}$
, respectively.
$q_{0}=(0:1:1),q_{1},q_{2},q_{3},q_{4},q_{5}$
, respectively.
A direct computation shows that
for
![]() $R=\tfrac {1}{8}z_{2}^{2}(z_{1}-z_{3})^{2}R_{4}R_{7}$
, where
$R=\tfrac {1}{8}z_{2}^{2}(z_{1}-z_{3})^{2}R_{4}R_{7}$
, where
 $$ \begin{align*} R_{4}=&z_{1}^{4}+2z_{1}^{3}z_{2}+z_{1}^{2}z_{2}^{2}-z_{1}^{2}z_{3}^{2}-z_{1}z_{2}z_{3}^{2}-z_{2}z_{3}^{3},\\ R_{7}=&z_{1}^{6}z_{2}+4z_{1}^{5}z_{2}^{2}+6z_{1}^{4}z_{2}^{3}+4z_{1}^{3}z_{2}^{4}+z_{1}^{2}z_{2}^{5}+z_{1}^{6}z_{3}-7z_{1}^{4}z_{2}^{2}z_{3}-11z_{1}^{3}z_{2}^{3}z_{3}-6z_{1}^{2}z_{2}^{4}z_{3}-z_{1}z_{2}^{5}z_{3}\\ &-z_{1}^{5}z_{3}^{2}+3z_{1}^{3}z_{2}^{2}z_{3}^{2}+2z_{1}^{2}z_{2}^{3}z_{3}^{2}+3z_{1}^{2}z_{2}^{2}z_{3}^{3}+5z_{1}z_{2}^{3}z_{3}^{3}+2z_{2}^{4}z_{3}^{3}-2z_{1}z_{2}^{2}z_{3}^{4}-2z_{2}^{3}z_{3}^{4}-z_{1}z_{2}z_{3}^{5}. \end{align*} $$
$$ \begin{align*} R_{4}=&z_{1}^{4}+2z_{1}^{3}z_{2}+z_{1}^{2}z_{2}^{2}-z_{1}^{2}z_{3}^{2}-z_{1}z_{2}z_{3}^{2}-z_{2}z_{3}^{3},\\ R_{7}=&z_{1}^{6}z_{2}+4z_{1}^{5}z_{2}^{2}+6z_{1}^{4}z_{2}^{3}+4z_{1}^{3}z_{2}^{4}+z_{1}^{2}z_{2}^{5}+z_{1}^{6}z_{3}-7z_{1}^{4}z_{2}^{2}z_{3}-11z_{1}^{3}z_{2}^{3}z_{3}-6z_{1}^{2}z_{2}^{4}z_{3}-z_{1}z_{2}^{5}z_{3}\\ &-z_{1}^{5}z_{3}^{2}+3z_{1}^{3}z_{2}^{2}z_{3}^{2}+2z_{1}^{2}z_{2}^{3}z_{3}^{2}+3z_{1}^{2}z_{2}^{2}z_{3}^{3}+5z_{1}z_{2}^{3}z_{3}^{3}+2z_{2}^{4}z_{3}^{3}-2z_{1}z_{2}^{2}z_{3}^{4}-2z_{2}^{3}z_{3}^{4}-z_{1}z_{2}z_{3}^{5}. \end{align*} $$
The images of the curves
![]() $z_{2}=0,\,z_{1}-z_{3}=0$
and
$z_{2}=0,\,z_{1}-z_{3}=0$
and
![]() $R_{4}=0$
by the rational self-map
$R_{4}=0$
by the rational self-map
![]() $F=(Q_{1}:Q_{2}:Q_{3})$
of
$F=(Q_{1}:Q_{2}:Q_{3})$
of
![]() $\mathbb {P}^{2}$
are the indeterminacy points
$\mathbb {P}^{2}$
are the indeterminacy points
![]() $q_{2}, q_{4}, q_{2}$
, respectively. The image of the curve
$q_{2}, q_{4}, q_{2}$
, respectively. The image of the curve
![]() $R_{7}=0$
under the map F is the quintic curve B. The image of the quintic curve B under the map F is the line
$R_{7}=0$
under the map F is the quintic curve B. The image of the quintic curve B under the map F is the line
![]() $L:z_{1}=0$
. The rational map F preserves L and the action of F on L is through the map
$L:z_{1}=0$
. The rational map F preserves L and the action of F on L is through the map
![]() $(z_{2}:z_{3})\to (z_{2}-z_{3}:z_{3})$
.
$(z_{2}:z_{3})\to (z_{2}-z_{3}:z_{3})$
.
From the above description and §2.3, the surface
![]() $Z_7^{s}$
is the minimal desingularization of the double cover
$Z_7^{s}$
is the minimal desingularization of the double cover
branched over
![]() $L+B$
. The birational map between X and
$L+B$
. The birational map between X and
![]() $Z_7$
is given by the equalities
$Z_7$
is given by the equalities
![]() $y_{i+1}=z_{i}$
for
$y_{i+1}=z_{i}$
for
![]() $i\in \{1,2,3\}$
and
$i\in \{1,2,3\}$
and
We continue to denote by ![]() the rational self-map
the rational self-map
Applying the results of §2.3, we obtain that:
Theorem 3.10. The dynamical system ![]() is semi-conjugated to
is semi-conjugated to
![]() $(\mathbb {P}^{2},F)$
.
$(\mathbb {P}^{2},F)$
.
Remark 3.11. a) The degrees of the coprime polynomials defining the rational maps
![]() $F,F^{2},F^{3}$
are
$F,F^{2},F^{3}$
are
![]() $6,21,82$
, respectively.
$6,21,82$
, respectively.
b) It would be interesting to construct rational self-maps on some other degree two K3 surfaces.
4 The Octagon and the operator 
4.1 The matroid
 $M_{8}$
constructed from the regular octagon.
$M_{8}$
constructed from the regular octagon.
Consider the
![]() $16$
lines in Figure 2: the black lines
$16$
lines in Figure 2: the black lines
![]() $\ell _{1},\dots ,\ell _{8}$
are the
$\ell _{1},\dots ,\ell _{8}$
are the
![]() $8$
lines of the regular octagon
$8$
lines of the regular octagon
![]() $\mathcal {C}_{1}$
and the blue lines
$\mathcal {C}_{1}$
and the blue lines
![]() $\ell _{1}',\dots ,\ell _{8}'$
are the 8 lines symmetries of
$\ell _{1}',\dots ,\ell _{8}'$
are the 8 lines symmetries of
![]() $\mathcal {C}_{0}$
. The image of
$\mathcal {C}_{0}$
. The image of
![]() $\mathcal {C}_{0}=\ell _{1}+\dots +\ell _{8}$
by the operator
$\mathcal {C}_{0}=\ell _{1}+\dots +\ell _{8}$
by the operator ![]() is the line arrangement
is the line arrangement
![]() $\mathcal {C}_{1}=\ell _{1}'+\dots +\ell _{8}'$
.
$\mathcal {C}_{1}=\ell _{1}'+\dots +\ell _{8}'$
.

Figure 2 Matroid
![]() $M_8$
(
$M_8$
(
![]() $\ell _i$
and
$\ell _i$
and
![]() $\ell _{i+4}$
meet at infinity at point
$\ell _{i+4}$
meet at infinity at point
![]() $p_{i,i+4}$
).
$p_{i,i+4}$
).
The
![]() $8$
lines
$8$
lines
![]() $\ell _{i},\ell _{j}$
of
$\ell _{i},\ell _{j}$
of
![]() $\mathcal {C}_{0}=(\ell _{1},\dots \ell _{8})$
meet in
$\mathcal {C}_{0}=(\ell _{1},\dots \ell _{8})$
meet in
![]() $28$
double points denoted by
$28$
double points denoted by
![]() $p_{i,j}$
(some points are at infinity). The lines
$p_{i,j}$
(some points are at infinity). The lines
![]() $\ell _{1}',\dots ,\ell _{8}'$
are the lines containing the points in sets
$\ell _{1}',\dots ,\ell _{8}'$
are the lines containing the points in sets
![]() $S_{1},\dots ,S_{8}$
which are respectively
$S_{1},\dots ,S_{8}$
which are respectively
 $$ \begin{align} \begin{array}{c} \{p_{1,8},p_{2,7},p_{3,6},p_{4,5}\},\{p_{1,7},p_{2,6},p_{3,5}\},\{p_{1,6},p_{2,5},p_{3,4},p_{7,8}\},\{p_{1,5},p_{2,4},p_{6,8}\},\\ \{p_{1,4},p_{2,3},p_{5,8},p_{6,7}\},\{p_{1,3},p_{4,8},p_{5,7}\},\{p_{1,2},p_{3,8},p_{4,7},p_{5,6}\},\{p_{2,8},p_{3,7},p_{4,6}\}. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{c} \{p_{1,8},p_{2,7},p_{3,6},p_{4,5}\},\{p_{1,7},p_{2,6},p_{3,5}\},\{p_{1,6},p_{2,5},p_{3,4},p_{7,8}\},\{p_{1,5},p_{2,4},p_{6,8}\},\\ \{p_{1,4},p_{2,3},p_{5,8},p_{6,7}\},\{p_{1,3},p_{4,8},p_{5,7}\},\{p_{1,2},p_{3,8},p_{4,7},p_{5,6}\},\{p_{2,8},p_{3,7},p_{4,6}\}. \end{array} \end{align} $$
These sets
![]() $S_{k},\,k=1,\dots ,8$
form a partition of the
$S_{k},\,k=1,\dots ,8$
form a partition of the
![]() $28$
double points of
$28$
double points of
![]() $\mathcal {C}_{0}$
; these
$\mathcal {C}_{0}$
; these
![]() $28$
points are the triple points of
$28$
points are the triple points of
![]() $\mathcal {C}_{0}\cup \mathcal {C}_{1}$
. One has the relation
$\mathcal {C}_{0}\cup \mathcal {C}_{1}$
. One has the relation ![]() (as unlabeled line arrangements).
(as unlabeled line arrangements).
Let
![]() $M_{8}$
be the matroid associated to the incidences between the
$M_{8}$
be the matroid associated to the incidences between the
![]() $16$
labeled lines
$16$
labeled lines
![]() $\ell _{1},\dots ,\ell _{8},\ell _{1}',\dots ,\ell _{8}'$
and the
$\ell _{1},\dots ,\ell _{8},\ell _{1}',\dots ,\ell _{8}'$
and the
![]() $28$
triple points: it is obtained from the matroid associated to the labeled line arrangement
$28$
triple points: it is obtained from the matroid associated to the labeled line arrangement
![]() $\mathcal {C}_{0}\cup \mathcal {C}_{1}$
, but we discard all non-bases coming from the central point, so that
$\mathcal {C}_{0}\cup \mathcal {C}_{1}$
, but we discard all non-bases coming from the central point, so that
![]() $M_{8}$
has
$M_{8}$
has
![]() $16$
atoms and only
$16$
atoms and only
![]() $28$
non-bases. We denote by
$28$
non-bases. We denote by
![]() $\mathcal {R}_{8}$
the moduli space of realizations of
$\mathcal {R}_{8}$
the moduli space of realizations of
![]() $M_{8}$
(over
$M_{8}$
(over
![]() $\mathbb {C})$
.
$\mathbb {C})$
.
4.2 The moduli space
 $ \mathcal {R}_{8}$
of
$ \mathcal {R}_{8}$
of
 $M_{8.}$
$M_{8.}$
A direct computation in OSCAR shows that the moduli space
![]() $\mathcal {R}_{8}$
is two-dimensional, and an open sub-set of the quartic surface
$\mathcal {R}_{8}$
is two-dimensional, and an open sub-set of the quartic surface
![]() $Z_{8}$
in
$Z_{8}$
in
![]() $\mathbb {P}^{3}$
with the equation
$\mathbb {P}^{3}$
with the equation
The surface
![]() $Z_{8}$
has singularities
$Z_{8}$
has singularities
![]() $A_{2},A_{2},A_{3},A_{4},A_{3},A_{1}$
at the respective points
$A_{2},A_{2},A_{3},A_{4},A_{3},A_{1}$
at the respective points
Its minimal desingularization
![]() $Z_{8}^{s}$
is a K3 surface. The realization
$Z_{8}^{s}$
is a K3 surface. The realization
![]() $\mathcal {A}(x)$
corresponding to a generic point
$\mathcal {A}(x)$
corresponding to a generic point
![]() $x=(x_{1},x_{2},x_{3})$
of
$x=(x_{1},x_{2},x_{3})$
of
![]() $Z_{8}$
in the affine chart
$Z_{8}$
in the affine chart
![]() $\mathbb {A}^{3}=\{y_{4}\neq 0\}$
is the union
$\mathbb {A}^{3}=\{y_{4}\neq 0\}$
is the union
![]() $\mathcal {A}(x)=\mathcal {C}_{0}(x)\cup \mathcal {C}_{1}(x)$
, where
$\mathcal {A}(x)=\mathcal {C}_{0}(x)\cup \mathcal {C}_{1}(x)$
, where
![]() $\mathcal {C}_{0}(x)$
is the line arrangement with eight lines with normal vectors the four vectors of the canonical basis and the following four vectors
$\mathcal {C}_{0}(x)$
is the line arrangement with eight lines with normal vectors the four vectors of the canonical basis and the following four vectors
 $$\begin{align*}\begin{array}{c} (x_{1}-x_{2}:x_{1}^{2}-x_{1}x_{2}-x_{1}x_{3}+x_{1}-x_{2}+x_{3}:x_{1}-x_{2}x_{3}-x_{2}+x_{3}),\\ (x_{1}x_{2}-x_{1}x_{3}-x_{2}+x_{3}:x_{1}x_{2}^{2}-x_{1}x_{2}-x_{1}x_{3}+x_{1}-x_{2}+x_{3}:x_{1}x_{2}x_{3}-2x_{1}x_{3}+x_{1}-x_{2}+x_{3})\\ (x_{1}-1:x_{1}x_{2}-x_{2}:x_{1}-x_{2}),(1:x_{1}:x_{3}). \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{c} (x_{1}-x_{2}:x_{1}^{2}-x_{1}x_{2}-x_{1}x_{3}+x_{1}-x_{2}+x_{3}:x_{1}-x_{2}x_{3}-x_{2}+x_{3}),\\ (x_{1}x_{2}-x_{1}x_{3}-x_{2}+x_{3}:x_{1}x_{2}^{2}-x_{1}x_{2}-x_{1}x_{3}+x_{1}-x_{2}+x_{3}:x_{1}x_{2}x_{3}-2x_{1}x_{3}+x_{1}-x_{2}+x_{3})\\ (x_{1}-1:x_{1}x_{2}-x_{2}:x_{1}-x_{2}),(1:x_{1}:x_{3}). \end{array} \end{align*}$$
Moreover,
![]() $\mathcal {C}_{1}(x)$
is the line arrangement with normal vectors
$\mathcal {C}_{1}(x)$
is the line arrangement with normal vectors
 $$\begin{align*}\begin{array}{c} (x_{1}x_{2}-x_{1}x_{3}-x_{2}+x_{3}:x_{1}x_{2}^{2}-x_{1}x_{2}-x_{1}x_{3}+x_{1}-x_{2}+x_{3}:x_{1}x_{2}-x_{1}x_{3}-x_{2}^{2}+x_{2}x_{3}),\\ (x_{1}^{2}x_{2}-x_{1}^{2}x_{3}-x_{1}x_{2}^{2}+x_{1}x_{2}x_{3}-x_{1}x_{2}+x_{1}x_{3}+x_{2}^{2}-x_{2}x_{3}:x_{1}^{3}x_{2}-x_{1}^{3}x_{3}-x_{1}^{2}x_{2}^{2}+x_{1}^{2}x_{3}^{2}\\ +2x_{1}x_{2}x_{3}-x_{1}x_{2}-2x_{1}x_{3}^{2}+x_{1}x_{3}+x_{2}^{2}-2x_{2}x_{3}+x_{3}^{2}:x_{1}^{2}x_{2}x_{3}-x_{1}^{2}x_{2}-x_{1}^{2}\\ x_{3}+x_{1}^{2}+x_{1}x_{2}^{2}-2x_{1}x_{2}-x_{1}x_{3}^{2}+2x_{1}x_{3}+x_{2}^{2}-2x_{2}x_{3}+x_{3}^{2}),\\ (x_{1}-x_{2}:x_{1}-x_{2}:x_{1}-x_{2}x_{3}-x_{2}+x_{3}),(x_{3}:x_{1}x_{2}:x_{3}),(0:1:1),\\ (x_{1}-1:0:x_{1}-x_{3}),(1:x_{1}:0),(1:x_{2}:x_{3}). \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{c} (x_{1}x_{2}-x_{1}x_{3}-x_{2}+x_{3}:x_{1}x_{2}^{2}-x_{1}x_{2}-x_{1}x_{3}+x_{1}-x_{2}+x_{3}:x_{1}x_{2}-x_{1}x_{3}-x_{2}^{2}+x_{2}x_{3}),\\ (x_{1}^{2}x_{2}-x_{1}^{2}x_{3}-x_{1}x_{2}^{2}+x_{1}x_{2}x_{3}-x_{1}x_{2}+x_{1}x_{3}+x_{2}^{2}-x_{2}x_{3}:x_{1}^{3}x_{2}-x_{1}^{3}x_{3}-x_{1}^{2}x_{2}^{2}+x_{1}^{2}x_{3}^{2}\\ +2x_{1}x_{2}x_{3}-x_{1}x_{2}-2x_{1}x_{3}^{2}+x_{1}x_{3}+x_{2}^{2}-2x_{2}x_{3}+x_{3}^{2}:x_{1}^{2}x_{2}x_{3}-x_{1}^{2}x_{2}-x_{1}^{2}\\ x_{3}+x_{1}^{2}+x_{1}x_{2}^{2}-2x_{1}x_{2}-x_{1}x_{3}^{2}+2x_{1}x_{3}+x_{2}^{2}-2x_{2}x_{3}+x_{3}^{2}),\\ (x_{1}-x_{2}:x_{1}-x_{2}:x_{1}-x_{2}x_{3}-x_{2}+x_{3}),(x_{3}:x_{1}x_{2}:x_{3}),(0:1:1),\\ (x_{1}-1:0:x_{1}-x_{3}),(1:x_{1}:0),(1:x_{2}:x_{3}). \end{array} \end{align*}$$
From the definition of the matroid
![]() $M_{8}$
, if
$M_{8}$
, if
![]() $\mathcal {A}_{0}=\mathcal {C}_{0}\cup \mathcal {C}_{1}$
is a realization of
$\mathcal {A}_{0}=\mathcal {C}_{0}\cup \mathcal {C}_{1}$
is a realization of
![]() $M_{8}$
and
$M_{8}$
and
![]() $\mathcal {C}_{0}$
(resp.
$\mathcal {C}_{0}$
(resp.
![]() $\mathcal {C}_{1}$
) denotes its first (resp. last) eight lines then,
$\mathcal {C}_{1}$
) denotes its first (resp. last) eight lines then, ![]() as unlabeled line arrangements. The following operator
as unlabeled line arrangements. The following operator ![]() gives a labeling to
gives a labeling to ![]() :
:
Definition 4.2. The operator ![]() associates to a labeled line arrangement
associates to a labeled line arrangement
![]() $L_{8}$
of
$L_{8}$
of
![]() $8$
lines
$8$
lines
![]() $\ell _{1},\dots ,\ell _{8}$
, the labeled line arrangement
$\ell _{1},\dots ,\ell _{8}$
, the labeled line arrangement
![]() $\ell _{1}',\dots ,\ell _{8}'$
where
$\ell _{1}',\dots ,\ell _{8}'$
where
![]() $\ell _{j}'$
is the set of lines containing all the points in
$\ell _{j}'$
is the set of lines containing all the points in
![]() $S_{k}$
defined in (4.1) (
$S_{k}$
defined in (4.1) (
![]() $\ell _{j}'$
is a line or the empty set).
$\ell _{j}'$
is a line or the empty set).
For a generic arrangement
![]() $L_{8}$
of eight lines, one has
$L_{8}$
of eight lines, one has ![]() . The operator
. The operator ![]() is constructed so that if
is constructed so that if
![]() $\mathcal {A}_{0}$
is any realization of
$\mathcal {A}_{0}$
is any realization of
![]() $M_{8}$
and
$M_{8}$
and
![]() $\mathcal {C}_{0}$
(resp.
$\mathcal {C}_{0}$
(resp.
![]() $\mathcal {C}_{1}$
) denotes its first (resp. last) eight lines then
$\mathcal {C}_{1}$
) denotes its first (resp. last) eight lines then ![]() as labeled line arrangements (and of course
as labeled line arrangements (and of course ![]() if one forgets the labels).
if one forgets the labels).
4.3 The operator  acts as a rational self-map on
acts as a rational self-map on
 $ \mathcal {R}_{8.}$
$ \mathcal {R}_{8.}$
A priori the line arrangement ![]() could be empty, however:
could be empty, however:
Theorem 4.3. Suppose that
![]() $\mathcal {A}_{0}=\mathcal {C}_{0}\cup \mathcal {C}_{1}$
is generic among the realizations of
$\mathcal {A}_{0}=\mathcal {C}_{0}\cup \mathcal {C}_{1}$
is generic among the realizations of
![]() $M_{8}$
. Then the labeled line arrangement
$M_{8}$
. Then the labeled line arrangement ![]() has
has
![]() $8$
lines and
$8$
lines and
![]() $\mathcal {A}_{1}=\mathcal {C}_{1}\cup \mathcal {C}_{2}$
is a realization of
$\mathcal {A}_{1}=\mathcal {C}_{1}\cup \mathcal {C}_{2}$
is a realization of
![]() $\mathcal {R}_{8}$
.
$\mathcal {R}_{8}$
.
Proof. Using the function field of
![]() $\mathcal {R}_{8}$
, we realize the generic element of
$\mathcal {R}_{8}$
, we realize the generic element of
![]() $\mathcal {R}_{8}$
using the formulas for
$\mathcal {R}_{8}$
using the formulas for
![]() $\mathcal {A}(x)$
. Then we compute
$\mathcal {A}(x)$
. Then we compute ![]() and obtain eight lines. Finally we check that
and obtain eight lines. Finally we check that
![]() $\mathcal {C}_{1}\cup \mathcal {C}_{2}$
defines the same matroid as
$\mathcal {C}_{1}\cup \mathcal {C}_{2}$
defines the same matroid as
![]() $\mathcal {A}_{0}$
.
$\mathcal {A}_{0}$
.
The operator ![]() acts on realizations of
acts on realizations of
![]() $M_{8}$
, sending
$M_{8}$
, sending
![]() $\mathcal {A}_{0}=\mathcal {C}_{0}\cup \mathcal {C}_{1}$
to
$\mathcal {A}_{0}=\mathcal {C}_{0}\cup \mathcal {C}_{1}$
to
![]() $\mathcal {A}_{1}=\mathcal {C}_{1}\cup \mathcal {C}_{2}$
, where
$\mathcal {A}_{1}=\mathcal {C}_{1}\cup \mathcal {C}_{2}$
, where ![]() . It therefore acts on the moduli space
. It therefore acts on the moduli space
![]() $Z_{8}$
: we denote by
$Z_{8}$
: we denote by
that action. In order to obtain the explicit polynomials defining ![]() , we remark that one may recover the coordinates
, we remark that one may recover the coordinates
![]() $x_{1},x_{2},x_{3}$
of the line arrangement
$x_{1},x_{2},x_{3}$
of the line arrangement
![]() $\mathcal {A}_{0}(x)$
from the two last normal vectors
$\mathcal {A}_{0}(x)$
from the two last normal vectors
![]() $(1:x_{1}:0),(1:x_{2}:x_{3})$
of
$(1:x_{1}:0),(1:x_{2}:x_{3})$
of
![]() $\mathcal {C}_{1}(x)$
. Then one computes the unique line arrangement
$\mathcal {C}_{1}(x)$
. Then one computes the unique line arrangement
![]() $\tilde {\mathcal {C}_{1}}\cup \tilde {\mathcal {C}_{2}}$
projectively equivalent to
$\tilde {\mathcal {C}_{1}}\cup \tilde {\mathcal {C}_{2}}$
projectively equivalent to
![]() $\mathcal {A}_{1}(x)=\mathcal {C}_{1}(x)\cup \mathcal {C}_{2}(x)$
such that the first four normal vectors are the canonical basis. The image of x by
$\mathcal {A}_{1}(x)=\mathcal {C}_{1}(x)\cup \mathcal {C}_{2}(x)$
such that the first four normal vectors are the canonical basis. The image of x by ![]() is the point
is the point
![]() $x'=(x_{1}',x_{2}',x_{3}')$
such that the two last normal vectors of
$x'=(x_{1}',x_{2}',x_{3}')$
such that the two last normal vectors of
![]() $\tilde {\mathcal {C}_{2}}$
are
$\tilde {\mathcal {C}_{2}}$
are
![]() $(1:x_{1}':0),(1:x_{2}':x_{3}')$
(and
$(1:x_{1}':0),(1:x_{2}':x_{3}')$
(and
![]() $\tilde {\mathcal {C}_{1}}\cup \tilde {\mathcal {C}_{2}}=\mathcal {A}_{0}(x')$
). Taking the homogenization to
$\tilde {\mathcal {C}_{1}}\cup \tilde {\mathcal {C}_{2}}=\mathcal {A}_{0}(x')$
). Taking the homogenization to
![]() $\mathbb {P}^{3}$
, one obtains that the map
$\mathbb {P}^{3}$
, one obtains that the map ![]() is defined by the four degree
is defined by the four degree
![]() $10$
coprime polynomials
$10$
coprime polynomials
![]() $P_{1},\dots ,P_{4}$
given in the ancillary file of the arXiv version of this paper. The base points of
$P_{1},\dots ,P_{4}$
given in the ancillary file of the arXiv version of this paper. The base points of ![]() are
are
 $$\begin{align*}\begin{array}{c} (-\sqrt{2}-1:\sqrt{2}+2:2\sqrt{2}+3:1),(\sqrt{2}-1:-\sqrt{2}+2:-2\sqrt{2}+3:1),\\ (i:0:1:1),(-i:0:1:1),(1:1:0:1),(0:1:1:0),(0:1:0:1). \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{c} (-\sqrt{2}-1:\sqrt{2}+2:2\sqrt{2}+3:1),(\sqrt{2}-1:-\sqrt{2}+2:-2\sqrt{2}+3:1),\\ (i:0:1:1),(-i:0:1:1),(1:1:0:1),(0:1:1:0),(0:1:0:1). \end{array} \end{align*}$$
The line arrangements
![]() $\mathcal {C}_{0}\cup \mathcal {C}_{1}$
associated to the first two points are the regular octagon and its lines of symmetries. The line arrangements
$\mathcal {C}_{0}\cup \mathcal {C}_{1}$
associated to the first two points are the regular octagon and its lines of symmetries. The line arrangements
![]() $\mathcal {C}_{0}$
associated to the third and fourth points are such that
$\mathcal {C}_{0}$
associated to the third and fourth points are such that ![]() is the Ceva line arrangement with
is the Ceva line arrangement with
![]() $12$
lines; it contains
$12$
lines; it contains
![]() $\mathcal {C}_{0}$
.
$\mathcal {C}_{0}$
.
Using the explicit polynomials
![]() $P_{1},\dots ,P_{4}$
, we obtain that:
$P_{1},\dots ,P_{4}$
, we obtain that:
Proposition 4.4. The degree of the rational self-map ![]() on
on
![]() $Z_8^{s}$
is
$Z_8^{s}$
is
![]() $4$
.
$4$
.
Proof. We again apply the method from [Reference Voisin15]. Let
![]() $f(x_{1},x_{2},x_{3})$
be the equation of the quartic
$f(x_{1},x_{2},x_{3})$
be the equation of the quartic
![]() $Z_8$
in the chart
$Z_8$
in the chart
![]() $U_{4}:y_{4}\neq 0$
. The space of global non-vanishing differential
$U_{4}:y_{4}\neq 0$
. The space of global non-vanishing differential
![]() $2$
-forms is generated by a form
$2$
-forms is generated by a form ![]() , which one can choose so that on an open set of
, which one can choose so that on an open set of
![]() $U_{4}$
one has:
$U_{4}$
one has: ![]() The rational self-map
The rational self-map ![]() preserves
preserves
![]() $U_{4}$
. A direct computation gives that
$U_{4}$
. A direct computation gives that ![]() The pull-back by
The pull-back by ![]() of the volume form
of the volume form ![]() is therefore
is therefore ![]() , thus the degree of
, thus the degree of ![]() is
is
![]() $4$
.
$4$
.
4.4 The dynamical system  is semi-conjugated to the plane.
is semi-conjugated to the plane.
The four polynomials
![]() $P_{1},\dots ,P_{4}$
such that
$P_{1},\dots ,P_{4}$
such that ![]() verify
verify
![]() $\deg _{y_{1}}(P_{1})=1$
and
$\deg _{y_{1}}(P_{1})=1$
and
![]() $\deg _{y_{k}}(P_{1})=0$
for
$\deg _{y_{k}}(P_{1})=0$
for
![]() $k\geq 2$
. Let
$k\geq 2$
. Let
![]() $\pi :Z_{8}\dashrightarrow \mathbb {P}^{2}$
be the double cover obtained by projecting from the double point
$\pi :Z_{8}\dashrightarrow \mathbb {P}^{2}$
be the double cover obtained by projecting from the double point
![]() $(1:0:0:0)$
of
$(1:0:0:0)$
of
![]() $Z_{8}$
.
$Z_{8}$
.
Lemma 4.5. The branch curve B of
![]() $\pi $
is the union of the conic
$\pi $
is the union of the conic
![]() $C=\{z_{1}^{2}-z_{2}z_{3}=0\}$
and the quartic curve
$C=\{z_{1}^{2}-z_{2}z_{3}=0\}$
and the quartic curve
Proof. The ramification locus of
![]() $\pi _{1}$
is the discriminant of the equation of
$\pi _{1}$
is the discriminant of the equation of
![]() $Z_8$
with respect to the variable
$Z_8$
with respect to the variable
![]() $y_{1}$
. The image of the ramification curve by
$y_{1}$
. The image of the ramification curve by
![]() $\pi _{1}$
is the curve B.
$\pi _{1}$
is the curve B.
The quartic Q has geometric genus
![]() $0$
and is singular at the points
$0$
and is singular at the points
![]() $(1:0:0),(1:1:1)$
with singularities
$(1:0:0),(1:1:1)$
with singularities
![]() $A_{3}$
and
$A_{3}$
and
![]() $A_{1}$
. The curve
$A_{1}$
. The curve
![]() $B=C+Q$
is singular at the points
$B=C+Q$
is singular at the points
with singularities
![]() $A_{3},A_{5},A_{5},D_{4}$
, respectively.
$A_{3},A_{5},A_{5},D_{4}$
, respectively.
Let us define the polynomials
![]() $Q_{k}=P_{k+1}(0,z_{1},z_{2},z_{3})$
$Q_{k}=P_{k+1}(0,z_{1},z_{2},z_{3})$
![]() $(k=1,2,3$
) and the rational self-map
$(k=1,2,3$
) and the rational self-map
![]() $\mu :\mathbb {P}^{2}\dashrightarrow \mathbb {P}^{2}$
,
$\mu :\mathbb {P}^{2}\dashrightarrow \mathbb {P}^{2}$
,
![]() $\mu =(Q_{1}:Q_{2}:Q_{3})$
. One has
$\mu =(Q_{1}:Q_{2}:Q_{3})$
. One has
![]() $ \mu ^{*}(B)=B+2D $
for a degree
$ \mu ^{*}(B)=B+2D $
for a degree
![]() $27$
curve D. Using §2.3, the double cover of
$27$
curve D. Using §2.3, the double cover of
![]() $\mathbb {P}^{2}$
branched over
$\mathbb {P}^{2}$
branched over
![]() $B=C+Q$
is birational to the surface
$B=C+Q$
is birational to the surface
![]() $Z_{8}$
and
$Z_{8}$
and ![]() is semi-conjugated to
is semi-conjugated to
![]() $(\mathbb {P}^{2},\mu )$
.
$(\mathbb {P}^{2},\mu )$
.
The indetermination points of
![]() $\mu $
are the
$\mu $
are the
![]() $9$
points
$9$
points
 $$\begin{align*}\begin{array}{c} (1:0:0),(0:1:0),(0:0:1),(1:1:1),(1:0:1),(1:1:0),\\ (0:1:1),(-\sqrt{2}+2:-2\sqrt{2}+3:1),(\sqrt{2}+2:2\sqrt{2}+3:1). \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{c} (1:0:0),(0:1:0),(0:0:1),(1:1:1),(1:0:1),(1:1:0),\\ (0:1:1),(-\sqrt{2}+2:-2\sqrt{2}+3:1),(\sqrt{2}+2:2\sqrt{2}+3:1). \end{array} \end{align*}$$
The image by
![]() $\mu $
of Q is the conic C; the rational map
$\mu $
of Q is the conic C; the rational map
![]() $\mu $
restricts to the identity on C.
$\mu $
restricts to the identity on C.
Remark 4.6. The choice for the labelings of the lines in the unlabeled line arrangement ![]() was made so that the defining polynomials of the rational self-map
was made so that the defining polynomials of the rational self-map ![]() are of low degree. Moreover, for the other choices we tried, the degrees of the polynomials defining the analog of
are of low degree. Moreover, for the other choices we tried, the degrees of the polynomials defining the analog of ![]() with respect to any variables
with respect to any variables
![]() $y_{i}$
were never
$y_{i}$
were never
![]() $1,0,0,0$
, so that it was not possible to understand that rational self-map
$1,0,0,0$
, so that it was not possible to understand that rational self-map ![]() as a semi-conjugacy with the plane.
as a semi-conjugacy with the plane.
4.5 The K3 surface
 $Z_{8}$
and the modular surface
$Z_{8}$
and the modular surface
 $\Xi _{1}(8).$
$\Xi _{1}(8).$
One has:
Proposition 4.7. The K3 surface
![]() $Z_8^{s}$
is the unique K3 surface with discriminant
$Z_8^{s}$
is the unique K3 surface with discriminant
![]() $-8$
and Picard number
$-8$
and Picard number
![]() $20$
.
$20$
.
Proof. The eight lines with equations
 $$\begin{align*}\begin{array}{c} (y_{1}=y_{3}=0),(y_{1}=y_{4}=0),(y_{2}=y_{3}=0),(y_{2}=y_{4}=0),(y_{3}=y_{4}=0),\\ (y_{1}-y_{4}=y_{2}-y_{4}=0),(y_{1}-y_{3}=y_{2}-y_{4}=0),(y_{2}-y_{4}=y_{3}-y_{4}=0) \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{c} (y_{1}=y_{3}=0),(y_{1}=y_{4}=0),(y_{2}=y_{3}=0),(y_{2}=y_{4}=0),(y_{3}=y_{4}=0),\\ (y_{1}-y_{4}=y_{2}-y_{4}=0),(y_{1}-y_{3}=y_{2}-y_{4}=0),(y_{2}-y_{4}=y_{3}-y_{4}=0) \end{array} \end{align*}$$
are contained in the surface
![]() $Z_8$
. Using Magma, one can compute that their strict transforms on
$Z_8$
. Using Magma, one can compute that their strict transforms on
![]() $Z_8^{s}$
together with the
$Z_8^{s}$
together with the
![]() $15 (-2)$
-curves coming from the resolutions of the singularities of
$15 (-2)$
-curves coming from the resolutions of the singularities of
![]() $Z_8$
, generate a rank
$Z_8$
, generate a rank
![]() $20$
lattice with discriminant
$20$
lattice with discriminant
![]() $-8$
. There is no K3 surface with Picard number
$-8$
. There is no K3 surface with Picard number
![]() $20$
and discriminant
$20$
and discriminant
![]() $-2$
and there is a unique K3 surface with Picard number 20 and discriminant −8 (see, e.g., [Reference Schütt10]) which yields the conclusion.
$-2$
and there is a unique K3 surface with Picard number 20 and discriminant −8 (see, e.g., [Reference Schütt10]) which yields the conclusion.
Proposition 4.8. The surface
![]() $Z_8$
is (isomorphic to) the elliptic modular surface
$Z_8$
is (isomorphic to) the elliptic modular surface
![]() $\Xi _{1}(8)$
above the modular curve
$\Xi _{1}(8)$
above the modular curve
![]() $X_{1}(8)$
.
$X_{1}(8)$
.
Proof. The projection map from the line
![]() $y_{2}-y_{4}=y_{3}-y_{4}=0$
induces a fibration
$y_{2}-y_{4}=y_{3}-y_{4}=0$
induces a fibration
![]() $Z_8\to \mathbb {P}^{1}$
. By evaluating the Equation of
$Z_8\to \mathbb {P}^{1}$
. By evaluating the Equation of
![]() $Z_8$
at
$Z_8$
at
![]() $(X,1+t(Y-1),Y,1)$
, one gets the cubic affine model
$(X,1+t(Y-1),Y,1)$
, one gets the cubic affine model
of the generic fiber, where t is the parameter of
![]() $\mathbb {P}^{1}$
. One computes that the Weierstrass model of it is the elliptic curve
$\mathbb {P}^{1}$
. One computes that the Weierstrass model of it is the elliptic curve
The associated elliptic surface is a smooth model of the K3 surface
![]() $Z_8$
: it is isomorphic to
$Z_8$
: it is isomorphic to
![]() $Z_8^{s}$
. One computes that the singular fibers of the fibration are
$Z_8^{s}$
. One computes that the singular fibers of the fibration are
![]() $ 2I_{8}+I_{4}+I_{2}+2I_{1}, $
at the points
$ 2I_{8}+I_{4}+I_{2}+2I_{1}, $
at the points
![]() $1,0,\infty ,1/2,t^{2}-t-1/4=0$
, respectively.
$1,0,\infty ,1/2,t^{2}-t-1/4=0$
, respectively.
By [Reference Top and Yui13, §2.3.3], the equation of a Weierstrass model of the elliptic surface
![]() $\Xi _{1}(8)$
above the modular curve
$\Xi _{1}(8)$
above the modular curve
![]() $X_{1}(8)$
is
$X_{1}(8)$
is
where
![]() $s=2t^{2}/(t^{2}-1)$
. To check that
$s=2t^{2}/(t^{2}-1)$
. To check that
![]() $\Xi _{1}(8)$
is isomorphic to
$\Xi _{1}(8)$
is isomorphic to
![]() $Z_8^{s}$
, one just has to compare the two j-invariants
$Z_8^{s}$
, one just has to compare the two j-invariants
![]() $j(E)(t)\in \mathbb {Q}(t)$
and
$j(E)(t)\in \mathbb {Q}(t)$
and
![]() $j(E')(t)\in \mathbb {Q}(t)$
. We compute that
$j(E')(t)\in \mathbb {Q}(t)$
. We compute that
![]() $j(E)(\tfrac {1}{2}(1-\tfrac {1}{t}))=j(E')(t)$
, therefore E is isomorphic to
$j(E)(\tfrac {1}{2}(1-\tfrac {1}{t}))=j(E')(t)$
, therefore E is isomorphic to
![]() $E'$
, and
$E'$
, and
![]() $\Xi _{1}(8)\simeq Z_8^{s}$
.
$\Xi _{1}(8)\simeq Z_8^{s}$
.
4.6 Action of 
The automorphism group of
![]() $M_{8}$
is generated by the involutions
$M_{8}$
is generated by the involutions
 $$\begin{align*}\begin{array}{c} s_{1}=(2,4)(3,7)(6,8)(9,11)(10,14)(13,15),s_{2}=(2,6)(4,8)(9,13)(11,15),\\ s_{3}=(1,2)(3,8)(4,7)(5,6)(9,13)(10,12)(14,16). \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{c} s_{1}=(2,4)(3,7)(6,8)(9,11)(10,14)(13,15),s_{2}=(2,6)(4,8)(9,13)(11,15),\\ s_{3}=(1,2)(3,8)(4,7)(5,6)(9,13)(10,12)(14,16). \end{array} \end{align*}$$
The group ![]() is the semi-direct product
is the semi-direct product
![]() $\mathbb {Z}/8\mathbb {Z}\rtimes (\mathbb {Z}/2\mathbb {Z})^{2}$
. One computes that it acts faithfully on the K3 surface
$\mathbb {Z}/8\mathbb {Z}\rtimes (\mathbb {Z}/2\mathbb {Z})^{2}$
. One computes that it acts faithfully on the K3 surface
![]() $Z_{8}$
. The map
$Z_{8}$
. The map
![]() $s_{2}$
(acting on
$s_{2}$
(acting on
![]() $Z_8$
) is given in the ancillary file of the arXiv version of this paper. It is a birational involution of
$Z_8$
) is given in the ancillary file of the arXiv version of this paper. It is a birational involution of
![]() $\mathbb {P}^{3}$
.
$\mathbb {P}^{3}$
.
The group of elements
![]() $\sigma $
commuting with the action of
$\sigma $
commuting with the action of ![]() is isomorphic to
is isomorphic to
![]() $(\mathbb {Z}/2\mathbb {Z})^{2}$
. The involution
$(\mathbb {Z}/2\mathbb {Z})^{2}$
. The involution
![]() $s=(1,5)(2,6)(3,7)(4,8)$
is the unique automorphism of
$s=(1,5)(2,6)(3,7)(4,8)$
is the unique automorphism of ![]() such that
such that ![]()
4.7 Periodic line arrangements.
Let us prove:
Proposition 4.9. The surface
![]() $Z_{8}$
contains a curve
$Z_{8}$
contains a curve
![]() $C_{3}$
of geometric genus
$C_{3}$
of geometric genus
![]() $5$
such that each point of
$5$
such that each point of
![]() $C_{3}$
is fixed by
$C_{3}$
is fixed by ![]() and for a generic point x of
and for a generic point x of
![]() $C_{3}$
, the associated line arrangement
$C_{3}$
, the associated line arrangement
![]() $\mathcal {C}_{0}(x)$
in
$\mathcal {C}_{0}(x)$
in
![]() $\mathbb {P}^{2}$
is periodic of period
$\mathbb {P}^{2}$
is periodic of period
![]() $3$
for the action of
$3$
for the action of ![]() .
.
Remark 4.10. We recall that ![]() is an operator acting on line arrangements, whereas
is an operator acting on line arrangements, whereas ![]() is the rational self-map induced by
is the rational self-map induced by ![]() : it acts on line arrangements modulo projective transformations. In particular, Proposition 4.9 implies that for a line arrangement
: it acts on line arrangements modulo projective transformations. In particular, Proposition 4.9 implies that for a line arrangement
![]() $\mathcal {C}$
corresponding to a point on the curve
$\mathcal {C}$
corresponding to a point on the curve
![]() $C_3$
, one has
$C_3$
, one has ![]() with
with ![]() , but
, but ![]() is projectively equivalent to
is projectively equivalent to
![]() $\mathcal {C}$
. The union of the line arrangements
$\mathcal {C}$
. The union of the line arrangements ![]() has 24 lines with
has 24 lines with
![]() $84$
triple points,
$84$
triple points,
![]() $24$
double points, and no other singularities.
$24$
double points, and no other singularities.
Proof. We searched by random an example of a ![]() -fixed point x over a finite field and we found the point
-fixed point x over a finite field and we found the point
![]() $x=(794:582:116:1)\in \mathbb {P}^{3}(\mathbb {F}_{1013})$
in the surface
$x=(794:582:116:1)\in \mathbb {P}^{3}(\mathbb {F}_{1013})$
in the surface
![]() $(\mathcal {R}_{8})_{/\mathbb {F}_{1013}}$
. The corresponding line arrangement
$(\mathcal {R}_{8})_{/\mathbb {F}_{1013}}$
. The corresponding line arrangement
![]() $\mathcal {C}_{0}\cup \mathcal {C}_{1}$
is
$\mathcal {C}_{0}\cup \mathcal {C}_{1}$
is
![]() $3$
-periodic for the operator
$3$
-periodic for the operator ![]() : the line arrangements
: the line arrangements
![]() $\mathcal {C}_{0}\cup \mathcal {C}_{1}$
,
$\mathcal {C}_{0}\cup \mathcal {C}_{1}$
,
![]() $\mathcal {C}_{1}\cup \mathcal {C}_{2}$
and
$\mathcal {C}_{1}\cup \mathcal {C}_{2}$
and
![]() $\mathcal {C}_{2}\cup \mathcal {C}_{0}$
are realizations of
$\mathcal {C}_{2}\cup \mathcal {C}_{0}$
are realizations of
![]() $M_8$
(over
$M_8$
(over
![]() $\mathbb {F}_{1013}$
), and
$\mathbb {F}_{1013}$
), and ![]() . One computes that the matroid
. One computes that the matroid
![]() $N_{24}$
associated to
$N_{24}$
associated to
![]() $\mathcal {C}_{0}\cup \mathcal {C}_{1}\cup \mathcal {C}_{2}$
has an irreducible one dimensional moduli space
$\mathcal {C}_{0}\cup \mathcal {C}_{1}\cup \mathcal {C}_{2}$
has an irreducible one dimensional moduli space
![]() $\mathcal {R}(N_{24})$
over
$\mathcal {R}(N_{24})$
over
![]() $\mathbb {C}$
and that the geometric genus of the compactification of
$\mathbb {C}$
and that the geometric genus of the compactification of
![]() $\mathcal {R}(N_{24})$
is
$\mathcal {R}(N_{24})$
is
![]() $5$
. Let
$5$
. Let
![]() $\mathcal {C}_{0}'\cup \mathcal {C}_{1}'\cup \mathcal {C}_{2}'$
be a realization (over
$\mathcal {C}_{0}'\cup \mathcal {C}_{1}'\cup \mathcal {C}_{2}'$
be a realization (over
![]() $\mathbb {C}$
) of
$\mathbb {C}$
) of
![]() $N_{24}$
. From the combinatorics of
$N_{24}$
. From the combinatorics of
![]() $M_8$
and
$M_8$
and
![]() $N_{24}$
, the line arrangements
$N_{24}$
, the line arrangements
![]() $\mathcal {C}_{0}'\cup \mathcal {C}_{1}'$
,
$\mathcal {C}_{0}'\cup \mathcal {C}_{1}'$
,
![]() $\mathcal {C}_{1}'\cup \mathcal {C}_{2}'$
and
$\mathcal {C}_{1}'\cup \mathcal {C}_{2}'$
and
![]() $\mathcal {C}_{2}'\cup \mathcal {C}_{0}'$
are realizations of
$\mathcal {C}_{2}'\cup \mathcal {C}_{0}'$
are realizations of
![]() $M_8$
, and
$M_8$
, and ![]() if the realization is generic. The natural map
if the realization is generic. The natural map
![]() $\mathcal {R}(N_{24})\to \mathcal {R}_{8}$
, which to a realization
$\mathcal {R}(N_{24})\to \mathcal {R}_{8}$
, which to a realization
![]() $\mathcal {C}_{0}'\cup \mathcal {C}_{1}'\cup \mathcal {C}_{2}'$
of
$\mathcal {C}_{0}'\cup \mathcal {C}_{1}'\cup \mathcal {C}_{2}'$
of
![]() $N_{24}$
associates
$N_{24}$
associates
![]() $\mathcal {C}_{0}'\cup \mathcal {C}_{1}'$
is one-to-one onto its image (a curve denoted
$\mathcal {C}_{0}'\cup \mathcal {C}_{1}'$
is one-to-one onto its image (a curve denoted
![]() $C_{3}$
) in
$C_{3}$
) in
![]() $\mathcal {R}_8$
, since one may recover
$\mathcal {R}_8$
, since one may recover
![]() $\mathcal {C}_{2}'$
(and therefore
$\mathcal {C}_{2}'$
(and therefore
![]() $\mathcal {C}_{0}'\cup \mathcal {C}_{1}'\cup \mathcal {C}_{2}'$
) as
$\mathcal {C}_{0}'\cup \mathcal {C}_{1}'\cup \mathcal {C}_{2}'$
) as ![]() . A computer computation gives that
. A computer computation gives that
![]() $C_3$
has genus
$C_3$
has genus
![]() $5$
and
$5$
and ![]() is projectively equivalent to
is projectively equivalent to
![]() $\eta $
, where
$\eta $
, where
![]() $\eta $
is the generic point of
$\eta $
is the generic point of
![]() $C_3$
, thus any specialization
$C_3$
, thus any specialization
![]() $\eta '$
is such that
$\eta '$
is such that ![]() , and the curve
, and the curve
![]() $C_3$
is point-wise fixed by
$C_3$
is point-wise fixed by ![]() .
.
Acknowledgements
The authors are grateful to Bert van Geemen and to Keiji Oguiso for interesting discussions.
Funding
LK is supported by the SFB-TRR 358 – 491392403 “Integral Structures in Geometry and Representation Theory” and the SPP 2458 – 539866293 “Combinatorial Synergies” (DFG). XR is thankful to the Max Planck Institute for Mathematics in Bonn for its hospitality and financial support. XR is also supported by the Centre Henri Lebesgue (ANR-11-LABX-0020-01).