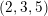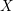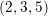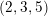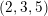1 Introduction
A distribution ![]() $D$ on a five-dimensional manifold
$D$ on a five-dimensional manifold ![]() $Y$ is called a
$Y$ is called a ![]() $(2,3,5)$-distribution if there is a local section
$(2,3,5)$-distribution if there is a local section ![]() $\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}$ of
$\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}$ of ![]() $D$ such that
$D$ such that
form a local frame of the tangent bundle to ![]() $Y$, in other words, if
$Y$, in other words, if ![]() $D$ has the weak growth
$D$ has the weak growth ![]() $(2,3,5)$, namely, if
$(2,3,5)$, namely, if ![]() $\operatorname{rank}(\unicode[STIX]{x2202}{\mathcal{D}})=3$ and
$\operatorname{rank}(\unicode[STIX]{x2202}{\mathcal{D}})=3$ and ![]() $\operatorname{rank}(\unicode[STIX]{x2202}^{(2)}{\mathcal{D}})=5$, where
$\operatorname{rank}(\unicode[STIX]{x2202}^{(2)}{\mathcal{D}})=5$, where ![]() $\unicode[STIX]{x2202}{\mathcal{D}}:=[{\mathcal{D}},{\mathcal{D}}]~(={\mathcal{D}}+[{\mathcal{D}},{\mathcal{D}}])$, the derived system, and
$\unicode[STIX]{x2202}{\mathcal{D}}:=[{\mathcal{D}},{\mathcal{D}}]~(={\mathcal{D}}+[{\mathcal{D}},{\mathcal{D}}])$, the derived system, and ![]() $\unicode[STIX]{x2202}^{(2)}{\mathcal{D}}:=[{\mathcal{D}},\unicode[STIX]{x2202}{\mathcal{D}}]~(={\mathcal{D}}+\unicode[STIX]{x2202}{\mathcal{D}}+[{\mathcal{D}},\unicode[STIX]{x2202}{\mathcal{D}}])$ for the sheaf
$\unicode[STIX]{x2202}^{(2)}{\mathcal{D}}:=[{\mathcal{D}},\unicode[STIX]{x2202}{\mathcal{D}}]~(={\mathcal{D}}+\unicode[STIX]{x2202}{\mathcal{D}}+[{\mathcal{D}},\unicode[STIX]{x2202}{\mathcal{D}}])$ for the sheaf ![]() ${\mathcal{D}}$ of section germs to
${\mathcal{D}}$ of section germs to ![]() $D$.
$D$.
The geometry and classification problem of ![]() $(2,3,5)$-distributions are studied after Cartan [Reference Cartan13], related to the simple Lie group
$(2,3,5)$-distributions are studied after Cartan [Reference Cartan13], related to the simple Lie group ![]() $G_{2}$, by many mathematicians [Reference Agrachev and Zelenko5, Reference Bryant9, Reference Leistner, Nurowski and Sagerschung19, Reference The26–Reference Zhitomirskii30]. The
$G_{2}$, by many mathematicians [Reference Agrachev and Zelenko5, Reference Bryant9, Reference Leistner, Nurowski and Sagerschung19, Reference The26–Reference Zhitomirskii30]. The ![]() $(2,3,5)$-distributions are related to many problems, for instance, to the problem of “rolling balls” [Reference Agrachev1, Reference An and Nurowski6–Reference Bor and Montgomery8], to indefinite conformal metrics [Reference Leistner, Nurowski and Sagerschung19, Reference Nurowski21], to nonlinear differential equations [Reference Randall22], and so on.
$(2,3,5)$-distributions are related to many problems, for instance, to the problem of “rolling balls” [Reference Agrachev1, Reference An and Nurowski6–Reference Bor and Montgomery8], to indefinite conformal metrics [Reference Leistner, Nurowski and Sagerschung19, Reference Nurowski21], to nonlinear differential equations [Reference Randall22], and so on.
In [Reference Ishikawa, Machida and Takahashi16–Reference Kitagawa18], we studied the global duality of ![]() $G_{2}$-homogeneous (flat)
$G_{2}$-homogeneous (flat) ![]() $(2,3,5)$-distribution and a Lagrangian cone structure from Cayley’s split Octonions and classified the related generic singularities. In [Reference Ishikawa, Kitagawa and Yukuno15], we associated locally with any given
$(2,3,5)$-distribution and a Lagrangian cone structure from Cayley’s split Octonions and classified the related generic singularities. In [Reference Ishikawa, Kitagawa and Yukuno15], we associated locally with any given ![]() $(2,3,5)$-distribution
$(2,3,5)$-distribution ![]() $D$ on a five-dimensional manifold
$D$ on a five-dimensional manifold ![]() $Y$, a Lagrangian cone structure
$Y$, a Lagrangian cone structure ![]() $C$ on another five-dimensional manifold
$C$ on another five-dimensional manifold ![]() $X$, which consists of abnormal or singular paths of
$X$, which consists of abnormal or singular paths of ![]() $(Y,D)$, in the sense of sub-Riemannian geometry or geometric control theory (see [Reference Agrachev and Sachkov2, Reference Montgomery20]). Moreover, it was shown in [Reference Ishikawa, Kitagawa and Yukuno15] that the original space
$(Y,D)$, in the sense of sub-Riemannian geometry or geometric control theory (see [Reference Agrachev and Sachkov2, Reference Montgomery20]). Moreover, it was shown in [Reference Ishikawa, Kitagawa and Yukuno15] that the original space ![]() $Y$ turns to be the totality of singular paths of the “Lagrangian cone structure”
$Y$ turns to be the totality of singular paths of the “Lagrangian cone structure” ![]() $(X,C)$, when the cone field
$(X,C)$, when the cone field ![]() $C$ is regarded as a control system on
$C$ is regarded as a control system on ![]() $X$.
$X$.
In this paper, we give the characterization of the class of Lagrangian cone structures corresponding to ![]() $(2,3,5)$-distributions, and, thus, we complete the duality between
$(2,3,5)$-distributions, and, thus, we complete the duality between ![]() $(2,3,5)$-distributions and Lagrangian cone structures (Theorem 3.1). The duality is actually understood via pseudo-product structure of
$(2,3,5)$-distributions and Lagrangian cone structures (Theorem 3.1). The duality is actually understood via pseudo-product structure of ![]() $G_{2}$-type
$G_{2}$-type ![]() $E=K\oplus L$ on a six-dimensional manifold
$E=K\oplus L$ on a six-dimensional manifold ![]() $Z$ (Section 2), which is regarded both as the prolongation of
$Z$ (Section 2), which is regarded both as the prolongation of ![]() $(Y,D)$ and
$(Y,D)$ and ![]() $(X,C)$ in the sense of Bryant [Reference Bryant9, Reference Bryant and Hsu10], via the double fibration
$(X,C)$ in the sense of Bryant [Reference Bryant9, Reference Bryant and Hsu10], via the double fibration
We realize, for the characterization of a class of Lagrangian cone structures, that the language of cone structures is actually lacking. We introduce, regarding the cone structures as control systems, the notions of linear approximations and osculating bundles of cone structures as well as the exact definition of nondegenerate Lagrangian cone structures (Definition 2.3).
We remark that our correspondence is purely local in nature. It is “spatially” local for ![]() $(Z,E)$ while “spatially and directionally” local for
$(Z,E)$ while “spatially and directionally” local for ![]() $(Y,D)$ and for
$(Y,D)$ and for ![]() $(X,C)$. Moreover, the “directional locality” for the distribution
$(X,C)$. Moreover, the “directional locality” for the distribution ![]() $(Y,D)$ is resolved by taking the linear hull; however, it is not the case for the cone structure
$(Y,D)$ is resolved by taking the linear hull; however, it is not the case for the cone structure ![]() $(X,C)$. This fact makes our duality delicate.
$(X,C)$. This fact makes our duality delicate.
It is clear that ![]() $(2,3,5)$-distributions form an open set, for Whitney
$(2,3,5)$-distributions form an open set, for Whitney ![]() $C^{\infty }$-topology, in the space of all distributions of rank
$C^{\infty }$-topology, in the space of all distributions of rank ![]() $2$ on a five-dimensional manifold. In particular, a
$2$ on a five-dimensional manifold. In particular, a ![]() $(2,3,5)$-distribution remains a
$(2,3,5)$-distribution remains a ![]() $(2,3,5)$-distribution by sufficiently small perturbations with compact supports. However, such a stability for cone structures corresponding to
$(2,3,5)$-distribution by sufficiently small perturbations with compact supports. However, such a stability for cone structures corresponding to ![]() $(2,3,5)$-distributions via the duality is not clear. We give a local example of nonflat perturbations of the global model of flat Lagrangian cone structure [Reference Ishikawa, Machida and Takahashi16], which corresponds to
$(2,3,5)$-distributions via the duality is not clear. We give a local example of nonflat perturbations of the global model of flat Lagrangian cone structure [Reference Ishikawa, Machida and Takahashi16], which corresponds to ![]() $(2,3,5)$-distributions (Example 4.3). The existence of nonflat global perturbations of Lagrangian cone structures, which correspond to
$(2,3,5)$-distributions (Example 4.3). The existence of nonflat global perturbations of Lagrangian cone structures, which correspond to ![]() $(2,3,5)$-distributions, is open. The classification of nondegenerate Lagrangian cone structures based on their symmetries is an interesting open problem, regarding our duality and the studies on
$(2,3,5)$-distributions, is open. The classification of nondegenerate Lagrangian cone structures based on their symmetries is an interesting open problem, regarding our duality and the studies on ![]() $G_{2}$-contact structures [Reference C̆ap and Slovák12, Reference Leistner, Nurowski and Sagerschung19, Reference The26]. The direct study on symmetries of nondegenerate Lagrangian cone structures should be desirable.
$G_{2}$-contact structures [Reference C̆ap and Slovák12, Reference Leistner, Nurowski and Sagerschung19, Reference The26]. The direct study on symmetries of nondegenerate Lagrangian cone structures should be desirable.
The cone structure was first given in [Reference Agrachev and Zelenko5] by a foliation on the space ![]() $P((\unicode[STIX]{x2202}D)^{\bot })\subset P(T^{\ast }Y)$ for the derived system
$P((\unicode[STIX]{x2202}D)^{\bot })\subset P(T^{\ast }Y)$ for the derived system ![]() $\unicode[STIX]{x2202}D$ of a
$\unicode[STIX]{x2202}D$ of a ![]() $(2,3,5)$-distribution
$(2,3,5)$-distribution ![]() $D$, which is an essentially same foliation in the space
$D$, which is an essentially same foliation in the space ![]() $P(D)\subset P(TY)$ of [Reference Ishikawa, Kitagawa and Yukuno15]. See also [Reference Agrachev and Zelenko5, Reference Doubrov and Zelenko14]. In fact, there exists the natural fiber-preserving diffeomorphism
$P(D)\subset P(TY)$ of [Reference Ishikawa, Kitagawa and Yukuno15]. See also [Reference Agrachev and Zelenko5, Reference Doubrov and Zelenko14]. In fact, there exists the natural fiber-preserving diffeomorphism ![]() $P(D)\rightarrow P((\unicode[STIX]{x2202}D)^{\bot })$ which preserves also the foliation induced from singular paths of
$P(D)\rightarrow P((\unicode[STIX]{x2202}D)^{\bot })$ which preserves also the foliation induced from singular paths of ![]() $D$. Moreover, the Lagrangian cone structure
$D$. Moreover, the Lagrangian cone structure ![]() $C\subset TX$, which is contained in a contact structure
$C\subset TX$, which is contained in a contact structure ![]() $D^{\prime }\subset TX$ on
$D^{\prime }\subset TX$ on ![]() $X$, has the essentially same information with the Jacobi curves introduced in [Reference Agrachev and Zelenko3, Reference Agrachev and Zelenko4]. In fact, each cone
$X$, has the essentially same information with the Jacobi curves introduced in [Reference Agrachev and Zelenko3, Reference Agrachev and Zelenko4]. In fact, each cone ![]() $C_{x}\subset D_{x}^{\prime },(x\in X)$ gives the (reduced) Jacobi curve associated with the singular path
$C_{x}\subset D_{x}^{\prime },(x\in X)$ gives the (reduced) Jacobi curve associated with the singular path ![]() $x$ of
$x$ of ![]() $D$ in Lagrangian Grassmannian of
$D$ in Lagrangian Grassmannian of ![]() $D_{x}^{\prime }$ by taking tangent planes to
$D_{x}^{\prime }$ by taking tangent planes to ![]() $C_{x}$.
$C_{x}$.
In [Reference Zelenko29], it was shown that the Cartan tensor of any ![]() $(2,3,5)$-distribution is given by the fundamental invariant of Jacobi curves of singular paths and, in particular, the Cartan tensor is determined by the projective equivalence classes of the pointwise curves
$(2,3,5)$-distribution is given by the fundamental invariant of Jacobi curves of singular paths and, in particular, the Cartan tensor is determined by the projective equivalence classes of the pointwise curves ![]() $P(C_{x}),x\in X$ of the corresponding Lagrangian cone structure
$P(C_{x}),x\in X$ of the corresponding Lagrangian cone structure ![]() $(X,C)$. We give a short proof (Proposition 4.1), related to the study on
$(X,C)$. We give a short proof (Proposition 4.1), related to the study on ![]() $G_{2}$-contact structures [Reference C̆ap and Slovák12, Reference Leistner, Nurowski and Sagerschung19], that the
$G_{2}$-contact structures [Reference C̆ap and Slovák12, Reference Leistner, Nurowski and Sagerschung19], that the ![]() $(2,3,5)$-distribution which corresponds to a cubic Lagrangian cone structure via our duality is necessarily flat, by using Zelenko’s theorem [Reference Zelenko29] (Proposition 4.1). Since the degrees of cone structures are invariant under isomorphisms of cone structures and by Theorem 3.1 of the present paper, we see that any cone structure which corresponds to a flat
$(2,3,5)$-distribution which corresponds to a cubic Lagrangian cone structure via our duality is necessarily flat, by using Zelenko’s theorem [Reference Zelenko29] (Proposition 4.1). Since the degrees of cone structures are invariant under isomorphisms of cone structures and by Theorem 3.1 of the present paper, we see that any cone structure which corresponds to a flat ![]() $(2,3,5)$ structure must be cubic. Then we can say that, to check the flatness of a
$(2,3,5)$ structure must be cubic. Then we can say that, to check the flatness of a ![]() $(2,3,5)$-distribution is easier, if it is given by a corresponding Lagrangian cone structure. In fact, the condition
$(2,3,5)$-distribution is easier, if it is given by a corresponding Lagrangian cone structure. In fact, the condition ![]() $\unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C$ of Theorem 3.1 is checked by straightforward computations of differentials and then it is sufficient to see whether the degree of the cone is cubic or not. However, it is a difficult task, given a
$\unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C$ of Theorem 3.1 is checked by straightforward computations of differentials and then it is sufficient to see whether the degree of the cone is cubic or not. However, it is a difficult task, given a ![]() $(2,3,5)$-distribution, to get the corresponding Lagrangian cone structure concretely.
$(2,3,5)$-distribution, to get the corresponding Lagrangian cone structure concretely.
In Section 2, we review the results given in the previous paper [Reference Ishikawa, Kitagawa and Yukuno15] with additional explanations. In particular, we give the exact definition of (nondegenerate) Lagrangian cone structures (Definition 2.3).
In Section 3, we complete the duality between ![]() $(2,3,5)$-distributions and nondegenerate Lagrangian cone structures with an additional condition via pseudo-product structures of type
$(2,3,5)$-distributions and nondegenerate Lagrangian cone structures with an additional condition via pseudo-product structures of type ![]() $G_{2}$.
$G_{2}$.
We conclude this paper by several remarks related to the duality in Section 4.
All manifolds and mappings are supposed to be of class ![]() $C^{\infty }$ unless otherwise stated.
$C^{\infty }$ unless otherwise stated.
2 Pseudo-product structures of  $G_{2}$-type
$G_{2}$-type
Let ![]() $D$ be a
$D$ be a ![]() $(2,3,5)$-distribution on a five-dimensional manifold
$(2,3,5)$-distribution on a five-dimensional manifold ![]() $Y$. Let
$Y$. Let ![]() $Z:=P(D)=(D-0)/\mathbb{R}^{\times }$ be the space of tangential lines in
$Z:=P(D)=(D-0)/\mathbb{R}^{\times }$ be the space of tangential lines in ![]() $D$,
$D$, ![]() $Z:=\{(y,\ell )\mid y\in Y,\ell \subset D_{y}(\subset T_{y}Y),\dim (\ell )=1\}$. Then
$Z:=\{(y,\ell )\mid y\in Y,\ell \subset D_{y}(\subset T_{y}Y),\dim (\ell )=1\}$. Then ![]() $\dim (Z)=6$ and the projection
$\dim (Z)=6$ and the projection ![]() $\unicode[STIX]{x1D70B}_{Y}:Z\rightarrow Y$ is an
$\unicode[STIX]{x1D70B}_{Y}:Z\rightarrow Y$ is an ![]() $\mathbb{R}P^{1}$-bundle.
$\mathbb{R}P^{1}$-bundle.
We define a subbundle ![]() $E\subset TZ$ of rank
$E\subset TZ$ of rank ![]() $2$, Cartan prolongation of
$2$, Cartan prolongation of ![]() $D\subset TY$, by setting for each
$D\subset TY$, by setting for each ![]() $(y,\ell )\in Z$,
$(y,\ell )\in Z$, ![]() $\ell \subset D_{y}$,
$\ell \subset D_{y}$, ![]() $E_{(y,\ell )}:=\unicode[STIX]{x1D70B}_{Y\ast }^{-1}(\ell )~(\subset T_{(y,\ell )}Z)$. Then
$E_{(y,\ell )}:=\unicode[STIX]{x1D70B}_{Y\ast }^{-1}(\ell )~(\subset T_{(y,\ell )}Z)$. Then ![]() $E$ is a distribution with (weak) growth
$E$ is a distribution with (weak) growth ![]() $(2,3,4,5,6)$:
$(2,3,4,5,6)$: ![]() $\operatorname{rank}(E)=2,\operatorname{rank}(\unicode[STIX]{x2202}E)=3,\operatorname{rank}(\unicode[STIX]{x2202}^{(2)}E)=4$,
$\operatorname{rank}(E)=2,\operatorname{rank}(\unicode[STIX]{x2202}E)=3,\operatorname{rank}(\unicode[STIX]{x2202}^{(2)}E)=4$, ![]() $\operatorname{rank}(\unicode[STIX]{x2202}^{(3)}E)=5$,
$\operatorname{rank}(\unicode[STIX]{x2202}^{(3)}E)=5$,![]() $\operatorname{rank}(\unicode[STIX]{x2202}^{(4)}E)=6$.
$\operatorname{rank}(\unicode[STIX]{x2202}^{(4)}E)=6$.
Then we see that there exists an intrinsic decomposition
of ![]() $E$ with
$E$ with ![]() $L:=\operatorname{Ker}(\unicode[STIX]{x1D70B}_{Y\ast })\subset E$ and a complementary line subbundle
$L:=\operatorname{Ker}(\unicode[STIX]{x1D70B}_{Y\ast })\subset E$ and a complementary line subbundle ![]() $K$ of
$K$ of ![]() $E$, a pseudo-product structure in the sense of Tanaka [Reference Tanaka24, Reference Tanaka25].
$E$, a pseudo-product structure in the sense of Tanaka [Reference Tanaka24, Reference Tanaka25].
We will explain this in terms of “geometric control theory” [Reference Agrachev and Sachkov2, Reference Montgomery20].
A control system ![]() $\mathbb{C}:{\mathcal{U}}\xrightarrow[{}]{F}TM\rightarrow M$ on a manifold
$\mathbb{C}:{\mathcal{U}}\xrightarrow[{}]{F}TM\rightarrow M$ on a manifold ![]() $M$ is given by a locally trivial fibration
$M$ is given by a locally trivial fibration ![]() $\unicode[STIX]{x1D70B}_{{\mathcal{U}}}:{\mathcal{U}}\rightarrow M$ over
$\unicode[STIX]{x1D70B}_{{\mathcal{U}}}:{\mathcal{U}}\rightarrow M$ over ![]() $M$ and a map
$M$ and a map ![]() $F:{\mathcal{U}}\rightarrow TM$ such that the following diagram commutes:
$F:{\mathcal{U}}\rightarrow TM$ such that the following diagram commutes:

Any section ![]() $s:M\rightarrow {\mathcal{U}}$ defines a vector field
$s:M\rightarrow {\mathcal{U}}$ defines a vector field ![]() $F\circ s:M\rightarrow TM$ over
$F\circ s:M\rightarrow TM$ over ![]() $M$. Via a local triviality on
$M$. Via a local triviality on ![]() $M$, a control system is given by a family of vector fields
$M$, a control system is given by a family of vector fields ![]() $f_{u}(x)=F(x,u)$ over
$f_{u}(x)=F(x,u)$ over ![]() $M$,
$M$, ![]() $(x,u)\in {\mathcal{U}}$,
$(x,u)\in {\mathcal{U}}$, ![]() $x\in M$.
$x\in M$.
A distribution ![]() $D\subset TM$ is regarded as a control system
$D\subset TM$ is regarded as a control system ![]() $\mathbb{D}:D{\hookrightarrow}TM\longrightarrow M$, by the inclusion.
$\mathbb{D}:D{\hookrightarrow}TM\longrightarrow M$, by the inclusion.
Two control systems ![]() $\mathbb{C}:{\mathcal{U}}\xrightarrow[{}]{F}TM\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{TM}}M$ and
$\mathbb{C}:{\mathcal{U}}\xrightarrow[{}]{F}TM\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{TM}}M$ and ![]() $\mathbb{C}^{\prime }:{\mathcal{U}}^{\prime }\xrightarrow[{}]{F^{\prime }}TM^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{TM^{\prime }}}M^{\prime }$ are called isomorphic if the diagram
$\mathbb{C}^{\prime }:{\mathcal{U}}^{\prime }\xrightarrow[{}]{F^{\prime }}TM^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{TM^{\prime }}}M^{\prime }$ are called isomorphic if the diagram

commutes for some diffeomorphisms ![]() $\unicode[STIX]{x1D713}$ and
$\unicode[STIX]{x1D713}$ and ![]() $\unicode[STIX]{x1D711}$. Here,
$\unicode[STIX]{x1D711}$. Here, ![]() $\unicode[STIX]{x1D711}_{\ast }$ is the differential of
$\unicode[STIX]{x1D711}_{\ast }$ is the differential of ![]() $\unicode[STIX]{x1D711}$.
$\unicode[STIX]{x1D711}$.
The pair ![]() $(\unicode[STIX]{x1D713},\unicode[STIX]{x1D711})$ of diffeomorphisms is called an isomorphism of the control systems
$(\unicode[STIX]{x1D713},\unicode[STIX]{x1D711})$ of diffeomorphisms is called an isomorphism of the control systems ![]() $\mathbb{C}$ and
$\mathbb{C}$ and ![]() $\mathbb{C}^{\prime }$.
$\mathbb{C}^{\prime }$.
Given a control system ![]() $\mathbb{C}:{\mathcal{U}}\xrightarrow[{}]{F}TM\rightarrow M$, an
$\mathbb{C}:{\mathcal{U}}\xrightarrow[{}]{F}TM\rightarrow M$, an ![]() $L^{\infty }$ (measurable, essentially bounded) map
$L^{\infty }$ (measurable, essentially bounded) map ![]() $c:[a,b]\rightarrow {\mathcal{U}}$ is called an admissible control if the curve
$c:[a,b]\rightarrow {\mathcal{U}}$ is called an admissible control if the curve
satisfies the differential equation
Then the Lipschitz curve ![]() $\unicode[STIX]{x1D6FE}$ is called a trajectory. If we write
$\unicode[STIX]{x1D6FE}$ is called a trajectory. If we write ![]() $c(t)=(x(t),u(t))$, then
$c(t)=(x(t),u(t))$, then ![]() $x(t)=\unicode[STIX]{x1D6FE}(t)$ and
$x(t)=\unicode[STIX]{x1D6FE}(t)$ and
We use the term “path” for a smooth (![]() $C^{\infty }$) immersive trajectory regarded up to parametrization.
$C^{\infty }$) immersive trajectory regarded up to parametrization.
The totality ![]() ${\mathcal{C}}$ of admissible controls
${\mathcal{C}}$ of admissible controls ![]() $c:[a,b]\rightarrow {\mathcal{U}}$ with a given initial point
$c:[a,b]\rightarrow {\mathcal{U}}$ with a given initial point ![]() $q_{0}\in M$ is a Banach manifold. The endpoint mapping
$q_{0}\in M$ is a Banach manifold. The endpoint mapping ![]() $\operatorname{End}:{\mathcal{C}}\rightarrow M$ is defined by
$\operatorname{End}:{\mathcal{C}}\rightarrow M$ is defined by
An admissible control ![]() $c:[a,b]\rightarrow {\mathcal{U}}$ with the initial point
$c:[a,b]\rightarrow {\mathcal{U}}$ with the initial point ![]() $\unicode[STIX]{x1D70B}_{{\mathcal{U}}}(c(a))=q_{0}$ is called singular or abnormal, if
$\unicode[STIX]{x1D70B}_{{\mathcal{U}}}(c(a))=q_{0}$ is called singular or abnormal, if ![]() $c\in {\mathcal{C}}$ is a singular point of
$c\in {\mathcal{C}}$ is a singular point of ![]() $\operatorname{End}$, namely if the differential
$\operatorname{End}$, namely if the differential ![]() $\operatorname{End}_{\ast }:T_{c}{\mathcal{C}}\rightarrow T_{\text{End(c)}}M$ is not surjective. If
$\operatorname{End}_{\ast }:T_{c}{\mathcal{C}}\rightarrow T_{\text{End(c)}}M$ is not surjective. If ![]() $c$ is a singular control, then the trajectory
$c$ is a singular control, then the trajectory ![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D70B}_{{\mathcal{U}}}\circ c$ is called a singular trajectory or an abnormal extremal.
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D70B}_{{\mathcal{U}}}\circ c$ is called a singular trajectory or an abnormal extremal.
Let ![]() $D\subset TY$ be a
$D\subset TY$ be a ![]() $(2,3,5)$-distribution. Then, it can be shown that for any point
$(2,3,5)$-distribution. Then, it can be shown that for any point ![]() $y$ of
$y$ of ![]() $Y$ and for any direction
$Y$ and for any direction ![]() $\ell \subset D_{y}$, there exists uniquely a singular
$\ell \subset D_{y}$, there exists uniquely a singular ![]() $D$-path (an immersed abnormal extremal for
$D$-path (an immersed abnormal extremal for ![]() $D$) through
$D$) through ![]() $y$ with the given direction
$y$ with the given direction ![]() $\ell$. Thus, the singular
$\ell$. Thus, the singular ![]() $D$-paths form another five-dimensional manifold
$D$-paths form another five-dimensional manifold ![]() $X$.
$X$.
Let ![]() $Z=P(D)=(D-0)/\mathbb{R}^{\times }$ be the space of tangential lines in
$Z=P(D)=(D-0)/\mathbb{R}^{\times }$ be the space of tangential lines in ![]() $D$,
$D$, ![]() $\dim (Z)=6$. Then
$\dim (Z)=6$. Then ![]() $Z$ is naturally foliated by the liftings of singular
$Z$ is naturally foliated by the liftings of singular ![]() $D$-paths, and we have locally double fibrations:
$D$-paths, and we have locally double fibrations:
If we put ![]() $L=\operatorname{Ker}(\unicode[STIX]{x1D70B}_{Y\ast }),K=\operatorname{Ker}(\unicode[STIX]{x1D70B}_{X\ast })$, then we have a decomposition
$L=\operatorname{Ker}(\unicode[STIX]{x1D70B}_{Y\ast }),K=\operatorname{Ker}(\unicode[STIX]{x1D70B}_{X\ast })$, then we have a decomposition ![]() $E=K\oplus L$ by subbundles of rank
$E=K\oplus L$ by subbundles of rank ![]() $1$.
$1$.
We denote, for any distribution ![]() $E$, by
$E$, by ![]() ${\mathcal{E}}$ the sheaf of local sections to
${\mathcal{E}}$ the sheaf of local sections to ![]() $E$. We set
$E$. We set
and so on. If ![]() $\unicode[STIX]{x2202}{\mathcal{E}}$ is generated by a local section of a distribution, then we denote it by
$\unicode[STIX]{x2202}{\mathcal{E}}$ is generated by a local section of a distribution, then we denote it by ![]() $\unicode[STIX]{x2202}E$.
$\unicode[STIX]{x2202}E$.
Definition 2.1. A distribution ![]() $(Z,E)$ of rank
$(Z,E)$ of rank ![]() $2$ on a six-dimensional manifold
$2$ on a six-dimensional manifold ![]() $Z$ with a decomposition
$Z$ with a decomposition ![]() $E=K\oplus L$ by subbundles
$E=K\oplus L$ by subbundles ![]() $K,L$ of rank
$K,L$ of rank ![]() $1$ is called a pseudo-product structures of
$1$ is called a pseudo-product structures of ![]() $G_{2}$-type if
$G_{2}$-type if ![]() $E$ has small growth
$E$ has small growth ![]() $(2,3,4,5,6)$ and, moreover, satisfies that
$(2,3,4,5,6)$ and, moreover, satisfies that
Then, by taking the gradation of the filtration
we have, at each point ![]() $z\in Z$, the symbol algebra
$z\in Z$, the symbol algebra
 $$\begin{eqnarray}\displaystyle & \displaystyle \mathfrak{m}=\mathfrak{g}_{-5}\oplus \mathfrak{g}_{-4}\oplus \mathfrak{g}_{-3}\oplus \mathfrak{g}_{-2}\oplus \mathfrak{g}_{-1}=\langle e_{6}\rangle \oplus \langle e_{5}\rangle \oplus \langle e_{4}\rangle \oplus \langle e_{3}\rangle \oplus \langle e_{1},e_{2}\rangle , & \displaystyle \nonumber\\ \displaystyle & \displaystyle [e_{1},e_{2}]=e_{3},\qquad [e_{1},e_{3}]=e_{4},\qquad [e_{2},e_{3}]=0,\qquad [e_{1},e_{4}]=e_{5}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle [e_{2},e_{4}]=0,\qquad [e_{1},e_{5}]=0,\qquad [e_{2},e_{5}]=e_{6}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathfrak{m}=\mathfrak{g}_{-5}\oplus \mathfrak{g}_{-4}\oplus \mathfrak{g}_{-3}\oplus \mathfrak{g}_{-2}\oplus \mathfrak{g}_{-1}=\langle e_{6}\rangle \oplus \langle e_{5}\rangle \oplus \langle e_{4}\rangle \oplus \langle e_{3}\rangle \oplus \langle e_{1},e_{2}\rangle , & \displaystyle \nonumber\\ \displaystyle & \displaystyle [e_{1},e_{2}]=e_{3},\qquad [e_{1},e_{3}]=e_{4},\qquad [e_{2},e_{3}]=0,\qquad [e_{1},e_{4}]=e_{5}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle [e_{2},e_{4}]=0,\qquad [e_{1},e_{5}]=0,\qquad [e_{2},e_{5}]=e_{6}, & \displaystyle \nonumber\end{eqnarray}$$ with the decomposition ![]() $\mathfrak{g}_{-1}=\mathfrak{k}\oplus \mathfrak{l}=\langle e_{1}\rangle \oplus \langle e_{2}\rangle$.
$\mathfrak{g}_{-1}=\mathfrak{k}\oplus \mathfrak{l}=\langle e_{1}\rangle \oplus \langle e_{2}\rangle$.
Then we have the following.
Theorem 2.2. There exists a natural bijective correspondence of local isomorphism classes between ![]() $(2,3,5)$-distributions and pseudo-product structures of
$(2,3,5)$-distributions and pseudo-product structures of ![]() $G_{2}$-type.
$G_{2}$-type.
Proof. First, let us make sure that the prolongation ![]() $E$ of a
$E$ of a ![]() $(2,3,5)$-distribution
$(2,3,5)$-distribution ![]() $D$ on a five-dimensional manifold
$D$ on a five-dimensional manifold ![]() $Y$ has small growth
$Y$ has small growth ![]() $(2,3,4,5,6)$.
$(2,3,4,5,6)$.
Let ![]() $\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}$ be a local frame of
$\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}$ be a local frame of ![]() $D$. Then, setting
$D$. Then, setting
we have a local frame ![]() $\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{3},\unicode[STIX]{x1D702}_{4},\unicode[STIX]{x1D702}_{5}$ of
$\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{3},\unicode[STIX]{x1D702}_{4},\unicode[STIX]{x1D702}_{5}$ of ![]() $TY$. For each
$TY$. For each ![]() $y\in Y$, directions in
$y\in Y$, directions in ![]() $D_{y}$ are, locally, parametrized via
$D_{y}$ are, locally, parametrized via ![]() $\unicode[STIX]{x1D702}_{1}(y)+t\unicode[STIX]{x1D702}_{2}(y)$
$\unicode[STIX]{x1D702}_{1}(y)+t\unicode[STIX]{x1D702}_{2}(y)$![]() $(t\in \mathbb{R})$. Then, for any system of local coordinates
$(t\in \mathbb{R})$. Then, for any system of local coordinates ![]() $y=(y_{1},y_{2},y_{3},y_{4},y_{5})$ of
$y=(y_{1},y_{2},y_{3},y_{4},y_{5})$ of ![]() $Y$ centered at base point of
$Y$ centered at base point of ![]() $Y$,
$Y$, ![]() $(y,t)$ form a system of local coordinates of
$(y,t)$ form a system of local coordinates of ![]() $Z$ such that
$Z$ such that ![]() $\unicode[STIX]{x1D70B}_{Y}$ is expressed by
$\unicode[STIX]{x1D70B}_{Y}$ is expressed by ![]() $(y,t)\mapsto y$. We regard
$(y,t)\mapsto y$. We regard ![]() $\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{3},\unicode[STIX]{x1D702}_{4},\unicode[STIX]{x1D702}_{5}$ as vector fields over
$\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{3},\unicode[STIX]{x1D702}_{4},\unicode[STIX]{x1D702}_{5}$ as vector fields over ![]() $Z$. Then
$Z$. Then
form a local frame of ![]() $E$, and
$E$, and ![]() $\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{3},\unicode[STIX]{x1D702}_{4},\unicode[STIX]{x1D702}_{5},\unicode[STIX]{x1D701}_{2}$ of
$\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{3},\unicode[STIX]{x1D702}_{4},\unicode[STIX]{x1D702}_{5},\unicode[STIX]{x1D701}_{2}$ of ![]() $TZ$.
$TZ$.
Since ![]() $[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}]=[\unicode[STIX]{x1D702}_{1}+t\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D701}_{2}]=-\unicode[STIX]{x1D702}_{2}$, we have
$[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}]=[\unicode[STIX]{x1D702}_{1}+t\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D701}_{2}]=-\unicode[STIX]{x1D702}_{2}$, we have
which is of rank ![]() $3$. Here,
$3$. Here, ![]() $\langle \unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D702}_{2}\rangle$ means the distribution generated by
$\langle \unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D702}_{2}\rangle$ means the distribution generated by ![]() $\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D702}_{2}$. Since
$\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D702}_{2}$. Since ![]() $[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D702}_{2}]=[\unicode[STIX]{x1D702}_{1}+t\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{2}]=\unicode[STIX]{x1D702}_{3}$ and
$[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D702}_{2}]=[\unicode[STIX]{x1D702}_{1}+t\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{2}]=\unicode[STIX]{x1D702}_{3}$ and ![]() $[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D702}_{2}]=0$, we have
$[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D702}_{2}]=0$, we have
which is of rank ![]() $4$. Since
$4$. Since ![]() $[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D702}_{3}]=[\unicode[STIX]{x1D702}_{1}+t\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{3}]=\unicode[STIX]{x1D702}_{4}+t\unicode[STIX]{x1D702}_{5}$ and
$[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D702}_{3}]=[\unicode[STIX]{x1D702}_{1}+t\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{3}]=\unicode[STIX]{x1D702}_{4}+t\unicode[STIX]{x1D702}_{5}$ and ![]() $[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D702}_{3}]=0$, we have
$[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D702}_{3}]=0$, we have
which is of rank ![]() $5$. Since
$5$. Since ![]() $[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D702}_{4}+t\unicode[STIX]{x1D702}_{5}]=\unicode[STIX]{x1D702}_{5}$, we have
$[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D702}_{4}+t\unicode[STIX]{x1D702}_{5}]=\unicode[STIX]{x1D702}_{5}$, we have ![]() $\unicode[STIX]{x2202}^{(4)}{\mathcal{E}}=TZ$. Therefore,
$\unicode[STIX]{x2202}^{(4)}{\mathcal{E}}=TZ$. Therefore, ![]() $E$ has small growth
$E$ has small growth ![]() $(2,3,4,5,6)$.
$(2,3,4,5,6)$.
Note that ![]() ${\mathcal{L}}$ is generated by
${\mathcal{L}}$ is generated by ![]() $\unicode[STIX]{x1D701}_{2}$. Moreover, there exists a generator of
$\unicode[STIX]{x1D701}_{2}$. Moreover, there exists a generator of ![]() ${\mathcal{K}}$ of form
${\mathcal{K}}$ of form ![]() $\unicode[STIX]{x1D701}_{1}+e(y,t)\unicode[STIX]{x1D701}_{2}$. In fact, the function
$\unicode[STIX]{x1D701}_{1}+e(y,t)\unicode[STIX]{x1D701}_{2}$. In fact, the function ![]() $e(y,t)$ is uniquely determined by the condition
$e(y,t)$ is uniquely determined by the condition ![]() $[{\mathcal{K}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$, which is equivalent to the condition
$[{\mathcal{K}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$, which is equivalent to the condition
Then other remaining conditions that ![]() $E=K\oplus L$ is a pseudo-product structure of type
$E=K\oplus L$ is a pseudo-product structure of type ![]() $G_{2}$ follow.
$G_{2}$ follow.
Conversely, suppose ![]() $E=K\oplus L$ is a pseudo-product structure of type
$E=K\oplus L$ is a pseudo-product structure of type ![]() $G_{2}$. Then
$G_{2}$. Then ![]() $L$ is the Cauchy characteristic of
$L$ is the Cauchy characteristic of ![]() $\unicode[STIX]{x2202}E$ (see [Reference Bryant, Chern, Gardner, Goldschmidt and Griffiths11]). Let
$\unicode[STIX]{x2202}E$ (see [Reference Bryant, Chern, Gardner, Goldschmidt and Griffiths11]). Let ![]() $Y$ be the leaf space of
$Y$ be the leaf space of ![]() $L$, which is a locally defined five-dimensional manifold. Moreover,
$L$, which is a locally defined five-dimensional manifold. Moreover, ![]() $Z$ has a system of local coordinates
$Z$ has a system of local coordinates ![]() $(y,t)$ centered at the base point such that
$(y,t)$ centered at the base point such that ![]() $\unicode[STIX]{x1D70B}_{Y}$ is given by
$\unicode[STIX]{x1D70B}_{Y}$ is given by ![]() $(y,t)\mapsto y$. Let
$(y,t)\mapsto y$. Let ![]() $D$ be the reduction of
$D$ be the reduction of ![]() $\unicode[STIX]{x2202}E$ by
$\unicode[STIX]{x2202}E$ by ![]() $L$. Take a local frame
$L$. Take a local frame ![]() $\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}$ of
$\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}$ of ![]() $D$ such that, regarded as vector fields over
$D$ such that, regarded as vector fields over ![]() $Z$,
$Z$, ![]() $\unicode[STIX]{x1D702}_{1}$ generates the quotient bundle
$\unicode[STIX]{x1D702}_{1}$ generates the quotient bundle ![]() $(\unicode[STIX]{x2202}E)/E$. Moreover,
$(\unicode[STIX]{x2202}E)/E$. Moreover, ![]() $\unicode[STIX]{x1D701}_{1}=\unicode[STIX]{x1D702}_{1}+\unicode[STIX]{x1D711}(y,t)\unicode[STIX]{x1D702}_{2}$ and
$\unicode[STIX]{x1D701}_{1}=\unicode[STIX]{x1D702}_{1}+\unicode[STIX]{x1D711}(y,t)\unicode[STIX]{x1D702}_{2}$ and ![]() $\unicode[STIX]{x1D701}_{2}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t$ generate
$\unicode[STIX]{x1D701}_{2}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t$ generate ![]() $K$ and
$K$ and ![]() $L$, respectively, for some function
$L$, respectively, for some function ![]() $\unicode[STIX]{x1D711}(y,t)$ with
$\unicode[STIX]{x1D711}(y,t)$ with ![]() $\unicode[STIX]{x1D711}(0,0)=0$. Since
$\unicode[STIX]{x1D711}(0,0)=0$. Since
we have that ![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}t\not =0$. Set
$\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}t\not =0$. Set ![]() $\unicode[STIX]{x1D701}_{3}:=\unicode[STIX]{x1D702}_{2}$. Then
$\unicode[STIX]{x1D701}_{3}:=\unicode[STIX]{x1D702}_{2}$. Then
Therefore, ![]() $\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2},[\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}]$ are linearly independent pointwise on
$\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2},[\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}]$ are linearly independent pointwise on ![]() $Y$. We set
$Y$. We set ![]() $\unicode[STIX]{x1D701}_{4}:=\unicode[STIX]{x1D702}_{3}=[\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}]$ as a vector field over
$\unicode[STIX]{x1D701}_{4}:=\unicode[STIX]{x1D702}_{3}=[\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2}]$ as a vector field over ![]() $Z$. Then
$Z$. Then
and ![]() $[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{4}]=[\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t,\unicode[STIX]{x1D702}_{3}]=0$. Set
$[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{4}]=[\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t,\unicode[STIX]{x1D702}_{3}]=0$. Set ![]() $\unicode[STIX]{x1D702}_{4}=[\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{3}],\unicode[STIX]{x1D702}_{5}=[\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{3}]$ and
$\unicode[STIX]{x1D702}_{4}=[\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{3}],\unicode[STIX]{x1D702}_{5}=[\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{3}]$ and ![]() $\unicode[STIX]{x1D701}_{5}=\unicode[STIX]{x1D702}_{4}+\unicode[STIX]{x1D711}\unicode[STIX]{x1D702}_{5}$. Then
$\unicode[STIX]{x1D701}_{5}=\unicode[STIX]{x1D702}_{4}+\unicode[STIX]{x1D711}\unicode[STIX]{x1D702}_{5}$. Then ![]() $\unicode[STIX]{x1D702}_{4}(0)\in (\unicode[STIX]{x2202}^{(3)}E)_{0}\setminus (\unicode[STIX]{x2202}^{(2)}E)_{0}$. Then we have that
$\unicode[STIX]{x1D702}_{4}(0)\in (\unicode[STIX]{x2202}^{(3)}E)_{0}\setminus (\unicode[STIX]{x2202}^{(2)}E)_{0}$. Then we have that ![]() $[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{5}](0)\not \in (\unicode[STIX]{x2202}^{(3)}E)_{0}$, while
$[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{5}](0)\not \in (\unicode[STIX]{x2202}^{(3)}E)_{0}$, while ![]() $[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{5}]=(\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}t)\unicode[STIX]{x1D702}_{5}(0)$. Therefore,
$[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{5}]=(\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}t)\unicode[STIX]{x1D702}_{5}(0)$. Therefore, ![]() $\unicode[STIX]{x1D702}_{5}(0)\not \in (\unicode[STIX]{x2202}^{(3)}E)_{0}$. Therefore,
$\unicode[STIX]{x1D702}_{5}(0)\not \in (\unicode[STIX]{x2202}^{(3)}E)_{0}$. Therefore, ![]() $\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{3},\unicode[STIX]{x1D702}_{4},\unicode[STIX]{x1D702}_{5}$ are linearly independent pointwise. Thus, we see that
$\unicode[STIX]{x1D702}_{1},\unicode[STIX]{x1D702}_{2},\unicode[STIX]{x1D702}_{3},\unicode[STIX]{x1D702}_{4},\unicode[STIX]{x1D702}_{5}$ are linearly independent pointwise. Thus, we see that ![]() $D$ is a
$D$ is a ![]() $(2,3,5)$-distribution.
$(2,3,5)$-distribution.
These correspondences induce the bijection between local isomorphism classes of ![]() $(2,3,5)$-distributions and pseudo-product structures of
$(2,3,5)$-distributions and pseudo-product structures of ![]() $G_{2}$-type on a
$G_{2}$-type on a ![]() $5$-manifold.◻
$5$-manifold.◻
Note that the original ![]() $(2,3,5)$-distribution
$(2,3,5)$-distribution ![]() $D$ is obtained as the linear hull of the cone field (“bowtie”) induced from
$D$ is obtained as the linear hull of the cone field (“bowtie”) induced from ![]() $K$:
$K$:
Also, the ![]() $(2,3,5)$-distribution
$(2,3,5)$-distribution ![]() $D$ is obtained as the reduction of
$D$ is obtained as the reduction of ![]() $\unicode[STIX]{x2202}E$ by Cauchy characteristic
$\unicode[STIX]{x2202}E$ by Cauchy characteristic ![]() $L=\operatorname{Ker}(\unicode[STIX]{x1D70B}_{Y\ast })$.
$L=\operatorname{Ker}(\unicode[STIX]{x1D70B}_{Y\ast })$.
On the other hand, we obtain a cone field ![]() $C\subset TX$ on
$C\subset TX$ on ![]() $X$ by setting, for each
$X$ by setting, for each ![]() $x\in X$,
$x\in X$,
Now, to make sure, we formulate exactly the notion of Lagrangian cone structures (see [Reference C̆ap and Slovák12]).
Definition 2.3. (1) Let ![]() $X$ be a manifold of dimension
$X$ be a manifold of dimension ![]() $m$. A subset
$m$. A subset ![]() $C\subset TX$ is called a cone structure if there is an
$C\subset TX$ is called a cone structure if there is an ![]() $\mathbb{R}^{\times }$-invariant subset
$\mathbb{R}^{\times }$-invariant subset ![]() $\text{}\underline{C}\subset \mathbb{R}^{m}$, a model cone, such that, for any
$\text{}\underline{C}\subset \mathbb{R}^{m}$, a model cone, such that, for any ![]() $x\in X$, there exist an open neighborhood
$x\in X$, there exist an open neighborhood ![]() $U$ of
$U$ of ![]() $x$ and a local triviality
$x$ and a local triviality ![]() $\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D70B}^{-1}(U)\rightarrow U\times \mathbb{R}^{m}$ of
$\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D70B}^{-1}(U)\rightarrow U\times \mathbb{R}^{m}$ of ![]() $\unicode[STIX]{x1D70B}:TX\rightarrow X$ over
$\unicode[STIX]{x1D70B}:TX\rightarrow X$ over ![]() $U$ satisfying
$U$ satisfying ![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70B}^{-1}(U)\cap C)=U\times \text{}\underline{C}$.
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D70B}^{-1}(U)\cap C)=U\times \text{}\underline{C}$.
(2) Suppose that the model cone ![]() $\text{}\underline{C}$ is nonsingular away from the origin in
$\text{}\underline{C}$ is nonsingular away from the origin in ![]() $\mathbb{R}^{m}$. Then
$\mathbb{R}^{m}$. Then ![]() $P(C)$ is a submanifold of
$P(C)$ is a submanifold of ![]() $P(TX)$. For each section
$P(TX)$. For each section ![]() $s:X\rightarrow P(C)$ for the projection
$s:X\rightarrow P(C)$ for the projection ![]() $P(C)\rightarrow X$, we have the subbundle
$P(C)\rightarrow X$, we have the subbundle ![]() $T_{s}C\subset TX$ by taking tangent planes of
$T_{s}C\subset TX$ by taking tangent planes of ![]() $C_{x}$ along the direction
$C_{x}$ along the direction ![]() $s(x)$ at every point
$s(x)$ at every point ![]() $x\in X$. We call the distribution
$x\in X$. We call the distribution ![]() $T_{s}C$ the linear approximation of
$T_{s}C$ the linear approximation of ![]() $C$ along
$C$ along ![]() $s$.
$s$.
(3) A cone structure ![]() $C\subset TX$ is called a Lagrangian cone structure if there exists a contact structure
$C\subset TX$ is called a Lagrangian cone structure if there exists a contact structure ![]() $D^{\prime }$ on
$D^{\prime }$ on ![]() $X$ such that
$X$ such that ![]() $C\subset D^{\prime }$ and, for any section
$C\subset D^{\prime }$ and, for any section ![]() $s:X\rightarrow P(C)$,
$s:X\rightarrow P(C)$, ![]() $T_{s}C$ is a Lagrangian subbundle of
$T_{s}C$ is a Lagrangian subbundle of ![]() $D^{\prime }$. The last condition is equivalent to that, for any
$D^{\prime }$. The last condition is equivalent to that, for any ![]() $x\in X$,
$x\in X$, ![]() $C_{x}\setminus \{0\}$ is a Lagrangian submanifold of the linear symplectic manifold
$C_{x}\setminus \{0\}$ is a Lagrangian submanifold of the linear symplectic manifold ![]() $D_{x}^{\prime }$ or, equivalently,
$D_{x}^{\prime }$ or, equivalently, ![]() $P(C_{x})$ is a Legendrian submanifold of the contact manifold
$P(C_{x})$ is a Legendrian submanifold of the contact manifold ![]() $P(D_{x}^{\prime })$ induced from the conformal symplectic vector space
$P(D_{x}^{\prime })$ induced from the conformal symplectic vector space ![]() $D_{x}^{\prime }$.
$D_{x}^{\prime }$.
(4) Let ![]() $\dim (X)=5$. A Lagrangian cone structure
$\dim (X)=5$. A Lagrangian cone structure ![]() $C\subset TX$ for a contact structure
$C\subset TX$ for a contact structure ![]() $D^{\prime }\subset TX$ is called nondegenerate if the spatial projective curve segment
$D^{\prime }\subset TX$ is called nondegenerate if the spatial projective curve segment ![]() $P(C_{x})\subset P(D_{x}^{\prime })\cong P^{3}$ is nondegenerate, i.e. the first, second, and third derivatives of a parametrization of
$P(C_{x})\subset P(D_{x}^{\prime })\cong P^{3}$ is nondegenerate, i.e. the first, second, and third derivatives of a parametrization of ![]() $P(C_{x})$ are linearly independent.
$P(C_{x})$ are linearly independent.
From condition (4), for each direction field ![]() $s$ of
$s$ of ![]() $C$, we define osculating bundles
$C$, we define osculating bundles ![]() $O_{s}^{(2)}C\subset TX$ of rank
$O_{s}^{(2)}C\subset TX$ of rank ![]() $3$ and
$3$ and ![]() $O_{s}^{(3)}C\subset TX$ of rank
$O_{s}^{(3)}C\subset TX$ of rank ![]() $4$, generated by osculating planes
$4$, generated by osculating planes ![]() $O_{2}$ and three-dimensional osculating spaces
$O_{2}$ and three-dimensional osculating spaces ![]() $O_{3}$ to
$O_{3}$ to ![]() $P(C_{x})$ with direction
$P(C_{x})$ with direction ![]() $s$. Then the contact structure
$s$. Then the contact structure ![]() $D^{\prime }$ coincides with
$D^{\prime }$ coincides with ![]() $O_{s}^{(3)}C$ which is independent of
$O_{s}^{(3)}C$ which is independent of ![]() $s$.
$s$.
Because distributions are regarded as cone structures of special type, the notion of Lagrangian cone structures is a natural generalization for that of Lagrangian subbundle of the tangent bundle over a contact manifold.
Lemma 2.4. In our case, the above ![]() $C\subset TX$ defined as (
$C\subset TX$ defined as (![]() $\triangle$ ) corresponding to a
$\triangle$ ) corresponding to a ![]() $(2,3,5)$-distribution
$(2,3,5)$-distribution ![]() $D\subset TY$ is a nondegenerate Lagrangian cone structure in the sense of Definition 2.3.
$D\subset TY$ is a nondegenerate Lagrangian cone structure in the sense of Definition 2.3.
Proof. By the condition ![]() $[{\mathcal{K}},\unicode[STIX]{x2202}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}$,
$[{\mathcal{K}},\unicode[STIX]{x2202}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}$, ![]() $C$ satisfies conditions (1) and (2) of Definition 2.3. By the condition
$C$ satisfies conditions (1) and (2) of Definition 2.3. By the condition ![]() $[{\mathcal{K}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$,
$[{\mathcal{K}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$, ![]() $K$ is the Cauchy characteristic of
$K$ is the Cauchy characteristic of ![]() $\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$. Then the distribution
$\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$. Then the distribution ![]() $D^{\prime }\subset TX$ induced from
$D^{\prime }\subset TX$ induced from ![]() $\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$ is a contact structure by the condition
$\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$ is a contact structure by the condition ![]() $[{\mathcal{L}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(4)}{\mathcal{E}}$. Moreover,
$[{\mathcal{L}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(4)}{\mathcal{E}}$. Moreover, ![]() $\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}$ projects to tangent spaces to
$\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}$ projects to tangent spaces to ![]() $C_{x}$ along
$C_{x}$ along ![]() $\unicode[STIX]{x1D70B}_{X}^{-1}(x)$. For any section
$\unicode[STIX]{x1D70B}_{X}^{-1}(x)$. For any section ![]() $s:X\rightarrow L$,
$s:X\rightarrow L$, ![]() $s(x)\not =0$, we have that the linear approximation
$s(x)\not =0$, we have that the linear approximation ![]() $T_{s}C$ is a Lagrangian subbundle of
$T_{s}C$ is a Lagrangian subbundle of ![]() $D^{\prime }$ by the condition
$D^{\prime }$ by the condition ![]() $[{\mathcal{L}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$. Therefore,
$[{\mathcal{L}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$. Therefore, ![]() $C$ satisfies also condition (3) of Definition 2.3. Thus,
$C$ satisfies also condition (3) of Definition 2.3. Thus, ![]() $(X,C)$ is a Lagrangian cone structure. Moreover, by the condition
$(X,C)$ is a Lagrangian cone structure. Moreover, by the condition ![]() $[{\mathcal{K}},\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$, condition (4) of Definition 2.3 is satisfied. Therefore,
$[{\mathcal{K}},\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$, condition (4) of Definition 2.3 is satisfied. Therefore, ![]() $(X,C)$ is a nondegenerate Lagrangian cone structure.◻
$(X,C)$ is a nondegenerate Lagrangian cone structure.◻
Now, we regard the cone field ![]() $C\subset TX$ as a control system over
$C\subset TX$ as a control system over ![]() $X$:
$X$:
for the subbundle ![]() $L$ of
$L$ of ![]() $TZ$. Then we have shown in [Reference Ishikawa, Kitagawa and Yukuno15] the following theorem.
$TZ$. Then we have shown in [Reference Ishikawa, Kitagawa and Yukuno15] the following theorem.
Theorem 2.5. (Duality theorem [Reference Ishikawa, Kitagawa and Yukuno15])
Singular paths of the control system
are given by ![]() $\unicode[STIX]{x1D70B}_{X}$-images of
$\unicode[STIX]{x1D70B}_{X}$-images of ![]() $\unicode[STIX]{x1D70B}_{Y}$-fibers.
$\unicode[STIX]{x1D70B}_{Y}$-fibers.
Therefore, for any ![]() $x\in X$ and for any direction
$x\in X$ and for any direction ![]() $\ell \subset C_{x}$, there exists uniquely a singular
$\ell \subset C_{x}$, there exists uniquely a singular ![]() $\mathbb{C}$-path passing through
$\mathbb{C}$-path passing through ![]() $x$ with the direction
$x$ with the direction ![]() $\ell$ at
$\ell$ at ![]() $x$.
$x$.
Thus, the original space ![]() $Y$ is identified with the space of singular paths for
$Y$ is identified with the space of singular paths for ![]() $(X,C)$, while
$(X,C)$, while ![]() $X$ is the space of singular paths for
$X$ is the space of singular paths for ![]() $(Y,D)$.
$(Y,D)$.
We recall the local characterization of singular controls.
For a control system ![]() $\mathbb{C}:{\mathcal{U}}\xrightarrow[{}]{F}TM\rightarrow M$ on a manifold
$\mathbb{C}:{\mathcal{U}}\xrightarrow[{}]{F}TM\rightarrow M$ on a manifold ![]() $M$, we consider the fiber product
$M$, we consider the fiber product ![]() ${\mathcal{U}}\times _{M}T^{\ast }M$ and define the Hamiltonian function
${\mathcal{U}}\times _{M}T^{\ast }M$ and define the Hamiltonian function ![]() $H:{\mathcal{U}}\times _{M}T^{\ast }M\rightarrow \mathbb{R}$ of the control system
$H:{\mathcal{U}}\times _{M}T^{\ast }M\rightarrow \mathbb{R}$ of the control system ![]() $F:{\mathcal{U}}\rightarrow TM$ by
$F:{\mathcal{U}}\rightarrow TM$ by
A singular control ![]() $(x(t),u(t))$ is characterized by the liftability to an abnormal bi-extremal
$(x(t),u(t))$ is characterized by the liftability to an abnormal bi-extremal ![]() $(x(t),p(t),u(t))$ satisfying the constrained Hamiltonian equation
$(x(t),p(t),u(t))$ satisfying the constrained Hamiltonian equation
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle {\dot{x}}_{i}(t)={\displaystyle \frac{\unicode[STIX]{x2202}H}{\unicode[STIX]{x2202}p_{i}}}(x(t),p(t),u(t)),\quad (1\leqslant i\leqslant m)\quad \\ \displaystyle {\dot{p}}_{i}(t)=-{\displaystyle \frac{\unicode[STIX]{x2202}H}{\unicode[STIX]{x2202}x_{i}}}(x(t),p(t),u(t)),\quad (1\leqslant i\leqslant m)\quad \\ \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}H}{\unicode[STIX]{x2202}u_{j}}}(x(t),p(t),u(t))=0,\quad (1\leqslant j\leqslant r),p(t)\not =0.\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle {\dot{x}}_{i}(t)={\displaystyle \frac{\unicode[STIX]{x2202}H}{\unicode[STIX]{x2202}p_{i}}}(x(t),p(t),u(t)),\quad (1\leqslant i\leqslant m)\quad \\ \displaystyle {\dot{p}}_{i}(t)=-{\displaystyle \frac{\unicode[STIX]{x2202}H}{\unicode[STIX]{x2202}x_{i}}}(x(t),p(t),u(t)),\quad (1\leqslant i\leqslant m)\quad \\ \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}H}{\unicode[STIX]{x2202}u_{j}}}(x(t),p(t),u(t))=0,\quad (1\leqslant j\leqslant r),p(t)\not =0.\quad \end{array}\right.\end{eqnarray}$$ Let ![]() $E\subset TZ$ be a distribution on a manifold
$E\subset TZ$ be a distribution on a manifold ![]() $Z$ regarded as a control system. A singular path
$Z$ regarded as a control system. A singular path ![]() $x(t)$ for
$x(t)$ for ![]() $E\subset TZ$ is called regular singular if it is associated with an abnormal bi-extremal
$E\subset TZ$ is called regular singular if it is associated with an abnormal bi-extremal ![]() $(x(t),p(t),u(t))$ such that
$(x(t),p(t),u(t))$ such that ![]() $p(t)\in (\unicode[STIX]{x2202}E)^{\bot }\setminus (\unicode[STIX]{x2202}^{(2)}E)^{\bot }\subset T^{\ast }Z$. A singular path
$p(t)\in (\unicode[STIX]{x2202}E)^{\bot }\setminus (\unicode[STIX]{x2202}^{(2)}E)^{\bot }\subset T^{\ast }Z$. A singular path ![]() $x(t)$ for
$x(t)$ for ![]() $E\subset TZ$ is called totally irregular singular if any associated abnormal bi-extremal
$E\subset TZ$ is called totally irregular singular if any associated abnormal bi-extremal ![]() $(x(t),p(t),u(t))$ satisfies that
$(x(t),p(t),u(t))$ satisfies that ![]() $p(t)\in (\unicode[STIX]{x2202}^{(2)}E)^{\bot }\subset T^{\ast }Z$.
$p(t)\in (\unicode[STIX]{x2202}^{(2)}E)^{\bot }\subset T^{\ast }Z$.
From the pseudo-product structure on ![]() $E\subset TZ$, we have the following.
$E\subset TZ$, we have the following.
Theorem 2.6. (Asymmetry theorem [Reference Ishikawa, Kitagawa and Yukuno15])
A singular path for ![]() $E{\hookrightarrow}TZ\rightarrow Z$ is either a
$E{\hookrightarrow}TZ\rightarrow Z$ is either a ![]() $\unicode[STIX]{x1D70B}_{Y}$-fiber or a
$\unicode[STIX]{x1D70B}_{Y}$-fiber or a ![]() $\unicode[STIX]{x1D70B}_{X}$-fiber. Each
$\unicode[STIX]{x1D70B}_{X}$-fiber. Each ![]() $\unicode[STIX]{x1D70B}_{Y}$-fiber is regular singular, while each
$\unicode[STIX]{x1D70B}_{Y}$-fiber is regular singular, while each ![]() $\unicode[STIX]{x1D70B}_{X}$-fiber is totally irregular singular.
$\unicode[STIX]{x1D70B}_{X}$-fiber is totally irregular singular.
3 Complete duality
The description of the duality on ![]() $(2,3,5)$-distributions
$(2,3,5)$-distributions ![]() $(Y,D)$ and nondegenerate Lagrangian cone structures
$(Y,D)$ and nondegenerate Lagrangian cone structures ![]() $(X,C)$ via
$(X,C)$ via ![]() $(Z,E)$ which is given in Section 2 should be completed by answering the question: What kinds of nondegenerate Lagrangian cone structures do they correspond to
$(Z,E)$ which is given in Section 2 should be completed by answering the question: What kinds of nondegenerate Lagrangian cone structures do they correspond to ![]() $(2,3,5)$-distributions?
$(2,3,5)$-distributions?
Then we have the following.
Theorem 3.1. There exist natural bijective correspondences of isomorphism classes:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \{(2,3,5)\text{-distributions }(Y,D)\}\!/\!\cong \nonumber\\ \displaystyle & & \displaystyle \qquad \longleftrightarrow \,\left\{\begin{array}{@{}c@{}}\text{pseudo-product structures of }G_{2}\text{-type }(Z,E):\\ (2,3,4,5,6)\text{-distributions }E\text{ with a decomposition}\\ E=K\oplus L,\operatorname{rank}(K)=\operatorname{rank}(L)=1,\\ \hspace{0.0pt}[{\mathcal{K}},{\mathcal{L}}]=\unicode[STIX]{x2202}{\mathcal{E}}~(:=[{\mathcal{E}},{\mathcal{E}}]={\mathcal{E}}+[{\mathcal{E}},{\mathcal{E}}]),\\ \hspace{0.0pt}[{\mathcal{K}},\unicode[STIX]{x2202}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(2)}{\mathcal{E}},[{\mathcal{L}},\unicode[STIX]{x2202}{\mathcal{E}}]=\unicode[STIX]{x2202}{\mathcal{E}},\\ \hspace{0.0pt}[{\mathcal{K}},\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}},[{\mathcal{L}},\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(2)}{\mathcal{E}},\\ \hspace{0.0pt}[{\mathcal{K}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}},[{\mathcal{L}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(4)}{\mathcal{E}}.\end{array}\right\}\!/\!\cong \nonumber\\ \displaystyle & & \displaystyle \qquad \longleftrightarrow \,\left\{\begin{array}{@{}c@{}}\text{nondegenerate Lagrangian cone structures }(X,C)\\ \text{on five-dimensional manifolds }X\text{ with the condition }\\ \unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C,\text{ for any direction field }s\text{ of }C.\end{array}\right\}\!/\!\cong \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \{(2,3,5)\text{-distributions }(Y,D)\}\!/\!\cong \nonumber\\ \displaystyle & & \displaystyle \qquad \longleftrightarrow \,\left\{\begin{array}{@{}c@{}}\text{pseudo-product structures of }G_{2}\text{-type }(Z,E):\\ (2,3,4,5,6)\text{-distributions }E\text{ with a decomposition}\\ E=K\oplus L,\operatorname{rank}(K)=\operatorname{rank}(L)=1,\\ \hspace{0.0pt}[{\mathcal{K}},{\mathcal{L}}]=\unicode[STIX]{x2202}{\mathcal{E}}~(:=[{\mathcal{E}},{\mathcal{E}}]={\mathcal{E}}+[{\mathcal{E}},{\mathcal{E}}]),\\ \hspace{0.0pt}[{\mathcal{K}},\unicode[STIX]{x2202}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(2)}{\mathcal{E}},[{\mathcal{L}},\unicode[STIX]{x2202}{\mathcal{E}}]=\unicode[STIX]{x2202}{\mathcal{E}},\\ \hspace{0.0pt}[{\mathcal{K}},\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}},[{\mathcal{L}},\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(2)}{\mathcal{E}},\\ \hspace{0.0pt}[{\mathcal{K}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}},[{\mathcal{L}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(4)}{\mathcal{E}}.\end{array}\right\}\!/\!\cong \nonumber\\ \displaystyle & & \displaystyle \qquad \longleftrightarrow \,\left\{\begin{array}{@{}c@{}}\text{nondegenerate Lagrangian cone structures }(X,C)\\ \text{on five-dimensional manifolds }X\text{ with the condition }\\ \unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C,\text{ for any direction field }s\text{ of }C.\end{array}\right\}\!/\!\cong \nonumber\end{eqnarray}$$Proof of Theorem 3.1.
Let ![]() $X$ be a five-dimensional manifold and
$X$ be a five-dimensional manifold and ![]() $C\subset TX$ a nondegenerate Lagrangian cone structure (Definition 2.3). Then
$C\subset TX$ a nondegenerate Lagrangian cone structure (Definition 2.3). Then ![]() $Z=P(C):=(C\setminus (\text{zero section}))/\mathbb{R}^{\times }$ is a six-dimensional manifold and
$Z=P(C):=(C\setminus (\text{zero section}))/\mathbb{R}^{\times }$ is a six-dimensional manifold and ![]() $\unicode[STIX]{x1D70B}_{X}:Z\rightarrow X$ is a
$\unicode[STIX]{x1D70B}_{X}:Z\rightarrow X$ is a ![]() $C^{\infty }$-fibration with projective curves
$C^{\infty }$-fibration with projective curves ![]() $P(C_{x})\subset P(T_{x}X)\cong P^{4}$ as fibers.
$P(C_{x})\subset P(T_{x}X)\cong P^{4}$ as fibers.
By the nondegeneracy condition, we have that the first, second, and third derivatives are linearly independent everywhere on ![]() $P(C_{x})$, for any
$P(C_{x})$, for any ![]() $x\in X$.
$x\in X$.
Then we define a subbundle ![]() $E\subset TZ$ of rank
$E\subset TZ$ of rank ![]() $2$ by setting
$2$ by setting
for each ![]() $(x,\ell )\in Z$ as the prolongation of the cone structure
$(x,\ell )\in Z$ as the prolongation of the cone structure ![]() $C\in TX$. We set
$C\in TX$. We set ![]() $K=\operatorname{Ker}((\unicode[STIX]{x1D70B}_{X})_{\ast })$.
$K=\operatorname{Ker}((\unicode[STIX]{x1D70B}_{X})_{\ast })$.
Let ![]() $x=(x_{1},x_{2},x_{3},x_{4},x_{5})$ be a system of local coordinates of
$x=(x_{1},x_{2},x_{3},x_{4},x_{5})$ be a system of local coordinates of ![]() $X$ and
$X$ and ![]() $x,\unicode[STIX]{x1D703}$ that of
$x,\unicode[STIX]{x1D703}$ that of ![]() $Z$ such that
$Z$ such that ![]() $\unicode[STIX]{x1D70B}_{X}:Z\rightarrow X$ is given by
$\unicode[STIX]{x1D70B}_{X}:Z\rightarrow X$ is given by ![]() $(x,\unicode[STIX]{x1D703})\mapsto x$ and
$(x,\unicode[STIX]{x1D703})\mapsto x$ and ![]() $E$ is generated by
$E$ is generated by ![]() $\unicode[STIX]{x1D701}_{1}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}$ and a vector field
$\unicode[STIX]{x1D701}_{1}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}$ and a vector field ![]() $\unicode[STIX]{x1D701}_{2}(x,\unicode[STIX]{x1D703})$ of form
$\unicode[STIX]{x1D701}_{2}(x,\unicode[STIX]{x1D703})$ of form
where ![]() $A,B,S,T$ are function germs of
$A,B,S,T$ are function germs of ![]() $x,\unicode[STIX]{x1D703}$. The projective curve
$x,\unicode[STIX]{x1D703}$. The projective curve ![]() $C_{x}\subset P(T_{x}X)$ is given by
$C_{x}\subset P(T_{x}X)$ is given by
in homogeneous coordinates, for each ![]() $x\in X$.
$x\in X$.
We have, on ![]() $Z$,
$Z$,
and
In local coordinates,
and
Any direction field ![]() $s$ of
$s$ of ![]() $C$ is given by
$C$ is given by ![]() $x\mapsto (x,\unicode[STIX]{x1D703}(x))$ for some functions
$x\mapsto (x,\unicode[STIX]{x1D703}(x))$ for some functions ![]() $\unicode[STIX]{x1D703}(x)$ of
$\unicode[STIX]{x1D703}(x)$ of ![]() $x$ and the linear approximation
$x$ and the linear approximation ![]() $T_{s}C$ of
$T_{s}C$ of ![]() $C$ along the direction field
$C$ along the direction field ![]() $s$ is generated by
$s$ is generated by ![]() $\unicode[STIX]{x1D701}_{2}(x,\unicode[STIX]{x1D703}(x)),\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}(x,\unicode[STIX]{x1D703}(x))$. Moreover, the osculating bundles
$\unicode[STIX]{x1D701}_{2}(x,\unicode[STIX]{x1D703}(x)),\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}(x,\unicode[STIX]{x1D703}(x))$. Moreover, the osculating bundles ![]() $O_{s}^{(2)}C$ and
$O_{s}^{(2)}C$ and ![]() $O_{s}^{(3)}C$ are generated by
$O_{s}^{(3)}C$ are generated by ![]() $\unicode[STIX]{x1D701}_{2}(x,\unicode[STIX]{x1D703}(x)),\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}(x,\unicode[STIX]{x1D703}(x)),\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D701}_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{2}}(x,\unicode[STIX]{x1D703}(x))$ and by
$\unicode[STIX]{x1D701}_{2}(x,\unicode[STIX]{x1D703}(x)),\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}(x,\unicode[STIX]{x1D703}(x)),\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D701}_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{2}}(x,\unicode[STIX]{x1D703}(x))$ and by ![]() $\unicode[STIX]{x1D701}_{2}(x,\unicode[STIX]{x1D703}(x))$,
$\unicode[STIX]{x1D701}_{2}(x,\unicode[STIX]{x1D703}(x))$, ![]() $\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}(x,\unicode[STIX]{x1D703}(x))$,
$\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}(x,\unicode[STIX]{x1D703}(x))$, ![]() $\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D701}_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{2}}(x,\unicode[STIX]{x1D703}(x))$,
$\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D701}_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{2}}(x,\unicode[STIX]{x1D703}(x))$, ![]() $\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D701}_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{3}}(x,\unicode[STIX]{x1D703}(x))$, respectively.
$\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D701}_{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{3}}(x,\unicode[STIX]{x1D703}(x))$, respectively.
By the condition ![]() $\unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C$, we have that
$\unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C$, we have that ![]() $[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3}]\equiv 0,\text{mod}.~\langle \unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{4}\rangle$. Then there exists uniquely a function
$[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3}]\equiv 0,\text{mod}.~\langle \unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{4}\rangle$. Then there exists uniquely a function ![]() $U(x,\unicode[STIX]{x1D703})$ such that
$U(x,\unicode[STIX]{x1D703})$ such that ![]() $\widetilde{\unicode[STIX]{x1D701}}_{2}=\unicode[STIX]{x1D701}_{2}+U\unicode[STIX]{x1D701}_{1}$ is the Cauchy characteristic vector field of
$\widetilde{\unicode[STIX]{x1D701}}_{2}=\unicode[STIX]{x1D701}_{2}+U\unicode[STIX]{x1D701}_{1}$ is the Cauchy characteristic vector field of ![]() $\unicode[STIX]{x2202}E$ so that
$\unicode[STIX]{x2202}E$ so that ![]() $[\widetilde{\unicode[STIX]{x1D701}}_{2},\unicode[STIX]{x1D701}_{3}]\equiv 0,\langle \text{mod}.~\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3}\rangle$.
$[\widetilde{\unicode[STIX]{x1D701}}_{2},\unicode[STIX]{x1D701}_{3}]\equiv 0,\langle \text{mod}.~\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3}\rangle$.
Taking the subbundle ![]() $L\subset E$ generated by
$L\subset E$ generated by ![]() $\widetilde{\unicode[STIX]{x1D701}}_{2}$, we have a pseudo-product structure
$\widetilde{\unicode[STIX]{x1D701}}_{2}$, we have a pseudo-product structure ![]() $E=K\oplus L$ on
$E=K\oplus L$ on ![]() $Z$ satisfying the conditions
$Z$ satisfying the conditions
By Jacobi identity, ![]() $[\widetilde{\unicode[STIX]{x1D701}}_{2},[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{3}]]+ [\!\unicode[STIX]{x1D701}_{1},[\unicode[STIX]{x1D701}_{3},\widetilde{\unicode[STIX]{x1D701}}_{2}]+[\unicode[STIX]{x1D701}_{3},[\widetilde{\unicode[STIX]{x1D701}}_{2},\unicode[STIX]{x1D701}_{1}]]=0,$ we have that
$[\widetilde{\unicode[STIX]{x1D701}}_{2},[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{3}]]+ [\!\unicode[STIX]{x1D701}_{1},[\unicode[STIX]{x1D701}_{3},\widetilde{\unicode[STIX]{x1D701}}_{2}]+[\unicode[STIX]{x1D701}_{3},[\widetilde{\unicode[STIX]{x1D701}}_{2},\unicode[STIX]{x1D701}_{1}]]=0,$ we have that
Therefore, the condition ![]() $[{\mathcal{L}},\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}$ is satisfied. Since
$[{\mathcal{L}},\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}$ is satisfied. Since ![]() $O_{s}^{(3)}C\subset TX$ is independent of
$O_{s}^{(3)}C\subset TX$ is independent of ![]() $s$ and is a contact structure on
$s$ and is a contact structure on ![]() $X$, we have that
$X$, we have that ![]() $[{\mathcal{K}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$ and that
$[{\mathcal{K}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}$ and that ![]() $[{\mathcal{L}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]$ generates the total tangent bundle
$[{\mathcal{L}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]$ generates the total tangent bundle ![]() $TZ$. Thus, the last condition
$TZ$. Thus, the last condition ![]() $[{\mathcal{L}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(4)}{\mathcal{E}}$ holds.
$[{\mathcal{L}},\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}]=\unicode[STIX]{x2202}^{(4)}{\mathcal{E}}$ holds.
Consequently, if ![]() $C$ is a nondegenerate Lagrangian cone structure with the condition that
$C$ is a nondegenerate Lagrangian cone structure with the condition that ![]() $\unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C$ for any direction field
$\unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C$ for any direction field ![]() $s$ of
$s$ of ![]() $C$, then
$C$, then ![]() $E=K\oplus L$ is a pseudo-product structure of
$E=K\oplus L$ is a pseudo-product structure of ![]() $G_{2}$-type.
$G_{2}$-type.
This completes the proof of Theorem 3.1. ◻
Remark 3.2. The cone structure ![]() $C\subset TX$ is regarded as the control system over
$C\subset TX$ is regarded as the control system over ![]() $X$,
$X$,
with ![]() $2$-control parameters. In local coordinates, the control system
$2$-control parameters. In local coordinates, the control system ![]() $\mathbb{C}$ is given by
$\mathbb{C}$ is given by
with the control parameters ![]() $r,\unicode[STIX]{x1D703}$.
$r,\unicode[STIX]{x1D703}$.
4  $(2,3,5)$-distributions and cubic Lagrangian cone structures
$(2,3,5)$-distributions and cubic Lagrangian cone structures
Let us denote by ![]() $G_{2}^{\prime }$ the automorphism group of the split octonion algebra
$G_{2}^{\prime }$ the automorphism group of the split octonion algebra ![]() $\mathbb{O}^{\prime }$. Then for a Borel group subgroup
$\mathbb{O}^{\prime }$. Then for a Borel group subgroup ![]() $B$ and parabolic subgroups
$B$ and parabolic subgroups ![]() $P_{1},P_{2}$ containing
$P_{1},P_{2}$ containing ![]() $B$ of
$B$ of ![]() $G_{2}^{\prime }$, we have a double fibration
$G_{2}^{\prime }$, we have a double fibration
a ![]() $(2,3,5)$-distribution
$(2,3,5)$-distribution ![]() $D\subset TY$ on
$D\subset TY$ on ![]() $Y$, a pseudo-product structure of type
$Y$, a pseudo-product structure of type ![]() $G_{2}$ as
$G_{2}$ as ![]() $E=K\oplus L\subset TZ$ on
$E=K\oplus L\subset TZ$ on ![]() $Z$, and a nondegenerate Lagrangian cubic cone structure
$Z$, and a nondegenerate Lagrangian cubic cone structure ![]() $C\subset TX$ (see [Reference Ishikawa, Machida and Takahashi16]). It is known also that
$C\subset TX$ (see [Reference Ishikawa, Machida and Takahashi16]). It is known also that ![]() $Y$ is diffeomorphic to
$Y$ is diffeomorphic to ![]() $S^{3}\times S^{2}$ (resp.
$S^{3}\times S^{2}$ (resp. ![]() $Z$ to
$Z$ to ![]() $S^{3}\times S^{3}$,
$S^{3}\times S^{3}$, ![]() $X$ to
$X$ to ![]() $S^{2}\times S^{3}$). On each of three places, there exists Cartan’s parabolic geometry as a natural nonflat geometry modeled on the homogeneous space. On
$S^{2}\times S^{3}$). On each of three places, there exists Cartan’s parabolic geometry as a natural nonflat geometry modeled on the homogeneous space. On ![]() $Y$, it is the geometry of
$Y$, it is the geometry of ![]() $(2,3,5)$-distributions. On
$(2,3,5)$-distributions. On ![]() $Z$, it is the geometry of pseudo-product structures of type
$Z$, it is the geometry of pseudo-product structures of type ![]() $G_{2}$. On
$G_{2}$. On ![]() $X$, it is
$X$, it is ![]() $G_{2}$-contact structures [Reference C̆ap and Slovák12, Reference Leistner, Nurowski and Sagerschung19]. Moreover, any
$G_{2}$-contact structures [Reference C̆ap and Slovák12, Reference Leistner, Nurowski and Sagerschung19]. Moreover, any ![]() $G_{2}$-contact structure is accompanied with and is recovered from a nondegenerate Lagrangian cubic cone structure.
$G_{2}$-contact structure is accompanied with and is recovered from a nondegenerate Lagrangian cubic cone structure.
Sato [Reference Sato23] has suggested to the first author that any ![]() $G_{2}$-contact structure corresponding to a
$G_{2}$-contact structure corresponding to a ![]() $(2,3,5)$-distribution should be flat, from the exact comparison of curvatures for associated Cartan connections on pseudo-product
$(2,3,5)$-distribution should be flat, from the exact comparison of curvatures for associated Cartan connections on pseudo-product ![]() $G_{2}$-structure and on
$G_{2}$-structure and on ![]() $G_{2}$-contact structures [Reference Tanaka24, Reference Yamaguchi27]. Here we would like to provide alternative proof for the fact. In fact, we have the following.
$G_{2}$-contact structures [Reference Tanaka24, Reference Yamaguchi27]. Here we would like to provide alternative proof for the fact. In fact, we have the following.
Proposition 4.1. Any ![]() $(2,3,5)$-distribution
$(2,3,5)$-distribution ![]() $(Y,D)$ which corresponds to a cubic cone structure
$(Y,D)$ which corresponds to a cubic cone structure ![]() $(X,C)$ must be flat. Any Lagrangian cone structure which corresponds to a flat
$(X,C)$ must be flat. Any Lagrangian cone structure which corresponds to a flat ![]() $(2,3,5)$-distributions must be cubic.
$(2,3,5)$-distributions must be cubic.
Proof of Proposition 4.1.
For each ![]() $x\in X$, the cone
$x\in X$, the cone ![]() $C_{x}\subset D_{x}^{\prime }(\subset T_{x}X)$ gives the (reduced) “Jacobi curve” in the sense of Agrachev and Zelenko [Reference Agrachev and Zelenko3–Reference Agrachev and Zelenko5, Reference Zelenko29]. Then, in [Reference Zelenko29], it is proved that “Cartan tensor” of
$C_{x}\subset D_{x}^{\prime }(\subset T_{x}X)$ gives the (reduced) “Jacobi curve” in the sense of Agrachev and Zelenko [Reference Agrachev and Zelenko3–Reference Agrachev and Zelenko5, Reference Zelenko29]. Then, in [Reference Zelenko29], it is proved that “Cartan tensor” of ![]() $D$ is recovered by a projective invariant, the fundamental invariant, a kind of cross ratio, of
$D$ is recovered by a projective invariant, the fundamental invariant, a kind of cross ratio, of ![]() $P(C_{x})$ pointwise. In fact, for the cone
$P(C_{x})$ pointwise. In fact, for the cone ![]() $C_{x}\subset D_{x}\cong \mathbb{R}^{4}$, there is associated a curve
$C_{x}\subset D_{x}\cong \mathbb{R}^{4}$, there is associated a curve ![]() $P(C_{x})$ in Grassmannian
$P(C_{x})$ in Grassmannian ![]() $\operatorname{Gr}(2,\mathbb{R}^{4})$, and the fundamental invariants is calculated from
$\operatorname{Gr}(2,\mathbb{R}^{4})$, and the fundamental invariants is calculated from ![]() $P(C_{x})$ in a projective invariant way.
$P(C_{x})$ in a projective invariant way.
Suppose a ![]() $(2,3,5)$-distribution
$(2,3,5)$-distribution ![]() $D$ corresponds to a cubic cone structure
$D$ corresponds to a cubic cone structure ![]() $C\subset D^{\prime }\subset TX$. Then the cone structure is nondegenerate. Since all nondegenerate cubic cones are projectively equivalent pointwise, the Cartan tensor of
$C\subset D^{\prime }\subset TX$. Then the cone structure is nondegenerate. Since all nondegenerate cubic cones are projectively equivalent pointwise, the Cartan tensor of ![]() $D$ coincides with the flat
$D$ coincides with the flat ![]() $(2,3,5)$-distribution. Therefore,
$(2,3,5)$-distribution. Therefore, ![]() $D$ must be flat.
$D$ must be flat.
Suppose a Lagrangian cone structure ![]() $(X,C)$ corresponds to a flat
$(X,C)$ corresponds to a flat ![]() $(2,3,5)$-distribution
$(2,3,5)$-distribution ![]() $(Y,D)$. The flat model
$(Y,D)$. The flat model ![]() $(Y_{0},D_{0})$ has the standard cubic dual
$(Y_{0},D_{0})$ has the standard cubic dual ![]() $(X_{0},C_{0})$ as in [Reference Ishikawa, Machida and Takahashi16]. Since
$(X_{0},C_{0})$ as in [Reference Ishikawa, Machida and Takahashi16]. Since ![]() $(Y,D)\equiv (Y_{0},D_{0})$, we see
$(Y,D)\equiv (Y_{0},D_{0})$, we see ![]() $(X,C)\equiv (X_{0},C_{0})$ by Theorem 3.1. Then
$(X,C)\equiv (X_{0},C_{0})$ by Theorem 3.1. Then ![]() $C$ is cubic because the degree is invariant under the isomorphism of cone structures.◻
$C$ is cubic because the degree is invariant under the isomorphism of cone structures.◻
Example 4.2. (Cubic Lagrangian cone structures not corresponding to  $(2,3,5)$-distributions)
$(2,3,5)$-distributions)
Consider a cubic cone structure ![]() $C$ on
$C$ on ![]() $(\mathbb{R}^{5},0)$ around the direction
$(\mathbb{R}^{5},0)$ around the direction ![]() $\unicode[STIX]{x1D703}=0$,
$\unicode[STIX]{x1D703}=0$,
 $$\begin{eqnarray}\displaystyle F(x;r,\unicode[STIX]{x1D703}) & = & \displaystyle r\biggl(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{1}}+\unicode[STIX]{x1D703}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{2}}+(\unicode[STIX]{x1D703}^{2}+a)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+(\unicode[STIX]{x1D703}^{3}-3\unicode[STIX]{x1D703}a)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\{x_{3}\unicode[STIX]{x1D703}-2x_{2}(\unicode[STIX]{x1D703}^{2}+a)+x_{1}(\unicode[STIX]{x1D703}^{3}-3\unicode[STIX]{x1D703}a)\}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(x;r,\unicode[STIX]{x1D703}) & = & \displaystyle r\biggl(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{1}}+\unicode[STIX]{x1D703}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{2}}+(\unicode[STIX]{x1D703}^{2}+a)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+(\unicode[STIX]{x1D703}^{3}-3\unicode[STIX]{x1D703}a)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\{x_{3}\unicode[STIX]{x1D703}-2x_{2}(\unicode[STIX]{x1D703}^{2}+a)+x_{1}(\unicode[STIX]{x1D703}^{3}-3\unicode[STIX]{x1D703}a)\}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}\biggr),\nonumber\end{eqnarray}$$ defined by a ![]() $C^{\infty }$ function
$C^{\infty }$ function ![]() $a(x_{1})$ with
$a(x_{1})$ with ![]() $a(0)=0$.
$a(0)=0$.
Then ![]() $C$ is a nondegenerate Lagrangian cone structure for the contact structure
$C$ is a nondegenerate Lagrangian cone structure for the contact structure ![]() $D^{\prime }:dx_{5}-x_{3}dx_{2}+2x_{2}dx_{3}-x_{1}dx_{4}=0$. Moreover,
$D^{\prime }:dx_{5}-x_{3}dx_{2}+2x_{2}dx_{3}-x_{1}dx_{4}=0$. Moreover, ![]() $C$ satisfies the condition
$C$ satisfies the condition ![]() $\unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C$ for any
$\unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C$ for any ![]() $s:X\rightarrow L\setminus \{0\}$, to correspond to a
$s:X\rightarrow L\setminus \{0\}$, to correspond to a ![]() $(2,3,5)$-distribution, if and only if
$(2,3,5)$-distribution, if and only if ![]() $a\not \equiv 0$. The case
$a\not \equiv 0$. The case ![]() $a\equiv 0$ corresponds to the
$a\equiv 0$ corresponds to the ![]() $G_{2}$-homogeneous flat case [Reference Ishikawa, Machida and Takahashi16].
$G_{2}$-homogeneous flat case [Reference Ishikawa, Machida and Takahashi16].
The following gives examples of nondegenerate Lagrangian noncubic cone structures which correspond to ![]() $(2,3,5)$-distributions and shows the necessity of the additional condition
$(2,3,5)$-distributions and shows the necessity of the additional condition ![]() $\unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C$ of Theorem 3.1.
$\unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C$ of Theorem 3.1.
Example 4.3. (Noncubic Lagrangian cone structures corresponding to  $(2,3,5)$-distributions)
$(2,3,5)$-distributions)
Consider a cone structure on ![]() $(\mathbb{R}^{5},0)$ around the direction
$(\mathbb{R}^{5},0)$ around the direction ![]() $\unicode[STIX]{x1D703}=0$,
$\unicode[STIX]{x1D703}=0$,
 $$\begin{eqnarray}\displaystyle F(x;r,\unicode[STIX]{x1D703}) & = & \displaystyle r\biggl(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{1}}+\unicode[STIX]{x1D703}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{2}}+(\unicode[STIX]{x1D703}^{2}+b)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+(\unicode[STIX]{x1D703}^{3}+c)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\{x_{3}\unicode[STIX]{x1D703}-2x_{2}(\unicode[STIX]{x1D703}^{2}+b)+x_{1}(\unicode[STIX]{x1D703}^{3}+c)\}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(x;r,\unicode[STIX]{x1D703}) & = & \displaystyle r\biggl(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{1}}+\unicode[STIX]{x1D703}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{2}}+(\unicode[STIX]{x1D703}^{2}+b)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+(\unicode[STIX]{x1D703}^{3}+c)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\{x_{3}\unicode[STIX]{x1D703}-2x_{2}(\unicode[STIX]{x1D703}^{2}+b)+x_{1}(\unicode[STIX]{x1D703}^{3}+c)\}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}\biggr),\nonumber\end{eqnarray}$$ where ![]() $b=b(\unicode[STIX]{x1D703}),c=c(\unicode[STIX]{x1D703})$, with
$b=b(\unicode[STIX]{x1D703}),c=c(\unicode[STIX]{x1D703})$, with ![]() $\operatorname{ord}_{0}b(\unicode[STIX]{x1D703})\geqslant 3,\operatorname{ord}_{0}c(\unicode[STIX]{x1D703})\geqslant 4$.
$\operatorname{ord}_{0}b(\unicode[STIX]{x1D703})\geqslant 3,\operatorname{ord}_{0}c(\unicode[STIX]{x1D703})\geqslant 4$.
Then ![]() $F$ is a nondegenerate Lagrangian cone structure for the contact structure
$F$ is a nondegenerate Lagrangian cone structure for the contact structure ![]() $D^{\prime }:dx_{5}-x_{3}dx_{2}+2x_{2}dx_{3}-x_{1}dx_{4}=0$. Moreover,
$D^{\prime }:dx_{5}-x_{3}dx_{2}+2x_{2}dx_{3}-x_{1}dx_{4}=0$. Moreover, ![]() $F$ satisfies the condition
$F$ satisfies the condition ![]() $\unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C$, for any direction field
$\unicode[STIX]{x2202}(T_{s}C)\subset O_{s}^{(2)}C$, for any direction field ![]() $s$, to correspond to a
$s$, to correspond to a ![]() $(2,3,5)$-distribution, if and only if
$(2,3,5)$-distribution, if and only if ![]() $c_{\unicode[STIX]{x1D703}}=3\unicode[STIX]{x1D703}b_{\unicode[STIX]{x1D703}}-3b$.
$c_{\unicode[STIX]{x1D703}}=3\unicode[STIX]{x1D703}b_{\unicode[STIX]{x1D703}}-3b$.
If ![]() $b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}\not =0$, for example, if
$b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}\not =0$, for example, if ![]() $b=\unicode[STIX]{x1D703}^{4},c=\frac{9}{5}\unicode[STIX]{x1D703}^{5}$, then
$b=\unicode[STIX]{x1D703}^{4},c=\frac{9}{5}\unicode[STIX]{x1D703}^{5}$, then ![]() $C$ is not cubic. Therefore, the corresponding
$C$ is not cubic. Therefore, the corresponding ![]() $(2,3,5)$-distribution is never flat.
$(2,3,5)$-distribution is never flat.
Here we present the computation of the prolongation ![]() $(Z,E)$ from the above example of cone structures. The bundle
$(Z,E)$ from the above example of cone structures. The bundle ![]() $E$ is generated by
$E$ is generated by
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle \unicode[STIX]{x1D701}_{1}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}},\\ \displaystyle \unicode[STIX]{x1D701}_{2}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{1}}+\unicode[STIX]{x1D703}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{2}}+(\unicode[STIX]{x1D703}^{2}+b)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+(\unicode[STIX]{x1D703}^{3}+c)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}+\{x_{3}\unicode[STIX]{x1D703}-2x_{2}(\unicode[STIX]{x1D703}^{2}+b)+x_{1}(\unicode[STIX]{x1D703}^{3}+c)\}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\displaystyle \unicode[STIX]{x1D701}_{1}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}},\\ \displaystyle \unicode[STIX]{x1D701}_{2}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{1}}+\unicode[STIX]{x1D703}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{2}}+(\unicode[STIX]{x1D703}^{2}+b)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+(\unicode[STIX]{x1D703}^{3}+c)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}+\{x_{3}\unicode[STIX]{x1D703}-2x_{2}(\unicode[STIX]{x1D703}^{2}+b)+x_{1}(\unicode[STIX]{x1D703}^{3}+c)\}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}\end{array}\right.\end{eqnarray}$$ on the space ![]() $Z$ with coordinates
$Z$ with coordinates ![]() $\unicode[STIX]{x1D703},x_{1},x_{2},x_{3},x_{4},x_{5}$. Then we have over
$\unicode[STIX]{x1D703},x_{1},x_{2},x_{3},x_{4},x_{5}$. Then we have over ![]() $Z$,
$Z$,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{3} & := & \displaystyle [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}]=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{2}}+(2\unicode[STIX]{x1D703}+b_{\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+(3\unicode[STIX]{x1D703}^{2}+c_{\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\{x_{3}-2x_{2}(2\unicode[STIX]{x1D703}+b_{\unicode[STIX]{x1D703}})+x_{1}(3\unicode[STIX]{x1D703}^{2}+c_{\unicode[STIX]{x1D703}})\}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{3} & := & \displaystyle [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}]=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{2}}+(2\unicode[STIX]{x1D703}+b_{\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+(3\unicode[STIX]{x1D703}^{2}+c_{\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\{x_{3}-2x_{2}(2\unicode[STIX]{x1D703}+b_{\unicode[STIX]{x1D703}})+x_{1}(3\unicode[STIX]{x1D703}^{2}+c_{\unicode[STIX]{x1D703}})\}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}},\nonumber\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D701}_{4}:=[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{3}]=(2+b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+(6\unicode[STIX]{x1D703}+c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}+\{-2x_{2}(2+b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})+x_{1}(6\unicode[STIX]{x1D703}+c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle [\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3}]=(c_{\unicode[STIX]{x1D703}}-3\unicode[STIX]{x1D703}b_{\unicode[STIX]{x1D703}}+3b)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D701}_{5}=[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{4}]=b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+(6+c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}+\{-2x_{2}b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}+x_{1}(6+c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle [\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{4}]=(c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}-3\unicode[STIX]{x1D703}b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{5}]=b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}+(-2x_{2}b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}+x_{1}c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D701}_{6}:=[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{5}]=3(2+a_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D701}_{4}:=[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{3}]=(2+b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+(6\unicode[STIX]{x1D703}+c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}+\{-2x_{2}(2+b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})+x_{1}(6\unicode[STIX]{x1D703}+c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle [\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3}]=(c_{\unicode[STIX]{x1D703}}-3\unicode[STIX]{x1D703}b_{\unicode[STIX]{x1D703}}+3b)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D701}_{5}=[\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{4}]=b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+(6+c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}+\{-2x_{2}b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}+x_{1}(6+c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle [\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{4}]=(c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}-3\unicode[STIX]{x1D703}b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}=0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{5}]=b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{3}}+c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{4}}+(-2x_{2}b_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}}+x_{1}c_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D701}_{6}:=[\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{5}]=3(2+a_{\unicode[STIX]{x1D703}\unicode[STIX]{x1D703}})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{5}}. & \displaystyle \nonumber\end{eqnarray}$$ We have that ![]() $\unicode[STIX]{x2202}{\mathcal{E}}=\langle \unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3}\rangle ,\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}=\langle \unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{4}\rangle ,\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}=\langle \unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{4},\unicode[STIX]{x1D701}_{5}\rangle$, and
$\unicode[STIX]{x2202}{\mathcal{E}}=\langle \unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3}\rangle ,\unicode[STIX]{x2202}^{(2)}{\mathcal{E}}=\langle \unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{4}\rangle ,\unicode[STIX]{x2202}^{(3)}{\mathcal{E}}=\langle \unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{4},\unicode[STIX]{x1D701}_{5}\rangle$, and ![]() $\unicode[STIX]{x2202}^{(4)}{\mathcal{E}}=\langle \unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{4},\unicode[STIX]{x1D701}_{5},\unicode[STIX]{x1D701}_{6}\rangle$. Then
$\unicode[STIX]{x2202}^{(4)}{\mathcal{E}}=\langle \unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{4},\unicode[STIX]{x1D701}_{5},\unicode[STIX]{x1D701}_{6}\rangle$. Then ![]() $E$ has the pseudo-product structure of
$E$ has the pseudo-product structure of ![]() $G_{2}$-type given by
$G_{2}$-type given by ![]() ${\mathcal{K}}=\langle \unicode[STIX]{x1D701}_{1}\rangle ,{\mathcal{L}}=\langle \unicode[STIX]{x1D701}_{2}\rangle$ and it descends to a nonflat
${\mathcal{K}}=\langle \unicode[STIX]{x1D701}_{1}\rangle ,{\mathcal{L}}=\langle \unicode[STIX]{x1D701}_{2}\rangle$ and it descends to a nonflat ![]() $(2,3,5)$-distribution.
$(2,3,5)$-distribution.
Acknowledgments
The authors are grateful to Professor Hajime Sato for valuable comments. They are grateful also to an anonymous referee for his/her helpful suggestions to improve the paper.