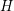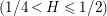1 Introduction
In this paper we study from the viewpoint of Malliavin calculus the following rough differential equation (RDE) driven by ![]() $d$-dimensional fractional Brownian motion (fBm)
$d$-dimensional fractional Brownian motion (fBm) ![]() $(w_{t})$ with Hurst parameter
$(w_{t})$ with Hurst parameter ![]() $H\in (1/4,1/2]$.
$H\in (1/4,1/2]$.
Here, ![]() $V_{i}$
$V_{i}$![]() $(0\leqslant i\leqslant d)$ is a sufficiently regular vector field on
$(0\leqslant i\leqslant d)$ is a sufficiently regular vector field on ![]() $\mathbf{R}^{n}$. When
$\mathbf{R}^{n}$. When ![]() $H=1/2$, fBm is the usual Brownian motion and this RDE coincides with the usual stochastic differential equation (SDE) of Stratonovich type.
$H=1/2$, fBm is the usual Brownian motion and this RDE coincides with the usual stochastic differential equation (SDE) of Stratonovich type.
Malliavin calculus for RDEs driven by fractional Brownian rough path or Gaussian rough path is a quite active topic now and a number of papers were published on it recently. See [Reference Baudoin, Nualart, Ouyang and TindelBNOT16, Reference Baudoin, Ouyang and ZhangBOZ15, Reference Baudoin, Ouyang and ZhangBOZ16, Reference Boedihardjo, Geng and QianBGQ16, Reference Cass and FrizCF10, Reference Cass, Friz and VictoirCFV09, Reference Cass, Hairer, Litterer and TindelCHLT15, Reference DriscollDri13, Reference Hairer and PillaiHP13, Reference Hu and TindelHT13, Reference InahamaIna14, Reference InahamaIna16b] among others.
Due to [Reference Cass, Hairer, Litterer and TindelCHLT15, Reference InahamaIna14] and the general theory of Malliavin calculus, under Hörmander’s bracket generating condition on ![]() $V_{i}$
$V_{i}$![]() $(0\leqslant i\leqslant d)$ at the starting point
$(0\leqslant i\leqslant d)$ at the starting point ![]() $a$, the solution
$a$, the solution ![]() $y_{t}$ has a smooth density
$y_{t}$ has a smooth density ![]() $p_{t}(a,a^{\prime })$ with respect to the Lebesgue measure for every
$p_{t}(a,a^{\prime })$ with respect to the Lebesgue measure for every ![]() $t>0$, that is, the function
$t>0$, that is, the function ![]() $a^{\prime }\mapsto p_{t}(a,a^{\prime })$ is smooth and
$a^{\prime }\mapsto p_{t}(a,a^{\prime })$ is smooth and ![]() $\mathbf{P}(y_{t}\in A)=\int _{A}p_{t}(a,a^{\prime })\,da^{\prime }$ holds for every Borel subset
$\mathbf{P}(y_{t}\in A)=\int _{A}p_{t}(a,a^{\prime })\,da^{\prime }$ holds for every Borel subset ![]() $A\subset \mathbf{R}^{n}$.
$A\subset \mathbf{R}^{n}$.
In this paper we are interested in short time asymptotics of this density function. We will prove in Theorem 2.3 a full asymptotic expansion of ![]() $p_{t}(a,a^{\prime })$ as
$p_{t}(a,a^{\prime })$ as ![]() $t{\searrow}0$ for
$t{\searrow}0$ for ![]() $a\neq a^{\prime }$ under, loosely speaking, Hörmander’s condition at
$a\neq a^{\prime }$ under, loosely speaking, Hörmander’s condition at ![]() $a$ and the “unique minimizer” condition (see (A1) and (A2) below, respectively).
$a$ and the “unique minimizer” condition (see (A1) and (A2) below, respectively).
This kind of short time asymptotic expansion of the density (under the unique minimizer condition) was first shown for ![]() $H\in (1/2,1)$ in the framework of Young integration theory by [Reference Baudoin and OuyangBO11, Reference InahamaIna16a], then for
$H\in (1/2,1)$ in the framework of Young integration theory by [Reference Baudoin and OuyangBO11, Reference InahamaIna16a], then for ![]() $H\in (1/3,1/2]$ by [Reference InahamaIna16b] in the framework of rough path theory. These results are not completely satisfactory, however, for the following two reasons. First, from the viewpoint of rough path theory, the condition on Hurst parameter should be
$H\in (1/3,1/2]$ by [Reference InahamaIna16b] in the framework of rough path theory. These results are not completely satisfactory, however, for the following two reasons. First, from the viewpoint of rough path theory, the condition on Hurst parameter should be ![]() $H>1/4$. Second, in these papers the ellipticity assumption on the vector fields is assumed. From the viewpoint of Malliavin calculus, it should be replaced by Hörmander’s condition.
$H>1/4$. Second, in these papers the ellipticity assumption on the vector fields is assumed. From the viewpoint of Malliavin calculus, it should be replaced by Hörmander’s condition.
The purpose of the present paper is to generalize this kind of off-diagonal asymptotic expansion to a satisfactory form by refining the arguments in [Reference InahamaIna16b]. Hence, this is a continuation of [Reference InahamaIna16b] and our proof, just like the one in [Reference InahamaIna16b], is based on Watanabe’s distributional Malliavin calculus [Reference WatanabeWat87, Reference Ikeda and WatanabeIW89].
Due to the generalizations, however, many parts of our proof become more complicated than their counterparts in [Reference InahamaIna16b]. Examples are as follows. In § 3.5 we calculate the Young translation of Besov rough path for the third level case. Since we work under Hörmander’s condition, we must calculate Malliavin covariance matrices more carefully in Section 5. In particular, we prove Kusuoka–Stroock type estimate (Proposition 5.3) and the uniform non-degeneracy for the scaled–shifted RDE (Proposition 5.4).
When ![]() $H=1/2$,
$H=1/2$, ![]() $p_{t}(a,a^{\prime })$ can also be viewed as the heat kernel of the corresponding parabolic equation and has been extensively studied by the analytic and the probabilistic methods. When it comes to off-diagonal asymptotic expansion under the unique minimizer condition, Ben Arous [Reference Ben ArousBA88] seems to be the most famous. In the special case
$p_{t}(a,a^{\prime })$ can also be viewed as the heat kernel of the corresponding parabolic equation and has been extensively studied by the analytic and the probabilistic methods. When it comes to off-diagonal asymptotic expansion under the unique minimizer condition, Ben Arous [Reference Ben ArousBA88] seems to be the most famous. In the special case ![]() $H=1/2$, our main result (Theorem 2.3) recovers the main result in [Reference Ben ArousBA88]. Therefore, Theorem 2.3 can be regarded as an “fBm-version” of [Reference Ben ArousBA88].
$H=1/2$, our main result (Theorem 2.3) recovers the main result in [Reference Ben ArousBA88]. Therefore, Theorem 2.3 can be regarded as an “fBm-version” of [Reference Ben ArousBA88].
The organization of this paper is as follows. In Section 2 we introduce the setting and assumptions and then state our main result. In Section 3 we gather basic results in rough path theory for later use, including many probabilistic properties of fractional Brownian rough path. In Section 4, a Taylor-like expansion of Lyons–Itô map, both in the deterministic and probabilistic senses, is given. In Section 5 we apply Malliavin calculus to an RDE driven by fractional Brownian rough path with Hurst parameter ![]() $H\in (1/4,1/2]$. Following [Reference Baudoin, Ouyang and ZhangBOZ15], [Reference Cass, Hairer, Litterer and TindelCHLT15] and [Reference Gess, Ouyang and TindelGOT17], we carefully prove a few important propositions. Those are used in Section 6 to prove our main theorem. In Section 7 we apply our main result to concrete examples. Section 8 is devoted to showing a technical lemma.
$H\in (1/4,1/2]$. Following [Reference Baudoin, Ouyang and ZhangBOZ15], [Reference Cass, Hairer, Litterer and TindelCHLT15] and [Reference Gess, Ouyang and TindelGOT17], we carefully prove a few important propositions. Those are used in Section 6 to prove our main theorem. In Section 7 we apply our main result to concrete examples. Section 8 is devoted to showing a technical lemma.
In what follows, we use the following notation. For ![]() $p\geqslant 0$,
$p\geqslant 0$, ![]() $\lfloor p\rfloor$ denotes the integer part of
$\lfloor p\rfloor$ denotes the integer part of ![]() $p$. For
$p$. For ![]() $1<p<\infty$,
$1<p<\infty$, ![]() $0<\unicode[STIX]{x1D6FC}<1$ and a metric space
$0<\unicode[STIX]{x1D6FC}<1$ and a metric space ![]() $E$,
$E$, ![]() $C^{p\text{-}\text{var}}([0,1];E)$ and
$C^{p\text{-}\text{var}}([0,1];E)$ and ![]() $C^{\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}([0,1];E)$ stand for the space of all continuous paths of bounded
$C^{\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}([0,1];E)$ stand for the space of all continuous paths of bounded ![]() $p$-variation and the space of all
$p$-variation and the space of all ![]() $\unicode[STIX]{x1D6FC}$-Hölder paths from
$\unicode[STIX]{x1D6FC}$-Hölder paths from ![]() $[0,1]$ to
$[0,1]$ to ![]() $E$, respectively. We denote by
$E$, respectively. We denote by ![]() $C_{o}^{p\text{-}\text{var}}([0,1];E)$ and
$C_{o}^{p\text{-}\text{var}}([0,1];E)$ and ![]() $C_{o}^{\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}([0,1];E)$ the subsets of
$C_{o}^{\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}([0,1];E)$ the subsets of ![]() $C^{p\text{-}\text{var}}([0,1];E)$ and
$C^{p\text{-}\text{var}}([0,1];E)$ and ![]() $C^{\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}([0,1];E)$, respectively, of the paths starting from
$C^{\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}([0,1];E)$, respectively, of the paths starting from ![]() $o\in E$. For a real symmetric matrix
$o\in E$. For a real symmetric matrix ![]() $A$,
$A$, ![]() $\unicode[STIX]{x1D706}_{\min }(A)$ and
$\unicode[STIX]{x1D706}_{\min }(A)$ and ![]() $\unicode[STIX]{x1D706}_{\max }(A)$ denote the smallest and the largest eigenvalues of
$\unicode[STIX]{x1D706}_{\max }(A)$ denote the smallest and the largest eigenvalues of ![]() $A$, respectively. A smooth vector field
$A$, respectively. A smooth vector field ![]() $F=\sum _{i=1}^{n}F^{i}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{i})$ on
$F=\sum _{i=1}^{n}F^{i}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}^{i})$ on ![]() $\mathbf{R}^{n}$ is often identified with the corresponding
$\mathbf{R}^{n}$ is often identified with the corresponding ![]() $\mathbf{R}^{n}$-valued smooth function
$\mathbf{R}^{n}$-valued smooth function ![]() $(F^{i}(\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{n}))_{1\leqslant i\leqslant n}$ on
$(F^{i}(\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{n}))_{1\leqslant i\leqslant n}$ on ![]() $\mathbf{R}^{n}$. Its Jacobi matrix is denoted by
$\mathbf{R}^{n}$. Its Jacobi matrix is denoted by ![]() $\unicode[STIX]{x1D6FB}F$, that is,
$\unicode[STIX]{x1D6FB}F$, that is, ![]() $(\unicode[STIX]{x1D6FB}F)_{ij}=\unicode[STIX]{x2202}F^{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}_{j}=\unicode[STIX]{x2202}F^{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}_{j}(1\leqslant i,j\leqslant n)$.
$(\unicode[STIX]{x1D6FB}F)_{ij}=\unicode[STIX]{x2202}F^{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}_{j}=\unicode[STIX]{x2202}F^{i}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}_{j}(1\leqslant i,j\leqslant n)$.
2 Setting and main result
2.1 Setting
In this subsection, we introduce a stochastic process that will play a main role in this paper. From now on we denote by ![]() $(w_{t})_{t\geqslant 0}$ the
$(w_{t})_{t\geqslant 0}$ the ![]() $d$-dimensional fBm with Hurst parameter
$d$-dimensional fBm with Hurst parameter ![]() $H$. Throughout this paper we assume
$H$. Throughout this paper we assume ![]() $1/4<H\leqslant 1/2$. It is a unique
$1/4<H\leqslant 1/2$. It is a unique ![]() $d$-dimensional, mean-zero, continuous Gaussian process with covariance
$d$-dimensional, mean-zero, continuous Gaussian process with covariance ![]() $\mathbf{E}[w_{s}^{i}w_{t}^{j}]=\unicode[STIX]{x1D6FF}_{ij}R(s,t)$ (
$\mathbf{E}[w_{s}^{i}w_{t}^{j}]=\unicode[STIX]{x1D6FF}_{ij}R(s,t)$ (![]() $s,t\geqslant 0$), where
$s,t\geqslant 0$), where
Note that, for any ![]() $c>0$,
$c>0$, ![]() $(w_{ct})_{t\geqslant 0}$ and
$(w_{ct})_{t\geqslant 0}$ and ![]() $(c^{H}w_{t})_{t\geqslant 0}$ have the same law. This property is called self-similarity or scale invariance. When
$(c^{H}w_{t})_{t\geqslant 0}$ have the same law. This property is called self-similarity or scale invariance. When ![]() $H=1/2$, it is the usual Brownian motion. In what follows the time interval will always be
$H=1/2$, it is the usual Brownian motion. In what follows the time interval will always be ![]() $[0,1]$. It is well known that
$[0,1]$. It is well known that ![]() $(w_{t})_{0\leqslant t\leqslant 1}$ admits a canonical rough path lift
$(w_{t})_{0\leqslant t\leqslant 1}$ admits a canonical rough path lift ![]() $\mathbf{w}=(\mathbf{w}^{1},\ldots ,\mathbf{w}^{\lfloor 1/H\rfloor })$, which is called fractional Brownian rough path [Reference Coutin and QianCQ02].
$\mathbf{w}=(\mathbf{w}^{1},\ldots ,\mathbf{w}^{\lfloor 1/H\rfloor })$, which is called fractional Brownian rough path [Reference Coutin and QianCQ02].
Let ![]() $V_{i}:\mathbf{R}^{n}\rightarrow \mathbf{R}^{n}$ be
$V_{i}:\mathbf{R}^{n}\rightarrow \mathbf{R}^{n}$ be ![]() $C_{b}^{\infty }$, that is,
$C_{b}^{\infty }$, that is, ![]() $V_{i}$ is a bounded smooth function with bounded derivatives of all order (
$V_{i}$ is a bounded smooth function with bounded derivatives of all order (![]() $0\leqslant i\leqslant d$). We shall identify
$0\leqslant i\leqslant d$). We shall identify ![]() $V_{i}$ with its corresponding vector field and denote the vector field by the same symbol. We consider the following RDE:
$V_{i}$ with its corresponding vector field and denote the vector field by the same symbol. We consider the following RDE:
where ![]() $a\in \mathbf{R}^{n}$ is a deterministic initial point. This RDE is driven by the Young pairing
$a\in \mathbf{R}^{n}$ is a deterministic initial point. This RDE is driven by the Young pairing ![]() $(\mathbf{w},\boldsymbol{\unicode[STIX]{x1D706}})$, where
$(\mathbf{w},\boldsymbol{\unicode[STIX]{x1D706}})$, where ![]() $\unicode[STIX]{x1D706}_{t}=t$. The unique solution is denoted by
$\unicode[STIX]{x1D706}_{t}=t$. The unique solution is denoted by ![]() $\mathbf{y}=(\mathbf{y}^{1},\ldots ,\mathbf{y}^{\lfloor 1/H\rfloor })$ and we set
$\mathbf{y}=(\mathbf{y}^{1},\ldots ,\mathbf{y}^{\lfloor 1/H\rfloor })$ and we set ![]() $y_{t}:=a+\mathbf{y}_{0,t}^{1}$ as usual. We will sometimes write
$y_{t}:=a+\mathbf{y}_{0,t}^{1}$ as usual. We will sometimes write ![]() $y_{t}=y_{t}(a)=y_{t}(a,\mathbf{w})$ etc. to make explicit the dependence on
$y_{t}=y_{t}(a)=y_{t}(a,\mathbf{w})$ etc. to make explicit the dependence on ![]() $a$ and
$a$ and ![]() $\mathbf{w}$. We often use a matrix notation for (2.1), that is, we set
$\mathbf{w}$. We often use a matrix notation for (2.1), that is, we set ![]() $b=V_{0}$ and
$b=V_{0}$ and ![]() $\unicode[STIX]{x1D70E}=[V_{1},\ldots ,V_{d}]$, which is
$\unicode[STIX]{x1D70E}=[V_{1},\ldots ,V_{d}]$, which is ![]() $n\times d$ matrix-valued, and write (2.1) as
$n\times d$ matrix-valued, and write (2.1) as
2.2 Assumptions
In this subsection, we introduce assumptions of the main theorem. First, we introduce the Hörmander condition:
Definition 2.1. (Hörmander condition) Set
For ![]() $x\in \mathbf{R}^{n}$,
$x\in \mathbf{R}^{n}$, ![]() ${\mathcal{V}}_{m}(x)$ (resp.
${\mathcal{V}}_{m}(x)$ (resp. ![]() ${\mathcal{V}}(x)$) stands for the subset of
${\mathcal{V}}(x)$) stands for the subset of ![]() $\mathbf{R}^{n}$ obtained by plugging
$\mathbf{R}^{n}$ obtained by plugging ![]() $x$ into the vector field of
$x$ into the vector field of ![]() ${\mathcal{V}}_{m}$ (resp.
${\mathcal{V}}_{m}$ (resp. ![]() ${\mathcal{V}}$). We say that the vector fields
${\mathcal{V}}$). We say that the vector fields ![]() $V_{0},V_{1},\ldots ,V_{d}$ satisfy the Hörmander condition at
$V_{0},V_{1},\ldots ,V_{d}$ satisfy the Hörmander condition at ![]() $x\in \mathbf{R}^{n}$ if
$x\in \mathbf{R}^{n}$ if ![]() ${\mathcal{V}}(x)$ linearly spans
${\mathcal{V}}(x)$ linearly spans ![]() $\mathbf{R}^{n}$.
$\mathbf{R}^{n}$.
We assume the following:
(A1)![]() $V_{0},V_{1},\ldots ,V_{d}$ satisfy the Hörmander condition at the initial point
$V_{0},V_{1},\ldots ,V_{d}$ satisfy the Hörmander condition at the initial point ![]() $a\in \mathbf{R}^{n}$.
$a\in \mathbf{R}^{n}$.
It is known that, under (A1), the law of the solution ![]() $y_{t}$ has a density
$y_{t}$ has a density ![]() $p_{t}(a,a^{\prime })$ with respect to the Lebesgue measure on
$p_{t}(a,a^{\prime })$ with respect to the Lebesgue measure on ![]() $\mathbf{R}^{n}$ for any
$\mathbf{R}^{n}$ for any ![]() $t>0$ (see [Reference Hairer and PillaiHP13, Reference Cass, Hairer, Litterer and TindelCHLT15]). Hence, for any Borel subset
$t>0$ (see [Reference Hairer and PillaiHP13, Reference Cass, Hairer, Litterer and TindelCHLT15]). Hence, for any Borel subset ![]() $A\subset \mathbf{R}^{n}$,
$A\subset \mathbf{R}^{n}$, ![]() $\mathbf{P}(y_{t}(a)\in A)=\int _{A}p_{t}(a,a^{\prime })\,da^{\prime }$.
$\mathbf{P}(y_{t}(a)\in A)=\int _{A}p_{t}(a,a^{\prime })\,da^{\prime }$.
Let ![]() $\mathfrak{H}=\mathfrak{H}^{H}$ be the Cameron–Martin space of fBm on the time interval
$\mathfrak{H}=\mathfrak{H}^{H}$ be the Cameron–Martin space of fBm on the time interval ![]() $[0,1]$. For every
$[0,1]$. For every ![]() $H\in (1/4,1/2]$, there exists
$H\in (1/4,1/2]$, there exists ![]() $q\in [1,2)$ such that every
$q\in [1,2)$ such that every ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ is continuous and of finite
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ is continuous and of finite![]() $q$-variation. For
$q$-variation. For ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}$, we denote by
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}$, we denote by ![]() $\unicode[STIX]{x1D719}_{t}^{0}=\unicode[STIX]{x1D719}_{t}^{0}(\unicode[STIX]{x1D6FE})$ the solution of the following Young ordinary differential equation (ODE):
$\unicode[STIX]{x1D719}_{t}^{0}=\unicode[STIX]{x1D719}_{t}^{0}(\unicode[STIX]{x1D6FE})$ the solution of the following Young ordinary differential equation (ODE):
Set, for ![]() $a^{\prime }\neq a$,
$a^{\prime }\neq a$, ![]() $K_{a}^{a^{\prime }}=\{\unicode[STIX]{x1D6FE}\in \mathfrak{H}\mid \unicode[STIX]{x1D719}_{1}^{0}(\unicode[STIX]{x1D6FE})=a^{\prime }\}$. We only consider the case where
$K_{a}^{a^{\prime }}=\{\unicode[STIX]{x1D6FE}\in \mathfrak{H}\mid \unicode[STIX]{x1D719}_{1}^{0}(\unicode[STIX]{x1D6FE})=a^{\prime }\}$. We only consider the case where ![]() $K_{a}^{a^{\prime }}$ is not empty. From goodness of the rate function in Schilder-type large deviation for fractional Brownian rough path, it follows that
$K_{a}^{a^{\prime }}$ is not empty. From goodness of the rate function in Schilder-type large deviation for fractional Brownian rough path, it follows that ![]() $\inf \{\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}\mid \unicode[STIX]{x1D6FE}\in K_{a}^{a^{\prime }}\}=\min \{\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}\mid \unicode[STIX]{x1D6FE}\in K_{a}^{a^{\prime }}\}$. Now we introduce the following assumption:
$\inf \{\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}\mid \unicode[STIX]{x1D6FE}\in K_{a}^{a^{\prime }}\}=\min \{\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}\mid \unicode[STIX]{x1D6FE}\in K_{a}^{a^{\prime }}\}$. Now we introduce the following assumption:
(A2)![]() $\bar{\unicode[STIX]{x1D6FE}}\in K_{a}^{a^{\prime }}$ which minimizes
$\bar{\unicode[STIX]{x1D6FE}}\in K_{a}^{a^{\prime }}$ which minimizes ![]() $\mathfrak{H}$-norm exists uniquely.
$\mathfrak{H}$-norm exists uniquely.
In what follows, ![]() $\bar{\unicode[STIX]{x1D6FE}}$ denotes the minimizer in (A2). Note that the map
$\bar{\unicode[STIX]{x1D6FE}}$ denotes the minimizer in (A2). Note that the map ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}{\hookrightarrow}C^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})\mapsto \unicode[STIX]{x1D719}_{1}^{0}(\unicode[STIX]{x1D6FE})\in \mathbf{R}^{n}$ is Fréchet differentiable;
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}{\hookrightarrow}C^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})\mapsto \unicode[STIX]{x1D719}_{1}^{0}(\unicode[STIX]{x1D6FE})\in \mathbf{R}^{n}$ is Fréchet differentiable; ![]() $D\unicode[STIX]{x1D719}_{1}^{0}(\unicode[STIX]{x1D6FE})$ stands for the Fréchet derivative and is expressed by
$D\unicode[STIX]{x1D719}_{1}^{0}(\unicode[STIX]{x1D6FE})$ stands for the Fréchet derivative and is expressed by
where ![]() $[\bullet ]^{k}$ and
$[\bullet ]^{k}$ and ![]() $[\bullet ]_{i}^{k}$ are the
$[\bullet ]_{i}^{k}$ are the ![]() $k$th component of the vector and the
$k$th component of the vector and the ![]() $(k,i)$-component of the matrix, respectively, and
$(k,i)$-component of the matrix, respectively, and ![]() $J(\unicode[STIX]{x1D6FE})$ and
$J(\unicode[STIX]{x1D6FE})$ and ![]() $K(\unicode[STIX]{x1D6FE})$ are the Jacobi process of
$K(\unicode[STIX]{x1D6FE})$ are the Jacobi process of ![]() $\unicode[STIX]{x1D719}^{0}(\unicode[STIX]{x1D6FE})$ and its inverse, respectively. We define the deterministic Malliavin covariance matrix
$\unicode[STIX]{x1D719}^{0}(\unicode[STIX]{x1D6FE})$ and its inverse, respectively. We define the deterministic Malliavin covariance matrix ![]() $Q(\unicode[STIX]{x1D6FE})=(Q(\unicode[STIX]{x1D6FE})_{kl})_{1\leqslant k,l\leqslant n}$ by
$Q(\unicode[STIX]{x1D6FE})=(Q(\unicode[STIX]{x1D6FE})_{kl})_{1\leqslant k,l\leqslant n}$ by
We assume that ![]() $Q$ is nondegenerate at the minimizer
$Q$ is nondegenerate at the minimizer ![]() $\bar{\unicode[STIX]{x1D6FE}}$:
$\bar{\unicode[STIX]{x1D6FE}}$:
(A3) There is a positive constant ![]() $c$ such that
$c$ such that ![]() $Q(\bar{\unicode[STIX]{x1D6FE}})\geqslant cI$, where
$Q(\bar{\unicode[STIX]{x1D6FE}})\geqslant cI$, where ![]() $I$ stands for the identity matrix.
$I$ stands for the identity matrix.
Finally, we assume that ![]() $\Vert \bullet \Vert _{\mathfrak{H}}^{2}/2$ is not so degenerate at
$\Vert \bullet \Vert _{\mathfrak{H}}^{2}/2$ is not so degenerate at ![]() $\bar{\unicode[STIX]{x1D6FE}}$ in the following sense:
$\bar{\unicode[STIX]{x1D6FE}}$ in the following sense:
(A4) At ![]() $\bar{\unicode[STIX]{x1D6FE}}$, the Hessian of the functional
$\bar{\unicode[STIX]{x1D6FE}}$, the Hessian of the functional ![]() $K_{a}^{a^{\prime }}\ni \unicode[STIX]{x1D6FE}\mapsto \Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}/2$ is strictly positive in the quadratic form sense. More precisely, if
$K_{a}^{a^{\prime }}\ni \unicode[STIX]{x1D6FE}\mapsto \Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}/2$ is strictly positive in the quadratic form sense. More precisely, if ![]() $(-\unicode[STIX]{x1D716}_{0},\unicode[STIX]{x1D716}_{0})\ni u\mapsto f(u)\in K_{a}^{a^{\prime }}$ is a smooth curve in
$(-\unicode[STIX]{x1D716}_{0},\unicode[STIX]{x1D716}_{0})\ni u\mapsto f(u)\in K_{a}^{a^{\prime }}$ is a smooth curve in ![]() $K_{a}^{a^{\prime }}$ such that
$K_{a}^{a^{\prime }}$ such that ![]() $f(0)=\bar{\unicode[STIX]{x1D6FE}}$ and
$f(0)=\bar{\unicode[STIX]{x1D6FE}}$ and ![]() $f^{\prime }(0)\neq 0$, then
$f^{\prime }(0)\neq 0$, then ![]() $(d/du)^{2}|_{u=0}\Vert f(u)\Vert _{\mathfrak{H}}^{2}/2>0$.
$(d/du)^{2}|_{u=0}\Vert f(u)\Vert _{\mathfrak{H}}^{2}/2>0$.
Remark 2.2. By a standard argument, (A3) is equivalent to the surjectivity of the tangent map ![]() $D\unicode[STIX]{x1D719}_{1}^{0}(\bar{\unicode[STIX]{x1D6FE}}):\mathfrak{H}\rightarrow \mathbf{R}^{n}$. By the implicit function theorem, this implies that
$D\unicode[STIX]{x1D719}_{1}^{0}(\bar{\unicode[STIX]{x1D6FE}}):\mathfrak{H}\rightarrow \mathbf{R}^{n}$. By the implicit function theorem, this implies that ![]() $K_{a}^{a^{\prime }}$ has a Hilbert-manifold structure near
$K_{a}^{a^{\prime }}$ has a Hilbert-manifold structure near ![]() $\bar{\unicode[STIX]{x1D6FE}}$. Therefore, “Hessian at
$\bar{\unicode[STIX]{x1D6FE}}$. Therefore, “Hessian at ![]() $\bar{\unicode[STIX]{x1D6FE}}$” and “a smooth curve near
$\bar{\unicode[STIX]{x1D6FE}}$” and “a smooth curve near ![]() $\bar{\unicode[STIX]{x1D6FE}}$” make sense.
$\bar{\unicode[STIX]{x1D6FE}}$” make sense.
2.3 Index sets
In this subsection we introduce several index sets for the exponent of the small time parameter ![]() $t>0$, which will be used in the asymptotic expansion. Unfortunately, these index sets are not subsets of
$t>0$, which will be used in the asymptotic expansion. Unfortunately, these index sets are not subsets of ![]() $\mathbf{N}=\{0,1,2,\ldots \}$ and are rather complicated in general. (However, they are discrete subsets of
$\mathbf{N}=\{0,1,2,\ldots \}$ and are rather complicated in general. (However, they are discrete subsets of ![]() $(\mathbf{Z}+H^{-1}\mathbf{Z})\cap [0,\infty )$ with the minimum
$(\mathbf{Z}+H^{-1}\mathbf{Z})\cap [0,\infty )$ with the minimum ![]() $0$.)
$0$.)
Set
We denote by ![]() $0=\unicode[STIX]{x1D705}_{0}<\unicode[STIX]{x1D705}_{1}<\unicode[STIX]{x1D705}_{2}<\cdots \,$ all the elements of
$0=\unicode[STIX]{x1D705}_{0}<\unicode[STIX]{x1D705}_{1}<\unicode[STIX]{x1D705}_{2}<\cdots \,$ all the elements of ![]() $\unicode[STIX]{x1D6EC}_{1}$ in increasing order. Several smallest elements are explicitly given as follows: for
$\unicode[STIX]{x1D6EC}_{1}$ in increasing order. Several smallest elements are explicitly given as follows: for ![]() $1/3<H<1/2$,
$1/3<H<1/2$,
and, for ![]() $1/4<H<1/3$,
$1/4<H<1/3$,
We also set
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6EC}_{2}=\{\unicode[STIX]{x1D705}-1\mid \unicode[STIX]{x1D705}\in \unicode[STIX]{x1D6EC}_{1}\setminus \{\unicode[STIX]{x1D705}_{0}\}\}=\bigg\{0,1,\frac{1}{H}-1,2,\frac{1}{H},3,\ldots \bigg\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6EC}_{2}^{\prime }=\{\unicode[STIX]{x1D705}-2\mid \unicode[STIX]{x1D705}\in \unicode[STIX]{x1D6EC}_{1}\setminus \{\unicode[STIX]{x1D705}_{0},\unicode[STIX]{x1D705}_{1}\}\}=\bigg\{0,\frac{1}{H}-2,1,\frac{1}{H}-1,2,\ldots \bigg\}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6EC}_{2}=\{\unicode[STIX]{x1D705}-1\mid \unicode[STIX]{x1D705}\in \unicode[STIX]{x1D6EC}_{1}\setminus \{\unicode[STIX]{x1D705}_{0}\}\}=\bigg\{0,1,\frac{1}{H}-1,2,\frac{1}{H},3,\ldots \bigg\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6EC}_{2}^{\prime }=\{\unicode[STIX]{x1D705}-2\mid \unicode[STIX]{x1D705}\in \unicode[STIX]{x1D6EC}_{1}\setminus \{\unicode[STIX]{x1D705}_{0},\unicode[STIX]{x1D705}_{1}\}\}=\bigg\{0,\frac{1}{H}-2,1,\frac{1}{H}-1,2,\ldots \bigg\}. & \displaystyle \nonumber\end{eqnarray}$$ Note that in the above explicit expression of these two index sets the elements are not sorted in increasing order when ![]() $1/4<H\leqslant 1/3$. Next we set
$1/4<H\leqslant 1/3$. Next we set
where ![]() $\mathbf{N}_{+}=\{1,2,\ldots \!\,\}$. In the sequel,
$\mathbf{N}_{+}=\{1,2,\ldots \!\,\}$. In the sequel, ![]() $0=\unicode[STIX]{x1D708}_{0}<\unicode[STIX]{x1D708}_{1}<\unicode[STIX]{x1D708}_{2}<\cdots \,$ and
$0=\unicode[STIX]{x1D708}_{0}<\unicode[STIX]{x1D708}_{1}<\unicode[STIX]{x1D708}_{2}<\cdots \,$ and ![]() $0=\unicode[STIX]{x1D70C}_{0}<\unicode[STIX]{x1D70C}_{1}<\unicode[STIX]{x1D70C}_{2}<\cdots \,$ stand for all the elements of
$0=\unicode[STIX]{x1D70C}_{0}<\unicode[STIX]{x1D70C}_{1}<\unicode[STIX]{x1D70C}_{2}<\cdots \,$ stand for all the elements of ![]() $\unicode[STIX]{x1D6EC}_{3}$ and
$\unicode[STIX]{x1D6EC}_{3}$ and ![]() $\unicode[STIX]{x1D6EC}_{3}^{\prime }$ in increasing order, respectively. Finally,
$\unicode[STIX]{x1D6EC}_{3}^{\prime }$ in increasing order, respectively. Finally,
We denote by ![]() $0=\unicode[STIX]{x1D706}_{0}<\unicode[STIX]{x1D706}_{1}<\unicode[STIX]{x1D706}_{2}<\cdots \,$ all the elements of
$0=\unicode[STIX]{x1D706}_{0}<\unicode[STIX]{x1D706}_{1}<\unicode[STIX]{x1D706}_{2}<\cdots \,$ all the elements of ![]() $\unicode[STIX]{x1D6EC}_{4}$ in increasing order.
$\unicode[STIX]{x1D6EC}_{4}$ in increasing order.
We remark that when ![]() $H=1/2$ and
$H=1/2$ and ![]() $H=1/3$, all these index sets
$H=1/3$, all these index sets ![]() $\unicode[STIX]{x1D6EC}_{i},\unicode[STIX]{x1D6EC}_{j}^{\prime }$ above are just
$\unicode[STIX]{x1D6EC}_{i},\unicode[STIX]{x1D6EC}_{j}^{\prime }$ above are just ![]() $\mathbf{N}$.
$\mathbf{N}$.
2.4 Statement of the main result
Now we state our main theorem. This is basically analogous to many preceding works on the standard Brownian motion such as [Reference Ben ArousBA88, Reference WatanabeWat87]. However, when ![]() $H\neq 1/2,1/3$ and the drift term exists, there are some differences. First, the exponents of
$H\neq 1/2,1/3$ and the drift term exists, there are some differences. First, the exponents of ![]() $t$ are not (a constant multiple of) natural numbers. Second, cancelation of “odd terms” (see e.g., [Reference WatanabeWat87, pp. 20 and 34]) does not occur in general. (These phenomena were already observed in [Reference InahamaIna16a] and [Reference InahamaIna16b] when
$t$ are not (a constant multiple of) natural numbers. Second, cancelation of “odd terms” (see e.g., [Reference WatanabeWat87, pp. 20 and 34]) does not occur in general. (These phenomena were already observed in [Reference InahamaIna16a] and [Reference InahamaIna16b] when ![]() $H\in (1/3,1)$.) Our proof uses the Watanabe distribution theory. Therefore, the asymptotic expansion is actually obtained at the level of Watanabe distributions.
$H\in (1/3,1)$.) Our proof uses the Watanabe distribution theory. Therefore, the asymptotic expansion is actually obtained at the level of Watanabe distributions.
Theorem 2.3. Assume ![]() $a\neq a^{\prime }$ and
$a\neq a^{\prime }$ and ![]() $\text{(A1)}$–
$\text{(A1)}$–![]() $\text{(A4)}$. Then, we have the following asymptotic expansion as
$\text{(A4)}$. Then, we have the following asymptotic expansion as ![]() $t{\searrow}0$:
$t{\searrow}0$:
for a certain positive constant ![]() $\unicode[STIX]{x1D6FC}_{0}$ and certain real constants
$\unicode[STIX]{x1D6FC}_{0}$ and certain real constants ![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}_{j}}\;(j=1,2,\ldots )$. Here,
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}_{j}}\;(j=1,2,\ldots )$. Here, ![]() $0=\unicode[STIX]{x1D706}_{0}<\unicode[STIX]{x1D706}_{1}<\unicode[STIX]{x1D706}_{2}<\cdots \,$ are all the elements of
$0=\unicode[STIX]{x1D706}_{0}<\unicode[STIX]{x1D706}_{1}<\unicode[STIX]{x1D706}_{2}<\cdots \,$ are all the elements of ![]() $\unicode[STIX]{x1D6EC}_{4}$ in increasing order.
$\unicode[STIX]{x1D6EC}_{4}$ in increasing order.
The above result improves that in [Reference InahamaIna16b]. The reason is as follows. First, we work under Hörmander condition instead of the ellipticity assumption. Second, the case ![]() $1/4<H\leqslant 1/3$ is also treated. Hence, we must calculate the third level rough paths.
$1/4<H\leqslant 1/3$ is also treated. Hence, we must calculate the third level rough paths.
Remark 2.4. If RDE (2.1) has no drift term, that is, ![]() $V_{0}\equiv 0$, then we can replace
$V_{0}\equiv 0$, then we can replace ![]() $\unicode[STIX]{x1D6EC}_{4}$ by
$\unicode[STIX]{x1D6EC}_{4}$ by ![]() $2\mathbf{N}$ in Theorem 2.3, namely,
$2\mathbf{N}$ in Theorem 2.3, namely,
as ![]() $t{\searrow}0$. The reason is as follows. First, if
$t{\searrow}0$. The reason is as follows. First, if ![]() $V_{0}\equiv 0$, the index sets
$V_{0}\equiv 0$, the index sets ![]() $\unicode[STIX]{x1D6EC}_{i}$,
$\unicode[STIX]{x1D6EC}_{i}$, ![]() $\unicode[STIX]{x1D6EC}_{j}^{\prime }$
$\unicode[STIX]{x1D6EC}_{j}^{\prime }$![]() $(1\leqslant i\leqslant 4,2\leqslant j\leqslant 3)$ in the sequel can be replaced by
$(1\leqslant i\leqslant 4,2\leqslant j\leqslant 3)$ in the sequel can be replaced by ![]() $\mathbf{N}$. Second, the odd-numbered terms in the asymptotics of the generalized Wiener functional are also odd as generalized Wiener functionals. Hence, their generalized expectations all vanish.
$\mathbf{N}$. Second, the odd-numbered terms in the asymptotics of the generalized Wiener functional are also odd as generalized Wiener functionals. Hence, their generalized expectations all vanish.
When ![]() $H=1/2$, (2.5) holds for the same reason. Thus, we reprove the main result of Ben Arous [Reference Ben ArousBA88] via rough path theory.
$H=1/2$, (2.5) holds for the same reason. Thus, we reprove the main result of Ben Arous [Reference Ben ArousBA88] via rough path theory.
3 Preliminaries
3.1 Rough path analysis
In this paper we basically work in Lyons’ original framework of rough path theory. (The only exception is § 5.2, where the controlled path theory is used.) We borrow most of notations and terminologies from [Reference Lyons and QianLQ02, Reference Lyons, Caruana and LévyLCL07, Reference Friz and VictoirFV10]. Let ![]() $p\in [2,4)$ be the roughness constant and let
$p\in [2,4)$ be the roughness constant and let ![]() $q\in [1,2)$ be such that
$q\in [1,2)$ be such that ![]() $1/p+1/q>1$. Set
$1/p+1/q>1$. Set ![]() $\unicode[STIX]{x1D6FC}=1/p$ and let
$\unicode[STIX]{x1D6FC}=1/p$ and let ![]() $m\in \mathbf{N}_{+}$ satisfy
$m\in \mathbf{N}_{+}$ satisfy ![]() $\unicode[STIX]{x1D6FC}-1/m>0$. We denote by
$\unicode[STIX]{x1D6FC}-1/m>0$. We denote by ![]() $G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$,
$G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$, ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC}}^{\text{H}}(\mathbf{R}^{d})$, and
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC}}^{\text{H}}(\mathbf{R}^{d})$, and ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})$ the geometric rough path spaces with
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})$ the geometric rough path spaces with ![]() $p$-variation,
$p$-variation, ![]() $\unicode[STIX]{x1D6FC}$-Hölder and
$\unicode[STIX]{x1D6FC}$-Hölder and ![]() $(\unicode[STIX]{x1D6FC},m)$-Besov topologies, respectively. In this paper,
$(\unicode[STIX]{x1D6FC},m)$-Besov topologies, respectively. In this paper, ![]() $\mathbf{x}=(\mathbf{x}^{1},\ldots ,\mathbf{x}^{\lfloor p\rfloor })$ stands for a generic element in these rough path spaces. Recall that the
$\mathbf{x}=(\mathbf{x}^{1},\ldots ,\mathbf{x}^{\lfloor p\rfloor })$ stands for a generic element in these rough path spaces. Recall that the ![]() $p$-variation,
$p$-variation, ![]() $\unicode[STIX]{x1D6FC}$-Hölder and
$\unicode[STIX]{x1D6FC}$-Hölder and ![]() $(\unicode[STIX]{x1D6FC},m)$-Besov topologies are induced by
$(\unicode[STIX]{x1D6FC},m)$-Besov topologies are induced by
 $$\begin{eqnarray}\displaystyle \Vert \mathbf{x}^{i}\Vert _{p/i\text{-}\text{var}} & = & \displaystyle \sup _{0=t_{0}<\cdots <t_{K}=1}\bigg(\mathop{\sum }_{k=1}^{K}|\mathbf{x}_{t_{k-1},t_{k}}^{i}|^{p/i}\bigg)^{i/p},\nonumber\\ \displaystyle \Vert \mathbf{x}^{i}\Vert _{i\unicode[STIX]{x1D6FC}\text{-}\text{Hol}} & = & \displaystyle \sup _{0\leqslant s<t\leqslant 1}\frac{|\mathbf{x}_{s,t}^{i}|}{|t-s|^{i\unicode[STIX]{x1D6FC}}},\nonumber\\ \displaystyle \Vert \mathbf{x}^{i}\Vert _{(i\unicode[STIX]{x1D6FC},m/i)\text{-}\text{Bes}} & = & \displaystyle \bigg(\iint _{0\leqslant s<t\leqslant 1}\frac{|\mathbf{x}_{s,t}^{i}|^{m/i}}{|t-s|^{1+i\unicode[STIX]{x1D6FC}\cdot m/i}}\,dsdt\bigg)^{i/m}\quad (i=1,\ldots ,\lfloor p\rfloor ).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \mathbf{x}^{i}\Vert _{p/i\text{-}\text{var}} & = & \displaystyle \sup _{0=t_{0}<\cdots <t_{K}=1}\bigg(\mathop{\sum }_{k=1}^{K}|\mathbf{x}_{t_{k-1},t_{k}}^{i}|^{p/i}\bigg)^{i/p},\nonumber\\ \displaystyle \Vert \mathbf{x}^{i}\Vert _{i\unicode[STIX]{x1D6FC}\text{-}\text{Hol}} & = & \displaystyle \sup _{0\leqslant s<t\leqslant 1}\frac{|\mathbf{x}_{s,t}^{i}|}{|t-s|^{i\unicode[STIX]{x1D6FC}}},\nonumber\\ \displaystyle \Vert \mathbf{x}^{i}\Vert _{(i\unicode[STIX]{x1D6FC},m/i)\text{-}\text{Bes}} & = & \displaystyle \bigg(\iint _{0\leqslant s<t\leqslant 1}\frac{|\mathbf{x}_{s,t}^{i}|^{m/i}}{|t-s|^{1+i\unicode[STIX]{x1D6FC}\cdot m/i}}\,dsdt\bigg)^{i/m}\quad (i=1,\ldots ,\lfloor p\rfloor ).\nonumber\end{eqnarray}$$ Next we introduce homogeneous norms to ![]() $G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$,
$G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$, ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC}}^{\text{H}}(\mathbf{R}^{d})$, and
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC}}^{\text{H}}(\mathbf{R}^{d})$, and ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})$ which are consistent with their topology. More explicitly, they are given by
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})$ which are consistent with their topology. More explicitly, they are given by
 $$\begin{eqnarray}\displaystyle & \displaystyle \Vert \mathbf{x}\Vert _{p\text{-}\text{var}}=\mathop{\sum }_{i=1}^{\lfloor p\rfloor }\Vert \mathbf{x}^{i}\Vert _{p/i\text{-}\text{var}}^{1/i},\qquad \Vert \mathbf{x}\Vert _{\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}=\mathop{\sum }_{i=1}^{\lfloor 1/\unicode[STIX]{x1D6FC}\rfloor }\Vert \mathbf{x}^{i}\Vert _{i\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}^{1/i}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \Vert \mathbf{x}\Vert _{(\unicode[STIX]{x1D6FC},m)\text{-}\text{Bes}}=\mathop{\sum }_{i=1}^{\lfloor 1/\unicode[STIX]{x1D6FC}\rfloor }\Vert \mathbf{x}^{i}\Vert _{(i\unicode[STIX]{x1D6FC},m/i)\text{-}\text{Bes}}^{1/i}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \Vert \mathbf{x}\Vert _{p\text{-}\text{var}}=\mathop{\sum }_{i=1}^{\lfloor p\rfloor }\Vert \mathbf{x}^{i}\Vert _{p/i\text{-}\text{var}}^{1/i},\qquad \Vert \mathbf{x}\Vert _{\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}=\mathop{\sum }_{i=1}^{\lfloor 1/\unicode[STIX]{x1D6FC}\rfloor }\Vert \mathbf{x}^{i}\Vert _{i\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}^{1/i}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \Vert \mathbf{x}\Vert _{(\unicode[STIX]{x1D6FC},m)\text{-}\text{Bes}}=\mathop{\sum }_{i=1}^{\lfloor 1/\unicode[STIX]{x1D6FC}\rfloor }\Vert \mathbf{x}^{i}\Vert _{(i\unicode[STIX]{x1D6FC},m/i)\text{-}\text{Bes}}^{1/i}. & \displaystyle \nonumber\end{eqnarray}$$ We denote by ![]() $\Vert \mathbf{x}^{i}\Vert _{p/i\text{-}\text{var};[s,t]}$,
$\Vert \mathbf{x}^{i}\Vert _{p/i\text{-}\text{var};[s,t]}$, ![]() $\Vert \mathbf{x}\Vert _{p\text{-}\text{var};[s,t]}$, etc. the norms restricted on the subinterval
$\Vert \mathbf{x}\Vert _{p\text{-}\text{var};[s,t]}$, etc. the norms restricted on the subinterval ![]() $[s,t]$.
$[s,t]$.
For a rough path ![]() $\mathbf{x}$, we write
$\mathbf{x}$, we write ![]() $x_{t}=\mathbf{x}_{0,t}^{1}$ as usual. For
$x_{t}=\mathbf{x}_{0,t}^{1}$ as usual. For ![]() $x\in C_{0}^{r\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ with
$x\in C_{0}^{r\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ with ![]() $r\in [1,2)$, we denote the natural lift of
$r\in [1,2)$, we denote the natural lift of ![]() $x$ (i.e., the smooth rough path lying above
$x$ (i.e., the smooth rough path lying above ![]() $x$) by the corresponding boldface letter
$x$) by the corresponding boldface letter ![]() $\mathbf{x}$. Note that, for
$\mathbf{x}$. Note that, for ![]() $x\in C_{0}^{r\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ and
$x\in C_{0}^{r\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ and ![]() $y\in C_{0}^{r\text{-}\text{var}}([0,1];\mathbf{R}^{e})$,
$y\in C_{0}^{r\text{-}\text{var}}([0,1];\mathbf{R}^{e})$, ![]() $(\mathbf{x},\mathbf{y})\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+e})$ stands for the natural lift of
$(\mathbf{x},\mathbf{y})\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+e})$ stands for the natural lift of ![]() $(x,y)\in C_{0}^{r\text{-}\text{var}}([0,1];\mathbf{R}^{d+e})$, not for the pair
$(x,y)\in C_{0}^{r\text{-}\text{var}}([0,1];\mathbf{R}^{d+e})$, not for the pair ![]() $(\mathbf{x},\mathbf{y})\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{e})$. In a similar way, for
$(\mathbf{x},\mathbf{y})\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{e})$. In a similar way, for ![]() $\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ and
$\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ and ![]() $h\in C_{0}^{q\text{-}\text{var}}(\mathbf{R}^{e})$ with
$h\in C_{0}^{q\text{-}\text{var}}(\mathbf{R}^{e})$ with ![]() $1/p+1/q>1$,
$1/p+1/q>1$, ![]() $(\mathbf{x},\mathbf{h})\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+e})$ stands for the Young pairing. For
$(\mathbf{x},\mathbf{h})\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+e})$ stands for the Young pairing. For ![]() $\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ and
$\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ and ![]() $h\in C_{0}^{q\text{-}\text{var}}(\mathbf{R}^{d})$ with
$h\in C_{0}^{q\text{-}\text{var}}(\mathbf{R}^{d})$ with ![]() $1/p+1/q>1$,
$1/p+1/q>1$, ![]() $\mathbf{x}+\mathbf{h}=\unicode[STIX]{x1D70F}_{h}(\mathbf{x})\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ stands for the Young translation. (See [Reference Friz and VictoirFV10, Section 9.4].) We denote by
$\mathbf{x}+\mathbf{h}=\unicode[STIX]{x1D70F}_{h}(\mathbf{x})\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ stands for the Young translation. (See [Reference Friz and VictoirFV10, Section 9.4].) We denote by ![]() $c\mathbf{x}$ the dilation of a rough path
$c\mathbf{x}$ the dilation of a rough path ![]() $\mathbf{x}$ by
$\mathbf{x}$ by ![]() $c\in \mathbf{R}$. These notations may be somewhat misleading. But, they make many operations intuitively clear and easy to understand when we treat rough paths over a direct sum of many vector spaces.
$c\in \mathbf{R}$. These notations may be somewhat misleading. But, they make many operations intuitively clear and easy to understand when we treat rough paths over a direct sum of many vector spaces.
Note that the spaces ![]() $G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$,
$G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$, ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC}}^{\text{H}}(\mathbf{R}^{d})$, and
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC}}^{\text{H}}(\mathbf{R}^{d})$, and ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})$ enjoy the next continuous embeddings. We have
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})$ enjoy the next continuous embeddings. We have ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d}){\hookrightarrow}G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ and
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d}){\hookrightarrow}G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ and
from [Reference Friz and VictoirFV10, Corollary A.3]. (The continuity of this embedding is not explicitly written in [Reference Friz and VictoirFV10], but can be shown by standard and slightly lengthy argument.) For ![]() $\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FD}\leqslant 1/\lfloor 1/\unicode[STIX]{x1D6FC}\rfloor$, a direct computation implies Besov–Hölder embedding
$\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FD}\leqslant 1/\lfloor 1/\unicode[STIX]{x1D6FC}\rfloor$, a direct computation implies Besov–Hölder embedding ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FD}}^{\text{H}}(\mathbf{R}^{d}){\hookrightarrow}G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})$.
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FD}}^{\text{H}}(\mathbf{R}^{d}){\hookrightarrow}G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})$.
For a control function ![]() $\unicode[STIX]{x1D714}$ in the sense of [Reference Lyons and QianLQ02, p. 16], we write
$\unicode[STIX]{x1D714}$ in the sense of [Reference Lyons and QianLQ02, p. 16], we write ![]() $\bar{\unicode[STIX]{x1D714}}:=\unicode[STIX]{x1D714}(0,1)$. For any
$\bar{\unicode[STIX]{x1D714}}:=\unicode[STIX]{x1D714}(0,1)$. For any ![]() $\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$,
$\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$,
defines a control function. (This control function is equivalent to the one defined by Carnot–Caratheodory metric.) Similarly, we set ![]() $\unicode[STIX]{x1D714}_{h}(s,t):=\Vert h\Vert _{q\text{-}\text{var};[s,t]}^{q}$ for
$\unicode[STIX]{x1D714}_{h}(s,t):=\Vert h\Vert _{q\text{-}\text{var};[s,t]}^{q}$ for ![]() $h\in C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{e})$.
$h\in C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{e})$.
For ![]() $\unicode[STIX]{x1D6FF}>0$ and
$\unicode[STIX]{x1D6FF}>0$ and ![]() $\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$, set
$\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$, set ![]() $\unicode[STIX]{x1D70F}_{0}(\unicode[STIX]{x1D6FF})=0$ and
$\unicode[STIX]{x1D70F}_{0}(\unicode[STIX]{x1D6FF})=0$ and
Define
Superadditivity of ![]() $\unicode[STIX]{x1D714}_{\mathbf{x}}$ yields
$\unicode[STIX]{x1D714}_{\mathbf{x}}$ yields ![]() $\unicode[STIX]{x1D6FF}N_{\unicode[STIX]{x1D6FF}}(\mathbf{x})\leqslant \overline{\unicode[STIX]{x1D714}_{\mathbf{x}}}$. This quantity (3.3) was first studied by Cass, Litterer, and Lyons [Reference Cass, Litterer and LyonsCLL13].
$\unicode[STIX]{x1D6FF}N_{\unicode[STIX]{x1D6FF}}(\mathbf{x})\leqslant \overline{\unicode[STIX]{x1D714}_{\mathbf{x}}}$. This quantity (3.3) was first studied by Cass, Litterer, and Lyons [Reference Cass, Litterer and LyonsCLL13].
Let ![]() $\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+1})$. We consider an RDE
$\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+1})$. We consider an RDE
It is well known that the solution map ![]() $G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+1})\ni \mathbf{x}\mapsto \mathbf{y}=(\mathbf{y}^{1},\ldots ,\mathbf{y}^{\lfloor p\rfloor })\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{n})$ is continuous. Set
$G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+1})\ni \mathbf{x}\mapsto \mathbf{y}=(\mathbf{y}^{1},\ldots ,\mathbf{y}^{\lfloor p\rfloor })\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{n})$ is continuous. Set ![]() $\unicode[STIX]{x1D6F7}(\mathbf{x})=\mathbf{y}$ and
$\unicode[STIX]{x1D6F7}(\mathbf{x})=\mathbf{y}$ and ![]() $y_{t}=a+\mathbf{y}_{0,t}^{1}$. The Jacobi process
$y_{t}=a+\mathbf{y}_{0,t}^{1}$. The Jacobi process ![]() $J=((J_{t}^{kl}=\frac{dy_{t}^{k}}{da^{l}})_{t\in [0,1]})_{1\leqslant k,l\leqslant n}$ and its inverse
$J=((J_{t}^{kl}=\frac{dy_{t}^{k}}{da^{l}})_{t\in [0,1]})_{1\leqslant k,l\leqslant n}$ and its inverse ![]() $K=(K^{kl})_{1\leqslant k,l\leqslant n}$ exist and satisfy
$K=(K^{kl})_{1\leqslant k,l\leqslant n}$ exist and satisfy
Here, ![]() $I$ stands for the identity matrix with size
$I$ stands for the identity matrix with size ![]() $n$. It is well known that the system of RDEs (3.4)–(3.6) is globally well-posed. In particular, the map
$n$. It is well known that the system of RDEs (3.4)–(3.6) is globally well-posed. In particular, the map ![]() $\mathbf{x}\mapsto (\mathbf{y},\mathbf{J},\mathbf{K})$ is continuous.
$\mathbf{x}\mapsto (\mathbf{y},\mathbf{J},\mathbf{K})$ is continuous.
Here, we make a remark on continuity of the solution map. Let ![]() $\unicode[STIX]{x1D706}$ be a one-dimensional path defined by
$\unicode[STIX]{x1D706}$ be a one-dimensional path defined by ![]() $\unicode[STIX]{x1D706}_{t}=t$. The solution map
$\unicode[STIX]{x1D706}_{t}=t$. The solution map ![]() $\mathbf{x}\mapsto (\mathbf{y},\mathbf{J},\mathbf{K})$ is continuous on
$\mathbf{x}\mapsto (\mathbf{y},\mathbf{J},\mathbf{K})$ is continuous on ![]() $G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+1})$ as stated above. In addition,
$G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+1})$ as stated above. In addition, ![]() $G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$ is embedded in
$G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$ is embedded in ![]() $G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+1})$ continuously. Hence, the composition
$G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+1})$ continuously. Hence, the composition ![]() $(\mathbf{x},c\unicode[STIX]{x1D706})\mapsto (\mathbf{x},c\boldsymbol{\unicode[STIX]{x1D706}})\mapsto (\mathbf{y},\mathbf{J},\mathbf{K})$ of the two maps is continuous on
$(\mathbf{x},c\unicode[STIX]{x1D706})\mapsto (\mathbf{x},c\boldsymbol{\unicode[STIX]{x1D706}})\mapsto (\mathbf{y},\mathbf{J},\mathbf{K})$ of the two maps is continuous on ![]() $G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$. This continuity plays an important role in §§ 6.1 and 5.3, in which we will use results on large deviation for fractional Brownian rough path.
$G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$. This continuity plays an important role in §§ 6.1 and 5.3, in which we will use results on large deviation for fractional Brownian rough path.
3.2 RDEs driven by fBm
In this paper, we consider the case ![]() $x=(w,\unicode[STIX]{x1D706})$, where
$x=(w,\unicode[STIX]{x1D706})$, where ![]() $w$ is an fBm with the Hurst parameter
$w$ is an fBm with the Hurst parameter ![]() $1/4<H\leqslant 1/2$ and
$1/4<H\leqslant 1/2$ and ![]() $\unicode[STIX]{x1D706}$ is a one-dimensional path defined by
$\unicode[STIX]{x1D706}$ is a one-dimensional path defined by ![]() $\unicode[STIX]{x1D706}_{t}=t$. Let
$\unicode[STIX]{x1D706}_{t}=t$. Let ![]() $p$ be larger than but sufficiently close to
$p$ be larger than but sufficiently close to ![]() $1/H$. Since
$1/H$. Since ![]() $w$ admits a canonical lift
$w$ admits a canonical lift ![]() $\mathbf{w}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ (see [Reference Coutin and QianCQ02]), we can deal with (2.1) in the framework of rough path analysis and obtain
$\mathbf{w}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ (see [Reference Coutin and QianCQ02]), we can deal with (2.1) in the framework of rough path analysis and obtain ![]() $\mathbf{y}=\unicode[STIX]{x1D6F7}(\mathbf{w},\boldsymbol{\unicode[STIX]{x1D706}})$. Next we introduce a scaled (and shifted) RDE of (2.1). For every
$\mathbf{y}=\unicode[STIX]{x1D6F7}(\mathbf{w},\boldsymbol{\unicode[STIX]{x1D706}})$. Next we introduce a scaled (and shifted) RDE of (2.1). For every ![]() $0<\unicode[STIX]{x1D716}<1$ and
$0<\unicode[STIX]{x1D716}<1$ and ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}$, we consider a scaled RDE
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}$, we consider a scaled RDE
and a scaled–shifted RDE
The solutions are respectively given by
It is known that the processes ![]() $(y_{t}^{\unicode[STIX]{x1D716}})$ and
$(y_{t}^{\unicode[STIX]{x1D716}})$ and ![]() $(y_{\unicode[STIX]{x1D716}^{1/H}t})$ have the same law. We denote the Jacobi processes and its inverses of
$(y_{\unicode[STIX]{x1D716}^{1/H}t})$ have the same law. We denote the Jacobi processes and its inverses of ![]() $y^{\unicode[STIX]{x1D716}}$ and
$y^{\unicode[STIX]{x1D716}}$ and ![]() ${\tilde{y}}^{\unicode[STIX]{x1D716}}$ by
${\tilde{y}}^{\unicode[STIX]{x1D716}}$ by ![]() $J^{\unicode[STIX]{x1D716}}$,
$J^{\unicode[STIX]{x1D716}}$, ![]() $K^{\unicode[STIX]{x1D716}}$,
$K^{\unicode[STIX]{x1D716}}$, ![]() $\tilde{J}^{\unicode[STIX]{x1D716}}$ and
$\tilde{J}^{\unicode[STIX]{x1D716}}$ and ![]() $\tilde{K}^{\unicode[STIX]{x1D716}}$. (In the next subsection, a brief summary of the Cameron–Martin space
$\tilde{K}^{\unicode[STIX]{x1D716}}$. (In the next subsection, a brief summary of the Cameron–Martin space ![]() $\mathfrak{H}$ and the Young translation by
$\mathfrak{H}$ and the Young translation by ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ will be given.)
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ will be given.)
We remark that everything in this subsection still holds if ![]() $p$-variation topology is replaced by
$p$-variation topology is replaced by ![]() $1/p$-Hölder topology. See [Reference Friz and VictoirFV10, Reference Friz and VictoirFV06].
$1/p$-Hölder topology. See [Reference Friz and VictoirFV10, Reference Friz and VictoirFV06].
3.3 The Cameron–Martin space and its isometric space
Next we introduce the Cameron–Martin space ![]() $\mathfrak{H}$ associated to a
$\mathfrak{H}$ associated to a ![]() $d$-dimensional fBm on the time interval
$d$-dimensional fBm on the time interval ![]() $[0,1]$. Let
$[0,1]$. Let ![]() $\mathfrak{E}_{1}$ be the linear span of
$\mathfrak{E}_{1}$ be the linear span of ![]() $\{R(t,\bullet )\}_{t\in [0,1]}$ and define the inner product
$\{R(t,\bullet )\}_{t\in [0,1]}$ and define the inner product
The Cameron–Martin space ![]() $\mathfrak{H}$ associated to a
$\mathfrak{H}$ associated to a ![]() $d$-dimensional fBm is given by the completion of
$d$-dimensional fBm is given by the completion of ![]() $\mathfrak{E}=\mathfrak{E}_{1}^{d}$ with respect to the norm
$\mathfrak{E}=\mathfrak{E}_{1}^{d}$ with respect to the norm ![]() $\Vert \bullet \Vert _{\mathfrak{H}}=\langle \bullet ,\bullet \rangle _{\mathfrak{H}}$, where
$\Vert \bullet \Vert _{\mathfrak{H}}=\langle \bullet ,\bullet \rangle _{\mathfrak{H}}$, where ![]() $\langle f,g\rangle _{\mathfrak{H}}=\sum _{i=1}^{d}\langle f^{i},g^{i}\rangle _{\mathfrak{E}_{1}}$ for
$\langle f,g\rangle _{\mathfrak{H}}=\sum _{i=1}^{d}\langle f^{i},g^{i}\rangle _{\mathfrak{E}_{1}}$ for ![]() $f=(f^{1},\ldots ,f^{d})^{\top }$,
$f=(f^{1},\ldots ,f^{d})^{\top }$, ![]() $g=(g^{1},\ldots ,g^{d})^{\top }\in \mathfrak{E}$. Note that
$g=(g^{1},\ldots ,g^{d})^{\top }\in \mathfrak{E}$. Note that ![]() $\mathfrak{H}$ is unitarily isometric to the first Wiener chaos
$\mathfrak{H}$ is unitarily isometric to the first Wiener chaos ![]() ${\mathcal{C}}_{1}$, which is the Hilbert space defined by the
${\mathcal{C}}_{1}$, which is the Hilbert space defined by the ![]() $\Vert \bullet \Vert _{L^{2}(\unicode[STIX]{x1D6FA};\mathbf{R})}$-completion of the linear span of
$\Vert \bullet \Vert _{L^{2}(\unicode[STIX]{x1D6FA};\mathbf{R})}$-completion of the linear span of ![]() $(w_{t})_{t\in [0,1]}$. From [Reference Friz and VictoirFV06, Corollary 1], we see the continuous embedding
$(w_{t})_{t\in [0,1]}$. From [Reference Friz and VictoirFV06, Corollary 1], we see the continuous embedding ![]() $\mathfrak{H}{\hookrightarrow}C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ for
$\mathfrak{H}{\hookrightarrow}C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ for ![]() $(H+1/2)^{-1}<q<2$. According to [Reference Friz, Gess, Gulisashvili and RiedelFGGR16], the embedding holds for
$(H+1/2)^{-1}<q<2$. According to [Reference Friz, Gess, Gulisashvili and RiedelFGGR16], the embedding holds for ![]() $q=(H+1/2)^{-1}$. (Note that if
$q=(H+1/2)^{-1}$. (Note that if ![]() $p>1/H$ is sufficiently close to
$p>1/H$ is sufficiently close to ![]() $1/H$, then
$1/H$, then ![]() $1/p+1/q>1$ holds since
$1/p+1/q>1$ holds since ![]() $H>1/4$. Therefore, the Young translation by
$H>1/4$. Therefore, the Young translation by ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ is well-defined on
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ is well-defined on ![]() $G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$.)
$G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$.)
Next we introduce another Hilbert space ![]() $\tilde{\mathfrak{H}}$, which is isometric to
$\tilde{\mathfrak{H}}$, which is isometric to ![]() $\mathfrak{H}$. Let
$\mathfrak{H}$. Let ![]() $\tilde{\mathfrak{E}}_{1}$ be the linear span of
$\tilde{\mathfrak{E}}_{1}$ be the linear span of ![]() $\{{\mathtt{1}_{[0,t]}\}}_{t\in [0,1]}$ and define an inner product by
$\{{\mathtt{1}_{[0,t]}\}}_{t\in [0,1]}$ and define an inner product by
We define ![]() $\tilde{\mathfrak{H}}$ by the completion of
$\tilde{\mathfrak{H}}$ by the completion of ![]() $\tilde{\mathfrak{E}}=\tilde{\mathfrak{E}}_{1}^{d}$ with respect to the norm
$\tilde{\mathfrak{E}}=\tilde{\mathfrak{E}}_{1}^{d}$ with respect to the norm ![]() $\Vert \bullet \Vert _{\tilde{\mathfrak{H}}}=\langle \bullet ,\bullet \rangle _{\tilde{\mathfrak{H}}}$, where
$\Vert \bullet \Vert _{\tilde{\mathfrak{H}}}=\langle \bullet ,\bullet \rangle _{\tilde{\mathfrak{H}}}$, where ![]() $\langle f,g\rangle _{\tilde{\mathfrak{H}}}=\sum _{i=1}^{d}\langle f^{i},g^{i}\rangle _{\tilde{\mathfrak{E}}_{1}}$ for
$\langle f,g\rangle _{\tilde{\mathfrak{H}}}=\sum _{i=1}^{d}\langle f^{i},g^{i}\rangle _{\tilde{\mathfrak{E}}_{1}}$ for ![]() $f=(f^{1},\ldots ,f^{d})^{\top }$,
$f=(f^{1},\ldots ,f^{d})^{\top }$, ![]() $g=(g^{1},\ldots ,g^{d})^{\top }\in \tilde{\mathfrak{E}}$. Note that
$g=(g^{1},\ldots ,g^{d})^{\top }\in \tilde{\mathfrak{E}}$. Note that ![]() $\tilde{\mathfrak{H}}=I_{1-}^{1/2-H}(L^{2}([0,1];\mathbf{R}^{d}))$ from [Reference Decreusefond and ÜstünelDÜ99] and [Reference NualartNua06, p. 284]. Here,
$\tilde{\mathfrak{H}}=I_{1-}^{1/2-H}(L^{2}([0,1];\mathbf{R}^{d}))$ from [Reference Decreusefond and ÜstünelDÜ99] and [Reference NualartNua06, p. 284]. Here, ![]() $I_{1-}^{1/2-H}$ denotes the fractional integral of order
$I_{1-}^{1/2-H}$ denotes the fractional integral of order ![]() $1/2-H$. Hence, the inclusions
$1/2-H$. Hence, the inclusions ![]() $C^{(H-\unicode[STIX]{x1D6FF})\text{-}\text{Hol}}([0,1];\mathbf{R}^{d})\subset \tilde{\mathfrak{H}}\subset L^{2}([0,1];\mathbf{R}^{d})$ hold for
$C^{(H-\unicode[STIX]{x1D6FF})\text{-}\text{Hol}}([0,1];\mathbf{R}^{d})\subset \tilde{\mathfrak{H}}\subset L^{2}([0,1];\mathbf{R}^{d})$ hold for ![]() $0<\unicode[STIX]{x1D6FF}<2(H-1/4)$. The linear map
$0<\unicode[STIX]{x1D6FF}<2(H-1/4)$. The linear map ![]() ${\mathcal{R}}=({\mathcal{R}}^{1},\ldots ,{\mathcal{R}}^{d})^{\top }:\tilde{{\mathcal{E}}}\rightarrow \mathfrak{H}$ defined by
${\mathcal{R}}=({\mathcal{R}}^{1},\ldots ,{\mathcal{R}}^{d})^{\top }:\tilde{{\mathcal{E}}}\rightarrow \mathfrak{H}$ defined by ![]() ${\mathcal{R}}^{i}\mathtt{1}_{[0,t]}=R(t,\bullet )$ extends to a unitary isometry from
${\mathcal{R}}^{i}\mathtt{1}_{[0,t]}=R(t,\bullet )$ extends to a unitary isometry from ![]() $\tilde{\mathfrak{H}}$ to
$\tilde{\mathfrak{H}}$ to ![]() $\mathfrak{H}$.
$\mathfrak{H}$.
Remark 3.1. Under the condition ![]() $1/4<H\leqslant 1/2$, we can choose two numbers
$1/4<H\leqslant 1/2$, we can choose two numbers ![]() $1/H<p<1+\lfloor 1/H\rfloor$ and
$1/H<p<1+\lfloor 1/H\rfloor$ and ![]() $(H+1/2)^{-1}<q<2$ with
$(H+1/2)^{-1}<q<2$ with ![]() $1/p+1/q>1$. For every
$1/p+1/q>1$. For every ![]() $A=(A_{1},\ldots ,A_{d})\in C^{p\text{-}\text{var}}([0,1];\mathbf{R}^{d})$, we can define
$A=(A_{1},\ldots ,A_{d})\in C^{p\text{-}\text{var}}([0,1];\mathbf{R}^{d})$, we can define ![]() $\unicode[STIX]{x1D719}_{A}\in \mathfrak{H}^{\ast }$ by
$\unicode[STIX]{x1D719}_{A}\in \mathfrak{H}^{\ast }$ by
where the right-hand side is the Young integral since ![]() $h\in \mathfrak{H}\subset C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$. By using the isometry between
$h\in \mathfrak{H}\subset C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$. By using the isometry between ![]() $\mathfrak{H}^{\ast }$ and
$\mathfrak{H}^{\ast }$ and ![]() ${\mathcal{C}}_{1}$, the definition of
${\mathcal{C}}_{1}$, the definition of ![]() $\tilde{\mathfrak{H}}$ and the inequality
$\tilde{\mathfrak{H}}$ and the inequality ![]() $\Vert \bullet \Vert _{L^{2}([0,1];\mathbf{R}^{d})}\leqslant c\Vert \bullet \Vert _{\tilde{\mathfrak{H}}}$ for some positive constant
$\Vert \bullet \Vert _{L^{2}([0,1];\mathbf{R}^{d})}\leqslant c\Vert \bullet \Vert _{\tilde{\mathfrak{H}}}$ for some positive constant ![]() $c$, we have
$c$, we have
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D719}_{A}\Vert _{\mathfrak{H}^{\ast }}^{2}=\mathbf{E}\Bigg[\Bigg(\mathop{\sum }_{i=1}^{d}\int _{0}^{1}A_{i}(s)\,dw_{s}^{i}\Bigg)^{2}\Bigg]=\Vert A\Vert _{\tilde{\mathfrak{ H}}}^{2}\geqslant c^{-2}\Vert A\Vert _{L^{2}([0,1];\mathbf{R}^{d})}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D719}_{A}\Vert _{\mathfrak{H}^{\ast }}^{2}=\mathbf{E}\Bigg[\Bigg(\mathop{\sum }_{i=1}^{d}\int _{0}^{1}A_{i}(s)\,dw_{s}^{i}\Bigg)^{2}\Bigg]=\Vert A\Vert _{\tilde{\mathfrak{ H}}}^{2}\geqslant c^{-2}\Vert A\Vert _{L^{2}([0,1];\mathbf{R}^{d})}^{2}.\end{eqnarray}$$3.4 Large deviations
Let ![]() $(1+\lfloor 1/H\rfloor )^{-1}<\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FD}<H$ and
$(1+\lfloor 1/H\rfloor )^{-1}<\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FD}<H$ and ![]() $m\in \mathbf{N}_{+}$ satisfy
$m\in \mathbf{N}_{+}$ satisfy ![]() $\unicode[STIX]{x1D6FC}-1/m>0$. Recall that fBm
$\unicode[STIX]{x1D6FC}-1/m>0$. Recall that fBm ![]() $(w_{t})$ admits a natural lift almost surely via the dyadic piecewise linear approximation and the lift
$(w_{t})$ admits a natural lift almost surely via the dyadic piecewise linear approximation and the lift ![]() $\mathbf{w}$ is a random variable taking values in
$\mathbf{w}$ is a random variable taking values in ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FD}}^{\text{H}}(\mathbf{R}^{d})$. For
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FD}}^{\text{H}}(\mathbf{R}^{d})$. For ![]() $0<\unicode[STIX]{x1D716}<1$, the law of
$0<\unicode[STIX]{x1D716}<1$, the law of ![]() $\unicode[STIX]{x1D716}\mathbf{w}$ on this space is denoted by
$\unicode[STIX]{x1D716}\mathbf{w}$ on this space is denoted by ![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{H}$. Note that the lift of Cameron–Martin space
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}^{H}$. Note that the lift of Cameron–Martin space ![]() $\mathfrak{H}$ is contained in
$\mathfrak{H}$ is contained in ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FD}}^{\text{H}}(\mathbf{R}^{d})$. Moreover, as
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FD}}^{\text{H}}(\mathbf{R}^{d})$. Moreover, as ![]() $\unicode[STIX]{x1D716}{\searrow}0$, Schilder-type large deviations hold for
$\unicode[STIX]{x1D716}{\searrow}0$, Schilder-type large deviations hold for ![]() $\{{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}\}}_{\unicode[STIX]{x1D716}>0}$. (See [Reference Friz and VictoirFV07] and [Reference Friz and VictoirFV10, Sections 13.6 and 15.7].) Because of the Besov–Hölder embedding mentioned above, these properties also hold in
$\{{\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}\}}_{\unicode[STIX]{x1D716}>0}$. (See [Reference Friz and VictoirFV07] and [Reference Friz and VictoirFV10, Sections 13.6 and 15.7].) Because of the Besov–Hölder embedding mentioned above, these properties also hold in ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})$. As usual, the good rate function
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})$. As usual, the good rate function ![]() ${\mathcal{I}}$ is given as follows:
${\mathcal{I}}$ is given as follows: ![]() ${\mathcal{I}}(\mathbf{x})=\Vert h\Vert _{\mathfrak{H}}^{2}/2$ if
${\mathcal{I}}(\mathbf{x})=\Vert h\Vert _{\mathfrak{H}}^{2}/2$ if ![]() $\mathbf{x}$ is the lift of some
$\mathbf{x}$ is the lift of some ![]() $h\in \mathfrak{H}$ and
$h\in \mathfrak{H}$ and ![]() ${\mathcal{I}}(\mathbf{x})=\infty$ if otherwise.
${\mathcal{I}}(\mathbf{x})=\infty$ if otherwise.
Next, set ![]() $\hat{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}\otimes \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D716}^{1/H}\unicode[STIX]{x1D706}}$, where
$\hat{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D716}}\otimes \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D716}^{1/H}\unicode[STIX]{x1D706}}$, where ![]() $\unicode[STIX]{x1D706}$ is a one-dimensional path defined by
$\unicode[STIX]{x1D706}$ is a one-dimensional path defined by ![]() $\unicode[STIX]{x1D706}_{t}=t$ and
$\unicode[STIX]{x1D706}_{t}=t$ and ![]() $\otimes$ stands for the product of probability measures. This measure is supported on
$\otimes$ stands for the product of probability measures. This measure is supported on ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$. The Young pairing map
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$. The Young pairing map ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle \rightarrow G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d+1})$ is continuous. The law of this map under
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle \rightarrow G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},m}^{\text{B}}(\mathbf{R}^{d+1})$ is continuous. The law of this map under ![]() $\hat{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D716}}$ is the law of
$\hat{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D716}}$ is the law of ![]() $(\unicode[STIX]{x1D716}\mathbf{w},\unicode[STIX]{x1D716}^{1/H}\boldsymbol{\unicode[STIX]{x1D706}})$, the Young pairing of
$(\unicode[STIX]{x1D716}\mathbf{w},\unicode[STIX]{x1D716}^{1/H}\boldsymbol{\unicode[STIX]{x1D706}})$, the Young pairing of ![]() $\unicode[STIX]{x1D716}\mathbf{w}$ and
$\unicode[STIX]{x1D716}\mathbf{w}$ and ![]() $\unicode[STIX]{x1D716}^{1/H}\unicode[STIX]{x1D706}$. Define
$\unicode[STIX]{x1D716}^{1/H}\unicode[STIX]{x1D706}$. Define ![]() $\hat{{\mathcal{I}}}(\mathbf{x},l)=\Vert h\Vert _{\mathfrak{H}}^{2}/2$ if
$\hat{{\mathcal{I}}}(\mathbf{x},l)=\Vert h\Vert _{\mathfrak{H}}^{2}/2$ if ![]() $\mathbf{x}$ is the lift of some
$\mathbf{x}$ is the lift of some ![]() $h\in \mathfrak{H}$ and
$h\in \mathfrak{H}$ and ![]() $l_{t}\equiv 0$ and define
$l_{t}\equiv 0$ and define ![]() $\hat{{\mathcal{I}}}(\mathbf{x},l)=\infty$ if otherwise. Here,
$\hat{{\mathcal{I}}}(\mathbf{x},l)=\infty$ if otherwise. Here, ![]() $l$ is a one-dimensional path. We can easily show that
$l$ is a one-dimensional path. We can easily show that ![]() ${\{\hat{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D716}}\}}_{\unicode[STIX]{x1D716}>0}$ also satisfies a large deviation principle as
${\{\hat{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D716}}\}}_{\unicode[STIX]{x1D716}>0}$ also satisfies a large deviation principle as ![]() $\unicode[STIX]{x1D716}{\searrow}0$ with a good rate function
$\unicode[STIX]{x1D716}{\searrow}0$ with a good rate function ![]() $\hat{{\mathcal{I}}}$. We will use this in Lemma 6.1 to show that we may localize on a neighborhood of the minimizer
$\hat{{\mathcal{I}}}$. We will use this in Lemma 6.1 to show that we may localize on a neighborhood of the minimizer ![]() $\bar{\unicode[STIX]{x1D6FE}}$ in order to obtain the asymptotic expansion. (The existence of
$\bar{\unicode[STIX]{x1D6FE}}$ in order to obtain the asymptotic expansion. (The existence of ![]() $\bar{\unicode[STIX]{x1D6FE}}$ is assumed in (A2).)
$\bar{\unicode[STIX]{x1D6FE}}$ is assumed in (A2).)
3.5 The Young translation
In this subsection, we show that the Young translation is well-defined and continuous. In this subsection, we fix ![]() $1/4<H\leqslant 1/2$. Let
$1/4<H\leqslant 1/2$. Let ![]() $(1+\lfloor 1/H\rfloor )^{-1}<\unicode[STIX]{x1D6FC}<H$ and choose
$(1+\lfloor 1/H\rfloor )^{-1}<\unicode[STIX]{x1D6FC}<H$ and choose ![]() $m\in \mathbf{N}_{+}$ such that
$m\in \mathbf{N}_{+}$ such that ![]() $H-\unicode[STIX]{x1D6FC}>2/m$. Set
$H-\unicode[STIX]{x1D6FC}>2/m$. Set ![]() $p=1/\unicode[STIX]{x1D6FC}$ and
$p=1/\unicode[STIX]{x1D6FC}$ and ![]() $q=(H+1/2-1/m)^{-1}$. Then we have
$q=(H+1/2-1/m)^{-1}$. Then we have ![]() $1/p+1/q>1$ and
$1/p+1/q>1$ and ![]() $1/q-1/2-\unicode[STIX]{x1D6FC}>1/m$. Since
$1/q-1/2-\unicode[STIX]{x1D6FC}>1/m$. Since ![]() $(H+1/2)^{-1}\leqslant q<2$, [Reference Friz and VictoirFV06, Corollary 1] implies
$(H+1/2)^{-1}\leqslant q<2$, [Reference Friz and VictoirFV06, Corollary 1] implies
Throughout this subsection, ![]() $c$ denotes a positive constant and may change from line to line.
$c$ denotes a positive constant and may change from line to line.
We define the Young translation ![]() $\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}^{1},\ldots ,\unicode[STIX]{x1D70F}^{\lfloor 1/\unicode[STIX]{x1D6FC}\rfloor })$ from
$\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70F}^{1},\ldots ,\unicode[STIX]{x1D70F}^{\lfloor 1/\unicode[STIX]{x1D6FC}\rfloor })$ from ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})\times \mathfrak{H}$ to
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})\times \mathfrak{H}$ to ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})$; for
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})$; for ![]() $\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})$ and
$\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})$ and ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}$, define
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}$, define
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FE}}(\mathbf{x})_{s,t}^{1} & = & \displaystyle \mathbf{x}_{s,t}^{1}+\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,t}^{1},\nonumber\\ \displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FE}}(\mathbf{x})_{s,t}^{2} & = & \displaystyle \mathbf{x}_{s,t}^{2}+A_{s,t}^{1}+A_{s,t}^{2}+\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,t}^{2},\nonumber\\ \displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FE}}(\mathbf{x})_{s,t}^{3} & = & \displaystyle \mathbf{x}_{s,t}^{3}+B_{s,t}^{1}+B_{s,t}^{2}+B_{s,t}^{3}+C_{s,t}^{1}+C_{s,t}^{2}+C_{s,t}^{3}+\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,t}^{3},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FE}}(\mathbf{x})_{s,t}^{1} & = & \displaystyle \mathbf{x}_{s,t}^{1}+\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,t}^{1},\nonumber\\ \displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FE}}(\mathbf{x})_{s,t}^{2} & = & \displaystyle \mathbf{x}_{s,t}^{2}+A_{s,t}^{1}+A_{s,t}^{2}+\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,t}^{2},\nonumber\\ \displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FE}}(\mathbf{x})_{s,t}^{3} & = & \displaystyle \mathbf{x}_{s,t}^{3}+B_{s,t}^{1}+B_{s,t}^{2}+B_{s,t}^{3}+C_{s,t}^{1}+C_{s,t}^{2}+C_{s,t}^{3}+\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,t}^{3},\nonumber\end{eqnarray}$$where
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \boldsymbol{\unicode[STIX]{x1D6FE}}_{s,t}^{1}=\unicode[STIX]{x1D6FE}_{t}-\unicode[STIX]{x1D6FE}_{s},\quad & \displaystyle \boldsymbol{\unicode[STIX]{x1D6FE}}_{s,t}^{i}=\int _{s}^{t}\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,u}^{i-1}\otimes d\unicode[STIX]{x1D6FE}_{u}\quad (i=2,3),\\ \displaystyle A_{s,t}^{1}=\int _{s}^{t}\mathbf{x}_{s,u}^{1}\otimes d\unicode[STIX]{x1D6FE}_{u},\quad & \displaystyle A_{s,t}^{2}=\int _{s}^{t}\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,u}^{1}\otimes dx_{u},\\ \displaystyle B_{s,t}^{1}=\int _{s}^{t}\mathbf{x}_{s,u}^{2}\otimes d\unicode[STIX]{x1D6FE}_{u},\quad & \displaystyle B_{s,t}^{2}=\int _{s}^{t}\int _{s}^{v}\mathbf{x}_{s,u}^{1}\otimes d\unicode[STIX]{x1D6FE}_{u}\otimes dx_{v},\\ \displaystyle B_{s,t}^{3}=-\int _{s}^{t}\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,u}^{1}\otimes d\mathbf{x}_{u,t}^{2},\quad & \displaystyle C_{s,t}^{1}=-\int _{s}^{t}\mathbf{x}_{s,u}^{1}\otimes d\boldsymbol{\unicode[STIX]{x1D6FE}}_{u,t}^{2},\\ \displaystyle C_{s,t}^{2}=\int _{s}^{t}\int _{s}^{v}\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,u}^{1}\otimes dx_{u}\otimes d\unicode[STIX]{x1D6FE}_{v},\quad & \displaystyle C_{s,t}^{3}=\int _{s}^{t}\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,u}^{2}\otimes dx_{u}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \boldsymbol{\unicode[STIX]{x1D6FE}}_{s,t}^{1}=\unicode[STIX]{x1D6FE}_{t}-\unicode[STIX]{x1D6FE}_{s},\quad & \displaystyle \boldsymbol{\unicode[STIX]{x1D6FE}}_{s,t}^{i}=\int _{s}^{t}\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,u}^{i-1}\otimes d\unicode[STIX]{x1D6FE}_{u}\quad (i=2,3),\\ \displaystyle A_{s,t}^{1}=\int _{s}^{t}\mathbf{x}_{s,u}^{1}\otimes d\unicode[STIX]{x1D6FE}_{u},\quad & \displaystyle A_{s,t}^{2}=\int _{s}^{t}\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,u}^{1}\otimes dx_{u},\\ \displaystyle B_{s,t}^{1}=\int _{s}^{t}\mathbf{x}_{s,u}^{2}\otimes d\unicode[STIX]{x1D6FE}_{u},\quad & \displaystyle B_{s,t}^{2}=\int _{s}^{t}\int _{s}^{v}\mathbf{x}_{s,u}^{1}\otimes d\unicode[STIX]{x1D6FE}_{u}\otimes dx_{v},\\ \displaystyle B_{s,t}^{3}=-\int _{s}^{t}\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,u}^{1}\otimes d\mathbf{x}_{u,t}^{2},\quad & \displaystyle C_{s,t}^{1}=-\int _{s}^{t}\mathbf{x}_{s,u}^{1}\otimes d\boldsymbol{\unicode[STIX]{x1D6FE}}_{u,t}^{2},\\ \displaystyle C_{s,t}^{2}=\int _{s}^{t}\int _{s}^{v}\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,u}^{1}\otimes dx_{u}\otimes d\unicode[STIX]{x1D6FE}_{v},\quad & \displaystyle C_{s,t}^{3}=\int _{s}^{t}\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,u}^{2}\otimes dx_{u}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$ We should understand the integrals in the Young sense since ![]() $1/p+1/q>1$. At first glance,
$1/p+1/q>1$. At first glance, ![]() $B^{3}$ and
$B^{3}$ and ![]() $C^{1}$ look strange. However, if
$C^{1}$ look strange. However, if ![]() $x$ and
$x$ and ![]() $\unicode[STIX]{x1D6FE}$ are smooth and
$\unicode[STIX]{x1D6FE}$ are smooth and ![]() $\mathbf{x}$ is the natural lift of
$\mathbf{x}$ is the natural lift of ![]() $x$, we have
$x$, we have
In the first equality, we used ![]() $\frac{d\mathbf{x}_{u,t}^{2}}{du}=-\frac{dx_{u}}{du}\otimes (x_{t}-x_{u})$. Since a similar equality for
$\frac{d\mathbf{x}_{u,t}^{2}}{du}=-\frac{dx_{u}}{du}\otimes (x_{t}-x_{u})$. Since a similar equality for ![]() $C_{s,t}^{3}$ holds, we see
$C_{s,t}^{3}$ holds, we see ![]() $B^{3}$ and
$B^{3}$ and ![]() $C^{1}$ are defined appropriately. Then we see the next proposition.
$C^{1}$ are defined appropriately. Then we see the next proposition.
Proposition 3.2. Let ![]() $H$,
$H$, ![]() $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and ![]() $m$ be as above. Then, the Young translation
$m$ be as above. Then, the Young translation ![]() $\unicode[STIX]{x1D70F}:G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})\times \mathfrak{H}\rightarrow G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})$ is well-defined and continuous. Moreover, restricted to every bounded subset of the domain,
$\unicode[STIX]{x1D70F}:G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})\times \mathfrak{H}\rightarrow G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})$ is well-defined and continuous. Moreover, restricted to every bounded subset of the domain, ![]() $\unicode[STIX]{x1D70F}$ is Lipschitz continuous.
$\unicode[STIX]{x1D70F}$ is Lipschitz continuous.
Proof. Let ![]() $0\leqslant s\leqslant u<v\leqslant t\leqslant 1$. Recall that
$0\leqslant s\leqslant u<v\leqslant t\leqslant 1$. Recall that ![]() $\mathbf{x}_{s,\cdot }^{i}$ and
$\mathbf{x}_{s,\cdot }^{i}$ and ![]() $\mathbf{x}_{\cdot ,t}^{i}$ have finite
$\mathbf{x}_{\cdot ,t}^{i}$ have finite ![]() $p$-variation and that
$p$-variation and that ![]() $\Vert \mathbf{x}_{s,\cdot }^{i}\Vert _{p\text{-}\text{var};[u,v]}$ and
$\Vert \mathbf{x}_{s,\cdot }^{i}\Vert _{p\text{-}\text{var};[u,v]}$ and ![]() $\Vert \mathbf{x}_{\cdot ,t}^{i}\Vert _{p\text{-}\text{var};[u,v]}$ are bounded above by
$\Vert \mathbf{x}_{\cdot ,t}^{i}\Vert _{p\text{-}\text{var};[u,v]}$ are bounded above by ![]() $c\Vert \mathbf{x}\Vert _{p\text{-}\text{var};[s,t]}^{i-1}\Vert \mathbf{x}\Vert _{p\text{-}\text{var};[u,v]}$ for
$c\Vert \mathbf{x}\Vert _{p\text{-}\text{var};[s,t]}^{i-1}\Vert \mathbf{x}\Vert _{p\text{-}\text{var};[u,v]}$ for ![]() $i=1,2,3$.
$i=1,2,3$.
We show well-definedness of the map ![]() $\unicode[STIX]{x1D70F}$. Since
$\unicode[STIX]{x1D70F}$. Since ![]() $1/q+1/q>1$, we can define
$1/q+1/q>1$, we can define ![]() $\boldsymbol{\unicode[STIX]{x1D6FE}}^{2}$ in the Young sense and see that it is of finite
$\boldsymbol{\unicode[STIX]{x1D6FE}}^{2}$ in the Young sense and see that it is of finite ![]() $q$-variation and satisfies
$q$-variation and satisfies
In this estimate, we used [Reference Friz and VictoirFV10, Theorem 6.8]. By the same reason, ![]() $A^{1}$ and
$A^{1}$ and ![]() $A^{2}$ are well-defined in the Young sense and they are of finite
$A^{2}$ are well-defined in the Young sense and they are of finite ![]() $q$- and
$q$- and ![]() $p$-variation, respectively; more precisely, it holds that
$p$-variation, respectively; more precisely, it holds that
Note that ![]() $B_{s,t}^{2}=\int _{s}^{t}A_{s,r}^{1}\otimes dx_{r}$ and
$B_{s,t}^{2}=\int _{s}^{t}A_{s,r}^{1}\otimes dx_{r}$ and ![]() $C_{s,t}^{2}=\int _{s}^{t}A_{s,r}^{2}\otimes d\unicode[STIX]{x1D6FE}_{r}$ can be defined and
$C_{s,t}^{2}=\int _{s}^{t}A_{s,r}^{2}\otimes d\unicode[STIX]{x1D6FE}_{r}$ can be defined and
By the same reason, we see that ![]() $B_{s,t}^{1}$,
$B_{s,t}^{1}$, ![]() $B_{s,t}^{3}$,
$B_{s,t}^{3}$, ![]() $C_{s,t}^{1}$, and
$C_{s,t}^{1}$, and ![]() $C_{s,t}^{3}$ are well-defined and
$C_{s,t}^{3}$ are well-defined and
 $$\begin{eqnarray}\displaystyle \Vert \boldsymbol{\unicode[STIX]{x1D6FE}}_{s,\cdot }^{3}\Vert _{q\text{-}\text{var};[u,v]} & {\leqslant} & \displaystyle c\Vert \boldsymbol{\unicode[STIX]{x1D6FE}}_{s,\cdot }^{2}\Vert _{q\text{-}\text{var};[s,t]}\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[u,v]},\nonumber\\ \displaystyle \Vert B_{s,\cdot }^{1}\Vert _{q\text{-}\text{var};[u,v]} & {\leqslant} & \displaystyle c\Vert \mathbf{x}_{s,\cdot }^{2}\Vert _{p\text{-}\text{var};[s,t]}\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[u,v]},\nonumber\\ \displaystyle \Vert B_{s,\cdot }^{3}\Vert _{p\text{-}\text{var};[u,v]} & {\leqslant} & \displaystyle c\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[s,t]}\Vert \mathbf{x}_{\cdot ,t}^{2}\Vert _{p\text{-}\text{var};[u,v]},\nonumber\\ \displaystyle \Vert C_{s,\cdot }^{1}\Vert _{q\text{-}\text{var};[u,v]} & {\leqslant} & \displaystyle c\Vert x\Vert _{p\text{-}\text{var};[s,t]}\Vert \boldsymbol{\unicode[STIX]{x1D6FE}}_{\cdot ,t}^{2}\Vert _{q\text{-}\text{var};[u,v]},\nonumber\\ \displaystyle \Vert C_{s,\cdot }^{3}\Vert _{p\text{-}\text{var};[u,v]} & {\leqslant} & \displaystyle c\Vert \boldsymbol{\unicode[STIX]{x1D6FE}}_{s,\cdot }^{2}\Vert _{q\text{-}\text{var};[s,t]}\Vert x\Vert _{p\text{-}\text{var};[u,v]}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \boldsymbol{\unicode[STIX]{x1D6FE}}_{s,\cdot }^{3}\Vert _{q\text{-}\text{var};[u,v]} & {\leqslant} & \displaystyle c\Vert \boldsymbol{\unicode[STIX]{x1D6FE}}_{s,\cdot }^{2}\Vert _{q\text{-}\text{var};[s,t]}\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[u,v]},\nonumber\\ \displaystyle \Vert B_{s,\cdot }^{1}\Vert _{q\text{-}\text{var};[u,v]} & {\leqslant} & \displaystyle c\Vert \mathbf{x}_{s,\cdot }^{2}\Vert _{p\text{-}\text{var};[s,t]}\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[u,v]},\nonumber\\ \displaystyle \Vert B_{s,\cdot }^{3}\Vert _{p\text{-}\text{var};[u,v]} & {\leqslant} & \displaystyle c\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[s,t]}\Vert \mathbf{x}_{\cdot ,t}^{2}\Vert _{p\text{-}\text{var};[u,v]},\nonumber\\ \displaystyle \Vert C_{s,\cdot }^{1}\Vert _{q\text{-}\text{var};[u,v]} & {\leqslant} & \displaystyle c\Vert x\Vert _{p\text{-}\text{var};[s,t]}\Vert \boldsymbol{\unicode[STIX]{x1D6FE}}_{\cdot ,t}^{2}\Vert _{q\text{-}\text{var};[u,v]},\nonumber\\ \displaystyle \Vert C_{s,\cdot }^{3}\Vert _{p\text{-}\text{var};[u,v]} & {\leqslant} & \displaystyle c\Vert \boldsymbol{\unicode[STIX]{x1D6FE}}_{s,\cdot }^{2}\Vert _{q\text{-}\text{var};[s,t]}\Vert x\Vert _{p\text{-}\text{var};[u,v]}.\nonumber\end{eqnarray}$$ By recalling upper bounds of ![]() $\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[u,v]}$,
$\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[u,v]}$, ![]() $\Vert \boldsymbol{\unicode[STIX]{x1D6FE}}_{s,\cdot }^{2}\Vert _{q\text{-}\text{var};[u,v]}$,
$\Vert \boldsymbol{\unicode[STIX]{x1D6FE}}_{s,\cdot }^{2}\Vert _{q\text{-}\text{var};[u,v]}$, ![]() $\Vert \boldsymbol{\unicode[STIX]{x1D6FE}}_{\cdot ,t}^{2}\Vert _{q\text{-}\text{var};[u,v]}$,
$\Vert \boldsymbol{\unicode[STIX]{x1D6FE}}_{\cdot ,t}^{2}\Vert _{q\text{-}\text{var};[u,v]}$, ![]() $\Vert x\Vert _{q\text{-}\text{var};[u,v]}$,
$\Vert x\Vert _{q\text{-}\text{var};[u,v]}$, ![]() $\Vert \mathbf{x}_{s,\cdot }^{2}\Vert _{q\text{-}\text{var};[u,v]}$, and
$\Vert \mathbf{x}_{s,\cdot }^{2}\Vert _{q\text{-}\text{var};[u,v]}$, and ![]() $\Vert \mathbf{x}_{\cdot ,t}^{2}\Vert _{q\text{-}\text{var};[u,v]}$, we have
$\Vert \mathbf{x}_{\cdot ,t}^{2}\Vert _{q\text{-}\text{var};[u,v]}$, we have
 $$\begin{eqnarray}\displaystyle |\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,t}^{2}| & {\leqslant} & \displaystyle c\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[s,t]}^{2}\leqslant c\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}(t-s)^{2(1/q-1/2)},\nonumber\\ \displaystyle |A_{s,t}^{1}|,|A_{s,t}^{2}| & {\leqslant} & \displaystyle c\Vert \mathbf{x}\Vert _{p\text{-}\text{var};[s,t]}\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[s,t]}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle c\Vert \mathbf{x}\Vert _{(\unicode[STIX]{x1D6FC},12m)\text{-}\text{Bes}}\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}\cdot (t-s)^{(\unicode[STIX]{x1D6FC}-1/12m)+(1/q-1/2)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\boldsymbol{\unicode[STIX]{x1D6FE}}_{s,t}^{2}| & {\leqslant} & \displaystyle c\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[s,t]}^{2}\leqslant c\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}(t-s)^{2(1/q-1/2)},\nonumber\\ \displaystyle |A_{s,t}^{1}|,|A_{s,t}^{2}| & {\leqslant} & \displaystyle c\Vert \mathbf{x}\Vert _{p\text{-}\text{var};[s,t]}\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[s,t]}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle c\Vert \mathbf{x}\Vert _{(\unicode[STIX]{x1D6FC},12m)\text{-}\text{Bes}}\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}\cdot (t-s)^{(\unicode[STIX]{x1D6FC}-1/12m)+(1/q-1/2)}.\nonumber\end{eqnarray}$$Here, we used (3.1). Moreover, we obtain
 $$\begin{eqnarray}\displaystyle |B_{s,t}^{1}|,|B_{s,t}^{2}|,|B_{s,t}^{3}| & {\leqslant} & \displaystyle c\Vert \mathbf{x}\Vert _{p\text{-}\text{var};[s,t]}^{2}\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[s,t]}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle c\Vert \mathbf{x}\Vert _{(\unicode[STIX]{x1D6FC},12m)\text{-}\text{Bes}}^{2}\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}\cdot (t-s)^{2(\unicode[STIX]{x1D6FC}-1/12m)+(1/q-1/2)},\nonumber\\ \displaystyle |C_{s,t}^{1}|,|C_{s,t}^{2}|,|C_{s,t}^{3}| & {\leqslant} & \displaystyle c\Vert \mathbf{x}\Vert _{p\text{-}\text{var};[s,t]}\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[s,t]}^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle c\Vert \mathbf{x}\Vert _{(\unicode[STIX]{x1D6FC},12m)\text{-}\text{Bes}}\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}\cdot (t-s)^{(\unicode[STIX]{x1D6FC}-1/12m)+2(1/q-1/2)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |B_{s,t}^{1}|,|B_{s,t}^{2}|,|B_{s,t}^{3}| & {\leqslant} & \displaystyle c\Vert \mathbf{x}\Vert _{p\text{-}\text{var};[s,t]}^{2}\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[s,t]}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle c\Vert \mathbf{x}\Vert _{(\unicode[STIX]{x1D6FC},12m)\text{-}\text{Bes}}^{2}\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}\cdot (t-s)^{2(\unicode[STIX]{x1D6FC}-1/12m)+(1/q-1/2)},\nonumber\\ \displaystyle |C_{s,t}^{1}|,|C_{s,t}^{2}|,|C_{s,t}^{3}| & {\leqslant} & \displaystyle c\Vert \mathbf{x}\Vert _{p\text{-}\text{var};[s,t]}\Vert \unicode[STIX]{x1D6FE}\Vert _{q\text{-}\text{var};[s,t]}^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle c\Vert \mathbf{x}\Vert _{(\unicode[STIX]{x1D6FC},12m)\text{-}\text{Bes}}\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}\cdot (t-s)^{(\unicode[STIX]{x1D6FC}-1/12m)+2(1/q-1/2)}.\nonumber\end{eqnarray}$$Note
 $$\begin{eqnarray}\displaystyle & \displaystyle \bigg(\unicode[STIX]{x1D6FC}-\frac{1}{12m}\bigg)+\bigg(\frac{1}{q}-\frac{1}{2}\bigg)=2\unicode[STIX]{x1D6FC}+\bigg(\frac{1}{q}-\frac{1}{2}-\unicode[STIX]{x1D6FC}-\frac{1}{12m}\bigg)>2\unicode[STIX]{x1D6FC}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle 2\bigg(\unicode[STIX]{x1D6FC}-\frac{1}{12m}\bigg)+\bigg(\frac{1}{q}-\frac{1}{2}\bigg)=3\unicode[STIX]{x1D6FC}+\bigg(\frac{1}{q}-\frac{1}{2}-\unicode[STIX]{x1D6FC}-\frac{2}{12m}\bigg)>3\unicode[STIX]{x1D6FC}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \bigg(\unicode[STIX]{x1D6FC}-\frac{1}{12m}\bigg)+2\bigg(\frac{1}{q}-\frac{1}{2}\bigg)=3\unicode[STIX]{x1D6FC}+2\bigg(\frac{1}{q}-\frac{1}{2}-\unicode[STIX]{x1D6FC}-\frac{1}{2\cdot 12m}\bigg)>3\unicode[STIX]{x1D6FC}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \frac{1}{q}-\frac{1}{2}=\unicode[STIX]{x1D6FC}+\bigg(\frac{1}{q}-\frac{1}{2}-\unicode[STIX]{x1D6FC}\bigg)>\unicode[STIX]{x1D6FC}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bigg(\unicode[STIX]{x1D6FC}-\frac{1}{12m}\bigg)+\bigg(\frac{1}{q}-\frac{1}{2}\bigg)=2\unicode[STIX]{x1D6FC}+\bigg(\frac{1}{q}-\frac{1}{2}-\unicode[STIX]{x1D6FC}-\frac{1}{12m}\bigg)>2\unicode[STIX]{x1D6FC}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle 2\bigg(\unicode[STIX]{x1D6FC}-\frac{1}{12m}\bigg)+\bigg(\frac{1}{q}-\frac{1}{2}\bigg)=3\unicode[STIX]{x1D6FC}+\bigg(\frac{1}{q}-\frac{1}{2}-\unicode[STIX]{x1D6FC}-\frac{2}{12m}\bigg)>3\unicode[STIX]{x1D6FC}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \bigg(\unicode[STIX]{x1D6FC}-\frac{1}{12m}\bigg)+2\bigg(\frac{1}{q}-\frac{1}{2}\bigg)=3\unicode[STIX]{x1D6FC}+2\bigg(\frac{1}{q}-\frac{1}{2}-\unicode[STIX]{x1D6FC}-\frac{1}{2\cdot 12m}\bigg)>3\unicode[STIX]{x1D6FC}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \frac{1}{q}-\frac{1}{2}=\unicode[STIX]{x1D6FC}+\bigg(\frac{1}{q}-\frac{1}{2}-\unicode[STIX]{x1D6FC}\bigg)>\unicode[STIX]{x1D6FC}. & \displaystyle \nonumber\end{eqnarray}$$ Hence, ![]() $A^{i}$ and
$A^{i}$ and ![]() $\boldsymbol{\unicode[STIX]{x1D6FE}}^{2}$ are of finite
$\boldsymbol{\unicode[STIX]{x1D6FE}}^{2}$ are of finite ![]() $2(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FF})$-Hölder norm for some
$2(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FF})$-Hölder norm for some ![]() $\unicode[STIX]{x1D6FF}>0$ and therefore they are of finite
$\unicode[STIX]{x1D6FF}>0$ and therefore they are of finite ![]() $(2\unicode[STIX]{x1D6FC},6m)$-Besov norm. We also see that
$(2\unicode[STIX]{x1D6FC},6m)$-Besov norm. We also see that ![]() $B^{i}$,
$B^{i}$, ![]() $C^{i}$ and
$C^{i}$ and ![]() $\boldsymbol{\unicode[STIX]{x1D6FE}}^{3}$ are of finite
$\boldsymbol{\unicode[STIX]{x1D6FE}}^{3}$ are of finite ![]() $(3\unicode[STIX]{x1D6FC},4m)$-Besov norm. Hence,
$(3\unicode[STIX]{x1D6FC},4m)$-Besov norm. Hence, ![]() $\unicode[STIX]{x1D70F}$ is well-defined.
$\unicode[STIX]{x1D70F}$ is well-defined.
The continuity follows from the continuous embedding ![]() $C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ and the continuity of the Young integration.◻
$C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ and the continuity of the Young integration.◻
4 Moment estimate for Taylor expansion of the Lyons–Itô map
In this section, we prove a Taylor-like expansion for ![]() ${\tilde{y}}^{\unicode[STIX]{x1D716}}$, which was defined in (3.8). The base point
${\tilde{y}}^{\unicode[STIX]{x1D716}}$, which was defined in (3.8). The base point ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ of the expansion is arbitrary, but fixed. We will show that
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ of the expansion is arbitrary, but fixed. We will show that ![]() ${\tilde{y}}^{\unicode[STIX]{x1D716}}$ admits the next expansion
${\tilde{y}}^{\unicode[STIX]{x1D716}}$ admits the next expansion
as ![]() $\unicode[STIX]{x1D716}{\searrow}0$ in appropriate senses. Here
$\unicode[STIX]{x1D716}{\searrow}0$ in appropriate senses. Here ![]() $\unicode[STIX]{x1D705}_{k}\in \unicode[STIX]{x1D6EC}_{1}$ and
$\unicode[STIX]{x1D705}_{k}\in \unicode[STIX]{x1D6EC}_{1}$ and ![]() $\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{k}}$ is a nice Wiener functional (for
$\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{k}}$ is a nice Wiener functional (for ![]() $\unicode[STIX]{x1D6EC}_{1}$ and
$\unicode[STIX]{x1D6EC}_{1}$ and ![]() $0=\unicode[STIX]{x1D705}_{0}<\unicode[STIX]{x1D705}_{1}<\unicode[STIX]{x1D705}_{2}<\cdots \,$, see § 2.3).
$0=\unicode[STIX]{x1D705}_{0}<\unicode[STIX]{x1D705}_{1}<\unicode[STIX]{x1D705}_{2}<\cdots \,$, see § 2.3).
Let us fix some notations for fractional order expansion (4.1). In this section, ![]() $H$ is not necessarily the Hurst parameter, but a positive parameter unless otherwise specified. For notational simplicity, however,
$H$ is not necessarily the Hurst parameter, but a positive parameter unless otherwise specified. For notational simplicity, however, ![]() $H\in (0,1/2]$ is assumed. For such
$H\in (0,1/2]$ is assumed. For such ![]() $H$, we define
$H$, we define ![]() $0=\unicode[STIX]{x1D705}_{0}<\unicode[STIX]{x1D705}_{1}<\unicode[STIX]{x1D705}_{2}<\cdots \,$ in the same way as § 2.3. We will work in
$0=\unicode[STIX]{x1D705}_{0}<\unicode[STIX]{x1D705}_{1}<\unicode[STIX]{x1D705}_{2}<\cdots \,$ in the same way as § 2.3. We will work in ![]() $1$-variation topology for a while. The ODE that corresponds to (3.8) leads
$1$-variation topology for a while. The ODE that corresponds to (3.8) leads
Here ![]() $x,h\in C_{0}^{1\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ and
$x,h\in C_{0}^{1\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ and ![]() $\unicode[STIX]{x1D706}_{t}=t$. Next we define
$\unicode[STIX]{x1D706}_{t}=t$. Next we define ![]() $\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m}}$ appeared in (4.1) formally; for intuitive derivation of
$\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m}}$ appeared in (4.1) formally; for intuitive derivation of ![]() $\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m}}$, see [Reference InahamaIna16a, Section 7]. By setting
$\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m}}$, see [Reference InahamaIna16a, Section 7]. By setting ![]() $\unicode[STIX]{x1D716}=0$ in (4.2), we can easily see that
$\unicode[STIX]{x1D716}=0$ in (4.2), we can easily see that ![]() $\unicode[STIX]{x1D719}^{0}=\unicode[STIX]{x1D719}^{0}(h)$ satisfies
$\unicode[STIX]{x1D719}^{0}=\unicode[STIX]{x1D719}^{0}(h)$ satisfies
An ODE for ![]() $\unicode[STIX]{x1D719}^{1}=\unicode[STIX]{x1D719}^{1}(x,h)$ is given by
$\unicode[STIX]{x1D719}^{1}=\unicode[STIX]{x1D719}^{1}(x,h)$ is given by
For ![]() $\unicode[STIX]{x1D705}_{m}\geqslant 2$,
$\unicode[STIX]{x1D705}_{m}\geqslant 2$, ![]() $\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m}}=\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m}}(x,h)$ satisfies
$\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m}}=\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m}}(x,h)$ satisfies
 $$\begin{eqnarray}\displaystyle & & \displaystyle d\unicode[STIX]{x1D719}_{t}^{\unicode[STIX]{x1D705}_{m}}-\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{t}^{0})\langle \unicode[STIX]{x1D719}_{t}^{\unicode[STIX]{x1D705}_{m}},dh_{t}\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k=1}^{\infty }\mathop{\sum }_{\unicode[STIX]{x1D705}_{i_{1}}+\cdots +\unicode[STIX]{x1D705}_{i_{k}}=\unicode[STIX]{x1D705}_{m}-1}\frac{\unicode[STIX]{x1D6FB}^{k}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{t}^{0})}{k!}\langle \unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{i_{1}}},\ldots ,\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{i_{k}}};dx_{t}\rangle \nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{k=2}^{\infty }\mathop{\sum }_{\unicode[STIX]{x1D705}_{i_{1}}+\cdots +\unicode[STIX]{x1D705}_{i_{k}}=\unicode[STIX]{x1D705}_{m}}\frac{\unicode[STIX]{x1D6FB}^{k}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{t}^{0})}{k!}\langle \unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{i_{1}}},\ldots ,\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{i_{k}}};dh_{t}\rangle \nonumber\\ \displaystyle & & \displaystyle \qquad +\mathop{\sum }_{k=1}^{\infty }\mathop{\sum }_{\unicode[STIX]{x1D705}_{i_{1}}+\cdots +\unicode[STIX]{x1D705}_{i_{k}}=\unicode[STIX]{x1D705}_{m}-1/H}\frac{\unicode[STIX]{x1D6FB}^{k}b(\unicode[STIX]{x1D719}_{t}^{0})}{k!}\langle \unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{i_{1}}},\ldots ,\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{i_{k}}}\rangle \,dt\quad \text{with }\unicode[STIX]{x1D719}_{0}^{\unicode[STIX]{x1D705}_{m}}=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle d\unicode[STIX]{x1D719}_{t}^{\unicode[STIX]{x1D705}_{m}}-\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{t}^{0})\langle \unicode[STIX]{x1D719}_{t}^{\unicode[STIX]{x1D705}_{m}},dh_{t}\rangle \nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k=1}^{\infty }\mathop{\sum }_{\unicode[STIX]{x1D705}_{i_{1}}+\cdots +\unicode[STIX]{x1D705}_{i_{k}}=\unicode[STIX]{x1D705}_{m}-1}\frac{\unicode[STIX]{x1D6FB}^{k}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{t}^{0})}{k!}\langle \unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{i_{1}}},\ldots ,\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{i_{k}}};dx_{t}\rangle \nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{k=2}^{\infty }\mathop{\sum }_{\unicode[STIX]{x1D705}_{i_{1}}+\cdots +\unicode[STIX]{x1D705}_{i_{k}}=\unicode[STIX]{x1D705}_{m}}\frac{\unicode[STIX]{x1D6FB}^{k}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}_{t}^{0})}{k!}\langle \unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{i_{1}}},\ldots ,\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{i_{k}}};dh_{t}\rangle \nonumber\\ \displaystyle & & \displaystyle \qquad +\mathop{\sum }_{k=1}^{\infty }\mathop{\sum }_{\unicode[STIX]{x1D705}_{i_{1}}+\cdots +\unicode[STIX]{x1D705}_{i_{k}}=\unicode[STIX]{x1D705}_{m}-1/H}\frac{\unicode[STIX]{x1D6FB}^{k}b(\unicode[STIX]{x1D719}_{t}^{0})}{k!}\langle \unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{i_{1}}},\ldots ,\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{i_{k}}}\rangle \,dt\quad \text{with }\unicode[STIX]{x1D719}_{0}^{\unicode[STIX]{x1D705}_{m}}=0.\end{eqnarray}$$ The summations in the first term on the right-hand side is taken over all ![]() $\unicode[STIX]{x1D705}_{i_{1}},\ldots ,\unicode[STIX]{x1D705}_{i_{k}}\in \unicode[STIX]{x1D6EC}_{1}\setminus \{0\}$ such that
$\unicode[STIX]{x1D705}_{i_{1}},\ldots ,\unicode[STIX]{x1D705}_{i_{k}}\in \unicode[STIX]{x1D6EC}_{1}\setminus \{0\}$ such that ![]() $\unicode[STIX]{x1D705}_{i_{1}}+\cdots +\unicode[STIX]{x1D705}_{i_{k}}=\unicode[STIX]{x1D705}_{m}-1$ holds. It is not allowed that
$\unicode[STIX]{x1D705}_{i_{1}}+\cdots +\unicode[STIX]{x1D705}_{i_{k}}=\unicode[STIX]{x1D705}_{m}-1$ holds. It is not allowed that ![]() $\unicode[STIX]{x1D705}_{i_{j}}=0$. So, the sum is actually a finite sum. The second and the third terms should be understood in the same way. An important observation is that the right-hand side of (4.5) does not involve
$\unicode[STIX]{x1D705}_{i_{j}}=0$. So, the sum is actually a finite sum. The second and the third terms should be understood in the same way. An important observation is that the right-hand side of (4.5) does not involve ![]() $\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m}}$, but only
$\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m}}$, but only ![]() $\unicode[STIX]{x1D719}^{0},\ldots ,\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m-1}}$. These ODEs have a rigorous meaning and can actually be solved by variation of constants method. So, we inductively define
$\unicode[STIX]{x1D719}^{0},\ldots ,\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m-1}}$. These ODEs have a rigorous meaning and can actually be solved by variation of constants method. So, we inductively define ![]() $\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m}}$ as a unique solution of (4.3), (4.4) and (4.5). Finally, set
$\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{m}}$ as a unique solution of (4.3), (4.4) and (4.5). Finally, set
Then, ![]() $(x,h)\mapsto (x,h,\unicode[STIX]{x1D706},{\tilde{y}}^{\unicode[STIX]{x1D716}},\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{0}},\ldots ,\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{k}},r_{\unicode[STIX]{x1D716}}^{\unicode[STIX]{x1D705}_{k+1}})$ is continuous from
$(x,h)\mapsto (x,h,\unicode[STIX]{x1D706},{\tilde{y}}^{\unicode[STIX]{x1D716}},\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{0}},\ldots ,\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D705}_{k}},r_{\unicode[STIX]{x1D716}}^{\unicode[STIX]{x1D705}_{k+1}})$ is continuous from ![]() $C_{0}^{1\text{-}\text{var}}([0,1];\mathbf{R}^{d})^{2}$ to
$C_{0}^{1\text{-}\text{var}}([0,1];\mathbf{R}^{d})^{2}$ to ![]() $C_{0}^{1\text{-}\text{var}}([0,1];(\mathbf{R}^{d})^{\oplus 2}\oplus \mathbf{R}\oplus (\mathbf{R}^{n})^{k+3})$.
$C_{0}^{1\text{-}\text{var}}([0,1];(\mathbf{R}^{d})^{\oplus 2}\oplus \mathbf{R}\oplus (\mathbf{R}^{n})^{k+3})$.
Furthermore, it is known that this map extends to a continuous map with respect to the rough path topology; more precisely, for ![]() $2\leqslant p<4$,
$2\leqslant p<4$, ![]() $1\leqslant q<2$ with
$1\leqslant q<2$ with ![]() $1/p+1/q>1$,
$1/p+1/q>1$,
is locally Lipschitz for any ![]() $k$. Here, (4.2) is viewed as an RDE driven by
$k$. Here, (4.2) is viewed as an RDE driven by ![]() $(\unicode[STIX]{x1D716}\mathbf{x}+\mathbf{h},\boldsymbol{\unicode[STIX]{x1D706}})$ in the same way as in (3.8).
$(\unicode[STIX]{x1D716}\mathbf{x}+\mathbf{h},\boldsymbol{\unicode[STIX]{x1D706}})$ in the same way as in (3.8).
Proposition 4.1. Assume ![]() $2\leqslant p<4$,
$2\leqslant p<4$, ![]() $1\leqslant q<2$ and
$1\leqslant q<2$ and ![]() $1/p+1/q>1$. Let
$1/p+1/q>1$. Let ![]() $(\mathbf{x},h)\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ and consider RDE (4.2) and keep the same notations as above. Then, the following hold.
$(\mathbf{x},h)\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ and consider RDE (4.2) and keep the same notations as above. Then, the following hold.
(1) For any
 $\unicode[STIX]{x1D70C}>0$ and
$\unicode[STIX]{x1D70C}>0$ and  $k=1,2,\ldots$, there exists a positive constant
$k=1,2,\ldots$, there exists a positive constant  $C=C(\unicode[STIX]{x1D70C},k)$ which satisfies that for any
$C=C(\unicode[STIX]{x1D70C},k)$ which satisfies that for any $$\begin{eqnarray}\Vert (\boldsymbol{\unicode[STIX]{x1D719}}^{\unicode[STIX]{x1D705}_{k}})^{1}\Vert _{p\text{-}\text{var}}\leqslant C(1+\overline{\unicode[STIX]{x1D714}_{\mathbf{x}}}^{1/p})^{\unicode[STIX]{x1D705}_{k}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert (\boldsymbol{\unicode[STIX]{x1D719}}^{\unicode[STIX]{x1D705}_{k}})^{1}\Vert _{p\text{-}\text{var}}\leqslant C(1+\overline{\unicode[STIX]{x1D714}_{\mathbf{x}}}^{1/p})^{\unicode[STIX]{x1D705}_{k}}\end{eqnarray}$$ $\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ and
$\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ and  $h\in C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ with
$h\in C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ with  $\Vert h\Vert _{q\text{-}\text{var}}\leqslant \unicode[STIX]{x1D70C}$.
$\Vert h\Vert _{q\text{-}\text{var}}\leqslant \unicode[STIX]{x1D70C}$.(2) For any
 $\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2}>0$ and
$\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2}>0$ and  $k=1,2,\ldots$, there exists a positive constant
$k=1,2,\ldots$, there exists a positive constant  $\tilde{C}=\tilde{C}(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2},k)$, which is independent of
$\tilde{C}=\tilde{C}(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2},k)$, which is independent of  $\unicode[STIX]{x1D716}$ and satisfies that for any
$\unicode[STIX]{x1D716}$ and satisfies that for any $$\begin{eqnarray}\Vert (\mathbf{r}_{\unicode[STIX]{x1D716}}^{\unicode[STIX]{x1D705}_{k+1}})^{1}\Vert _{p\text{-}\text{var}}\leqslant \tilde{C}(\unicode[STIX]{x1D716}+\unicode[STIX]{x1D716}\overline{\unicode[STIX]{x1D714}_{\mathbf{x}}}^{1/p})^{\unicode[STIX]{x1D705}_{k+1}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert (\mathbf{r}_{\unicode[STIX]{x1D716}}^{\unicode[STIX]{x1D705}_{k+1}})^{1}\Vert _{p\text{-}\text{var}}\leqslant \tilde{C}(\unicode[STIX]{x1D716}+\unicode[STIX]{x1D716}\overline{\unicode[STIX]{x1D714}_{\mathbf{x}}}^{1/p})^{\unicode[STIX]{x1D705}_{k+1}}\end{eqnarray}$$ $\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ with
$\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$ with  $\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}\mathbf{x}}}^{1/p}=\unicode[STIX]{x1D716}\overline{\unicode[STIX]{x1D714}_{\mathbf{x}}}^{1/p}\leqslant \unicode[STIX]{x1D70C}_{1}$ and any
$\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D716}\mathbf{x}}}^{1/p}=\unicode[STIX]{x1D716}\overline{\unicode[STIX]{x1D714}_{\mathbf{x}}}^{1/p}\leqslant \unicode[STIX]{x1D70C}_{1}$ and any  $h\in C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ with
$h\in C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ with  $\Vert h\Vert _{q\text{-}\text{var}}\leqslant \unicode[STIX]{x1D70C}_{2}$.
$\Vert h\Vert _{q\text{-}\text{var}}\leqslant \unicode[STIX]{x1D70C}_{2}$.
Proof. This is essentially shown in [Reference InahamaIna10]. The only difference is that the index set in [Reference InahamaIna10] is ![]() $\mathbf{N}$ while it is
$\mathbf{N}$ while it is ![]() $\unicode[STIX]{x1D6EC}_{1}$ here. But, this is a trivial issue.◻
$\unicode[STIX]{x1D6EC}_{1}$ here. But, this is a trivial issue.◻
Now, we provide an ![]() $L^{r}$-version of the above proposition. By integrability lemmas of
$L^{r}$-version of the above proposition. By integrability lemmas of ![]() $\overline{\unicode[STIX]{x1D714}_{\mathbf{x}}}$ and
$\overline{\unicode[STIX]{x1D714}_{\mathbf{x}}}$ and ![]() $N_{\unicode[STIX]{x1D6FF}}(\mathbf{x})$, which are found in [Reference Friz and OberhauserFO10, Proposition 7] and [Reference Cass, Litterer and LyonsCLL13, Theorem 6.3 and Remark 6.4], respectively, the following theorem applies to fractional Brownian rough path
$N_{\unicode[STIX]{x1D6FF}}(\mathbf{x})$, which are found in [Reference Friz and OberhauserFO10, Proposition 7] and [Reference Cass, Litterer and LyonsCLL13, Theorem 6.3 and Remark 6.4], respectively, the following theorem applies to fractional Brownian rough path ![]() $\mathbf{w}$ and
$\mathbf{w}$ and ![]() $h\in \mathfrak{H}$ when
$h\in \mathfrak{H}$ when ![]() $H\in (1/4,1/2]$. More precisely, for every
$H\in (1/4,1/2]$. More precisely, for every ![]() $H\in (1/4,1/2]$, and
$H\in (1/4,1/2]$, and ![]() $p>1/H$ that is sufficiently close to
$p>1/H$ that is sufficiently close to ![]() $1/H$, we can let
$1/H$, we can let ![]() $H$ be the Hurst parameter itself and take
$H$ be the Hurst parameter itself and take ![]() $\mathbf{x}=\mathbf{w}$ and
$\mathbf{x}=\mathbf{w}$ and ![]() $h\in \mathfrak{H}$ in Theorem 4.2.
$h\in \mathfrak{H}$ in Theorem 4.2.
Theorem 4.2. Assume ![]() $2\leqslant p<4$,
$2\leqslant p<4$, ![]() $1\leqslant q<2$ and
$1\leqslant q<2$ and ![]() $1/p+1/q>1$. Let
$1/p+1/q>1$. Let ![]() $h\in C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ and let
$h\in C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ and let ![]() $\mathbf{x}$ be a
$\mathbf{x}$ be a ![]() $G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$-valued random variable such that
$G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})$-valued random variable such that ![]() $\overline{\unicode[STIX]{x1D714}_{\mathbf{x}}}=\unicode[STIX]{x1D714}_{\mathbf{x}}(0,1)\in \bigcap _{1\leqslant r<\infty }L^{r}$ and
$\overline{\unicode[STIX]{x1D714}_{\mathbf{x}}}=\unicode[STIX]{x1D714}_{\mathbf{x}}(0,1)\in \bigcap _{1\leqslant r<\infty }L^{r}$ and ![]() $\exp (N_{\unicode[STIX]{x1D6FF}}(\mathbf{x}))\in \bigcap _{1\leqslant r<\infty }L^{r}$ for every
$\exp (N_{\unicode[STIX]{x1D6FF}}(\mathbf{x}))\in \bigcap _{1\leqslant r<\infty }L^{r}$ for every ![]() $\unicode[STIX]{x1D6FF}>0$. We consider RDE (4.2).
$\unicode[STIX]{x1D6FF}>0$. We consider RDE (4.2).
Then, for any ![]() $\mathbf{x}$,
$\mathbf{x}$, ![]() $h$ and
$h$ and ![]() $k\in \mathbf{N}$, there exist control functions
$k\in \mathbf{N}$, there exist control functions ![]() $\unicode[STIX]{x1D702}_{k}=\unicode[STIX]{x1D702}_{k,\mathbf{x},h}$ such that the following hold:
$\unicode[STIX]{x1D702}_{k}=\unicode[STIX]{x1D702}_{k,\mathbf{x},h}$ such that the following hold:
(1)
 $\unicode[STIX]{x1D702}_{k}$ are nondecreasing in
$\unicode[STIX]{x1D702}_{k}$ are nondecreasing in  $k$, that is,
$k$, that is,  $\unicode[STIX]{x1D702}_{k,\mathbf{x},h}(s,t)\leqslant \unicode[STIX]{x1D702}_{k+1,\mathbf{x},h}(s,t)$ for all
$\unicode[STIX]{x1D702}_{k,\mathbf{x},h}(s,t)\leqslant \unicode[STIX]{x1D702}_{k+1,\mathbf{x},h}(s,t)$ for all  $k,\mathbf{x},h,(s,t)$.
$k,\mathbf{x},h,(s,t)$.(2)
 $\overline{\unicode[STIX]{x1D702}_{k,\mathbf{x},h}}\in \bigcap _{1\leqslant r<\infty }L^{r}$ for all
$\overline{\unicode[STIX]{x1D702}_{k,\mathbf{x},h}}\in \bigcap _{1\leqslant r<\infty }L^{r}$ for all  $k,h$.
$k,h$.(3) For all
 $\unicode[STIX]{x1D716}\in (0,1]$,
$\unicode[STIX]{x1D716}\in (0,1]$,  $k\in \mathbf{N}$,
$k\in \mathbf{N}$,  $h$,
$h$,  $\mathbf{x}$,
$\mathbf{x}$,  $0\leqslant s\leqslant t\leqslant 1$, and
$0\leqslant s\leqslant t\leqslant 1$, and  $1\leqslant j\leqslant \lfloor p\rfloor$, we have
$1\leqslant j\leqslant \lfloor p\rfloor$, we have  $$\begin{eqnarray}|(\mathbf{x},\mathbf{h},\tilde{\mathbf{y}}^{\unicode[STIX]{x1D716}},\boldsymbol{\unicode[STIX]{x1D719}}^{0},\boldsymbol{\unicode[STIX]{x1D719}}^{\unicode[STIX]{x1D705}_{1}},\ldots ,\boldsymbol{\unicode[STIX]{x1D719}}^{\unicode[STIX]{x1D705}_{k}},\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D705}_{k+1}}\mathbf{r}_{\unicode[STIX]{x1D716}}^{\unicode[STIX]{x1D705}_{k+1}})_{s,t}^{j}|\leqslant \unicode[STIX]{x1D702}_{k,\mathbf{x},h}(s,t)^{j/p}.\end{eqnarray}$$
$$\begin{eqnarray}|(\mathbf{x},\mathbf{h},\tilde{\mathbf{y}}^{\unicode[STIX]{x1D716}},\boldsymbol{\unicode[STIX]{x1D719}}^{0},\boldsymbol{\unicode[STIX]{x1D719}}^{\unicode[STIX]{x1D705}_{1}},\ldots ,\boldsymbol{\unicode[STIX]{x1D719}}^{\unicode[STIX]{x1D705}_{k}},\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D705}_{k+1}}\mathbf{r}_{\unicode[STIX]{x1D716}}^{\unicode[STIX]{x1D705}_{k+1}})_{s,t}^{j}|\leqslant \unicode[STIX]{x1D702}_{k,\mathbf{x},h}(s,t)^{j/p}.\end{eqnarray}$$
In particular, for all ![]() $k\in \mathbf{N}$ and
$k\in \mathbf{N}$ and ![]() $h$,
$h$, ![]() $\Vert (\boldsymbol{\unicode[STIX]{x1D719}}^{\unicode[STIX]{x1D705}_{k}})^{1}\Vert _{p\text{-}\text{var}}\in \bigcap _{1\leqslant r<\infty }L^{r}$ and
$\Vert (\boldsymbol{\unicode[STIX]{x1D719}}^{\unicode[STIX]{x1D705}_{k}})^{1}\Vert _{p\text{-}\text{var}}\in \bigcap _{1\leqslant r<\infty }L^{r}$ and ![]() $\Vert (\mathbf{r}_{\unicode[STIX]{x1D716}}^{\unicode[STIX]{x1D705}_{k+1}})^{1}\Vert _{p\text{-}\text{var}}=O(\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D705}_{k+1}})$ in
$\Vert (\mathbf{r}_{\unicode[STIX]{x1D716}}^{\unicode[STIX]{x1D705}_{k+1}})^{1}\Vert _{p\text{-}\text{var}}=O(\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D705}_{k+1}})$ in ![]() $L^{r}$ for any
$L^{r}$ for any ![]() $1\leqslant r<\infty$.
$1\leqslant r<\infty$.
Proof. One can prove this by combining Proposition 4.1 above and computing ![]() $N_{\unicode[STIX]{x1D6FF}}(\mathbf{x})$ in the same way as [Reference InahamaIna16b]. For
$N_{\unicode[STIX]{x1D6FF}}(\mathbf{x})$ in the same way as [Reference InahamaIna16b]. For ![]() $k=0$, (4.2) and (4.3) imply
$k=0$, (4.2) and (4.3) imply
Since the first term on the right-hand side can be interpreted as a rough integration of one form along ![]() $(\mathbf{x},\mathbf{h},\tilde{\mathbf{y}}^{\unicode[STIX]{x1D716}},\boldsymbol{\unicode[STIX]{x1D719}}^{0})$, there exists a control function
$(\mathbf{x},\mathbf{h},\tilde{\mathbf{y}}^{\unicode[STIX]{x1D716}},\boldsymbol{\unicode[STIX]{x1D719}}^{0})$, there exists a control function ![]() $\unicode[STIX]{x1D702}_{\mathbf{x},h}^{\prime }$ determined by
$\unicode[STIX]{x1D702}_{\mathbf{x},h}^{\prime }$ determined by ![]() $\unicode[STIX]{x1D714}_{\mathbf{x}}$ and
$\unicode[STIX]{x1D714}_{\mathbf{x}}$ and ![]() $\unicode[STIX]{x1D714}_{h}$ such that
$\unicode[STIX]{x1D714}_{h}$ such that
for ![]() $1\leqslant j\leqslant \lfloor p\rfloor$. The second and third terms can admit
$1\leqslant j\leqslant \lfloor p\rfloor$. The second and third terms can admit
where ![]() $\unicode[STIX]{x1D702}_{\mathbf{x},h}^{\prime \prime }$ is a control function determined by
$\unicode[STIX]{x1D702}_{\mathbf{x},h}^{\prime \prime }$ is a control function determined by ![]() $\unicode[STIX]{x1D714}_{\mathbf{x}}$,
$\unicode[STIX]{x1D714}_{\mathbf{x}}$, ![]() $\unicode[STIX]{x1D714}_{h}$ and
$\unicode[STIX]{x1D714}_{h}$ and ![]() $N_{\unicode[STIX]{x1D6FF}}(\mathbf{x})$. These three equations correspond to (3.16), (3.17) and (3.20) in [Reference InahamaIna16b]. Hence, the assertion for
$N_{\unicode[STIX]{x1D6FF}}(\mathbf{x})$. These three equations correspond to (3.16), (3.17) and (3.20) in [Reference InahamaIna16b]. Hence, the assertion for ![]() $k=0$ holds from these estimates and a property of Young pairing (
$k=0$ holds from these estimates and a property of Young pairing (![]() $\unicode[STIX]{x1D702}_{1,\mathbf{x},h}$ appeared in the assertion consists of
$\unicode[STIX]{x1D702}_{1,\mathbf{x},h}$ appeared in the assertion consists of ![]() $\unicode[STIX]{x1D702}_{\mathbf{x},h}^{\prime }$ and
$\unicode[STIX]{x1D702}_{\mathbf{x},h}^{\prime }$ and ![]() $\unicode[STIX]{x1D702}_{\mathbf{x},h}^{\prime \prime }$). For details of the discussion above and the proof of the assertion for general
$\unicode[STIX]{x1D702}_{\mathbf{x},h}^{\prime \prime }$). For details of the discussion above and the proof of the assertion for general ![]() $k$, we consult on [Reference InahamaIna16b, Section 3].◻
$k$, we consult on [Reference InahamaIna16b, Section 3].◻
5 Malliavin calculus for the solution of RDE driven by fBm
Our main purpose in this section is to prove that ![]() $y_{1}^{\unicode[STIX]{x1D716}}$ and
$y_{1}^{\unicode[STIX]{x1D716}}$ and ![]() ${\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}$ are nondegenerate uniformly in the sense of Malliavin in
${\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}$ are nondegenerate uniformly in the sense of Malliavin in ![]() $\unicode[STIX]{x1D716}$. Here,
$\unicode[STIX]{x1D716}$. Here, ![]() $y^{\unicode[STIX]{x1D716}}$ and
$y^{\unicode[STIX]{x1D716}}$ and ![]() ${\tilde{y}}^{\unicode[STIX]{x1D716}}$ are solutions to (3.7) and (3.8), respectively. Throughout this section,
${\tilde{y}}^{\unicode[STIX]{x1D716}}$ are solutions to (3.7) and (3.8), respectively. Throughout this section, ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ in the definition of
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ in the definition of ![]() ${\tilde{y}}_{t}^{\unicode[STIX]{x1D716}}$ in (3.8) will be fixed.
${\tilde{y}}_{t}^{\unicode[STIX]{x1D716}}$ in (3.8) will be fixed.
5.1 Notation and results of this section
We recall Watanabe’s theory of generalized Wiener functionals (Watanabe distributions) in Malliavin calculus. We borrow the notations used in this paper from Ikeda and Watanabe [Reference Ikeda and WatanabeIW89, V.8-V.10]. We also refer to Nualart [Reference NualartNua06], Shigekawa [Reference ShigekawaShi04], Matsumoto and Taniguchi [Reference Matsumoto and TaniguchiMT17] and Hu [Reference HuHu17].
We introduce a measure. Let ![]() $\mathbf{P}=\mathbf{P}^{H}$ be the law of the fBm with Hurst parameter
$\mathbf{P}=\mathbf{P}^{H}$ be the law of the fBm with Hurst parameter ![]() $H$. This is a probability measure on
$H$. This is a probability measure on ![]() $\unicode[STIX]{x1D6FA}=\overline{\mathfrak{H}}$, which is the closure of the Cameron–Martin space
$\unicode[STIX]{x1D6FA}=\overline{\mathfrak{H}}$, which is the closure of the Cameron–Martin space ![]() $\mathfrak{H}=\mathfrak{H}^{H}$ in
$\mathfrak{H}=\mathfrak{H}^{H}$ in ![]() $C_{0}^{p\text{-}\text{var}}([0,1];\mathbf{R}^{d})$. Then, the triple
$C_{0}^{p\text{-}\text{var}}([0,1];\mathbf{R}^{d})$. Then, the triple ![]() $(\unicode[STIX]{x1D6FA},\mathfrak{H},\mathbf{P})$ is an abstract Wiener space. We denote by
$(\unicode[STIX]{x1D6FA},\mathfrak{H},\mathbf{P})$ is an abstract Wiener space. We denote by ![]() $\mathbf{D}_{r,s}(K)$ the
$\mathbf{D}_{r,s}(K)$ the ![]() $K$-valued Gaussian–Sobolev space, where
$K$-valued Gaussian–Sobolev space, where ![]() $1<r<\infty$,
$1<r<\infty$, ![]() $s\in \mathbf{R}$ and
$s\in \mathbf{R}$ and ![]() $K$ is a real separable Hilbert space. Note that
$K$ is a real separable Hilbert space. Note that ![]() $r$ and
$r$ and ![]() $s$ stand for the integrability index and the differentiability index, respectively. As usual, we set the spaces
$s$ stand for the integrability index and the differentiability index, respectively. As usual, we set the spaces ![]() $\mathbf{D}_{\infty }(K)=\bigcap _{s=1}^{\infty }\bigcap _{1<r<\infty }\mathbf{D}_{r,s}(K)$ and
$\mathbf{D}_{\infty }(K)=\bigcap _{s=1}^{\infty }\bigcap _{1<r<\infty }\mathbf{D}_{r,s}(K)$ and ![]() $\tilde{\mathbf{D}}_{\infty }(K)=\bigcap _{s=1}^{\infty }\bigcup _{1<r<\infty }\mathbf{D}_{r,s}(K)$ of test functions and the spaces
$\tilde{\mathbf{D}}_{\infty }(K)=\bigcap _{s=1}^{\infty }\bigcup _{1<r<\infty }\mathbf{D}_{r,s}(K)$ of test functions and the spaces ![]() $\mathbf{D}_{-\infty }(K)=\bigcup _{s=1}^{\infty }\bigcup _{1<r<\infty }\mathbf{D}_{r,-s}(K)$ and
$\mathbf{D}_{-\infty }(K)=\bigcup _{s=1}^{\infty }\bigcup _{1<r<\infty }\mathbf{D}_{r,-s}(K)$ and ![]() $\tilde{\mathbf{D}}_{-\infty }(K)=\bigcup _{s=1}^{\infty }\bigcap _{1<r<\infty }\mathbf{D}_{n,-s}(K)$ of Watanabe distributions. For
$\tilde{\mathbf{D}}_{-\infty }(K)=\bigcup _{s=1}^{\infty }\bigcap _{1<r<\infty }\mathbf{D}_{n,-s}(K)$ of Watanabe distributions. For ![]() $F\in \mathbf{D}_{r,s}(K)$,
$F\in \mathbf{D}_{r,s}(K)$, ![]() $D^{k}F$ denotes the
$D^{k}F$ denotes the ![]() $k$th derivative of
$k$th derivative of ![]() $F$ for
$F$ for ![]() $k\in \mathbf{N}_{+}$.
$k\in \mathbf{N}_{+}$.
We set ![]() $V_{0}^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}^{1/H}V_{0}$,
$V_{0}^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}^{1/H}V_{0}$, ![]() $V_{i}^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}V_{i}$ (
$V_{i}^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}V_{i}$ (![]() $1\leqslant i\leqslant d$), and
$1\leqslant i\leqslant d$), and ![]() $\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}=[V_{1}^{\unicode[STIX]{x1D716}},\ldots ,V_{d}^{\unicode[STIX]{x1D716}}]$, which is viewed as an
$\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}=[V_{1}^{\unicode[STIX]{x1D716}},\ldots ,V_{d}^{\unicode[STIX]{x1D716}}]$, which is viewed as an ![]() $n\times d$ matrix. It holds that
$n\times d$ matrix. It holds that ![]() $\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D70E}$. Set
$\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D70E}$. Set ![]() $\tilde{A}^{\unicode[STIX]{x1D716}}(s)=\tilde{J}_{1}^{\unicode[STIX]{x1D716}}\tilde{K}_{s}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}({\tilde{y}}_{s}^{\unicode[STIX]{x1D716}})$, whose size is again
$\tilde{A}^{\unicode[STIX]{x1D716}}(s)=\tilde{J}_{1}^{\unicode[STIX]{x1D716}}\tilde{K}_{s}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}({\tilde{y}}_{s}^{\unicode[STIX]{x1D716}})$, whose size is again ![]() $n\times d$. Let
$n\times d$. Let ![]() $\tilde{A}^{\unicode[STIX]{x1D716},k}(s)$ and
$\tilde{A}^{\unicode[STIX]{x1D716},k}(s)$ and ![]() $\tilde{A}_{i}^{\unicode[STIX]{x1D716},k}(s)$ denote the
$\tilde{A}_{i}^{\unicode[STIX]{x1D716},k}(s)$ denote the ![]() $k$th row and the
$k$th row and the ![]() $(k,i)$-component of
$(k,i)$-component of ![]() $\tilde{A}^{\unicode[STIX]{x1D716}}(s)$, respectively.
$\tilde{A}^{\unicode[STIX]{x1D716}}(s)$, respectively.
Under this setting, we see that ![]() ${\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}$ is differentiable in the sense of Malliavin and the derivatives admit good estimate as follows:
${\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}$ is differentiable in the sense of Malliavin and the derivatives admit good estimate as follows:
Proposition 5.1. We have ![]() ${\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}\in \mathbf{D}_{\infty }(\mathbf{R}^{n})$ and
${\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}\in \mathbf{D}_{\infty }(\mathbf{R}^{n})$ and
In addition, for any ![]() $m=0,1,2,\ldots$ and
$m=0,1,2,\ldots$ and ![]() $1<r<\infty$, there exists a positive constant
$1<r<\infty$, there exists a positive constant ![]() $c=c_{m,r}$ such that
$c=c_{m,r}$ such that
Proof. Malliavin differentiability of solutions of RDEs driven by Gaussian rough path was studied in [Reference InahamaIna14]. A slight modification of that argument proves this proposition. ◻
Proposition 5.2. We have the following asymptotic expansion as ![]() $\unicode[STIX]{x1D716}{\searrow}0$:
$\unicode[STIX]{x1D716}{\searrow}0$:
This means that for each ![]() $k$, (i)
$k$, (i) ![]() $\unicode[STIX]{x1D719}_{1}^{\unicode[STIX]{x1D705}_{k}}\in \mathbf{D}_{\infty }(\mathbf{R}^{n})$ and (ii)
$\unicode[STIX]{x1D719}_{1}^{\unicode[STIX]{x1D705}_{k}}\in \mathbf{D}_{\infty }(\mathbf{R}^{n})$ and (ii) ![]() $\mathbf{D}_{r,s}$-norm of
$\mathbf{D}_{r,s}$-norm of ![]() $r_{\unicode[STIX]{x1D716},1}^{\unicode[STIX]{x1D705}_{k+1}}$ is
$r_{\unicode[STIX]{x1D716},1}^{\unicode[STIX]{x1D705}_{k+1}}$ is ![]() $O(\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D705}_{k+1}})$ for any
$O(\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D705}_{k+1}})$ for any ![]() $1<r<\infty$ and
$1<r<\infty$ and ![]() $s\geqslant 0$. Here,
$s\geqslant 0$. Here, ![]() $r_{\unicode[STIX]{x1D716},1}^{\unicode[STIX]{x1D705}_{k+1}}$ is defined by (4.6).
$r_{\unicode[STIX]{x1D716},1}^{\unicode[STIX]{x1D705}_{k+1}}$ is defined by (4.6).
Proof. We can show the assertion in the same way as [Reference InahamaIna16b, Proposition 4.3]. Indeed, it follows from Theorem 4.2, Proposition 5.1, Meyer’s inequality and the fact that ![]() $\unicode[STIX]{x1D719}_{1}^{\unicode[STIX]{x1D705}_{k}}$ belongs to the
$\unicode[STIX]{x1D719}_{1}^{\unicode[STIX]{x1D705}_{k}}$ belongs to the ![]() $\mathbf{R}^{n}$-valued inhomogeneous Wiener chaos of order
$\mathbf{R}^{n}$-valued inhomogeneous Wiener chaos of order ![]() $\lfloor \unicode[STIX]{x1D705}_{k}\rfloor$.◻
$\lfloor \unicode[STIX]{x1D705}_{k}\rfloor$.◻
The Malliavin covariance matrices ![]() $Q=(Q_{kl})_{1\leqslant l,k\leqslant n}$ of
$Q=(Q_{kl})_{1\leqslant l,k\leqslant n}$ of ![]() $y_{1}$,
$y_{1}$, ![]() $Q^{\unicode[STIX]{x1D716}}=(Q_{kl}^{\unicode[STIX]{x1D716}})_{1\leqslant l,k\leqslant n}$ of
$Q^{\unicode[STIX]{x1D716}}=(Q_{kl}^{\unicode[STIX]{x1D716}})_{1\leqslant l,k\leqslant n}$ of ![]() $y_{1}^{\unicode[STIX]{x1D716}}$, and
$y_{1}^{\unicode[STIX]{x1D716}}$, and ![]() $\tilde{Q}^{\unicode[STIX]{x1D716}}=(\tilde{Q}_{kl}^{\unicode[STIX]{x1D716}})_{1\leqslant l,k\leqslant n}$ of
$\tilde{Q}^{\unicode[STIX]{x1D716}}=(\tilde{Q}_{kl}^{\unicode[STIX]{x1D716}})_{1\leqslant l,k\leqslant n}$ of ![]() ${\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}$ are defined by
${\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}$ are defined by
respectively. In this paper we do not express these covariance matrices as two-parameter Young integrals (cf. [Reference Cass, Hairer, Litterer and TindelCHLT15, (6.1)]). In this notation, we will state the following two propositions.
The first one is Kusuoka–Stroock type estimate for the solution of the scaled RDE. Although this is not surprising, there seems to be no literature that actually proves it.
Proposition 5.3. Suppose that (A1) holds. Then, there are positive constants ![]() $c$ and
$c$ and ![]() $\unicode[STIX]{x1D707}$ such that for every
$\unicode[STIX]{x1D707}$ such that for every ![]() $0<\unicode[STIX]{x1D716}<1$ and
$0<\unicode[STIX]{x1D716}<1$ and ![]() $1<r<\infty$, we have
$1<r<\infty$, we have
Here, ![]() $c=c(r)$ can be chosen independent of
$c=c(r)$ can be chosen independent of ![]() $\unicode[STIX]{x1D716}$, while
$\unicode[STIX]{x1D716}$, while ![]() $\unicode[STIX]{x1D707}$ is independent of both
$\unicode[STIX]{x1D707}$ is independent of both ![]() $r$ and
$r$ and ![]() $\unicode[STIX]{x1D716}$.
$\unicode[STIX]{x1D716}$.
The second one is about the uniform non-degeneracy in the sense of Malliavin calculus of the solution of the scaled–shifted RDE under (A3). The Schilder-type large deviations for fractional Brownian rough path are used in the proof.
Proposition 5.4. Suppose that (A1) holds. Let ![]() $\unicode[STIX]{x1D6FE}$ in the definition of
$\unicode[STIX]{x1D6FE}$ in the definition of ![]() ${\tilde{y}}^{\unicode[STIX]{x1D716}}$ in (3.8) satisfy
${\tilde{y}}^{\unicode[STIX]{x1D716}}$ in (3.8) satisfy ![]() $Q(\unicode[STIX]{x1D6FE})\geqslant cI$ for some
$Q(\unicode[STIX]{x1D6FE})\geqslant cI$ for some ![]() $c>0$. Then, for every
$c>0$. Then, for every ![]() $1<r<\infty$, we have
$1<r<\infty$, we have
Let ![]() $a^{\prime }\in \mathbf{R}^{n}$. Then, we have
$a^{\prime }\in \mathbf{R}^{n}$. Then, we have
It follows from Proposition 5.4 and this identity that ![]() $({\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}-a^{\prime })/\unicode[STIX]{x1D716}$ with
$({\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}-a^{\prime })/\unicode[STIX]{x1D716}$ with ![]() $\unicode[STIX]{x1D6FE}=\bar{\unicode[STIX]{x1D6FE}}$ is uniformly nondegenerate in the sense of Malliavin calculus under (A1), (A2) and (A3).
$\unicode[STIX]{x1D6FE}=\bar{\unicode[STIX]{x1D6FE}}$ is uniformly nondegenerate in the sense of Malliavin calculus under (A1), (A2) and (A3).
Propositions 5.3 and 5.4 will be proved in §§ 5.2 and 5.3, respectively.
5.2 Covariance matrix of the solution of scaled RDE driven by fBm
In this subsection, we show Proposition 5.3. Set
Then we see Proposition 5.3 from the following three lemmas.
Lemma 5.5. For every ![]() $0<\unicode[STIX]{x1D716}<1$, we have
$0<\unicode[STIX]{x1D716}<1$, we have
Here, ![]() $c$ is a positive constant independent of
$c$ is a positive constant independent of ![]() $\unicode[STIX]{x1D716}$.
$\unicode[STIX]{x1D716}$.
Lemma 5.6. Suppose that (A1) holds. Then, there are positive constants ![]() $c$ and
$c$ and ![]() $\unicode[STIX]{x1D707}$ such that for every
$\unicode[STIX]{x1D707}$ such that for every ![]() $0<\unicode[STIX]{x1D716}<1$ and
$0<\unicode[STIX]{x1D716}<1$ and ![]() $1<r<\infty$, we have
$1<r<\infty$, we have
Here, ![]() $c=c(r)$ can be chosen independent of
$c=c(r)$ can be chosen independent of ![]() $\unicode[STIX]{x1D716}$, while
$\unicode[STIX]{x1D716}$, while ![]() $\unicode[STIX]{x1D707}$ is independent of both
$\unicode[STIX]{x1D707}$ is independent of both ![]() $r$ and
$r$ and ![]() $\unicode[STIX]{x1D716}$.
$\unicode[STIX]{x1D716}$.
Lemma 5.7. [Reference Cass, Litterer and LyonsCLL13]
Let ![]() $p>1/H$. For every
$p>1/H$. For every ![]() $1<r<\infty$, we have
$1<r<\infty$, we have
Now we show Proposition 5.3 by using lemmas above.
Proof of Proposition 5.3.
From Lemma 5.5, we see
Hence,
Noting ![]() $\unicode[STIX]{x1D706}_{\min }(J_{1}^{\unicode[STIX]{x1D716}}(J_{1}^{\unicode[STIX]{x1D716}})^{\top })^{-1}=\unicode[STIX]{x1D706}_{\max }(K_{1}^{\unicode[STIX]{x1D716}}(K_{1}^{\unicode[STIX]{x1D716}})^{\top })$ and applying Lemmas 5.6 and 5.7, we see the assertion.
$\unicode[STIX]{x1D706}_{\min }(J_{1}^{\unicode[STIX]{x1D716}}(J_{1}^{\unicode[STIX]{x1D716}})^{\top })^{-1}=\unicode[STIX]{x1D706}_{\max }(K_{1}^{\unicode[STIX]{x1D716}}(K_{1}^{\unicode[STIX]{x1D716}})^{\top })$ and applying Lemmas 5.6 and 5.7, we see the assertion.
Next we show Lemma 5.5.
Proof of Lemma 5.5.
Set ![]() $A^{\unicode[STIX]{x1D716}}(s)=\mathtt{1}_{[0,1]}(s)J_{1}^{\unicode[STIX]{x1D716}}K_{s}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}(y_{s}^{\unicode[STIX]{x1D716}})$ and let
$A^{\unicode[STIX]{x1D716}}(s)=\mathtt{1}_{[0,1]}(s)J_{1}^{\unicode[STIX]{x1D716}}K_{s}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}(y_{s}^{\unicode[STIX]{x1D716}})$ and let ![]() $A^{\unicode[STIX]{x1D716},k}(s)$ denote the
$A^{\unicode[STIX]{x1D716},k}(s)$ denote the ![]() $k$th row of
$k$th row of ![]() $A^{\unicode[STIX]{x1D716}}(s)$. Then, for every
$A^{\unicode[STIX]{x1D716}}(s)$. Then, for every ![]() $v=(v_{1},\ldots ,v_{n})^{\top }\in \mathbf{R}^{n}$, we have
$v=(v_{1},\ldots ,v_{n})^{\top }\in \mathbf{R}^{n}$, we have ![]() $\langle v,Q^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}=\Vert \!\sum _{k=1}^{n}v_{k}Dy_{1}^{\unicode[STIX]{x1D716},k}\Vert _{\mathfrak{H}}^{2}$. It follows from the Riesz representation theorem and Remark 3.1 that
$\langle v,Q^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}=\Vert \!\sum _{k=1}^{n}v_{k}Dy_{1}^{\unicode[STIX]{x1D716},k}\Vert _{\mathfrak{H}}^{2}$. It follows from the Riesz representation theorem and Remark 3.1 that
 $$\begin{eqnarray}\biggl\|\mathop{\sum }_{k=1}^{n}v_{k}Dy_{1}^{\unicode[STIX]{x1D716},k}\biggr\|_{\mathfrak{ H}}^{2}=\biggl\|\mathop{\sum }_{k=1}^{n}v_{k}Dy_{1}^{\unicode[STIX]{x1D716},k}\biggr\|_{\mathfrak{ H}^{\ast }}^{2}\geqslant c\biggl\|\mathop{\sum }_{k=1}^{n}v_{k}A^{\unicode[STIX]{x1D716},k}\biggr\|_{L^{2}([0,1];\mathbf{R}^{d})}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl\|\mathop{\sum }_{k=1}^{n}v_{k}Dy_{1}^{\unicode[STIX]{x1D716},k}\biggr\|_{\mathfrak{ H}}^{2}=\biggl\|\mathop{\sum }_{k=1}^{n}v_{k}Dy_{1}^{\unicode[STIX]{x1D716},k}\biggr\|_{\mathfrak{ H}^{\ast }}^{2}\geqslant c\biggl\|\mathop{\sum }_{k=1}^{n}v_{k}A^{\unicode[STIX]{x1D716},k}\biggr\|_{L^{2}([0,1];\mathbf{R}^{d})}^{2}.\end{eqnarray}$$ Here, ![]() $c$ is a positive constant independent of
$c$ is a positive constant independent of ![]() $v$ and
$v$ and ![]() $\unicode[STIX]{x1D716}$. Noting
$\unicode[STIX]{x1D716}$. Noting ![]() $|\sum _{k=1}^{n}v_{k}A^{\unicode[STIX]{x1D716},k}(s)|_{\mathbf{R}^{d}}^{2}=\langle v,A^{\unicode[STIX]{x1D716}}(s)A^{\unicode[STIX]{x1D716}}(s)^{\top }v\rangle _{\mathbf{R}^{n}}$, we have
$|\sum _{k=1}^{n}v_{k}A^{\unicode[STIX]{x1D716},k}(s)|_{\mathbf{R}^{d}}^{2}=\langle v,A^{\unicode[STIX]{x1D716}}(s)A^{\unicode[STIX]{x1D716}}(s)^{\top }v\rangle _{\mathbf{R}^{n}}$, we have
 $$\begin{eqnarray}\biggl\|\mathop{\sum }_{k=1}^{n}v_{k}A^{\unicode[STIX]{x1D716},k}\biggr\|_{L^{2}([0,1];\mathbf{R}^{d})}^{2}=\int _{0}^{1}\langle v,A^{\unicode[STIX]{x1D716}}(s)A^{\unicode[STIX]{x1D716}}(s)^{\top }v\rangle _{\boldsymbol{ R}^{n}}\,ds=\langle v,J_{1}^{\unicode[STIX]{x1D716}}C_{\unicode[STIX]{x1D716}}(J_{1}^{\unicode[STIX]{x1D716}})^{\top }v\rangle _{\boldsymbol{ R}^{n}}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl\|\mathop{\sum }_{k=1}^{n}v_{k}A^{\unicode[STIX]{x1D716},k}\biggr\|_{L^{2}([0,1];\mathbf{R}^{d})}^{2}=\int _{0}^{1}\langle v,A^{\unicode[STIX]{x1D716}}(s)A^{\unicode[STIX]{x1D716}}(s)^{\top }v\rangle _{\boldsymbol{ R}^{n}}\,ds=\langle v,J_{1}^{\unicode[STIX]{x1D716}}C_{\unicode[STIX]{x1D716}}(J_{1}^{\unicode[STIX]{x1D716}})^{\top }v\rangle _{\boldsymbol{ R}^{n}}.\end{eqnarray}$$These imply
Hence,
The proof has been completed.
In the rest of this subsection we show Lemma 5.6, following [Reference Cass, Hairer, Litterer and TindelCHLT15] closely. To end this, we regard (3.7) as an RDE driven by ![]() $\mathbf{w}$ with the coefficients
$\mathbf{w}$ with the coefficients ![]() $V_{0}^{\unicode[STIX]{x1D716}}$,
$V_{0}^{\unicode[STIX]{x1D716}}$, ![]() $V_{1}^{\unicode[STIX]{x1D716}},\ldots ,V_{d}^{\unicode[STIX]{x1D716}}$. (Except in the rest of this subsection, we regard (3.7) as an RDE driven by
$V_{1}^{\unicode[STIX]{x1D716}},\ldots ,V_{d}^{\unicode[STIX]{x1D716}}$. (Except in the rest of this subsection, we regard (3.7) as an RDE driven by ![]() $\unicode[STIX]{x1D716}\mathbf{w}$ with the coefficients
$\unicode[STIX]{x1D716}\mathbf{w}$ with the coefficients ![]() $V_{0},V_{1},\ldots ,V_{d}$.) Keeping this in mind, we introduce a quantity which plays an important role in a Norris-type lemma. Note that the quantity is defined in the framework of the controlled path theory. Let
$V_{0},V_{1},\ldots ,V_{d}$.) Keeping this in mind, we introduce a quantity which plays an important role in a Norris-type lemma. Note that the quantity is defined in the framework of the controlled path theory. Let ![]() $(1+\lfloor 1/H\rfloor )^{-1}<\unicode[STIX]{x1D6FC}<H$. Fix
$(1+\lfloor 1/H\rfloor )^{-1}<\unicode[STIX]{x1D6FC}<H$. Fix ![]() $a\in \mathbf{R}^{n}$ and
$a\in \mathbf{R}^{n}$ and ![]() $0<\unicode[STIX]{x1D703}<1$. For every
$0<\unicode[STIX]{x1D703}<1$. For every ![]() $0<\unicode[STIX]{x1D716}<1$, define
$0<\unicode[STIX]{x1D716}<1$, define
Here, ![]() ${\mathcal{N}}_{\mathbf{w},\unicode[STIX]{x1D6FC}}=\sum _{i=1}^{\lfloor 1/H\rfloor }\Vert \mathbf{w}^{i}\Vert _{i\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}$ and
${\mathcal{N}}_{\mathbf{w},\unicode[STIX]{x1D6FC}}=\sum _{i=1}^{\lfloor 1/H\rfloor }\Vert \mathbf{w}^{i}\Vert _{i\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}$ and ![]() $Q_{\mathbf{w}}^{\unicode[STIX]{x1D6FC}}$ stands for the Banach space of controlled paths with respect to
$Q_{\mathbf{w}}^{\unicode[STIX]{x1D6FC}}$ stands for the Banach space of controlled paths with respect to ![]() $\mathbf{w}$. We refer to [Reference Hairer and PillaiHP13, Definition 3] and [Reference Cass, Hairer, Litterer and TindelCHLT15, Definition 5.2] for
$\mathbf{w}$. We refer to [Reference Hairer and PillaiHP13, Definition 3] and [Reference Cass, Hairer, Litterer and TindelCHLT15, Definition 5.2] for ![]() $L_{\unicode[STIX]{x1D703}}(w)$, which is called the modulus of
$L_{\unicode[STIX]{x1D703}}(w)$, which is called the modulus of ![]() $\unicode[STIX]{x1D703}$-Hölder roughness of
$\unicode[STIX]{x1D703}$-Hölder roughness of ![]() $w$, and to [Reference Cass, Hairer, Litterer and TindelCHLT15, Definition 5.1] for
$w$, and to [Reference Cass, Hairer, Litterer and TindelCHLT15, Definition 5.1] for ![]() $\Vert (y^{\unicode[STIX]{x1D716}},J^{\unicode[STIX]{x1D716}},K^{\unicode[STIX]{x1D716}})\Vert _{Q_{\mathbf{w}}^{\unicode[STIX]{x1D6FC}}}$.
$\Vert (y^{\unicode[STIX]{x1D716}},J^{\unicode[STIX]{x1D716}},K^{\unicode[STIX]{x1D716}})\Vert _{Q_{\mathbf{w}}^{\unicode[STIX]{x1D6FC}}}$.
Although we do not discuss the details of ![]() ${\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)$ for concise, we note that expectations of
${\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)$ for concise, we note that expectations of ![]() $r$th power of
$r$th power of ![]() ${\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)$ are bounded in
${\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)$ are bounded in ![]() $\unicode[STIX]{x1D716}$ (Lemma 5.8) and it gives a good estimate of
$\unicode[STIX]{x1D716}$ (Lemma 5.8) and it gives a good estimate of ![]() $\langle v,C^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}$ (Lemma 5.10). Combining these two lemmas, we can prove Lemma 5.6.
$\langle v,C^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}$ (Lemma 5.10). Combining these two lemmas, we can prove Lemma 5.6.
Let us start to prove Lemma 5.6 with the next lemma.
Lemma 5.8. For every ![]() $1<r<\infty$, we have
$1<r<\infty$, we have
Proof. We see ![]() $\mathbf{E}[L_{\unicode[STIX]{x1D703}}(w)^{-r}]<\infty$ for all
$\mathbf{E}[L_{\unicode[STIX]{x1D703}}(w)^{-r}]<\infty$ for all ![]() $r>1$ from [Reference Hairer and PillaiHP13, Lemma 3] and [Reference Cass, Hairer, Litterer and TindelCHLT15, Corollary 5.10]. We obtain
$r>1$ from [Reference Hairer and PillaiHP13, Lemma 3] and [Reference Cass, Hairer, Litterer and TindelCHLT15, Corollary 5.10]. We obtain ![]() $\sup _{0<\unicode[STIX]{x1D716}<1}\mathbf{E}[\Vert (y^{\unicode[STIX]{x1D716}},J^{\unicode[STIX]{x1D716}},K^{\unicode[STIX]{x1D716}})\Vert _{Q_{\mathbf{w}}^{\unicode[STIX]{x1D6FC}}}^{r}]\infty$ for all
$\sup _{0<\unicode[STIX]{x1D716}<1}\mathbf{E}[\Vert (y^{\unicode[STIX]{x1D716}},J^{\unicode[STIX]{x1D716}},K^{\unicode[STIX]{x1D716}})\Vert _{Q_{\mathbf{w}}^{\unicode[STIX]{x1D6FC}}}^{r}]\infty$ for all ![]() $r>1$ by reading carefully [Reference Cass, Hairer, Litterer and TindelCHLT15, Corollary 8.1] and using Lemma 5.7. Finally, since
$r>1$ by reading carefully [Reference Cass, Hairer, Litterer and TindelCHLT15, Corollary 8.1] and using Lemma 5.7. Finally, since ![]() $\Vert \mathbf{w}^{i}\Vert _{i\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}^{1/i}$ has a Gaussian tail, we see
$\Vert \mathbf{w}^{i}\Vert _{i\unicode[STIX]{x1D6FC}\text{-}\text{Hol}}^{1/i}$ has a Gaussian tail, we see ![]() $\mathbf{E}[{\mathcal{N}}_{\mathbf{w},\unicode[STIX]{x1D6FC}}^{r}]<\infty$. The proof is finished.◻
$\mathbf{E}[{\mathcal{N}}_{\mathbf{w},\unicode[STIX]{x1D6FC}}^{r}]<\infty$. The proof is finished.◻
Before stating the next lemma, we make a remark.
Remark 5.9. For every ![]() $v=(v_{1},\ldots ,v_{n})^{\top }\in \mathbf{R}^{n}$, we have
$v=(v_{1},\ldots ,v_{n})^{\top }\in \mathbf{R}^{n}$, we have
which follows from
and
 $$\begin{eqnarray}\displaystyle \langle v,K_{s}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}(y_{s}^{\unicode[STIX]{x1D716}})\{K_{s}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}(y_{s}^{\unicode[STIX]{x1D716}})\}^{\top }v\rangle _{\mathbf{R}^{n}} & = & \displaystyle \langle \{K_{s}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}(y_{s}^{\unicode[STIX]{x1D716}})\}^{\top }v,\{K_{s}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}(y_{s}^{\unicode[STIX]{x1D716}})\}^{\top }v\rangle _{\mathbf{R}^{d}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{d}\langle v,K_{s}^{\unicode[STIX]{x1D716}}V_{i}^{\unicode[STIX]{x1D716}}(y_{s}^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle v,K_{s}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}(y_{s}^{\unicode[STIX]{x1D716}})\{K_{s}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}(y_{s}^{\unicode[STIX]{x1D716}})\}^{\top }v\rangle _{\mathbf{R}^{n}} & = & \displaystyle \langle \{K_{s}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}(y_{s}^{\unicode[STIX]{x1D716}})\}^{\top }v,\{K_{s}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D716}}(y_{s}^{\unicode[STIX]{x1D716}})\}^{\top }v\rangle _{\mathbf{R}^{d}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{d}\langle v,K_{s}^{\unicode[STIX]{x1D716}}V_{i}^{\unicode[STIX]{x1D716}}(y_{s}^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}^{2}.\nonumber\end{eqnarray}$$ We denote by ![]() ${\mathcal{V}}_{m}^{\unicode[STIX]{x1D716}}$ and
${\mathcal{V}}_{m}^{\unicode[STIX]{x1D716}}$ and ![]() ${\mathcal{V}}^{\unicode[STIX]{x1D716}}$ sets of vectors which are defined by replacing
${\mathcal{V}}^{\unicode[STIX]{x1D716}}$ sets of vectors which are defined by replacing ![]() $V_{i}$ by
$V_{i}$ by ![]() $V_{i}^{\unicode[STIX]{x1D716}}$ in Definition 2.1. Then, we see the relationship of
$V_{i}^{\unicode[STIX]{x1D716}}$ in Definition 2.1. Then, we see the relationship of ![]() ${\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)$ and
${\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)$ and ![]() $\langle v,C^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}$ from the following lemma.
$\langle v,C^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}$ from the following lemma.
Lemma 5.10. Let ![]() $m\in \mathbf{N}$. For every
$m\in \mathbf{N}$. For every ![]() $0<\unicode[STIX]{x1D716}<1$,
$0<\unicode[STIX]{x1D716}<1$, ![]() $W\in {\mathcal{V}}_{m}^{\unicode[STIX]{x1D716}}$,
$W\in {\mathcal{V}}_{m}^{\unicode[STIX]{x1D716}}$, ![]() $v\in \mathbf{R}^{n}$ with
$v\in \mathbf{R}^{n}$ with ![]() $|v|=1$ and
$|v|=1$ and ![]() $0\leqslant s\leqslant 1$, we have
$0\leqslant s\leqslant 1$, we have
where ![]() $c_{m}$,
$c_{m}$, ![]() $\unicode[STIX]{x1D707}(m)$ and
$\unicode[STIX]{x1D707}(m)$ and ![]() $\unicode[STIX]{x1D70B}(m)$ are certain positive constants independent of
$\unicode[STIX]{x1D70B}(m)$ are certain positive constants independent of ![]() $\unicode[STIX]{x1D716}$,
$\unicode[STIX]{x1D716}$, ![]() $W$,
$W$, ![]() $v$ and
$v$ and ![]() $s$.
$s$.
Proof. The proof is done by induction on ![]() $m$. Let
$m$. Let ![]() $m=0$. Then,
$m=0$. Then, ![]() $W=V_{i}^{\unicode[STIX]{x1D716}}$ for some
$W=V_{i}^{\unicode[STIX]{x1D716}}$ for some ![]() $1\leqslant i\leqslant d$. Since
$1\leqslant i\leqslant d$. Since ![]() $f_{i}^{\unicode[STIX]{x1D716}}=\langle v,K^{\unicode[STIX]{x1D716}}V_{i}^{\unicode[STIX]{x1D716}}(y^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}$ is
$f_{i}^{\unicode[STIX]{x1D716}}=\langle v,K^{\unicode[STIX]{x1D716}}V_{i}^{\unicode[STIX]{x1D716}}(y^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}$ is ![]() $\unicode[STIX]{x1D6FC}$-Hölder continuous, we can use [Reference Hairer and PillaiHP11, Lemma A.3] to obtain
$\unicode[STIX]{x1D6FC}$-Hölder continuous, we can use [Reference Hairer and PillaiHP11, Lemma A.3] to obtain
Since
holds and ![]() $\Vert f_{i}^{\unicode[STIX]{x1D716}}\Vert _{L^{2}([0,1];\mathbf{R})}\leqslant \langle v,C^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}^{1/2}$ follows from (5.3), we have
$\Vert f_{i}^{\unicode[STIX]{x1D716}}\Vert _{L^{2}([0,1];\mathbf{R})}\leqslant \langle v,C^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}^{1/2}$ follows from (5.3), we have
This is the conclusion for ![]() $m=0$.
$m=0$.
Assuming the conclusion to hold for ![]() $m-1$, we will prove it for
$m-1$, we will prove it for ![]() $m$. Note that for every
$m$. Note that for every ![]() $W\in {\mathcal{V}}_{m}^{\unicode[STIX]{x1D716}}$, there exists
$W\in {\mathcal{V}}_{m}^{\unicode[STIX]{x1D716}}$, there exists ![]() $U\in {\mathcal{V}}_{m-1}^{\unicode[STIX]{x1D716}}$ and
$U\in {\mathcal{V}}_{m-1}^{\unicode[STIX]{x1D716}}$ and ![]() $0\leqslant i\leqslant d$ such that
$0\leqslant i\leqslant d$ such that ![]() $W=[V_{i}^{\unicode[STIX]{x1D716}},U]$. We have
$W=[V_{i}^{\unicode[STIX]{x1D716}},U]$. We have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \langle v,K_{t}^{\unicode[STIX]{x1D716}}U(y_{t}^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}-\langle v,U(a)\rangle _{\mathbf{R}^{n}}\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{i=1}^{d}\int _{0}^{t}\langle v,K_{s}^{\unicode[STIX]{x1D716}}[V_{i}^{\unicode[STIX]{x1D716}},U](y_{s}^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}\,dw_{s}^{i}+\int _{0}^{t}\langle v,K_{s}^{\unicode[STIX]{x1D716}}[V_{0},U](y_{s}^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}\,ds.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \langle v,K_{t}^{\unicode[STIX]{x1D716}}U(y_{t}^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}-\langle v,U(a)\rangle _{\mathbf{R}^{n}}\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{i=1}^{d}\int _{0}^{t}\langle v,K_{s}^{\unicode[STIX]{x1D716}}[V_{i}^{\unicode[STIX]{x1D716}},U](y_{s}^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}\,dw_{s}^{i}+\int _{0}^{t}\langle v,K_{s}^{\unicode[STIX]{x1D716}}[V_{0},U](y_{s}^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}\,ds.\nonumber\end{eqnarray}$$ From a Norris-type lemma ([Reference Cass, Hairer, Litterer and TindelCHLT15, Theorem 5.6], [Reference Hairer and PillaiHP13, Theorem 3.1]), there exist positive constants ![]() $Q$ and
$Q$ and ![]() $R$ such that
$R$ such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \Vert \langle v,K_{\bullet }^{\unicode[STIX]{x1D716}}W(y_{\bullet }^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}\Vert _{\infty }\nonumber\\ \displaystyle & & \displaystyle \qquad \leqslant M{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{Q}\Vert \langle v,K_{\bullet }^{\unicode[STIX]{x1D716}}U(y_{\bullet }^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}-\langle v,U(a)\rangle _{\mathbf{R}^{n}}\Vert _{\infty }^{R}\nonumber\\ \displaystyle & & \displaystyle \qquad \leqslant M{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{Q}(2c_{m-1}{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{\unicode[STIX]{x1D707}(m-1)}\langle v,C^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}^{\unicode[STIX]{x1D70B}(m-1)})^{R}\nonumber\\ \displaystyle & & \displaystyle \qquad =M(2c_{m-1})^{R}{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{Q+\unicode[STIX]{x1D707}(m-1)R}\langle v,C^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}^{\unicode[STIX]{x1D70B}(m-1)R}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \Vert \langle v,K_{\bullet }^{\unicode[STIX]{x1D716}}W(y_{\bullet }^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}\Vert _{\infty }\nonumber\\ \displaystyle & & \displaystyle \qquad \leqslant M{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{Q}\Vert \langle v,K_{\bullet }^{\unicode[STIX]{x1D716}}U(y_{\bullet }^{\unicode[STIX]{x1D716}})\rangle _{\mathbf{R}^{n}}-\langle v,U(a)\rangle _{\mathbf{R}^{n}}\Vert _{\infty }^{R}\nonumber\\ \displaystyle & & \displaystyle \qquad \leqslant M{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{Q}(2c_{m-1}{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{\unicode[STIX]{x1D707}(m-1)}\langle v,C^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}^{\unicode[STIX]{x1D70B}(m-1)})^{R}\nonumber\\ \displaystyle & & \displaystyle \qquad =M(2c_{m-1})^{R}{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{Q+\unicode[STIX]{x1D707}(m-1)R}\langle v,C^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}^{\unicode[STIX]{x1D70B}(m-1)R}\nonumber\end{eqnarray}$$ for some ![]() $M$ depending only on
$M$ depending only on ![]() $d$ and
$d$ and ![]() $n$. This is the conclusion for
$n$. This is the conclusion for ![]() $m$. The proof is finished.◻
$m$. The proof is finished.◻
We are now in a position to show Lemma 5.6.
Proof of Lemma 5.6.
Let ![]() $\unicode[STIX]{x1D708}$ be a positive constant specified later. We will show that, for every
$\unicode[STIX]{x1D708}$ be a positive constant specified later. We will show that, for every ![]() $1<r<\infty$, there exist positive constants
$1<r<\infty$, there exist positive constants ![]() $c_{r,1}$ and
$c_{r,1}$ and ![]() $c_{r,2}$ such that
$c_{r,2}$ such that
for any ![]() $0<\unicode[STIX]{x1D716}<1$ and
$0<\unicode[STIX]{x1D716}<1$ and ![]() $0<\unicode[STIX]{x1D709}<1$. Due to Lemma 8.1, these two estimates are sufficient for Lemma 5.6. Indeed the assertion holds with
$0<\unicode[STIX]{x1D709}<1$. Due to Lemma 8.1, these two estimates are sufficient for Lemma 5.6. Indeed the assertion holds with ![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D708}+1$.
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D708}+1$.
Because (5.4) follows from Lemma 5.7, we show (5.5) in the rest of the proof. Since the vector fields ![]() $V_{0},V_{1},\ldots ,V_{d}$ satisfy the Hörmander condition at
$V_{0},V_{1},\ldots ,V_{d}$ satisfy the Hörmander condition at ![]() $a$, we can choose
$a$, we can choose ![]() $W_{1},\ldots ,W_{n}\in {\mathcal{V}}$ so that
$W_{1},\ldots ,W_{n}\in {\mathcal{V}}$ so that ![]() $W_{1}(a),\ldots ,W_{n}(a)$ linearly spans
$W_{1}(a),\ldots ,W_{n}(a)$ linearly spans ![]() $\mathbf{R}^{n}$. Then, for every
$\mathbf{R}^{n}$. Then, for every ![]() $1\leqslant k\leqslant n$, there exists a non-negative integer
$1\leqslant k\leqslant n$, there exists a non-negative integer ![]() $i_{k}\in \mathbf{N}$ such that
$i_{k}\in \mathbf{N}$ such that ![]() $W_{k}\in {\mathcal{V}}_{i_{k}}$. From the definition of
$W_{k}\in {\mathcal{V}}_{i_{k}}$. From the definition of ![]() ${\mathcal{V}}_{i_{k}}^{\unicode[STIX]{x1D716}}$, we can choose a positive constant
${\mathcal{V}}_{i_{k}}^{\unicode[STIX]{x1D716}}$, we can choose a positive constant ![]() $\unicode[STIX]{x1D70C}_{k}$ such that
$\unicode[STIX]{x1D70C}_{k}$ such that ![]() $W_{k}^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70C}_{k}}W_{k}\in {\mathcal{V}}_{i_{k}}^{\unicode[STIX]{x1D716}}$. Set
$W_{k}^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70C}_{k}}W_{k}\in {\mathcal{V}}_{i_{k}}^{\unicode[STIX]{x1D716}}$. Set ![]() $\unicode[STIX]{x1D70C}=\max \{\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{n}\}$. We define
$\unicode[STIX]{x1D70C}=\max \{\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{n}\}$. We define
for every ![]() $u\in \mathbf{R}^{n}$ with
$u\in \mathbf{R}^{n}$ with ![]() $|u|=1$. Then,
$|u|=1$. Then, ![]() $\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D716}}(u)\geqslant \unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D719}(u)$ for any
$\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D716}}(u)\geqslant \unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D719}(u)$ for any ![]() $|u|=1$. Since
$|u|=1$. Since ![]() $W_{1}^{\unicode[STIX]{x1D716}}(a),\ldots ,W_{n}^{\unicode[STIX]{x1D716}}(a)$ spans linearly
$W_{1}^{\unicode[STIX]{x1D716}}(a),\ldots ,W_{n}^{\unicode[STIX]{x1D716}}(a)$ spans linearly ![]() $\mathbf{R}^{n}$ and
$\mathbf{R}^{n}$ and ![]() $\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D716}}$ is continuous,
$\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D716}}$ is continuous, ![]() $\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D716}}$ attains the positive minimum. Let
$\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D716}}$ attains the positive minimum. Let ![]() $c_{m}$,
$c_{m}$, ![]() $\unicode[STIX]{x1D707}(m)$ and
$\unicode[STIX]{x1D707}(m)$ and ![]() $\unicode[STIX]{x1D70B}(m)$ be the same symbols as Lemma 5.10 and set
$\unicode[STIX]{x1D70B}(m)$ be the same symbols as Lemma 5.10 and set ![]() $c=\max \{c_{i_{1}},\ldots ,c_{i_{n}}\}$,
$c=\max \{c_{i_{1}},\ldots ,c_{i_{n}}\}$, ![]() $\unicode[STIX]{x1D707}=\max \{\unicode[STIX]{x1D707}_{i_{1}},\ldots ,\unicode[STIX]{x1D707}_{i_{n}}\}$, and
$\unicode[STIX]{x1D707}=\max \{\unicode[STIX]{x1D707}_{i_{1}},\ldots ,\unicode[STIX]{x1D707}_{i_{n}}\}$, and ![]() $\unicode[STIX]{x1D70B}=\min \{\unicode[STIX]{x1D70B}_{i_{1}},\ldots ,\unicode[STIX]{x1D70B}_{i_{n}}\}$. Set
$\unicode[STIX]{x1D70B}=\min \{\unicode[STIX]{x1D70B}_{i_{1}},\ldots ,\unicode[STIX]{x1D70B}_{i_{n}}\}$. Set ![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70B}$.
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70B}$.
We choose ![]() $v\in \mathbf{R}^{n}$ with
$v\in \mathbf{R}^{n}$ with ![]() $|v|=1$ and
$|v|=1$ and ![]() $\unicode[STIX]{x1D716}>0$ arbitrarily. For
$\unicode[STIX]{x1D716}>0$ arbitrarily. For ![]() $v$ and
$v$ and ![]() $\unicode[STIX]{x1D716}$, there exists
$\unicode[STIX]{x1D716}$, there exists ![]() $1\leqslant k_{0}\equiv k_{0}(v,\unicode[STIX]{x1D716})\leqslant n$ such that
$1\leqslant k_{0}\equiv k_{0}(v,\unicode[STIX]{x1D716})\leqslant n$ such that ![]() $\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D716}}(v)=|\langle v,W_{k_{0}}^{\unicode[STIX]{x1D716}}(a)\rangle _{\boldsymbol{ R}^{n}}|$. From Lemma 5.10 and the above, we have
$\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D716}}(v)=|\langle v,W_{k_{0}}^{\unicode[STIX]{x1D716}}(a)\rangle _{\boldsymbol{ R}^{n}}|$. From Lemma 5.10 and the above, we have
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \{|\langle v,W_{k_{0}}^{\unicode[STIX]{x1D716}}(a)\rangle _{\boldsymbol{ R}^{n}}|<c_{i_{k_{0}}}{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{\unicode[STIX]{x1D707}(i_{k_{0}})}\unicode[STIX]{x1D709}^{\unicode[STIX]{x1D70B}(i_{k_{0}})}\}\nonumber\\ \displaystyle & & \displaystyle \qquad \subset \{\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D719}(v)<c{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D709}^{\unicode[STIX]{x1D70B}}\}\nonumber\\ \displaystyle & & \displaystyle \qquad =\{\unicode[STIX]{x1D719}(v)<c{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D709}^{\unicode[STIX]{x1D70B}}\}\nonumber\\ \displaystyle & & \displaystyle \qquad \subset \{\min _{|v|=1}\unicode[STIX]{x1D719}(v)<c{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D709}^{\unicode[STIX]{x1D70B}}\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \{|\langle v,W_{k_{0}}^{\unicode[STIX]{x1D716}}(a)\rangle _{\boldsymbol{ R}^{n}}|<c_{i_{k_{0}}}{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{\unicode[STIX]{x1D707}(i_{k_{0}})}\unicode[STIX]{x1D709}^{\unicode[STIX]{x1D70B}(i_{k_{0}})}\}\nonumber\\ \displaystyle & & \displaystyle \qquad \subset \{\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D719}(v)<c{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D709}^{\unicode[STIX]{x1D70B}}\}\nonumber\\ \displaystyle & & \displaystyle \qquad =\{\unicode[STIX]{x1D719}(v)<c{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D709}^{\unicode[STIX]{x1D70B}}\}\nonumber\\ \displaystyle & & \displaystyle \qquad \subset \{\min _{|v|=1}\unicode[STIX]{x1D719}(v)<c{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D709}^{\unicode[STIX]{x1D70B}}\}.\nonumber\end{eqnarray}$$From the Markov inequality, we see
Noting ![]() $\mathbf{E}[{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{\unicode[STIX]{x1D707}r/\unicode[STIX]{x1D70B}}]$ are bounded from above in
$\mathbf{E}[{\mathcal{L}}_{w}^{\unicode[STIX]{x1D716}}(a,\unicode[STIX]{x1D703},1)^{\unicode[STIX]{x1D707}r/\unicode[STIX]{x1D70B}}]$ are bounded from above in ![]() $\unicode[STIX]{x1D716}$, we obtain (5.5).
$\unicode[STIX]{x1D716}$, we obtain (5.5).
5.3 Covariance matrix of the solution of scaled–shifted RDE driven by fBm
In this subsection, we will show Proposition 5.4. Let ![]() $1/H<p<\lfloor 1/H\rfloor +1$ and
$1/H<p<\lfloor 1/H\rfloor +1$ and ![]() $(H+1/2)^{-1}<q<2$ satisfy
$(H+1/2)^{-1}<q<2$ satisfy ![]() $1/p+1/q>1$. We start our discussion with making a remark on continuity of
$1/p+1/q>1$. We start our discussion with making a remark on continuity of ![]() $Q$ on
$Q$ on ![]() $G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$, where
$G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$, where ![]() $\unicode[STIX]{x1D706}$ is a one-dimensional path defined by
$\unicode[STIX]{x1D706}$ is a one-dimensional path defined by ![]() $\unicode[STIX]{x1D706}_{t}=t$. Recall that the solution maps
$\unicode[STIX]{x1D706}_{t}=t$. Recall that the solution maps ![]() $(\mathbf{x},c\unicode[STIX]{x1D706})\mapsto y,J,K$ are continuous on
$(\mathbf{x},c\unicode[STIX]{x1D706})\mapsto y,J,K$ are continuous on ![]() $G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$, where
$G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$, where ![]() $y$,
$y$, ![]() $J$ and
$J$ and ![]() $K$ are solutions to (3.4), (3.5) and (3.6) driven by
$K$ are solutions to (3.4), (3.5) and (3.6) driven by ![]() $(x,c\unicode[STIX]{x1D706})$, respectively. Furthermore,
$(x,c\unicode[STIX]{x1D706})$, respectively. Furthermore, ![]() $Dy_{1}$ is continuous in
$Dy_{1}$ is continuous in ![]() $y$,
$y$, ![]() $J$ and
$J$ and ![]() $K$ since the right-hand side of (5.1) is Young integration and Young integration is continuous in both integrands and integrators. Note that the embedding
$K$ since the right-hand side of (5.1) is Young integration and Young integration is continuous in both integrands and integrators. Note that the embedding ![]() $\mathfrak{H}\subset C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ with
$\mathfrak{H}\subset C_{0}^{q\text{-}\text{var}}([0,1];\mathbf{R}^{d})$ with ![]() $1/p+1/q>1$ holds. Hence, we see that
$1/p+1/q>1$ holds. Hence, we see that ![]() $Q$ is continuous on
$Q$ is continuous on ![]() $G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$. We are now in a position to prove Proposition 5.4.
$G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$. We are now in a position to prove Proposition 5.4.
Proof of Proposition 5.4.
From the continuity of ![]() $Q$ at
$Q$ at ![]() $(\boldsymbol{\unicode[STIX]{x1D6FE}},0)\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$ and the assumption on
$(\boldsymbol{\unicode[STIX]{x1D6FE}},0)\in G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$ and the assumption on ![]() $\unicode[STIX]{x1D6FE}$, there exists an open set
$\unicode[STIX]{x1D6FE}$, there exists an open set ![]() $O\subset G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$ such that
$O\subset G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle$ such that
for any ![]() $(\mathbf{x},k)\in O$. Note that
$(\mathbf{x},k)\in O$. Note that ![]() $O$ contains
$O$ contains ![]() $(\mathbf{0},0)$. (Here,
$(\mathbf{0},0)$. (Here, ![]() $(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FE}}(\mathbf{x}),\mathbf{k})$ is the Young pairing and
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FE}}(\mathbf{x}),\mathbf{k})$ is the Young pairing and ![]() $(\mathbf{x},k)$ is a pair. In this proof, both of them will appear.)
$(\mathbf{x},k)$ is a pair. In this proof, both of them will appear.)
We decompose ![]() $\mathbf{E}[|\!\det \tilde{Q}^{\unicode[STIX]{x1D716}}|^{-r}]$ into expectations on
$\mathbf{E}[|\!\det \tilde{Q}^{\unicode[STIX]{x1D716}}|^{-r}]$ into expectations on ![]() $U_{\unicode[STIX]{x1D716}}=\{w\in \unicode[STIX]{x1D6FA}\mid (\unicode[STIX]{x1D716}\mathbf{w},\unicode[STIX]{x1D716}^{1/H}\unicode[STIX]{x1D706})\in O\}$ and
$U_{\unicode[STIX]{x1D716}}=\{w\in \unicode[STIX]{x1D6FA}\mid (\unicode[STIX]{x1D716}\mathbf{w},\unicode[STIX]{x1D716}^{1/H}\unicode[STIX]{x1D706})\in O\}$ and ![]() $U_{\unicode[STIX]{x1D716}}^{\complement }$. First, we study the expectation on
$U_{\unicode[STIX]{x1D716}}^{\complement }$. First, we study the expectation on ![]() $U_{\unicode[STIX]{x1D716}}$. Since
$U_{\unicode[STIX]{x1D716}}$. Since ![]() $\tilde{Q}^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}^{2}Q(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D716}\mathbf{w}),\unicode[STIX]{x1D716}^{1/H}\boldsymbol{\unicode[STIX]{x1D706}})$ and (5.6), we see
$\tilde{Q}^{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}^{2}Q(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D716}\mathbf{w}),\unicode[STIX]{x1D716}^{1/H}\boldsymbol{\unicode[STIX]{x1D706}})$ and (5.6), we see
which implies
Next we consider the expectation on ![]() $U_{\unicode[STIX]{x1D716}}^{\complement }$. From the Hölder inequality, we have
$U_{\unicode[STIX]{x1D716}}^{\complement }$. From the Hölder inequality, we have
Since the rate function of the Schilder-type large deviation principle is good, we see that there exists a positive constant ![]() $c_{2}$ such that
$c_{2}$ such that
for small ![]() $\unicode[STIX]{x1D716}>0$. Here, we choose
$\unicode[STIX]{x1D716}>0$. Here, we choose ![]() $1<q<\infty$ so that
$1<q<\infty$ so that ![]() $(q-1)\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}<c_{2}$ and set
$(q-1)\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}<c_{2}$ and set ![]() $1<q^{\prime }<\infty$ as the Hölder conjugate of
$1<q^{\prime }<\infty$ as the Hölder conjugate of ![]() $q$. The Girsanov theorem and Proposition 5.3 imply
$q$. The Girsanov theorem and Proposition 5.3 imply
 $$\begin{eqnarray}\displaystyle \mathbf{E}[|\!\det \tilde{Q}^{\unicode[STIX]{x1D716}}|^{-2r}]^{1/2} & = & \displaystyle \mathbf{E}\biggl[|\!\det Q^{\unicode[STIX]{x1D716}}|^{-2r}\exp \biggl(\langle w,\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D716}}\rangle -\frac{\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}}{2\unicode[STIX]{x1D716}^{2}}\biggr)\biggr]^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathbf{E}[|\!\det Q^{\unicode[STIX]{x1D716}}|^{-2rq^{\prime }}]^{1/2q^{\prime }}\mathbf{E}\bigg[\exp \biggl(q\bigg\{\langle w,\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D716}}\rangle -\frac{\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}}{2\unicode[STIX]{x1D716}^{2}}\bigg\}\biggr)\bigg]^{1/2q}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (c_{3}\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D707}})^{r}\exp \bigg(\frac{(q-1)\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}}{4\unicode[STIX]{x1D716}^{2}}\bigg).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{E}[|\!\det \tilde{Q}^{\unicode[STIX]{x1D716}}|^{-2r}]^{1/2} & = & \displaystyle \mathbf{E}\biggl[|\!\det Q^{\unicode[STIX]{x1D716}}|^{-2r}\exp \biggl(\langle w,\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D716}}\rangle -\frac{\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}}{2\unicode[STIX]{x1D716}^{2}}\biggr)\biggr]^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathbf{E}[|\!\det Q^{\unicode[STIX]{x1D716}}|^{-2rq^{\prime }}]^{1/2q^{\prime }}\mathbf{E}\bigg[\exp \biggl(q\bigg\{\langle w,\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D716}}\rangle -\frac{\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}}{2\unicode[STIX]{x1D716}^{2}}\bigg\}\biggr)\bigg]^{1/2q}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (c_{3}\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D707}})^{r}\exp \bigg(\frac{(q-1)\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}}{4\unicode[STIX]{x1D716}^{2}}\bigg).\nonumber\end{eqnarray}$$From the above, we see
The estimates (5.7) and (5.8) imply
 $$\begin{eqnarray}\displaystyle \mathbf{E}[|\!\det \unicode[STIX]{x1D716}^{-2}\tilde{Q}^{\unicode[STIX]{x1D716}}|^{-r}] & = & \displaystyle \unicode[STIX]{x1D716}^{2nr}\mathbf{E}[|\!\det \tilde{Q}^{\unicode[STIX]{x1D716}}|^{-r}]\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D716}^{2nr}\bigg\{(c_{1}\unicode[STIX]{x1D716}^{2})^{-nr}+c_{3}^{r}\unicode[STIX]{x1D716}^{-r\unicode[STIX]{x1D707}}\exp \bigg(-\frac{c_{2}-(q-1)\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}}{4\unicode[STIX]{x1D716}^{2}}\bigg)\bigg\}\nonumber\\ \displaystyle & = & \displaystyle c_{1}^{-nr}+c_{3}^{r}\unicode[STIX]{x1D716}^{(2n-\unicode[STIX]{x1D707})r}\exp \bigg(-\frac{c_{2}-(q-1)\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}}{4\unicode[STIX]{x1D716}^{2}}\bigg).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{E}[|\!\det \unicode[STIX]{x1D716}^{-2}\tilde{Q}^{\unicode[STIX]{x1D716}}|^{-r}] & = & \displaystyle \unicode[STIX]{x1D716}^{2nr}\mathbf{E}[|\!\det \tilde{Q}^{\unicode[STIX]{x1D716}}|^{-r}]\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D716}^{2nr}\bigg\{(c_{1}\unicode[STIX]{x1D716}^{2})^{-nr}+c_{3}^{r}\unicode[STIX]{x1D716}^{-r\unicode[STIX]{x1D707}}\exp \bigg(-\frac{c_{2}-(q-1)\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}}{4\unicode[STIX]{x1D716}^{2}}\bigg)\bigg\}\nonumber\\ \displaystyle & = & \displaystyle c_{1}^{-nr}+c_{3}^{r}\unicode[STIX]{x1D716}^{(2n-\unicode[STIX]{x1D707})r}\exp \bigg(-\frac{c_{2}-(q-1)\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}}{4\unicode[STIX]{x1D716}^{2}}\bigg).\nonumber\end{eqnarray}$$ The right-hand side is bounded as ![]() $\unicode[STIX]{x1D716}{\searrow}0$. The proof has finished.◻
$\unicode[STIX]{x1D716}{\searrow}0$. The proof has finished.◻
6 Off-diagonal short time asymptotics
In this section, following Watanabe [Reference WatanabeWat87], we prove the short time asymptotics of kernel function ![]() $p_{t}(a,a^{\prime })$ when
$p_{t}(a,a^{\prime })$ when ![]() $a\neq a^{\prime }$ and
$a\neq a^{\prime }$ and ![]() $1/4<H\leqslant 1/2$. Unlike in [Reference WatanabeWat87], we can localize around the energy minimizing path in the geometric rough path space in this paper, since the Lyons–Itô map is continuous in this setting. (The case
$1/4<H\leqslant 1/2$. Unlike in [Reference WatanabeWat87], we can localize around the energy minimizing path in the geometric rough path space in this paper, since the Lyons–Itô map is continuous in this setting. (The case ![]() $H>1/2$ was done in [Reference InahamaIna16a] and the case
$H>1/2$ was done in [Reference InahamaIna16a] and the case ![]() $1/3<H\leqslant 1/2$ was done in [Reference InahamaIna16b].)
$1/3<H\leqslant 1/2$ was done in [Reference InahamaIna16b].)
Hereafter in this section, we fix ![]() $1/4<H\leqslant 1/2$. Let
$1/4<H\leqslant 1/2$. Let ![]() $(1+\lfloor 1/H\rfloor )^{-1}<\unicode[STIX]{x1D6FC}<H$ and choose
$(1+\lfloor 1/H\rfloor )^{-1}<\unicode[STIX]{x1D6FC}<H$ and choose ![]() $m\in \mathbf{N}_{+}$ such that
$m\in \mathbf{N}_{+}$ such that ![]() $H-\unicode[STIX]{x1D6FC}>2/m$. Set
$H-\unicode[STIX]{x1D6FC}>2/m$. Set ![]() $p=1/\unicode[STIX]{x1D6FC}$ and
$p=1/\unicode[STIX]{x1D6FC}$ and ![]() $q=(H+1/2-1/m)^{-1}$.
$q=(H+1/2-1/m)^{-1}$.
6.1 Localization around energy minimizing path
Let us introduce a cut-off function for the localization. Let ![]() $\bar{\unicode[STIX]{x1D6FE}}\in \mathfrak{H}$ be as in (A2) and
$\bar{\unicode[STIX]{x1D6FE}}\in \mathfrak{H}$ be as in (A2) and ![]() $\unicode[STIX]{x1D716}>0$. Since
$\unicode[STIX]{x1D716}>0$. Since ![]() $\Vert \mathbf{w}^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{12m/i}$ is an element of an inhomogeneous Wiener chaos of order
$\Vert \mathbf{w}^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{12m/i}$ is an element of an inhomogeneous Wiener chaos of order ![]() $12m$, so is its Cameron–Martin shift
$12m$, so is its Cameron–Martin shift ![]() $\Vert \unicode[STIX]{x1D70F}_{-\bar{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D716}\mathbf{w})^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{12m/i}$. Here,
$\Vert \unicode[STIX]{x1D70F}_{-\bar{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D716}\mathbf{w})^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{12m/i}$. Here, ![]() $\unicode[STIX]{x1D70F}_{-\bar{\unicode[STIX]{x1D6FE}}}$ is the Young translation by
$\unicode[STIX]{x1D70F}_{-\bar{\unicode[STIX]{x1D6FE}}}$ is the Young translation by ![]() $-\bar{\unicode[STIX]{x1D6FE}}$. It is a continuous map from
$-\bar{\unicode[STIX]{x1D6FE}}$. It is a continuous map from ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})$ to itself. So, this Wiener functional is defined for almost all
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})$ to itself. So, this Wiener functional is defined for almost all ![]() $w\in \unicode[STIX]{x1D6FA}$. For any
$w\in \unicode[STIX]{x1D6FA}$. For any ![]() $r\in (1,\infty )$,
$r\in (1,\infty )$, ![]() $L^{r}$-norm of this Wiener functional is bounded in
$L^{r}$-norm of this Wiener functional is bounded in ![]() $\unicode[STIX]{x1D716}$. Hence, so is its
$\unicode[STIX]{x1D716}$. Hence, so is its ![]() $\mathbf{D}_{r,k}$-norm for any
$\mathbf{D}_{r,k}$-norm for any ![]() $r,k$. Due to this fact, the localization is allowed even in the framework of Watanabe distribution theory. This is the reason why we use this Besov-type norm on the geometric rough path space. Let
$r,k$. Due to this fact, the localization is allowed even in the framework of Watanabe distribution theory. This is the reason why we use this Besov-type norm on the geometric rough path space. Let ![]() $\unicode[STIX]{x1D713}:\mathbf{R}\rightarrow [0,1]$ be a smooth function such that
$\unicode[STIX]{x1D713}:\mathbf{R}\rightarrow [0,1]$ be a smooth function such that ![]() $\unicode[STIX]{x1D713}(u)=1$ if
$\unicode[STIX]{x1D713}(u)=1$ if ![]() $|u|\leqslant 1/2$ and
$|u|\leqslant 1/2$ and ![]() $\unicode[STIX]{x1D713}(u)=0$ if
$\unicode[STIX]{x1D713}(u)=0$ if ![]() $|u|\geqslant 1$. For each
$|u|\geqslant 1$. For each ![]() $\unicode[STIX]{x1D702}>0$ and
$\unicode[STIX]{x1D702}>0$ and ![]() $\unicode[STIX]{x1D716}>0$, we set
$\unicode[STIX]{x1D716}>0$, we set
 $$\begin{eqnarray}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D716},w)=\mathop{\prod }_{i=1}^{\lfloor 1/H\rfloor }\unicode[STIX]{x1D713}\bigg(\frac{\Vert \unicode[STIX]{x1D70F}_{-\bar{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D716}\mathbf{w})^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{12m/i}}{\unicode[STIX]{x1D702}^{12m}}\bigg).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D716},w)=\mathop{\prod }_{i=1}^{\lfloor 1/H\rfloor }\unicode[STIX]{x1D713}\bigg(\frac{\Vert \unicode[STIX]{x1D70F}_{-\bar{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D716}\mathbf{w})^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{12m/i}}{\unicode[STIX]{x1D702}^{12m}}\bigg).\end{eqnarray}$$ The following lemma states that only rough paths sufficiently close to the lift of the minimizer ![]() $\bar{\unicode[STIX]{x1D6FE}}$ contribute to the asymptotics. The keys of the proof are (i) the Schilder-type large deviations for fractional Brownian rough path and (ii) the Kusuoka–Stroock type estimate of the Malliavin covariance of
$\bar{\unicode[STIX]{x1D6FE}}$ contribute to the asymptotics. The keys of the proof are (i) the Schilder-type large deviations for fractional Brownian rough path and (ii) the Kusuoka–Stroock type estimate of the Malliavin covariance of ![]() $y_{1}^{\unicode[STIX]{x1D716}}$ (Proposition 5.3).
$y_{1}^{\unicode[STIX]{x1D716}}$ (Proposition 5.3).
Lemma 6.1. Suppose that ![]() $\text{(A1)}$ and
$\text{(A1)}$ and ![]() $\text{(A2)}$ hold. Then, for any
$\text{(A2)}$ hold. Then, for any ![]() $\unicode[STIX]{x1D702}>0$, there exists
$\unicode[STIX]{x1D702}>0$, there exists ![]() $c=c_{\unicode[STIX]{x1D702}}>0$ such that
$c=c_{\unicode[STIX]{x1D702}}>0$ such that
Proof. We show the assertion for ![]() $1/4<H\leqslant 1/3$. We can show it for
$1/4<H\leqslant 1/3$. We can show it for ![]() $1/3<H\leqslant 1/2$ more easily.
$1/3<H\leqslant 1/2$ more easily.
Set ![]() $p_{\unicode[STIX]{x1D716}}=\mathbf{E}[(1-\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D716},w))\unicode[STIX]{x1D6FF}_{a^{\prime }}(y_{1}^{\unicode[STIX]{x1D716}})]$. We take
$p_{\unicode[STIX]{x1D716}}=\mathbf{E}[(1-\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D716},w))\unicode[STIX]{x1D6FF}_{a^{\prime }}(y_{1}^{\unicode[STIX]{x1D716}})]$. We take ![]() $\unicode[STIX]{x1D702}^{\prime }>0$ arbitrarily and fix it for a while. It is obvious that
$\unicode[STIX]{x1D702}^{\prime }>0$ arbitrarily and fix it for a while. It is obvious that
Set ![]() $A(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{3})=1-\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709}_{1})\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709}_{3})$ for
$A(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{3})=1-\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709}_{1})\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709}_{2})\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709}_{3})$ for ![]() $\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{3})\in \mathbf{R}^{3}$ and write
$\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{3})\in \mathbf{R}^{3}$ and write ![]() $(\unicode[STIX]{x1D709}_{i};i=1,2,3)=(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{3})$. Set
$(\unicode[STIX]{x1D709}_{i};i=1,2,3)=(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{3})$. Set ![]() $g(u)=u\vee 0$ for
$g(u)=u\vee 0$ for ![]() $u\in \mathbf{R}$. Then, in the sense of distributional derivative,
$u\in \mathbf{R}$. Then, in the sense of distributional derivative, ![]() $g^{\prime \prime }=\unicode[STIX]{x1D6FF}_{0}$. Take a bounded continuous function
$g^{\prime \prime }=\unicode[STIX]{x1D6FF}_{0}$. Take a bounded continuous function ![]() $C:\mathbf{R}^{n}\rightarrow \mathbf{R}$ such that
$C:\mathbf{R}^{n}\rightarrow \mathbf{R}$ such that ![]() $C(u_{1},\ldots ,u_{n})=g(u_{1}-a_{1}^{\prime })g(u_{2}-a_{2}^{\prime })\cdots g(u_{n}-a_{n}^{\prime })$ if
$C(u_{1},\ldots ,u_{n})=g(u_{1}-a_{1}^{\prime })g(u_{2}-a_{2}^{\prime })\cdots g(u_{n}-a_{n}^{\prime })$ if ![]() $|u-a^{\prime }|\leqslant 2\unicode[STIX]{x1D702}^{\prime }$. Then,
$|u-a^{\prime }|\leqslant 2\unicode[STIX]{x1D702}^{\prime }$. Then,
Now, we use integration by parts formula for generalized expectations as in [Reference WatanabeWat87, Reference Ikeda and WatanabeIW89] to see that ![]() $p_{\unicode[STIX]{x1D716}}$ is equal to a finite sum of the following form;
$p_{\unicode[STIX]{x1D716}}$ is equal to a finite sum of the following form;
Here ![]() $j=(j_{1},j_{2},j_{3})$ and
$j=(j_{1},j_{2},j_{3})$ and ![]() $k$ run over finite subsets of
$k$ run over finite subsets of ![]() $\mathbf{N}^{3}$ and
$\mathbf{N}^{3}$ and ![]() $\mathbf{N}$, respectively,
$\mathbf{N}$, respectively, ![]() $\unicode[STIX]{x1D6FB}^{j}A=\unicode[STIX]{x2202}_{1}^{j_{1}}\unicode[STIX]{x2202}_{2}^{j_{2}}\unicode[STIX]{x2202}_{3}^{j_{3}}A$ and
$\unicode[STIX]{x1D6FB}^{j}A=\unicode[STIX]{x2202}_{1}^{j_{1}}\unicode[STIX]{x2202}_{2}^{j_{2}}\unicode[STIX]{x2202}_{3}^{j_{3}}A$ and ![]() $F_{j,k}(\unicode[STIX]{x1D716},w)$ is a polynomial in components of the following (i)–(iv): (i)
$F_{j,k}(\unicode[STIX]{x1D716},w)$ is a polynomial in components of the following (i)–(iv): (i) ![]() $y_{1}^{\unicode[STIX]{x1D716}}$ and its derivatives, (ii)
$y_{1}^{\unicode[STIX]{x1D716}}$ and its derivatives, (ii) ![]() $\Vert \unicode[STIX]{x1D70F}_{-\bar{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D716}\mathbf{w})^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{12m/i}$ and its derivatives, (iii)
$\Vert \unicode[STIX]{x1D70F}_{-\bar{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D716}\mathbf{w})^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{12m/i}$ and its derivatives, (iii) ![]() $Q^{\unicode[STIX]{x1D716}}$, which is Malliavin covariance matrix of
$Q^{\unicode[STIX]{x1D716}}$, which is Malliavin covariance matrix of ![]() $y_{1}^{\unicode[STIX]{x1D716}}$ and its derivatives, and (iv)
$y_{1}^{\unicode[STIX]{x1D716}}$ and its derivatives, and (iv) ![]() $(Q^{\unicode[STIX]{x1D716}})^{-1}$. Note that the derivatives of
$(Q^{\unicode[STIX]{x1D716}})^{-1}$. Note that the derivatives of ![]() $(Q^{\unicode[STIX]{x1D716}})^{-1}$ do not appear.
$(Q^{\unicode[STIX]{x1D716}})^{-1}$ do not appear.
From Propositions 5.1 and 5.3, there exists ![]() $\unicode[STIX]{x1D70C}>0$ such that
$\unicode[STIX]{x1D70C}>0$ such that ![]() $|(Q^{\unicode[STIX]{x1D716}})^{-1}|=O(\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D70C}})$ in
$|(Q^{\unicode[STIX]{x1D716}})^{-1}|=O(\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D70C}})$ in ![]() $L^{r}$ as
$L^{r}$ as ![]() $\unicode[STIX]{x1D716}{\searrow}0$ for all
$\unicode[STIX]{x1D716}{\searrow}0$ for all ![]() $1<r<\infty$. (Recall a well-known formula to obtain the inverse matrix
$1<r<\infty$. (Recall a well-known formula to obtain the inverse matrix ![]() $A^{-1}$ with the adjugate matrix of
$A^{-1}$ with the adjugate matrix of ![]() $A$ divided by
$A$ divided by ![]() $\det A$.) Therefore, there exists
$\det A$.) Therefore, there exists ![]() $\unicode[STIX]{x1D70C}>0$ such that
$\unicode[STIX]{x1D70C}>0$ such that ![]() $|F_{j,k}(\unicode[STIX]{x1D716})|=O(\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D70C}})$ in any
$|F_{j,k}(\unicode[STIX]{x1D716})|=O(\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D70C}})$ in any ![]() $L^{r}$-norm. (
$L^{r}$-norm. (![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(r)>0$ may change from line to line.) By Hölder’s inequality, we have
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}(r)>0$ may change from line to line.) By Hölder’s inequality, we have
 $$\begin{eqnarray}\displaystyle \qquad p_{\unicode[STIX]{x1D716}} & {\leqslant} & \displaystyle \frac{c}{\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70C}}}\mathop{\sum }_{j,k}\mathbf{E}\bigg[\bigg|\unicode[STIX]{x1D6FB}^{j}A\bigg(\frac{\Vert \unicode[STIX]{x1D70F}_{-\bar{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D716}\mathbf{w})^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{12m}}{\unicode[STIX]{x1D702}^{12m}};i=1,2,3\bigg)\bigg|^{r^{\prime }}\bigg|\unicode[STIX]{x1D713}^{(k)}\bigg(\frac{|y_{1}^{\unicode[STIX]{x1D716}}-a^{\prime }|^{2}}{{\unicode[STIX]{x1D702}^{\prime }}^{2}}\bigg)\bigg|^{r^{\prime }}\bigg]^{1/r^{\prime }}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{c}{\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70C}}}\mathbf{P}\bigg[\mathop{\bigcup }_{i=1}^{3}\bigg\{\Vert \unicode[STIX]{x1D70F}_{-\bar{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D716}\mathbf{w})^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{1/i}\geqslant \frac{\unicode[STIX]{x1D702}}{2^{1/(12m)}}\bigg\}\cap \{|y_{1}^{\unicode[STIX]{x1D716}}-a^{\prime }|\leqslant \unicode[STIX]{x1D702}^{\prime }\}\bigg]^{1/r^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \qquad p_{\unicode[STIX]{x1D716}} & {\leqslant} & \displaystyle \frac{c}{\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70C}}}\mathop{\sum }_{j,k}\mathbf{E}\bigg[\bigg|\unicode[STIX]{x1D6FB}^{j}A\bigg(\frac{\Vert \unicode[STIX]{x1D70F}_{-\bar{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D716}\mathbf{w})^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{12m}}{\unicode[STIX]{x1D702}^{12m}};i=1,2,3\bigg)\bigg|^{r^{\prime }}\bigg|\unicode[STIX]{x1D713}^{(k)}\bigg(\frac{|y_{1}^{\unicode[STIX]{x1D716}}-a^{\prime }|^{2}}{{\unicode[STIX]{x1D702}^{\prime }}^{2}}\bigg)\bigg|^{r^{\prime }}\bigg]^{1/r^{\prime }}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{c}{\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D70C}}}\mathbf{P}\bigg[\mathop{\bigcup }_{i=1}^{3}\bigg\{\Vert \unicode[STIX]{x1D70F}_{-\bar{\unicode[STIX]{x1D6FE}}}(\unicode[STIX]{x1D716}\mathbf{w})^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{1/i}\geqslant \frac{\unicode[STIX]{x1D702}}{2^{1/(12m)}}\bigg\}\cap \{|y_{1}^{\unicode[STIX]{x1D716}}-a^{\prime }|\leqslant \unicode[STIX]{x1D702}^{\prime }\}\bigg]^{1/r^{\prime }}.\end{eqnarray}$$ Here, ![]() $1/r+1/r^{\prime }=1$ and
$1/r+1/r^{\prime }=1$ and ![]() $c=c(r,r^{\prime },\unicode[STIX]{x1D702},\unicode[STIX]{x1D702}^{\prime })$ is a positive constant, which may change from line to line. Set
$c=c(r,r^{\prime },\unicode[STIX]{x1D702},\unicode[STIX]{x1D702}^{\prime })$ is a positive constant, which may change from line to line. Set ![]() $U_{\unicode[STIX]{x1D702}^{\prime \prime }}=\bigcap _{i=1}^{3}\{\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})\mid \Vert \mathbf{x}^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{1/i}<\unicode[STIX]{x1D702}^{\prime \prime }\}$ for
$U_{\unicode[STIX]{x1D702}^{\prime \prime }}=\bigcap _{i=1}^{3}\{\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})\mid \Vert \mathbf{x}^{i}\Vert _{(i\unicode[STIX]{x1D6FC},12m/i)\text{-}\text{Bes}}^{1/i}<\unicode[STIX]{x1D702}^{\prime \prime }\}$ for ![]() $\unicode[STIX]{x1D702}^{\prime \prime }>0$. Then this forms a fundamental system of open neighborhoods around
$\unicode[STIX]{x1D702}^{\prime \prime }>0$. Then this forms a fundamental system of open neighborhoods around ![]() $(\mathbf{x}^{1},\mathbf{x}^{2},\mathbf{x}^{3})\equiv (0,0,0)$ with respect to
$(\mathbf{x}^{1},\mathbf{x}^{2},\mathbf{x}^{3})\equiv (0,0,0)$ with respect to ![]() $(\unicode[STIX]{x1D6FC},12m)$-Besov topology. By Proposition 3.2,
$(\unicode[STIX]{x1D6FC},12m)$-Besov topology. By Proposition 3.2, ![]() $\unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{\unicode[STIX]{x1D702}^{\prime \prime }})=\{\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})\mid \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}(\mathbf{x})\in U_{\unicode[STIX]{x1D702}^{\prime \prime }}\}$ is an open neighborhood of
$\unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{\unicode[STIX]{x1D702}^{\prime \prime }})=\{\mathbf{x}\in G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})\mid \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}(\mathbf{x})\in U_{\unicode[STIX]{x1D702}^{\prime \prime }}\}$ is an open neighborhood of ![]() $\bar{\boldsymbol{\unicode[STIX]{x1D6FE}}}$ in
$\bar{\boldsymbol{\unicode[STIX]{x1D6FE}}}$ in ![]() $(\unicode[STIX]{x1D6FC},12m)$-geometric rough path space. The first set on the most right-hand side of (6.1) can be written as
$(\unicode[STIX]{x1D6FC},12m)$-geometric rough path space. The first set on the most right-hand side of (6.1) can be written as ![]() $\{\unicode[STIX]{x1D716}\mathbf{w}\notin \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{2^{-1/(12m)}\unicode[STIX]{x1D702}})\}$.
$\{\unicode[STIX]{x1D716}\mathbf{w}\notin \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{2^{-1/(12m)}\unicode[STIX]{x1D702}})\}$.
First taking ![]() $\limsup _{\unicode[STIX]{x1D716}{\searrow}0}\unicode[STIX]{x1D716}^{2}\log$ and then letting
$\limsup _{\unicode[STIX]{x1D716}{\searrow}0}\unicode[STIX]{x1D716}^{2}\log$ and then letting ![]() $r^{\prime }{\searrow}1$, we obtain
$r^{\prime }{\searrow}1$, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \limsup _{\unicode[STIX]{x1D716}{\searrow}0}\unicode[STIX]{x1D716}^{2}\log p_{\unicode[STIX]{x1D716}}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \limsup _{\unicode[STIX]{x1D716}{\searrow}0}\unicode[STIX]{x1D716}^{2}\log \mathbf{P}[w\in \unicode[STIX]{x1D6FA}\mid \unicode[STIX]{x1D716}\mathbf{w}\notin \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{2^{-1/(12m)}\unicode[STIX]{x1D702}}),|y_{1}^{\unicode[STIX]{x1D716}}-a^{\prime }|\leqslant \unicode[STIX]{x1D702}^{\prime }]\nonumber\\ \displaystyle & & \displaystyle \quad =\limsup _{\unicode[STIX]{x1D716}{\searrow}0}\unicode[STIX]{x1D716}^{2}\log \hat{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D716}}\big[\big\{(\mathbf{x},l)\in G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle \,\Big|\,\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \mathbf{x}\in \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{2^{-1/(12m)}\unicode[STIX]{x1D702}})^{\complement },|a+\unicode[STIX]{x1D6F7}(\mathbf{x},\mathbf{l})_{0,1}^{1}-a^{\prime }|\leqslant \unicode[STIX]{x1D702}^{\prime }\big\}\big]\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant -\!\inf \bigg\{\frac{\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}}{2}\,\bigg|\,\unicode[STIX]{x1D6FE}\in \mathfrak{H},\boldsymbol{\unicode[STIX]{x1D6FE}}\in \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{2^{-1/(12m)}\unicode[STIX]{x1D702}})^{c},|a+\unicode[STIX]{x1D6F7}(\boldsymbol{\unicode[STIX]{x1D6FE}},\mathbf{0})_{0,1}^{1}-a^{\prime }|\leqslant \unicode[STIX]{x1D702}^{\prime }\bigg\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \limsup _{\unicode[STIX]{x1D716}{\searrow}0}\unicode[STIX]{x1D716}^{2}\log p_{\unicode[STIX]{x1D716}}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \limsup _{\unicode[STIX]{x1D716}{\searrow}0}\unicode[STIX]{x1D716}^{2}\log \mathbf{P}[w\in \unicode[STIX]{x1D6FA}\mid \unicode[STIX]{x1D716}\mathbf{w}\notin \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{2^{-1/(12m)}\unicode[STIX]{x1D702}}),|y_{1}^{\unicode[STIX]{x1D716}}-a^{\prime }|\leqslant \unicode[STIX]{x1D702}^{\prime }]\nonumber\\ \displaystyle & & \displaystyle \quad =\limsup _{\unicode[STIX]{x1D716}{\searrow}0}\unicode[STIX]{x1D716}^{2}\log \hat{\unicode[STIX]{x1D708}}^{\unicode[STIX]{x1D716}}\big[\big\{(\mathbf{x},l)\in G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle \,\Big|\,\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \mathbf{x}\in \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{2^{-1/(12m)}\unicode[STIX]{x1D702}})^{\complement },|a+\unicode[STIX]{x1D6F7}(\mathbf{x},\mathbf{l})_{0,1}^{1}-a^{\prime }|\leqslant \unicode[STIX]{x1D702}^{\prime }\big\}\big]\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant -\!\inf \bigg\{\frac{\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}}{2}\,\bigg|\,\unicode[STIX]{x1D6FE}\in \mathfrak{H},\boldsymbol{\unicode[STIX]{x1D6FE}}\in \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{2^{-1/(12m)}\unicode[STIX]{x1D702}})^{c},|a+\unicode[STIX]{x1D6F7}(\boldsymbol{\unicode[STIX]{x1D6FE}},\mathbf{0})_{0,1}^{1}-a^{\prime }|\leqslant \unicode[STIX]{x1D702}^{\prime }\bigg\}.\end{eqnarray}$$ Here, ![]() $\unicode[STIX]{x1D6F7}:G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+1})\rightarrow G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{n})$ denotes the Lyons–Itô map that corresponds to the coefficient
$\unicode[STIX]{x1D6F7}:G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+1})\rightarrow G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{n})$ denotes the Lyons–Itô map that corresponds to the coefficient ![]() $[\unicode[STIX]{x1D70E},b]$ and we used the embeddings
$[\unicode[STIX]{x1D70E},b]$ and we used the embeddings ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle {\hookrightarrow}G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d+1}){\hookrightarrow}G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+1})$ implicitly. In the last inequality we used large deviation upper estimate for a closed set. Notice also that
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})\times \mathbf{R}\langle \unicode[STIX]{x1D706}\rangle {\hookrightarrow}G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d+1}){\hookrightarrow}G\unicode[STIX]{x1D6FA}_{p}(\mathbf{R}^{d+1})$ implicitly. In the last inequality we used large deviation upper estimate for a closed set. Notice also that ![]() $a+\unicode[STIX]{x1D6F7}(\boldsymbol{\unicode[STIX]{x1D6FE}},0)^{1}=\unicode[STIX]{x1D719}^{0}(\unicode[STIX]{x1D6FE})$.
$a+\unicode[STIX]{x1D6F7}(\boldsymbol{\unicode[STIX]{x1D6FE}},0)^{1}=\unicode[STIX]{x1D719}^{0}(\unicode[STIX]{x1D6FE})$.
Now let ![]() $\unicode[STIX]{x1D702}^{\prime }$ tend to
$\unicode[STIX]{x1D702}^{\prime }$ tend to ![]() $0$. As
$0$. As ![]() $\unicode[STIX]{x1D702}^{\prime }$ decreases, the most right-hand side of (6.2) decreases. The proof is finished if the limit is strictly smaller than
$\unicode[STIX]{x1D702}^{\prime }$ decreases, the most right-hand side of (6.2) decreases. The proof is finished if the limit is strictly smaller than ![]() $-\Vert \bar{\unicode[STIX]{x1D6FE}}\Vert _{\mathfrak{H}}^{2}/2$. Assume otherwise. Then, there exists
$-\Vert \bar{\unicode[STIX]{x1D6FE}}\Vert _{\mathfrak{H}}^{2}/2$. Assume otherwise. Then, there exists ![]() $\{\unicode[STIX]{x1D6FE}_{k}\}_{k=1}^{\infty }\subset \mathfrak{H}$ such that
$\{\unicode[STIX]{x1D6FE}_{k}\}_{k=1}^{\infty }\subset \mathfrak{H}$ such that
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{\unicode[STIX]{x1D6FE}}_{k}\in \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{2^{-1/(12m)}\unicode[STIX]{x1D702}})^{c},\quad |a+\unicode[STIX]{x1D6F7}(\boldsymbol{\unicode[STIX]{x1D6FE}}_{k},0)_{0,1}^{1}-a^{\prime }|\leqslant \frac{1}{k}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \liminf _{k\rightarrow \infty }\bigg(-\frac{\Vert \unicode[STIX]{x1D6FE}_{k}\Vert _{\mathfrak{H}}^{2}}{2}\bigg)\geqslant -\frac{\Vert \bar{\unicode[STIX]{x1D6FE}}\Vert _{\mathfrak{H}}^{2}}{2}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{\unicode[STIX]{x1D6FE}}_{k}\in \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{2^{-1/(12m)}\unicode[STIX]{x1D702}})^{c},\quad |a+\unicode[STIX]{x1D6F7}(\boldsymbol{\unicode[STIX]{x1D6FE}}_{k},0)_{0,1}^{1}-a^{\prime }|\leqslant \frac{1}{k}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \liminf _{k\rightarrow \infty }\bigg(-\frac{\Vert \unicode[STIX]{x1D6FE}_{k}\Vert _{\mathfrak{H}}^{2}}{2}\bigg)\geqslant -\frac{\Vert \bar{\unicode[STIX]{x1D6FE}}\Vert _{\mathfrak{H}}^{2}}{2}. & \displaystyle \nonumber\end{eqnarray}$$ In particular, ![]() $\{\unicode[STIX]{x1D6FE}_{k}\}$ is bounded in
$\{\unicode[STIX]{x1D6FE}_{k}\}$ is bounded in ![]() $\mathfrak{H}$. Hence, by goodness of the rate function, the lift
$\mathfrak{H}$. Hence, by goodness of the rate function, the lift ![]() $\{\boldsymbol{\unicode[STIX]{x1D6FE}}_{k}\}$ is precompact in
$\{\boldsymbol{\unicode[STIX]{x1D6FE}}_{k}\}$ is precompact in ![]() $G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})$. By taking a subsequence if necessary, we may assume
$G\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC},12m}^{\text{B}}(\mathbf{R}^{d})$. By taking a subsequence if necessary, we may assume ![]() $\{\unicode[STIX]{x1D6FE}_{k}\}$ converges to some
$\{\unicode[STIX]{x1D6FE}_{k}\}$ converges to some ![]() $\mathbf{z}$ in
$\mathbf{z}$ in ![]() $(\unicode[STIX]{x1D6FC},12m)$-Besov topology. By the continuity of
$(\unicode[STIX]{x1D6FC},12m)$-Besov topology. By the continuity of ![]() $\unicode[STIX]{x1D6F7}$, we have
$\unicode[STIX]{x1D6F7}$, we have ![]() $a+\unicode[STIX]{x1D6F7}(\mathbf{z},0)_{0,1}^{1}=a^{\prime }$. Since
$a+\unicode[STIX]{x1D6F7}(\mathbf{z},0)_{0,1}^{1}=a^{\prime }$. Since ![]() $\mathbf{z}\in \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{2^{-1/(12m)}\unicode[STIX]{x1D702}})^{c}$,
$\mathbf{z}\in \unicode[STIX]{x1D70F}_{\bar{\unicode[STIX]{x1D6FE}}}^{-1}(U_{2^{-1/(12m)}\unicode[STIX]{x1D702}})^{c}$, ![]() $\mathbf{z}\neq \bar{\boldsymbol{\unicode[STIX]{x1D6FE}}}$. From the lower semicontinuity of the rate function, we see that
$\mathbf{z}\neq \bar{\boldsymbol{\unicode[STIX]{x1D6FE}}}$. From the lower semicontinuity of the rate function, we see that ![]() $\mathbf{z}$ is the lift of some
$\mathbf{z}$ is the lift of some ![]() $z\in \mathfrak{H}$ and
$z\in \mathfrak{H}$ and ![]() $\Vert z\Vert _{\mathfrak{H}}^{2}/2\leqslant \Vert \bar{\unicode[STIX]{x1D6FE}}\Vert _{\mathfrak{H}}^{2}/2$. This clearly contradicts (A2).◻
$\Vert z\Vert _{\mathfrak{H}}^{2}/2\leqslant \Vert \bar{\unicode[STIX]{x1D6FE}}\Vert _{\mathfrak{H}}^{2}/2$. This clearly contradicts (A2).◻
6.2 Proof of Theorem 2.3
Now, let us calculate the kernel ![]() $p_{t}(a,a^{\prime })$. We see that
$p_{t}(a,a^{\prime })$. We see that ![]() $p_{\unicode[STIX]{x1D716}^{1/H}}(a,a^{\prime })=\mathbf{E}[\unicode[STIX]{x1D6FF}_{a^{\prime }}(y_{1}^{\unicode[STIX]{x1D716}})]=I_{1}(\unicode[STIX]{x1D716})+I_{2}(\unicode[STIX]{x1D716})$, where
$p_{\unicode[STIX]{x1D716}^{1/H}}(a,a^{\prime })=\mathbf{E}[\unicode[STIX]{x1D6FF}_{a^{\prime }}(y_{1}^{\unicode[STIX]{x1D716}})]=I_{1}(\unicode[STIX]{x1D716})+I_{2}(\unicode[STIX]{x1D716})$, where
As we have shown in Lemma 6.1, the second term ![]() $I_{2}(\unicode[STIX]{x1D716})$ on the right-hand side does not contribute to the asymptotic expansion for any
$I_{2}(\unicode[STIX]{x1D716})$ on the right-hand side does not contribute to the asymptotic expansion for any ![]() $\unicode[STIX]{x1D702}>0$. So, we have only to calculate the first term
$\unicode[STIX]{x1D702}>0$. So, we have only to calculate the first term ![]() $I_{1}(\unicode[STIX]{x1D716})$ for some
$I_{1}(\unicode[STIX]{x1D716})$ for some ![]() $\unicode[STIX]{x1D702}>0$.
$\unicode[STIX]{x1D702}>0$.
However, the proof of the asymptotic expansion of ![]() $I_{1}(\unicode[STIX]{x1D716})$ in the case
$I_{1}(\unicode[STIX]{x1D716})$ in the case ![]() $H\in (1/4,1/3]$ is essentially the same as in the case
$H\in (1/4,1/3]$ is essentially the same as in the case ![]() $H\in (1/3,1/2]$ (see [Reference InahamaIna16b, Subsections 5.2–5.3]). Therefore, for the sake of brevity, we will give a sketch of the proof only.
$H\in (1/3,1/2]$ (see [Reference InahamaIna16b, Subsections 5.2–5.3]). Therefore, for the sake of brevity, we will give a sketch of the proof only.
Sketch of the proof of Theorem 2.3.
By the Cameron–Martin formula, we have
Moreover, there exists ![]() $\bar{\unicode[STIX]{x1D708}}\in \mathbf{R}^{n}$ such that
$\bar{\unicode[STIX]{x1D708}}\in \mathbf{R}^{n}$ such that ![]() $\langle \bar{\unicode[STIX]{x1D6FE}},w\rangle =\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{1}(w,\bar{\unicode[STIX]{x1D6FE}})\rangle$ for all
$\langle \bar{\unicode[STIX]{x1D6FE}},w\rangle =\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{1}(w,\bar{\unicode[STIX]{x1D6FE}})\rangle$ for all ![]() $w$, where the inner product on the right-hand side is a standard one on
$w$, where the inner product on the right-hand side is a standard one on ![]() $\mathbf{R}^{n}$. (In fact,
$\mathbf{R}^{n}$. (In fact, ![]() $\bar{\unicode[STIX]{x1D708}}$ is a covector that appears in the Lagrange multiplier method for
$\bar{\unicode[STIX]{x1D708}}$ is a covector that appears in the Lagrange multiplier method for ![]() $\unicode[STIX]{x1D719}_{1}^{0}$ and
$\unicode[STIX]{x1D719}_{1}^{0}$ and ![]() $\unicode[STIX]{x1D6FE}\mapsto \Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}/2$ at
$\unicode[STIX]{x1D6FE}\mapsto \Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}/2$ at ![]() $\bar{\unicode[STIX]{x1D6FE}}$. Note that
$\bar{\unicode[STIX]{x1D6FE}}$. Note that ![]() $\unicode[STIX]{x1D719}_{1}^{1}$ is a continuous extension of
$\unicode[STIX]{x1D719}_{1}^{1}$ is a continuous extension of ![]() $\unicode[STIX]{x1D6FE}\mapsto D_{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D719}_{1}^{0}(\bar{\unicode[STIX]{x1D6FE}})$.) Hence, we have
$\unicode[STIX]{x1D6FE}\mapsto D_{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D719}_{1}^{0}(\bar{\unicode[STIX]{x1D6FE}})$.) Hence, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D716}^{n}\exp \bigg(\frac{\Vert \bar{\unicode[STIX]{x1D6FE}}\Vert _{\mathfrak{H}}^{2}}{2\unicode[STIX]{x1D716}^{2}}\bigg)I_{1}(\unicode[STIX]{x1D716})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D716}^{n}\mathbf{E}\bigg[\exp \bigg(-\frac{1}{\unicode[STIX]{x1D716}}\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{1}\rangle \bigg)\unicode[STIX]{x1D6FF}_{a^{\prime }}(a^{\prime }+\unicode[STIX]{x1D716}\unicode[STIX]{x1D719}_{1}^{1}+r_{\unicode[STIX]{x1D716},1}^{2})\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}\bigg(\unicode[STIX]{x1D716},w+\frac{\bar{\unicode[STIX]{x1D6FE}}}{\unicode[STIX]{x1D716}}\bigg)\bigg]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbf{E}\bigg[\exp \bigg(-\frac{1}{\unicode[STIX]{x1D716}}\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{1}\rangle \bigg)\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D719}_{1}^{1}+\unicode[STIX]{x1D716}^{-1}r_{\unicode[STIX]{x1D716},1}^{2})\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}\bigg(\unicode[STIX]{x1D716},w+\frac{\bar{\unicode[STIX]{x1D6FE}}}{\unicode[STIX]{x1D716}}\bigg)\bigg]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbf{E}\bigg[\exp \bigg(\frac{\langle \bar{\unicode[STIX]{x1D708}},r_{\unicode[STIX]{x1D716},1}^{2}\rangle }{\unicode[STIX]{x1D716}^{2}}\bigg)\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D719}_{1}^{1}+\unicode[STIX]{x1D716}^{-1}r_{\unicode[STIX]{x1D716},1}^{2})\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}\bigg(\unicode[STIX]{x1D716},w+\frac{\bar{\unicode[STIX]{x1D6FE}}}{\unicode[STIX]{x1D716}}\bigg)\bigg]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbf{E}\bigg[F(\unicode[STIX]{x1D716},w)\unicode[STIX]{x1D6FF}_{0}\bigg(\frac{{\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}-a^{\prime }}{\unicode[STIX]{x1D716}}\bigg)\bigg],\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D716}^{n}\exp \bigg(\frac{\Vert \bar{\unicode[STIX]{x1D6FE}}\Vert _{\mathfrak{H}}^{2}}{2\unicode[STIX]{x1D716}^{2}}\bigg)I_{1}(\unicode[STIX]{x1D716})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D716}^{n}\mathbf{E}\bigg[\exp \bigg(-\frac{1}{\unicode[STIX]{x1D716}}\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{1}\rangle \bigg)\unicode[STIX]{x1D6FF}_{a^{\prime }}(a^{\prime }+\unicode[STIX]{x1D716}\unicode[STIX]{x1D719}_{1}^{1}+r_{\unicode[STIX]{x1D716},1}^{2})\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}\bigg(\unicode[STIX]{x1D716},w+\frac{\bar{\unicode[STIX]{x1D6FE}}}{\unicode[STIX]{x1D716}}\bigg)\bigg]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbf{E}\bigg[\exp \bigg(-\frac{1}{\unicode[STIX]{x1D716}}\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{1}\rangle \bigg)\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D719}_{1}^{1}+\unicode[STIX]{x1D716}^{-1}r_{\unicode[STIX]{x1D716},1}^{2})\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}\bigg(\unicode[STIX]{x1D716},w+\frac{\bar{\unicode[STIX]{x1D6FE}}}{\unicode[STIX]{x1D716}}\bigg)\bigg]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbf{E}\bigg[\exp \bigg(\frac{\langle \bar{\unicode[STIX]{x1D708}},r_{\unicode[STIX]{x1D716},1}^{2}\rangle }{\unicode[STIX]{x1D716}^{2}}\bigg)\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D719}_{1}^{1}+\unicode[STIX]{x1D716}^{-1}r_{\unicode[STIX]{x1D716},1}^{2})\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}\bigg(\unicode[STIX]{x1D716},w+\frac{\bar{\unicode[STIX]{x1D6FE}}}{\unicode[STIX]{x1D716}}\bigg)\bigg]\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbf{E}\bigg[F(\unicode[STIX]{x1D716},w)\unicode[STIX]{x1D6FF}_{0}\bigg(\frac{{\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}-a^{\prime }}{\unicode[STIX]{x1D716}}\bigg)\bigg],\nonumber\end{eqnarray}$$where
for any positive constant ![]() $\unicode[STIX]{x1D702}^{\prime }$. Here we have used
$\unicode[STIX]{x1D702}^{\prime }$. Here we have used ![]() $\unicode[STIX]{x1D6FF}_{0}(\bullet )=\unicode[STIX]{x1D713}(|\bullet |^{2}/{\unicode[STIX]{x1D702}^{\prime }}^{2})\unicode[STIX]{x1D6FF}_{0}(\bullet )$.
$\unicode[STIX]{x1D6FF}_{0}(\bullet )=\unicode[STIX]{x1D713}(|\bullet |^{2}/{\unicode[STIX]{x1D702}^{\prime }}^{2})\unicode[STIX]{x1D6FF}_{0}(\bullet )$.
By a slight modification of Watanabe’s asymptotic expansion theory and uniform non-degeneracy (Proposition 5.4), ![]() $\unicode[STIX]{x1D6FF}_{0}(({\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}-a^{\prime })/\unicode[STIX]{x1D716})$ admits the following asymptotic expansion as
$\unicode[STIX]{x1D6FF}_{0}(({\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}-a^{\prime })/\unicode[STIX]{x1D716})$ admits the following asymptotic expansion as ![]() $\unicode[STIX]{x1D716}{\searrow}0$ in
$\unicode[STIX]{x1D716}{\searrow}0$ in ![]() $\tilde{\mathbf{D}}_{-\infty }$-topology as follows: for some
$\tilde{\mathbf{D}}_{-\infty }$-topology as follows: for some ![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D708}_{j}}\in \tilde{\mathbf{D}}_{-\infty }$ (
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D708}_{j}}\in \tilde{\mathbf{D}}_{-\infty }$ (![]() $j=1,2,\ldots$),
$j=1,2,\ldots$),
(see [Reference Ikeda and WatanabeIW89, Theorem 9.3, p. 387]). Recall that ![]() $0=\unicode[STIX]{x1D708}_{0}<\unicode[STIX]{x1D708}_{1}<\unicode[STIX]{x1D708}_{2}<\cdots \,$ are all the elements of
$0=\unicode[STIX]{x1D708}_{0}<\unicode[STIX]{x1D708}_{1}<\unicode[STIX]{x1D708}_{2}<\cdots \,$ are all the elements of ![]() $\unicode[STIX]{x1D6EC}_{3}$ in increasing order. Moreover, since
$\unicode[STIX]{x1D6EC}_{3}$ in increasing order. Moreover, since ![]() $\unicode[STIX]{x1D719}_{1}^{1}$ is a Gaussian random vector whose covariance matrix equals
$\unicode[STIX]{x1D719}_{1}^{1}$ is a Gaussian random vector whose covariance matrix equals ![]() $Q(\bar{\unicode[STIX]{x1D6FE}})$,
$Q(\bar{\unicode[STIX]{x1D6FE}})$, ![]() $\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D719}_{1}^{1})$ is actually a nontrivial finite measure with its total mass
$\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D719}_{1}^{1})$ is actually a nontrivial finite measure with its total mass ![]() $\mathbf{E}[\unicode[STIX]{x1D719}_{1}^{1}]=(2\unicode[STIX]{x1D70B})^{-n/2}(\det Q(\bar{\unicode[STIX]{x1D6FE}}))^{-1/2}>0$.
$\mathbf{E}[\unicode[STIX]{x1D719}_{1}^{1}]=(2\unicode[STIX]{x1D70B})^{-n/2}(\det Q(\bar{\unicode[STIX]{x1D6FE}}))^{-1/2}>0$.
Therefore, our problem reduces to showing ![]() $F(\unicode[STIX]{x1D716},\bullet )$ belongs to
$F(\unicode[STIX]{x1D716},\bullet )$ belongs to ![]() $\tilde{\mathbf{D}}_{\infty }$ and admits asymptotic expansion in
$\tilde{\mathbf{D}}_{\infty }$ and admits asymptotic expansion in ![]() $\tilde{\mathbf{D}}_{\infty }$-topology with the index set
$\tilde{\mathbf{D}}_{\infty }$-topology with the index set ![]() $\unicode[STIX]{x1D6EC}_{3}^{\prime }$. However, this is highly nontrivial since
$\unicode[STIX]{x1D6EC}_{3}^{\prime }$. However, this is highly nontrivial since ![]() $\exp (\langle \bar{\unicode[STIX]{x1D708}},r_{\unicode[STIX]{x1D716},1}^{2}\rangle /\unicode[STIX]{x1D716}^{2})$ itself does not have nice integrability. This is why the two technical factors are involved in the definition of
$\exp (\langle \bar{\unicode[STIX]{x1D708}},r_{\unicode[STIX]{x1D716},1}^{2}\rangle /\unicode[STIX]{x1D716}^{2})$ itself does not have nice integrability. This is why the two technical factors are involved in the definition of ![]() $F(\unicode[STIX]{x1D716},\bullet )$.
$F(\unicode[STIX]{x1D716},\bullet )$.
Let us observe the two technical factors. First, ![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D716},w+\bar{\unicode[STIX]{x1D6FE}}/\unicode[STIX]{x1D716})$ and its derivatives vanish outside
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D716},w+\bar{\unicode[STIX]{x1D6FE}}/\unicode[STIX]{x1D716})$ and its derivatives vanish outside ![]() $\{w~|~\unicode[STIX]{x1D716}\mathbf{w}\in U_{\unicode[STIX]{x1D702}}\}$ and
$\{w~|~\unicode[STIX]{x1D716}\mathbf{w}\in U_{\unicode[STIX]{x1D702}}\}$ and ![]() $\unicode[STIX]{x1D713}({\unicode[STIX]{x1D702}^{\prime }}^{-2}|({\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}-a^{\prime })/\unicode[STIX]{x1D716}|^{2})$ and its derivatives vanish outside
$\unicode[STIX]{x1D713}({\unicode[STIX]{x1D702}^{\prime }}^{-2}|({\tilde{y}}_{1}^{\unicode[STIX]{x1D716}}-a^{\prime })/\unicode[STIX]{x1D716}|^{2})$ and its derivatives vanish outside ![]() $\{|r_{\unicode[STIX]{x1D716},1}^{1}/\unicode[STIX]{x1D716}|\leqslant \unicode[STIX]{x1D702}^{\prime }\}$. Second, as
$\{|r_{\unicode[STIX]{x1D716},1}^{1}/\unicode[STIX]{x1D716}|\leqslant \unicode[STIX]{x1D702}^{\prime }\}$. Second, as ![]() $\unicode[STIX]{x1D716}{\searrow}0$,
$\unicode[STIX]{x1D716}{\searrow}0$,
in ![]() $\mathbf{D}_{\infty }$-topology for any (large)
$\mathbf{D}_{\infty }$-topology for any (large) ![]() $M>0$. Therefore, these two Wiener functionals have no influence in the coefficient of the expansion of
$M>0$. Therefore, these two Wiener functionals have no influence in the coefficient of the expansion of ![]() $F(\unicode[STIX]{x1D716},\bullet )$.
$F(\unicode[STIX]{x1D716},\bullet )$.
The expansion of ![]() $\langle \bar{\unicode[STIX]{x1D708}},r_{\unicode[STIX]{x1D716},1}^{2}\rangle /\unicode[STIX]{x1D716}^{2}=\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{2}+r_{\unicode[STIX]{x1D716},1}^{\unicode[STIX]{x1D705}_{3}}/\unicode[STIX]{x1D716}^{2}\rangle$ is indexed by
$\langle \bar{\unicode[STIX]{x1D708}},r_{\unicode[STIX]{x1D716},1}^{2}\rangle /\unicode[STIX]{x1D716}^{2}=\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{2}+r_{\unicode[STIX]{x1D716},1}^{\unicode[STIX]{x1D705}_{3}}/\unicode[STIX]{x1D716}^{2}\rangle$ is indexed by ![]() $\unicode[STIX]{x1D6EC}_{2}^{\prime }$. Hence, if the integrability issue were left aside, we would easily have an expansion of the following type:
$\unicode[STIX]{x1D6EC}_{2}^{\prime }$. Hence, if the integrability issue were left aside, we would easily have an expansion of the following type:
where ![]() $0=\unicode[STIX]{x1D70C}_{0}<\unicode[STIX]{x1D70C}_{1}<\unicode[STIX]{x1D70C}_{2}<\cdots \,$ are all the elements of
$0=\unicode[STIX]{x1D70C}_{0}<\unicode[STIX]{x1D70C}_{1}<\unicode[STIX]{x1D70C}_{2}<\cdots \,$ are all the elements of ![]() $\unicode[STIX]{x1D6EC}_{3}^{\prime }$ in increasing order. Due to (6.4), it also should hold that
$\unicode[STIX]{x1D6EC}_{3}^{\prime }$ in increasing order. Due to (6.4), it also should hold that
Once (6.6) is actually shown, then we prove our main theorem (Theorem 2.3). Moreover, ![]() $\unicode[STIX]{x1D6FC}_{0}:=\mathbf{E}[e^{\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{2}\rangle }\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D719}_{1}^{1})]>0$ is finite due to Assumption (A4).
$\unicode[STIX]{x1D6FC}_{0}:=\mathbf{E}[e^{\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{2}\rangle }\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D719}_{1}^{1})]>0$ is finite due to Assumption (A4).
Roughly speaking, the proof of (6.6) goes in the following way. First, Assumption (A4) implies ![]() $\mathbf{E}[e^{\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{2}\rangle }\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D719}_{1}^{1})]<\infty$ since
$\mathbf{E}[e^{\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{2}\rangle }\unicode[STIX]{x1D6FF}_{0}(\unicode[STIX]{x1D719}_{1}^{1})]<\infty$ since ![]() $\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{2}\rangle$ belongs to the inhomogeneous Wiener chaos of order 2 whose main term corresponds to the Hessian in (A4). Though it is not at all obvious, the Hessian is actually Hilbert–Schmidt on
$\langle \bar{\unicode[STIX]{x1D708}},\unicode[STIX]{x1D719}_{1}^{2}\rangle$ belongs to the inhomogeneous Wiener chaos of order 2 whose main term corresponds to the Hessian in (A4). Though it is not at all obvious, the Hessian is actually Hilbert–Schmidt on ![]() $\mathfrak{H}\times \mathfrak{H}$.
$\mathfrak{H}\times \mathfrak{H}$.
However, what we want to estimate is something like
Here, thanks to the factor ![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D716},w+\bar{\unicode[STIX]{x1D6FE}}/\unicode[STIX]{x1D716})$, we may assume
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D702}}(\unicode[STIX]{x1D716},w+\bar{\unicode[STIX]{x1D6FE}}/\unicode[STIX]{x1D716})$, we may assume ![]() $\unicode[STIX]{x1D716}\mathbf{w}$ stay in the bounded set
$\unicode[STIX]{x1D716}\mathbf{w}$ stay in the bounded set ![]() $U_{\unicode[STIX]{x1D702}}$ in the geometric rough path space. Hence, we can use the deterministic version of Taylor expansion of the Lyons–Itô map (Proposition 4.1) to prove that
$U_{\unicode[STIX]{x1D702}}$ in the geometric rough path space. Hence, we can use the deterministic version of Taylor expansion of the Lyons–Itô map (Proposition 4.1) to prove that ![]() $\langle \bar{\unicode[STIX]{x1D708}},r_{\unicode[STIX]{x1D716},1}^{\unicode[STIX]{x1D705}_{3}}\rangle /\unicode[STIX]{x1D716}^{2}$ and
$\langle \bar{\unicode[STIX]{x1D708}},r_{\unicode[STIX]{x1D716},1}^{\unicode[STIX]{x1D705}_{3}}\rangle /\unicode[STIX]{x1D716}^{2}$ and ![]() $r_{\unicode[STIX]{x1D716},1}^{2}/\unicode[STIX]{x1D716}$ are actually so “small” that adding them does not destroy the integrability we need.◻
$r_{\unicode[STIX]{x1D716},1}^{2}/\unicode[STIX]{x1D716}$ are actually so “small” that adding them does not destroy the integrability we need.◻
7 Examples
In this section, we provide two examples to which our main theorem (Theorem 2.3) applies. First, we recall the case of near points under the ellipticity condition.
Example 7.1. Assume the ellipticity condition at the starting point ![]() $a$, that is,
$a$, that is, ![]() $\{V_{1}(a),\ldots ,V_{d}(a)\}$ linearly spans
$\{V_{1}(a),\ldots ,V_{d}(a)\}$ linearly spans ![]() $\mathbf{R}^{n}$. Obviously, this implies (A1). If the end point
$\mathbf{R}^{n}$. Obviously, this implies (A1). If the end point ![]() $a^{\prime }$ is sufficiently close to the starting point
$a^{\prime }$ is sufficiently close to the starting point ![]() $a$, then (A2), (A3) and (A4) are also satisfied. Therefore, our main theorem can be used.
$a$, then (A2), (A3) and (A4) are also satisfied. Therefore, our main theorem can be used.
This was shown in [Reference InahamaIna16a] when ![]() $H\in (1/2,1)$. The same proof works when
$H\in (1/2,1)$. The same proof works when ![]() $H\in (1/4,1/2]$, too. The key of the proof is the implicit function theorem. Note that under the ellipticity assumption, the deterministic Malliavin covariance
$H\in (1/4,1/2]$, too. The key of the proof is the implicit function theorem. Note that under the ellipticity assumption, the deterministic Malliavin covariance ![]() $Q(\unicode[STIX]{x1D6FE})$ is never degenerate and the implicit function theorem is available at every
$Q(\unicode[STIX]{x1D6FE})$ is never degenerate and the implicit function theorem is available at every ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}$.
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}$.
Second, we provide an example, in which the coefficient vector fields satisfy the Hörmander condition, but not the ellipticity condition. This model was already studied in [Reference DriscollDri13].
Example 7.2. (The “fractional diffusion” process on the Heisenberg group). Let ![]() $d=2$,
$d=2$, ![]() $n=3$ and
$n=3$ and
Then, (A1) is satisfied at every point since ![]() $[V_{1},V_{2}]=-4\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x^{3}$. Fortunately, we can write down the solutions for (2.1) and (2.2) for any given initial condition
$[V_{1},V_{2}]=-4\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x^{3}$. Fortunately, we can write down the solutions for (2.1) and (2.2) for any given initial condition ![]() $a=(a^{1},a^{2},a^{3})$ as follows:
$a=(a^{1},a^{2},a^{3})$ as follows:
 $$\begin{eqnarray}\displaystyle y_{t} & = & \displaystyle (a^{1}+\mathbf{w}_{0,t}^{1,1},a^{2}+\mathbf{w}_{0,t}^{1,2},a^{3}+2(a^{2}\mathbf{w}_{0,t}^{1,1}-a^{1}\mathbf{w}_{0,t}^{1,2})+2(\mathbf{w}_{0,t}^{2,21}-\mathbf{w}_{0,t}^{2,12})),\nonumber\\ \displaystyle \unicode[STIX]{x1D719}_{t}^{0}(\unicode[STIX]{x1D6FE}) & = & \displaystyle (a^{1}+\unicode[STIX]{x1D6FE}_{t}^{1},\,a^{2}+\unicode[STIX]{x1D6FE}_{t}^{2},\,a^{3}+2(a^{2}\unicode[STIX]{x1D6FE}_{t}^{1}-a^{1}\unicode[STIX]{x1D6FE}_{t}^{2})+2(\boldsymbol{\unicode[STIX]{x1D6FE}}_{0,t}^{2,21}-\boldsymbol{\unicode[STIX]{x1D6FE}}_{0,t}^{2,12})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{t} & = & \displaystyle (a^{1}+\mathbf{w}_{0,t}^{1,1},a^{2}+\mathbf{w}_{0,t}^{1,2},a^{3}+2(a^{2}\mathbf{w}_{0,t}^{1,1}-a^{1}\mathbf{w}_{0,t}^{1,2})+2(\mathbf{w}_{0,t}^{2,21}-\mathbf{w}_{0,t}^{2,12})),\nonumber\\ \displaystyle \unicode[STIX]{x1D719}_{t}^{0}(\unicode[STIX]{x1D6FE}) & = & \displaystyle (a^{1}+\unicode[STIX]{x1D6FE}_{t}^{1},\,a^{2}+\unicode[STIX]{x1D6FE}_{t}^{2},\,a^{3}+2(a^{2}\unicode[STIX]{x1D6FE}_{t}^{1}-a^{1}\unicode[STIX]{x1D6FE}_{t}^{2})+2(\boldsymbol{\unicode[STIX]{x1D6FE}}_{0,t}^{2,21}-\boldsymbol{\unicode[STIX]{x1D6FE}}_{0,t}^{2,12})).\nonumber\end{eqnarray}$$ Here, ![]() $\boldsymbol{\unicode[STIX]{x1D6FE}}=(\boldsymbol{\unicode[STIX]{x1D6FE}}^{1},\ldots ,\boldsymbol{\unicode[STIX]{x1D6FE}}^{\lfloor 1/H\rfloor })$ is the natural lift of
$\boldsymbol{\unicode[STIX]{x1D6FE}}=(\boldsymbol{\unicode[STIX]{x1D6FE}}^{1},\ldots ,\boldsymbol{\unicode[STIX]{x1D6FE}}^{\lfloor 1/H\rfloor })$ is the natural lift of ![]() $\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{t}^{1},\unicode[STIX]{x1D6FE}_{t}^{2})_{0\leqslant t\leqslant 1}\in \mathfrak{H}$ by means of Young integration and
$\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{t}^{1},\unicode[STIX]{x1D6FE}_{t}^{2})_{0\leqslant t\leqslant 1}\in \mathfrak{H}$ by means of Young integration and ![]() $\boldsymbol{\unicode[STIX]{x1D6FE}}^{2,ij}$ stands for the
$\boldsymbol{\unicode[STIX]{x1D6FE}}^{2,ij}$ stands for the ![]() $(i,j)$-component of
$(i,j)$-component of ![]() $\boldsymbol{\unicode[STIX]{x1D6FE}}^{2}$.
$\boldsymbol{\unicode[STIX]{x1D6FE}}^{2}$.
Let ![]() $a=(0,0,0),a^{\prime }=(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702},0)\in \mathbf{R}^{3}$ with
$a=(0,0,0),a^{\prime }=(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702},0)\in \mathbf{R}^{3}$ with ![]() $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\neq (0,0)$. Then, (A2), (A3) and (A4) are also satisfied. (For a proof, see Lemma 7.4.)
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\neq (0,0)$. Then, (A2), (A3) and (A4) are also satisfied. (For a proof, see Lemma 7.4.)
Therefore, by Theorem 2.3 and Remark 2.4, we have the following asymptotics:
as ![]() $t{\searrow}0$ for some
$t{\searrow}0$ for some ![]() $\unicode[STIX]{x1D6FC}_{0}>0$ and
$\unicode[STIX]{x1D6FC}_{0}>0$ and ![]() $\unicode[STIX]{x1D6FC}_{2j}\in \mathbf{R}$
$\unicode[STIX]{x1D6FC}_{2j}\in \mathbf{R}$![]() $(j=1,2,\ldots \,)$.
$(j=1,2,\ldots \,)$.
Remark 7.3. We make two remarks on Example 7.2.
∙ The definitions of
 $V_{1}$ and
$V_{1}$ and  $V_{2}$ slightly differ from literature to literature.
$V_{2}$ slightly differ from literature to literature.∙
 $V_{1}$ and
$V_{1}$ and  $V_{2}$ are not of
$V_{2}$ are not of  $C_{b}^{\infty }$. So, precisely speaking, we cannot use Theorem 2.3 directly. However, there is no problem since the solution
$C_{b}^{\infty }$. So, precisely speaking, we cannot use Theorem 2.3 directly. However, there is no problem since the solution  $(y_{t})$ has a very explicit expression. (The main purpose of imposing
$(y_{t})$ has a very explicit expression. (The main purpose of imposing  $C_{b}^{\infty }$-condition is to ensure the existence of a global solution.)
$C_{b}^{\infty }$-condition is to ensure the existence of a global solution.)
Lemma 7.4. Let the notation be as in Example 7.2. Then, (A2), (A3) and (A4) are satisfied for ![]() $a=(0,0,0),a^{\prime }=(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702},0)\in \mathbf{R}^{3}$ with
$a=(0,0,0),a^{\prime }=(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702},0)\in \mathbf{R}^{3}$ with ![]() $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\neq (0,0)$. Moreover,
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\neq (0,0)$. Moreover, ![]() $\bar{\unicode[STIX]{x1D6FE}}_{t}=(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})R(1,t)$ and
$\bar{\unicode[STIX]{x1D6FE}}_{t}=(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})R(1,t)$ and ![]() $\Vert \bar{\unicode[STIX]{x1D6FE}}\Vert _{\mathfrak{H}}^{2}=\unicode[STIX]{x1D709}^{2}+\unicode[STIX]{x1D702}^{2}$.
$\Vert \bar{\unicode[STIX]{x1D6FE}}\Vert _{\mathfrak{H}}^{2}=\unicode[STIX]{x1D709}^{2}+\unicode[STIX]{x1D702}^{2}$.
Proof. First, note that we may assume without loss of generality that ![]() $a^{\prime }=(\unicode[STIX]{x1D709},0,0)$ with
$a^{\prime }=(\unicode[STIX]{x1D709},0,0)$ with ![]() $\unicode[STIX]{x1D709}>0$. The reason is as follows. If
$\unicode[STIX]{x1D709}>0$. The reason is as follows. If ![]() $(w_{t})$ is a two-dimensional fBm and
$(w_{t})$ is a two-dimensional fBm and ![]() $A\in \text{SO}(2)$, then
$A\in \text{SO}(2)$, then ![]() $\tilde{w}:=Aw$ is again a two-dimensional fBm and
$\tilde{w}:=Aw$ is again a two-dimensional fBm and ![]() $\mathbf{w}_{0,t}^{2,21}-\mathbf{w}_{0,t}^{2,12}=\tilde{\mathbf{w}}_{0,t}^{2,21}-\tilde{\mathbf{w}}_{0,t}^{2,12}$. So, if we choose suitable
$\mathbf{w}_{0,t}^{2,21}-\mathbf{w}_{0,t}^{2,12}=\tilde{\mathbf{w}}_{0,t}^{2,21}-\tilde{\mathbf{w}}_{0,t}^{2,12}$. So, if we choose suitable ![]() $A$, the problem reduces to the case
$A$, the problem reduces to the case ![]() $a^{\prime }=(\unicode[STIX]{x1D709},0,0)$ with
$a^{\prime }=(\unicode[STIX]{x1D709},0,0)$ with ![]() $\unicode[STIX]{x1D709}>0$.
$\unicode[STIX]{x1D709}>0$.
Next, we fix some notation. We write ![]() $G(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D719}_{1}^{0}(\unicode[STIX]{x1D6FE})$ for any
$G(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D719}_{1}^{0}(\unicode[STIX]{x1D6FE})$ for any ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ or any two-dimensional continuous path
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ or any two-dimensional continuous path ![]() $\unicode[STIX]{x1D6FE}$ such that the Young ODE (2.2) makes sense. Explicitly,
$\unicode[STIX]{x1D6FE}$ such that the Young ODE (2.2) makes sense. Explicitly, ![]() $G(\unicode[STIX]{x1D6FE})=(\unicode[STIX]{x1D6FE}_{1}^{1},\unicode[STIX]{x1D6FE}_{1}^{2},2\int _{0}^{1}(\unicode[STIX]{x1D6FE}_{s}^{2}\,d\unicode[STIX]{x1D6FE}_{s}^{1}-\unicode[STIX]{x1D6FE}_{s}^{1}\,d\unicode[STIX]{x1D6FE}_{s}^{2}))$. We denote by
$G(\unicode[STIX]{x1D6FE})=(\unicode[STIX]{x1D6FE}_{1}^{1},\unicode[STIX]{x1D6FE}_{1}^{2},2\int _{0}^{1}(\unicode[STIX]{x1D6FE}_{s}^{2}\,d\unicode[STIX]{x1D6FE}_{s}^{1}-\unicode[STIX]{x1D6FE}_{s}^{1}\,d\unicode[STIX]{x1D6FE}_{s}^{2}))$. We denote by ![]() $\mathfrak{H}_{H}(\mathbf{R}^{m})$ the Cameron–Martin space of an
$\mathfrak{H}_{H}(\mathbf{R}^{m})$ the Cameron–Martin space of an ![]() $m$-dimensional fBm (so
$m$-dimensional fBm (so ![]() $\mathfrak{H}=\mathfrak{H}_{H}(\mathbf{R}^{2})$). We write
$\mathfrak{H}=\mathfrak{H}_{H}(\mathbf{R}^{2})$). We write ![]() $I(\unicode[STIX]{x1D6FE})=\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}_{H}(\mathbf{R}^{m})}^{2}/2$ for
$I(\unicode[STIX]{x1D6FE})=\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}_{H}(\mathbf{R}^{m})}^{2}/2$ for ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}_{H}(\mathbf{R}^{m})$, but suppress the dimension
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}_{H}(\mathbf{R}^{m})$, but suppress the dimension ![]() $m$. Recall that there exists a real-valued kernel
$m$. Recall that there exists a real-valued kernel ![]() $K(t,s)=K_{H}(t,s)$,
$K(t,s)=K_{H}(t,s)$, ![]() $0<s<t$, with the following properties:
$0<s<t$, with the following properties:
(1) If
 $(b_{t})$ is an
$(b_{t})$ is an  $m$-dimensional Brownian motion, then
$m$-dimensional Brownian motion, then  $(w_{t})$, defined by
$(w_{t})$, defined by  $w_{t}=\int _{0}^{t}K(t,s)\,db_{s}$, is an
$w_{t}=\int _{0}^{t}K(t,s)\,db_{s}$, is an  $m$-dimensional fBm with Hurst parameter
$m$-dimensional fBm with Hurst parameter  $H$.
$H$.(2) Set
 $({\mathcal{K}}f)_{t}=\int _{0}^{t}K(t,s)f_{s}\,ds$. Then,
$({\mathcal{K}}f)_{t}=\int _{0}^{t}K(t,s)f_{s}\,ds$. Then,  ${\mathcal{K}}={\mathcal{K}}_{H}$ is a unitary isometry from
${\mathcal{K}}={\mathcal{K}}_{H}$ is a unitary isometry from  $L^{2}([0,1];\mathbf{R}^{m})$ to
$L^{2}([0,1];\mathbf{R}^{m})$ to  $\mathfrak{H}_{H}(\mathbf{R}^{m})$.
$\mathfrak{H}_{H}(\mathbf{R}^{m})$.(3)
 $R(t,t^{\prime })=\int _{0}^{t\wedge t^{\prime }}K(t,s)K(t^{\prime },s)\,ds$.
$R(t,t^{\prime })=\int _{0}^{t\wedge t^{\prime }}K(t,s)K(t^{\prime },s)\,ds$.
For proofs, see [Reference NualartNua06, Section 5.1] and [Reference Biagini, Hu, Øksendal and ZhangBHØZ08, Section 1.2]. There, an explicit expression of ![]() $K$ is also given, but it is not used here.
$K$ is also given, but it is not used here.
Now we consider a one-dimensional problem before showing (A2). Let ![]() $m=1$. We now prove that
$m=1$. We now prove that ![]() $\unicode[STIX]{x1D709}R(1,\bullet )$ is a unique minimizer of
$\unicode[STIX]{x1D709}R(1,\bullet )$ is a unique minimizer of ![]() $I$ among
$I$ among ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}_{H}(\mathbf{R}^{1})$ that connect
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}_{H}(\mathbf{R}^{1})$ that connect ![]() $0$ and
$0$ and ![]() $\unicode[STIX]{x1D709}>0$ at time
$\unicode[STIX]{x1D709}>0$ at time ![]() $1$, that is,
$1$, that is,
From (2) and (3) above we see that ![]() $({\mathcal{K}}K(1,\ast ))_{\bullet }=R(1,\bullet )\in \mathfrak{H}_{H}(\mathbf{R}^{1})$ and
$({\mathcal{K}}K(1,\ast ))_{\bullet }=R(1,\bullet )\in \mathfrak{H}_{H}(\mathbf{R}^{1})$ and
Take ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}_{H}(\mathbf{R}^{1})$ with
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}_{H}(\mathbf{R}^{1})$ with ![]() $\unicode[STIX]{x1D6FE}_{1}=\unicode[STIX]{x1D709}$ arbitrarily. Since
$\unicode[STIX]{x1D6FE}_{1}=\unicode[STIX]{x1D709}$ arbitrarily. Since ![]() ${\mathcal{K}}$ is an isometry, there exists
${\mathcal{K}}$ is an isometry, there exists ![]() $f\in L^{2}([0,1];\mathbf{R}^{1})$ such that
$f\in L^{2}([0,1];\mathbf{R}^{1})$ such that ![]() $\unicode[STIX]{x1D6FE}={\mathcal{K}}(f+\unicode[STIX]{x1D709}K(1,\bullet ))$ uniquely. From
$\unicode[STIX]{x1D6FE}={\mathcal{K}}(f+\unicode[STIX]{x1D709}K(1,\bullet ))$ uniquely. From ![]() $({\mathcal{K}}K(1,\ast ))_{\bullet }=R(1,\bullet )$ and
$({\mathcal{K}}K(1,\ast ))_{\bullet }=R(1,\bullet )$ and ![]() $\unicode[STIX]{x1D6FE}_{1}=\unicode[STIX]{x1D709}$, we have
$\unicode[STIX]{x1D6FE}_{1}=\unicode[STIX]{x1D709}$, we have ![]() $({\mathcal{K}}f)_{1}=0$, which implies
$({\mathcal{K}}f)_{1}=0$, which implies ![]() $K(1,\bullet )$ and
$K(1,\bullet )$ and ![]() $f$ are orthogonal in
$f$ are orthogonal in ![]() $L^{2}([0,1];\mathbf{R}^{1})$. Hence we can deduce
$L^{2}([0,1];\mathbf{R}^{1})$. Hence we can deduce ![]() $\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}=\Vert f+\unicode[STIX]{x1D709}K(1,\bullet )\Vert _{L^{2}([0,1];\mathbf{R}^{1})}^{2}=\Vert f\Vert _{L^{2}([0,1];\mathbf{R}^{1})}^{2}+\unicode[STIX]{x1D709}^{2}$. The minimum of
$\Vert \unicode[STIX]{x1D6FE}\Vert _{\mathfrak{H}}^{2}=\Vert f+\unicode[STIX]{x1D709}K(1,\bullet )\Vert _{L^{2}([0,1];\mathbf{R}^{1})}^{2}=\Vert f\Vert _{L^{2}([0,1];\mathbf{R}^{1})}^{2}+\unicode[STIX]{x1D709}^{2}$. The minimum of ![]() $I(\unicode[STIX]{x1D6FE})$ is achieved only when
$I(\unicode[STIX]{x1D6FE})$ is achieved only when ![]() $f=0$. Thus, we have shown (7.1). It is easy to see from (7.1) that (A2) holds with
$f=0$. Thus, we have shown (7.1). It is easy to see from (7.1) that (A2) holds with ![]() $\bar{\unicode[STIX]{x1D6FE}}=(\unicode[STIX]{x1D709},0)R(1,\bullet )\in \mathfrak{H}$.
$\bar{\unicode[STIX]{x1D6FE}}=(\unicode[STIX]{x1D709},0)R(1,\bullet )\in \mathfrak{H}$.
Next, we prove (A3). Recall that non-degeneracy of the deterministic Malliavin covariance matrix ![]() $Q(\bar{\unicode[STIX]{x1D6FE}})$ of
$Q(\bar{\unicode[STIX]{x1D6FE}})$ of ![]() $G$ at
$G$ at ![]() $\bar{\unicode[STIX]{x1D6FE}}$ is equivalent to the surjectivity of the tangent map
$\bar{\unicode[STIX]{x1D6FE}}$ is equivalent to the surjectivity of the tangent map ![]() $DG(\bar{\unicode[STIX]{x1D6FE}}):\mathfrak{H}\rightarrow \mathbf{R}^{3}$. Note that
$DG(\bar{\unicode[STIX]{x1D6FE}}):\mathfrak{H}\rightarrow \mathbf{R}^{3}$. Note that ![]() $\bar{\unicode[STIX]{x1D6FE}}\in \mathfrak{H}_{1/2}(\mathbf{R}^{2})$ since
$\bar{\unicode[STIX]{x1D6FE}}\in \mathfrak{H}_{1/2}(\mathbf{R}^{2})$ since ![]() $H>1/4$. From the third assertion in [Reference BismutBis84, Theorem 1.10 in Chapter 1], we see that
$H>1/4$. From the third assertion in [Reference BismutBis84, Theorem 1.10 in Chapter 1], we see that ![]() $DG(\unicode[STIX]{x1D6FE})$ is surjective for every
$DG(\unicode[STIX]{x1D6FE})$ is surjective for every ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}_{1/2}(\mathbf{R}^{2})$ with
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}_{1/2}(\mathbf{R}^{2})$ with ![]() $\unicode[STIX]{x1D6FE}\neq 0$ (in the reference, it is assumed that the distribution linearly spanned by
$\unicode[STIX]{x1D6FE}\neq 0$ (in the reference, it is assumed that the distribution linearly spanned by ![]() $\{V_{1},V_{2}\}$ is fat). Since
$\{V_{1},V_{2}\}$ is fat). Since ![]() $C^{1}$-paths which start at
$C^{1}$-paths which start at ![]() $0$ are dense in
$0$ are dense in ![]() $\mathfrak{H}_{1/2}(\mathbf{R}^{2})$, there are three
$\mathfrak{H}_{1/2}(\mathbf{R}^{2})$, there are three ![]() $C^{1}$-paths
$C^{1}$-paths ![]() $h_{1},h_{2},h_{3}$ which start at
$h_{1},h_{2},h_{3}$ which start at ![]() $0$ such that
$0$ such that ![]() ${\{D_{h_{i}}G(\bar{\unicode[STIX]{x1D6FE}})\}}_{1\leqslant i\leqslant 3}$ spans
${\{D_{h_{i}}G(\bar{\unicode[STIX]{x1D6FE}})\}}_{1\leqslant i\leqslant 3}$ spans ![]() $\mathbf{R}^{3}$. Recalling that
$\mathbf{R}^{3}$. Recalling that ![]() $C^{1}$-paths which start at
$C^{1}$-paths which start at ![]() $0$ belong to
$0$ belong to ![]() $\mathfrak{H}$ (see [Reference Friz and VictoirFV06]), we conclude that the tangent map of
$\mathfrak{H}$ (see [Reference Friz and VictoirFV06]), we conclude that the tangent map of ![]() $G:\mathfrak{H}\rightarrow \mathbf{R}^{3}$ at
$G:\mathfrak{H}\rightarrow \mathbf{R}^{3}$ at ![]() $\bar{\unicode[STIX]{x1D6FE}}$ is also surjective, which is equivalent to (A3).
$\bar{\unicode[STIX]{x1D6FE}}$ is also surjective, which is equivalent to (A3).
Finally, we prove (A4). Let ![]() $\bar{\unicode[STIX]{x1D708}}=\bar{\unicode[STIX]{x1D708}}(\bar{\unicode[STIX]{x1D6FE}})\in \mathbf{R}^{3}$ be the Lagrange multiplier at
$\bar{\unicode[STIX]{x1D708}}=\bar{\unicode[STIX]{x1D708}}(\bar{\unicode[STIX]{x1D6FE}})\in \mathbf{R}^{3}$ be the Lagrange multiplier at ![]() $\bar{\unicode[STIX]{x1D6FE}}$ for
$\bar{\unicode[STIX]{x1D6FE}}$ for ![]() $I$ under the condition that
$I$ under the condition that ![]() $G=a^{\prime }$. Let
$G=a^{\prime }$. Let ![]() $f:(-\unicode[STIX]{x1D716}_{0},\unicode[STIX]{x1D716}_{0})\rightarrow K_{a}^{a^{\prime }}$ be as in (A4). Then, in the same way as [Reference InahamaIna16b, Proposition 5.5], we have
$f:(-\unicode[STIX]{x1D716}_{0},\unicode[STIX]{x1D716}_{0})\rightarrow K_{a}^{a^{\prime }}$ be as in (A4). Then, in the same way as [Reference InahamaIna16b, Proposition 5.5], we have
where ![]() $D^{2}G(\bar{\unicode[STIX]{x1D6FE}})\langle k,k\rangle =D_{k}^{2}G(\bar{\unicode[STIX]{x1D6FE}})$. It is well known that
$D^{2}G(\bar{\unicode[STIX]{x1D6FE}})\langle k,k\rangle =D_{k}^{2}G(\bar{\unicode[STIX]{x1D6FE}})$. It is well known that
By straightforward computation, we have for every ![]() $\unicode[STIX]{x1D6FE},h\in \mathfrak{H}$
$\unicode[STIX]{x1D6FE},h\in \mathfrak{H}$
Thanks to the explicit forms of ![]() $\bar{\unicode[STIX]{x1D6FE}}$ and
$\bar{\unicode[STIX]{x1D6FE}}$ and ![]() $G$, we can easily see that
$G$, we can easily see that ![]() $D_{\bar{\unicode[STIX]{x1D6FE}}}G^{j}(\bar{\unicode[STIX]{x1D6FE}})=(\unicode[STIX]{x1D709},0,0)$. Since the second component of
$D_{\bar{\unicode[STIX]{x1D6FE}}}G^{j}(\bar{\unicode[STIX]{x1D6FE}})=(\unicode[STIX]{x1D709},0,0)$. Since the second component of ![]() $\bar{\unicode[STIX]{x1D6FE}}$ is zero, the second and the third components of
$\bar{\unicode[STIX]{x1D6FE}}$ is zero, the second and the third components of ![]() $D_{h}G(\bar{\unicode[STIX]{x1D6FE}})$ do not depend on
$D_{h}G(\bar{\unicode[STIX]{x1D6FE}})$ do not depend on ![]() $h^{1}$, the first component of
$h^{1}$, the first component of ![]() $h$. This implies that
$h$. This implies that
 $$\begin{eqnarray}Q(\bar{\unicode[STIX]{x1D6FE}})=\left(\begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & \ast \\ 0 & \ast & \ast \end{array}\right),\qquad Q(\bar{\unicode[STIX]{x1D6FE}})^{-1}=\left(\begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & \ast & \ast \\ 0 & \ast & \ast \end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}Q(\bar{\unicode[STIX]{x1D6FE}})=\left(\begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & 1 & \ast \\ 0 & \ast & \ast \end{array}\right),\qquad Q(\bar{\unicode[STIX]{x1D6FE}})^{-1}=\left(\begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & \ast & \ast \\ 0 & \ast & \ast \end{array}\right)\end{eqnarray}$$ and hence ![]() $\bar{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D709},0,0)$. Since
$\bar{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D709},0,0)$. Since ![]() $G^{1}$ is linear,
$G^{1}$ is linear, ![]() $D^{2}G^{1}\equiv 0$. Thus, we have shown that
$D^{2}G^{1}\equiv 0$. Thus, we have shown that ![]() $\langle \bar{\unicode[STIX]{x1D708}},D^{2}G(\bar{\unicode[STIX]{x1D6FE}})\langle f^{\prime }(0),f^{\prime }(0)\rangle \rangle _{\mathbf{R}^{3}}=0$, which clearly implies (A4).◻
$\langle \bar{\unicode[STIX]{x1D708}},D^{2}G(\bar{\unicode[STIX]{x1D6FE}})\langle f^{\prime }(0),f^{\prime }(0)\rangle \rangle _{\mathbf{R}^{3}}=0$, which clearly implies (A4).◻
Remark 7.5. When ![]() $H=1/2$, Young ODE (2.2) controlled by
$H=1/2$, Young ODE (2.2) controlled by ![]() $\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ is called skeleton ODE in probability theory and has been thoroughly studied in both probability theory and control theory. In that case, (A1)–(A4) are known to be a natural set of assumptions with many concrete examples.
$\unicode[STIX]{x1D6FE}\in \mathfrak{H}$ is called skeleton ODE in probability theory and has been thoroughly studied in both probability theory and control theory. In that case, (A1)–(A4) are known to be a natural set of assumptions with many concrete examples.
On the other hand, when ![]() $H\neq 1/2$, not much seems to be known for this ODE. This is the main reason why we cannot systematically find examples for our main theorem in this section. Therefore, we believe that a “fractional version of the control theory of ODEs” needs to be investigated for future developments of this topic. (The fraction version could also be useful in relaxing the unique minimizer assumption (A2).)
$H\neq 1/2$, not much seems to be known for this ODE. This is the main reason why we cannot systematically find examples for our main theorem in this section. Therefore, we believe that a “fractional version of the control theory of ODEs” needs to be investigated for future developments of this topic. (The fraction version could also be useful in relaxing the unique minimizer assumption (A2).)
8 Technical lemma
The following lemma to be used in the proof of Lemma 5.6 is a slight modification of [Reference NualartNua06, Lemma 2.3.1]. For readers’ convenience, we prove it in this section.
Lemma 8.1. Let ![]() ${\{A^{\unicode[STIX]{x1D716}}\}}_{0<\unicode[STIX]{x1D716}<1}$ be a family of real symmetric non-negative definite
${\{A^{\unicode[STIX]{x1D716}}\}}_{0<\unicode[STIX]{x1D716}<1}$ be a family of real symmetric non-negative definite ![]() $n\times n$ random matrices. Let
$n\times n$ random matrices. Let ![]() $\unicode[STIX]{x1D707}_{1}$ and
$\unicode[STIX]{x1D707}_{1}$ and ![]() $\unicode[STIX]{x1D707}_{2}$ be non-negative constants. We assume that for every
$\unicode[STIX]{x1D707}_{2}$ be non-negative constants. We assume that for every ![]() $1<p<\infty$, there exist positive constants
$1<p<\infty$, there exist positive constants ![]() $c_{p,1}$ and
$c_{p,1}$ and ![]() $c_{p,2}$ such that
$c_{p,2}$ such that
for any ![]() $0<\unicode[STIX]{x1D716}<1$ and
$0<\unicode[STIX]{x1D716}<1$ and ![]() $0<\unicode[STIX]{x1D709}<1$. Then, for all
$0<\unicode[STIX]{x1D709}<1$. Then, for all ![]() $0<\unicode[STIX]{x1D716}<1$,
$0<\unicode[STIX]{x1D716}<1$, ![]() $\unicode[STIX]{x1D707}>\unicode[STIX]{x1D707}_{1}\vee \unicode[STIX]{x1D707}_{2}$ and
$\unicode[STIX]{x1D707}>\unicode[STIX]{x1D707}_{1}\vee \unicode[STIX]{x1D707}_{2}$ and ![]() $1<r<\infty$, we have
$1<r<\infty$, we have
Here, ![]() $c$ is a positive constant, which is independent of
$c$ is a positive constant, which is independent of ![]() $\unicode[STIX]{x1D716}$ and
$\unicode[STIX]{x1D716}$ and ![]() $\unicode[STIX]{x1D707}$ but depends on
$\unicode[STIX]{x1D707}$ but depends on ![]() $r$.
$r$.
Proof. Fix ![]() $0<\unicode[STIX]{x1D716}<1$. Let
$0<\unicode[STIX]{x1D716}<1$. Let ![]() $\unicode[STIX]{x1D707}>\unicode[STIX]{x1D707}_{1}\vee \unicode[STIX]{x1D707}_{2}$ and set
$\unicode[STIX]{x1D707}>\unicode[STIX]{x1D707}_{1}\vee \unicode[STIX]{x1D707}_{2}$ and set
First of all, we show that, for every ![]() $r\geqslant r_{0}$, there exists a positive constant
$r\geqslant r_{0}$, there exists a positive constant ![]() $\tilde{c}_{r}$ such that
$\tilde{c}_{r}$ such that
for all ![]() $0<\unicode[STIX]{x1D709}<1$. Here, we can choose
$0<\unicode[STIX]{x1D709}<1$. Here, we can choose ![]() $\tilde{c}_{r}$ as a constant which is independent of
$\tilde{c}_{r}$ as a constant which is independent of ![]() $\unicode[STIX]{x1D716}$,
$\unicode[STIX]{x1D716}$, ![]() $\unicode[STIX]{x1D709}$, and
$\unicode[STIX]{x1D709}$, and ![]() $\unicode[STIX]{x1D707}$ but depends on
$\unicode[STIX]{x1D707}$ but depends on ![]() $r$. Note that the restriction
$r$. Note that the restriction ![]() $r\geqslant r_{0}$ and
$r\geqslant r_{0}$ and ![]() $\unicode[STIX]{x1D707}>\unicode[STIX]{x1D707}_{1}\vee \unicode[STIX]{x1D707}_{2}$ imply
$\unicode[STIX]{x1D707}>\unicode[STIX]{x1D707}_{1}\vee \unicode[STIX]{x1D707}_{2}$ imply ![]() $r\unicode[STIX]{x1D707}\geqslant (r+1+2n)\unicode[STIX]{x1D707}_{i}$ for
$r\unicode[STIX]{x1D707}\geqslant (r+1+2n)\unicode[STIX]{x1D707}_{i}$ for ![]() $i=1,2$. Note
$i=1,2$. Note
The first term satisfies ![]() $\mathbf{P}(|A^{\unicode[STIX]{x1D716}}|\geqslant 1/\unicode[STIX]{x1D709})\leqslant c_{r+1,1}(\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D707}_{1}}\unicode[STIX]{x1D709})^{r+1}\leqslant c_{r+1,1}\unicode[STIX]{x1D716}^{-r\unicode[STIX]{x1D707}}\unicode[STIX]{x1D709}^{r+1}$ from the assumption and
$\mathbf{P}(|A^{\unicode[STIX]{x1D716}}|\geqslant 1/\unicode[STIX]{x1D709})\leqslant c_{r+1,1}(\unicode[STIX]{x1D716}^{-\unicode[STIX]{x1D707}_{1}}\unicode[STIX]{x1D709})^{r+1}\leqslant c_{r+1,1}\unicode[STIX]{x1D716}^{-r\unicode[STIX]{x1D707}}\unicode[STIX]{x1D709}^{r+1}$ from the assumption and ![]() $r\unicode[STIX]{x1D707}\geqslant (r+1)\unicode[STIX]{x1D707}_{1}$. The second term is estimated as follows. We denote by
$r\unicode[STIX]{x1D707}\geqslant (r+1)\unicode[STIX]{x1D707}_{1}$. The second term is estimated as follows. We denote by ![]() $S^{n-1}$ and
$S^{n-1}$ and ![]() $B(v,\unicode[STIX]{x1D70C})$ the unit sphere centered at the origin and the open ball with center
$B(v,\unicode[STIX]{x1D70C})$ the unit sphere centered at the origin and the open ball with center ![]() $v\in \mathbf{R}^{n}$ and radius
$v\in \mathbf{R}^{n}$ and radius ![]() $\unicode[STIX]{x1D70C}>0$. Since
$\unicode[STIX]{x1D70C}>0$. Since ![]() $S^{n-1}$ is compact, there exist vectors
$S^{n-1}$ is compact, there exist vectors ![]() $v_{1},\ldots ,v_{m}\in S^{n-1}$ so that
$v_{1},\ldots ,v_{m}\in S^{n-1}$ so that ![]() $\{B(v_{i},\unicode[STIX]{x1D709}^{2}/2)\}_{i=1}^{m}$ covers
$\{B(v_{i},\unicode[STIX]{x1D709}^{2}/2)\}_{i=1}^{m}$ covers ![]() $S^{n-1}$. In addition,
$S^{n-1}$. In addition, ![]() $\unicode[STIX]{x1D706}_{\min }(A^{\unicode[STIX]{x1D716}})=\inf _{v\in S^{n-1}}\langle v,A^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}$ holds. From these facts, on the event
$\unicode[STIX]{x1D706}_{\min }(A^{\unicode[STIX]{x1D716}})=\inf _{v\in S^{n-1}}\langle v,A^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}$ holds. From these facts, on the event ![]() $\{\unicode[STIX]{x1D706}_{\min }(A^{\unicode[STIX]{x1D716}})<\unicode[STIX]{x1D709},|A^{\unicode[STIX]{x1D716}}|<1/\unicode[STIX]{x1D709}\}$, we can choose
$\{\unicode[STIX]{x1D706}_{\min }(A^{\unicode[STIX]{x1D716}})<\unicode[STIX]{x1D709},|A^{\unicode[STIX]{x1D716}}|<1/\unicode[STIX]{x1D709}\}$, we can choose ![]() $v\in S^{n-1}$ such that
$v\in S^{n-1}$ such that ![]() $\langle v,A^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}<\unicode[STIX]{x1D709}$ with
$\langle v,A^{\unicode[STIX]{x1D716}}v\rangle _{\mathbf{R}^{n}}<\unicode[STIX]{x1D709}$ with ![]() $v\in B(v_{i},\unicode[STIX]{x1D709}^{2}/2)$ for some
$v\in B(v_{i},\unicode[STIX]{x1D709}^{2}/2)$ for some ![]() $1\leqslant i\leqslant m$. Hence,
$1\leqslant i\leqslant m$. Hence,
which implies
Moreover, we see that the number ![]() $m$ of the vectors may depend on
$m$ of the vectors may depend on ![]() $\unicode[STIX]{x1D709}$; however
$\unicode[STIX]{x1D709}$; however ![]() $m\leqslant c_{n}\unicode[STIX]{x1D709}^{-2n}$ holds, where
$m\leqslant c_{n}\unicode[STIX]{x1D709}^{-2n}$ holds, where ![]() $c_{n}$ is a constant depending only on
$c_{n}$ is a constant depending only on ![]() $n$. Therefore, the term
$n$. Therefore, the term ![]() $\mathbf{P}(\unicode[STIX]{x1D706}_{\min }(A^{\unicode[STIX]{x1D716}})<\unicode[STIX]{x1D709},|A^{\unicode[STIX]{x1D716}}|\leqslant 1/\unicode[STIX]{x1D709})$ is estimated by
$\mathbf{P}(\unicode[STIX]{x1D706}_{\min }(A^{\unicode[STIX]{x1D716}})<\unicode[STIX]{x1D709},|A^{\unicode[STIX]{x1D716}}|\leqslant 1/\unicode[STIX]{x1D709})$ is estimated by
where ![]() $c_{r,n}=2^{r+1+2n}c_{n}c_{r+1+2n,2}$. In the last estimate, we used
$c_{r,n}=2^{r+1+2n}c_{n}c_{r+1+2n,2}$. In the last estimate, we used ![]() $r\unicode[STIX]{x1D707}\geqslant (r+1+2n)\unicode[STIX]{x1D707}_{2}$. The estimates above imply
$r\unicode[STIX]{x1D707}\geqslant (r+1+2n)\unicode[STIX]{x1D707}_{2}$. The estimates above imply
which implies (8.1) with ![]() $\tilde{c}_{r}=c_{r+1,1}+c_{r,n}$.
$\tilde{c}_{r}=c_{r+1,1}+c_{r,n}$.
Next, we complete the proof. It follows from (8.1) that, for all ![]() $r\geqslant r_{0}$,
$r\geqslant r_{0}$,
 $$\begin{eqnarray}\displaystyle \mathbf{E}[\unicode[STIX]{x1D706}_{\min }(A^{\unicode[STIX]{x1D716}})^{-r}] & = & \displaystyle r\int _{0}^{\infty }\unicode[STIX]{x1D709}^{-r-1}\mathbf{P}(\unicode[STIX]{x1D706}_{\min }(A^{\unicode[STIX]{x1D716}})<\unicode[STIX]{x1D709})\,d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle r\int _{0}^{1}\unicode[STIX]{x1D709}^{-r-1}\tilde{c}_{r}\unicode[STIX]{x1D716}^{-r\unicode[STIX]{x1D707}}\unicode[STIX]{x1D709}^{r+1}\,d\unicode[STIX]{x1D709}+r\int _{1}^{\infty }\unicode[STIX]{x1D709}^{-r-1}d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & = & \displaystyle r\tilde{c}_{r}\unicode[STIX]{x1D716}^{-r\unicode[STIX]{x1D707}}+1\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (1+r\tilde{c}_{r})\unicode[STIX]{x1D716}^{-r\unicode[STIX]{x1D707}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{E}[\unicode[STIX]{x1D706}_{\min }(A^{\unicode[STIX]{x1D716}})^{-r}] & = & \displaystyle r\int _{0}^{\infty }\unicode[STIX]{x1D709}^{-r-1}\mathbf{P}(\unicode[STIX]{x1D706}_{\min }(A^{\unicode[STIX]{x1D716}})<\unicode[STIX]{x1D709})\,d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle r\int _{0}^{1}\unicode[STIX]{x1D709}^{-r-1}\tilde{c}_{r}\unicode[STIX]{x1D716}^{-r\unicode[STIX]{x1D707}}\unicode[STIX]{x1D709}^{r+1}\,d\unicode[STIX]{x1D709}+r\int _{1}^{\infty }\unicode[STIX]{x1D709}^{-r-1}d\unicode[STIX]{x1D709}\nonumber\\ \displaystyle & = & \displaystyle r\tilde{c}_{r}\unicode[STIX]{x1D716}^{-r\unicode[STIX]{x1D707}}+1\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (1+r\tilde{c}_{r})\unicode[STIX]{x1D716}^{-r\unicode[STIX]{x1D707}}.\nonumber\end{eqnarray}$$ For ![]() $1\leqslant r<r_{0}$, we have
$1\leqslant r<r_{0}$, we have
These imply the assertion. ◻