Introduction
In our investigations of post-mining mineralisation in mines of the southwestern United States, we encountered an unusual and still actively forming bat-guano assemblage at depth (125 feet) in the Rowley mine near Theba, Arizona. Previously, from this assemblage, we reported on the new mineral rowleyite, [Na(NH4,K)9Cl4][V5+,4+2(P,As)O8]6·n[H2O,Na,NH4,K,Cl], which has a microporous vanadate–phosphate framework structure (Kampf et al., Reference Kampf, Cooper, Nash, Cerling, Marty, Hummer, Celestian, Rose and Trebisky2017) and the new mineral phoxite, (NH4)2Mg2(C2O4)(PO3OH)2(H2O)4, which is the first mineral found to contain both phosphate and oxalate groups (Kampf et al., 2019). Herein, we report on the new mineral davidbrownite-(NH4), (NH4,K)5(V4+O)2(C2O4)[PO2.75(OH)1.25]4·3H2O, which is the second mineral containing both phosphate and oxalate groups and which has a novel structure that includes multiple strong hydrogen bonds.
The name davidbrownite-(NH4) honours British–Canadian crystallographer Dr. I. David Brown (born April 11, 1932) in Edgeware, Middlesex, UK. Dr. Brown did his PhD at the Royal Institution of Great Britain and Eidgenössische Technische Hochschule (ETH) Zürich, before moving in 1959 to McMaster University, Hamilton, Ontario, Canada, for a post-doctoral position. Following his post-doctoral years, Dr. Brown joined the Physics Department (now the Department of Physics and Astronomy) at McMaster where he has stayed for his entire professional career, and is now Professor Emeritus. Dr. Brown is well known for developing Bond-Valence Theory (Brown, Reference Brown2002, Reference Brown2016), which is used extensively by mineralogical crystallographers the world over to both validate structural arrangements derived from crystal-structure solution and refinement, and to derive many crystal-chemical details (e.g. the presence of hydrogen and its speciation in structures, the arrangements of hydrogen bonds) that are not revealed directly by crystal-structure refinement. Dr. Brown has given his permission for this mineral to be named in his honour. For naming and species definition, the total occupancy of the three large cation sites in the structure is employed; thereby, the ‘-(NH4)’ suffix in the name reflects the fact that NH4+ > K+. If an analogue with K+ > NH4+ were found, it would be named davidbrownite-(K).
The new mineral and name were approved by the Commission on New Minerals, Nomenclature and Classification of the International Mineralogical Association (IMA2018-129, Kampf et al., Reference Kampf, Cooper, Rossman, Nash, Hawthorne and Marty2019b). Three small cotype specimens are deposited in the collections of the Natural History Museum of Los Angeles County, Los Angeles, California, USA, catalogue numbers 66951, 66955 and 66959.
Occurrence
Davidbrownite-(NH4) was found on the 125-foot level of the Rowley mine, ~20 km NW of Theba, Maricopa County, Arizona, USA (33°2′57″N 113°1′49.59″W). The Rowley mine (in the Painted Rock mining district) is a former Cu–Pb–Au–Ag–Mo–V–baryte–fluorite mine that exploited veins presumed to be related to the intrusion of an andesite porphyry dyke into Tertiary volcanic rocks. Although the mine has not been operated for ore since 1923, collectors took notice of the mine as a source of fine wulfenite crystals around 1945. The most detailed recent account of the history, geology and mineralogy of the mine was by Wilson and Miller (Reference Wilson and Miller1974).
The new mineral occurs in a hot and humid area of the mine in an unusual bat-guano-related, post-mining assemblage of phases that include a variety of vanadates, phosphates, oxalates and chlorides, some containing NH4+. This secondary mineral assemblage is found growing on baryte–quartz-rich matrix and, besides davidbrownite-(NH4) includes antipinite, fluorite, mimetite, mottramite, phoxite (Kampf et al., Reference Kampf, Celestian, Nash and Marty2019a), quartz, rowleyite (Kampf et al., Reference Kampf, Cooper, Nash, Cerling, Marty, Hummer, Celestian, Rose and Trebisky2017), salammoniac, struvite, vanadinite, willemite, wulfenite and several other potentially new minerals.
Physical and optical properties
Crystals of davidbrownite-(NH4) are needles or narrow blades, up to ~0.2 mm long, usually growing in sprays (Fig. 1). The blades are elongate on [010], more or less flattened on {100} and exhibit the crystal forms {100}, {001} and {230} (Fig. 2). No twinning was observed. The colour is light green blue (close to Pantone 317 C), the streak is white, the lustre is vitreous, the Mohs hardness is ~2, the tenacity is brittle and the fracture is splintery. There are two good cleavages in the [010] zone, probably {100} and {001}. The density measured by flotation in a mixture of methylene iodide and toluene is 2.12(2) g cm–3. The calculated density is 2.107 g cm–3 using the empirical formula and 2.116 g cm–3 using the ideal formula. Davidbrownite-(NH4) is non-fluorescent in longwave and shortwave ultraviolet light. The mineral is insoluble at room temperature in H2O, but easily soluble in dilute HCl.

Fig. 1. Sprays of davidbrownite-(NH4) needles with deep blue antipinite on quartz–baryte matrix; Field of view 1.14 mm. Specimen number 66951.

Fig. 2. Crystal drawing of davidbrownite-(NH4); clinographic projection in a non-standard orientation, b vertical.
Davidbrownite-(NH4) is optically biaxial (+) with α = 1.540(2), β = 1.550(5) and γ = 1.582(2) determined in white light. The 2V measured using extinction data with EXCALIBR (Gunter et al., Reference Gunter, Bandli, Bloss, Evans, Su and Weaver2004) is 58.5(5)° and the calculated 2V is 59.4°. Moderate r > v dispersion was observed. The optical orientation is Z = b and Y ≈ a. Pleochroism is distinct: X = pale blue, Y = nearly colourless and Z = light blue; Y < X < Z.
Raman and ATR-IR spectroscopy
The Raman spectrum (Fig. 3) was recorded using a Renishaw M1000 micro-Raman spectrometer with a 514.5 nm green laser, with ~1 μm diameter beam and with 2 mW on the unoriented sample. The attenuated total reflectance (ATR) infrared (IR) spectrum (Fig. 4) was recorded using a SensIR Durascope ATR accessory with a Thermo-Nicolet iS50 FTIR spectrometer on a small amount of powdered material.

Fig. 3. Raman spectrum of davidbrownite-(NH4).
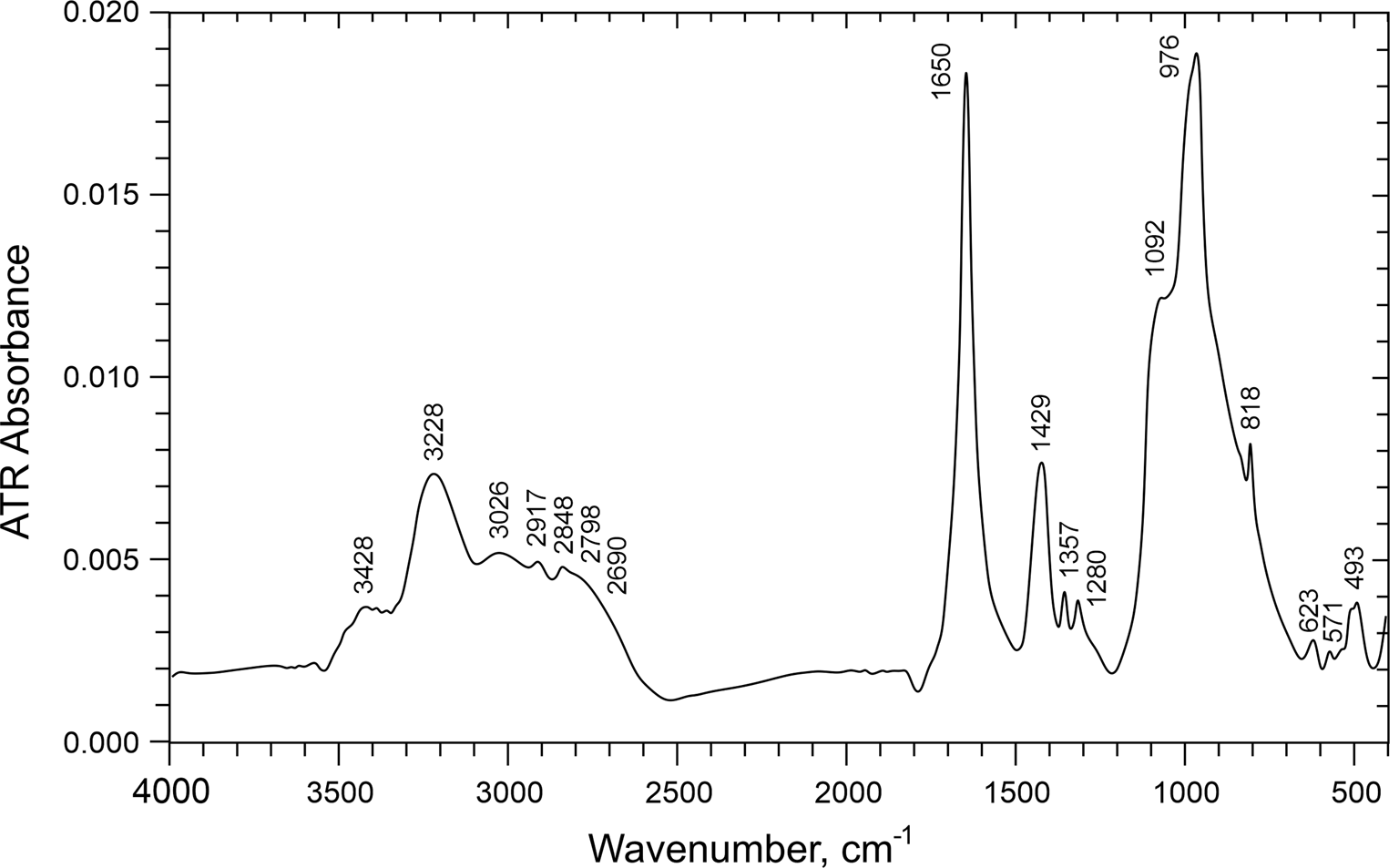
Fig. 4. ATR-IR spectrum of davidbrownite-(NH4).
Weak Raman bands and a stronger infrared band in the 1700–1600 cm–1 region, as seen in the davidbrownite-(NH4) spectra, are consistent with the spectroscopic features of oxalate groups in potassium manganese oxalotophosphite (Orive et al., Reference Orive, Sivasamy, Fernández de Luis, Mosquera and Arriortua2018), ammonium vanadyl oxalatophosphite (Kouvatas et al., Reference Kouvatas, Alonzo, Bataille, Le Pollès, Roiland, Louarn and Le Fur2017) and various minerals with essential (Frost and Weier, Reference Frost and Weier2003) and non-essential (Chukanov et al., Reference Chukanov, Pekov, Olysych, Zubkova and Vigasina2011) oxalate. The strong Raman band at 1499 cm–1 corresponds to the strong C–O stretch seen in other oxalates such as the 1496 cm–1 band in potassium–oxalate solution (Edwards et al., Reference Edwards, Farwell, Rose and Smith1991), which also has a less-intense 1459 cm–1 band comparable to the 1453 cm–1 band in the davidbrownite-(NH4) spectra.
Ammonium features are commonly observed in the 3600–2800 cm–1 range that overlaps the OH stretching region (Beran et al., Reference Beran, Armstrong and Rossman1992). Davidbrownite-(NH4) has several IR absorption and Raman features in this region; however, without detailed deuteration studies of synthetic material, definitive distinction of NH4 and OH features in this and other regions is not possible. The IR band at 1429 cm–1 is consistent with NH4 deformation.
Phosphate bands commonly occur between 1100 and 1000 cm–1, as noted for vanadyl oxalatophosphate (Kouvatas et al., Reference Kouvatas, Alonzo, Bataille, Le Pollès, Roiland, Louarn and Le Fur2017), and these authors assigned V = O stretching to a band at 973 cm–1. Comparable features are seen in these regions of the davidbrownite-(NH4) spectra.
The structure of davidbrownite-(NH4) (see below) suggests that there are probably strong hydrogen bonds (short O–O distances). Using the O–O distances from the structure refinement and the band positions from fig. 1 of Libowitzky (Reference Libowitzky1999), estimated approximate infrared band positions for the hydrogen-bonded OH units can be derived (Table 1). Low energy features from strong hydrogen bonds tend to give broad infrared bands (Hammer et al., Reference Hammer, Libowitzky and Rossman1998). Several of the possible weak hydrogen bonds are consistent with spectral features in the 3500–3200 cm–1 region, but with the exception of the 3428 cm–1 feature, do not correspond well with the approximate predictions. The strong hydrogen bond predicted to be in the 1680 cm–1 region is near the 1650 cm–1 band, but this band position is appropriate for the oxalate antisymmetric stretching mode and is extremely narrow compared to strong OH bands at such low wavenumbers. Clear evidence of the other two strong hydrogen bonds in the predicted positions is not apparent from the infrared spectrum, although the weak absorption in the 1700–2500 cm–1 region could possibly be from hydrogen-bonded OH acid-phosphate groups.
Table 1. Predicted O···H absorption bands from the possible hydrogen-bond Odonor–Oacceptor distances.

*See table 1 of Libowitzky (Reference Libowitzky1999).
Chemical analysis
Electron probe microanalyses (EPMA) of davidbrownite-(NH4) (four points) were undertaken at the University of Utah on a Cameca SX-50 electron microprobe with four wavelength dispersive spectrometers using Probe for EPMA software. Analytical conditions were 15 kV accelerating voltage, 10 nA beam current and beam diameters of 5 and 10 μm. Raw X-ray intensities were corrected for matrix effects with a φρ(z) algorithm (Pouchou and Pichoir, Reference Pouchou, Pichoir, Heinrich and Newbury1991). Intensities for Na, K and P were corrected for time-dependent variation in intensity during analyses. The crystals fragmented when polished, so the analyses were done on unpolished but smooth crystal faces. Because insufficient material is available for a direct determination of H (H2O) or C (C2O3), they were calculated on the basis of the structure determination. The high analytical total is probably due to the partial loss of H2O under vacuum, which results in higher concentrations for the remaining constituents. Analytical data are given in Table 2.
Table 2. Analytical data (wt.%) for davidbrownite-(NH4).

* Based on the structure; S.D. – standard deviation.
The empirical formula (based on V + Mg + Al + P + As = 6 and O = 25 atoms per formula unit) is [(NH4)3.11K1.73Na0.09]Σ4.93[(V4+1.92Mg0.01Al0.02)Σ1.95O2](C2O4)[(P3.94As0.12)Σ4.06O10.94(OH)5.06]·3H2O. The simplified formula is (NH4,K)5(V4+O)2(C2O4)[PO2.75(OH)1.25]4·3H2O, which for 3 NH4 and 2 K per formula unit (pfu) requires (NH4)2O 9.85, K2O 11.88, VO2 20.91, P2O5 35.79, C2O3 9.08, H2O 12.49, total 100 wt.%. The end-member formula is (NH4)5(V4+O)2(C2O4)[PO2.75(OH)1.25]4·3H2O. The Gladstone–Dale compatibility (Mandarino, Reference Mandarino2007) 1 – (K p/K c) is –0.032 in the range of excellent compatibility for the empirical formula.
X-ray crystallography and structure determination
Powder X-ray studies were done using a Rigaku R-Axis Rapid II curved imaging plate microdiffractometer with monochromatised MoKα radiation. A Gandolfi-like motion on the φ and ω axes was used to randomise the sample. Observed d values and intensities were derived by profile fitting using JADE 2010 software (Materials Data, Inc.). The powder data are presented in Table 3. Unit-cell parameters refined from the powder data using JADE 2010 with whole pattern fitting are a = 10.370(13), b = 8.914(14), c = 13.470(14) Å, β = 92.70(2)° and V = 1244(3) Å3.
Table 3. Powder X-ray data (d in Å) for davidbrownite-(NH4).

The strongest lines are given in bold.
Single-crystal X-ray studies were done using a Bruker D8 three-circle diffractometer equipped with a rotating anode generator (MoKα X-radiation), multilayer optics and an APEX-II CCD area detector. The unit-cell dimensions were obtained by least-squares refinement of 3578 reflections with I > 10σI. Systematically absent reflections are consistent with the space group P21/c. Empirical absorption corrections (SADABS; Sheldrick, Reference Sheldrick2015) were applied and equivalent reflections were merged. The structure was solved by direct methods using SHELXS-2013 and the structure was refined to convergence using SHELXL-2016 (Sheldrick, Reference Sheldrick2015). The partly occupied interstitial H2O sites showed very anisotropic displacement behaviour; however, attempts to split the sites led to instability in the refinement and provided no additional useful crystal-chemical information. Data collection and refinement details are given in Table 4, atom coordinates and displacement parameters in Table 5, selected bond distances in Table 6 and a bond-valence analysis in Table 7. The crystallographic information files have been deposited with the Principal Editor of Mineralogical Magazine and are available as Supplementary material (see below).
Table 4. Data collection and structure refinement details for davidbrownite-(NH4).

* Note that H atoms inferred from bond-valence considerations have been included in the structural formula even though they were not located in the structure refinement.
R int = Σ|F o2–F o2(mean)|/Σ[F o2]. GoF = S = {Σ[w(F o2–F c2)2]/(n–p)}1/2. R 1 = Σ||F o|–|F c||/Σ|F o|. wR 2 = {Σ[w(F o2–F c2)2]/Σ[w(F o2)2]}1/2; w = 1/[σ2(F o2) + (aP)2 + bP] where a is 0.0801, b is 0.9668 and P is [2F c2 + Max(F o2,0)]/3.
Table 5. Atom positions and displacement parameters (Å2) for davidbrownite-(NH4).

Table 6. Selected interatomic distances (Å) in davidbrownite-(NH4).

* Not included in coordination; §A3 bonds to O occupying adjacent A3 site.
Table 7. Bond valences for davidbrownite-(NH4) (not including hydrogen-bond contributions). Values are in valence units (vu).

Bond-valence parameters for NH4+–O are from Garcia-Rodriguez et al. (Reference García-Rodríguez, Rute-Pérez, Piñero and González-Silgo2000); all others are from Gagné and Hawthorne (Reference Gagné and Hawthorne2015). The bond valences for the A1, A2 and A3 sites are based only on the dominant cation in each site, as noted. All of the bond valences for A3 contribute to only ½ of the listed values in the horizontal direction.
Discussion of the structure
The structure consists of an ordered VO6–(PΦ)4–C2O4 structural unit (Φ = O and OH) and a disordered K–NH4–H2O interstitial complex. The H positions could not be located, and correct identification of O and OH anions bonded to the P atoms (in less typical fashion) was essential to complete an understanding of the structural unit, which then provided the necessary constraint to allow us to decipher the complex disordered interstitial region of the structure.
VO6–(PΦ)4–C2O4 structural unit
The V atoms are coordinated by six O atoms. Three of these O atoms, O3, O4 and O9, are shared with phosphate groups with V–O bond distances ranging from 1.969 to 2.026 Å, two O atoms, O1 and O2, are shared with the oxalate C2O4 group with longer V–O bonds of 2.272 and 2.058 Å, respectively, and one O atom, O11, forms a short vanadyl V = O bond of 1.601 Å. The long V–O bond of 2.272 Å is trans to the short vanadyl bond, giving a typical [1 + 4 + 1]-coordination (Schindler et al., Reference Schindler, Hawthorne and Baur2000). The interpreted 4+ oxidation state of the V atoms is in agreement with the observed <[6]V–Oeq> distance of 2.01 Å and derived bond-valence sum (Table 6) (Schindler et al., Reference Schindler, Hawthorne and Baur2000; Gagné and Hawthorne, Reference Gagné and Hawthorne2015). The chemistry indicated the presence of minor As, which is presumed to occupy the P sites (~3% As occupancy). As such, the site occupancies of the P1 and P2 sites were refined with joint occupancy by P and As, resulting in a total of ~3.6% As at the two sites. (Table 5).
Pairs of VO6 octahedra are linked by the bridging oxalate group, forming [V2C2O12] dimers. Two of the O atoms (O3 and O4) of the P1 phosphate group are shared with the V atoms, with two P1 tetrahedra forming a double bridge between VO6 octahedra. One O atom (O9) of the P2 phosphate group links to the V atom. The linkages between the VO6 octahedra, oxalate groups and P1 phosphate groups gives a straight chain parallel to [010] that is decorated by P2 phosphate groups (Fig. 5).

Fig. 5. The chain in the structure of davidbrownite-(NH4), viewed down [10![]() $\bar{1}$] with [010] horizontal. The O atoms are numbered.
$\bar{1}$] with [010] horizontal. The O atoms are numbered.
The five anions of the phosphate groups that are not bonded to V atoms, O5, OH6, O7, OH8 and OH10, have incident bond-valence sums ranging from ~1.2–1.5 valence units (vu) from their neighbouring cations (Table 7); however, bond-valence contributions from the disordered interstitial constituents are regarded as approximate. These five anions form three close pairings between neighbouring phosphate groups OH8···OH8 (2.469 Å), OH6···O7 (2.500 Å) and OH10···O5 (2.573 Å), and very strong hydrogen bonding from OH groups is inferred (Fig. 6). In the absence of H positions, reliable hydrogen-bond valences can be determined from OD···OA (D = hydrogen-bond donor; A = hydrogen-bond acceptor) distances (Brown, Reference Brown2002). Our observed OD···OA distances of 2.469, 2.500 and 2.573 Å are consistent with H-bond valences of 0.45, 0.40 and 0.35 vu, respectively (Brown, Reference Brown2002), and donor valences (i.e. 1 – hydrogen-bond valence) of 0.55, 0.60 and 0.65 vu. Adding these respective H bond-valence contributions to the anions with the donor oxygens identified as OH8, OH6 and OH10 produces satisfactory bond-valence sums at the anions. In the extreme case of the very close approach between OH8 anions belonging to neighbouring separate P2 tetrahedra, the single H position is presumed to lie very close to the mid-point (i.e. a near-symmetrical hydrogen bond) and the hydrogen-bond valence ≈ donor bond valence. Thus, there are two OH8 anions pfu, but only a single associated H atom pfu, and the OH8 anion receives an average bond valence from the H atom of (0.45 + 0.55)/2 = 0.5 vu. It should be noted that two factors complicate rigorous bond-valence interpretations at these anions: (1) interstitial identity and position of the disordered (K, NH4 and H2O), which are presumably coupled to (2) the increased positional disorder observed for the anions themselves (i.e. larger displacement parameters for O5, OH6, O7, OH8 and OH10, Table 5). Similar strong hydrogen bonds between phosphate O atoms were noted in the structure of Ca2(NH4)H7(PO4)4·2H2O (Takagi et al., Reference Takagi, Mathew and Brown1980). In davidbrownite-(NH4), OH6 bonds to the P1 tetrahedron and OH8 and OH10 bond to the P2 tetrahedron giving [P1O3(OH)]2 and [P2O2(OH)O]2–H (or [P2O2(OH)O–H–O(OH)O2P2] written symmetrically) pfu for a combined composition of [PO2.75(OH)1.25]4 pfu. The chain structural units have the formula {(V4+O)2(C2O4)[PO2.75(OH)1.25]4}5–, which is balanced by five large monovalent cations pfu in the interstitial complex (see below).

Fig. 6. The chains in the structure of davidbrownite-(NH4), viewed down [010]. The strong hydrogen bonds (OH10–O5, OH6–O7 and OH8–OH8) are shown as blue lines. The O atoms participating in these bonds are labelled and their bond distances are shown. The NH4, K and H2O sites are omitted. The unit cell outline is shown with dashed lines.
NH4–K–H2O interstitial complex
Two fully occupied large-cation sites (A1 and A2) were refined with joint occupancy by N (NH4) and K. The A1 site is occupied dominantly by NH4 [N0.658(8)K0.342(8)] and the A2 site is occupied dominantly by K [K0.673(7)N0.327(7)]. Another site, A3, is interpreted as being partly occupied by both large cations and the O of an H2O group, and this site is located ~1 Å from a low occupancy O (H2O) site (OWA3). To best fit the formula, the A3 site was refined as half occupied jointly by N and K (to provide a 1+ charge pfu) with the remaining site scattering accounted for by O, whose occupancy was linked to the OWA3 occupancy such that the total of the occupancies of the A3 and OWA3 sites is 1. The refined occupancies of the A3 and OWA3 sites are [N0.429(13)K0.071(13)O0.21(3)] and O0.29(3), respectively. Note that the minor Na, indicated by the EPMA, is probably disordered over the A1, A2 and A3 sites. One additional H2O group is split over sites (OWa/OWb/OWc), and the site-occupancies coupled to full occupancy. The combined A3 and OWA3 sites contribute one H2O, and the combined (OWa/OWb/OWc) sites contribute two H2O pfu, providing a total of three H2O pfu. The complete structure is shown in Fig. 7.

Fig. 7. The davidbrownite-(NH4) structure viewed down [100]. The unit-cell outline is shown with dashed lines.
Lewis acid–base considerations
Hawthorne (Reference Hawthorne1985) first introduced the concept of binary structural representation in which a structure can be considered a combination of a strongly bonded ‘structural unit’ (usually anionic) and a weakly bonded ‘interstitial complex’; this concept was expanded by Schindler and Hawthorne (Reference Schindler and Hawthorne2001) and Hawthorne and Schindler (Reference Hawthorne and Schindler2008). The structural unit is (usually) a complex oxyanion and can be characterised by its Lewis basicity. The interstitial complex is (usually) a complex cation and can be characterised by its Lewis acidity. The interaction between the structural unit and the interstitial complex can be examined using the ‘principle of correspondence of Lewis acidity–basicity’ (Hawthorne and Schindler, Reference Hawthorne and Schindler2008). Calculation of the Lewis basicity of the structural unit requires the relation between the charge deficiency per anion of the structural unit and the average number of bonds from the interstitial complex and adjacent structural units. This relation is derived from experimental structure data on particular oxysalt minerals, but is not yet available for phosphate minerals. In the absence of this relation, we may approximate the relation by specifying the average coordination number of a structural unit. Previous work used the coordination numbers [4] for silicate minerals and [3] for sulfate minerals (Hawthorne, Reference Hawthorne and Merlino1997); the pentavalent nature of P suggests that we may use a coordination number intermediate between quadrivalent and hexavalent oxysalts: [3.5].
Let us write the formula of davidbrownite-(NH4) as follows, where the structural unit is enclosed in square brackets and the interstitial complex is enclosed in curly brackets: {(NH4,K)5(H2O)3}5+[(V4+O)2(C3+2O4)[PO3(OH)]4H]5–. The Lewis basicity of the structural unit is defined as the effective charge of the structural unit divided by the number of bonds needed by the structural unit. The number of anions in the structural unit is 22 and hence the number of bonds needed by the structural unit is 22 × 3.5 = 77. The number of bonds within the structural unit is P–O(4 × 4) + V–O(6 × 2) + C–O(2 × 2) + H–O(2 × 5) = 42, and hence the number of bonds needed by the structural unit from the interstitial complex is 77–42 = 35. The charge on the structural unit is 5– and hence the Lewis basicity of the structural unit is 5 / 35 = 0.14 vu. The interstitial complex, {(NH4,K)5(H2O)3}5+, contains three cation sites, A1, A2 and A3, and four H2O sites, OWa, OWb, OWc and OWA3. The A1, A2 and A3 sites have aggregate cation occupancies of 1.0, 1.0 and 0.5, and OWa, OWb, OWc have H2O occupancies of 0.47, 0.42 and 0.11, respectively. We may calculate the Lewis acidity of the interstitial complex by dividing its aggregate charge by the number of bonds in the interstitial complex. The bond lengths involving the A1, A2 and A3 sites are listed in Table 6. However, the OW sites are all partly occupied and these partial occupancies have to be taken into account in calculating the coordination numbers; this leads to the following coordination numbers for A1, A2 and A3: [7], [8] and [5.4], respectively. Each of the H2O groups is bonded to two cations and hence they are all non-transformer H2O groups (Hawthorne, Reference Hawthorne2012) and will not affect the number of bonds from the interstitial complex to the structural unit. As the A1 and A2 sites are fully occupied and the A3 site is half-occupied (Table 5), this gives a total of 7 × 2 + 8 × 2 + 5.4 = 35.4 bonds from the interstitial complex to the structural unit. Thus, the Lewis acidity of the interstitial complex is 5 / 35.4 = 0.14 vu and the principle of correspondence of Lewis acidity–basicity holds. We have not made any predictions here, but we may draw some interesting conclusions. If the OWa, OWb and OWc sites were fully occupied, the Lewis acidity of the interstitial complex would be 0.11 vu, deviating somewhat from the principle of correspondence of Lewis acidity–basicity. This suggests that the partial occupancies of the H2O sites are not random long-range disordered but are constrained by the Lewis basicity of the structural unit. Moreover, the partly occupied H2O sites may couple to the type of interstitial cation occupying the locally associated A1, A2 and A3 sites. If this is the case, it suggests that davidbrownite-(NH4) (and possibly many other associated secondary minerals) may be less disordered than their chemical formulae suggest.
Relation to other structures
While there are no other minerals with similar structures, a variety of phases have been synthesised that contain V4+ coordinated by both oxalate and phosphate anions (cf. Tsai et al., Reference Tsai, Wang, Huang and Lii1999; Do et al., Reference Do, Bontchev and Jacobson2000, Reference Do, Bontchev and Jacobson2001; Colin et al., Reference Colin, Bataille, Ashbrook, Audebrand, Le Pollès, Pivan and Le Fur2006; Nagarathinam et al., Reference Nagarathinam, Saravanan, Phua, Reddy, Chowdari and Vittal2012; Kouvatas et al., Reference Kouvatas, Alonzo, Bataille, Le Pollès, Roiland, Louarn and Le Fur2017). Some of these phases, referred to as vanadyl oxalatophosphates, and particularly those with framework structures, have potential technological applications. We have not encountered any reports of vanadyl oxalatophosphate structures with the same chain topology as davidbrownite-(NH4); however, similar linkages have been reported in several phases, in particular, (NH4)2[VO(HPO4)]2(C2O4)·5H2O (Do et al., Reference Do, Bontchev and Jacobson2000) and Na2[(VO)2(HPO4)2C2O4]·2H2O (Colin et al., Reference Colin, Bataille, Ashbrook, Audebrand, Le Pollès, Pivan and Le Fur2006), both of which have layer structures. A vanadyl oxalatophosphite chain with topology similar to that of the chain in davidbrownite-(NH4) was reported in (NH4)2(VOHPO3)2C2O4·2.9H2O (Kouvatas et al., Reference Kouvatas, Alonzo, Bataille, Le Pollès, Roiland, Louarn and Le Fur2017).
Acknowledgements
One anonymous reviewer, Igor V. Pekov and Structures Editor Peter Leverett are thanked for constructive comments, which improved the manuscript. Keith Wentz, claim holder of the Rowley mine, is thanked for allowing underground access for the study of the occurrence and the collecting of specimens. This study was funded, in part, by the John Jago Trelawney Endowment to the Mineral Sciences Department of the Natural History Museum of Los Angeles County, by NSF grant EAR-1322082 to GRR and by a Natural Sciences and Engineering Research Council Discovery Grant and a Canada Foundation for Innovation Grant to FCH.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1180/mgm.2019.56

















