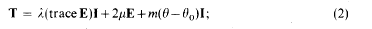We consider a body which occupies the open, bounded, regular region B, whose boundary is ∂B and whose closure is  . We denote by da the element of surface area, by dυ the element of volume, and by n the outward unit normal. We suppose the behaviour of the body to be described by the equations of the quasi-static theory of homogeneous and isotropic thermoelasticity. These equations, which are obtained from the equations of the dynamical theory (see, for example, Carlson [1], Chadwick [2] or Boley and Weiner [3]) by omitting the inertial term pű from the right-hand side of the equation of motion (4), are:
. We denote by da the element of surface area, by dυ the element of volume, and by n the outward unit normal. We suppose the behaviour of the body to be described by the equations of the quasi-static theory of homogeneous and isotropic thermoelasticity. These equations, which are obtained from the equations of the dynamical theory (see, for example, Carlson [1], Chadwick [2] or Boley and Weiner [3]) by omitting the inertial term pű from the right-hand side of the equation of motion (4), are: