In this paper we study the number of rational points on curves in an ensemble of abelian covers of the projective line: let  $\ell$ be a prime,
$\ell$ be a prime, 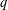 $q$ a prime power and consider the ensemble
$q$ a prime power and consider the ensemble 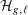 ${\mathcal{H}}_{g,\ell }$ of
${\mathcal{H}}_{g,\ell }$ of 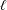 $\ell$-cyclic covers of
$\ell$-cyclic covers of 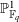 $\mathbb{P}_{\mathbb{F}_{q}}^{1}$ of genus
$\mathbb{P}_{\mathbb{F}_{q}}^{1}$ of genus 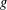 $g$. We assume that
$g$. We assume that 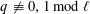 $q\not \equiv 0,1~\text{mod}~\ell$. If
$q\not \equiv 0,1~\text{mod}~\ell$. If 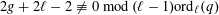 $2g+2\ell -2\not \equiv 0~\text{mod}~(\ell -1)\operatorname{ord}_{\ell }(q)$, then
$2g+2\ell -2\not \equiv 0~\text{mod}~(\ell -1)\operatorname{ord}_{\ell }(q)$, then 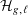 ${\mathcal{H}}_{g,\ell }$ is empty. Otherwise, the number of rational points on a random curve in
${\mathcal{H}}_{g,\ell }$ is empty. Otherwise, the number of rational points on a random curve in 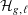 ${\mathcal{H}}_{g,\ell }$ distributes as
${\mathcal{H}}_{g,\ell }$ distributes as 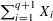 $\sum _{i=1}^{q+1}X_{i}$ as
$\sum _{i=1}^{q+1}X_{i}$ as 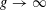 $g\rightarrow \infty$, where
$g\rightarrow \infty$, where 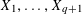 $X_{1},\ldots ,X_{q+1}$ are independent and identically distributed random variables taking the values
$X_{1},\ldots ,X_{q+1}$ are independent and identically distributed random variables taking the values 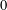 $0$ and
$0$ and 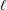 $\ell$ with probabilities
$\ell$ with probabilities 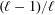 $(\ell -1)/\ell$ and
$(\ell -1)/\ell$ and 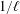 $1/\ell$, respectively. The novelty of our result is that it works in the absence of a primitive
$1/\ell$, respectively. The novelty of our result is that it works in the absence of a primitive 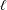 $\ell$th root of unity, the presence of which was crucial in previous studies.
$\ell$th root of unity, the presence of which was crucial in previous studies.
 $A(X\oplus X)$ INTO
$A(X\oplus X)$ INTO  $A(X)$
$A(X)$
 $m$
$m$
 $L$-FUNCTIONS
$L$-FUNCTIONS