Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-06T11:07:05.105Z Has data issue: false hasContentIssue false
  • English
  • Français

ON IMPROVING ROTH’S THEOREM IN THE PRIMES

Part of: Sequences and sets Multiplicative number theory Additive number theory; partitions

Published online by Cambridge University Press:  09 October 2014

Eric Naslund
Eric Naslund*
Affiliation:
Princeton University Mathematics Department, Fine Hall Room 304, Princeton, NJ 08544-1044, USA email naslund@math.princeton.edu
Get access

Abstract

Let $A\subset \{1,\dots ,N\}$ be a set of prime numbers containing no non-trivial arithmetic progressions. Suppose that $A$ has relative density 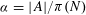${\it\alpha}=|A|/{\it\pi}(N)$, where ${\it\pi}(N)$ denotes the number of primes in the set $\{1,\dots ,N\}$. By modifying Helfgott and De Roton’s work [Improving Roth’s theorem in the primes. Int. Math. Res. Not. IMRN2011 (4) (2011), 767–783], we improve their bound and show that

$$\begin{eqnarray}{\it\alpha}\ll \frac{(\log \log \log N)^{6}}{\log \log N}.\end{eqnarray}$$

MSC classification

Primary: 11B25: Arithmetic progressions 11N13: Primes in progressions 11N36: Applications of sieve methods 11P32: Goldbach-type theorems; other additive questions involving primes 11B30: Arithmetic combinatorics; higher degree uniformity
Type
Research Article
Information
Mathematika , Volume 61 , Issue 1 , January 2015 , pp. 49 - 62
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bourgain, J., On triples in arithmetic progression. Geom. Funct. Anal. 9(5) 1999, 968–984.CrossRefGoogle Scholar
Bourgain, J., Roth’s theorem on progressions revisited. J. Anal. Math. 104 2008, 155–192.CrossRefGoogle Scholar
Erdös, P. and Turán, P., On some sequences of integers. J. Lond. Math. Soc. S1–11(4) 1936, 261–264.Google Scholar
Green, B., Roth’s theorem in the primes. Ann. of Math. (2) 161(3) 2005, 1609–1636.Google Scholar
Green, B. and Tao, T., Restriction theory of the Selberg sieve, with applications. J. Théor. Nombres Bordeaux 18(1) 2006, 147–182.Google Scholar
Halberstam, H. and Richert, H.-E., Sieve Methods (London Mathematical Society Monographs 4), Academic Press (London, 1974).Google Scholar
Heath-Brown, D. R., Integer sets containing no arithmetic progressions. J. Lond. Math. Soc. (2) 35(3) 1987, 385–394.CrossRefGoogle Scholar
Helfgott, H. A. and de Roton, A., Improving Roth’s theorem in the primes. Int. Math. Res. Not. IMRN 2011(4) 2011, 767–783.Google Scholar
Klimov, N. I., Combination of elementary and analytic methods in the theory of numbers. Uspehi Mat. Nauk (N.S.) 13(3(81)) 1958, 145–164.Google Scholar
Roth, K. F., On certain sets of integers. J. Lond. Math. Soc. 28 1953, 104–109.CrossRefGoogle Scholar
Sanders, T., On Roth’s theorem on progressions. Ann. of Math. (2) 174(1) 2011, 619–636.Google Scholar
Szemerédi, E., Integer sets containing no arithmetic progressions. Acta Math. Hungar. 56(1–2) 1990, 155–158.Google Scholar
van der Corput, J. G., Über Summen von Primzahlen und Primzahlquadraten. Math. Ann. 116(1) 1939, 1–50.CrossRefGoogle Scholar