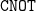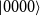1. Introduction
The original idea of using the hyperdeterminant to classify multipartite entanglement goes back to Miyake (Miyake and Wadati, Reference Miyake and Wadati2002; Miyake, Reference Miyake2003). The hyperdeterminant (in the sense of Gelfand et al. Reference Gelfand, Kapranov and Zelevisnky1992) is a generalization of the determinant to higher dimensions. Let
![]() $|{\psi}\rangle=\sum_{i_0, i_1,\dots,i_{n-1}\in\{0,1\}}a_{i_0 i_1\dots i_{n-1}}|{i_0i_1\dots i_{n-1}}\rangle$
be the state vector of an n-qubit system in the Hilbert space
$|{\psi}\rangle=\sum_{i_0, i_1,\dots,i_{n-1}\in\{0,1\}}a_{i_0 i_1\dots i_{n-1}}|{i_0i_1\dots i_{n-1}}\rangle$
be the state vector of an n-qubit system in the Hilbert space
![]() $\mathcal{H}^{\otimes n}=(\mathbb{C}^2)^{\otimes n}$
; then, the hyperdeterminant of the format
$\mathcal{H}^{\otimes n}=(\mathbb{C}^2)^{\otimes n}$
; then, the hyperdeterminant of the format
![]() $2^n$
, denoted in this paper by
$2^n$
, denoted in this paper by
![]() $\Delta_n$
, is an homogenous multivariate polynomial in the
$\Delta_n$
, is an homogenous multivariate polynomial in the
![]() $2^n$
variables
$2^n$
variables
![]() $a_{i_0 i_1\dots i_{n-1}}$
, with coefficients in
$a_{i_0 i_1\dots i_{n-1}}$
, with coefficients in
![]() $\mathbb{Z}$
. It is invariant (up to a sign) by permutation of the qubits and also invariant by the action of the group SLOCC, the group of stochastic local operations assisted by classical communication, assimilated to the Cartesian product
$\mathbb{Z}$
. It is invariant (up to a sign) by permutation of the qubits and also invariant by the action of the group SLOCC, the group of stochastic local operations assisted by classical communication, assimilated to the Cartesian product
![]() $SL(2,\mathbb{C})^n$
. According to Miyake (Miyake and Wadati, Reference Miyake and Wadati2002; Miyake, Reference Miyake2003), the more generic entanglement holds only for the states on which the hyperdeterminant does not vanish and the absolute value of
$SL(2,\mathbb{C})^n$
. According to Miyake (Miyake and Wadati, Reference Miyake and Wadati2002; Miyake, Reference Miyake2003), the more generic entanglement holds only for the states on which the hyperdeterminant does not vanish and the absolute value of
![]() $\Delta_n$
quantifies the amount of generic entanglement.
$\Delta_n$
quantifies the amount of generic entanglement.
In this article, we focus on a four-qubit quantum system. In this case, the hyperdeterminant
![]() $\Delta_4$
is a polynomial of degree 24 in 16 unknowns which has 2,894,276 terms and a rich geometric structure related with the triangulations of the 4-cube (Huggins et al., Reference Huggins, Sturmfels, Yu and Yuster2008). Despite of its huge size, it is still maniable and computable by several methods. Since the formula given by Schläfli in 1852 Gelfand et al. (Reference Gelfand, Kapranov and Zelevisnky1992), Chapter 14, Section 4, other methods have been developed including an expression of
$\Delta_4$
is a polynomial of degree 24 in 16 unknowns which has 2,894,276 terms and a rich geometric structure related with the triangulations of the 4-cube (Huggins et al., Reference Huggins, Sturmfels, Yu and Yuster2008). Despite of its huge size, it is still maniable and computable by several methods. Since the formula given by Schläfli in 1852 Gelfand et al. (Reference Gelfand, Kapranov and Zelevisnky1992), Chapter 14, Section 4, other methods have been developed including an expression of
![]() $\Delta_4$
in terms of fundamental SLOCC invariant polynomials of lower degree (Luque and Thibon Reference Luque and Thibon2003) and more recently an evaluation of
$\Delta_4$
in terms of fundamental SLOCC invariant polynomials of lower degree (Luque and Thibon Reference Luque and Thibon2003) and more recently an evaluation of
![]() $\Delta_4$
via neural networks (Jaffali and Oeding Reference Jaffali and Oeding2020).
$\Delta_4$
via neural networks (Jaffali and Oeding Reference Jaffali and Oeding2020).
Following Miyake, we consider as Gour and Wallach (Reference Gour and Wallach2012), that a four-qubit state with the highest amount of generic entanglement can be defined as a state maximizing the absolute value of
![]() $\Delta_4$
. In the rest of the paper, we refer to this type of state as a maximum hyperdeterminant state (sometimes abbreviated as MHS). Gour and Wallach (Reference Gour and Wallach2012) conjectured that the state
$\Delta_4$
. In the rest of the paper, we refer to this type of state as a maximum hyperdeterminant state (sometimes abbreviated as MHS). Gour and Wallach (Reference Gour and Wallach2012) conjectured that the state
![]() $|L\rangle$
(see Figure 1) is the unique maximum hyperdeterminant state, up to a local unitary operation. This conjecture was proved in 2013 by Chen and Djokovic (Reference Chen and Djokovic2013) and the maximal value of
$|L\rangle$
(see Figure 1) is the unique maximum hyperdeterminant state, up to a local unitary operation. This conjecture was proved in 2013 by Chen and Djokovic (Reference Chen and Djokovic2013) and the maximal value of
![]() $|\Delta_4|$
is
$|\Delta_4|$
is
![]() $\frac{1}{2^83^9}=\frac{1}{{5,038,848}}\simeq 1.98\times10^{-7}$
. As
$\frac{1}{2^83^9}=\frac{1}{{5,038,848}}\simeq 1.98\times10^{-7}$
. As
![]() $\Delta_4$
is a SLOCC-invariant polynomial, a simple consequence of this result is that the SLOCC orbit of
$\Delta_4$
is a SLOCC-invariant polynomial, a simple consequence of this result is that the SLOCC orbit of
![]() $|L\rangle$
corresponds to its LU orbit (about the LU orbits and LU-invariant polynomials of four qubits, we refer the reader to Luque et al., Reference Luque, Thibon and Toumazet2007). Another interesting property of the state
$|L\rangle$
corresponds to its LU orbit (about the LU orbits and LU-invariant polynomials of four qubits, we refer the reader to Luque et al., Reference Luque, Thibon and Toumazet2007). Another interesting property of the state
![]() $|L\rangle$
is to be the only state (up to local unitary operations) maximizing the average Tsallis
$|L\rangle$
is to be the only state (up to local unitary operations) maximizing the average Tsallis
![]() $\alpha$
-entropy of entanglement, for all
$\alpha$
-entropy of entanglement, for all
![]() $\alpha > 2$
(Gour and Wallach, Reference Gour and Wallach2010). Let us also mention two other maximum hyperdeterminant states, which have the property of having real coordinates (see Figure 1):
$\alpha > 2$
(Gour and Wallach, Reference Gour and Wallach2010). Let us also mention two other maximum hyperdeterminant states, which have the property of having real coordinates (see Figure 1):
![]() $|{\Phi_5}\rangle$
(reported by Osterloh and Siewert Reference Osterloh and Siewert2006 and by Alsina Reference Alsina2017) and
$|{\Phi_5}\rangle$
(reported by Osterloh and Siewert Reference Osterloh and Siewert2006 and by Alsina Reference Alsina2017) and
![]() $|{M_{2222}}\rangle$
(reported by Jaffali Reference Jaffali2020).
$|{M_{2222}}\rangle$
(reported by Jaffali Reference Jaffali2020).

Figure 1. 4-qubits states for which
![]() $|\Delta_4|$
is maximal.
$|\Delta_4|$
is maximal.
In Quantum Information and Computation, entangled states, and in particular maximally entangled states, play the role of an important physical resource (see e.g. the introduction of Chen and Djokovic, Reference Chen and Djokovic2013). Despite of that, to our knowledge, there is no proposal in the academic literature for quantum circuits capable of producing the state
![]() $|L\rangle$
or any other MHS. The goal of this work is merely to fill this gap by describing a family of quantum circuits that enable the generation of maximum hyperdeterminant states. We show that a MHS can be obtained by the action a certain type of
$|L\rangle$
or any other MHS. The goal of this work is merely to fill this gap by describing a family of quantum circuits that enable the generation of maximum hyperdeterminant states. We show that a MHS can be obtained by the action a certain type of
![]() $\mathtt{CNOT}$
gate circuits on a fully factorized state, namely a state of the LU orbit of
$\mathtt{CNOT}$
gate circuits on a fully factorized state, namely a state of the LU orbit of
![]() $|0000\rangle$
. As a consequence of this result, one can construct quantum circuits of relatively small depth generating the three states
$|0000\rangle$
. As a consequence of this result, one can construct quantum circuits of relatively small depth generating the three states
![]() $|L\rangle$
,
$|L\rangle$
,
![]() $|{\Phi_5}\rangle$
and
$|{\Phi_5}\rangle$
and
![]() $|{M_{2222}}\rangle$
.
$|{M_{2222}}\rangle$
.
The paper is structured as follows. Section 2 is a reminder on quantum circuits of
![]() $\mathtt{CNOT}$
gates and
$\mathtt{CNOT}$
gates and
![]() $\mathtt{SWAP}$
gates, where we introduce most of our notations and give some useful conjugation rules between these gates. In Section 3, we present the methodology and algorithms used in our numerical approach to find circuits generating maximum hyperdeterminant states. The two next Sections (4 and 5) are dedicated to the description of these circuits. Finally, in Section 6, we propose three simple quantum circuits generating the states
$\mathtt{SWAP}$
gates, where we introduce most of our notations and give some useful conjugation rules between these gates. In Section 3, we present the methodology and algorithms used in our numerical approach to find circuits generating maximum hyperdeterminant states. The two next Sections (4 and 5) are dedicated to the description of these circuits. Finally, in Section 6, we propose three simple quantum circuits generating the states
![]() $|L\rangle$
,
$|L\rangle$
,
![]() $|{\Phi_5}\rangle$
and
$|{\Phi_5}\rangle$
and
![]() $M_{2222}$
, as well as an implementation of a circuit generating the state
$M_{2222}$
, as well as an implementation of a circuit generating the state
![]() $|L\rangle$
into a quantum computer provided by the IBM quantum experience at https://quantum-computing.ibm.com/.
$|L\rangle$
into a quantum computer provided by the IBM quantum experience at https://quantum-computing.ibm.com/.
This article goes along with a Python module than can be downloaded at https://github.com/marcbataille/maximum-hyperdeterminant-states. Our module relies on the Python module SymPy (a Computer Algebra System), allowing us to perform symbolic and exact computation. It provides an implementation in the Python language of the different algorithms, quantum gates and quantum states used in this work. As the proof of some assertions (mostly numerical equalities) consists only of basic linear algebra and calculus, we chose to refer the reader to the corresponding function of the module that does the job.
2. Quantum Circuits of
 $\mathtt{CNOT}$
and
$\mathtt{CNOT}$
and
 $\mathtt{SWAP}$
Gates
$\mathtt{SWAP}$
Gates
In this section, we introduce the main notations and conventions of the paper and we recall the definition of some classical quantum gates (Table 1) as well as some properties of the
![]() $\mathtt{CNOT}$
gates and
$\mathtt{CNOT}$
gates and
![]() $\mathtt{SWAP}$
gates often used in the rest of the article.
$\mathtt{SWAP}$
gates often used in the rest of the article.
Table 1. Classical single-qubit unitary gates

Let
![]() $n\geqslant 1$
be the number of qubits of the considered quantum register. We label each qubit from 0 to
$n\geqslant 1$
be the number of qubits of the considered quantum register. We label each qubit from 0 to
![]() $n-1$
, thus following the usual convention. For coherence, we also number the lines and columns of a
$n-1$
, thus following the usual convention. For coherence, we also number the lines and columns of a
![]() $n\times n$
matrix from 0 to
$n\times n$
matrix from 0 to
![]() $n-1,$
and we consider that a permutation in the symmetric group
$n-1,$
and we consider that a permutation in the symmetric group
![]() $\mathfrak{S}_{n}$
is a bijection of
$\mathfrak{S}_{n}$
is a bijection of
![]() $\{0,\dots,n-1\}$
.
$\{0,\dots,n-1\}$
.
If two normalized vectors
![]() $|{\psi}\rangle$
and
$|{\psi}\rangle$
and
![]() $|{\psi'}\rangle$
of the Hilbert space
$|{\psi'}\rangle$
of the Hilbert space
![]() $\mathcal{H}^{\otimes n}$
are equal up to a global phase, then they represent physically the same state and we write
$\mathcal{H}^{\otimes n}$
are equal up to a global phase, then they represent physically the same state and we write
![]() $|{\psi}\rangle\simeq|{\psi'}\rangle$
. In the same way, we write
$|{\psi}\rangle\simeq|{\psi'}\rangle$
. In the same way, we write
![]() $U\simeq U'$
for two unitary operators which are equal up to a global phase. In the design of quantum circuits, we use the following correspondences between the classical gates :
$U\simeq U'$
for two unitary operators which are equal up to a global phase. In the design of quantum circuits, we use the following correspondences between the classical gates :
When one applies locally a single-qubit gate U to the qubit i of a n-qubit register, the corresponding action on the n-qubit system is that of the unitary operator
where
![]() $\otimes$
is the Kronecker product of matrices and I the identity matrix in dimension 2. As an example, if
$\otimes$
is the Kronecker product of matrices and I the identity matrix in dimension 2. As an example, if
![]() $n=4$
,
$n=4$
,
![]() $H_1= I\otimes H\otimes I\otimes I$
and
$H_1= I\otimes H\otimes I\otimes I$
and
![]() $H_0H_3=H\otimes I\otimes I\otimes H$
. We also use vectors of
$H_0H_3=H\otimes I\otimes I\otimes H$
. We also use vectors of
![]() $\mathbb{F}_{2}^n$
as labels to indicate the set of qubits to which the single-qubit unitary U is applied. Let
$\mathbb{F}_{2}^n$
as labels to indicate the set of qubits to which the single-qubit unitary U is applied. Let
![]() $v=[v_0 \dots v_{n-1}]^t$
be a (column) vector of
$v=[v_0 \dots v_{n-1}]^t$
be a (column) vector of
![]() $\mathbb{F}_{2}^n$
, we denote by
$\mathbb{F}_{2}^n$
, we denote by
![]() $U_{v}$
the product
$U_{v}$
the product
![]() $\prod_iU_i^{v_i}$
.
$\prod_iU_i^{v_i}$
.
A
![]() $\mathtt{CNOT}$
gate with target on qubit i and control on qubit j is denoted by
$\mathtt{CNOT}$
gate with target on qubit i and control on qubit j is denoted by
![]() $X_{[i\;j]}$
(not to be confused with
$X_{[i\;j]}$
(not to be confused with
![]() $X_i$
which denotes a Pauli-
$X_i$
which denotes a Pauli-
![]() $\mathtt X$
gate applied on qubit i). The group generated by the
$\mathtt X$
gate applied on qubit i). The group generated by the
![]() $\mathtt{CNOT}$
gates acting on an n-qubit quantum system is denoted by
$\mathtt{CNOT}$
gates acting on an n-qubit quantum system is denoted by
![]() ${{\left\rangle\mathtt{CNOT}\right\rangle}_{n}}$
. Let us denote by
${{\left\rangle\mathtt{CNOT}\right\rangle}_{n}}$
. Let us denote by
![]() ${\mathrm{GL}_{n}(\mathbb{F}_2)}$
the general linear group over
${\mathrm{GL}_{n}(\mathbb{F}_2)}$
the general linear group over
![]() $\mathbb{F}_{2}$
in dimension n. A transvection matrix
$\mathbb{F}_{2}$
in dimension n. A transvection matrix
![]() $[i\;j]$
(
$[i\;j]$
(
![]() $i,j=1\dots n-1$
and
$i,j=1\dots n-1$
and
![]() $i\neq j$
) is the matrix of
$i\neq j$
) is the matrix of
![]() ${\mathrm{GL}_{n}(\mathbb{F}_2)}$
defined by
${\mathrm{GL}_{n}(\mathbb{F}_2)}$
defined by
![]() $[i\;j]=I_n+E_{ij}$
, where
$[i\;j]=I_n+E_{ij}$
, where
![]() $I_n$
is the identity in dimension n and
$I_n$
is the identity in dimension n and
![]() $E_{ij}$
is the matrix with all entries equal to zero but the entry (i,j) that is equal to 1. We recall that the transvection matrices generate the group
$E_{ij}$
is the matrix with all entries equal to zero but the entry (i,j) that is equal to 1. We recall that the transvection matrices generate the group
![]() ${\mathrm{GL}_{n}(\mathbb{F}_2)}$
and that multiplying a matrix M to the left by a transvection matrix
${\mathrm{GL}_{n}(\mathbb{F}_2)}$
and that multiplying a matrix M to the left by a transvection matrix
![]() $[i\;j]$
is equivalent to adding the row j to the row i of M. From these facts, one can deduce that the group
$[i\;j]$
is equivalent to adding the row j to the row i of M. From these facts, one can deduce that the group
![]() ${{\left\rangle\mathtt{CNOT}\right\rangle}_{n}}$
is isomorphic to
${{\left\rangle\mathtt{CNOT}\right\rangle}_{n}}$
is isomorphic to
![]() ${\mathrm{GL}_{n}(\mathbb{F}_2)}$
, a possible isomorphism associating, to any gate
${\mathrm{GL}_{n}(\mathbb{F}_2)}$
, a possible isomorphism associating, to any gate
![]() $X_{[i\;j]}$
, the transvection matrix
$X_{[i\;j]}$
, the transvection matrix
![]() $[i\;j]$
(see Bataille, Reference Bataille2022 for more details). The order of
$[i\;j]$
(see Bataille, Reference Bataille2022 for more details). The order of
![]() ${{\left\rangle\mathtt{CNOT}\right\rangle}_{n}}$
is therefore equal to the order of
${{\left\rangle\mathtt{CNOT}\right\rangle}_{n}}$
is therefore equal to the order of
![]() ${\mathrm{GL}_{n}(\mathbb{F}_2)}$
:
${\mathrm{GL}_{n}(\mathbb{F}_2)}$
:
Let A be any matrix in
![]() ${\mathrm{GL}_{n}(\mathbb{F}_2)}$
, we denote by
${\mathrm{GL}_{n}(\mathbb{F}_2)}$
, we denote by
![]() $X_A$
the element of
$X_A$
the element of
![]() ${{\left\rangle\mathtt{CNOT}\right\rangle}_{n}}$
associated with A, that is
${{\left\rangle\mathtt{CNOT}\right\rangle}_{n}}$
associated with A, that is
![]() $X_A$
is the product of any sequence of
$X_A$
is the product of any sequence of
![]() $\mathtt{CNOT}$
gates
$\mathtt{CNOT}$
gates
![]() $X_{[i_1\;j_i]},\dots, X_{[i_p\;j_p]}$
such that A can be decomposed in the product of the transvection matrices
$X_{[i_1\;j_i]},\dots, X_{[i_p\;j_p]}$
such that A can be decomposed in the product of the transvection matrices
![]() $[i_1\;j_i],\dots,[i_p\;j_p]$
.
$[i_1\;j_i],\dots,[i_p\;j_p]$
.
The
![]() $\mathtt{SWAP}$
gate that exchanges qubits i and j is denoted by
$\mathtt{SWAP}$
gate that exchanges qubits i and j is denoted by
![]() $S_{(i\;j)}$
. Let
$S_{(i\;j)}$
. Let
![]() $\sigma$
be a permutation of the symmetric group
$\sigma$
be a permutation of the symmetric group
![]() $\mathfrak{S}_{n}$
. We also denote by
$\mathfrak{S}_{n}$
. We also denote by
![]() $\sigma$
the permutation matrix associated with the permutation
$\sigma$
the permutation matrix associated with the permutation
![]() $\sigma$
. Consequently,
$\sigma$
. Consequently,
![]() $(i\;j)$
denotes the transposition of
$(i\;j)$
denotes the transposition of
![]() $\mathfrak{S}_{n}$
that exchanges i and j as well as the corresponding transposition matrix in
$\mathfrak{S}_{n}$
that exchanges i and j as well as the corresponding transposition matrix in
![]() ${\mathrm{GL}_{n}(\mathbb{F}_2)}$
. The permutation matrix
${\mathrm{GL}_{n}(\mathbb{F}_2)}$
. The permutation matrix
![]() $\sigma$
is defined as the matrix
$\sigma$
is defined as the matrix
![]() $A=(a_{ij})$
in
$A=(a_{ij})$
in
![]() ${\mathrm{GL}_{n}(\mathbb{F}_2)}$
such that
${\mathrm{GL}_{n}(\mathbb{F}_2)}$
such that
![]() $a_{ij}=1$
if and only if
$a_{ij}=1$
if and only if
![]() $i=\sigma(j)$
. We recall that multiplying a matrix M to the left by a permutation matrix
$i=\sigma(j)$
. We recall that multiplying a matrix M to the left by a permutation matrix
![]() $\sigma$
is equivalent to applying the permutation
$\sigma$
is equivalent to applying the permutation
![]() $\sigma$
to the rows of M. In this case, each row
$\sigma$
to the rows of M. In this case, each row
![]() $R_i$
is replaced by the row
$R_i$
is replaced by the row
![]() $R_{\sigma^{-1}(i)}$
. The group of permutation matrices is a subgroup of
$R_{\sigma^{-1}(i)}$
. The group of permutation matrices is a subgroup of
![]() ${\mathrm{GL}_{n}(\mathbb{F}_2)}$
which is isomorphic to the group generated by the
${\mathrm{GL}_{n}(\mathbb{F}_2)}$
which is isomorphic to the group generated by the
![]() $\mathtt{SWAP}$
gates acting on n qubits : to each
$\mathtt{SWAP}$
gates acting on n qubits : to each
![]() $\mathtt{SWAP}$
gate
$\mathtt{SWAP}$
gate
![]() $S_{(i\;j)}$
corresponds the transposition matrix
$S_{(i\;j)}$
corresponds the transposition matrix
![]() $(i\;j)$
. We denote by
$(i\;j)$
. We denote by
![]() $S_{\sigma}$
the product of any sequence of
$S_{\sigma}$
the product of any sequence of
![]() $\mathtt{SWAP}$
gates
$\mathtt{SWAP}$
gates
![]() $S_{(i_1\;j_1)},\dots, S_{(i_p\;j_p)}$
such that
$S_{(i_1\;j_1)},\dots, S_{(i_p\;j_p)}$
such that
![]() $\sigma=(i_1\;j_1)\dots (i_p\;j_p)$
.
$\sigma=(i_1\;j_1)\dots (i_p\;j_p)$
.
Let
![]() $\tau$
be a transposition of
$\tau$
be a transposition of
![]() $\mathfrak{S}_{n}$
, it is easy to check that
$\mathfrak{S}_{n}$
, it is easy to check that
![]() $S_{\tau}X_{[i\;j]}S_{\tau}=X_{[\tau(i)\;\tau(j)]}$
. Hence, by induction, one has for any permutation
$S_{\tau}X_{[i\;j]}S_{\tau}=X_{[\tau(i)\;\tau(j)]}$
. Hence, by induction, one has for any permutation
![]() $\sigma$
:
$\sigma$
:
Let U be a single-qubit unitary matrix and
![]() $U_i$
the unitary corresponding to the action of U on qubit i (Identity (6)). One has, for any permutation
$U_i$
the unitary corresponding to the action of U on qubit i (Identity (6)). One has, for any permutation
![]() $\sigma$
$\sigma$
and for any vector v in
![]() $\mathbb{F}_{2}^{n}$
$\mathbb{F}_{2}^{n}$
where
![]() $\sigma v$
is the matrix product between
$\sigma v$
is the matrix product between
![]() $\sigma$
and v.
$\sigma$
and v.
The Pauli group for n qubits is the subgroup of the unitary group
![]() $U(2^n)$
generated by the Pauli gates
$U(2^n)$
generated by the Pauli gates
![]() $X_i,Y_i$
and
$X_i,Y_i$
and
![]() $Z_i$
(
$Z_i$
(
![]() $0\leqslant i \leqslant n-1$
). Since
$0\leqslant i \leqslant n-1$
). Since
![]() $Y=\mathrm{i} XZ$
and
$Y=\mathrm{i} XZ$
and
![]() $XZ=-ZX$
, any element of this group can be written uniquely in the form
$XZ=-ZX$
, any element of this group can be written uniquely in the form
where u and v are two vectors of the space
![]() $\mathbb{F}_{2}^n$
and
$\mathbb{F}_{2}^n$
and
![]() $\lambda\in\{0,1,2,3\}$
. The
$\lambda\in\{0,1,2,3\}$
. The
![]() $\mathtt{CNOT}$
gates normalize the Pauli group, and it is not difficult to prove the following conjugation rules of a Pauli gate by a
$\mathtt{CNOT}$
gates normalize the Pauli group, and it is not difficult to prove the following conjugation rules of a Pauli gate by a
![]() $\mathtt{CNOT}$
gate:
$\mathtt{CNOT}$
gate:
![]() $X_{[ij]}Z_iX_{[ij]}=Z_iZ_j$
,
$X_{[ij]}Z_iX_{[ij]}=Z_iZ_j$
,
![]() $X_{[ij]}Z_jX_{[ij]}=Z_j$
,
$X_{[ij]}Z_jX_{[ij]}=Z_j$
,
![]() $X_{[ij]}X_iX_{[ij]}=X_i$
and
$X_{[ij]}X_iX_{[ij]}=X_i$
and
![]() $X_{[ij]}X_jX_{[ij]}=X_iX_j$
. These rules can be generalized by induction as
$X_{[ij]}X_jX_{[ij]}=X_iX_j$
. These rules can be generalized by induction as
where u and v are vectors in
![]() $\mathbb{F}_{2}^n$
, A is a matrix in
$\mathbb{F}_{2}^n$
, A is a matrix in
![]() ${\mathrm{GL}_{n}(\mathbb{F}_2)}$
and
${\mathrm{GL}_{n}(\mathbb{F}_2)}$
and
![]() $A^{-t}$
a shorthand for
$A^{-t}$
a shorthand for
![]() $\left(A^{-1}\right)^{t}$
.
$\left(A^{-1}\right)^{t}$
.
3. Methodology used in the Numerical Exploration
We address the following problem, that we have already formulated in Bataille (Reference Bataille2022) : is it possible to generate a state maximizing
![]() $|\Delta_4|$
by applying a
$|\Delta_4|$
by applying a
![]() $\mathtt{CNOT}$
gate circuit to a state of the LU orbit of
$\mathtt{CNOT}$
gate circuit to a state of the LU orbit of
![]() $|0000\rangle$
?
$|0000\rangle$
?
We use the classical Z-Y decomposition of a single-qubit unitary operator in the form
![]() $\mathrm{e} ^{\mathrm{i}\varphi}R_z(\alpha)R_y(\beta)R_z(\alpha')$
(see e.g. Nielsen and Chuang, Reference Nielsen and Chuang2011, Th. 4.1). Using this decomposition, any fully factorized unitary operator U depends, up to a global phase, on the 12 real parameters of the matrix
$\mathrm{e} ^{\mathrm{i}\varphi}R_z(\alpha)R_y(\beta)R_z(\alpha')$
(see e.g. Nielsen and Chuang, Reference Nielsen and Chuang2011, Th. 4.1). Using this decomposition, any fully factorized unitary operator U depends, up to a global phase, on the 12 real parameters of the matrix
 \begin{equation} \mathcal P=\begin{bmatrix}\alpha_0&\quad \beta_0&\quad \alpha_0'\\ \alpha_1&\quad \beta_1&\quad \alpha_1'\\ \alpha_2&\quad \beta_2&\quad \alpha_2'\\ \alpha_3&\quad \beta_3&\quad \alpha_3'\end{bmatrix}.\end{equation}
\begin{equation} \mathcal P=\begin{bmatrix}\alpha_0&\quad \beta_0&\quad \alpha_0'\\ \alpha_1&\quad \beta_1&\quad \alpha_1'\\ \alpha_2&\quad \beta_2&\quad \alpha_2'\\ \alpha_3&\quad \beta_3&\quad \alpha_3'\end{bmatrix}.\end{equation}
Let us define the unitary
![]() $U(\mathcal P)$
by
$U(\mathcal P)$
by
As a rotation around the
![]() $\hat z$
axis applied to
$\hat z$
axis applied to
![]() $|0\rangle$
is just a change of phase, it is possible to write any state vector of the LU orbit of
$|0\rangle$
is just a change of phase, it is possible to write any state vector of the LU orbit of
![]() $|0000\rangle$
(up to a global phase), by using only two parameters for each qubit. So, any state in the LU orbit of
$|0000\rangle$
(up to a global phase), by using only two parameters for each qubit. So, any state in the LU orbit of
![]() $|0000\rangle$
is equal (up to a global phase) to the state
$|0000\rangle$
is equal (up to a global phase) to the state
![]() $|{\mathcal P}\rangle$
defined by
$|{\mathcal P}\rangle$
defined by
Using the definition of the rotation matrices around the
![]() $\hat z$
and
$\hat z$
and
![]() $\hat y$
axes, one has
$\hat y$
axes, one has
 \begin{align*} \text{where }(a_0,a_1)&=\left(\mathrm{e}^{-\mathrm{i}\alpha_0/2}\cos\frac{\beta_0}{2}, \mathrm{e}^{\mathrm{i}\alpha_0/2}\sin\frac{\beta_0}{2}\right),\\ (b_0,b_1)&=\left(\mathrm{e}^{-\mathrm{i}\alpha_1/2}\cos\frac{\beta_1}{2},\mathrm{e}^{\mathrm{i}\alpha_1/2}\sin\frac{\beta_1}{2}\right),\\ (c_0,c_1)&=\left(\mathrm{e}^{-\mathrm{i}\alpha_2/2}\cos\frac{\beta_2}{2},\mathrm{e}^{\mathrm{i}\alpha_2/2}\sin\frac{\beta_2}{2}\right),\\ (d_0,d_1)&=\left(\mathrm{e}^{-\mathrm{i}\alpha_3/2}\cos\frac{\beta_3}{2},\mathrm{e}^{\mathrm{i}\alpha_3/2}\sin\frac{\beta_3}{2}\right).\end{align*}
\begin{align*} \text{where }(a_0,a_1)&=\left(\mathrm{e}^{-\mathrm{i}\alpha_0/2}\cos\frac{\beta_0}{2}, \mathrm{e}^{\mathrm{i}\alpha_0/2}\sin\frac{\beta_0}{2}\right),\\ (b_0,b_1)&=\left(\mathrm{e}^{-\mathrm{i}\alpha_1/2}\cos\frac{\beta_1}{2},\mathrm{e}^{\mathrm{i}\alpha_1/2}\sin\frac{\beta_1}{2}\right),\\ (c_0,c_1)&=\left(\mathrm{e}^{-\mathrm{i}\alpha_2/2}\cos\frac{\beta_2}{2},\mathrm{e}^{\mathrm{i}\alpha_2/2}\sin\frac{\beta_2}{2}\right),\\ (d_0,d_1)&=\left(\mathrm{e}^{-\mathrm{i}\alpha_3/2}\cos\frac{\beta_3}{2},\mathrm{e}^{\mathrm{i}\alpha_3/2}\sin\frac{\beta_3}{2}\right).\end{align*}
Any state resulting from the action of an unitary operator in
![]() ${{\left\rangle\mathtt{CNOT}\right\rangle}_{4}}$
, on a state of the LU orbit of
${{\left\rangle\mathtt{CNOT}\right\rangle}_{4}}$
, on a state of the LU orbit of
![]() $|0000\rangle$
can be written (up to a global phase) in the form
$|0000\rangle$
can be written (up to a global phase) in the form
where A is a matrix in
![]() ${\mathrm{GL}_{4}(\mathbb{F}_2)}$
and
${\mathrm{GL}_{4}(\mathbb{F}_2)}$
and
![]() $\mathcal P$
a matrix of parameters. In order to determine the states of type
$\mathcal P$
a matrix of parameters. In order to determine the states of type
![]() $X_A|{\mathcal P}\rangle$
capable of maximizing
$X_A|{\mathcal P}\rangle$
capable of maximizing
![]() $|\Delta_4|$
, it is sufficient to consider the right cosets of the subgroup of
$|\Delta_4|$
, it is sufficient to consider the right cosets of the subgroup of
![]() ${{\left\rangle\mathtt{CNOT}\right\rangle}_{4}}$
generated by the
${{\left\rangle\mathtt{CNOT}\right\rangle}_{4}}$
generated by the
![]() $\mathtt{SWAP}$
gates (group
$\mathtt{SWAP}$
gates (group
![]() ${{\left\rangle\mathtt{SWAP}\right\rangle}_{4}}\simeq \mathfrak{S}_{4})$
, because
${{\left\rangle\mathtt{SWAP}\right\rangle}_{4}}\simeq \mathfrak{S}_{4})$
, because
![]() $|\Delta_4|$
is invariant under permutation of the qubits, that is
$|\Delta_4|$
is invariant under permutation of the qubits, that is
![]() $|\Delta_4(X_A|{\mathcal P}\rangle\!)|=|\Delta_4(X_{\sigma A}|{\mathcal P}\rangle\!)|$
for any permutation matrix
$|\Delta_4(X_A|{\mathcal P}\rangle\!)|=|\Delta_4(X_{\sigma A}|{\mathcal P}\rangle\!)|$
for any permutation matrix
![]() $\sigma$
. The order of the group
$\sigma$
. The order of the group
![]() ${{\left\rangle\mathtt{CNOT}\right\rangle}_{4}}$
is 20,160 (see Identity (7)), so the number of right cosets of
${{\left\rangle\mathtt{CNOT}\right\rangle}_{4}}$
is 20,160 (see Identity (7)), so the number of right cosets of
![]() ${{\left\rangle\mathtt{SWAP}\right\rangle}_{4}}$
in
${{\left\rangle\mathtt{SWAP}\right\rangle}_{4}}$
in
![]() ${{\left\rangle\mathtt{CNOT}\right\rangle}_{4}}$
is
${{\left\rangle\mathtt{CNOT}\right\rangle}_{4}}$
is
![]() $20{,}160/24=840$
. For each coset, we compute a representative of minimal length in the generators
$20{,}160/24=840$
. For each coset, we compute a representative of minimal length in the generators
![]() $X_{[i\;j]}$
(function right_cosets_perm_GL4 of the Python module).
$X_{[i\;j]}$
(function right_cosets_perm_GL4 of the Python module).
The computation of
![]() $\Delta_4$
for a given state is performed using the algorithm proposed by Luque and Thibon in (2003), Section IV (function hyper_det of the Python module). After eliminating all coset representatives
$\Delta_4$
for a given state is performed using the algorithm proposed by Luque and Thibon in (2003), Section IV (function hyper_det of the Python module). After eliminating all coset representatives
![]() $X_A$
such that
$X_A$
such that
![]() $|\Delta_4(X_A|{\mathcal P}\rangle\!)|$
vanishes for any
$|\Delta_4(X_A|{\mathcal P}\rangle\!)|$
vanishes for any
![]() $\mathcal P$
, we obtain a list of 333 representatives (function non_zero_HD_strings of the Python module). For each of them, we use a random walk on the search space defined by the eight parameters
$\mathcal P$
, we obtain a list of 333 representatives (function non_zero_HD_strings of the Python module). For each of them, we use a random walk on the search space defined by the eight parameters
![]() $\alpha_i$
and
$\alpha_i$
and
![]() $\beta_i$
of
$\beta_i$
of
![]() $|{\mathcal P}\rangle$
in order to maximize the value of
$|{\mathcal P}\rangle$
in order to maximize the value of
![]() $|\Delta_4(X_A|{\mathcal P}\rangle\!)|$
(function search_max_HD of the Python module). We check that it is possible to reach the maximal value of
$|\Delta_4(X_A|{\mathcal P}\rangle\!)|$
(function search_max_HD of the Python module). We check that it is possible to reach the maximal value of
![]() $\frac{1}{2^83^9}$
for
$\frac{1}{2^83^9}$
for
![]() $|\Delta_4|$
(accuracy
$|\Delta_4|$
(accuracy
![]() $10^{-22}$
) for only 12 coset representatives. These cosets are described in Section 5. Finally, from the approximate values of
$10^{-22}$
) for only 12 coset representatives. These cosets are described in Section 5. Finally, from the approximate values of
![]() $\mathcal P$
computed by the random walk heuristic, we guess possible exact values for the parameters of
$\mathcal P$
computed by the random walk heuristic, we guess possible exact values for the parameters of
![]() $\mathcal P$
and we check (by CAS) that these exact values of
$\mathcal P$
and we check (by CAS) that these exact values of
![]() $\mathcal P$
satisfy the equality
$\mathcal P$
satisfy the equality
![]() $|\Delta_4(X_A|{\mathcal P}\rangle\!)|=\frac{1}{2^83^9}$
.
$|\Delta_4(X_A|{\mathcal P}\rangle\!)|=\frac{1}{2^83^9}$
.
4. A
 $\mathtt{CNOT}$
Circuit to Reach the Maximum of
$\mathtt{CNOT}$
Circuit to Reach the Maximum of
 $\boldsymbol{|\Delta}_{\mathrm{4}}|$
$\boldsymbol{|\Delta}_{\mathrm{4}}|$
Let
![]() $i,j,k,\ell$
be distinct integers in
$i,j,k,\ell$
be distinct integers in
![]() $\{0,1,2,3\}$
. We define as follows
$\{0,1,2,3\}$
. We define as follows
![]() $M_{k}^{(i,j)}$
, a product of
$M_{k}^{(i,j)}$
, a product of
![]() $\mathtt{CNOT}$
gates, and
$\mathtt{CNOT}$
gates, and
![]() $A_{k}^{(i,j)}$
the bit matrix of
$A_{k}^{(i,j)}$
the bit matrix of
![]() ${\mathrm{GL}_{4}(\mathbb{F}_2)}$
associated with
${\mathrm{GL}_{4}(\mathbb{F}_2)}$
associated with
![]() $M_{k}^{(i,j)}$
.
$M_{k}^{(i,j)}$
.
In this section, we show how to reach the maximum of
![]() $|\Delta_4|$
using the operator
$|\Delta_4|$
using the operator
The results are extended to any operator of type
![]() $M_{k}^{(i,j)}$
in the next section. Since
$M_{k}^{(i,j)}$
in the next section. Since
 \begin{equation*} A_{2}^{(0,1)}=[0\;1][1\;2][2\;0][0\;3][3\;1]=\begin{bmatrix}0&\quad 1&\quad 1&\quad 0\\1&\quad 0&\quad 1&\quad 1\\1&\quad 1&\quad 1&\quad 1\\0&\quad 1&\quad 0&\quad 1\end{bmatrix} \end{equation*}
\begin{equation*} A_{2}^{(0,1)}=[0\;1][1\;2][2\;0][0\;3][3\;1]=\begin{bmatrix}0&\quad 1&\quad 1&\quad 0\\1&\quad 0&\quad 1&\quad 1\\1&\quad 1&\quad 1&\quad 1\\0&\quad 1&\quad 0&\quad 1\end{bmatrix} \end{equation*}
and
 \begin{equation*}A_{3}^{(0,1)}=[0\;1][1\;3][3\;0][0\;2][2\;1]=\begin{bmatrix}0&\quad 1&\quad 0&\quad 1\\1&\quad 0&\quad 1&\quad 1\\0&\quad 1&\quad 1&\quad 0\\1&\quad 1&\quad 1&\quad 1\end{bmatrix}, \end{equation*}
\begin{equation*}A_{3}^{(0,1)}=[0\;1][1\;3][3\;0][0\;2][2\;1]=\begin{bmatrix}0&\quad 1&\quad 0&\quad 1\\1&\quad 0&\quad 1&\quad 1\\0&\quad 1&\quad 1&\quad 0\\1&\quad 1&\quad 1&\quad 1\end{bmatrix}, \end{equation*}
we remark that
![]() $A_{3}^{(0,1)}=(0\;2\;3)A_{2}^{(0,1)}$
. Hence,
$A_{3}^{(0,1)}=(0\;2\;3)A_{2}^{(0,1)}$
. Hence,
which means that
![]() $M_{3}^{(0,1)}$
and
$M_{3}^{(0,1)}$
and
![]() $M_{2}^{(0,1)}$
represent the same coset. This coset is denoted by
$M_{2}^{(0,1)}$
represent the same coset. This coset is denoted by
![]() $\overline{(0,1)}$
.
$\overline{(0,1)}$
.
Proposition 1. Let
![]() $\mathcal P_{\mathrm{max}}$
and
$\mathcal P_{\mathrm{max}}$
and
![]() $\mathcal P_{\mathrm{max}}'$
be the two matrices of parameters defined by
$\mathcal P_{\mathrm{max}}'$
be the two matrices of parameters defined by
 \begin{equation}\mathcal P_{\mathrm{max}}=\begin{bmatrix}\pi/2&\quad \pi/2&\quad 0\\ \pi/2&\quad \pi/2&\quad 0\\[3pt] \pi/4&\quad \cos^{-1}\frac{\sqrt 3}{3}&\quad 0\\[3pt] \pi/4&\quad \cos^{-1}\frac{\sqrt 3}{3}&\quad 0\end{bmatrix},\qquad\mathcal P_{\mathrm{max}}'=\begin{bmatrix}\pi/2&\quad \pi/2&\quad 0\\ \pi/2&\quad \pi/2&\quad 0\\[3pt] 3\pi/4&\quad \cos^{-1}\frac{\sqrt 3}{3}&\quad 0\\[3pt] 3\pi/4&\quad \cos^{-1}\frac{\sqrt 3}{3}&\quad 0\end{bmatrix},\end{equation}
\begin{equation}\mathcal P_{\mathrm{max}}=\begin{bmatrix}\pi/2&\quad \pi/2&\quad 0\\ \pi/2&\quad \pi/2&\quad 0\\[3pt] \pi/4&\quad \cos^{-1}\frac{\sqrt 3}{3}&\quad 0\\[3pt] \pi/4&\quad \cos^{-1}\frac{\sqrt 3}{3}&\quad 0\end{bmatrix},\qquad\mathcal P_{\mathrm{max}}'=\begin{bmatrix}\pi/2&\quad \pi/2&\quad 0\\ \pi/2&\quad \pi/2&\quad 0\\[3pt] 3\pi/4&\quad \cos^{-1}\frac{\sqrt 3}{3}&\quad 0\\[3pt] 3\pi/4&\quad \cos^{-1}\frac{\sqrt 3}{3}&\quad 0\end{bmatrix},\end{equation}
then the states
and
maximize the absolute value of the four-qubit hyperdeterminant. One has
and
where
 \begin{align*}|{w_1}\rangle& =\frac{1}{\sqrt 8}(\!|0001\rangle+\mathrm{i}|0011\rangle+|0101\rangle-\mathrm{i}|0111\rangle\\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad +|1000\rangle+\mathrm{i}|{1010}\rangle+|1100\rangle-\mathrm{i}|1110\rangle\!),\\ |{w_2}\rangle&=\frac{1}{2}({-}|0000\rangle-\mathrm{i}|0110\rangle-\mathrm{i}|1011\rangle +|1101\rangle\!),\\ |{w_3}\rangle&=\frac{1}{2}(\!|0010\rangle+\mathrm{i}|0100\rangle-\mathrm{i}|1001\rangle + |1111\rangle\!). \end{align*}
\begin{align*}|{w_1}\rangle& =\frac{1}{\sqrt 8}(\!|0001\rangle+\mathrm{i}|0011\rangle+|0101\rangle-\mathrm{i}|0111\rangle\\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad +|1000\rangle+\mathrm{i}|{1010}\rangle+|1100\rangle-\mathrm{i}|1110\rangle\!),\\ |{w_2}\rangle&=\frac{1}{2}({-}|0000\rangle-\mathrm{i}|0110\rangle-\mathrm{i}|1011\rangle +|1101\rangle\!),\\ |{w_3}\rangle&=\frac{1}{2}(\!|0010\rangle+\mathrm{i}|0100\rangle-\mathrm{i}|1001\rangle + |1111\rangle\!). \end{align*}
Proof. The different assertions can be checked using the function
check_psi_max_is_MHS of the Python module.![]()
In our numerical search for matrices of parameters
![]() $\mathcal P$
such that
$\mathcal P$
such that
![]() $M_{2}^{(0,1)}|{\mathcal P}\rangle$
maximizes
$M_{2}^{(0,1)}|{\mathcal P}\rangle$
maximizes
![]() $\Delta_4$
, it appears that all values of
$\Delta_4$
, it appears that all values of
![]() $\mathcal P$
computed by the random walk heuristic are related to
$\mathcal P$
computed by the random walk heuristic are related to
![]() $\mathcal P_{\mathrm{max}}$
or to
$\mathcal P_{\mathrm{max}}$
or to
![]() $\mathcal P_{\mathrm{max}}'$
by simple operations. These operations are described by the following lemma and its corollary. Numerical results suggest that these operations applied to the matrices
$\mathcal P_{\mathrm{max}}'$
by simple operations. These operations are described by the following lemma and its corollary. Numerical results suggest that these operations applied to the matrices
![]() $\mathcal P_{\mathrm{max}}$
or
$\mathcal P_{\mathrm{max}}$
or
![]() $\mathcal P_{\mathrm{max}}'$
are sufficient to describe all the possible matrices
$\mathcal P_{\mathrm{max}}'$
are sufficient to describe all the possible matrices
![]() $\mathcal P$
such that
$\mathcal P$
such that
![]() $M_{2}^{(0,1)}|{\mathcal P}\rangle$
is a MHS (Conjecture 7).
$M_{2}^{(0,1)}|{\mathcal P}\rangle$
is a MHS (Conjecture 7).
Lemma 2. Let
![]() $\mathcal P$
be a matrix of parameters and, for any k in
$\mathcal P$
be a matrix of parameters and, for any k in
![]() $\{0,1,2,3\}$
, let us denote by
$\{0,1,2,3\}$
, let us denote by
![]() $\mathcal P_{\alpha_k+\pi}$
the matrix obtained from
$\mathcal P_{\alpha_k+\pi}$
the matrix obtained from
![]() $\mathcal P$
by adding
$\mathcal P$
by adding
![]() $\pi$
to the parameter
$\pi$
to the parameter
![]() $\alpha_k$
,
$\alpha_k$
,
![]() $\mathcal P_{-\beta_k}$
, the matrix obtained from
$\mathcal P_{-\beta_k}$
, the matrix obtained from
![]() $\mathcal P$
by taking the opposite of
$\mathcal P$
by taking the opposite of
![]() $\beta_k$
,
$\beta_k$
,
![]() $\mathcal P_{-\alpha_k,\beta_k+\pi}$
, the matrix obtained from
$\mathcal P_{-\alpha_k,\beta_k+\pi}$
, the matrix obtained from
![]() $\mathcal P$
by taking the opposite of
$\mathcal P$
by taking the opposite of
![]() $\alpha_k$
and adding
$\alpha_k$
and adding
![]() $\pi$
to
$\pi$
to
![]() $\beta_k$
,
$\beta_k$
,
then:
Proof. We prove only Identity (30), the proofs of Identities (28) and (29) being similar. Without loss of generality, we suppose that the last column of the matrix
![]() $\mathcal P$
is null and
$\mathcal P$
is null and
![]() $k=0$
. On the one hand:
$k=0$
. On the one hand:
where
![]() $(a_0,a_1)=\left(\mathrm{e}^{-\mathrm{i}\alpha_0/2}\cos\!\frac{\beta_0}{2}, \mathrm{e}^{\mathrm{i}\alpha_0/2}\sin\!\frac{\beta_0}{2}\right)$
. On the other hand:
$(a_0,a_1)=\left(\mathrm{e}^{-\mathrm{i}\alpha_0/2}\cos\!\frac{\beta_0}{2}, \mathrm{e}^{\mathrm{i}\alpha_0/2}\sin\!\frac{\beta_0}{2}\right)$
. On the other hand:
where
![]() $(a_0',a_1')=\left(\mathrm{e}^{-\mathrm{i}({-}\alpha_0/2)}\cos\frac{\beta_0 + \pi}{2}, \mathrm{e}^{-\mathrm{i}\alpha_0/2}\sin\frac{\beta_0+\pi}{2}\right)=({-}a_1,a_0)$
.
$(a_0',a_1')=\left(\mathrm{e}^{-\mathrm{i}({-}\alpha_0/2)}\cos\frac{\beta_0 + \pi}{2}, \mathrm{e}^{-\mathrm{i}\alpha_0/2}\sin\frac{\beta_0+\pi}{2}\right)=({-}a_1,a_0)$
.
Hence
![]() $-\mathrm{i} Y_0|{\mathcal P}\rangle=|{\mathcal P_{-\alpha_0,\beta_0+\pi}}\rangle$
.
$-\mathrm{i} Y_0|{\mathcal P}\rangle=|{\mathcal P_{-\alpha_0,\beta_0+\pi}}\rangle$
.![]()
Corollary 3. Let A be a matrix in
![]() ${\mathrm{GL}_{4}(\mathbb{F}_2)}$
and
${\mathrm{GL}_{4}(\mathbb{F}_2)}$
and
![]() $\mathcal P$
a matrix of parameters. If
$\mathcal P$
a matrix of parameters. If
![]() $|\Delta_4|$
is maximal for
$|\Delta_4|$
is maximal for
![]() $X_A|{\mathcal P}\rangle$
, then
$X_A|{\mathcal P}\rangle$
, then
![]() $|\Delta_4|$
is also maximal for
$|\Delta_4|$
is also maximal for
![]() $X_A|{\mathcal P_{\alpha_k+\pi}}\rangle$
,
$X_A|{\mathcal P_{\alpha_k+\pi}}\rangle$
,
![]() $X_A|{\mathcal P_{-\beta_k}}\rangle$
and
$X_A|{\mathcal P_{-\beta_k}}\rangle$
and
![]() $X_A|{\mathcal P_{-\alpha_k,\beta_k+\pi}}\rangle$
, for any k in
$X_A|{\mathcal P_{-\alpha_k,\beta_k+\pi}}\rangle$
, for any k in
![]() $\{0,1,2,3\}$
.
$\{0,1,2,3\}$
.
Proof. Suppose that
![]() $|\Delta_4|$
is maximal for
$|\Delta_4|$
is maximal for
![]() $X_A|{\mathcal P}\rangle$
. Let
$X_A|{\mathcal P}\rangle$
. Let
![]() $\mathcal P'\in\{\mathcal P_{\alpha_k+\pi}, \mathcal P_{-\beta_k}, \mathcal P_{-\alpha_k,\ \beta_k+\pi}\}$
. From Lemma 2 and Identity (11), there exists two vectors u and v in
$\mathcal P'\in\{\mathcal P_{\alpha_k+\pi}, \mathcal P_{-\beta_k}, \mathcal P_{-\alpha_k,\ \beta_k+\pi}\}$
. From Lemma 2 and Identity (11), there exists two vectors u and v in
![]() $\mathbb{F}_{2}^4$
such that
$\mathbb{F}_{2}^4$
such that
![]() $|{\mathcal P'}\rangle\simeq X_uZ_v|{\mathcal P}\rangle$
. Hence,
$|{\mathcal P'}\rangle\simeq X_uZ_v|{\mathcal P}\rangle$
. Hence,
![]() $X_A|{\mathcal P'}\rangle\simeq X_AX_uZ_v|{\mathcal P}\rangle\simeq X_AX_uZ_vX_A^{-1}X_A|{\mathcal P}\rangle$
. So, using Identity (12), we deduce that
$X_A|{\mathcal P'}\rangle\simeq X_AX_uZ_v|{\mathcal P}\rangle\simeq X_AX_uZ_vX_A^{-1}X_A|{\mathcal P}\rangle$
. So, using Identity (12), we deduce that
![]() $X_A|{\mathcal P'}\rangle\simeq X_{Au}Z_{A^{-t}v}X_A|{\mathcal P}\rangle$
. Consequently,
$X_A|{\mathcal P'}\rangle\simeq X_{Au}Z_{A^{-t}v}X_A|{\mathcal P}\rangle$
. Consequently,
![]() $X_A|{\mathcal P'}\rangle$
is in the LU orbit of
$X_A|{\mathcal P'}\rangle$
is in the LU orbit of
![]() $X_A|{\mathcal P}\rangle$
, which implies that
$X_A|{\mathcal P}\rangle$
, which implies that
![]() $|\Delta_4|$
is maximal for the state
$|\Delta_4|$
is maximal for the state
![]() $X_A|{\mathcal P'}\rangle$
.
$X_A|{\mathcal P'}\rangle$
.![]()
Example 4. Let us apply the following sequence of operations on
![]() $\mathcal P_{\mathrm{max}}$
:
$\mathcal P_{\mathrm{max}}$
:
![]() $\alpha_0\leftarrow\alpha_0+\pi$
,
$\alpha_0\leftarrow\alpha_0+\pi$
,
![]() $\beta_2\leftarrow-\beta_2$
,
$\beta_2\leftarrow-\beta_2$
,
![]() $\alpha_3\leftarrow -\alpha_3$
,
$\alpha_3\leftarrow -\alpha_3$
,
![]() $\beta_3\leftarrow\beta_3+\pi$
.
$\beta_3\leftarrow\beta_3+\pi$
.
The resulting matrix of parameters is
 $\mathcal P=\begin{bmatrix}3\pi/2&\quad \pi/2&\quad 0\\ \pi/2&\quad \pi/2&\quad 0\\[4pt] \pi/4&\quad -\cos^{-1}\frac{\sqrt 3}{3}&\quad 0\\[4pt] -\pi/4&\quad \cos^{-1}\frac{\sqrt 3}{3}+\pi&\quad 0\end{bmatrix}$
and
$\mathcal P=\begin{bmatrix}3\pi/2&\quad \pi/2&\quad 0\\ \pi/2&\quad \pi/2&\quad 0\\[4pt] \pi/4&\quad -\cos^{-1}\frac{\sqrt 3}{3}&\quad 0\\[4pt] -\pi/4&\quad \cos^{-1}\frac{\sqrt 3}{3}+\pi&\quad 0\end{bmatrix}$
and
Let
![]() $u=[0\;0\;0\;1]^t$
and
$u=[0\;0\;0\;1]^t$
and
![]() $v=[1\;0\;1\;1]^t$
. One has :
$v=[1\;0\;1\;1]^t$
. One has :
 \begin{equation*} A^{(0,1)}_2=\begin{bmatrix}0&\quad 1&\quad 1&\quad 0\\1&\quad 0&\quad 1&\quad 1\\1&\quad 1&\quad 1&\quad 1\\0&\quad 1&\quad 0&\quad 1\end{bmatrix},\qquad A^{(0,1)}_2u=[0\;1\;1\;1]^t\end{equation*}
\begin{equation*} A^{(0,1)}_2=\begin{bmatrix}0&\quad 1&\quad 1&\quad 0\\1&\quad 0&\quad 1&\quad 1\\1&\quad 1&\quad 1&\quad 1\\0&\quad 1&\quad 0&\quad 1\end{bmatrix},\qquad A^{(0,1)}_2u=[0\;1\;1\;1]^t\end{equation*}
and
 \begin{equation*}\left(A^{(0,1)}_2\right)^{-t}=\begin{bmatrix}1&\quad 0&\quad 1&\quad 0\\1&\quad 1&\quad 1&\quad 1\\0&\quad 1&\quad 1&\quad 1\\1&\quad 0&\quad 0&\quad 1\end{bmatrix}, \qquad\left(A^{(0,1)}_2\right)^{-t}v=[0\;1\;0\;0]^t.\end{equation*}
\begin{equation*}\left(A^{(0,1)}_2\right)^{-t}=\begin{bmatrix}1&\quad 0&\quad 1&\quad 0\\1&\quad 1&\quad 1&\quad 1\\0&\quad 1&\quad 1&\quad 1\\1&\quad 0&\quad 0&\quad 1\end{bmatrix}, \qquad\left(A^{(0,1)}_2\right)^{-t}v=[0\;1\;0\;0]^t.\end{equation*}
Hence
![]() $M^{(0,1)}_2|{\mathcal P}\rangle\simeq X_1X_2X_3Z_1|{\psi_{\mathrm{max}}}\rangle$
.
$M^{(0,1)}_2|{\mathcal P}\rangle\simeq X_1X_2X_3Z_1|{\psi_{\mathrm{max}}}\rangle$
.
Remark 5. We observe that the matrices
![]() $\mathcal P_{\mathrm{max}}$
and
$\mathcal P_{\mathrm{max}}$
and
![]() $\mathcal P_{\mathrm{max}}'$
are not related by the operations on parameters described in Lemma 2, that is there does not exist any gate
$\mathcal P_{\mathrm{max}}'$
are not related by the operations on parameters described in Lemma 2, that is there does not exist any gate
![]() $X_uZ_v$
in the four-qubit Pauli group such that
$X_uZ_v$
in the four-qubit Pauli group such that
![]() $|{\mathcal P_{\mathrm{max}}'}\rangle\simeq X_uZ_v|{\mathcal P_{\mathrm{max}}}\rangle$
. This implies that the state
$|{\mathcal P_{\mathrm{max}}'}\rangle\simeq X_uZ_v|{\mathcal P_{\mathrm{max}}}\rangle$
. This implies that the state
![]() $|{\psi_{\mathrm{max}}}\rangle$
and the state
$|{\psi_{\mathrm{max}}}\rangle$
and the state
![]() $|{\psi_{\mathrm{max}}'}\rangle$
define distinct orbits by the action of the four-qubit Pauli group. Actually, from Identities (22) and (4), one has
$|{\psi_{\mathrm{max}}'}\rangle$
define distinct orbits by the action of the four-qubit Pauli group. Actually, from Identities (22) and (4), one has
![]() $|{\mathcal P_{\mathrm{max}}'}\rangle\simeq P_2P_3|{\mathcal P_{\mathrm{max}}}\rangle$
. Using the method described in Section 3, we compute a matrix of parameters
$|{\mathcal P_{\mathrm{max}}'}\rangle\simeq P_2P_3|{\mathcal P_{\mathrm{max}}}\rangle$
. Using the method described in Section 3, we compute a matrix of parameters
 $\mathcal P_{\psi\rightarrow\psi'}=\begin{bmatrix}-\pi/2&\quad -\pi/2&\quad -\pi/2\\\pi/2&\quad \pi&\quad \pi\\0&\quad \pi/2&\quad \pi\\-\pi/2&\quad -\pi/2&\quad -\pi/2\end{bmatrix}$
and a phase
$\mathcal P_{\psi\rightarrow\psi'}=\begin{bmatrix}-\pi/2&\quad -\pi/2&\quad -\pi/2\\\pi/2&\quad \pi&\quad \pi\\0&\quad \pi/2&\quad \pi\\-\pi/2&\quad -\pi/2&\quad -\pi/2\end{bmatrix}$
and a phase
![]() $\varphi=-\frac{\pi}{3}$
such that
$\varphi=-\frac{\pi}{3}$
such that
![]() $|{\psi_{\mathrm{max}}'}\rangle=\mathrm{e}^{\mathrm{i}\varphi}U(\mathcal P_{\psi \rightarrow \psi'})|{\psi_{\mathrm{max}}}\rangle$
. Then, using Identities (4) and (5), we obtain
$|{\psi_{\mathrm{max}}'}\rangle=\mathrm{e}^{\mathrm{i}\varphi}U(\mathcal P_{\psi \rightarrow \psi'})|{\psi_{\mathrm{max}}}\rangle$
. Then, using Identities (4) and (5), we obtain
This last identity can be checked using the function check_psi_to_psi_prime of the Python module.
Remark 6. Since
![]() $M_{3}^{(0,1)}=S_{(0\;2\;3)}M_{2}^{(0,1)}$
, it is easy to see that the set of all matrices of parameters
$M_{3}^{(0,1)}=S_{(0\;2\;3)}M_{2}^{(0,1)}$
, it is easy to see that the set of all matrices of parameters
![]() $\mathcal P$
having their last column null such that
$\mathcal P$
having their last column null such that
![]() $M^{(0,1)}_3|{\mathcal P}\rangle$
maximizes
$M^{(0,1)}_3|{\mathcal P}\rangle$
maximizes
![]() $|\Delta_4|$
is equal to the set of all matrices of parameters
$|\Delta_4|$
is equal to the set of all matrices of parameters
![]() $\mathcal P$
having their last column null such that
$\mathcal P$
having their last column null such that
![]() $M^{(0,1)}_2|{\mathcal P}\rangle$
maximizes
$M^{(0,1)}_2|{\mathcal P}\rangle$
maximizes
![]() $|\Delta_4|$
. We denote this set by
$|\Delta_4|$
. We denote this set by
![]() $\mathrm{PMAX}^{(0,1)}$
.
$\mathrm{PMAX}^{(0,1)}$
.
Conjecture 7. Any matrix in
![]() $\mathrm{PMAX}^{(0,1)}$
can be obtain from
$\mathrm{PMAX}^{(0,1)}$
can be obtain from
![]() $\mathcal P_{\mathrm{max}}$
or from
$\mathcal P_{\mathrm{max}}$
or from
![]() $\mathcal P_{\mathrm{max}}'$
by a sequence of the operations on parameters described by Lemma 2.
$\mathcal P_{\mathrm{max}}'$
by a sequence of the operations on parameters described by Lemma 2.
5. All
 $\mathtt{CNOT}$
Circuits to Reach the Maximum of
$\mathtt{CNOT}$
Circuits to Reach the Maximum of
 $|\Delta_4|$
$|\Delta_4|$
We generalize the results of the previous section by describing all the four-qubit
![]() $\mathtt{CNOT}$
circuits that enable to produce a state maximizing
$\mathtt{CNOT}$
circuits that enable to produce a state maximizing
![]() $|\Delta_4|$
when they act on the LU orbit of
$|\Delta_4|$
when they act on the LU orbit of
![]() $|0000\rangle$
.
$|0000\rangle$
.
Proposition 8. Let
![]() $i,j,k,\ell$
be distinct integers in
$i,j,k,\ell$
be distinct integers in
![]() $\{0,1,2,3\}$
, then
$\{0,1,2,3\}$
, then
![]() $M_{k}^{(i,j)}$
and
$M_{k}^{(i,j)}$
and
![]() $M_{\ell}^{(i,j)}$
define the same right coset of the subgroup
$M_{\ell}^{(i,j)}$
define the same right coset of the subgroup
![]() ${{\left\rangle\mathtt{SWAP}\right\rangle}_{4}}$
in
${{\left\rangle\mathtt{SWAP}\right\rangle}_{4}}$
in
![]() ${{\left\rangle\mathtt{CNOT}\right\rangle}_{4}}$
. This right coset is denoted by
${{\left\rangle\mathtt{CNOT}\right\rangle}_{4}}$
. This right coset is denoted by
![]() $\overline{(i,j)}$
:
$\overline{(i,j)}$
:
Proof. Let
![]() $\sigma$
be the permutation
$\sigma$
be the permutation
 $\begin{pmatrix}0&1&2&3\\i&j&k&\ell\end{pmatrix}$
. Using Identity (8), we conjugate each member of the equality
$\begin{pmatrix}0&1&2&3\\i&j&k&\ell\end{pmatrix}$
. Using Identity (8), we conjugate each member of the equality
![]() $M_{3}^{(0,1)}=S_{(0\;2\;3)}M_{2}^{(0,1)}$
(Identity (21)) by
$M_{3}^{(0,1)}=S_{(0\;2\;3)}M_{2}^{(0,1)}$
(Identity (21)) by
![]() $S_{\sigma}$
and obtain
$S_{\sigma}$
and obtain
![]() $M_{\ell}^{(i,j)}=S_{(ik\ell)}M_{k}^{(i,j)}$
.
$M_{\ell}^{(i,j)}=S_{(ik\ell)}M_{k}^{(i,j)}$
.![]()
Proposition 9. Let i,j,i′,j′ in
![]() $\{0,1,2,3\}$
such that
$\{0,1,2,3\}$
such that
![]() $i\neq j$
and
$i\neq j$
and
![]() $i'\neq j'$
. If (i,j) and (i′,j′) are distinct couples, then
$i'\neq j'$
. If (i,j) and (i′,j′) are distinct couples, then
![]() $\overline{(i,j)}$
and
$\overline{(i,j)}$
and
![]() $\overline{(i',j')}$
are distinct cosets.
$\overline{(i',j')}$
are distinct cosets.
Proof. We check that for any i,j,k,i′,j′,k′ in
![]() $\{0,1,2,3\}$
(i,j,k distinct and i′,j′,k′ distinct), if
$\{0,1,2,3\}$
(i,j,k distinct and i′,j′,k′ distinct), if
![]() $A_{k}^{(i,j)}=\sigma A_{k'}^{(i',j')}$
for some permutation matrix
$A_{k}^{(i,j)}=\sigma A_{k'}^{(i',j')}$
for some permutation matrix
![]() $\sigma$
, then
$\sigma$
, then
![]() $(i,j) = (i',j')$
(function check_distinct_cosets of the Python module).
$(i,j) = (i',j')$
(function check_distinct_cosets of the Python module).![]()
Proposition 10. For any permutation
![]() $\sigma$
, one has :
$\sigma$
, one has :
![]() $S_{\sigma}\overline{(i,j)}S_{\sigma}^{-1}=\overline{(\sigma(i),\sigma(j))}$
.
$S_{\sigma}\overline{(i,j)}S_{\sigma}^{-1}=\overline{(\sigma(i),\sigma(j))}$
.
Proof. Using Identity (8), one has:
![]() $S_{\sigma}M_{k}^{(i,j)}S_{\sigma}^{-1}=M_{\sigma(k)}^{(\sigma(i),\sigma(j))}$
. The result follows from Proposition 8.
$S_{\sigma}M_{k}^{(i,j)}S_{\sigma}^{-1}=M_{\sigma(k)}^{(\sigma(i),\sigma(j))}$
. The result follows from Proposition 8.![]()
Remark 6 can be generalized to any coset
![]() $\overline{(i,j),}$
and one can define
$\overline{(i,j),}$
and one can define
![]() $\mathrm{PMAX}^{(i,j)}$
as being the set of all matrices
$\mathrm{PMAX}^{(i,j)}$
as being the set of all matrices
![]() $\mathcal P$
having their last column such that the state
$\mathcal P$
having their last column such that the state
![]() $M_{k}^{(i,j)}|{\mathcal P}\rangle$
maximizes
$M_{k}^{(i,j)}|{\mathcal P}\rangle$
maximizes
![]() $|\Delta_4|$
.
$|\Delta_4|$
.
Proposition 11. Let i,j be distinct integers in
![]() $\{0,1,2,3\}$
and
$\{0,1,2,3\}$
and
![]() $\sigma$
be a permutation such that
$\sigma$
be a permutation such that
![]() $\sigma(0)=i$
and
$\sigma(0)=i$
and
![]() $\sigma(1)=j$
, then :
$\sigma(1)=j$
, then :
Proof. We prove that
![]() $\mathrm{PMAX}^{(i,j)}\subset\sigma \mathrm{PMAX}^{(0,1)}$
, the other inclusion being similar. Let
$\mathrm{PMAX}^{(i,j)}\subset\sigma \mathrm{PMAX}^{(0,1)}$
, the other inclusion being similar. Let
![]() $\mathcal P$
be a matrix of parameters in
$\mathcal P$
be a matrix of parameters in
![]() $\mathrm{PMAX}^{(i,j)}$
and let
$\mathrm{PMAX}^{(i,j)}$
and let
![]() $|{\psi}\rangle =M_{k}^{(i,j)}|{\mathcal P}\rangle$
. Then
$|{\psi}\rangle =M_{k}^{(i,j)}|{\mathcal P}\rangle$
. Then
![]() $|{\psi}\rangle$
maximizes
$|{\psi}\rangle$
maximizes
![]() $|\Delta_4|$
and so does
$|\Delta_4|$
and so does
![]() $S_{\sigma}^{-1}|{\psi}\rangle$
. One has :
$S_{\sigma}^{-1}|{\psi}\rangle$
. One has :
where
![]() $k'\in\{2,3\}$
. Moreover,
$k'\in\{2,3\}$
. Moreover,
![]() $S_{\sigma}^{-1}|{\mathcal P}\rangle=S_{\sigma}^{-1}U(\mathcal P)|0000\rangle=S_{\sigma}^{-1}U(\mathcal P)S_{\sigma}|0000\rangle$
and, by using Identity (9), one obtains
$S_{\sigma}^{-1}|{\mathcal P}\rangle=S_{\sigma}^{-1}U(\mathcal P)|0000\rangle=S_{\sigma}^{-1}U(\mathcal P)S_{\sigma}|0000\rangle$
and, by using Identity (9), one obtains
![]() $S_{\sigma}^{-1}|{\mathcal P}\rangle=|{\sigma^{-1}\mathcal P}\rangle$
, hence
$S_{\sigma}^{-1}|{\mathcal P}\rangle=|{\sigma^{-1}\mathcal P}\rangle$
, hence
As
![]() $S_{\sigma}^{-1}|{\psi}\rangle$
maximizes
$S_{\sigma}^{-1}|{\psi}\rangle$
maximizes
![]() $|\Delta_4|$
, then
$|\Delta_4|$
, then
![]() $\sigma^{-1}\mathcal P \in \mathrm{PMAX}^{(0,1)}$
, so
$\sigma^{-1}\mathcal P \in \mathrm{PMAX}^{(0,1)}$
, so
![]() $\mathcal P\in \sigma \mathrm{PMAX}^{(0,1)}$
and we deduce that
$\mathcal P\in \sigma \mathrm{PMAX}^{(0,1)}$
and we deduce that
![]() $\mathrm{PMAX}^{(i,j)}\subset\sigma \mathrm{PMAX}^{(0,1)}$
.
$\mathrm{PMAX}^{(i,j)}\subset\sigma \mathrm{PMAX}^{(0,1)}$
.![]()
Our numerical results based on the use of the random walk heuristic suggest the following conjecture.
Conjecture 12. Any four-qubit
![]() $\mathtt{CNOT}$
circuit capable of maximizing
$\mathtt{CNOT}$
circuit capable of maximizing
![]() $|\Delta_4|$
by acting on the LU orbit of
$|\Delta_4|$
by acting on the LU orbit of
![]() $|0000\rangle$
belongs to one of the 12 cosets
$|0000\rangle$
belongs to one of the 12 cosets
![]() $\overline{(i,j)}$
.
$\overline{(i,j)}$
.
Example 13. Let
![]() $\sigma=(013)$
. The unitary
$\sigma=(013)$
. The unitary
![]() $S_{\sigma}M_{2}^{(0,1)}$
acting on the state
$S_{\sigma}M_{2}^{(0,1)}$
acting on the state
![]() $|{\mathcal P_{\mathrm{max}}}\rangle$
generates the state
$|{\mathcal P_{\mathrm{max}}}\rangle$
generates the state
![]() $S_{(013)}|{\psi_{\mathrm{max}}}\rangle$
that maximizes
$S_{(013)}|{\psi_{\mathrm{max}}}\rangle$
that maximizes
![]() $|\Delta_4|$
. This state can be produced by the unitary
$|\Delta_4|$
. This state can be produced by the unitary
![]() $M_{\sigma(2)}^{(\sigma(0),\sigma(1))}=M_{2}^{(1,3)}$
acting on the state
$M_{\sigma(2)}^{(\sigma(0),\sigma(1))}=M_{2}^{(1,3)}$
acting on the state
![]() $|{\sigma\mathcal P_{\mathrm{max}}}\rangle$
, where
$|{\sigma\mathcal P_{\mathrm{max}}}\rangle$
, where
 \[\sigma\mathcal P_{\mathrm{max}}=\sigma\!\begin{bmatrix}\pi/2& \quad \pi/2& \quad 0\\ \pi/2& \quad \pi/2& \quad 0\\[3pt] \pi/4& \quad \cos^{-1}\frac{\sqrt 3}{3}& \quad 0\\[3pt] \pi/4& \quad \cos^{-1}\frac{\sqrt 3}{3}& \quad 0\end{bmatrix}=\begin{bmatrix} \pi/4& \quad \cos^{-1}\frac{\sqrt 3}{3}& \quad 0\\ \pi/2& \quad \pi/2& \quad 0\\[3pt] \pi/4& \quad \cos^{-1}\frac{\sqrt 3}{3}& \quad 0\\[3pt] \pi/2& \quad \pi/2& \quad 0\end{bmatrix}.\]
\[\sigma\mathcal P_{\mathrm{max}}=\sigma\!\begin{bmatrix}\pi/2& \quad \pi/2& \quad 0\\ \pi/2& \quad \pi/2& \quad 0\\[3pt] \pi/4& \quad \cos^{-1}\frac{\sqrt 3}{3}& \quad 0\\[3pt] \pi/4& \quad \cos^{-1}\frac{\sqrt 3}{3}& \quad 0\end{bmatrix}=\begin{bmatrix} \pi/4& \quad \cos^{-1}\frac{\sqrt 3}{3}& \quad 0\\ \pi/2& \quad \pi/2& \quad 0\\[3pt] \pi/4& \quad \cos^{-1}\frac{\sqrt 3}{3}& \quad 0\\[3pt] \pi/2& \quad \pi/2& \quad 0\end{bmatrix}.\]
6. Circuits Generating the States
 $|L\rangle$
,
$|L\rangle$
,
 $|{\Phi_5}\rangle$
and
$|{\Phi_5}\rangle$
and
 $|{M_{2222}}\rangle$
$|{M_{2222}}\rangle$
Let
![]() $|{\psi}\rangle$
be a state in the set
$|{\psi}\rangle$
be a state in the set
![]() $\{|L\rangle, |{\Phi_5}\rangle, |{M_{2222}}\rangle\}$
. Following the Gour-Wallach conjecture (Gour and Wallach, Reference Gour and Wallach2012) proved by Chen and Djokovic (Reference Chen and Djokovic2013), there exists a matrix
$\{|L\rangle, |{\Phi_5}\rangle, |{M_{2222}}\rangle\}$
. Following the Gour-Wallach conjecture (Gour and Wallach, Reference Gour and Wallach2012) proved by Chen and Djokovic (Reference Chen and Djokovic2013), there exists a matrix
![]() $\mathcal P$
of parameters and a phase
$\mathcal P$
of parameters and a phase
![]() $\varphi$
such that
$\varphi$
such that
In order to compute
![]() $\mathcal P$
and
$\mathcal P$
and
![]() $\varphi$
, one can try to solve a 16 equations non-linear system but its resolution seems to be out of reach of current equation solvers (we used Maple and Python SymPy solvers). However, one can turn the problem of finding a solution of (34) into an optimization problem thanks to this simple remark :
$\varphi$
, one can try to solve a 16 equations non-linear system but its resolution seems to be out of reach of current equation solvers (we used Maple and Python SymPy solvers). However, one can turn the problem of finding a solution of (34) into an optimization problem thanks to this simple remark :
![]() $|{\psi}\rangle=\mathrm{e}^{\mathrm{i}\varphi}U(\mathcal{P})|{\psi_{\mathrm{max}}}\rangle$
if and only if the sum of the absolute values of the 16 coordinates of
$|{\psi}\rangle=\mathrm{e}^{\mathrm{i}\varphi}U(\mathcal{P})|{\psi_{\mathrm{max}}}\rangle$
if and only if the sum of the absolute values of the 16 coordinates of
![]() $|{\psi}\rangle-\mathrm{e}^{\mathrm{i}\varphi}U(\mathcal{P})|L\rangle$
vanishes. Again, we use a random walk on a search space of 13 parameters (the 12 parameters of
$|{\psi}\rangle-\mathrm{e}^{\mathrm{i}\varphi}U(\mathcal{P})|L\rangle$
vanishes. Again, we use a random walk on a search space of 13 parameters (the 12 parameters of
![]() $\mathcal P$
plus the phase
$\mathcal P$
plus the phase
![]() $\varphi$
) to minimize this sum and obtain an approximate solution of the system (function search_LU_from_state1_to_state2 of the Python module). From this approximate solution, we guess a possible form of an exact solution. Then, we check by CAS (using the Python module SymPy) that this form is indeed an exact solution. The results are summarized in Figure 2. Finally, using Identities (4) and (5), and combining the results in Figure 2 with those of Proposition 1, it is possible to build simple quantum circuits generating the states
$\varphi$
) to minimize this sum and obtain an approximate solution of the system (function search_LU_from_state1_to_state2 of the Python module). From this approximate solution, we guess a possible form of an exact solution. Then, we check by CAS (using the Python module SymPy) that this form is indeed an exact solution. The results are summarized in Figure 2. Finally, using Identities (4) and (5), and combining the results in Figure 2 with those of Proposition 1, it is possible to build simple quantum circuits generating the states
![]() $|L\rangle$
,
$|L\rangle$
,
![]() $|{\Phi_5}\rangle$
and
$|{\Phi_5}\rangle$
and
![]() $|{M_{2222}}\rangle$
. These circuits are depicted in Figure 3, and one can check that they are correct by using the function check_circuits of the Python module.
$|{M_{2222}}\rangle$
. These circuits are depicted in Figure 3, and one can check that they are correct by using the function check_circuits of the Python module.

Figure 2. LU operators generating the states
![]() $|L\rangle$
,
$|L\rangle$
,
![]() $|{\Phi_5}\rangle$
and
$|{\Phi_5}\rangle$
and
![]() $|{M_{2222}}\rangle$
, from the state
$|{M_{2222}}\rangle$
, from the state
![]() $|{\psi_{\mathrm{max}}}\rangle$
.
$|{\psi_{\mathrm{max}}}\rangle$
.

Figure 3. Quantum circuits generating the states
![]() $|L\rangle$
,
$|L\rangle$
,
![]() $|{\Phi_5}\rangle$
and
$|{\Phi_5}\rangle$
and
![]() $|{M_{2222}}\rangle$
up to a global phase. For better readability, most of the rotations around the
$|{M_{2222}}\rangle$
up to a global phase. For better readability, most of the rotations around the
![]() $\hat y$
and
$\hat y$
and
![]() $\hat z$
axes defined by the matrices of parameters are written using the universal single-qubit gates H,P,T (see Identity (4)).
$\hat z$
axes defined by the matrices of parameters are written using the universal single-qubit gates H,P,T (see Identity (4)).
We implemented the circuit generating the state
![]() $|L\rangle$
in one of the quantum computers publicly available at https://quantum-computing.ibm.com/. In those computers, full connectivity between the qubits is not achieved and the direct connections allowed between two qubits are given by a graph. Moreover, due to the noise in the gates, and particularly in the 2-qubit gates, it is of crucial importance to use as few
$|L\rangle$
in one of the quantum computers publicly available at https://quantum-computing.ibm.com/. In those computers, full connectivity between the qubits is not achieved and the direct connections allowed between two qubits are given by a graph. Moreover, due to the noise in the gates, and particularly in the 2-qubit gates, it is of crucial importance to use as few
![]() $\mathtt{CNOT}$
gates as possible. We chose the 5-qubit ibmq_quito computer because its graph is
$\mathtt{CNOT}$
gates as possible. We chose the 5-qubit ibmq_quito computer because its graph is
![]() $\{\{1, 0\}, \{1, 2\}, \{1, 3\}, \{3, 4\}\}$
; hence, the gates
$\{\{1, 0\}, \{1, 2\}, \{1, 3\}, \{3, 4\}\}$
; hence, the gates
![]() $X_{[0\;1]}, X_{[1\;2]}$
and
$X_{[0\;1]}, X_{[1\;2]}$
and
![]() $X_{[3\;1]}$
of the
$X_{[3\;1]}$
of the
![]() $\mathtt{CNOT}$
subcircuit that implements the operator
$\mathtt{CNOT}$
subcircuit that implements the operator
![]() $M^{(0,1)}_2=X_{[0\;1]}X_{[1\;2]}X_{[2\;0]}X_{[0\;3]}X_{[3\;1]}$
are already native gates. The two other gates of the
$M^{(0,1)}_2=X_{[0\;1]}X_{[1\;2]}X_{[2\;0]}X_{[0\;3]}X_{[3\;1]}$
are already native gates. The two other gates of the
![]() $\mathtt{CNOT}$
subcircuit, namely
$\mathtt{CNOT}$
subcircuit, namely
![]() $X_{[2\;0]}$
and
$X_{[2\;0]}$
and
![]() $X_{[0\;3],}$
are not native
$X_{[0\;3],}$
are not native
![]() $\mathtt{CNOT}$
gates and can be simulated thanks to the use of
$\mathtt{CNOT}$
gates and can be simulated thanks to the use of
![]() $\mathtt{SWAP}$
gates. Finally, the operator
$\mathtt{SWAP}$
gates. Finally, the operator
![]() $M^{(0,1)}_2$
can be implemented using only 11 native
$M^{(0,1)}_2$
can be implemented using only 11 native
![]() $\mathtt{CNOT}$
gates:
$\mathtt{CNOT}$
gates:
 \begin{equation}M^{(0,1)}_2 = X_{[0\;1]}X_{[1\;2]}\underbrace{X_{[0\;1]}X_{[1\;0]}X_{[0\;1]}}_{S_{(0\;1)}}X_{[2\;1]}X_{[1\;3]}\underbrace{X_{[0\;1]}X_{[1\;0]}X_{[0\;1]}}_{S_{(0\;1)}}X_{[3\;1]}.\end{equation}
\begin{equation}M^{(0,1)}_2 = X_{[0\;1]}X_{[1\;2]}\underbrace{X_{[0\;1]}X_{[1\;0]}X_{[0\;1]}}_{S_{(0\;1)}}X_{[2\;1]}X_{[1\;3]}\underbrace{X_{[0\;1]}X_{[1\;0]}X_{[0\;1]}}_{S_{(0\;1)}}X_{[3\;1]}.\end{equation}
After compilation by the IBM algorithm (the process is called transpilation on the website), the quantum circuit implementing the state
![]() $|L\rangle$
uses 22 single-qubit native gates, 11
$|L\rangle$
uses 22 single-qubit native gates, 11
![]() $\mathtt{CNOT}$
gates and has a total depth of 18 (see Figure 4). However, despite of this moderate length, we observed after measurement the apparition of a large quantity of scorias (see the bar chart in Figure 4). Indeed, from Identity (1), one has
$\mathtt{CNOT}$
gates and has a total depth of 18 (see Figure 4). However, despite of this moderate length, we observed after measurement the apparition of a large quantity of scorias (see the bar chart in Figure 4). Indeed, from Identity (1), one has
so, ideally, the states
![]() $|0001\rangle, |0010\rangle, |0100\rangle, |1000\rangle, |0111\rangle |1011\rangle, |1101\rangle,$
or
$|0001\rangle, |0010\rangle, |0100\rangle, |1000\rangle, |0111\rangle |1011\rangle, |1101\rangle,$
or
![]() $|1110\rangle$
should not appear after measurement. The main causes of this problem are, on one hand, the measurement errors (average readout error is about 3 percent on this device), and on the other hand, the noise in the gates (
$|1110\rangle$
should not appear after measurement. The main causes of this problem are, on one hand, the measurement errors (average readout error is about 3 percent on this device), and on the other hand, the noise in the gates (
![]() $\mathtt{CNOT}$
gate average error is about
$\mathtt{CNOT}$
gate average error is about
![]() $1.3$
percent). This suggests that there are still significant technological challenges to overcome before we can implement the state
$1.3$
percent). This suggests that there are still significant technological challenges to overcome before we can implement the state
![]() $|L\rangle$
in a reliable fashion.
$|L\rangle$
in a reliable fashion.

Figure 4. Implementation in the ibmq_quito quantum computer of a circuit generating the state
![]() $|L\rangle$
. The bar chart is based on 2000 measurements.
$|L\rangle$
. The bar chart is based on 2000 measurements.
7. Conclusion and Perspectives
In this work, we described how a
![]() $\mathtt{CNOT}$
circuit acting on a factorized state can produce four-qubit maximum hyperdeterminant states and we proposed a quantum circuit generating the state
$\mathtt{CNOT}$
circuit acting on a factorized state can produce four-qubit maximum hyperdeterminant states and we proposed a quantum circuit generating the state
![]() $|L\rangle$
, whose interesting properties where described by Gour and Wallach (Reference Gour and Wallach2012) and by Chen and Djokovic (Reference Chen and Djokovic2013). It would be interesting to know whether it is possible to generalize this result when the number of qubits n is greater than 4. Is it still possible to reach a MHS by a
$|L\rangle$
, whose interesting properties where described by Gour and Wallach (Reference Gour and Wallach2012) and by Chen and Djokovic (Reference Chen and Djokovic2013). It would be interesting to know whether it is possible to generalize this result when the number of qubits n is greater than 4. Is it still possible to reach a MHS by a
![]() $\mathtt{CNOT}$
circuit acting on a factorized state? What would be in this case the generalization of the unitary
$\mathtt{CNOT}$
circuit acting on a factorized state? What would be in this case the generalization of the unitary
![]() $M^{(i,j)}_k$
to higher dimensions? However, answering these questions seems to be currently out of reach because an explicit polynomial expression of the hyperdeterminant is known only up to 4 qubits. A first approach would be to know if a generically entangled state (i.e. a state
$M^{(i,j)}_k$
to higher dimensions? However, answering these questions seems to be currently out of reach because an explicit polynomial expression of the hyperdeterminant is known only up to 4 qubits. A first approach would be to know if a generically entangled state (i.e. a state
![]() $|{\psi}\rangle$
such that
$|{\psi}\rangle$
such that
![]() $\Delta_n(\!|{\psi}\rangle\!)\neq 0$
) can be produced by a
$\Delta_n(\!|{\psi}\rangle\!)\neq 0$
) can be produced by a
![]() $\mathtt{CNOT}$
circuit acting on a factorized state in the case of any n-qubit system. Indeed, the vanishing of
$\mathtt{CNOT}$
circuit acting on a factorized state in the case of any n-qubit system. Indeed, the vanishing of
![]() $\Delta_n$
can be tested using the following criterion Gelfand et al. (Reference Gelfand, Kapranov and Zelevisnky1992), p. 445: let
$\Delta_n$
can be tested using the following criterion Gelfand et al. (Reference Gelfand, Kapranov and Zelevisnky1992), p. 445: let
![]() $A = \displaystyle\sum_{0\leqslant i_0,\dots,i_{n-1}\leqslant 1}a_{i_0\dots i_{n-1}}x^{(0)}_{i_0}\dots x^{(n-1)}_{i_{n-1}}$
be the multilinear form associated with the n-qubit state
$A = \displaystyle\sum_{0\leqslant i_0,\dots,i_{n-1}\leqslant 1}a_{i_0\dots i_{n-1}}x^{(0)}_{i_0}\dots x^{(n-1)}_{i_{n-1}}$
be the multilinear form associated with the n-qubit state
![]() $|{\psi}\rangle= \displaystyle\sum_{0\leqslant i_0,\dots,i_{n-1}\leqslant 1}a_{i_0\dots i_{n-1}}|{i_0\dots i_{n-1}}\rangle$
, then the condition
$|{\psi}\rangle= \displaystyle\sum_{0\leqslant i_0,\dots,i_{n-1}\leqslant 1}a_{i_0\dots i_{n-1}}|{i_0\dots i_{n-1}}\rangle$
, then the condition
![]() $\Delta_n(\!|{\psi}\rangle\!)= 0$
means that the system
$\Delta_n(\!|{\psi}\rangle\!)= 0$
means that the system
 \begin{equation} \left\{A=\frac{\partial A}{\partial x^{(0)}_{0}}=\frac{\partial A}{\partial x^{(0)}_{1}}=\dots=\frac{\partial A}{\partial x^{(n-1)}_{0}}=\frac{\partial A}{\partial x^{(n-1)}_{1}}=0\right\} \end{equation}
\begin{equation} \left\{A=\frac{\partial A}{\partial x^{(0)}_{0}}=\frac{\partial A}{\partial x^{(0)}_{1}}=\dots=\frac{\partial A}{\partial x^{(n-1)}_{0}}=\frac{\partial A}{\partial x^{(n-1)}_{1}}=0\right\} \end{equation}
has a solution
![]() $\left(x^{(0)}_{0}, x^{(0)}_{1},\dots, x^{(n-1)}_{0}, x^{(n-1)}_{1}\right)$
such that
$\left(x^{(0)}_{0}, x^{(0)}_{1},\dots, x^{(n-1)}_{0}, x^{(n-1)}_{1}\right)$
such that
![]() $\left( x^{(i)}_{0}, x^{(i)}_{1}\right)\neq (0,0)$
for any
$\left( x^{(i)}_{0}, x^{(i)}_{1}\right)\neq (0,0)$
for any
![]() $i=0\dots n-1$
. Such a solution is called non-trivial. Therefore, to show that a state
$i=0\dots n-1$
. Such a solution is called non-trivial. Therefore, to show that a state
![]() $|{\psi}\rangle$
is generically entangled, it is sufficient to prove that the system corresponding to
$|{\psi}\rangle$
is generically entangled, it is sufficient to prove that the system corresponding to
![]() $|{\psi}\rangle$
has no solutions apart from the trivial solutions. We will go back to these questions in future works.
$|{\psi}\rangle$
has no solutions apart from the trivial solutions. We will go back to these questions in future works.
Acknowledgements
The author acknowledges the use of the IBM Quantum Experience at https://quantum-computing.ibm.com/. The views expressed are those of the author and do not reflect the official policy or position of IBM or the IBM Quantum Experience team. Part of this work was performed using computing resources of the CRIANN (Normandy, France).
Conflicts of interest
The author declares none.