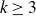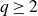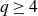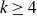1. Introduction
For a k-uniform hypergraph H and a positive integer q, we denote by
![]() $r_k(H;\, q)$
the q-colour Ramsey number of H defined as the minimum integer N such that any q-colouring of the complete k-uniform hypergraph on N vertices, denoted by
$r_k(H;\, q)$
the q-colour Ramsey number of H defined as the minimum integer N such that any q-colouring of the complete k-uniform hypergraph on N vertices, denoted by
![]() $K_N^{(k)}$
, contains a monochromatic copy of H. When
$K_N^{(k)}$
, contains a monochromatic copy of H. When
![]() $H = K^{(k)}_n,$
we simply write
$H = K^{(k)}_n,$
we simply write
![]() $r_k(n;\, q)$
. The existence of these numbers was famously shown by Ramsey [
Reference Ramsey21
] in 1930. Since then, finding good bounds on
$r_k(n;\, q)$
. The existence of these numbers was famously shown by Ramsey [
Reference Ramsey21
] in 1930. Since then, finding good bounds on
![]() $r_k(H;\,q)$
for various (hyper)graphs H has been one of the most major areas of study in Discrete mathematics. The first important results in this direction were exponential bounds on the so-called diagonal graph Ramsey number, namely that
$r_k(H;\,q)$
for various (hyper)graphs H has been one of the most major areas of study in Discrete mathematics. The first important results in this direction were exponential bounds on the so-called diagonal graph Ramsey number, namely that
![]() $\sqrt{2}^n \lt r_2(n;\, 2) \lt 4^n,$
where the upper bound was proven by Erdős and Szekeres [
Reference Erdős and Szekeres14
] and the lower bound by Erdős [
Reference Erdős8
] as one of the first applications of the probabilistic method. Both of these arguments easily extend to give similar bounds for any fixed number of colours q. Despite a great amount of interest and the fact that these bounds are at least 70 years old, until very recently they have been only improved by lower order terms. In March 2023, a major breakthrough was obtained by Campos, Griffiths, Morris and Sahasrabudhe [
Reference Campos, Griffiths, Morris and Sahasrabudhe2
], who improved the upper bound to
$\sqrt{2}^n \lt r_2(n;\, 2) \lt 4^n,$
where the upper bound was proven by Erdős and Szekeres [
Reference Erdős and Szekeres14
] and the lower bound by Erdős [
Reference Erdős8
] as one of the first applications of the probabilistic method. Both of these arguments easily extend to give similar bounds for any fixed number of colours q. Despite a great amount of interest and the fact that these bounds are at least 70 years old, until very recently they have been only improved by lower order terms. In March 2023, a major breakthrough was obtained by Campos, Griffiths, Morris and Sahasrabudhe [
Reference Campos, Griffiths, Morris and Sahasrabudhe2
], who improved the upper bound to
![]() $(4-\epsilon)^n$
.
$(4-\epsilon)^n$
.
In the case of hypergraphs, Erdős and Rado [
Reference Erdős and Rado13
] showed that for some constant
![]() $c = c(k, q),$
the Ramsey numbers satisfy
$c = c(k, q),$
the Ramsey numbers satisfy
![]() $r_k(n;\, q) \le \mathrm{tw}_k(cn),$
where
$r_k(n;\, q) \le \mathrm{tw}_k(cn),$
where
![]() $\mathrm{tw}_k(x)$
denotes the tower function defined as
$\mathrm{tw}_k(x)$
denotes the tower function defined as
![]() $\mathrm{tw}_1(x) = x$
and
$\mathrm{tw}_1(x) = x$
and
![]() $\mathrm{tw}_k(x) = 2^{\mathrm{tw}_{k-1}(x)}$
for
$\mathrm{tw}_k(x) = 2^{\mathrm{tw}_{k-1}(x)}$
for
![]() $k\ge 2.$
On the other hand, an ingenious construction of Erdős and Hajnal (see e.g. [
Reference Graham, Rothschild and Spencer17
]), known as the stepping-up lemma, allows one to obtain a lower bound for hypergraphs of uniformity
$k\ge 2.$
On the other hand, an ingenious construction of Erdős and Hajnal (see e.g. [
Reference Graham, Rothschild and Spencer17
]), known as the stepping-up lemma, allows one to obtain a lower bound for hypergraphs of uniformity
![]() $k+1$
from lower bounds for uniformity k, essentially gaining an extra exponential. However, this construction only works if the number of colors, q, is at least 4 or the uniformity, k, is at least
$k+1$
from lower bounds for uniformity k, essentially gaining an extra exponential. However, this construction only works if the number of colors, q, is at least 4 or the uniformity, k, is at least
![]() $3.$
In particular, we have the bounds
$3.$
In particular, we have the bounds
![]() $r_k(n;\, 2) \ge \mathrm{tw}_{k-1}(c n^2)$
and
$r_k(n;\, 2) \ge \mathrm{tw}_{k-1}(c n^2)$
and
![]() $r_k(n;\, 4) \ge \mathrm{tw}_k(cn).$
The first bound comes from applying a random construction for uniformity 3 and then applying the stepping-up lemma. Erdős, Hajnal and Rado [
Reference Erdős, Hajnal and Rado12
] conjectured that
$r_k(n;\, 4) \ge \mathrm{tw}_k(cn).$
The first bound comes from applying a random construction for uniformity 3 and then applying the stepping-up lemma. Erdős, Hajnal and Rado [
Reference Erdős, Hajnal and Rado12
] conjectured that
![]() $r_3(n;\,2) \gt 2^{2^{cn}}$
, which would, by the stepping-up lemma, imply
$r_3(n;\,2) \gt 2^{2^{cn}}$
, which would, by the stepping-up lemma, imply
![]() $r_k(n;\,2) \ge \mathrm{tw}_k(c_kn),$
thus determining the correct tower height of these numbers. However, this remains a major open problem.
$r_k(n;\,2) \ge \mathrm{tw}_k(c_kn),$
thus determining the correct tower height of these numbers. However, this remains a major open problem.
Given the difficulty of finding good bounds for complete graphs and hypergraphs, Burr and Erdős [
Reference Burr and Erdős1
] initiated the study of Ramsey numbers of sparse graphs and, in particular, conjectured that for any integer
![]() $\Delta,$
there is
$\Delta,$
there is
![]() $c(\Delta)$
such that
$c(\Delta)$
such that
![]() $r_2(G;\, 2) \le c(\Delta) n$
for any n-vertex graph with maximum degree at most
$r_2(G;\, 2) \le c(\Delta) n$
for any n-vertex graph with maximum degree at most
![]() $\Delta.$
This conjecture was proven by Chvátal, Rödl, Szemerédi and Trotter [
Reference Chvatál, Rödl, Szemerédi and Trotter3
] using Szemerédi’s celebrated regularity lemma. The development of the hypergraph regularity lemma lead to the generalisation of this result to bounded degree hypergraphs proven by Cooley, Fountoulakis, Kühn and Osthus [
Reference Cooley, Fountoulakis, Kühn and Osthus7
]. Burr and Erdős also made the stronger conjecture that
$\Delta.$
This conjecture was proven by Chvátal, Rödl, Szemerédi and Trotter [
Reference Chvatál, Rödl, Szemerédi and Trotter3
] using Szemerédi’s celebrated regularity lemma. The development of the hypergraph regularity lemma lead to the generalisation of this result to bounded degree hypergraphs proven by Cooley, Fountoulakis, Kühn and Osthus [
Reference Cooley, Fountoulakis, Kühn and Osthus7
]. Burr and Erdős also made the stronger conjecture that
![]() $r_2(G;\, 2) \lt c(d) n$
should also hold for all d-degenerate graphs on n vertices and it was proved by Lee [
Reference Lee20
].
$r_2(G;\, 2) \lt c(d) n$
should also hold for all d-degenerate graphs on n vertices and it was proved by Lee [
Reference Lee20
].
In 1973, Erdős and Graham [
Reference Erdős and Graham11
] posed a natural question of maximising the Ramsey number of a graph as a function of the number of its edges. Since Ramsey numbers of sparse graphs grow slowly, it is natural to guess that in order to maximise the Ramsey number of a graph with m edges, one should make it as dense as possible. This has motivated Erdős and Graham to conjecture that among all graphs with
![]() $m = \binom{n}{2}$
edges, the complete graph
$m = \binom{n}{2}$
edges, the complete graph
![]() $K_n$
has the largest Ramsey number. This conjecture appears extremely difficult and there has been no real progress on it. Therefore Erdős [
Reference Erdős10
] made a weaker conjecture that there is a constant c such that
$K_n$
has the largest Ramsey number. This conjecture appears extremely difficult and there has been no real progress on it. Therefore Erdős [
Reference Erdős10
] made a weaker conjecture that there is a constant c such that
![]() $r_2(G;\, 2) \le 2^{c \sqrt{m}}$
for any graph G with m edges and no isolated vertices, which would be sharp by the above-mentioned lower bound for the Ramsey number of the complete graph. This conjecture has been resolved by Sudakov [
Reference Sudakov22
]. In contrast to many results mentioned above, the argument in [
Reference Sudakov22
] only works for two colours and it would be interesting to extend this result to more colours.
$r_2(G;\, 2) \le 2^{c \sqrt{m}}$
for any graph G with m edges and no isolated vertices, which would be sharp by the above-mentioned lower bound for the Ramsey number of the complete graph. This conjecture has been resolved by Sudakov [
Reference Sudakov22
]. In contrast to many results mentioned above, the argument in [
Reference Sudakov22
] only works for two colours and it would be interesting to extend this result to more colours.
In this paper we consider the Erdős and Graham question for hypergaphs. Naively one might expect that for fixed k and q, there exists
![]() $c = c(k, q)$
such that any k-uniform hypergraph H with m edges satisfies
$c = c(k, q)$
such that any k-uniform hypergraph H with m edges satisfies
![]() $r_k(H;\, q) \le \mathrm{tw}_k(c m^{1/k})$
, i.e., the complete hypergraph is a maximiser. This however, was shown to be false by Conlon, Fox and Sudakov [
Reference Conlon, Fox and Sudakov4
] who constructed a 3-uniform hypergraph with m edges whose 4-colour Ramsey number at least
$r_k(H;\, q) \le \mathrm{tw}_k(c m^{1/k})$
, i.e., the complete hypergraph is a maximiser. This however, was shown to be false by Conlon, Fox and Sudakov [
Reference Conlon, Fox and Sudakov4
] who constructed a 3-uniform hypergraph with m edges whose 4-colour Ramsey number at least
![]() $2^{2^{c \sqrt{m}}}$
for some positive absolute constant c. On the other hand, they showed that any k-uniform hypergraph H with m edges satisfies
$2^{2^{c \sqrt{m}}}$
for some positive absolute constant c. On the other hand, they showed that any k-uniform hypergraph H with m edges satisfies
![]() $r_k(H;\, q) \le \mathrm{tw}_k(c \sqrt{m}),$
for
$r_k(H;\, q) \le \mathrm{tw}_k(c \sqrt{m}),$
for
![]() $k \ge 4,$
while
$k \ge 4,$
while
![]() $r_k(H;\, q) \le \mathrm{tw}_k(c \sqrt{m} \log m)$
for
$r_k(H;\, q) \le \mathrm{tw}_k(c \sqrt{m} \log m)$
for
![]() $k=3,$
where the constant c depends only on k and q. In a survey on graph Ramsey theory [
Reference Conlon, Fox and Sudakov5
], they further asked whether it is possible to remove the logarithmic factor for the 3-uniform case.
$k=3,$
where the constant c depends only on k and q. In a survey on graph Ramsey theory [
Reference Conlon, Fox and Sudakov5
], they further asked whether it is possible to remove the logarithmic factor for the 3-uniform case.
Problem 1·1. Show that for any
![]() $q \ge 2,$
there exists
$q \ge 2,$
there exists
![]() $c_q$
such that
$c_q$
such that
![]() $r_3(H;\, q) \le 2^{2^{c_q \sqrt{m}}}$
for any 3-uniform hypergraph H with m edges and no isolated vertices.
$r_3(H;\, q) \le 2^{2^{c_q \sqrt{m}}}$
for any 3-uniform hypergraph H with m edges and no isolated vertices.
In the present paper, we resolve Problem 1·1. Moreover, our proof extends to larger uniformities as well so we present a unified proof for all
![]() $k \ge 3$
.
$k \ge 3$
.
Theorem 1·2. For any
![]() $k \ge 3,$
and any fixed number of colours q, there is a constant
$k \ge 3,$
and any fixed number of colours q, there is a constant
![]() $C_{k, q}$
such that the q-colour Ramsey number of any k-uniform hypergraph H with m edges and no isolated vertices is at most
$C_{k, q}$
such that the q-colour Ramsey number of any k-uniform hypergraph H with m edges and no isolated vertices is at most
![]() $\mathrm{tw}_k(C_{k,q} \sqrt{m}).$
$\mathrm{tw}_k(C_{k,q} \sqrt{m}).$
We also provide a construction showing that the above bound is tight up to a constant factor in front of
![]() $\sqrt m$
. Although in the graph case the tightness follows simply by considering a clique of appropriate size, for higher uniformities the construction is rather involved and is obtained by using the paths in expander graphs. Due to our reliance on the stepping-up lemma, the construction requires 4 colours.
$\sqrt m$
. Although in the graph case the tightness follows simply by considering a clique of appropriate size, for higher uniformities the construction is rather involved and is obtained by using the paths in expander graphs. Due to our reliance on the stepping-up lemma, the construction requires 4 colours.
Theorem 1·3. For any
![]() $k \ge 2,$
there exist a constant
$k \ge 2,$
there exist a constant
![]() $c_k \gt 0$
such that for any positive integer m there is a k-uniform hypergraph with m hyperedges and no isolated vertices whose 4-colour Ramsey number is at least
$c_k \gt 0$
such that for any positive integer m there is a k-uniform hypergraph with m hyperedges and no isolated vertices whose 4-colour Ramsey number is at least
![]() $\mathrm{tw}_k(c_k \sqrt{m}).$
$\mathrm{tw}_k(c_k \sqrt{m}).$
The rest of this short paper is organised as follows. In Section 2 we prove Theorem 1·2 and in Section 3 we prove Theorem 1·3. We systematically ignore floor and ceiling signs whenever they are not crucial for the argument. In the use of asymptotic notation we sometimes omit the dependence on the uniformity, k, and the number of colours, q, since we treat them as constants.
2. Proof of Theorem 1·2
Before presenting the proof, let us give a brief outline. The main new idea is to show that every hypergraph with m edges has a strong colouring (see Definition 2·2) with
![]() $t = O(\sqrt{m})$
colours such that the product of the sizes of the colour classes is
$t = O(\sqrt{m})$
colours such that the product of the sizes of the colour classes is
![]() $2^{O(\sqrt{m})}.$
Given a coloured complete k-uniform hypergraph G on
$2^{O(\sqrt{m})}.$
Given a coloured complete k-uniform hypergraph G on
![]() $\mathrm{tw}_k(C \sqrt{m})$
vertices, we then apply Erdős and Rado’s upper bound on hypergraph Ramsey numbers mentioned in the introduction along with a simple supersaturation argument to find many monochromatic cliques of size t in G. Then, it is enough to find a set of cliques of one colour which form a complete t-partite hypergraph with part sizes corresponding to the colour classes of the given strong colouring. This will follow from a version of the hypergraph extension of the Kővári–Sós–Turán theorem [
Reference Kővári, Sós and Turán19
]. Such an extension was first proved by Erdős [
Reference Erdős9
]. In our setting, the number of parts and their sizes are allowed to grow with the size of the hypergraph. The aforementioned result of Erdős does not provide such a bound, though it can easily be extracted from most of the known proofs.
$\mathrm{tw}_k(C \sqrt{m})$
vertices, we then apply Erdős and Rado’s upper bound on hypergraph Ramsey numbers mentioned in the introduction along with a simple supersaturation argument to find many monochromatic cliques of size t in G. Then, it is enough to find a set of cliques of one colour which form a complete t-partite hypergraph with part sizes corresponding to the colour classes of the given strong colouring. This will follow from a version of the hypergraph extension of the Kővári–Sós–Turán theorem [
Reference Kővári, Sós and Turán19
]. Such an extension was first proved by Erdős [
Reference Erdős9
]. In our setting, the number of parts and their sizes are allowed to grow with the size of the hypergraph. The aforementioned result of Erdős does not provide such a bound, though it can easily be extracted from most of the known proofs.
Let
![]() $K_{s_1, \ldots, s_t}$
denote the complete t-partite t-uniform hypergraph with part sizes
$K_{s_1, \ldots, s_t}$
denote the complete t-partite t-uniform hypergraph with part sizes
![]() $s_1, \ldots, s_t$
and denote by
$s_1, \ldots, s_t$
and denote by
![]() $\mathrm{ex}(n, K_{s_1, \ldots, s_t})$
the maximum number of edges in a t-uniform hypergraph not containing
$\mathrm{ex}(n, K_{s_1, \ldots, s_t})$
the maximum number of edges in a t-uniform hypergraph not containing
![]() $K_{s_1, \ldots, s_t}$
as a subgraph.
$K_{s_1, \ldots, s_t}$
as a subgraph.
We require an upper bound on
![]() $\mathrm{ex}(n, K_{s_1, \ldots s_t}),$
where the number of parts and their sizes are allowed to grow with n. Such an upper bound is surely widely known, but we have not found a reference which contains the bound we need. Hence, we include the short proof for completeness. Note that the exponent of n in our bound is not best possible, however, it is sufficient for our purposes and allows for a cleaner proof.
$\mathrm{ex}(n, K_{s_1, \ldots s_t}),$
where the number of parts and their sizes are allowed to grow with n. Such an upper bound is surely widely known, but we have not found a reference which contains the bound we need. Hence, we include the short proof for completeness. Note that the exponent of n in our bound is not best possible, however, it is sufficient for our purposes and allows for a cleaner proof.
Lemma 2·1. Let
![]() $s_1, \ldots, s_t$
be positive integers and denote
$s_1, \ldots, s_t$
be positive integers and denote
![]() $P = \prod_{i=1}^t s_i.$
Then, for all
$P = \prod_{i=1}^t s_i.$
Then, for all
![]() $n \ge 1,$
$n \ge 1,$
Proof. We prove the statement by induction on t. For
![]() $t=1,$
the claim is trivial. Assume now
$t=1,$
the claim is trivial. Assume now
![]() $t \ge 2$
and let H be a t-uniform hypergraph with
$t \ge 2$
and let H be a t-uniform hypergraph with
![]() $m \ge P n^{t - P^{-1}}$
edges. We need to show that H contains a copy of
$m \ge P n^{t - P^{-1}}$
edges. We need to show that H contains a copy of
![]() $K_{s_1, \ldots, s_t}.$
For
$K_{s_1, \ldots, s_t}.$
For
![]() $W \in \binom{V(H)}{s_t},$
let
$W \in \binom{V(H)}{s_t},$
let
For
![]() $f \in \binom{V(H)}{t-1},$
let d(f) denote the number of edges of H containing the set f. Double counting, we have
$f \in \binom{V(H)}{t-1},$
let d(f) denote the number of edges of H containing the set f. Double counting, we have
 \begin{align*} \sum_{W \in \binom{V(H)}{s_t}} |N(W)| = \sum_{f \in \binom{V(H)}{t-1}} \binom{d(f)}{s_t}. \end{align*}
\begin{align*} \sum_{W \in \binom{V(H)}{s_t}} |N(W)| = \sum_{f \in \binom{V(H)}{t-1}} \binom{d(f)}{s_t}. \end{align*}
Using that
![]() $\binom{x}{s}$
is convex and
$\binom{x}{s}$
is convex and
![]() $\sum_{f \in \binom{V(H)}{t-1}} d(f) = tm,$
we can apply Jensen’s inequality to obtain
$\sum_{f \in \binom{V(H)}{t-1}} d(f) = tm,$
we can apply Jensen’s inequality to obtain
 \begin{align*} \sum_{W \in \binom{V(H)}{s_t}} |N(W)| & \ge \binom{n}{t-1} \binom{tm / \binom{n}{t-1}}{s_t} \ge \frac{n \cdots (n-t+2)}{(t-1)!} \cdot \left(\frac{t! m}{s_t \cdot n \cdots (n-t+2)}\right)^{s_t}\\& \ge \frac{m^{s_t}}{s_t^{s_t} \cdot n^{(t-1)(s_t-1)}}. \end{align*}
\begin{align*} \sum_{W \in \binom{V(H)}{s_t}} |N(W)| & \ge \binom{n}{t-1} \binom{tm / \binom{n}{t-1}}{s_t} \ge \frac{n \cdots (n-t+2)}{(t-1)!} \cdot \left(\frac{t! m}{s_t \cdot n \cdots (n-t+2)}\right)^{s_t}\\& \ge \frac{m^{s_t}}{s_t^{s_t} \cdot n^{(t-1)(s_t-1)}}. \end{align*}
Denoting
![]() $P' = \prod_{i=1}^{t-1} s_i = P / s_t,$
by the pigeonhole principle, there is a set W with
$P' = \prod_{i=1}^{t-1} s_i = P / s_t,$
by the pigeonhole principle, there is a set W with
By the induction hypothesis, the
![]() $(t-1)$
-uniform hypergraph formed by the edge set N(W) contains a copy of
$(t-1)$
-uniform hypergraph formed by the edge set N(W) contains a copy of
![]() $K_{s_1, \ldots, s_{t-1}},$
which together with W forms
$K_{s_1, \ldots, s_{t-1}},$
which together with W forms
![]() $K_{s_1, \ldots, s_t},$
as required.
$K_{s_1, \ldots, s_t},$
as required.
Definition 2·2. A strong colouring of a hypergraph H is a partition of V(H) into colour classes
![]() $V_1, \ldots, V_t$
such that every edge of H contains at most one vertex from each of the sets
$V_1, \ldots, V_t$
such that every edge of H contains at most one vertex from each of the sets
![]() $V_1, \ldots, V_t.$
$V_1, \ldots, V_t.$
Lemma 2·3. Fix
![]() $k \ge 2$
and let H be a k-uniform hypergraph with m edges and no isolated vertices. Then, there is a strong colouring
$k \ge 2$
and let H be a k-uniform hypergraph with m edges and no isolated vertices. Then, there is a strong colouring
![]() $V_1\, {\cdot\!\!\cup} \ldots\, {\cdot\!\!\cup} V_t$
of H such that
$V_1\, {\cdot\!\!\cup} \ldots\, {\cdot\!\!\cup} V_t$
of H such that
![]() $t = O(\sqrt{m})$
and moreover,
$t = O(\sqrt{m})$
and moreover,
![]() $\prod_{i=1}^t |V_i| \le 2^{O(\sqrt{m})}.$
$\prod_{i=1}^t |V_i| \le 2^{O(\sqrt{m})}.$
Proof. We first partition the vertices of H according to their degree as follows. Set
![]() $\Delta := \sqrt{m}$
and denote
$\Delta := \sqrt{m}$
and denote
![]() $s = \lfloor{\log_2 \Delta}\rfloor + 1.$
Let
$s = \lfloor{\log_2 \Delta}\rfloor + 1.$
Let
![]() $U_0 = \{ v \in V(H) \, \vert \, d(v) \gt \Delta \}$
and for
$U_0 = \{ v \in V(H) \, \vert \, d(v) \gt \Delta \}$
and for
![]() $1 \le i \le s,$
let
$1 \le i \le s,$
let
![]() $U_i = \{ v \in V(H) \, \vert \, \Delta / 2^i \lt d(v) \le \Delta / 2^{i-1} \}.$
Since V(H) has no isolated vertices, it is clear that
$U_i = \{ v \in V(H) \, \vert \, \Delta / 2^i \lt d(v) \le \Delta / 2^{i-1} \}.$
Since V(H) has no isolated vertices, it is clear that
![]() $U_0\, {\cdot\!\!\cup} \ldots\, {\cdot\!\!\cup} U_s$
is a partition of
$U_0\, {\cdot\!\!\cup} \ldots\, {\cdot\!\!\cup} U_s$
is a partition of
![]() $V(H).$
We colour each of the sets
$V(H).$
We colour each of the sets
![]() $U_i$
using distinct colours. Each vertex in
$U_i$
using distinct colours. Each vertex in
![]() $U_0$
receives a distinct colour. For
$U_0$
receives a distinct colour. For
![]() $i \ge 1,$
the vertices in
$i \ge 1,$
the vertices in
![]() $U_i$
are greedily coloured one by one using at most
$U_i$
are greedily coloured one by one using at most
![]() $t_i := k \Delta / 2^{i-1}$
colours. This is possible since having coloured some vertices in
$t_i := k \Delta / 2^{i-1}$
colours. This is possible since having coloured some vertices in
![]() $U_i,$
the next vertex
$U_i,$
the next vertex
![]() $v \in U_i$
to be coloured shares an edge with at most
$v \in U_i$
to be coloured shares an edge with at most
![]() $(k-1) d(v) \le (k-1) \Delta / 2^{i-1} \le t_i - 1$
previously coloured vertices in
$(k-1) d(v) \le (k-1) \Delta / 2^{i-1} \le t_i - 1$
previously coloured vertices in
![]() $U_i.$
$U_i.$
Let
![]() $V_1, \ldots, V_t$
denote the colour classes produced by the colouring described above. It remains to verify that it satisfies the desired properties. To this end, for
$V_1, \ldots, V_t$
denote the colour classes produced by the colouring described above. It remains to verify that it satisfies the desired properties. To this end, for
![]() $0 \le i \le s,$
we denote
$0 \le i \le s,$
we denote
![]() $n_i = |U_i|$
and
$n_i = |U_i|$
and
![]() $m_i = \sum_{v \in U_i} d(v).$
Clearly,
$m_i = \sum_{v \in U_i} d(v).$
Clearly,
![]() $\sum_{i=0}^s m_i = \sum_{v \in V(H)} d(v) = km$
and for
$\sum_{i=0}^s m_i = \sum_{v \in V(H)} d(v) = km$
and for
![]() $0 \le i \le s,$
we have
$0 \le i \le s,$
we have
![]() $km \ge m_i \ge n_i \cdot \Delta / 2^i.$
In particular,
$km \ge m_i \ge n_i \cdot \Delta / 2^i.$
In particular,
![]() $n_0 \le km / \Delta = k \sqrt{m}$
.
$n_0 \le km / \Delta = k \sqrt{m}$
.
The number of colours used, t, satisfies
Recall that
![]() $t_i = k \Delta / 2^{i-1}$
and
$t_i = k \Delta / 2^{i-1}$
and
![]() $n_i \le 2^i m_i / \Delta \le 2^i km / \Delta.$
By the AM-GM inequality, the product of the sizes of the colour classes used to colour
$n_i \le 2^i m_i / \Delta \le 2^i km / \Delta.$
By the AM-GM inequality, the product of the sizes of the colour classes used to colour
![]() $U_i, i \ge 1$
is at most
$U_i, i \ge 1$
is at most
 \begin{align*} \left(\frac{n_i}{t_i}\right)^{t_i} \lt \left( \frac{4^i m}{\Delta^2} \right)^{k \Delta / 2^{i-1}} = (4^i)^{k\Delta / 2^{i-1}} =2^{k\Delta i/2^{i-2}}. \end{align*}
\begin{align*} \left(\frac{n_i}{t_i}\right)^{t_i} \lt \left( \frac{4^i m}{\Delta^2} \right)^{k \Delta / 2^{i-1}} = (4^i)^{k\Delta / 2^{i-1}} =2^{k\Delta i/2^{i-2}}. \end{align*}
Multiplying the above bound for all
![]() $1 \le i \le s$
and using that the series
$1 \le i \le s$
and using that the series
![]() $\sum_{i=1}^\infty i / 2^{i-2}$
converges, we obtain
$\sum_{i=1}^\infty i / 2^{i-2}$
converges, we obtain
 \begin{align*} \prod_{j=1}^t |V_j| \le \prod_{i=1}^s 2^{k\Delta i/2^{i-2}} = 2^{O_k(\sqrt{m})}. \end{align*}
\begin{align*} \prod_{j=1}^t |V_j| \le \prod_{i=1}^s 2^{k\Delta i/2^{i-2}} = 2^{O_k(\sqrt{m})}. \end{align*}
As mentioned in the outline, we will use the following bound on the Ramsey number of a complete k-uniform hypergraph.
Theorem 2·4 (Erdős, Rado [
Reference Erdős and Rado13
]). For positive integers q, k there is a constant
![]() $C' = C'(q, k)$
such that
$C' = C'(q, k)$
such that
![]() $r_k(n;\, q) \le \mathrm{tw}_k(C'n).$
$r_k(n;\, q) \le \mathrm{tw}_k(C'n).$
Proof of Theorem 1·2. Let
![]() $m = e(H)$
and let
$m = e(H)$
and let
![]() $N = \mathrm{tw}_k(C \sqrt{m})$
where
$N = \mathrm{tw}_k(C \sqrt{m})$
where
![]() $C = C(k, q)$
is a large constant to be chosen implicitly later. Consider an arbitrary q-colouring of the complete k-uniform hypergraph on N vertices and call this colored hypergraph G. We need to show that G contains a monochromatic copy of H.
$C = C(k, q)$
is a large constant to be chosen implicitly later. Consider an arbitrary q-colouring of the complete k-uniform hypergraph on N vertices and call this colored hypergraph G. We need to show that G contains a monochromatic copy of H.
Let
![]() $V_1\, {\cdot\!\!\cup} \ldots\, {\cdot\!\!\cup} V_t = V(H)$
be a strong colouring of H satisfying
$V_1\, {\cdot\!\!\cup} \ldots\, {\cdot\!\!\cup} V_t = V(H)$
be a strong colouring of H satisfying
![]() $t \le O(\sqrt{m})$
and
$t \le O(\sqrt{m})$
and
![]() $P := \prod_{i=1}^t |V_i| \le 2^{O(\sqrt{m})}$
given by Lemma 2·3. We remark that P will correspond to the value of P in our application of Lemma 2·1. We denote
$P := \prod_{i=1}^t |V_i| \le 2^{O(\sqrt{m})}$
given by Lemma 2·3. We remark that P will correspond to the value of P in our application of Lemma 2·1. We denote
![]() $s_i = |V_i|$
for
$s_i = |V_i|$
for
![]() $i \in [t].$
Let
$i \in [t].$
Let
![]() $R = r_k(t;\, q) \le \mathrm{tw}_k(O(\sqrt{m})),$
where the bound holds by Theorem 2·4. A standard supersaturation argument allows us to find many monochromatic copies of
$R = r_k(t;\, q) \le \mathrm{tw}_k(O(\sqrt{m})),$
where the bound holds by Theorem 2·4. A standard supersaturation argument allows us to find many monochromatic copies of
![]() $K^{(k)}_t$
in G of the same colour. Indeed, by definition, every set of R vertices of G contains a monochromatic copy of
$K^{(k)}_t$
in G of the same colour. Indeed, by definition, every set of R vertices of G contains a monochromatic copy of
![]() $K^{(k)}_t$
. On the other hand, any copy of
$K^{(k)}_t$
. On the other hand, any copy of
![]() $K^{(k)}_t$
is contained in
$K^{(k)}_t$
is contained in
![]() $\binom{N-t}{R-t}$
sets of R vertices of G. Putting these two facts together and applying the pigeonhole principle, there is a colour, say red, such that the number of red copies of
$\binom{N-t}{R-t}$
sets of R vertices of G. Putting these two facts together and applying the pigeonhole principle, there is a colour, say red, such that the number of red copies of
![]() $K^{(k)}_t$
in G is at least
$K^{(k)}_t$
in G is at least
We construct an auxiliary t-uniform hypergraph
![]() $\Gamma$
on the vertex set V(G) where a t-set forms an edge if it forms a red t-clique in G. Provided that
$\Gamma$
on the vertex set V(G) where a t-set forms an edge if it forms a red t-clique in G. Provided that
![]() $e(\Gamma) \gt \mathrm{ex}(N, K^{(t)}_{s_1, \ldots, s_t}),$
there must exist a copy of
$e(\Gamma) \gt \mathrm{ex}(N, K^{(t)}_{s_1, \ldots, s_t}),$
there must exist a copy of
![]() $K^{(t)}_{s_1, \ldots, s_t}$
in
$K^{(t)}_{s_1, \ldots, s_t}$
in
![]() $\Gamma$
which corresponds to a red complete t-partite k-uniform hypergraph with part sizes
$\Gamma$
which corresponds to a red complete t-partite k-uniform hypergraph with part sizes
![]() $s_1, \ldots, s_t$
in G and by the existence of the strong colouring
$s_1, \ldots, s_t$
in G and by the existence of the strong colouring
![]() $V(H) = V_1\, {\cdot\!\!\cup} \ldots\, {\cdot\!\!\cup} V_t,$
it contains a red subgraph isomorphic to H.
$V(H) = V_1\, {\cdot\!\!\cup} \ldots\, {\cdot\!\!\cup} V_t,$
it contains a red subgraph isomorphic to H.
It remains to ensure that
![]() $e(\Gamma) \gt \mathrm{ex}(N, K^{(t)}_{s_1, \ldots, s_t}).$
Recall that
$e(\Gamma) \gt \mathrm{ex}(N, K^{(t)}_{s_1, \ldots, s_t}).$
Recall that
![]() $P = \prod_{i=1}^{t} |V_i| = 2^{O(\sqrt{m})}$
. Hence, by (1) and Lemma 2·1, it is enough to show that
$P = \prod_{i=1}^{t} |V_i| = 2^{O(\sqrt{m})}$
. Hence, by (1) and Lemma 2·1, it is enough to show that
or equivalently,
It will be convenient to compare the logarithms of the two sides. We remind the reader that
![]() $\mathrm{tw}_k(x) = 2^{\mathrm{tw}_{k-1}(x)}$
for
$\mathrm{tw}_k(x) = 2^{\mathrm{tw}_{k-1}(x)}$
for
![]() $k \ge 2.$
Thus, we have
$k \ge 2.$
Thus, we have
where in the last inequality we used that
![]() $k \ge 3.$
On the other hand,
$k \ge 3.$
On the other hand,
where in the last inequality we used that
![]() $k\ge 3$
and chose C to be large enough compared to the implicit constant in the O notation. It follows that for large enough C, we have
$k\ge 3$
and chose C to be large enough compared to the implicit constant in the O notation. It follows that for large enough C, we have
![]() $R^t q \lt N^{2^{-O(\sqrt{m})}},$
as needed.
$R^t q \lt N^{2^{-O(\sqrt{m})}},$
as needed.
3. Proof of Theorem 1·3
In this section, we prove Theorem 1·3. We shall start with a few definitions which are used in the proof and present a variant of the step-up colouring that we use. After that, we give an informal discussion of the main ideas behind the proof and then we present the proof itself.
3·1. Setup
To begin, we recall an important function used in this construction. For a nonnegative integer x, let
![]() $x = \sum_{i=0}^{\infty} a_i 2^i$
be its unique binary representation (where
$x = \sum_{i=0}^{\infty} a_i 2^i$
be its unique binary representation (where
![]() $a_i = 0$
for all but finitely many i). We denote
$a_i = 0$
for all but finitely many i). We denote
![]() $\mathrm{bit}(x, i) = a_i.$
Then
$\mathrm{bit}(x, i) = a_i.$
Then
![]() $\delta(x, y) := \max \{ i \in \mathbb{Z}_{\ge 0} \, \vert \, \mathrm{bit}(x, i) \neq \mathrm{bit}(y, i)\}.$
For nonnegative integers
$\delta(x, y) := \max \{ i \in \mathbb{Z}_{\ge 0} \, \vert \, \mathrm{bit}(x, i) \neq \mathrm{bit}(y, i)\}.$
For nonnegative integers
![]() $x_1 \lt x_2 \lt \ldots \lt x_t,$
we denote
$x_1 \lt x_2 \lt \ldots \lt x_t,$
we denote
![]() $\delta(\{x_1, \ldots, x_t\}) = (\delta_1, \ldots, \delta_{t-1})$
where for
$\delta(\{x_1, \ldots, x_t\}) = (\delta_1, \ldots, \delta_{t-1})$
where for
![]() $i \in [t-1],$
$i \in [t-1],$
![]() $\delta_i = \delta(x_i, x_{i+1}).$
The following properties of this function are well known and easy to verify.
$\delta_i = \delta(x_i, x_{i+1}).$
The following properties of this function are well known and easy to verify.
-
(P1)
 $x \lt y \iff \mathrm{bit}(x, \delta(x, y)) \lt \mathrm{bit}(y, \delta(x, y))$
.
$x \lt y \iff \mathrm{bit}(x, \delta(x, y)) \lt \mathrm{bit}(y, \delta(x, y))$
. -
(P2) For any
 $x \lt y \lt z,$
$x \lt y \lt z,$
 $\delta(x, y) \neq \delta(y, z)$
.
$\delta(x, y) \neq \delta(y, z)$
. -
(P3) For any
 $x_1 \lt x_2 \lt \ldots \lt x_k,$
$x_1 \lt x_2 \lt \ldots \lt x_k,$
 $\delta(x_1, x_k) = \max_{1 \le i \le k-1} \delta(x_i, x_{i+1})$
.
$\delta(x_1, x_k) = \max_{1 \le i \le k-1} \delta(x_i, x_{i+1})$
.
Let us now define the colouring which will be used to prove Theorem 1·3. For a positive integer n, we start with a red-blue colouring
![]() $\phi_n^{(2)}$
of the complete graph with vertex set
$\phi_n^{(2)}$
of the complete graph with vertex set
![]() $\{0, \ldots, N_2-1\}$
, where
$\{0, \ldots, N_2-1\}$
, where
![]() $N_2 = N_2(n) = 2^{n/2}$
, containing no monochromatic clique of size n. Such a colouring exists by the well known result of Erdős mentioned in the introduction. For
$N_2 = N_2(n) = 2^{n/2}$
, containing no monochromatic clique of size n. Such a colouring exists by the well known result of Erdős mentioned in the introduction. For
![]() $k \ge 3,$
the colouring
$k \ge 3,$
the colouring
![]() $\phi_n^{(k)}$
is on the vertex set
$\phi_n^{(k)}$
is on the vertex set
![]() $\{0, \ldots, N_k - 1\},$
where
$\{0, \ldots, N_k - 1\},$
where
![]() $N_k = N_k(n) = 2^{N_{k-1}(n)} = \mathrm{tw}_k(n/2)$
and is defined as follows. For a set
$N_k = N_k(n) = 2^{N_{k-1}(n)} = \mathrm{tw}_k(n/2)$
and is defined as follows. For a set
![]() $\{x_1, \ldots, x_k\}$
with
$\{x_1, \ldots, x_k\}$
with
![]() $0 \le x_1 \lt \ldots \lt x_k \lt N_k,$
we consider the vector
$0 \le x_1 \lt \ldots \lt x_k \lt N_k,$
we consider the vector
![]() $\delta(\{x_1, \ldots, x_k\}) = (\delta_1, \ldots, \delta_{k-1}).$
Note that
$\delta(\{x_1, \ldots, x_k\}) = (\delta_1, \ldots, \delta_{k-1}).$
Note that
![]() $0 \le \delta_i \lt N_{k-1}$
for all
$0 \le \delta_i \lt N_{k-1}$
for all
![]() $i \in [k-1]$
. Hence for distinct
$i \in [k-1]$
. Hence for distinct
![]() $\delta_i$
, the set
$\delta_i$
, the set
![]() $\{\delta_1, \ldots, \delta_{k-1}\}$
forms an edge of the complete
$\{\delta_1, \ldots, \delta_{k-1}\}$
forms an edge of the complete
![]() $(k-1)$
-uniform hypegraph on
$(k-1)$
-uniform hypegraph on
![]() $\{0, \ldots, N_{k-1}-1\}$
with colour
$\{0, \ldots, N_{k-1}-1\}$
with colour
![]() $\phi^{(k-1)}_n(\{\delta_1, \ldots, \delta_{k-1}\})$
. For
$\phi^{(k-1)}_n(\{\delta_1, \ldots, \delta_{k-1}\})$
. For
![]() $k = 3,$
the 4-colouring is given as:
$k = 3,$
the 4-colouring is given as:
 \begin{align*} \phi^{(3)}_n(\{x_1, x_2, x_3\}) = \begin{cases} C_1, &\text{if } \delta_1 \lt \delta_2 \text{ and } \phi_n^{(2)}(\{\delta_1, \delta_2\}) \text{ is red;}\\ C_2, &\text{if } \delta_1 \lt \delta_2 \text{ and } \phi_n^{(2)}(\{\delta_1, \delta_2\}) \text{ is blue;}\\ C_3, &\text{if } \delta_1 \gt \delta_2 \text{ and } \phi_n^{(2)}(\{\delta_1, \delta_2\}) \text{ is red;}\\ C_4, &\text{if } \delta_1 \gt \delta_2 \text{ and } \phi_n^{(2)}(\{\delta_1, \delta_2\}) \text{ is blue.} \end{cases}\end{align*}
\begin{align*} \phi^{(3)}_n(\{x_1, x_2, x_3\}) = \begin{cases} C_1, &\text{if } \delta_1 \lt \delta_2 \text{ and } \phi_n^{(2)}(\{\delta_1, \delta_2\}) \text{ is red;}\\ C_2, &\text{if } \delta_1 \lt \delta_2 \text{ and } \phi_n^{(2)}(\{\delta_1, \delta_2\}) \text{ is blue;}\\ C_3, &\text{if } \delta_1 \gt \delta_2 \text{ and } \phi_n^{(2)}(\{\delta_1, \delta_2\}) \text{ is red;}\\ C_4, &\text{if } \delta_1 \gt \delta_2 \text{ and } \phi_n^{(2)}(\{\delta_1, \delta_2\}) \text{ is blue.} \end{cases}\end{align*}
We denote by
![]() $\mathrm{arg\,max}_{i \in [k-1]} \delta_i$
the unique index
$\mathrm{arg\,max}_{i \in [k-1]} \delta_i$
the unique index
![]() $j \in [k-1]$
such that
$j \in [k-1]$
such that
![]() $\delta_j = \max_{i \in [k-1]} \delta_i$
, where the uniqueness follows from Properties (P2) and (P3). For
$\delta_j = \max_{i \in [k-1]} \delta_i$
, where the uniqueness follows from Properties (P2) and (P3). For
![]() $k \ge 4,$
the colouring is given as:
$k \ge 4,$
the colouring is given as:
 \begin{align*} \phi^{(k)}_n(\{x_1, \ldots, x_k\}) =\begin{cases} \phi^{(k-1)}_n(\{\delta_1, \ldots, \delta_{k-1}\}), &\text{if } \delta \text{ is a monotone sequence;}\\ C_1, &\text{if } \delta \text{ is not monotone and } \mathrm{arg\,max}_{i \in [k-1]}\\ & \qquad\qquad \delta_i \in \{1, k-1\}; \\ C_2, &\text{if } \mathrm{arg\,max}_{i \in [k-1]} \delta_i \not\in \{1, k-1\}.\end{cases}\end{align*}
\begin{align*} \phi^{(k)}_n(\{x_1, \ldots, x_k\}) =\begin{cases} \phi^{(k-1)}_n(\{\delta_1, \ldots, \delta_{k-1}\}), &\text{if } \delta \text{ is a monotone sequence;}\\ C_1, &\text{if } \delta \text{ is not monotone and } \mathrm{arg\,max}_{i \in [k-1]}\\ & \qquad\qquad \delta_i \in \{1, k-1\}; \\ C_2, &\text{if } \mathrm{arg\,max}_{i \in [k-1]} \delta_i \not\in \{1, k-1\}.\end{cases}\end{align*}
3·2. Proof outline
Let us now discuss the main ideas of our proof. First, we recall Erdős and Hajnal’s proof of the lower bound
![]() $r_k(n;\, 4) \ge \mathrm{tw}_k(2^{-k} n).$
Their proof uses a slightly different colouring than given above, but the same proof works with our colouring, so we consider it instead. Suppose that
$r_k(n;\, 4) \ge \mathrm{tw}_k(2^{-k} n).$
Their proof uses a slightly different colouring than given above, but the same proof works with our colouring, so we consider it instead. Suppose that
![]() $\phi^{(k)}_n$
contains a monochromatic clique of size
$\phi^{(k)}_n$
contains a monochromatic clique of size
![]() $n_k = 2^k n$
. Denote by
$n_k = 2^k n$
. Denote by
![]() $x_1 \lt x_2 \lt \ldots \lt x_{n_k}$
the vertices of this clique and let
$x_1 \lt x_2 \lt \ldots \lt x_{n_k}$
the vertices of this clique and let
![]() $\delta = (\delta_1, \ldots, \delta_{n_k-1}) = \delta(\{x_1, \ldots, x_{n_k}\}).$
It is not difficult to show that
$\delta = (\delta_1, \ldots, \delta_{n_k-1}) = \delta(\{x_1, \ldots, x_{n_k}\}).$
It is not difficult to show that
![]() $\delta$
must contain a monotone contiguous subsequence
$\delta$
must contain a monotone contiguous subsequence
![]() $\delta' = (\delta_a, \delta_{a+1}, \ldots, \delta_b)$
of length at least
$\delta' = (\delta_a, \delta_{a+1}, \ldots, \delta_b)$
of length at least
![]() $n_k/2.$
By Property (P3) and the definition of
$n_k/2.$
By Property (P3) and the definition of
![]() $\phi^{(k)}_n,$
it follows that
$\phi^{(k)}_n,$
it follows that
![]() $\{\delta_a, \delta_{a+1}, \ldots \delta_b\}$
forms a monochromatic clique in
$\{\delta_a, \delta_{a+1}, \ldots \delta_b\}$
forms a monochromatic clique in
![]() $\phi^{(k-1)}_n$
of size at least
$\phi^{(k-1)}_n$
of size at least
![]() $n_k/2.$
Applying the same argument to this clique in
$n_k/2.$
Applying the same argument to this clique in
![]() $\phi^{(k-1)}_n$
, we find a monochromatic clique of size at least
$\phi^{(k-1)}_n$
, we find a monochromatic clique of size at least
![]() $n_k / 4$
in
$n_k / 4$
in
![]() $\phi^{(k-2)}_n$
and so on. After
$\phi^{(k-2)}_n$
and so on. After
![]() $k-2$
steps, we thus reach a monochromatic clique of size 4n in
$k-2$
steps, we thus reach a monochromatic clique of size 4n in
![]() $\phi^{(2)}_n,$
a contradiction.
$\phi^{(2)}_n,$
a contradiction.
We will show that instead of a clique, we can take a much sparser hypergraph
![]() $H_k$
on
$H_k$
on
![]() $n_k = \alpha_k n$
vertices with
$n_k = \alpha_k n$
vertices with
![]() $m = O(n_k^2) = O_k(n^2)$
edges and reach a similar conclusion, i.e. that
$m = O(n_k^2) = O_k(n^2)$
edges and reach a similar conclusion, i.e. that
![]() $\phi^{(k-1)}_n$
contains a monochromatic copy of some
$\phi^{(k-1)}_n$
contains a monochromatic copy of some
![]() $(k-1)$
-uniform hypergraph
$(k-1)$
-uniform hypergraph
![]() $H_{k-1}$
on
$H_{k-1}$
on
![]() $\alpha_{k-1} n$
vertices, where
$\alpha_{k-1} n$
vertices, where
![]() $H_{k-1}$
is “of the same form” as
$H_{k-1}$
is “of the same form” as
![]() $H_k.$
For the argument to work, we need to make sure of a few a things. With
$H_k.$
For the argument to work, we need to make sure of a few a things. With
![]() $x_1 \lt x_2 \lt \ldots \lt x_{n_k}$
and
$x_1 \lt x_2 \lt \ldots \lt x_{n_k}$
and
![]() $\delta = (\delta_1, \ldots, \delta_{n_{k-1}})$
defined as above, we need that
$\delta = (\delta_1, \ldots, \delta_{n_{k-1}})$
defined as above, we need that
![]() $\delta$
contains a monotone subsequence of length
$\delta$
contains a monotone subsequence of length
![]() $\Omega(n_k).$
Furthermore, this monotone subsequence should imply the existence of a hypergraph
$\Omega(n_k).$
Furthermore, this monotone subsequence should imply the existence of a hypergraph
![]() $H_{k-1}$
on
$H_{k-1}$
on
![]() $\alpha_{k-1}n$
vertices on which we can apply induction. We remark here that
$\alpha_{k-1}n$
vertices on which we can apply induction. We remark here that
![]() $H_{k-1}$
will not be a fixed hypergraph, but rather some large enough hypergraph of the same form as
$H_{k-1}$
will not be a fixed hypergraph, but rather some large enough hypergraph of the same form as
![]() $H_k$
. Finally, after
$H_k$
. Finally, after
![]() $k-2$
steps, we should reach a graph containing a clique of size n to obtain a contradiction. Given that this argument works for a clique and we want a much sparser hypergraph, it should be no surprise that our construction is based on an expander graph. We next define our construction formally and carry out the outlined proof strategy.
$k-2$
steps, we should reach a graph containing a clique of size n to obtain a contradiction. Given that this argument works for a clique and we want a much sparser hypergraph, it should be no surprise that our construction is based on an expander graph. We next define our construction formally and carry out the outlined proof strategy.
3·3. Formal proof
Given a graph G and an integer
![]() $k \ge 2,$
we define a k-uniform hypergraph
$k \ge 2,$
we define a k-uniform hypergraph
![]() $H = H(G, k)$
on the same vertex set where for every path
$H = H(G, k)$
on the same vertex set where for every path
![]() $(v_1, \ldots, v_{k-1})$
in G and any vertex
$(v_1, \ldots, v_{k-1})$
in G and any vertex
![]() $v_k \in V(G)$
not on this path, we put the k-edge
$v_k \in V(G)$
not on this path, we put the k-edge
![]() $\{v_1, \ldots, v_k\}$
in H. Note that for
$\{v_1, \ldots, v_k\}$
in H. Note that for
![]() $k=2,$
H(G, k) is simply the complete graph on the vertex set
$k=2,$
H(G, k) is simply the complete graph on the vertex set
![]() $V(G).$
$V(G).$
Given a k-uniform hypergraph
![]() $\Gamma$
with a colouring
$\Gamma$
with a colouring
![]() $\phi \colon E(\Gamma) \rightarrow \mathcal{C}$
and a hypergraph H, a set of vertices
$\phi \colon E(\Gamma) \rightarrow \mathcal{C}$
and a hypergraph H, a set of vertices
![]() $X \subseteq V(\Gamma)$
forms a monochromatic copy of H if there exists a bijection
$X \subseteq V(\Gamma)$
forms a monochromatic copy of H if there exists a bijection
![]() $\Psi \colon V(H) \rightarrow X$
such that
$\Psi \colon V(H) \rightarrow X$
such that
![]() $\phi(\Psi(e)) = \phi(\Psi(e'))$
for all
$\phi(\Psi(e)) = \phi(\Psi(e'))$
for all
![]() $e, e' \in E(H).$
$e, e' \in E(H).$
We shall need the following simple lemma about sparse random graphs.
Lemma 3·1. For any
![]() $d \ge 10^9$
and M sufficiently large, there is a graph G on M vertices such that:
$d \ge 10^9$
and M sufficiently large, there is a graph G on M vertices such that:
-
(a) for all disjoint subsets
 $S, T \subseteq V(G)$
with
$S, T \subseteq V(G)$
with
 $ |S|, |T| \ge \frac{M}{d^{1/3}}$
, we have and
$ |S|, |T| \ge \frac{M}{d^{1/3}}$
, we have and \begin{align*} \big|e_G(S, T) - \frac{d}{M}|S||T|\big| \le \frac{1}{2} \frac{d}{M}|S||T|; \end{align*}
\begin{align*} \big|e_G(S, T) - \frac{d}{M}|S||T|\big| \le \frac{1}{2} \frac{d}{M}|S||T|; \end{align*}
-
(b) the maximum degree of G is at most 2d.
Proof. Let
![]() $H \sim G(M, d/M),$
that is, H is a random graph on M vertices where every possible edge is present with probability
$H \sim G(M, d/M),$
that is, H is a random graph on M vertices where every possible edge is present with probability
![]() $d/M$
independently. Let G be the graph obtained from H by removing all edges incident to vertices of degree greater than 2d. Thus, G satisfies b) deterministically. The expected number of edges removed from H to obtain G is at most
$d/M$
independently. Let G be the graph obtained from H by removing all edges incident to vertices of degree greater than 2d. Thus, G satisfies b) deterministically. The expected number of edges removed from H to obtain G is at most
 \begin{align*} \sum_{\{u,v\}\subseteq V(H)} &\mathbb{P}[uv \in E(H)] \cdot \mathbb{P}[\max\{d_H(u), d_H(v)\} \gt 2d \, \vert \, uv \in E(H)]\\ &\le \binom{M}{2} \frac{d}{M} \cdot 2 \mathbb{P}[\mathrm{Bin}(M-2, d/M) \ge 2d] \le 2Md e^{-d/3} \lt M, \end{align*}
\begin{align*} \sum_{\{u,v\}\subseteq V(H)} &\mathbb{P}[uv \in E(H)] \cdot \mathbb{P}[\max\{d_H(u), d_H(v)\} \gt 2d \, \vert \, uv \in E(H)]\\ &\le \binom{M}{2} \frac{d}{M} \cdot 2 \mathbb{P}[\mathrm{Bin}(M-2, d/M) \ge 2d] \le 2Md e^{-d/3} \lt M, \end{align*}
where we used a standard Chernoff bound (e.g. [
Reference Janson and Rucinski18
, corollary 2·3]) and that
![]() $d \ge 10^9.$
By Markov’s inequality, with probability at least
$d \ge 10^9.$
By Markov’s inequality, with probability at least
![]() $3/4,$
we have
$3/4,$
we have
![]() $e(H) - e(G) \le 4M.$
For fixed disjoint sets of vertices S and T of size at least
$e(H) - e(G) \le 4M.$
For fixed disjoint sets of vertices S and T of size at least
![]() ${M}/{d^{1/3}}$
using the same form of the Chernoff bound, we have
${M}/{d^{1/3}}$
using the same form of the Chernoff bound, we have
Taking a union bound over all sets S, T as above, with probability at least
![]() $1 - 2^M \cdot 2^M \cdot 2e^{-20M} \gt 3/4$
, we have
$1 - 2^M \cdot 2^M \cdot 2e^{-20M} \gt 3/4$
, we have
By a union bound, with probability at least
![]() $1/2$
we have
$1/2$
we have
![]() $e(H) - e(G) \leq 4M$
and (2). Noting that
$e(H) - e(G) \leq 4M$
and (2). Noting that
![]() $4M \le ({1}/{4}) ({d}/{M}) \left({M}/{d^{1/3}} \right)^2,$
it follows that G satisfies (a) with probability at least
$4M \le ({1}/{4}) ({d}/{M}) \left({M}/{d^{1/3}} \right)^2,$
it follows that G satisfies (a) with probability at least
![]() $1/2,$
finishing the proof.
$1/2,$
finishing the proof.
Proof of Theorem 1·3. Fix
![]() $k \ge 3,$
let n be a large enough integer, set
$k \ge 3,$
let n be a large enough integer, set
![]() $d = 10^{20k}$
and let G be a graph on
$d = 10^{20k}$
and let G be a graph on
![]() $n_k = dn$
vertices satisfying (a) and (b) for d whose existence is given by Lemma 3·1. Let
$n_k = dn$
vertices satisfying (a) and (b) for d whose existence is given by Lemma 3·1. Let
![]() $H_k = H(G, k).$
We will show that there is no monochromatic copy of
$H_k = H(G, k).$
We will show that there is no monochromatic copy of
![]() $H_k$
in
$H_k$
in
![]() $\phi^{(k)}_n,$
where we remind the reader that
$\phi^{(k)}_n,$
where we remind the reader that
![]() $\phi^{(k)}_n$
is a colouring of the complete k-graph with vertex set
$\phi^{(k)}_n$
is a colouring of the complete k-graph with vertex set
![]() $\{0, \ldots, N_k(n)-1\},$
where
$\{0, \ldots, N_k(n)-1\},$
where
![]() $N_k(n) = \mathrm{tw}_k(n/2)$
. This would prove the theorem since, by construction,
$N_k(n) = \mathrm{tw}_k(n/2)$
. This would prove the theorem since, by construction,
![]() $e(H_k) \le n_k \cdot \#\{\text{paths of length } k-2 \text{ in } G\} \le n_k^2 (2d)^{k-2} = O(n^2)$
, while
$e(H_k) \le n_k \cdot \#\{\text{paths of length } k-2 \text{ in } G\} \le n_k^2 (2d)^{k-2} = O(n^2)$
, while
![]() $r_k(H_k;\, 4) \gt N_k(n) = \mathrm{tw}_k(n/2) = \mathrm{tw}_k(\Omega(\sqrt{e(H)})).$
We make repeated use of the following lemma.
$r_k(H_k;\, 4) \gt N_k(n) = \mathrm{tw}_k(n/2) = \mathrm{tw}_k(\Omega(\sqrt{e(H)})).$
We make repeated use of the following lemma.
Lemma 3·2. Let
![]() $U \subseteq V(G), |U| \ge n_k / (1000^{k-1})$
and let
$U \subseteq V(G), |U| \ge n_k / (1000^{k-1})$
and let
![]() $\ell \ge 3$
be an integer. Denote
$\ell \ge 3$
be an integer. Denote
![]() $H = H(G[U], \ell)$
and suppose there is a monochromatic copy of H in
$H = H(G[U], \ell)$
and suppose there is a monochromatic copy of H in
![]() $\phi^{(\ell)}_n.$
Then, there exists a set
$\phi^{(\ell)}_n.$
Then, there exists a set
![]() $U' \subseteq U$
such that
$U' \subseteq U$
such that
![]() $|U'| \ge |U| / 1000$
and there exists a monochromatic copy of the
$|U'| \ge |U| / 1000$
and there exists a monochromatic copy of the
![]() $(\ell-1)$
-uniform hypergraph
$(\ell-1)$
-uniform hypergraph
![]() $H' = H(G[U'], \ell-1)$
in
$H' = H(G[U'], \ell-1)$
in
![]() $\phi^{(\ell-1)}_n.$
$\phi^{(\ell-1)}_n.$
First, let us finish the proof of Theorem 1·3 given Lemma 3·2. By repeated uses of the lemma, it follows that there are subsets
![]() $V(G) = U_k \supseteq U_{k-1} \supseteq \ldots \supseteq U_2$
such that there is a monochromatic copy of
$V(G) = U_k \supseteq U_{k-1} \supseteq \ldots \supseteq U_2$
such that there is a monochromatic copy of
![]() $H(G[U_\ell], \ell)$
in
$H(G[U_\ell], \ell)$
in
![]() $\phi^{(\ell)}_n$
for all
$\phi^{(\ell)}_n$
for all
![]() $2 \le \ell \le k$
and
$2 \le \ell \le k$
and
![]() $|U_\ell| \ge |U_{\ell+1}| / 1000$
for all
$|U_\ell| \ge |U_{\ell+1}| / 1000$
for all
![]() $2 \le \ell \le k-1.$
Hence, we have
$2 \le \ell \le k-1.$
Hence, we have
![]() $|U_2| \ge n_k / 1000^k = 10^{20k} n / 1000^k \gt n$
and a monochromatic copy of
$|U_2| \ge n_k / 1000^k = 10^{20k} n / 1000^k \gt n$
and a monochromatic copy of
![]() $H(G[U_2], 2)$
in
$H(G[U_2], 2)$
in
![]() $\phi^{(2)}_n.$
Recall that by definition,
$\phi^{(2)}_n.$
Recall that by definition,
![]() $H(G[U_2], 2)$
is a clique on
$H(G[U_2], 2)$
is a clique on
![]() $|U_2| \gt n$
vertices, hence there is no monochromatic copy of
$|U_2| \gt n$
vertices, hence there is no monochromatic copy of
![]() $H(G[U_2], 2)$
in
$H(G[U_2], 2)$
in
![]() $\phi^{(2)}_n,$
a contradiction.
$\phi^{(2)}_n,$
a contradiction.
Proof of Lemma 3·2. Let
![]() $s = |U| = |V(H)|,$
let
$s = |U| = |V(H)|,$
let
![]() $X = \{x_1, \ldots, x_s\} \subseteq \{0, \ldots, N_\ell - 1\},$
where
$X = \{x_1, \ldots, x_s\} \subseteq \{0, \ldots, N_\ell - 1\},$
where
![]() $x_1 \lt \ldots \lt x_s$
, form a mononchromatic copy of H and denote by
$x_1 \lt \ldots \lt x_s$
, form a mononchromatic copy of H and denote by
![]() $\Psi \colon V(H) \rightarrow \{ 0, \ldots, N_\ell-1 \}$
the given monochromatic embedding.
$\Psi \colon V(H) \rightarrow \{ 0, \ldots, N_\ell-1 \}$
the given monochromatic embedding.
Claim 3·3. There is a set
![]() $Y = \{y_1, \ldots, y_t\} \subseteq X$
of size
$Y = \{y_1, \ldots, y_t\} \subseteq X$
of size
![]() $t \ge s / 200$
where
$t \ge s / 200$
where
![]() $y_1 \lt \ldots \lt y_t$
such that
$y_1 \lt \ldots \lt y_t$
such that
![]() $\delta(\{y_1, \ldots, y_t\})$
is a monotone sequence.
$\delta(\{y_1, \ldots, y_t\})$
is a monotone sequence.
First we finish the proof of the lemma given Claim 3·3. Let
![]() $Y \subseteq X$
with
$Y \subseteq X$
with
![]() $|Y| = t \ge s / 200$
be given by Claim 3·3 and assume that
$|Y| = t \ge s / 200$
be given by Claim 3·3 and assume that
![]() $\delta(Y)$
is increasing, the other case being analogous. We denote
$\delta(Y)$
is increasing, the other case being analogous. We denote
![]() $L = \{\Psi^{-1}(y_1), \ldots, \Psi^{-1}(y_{t/2})\} \subseteq U$
and let
$L = \{\Psi^{-1}(y_1), \ldots, \Psi^{-1}(y_{t/2})\} \subseteq U$
and let
![]() $U' \subseteq U$
be the set of all vertices
$U' \subseteq U$
be the set of all vertices
![]() $\Psi^{-1}(y_j)$
with
$\Psi^{-1}(y_j)$
with
![]() $t/2 \lt j \le t$
which in G have at least one neighbour in L. We have that
$t/2 \lt j \le t$
which in G have at least one neighbour in L. We have that
![]() $|U'| \ge t / 4,$
as otherwise there is a set of
$|U'| \ge t / 4,$
as otherwise there is a set of
![]() $t/4$
vertices with no edges toward L, contradicting (a) since
$t/4$
vertices with no edges toward L, contradicting (a) since
Let us verify that
![]() $\phi_n^{(\ell-1)}$
contains a monochromatic copy of
$\phi_n^{(\ell-1)}$
contains a monochromatic copy of
![]() $H' = H(G[U'], \ell-1).$
Let
$H' = H(G[U'], \ell-1).$
Let
![]() $z_1, z_2, \ldots, z_{t'}$
be the elements of
$z_1, z_2, \ldots, z_{t'}$
be the elements of
![]() $\Psi(U')$
in increasing order and recall that
$\Psi(U')$
in increasing order and recall that
![]() $y_i \lt z_j$
for all
$y_i \lt z_j$
for all
![]() $i \in [t/2], j \in [t'].$
Denote
$i \in [t/2], j \in [t'].$
Denote
![]() $a_1 = \delta(y_1, z_1)$
and
$a_1 = \delta(y_1, z_1)$
and
![]() $a_i = \delta(z_{i-1}, z_i)$
for
$a_i = \delta(z_{i-1}, z_i)$
for
![]() $2 \le i \le t'.$
We will show that the set
$2 \le i \le t'.$
We will show that the set
![]() $\mathcal{A} = \{a_1, \ldots, a_{t'}\}$
forms a monochromatic copy of H’ in
$\mathcal{A} = \{a_1, \ldots, a_{t'}\}$
forms a monochromatic copy of H’ in
![]() $\phi^{(\ell-1)}_n$
with the natural correspondence
$\phi^{(\ell-1)}_n$
with the natural correspondence
![]() $\Psi' \colon U' \rightarrow \mathcal{A}$
defined by
$\Psi' \colon U' \rightarrow \mathcal{A}$
defined by
![]() $\Psi'(\Psi^{-1}(z_i)) = a_i$
for all
$\Psi'(\Psi^{-1}(z_i)) = a_i$
for all
![]() $i \in [t']$
. We do so by showing that, for an edge
$i \in [t']$
. We do so by showing that, for an edge
![]() $e \in E(H'),$
the colour
$e \in E(H'),$
the colour
![]() $\phi^{(\ell-1)}_n(\Psi'(e))$
is inherited from the colour of
$\phi^{(\ell-1)}_n(\Psi'(e))$
is inherited from the colour of
![]() $\phi_n^{(\ell)}(\Psi(f))$
of some edge
$\phi_n^{(\ell)}(\Psi(f))$
of some edge
![]() $f \in E(H).$
$f \in E(H).$
By monotonicity of
![]() $\delta(\{y_1, \ldots, y_t\}),$
using (P3), we have
$\delta(\{y_1, \ldots, y_t\}),$
using (P3), we have
![]() $\delta(z_i, z_j) = a_j$
for any
$\delta(z_i, z_j) = a_j$
for any
![]() $1 \le i \lt j \le t'$
and
$1 \le i \lt j \le t'$
and
![]() $\delta(y_i, z_j) = a_j$
for any
$\delta(y_i, z_j) = a_j$
for any
![]() $i \in [t/2]$
and
$i \in [t/2]$
and
![]() $j \in [t'].$
Now, consider an arbitrary edge
$j \in [t'].$
Now, consider an arbitrary edge
![]() $e = \{\Psi^{-1}(z_{j_1}), \ldots, \Psi^{-1}(z_{j_{\ell-1}})\} \in E(H'),$
where
$e = \{\Psi^{-1}(z_{j_1}), \ldots, \Psi^{-1}(z_{j_{\ell-1}})\} \in E(H'),$
where
![]() $j_1 \lt j_2 \lt \ldots \lt j_{\ell-1}.$
By construction, some
$j_1 \lt j_2 \lt \ldots \lt j_{\ell-1}.$
By construction, some
![]() $\ell-2$
of these vertices form a path P’ in G. By definition of U’, any vertex on this path, in particular one of its endpoints, has a neighbour L. So, we can attach a vertex
$\ell-2$
of these vertices form a path P’ in G. By definition of U’, any vertex on this path, in particular one of its endpoints, has a neighbour L. So, we can attach a vertex
![]() $w \in L$
to one of the endpoints of P’ to obtain a path on
$w \in L$
to one of the endpoints of P’ to obtain a path on
![]() $\ell-1$
vertices in G. Hence,
$\ell-1$
vertices in G. Hence,
![]() $f = e \cup \{w\}$
is a set of
$f = e \cup \{w\}$
is a set of
![]() $\ell$
vertices, some
$\ell$
vertices, some
![]() $\ell-1$
of which form a path in G, implying that f is an edge of H. Note that
$\ell-1$
of which form a path in G, implying that f is an edge of H. Note that
![]() $\delta(\Psi(f)) = (a_{j_1}, a_{j_2}, \ldots, a_{j_{\ell-1}}),$
which is an increasing sequence. If
$\delta(\Psi(f)) = (a_{j_1}, a_{j_2}, \ldots, a_{j_{\ell-1}}),$
which is an increasing sequence. If
![]() $\ell \ge 4,$
we have
$\ell \ge 4,$
we have
![]() $\phi^{(\ell)}_n(\Psi(f)) = \phi^{(\ell-1)}_n(\delta(\Psi(f))) = \phi^{(\ell-1)}_n(\Psi'(e)).$
In the case
$\phi^{(\ell)}_n(\Psi(f)) = \phi^{(\ell-1)}_n(\delta(\Psi(f))) = \phi^{(\ell-1)}_n(\Psi'(e)).$
In the case
![]() $\ell = 3,$
if
$\ell = 3,$
if
![]() $\phi^{(2)}_n(\Psi'(e)) = \mathrm{red},$
then
$\phi^{(2)}_n(\Psi'(e)) = \mathrm{red},$
then
![]() $\phi^{(\ell)}_n = C_1$
, and if
$\phi^{(\ell)}_n = C_1$
, and if
![]() $\phi^{(2)}_n(\Psi'(e)) = \mathrm{blue}$
, then
$\phi^{(2)}_n(\Psi'(e)) = \mathrm{blue}$
, then
![]() $\phi^{(\ell)}_n = C_2$
. In either case, it follows that
$\phi^{(\ell)}_n = C_2$
. In either case, it follows that
![]() $\mathcal{A}$
forms a monochromatic copy of H’ in
$\mathcal{A}$
forms a monochromatic copy of H’ in
![]() $\phi_n^{(\ell-1)},$
as needed.
$\phi_n^{(\ell-1)},$
as needed.
Proof of Claim 3·3. Consider the following procedure. Start with
![]() $Z = X.$
At each step, let q be the largest integer such that not all elements of Z have the same bit at position q. Consider the partition
$Z = X.$
At each step, let q be the largest integer such that not all elements of Z have the same bit at position q. Consider the partition
![]() $Z = Z_0\, {\cdot\!\!\cup} Z_1,$
where
$Z = Z_0\, {\cdot\!\!\cup} Z_1,$
where
![]() $Z_p$
denotes the set of elements
$Z_p$
denotes the set of elements
![]() $z \in Z$
with
$z \in Z$
with
![]() $\mathrm{bit}(z, q) = p.$
Then, let Z be the larger of
$\mathrm{bit}(z, q) = p.$
Then, let Z be the larger of
![]() $Z_0, Z_1$
and continue the procedure. Eventually we reach a point where
$Z_0, Z_1$
and continue the procedure. Eventually we reach a point where
![]() $s/4 \le |Z| \le s/2,$
where the lower bound follows since
$s/4 \le |Z| \le s/2,$
where the lower bound follows since
![]() $|Z|$
drops by a factor of at most 2 in each step. Let
$|Z|$
drops by a factor of at most 2 in each step. Let
![]() $Z^*$
denote the final set Z and let
$Z^*$
denote the final set Z and let
![]() $q^*$
be the last value of q before this point. Then, for all distinct
$q^*$
be the last value of q before this point. Then, for all distinct
![]() $u, v \in Z^*, w \in X \setminus Z^*,$
we have
$u, v \in Z^*, w \in X \setminus Z^*,$
we have
![]() $\delta(u, v) \lt q^* \le \delta(u, w).$
Also, note that the elements of
$\delta(u, v) \lt q^* \le \delta(u, w).$
Also, note that the elements of
![]() $Z^*$
form an interval in the ordered set X. Indeed, at each step all elements in
$Z^*$
form an interval in the ordered set X. Indeed, at each step all elements in
![]() $Z_0$
are smaller than all elements of
$Z_0$
are smaller than all elements of
![]() $Z_1,$
since all elements in Z have the same bit on all positions larger than q. Hence, if Z was an interval in the ordered set X before step i, it is also an interval after step i. We shall assume that at least
$Z_1,$
since all elements in Z have the same bit on all positions larger than q. Hence, if Z was an interval in the ordered set X before step i, it is also an interval after step i. We shall assume that at least
![]() $s/4$
vertices in
$s/4$
vertices in
![]() $X \setminus Z^*$
are smaller than all elements of
$X \setminus Z^*$
are smaller than all elements of
![]() $Z^*,$
the other case being analogous. Let W denote the set of elements in
$Z^*,$
the other case being analogous. Let W denote the set of elements in
![]() $X \setminus Z^*$
smaller than every element of
$X \setminus Z^*$
smaller than every element of
![]() $Z^*.$
Now, let
$Z^*.$
Now, let
![]() $A = \Psi^{-1}(W) \subseteq U$
and let B be the set of all vertices in
$A = \Psi^{-1}(W) \subseteq U$
and let B be the set of all vertices in
![]() $\Psi^{-1}(Z^*) \subseteq U$
that have at least one neighbour of G in A. By a), it follows that
$\Psi^{-1}(Z^*) \subseteq U$
that have at least one neighbour of G in A. By a), it follows that
as otherwise we obtain a set of
![]() $s/8$
vertices with no edge towards A, which is a contradiction since
$s/8$
vertices with no edge towards A, which is a contradiction since
![]() $|A| \ge s/8 \ge n_k / 1000^k \gt n_k / d^{1/3}.$
$|A| \ge s/8 \ge n_k / 1000^k \gt n_k / d^{1/3}.$
Now, we analyse the set
![]() $S_1 := \Psi(B)$
using a similar procedure as above in steps
$S_1 := \Psi(B)$
using a similar procedure as above in steps
![]() $i=1, \ldots, h,$
where the number of steps, h, is to be determined by the procedure. At the beginning of step i, we have a set
$i=1, \ldots, h,$
where the number of steps, h, is to be determined by the procedure. At the beginning of step i, we have a set
![]() $S_i$
of size at least
$S_i$
of size at least
![]() $2.$
Let
$2.$
Let
![]() $q_i$
be the largest integer such that not all elements of
$q_i$
be the largest integer such that not all elements of
![]() $S_i$
have the same bit at position
$S_i$
have the same bit at position
![]() $q_i.$
Let
$q_i.$
Let
![]() $S_i = S^0_i\, {\cdot\!\!\cup} S^1_i,$
where
$S_i = S^0_i\, {\cdot\!\!\cup} S^1_i,$
where
![]() $S^p_i$
consists of the elements
$S^p_i$
consists of the elements
![]() $z \in S_i$
with
$z \in S_i$
with
![]() $\mathrm{bit}(z, q_i) = p.$
Let
$\mathrm{bit}(z, q_i) = p.$
Let
![]() $p_i \in \{0,1\}$
be such that
$p_i \in \{0,1\}$
be such that
![]() $|S^{p_i}_i| \ge |S^{1-p_i}_i|.$
Let
$|S^{p_i}_i| \ge |S^{1-p_i}_i|.$
Let
![]() $S_{i+1} = S^{p_i}_i.$
If
$S_{i+1} = S^{p_i}_i.$
If
![]() $|S_{i+1}| \lt s / 100,$
stop the process, otherwise continue to step
$|S_{i+1}| \lt s / 100,$
stop the process, otherwise continue to step
![]() $i+1.$
$i+1.$
Assume first that the procedure runs for at least
![]() $s / 100$
steps. Then, there is a set
$s / 100$
steps. Then, there is a set
![]() $I, |I| \ge s / 200$
and
$I, |I| \ge s / 200$
and
![]() $p \in \{0, 1\}$
such that for all
$p \in \{0, 1\}$
such that for all
![]() $i \in I,$
we have
$i \in I,$
we have
![]() $p_i = p$
and so
$p_i = p$
and so
![]() $S_{i+1} = S^p_i.$
For each
$S_{i+1} = S^p_i.$
For each
![]() $i \in I,$
let
$i \in I,$
let
![]() $y_i$
be an arbitrary element in
$y_i$
be an arbitrary element in
![]() $S^{1-p}_i$
and let
$S^{1-p}_i$
and let
![]() $Y = \{y_i, \vert \, i \in I\}.$
Using 3, we have
$Y = \{y_i, \vert \, i \in I\}.$
Using 3, we have
![]() $\delta(y_i, y_{i'}) = q_i$
for any
$\delta(y_i, y_{i'}) = q_i$
for any
![]() $i, i' \in I, i\lt i'.$
Moreover, the sequence
$i, i' \in I, i\lt i'.$
Moreover, the sequence
![]() $(y_i)_{i\in I}$
is increasing if
$(y_i)_{i\in I}$
is increasing if
![]() $p=1,$
and decreasing otherwise. Observing that
$p=1,$
and decreasing otherwise. Observing that
![]() $q_i \gt q_{i'}$
for
$q_i \gt q_{i'}$
for
![]() $i \lt i',$
it follows that Y is the desired set.
$i \lt i',$
it follows that Y is the desired set.
Therefore, we may assume that the above procedure runs for
![]() $h \lt s / 100$
steps and we will show that this leads to a contradiction. First, we require the following claim.
$h \lt s / 100$
steps and we will show that this leads to a contradiction. First, we require the following claim.
Claim 3·4. There exists
![]() $i \in [h]$
such that
$i \in [h]$
such that
![]() $|S^{1-p_i}_i| \ge 2$
and there is a path P of length
$|S^{1-p_i}_i| \ge 2$
and there is a path P of length
![]() $\ell-2$
in G with an endpoint
$\ell-2$
in G with an endpoint
![]() $v \in \Psi^{-1}(S^{1-p_i}_i)$
and having its remaining vertices in
$v \in \Psi^{-1}(S^{1-p_i}_i)$
and having its remaining vertices in
![]() $\Psi^{-1}(S^{p_i}_i).$
$\Psi^{-1}(S^{p_i}_i).$
Proof of Claim 3·4. Let
![]() $Q = \bigcup_{i \in [h], |S^{1-p_i}_i| \ge 2} \Psi^{-1}(S^{1-p_i}_i)$
and
$Q = \bigcup_{i \in [h], |S^{1-p_i}_i| \ge 2} \Psi^{-1}(S^{1-p_i}_i)$
and
![]() $T_0 = \Psi^{-1}(S_{h+1}),$
where
$T_0 = \Psi^{-1}(S_{h+1}),$
where
![]() $S_{h+1}$
is the final set after halting the procedure. Note that
$S_{h+1}$
is the final set after halting the procedure. Note that
![]() $|T_0| \ge s / 200.$
We repeatedly remove from
$|T_0| \ge s / 200.$
We repeatedly remove from
![]() $T_0$
vertices that have fewer than
$T_0$
vertices that have fewer than
![]() $\ell$
neighbours in G in the current set
$\ell$
neighbours in G in the current set
![]() $T_0.$
Let T denote the final set after these deletions. Then,
$T_0.$
Let T denote the final set after these deletions. Then,
![]() $|T| \ge s / 400 \ge n_k / (1000)^k,$
as otherwise at the point when we removed half of the vertices, we have two sets of size
$|T| \ge s / 400 \ge n_k / (1000)^k,$
as otherwise at the point when we removed half of the vertices, we have two sets of size
![]() $q \ge s/400 \ge n / d^{1/3}$
with at most
$q \ge s/400 \ge n / d^{1/3}$
with at most
![]() $\ell q$
edges between them, contradicting that G satisfies a). Using a) again, it follows that there is an edge vu with
$\ell q$
edges between them, contradicting that G satisfies a). Using a) again, it follows that there is an edge vu with
![]() $v \in Q$
and
$v \in Q$
and
![]() $u \in T$
since
$u \in T$
since
![]() $|Q| \ge |S_1| - |S_{h+1}| - h \ge s/8 - s/100 - s/100 \gt s/16 \gt n / d^{1/3}.$
Since G[T] has minimum degree at least
$|Q| \ge |S_1| - |S_{h+1}| - h \ge s/8 - s/100 - s/100 \gt s/16 \gt n / d^{1/3}.$
Since G[T] has minimum degree at least
![]() $\ell,$
we can extend this edge to a path of length
$\ell,$
we can extend this edge to a path of length
![]() $\ell-2$
using only vertices in T. Let i be the index such that
$\ell-2$
using only vertices in T. Let i be the index such that
![]() $v \in \Psi^{-1}(S^{1-p_i}_i).$
Note that
$v \in \Psi^{-1}(S^{1-p_i}_i).$
Note that
![]() $S_j^{p_j} \subseteq S_{j-1}^{p_{j-1}}$
for all
$S_j^{p_j} \subseteq S_{j-1}^{p_{j-1}}$
for all
![]() $2 \le j \le h$
and
$2 \le j \le h$
and
![]() $T \subseteq \Psi^{-1}(S_{h+1}) = \Psi^{-1}(S_h^{p_h}).$
It follows that
$T \subseteq \Psi^{-1}(S_{h+1}) = \Psi^{-1}(S_h^{p_h}).$
It follows that
![]() $T \subseteq \Psi^{-1}(S_i^{p_i}),$
so the abovementioned path indeed has all vertices but the first in
$T \subseteq \Psi^{-1}(S_i^{p_i}),$
so the abovementioned path indeed has all vertices but the first in
![]() $\Psi^{-1}(S_i^{p_i}).$
By definition of Q, we also have
$\Psi^{-1}(S_i^{p_i}).$
By definition of Q, we also have
![]() $|S^{1-p_i}_i| \ge 2,$
as needed.
$|S^{1-p_i}_i| \ge 2,$
as needed.
Let i, v, P be given by Claim 3·4 and let w be an arbitrary vertex in
![]() $\Psi^{-1}(S^{1-p_i}_i)$
distinct from v. We will show that then
$\Psi^{-1}(S^{1-p_i}_i)$
distinct from v. We will show that then
![]() $\Psi$
is not a valid embedding, that is, we will find two edges of H whose images get different colours. Let
$\Psi$
is not a valid embedding, that is, we will find two edges of H whose images get different colours. Let
![]() $e = P \cup \{w\} \in E(H).$
We now find another edge
$e = P \cup \{w\} \in E(H).$
We now find another edge
![]() $f \in E(H)$
whose image under
$f \in E(H)$
whose image under
![]() $\Psi$
gets a different colour than e.
$\Psi$
gets a different colour than e.
Consider first the case
![]() $\ell = 3.$
Then, the path P consists of a single edge vu for some
$\ell = 3.$
Then, the path P consists of a single edge vu for some
![]() $u \in \Psi^{-1}(S^{p_i}_i).$
Let u’ be an arbitrary vertex in
$u \in \Psi^{-1}(S^{p_i}_i).$
Let u’ be an arbitrary vertex in
![]() $S^{p_i}_i$
distinct form u, which clearly exists since
$S^{p_i}_i$
distinct form u, which clearly exists since
![]() $|S^{p_i}_i| \ge |S^{1-p_i}_i| \ge 2,$
and let
$|S^{p_i}_i| \ge |S^{1-p_i}_i| \ge 2,$
and let
![]() $f = \{ v,u,u' \}.$
Note that, by construction,
$f = \{ v,u,u' \}.$
Note that, by construction,
![]() $\delta(u, u'), \delta(v, w) \lt q_i,$
while
$\delta(u, u'), \delta(v, w) \lt q_i,$
while
![]() $\delta(z, z') = q_i$
for any
$\delta(z, z') = q_i$
for any
![]() $(z, z') \in S_i^{p_i} \times S_i^{1-p_i}$
. It follows that if
$(z, z') \in S_i^{p_i} \times S_i^{1-p_i}$
. It follows that if
![]() $p_i = 1,$
then
$p_i = 1,$
then
![]() $\delta(\Psi(e))$
is increasing, while
$\delta(\Psi(e))$
is increasing, while
![]() $\delta(\Psi(f))$
is decreasing whereas if
$\delta(\Psi(f))$
is decreasing whereas if
![]() $p_i = 0,$
then
$p_i = 0,$
then
![]() $\delta(\Psi(e))$
is decreasing, while
$\delta(\Psi(e))$
is decreasing, while
![]() $\delta(\Psi(f))$
is increasing. In either case,
$\delta(\Psi(f))$
is increasing. In either case,
![]() $\Psi(e)$
and
$\Psi(e)$
and
![]() $\Psi(f)$
are coloured differently by
$\Psi(f)$
are coloured differently by
![]() $\phi_n^{(3)}$
, as claimed.
$\phi_n^{(3)}$
, as claimed.
Now, consider
![]() $\ell \ge 4$
and see Figure 1 for an illustration. Recall that
$\ell \ge 4$
and see Figure 1 for an illustration. Recall that
![]() $e = P \cup \{w\},$
so e has exactly two vertices in
$e = P \cup \{w\},$
so e has exactly two vertices in
![]() $\Psi^{-1}(S^{1-p_i}_i)$
and the other vertices are in
$\Psi^{-1}(S^{1-p_i}_i)$
and the other vertices are in
![]() $\Psi^{-1}(S^{p_i}_i).$
Let
$\Psi^{-1}(S^{p_i}_i).$
Let
![]() $\delta = (\delta_1, \ldots, \delta_{\ell-1}) = \delta(\Psi(e)).$
Then,
$\delta = (\delta_1, \ldots, \delta_{\ell-1}) = \delta(\Psi(e)).$
Then,
![]() $\mathrm{arg\,max}_{j \in [\ell-1]} \delta_j = 2$
if
$\mathrm{arg\,max}_{j \in [\ell-1]} \delta_j = 2$
if
![]() $p_i = 1$
and
$p_i = 1$
and
![]() $\mathrm{arg\,max}_{j \in [\ell-1]} \delta_j = k-2$
if
$\mathrm{arg\,max}_{j \in [\ell-1]} \delta_j = k-2$
if
![]() $p_i = 0.$
In either case,
$p_i = 0.$
In either case,
![]() $\phi_n^{(\ell)}(\Psi(e)) = C_2.$
We will find an edge
$\phi_n^{(\ell)}(\Psi(e)) = C_2.$
We will find an edge
![]() $f \in E(H)$
whose image receives colour
$f \in E(H)$
whose image receives colour
![]() $C_1$
. Recall that every vertex in
$C_1$
. Recall that every vertex in
![]() $B \supseteq \Psi^{-1}(S^{1-p_i}_i)$
has a neighbour in A. Hence, we can extend P by attaching a vertex
$B \supseteq \Psi^{-1}(S^{1-p_i}_i)$
has a neighbour in A. Hence, we can extend P by attaching a vertex
![]() $a \in A$
to v and then remove its last vertex (which is in
$a \in A$
to v and then remove its last vertex (which is in
![]() $\Psi^{-1}(S_i^{p_i})$
) to obtain a path P’ of length
$\Psi^{-1}(S_i^{p_i})$
) to obtain a path P’ of length
![]() $\ell-2$
whose first vertex is
$\ell-2$
whose first vertex is
![]() $a \in A,$
the second vertex is
$a \in A,$
the second vertex is
![]() $v \in \Psi^{-1}(S^{1-p_i}_i)$
and the remaining vertices are in
$v \in \Psi^{-1}(S^{1-p_i}_i)$
and the remaining vertices are in
![]() $\Psi^{-1}(S^{p_i}_i).$
$\Psi^{-1}(S^{p_i}_i).$

Figure 1. The two chosen edges in the case
![]() $\ell=5$
. Sets
$\ell=5$
. Sets
![]() $\Psi(A), \Psi(B), S_i^0$
and
$\Psi(A), \Psi(B), S_i^0$
and
![]() $S_i^1$
are depicted by ovals. The vertices appearing in both e and f are depicted by points, the vertices in
$S_i^1$
are depicted by ovals. The vertices appearing in both e and f are depicted by points, the vertices in
![]() $e \setminus f$
by squares and the vertices in
$e \setminus f$
by squares and the vertices in
![]() $f \setminus e$
by crosses. The vertices further to the right are mapped by
$f \setminus e$
by crosses. The vertices further to the right are mapped by
![]() $\Psi$
to larger values. The black triangles correspond to the value of
$\Psi$
to larger values. The black triangles correspond to the value of
![]() $\delta$
of consecutive vertices, where higher triangles represent larger bit positions. The curves connecting the points and crosses represent edges between the corresponding vertices in G.
$\delta$
of consecutive vertices, where higher triangles represent larger bit positions. The curves connecting the points and crosses represent edges between the corresponding vertices in G.
If
![]() $p_i = 1,$
then let
$p_i = 1,$
then let
![]() $f = V(P') \cup \{w\} \in E(H).$
Consider
$f = V(P') \cup \{w\} \in E(H).$
Consider
![]() $\delta = (\delta_1, \ldots, \delta_{\ell-1}) = \delta(\Psi(f)).$
Since f has one vertex in A and the rest are in B, it follows that
$\delta = (\delta_1, \ldots, \delta_{\ell-1}) = \delta(\Psi(f)).$
Since f has one vertex in A and the rest are in B, it follows that
![]() $\mathrm{arg\,max}_{j \in [\ell-1]} \delta_j = 1.$
Additionally,
$\mathrm{arg\,max}_{j \in [\ell-1]} \delta_j = 1.$
Additionally,
![]() $\Psi(f)$
has two vertices in
$\Psi(f)$
has two vertices in
![]() $S_i^0$
and the remaining ones are in
$S_i^0$
and the remaining ones are in
![]() $S_i^1.$
Hence,
$S_i^1.$
Hence,
![]() $\delta_2 \lt q_i = \delta_3,$
so
$\delta_2 \lt q_i = \delta_3,$
so
![]() $\delta$
is not monotone, implying that
$\delta$
is not monotone, implying that
![]() $\phi_n^{(\ell)}(\Psi(f)) = C_1.$
$\phi_n^{(\ell)}(\Psi(f)) = C_1.$
If
![]() $p_i = 0,$
then let u be an arbitrary vertex in
$p_i = 0,$
then let u be an arbitrary vertex in
![]() $\Psi^{-1}(S^0_i) \setminus V(P'),$
which exists since
$\Psi^{-1}(S^0_i) \setminus V(P'),$
which exists since
![]() $|S^0_i| \ge s / 100 \ge \ell.$
Let
$|S^0_i| \ge s / 100 \ge \ell.$
Let
![]() $f = V(P') \cup \{ u\} \in E(H)$
and denote
$f = V(P') \cup \{ u\} \in E(H)$
and denote
![]() $\delta = (\delta_1, \ldots, \delta_{\ell-1}) = \delta(\Psi(f)).$
As before, we have
$\delta = (\delta_1, \ldots, \delta_{\ell-1}) = \delta(\Psi(f)).$
As before, we have
![]() $\mathrm{arg\,max}_{j \in [\ell-1]} \delta_j = 1.$
The largest element of
$\mathrm{arg\,max}_{j \in [\ell-1]} \delta_j = 1.$
The largest element of
![]() $\Psi(f)$
is
$\Psi(f)$
is
![]() $\Psi(v) \in S^1_i,$
while the second and third largest elements are in
$\Psi(v) \in S^1_i,$
while the second and third largest elements are in
![]() $S^0_i.$
Hence,
$S^0_i.$
Hence,
![]() $\delta_{\ell-1} \gt \delta_{\ell-2} \lt \delta_1,$
which gives
$\delta_{\ell-1} \gt \delta_{\ell-2} \lt \delta_1,$
which gives
![]() $\phi_n^{(\ell)}(\Psi(f)) = C_1.$
$\phi_n^{(\ell)}(\Psi(f)) = C_1.$
4. Concluding remarks
There are many remaining interesting problems on Ramsey numbers of hypergraphs. Maybe most notably, while for four or more colours we have lower bound constructions on hypergraph Ramsey numbers for cliques and certain other hypergraphs essentially matching the upper bounds, the bounds are still far apart for two and three colours. It would be interesting to close the gap in these cases.
Another well-studied question is to bound the q-colour Ramsey number of bounded degree k-uniform hypergraphs on n vertices. It is known that there is a constant
![]() $c = c(k, q, \Delta)$
such that
$c = c(k, q, \Delta)$
such that
![]() $r(H;q) \le c(k, q, \Delta) n$
for any n-vertex k-uniform hypergraph H with maximum degree at most
$r(H;q) \le c(k, q, \Delta) n$
for any n-vertex k-uniform hypergraph H with maximum degree at most
![]() $\Delta$
and the main question is to understand the value of the factor
$\Delta$
and the main question is to understand the value of the factor
![]() $c(k, q, \Delta)$
as a function of the maximum degree. In the graph case with two colours, the best lower bound is
$c(k, q, \Delta)$
as a function of the maximum degree. In the graph case with two colours, the best lower bound is
![]() $c(2, 2, \Delta) = 2^{\Omega(\Delta)}$
due to Graham, Rödl and Ruciński [
Reference Graham, Rődl and Ruciński16
], while the best upper bound is
$c(2, 2, \Delta) = 2^{\Omega(\Delta)}$
due to Graham, Rödl and Ruciński [
Reference Graham, Rődl and Ruciński16
], while the best upper bound is
![]() $c(2, 2, \Delta) \lt 2^{O(\Delta \log \Delta)}$
due to Conlon, Fox and Sudakov [
Reference Conlon, Fox and Sudakov6
]. For more than two colours the known upper bound proved in [
Reference Fox and Sudakov15
] is much worse and is of the form
$c(2, 2, \Delta) \lt 2^{O(\Delta \log \Delta)}$
due to Conlon, Fox and Sudakov [
Reference Conlon, Fox and Sudakov6
]. For more than two colours the known upper bound proved in [
Reference Fox and Sudakov15
] is much worse and is of the form
![]() $c(2, q, \Delta) \le 2^{c_q \Delta^2}$
. Turning to hypergraphs, [
Reference Conlon, Fox and Sudakov4
] showed
$c(2, q, \Delta) \le 2^{c_q \Delta^2}$
. Turning to hypergraphs, [
Reference Conlon, Fox and Sudakov4
] showed
![]() $c(3, q, \Delta) \le \mathrm{tw}_3(c' \Delta \log \Delta)$
and
$c(3, q, \Delta) \le \mathrm{tw}_3(c' \Delta \log \Delta)$
and
![]() $c(k, q, \Delta) \le \mathrm{tw}_k(c' \Delta)$
for
$c(k, q, \Delta) \le \mathrm{tw}_k(c' \Delta)$
for
![]() $k \ge 4,$
where c’ is a constant depending on k and q. It is an outstanding open problem to show that
$k \ge 4,$
where c’ is a constant depending on k and q. It is an outstanding open problem to show that
![]() $c(k, q, \Delta) \le \mathrm{tw}_k(c' \Delta)$
also when
$c(k, q, \Delta) \le \mathrm{tw}_k(c' \Delta)$
also when
![]() $k=2, 3$
, i.e., for graphs and 3-uniform hypergraphs. Such a result would provide a different proof of the upper bound for 3-uniform hypergraphs, presented in this paper. Conlon, Fox and Sudakov [
Reference Conlon, Fox and Sudakov4
] also constructed, for any positive integer
$k=2, 3$
, i.e., for graphs and 3-uniform hypergraphs. Such a result would provide a different proof of the upper bound for 3-uniform hypergraphs, presented in this paper. Conlon, Fox and Sudakov [
Reference Conlon, Fox and Sudakov4
] also constructed, for any positive integer
![]() $\Delta$
, a 3-uniform n-vertex hypergraph H with maximum degree
$\Delta$
, a 3-uniform n-vertex hypergraph H with maximum degree
![]() $\Delta$
and
$\Delta$
and
![]() $r(H; 4) \ge \mathrm{tw}_3(c' \Delta) n$
for some absolute constant
$r(H; 4) \ge \mathrm{tw}_3(c' \Delta) n$
for some absolute constant
![]() $c'.$
The hypergraph we constructed in the proof of Theorem 1·3 has n vertices, maximum degree
$c'.$
The hypergraph we constructed in the proof of Theorem 1·3 has n vertices, maximum degree
![]() $\Delta \le c_k n$
and 4-colour Ramsey number at least
$\Delta \le c_k n$
and 4-colour Ramsey number at least
![]() $\mathrm{tw}_k(c'_k n) n,$
so it can be viewed as a generalization of the aforementioned result to larger uniformities. These results show that in general, it is necessary to have
$\mathrm{tw}_k(c'_k n) n,$
so it can be viewed as a generalization of the aforementioned result to larger uniformities. These results show that in general, it is necessary to have
![]() $c(k, 4, \Delta) \ge \mathrm{tw}_k(c'_k \Delta).$
However, both our construction and that in [
Reference Conlon, Fox and Sudakov4
] have
$c(k, 4, \Delta) \ge \mathrm{tw}_k(c'_k \Delta).$
However, both our construction and that in [
Reference Conlon, Fox and Sudakov4
] have
![]() $\Delta = \Theta(n)$
and it would be interesting to find a construction which works for any
$\Delta = \Theta(n)$
and it would be interesting to find a construction which works for any
![]() $\Delta$
and sufficiently large n similar to the abovementioned lower bound of Graham, Rödl and Ruciński which works for any
$\Delta$
and sufficiently large n similar to the abovementioned lower bound of Graham, Rödl and Ruciński which works for any
![]() $\Delta$
and
$\Delta$
and
![]() $n \gg \Delta.$
$n \gg \Delta.$
Finally, we think it would be interesting to study the following generalization of Ramsey numbers. For a k-uniform hypergraph H and positive integers N and q with
![]() $q \leq e(H)$
, let f(N,H,q) be the minimum number r such that in every r-colouring of the edges of
$q \leq e(H)$
, let f(N,H,q) be the minimum number r such that in every r-colouring of the edges of
![]() $K_N^{(k)}$
there is a copy of H receiving fewer than q colours. The case
$K_N^{(k)}$
there is a copy of H receiving fewer than q colours. The case
![]() $q=2$
is just the inverse (as a function of the number of colours) of the Ramsey number of H. The case H is a clique was introduced by Erdős and Gyarfas and has been well-studied (see for example [
Reference Conlon, Fox and Sudakov5
]).
$q=2$
is just the inverse (as a function of the number of colours) of the Ramsey number of H. The case H is a clique was introduced by Erdős and Gyarfas and has been well-studied (see for example [
Reference Conlon, Fox and Sudakov5
]).