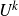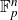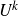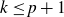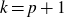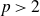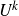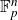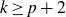1. Introduction
The inverse theorem for the Gowers
![]() $U^k$
-norm states that a bounded function
$U^k$
-norm states that a bounded function
![]() $f\colon G\to\mathbb C$
has large
$f\colon G\to\mathbb C$
has large
![]() $U^k$
-norm if and only if f correlates with a certain structured object. When
$U^k$
-norm if and only if f correlates with a certain structured object. When
![]() $G=\mathbb Z/N\mathbb Z$
, these structured objects are quite complicated and need the theory of nilsequences to describe. When
$G=\mathbb Z/N\mathbb Z$
, these structured objects are quite complicated and need the theory of nilsequences to describe. When
![]() $G=\mathbb F_p^n$
, the situation is somewhat simpler. When
$G=\mathbb F_p^n$
, the situation is somewhat simpler. When
![]() $p \geq k$
, a bounded function
$p \geq k$
, a bounded function
![]() $f\colon\mathbb F_p^n\to\mathbb C$
has large
$f\colon\mathbb F_p^n\to\mathbb C$
has large
![]() $U^k$
-norm if and only if f has non-negligible correlation with a polynomial phase function, i.e.,
$U^k$
-norm if and only if f has non-negligible correlation with a polynomial phase function, i.e.,
![]() $e^{2\pi i P(x)/p}$
where
$e^{2\pi i P(x)/p}$
where
![]() $P\colon\mathbb F_p^n\to\mathbb F_p$
is a polynomial of degree at most
$P\colon\mathbb F_p^n\to\mathbb F_p$
is a polynomial of degree at most
![]() $k-1$
.
$k-1$
.
The situation when p is small compared to k is more delicate. Green and Tao [Reference B. and T.3] and independently Lovett, Meshulam and Samorodnitsky [Reference S., R. and A.4] showed that the corresponding conjecture is false for
![]() $k=4$
and
$k=4$
and
![]() $p=2$
. In other words, there exist bounded functions
$p=2$
. In other words, there exist bounded functions
![]() $f\colon\mathbb F_2^n\to\mathbb C$
with large
$f\colon\mathbb F_2^n\to\mathbb C$
with large
![]() $U^4$
-norm but with correlation
$U^4$
-norm but with correlation
![]() $o_{n\to\infty}(1)$
with every cubic phase function. Tao and Ziegler [Reference T. and T.7] clarified this situation by proving that for all k and p, a bounded function
$o_{n\to\infty}(1)$
with every cubic phase function. Tao and Ziegler [Reference T. and T.7] clarified this situation by proving that for all k and p, a bounded function
![]() $f\colon\mathbb F_p^n\to\mathbb C$
has large
$f\colon\mathbb F_p^n\to\mathbb C$
has large
![]() $U^k$
-norm if and only if f has non-negligible correlation with a non-classical polynomial phase function, i.e.,
$U^k$
-norm if and only if f has non-negligible correlation with a non-classical polynomial phase function, i.e.,
![]() $e^{2\pi i P(x)}$
where
$e^{2\pi i P(x)}$
where
![]() $P\colon\mathbb F_p^n\to\mathbb R/\mathbb Z$
is a non-classical polynomial of degree at most
$P\colon\mathbb F_p^n\to\mathbb R/\mathbb Z$
is a non-classical polynomial of degree at most
![]() $k-1$
. (See Section 2 for the relevant definitions.)
$k-1$
. (See Section 2 for the relevant definitions.)
A natural question which remains from the above discussion is to determine for which pairs p, k does the
![]() $U^k$
-inverse theorem over
$U^k$
-inverse theorem over
![]() $\mathbb F_p^n$
hold with classical polynomials. In the positive direction, it is known due to Samorodnitsky [Reference A.5] that the
$\mathbb F_p^n$
hold with classical polynomials. In the positive direction, it is known due to Samorodnitsky [Reference A.5] that the
![]() $U^3$
-inverse theorem over
$U^3$
-inverse theorem over
![]() $\mathbb F_2^n$
holds with classical polynomials. In the negative direction, Lovett, Meshulam and Samorodnitsky [Reference S., R. and A.4] proved that the
$\mathbb F_2^n$
holds with classical polynomials. In the negative direction, Lovett, Meshulam and Samorodnitsky [Reference S., R. and A.4] proved that the
![]() $U^{p^\ell}$
-inverse theorem over
$U^{p^\ell}$
-inverse theorem over
![]() $\mathbb F_p^n$
requires non-classical polynomials for all p and
$\mathbb F_p^n$
requires non-classical polynomials for all p and
![]() $\ell\geq 2$
. (A curious feature of this problem is that it is not monotone in k, e.g., the Lovett–Meshulam–Samorodnitsky result does not imply that non-classical polynomials are necessary in the
$\ell\geq 2$
. (A curious feature of this problem is that it is not monotone in k, e.g., the Lovett–Meshulam–Samorodnitsky result does not imply that non-classical polynomials are necessary in the
![]() $U^k$
-inverse theorem for all
$U^k$
-inverse theorem for all
![]() $k\geq p^2$
.)
$k\geq p^2$
.)
In this paper we completely characterize when classical polynomials suffice in the statement of the inverse theorem. We first prove the inverse theorem for the Gowers
![]() $U^{p+1}$
-norm with classical polynomials. This result is proved via a short deduction from the usual inverse theorem for the
$U^{p+1}$
-norm with classical polynomials. This result is proved via a short deduction from the usual inverse theorem for the
![]() $U^{p+1}$
-norm that involves non-classical polynomials.Footnote 1
$U^{p+1}$
-norm that involves non-classical polynomials.Footnote 1
Theorem 1·1 Fix a prime p and
![]() $\delta>0$
. There exists
$\delta>0$
. There exists
![]() $\epsilon>0$
such that the following holds. Let V be a finite-dimensional
$\epsilon>0$
such that the following holds. Let V be a finite-dimensional
![]() $\mathbb{F}_p$
-vector space. Given a function
$\mathbb{F}_p$
-vector space. Given a function
![]() $f\colon V\to\mathbb{C}$
satisfying
$f\colon V\to\mathbb{C}$
satisfying
![]() $\|f\|_\infty\le1$
and
$\|f\|_\infty\le1$
and
![]() $\|f\|_{U^{p+1}}>\delta$
, there exists a classical polynomial
$\|f\|_{U^{p+1}}>\delta$
, there exists a classical polynomial
![]() $P\in\operatorname{\rm{Poly}}_{\leqslant p}(V\to\mathbb{F}_p)$
such that
$P\in\operatorname{\rm{Poly}}_{\leqslant p}(V\to\mathbb{F}_p)$
such that
Second, we give an example showing that non-classical polynomials are necessary in the
![]() $U^k$
-inverse theorem for all
$U^k$
-inverse theorem for all
![]() $k\geq p+2$
.
$k\geq p+2$
.
Theorem 1·2 Fix a prime p and an integer
![]() $k\geq p+2$
. For all n, there exists a function
$k\geq p+2$
. For all n, there exists a function
![]() $f\colon\mathbb F_p^n\to \mathbb C$
satisfying
$f\colon\mathbb F_p^n\to \mathbb C$
satisfying
![]() $\|f\|_{\infty}\leq 1$
and
$\|f\|_{\infty}\leq 1$
and
![]() $\|f\|_{U^k}=1$
such that for all (classical) polynomials
$\|f\|_{U^k}=1$
such that for all (classical) polynomials
![]() $P\in\operatorname{\rm{Poly}}_{\leqslant k-1}(\mathbb F_p^n\to\mathbb F_p)$
,
$P\in\operatorname{\rm{Poly}}_{\leqslant k-1}(\mathbb F_p^n\to\mathbb F_p)$
,
Our example is fairly simple to write down. For
![]() $k\geq p+2$
, we write
$k\geq p+2$
, we write
![]() $k-1=r+(p-1)\ell$
where
$k-1=r+(p-1)\ell$
where
![]() $\ell\geq 1$
and
$\ell\geq 1$
and
![]() $0<r<p$
. Then our function is
$0<r<p$
. Then our function is
(where
![]() $|\cdot|\colon\mathbb F_p\to\{0,\ldots,p-1\}$
is the standard map). Note that this function f is a non-classical polynomial phase function of degree
$|\cdot|\colon\mathbb F_p\to\{0,\ldots,p-1\}$
is the standard map). Note that this function f is a non-classical polynomial phase function of degree
![]() $k-1$
, so the content of this result is that it does not correlate with any classical polynomial phase functions of the same degree.
$k-1$
, so the content of this result is that it does not correlate with any classical polynomial phase functions of the same degree.
The o(1) correlation in Theorem 1·2 is fairly bad – the inverse of many iterated logarithms. This is due to our use of a Ramsey-theoretic argument inspired by an argument of Alon and Beigel. (A similar argument appeared in the previous works [Reference B. and T.3,Reference S., R. and A.4].) We conjecture that this bound on the correlation can be improved.
Conjecture 1·3 Fix a prime p and an integer
![]() $k\geq p+2$
. For all n there exist
$k\geq p+2$
. For all n there exist
![]() $f\colon\mathbb F_p^n\to\mathbb C$
satisfying
$f\colon\mathbb F_p^n\to\mathbb C$
satisfying
![]() $\|f\|_{\infty}\leq 1$
and
$\|f\|_{\infty}\leq 1$
and
![]() $\|f\|_{U^k}\geq c_{p,k}>0$
such that for all (classical) polynomials
$\|f\|_{U^k}\geq c_{p,k}>0$
such that for all (classical) polynomials
![]() $P\in\operatorname{\rm{Poly}}_{\leqslant k-1}(\mathbb F_p^n\to\mathbb F_p)$
,
$P\in\operatorname{\rm{Poly}}_{\leqslant k-1}(\mathbb F_p^n\to\mathbb F_p)$
,
In fact, we believe that this conjecture is true with the same functions that we use to prove Theorem 1·2.
Structure of the paper:
in Section 2 we give the definition of the Gowers
![]() $U^k$
-norm and of non-classical polynomials. In Section 3 we prove Theorem 1·1. We prove Theorem 1·2 in the remainder of the paper. Section 4 develops the symmetrization tool that we use and Section 5 gives the full proof.
$U^k$
-norm and of non-classical polynomials. In Section 3 we prove Theorem 1·1. We prove Theorem 1·2 in the remainder of the paper. Section 4 develops the symmetrization tool that we use and Section 5 gives the full proof.
Notation:
we use
![]() $|\cdot|$
for the standard map
$|\cdot|$
for the standard map
![]() $\mathbb{F}_p\to\{0,\ldots,p-1\}$
. We often treat
$\mathbb{F}_p\to\{0,\ldots,p-1\}$
. We often treat
![]() $\mathbb F_p$
as an additive subgroup of
$\mathbb F_p$
as an additive subgroup of
![]() $\mathbb R/\mathbb Z$
via the map
$\mathbb R/\mathbb Z$
via the map
![]() $x\mapsto |x|/p$
and, by some abuse of notation, freely switch between these two viewpoints. We use
$x\mapsto |x|/p$
and, by some abuse of notation, freely switch between these two viewpoints. We use
![]() $e\colon\mathbb R/\mathbb Z\to\mathbb C$
for the function
$e\colon\mathbb R/\mathbb Z\to\mathbb C$
for the function
![]() $e(x)=e^{2\pi i x}$
and
$e(x)=e^{2\pi i x}$
and
![]() $e_p\colon\mathbb F_p\to\mathbb C$
for the function
$e_p\colon\mathbb F_p\to\mathbb C$
for the function
![]() $e_p(x)=e^{2\pi i |x|/p}$
.
$e_p(x)=e^{2\pi i |x|/p}$
.
2. Background on non-classical polynomials
Definition 2·1 Fix a prime p, a finite-dimensional
![]() $\mathbb{F}_p$
-vector space V, and an abelian group G. Given a function
$\mathbb{F}_p$
-vector space V, and an abelian group G. Given a function
![]() $f\colon V\to G$
and a shift
$f\colon V\to G$
and a shift
![]() $h\in V$
, define the additive derivative
$h\in V$
, define the additive derivative
![]() $\Delta_hf\colon V\to G$
by
$\Delta_hf\colon V\to G$
by
Given a function
![]() $f\colon V\to\mathbb{C}$
and a shift
$f\colon V\to\mathbb{C}$
and a shift
![]() $h\in V$
, define the multiplicative derivative
$h\in V$
, define the multiplicative derivative
![]() $\partial_hf\colon V\to\mathbb{C}$
by
$\partial_hf\colon V\to\mathbb{C}$
by
Definition 2·2 Fix a prime p and a finite-dimensional
![]() $\mathbb{F}_p$
-vector space V. Given a function
$\mathbb{F}_p$
-vector space V. Given a function
![]() $f\colon V\to\mathbb{C}$
and
$f\colon V\to\mathbb{C}$
and
![]() $d\ge 1$
, the Gowers uniformity norm
$d\ge 1$
, the Gowers uniformity norm
![]() $\|f\|_{U^d}$
is defined by
$\|f\|_{U^d}$
is defined by
See [Reference T. and T.7, lemma B.1] for some basic facts about the Gowers uniformity norms.
Definition 2·3 Fix a prime p and a non-negative integer
![]() $d\ge0$
. Let V be a finite-dimensional
$d\ge0$
. Let V be a finite-dimensional
![]() $\mathbb{F}_p$
-vector space. A non-classical polynomial of degree at most d is a map
$\mathbb{F}_p$
-vector space. A non-classical polynomial of degree at most d is a map
![]() $P\colon V\to\mathbb{R}/\mathbb{Z}$
that satisfies
$P\colon V\to\mathbb{R}/\mathbb{Z}$
that satisfies
for all
![]() $h_1,\ldots,h_{d+1},x\in V$
. We write
$h_1,\ldots,h_{d+1},x\in V$
. We write
![]() $\operatorname{\textrm{Poly}}_{\leqslant d}(V\to\mathbb{R}/\mathbb{Z})$
for the set of non-classical polynomials of degree at most d.
$\operatorname{\textrm{Poly}}_{\leqslant d}(V\to\mathbb{R}/\mathbb{Z})$
for the set of non-classical polynomials of degree at most d.
A classical polynomial is a map
![]() $V\to\mathbb{F}_p$
satisfying the same property. By composing with the standard map
$V\to\mathbb{F}_p$
satisfying the same property. By composing with the standard map
![]() $x\mapsto |x|/p$
we can view
$x\mapsto |x|/p$
we can view
![]() $\operatorname{\textrm{Poly}}_{\leqslant d}(V\to\mathbb{F}_p)$
as a subset of
$\operatorname{\textrm{Poly}}_{\leqslant d}(V\to\mathbb{F}_p)$
as a subset of
![]() $\operatorname{\textrm{Poly}}_{\leqslant d}(V\to\mathbb{R}/\mathbb{Z})$
.
$\operatorname{\textrm{Poly}}_{\leqslant d}(V\to\mathbb{R}/\mathbb{Z})$
.
See [Reference T. and T.7, lemma 1·7] for some properties of non-classical polynomials. We give one property below which will be used several times in this paper.
Lemma 2·4 ([Reference T. and T.7, lemma 1·7(iii)]) Fix a prime p and a finite-dimensional
![]() $\mathbb{F}_p$
-vector space
$\mathbb{F}_p$
-vector space
![]() $V=\mathbb{F}_p^n$
. Then
$V=\mathbb{F}_p^n$
. Then
![]() $P\colon V\to\mathbb{R}/\mathbb{Z}$
is a non-classical polynomial of degree at most d if and only if it can be expressed in the form
$P\colon V\to\mathbb{R}/\mathbb{Z}$
is a non-classical polynomial of degree at most d if and only if it can be expressed in the form
 \begin{equation*}P(x_1,\ldots,x_n)=\alpha+\sum_{\genfrac{}{}{0pt}{}{0\le i_1,\ldots,i_n<p,\, j\ge 0:}{0<i_1+\cdots+i_n\le d-j(p-1)}}\frac{c_{i_1,\ldots,i_n,j}|x_1|^{i_1}\cdots|x_n|^{i_n}}{p^{j+1}}\ (\mathrm{mod}\ 1),\end{equation*}
\begin{equation*}P(x_1,\ldots,x_n)=\alpha+\sum_{\genfrac{}{}{0pt}{}{0\le i_1,\ldots,i_n<p,\, j\ge 0:}{0<i_1+\cdots+i_n\le d-j(p-1)}}\frac{c_{i_1,\ldots,i_n,j}|x_1|^{i_1}\cdots|x_n|^{i_n}}{p^{j+1}}\ (\mathrm{mod}\ 1),\end{equation*}
for some
![]() $\alpha\in\mathbb{R}/\mathbb{Z}$
and coefficients
$\alpha\in\mathbb{R}/\mathbb{Z}$
and coefficients
![]() $c_{i_1,\ldots,i_n,j}\in\{0,\ldots,p-1\}$
. Furthermore, this representation is unique.
$c_{i_1,\ldots,i_n,j}\in\{0,\ldots,p-1\}$
. Furthermore, this representation is unique.
Define
![]() $\mathbb U_k\subset\mathbb R/\mathbb Z$
to be
$\mathbb U_k\subset\mathbb R/\mathbb Z$
to be
![]() $\{0,1/p^k,\ldots,(p^k-1)/p^k\}$
. As a corollary we see that in characteristic p, every non-classical polynomial of degree at most d takes values in a coset of
$\{0,1/p^k,\ldots,(p^k-1)/p^k\}$
. As a corollary we see that in characteristic p, every non-classical polynomial of degree at most d takes values in a coset of
![]() $\mathbb{U}_{\lfloor(d-1)/(p-1)\rfloor+1}$
.
$\mathbb{U}_{\lfloor(d-1)/(p-1)\rfloor+1}$
.
Finally we state the inverse theorem of Tao and Ziegler.
Theorem 2·5 ([Reference T. and T.7, theorem 1·10]) Fix a prime p, a positive integer k, and a parameter
![]() $\delta>0$
. There exists
$\delta>0$
. There exists
![]() $\epsilon>0$
such that the following holds. Let V be a finite-dimensional
$\epsilon>0$
such that the following holds. Let V be a finite-dimensional
![]() $\mathbb{F}_p$
-vector space. Given a function
$\mathbb{F}_p$
-vector space. Given a function
![]() $f\colon V\to\mathbb{C}$
satisfying
$f\colon V\to\mathbb{C}$
satisfying
![]() $\|f\|_\infty\le1$
and
$\|f\|_\infty\le1$
and
![]() $\|f\|_{U^k}>\delta$
, there exists a non-classical polynomial
$\|f\|_{U^k}>\delta$
, there exists a non-classical polynomial
![]() $P\in\operatorname{\rm{Poly}}_{\leqslant k-1}(V\to\mathbb{R}/\mathbb{Z})$
such that
$P\in\operatorname{\rm{Poly}}_{\leqslant k-1}(V\to\mathbb{R}/\mathbb{Z})$
such that
Earlier works of Bergelson, Tao and Ziegler [Reference V., T. and T.2] and Tao and Ziegler [Reference T. and T.6] show this result in the high-characteristic regime
![]() $p\geq k$
, with the additional guarantee that P is a classical polynomial of degree at most
$p\geq k$
, with the additional guarantee that P is a classical polynomial of degree at most
![]() $k-1$
.
$k-1$
.
3. Classical polynomials for the
 $U^{p+1}$
-inverse theorem
$U^{p+1}$
-inverse theorem
The inverse theorem for the
![]() $U^k$
-norm does not require non-classical polynomials when
$U^k$
-norm does not require non-classical polynomials when
![]() $p\geq k$
for the simple reason that every non-classical polynomial of degree at most
$p\geq k$
for the simple reason that every non-classical polynomial of degree at most
![]() $p-1$
is a classical polynomial of the same degree (up to a constant shift). To prove Theorem 1·1, about the
$p-1$
is a classical polynomial of the same degree (up to a constant shift). To prove Theorem 1·1, about the
![]() $U^{p+1}$
-inverse theorem, we use the following fact. Every non-classical polynomial of degree p agrees with a classical polynomial on a codimension 1 hyperplane (up to a constant shift).
$U^{p+1}$
-inverse theorem, we use the following fact. Every non-classical polynomial of degree p agrees with a classical polynomial on a codimension 1 hyperplane (up to a constant shift).
Proposition 3·1 Let
![]() $P\in\operatorname{\rm{Poly}}_{\leqslant p}(V\to\mathbb{R}/\mathbb{Z})$
be a non-classical polynomial of degree at most p. Then there exists a codimension 1 hyperplane
$P\in\operatorname{\rm{Poly}}_{\leqslant p}(V\to\mathbb{R}/\mathbb{Z})$
be a non-classical polynomial of degree at most p. Then there exists a codimension 1 hyperplane
![]() $U\le V$
, a classical polynomial
$U\le V$
, a classical polynomial
![]() $Q\in {\rm{Poly}}_{\leqslant p}(V\to\mathbb F_p)$
, and
$Q\in {\rm{Poly}}_{\leqslant p}(V\to\mathbb F_p)$
, and
![]() $\alpha\in\mathbb R/\mathbb Z$
such that
$\alpha\in\mathbb R/\mathbb Z$
such that
![]() $P(x)=\alpha+|Q(x)|/p$
for all
$P(x)=\alpha+|Q(x)|/p$
for all
![]() $x\in U$
.
$x\in U$
.
Proof. Pick an isomorphism
![]() $V\simeq \mathbb F_p^n$
. By Lemma 2·4, we have
$V\simeq \mathbb F_p^n$
. By Lemma 2·4, we have
for
![]() $\alpha\in\mathbb{R}/\mathbb{Z}$
, a polynomial P
$\alpha\in\mathbb{R}/\mathbb{Z}$
, a polynomial P
![]() $^{\prime}$
taking values in
$^{\prime}$
taking values in
![]() $\mathbb U_1=\{0,1/p,\ldots,(p-1)/p\}$
, and
$\mathbb U_1=\{0,1/p,\ldots,(p-1)/p\}$
, and
![]() $c_1,\ldots,c_n\in\{0,\ldots,p-1\}$
. Define the codimension 1 hyperplane
$c_1,\ldots,c_n\in\{0,\ldots,p-1\}$
. Define the codimension 1 hyperplane
![]() $U\le V$
by
$U\le V$
by
![]() $c_1x_1+\cdots+c_nx_n=0$
. Note that for
$c_1x_1+\cdots+c_nx_n=0$
. Note that for
![]() $(x_1,\ldots,x_n)\in U$
, we have
$(x_1,\ldots,x_n)\in U$
, we have
![]() $c_1|x_1|+\cdots+c_n|x_n|\equiv0\ (\mathrm{mod}\ p)$
. Thus
$c_1|x_1|+\cdots+c_n|x_n|\equiv0\ (\mathrm{mod}\ p)$
. Thus
![]() $P|_U$
takes values in
$P|_U$
takes values in
![]() $\alpha+\mathbb U_1$
. Thus by our identification of
$\alpha+\mathbb U_1$
. Thus by our identification of
![]() $\mathbb U_1$
with
$\mathbb U_1$
with
![]() $\mathbb F_p$
,
$\mathbb F_p$
,
![]() $P|_U-\alpha$
is a classical polynomial of degree at most p.
$P|_U-\alpha$
is a classical polynomial of degree at most p.
Proof of Theorem 1·1. By the usual inverse theorem, Theorem 2·5, there exists
![]() $P\in\operatorname{\textrm{Poly}}_{\leqslant p}(V\to\mathbb{R}/\mathbb{Z})$
such that
$P\in\operatorname{\textrm{Poly}}_{\leqslant p}(V\to\mathbb{R}/\mathbb{Z})$
such that
![]() $|\mathbb{E}_{x\in V}f(x)e(\!-P(x))|\ge\epsilon$
. By Proposition 3·1, there exists a codimension 1 hyperplane U and
$|\mathbb{E}_{x\in V}f(x)e(\!-P(x))|\ge\epsilon$
. By Proposition 3·1, there exists a codimension 1 hyperplane U and
![]() $\alpha\in\mathbb{R}/\mathbb{Z}$
such that
$\alpha\in\mathbb{R}/\mathbb{Z}$
such that
![]() $P|_U$
takes values in
$P|_U$
takes values in
![]() $\alpha+\mathbb U_1$
, i.e.,
$\alpha+\mathbb U_1$
, i.e.,
![]() $P|_U-\alpha$
is classical. Pick an isomorphism
$P|_U-\alpha$
is classical. Pick an isomorphism
![]() $V\simeq\mathbb{F}_p^n$
such that U is the hyperplane defined by
$V\simeq\mathbb{F}_p^n$
such that U is the hyperplane defined by
![]() $x_1=0$
. In this basis, there exists a classical polynomial
$x_1=0$
. In this basis, there exists a classical polynomial
![]() $Q\in\operatorname{\textrm{Poly}}_{\leqslant p}(\mathbb{F}_p^n\to\mathbb{F}_p)$
and
$Q\in\operatorname{\textrm{Poly}}_{\leqslant p}(\mathbb{F}_p^n\to\mathbb{F}_p)$
and
![]() $c\in\{0,\ldots,p-1\}$
so that
$c\in\{0,\ldots,p-1\}$
so that
Thus we have
 \begin{align*}\epsilon&\le|\mathbb{E}_{x\in\mathbb{F}_p^n}f(x)e(\!-P(x))|\\[3pt]&\le\mathbb{E}_{x_1\in\mathbb{F}_p}\bigg|\mathbb{E}_{y\in\mathbb{F}_p^{n-1}}f(x_1,y)e(\!-P(x_1,y))\bigg|\\[3pt] &=\mathbb{E}_{x_1\in\mathbb{F}_p}\bigg|\mathbb{E}_{y\in\mathbb{F}_p^{n-1}}f(x_1,y)e_p(\!-Q(x_1,y))\bigg|\\[3pt] &\le\bigg(\mathbb{E}_{x_1\in\mathbb{F}_p}\bigg|\mathbb{E}_{y\in\mathbb{F}_p^{n-1}}f(x_1,y)e_p(\!-Q(x_1,y))\bigg|^2\bigg)^{1/2}.\end{align*}
\begin{align*}\epsilon&\le|\mathbb{E}_{x\in\mathbb{F}_p^n}f(x)e(\!-P(x))|\\[3pt]&\le\mathbb{E}_{x_1\in\mathbb{F}_p}\bigg|\mathbb{E}_{y\in\mathbb{F}_p^{n-1}}f(x_1,y)e(\!-P(x_1,y))\bigg|\\[3pt] &=\mathbb{E}_{x_1\in\mathbb{F}_p}\bigg|\mathbb{E}_{y\in\mathbb{F}_p^{n-1}}f(x_1,y)e_p(\!-Q(x_1,y))\bigg|\\[3pt] &\le\bigg(\mathbb{E}_{x_1\in\mathbb{F}_p}\bigg|\mathbb{E}_{y\in\mathbb{F}_p^{n-1}}f(x_1,y)e_p(\!-Q(x_1,y))\bigg|^2\bigg)^{1/2}.\end{align*}
By Parseval and the pigeonhole principle, there exists
![]() $a\in\mathbb{F}_p$
such that
$a\in\mathbb{F}_p$
such that
Therefore f has correlation at least
![]() $\epsilon/\sqrt{p}$
with the classical polynomial
$\epsilon/\sqrt{p}$
with the classical polynomial
![]() $Q(x_1,\ldots,x_n)+ax_1$
.
$Q(x_1,\ldots,x_n)+ax_1$
.
4. Symmetrisation techniques
We now extend a symmetrisation technique of Alon and Beigel [Reference N. and R.1] which will be needed to prove the non-correlation property of our example. The original version of this technique uses Ramsey theory to show that if a function correlates with a bounded degree multilinear polynomial, then some restriction of coordinates correlates with a symmetric polynomial. This result was used in the previous works [Reference B. and T.3,Reference S., R. and A.4] on this problem.
For our application we need a result which applies to arbitrary polynomials. We show that if a function correlates with a bounded degree polynomial, then some restriction of coordinates correlates with a so-called quasisymmetric polynomial. These are a generalisation of the notion of symmetric polynomials which have found extensive use in enumerative and algebraic combinatorics.
Definition 4·1 For a prime p and a tuple
![]() $(\alpha_1,\ldots,\alpha_s)$
of positive integers satisfying
$(\alpha_1,\ldots,\alpha_s)$
of positive integers satisfying
![]() $\alpha_i<p$
for all i, the elementary quasisymmetric polynomial associated to
$\alpha_i<p$
for all i, the elementary quasisymmetric polynomial associated to
![]() $(\alpha_1,\ldots,\alpha_s)$
in n variables is the polynomial
$(\alpha_1,\ldots,\alpha_s)$
in n variables is the polynomial
![]() $Q_\alpha\colon\mathbb F_p^n\to\mathbb F_p$
defined by
$Q_\alpha\colon\mathbb F_p^n\to\mathbb F_p$
defined by
 \begin{equation*}Q_\alpha(x_1,\ldots,x_n) = \sum_{1\le i_1 < \cdots < i_s\le n}\prod_{j=1}^s x_{i_j}^{\alpha_j}.\end{equation*}
\begin{equation*}Q_\alpha(x_1,\ldots,x_n) = \sum_{1\le i_1 < \cdots < i_s\le n}\prod_{j=1}^s x_{i_j}^{\alpha_j}.\end{equation*}
We additionally note the total degree is
![]() $|\alpha|:=\alpha_1+\cdots+\alpha_s$
.
$|\alpha|:=\alpha_1+\cdots+\alpha_s$
.
Theorem 4·2 Fix a prime p and an integer
![]() $d\ge 1$
. For any n, there exists
$d\ge 1$
. For any n, there exists
![]() $m=\omega_{p,d;n\to\infty}(1)$
such that the following holds. Let
$m=\omega_{p,d;n\to\infty}(1)$
such that the following holds. Let
![]() $P(x_1,\ldots,x_n)$
be a polynomial of degree at most d with coefficients in
$P(x_1,\ldots,x_n)$
be a polynomial of degree at most d with coefficients in
![]() $\mathbb{F}_p$
. There exists
$\mathbb{F}_p$
. There exists
![]() $I\subseteq[n]$
of size
$I\subseteq[n]$
of size
![]() $|I|=m$
such that for any
$|I|=m$
such that for any
![]() $y_{[n]\setminus I}\in\mathbb{F}_p^{[n]\setminus I}$
, the function
$y_{[n]\setminus I}\in\mathbb{F}_p^{[n]\setminus I}$
, the function
![]() $P(x_I,y_{[n]\setminus I})$
(viewed as a polynomial in the
$P(x_I,y_{[n]\setminus I})$
(viewed as a polynomial in the
![]() $x_I$
) can be written as a quasisymmetric polynomial of degree d plus an arbitrary polynomial of degree at most
$x_I$
) can be written as a quasisymmetric polynomial of degree d plus an arbitrary polynomial of degree at most
![]() $d-1$
.
$d-1$
.
Proof. We can uniquely express P in the form
 \begin{equation*}P(x_1,\ldots,x_n)=\sum_{s=0}^d\sum_{1\leq i_1<\cdots<i_s\leq n}\sum_{\substack{\alpha\in\{1,\ldots,p-1\}^s\\[2pt]|\alpha|\leq d}}c_{i_1,\ldots,i_s,\alpha}\prod_{j=1}^s x_{i_j}^{\alpha_j},\end{equation*}
\begin{equation*}P(x_1,\ldots,x_n)=\sum_{s=0}^d\sum_{1\leq i_1<\cdots<i_s\leq n}\sum_{\substack{\alpha\in\{1,\ldots,p-1\}^s\\[2pt]|\alpha|\leq d}}c_{i_1,\ldots,i_s,\alpha}\prod_{j=1}^s x_{i_j}^{\alpha_j},\end{equation*}
where the
![]() $c_{i_1,\ldots,i_s,\alpha}\in\mathbb F_p$
are arbitrary.
$c_{i_1,\ldots,i_s,\alpha}\in\mathbb F_p$
are arbitrary.
Define
![]() $\Lambda=\{\lambda\in\{0,\ldots,p-1\}^d:|\lambda|=d\}$
. We define a colouring of the complete d-uniform hypergraph on n vertices where the set of colours is
$\Lambda=\{\lambda\in\{0,\ldots,p-1\}^d:|\lambda|=d\}$
. We define a colouring of the complete d-uniform hypergraph on n vertices where the set of colours is
![]() $\mathbb F_p^{\Lambda}$
. For an edge
$\mathbb F_p^{\Lambda}$
. For an edge
![]() $\{i_1,\ldots,i_d\}$
with
$\{i_1,\ldots,i_d\}$
with
![]() $1\leq i_1<\cdots<i_d\leq n$
, let the colour of this edge be given by
$1\leq i_1<\cdots<i_d\leq n$
, let the colour of this edge be given by
![]() $c_{i_1,\ldots,i_d}\colon \Lambda\to\mathbb F_p$
. We define
$c_{i_1,\ldots,i_d}\colon \Lambda\to\mathbb F_p$
. We define
![]() $c_{i_1,\ldots,i_d}(\lambda)=c_{j_1,\ldots,j_s,\alpha}$
where
$c_{i_1,\ldots,i_d}(\lambda)=c_{j_1,\ldots,j_s,\alpha}$
where
![]() $\alpha$
is formed by removing the 0’s from the tuple
$\alpha$
is formed by removing the 0’s from the tuple
![]() $\lambda$
and
$\lambda$
and
![]() $(j_1,\ldots,j_s)$
is formed from
$(j_1,\ldots,j_s)$
is formed from
![]() $(i_1,\ldots,i_d)$
by removing the coordinate
$(i_1,\ldots,i_d)$
by removing the coordinate
![]() $i_k$
if
$i_k$
if
![]() $\lambda_k=0$
.
$\lambda_k=0$
.
Applying the hypergraph Ramsey theorem, there exists a subset
![]() $I\subseteq[n]$
such that the induced subhypergraph on vertex set I is coloured monochromatically with colour
$I\subseteq[n]$
such that the induced subhypergraph on vertex set I is coloured monochromatically with colour
![]() $c\colon\Lambda\to\mathbb F_p$
and
$c\colon\Lambda\to\mathbb F_p$
and
![]() $|I|=\omega_{p,d;n\to\infty}(1)$
. Unwinding the definitions, we see that
$|I|=\omega_{p,d;n\to\infty}(1)$
. Unwinding the definitions, we see that
 \begin{equation*}P(x_{I},y_{[n]\setminus I}) = \sum_{s=0}^d\sum_{\substack{\alpha\in\{1,\ldots,p-1\}^s\\[2pt] |\alpha|=d}}c(\alpha,\underbrace{0,\ldots,0}_{d-s\text{ 0's}})Q_\alpha(x_I)+ \text{mixed terms}.\end{equation*}
\begin{equation*}P(x_{I},y_{[n]\setminus I}) = \sum_{s=0}^d\sum_{\substack{\alpha\in\{1,\ldots,p-1\}^s\\[2pt] |\alpha|=d}}c(\alpha,\underbrace{0,\ldots,0}_{d-s\text{ 0's}})Q_\alpha(x_I)+ \text{mixed terms}.\end{equation*}
Now the mixed terms involve at least one factor of
![]() $y_{[n]\setminus I}$
, so their total
$y_{[n]\setminus I}$
, so their total
![]() $x_I$
-degree is strictly smaller than d.
$x_I$
-degree is strictly smaller than d.
5. Non-classical polynomials are necessary
In this section we prove Theorem 1·2, namely that non-classical polynomials are necessary in the
![]() $U^{k+1}$
-inverse theorem when
$U^{k+1}$
-inverse theorem when
![]() $k> p$
. To do this, we use the function
$k> p$
. To do this, we use the function
![]() $f_n^{(k)}\colon\mathbb{F}_p^n\to\mathbb{R}/\mathbb{Z}$
defined by
$f_n^{(k)}\colon\mathbb{F}_p^n\to\mathbb{R}/\mathbb{Z}$
defined by
where
![]() $k=r+(p-1)\ell$
with
$k=r+(p-1)\ell$
with
![]() $\ell\geq 1$
and
$\ell\geq 1$
and
![]() $0<r<p$
. Note that
$0<r<p$
. Note that
![]() $f_n^{(k)}$
is a non-classical polynomial of degree k, so
$f_n^{(k)}$
is a non-classical polynomial of degree k, so
![]() $\|e(f_n^{(k)})\|_{U^{k+1}}=1$
.
$\|e(f_n^{(k)})\|_{U^{k+1}}=1$
.
In order to motivate our proof, suppose for the sake of contradiction that
![]() $f_n^{(k)}$
has correlation at least
$f_n^{(k)}$
has correlation at least
![]() $\epsilon$
with some classical polynomial of degree at most k. By Theorem 4·2, we will be able to reduce to the situation
$\epsilon$
with some classical polynomial of degree at most k. By Theorem 4·2, we will be able to reduce to the situation
where g is a homogeneous quasisymmetric polynomial of degree k and h is a classical polynomial of degree at most
![]() $k-1$
. By the monotonicity of the Gowers norms (alternatively by the Gowers–Cauchy–Schwarz inequality), we deduce
$k-1$
. By the monotonicity of the Gowers norms (alternatively by the Gowers–Cauchy–Schwarz inequality), we deduce
 \begin{align*}\epsilon^{2^k}&\leq\left|\mathbb E_{x}e(f_n^{(k)}(x)+g(x)+h(x))\right|^{2^k}\\[2pt] &=\mathbb E_{x,h_1,\ldots,h_k}(\partial_{h_1}\cdots\partial_{h_k}e(f_n^{(k)}+g+h))(x)\\[2pt] &=\mathbb E_{h_1,\ldots,h_k}e(\Delta_{h_1}\cdots\Delta_{h_k}(f_n^{(k)}+g)).\end{align*}
\begin{align*}\epsilon^{2^k}&\leq\left|\mathbb E_{x}e(f_n^{(k)}(x)+g(x)+h(x))\right|^{2^k}\\[2pt] &=\mathbb E_{x,h_1,\ldots,h_k}(\partial_{h_1}\cdots\partial_{h_k}e(f_n^{(k)}+g+h))(x)\\[2pt] &=\mathbb E_{h_1,\ldots,h_k}e(\Delta_{h_1}\cdots\Delta_{h_k}(f_n^{(k)}+g)).\end{align*}
Since
![]() $f_n^{(k)}$
and g are polynomials of degree k, the iterated derivatives
$f_n^{(k)}$
and g are polynomials of degree k, the iterated derivatives
![]() $(\Delta_{h_1}\cdots\Delta_{h_k}f_n^{(k)})(x)$
and
$(\Delta_{h_1}\cdots\Delta_{h_k}f_n^{(k)})(x)$
and
![]() $(\Delta_{h_1}\cdots\Delta_{h_k}g)(x)$
are constants independent of x. Furthermore, they take values in
$(\Delta_{h_1}\cdots\Delta_{h_k}g)(x)$
are constants independent of x. Furthermore, they take values in
![]() $\mathbb U_1$
which (with some abuse of notation) we identify with
$\mathbb U_1$
which (with some abuse of notation) we identify with
![]() $\mathbb F_p$
. Many results on these objects are known, including the fact that in general they are multilinear functions of
$\mathbb F_p$
. Many results on these objects are known, including the fact that in general they are multilinear functions of
![]() $h_1,\ldots, h_k$
(see [Reference T. and T.7, section 4]). For the purposes of this paper, it is sufficient to do the following explicit computation.
$h_1,\ldots, h_k$
(see [Reference T. and T.7, section 4]). For the purposes of this paper, it is sufficient to do the following explicit computation.
Lemma 5·1 For
![]() $k=r+(p-1)\ell$
with
$k=r+(p-1)\ell$
with
![]() $\ell\geq 0$
and
$\ell\geq 0$
and
![]() $0<r<p$
,
$0<r<p$
,
and for
![]() $\alpha=(\alpha_1,\ldots,\alpha_s)$
with
$\alpha=(\alpha_1,\ldots,\alpha_s)$
with
![]() $\alpha_1+\cdots+\alpha_s=k$
and
$\alpha_1+\cdots+\alpha_s=k$
and
![]() $0\leq \alpha_i<p$
,
$0\leq \alpha_i<p$
,
where the sum is over sequences
![]() $1\leq i_1\leq\cdots\leq i_k\leq n$
that satisfy
$1\leq i_1\leq\cdots\leq i_k\leq n$
that satisfy
![]() $i_{\alpha_1+\cdots+\alpha_j+1}=\cdots=i_{\alpha_1+\cdots+\alpha_j+\alpha_{j+1}}$
and
$i_{\alpha_1+\cdots+\alpha_j+1}=\cdots=i_{\alpha_1+\cdots+\alpha_j+\alpha_{j+1}}$
and
![]() $i_{\alpha_1+\cdots+\alpha_j}<i_{\alpha_1+\cdots+\alpha_j+1}$
for all j.
$i_{\alpha_1+\cdots+\alpha_j}<i_{\alpha_1+\cdots+\alpha_j+1}$
for all j.
Proof. For classical polynomials
![]() $P,Q\colon\mathbb F_p^n\to\mathbb F_p$
, of degrees
$P,Q\colon\mathbb F_p^n\to\mathbb F_p$
, of degrees
![]() $d_1,d_2$
, the discrete Leibniz rule,
$d_1,d_2$
, the discrete Leibniz rule,
![]() $\Delta_h(PQ)=(\Delta_h P)Q+P(\Delta_h Q)+(\Delta_h P)(\Delta_h Q)$
, can be easily verified. This implies the more convenient
$\Delta_h(PQ)=(\Delta_h P)Q+P(\Delta_h Q)+(\Delta_h P)(\Delta_h Q)$
, can be easily verified. This implies the more convenient
Note that taking d discrete derivatives kills
![]() $\textrm{Poly}_{\leqslant d}(\mathbb F_p^n\to\mathbb F_p)$
, so if
$\textrm{Poly}_{\leqslant d}(\mathbb F_p^n\to\mathbb F_p)$
, so if
![]() $P\equiv Q \pmod{\textrm{Poly}_{\leqslant d}(\mathbb F_p^n\to\mathbb F_p)}$
, then
$P\equiv Q \pmod{\textrm{Poly}_{\leqslant d}(\mathbb F_p^n\to\mathbb F_p)}$
, then
![]() $\Delta_{h_1}\cdots\Delta_{h_d}P(x)=\Delta_{h_1}\cdots\Delta_{h_d}Q(x)$
.
$\Delta_{h_1}\cdots\Delta_{h_d}P(x)=\Delta_{h_1}\cdots\Delta_{h_d}Q(x)$
.
We compute
![]() $\tau_\alpha$
first. Define
$\tau_\alpha$
first. Define
![]() $f\in \textrm{Poly}_{\leqslant k}(V\to\mathbb F_p)$
by
$f\in \textrm{Poly}_{\leqslant k}(V\to\mathbb F_p)$
by
![]() $f(x)=x_{i_1}\cdots x_{i_k}$
. By many applications of the discrete Leibniz rule, we see that
$f(x)=x_{i_1}\cdots x_{i_k}$
. By many applications of the discrete Leibniz rule, we see that
Extending this result by linearity gives the formula for
![]() $\tau_\alpha$
.
$\tau_\alpha$
.
Now for
![]() $\iota_k$
. For any
$\iota_k$
. For any
![]() $k\geq 1$
, write
$k\geq 1$
, write
![]() $k=r+(p-1)\ell$
with
$k=r+(p-1)\ell$
with
![]() $0<r<p$
and
$0<r<p$
and
![]() $\ell\geq 0$
. Define
$\ell\geq 0$
. Define
![]() $Q_k\in \textrm{Poly}_{\leqslant k}(\mathbb F_p\to\mathbb R/\mathbb Z)$
by
$Q_k\in \textrm{Poly}_{\leqslant k}(\mathbb F_p\to\mathbb R/\mathbb Z)$
by
![]() $Q_k(x)=|x|^r/p^{\ell+1}$
. By linearity, it suffices to prove that
$Q_k(x)=|x|^r/p^{\ell+1}$
. By linearity, it suffices to prove that
![]() $\Delta_{h_1}\cdots\Delta_{h_k} Q_k(x)=r!(\!-1)^\ell h_1\cdots h_k$
. We prove that
$\Delta_{h_1}\cdots\Delta_{h_k} Q_k(x)=r!(\!-1)^\ell h_1\cdots h_k$
. We prove that
![]() $\Delta_hQ_k(x)\equiv r|h|Q_{k-1}(x) \pmod{\textrm{Poly}_{\leqslant k-2}(\mathbb F_p\to\mathbb R/\mathbb Z)}$
for
$\Delta_hQ_k(x)\equiv r|h|Q_{k-1}(x) \pmod{\textrm{Poly}_{\leqslant k-2}(\mathbb F_p\to\mathbb R/\mathbb Z)}$
for
![]() $k\geq 2$
, while obviously
$k\geq 2$
, while obviously
![]() $\Delta_hQ_1(x)=|h|/p$
. Iterating (and applying the fact that
$\Delta_hQ_1(x)=|h|/p$
. Iterating (and applying the fact that
![]() $(p-1)!\equiv -1\pmod p$
) gives the desired result.
$(p-1)!\equiv -1\pmod p$
) gives the desired result.
We break into two cases. First, if
![]() $r=1$
(and
$r=1$
(and
![]() $\ell\geq 1$
) then
$\ell\geq 1$
) then
 \begin{align*}\Delta_hQ_k(x)&=\frac{|x+h|-|x|}{p^{\ell+1}}\\[2pt] &=\frac{|h|}{p^{\ell+1}}-\frac{\mathbb{1}(|x|+|h|\geq p)}{p^\ell}\\[2pt] &=\frac{|h|}{p^{\ell+1}}-\sum_{c=p-|h|}^{p-1}\frac{\mathbb{1}(|x|=c)}{p^\ell}\\[2pt] &=\frac{|h|}{p^{\ell+1}}+|h|\frac{|x|^{p-1}}{p^\ell}-\sum_{c=p-|h|}^{p-1}\frac{\mathbb{1}(|x|=c)+|x|^{p-1}}{p^\ell}.\end{align*}
\begin{align*}\Delta_hQ_k(x)&=\frac{|x+h|-|x|}{p^{\ell+1}}\\[2pt] &=\frac{|h|}{p^{\ell+1}}-\frac{\mathbb{1}(|x|+|h|\geq p)}{p^\ell}\\[2pt] &=\frac{|h|}{p^{\ell+1}}-\sum_{c=p-|h|}^{p-1}\frac{\mathbb{1}(|x|=c)}{p^\ell}\\[2pt] &=\frac{|h|}{p^{\ell+1}}+|h|\frac{|x|^{p-1}}{p^\ell}-\sum_{c=p-|h|}^{p-1}\frac{\mathbb{1}(|x|=c)+|x|^{p-1}}{p^\ell}.\end{align*}
Now
![]() $\mathbb{1}(|x|=c)\equiv 1-(|x|-c)^{p-1}\pmod p$
, say
$\mathbb{1}(|x|=c)\equiv 1-(|x|-c)^{p-1}\pmod p$
, say
![]() $\mathbb{1}(|x|=c)=1-(|x|-c)^{p-1}+pE_{c,p}(x)$
for some function
$\mathbb{1}(|x|=c)=1-(|x|-c)^{p-1}+pE_{c,p}(x)$
for some function
![]() $E_{c,p}$
. Then we see
$E_{c,p}$
. Then we see
 \begin{equation*}\Delta_hQ_k(x)-|h|\frac{|x|^{p-1}}{p^\ell}=\frac{|h|}{p^{\ell+1}}-\sum_{c=p-|h|}^{p-1}\frac{1-(|x|-c)^{p-1}+|x|^{p-1}}{p^\ell}-\sum_{c=p-|h|}^{p-1}\frac{E_{c,p}(x)}{p^{\ell-1}}.\end{equation*}
\begin{equation*}\Delta_hQ_k(x)-|h|\frac{|x|^{p-1}}{p^\ell}=\frac{|h|}{p^{\ell+1}}-\sum_{c=p-|h|}^{p-1}\frac{1-(|x|-c)^{p-1}+|x|^{p-1}}{p^\ell}-\sum_{c=p-|h|}^{p-1}\frac{E_{c,p}(x)}{p^{\ell-1}}.\end{equation*}
We know that every term in this equation is a non-classical polynomial of degree at most
![]() $k-1$
except for the last term. Thus we conclude that the last term is also a non-classical polynomial of degree
$k-1$
except for the last term. Thus we conclude that the last term is also a non-classical polynomial of degree
![]() $k-1$
. Furthermore, of the three terms on the right-hand side, the first is a constant, the second is a non-classical polynomial of degree at most
$k-1$
. Furthermore, of the three terms on the right-hand side, the first is a constant, the second is a non-classical polynomial of degree at most
![]() $(p-1)(\ell-1)+(p-2)=k-2$
(since the
$(p-1)(\ell-1)+(p-2)=k-2$
(since the
![]() $|x|^{p-1}/p^\ell$
terms cancel), and the third has degree at most
$|x|^{p-1}/p^\ell$
terms cancel), and the third has degree at most
![]() $(p-1)(\ell-1)=k-p$
(since it takes values in
$(p-1)(\ell-1)=k-p$
(since it takes values in
![]() $\mathbb U_{\ell-1}$
). Thus the right-hand side lies in
$\mathbb U_{\ell-1}$
). Thus the right-hand side lies in
![]() $\textrm{Poly}_{\leqslant k-2}(\mathbb F_p\to\mathbb R/\mathbb Z)$
, proving the desired result in the
$\textrm{Poly}_{\leqslant k-2}(\mathbb F_p\to\mathbb R/\mathbb Z)$
, proving the desired result in the
![]() $r=1$
case.
$r=1$
case.
Now assume that
![]() $k=r+(p-1)\ell$
where
$k=r+(p-1)\ell$
where
![]() $r\geq 2$
. We compute
$r\geq 2$
. We compute
 \begin{align*}\Delta_h Q_k(x)&=\frac{|x+h|^r-|x|^r}{p^{\ell+1}}\\[2pt] &=\frac{(|x|+|h|)^r-|x|^r}{p^{\ell+1}}-\mathbb{1}(|x|+|h|\geq p)\frac{(|x|+|h|)^r-(|x|+|h|-p)^r}{p^{\ell+1}}\\[2pt] &=\frac{\sum_{i=1}^r\binom ri |h|^i|x|^{r-i}}{p^{\ell+1}}-\mathbb{1}(|x|+|h|\geq p)\left(\sum_{i=1}^r\frac{(\!-1)^{i-1}\binom ri (|x|+|h|)^{r-i}}{p^{\ell+1-i}}\right).\end{align*}
\begin{align*}\Delta_h Q_k(x)&=\frac{|x+h|^r-|x|^r}{p^{\ell+1}}\\[2pt] &=\frac{(|x|+|h|)^r-|x|^r}{p^{\ell+1}}-\mathbb{1}(|x|+|h|\geq p)\frac{(|x|+|h|)^r-(|x|+|h|-p)^r}{p^{\ell+1}}\\[2pt] &=\frac{\sum_{i=1}^r\binom ri |h|^i|x|^{r-i}}{p^{\ell+1}}-\mathbb{1}(|x|+|h|\geq p)\left(\sum_{i=1}^r\frac{(\!-1)^{i-1}\binom ri (|x|+|h|)^{r-i}}{p^{\ell+1-i}}\right).\end{align*}
We rewrite this as
 \begin{equation*}\begin{split}\Delta_h Q_k(x)-r|h|\frac{|x|^{r-1}}{p^{\ell+1}}=&\frac{\sum_{i=2}^r\binom ri |h|^i|x|^{r-i}}{p^{\ell+1}}\\[2pt] \quad&-\mathbb{1}(|x|+|h|\geq p)\left(\sum_{i=1}^r\frac{(\!-1)^{i-1}\binom ri (|x|+|h|)^{r-i}}{p^{\ell+1-i}}\right).\end{split}\end{equation*}
\begin{equation*}\begin{split}\Delta_h Q_k(x)-r|h|\frac{|x|^{r-1}}{p^{\ell+1}}=&\frac{\sum_{i=2}^r\binom ri |h|^i|x|^{r-i}}{p^{\ell+1}}\\[2pt] \quad&-\mathbb{1}(|x|+|h|\geq p)\left(\sum_{i=1}^r\frac{(\!-1)^{i-1}\binom ri (|x|+|h|)^{r-i}}{p^{\ell+1-i}}\right).\end{split}\end{equation*}
We know that every term in this equation is a non-classical polynomial of degree at most
![]() $k-1$
except for the last term, implying that the last term is also a non-classical polynomial of degree
$k-1$
except for the last term, implying that the last term is also a non-classical polynomial of degree
![]() $k-1$
. Furthermore, of the two terms on the right-hand side, the first is a non-classical polynomial of degree at most
$k-1$
. Furthermore, of the two terms on the right-hand side, the first is a non-classical polynomial of degree at most
![]() $(p-1)\ell+r-2=k-2$
and the second has degree at most
$(p-1)\ell+r-2=k-2$
and the second has degree at most
![]() $(p-1)\ell=k-r$
(since it takes values in
$(p-1)\ell=k-r$
(since it takes values in
![]() $\mathbb U_{\ell-1}$
). Thus the right-hand side lies in
$\mathbb U_{\ell-1}$
). Thus the right-hand side lies in
![]() $\textrm{Poly}_{\leqslant k-2}(\mathbb F_p\to\mathbb R/\mathbb Z)$
, proving the desired result in the
$\textrm{Poly}_{\leqslant k-2}(\mathbb F_p\to\mathbb R/\mathbb Z)$
, proving the desired result in the
![]() $r\geq 2$
case. This completes the proof.
$r\geq 2$
case. This completes the proof.
Define the maps
![]() $I_k,T_\alpha\colon \Big(\mathbb F_p^n\Big)^{k-1}\to\mathbb F_p^n$
by the equations
$I_k,T_\alpha\colon \Big(\mathbb F_p^n\Big)^{k-1}\to\mathbb F_p^n$
by the equations
![]() $\iota_k(h_1,\ldots,h_k)=I_k(h_1,\ldots,h_{k-1})\cdot h_k$
and
$\iota_k(h_1,\ldots,h_k)=I_k(h_1,\ldots,h_{k-1})\cdot h_k$
and
![]() $\tau_\alpha(h_1,\ldots,h_k)=T_\alpha(h_1,\ldots,h_{k-1})\cdot h_k$
. From Lemma 5·1, clearly
$\tau_\alpha(h_1,\ldots,h_k)=T_\alpha(h_1,\ldots,h_{k-1})\cdot h_k$
. From Lemma 5·1, clearly
![]() $I_k(h_1,\ldots,h_{k-1})_i=(\!-1)^\ell r!(h_1)_i\cdots(h_{k-1})_i$
. To continue the argument we will need to show that
$I_k(h_1,\ldots,h_{k-1})_i=(\!-1)^\ell r!(h_1)_i\cdots(h_{k-1})_i$
. To continue the argument we will need to show that
![]() $T_\alpha$
can be expressed in a particularly convenient form.
$T_\alpha$
can be expressed in a particularly convenient form.
Lemma 5·2 For
![]() $\alpha=(\alpha_1,\ldots,\alpha_s)$
with
$\alpha=(\alpha_1,\ldots,\alpha_s)$
with
![]() $\alpha_1+\cdots+\alpha_s=k$
and
$\alpha_1+\cdots+\alpha_s=k$
and
![]() $0<\alpha_i<p$
for all i,
$0<\alpha_i<p$
for all i,
for some functions
![]() $C_{i,\alpha,J}(\cdot,\cdot)$
, evaluated at the tuple of
$C_{i,\alpha,J}(\cdot,\cdot)$
, evaluated at the tuple of
![]() $(h_j)_{i'}$
for all
$(h_j)_{i'}$
for all
![]() $j\in[k-1]$
and
$j\in[k-1]$
and
![]() $i'<i$
and the tuple of
$i'<i$
and the tuple of
![]() $\tau_\beta(h_I)$
for all
$\tau_\beta(h_I)$
for all
![]() $I\subseteq[k-1]$
and
$I\subseteq[k-1]$
and
![]() $\beta=(\beta_1,\ldots,\beta_t)$
with
$\beta=(\beta_1,\ldots,\beta_t)$
with
![]() $\beta_1+\cdots+\beta_t= |I|$
and
$\beta_1+\cdots+\beta_t= |I|$
and
![]() $0<\beta_i<p$
for all i. Furthermore,
$0<\beta_i<p$
for all i. Furthermore,
Proof. Fix
![]() $i\in[n]$
for the rest of the proof. We introduce some notation. We have
$i\in[n]$
for the rest of the proof. We introduce some notation. We have
![]() $h_1,\ldots,h_{k-1}\in\mathbb F_p^n$
. For
$h_1,\ldots,h_{k-1}\in\mathbb F_p^n$
. For
![]() $I\subseteq[k-1]$
, we write
$I\subseteq[k-1]$
, we write
![]() $h_I=(h_j)_{j\in I}$
. We use
$h_I=(h_j)_{j\in I}$
. We use
For
![]() $\alpha=(\alpha_1,\ldots,\alpha_s)$
we write
$\alpha=(\alpha_1,\ldots,\alpha_s)$
we write
![]() $\alpha_{<\ell}=(\alpha_1,\ldots,\alpha_{\ell-1})$
and
$\alpha_{<\ell}=(\alpha_1,\ldots,\alpha_{\ell-1})$
and
![]() $\alpha_{>\ell}=(\alpha_{\ell+1},\ldots,\alpha_s)$
. We define
$\alpha_{>\ell}=(\alpha_{\ell+1},\ldots,\alpha_s)$
. We define
![]() $\alpha_{\leqslant\ell}$
analogously. Recall that we use
$\alpha_{\leqslant\ell}$
analogously. Recall that we use
![]() $|\alpha|=\alpha_1+\cdots+\alpha_s$
.
$|\alpha|=\alpha_1+\cdots+\alpha_s$
.
By inspection, we can write
 \begin{equation}T_{\alpha}(h_{[k-1]})_i=\sum_{\ell=1}^s\alpha_\ell!\sum_{\substack{I\sqcup J\sqcup K=[k-1]: \\[2pt] |I|=|\alpha_{<\ell}|,\\[2pt] |J|=\alpha_{\ell}-1, \\[2pt] |K|=|\alpha_{>\ell}|}}\left(\prod_{j\in J}(h_j)_i\right)\tau_{\alpha_{<\ell}}(h_{I,<})\tau_{\alpha_{>\ell}}(h_{K,>}).\end{equation}
\begin{equation}T_{\alpha}(h_{[k-1]})_i=\sum_{\ell=1}^s\alpha_\ell!\sum_{\substack{I\sqcup J\sqcup K=[k-1]: \\[2pt] |I|=|\alpha_{<\ell}|,\\[2pt] |J|=\alpha_{\ell}-1, \\[2pt] |K|=|\alpha_{>\ell}|}}\left(\prod_{j\in J}(h_j)_i\right)\tau_{\alpha_{<\ell}}(h_{I,<})\tau_{\alpha_{>\ell}}(h_{K,>}).\end{equation}
We now remove the terms depending on
![]() $h_{[k-1],>}$
. Take
$h_{[k-1],>}$
. Take
![]() $\beta=(\beta_1,\ldots,\beta_t)$
with
$\beta=(\beta_1,\ldots,\beta_t)$
with
![]() $0< \beta_i<p$
for all i and
$0< \beta_i<p$
for all i and
![]() $L\subseteq[k-1]$
with
$L\subseteq[k-1]$
with
![]() $|L|=|\beta|$
. We have the identity
$|L|=|\beta|$
. We have the identity
 \begin{equation}\begin{aligned}\tau_\beta(h_{L,>})=\tau_\beta(h_L)&-\sum_{\ell=1}^t\sum_{\substack{I\sqcup K=L: \\[2pt] |I|=|\beta_{\leqslant\ell}|, \\[2pt] |K|=|\beta_{>\ell}|}}\tau_{\beta_{\leqslant\ell}}(h_{I,<})\tau_{\beta_{>\ell}}(h_{K,>})\\[2pt] &-\sum_{\ell=1}^t\beta_\ell!\sum_{\substack{I\sqcup J\sqcup K=L: \\[2pt] |I|=|\beta_{<\ell}|,\\[2pt] |J|=\beta_{\ell}, \\[2pt] |K|=|\beta_{>\ell}|}}\left(\prod_{j\in J}(h_j)_i\right)\tau_{\beta_{<\ell}}(h_{I,<})\tau_{\beta_{>\ell}}(h_{K,>}).\end{aligned}\end{equation}
\begin{equation}\begin{aligned}\tau_\beta(h_{L,>})=\tau_\beta(h_L)&-\sum_{\ell=1}^t\sum_{\substack{I\sqcup K=L: \\[2pt] |I|=|\beta_{\leqslant\ell}|, \\[2pt] |K|=|\beta_{>\ell}|}}\tau_{\beta_{\leqslant\ell}}(h_{I,<})\tau_{\beta_{>\ell}}(h_{K,>})\\[2pt] &-\sum_{\ell=1}^t\beta_\ell!\sum_{\substack{I\sqcup J\sqcup K=L: \\[2pt] |I|=|\beta_{<\ell}|,\\[2pt] |J|=\beta_{\ell}, \\[2pt] |K|=|\beta_{>\ell}|}}\left(\prod_{j\in J}(h_j)_i\right)\tau_{\beta_{<\ell}}(h_{I,<})\tau_{\beta_{>\ell}}(h_{K,>}).\end{aligned}\end{equation}
Repeatedly applying this identity eventually puts
![]() $T_{\alpha}(h_{[k-1]})_i$
into the desired form. To see this, note that applying this identity to
$T_{\alpha}(h_{[k-1]})_i$
into the desired form. To see this, note that applying this identity to
![]() $\tau_\beta(h_{L,>})$
produces many terms of the form
$\tau_\beta(h_{L,>})$
produces many terms of the form
![]() $\tau_{\beta_{>\ell}}(h_{K,>})$
but all of these satisfy
$\tau_{\beta_{>\ell}}(h_{K,>})$
but all of these satisfy
![]() $|\beta_{>\ell}|=|K|<|\beta|=|L|$
, so we always make progress.
$|\beta_{>\ell}|=|K|<|\beta|=|L|$
, so we always make progress.
Finally we need to compute
![]() $C_{i,\alpha,[k-1]}$
. Obviously this coefficient is a constant since the final decomposition that we produce is multilinear in the
$C_{i,\alpha,[k-1]}$
. Obviously this coefficient is a constant since the final decomposition that we produce is multilinear in the
![]() $h_1,\ldots,h_{k-1}$
. Furthermore, the only way to produce a term that is a multiple of
$h_1,\ldots,h_{k-1}$
. Furthermore, the only way to produce a term that is a multiple of
![]() $(h_1)_i\cdots(h_{k-1})_i$
is to have no factors of
$(h_1)_i\cdots(h_{k-1})_i$
is to have no factors of
![]() $\tau_{\beta_{<\ell}}(h_{I,<})$
in that term. (However, we have a choice of I, J, K in (5·2).) This means that in the initial decomposition we need to be in the
$\tau_{\beta_{<\ell}}(h_{I,<})$
in that term. (However, we have a choice of I, J, K in (5·2).) This means that in the initial decomposition we need to be in the
![]() $\ell=1$
case of the sum and every time we use the identity (5·3) we need to be in the
$\ell=1$
case of the sum and every time we use the identity (5·3) we need to be in the
![]() $\ell=1$
case of the second sum. Again, in every subsequent choice although
$\ell=1$
case of the second sum. Again, in every subsequent choice although
![]() $\ell = 1$
is fixed, we have a choice of I, J, K. Tracing through all of these reductions, we see that we produce the coefficient
$\ell = 1$
is fixed, we have a choice of I, J, K. Tracing through all of these reductions, we see that we produce the coefficient
 \begin{equation*}\alpha_1!\binom{k-1}{\alpha_1-1}\prod_{j=2}^s\bigg(\!-(\alpha_j!)\binom{k-\alpha_1-\cdots-\alpha_{j-1}}{\alpha_j}\bigg) = (\!-1)^{s-1}\alpha_1(k-1)!.\end{equation*}
\begin{equation*}\alpha_1!\binom{k-1}{\alpha_1-1}\prod_{j=2}^s\bigg(\!-(\alpha_j!)\binom{k-\alpha_1-\cdots-\alpha_{j-1}}{\alpha_j}\bigg) = (\!-1)^{s-1}\alpha_1(k-1)!.\end{equation*}
This proves the desired result.
So far we have developed the tools to, starting with the assumption of correlation with a classical polynomial, reduce to a situation in which
 \begin{align*}\epsilon^{2^k}&\leq\mathbb E\left[e_p\left(\iota_k-\sum_\alpha c_\alpha \tau_\alpha\right)\right]=\mathbb P\left(I_k+\sum_\alpha c_\alpha T_\alpha=0\right)\\[2pt] &=\mathbb P_{h_1,\ldots,h_{k-1}\sim\mathbb F_p^n}\left(\forall i\in[n],\: I_k(h_1,\ldots,h_{k-1})_i+\sum_\alpha c_\alpha T_\alpha(h_1,\ldots,h_{k-1})_i=0\right).\end{align*}
\begin{align*}\epsilon^{2^k}&\leq\mathbb E\left[e_p\left(\iota_k-\sum_\alpha c_\alpha \tau_\alpha\right)\right]=\mathbb P\left(I_k+\sum_\alpha c_\alpha T_\alpha=0\right)\\[2pt] &=\mathbb P_{h_1,\ldots,h_{k-1}\sim\mathbb F_p^n}\left(\forall i\in[n],\: I_k(h_1,\ldots,h_{k-1})_i+\sum_\alpha c_\alpha T_\alpha(h_1,\ldots,h_{k-1})_i=0\right).\end{align*}
Therefore, we need a bound on the probability that a multiaffine function equals zero.
Lemma 5·3 Let
![]() $L\colon\mathbb F_p^r\to\mathbb F_p$
be a multiaffine function whose leading coefficient (i.e., coefficient of
$L\colon\mathbb F_p^r\to\mathbb F_p$
be a multiaffine function whose leading coefficient (i.e., coefficient of
![]() $x_1\cdots x_r$
) is non-zero. Then
$x_1\cdots x_r$
) is non-zero. Then
Proof. We prove this result by induction on r. The bound is trivially true for
![]() $r=0$
.
$r=0$
.
For
![]() $r\geq 1$
, we can write
$r\geq 1$
, we can write
where M and N are multiaffine and the leading coefficient of M is non-zero. Then for each fixed
![]() $x_1,\ldots,x_{r-1}$
, there is at most 1 choice of
$x_1,\ldots,x_{r-1}$
, there is at most 1 choice of
![]() $x_r$
that makes L vanish unless
$x_r$
that makes L vanish unless
![]() $M(x_1,\ldots,x_r)=0$
. Then
$M(x_1,\ldots,x_r)=0$
. Then
The second term can be handled by the inductive hypothesis, completing the desired induction.
We now have the tools to prove the main theorem. The probability we are considering is the probability that n multiaffine functions vanish simultaneously. If these were independent, by the above lemma, we could bound the probability by
![]() $(1-c_{p,k})^n=o_{p,k;n\to\infty}(1)$
.
$(1-c_{p,k})^n=o_{p,k;n\to\infty}(1)$
.
In order to introduce such independence, we can take a union bound over all possible
![]() $\tau_\beta(h_I)$
. Then Lemma 5·2 shows that our multiaffine forms have the following property: if we plug in values for
$\tau_\beta(h_I)$
. Then Lemma 5·2 shows that our multiaffine forms have the following property: if we plug in values for
![]() $((h_1)_{i'},\ldots,(h_{k-1})_{i'})_{i' < i}$
and
$((h_1)_{i'},\ldots,(h_{k-1})_{i'})_{i' < i}$
and
![]() $\tau_\beta(h_I)$
for all
$\tau_\beta(h_I)$
for all
![]() $\beta,I$
, then
$\beta,I$
, then
![]() $T_\alpha(h_1,\ldots,h_{k-1})_i$
is multiaffine in
$T_\alpha(h_1,\ldots,h_{k-1})_i$
is multiaffine in
![]() $(h_1)_i,\ldots,(h_{k-1})_i$
with non-zero leading coefficient. Then we may reveal
$(h_1)_i,\ldots,(h_{k-1})_i$
with non-zero leading coefficient. Then we may reveal
![]() $((h_1)_i,\ldots,(h_{k-1})_i)$
one-by-one for
$((h_1)_i,\ldots,(h_{k-1})_i)$
one-by-one for
![]() $i\in[n]$
, and find that the total probability is bounded by
$i\in[n]$
, and find that the total probability is bounded by
![]() $(1-c_{p,k})^{n}$
. As the number of possible choices in the union bound is
$(1-c_{p,k})^{n}$
. As the number of possible choices in the union bound is
![]() $O_{p,k}(1)$
we will be able to prove the desired bound.
$O_{p,k}(1)$
we will be able to prove the desired bound.
Proof of Theorem 1·2. Take
![]() $k\geq p+1$
. Consider
$k\geq p+1$
. Consider
![]() $f_n^{(k)}\colon\mathbb F_p^n\to\mathbb R/\mathbb Z$
defined in (5·1). Since
$f_n^{(k)}\colon\mathbb F_p^n\to\mathbb R/\mathbb Z$
defined in (5·1). Since
![]() $f_n^{(k)}$
is a non-classical polynomial of degree k, we know that
$f_n^{(k)}$
is a non-classical polynomial of degree k, we know that
![]() $\|e(f_n^{(k)})\|_{U^{k+1}}=1$
. For a classical polynomial
$\|e(f_n^{(k)})\|_{U^{k+1}}=1$
. For a classical polynomial
![]() $P\in \textrm{Poly}_{\leqslant k}(\mathbb F_p^n\to\mathbb F_p)$
, set
$P\in \textrm{Poly}_{\leqslant k}(\mathbb F_p^n\to\mathbb F_p)$
, set
![]() $\epsilon=|\mathbb E_x e(f_n^{(k)}(x)+|P(x)|/p)|$
. We will prove that
$\epsilon=|\mathbb E_x e(f_n^{(k)}(x)+|P(x)|/p)|$
. We will prove that
![]() $\epsilon=o_{p,k;n\to\infty}(1)$
.
$\epsilon=o_{p,k;n\to\infty}(1)$
.
By Theorem 4·2, there exists
![]() $m=\omega_{p,k;n\to\infty}(1)$
and a subset
$m=\omega_{p,k;n\to\infty}(1)$
and a subset
![]() $I\subseteq[n]$
such that for all
$I\subseteq[n]$
such that for all
![]() $y_{[n]\setminus I}\in\mathbb F_p^{[n]\setminus I}$
,
$y_{[n]\setminus I}\in\mathbb F_p^{[n]\setminus I}$
,
where Q is a homogeneous quasisymmetric polynomial of degree k and
![]() $P_{y_{[n]\setminus I}}$
is a polynomial of degree at most
$P_{y_{[n]\setminus I}}$
is a polynomial of degree at most
![]() $k-1$
.
$k-1$
.
Without loss of generality, assume that
![]() $I=[m]$
. Then
$I=[m]$
. Then
Then by the pigeonhole principle, there exists
![]() $y\in\mathbb F_p^{n-m}$
such that the inner expectation is at least
$y\in\mathbb F_p^{n-m}$
such that the inner expectation is at least
![]() $\epsilon$
. Fix this choice of y for the rest of the proof. Note that
$\epsilon$
. Fix this choice of y for the rest of the proof. Note that
![]() $f_n^{(k)}(x,y)=f_m^{(k)}(x)+c_y$
where
$f_n^{(k)}(x,y)=f_m^{(k)}(x)+c_y$
where
![]() $c_y=f_{n-m}^{(k)}(y)\in\mathbb R/\mathbb Z$
is a constant. Thus we have
$c_y=f_{n-m}^{(k)}(y)\in\mathbb R/\mathbb Z$
is a constant. Thus we have
Note that the right-hand side is a
![]() $U^1$
-norm. Using the monotonicity of the Gowers norms (see, e.g., [Reference T. and T.7, lemma B.1.(ii)]) we deduce
$U^1$
-norm. Using the monotonicity of the Gowers norms (see, e.g., [Reference T. and T.7, lemma B.1.(ii)]) we deduce
 \begin{align*}\epsilon^{2^k}&\leq\|e(f_m^{(k)}+|Q|/p+|P_y|/p+c_y)\|_{U^1}^{2^k}\\[2pt] &\leq\|e(f_m^{(k)}+|Q|/p+|P_y|/p+c_y)\|_{U^k}^{2^k}\\[2pt] &=\mathbb E_{x,h_1,\ldots,h_k}\partial_{h_1}\cdots\partial_{h_k}e(f_m^{(k)}+|Q|/p+|P_y|/p+c_y)(x)\\[2pt] &=\mathbb E_{x,h_1,\ldots,h_k}e(\Delta_{h_1}\cdots\Delta_{h_k}(f_m^{(k)}+|Q|/p+|P_y|/p+c_y)(x)).\end{align*}
\begin{align*}\epsilon^{2^k}&\leq\|e(f_m^{(k)}+|Q|/p+|P_y|/p+c_y)\|_{U^1}^{2^k}\\[2pt] &\leq\|e(f_m^{(k)}+|Q|/p+|P_y|/p+c_y)\|_{U^k}^{2^k}\\[2pt] &=\mathbb E_{x,h_1,\ldots,h_k}\partial_{h_1}\cdots\partial_{h_k}e(f_m^{(k)}+|Q|/p+|P_y|/p+c_y)(x)\\[2pt] &=\mathbb E_{x,h_1,\ldots,h_k}e(\Delta_{h_1}\cdots\Delta_{h_k}(f_m^{(k)}+|Q|/p+|P_y|/p+c_y)(x)).\end{align*}
Taking k discrete derivatives kills (non-classical) polynomials of degree at most
![]() $k-1$
and turns those of degree k into constants. Thus the final expression is equal to
$k-1$
and turns those of degree k into constants. Thus the final expression is equal to
Since Q is a homogeneous quasisymmetric polynomial of degree k, it can be written as
![]() $\sum_\alpha c_\alpha Q_\alpha$
where
$\sum_\alpha c_\alpha Q_\alpha$
where
![]() $\alpha$
ranges over all tuples
$\alpha$
ranges over all tuples
![]() $(\alpha_1,\ldots,\alpha_s)$
with
$(\alpha_1,\ldots,\alpha_s)$
with
![]() $|\alpha|=k$
and
$|\alpha|=k$
and
![]() $0<\alpha_i<p$
for all i and the
$0<\alpha_i<p$
for all i and the
![]() $c_{\alpha}\in\mathbb F_p$
are arbitrary coefficients.
$c_{\alpha}\in\mathbb F_p$
are arbitrary coefficients.
We computed
![]() $\Delta_{h_1}\cdots\Delta_{h_k}f_m^{(k)}$
and
$\Delta_{h_1}\cdots\Delta_{h_k}f_m^{(k)}$
and
![]() $\Delta_{h_1}\cdots\Delta_{h_k}Q_{\alpha}$
in Lemma 5·1. These are the k-linear forms denoted
$\Delta_{h_1}\cdots\Delta_{h_k}Q_{\alpha}$
in Lemma 5·1. These are the k-linear forms denoted
![]() $\iota_k,\tau_\alpha\colon(\mathbb F_p^m)^k\to\mathbb F_p$
respectively. Thus so far we have shown that
$\iota_k,\tau_\alpha\colon(\mathbb F_p^m)^k\to\mathbb F_p$
respectively. Thus so far we have shown that
 \begin{equation*}\epsilon^{2^k}\leq \mathbb E_{h_1,\ldots,h_k}e_p\left(\iota_k(h_1,\ldots,h_k)+\sum_\alpha c_\alpha\tau_\alpha(h_1,\ldots,h_k)\right).\end{equation*}
\begin{equation*}\epsilon^{2^k}\leq \mathbb E_{h_1,\ldots,h_k}e_p\left(\iota_k(h_1,\ldots,h_k)+\sum_\alpha c_\alpha\tau_\alpha(h_1,\ldots,h_k)\right).\end{equation*}
For an arbitrary k-linear form
![]() $\sigma\colon\Big(\mathbb F_p^m\Big)^k\to\mathbb F_p$
, there is a unique
$\sigma\colon\Big(\mathbb F_p^m\Big)^k\to\mathbb F_p$
, there is a unique
![]() $(k-1)$
-linear function
$(k-1)$
-linear function
![]() $S\colon\Big(\mathbb F_p^m\Big)^{k-1}\to\mathbb F_p^m$
that satisfies
$S\colon\Big(\mathbb F_p^m\Big)^{k-1}\to\mathbb F_p^m$
that satisfies
![]() $\sigma(h_1,\ldots,h_k)=S(h_1,\ldots,h_{k-1})\cdot h_k$
. Furthermore, we have
$\sigma(h_1,\ldots,h_k)=S(h_1,\ldots,h_{k-1})\cdot h_k$
. Furthermore, we have
From this we conclude
 \begin{equation*}\epsilon^{2^k}\leq\mathbb P_{h_1,\ldots,h_{k-1}}\left(\forall i\in[m],\: I_k(h_1,\ldots,h_{k-1})_i+\sum_\alpha c_{\alpha}T_\alpha(h_1,\ldots,h_{k-1})_i=0\right).\end{equation*}
\begin{equation*}\epsilon^{2^k}\leq\mathbb P_{h_1,\ldots,h_{k-1}}\left(\forall i\in[m],\: I_k(h_1,\ldots,h_{k-1})_i+\sum_\alpha c_{\alpha}T_\alpha(h_1,\ldots,h_{k-1})_i=0\right).\end{equation*}
Recall that
![]() $I_k(h_1,\ldots,h_{k-1})_i=(\!-1)^\ell r!(h_1)_i\cdots (h_{k-1})_i$
where
$I_k(h_1,\ldots,h_{k-1})_i=(\!-1)^\ell r!(h_1)_i\cdots (h_{k-1})_i$
where
![]() $k=r+(p-1)\ell$
with
$k=r+(p-1)\ell$
with
![]() $\ell\geq 1$
and
$\ell\geq 1$
and
![]() $0<r<p$
. Note that
$0<r<p$
. Note that
![]() $(\!-1)^\ell r!\neq 0$
in
$(\!-1)^\ell r!\neq 0$
in
![]() $\mathbb F_p$
. Furthermore, Lemma 5·2 states that
$\mathbb F_p$
. Furthermore, Lemma 5·2 states that
In other words
![]() $T_{\alpha}(h_1,\ldots,h_{k-1})_i$
, viewed just as a function of
$T_{\alpha}(h_1,\ldots,h_{k-1})_i$
, viewed just as a function of
![]() $(h_1)_i,\ldots,(h_{k-1})_i$
is multiaffine with coefficients given by
$(h_1)_i,\ldots,(h_{k-1})_i$
is multiaffine with coefficients given by
![]() $C_{i,\alpha, J}$
. Additionally, Lemma 5·2 also gives the critical fact that the leading coefficient,
$C_{i,\alpha, J}$
. Additionally, Lemma 5·2 also gives the critical fact that the leading coefficient,
![]() $C_{i,\alpha,[k-1]}$
, is equal to
$C_{i,\alpha,[k-1]}$
, is equal to
![]() $(\!-1)^{s-1}\alpha_1(k-1)!$
for all i. Since
$(\!-1)^{s-1}\alpha_1(k-1)!$
for all i. Since
![]() $k\geq p+1$
, we have that
$k\geq p+1$
, we have that
![]() $C_{i,\alpha,[k-1]}=0$
(recall that the coefficients live in
$C_{i,\alpha,[k-1]}=0$
(recall that the coefficients live in
![]() $\mathbb F_p$
).
$\mathbb F_p$
).
This implies that
![]() $I_k(h_1,\ldots,h_{k-1})_i+\sum_\alpha c_{\alpha}T_\alpha(h_1,\ldots,h_{k-1})_i$
, viewed just as a function of
$I_k(h_1,\ldots,h_{k-1})_i+\sum_\alpha c_{\alpha}T_\alpha(h_1,\ldots,h_{k-1})_i$
, viewed just as a function of
![]() $(h_1)_i,\ldots,(h_{k-1})_i$
is multiaffine with non-zero leading coefficient, say
$(h_1)_i,\ldots,(h_{k-1})_i$
is multiaffine with non-zero leading coefficient, say
where
![]() $C_{i,[k-1]}=(\!-1)^\ell r!\neq 0$
for all i.
$C_{i,[k-1]}=(\!-1)^\ell r!\neq 0$
for all i.
By Lemma 5·3, if the coefficients are fixed then this function vanishes with probability at most
![]() $1-c_{p,k}<1$
. To complete the proof, we need to show that we can approximately decouple these events. Formally,
$1-c_{p,k}<1$
. To complete the proof, we need to show that we can approximately decouple these events. Formally,
 \begin{align*}\epsilon^{2^k}&\leq\mathbb P_{h_1,\ldots,h_{k-1}}\left(\forall i\in[m],\: \sum_{J\subseteq[k-1]}C_{i,J}(h_{[k-1],<i},(\tau_\beta(h_I))_{\beta,I})\prod_{j\in J}(h_j)_i=0\right)\\[2pt] &=\sum_{(A_{\beta,I})_{\beta, I}}\mathbb P_{h_1,\ldots,h_{k-1}}\left(\forall \beta, I,\: \tau_\beta(h_I)=A_{\beta,I}\right.\\[2pt] &\qquad\qquad\qquad\left. \cap \sum_{J\subseteq[k-1]}C_{i,J}(h_{[k-1],<i},(\tau_\beta(h_I))_{\beta,I})\prod_{j\in J}(h_j)_i=0 \right)\\[2pt] &\le \sum_{(A_{\beta,I})_{\beta, I}}\mathbb P_{h_1,\ldots,h_{k-1}}\left( \sum_{J\subseteq[k-1]}C_{i,J}(h_{[k-1],<i},(A_{\beta,I})_{\beta,I})\prod_{j\in J}(h_j)_i=0 \right).\\\end{align*}
\begin{align*}\epsilon^{2^k}&\leq\mathbb P_{h_1,\ldots,h_{k-1}}\left(\forall i\in[m],\: \sum_{J\subseteq[k-1]}C_{i,J}(h_{[k-1],<i},(\tau_\beta(h_I))_{\beta,I})\prod_{j\in J}(h_j)_i=0\right)\\[2pt] &=\sum_{(A_{\beta,I})_{\beta, I}}\mathbb P_{h_1,\ldots,h_{k-1}}\left(\forall \beta, I,\: \tau_\beta(h_I)=A_{\beta,I}\right.\\[2pt] &\qquad\qquad\qquad\left. \cap \sum_{J\subseteq[k-1]}C_{i,J}(h_{[k-1],<i},(\tau_\beta(h_I))_{\beta,I})\prod_{j\in J}(h_j)_i=0 \right)\\[2pt] &\le \sum_{(A_{\beta,I})_{\beta, I}}\mathbb P_{h_1,\ldots,h_{k-1}}\left( \sum_{J\subseteq[k-1]}C_{i,J}(h_{[k-1],<i},(A_{\beta,I})_{\beta,I})\prod_{j\in J}(h_j)_i=0 \right).\\\end{align*}
The final replacement simply comes by substituting in the values
![]() $A_{\beta,I}$
.
$A_{\beta,I}$
.
Now for each
![]() $i\in[m]$
, let
$i\in[m]$
, let
![]() $E_i$
be the event that
$E_i$
be the event that
We wish to bound
Since the event we are conditioning on only depends on
![]() $h_{[k-1],<i}$
, the conditional distribution of
$h_{[k-1],<i}$
, the conditional distribution of
![]() $(h_1)_i,\ldots,(h_{k-1})_i$
is still uniform. Thus we can upper bound the above probability by
$(h_1)_i,\ldots,(h_{k-1})_i$
is still uniform. Thus we can upper bound the above probability by
 \begin{align*}\sup_{h_{[k-1],<i}}\mathbb P_{(h_1)_i,\ldots,(h_{k-1})_i\sim\mathbb F_p}\left(\sum_{J\subseteq[k-1]}C_{i,J}(h_{[k-1],<i},(A_{\beta,I})_{\beta,I})\prod_{j\in J}(h_j)_i=0\right).\end{align*}
\begin{align*}\sup_{h_{[k-1],<i}}\mathbb P_{(h_1)_i,\ldots,(h_{k-1})_i\sim\mathbb F_p}\left(\sum_{J\subseteq[k-1]}C_{i,J}(h_{[k-1],<i},(A_{\beta,I})_{\beta,I})\prod_{j\in J}(h_j)_i=0\right).\end{align*}
By Lemma 5·3, and the fact that
![]() $C_{i,[k-1]}=(\!-1)^\ell r!\neq 0$
always, this probability is upper-bounded by
$C_{i,[k-1]}=(\!-1)^\ell r!\neq 0$
always, this probability is upper-bounded by
![]() $1-c_{p,k}<1$
. Putting everything together, we have shown that
$1-c_{p,k}<1$
. Putting everything together, we have shown that
![]() $\epsilon^{2^k}\leq O_{p,k}((1-c_{p,k})^{m})$
. (The hidden constant is the number of terms in the sum over
$\epsilon^{2^k}\leq O_{p,k}((1-c_{p,k})^{m})$
. (The hidden constant is the number of terms in the sum over
![]() $(A_{\beta,I})_{\beta, I}$
, which depends on p, k but not on m, n. It can be bounded by
$(A_{\beta,I})_{\beta, I}$
, which depends on p, k but not on m, n. It can be bounded by
![]() $p^{4^k}$
.) We showed that
$p^{4^k}$
.) We showed that
![]() $m=\omega_{p,k;n\to\infty}(1)$
, implying that
$m=\omega_{p,k;n\to\infty}(1)$
, implying that
![]() $\epsilon=o_{p,k;n\to\infty}(1)$
.
$\epsilon=o_{p,k;n\to\infty}(1)$
.