Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-05T20:44:28.645Z Has data issue: false hasContentIssue false
  • English
  • Français

A modified form of Siegel's mean-value theorem

Published online by Cambridge University Press:  24 October 2008

A. M. Macbeath  and
C. A. Rogers
A. M. Macbeath
Affiliation:
Queen's CollegeDundee
C. A. Rogers
Affiliation:
The UniversityBirmingham
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Minkowski–Hlawka theorem† asserts that, if S is any n-dimensional star body, with the origin o as centre, and with volume less than 2ζ(n), then there is a lattice of determinant 1 which has no point other than o in S. One of the methods used to prove this theorem splits up into three stages, (a) A function ρ(x) is considered, and it is shown that some suitably defined mean value of the sum

taken over a suitable set of lattices Λ of determinant 1, is equal, or approximately equal, to the integral

over the whole space. (b) By taking ρ(x) to be equal, or approximately equal, to

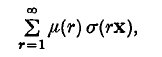
where σ(x) is the characteristic function of S, and μ(r) is the Möbius function, it is shown that a corresponding mean value of the sum

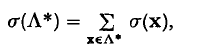
where Λ* is the set of primitive points of the lattice Λ, is equal, or approximately equal, to

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 51 , Issue 4 , October 1955 , pp. 565 - 576
Copyright
Copyright © Cambridge Philosophical Society 1955

References

REFERENCES

(1)Cassels, J. W. S.Proc. Camb. phil. Soc. 49 (1953), 165–6.CrossRefGoogle Scholar
(2)Davenport, H. and Rogers, C. A.Duke math. J. 14 (1947), 367–75.CrossRefGoogle Scholar
(3)Halmos, P. R.Measure theory (New York, 1950).CrossRefGoogle Scholar
(4)Hlawka, E.Math. Z. 49 (1944), 285–312.CrossRefGoogle Scholar
(5)Mahler, K.Duke math. J. 13 (1946), 611–21.CrossRefGoogle Scholar
(6)Minkowski, H.Gesammelte Abhandlungen (Leipzig, 1911).Google Scholar
(7)Rogers, C. A.Ann. Math., Princeton (2), 48 (1947), 994–1002.CrossRefGoogle Scholar
(8)Siegel, C. L.Ann. Math., Princeton (2), 46 (1945), 340–7.CrossRefGoogle Scholar