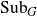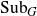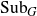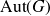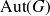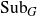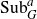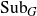1. Introduction
Let X be a (Hausdorff) topological space and let T be a homeomorphism of X. The map T is said to be distal if for any pair of distinct points
![]() $x,y \in {X}$
, the closure of the double orbit
$x,y \in {X}$
, the closure of the double orbit
![]() $\{(T^{n}(x),T^{n}(y))\mid n\in{{\mathbb Z}}\}$
in
$\{(T^{n}(x),T^{n}(y))\mid n\in{{\mathbb Z}}\}$
in
![]() $X\times X$
does not intersect the diagonal, i.e. for
$X\times X$
does not intersect the diagonal, i.e. for
![]() $x,y\in X$
with
$x,y\in X$
with
![]() $x\neq y$
,
$x\neq y$
,
![]() $\overline{\{(T^{n}(x),T^{n}(y))\mid n\in{{\mathbb Z}}\}}\cap\{(d,d)\mid d\in{X}\} =\emptyset$
. The notion of distality was introduced by David Hilbert (see Ellis [Reference Ellis12], Moore [Reference Moore21]) and studied by many in different contexts (see Abels [Reference Abels1, Reference Abels2], Furstenberg [Reference Furstenberg13], Raja–Shah [Reference Raja and SHAH25, Reference Raja and SHAH26], Shah [Reference Shah28] and the references cited therein). For a semigroup
$\overline{\{(T^{n}(x),T^{n}(y))\mid n\in{{\mathbb Z}}\}}\cap\{(d,d)\mid d\in{X}\} =\emptyset$
. The notion of distality was introduced by David Hilbert (see Ellis [Reference Ellis12], Moore [Reference Moore21]) and studied by many in different contexts (see Abels [Reference Abels1, Reference Abels2], Furstenberg [Reference Furstenberg13], Raja–Shah [Reference Raja and SHAH25, Reference Raja and SHAH26], Shah [Reference Shah28] and the references cited therein). For a semigroup
![]() $\Gamma$
which acts on X by homeomorphisms, i.e.
$\Gamma$
which acts on X by homeomorphisms, i.e.
![]() $\Gamma\to \rm Homeo(X)$
is a homomorphism, we say that
$\Gamma\to \rm Homeo(X)$
is a homomorphism, we say that
![]() $\Gamma$
acts distally on X if for any two distinct points
$\Gamma$
acts distally on X if for any two distinct points
![]() $x,y\in X$
, the closure of
$x,y\in X$
, the closure of
![]() $\{(\gamma(x), \gamma(y))\mid \gamma\in\Gamma\}$
does not intersect the diagonal. Let G be a locally compact (Hausdorff) group with the identity e and let
$\{(\gamma(x), \gamma(y))\mid \gamma\in\Gamma\}$
does not intersect the diagonal. Let G be a locally compact (Hausdorff) group with the identity e and let
![]() $T\in{\rm Aut}(G)$
, the group of automorphisms (homeomorphisms which are homomorphisms) of G. Then T is distal (on G) if and only if the closure of the T-orbit
$T\in{\rm Aut}(G)$
, the group of automorphisms (homeomorphisms which are homomorphisms) of G. Then T is distal (on G) if and only if the closure of the T-orbit
![]() $\{T^n(x)\mid n\in {\mathbb Z}\}$
of x does not contain the identity e unless
$\{T^n(x)\mid n\in {\mathbb Z}\}$
of x does not contain the identity e unless
![]() $x=e$
. If a group
$x=e$
. If a group
![]() $\Gamma$
acts on G by automorphisms, then the
$\Gamma$
acts on G by automorphisms, then the
![]() $\Gamma$
-action on G is distal if and only if
$\Gamma$
-action on G is distal if and only if
![]() $e\not\in\overline{\Gamma(x)}$
unless
$e\not\in\overline{\Gamma(x)}$
unless
![]() $x=e$
.
$x=e$
.
Let G be a locally compact (Hausdorff) group and let
![]() ${\rm Sub}_G$
be the set of all closed subgroups of G equipped with the Chabauty topology (see [Reference Chabauty9]). Note that
${\rm Sub}_G$
be the set of all closed subgroups of G equipped with the Chabauty topology (see [Reference Chabauty9]). Note that
![]() ${\rm Sub}_G$
is compact and Hausdorff. Also, it is metrisable if G is second countable [Reference Benedetti and Petronio7]. For various groups G, the space
${\rm Sub}_G$
is compact and Hausdorff. Also, it is metrisable if G is second countable [Reference Benedetti and Petronio7]. For various groups G, the space
![]() ${\rm Sub}_G$
has been identified and studied extensively, e.g.
${\rm Sub}_G$
has been identified and studied extensively, e.g.
![]() ${\rm Sub}_{{\mathbb R}^2}$
is homeomorphic to
${\rm Sub}_{{\mathbb R}^2}$
is homeomorphic to
![]() ${\mathbb S}^4$
, the unit sphere in
${\mathbb S}^4$
, the unit sphere in
![]() ${\mathbb R}^5$
[Reference Pourezza and HUBBARD23],
${\mathbb R}^5$
[Reference Pourezza and HUBBARD23],
![]() ${\rm Sub}_{{\mathbb R}}$
is homeomorphic to
${\rm Sub}_{{\mathbb R}}$
is homeomorphic to
![]() $[0,\infty]$
with a compact topology and
$[0,\infty]$
with a compact topology and
![]() ${\rm Sub}_{{\mathbb Z}}$
is homeomorphic to the subspace
${\rm Sub}_{{\mathbb Z}}$
is homeomorphic to the subspace
![]() $\{0\}\cup\{{{1}/{n}}\mid n\in{\mathbb N}\}$
of [0,1] with the usual topology. The space of G-invariant measures on
$\{0\}\cup\{{{1}/{n}}\mid n\in{\mathbb N}\}$
of [0,1] with the usual topology. The space of G-invariant measures on
![]() ${\rm Sub}_G$
and the subspace of lattices have also been studied extensively. We refer the reader to Bridson et al [Reference Bridson, De La Harpe and Kleptsyn8], Abert et al [Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and Samet4] and the references cited therein.
${\rm Sub}_G$
and the subspace of lattices have also been studied extensively. We refer the reader to Bridson et al [Reference Bridson, De La Harpe and Kleptsyn8], Abert et al [Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and Samet4] and the references cited therein.
There is a natural group action of
![]() ${\rm Aut}(G)$
on
${\rm Aut}(G)$
on
![]() ${\rm Sub}_G$
; namely,
${\rm Sub}_G$
; namely,
![]() $(T,H)\mapsto T(H)$
,
$(T,H)\mapsto T(H)$
,
![]() $T\in {\rm Aut}(G)$
,
$T\in {\rm Aut}(G)$
,
![]() $H\in{\rm Sub}_G$
. Since the image of
$H\in{\rm Sub}_G$
. Since the image of
![]() ${\rm Aut}(G)$
under this action is a large subclass of homeomorphisms of
${\rm Aut}(G)$
under this action is a large subclass of homeomorphisms of
![]() ${\rm Sub}_G$
, it would be significant to study the dynamics of this special subclass. Here, we would like to study the action of an automorphism of G on
${\rm Sub}_G$
, it would be significant to study the dynamics of this special subclass. Here, we would like to study the action of an automorphism of G on
![]() ${\rm Sub}_G$
in terms of distality. We show that the distality of the T-action on
${\rm Sub}_G$
in terms of distality. We show that the distality of the T-action on
![]() ${\rm Sub}_G$
implies the distality of the T-action on G for a large class of locally compact groups G; namely the class of those locally compact Hausdorff first countable (metrisable) groups which do not admit nontrivial compact connected normal subgroups (more generally, see Theorem 3·6). Conversely, not all distal automorphisms of G act distally on
${\rm Sub}_G$
implies the distality of the T-action on G for a large class of locally compact groups G; namely the class of those locally compact Hausdorff first countable (metrisable) groups which do not admit nontrivial compact connected normal subgroups (more generally, see Theorem 3·6). Conversely, not all distal automorphisms of G act distally on
![]() ${\rm Sub}_G$
; see Example 3·2. In fact we know that any unipotent automorphism of a connected Lie group G is distal [Reference Abels1, Reference Abels2], but it does not act distally on
${\rm Sub}_G$
; see Example 3·2. In fact we know that any unipotent automorphism of a connected Lie group G is distal [Reference Abels1, Reference Abels2], but it does not act distally on
![]() ${\rm Sub}_G$
unless it is trivial (see Theorem 4·3).
${\rm Sub}_G$
unless it is trivial (see Theorem 4·3).
Ellis [Reference Ellis12] characterised distal maps on compact spaces. If X is compact and T is a homeomorphism of X, then T is distal if and only if E(T), the closure of
![]() $\{T^n\mid n\in{{\mathbb N}}\}$
in
$\{T^n\mid n\in{{\mathbb N}}\}$
in
![]() $X^X$
is a group, where
$X^X$
is a group, where
![]() $X^X$
is endowed with the product topology. Furstenberg [Reference Furstenberg13] has a characterisation of minimal distal maps on compact metric spaces. Here we show that for a large class of connected Lie groups G, if an automorphism T acts distally on
$X^X$
is endowed with the product topology. Furstenberg [Reference Furstenberg13] has a characterisation of minimal distal maps on compact metric spaces. Here we show that for a large class of connected Lie groups G, if an automorphism T acts distally on
![]() ${\rm Sub}_G$
, a stronger result holds; namely, T is contained in a compact subgroup of
${\rm Sub}_G$
, a stronger result holds; namely, T is contained in a compact subgroup of
![]() ${\rm Aut}(G)$
. For a class of connected Lie groups G which do not admit any compact central subgroup of positive dimension, we characterise automorphisms T which act distally on
${\rm Aut}(G)$
. For a class of connected Lie groups G which do not admit any compact central subgroup of positive dimension, we characterise automorphisms T which act distally on
![]() ${\rm Sub}_G$
in terms of compactness of the closed group generated by T in
${\rm Sub}_G$
in terms of compactness of the closed group generated by T in
![]() ${\rm Aut}(G)$
(more generally see Theorem 4·1). For connected Lie groups, our results actually hold under a much weaker condition: e.g. if T acts distally on
${\rm Aut}(G)$
(more generally see Theorem 4·1). For connected Lie groups, our results actually hold under a much weaker condition: e.g. if T acts distally on
![]() ${\rm Sub}^a_G$
, the space of closed abelian subgroups of G. Note that
${\rm Sub}^a_G$
, the space of closed abelian subgroups of G. Note that
![]() ${\rm Sub}^a_G$
is closed in
${\rm Sub}^a_G$
is closed in
![]() ${\rm Sub}_G$
and hence compact, and it is invariant under the action of
${\rm Sub}_G$
and hence compact, and it is invariant under the action of
![]() ${\rm Aut}(G)$
. If
${\rm Aut}(G)$
. If
![]() $T\in{\rm Aut}(G)$
acts distally on
$T\in{\rm Aut}(G)$
acts distally on
![]() ${\rm Sub}_G$
, then it acts distally on
${\rm Sub}_G$
, then it acts distally on
![]() ${\rm Sub}^a_G$
. The converse holds for a large class of connected Lie groups as shown in Theorem 4·1.
${\rm Sub}^a_G$
. The converse holds for a large class of connected Lie groups as shown in Theorem 4·1.
We now discuss a class of automorphisms satisfying a certain weaker condition than those acting distally on
![]() ${\rm Sub}_G$
. For this, we introduce a subclass (NC) of
${\rm Sub}_G$
. For this, we introduce a subclass (NC) of
![]() ${\rm Aut}(G)$
: An automorphism T of a locally compact group G is said to belong to
${\rm Aut}(G)$
: An automorphism T of a locally compact group G is said to belong to
![]() ${\rm (NC)}$
, if for any discrete (closed) nontrivial cyclic subgroup A of G,
${\rm (NC)}$
, if for any discrete (closed) nontrivial cyclic subgroup A of G,
![]() $T^{n_k}(A)\not\to \{e\}$
in
$T^{n_k}(A)\not\to \{e\}$
in
![]() ${\rm Sub}_G$
for any sequence
${\rm Sub}_G$
for any sequence
![]() $\{n_k\}\subset{\mathbb Z}$
such that
$\{n_k\}\subset{\mathbb Z}$
such that
![]() ${n_k}\to\infty$
or
${n_k}\to\infty$
or
![]() ${n_k}\to -\infty$
.
${n_k}\to -\infty$
.
Since the cyclic groups are the most basic kind of groups and if the action of the group generated by an automorphism on
![]() ${\rm Sub}_G$
does not ‘contract’ any nontrivial closed cyclic group to the trivial group
${\rm Sub}_G$
does not ‘contract’ any nontrivial closed cyclic group to the trivial group
![]() $\{e\}$
, we call the class of such automorphisms
$\{e\}$
, we call the class of such automorphisms
![]() ${\rm (NC)}$
, where NC stands for ‘non-contracting’. Calling such an automorphism T itself “non-contracting” could be misleading as it could imply that the contraction group of T is trivial.
${\rm (NC)}$
, where NC stands for ‘non-contracting’. Calling such an automorphism T itself “non-contracting” could be misleading as it could imply that the contraction group of T is trivial.
For
![]() $G={\mathbb R}^n$
and
$G={\mathbb R}^n$
and
![]() $T=\alpha\,{\rm Id}$
for any
$T=\alpha\,{\rm Id}$
for any
![]() $\alpha\in {\mathbb R}\setminus \{0,1,-1\}$
, does not belong to
$\alpha\in {\mathbb R}\setminus \{0,1,-1\}$
, does not belong to
![]() ${\rm (NC)}$
, as for any cyclic group A in
${\rm (NC)}$
, as for any cyclic group A in
![]() ${\mathbb R}^n$
, either
${\mathbb R}^n$
, either
![]() $T^n(A)\to\{e\}$
or
$T^n(A)\to\{e\}$
or
![]() $T^{-n}(A)\to\{e\}$
as
$T^{-n}(A)\to\{e\}$
as
![]() $n\to\infty$
. All Lie groups and all connected locally compact non-compact groups admit nontrivial discrete cyclic subgroups. However, there are some totally disconnected groups which do not admit such subgroups, e.g.
$n\to\infty$
. All Lie groups and all connected locally compact non-compact groups admit nontrivial discrete cyclic subgroups. However, there are some totally disconnected groups which do not admit such subgroups, e.g.
![]() ${\mathbb Q}_p$
, p a prime, has no nontrivial closed discrete cyclic subgroups.
${\mathbb Q}_p$
, p a prime, has no nontrivial closed discrete cyclic subgroups.
If T acts distally on
![]() ${\rm Sub}^a_G$
, then
${\rm Sub}^a_G$
, then
![]() $T\in {\rm (NC)}$
. Some of the results, mainly those about the distal actions of T on
$T\in {\rm (NC)}$
. Some of the results, mainly those about the distal actions of T on
![]() ${\rm Sub}^a_G$
, for connected Lie groups G without compact central subgroups of positive dimension, are proven under a weaker assumption that
${\rm Sub}^a_G$
, for connected Lie groups G without compact central subgroups of positive dimension, are proven under a weaker assumption that
![]() $T\in {\rm (NC)}$
. All automorphisms contained in compact subgroups of
$T\in {\rm (NC)}$
. All automorphisms contained in compact subgroups of
![]() ${\rm Aut}(G)$
belong to
${\rm Aut}(G)$
belong to
![]() ${\rm (NC)}$
. The converse also holds for a large class of connected Lie groups; one of the main results shows that if G is a connected Lie group without any compact central subgroup of positive dimension, then T belongs to (NC) if and only if T is contained in a compact subgroup of
${\rm (NC)}$
. The converse also holds for a large class of connected Lie groups; one of the main results shows that if G is a connected Lie group without any compact central subgroup of positive dimension, then T belongs to (NC) if and only if T is contained in a compact subgroup of
![]() ${\rm Aut}(G)$
(see Theorem 4·1)
${\rm Aut}(G)$
(see Theorem 4·1)
Note that the projective space
![]() ${\mathbb R}{\mathbb P}^n$
can be identified with
${\mathbb R}{\mathbb P}^n$
can be identified with
![]() ${\mathbb L}^n$
, the set of lines in
${\mathbb L}^n$
, the set of lines in
![]() ${\mathbb R}^{n+1}$
, which is a closed subset of
${\mathbb R}^{n+1}$
, which is a closed subset of
![]() ${\rm Sub}^a_{{\mathbb R}^{n+1}}$
invariant under the action of
${\rm Sub}^a_{{\mathbb R}^{n+1}}$
invariant under the action of
![]() ${\rm GL}(n+1,{\mathbb R})$
. The action of
${\rm GL}(n+1,{\mathbb R})$
. The action of
![]() ${\rm GL}(n+1, {\mathbb R})$
on
${\rm GL}(n+1, {\mathbb R})$
on
![]() ${\mathbb R}{\mathbb P}^n$
has been studied extensively by many mathematicians. Shah and Yadav in [Reference Shah and YADAV30] show that for
${\mathbb R}{\mathbb P}^n$
has been studied extensively by many mathematicians. Shah and Yadav in [Reference Shah and YADAV30] show that for
![]() $T\in{\rm SL}(n+1,{\mathbb R})$
, if the homeomorphism of the unit n-sphere
$T\in{\rm SL}(n+1,{\mathbb R})$
, if the homeomorphism of the unit n-sphere
![]() ${\mathbb S}^n$
corresponding to T is distal, then T is contained in a compact subgroup of
${\mathbb S}^n$
corresponding to T is distal, then T is contained in a compact subgroup of
![]() ${\rm SL}(n+1,{\mathbb R})$
(more generally, see [Reference Shah and YADAV30, Corollary 5]). This in turn implies that if the action of such T on
${\rm SL}(n+1,{\mathbb R})$
(more generally, see [Reference Shah and YADAV30, Corollary 5]). This in turn implies that if the action of such T on
![]() ${\mathbb R}{\mathbb P}^n$
, and hence on
${\mathbb R}{\mathbb P}^n$
, and hence on
![]() ${\mathbb L}^n$
is distal, then T is contained in a compact subgroup of
${\mathbb L}^n$
is distal, then T is contained in a compact subgroup of
![]() ${\rm SL}(n+1,{\mathbb R})$
. It is easy to show that for
${\rm SL}(n+1,{\mathbb R})$
. It is easy to show that for
![]() $T\in {\rm GL}(n+1,{\mathbb R})$
, if T belongs to
$T\in {\rm GL}(n+1,{\mathbb R})$
, if T belongs to
![]() ${\rm (NC)}$
, then T acts distally on
${\rm (NC)}$
, then T acts distally on
![]() ${\mathbb L}^n\cong{\mathbb R}{\mathbb P}^n$
(this also follows from Theorem 4·1). The converse is not true as
${\mathbb L}^n\cong{\mathbb R}{\mathbb P}^n$
(this also follows from Theorem 4·1). The converse is not true as
![]() $T=\alpha\,{\rm Id}$
on
$T=\alpha\,{\rm Id}$
on
![]() ${\mathbb R}^{n+1}$
, (
${\mathbb R}^{n+1}$
, (
![]() $|\alpha|\ne 0,1$
), acts trivially on
$|\alpha|\ne 0,1$
), acts trivially on
![]() ${\mathbb R}{\mathbb P}^n\cong{\mathbb L}^n$
but it does not belong to
${\mathbb R}{\mathbb P}^n\cong{\mathbb L}^n$
but it does not belong to
![]() ${\rm (NC)}$
, as observed above. Therefore, in case of automorphisms T of
${\rm (NC)}$
, as observed above. Therefore, in case of automorphisms T of
![]() $G={\mathbb R}^{n+1}$
, the statements in Theorem 4·1 are not equivalent to the statement that T acts distally on a smaller non-discrete compact T-invariant subset
$G={\mathbb R}^{n+1}$
, the statements in Theorem 4·1 are not equivalent to the statement that T acts distally on a smaller non-discrete compact T-invariant subset
![]() ${\mathbb L}^n\subset {\rm Sub}^a_G$
.
${\mathbb L}^n\subset {\rm Sub}^a_G$
.
In Theorem 4·1, the condition on the center of G is necessary as illustrated by the example in Remark 3·8. Moreover, Example 4·7 shows that for a certain group G, there are nontrivial automorphisms contained in a connected unipotent subgroup of
![]() $({\rm Aut}(G))^0$
which belong to (NC), where
$({\rm Aut}(G))^0$
which belong to (NC), where
![]() $({\rm Aut}(G))^0$
is the connected component of the identity in
$({\rm Aut}(G))^0$
is the connected component of the identity in
![]() ${\rm Aut}(G)$
with respect to the compact-open topology. Therefore, the condition on the center in Theorem 4·1 is also necessary even if we restrict to the subclass of unipotent automorphisms or those belonging to
${\rm Aut}(G)$
with respect to the compact-open topology. Therefore, the condition on the center in Theorem 4·1 is also necessary even if we restrict to the subclass of unipotent automorphisms or those belonging to
![]() $({\rm Aut}(G))^0$
. However for these subclasses, we show that a part of Theorem 4·1 can be generalised to any connected Lie group G, i.e.
$({\rm Aut}(G))^0$
. However for these subclasses, we show that a part of Theorem 4·1 can be generalised to any connected Lie group G, i.e.
![]() $T\in ({\rm Aut}(G))^0$
acts distally on
$T\in ({\rm Aut}(G))^0$
acts distally on
![]() ${\rm Sub}^a_G$
if and only if T is contained in a compact subgroup of
${\rm Sub}^a_G$
if and only if T is contained in a compact subgroup of
![]() ${\rm Aut}(G)$
(see Theorem 4·4). We also show that for a unipotent automorphism T of G, T acts distally on
${\rm Aut}(G)$
(see Theorem 4·4). We also show that for a unipotent automorphism T of G, T acts distally on
![]() ${\rm Sub}^a_G$
if and only if
${\rm Sub}^a_G$
if and only if
![]() $T={\rm Id}$
, the identity map of G (see Theorem 4·3).
$T={\rm Id}$
, the identity map of G (see Theorem 4·3).
The group G acts on
![]() ${\rm Sub}_G$
via
${\rm Sub}_G$
via
![]() ${\rm Inn}(G)$
, the group of inner automorphisms of G. We study this action and characterise the class of connected Lie groups G which act distally on
${\rm Inn}(G)$
, the group of inner automorphisms of G. We study this action and characterise the class of connected Lie groups G which act distally on
![]() ${\rm Sub}^a_G$
. Namely, we show that G acts distally on
${\rm Sub}^a_G$
. Namely, we show that G acts distally on
![]() ${\rm Sub}^a_G$
if and only if every inner automorphism of G acts distally on
${\rm Sub}^a_G$
if and only if every inner automorphism of G acts distally on
![]() ${\rm Sub}^a_G$
, and that the latter statement is equivalent to the statement that G is either compact or
${\rm Sub}^a_G$
, and that the latter statement is equivalent to the statement that G is either compact or
![]() $G={\mathbb R}^n\times K$
, where K is a compact group and
$G={\mathbb R}^n\times K$
, where K is a compact group and
![]() $n\in{\mathbb N}$
(more generally, see Corollary 4·5).
$n\in{\mathbb N}$
(more generally, see Corollary 4·5).
Baik and Clavier in [Reference Baik and Clavier6] show that for
![]() $G={\rm PSL}(2, {\mathbb C})$
, a specific subspace of
$G={\rm PSL}(2, {\mathbb C})$
, a specific subspace of
![]() ${\rm Sub}^a_G$
is homeomorphic to the one-point compactification of
${\rm Sub}^a_G$
is homeomorphic to the one-point compactification of
![]() ${\mathbb S}^2\times{\mathbb R}^4$
. They also describe the space which is the closure of all cyclic subgroups of G, where
${\mathbb S}^2\times{\mathbb R}^4$
. They also describe the space which is the closure of all cyclic subgroups of G, where
![]() $G={\rm PSL}(2, {\mathbb R})$
or
$G={\rm PSL}(2, {\mathbb R})$
or
![]() $G={\rm PSL}(2, {\mathbb C})$
in [Reference Baik and ClavierL5, Reference Baik and Clavier6] respectively. Bridson, de la Harpe and Kleptsyn in [Reference Bridson, De La Harpe and Kleptsyn8] describe the structure of
$G={\rm PSL}(2, {\mathbb C})$
in [Reference Baik and ClavierL5, Reference Baik and Clavier6] respectively. Bridson, de la Harpe and Kleptsyn in [Reference Bridson, De La Harpe and Kleptsyn8] describe the structure of
![]() ${\rm Sub}^a_{\mathbb H}$
and various other subspaces of
${\rm Sub}^a_{\mathbb H}$
and various other subspaces of
![]() ${\rm Sub}_{\mathbb H}$
, for the 3-dimensional Heisenberg group
${\rm Sub}_{\mathbb H}$
, for the 3-dimensional Heisenberg group
![]() ${\mathbb H}$
, and they also study and describe the action of
${\mathbb H}$
, and they also study and describe the action of
![]() ${\rm Aut}(G)$
on some of these spaces in detail. One can correlate the image of
${\rm Aut}(G)$
on some of these spaces in detail. One can correlate the image of
![]() ${\rm Aut}(G)$
to a subclass of homeomorphisms of these spaces, and our results imply in particular that such a homeomorphism is distal if and only if it generates a compact group (as a closed group) in
${\rm Aut}(G)$
to a subclass of homeomorphisms of these spaces, and our results imply in particular that such a homeomorphism is distal if and only if it generates a compact group (as a closed group) in
![]() ${\rm Aut}(G)$
, for a large class of connected Lie groups G which include those mentioned above from [Reference Baik and ClavierL5, Reference Baik and Clavier6, Reference Bridson, De La Harpe and Kleptsyn8].
${\rm Aut}(G)$
, for a large class of connected Lie groups G which include those mentioned above from [Reference Baik and ClavierL5, Reference Baik and Clavier6, Reference Bridson, De La Harpe and Kleptsyn8].
Throughout, we will assume that all groups are locally compact and Hausdorff. We will often assume that they are second countable. A locally compact Hausdorff group is second countable if and only if it is first countable (metrisable) and
![]() $\sigma$
-compact. In particular, a locally compact Hausdorff first countable group is second countable if it is compactly generated or, more generally, its quotient modulo any open almost connected subgroup is countable. A closed subgroup of a connected Lie group is locally compact, Hausdorff and second countable. Let
$\sigma$
-compact. In particular, a locally compact Hausdorff first countable group is second countable if it is compactly generated or, more generally, its quotient modulo any open almost connected subgroup is countable. A closed subgroup of a connected Lie group is locally compact, Hausdorff and second countable. Let
![]() $G^0$
denote the connected component of the identity e in G. It is a closed (normal) characteristic subgroup of G.
$G^0$
denote the connected component of the identity e in G. It is a closed (normal) characteristic subgroup of G.
2. Actions of automorphisms of G on
 ${\rm Sub}_G$
${\rm Sub}_G$
In this section we discuss basic properties of the Chabauty topology on
![]() ${\rm Sub}_G$
, and discuss certain elementary results about convergence of sequences in
${\rm Sub}_G$
, and discuss certain elementary results about convergence of sequences in
![]() ${\rm Sub}_G$
and the action of
${\rm Sub}_G$
and the action of
![]() ${\rm Aut}(G)$
on
${\rm Aut}(G)$
on
![]() ${\rm Sub}_G$
.
${\rm Sub}_G$
.
Let G be a locally compact (Hausdorff) group. A sub-basis of the Chabauty topology on
![]() ${\rm Sub}_G$
is given by the sets of the form
${\rm Sub}_G$
is given by the sets of the form
![]() $\mathcal{O}_1(K)=\{A\in {\rm Sub}_G\mid A\cap K=\emptyset\}$
and
$\mathcal{O}_1(K)=\{A\in {\rm Sub}_G\mid A\cap K=\emptyset\}$
and
![]() $\mathcal{O}_2(U)=\{A\in {\rm Sub}_G\mid A\cap U\neq\emptyset\}$
, where K is a compact and U is an open subset of G. As observed earlier,
$\mathcal{O}_2(U)=\{A\in {\rm Sub}_G\mid A\cap U\neq\emptyset\}$
, where K is a compact and U is an open subset of G. As observed earlier,
![]() ${\rm Sub}_G$
is compact and Hausdorff, and if G is second countable, then both G and
${\rm Sub}_G$
is compact and Hausdorff, and if G is second countable, then both G and
![]() ${\rm Sub}_G$
are metrisable. For more details on the Chabauty topology, see [Reference Bridson, De La Harpe and Kleptsyn8, Reference Pourezza and HUBBARD23].
${\rm Sub}_G$
are metrisable. For more details on the Chabauty topology, see [Reference Bridson, De La Harpe and Kleptsyn8, Reference Pourezza and HUBBARD23].
Recall that
![]() ${\rm Aut}(G)$
is the group of all automorphisms of G. There is a natural group action of
${\rm Aut}(G)$
is the group of all automorphisms of G. There is a natural group action of
![]() ${\rm Aut}(G)$
on
${\rm Aut}(G)$
on
![]() ${\rm Sub}_G$
defined as follows:
${\rm Sub}_G$
defined as follows:
It is easy to see that the map
![]() $H\mapsto T(H)$
defines a homeomorphism of
$H\mapsto T(H)$
defines a homeomorphism of
![]() ${\rm Sub}_G$
for every
${\rm Sub}_G$
for every
![]() $T\in{\rm Aut}(G)$
(see e.g. [Reference Hamrouni and KADRI14, Proposition 2.1]), and the corresponding map
$T\in{\rm Aut}(G)$
(see e.g. [Reference Hamrouni and KADRI14, Proposition 2.1]), and the corresponding map
![]() ${\rm Aut}(G)\to {\rm Homeo}({\rm Sub}_{\rm G})$
is a group homomorphism.
${\rm Aut}(G)\to {\rm Homeo}({\rm Sub}_{\rm G})$
is a group homomorphism.
All our groups G are locally compact (Hausdorff) and we now assume that they are second countable, which ensures that
![]() ${\rm Sub}_G$
is metrisable and also that G is metrisable.
${\rm Sub}_G$
is metrisable and also that G is metrisable.
We first state a criterion (cf. [Reference Benedetti and Petronio7, p. 161]) for the convergence of a sequence in
![]() ${\rm Sub}_G$
in the following lemma, which will be used often.
${\rm Sub}_G$
in the following lemma, which will be used often.
Lemma 2·1. Let G be as above. A sequence
![]() $\{H_n\}\subset {\rm Sub}_G$
converges to
$\{H_n\}\subset {\rm Sub}_G$
converges to
![]() $H\in {\rm Sub}_G$
if and only if the following hold:
$H\in {\rm Sub}_G$
if and only if the following hold:
-
(i) For
 $g\in G$
, if there exists a subsequence
$g\in G$
, if there exists a subsequence
 $\{H_{n_k}\}$
of
$\{H_{n_k}\}$
of
 $\{H_n\}$
with
$\{H_n\}$
with
 $h_k\in H_{n_k}$
,
$h_k\in H_{n_k}$
,
 $k\in{\mathbb N}$
, such that
$k\in{\mathbb N}$
, such that
 $h_k\to g$
in G, then
$h_k\to g$
in G, then
 $g\in H$
.
$g\in H$
. -
(ii) For every
 $h\in H$
, there exists a sequence
$h\in H$
, there exists a sequence
 $\{h_n\}_{n\in{\mathbb N}}$
such that
$\{h_n\}_{n\in{\mathbb N}}$
such that
 $h_n\in H_n$
,
$h_n\in H_n$
,
 $n\in{\mathbb N}$
, and
$n\in{\mathbb N}$
, and
 $h_n\to h$
.
$h_n\to h$
.
The following lemma lists some elementary facts about the convergence in
![]() ${\rm Sub}_G$
and also the interplay of the action of
${\rm Sub}_G$
and also the interplay of the action of
![]() ${\rm Aut}(G)$
and the convergence.
${\rm Aut}(G)$
and the convergence.
Lemma 2·2. Let G be as above. The following statements hold:
-
(i) Let
 $H_n, L_n\in{\rm Sub}_G$
be such that
$H_n, L_n\in{\rm Sub}_G$
be such that
 $H_n\subset L_n$
,
$H_n\subset L_n$
,
 $n\in{\mathbb N}$
,
$n\in{\mathbb N}$
,
 $H_n\to H$
and
$H_n\to H$
and
 $L_n\to L$
in
$L_n\to L$
in
 ${\rm Sub}_G$
. Then
${\rm Sub}_G$
. Then
 $H\subset L$
.
$H\subset L$
. -
(ii) Let
 $H, L_n\in{\rm Sub}_G$
be such that
$H, L_n\in{\rm Sub}_G$
be such that
 $H\subset L_n$
for all
$H\subset L_n$
for all
 $n\in{\mathbb N}$
, and
$n\in{\mathbb N}$
, and
 $L_n\to L$
in
$L_n\to L$
in
 ${\rm Sub}_G$
. Then
${\rm Sub}_G$
. Then
 $H\subset L$
.
$H\subset L$
. -
(iii) Let
 $H_0,L_0\in{\rm Sub}_G$
be such that
$H_0,L_0\in{\rm Sub}_G$
be such that
 $H_0\subset L_0$
and
$H_0\subset L_0$
and
 $T_n(H_0)\to H$
and
$T_n(H_0)\to H$
and
 $T_n(L_0)\to L$
, for some
$T_n(L_0)\to L$
, for some
 $\{T_n\}\subset {\rm Aut}(G)$
. Then
$\{T_n\}\subset {\rm Aut}(G)$
. Then
 $H\subset L$
.
$H\subset L$
. -
(iv) Let
 $T\in{\rm Aut}(G)$
and let
$T\in{\rm Aut}(G)$
and let
 $H, L\in{\rm Sub}_G$
be such that
$H, L\in{\rm Sub}_G$
be such that
 $T(H)=H$
and
$T(H)=H$
and
 $H\subset L$
. If L′ is any limit point of
$H\subset L$
. If L′ is any limit point of
 $\{T^n(L)\}_{n\in{\mathbb Z}}$
, then
$\{T^n(L)\}_{n\in{\mathbb Z}}$
, then
 $H\subset L'$
.
$H\subset L'$
.
Proof. (i) Let
![]() $h\in H$
. As
$h\in H$
. As
![]() $H_n\to H$
, Lemma 2·1 (ii) implies that there exists a sequence
$H_n\to H$
, Lemma 2·1 (ii) implies that there exists a sequence
![]() $\{h_n\}$
such that
$\{h_n\}$
such that
![]() $h_n\in H_n$
for all n, and
$h_n\in H_n$
for all n, and
![]() $h_n\to h$
. Since
$h_n\to h$
. Since
![]() $H_n\subset L_n$
, we have that
$H_n\subset L_n$
, we have that
![]() $h_n\in L_n$
, for all n. As
$h_n\in L_n$
, for all n. As
![]() $L_n\to L$
, Lemma 2·1 (i) implies that
$L_n\to L$
, Lemma 2·1 (i) implies that
![]() $h\in L$
. Hence
$h\in L$
. Hence
![]() $H\subset L$
.
$H\subset L$
.
(i)
![]() $\Rightarrow$
(ii) as we can put
$\Rightarrow$
(ii) as we can put
![]() $H_n=H$
in (1), for all n.
$H_n=H$
in (1), for all n.
(i)
![]() $\Rightarrow$
(iii) as we can take
$\Rightarrow$
(iii) as we can take
![]() $H_n=T_n(H_0)$
and
$H_n=T_n(H_0)$
and
![]() $L_n=T_n(L_0)$
in (1), for all n.
$L_n=T_n(L_0)$
in (1), for all n.
(ii)
![]() $\Rightarrow$
(iv) is obvious.
$\Rightarrow$
(iv) is obvious.
The following elementary result about the relation between the convergence of a sequence of subgroups and that of the corresponding sequence in the quotient group will be useful.
Lemma 2·3. For G as above and a closed normal subgroup H of G, let
![]() $\pi:G\to G/H$
be the cannonical projection. Suppose
$\pi:G\to G/H$
be the cannonical projection. Suppose
![]() $\{L_n\}\subset{\rm Sub}_G$
is such that
$\{L_n\}\subset{\rm Sub}_G$
is such that
![]() $H\subset\cap_{n\in{\mathbb N}}L_n$
. Then the following hold:
$H\subset\cap_{n\in{\mathbb N}}L_n$
. Then the following hold:
-
(i) If
 $L_n\to L$
in
$L_n\to L$
in
 ${\rm Sub}_G$
, then
${\rm Sub}_G$
, then
 $\pi(L_n)\to\pi(L)$
.
$\pi(L_n)\to\pi(L)$
. -
(ii) If
 $\pi(L_n)\to L'$
, then
$\pi(L_n)\to L'$
, then
 $L_n\to \pi^{-1}(L')$
.
$L_n\to \pi^{-1}(L')$
.
Proof. (i) Suppose
![]() $L_n\to L$
. Observe that
$L_n\to L$
. Observe that
![]() $\{\pi(L_n)\}$
is relatively compact as
$\{\pi(L_n)\}$
is relatively compact as
![]() ${\rm Sub}_{G/H}$
is compact. Let L
′ be a limit point of
${\rm Sub}_{G/H}$
is compact. Let L
′ be a limit point of
![]() $\{\pi(L_n)\}$
. As
$\{\pi(L_n)\}$
. As
![]() ${\rm Sub}_{G/H}$
is metrisable, there exists
${\rm Sub}_{G/H}$
is metrisable, there exists
![]() $\{n_k\}\subset{\mathbb N}$
such that
$\{n_k\}\subset{\mathbb N}$
such that
![]() $\pi(L_{n_k})\to L'$
. First we show that
$\pi(L_{n_k})\to L'$
. First we show that
![]() $\pi(L)\subset L'$
. By Lemma 2·1 (ii), for any
$\pi(L)\subset L'$
. By Lemma 2·1 (ii), for any
![]() $x\in L$
, there exists
$x\in L$
, there exists
![]() $\{x_n\}$
such that
$\{x_n\}$
such that
![]() $x_n\in L_n$
,
$x_n\in L_n$
,
![]() $n\in{\mathbb N}$
, and
$n\in{\mathbb N}$
, and
![]() $x_n\to x$
in G. This implies that
$x_n\to x$
in G. This implies that
![]() $\pi(x_n)\to\pi(x)$
(as
$\pi(x_n)\to\pi(x)$
(as
![]() $\pi$
is continuous). Therefore,
$\pi$
is continuous). Therefore,
![]() $\pi(x)\in L'$
, and hence
$\pi(x)\in L'$
, and hence
![]() $\pi(L)\subset L'$
.
$\pi(L)\subset L'$
.
Now we show that
![]() $L'\subset\pi(L)$
. Suppose
$L'\subset\pi(L)$
. Suppose
![]() $x'\in L'$
. Again by Lemma 2·1 (ii), there exists
$x'\in L'$
. Again by Lemma 2·1 (ii), there exists
![]() $\{x^{\prime}_k\}$
such that
$\{x^{\prime}_k\}$
such that
![]() $x^{\prime}_k\in\pi(L_{n_k})$
,
$x^{\prime}_k\in\pi(L_{n_k})$
,
![]() $k\in{\mathbb N}$
, and
$k\in{\mathbb N}$
, and
![]() $x^{\prime}_k\to x'$
in
$x^{\prime}_k\to x'$
in
![]() $G/H$
. For
$G/H$
. For
![]() $k\in{\mathbb N}$
, let
$k\in{\mathbb N}$
, let
![]() $x_k\in L_{n_k}$
be such that
$x_k\in L_{n_k}$
be such that
![]() $\pi(x_k)=x^{\prime}_k$
. There exists a sequence
$\pi(x_k)=x^{\prime}_k$
. There exists a sequence
![]() $\{h_k\}\subset H$
such that
$\{h_k\}\subset H$
such that
![]() $x_kh_k\to x$
, for some
$x_kh_k\to x$
, for some
![]() $x\in G$
. Now
$x\in G$
. Now
![]() $x_kh_k\in L_{n_k}$
as
$x_kh_k\in L_{n_k}$
as
![]() $H\subset L_{n_k}$
, for all k, and hence
$H\subset L_{n_k}$
, for all k, and hence
![]() $x\in L$
(by Lemma 2·1 (i)). Moreover,
$x\in L$
(by Lemma 2·1 (i)). Moreover,
![]() $x'=\pi(x)\in \pi(L)$
, and hence
$x'=\pi(x)\in \pi(L)$
, and hence
![]() $\pi(L)=L'$
. Since this holds for all limit points of
$\pi(L)=L'$
. Since this holds for all limit points of
![]() $\{\pi(L_n)\}$
, we have that
$\{\pi(L_n)\}$
, we have that
![]() $\pi(L_n)\to\pi(L)$
.
$\pi(L_n)\to\pi(L)$
.
(ii) Suppose
![]() $\pi(L_n)\to L'$
. Here,
$\pi(L_n)\to L'$
. Here,
![]() $\{L_n\}$
is relatively compact as
$\{L_n\}$
is relatively compact as
![]() ${\rm Sub}_G$
is compact. Let
${\rm Sub}_G$
is compact. Let
![]() $L\in{\rm Sub}_G$
be a limit point of
$L\in{\rm Sub}_G$
be a limit point of
![]() $\{L_n\}$
. We show that
$\{L_n\}$
. We show that
![]() $L=\pi^{-1}(L')$
. As
$L=\pi^{-1}(L')$
. As
![]() ${\rm Sub}_G$
is metrisable, there exists a subsequence
${\rm Sub}_G$
is metrisable, there exists a subsequence
![]() $\{L_{n_k}\}$
of
$\{L_{n_k}\}$
of
![]() $\{L_n\}$
such that
$\{L_n\}$
such that
![]() $L_{n_k}\to L$
. From (i), we get that
$L_{n_k}\to L$
. From (i), we get that
![]() $\pi(L)=L'$
. As
$\pi(L)=L'$
. As
![]() $H\subset L_{n_k}$
, for all k,
$H\subset L_{n_k}$
, for all k,
![]() $H\subset L$
(from Lemma 2·2 (ii)), which in turn implies that
$H\subset L$
(from Lemma 2·2 (ii)), which in turn implies that
![]() $L=\pi^{-1}(L')$
. Since this holds for all the limit points L of
$L=\pi^{-1}(L')$
. Since this holds for all the limit points L of
![]() $\{L_n\}$
, it follows that
$\{L_n\}$
, it follows that
![]() $L_n\to\pi^{-1}(L')$
$L_n\to\pi^{-1}(L')$
Recall that for a locally compact (Hausdorff) group G, if
![]() ${\rm Aut}(G)$
is endowed with the compact-open topology, the map
${\rm Aut}(G)$
is endowed with the compact-open topology, the map
![]() ${\rm Aut}(G)\times G\to G$
,
${\rm Aut}(G)\times G\to G$
,
![]() $(T,x)\mapsto T(x)$
,
$(T,x)\mapsto T(x)$
,
![]() $T\in {\rm Aut}(G)$
,
$T\in {\rm Aut}(G)$
,
![]() $x\in G$
, is continuous. If
$x\in G$
, is continuous. If
![]() ${\rm Aut}(G)$
is endowed with the modified compact-open topology (which is finer than the compact-open topology), then
${\rm Aut}(G)$
is endowed with the modified compact-open topology (which is finer than the compact-open topology), then
![]() ${\rm Aut}(G)$
is a topological group [Reference Stroppel32, 9·17], and we show that the action of the group
${\rm Aut}(G)$
is a topological group [Reference Stroppel32, 9·17], and we show that the action of the group
![]() ${\rm Aut}(G)$
on
${\rm Aut}(G)$
on
![]() ${\rm Sub}_G$
is continuous. Note that for a connected Lie group G with the Lie algebra
${\rm Sub}_G$
is continuous. Note that for a connected Lie group G with the Lie algebra
![]() $\mathcal G$
,
$\mathcal G$
,
![]() ${\rm Aut}(G)$
is a Lie group as a closed subgroup of
${\rm Aut}(G)$
is a Lie group as a closed subgroup of
![]() ${\rm GL}(\mathcal G)$
and, the topology on
${\rm GL}(\mathcal G)$
and, the topology on
![]() ${\rm Aut}(G)$
inherited from
${\rm Aut}(G)$
inherited from
![]() ${\rm GL}(\mathcal G)$
coincides with the compact-open topology, as well as with the modified compact-open topology [Reference Arens3, Reference Hochschild16].
${\rm GL}(\mathcal G)$
coincides with the compact-open topology, as well as with the modified compact-open topology [Reference Arens3, Reference Hochschild16].
Lemma 2·4. Let G be a locally compact Hausdorff group and let
![]() ${\rm Aut}(G)$
be endowed with the modified compact-open topology. Then the map
${\rm Aut}(G)$
be endowed with the modified compact-open topology. Then the map
![]() ${\rm Aut}(G)\times{\rm Sub}_G\to{\rm Sub}_G$
,
${\rm Aut}(G)\times{\rm Sub}_G\to{\rm Sub}_G$
,
![]() $(T,H)\mapsto T(H)$
,
$(T,H)\mapsto T(H)$
,
![]() $T\in{\rm Aut}(G)$
,
$T\in{\rm Aut}(G)$
,
![]() $H\in {\rm Sub}(H)$
, is continuous.
$H\in {\rm Sub}(H)$
, is continuous.
Proof. For a compact set C and an open set U in G, let
![]() $\lfloor C,U\rfloor=\{\phi\in{\rm Aut}(G)\mid \phi(C)\subset U\}$
and
$\lfloor C,U\rfloor=\{\phi\in{\rm Aut}(G)\mid \phi(C)\subset U\}$
and
![]() $\lfloor C,U\rfloor^{-1}=\{\phi\in{\rm Aut}(G)\mid \phi^{-1}\in \lfloor C,U\rfloor\}$
. They are open in
$\lfloor C,U\rfloor^{-1}=\{\phi\in{\rm Aut}(G)\mid \phi^{-1}\in \lfloor C,U\rfloor\}$
. They are open in
![]() ${\rm Aut}(G)$
and the collection of all such sets form a sub-basis for the modified compact-open topology on
${\rm Aut}(G)$
and the collection of all such sets form a sub-basis for the modified compact-open topology on
![]() ${\rm Aut}(G)$
[Reference Stroppel32].
${\rm Aut}(G)$
[Reference Stroppel32].
Let
![]() $T\in{\rm Aut}(G)$
and
$T\in{\rm Aut}(G)$
and
![]() $H\in {\rm Sub}_G$
. Then T(H) belongs to either
$H\in {\rm Sub}_G$
. Then T(H) belongs to either
![]() $O_1(K)$
or
$O_1(K)$
or
![]() $O_2(U)$
for some compact set K or an open set U in G, where
$O_2(U)$
for some compact set K or an open set U in G, where
![]() $O_1(K)$
and
$O_1(K)$
and
![]() $O_2(U)$
are open sets in the sub-basis of the topology on
$O_2(U)$
are open sets in the sub-basis of the topology on
![]() ${\rm Sub}_G$
. Suppose
${\rm Sub}_G$
. Suppose
![]() $T(H)\in O_1(K)=\{L\in{\rm Sub}_G\mid L\cap K=\emptyset\}$
. Then
$T(H)\in O_1(K)=\{L\in{\rm Sub}_G\mid L\cap K=\emptyset\}$
. Then
![]() $H\cap T^{-1}(K)=\emptyset$
. As H is closed,
$H\cap T^{-1}(K)=\emptyset$
. As H is closed,
![]() $T^{-1}(K)$
is compact and since G is locally compact, there exists an open relatively compact set W containing
$T^{-1}(K)$
is compact and since G is locally compact, there exists an open relatively compact set W containing
![]() $T^{-1}(K)$
such that
$T^{-1}(K)$
such that
![]() $H\cap \overline{W}=\emptyset$
. Then
$H\cap \overline{W}=\emptyset$
. Then
![]() $\lfloor K,W\rfloor^{-1}\times O_1(\overline{W})$
is open in
$\lfloor K,W\rfloor^{-1}\times O_1(\overline{W})$
is open in
![]() ${\rm Aut}(G)\times {\rm Sub}_G$
, it contains (T,H) and if
${\rm Aut}(G)\times {\rm Sub}_G$
, it contains (T,H) and if
![]() $\phi\in \lfloor K,W\rfloor^{-1}$
and
$\phi\in \lfloor K,W\rfloor^{-1}$
and
![]() $L\in O_1(\overline{W})$
, then
$L\in O_1(\overline{W})$
, then
![]() $\phi(L)\in O_1(K)$
.
$\phi(L)\in O_1(K)$
.
Now suppose
![]() $T(H)\in O_2(U)=\{L\in{\rm Sub}_G\mid L\cap U\ne\emptyset\}$
. Since
$T(H)\in O_2(U)=\{L\in{\rm Sub}_G\mid L\cap U\ne\emptyset\}$
. Since
![]() $T(H)\cap U\ne\emptyset$
, there exists
$T(H)\cap U\ne\emptyset$
, there exists
![]() $x\in H$
such that
$x\in H$
such that
![]() $T(x)\in U$
. Since G is locally compact and U is open, there exists an open relatively compact set
$T(x)\in U$
. Since G is locally compact and U is open, there exists an open relatively compact set
![]() $W_1$
such that
$W_1$
such that
![]() $T(x)\in W_1\subset \overline{W}_1\subset U$
. Let
$T(x)\in W_1\subset \overline{W}_1\subset U$
. Let
![]() $V=T^{-1}(W_1)$
. Then V is relatively compact. As
$V=T^{-1}(W_1)$
. Then V is relatively compact. As
![]() $x\in V$
and
$x\in V$
and
![]() $T(\overline{V})\subset U$
, we get that
$T(\overline{V})\subset U$
, we get that
![]() $(T,H)\in \lfloor\overline{V},U\rfloor\times O_2(V)$
which is open in
$(T,H)\in \lfloor\overline{V},U\rfloor\times O_2(V)$
which is open in
![]() ${\rm Aut}(G)\times{\rm Sub}_G$
. Moreover, if
${\rm Aut}(G)\times{\rm Sub}_G$
. Moreover, if
![]() $\phi\in \lfloor\overline{V},U\rfloor$
and
$\phi\in \lfloor\overline{V},U\rfloor$
and
![]() $L\in O_2(V)$
, then
$L\in O_2(V)$
, then
![]() $\phi(L)\cap U\ne\emptyset$
. Therefore, the map
$\phi(L)\cap U\ne\emptyset$
. Therefore, the map
![]() ${\rm Aut}(G)\times{\rm Sub}_G\to{\rm Sub}_G$
as above is continuous.
${\rm Aut}(G)\times{\rm Sub}_G\to{\rm Sub}_G$
as above is continuous.
3. Distality of automorphisms on G and
 ${\rm Sub}_G$
${\rm Sub}_G$
In this section, for
![]() $T\in{\rm Aut}(G)$
, we show that the distality of the T-action on
$T\in{\rm Aut}(G)$
, we show that the distality of the T-action on
![]() ${\rm Sub}_G$
implies the distality of the corresponding action on
${\rm Sub}_G$
implies the distality of the corresponding action on
![]() ${\rm Sub}_{G/H}$
for any closed normal T-invariant subgroup H of G. We also compare the distality of the T-action on
${\rm Sub}_{G/H}$
for any closed normal T-invariant subgroup H of G. We also compare the distality of the T-action on
![]() ${\rm Sub}_G$
and that of T on G. [Reference Shah28, theorem 1·3] shows that an automorphism T of G is distal if and only if for any closed normal T-invariant subgroup H,
${\rm Sub}_G$
and that of T on G. [Reference Shah28, theorem 1·3] shows that an automorphism T of G is distal if and only if for any closed normal T-invariant subgroup H,
![]() $T|_H$
is distal and T acts distally on
$T|_H$
is distal and T acts distally on
![]() $G/H$
. Lemma 3·1 and Example 3·2 illustrate that only a partial analogue of this theorem holds for the action of automorphisms on
$G/H$
. Lemma 3·1 and Example 3·2 illustrate that only a partial analogue of this theorem holds for the action of automorphisms on
![]() ${\rm Sub}_G$
. We prove some results about the distality of automorphisms on a connected Lie group which belong to
${\rm Sub}_G$
. We prove some results about the distality of automorphisms on a connected Lie group which belong to
![]() ${\rm (NC)}$
. We also prove a result on the structure of a nilpotent group admitting a unipotent automorphism which is a generalisation of Kolchin’s Theorem for vector spaces; this will be useful to prove some of the main results. We end the section with a useful lemma about a criterion for the behaviour of an automorphism which implies that it does not belong to
${\rm (NC)}$
. We also prove a result on the structure of a nilpotent group admitting a unipotent automorphism which is a generalisation of Kolchin’s Theorem for vector spaces; this will be useful to prove some of the main results. We end the section with a useful lemma about a criterion for the behaviour of an automorphism which implies that it does not belong to
![]() ${\rm (NC)}$
.
${\rm (NC)}$
.
Lemma 3·1. Let G be a locally compact Hausdorff group,
![]() $T\in{\rm Aut}(G)$
and let H be a closed normal T-invariant subgroup of G. Let
$T\in{\rm Aut}(G)$
and let H be a closed normal T-invariant subgroup of G. Let
![]() $\overline{T}\in{\rm Aut}(G/H)$
be the corresponding map defined as
$\overline{T}\in{\rm Aut}(G/H)$
be the corresponding map defined as
![]() $\overline{T}(gH)=T(g)H$
, for all
$\overline{T}(gH)=T(g)H$
, for all
![]() $g\in G$
. If T acts distally on
$g\in G$
. If T acts distally on
![]() ${\rm Sub}_G$
, then T acts distally on
${\rm Sub}_G$
, then T acts distally on
![]() ${\rm Sub}_H$
and
${\rm Sub}_H$
and
![]() $\overline{T}$
acts distally on
$\overline{T}$
acts distally on
![]() ${\rm Sub}_{G/H}$
.
${\rm Sub}_{G/H}$
.
Proof. Suppose T acts distally on
![]() ${\rm Sub}_G$
. As
${\rm Sub}_G$
. As
![]() ${\rm Sub}_H$
is closed and T-invariant, it is easy to see that T acts distally on
${\rm Sub}_H$
is closed and T-invariant, it is easy to see that T acts distally on
![]() ${\rm Sub}_H$
. Now we show that
${\rm Sub}_H$
. Now we show that
![]() $\overline{T}$
acts distally on
$\overline{T}$
acts distally on
![]() ${\rm Sub}_{G/H}$
. Suppose G is second countable. For
${\rm Sub}_{G/H}$
. Suppose G is second countable. For
![]() $i=1,2$
, suppose
$i=1,2$
, suppose
![]() $H_i\in{\rm Sub}_{G/H}$
and a sequence
$H_i\in{\rm Sub}_{G/H}$
and a sequence
![]() $\{n_k\}\subset{\mathbb Z}$
are such that
$\{n_k\}\subset{\mathbb Z}$
are such that
![]() $\overline{T}^{n_k}(H_i)\to L$
in
$\overline{T}^{n_k}(H_i)\to L$
in
![]() ${\rm Sub}_{G/H}$
. Then
${\rm Sub}_{G/H}$
. Then
![]() $T(H)=H\subset \pi^{-1}(H_i)$
. By Lemma 2·3 (ii),
$T(H)=H\subset \pi^{-1}(H_i)$
. By Lemma 2·3 (ii),
![]() $T^{n_k}(\pi^{-1}(H_i))\to\pi^{-1}(L)$
, for
$T^{n_k}(\pi^{-1}(H_i))\to\pi^{-1}(L)$
, for
![]() $i=1,2$
. As T is distal on
$i=1,2$
. As T is distal on
![]() ${\rm Sub}_G$
,
${\rm Sub}_G$
,
![]() $\pi^{-1}(H_1)=\pi^{-1}(H_2)$
, and hence
$\pi^{-1}(H_1)=\pi^{-1}(H_2)$
, and hence
![]() $H_1=H_2$
. Thus,
$H_1=H_2$
. Thus,
![]() $\overline{T}$
acts distally on
$\overline{T}$
acts distally on
![]() ${\rm Sub}_{G/H}$
in this case.
${\rm Sub}_{G/H}$
in this case.
Now suppose G is not second countable. Let
![]() $S_H:=\{L\in{\rm Sub}_G\mid H\subset L\}$
. As
$S_H:=\{L\in{\rm Sub}_G\mid H\subset L\}$
. As
![]() $T(H)=H$
, it follows that
$T(H)=H$
, it follows that
![]() $S_H$
is a closed T-invariant subspace of
$S_H$
is a closed T-invariant subspace of
![]() ${\rm Sub}_G$
. Let
${\rm Sub}_G$
. Let
![]() $\bar\pi:S_H\to{\rm Sub}_{G/H}$
,
$\bar\pi:S_H\to{\rm Sub}_{G/H}$
,
![]() $\bar\pi(L)=\pi(L)=L/H$
,
$\bar\pi(L)=\pi(L)=L/H$
,
![]() $L\in S_H$
. Then
$L\in S_H$
. Then
![]() $\bar\pi$
is a homeomorphism such that
$\bar\pi$
is a homeomorphism such that
![]() $\overline{T}\circ\bar\pi=\bar\pi\circ T$
. As T acts distally on
$\overline{T}\circ\bar\pi=\bar\pi\circ T$
. As T acts distally on
![]() ${\rm Sub}_G$
, it acts distally on
${\rm Sub}_G$
, it acts distally on
![]() $S_H$
. Now using the homeomorphism
$S_H$
. Now using the homeomorphism
![]() $\bar\pi$
, it is easy to see that
$\bar\pi$
, it is easy to see that
![]() $\overline{T}$
acts distally on
$\overline{T}$
acts distally on
![]() ${\rm Sub}_{G/H}$
.
${\rm Sub}_{G/H}$
.
The converse of the lemma does not hold as illustrated by the following.
Example 3·2. Let
![]() $T= \begin{bmatrix} 1 & 1\\ 0 & 1 \end{bmatrix}$
in
$T= \begin{bmatrix} 1 & 1\\ 0 & 1 \end{bmatrix}$
in
![]() ${\rm GL}(2,{\mathbb R})$
. It is clear that the T-action on
${\rm GL}(2,{\mathbb R})$
. It is clear that the T-action on
![]() ${\mathbb R}^2$
is distal. Also, for
${\mathbb R}^2$
is distal. Also, for
![]() $H={\mathbb R}\times\{0\}$
, T acts trivially on H and on
$H={\mathbb R}\times\{0\}$
, T acts trivially on H and on
![]() ${\mathbb R}^2/H$
, hence it acts trivially on both
${\mathbb R}^2/H$
, hence it acts trivially on both
![]() ${\rm Sub}_H$
and
${\rm Sub}_H$
and
![]() ${\rm Sub}_{{\mathbb R}^2/H}$
, but the T-action on
${\rm Sub}_{{\mathbb R}^2/H}$
, but the T-action on
![]() ${\rm Sub}_{{\mathbb R}^2}$
is not distal, as
${\rm Sub}_{{\mathbb R}^2}$
is not distal, as
![]() $T(H)=H$
and for
$T(H)=H$
and for
![]() $H_1=\{0\}\times{\mathbb R}$
,
$H_1=\{0\}\times{\mathbb R}$
,
![]() $T^n(H_1)\rightarrow H$
in
$T^n(H_1)\rightarrow H$
in
![]() ${\rm Sub}_{{\mathbb R}^2}$
as
${\rm Sub}_{{\mathbb R}^2}$
as
![]() $n\to\pm\infty$
.
$n\to\pm\infty$
.
Recall that
![]() $T\in{\rm Aut}(G)$
belongs to
$T\in{\rm Aut}(G)$
belongs to
![]() ${\rm (NC)}$
if for any discrete (closed) nontrivial cyclic subgroup A of G,
${\rm (NC)}$
if for any discrete (closed) nontrivial cyclic subgroup A of G,
![]() $T^{n_k}(A)\not\to \{e\}$
in
$T^{n_k}(A)\not\to \{e\}$
in
![]() ${\rm Sub}_G$
for any sequence
${\rm Sub}_G$
for any sequence
![]() $\{n_k\}\subset{\mathbb Z}$
such that
$\{n_k\}\subset{\mathbb Z}$
such that
![]() ${n_k}\to\infty$
or
${n_k}\to\infty$
or
![]() ${n_k}\to -\infty$
. Note that for T as in Example 3·2 and
${n_k}\to -\infty$
. Note that for T as in Example 3·2 and
![]() $G={\mathbb R}^2$
,
$G={\mathbb R}^2$
,
![]() $T\notin{\rm (NC)}$
. This is because one can choose a discrete cyclic subgroup
$T\notin{\rm (NC)}$
. This is because one can choose a discrete cyclic subgroup
![]() $A=\{0\}\times{\mathbb Z}$
, for which
$A=\{0\}\times{\mathbb Z}$
, for which
![]() $T^n(A)=\{(nz,z)\mid z\in {\mathbb Z}\}$
,
$T^n(A)=\{(nz,z)\mid z\in {\mathbb Z}\}$
,
![]() $n\in{\mathbb Z}$
, and
$n\in{\mathbb Z}$
, and
![]() $T^n(A)\to\{(0,0)\}$
as
$T^n(A)\to\{(0,0)\}$
as
![]() $n\to\pm\infty$
.
$n\to\pm\infty$
.
A topological group is said to be monothetic if it has a dense cyclic subgroup. Monothetic groups are abelian. In a locally compact group, a closed monothetic subgroup is either compact or a discrete infinite cyclic group. The following lemma will be useful.
Lemma 3·3. Let G be a locally compact Hausdorff second countable group and let
![]() $T\in {\rm Aut}(G)$
. Let Z be a closed central T-invariant subgroup of G and let
$T\in {\rm Aut}(G)$
. Let Z be a closed central T-invariant subgroup of G and let
![]() $\overline{T}$
be the corresponding automorphism on
$\overline{T}$
be the corresponding automorphism on
![]() $G/Z$
. Suppose T acts distally on
$G/Z$
. Suppose T acts distally on
![]() ${\rm Sub}^a_G$
. Then
${\rm Sub}^a_G$
. Then
![]() $\overline{T}$
satisfies the following: for any two closed monothetic subgroups
$\overline{T}$
satisfies the following: for any two closed monothetic subgroups
![]() $A_1$
and
$A_1$
and
![]() $A_2$
in
$A_2$
in
![]() $G/Z$
, if for a sequence
$G/Z$
, if for a sequence
![]() $\{n_k\}\subset{\mathbb Z}$
,
$\{n_k\}\subset{\mathbb Z}$
,
![]() $\overline{T}^{n_k}(A_i)\to B$
,
$\overline{T}^{n_k}(A_i)\to B$
,
![]() $i=1,2$
, for some closed subgroup B in
$i=1,2$
, for some closed subgroup B in
![]() $G/Z$
, then
$G/Z$
, then
![]() $A_1=A_2$
. In particular,
$A_1=A_2$
. In particular,
![]() $\overline{T}\in {\rm (NC)}$
in
$\overline{T}\in {\rm (NC)}$
in
![]() ${\rm Aut}(G/Z)$
.
${\rm Aut}(G/Z)$
.
Proof. Let
![]() $\pi:G\to G/Z$
be the natural projection. Since each
$\pi:G\to G/Z$
be the natural projection. Since each
![]() $A_i$
is monothetic and Z is a central subgroup of G, it is easy to see that each
$A_i$
is monothetic and Z is a central subgroup of G, it is easy to see that each
![]() $\pi^{-1}(A_i)$
is abelian. By Lemma 2·3 (ii),
$\pi^{-1}(A_i)$
is abelian. By Lemma 2·3 (ii),
![]() $T^{n_k}(\pi^{-1}(A_i))\to\pi^{-1}(B)$
,
$T^{n_k}(\pi^{-1}(A_i))\to\pi^{-1}(B)$
,
![]() $i=1,2$
. Therefore,
$i=1,2$
. Therefore,
![]() $\pi^{-1}(B)\in {\rm Sub}^a_G$
. As T acts distally on
$\pi^{-1}(B)\in {\rm Sub}^a_G$
. As T acts distally on
![]() ${\rm Sub}_G$
, we get that
${\rm Sub}_G$
, we get that
![]() $\pi^{-1}(A_1)=\pi^{-1}(A_2)$
and hence that
$\pi^{-1}(A_1)=\pi^{-1}(A_2)$
and hence that
![]() $A_1=A_2$
. The second assertion follows from the first.
$A_1=A_2$
. The second assertion follows from the first.
The following useful lemma can be proved easily using Lemma 2·4. The lemma will apply in particular to the case of a connected Lie group G (with the Lie algebra
![]() $\mathcal G$
) as
$\mathcal G$
) as
![]() ${\rm Aut}(G)$
is a Lie group whose topology (inherited from
${\rm Aut}(G)$
is a Lie group whose topology (inherited from
![]() ${\rm GL}(\mathcal G)$
) coincides with the compact-open topology, as well as with the modified compact-open topology.
${\rm GL}(\mathcal G)$
) coincides with the compact-open topology, as well as with the modified compact-open topology.
Lemma 3·4. Let G be a locally compact Hausdorff group and let
![]() $T\in{\rm Aut}(G)$
be such that
$T\in{\rm Aut}(G)$
be such that
![]() $T=S\phi=\phi S$
for some
$T=S\phi=\phi S$
for some
![]() $\phi,S\in {\rm Aut}(G)$
, where
$\phi,S\in {\rm Aut}(G)$
, where
![]() $\phi$
is contained in a compact subgroup of
$\phi$
is contained in a compact subgroup of
![]() ${\rm Aut}(G)$
with respect to the modified compact-open topology. Then
${\rm Aut}(G)$
with respect to the modified compact-open topology. Then
![]() $T\in{\rm (NC)}$
if and only if
$T\in{\rm (NC)}$
if and only if
![]() $S\in{\rm (NC)}$
.
$S\in{\rm (NC)}$
.
For a locally compact group G,
![]() $T\in{\rm Aut}(G)$
and a compact T-invariant subgroup K of G,
$T\in{\rm Aut}(G)$
and a compact T-invariant subgroup K of G,
![]() $C_K(T)=\{x\in G\mid T^n(x)K\to K\mbox{ in } G/K\mbox{ as } n\to\infty\}$
is known as the K-contraction group of T. The group
$C_K(T)=\{x\in G\mid T^n(x)K\to K\mbox{ in } G/K\mbox{ as } n\to\infty\}$
is known as the K-contraction group of T. The group
![]() $C(T)=C_{\{e\}}(T)$
is known as the contraction group of T. It has been shown in [Reference Raja and SHAH26] that T is distal if and only if both C(T) and
$C(T)=C_{\{e\}}(T)$
is known as the contraction group of T. It has been shown in [Reference Raja and SHAH26] that T is distal if and only if both C(T) and
![]() $C(T^{-1})$
are trivial. For a connected Lie group G, it is well–known that
$C(T^{-1})$
are trivial. For a connected Lie group G, it is well–known that
![]() $C_K(T)=C(T)K$
[Reference Hazod and SIEBERT15]; see [Reference Raja and SHAH26] for a more general result on this decomposition.
$C_K(T)=C(T)K$
[Reference Hazod and SIEBERT15]; see [Reference Raja and SHAH26] for a more general result on this decomposition.
For an almost connected locally compact group G, let K be the largest compact normal subgroup. Then K is characteristic in G and
![]() $G/K$
is a Lie group. As observed in [Reference Raja and SHAH26], every inner automorphism of G acts distally on K. If any
$G/K$
is a Lie group. As observed in [Reference Raja and SHAH26], every inner automorphism of G acts distally on K. If any
![]() $T\in{\rm Aut}(G)$
acts distally on K, then C(T) is closed [Reference Raja and SHAH26, proposition 4·3]. The following useful lemma gives a more general result in the case of connected Lie groups. Note that the largest compact connected central subgroup of G is characteristic in G.
$T\in{\rm Aut}(G)$
acts distally on K, then C(T) is closed [Reference Raja and SHAH26, proposition 4·3]. The following useful lemma gives a more general result in the case of connected Lie groups. Note that the largest compact connected central subgroup of G is characteristic in G.
Lemma 3·5. Let G be a connected Lie group and let C be the largest compact connected central subgroup of G. Let
![]() $T\in{\rm Aut}(G)$
. Then the following hold:
$T\in{\rm Aut}(G)$
. Then the following hold:
-
(i)
 $\overline{C(T)}\subset C(T)C$
.
$\overline{C(T)}\subset C(T)C$
. -
(ii) If T acts distally on C, then C(T) is closed. In particular, if G does not have any compact central subgroup of positive dimension, then C(T) is closed.
Proof. (i) Let
![]() $D=\{d_n\}$
be a countable subgroup in C(T) which is dense in
$D=\{d_n\}$
be a countable subgroup in C(T) which is dense in
![]() $\overline{C(T)}$
and let
$\overline{C(T)}$
and let
![]() $\mu=\sum_{n\in{\mathbb N}} 2^{-n}\delta_{d_n}$
be a probability measure on G. It is easy to see that
$\mu=\sum_{n\in{\mathbb N}} 2^{-n}\delta_{d_n}$
be a probability measure on G. It is easy to see that
![]() $T^i(\mu)\to\delta_e$
as
$T^i(\mu)\to\delta_e$
as
![]() $i\to\infty$
. Now we can apply [Reference Dani and SHAH11, theorem 1·1] and get that
$i\to\infty$
. Now we can apply [Reference Dani and SHAH11, theorem 1·1] and get that
![]() $\overline{C(T)}= \textrm{supp}\mu\subset C_C(T)$
. As G is a connected Lie group, we have that
$\overline{C(T)}= \textrm{supp}\mu\subset C_C(T)$
. As G is a connected Lie group, we have that
![]() $C_C(T)=C(T)C$
[Reference Hazod and SIEBERT15, theorem 2·4]. Therefore, we get that
$C_C(T)=C(T)C$
[Reference Hazod and SIEBERT15, theorem 2·4]. Therefore, we get that
![]() $\overline{C(T)}\subset C(T)C$
and (1) follows. Moreover,
$\overline{C(T)}\subset C(T)C$
and (1) follows. Moreover,
![]() $C(T)C=\overline{C(T)}C$
and hence C(T)C is closed.
$C(T)C=\overline{C(T)}C$
and hence C(T)C is closed.
(ii) Now suppose T acts distally on C. Then
![]() $C(T)\cap C=\{e\}$
. Let
$C(T)\cap C=\{e\}$
. Let
![]() $G'=C(T)C=\overline{C(T)}C$
. Then G
′ is a closed T-invariant subgroup of G and
$G'=C(T)C=\overline{C(T)}C$
. Then G
′ is a closed T-invariant subgroup of G and
![]() $G'=C_C(\tau)$
, where
$G'=C_C(\tau)$
, where
![]() $\tau=T|_{G'}$
. As
$\tau=T|_{G'}$
. As
![]() $C(T)=C(\tau)$
,
$C(T)=C(\tau)$
,
![]() $C(\tau)\cap C=\{e\}$
. By [Reference Hazod and SIEBERT15, corollary 2·7], we get that
$C(\tau)\cap C=\{e\}$
. By [Reference Hazod and SIEBERT15, corollary 2·7], we get that
![]() $C(\tau)$
is closed in G
′. As G
′ is closed in G, we get that C(T) is closed. In particular, if G does not have any compact central subgroup of positive dimension, i.e. if C is trivial, then C(T) is closed.
$C(\tau)$
is closed in G
′. As G
′ is closed in G, we get that C(T) is closed. In particular, if G does not have any compact central subgroup of positive dimension, i.e. if C is trivial, then C(T) is closed.
For
![]() $T\in{\rm Aut}(G)$
, if the T-action on G is distal, it does not imply that the T-action on
$T\in{\rm Aut}(G)$
, if the T-action on G is distal, it does not imply that the T-action on
![]() ${\rm Sub}_G$
is distal; see Example 3·2. Conversely, the following theorem shows that for a large class of locally compact groups G, the distality of the T-action on
${\rm Sub}_G$
is distal; see Example 3·2. Conversely, the following theorem shows that for a large class of locally compact groups G, the distality of the T-action on
![]() ${\rm Sub}_G$
implies the distality of the T-action on G.
${\rm Sub}_G$
implies the distality of the T-action on G.
Theorem 3·6. Let G be a locally compact first countable (metrisable) group,
![]() $T\in{\rm Aut}(G)$
and let K be the largest compact normal subgroup of
$T\in{\rm Aut}(G)$
and let K be the largest compact normal subgroup of
![]() $G^0$
. Suppose T acts distally on
$G^0$
. Suppose T acts distally on
![]() ${\rm Sub}_G$
. Then the T-action on
${\rm Sub}_G$
. Then the T-action on
![]() $G/K^0$
is distal. Moreover, if T acts distally on
$G/K^0$
is distal. Moreover, if T acts distally on
![]() $K^0$
, then T acts distally on G.
$K^0$
, then T acts distally on G.
Proof. Let G be as above and let
![]() $T\in{\rm Aut}(G)$
. Suppose T acts distally on
$T\in{\rm Aut}(G)$
. Suppose T acts distally on
![]() ${\rm Sub}_G$
. Let K be as in the hypothesis. Note that
${\rm Sub}_G$
. Let K be as in the hypothesis. Note that
![]() $K^0$
is characteristic in G. In particular, it is T-invariant. We want to first show that the T-action on
$K^0$
is characteristic in G. In particular, it is T-invariant. We want to first show that the T-action on
![]() $G/K^0$
is distal.
$G/K^0$
is distal.
Since T acts distally on
![]() ${\rm Sub}_G$
, by Lemma 3·1, T acts distally on
${\rm Sub}_G$
, by Lemma 3·1, T acts distally on
![]() ${\rm Sub}_{G/K^0}$
. Hence, without loss of any generality, we may assume that K as above is totally disconnected and show that T is distal. By [Reference Raja and SHAH26, theorem 4·1], T is distal if and only if both C(T) and
${\rm Sub}_{G/K^0}$
. Hence, without loss of any generality, we may assume that K as above is totally disconnected and show that T is distal. By [Reference Raja and SHAH26, theorem 4·1], T is distal if and only if both C(T) and
![]() $C(T^{-1})$
are trivial.
$C(T^{-1})$
are trivial.
Step 1.
We first assume that G is second countable. Suppose G is totally disconnected. Then
![]() $K=\{e\}$
. If possible, suppose that C(T) is nontrivial. Since G is totally disconnected, there exists a neighbourhood basis of open compact subgroups
$K=\{e\}$
. If possible, suppose that C(T) is nontrivial. Since G is totally disconnected, there exists a neighbourhood basis of open compact subgroups
![]() $\{C_m\}_{m\in{\mathbb N}}$
at the identity e in G. Choose m such that
$\{C_m\}_{m\in{\mathbb N}}$
at the identity e in G. Choose m such that
![]() $C(T)\not\subset C_m$
. Let
$C(T)\not\subset C_m$
. Let
![]() $H=C_m\cap \overline{C(T)}$
. As
$H=C_m\cap \overline{C(T)}$
. As
![]() ${\rm Sub}_G$
is compact, there exists a sequence
${\rm Sub}_G$
is compact, there exists a sequence
![]() $\{n_k\}\subset{\mathbb N}$
such that
$\{n_k\}\subset{\mathbb N}$
such that
![]() $T^{-n_k}(H)\to L$
for some
$T^{-n_k}(H)\to L$
for some
![]() $L\in{\rm Sub}_G$
. As
$L\in{\rm Sub}_G$
. As
![]() $\overline{C(T)}$
is T-invariant and
$\overline{C(T)}$
is T-invariant and
![]() $H\subset \overline{C(T)}$
, by Lemma 2·2 (iii) we get that
$H\subset \overline{C(T)}$
, by Lemma 2·2 (iii) we get that
![]() $L\subset \overline{C(T)}$
. Let
$L\subset \overline{C(T)}$
. Let
![]() $x\in C(T)$
. Since
$x\in C(T)$
. Since
![]() $C_m$
is an open subgroup in G and C(T) is T-invariant, we get that
$C_m$
is an open subgroup in G and C(T) is T-invariant, we get that
![]() $T^n(x)\in C_m\cap C(T)\subset H$
for all large n, and hence, that
$T^n(x)\in C_m\cap C(T)\subset H$
for all large n, and hence, that
![]() $x=T^{-n}(T^n(x))\in T^{-n}(H)$
for all large n. Therefore,
$x=T^{-n}(T^n(x))\in T^{-n}(H)$
for all large n. Therefore,
![]() $x\in L$
and hence,
$x\in L$
and hence,
![]() $C(T)\subset L$
. As L is closed,
$C(T)\subset L$
. As L is closed,
![]() $\overline{C(T)}\subset L$
. Thus, we have that
$\overline{C(T)}\subset L$
. Thus, we have that
![]() $\overline{C(T)}=L$
, i.e.
$\overline{C(T)}=L$
, i.e.
![]() $T^{-n_k}(H)\to\overline{C(T)}$
. As
$T^{-n_k}(H)\to\overline{C(T)}$
. As
![]() $\overline{C(T)}$
is T-invariant and
$\overline{C(T)}$
is T-invariant and
![]() $H\ne \overline{C(T)}$
, we get that T does not act distally on
$H\ne \overline{C(T)}$
, we get that T does not act distally on
![]() ${\rm Sub}_G$
, a contradiction. Therefore, C(T) is trivial. Interchanging T and
${\rm Sub}_G$
, a contradiction. Therefore, C(T) is trivial. Interchanging T and
![]() $T^{-1}$
and arguing as above, we can show that
$T^{-1}$
and arguing as above, we can show that
![]() $C(T^{-1})$
is trivial.
$C(T^{-1})$
is trivial.
Step 2.
Suppose G is not totally disconnected. Note that
![]() $G^0$
is T-invariant and
$G^0$
is T-invariant and
![]() $G/G^0$
is totally disconnected. Let
$G/G^0$
is totally disconnected. Let
![]() $\overline{T}:G/G^0\to G/G^0$
be the automorphism corresponding to T. Then from Lemma 3·1,
$\overline{T}:G/G^0\to G/G^0$
be the automorphism corresponding to T. Then from Lemma 3·1,
![]() $\overline{T}$
acts distally on
$\overline{T}$
acts distally on
![]() ${\rm Sub}_{G/G^0}$
. Hence, from the assertion in Step 1,
${\rm Sub}_{G/G^0}$
. Hence, from the assertion in Step 1,
![]() $C(\overline{T})$
and
$C(\overline{T})$
and
![]() $C(\overline{T}^{-1})$
are trivial. Therefore,
$C(\overline{T}^{-1})$
are trivial. Therefore,
![]() $C(T)\cup C(T^{-1})\subset G^0$
. As K is totally disconnected and normal in
$C(T)\cup C(T^{-1})\subset G^0$
. As K is totally disconnected and normal in
![]() $G^0$
, by [Reference Shah29, lemma 2·2], it is central in
$G^0$
, by [Reference Shah29, lemma 2·2], it is central in
![]() $G^0$
(this also follows from [Reference Iwasawa18, theorem 1′]). Now
$G^0$
(this also follows from [Reference Iwasawa18, theorem 1′]). Now
![]() ${\rm Sub}_K={\rm Sub}^a_K$
. From Step 1, if T acts distally on
${\rm Sub}_K={\rm Sub}^a_K$
. From Step 1, if T acts distally on
![]() ${\rm Sub}^a_K$
, we get that T acts distally on K. Now it is enough to show that T acts distally on
${\rm Sub}^a_K$
, we get that T acts distally on K. Now it is enough to show that T acts distally on
![]() $G/K$
. As T acts distally on
$G/K$
. As T acts distally on
![]() ${\rm Sub}_{G/K}$
, replacing G by
${\rm Sub}_{G/K}$
, replacing G by
![]() $G/K$
and T by the corresponding automorphism of
$G/K$
and T by the corresponding automorphism of
![]() $G/K$
, we may assume that G is a connected Lie group without any nontrivial compact normal subgroup. We have also assumed that T acts distally on
$G/K$
, we may assume that G is a connected Lie group without any nontrivial compact normal subgroup. We have also assumed that T acts distally on
![]() ${\rm Sub}_G$
. We want to show that T is distal.
${\rm Sub}_G$
. We want to show that T is distal.
Step 3.
We prove a more general statement: if G is any connected Lie group,
![]() $T\in{\rm Aut}(G)$
acts distally on the largest compact connected central subgroup of G and if
$T\in{\rm Aut}(G)$
acts distally on the largest compact connected central subgroup of G and if
![]() $T\in{\rm (NC)}$
, then T is distal.
$T\in{\rm (NC)}$
, then T is distal.
Assume that G and T are as above. By Lemma 3·5 (ii), both C(T) and
![]() $C(T^{-1})$
are closed, and hence, simply connected and nilpotent.
$C(T^{-1})$
are closed, and hence, simply connected and nilpotent.
If possible, suppose C(T) is nontrivial. Let
![]() $V=Z(C(T))$
, the center of C(T). Then
$V=Z(C(T))$
, the center of C(T). Then
![]() $V\cong{\mathbb R}^m$
, for some
$V\cong{\mathbb R}^m$
, for some
![]() $m\in{\mathbb N}$
. Let
$m\in{\mathbb N}$
. Let
![]() $T_1=T|_{V}$
be the restriction of T to V. Then
$T_1=T|_{V}$
be the restriction of T to V. Then
![]() $T_1\in{\rm GL}(V)$
and
$T_1\in{\rm GL}(V)$
and
![]() $C(T_1)=V$
, which is turn implies that all the eigenvalues of
$C(T_1)=V$
, which is turn implies that all the eigenvalues of
![]() $T_1$
have absolute value less than 1. Suppose
$T_1$
have absolute value less than 1. Suppose
![]() $T_1$
has a real eigenvalue
$T_1$
has a real eigenvalue
![]() $\lambda$
. Then
$\lambda$
. Then
![]() $0<|\lambda|<1$
and there exists a subspace
$0<|\lambda|<1$
and there exists a subspace
![]() $W\cong{\mathbb R}$
in V such that
$W\cong{\mathbb R}$
in V such that
![]() $T_1(x)=\lambda x$
for all
$T_1(x)=\lambda x$
for all
![]() $x\in W$
. For the discrete subgroup
$x\in W$
. For the discrete subgroup
![]() ${\mathbb Z}$
in
${\mathbb Z}$
in
![]() ${\mathbb R}\cong W$
, it is easy to see that
${\mathbb R}\cong W$
, it is easy to see that
![]() $T_1^{-n}({\mathbb Z})=\lambda^{-n}{\mathbb Z}\to\{0\}$
as
$T_1^{-n}({\mathbb Z})=\lambda^{-n}{\mathbb Z}\to\{0\}$
as
![]() $n\to\infty$
in
$n\to\infty$
in
![]() ${\rm Sub}_{\mathbb R}$
[Reference Baik and ClavierL5]. As
${\rm Sub}_{\mathbb R}$
[Reference Baik and ClavierL5]. As
![]() $T|_W=T_1|_W$
, this leads to a contradiction as
$T|_W=T_1|_W$
, this leads to a contradiction as
![]() $T\in{\rm (NC)}$
.
$T\in{\rm (NC)}$
.
Now suppose all the eigenvalues of
![]() $T_1$
are complex. There exists a
$T_1$
are complex. There exists a
![]() $T_1$
-invariant subspace
$T_1$
-invariant subspace
![]() $W'\cong{\mathbb R}^2$
in V such that
$W'\cong{\mathbb R}^2$
in V such that
![]() $T_1|_{W'}$
has a complex eigenvalue of the form
$T_1|_{W'}$
has a complex eigenvalue of the form
![]() $r(\cos\theta+i\sin\theta)$
, where
$r(\cos\theta+i\sin\theta)$
, where
![]() $r\in{\mathbb R}$
and
$r\in{\mathbb R}$
and
![]() $0<r<1$
. Let
$0<r<1$
. Let
![]() $T_2\in {\rm GL}(2,{\mathbb R})$
be such that
$T_2\in {\rm GL}(2,{\mathbb R})$
be such that
![]() $T|_{W'}=T_1|_{W'}=T_2$
(under the isomorphism of
$T|_{W'}=T_1|_{W'}=T_2$
(under the isomorphism of
![]() ${\mathbb R}^2$
with W
′). Then
${\mathbb R}^2$
with W
′). Then
![]() $T_2=rA_\theta$
, where
$T_2=rA_\theta$
, where
![]() $A_\theta=AR_\theta A^{-1}$
for some
$A_\theta=AR_\theta A^{-1}$
for some
![]() $A\in {\rm GL}(2,{\mathbb R})$
, and
$A\in {\rm GL}(2,{\mathbb R})$
, and
![]() $R_\theta$
is the rotation by the angle
$R_\theta$
is the rotation by the angle
![]() $\theta$
on
$\theta$
on
![]() ${\mathbb R}^2$
. Here,
${\mathbb R}^2$
. Here,
![]() $A_\theta$
generates a relatively compact group in
$A_\theta$
generates a relatively compact group in
![]() ${\rm GL}(2,{\mathbb R})$
. Let
${\rm GL}(2,{\mathbb R})$
. Let
![]() $Z=\{(m,0)\mid m\in{\mathbb Z}\}$
. Then
$Z=\{(m,0)\mid m\in{\mathbb Z}\}$
. Then
![]() $Z\in{\rm Sub}_{{\mathbb R}^2}$
. Since
$Z\in{\rm Sub}_{{\mathbb R}^2}$
. Since
![]() $0<r<1$
, we have
$0<r<1$
, we have
![]() $r ^{-n}Z\to\{(0,0)\}$
as
$r ^{-n}Z\to\{(0,0)\}$
as
![]() $n\to\infty$
[Reference Baik and ClavierL5], and that
$n\to\infty$
[Reference Baik and ClavierL5], and that
![]() $r\,{\rm Id}\not\in{\rm (NC)}$
. Since
$r\,{\rm Id}\not\in{\rm (NC)}$
. Since
![]() $T_2=(r\,{\rm Id})A_\theta=A_\theta(r\,{\rm Id})$
, and
$T_2=(r\,{\rm Id})A_\theta=A_\theta(r\,{\rm Id})$
, and
![]() $A_\theta$
generates a relatively compact group, by Lemma 3·4, we get that
$A_\theta$
generates a relatively compact group, by Lemma 3·4, we get that
![]() $T_2\not\in{\rm (NC)}$
. As
$T_2\not\in{\rm (NC)}$
. As
![]() $T_2=T|_{W'}$
, this leads to a contradiction. Hence C(T) is trivial. Replacing T by
$T_2=T|_{W'}$
, this leads to a contradiction. Hence C(T) is trivial. Replacing T by
![]() $T^{-1}$
and arguing as above, we get that
$T^{-1}$
and arguing as above, we get that
![]() $C(T^{-1})$
is also trivial. Therefore, T is distal.
$C(T^{-1})$
is also trivial. Therefore, T is distal.
We have proved the first assertion in case G is second countable. Now suppose G is not second countable. As noted before step 1, K can be assumed to be totally disconnected and T acts distally on
![]() ${\rm Sub}_G$
. We need to show that T is distal. Suppose
${\rm Sub}_G$
. We need to show that T is distal. Suppose
![]() $x\in G$
is such that
$x\in G$
is such that
![]() $T^{n_k}(x)\to e$
in G for sone sequence
$T^{n_k}(x)\to e$
in G for sone sequence
![]() $\{n_k\}\subset {\mathbb Z}$
. Let
$\{n_k\}\subset {\mathbb Z}$
. Let
![]() $L_x$
be the subgroup generated by
$L_x$
be the subgroup generated by
![]() $O_x=\{T^n(x)\mid n\in{\mathbb Z}\}$
in G and let
$O_x=\{T^n(x)\mid n\in{\mathbb Z}\}$
in G and let
![]() $H=\overline{L_xG^0}$
. Then H is a closed T-invariant subgroup of G. As
$H=\overline{L_xG^0}$
. Then H is a closed T-invariant subgroup of G. As
![]() $O_x$
, and hence,
$O_x$
, and hence,
![]() $L_x$
is countable, we have that
$L_x$
is countable, we have that
![]() $H/H'$
is countable for some open almost connected subgroup H
′ of H. Since H
′ is compactly generated and first countable, and hence second countable, we get that H is second countable. As
$H/H'$
is countable for some open almost connected subgroup H
′ of H. Since H
′ is compactly generated and first countable, and hence second countable, we get that H is second countable. As
![]() $H^0=G^0$
, K is the largest compact normal subgroup of
$H^0=G^0$
, K is the largest compact normal subgroup of
![]() $H^0$
and K is totally disconnected. Since T acts distally on
$H^0$
and K is totally disconnected. Since T acts distally on
![]() ${\rm Sub}_G$
and since
${\rm Sub}_G$
and since
![]() ${\rm Sub}_H$
is closed in
${\rm Sub}_H$
is closed in
![]() ${\rm Sub}_G$
, we have that
${\rm Sub}_G$
, we have that
![]() $T|_H$
acts distally on
$T|_H$
acts distally on
![]() ${\rm Sub}_H$
. As H is second countable, we get from above that
${\rm Sub}_H$
. As H is second countable, we get from above that
![]() $T|_H$
is distal. Therefore,
$T|_H$
is distal. Therefore,
![]() $x=e$
and T is distal.
$x=e$
and T is distal.
We have proved that if T acts distally on
![]() ${\rm Sub}_G$
, then T acts distally on
${\rm Sub}_G$
, then T acts distally on
![]() $G/K^0$
, where K is the largest compact normal subgroup of
$G/K^0$
, where K is the largest compact normal subgroup of
![]() $G^0$
. Moreover, if T also acts distally on
$G^0$
. Moreover, if T also acts distally on
![]() $K^0$
, then it is easy to show that T acts distally on G.
$K^0$
, then it is easy to show that T acts distally on G.
We get a stronger result in case of Lie groups as follows.
Corollary 3·7. Let G be a Lie group with not necessarily finitely many connected components and let
![]() $T\in{\rm Aut}(G)$
and let C be the largest compact connected central subgroup of
$T\in{\rm Aut}(G)$
and let C be the largest compact connected central subgroup of
![]() $G^0$
. Then the following hold:
$G^0$
. Then the following hold:
-
(a) If T acts distally on C and
 $T\in{\rm (NC)}$
, then T acts distally on G.
$T\in{\rm (NC)}$
, then T acts distally on G. -
(b) If T acts distally on
 ${\rm Sub}^a_G$
, then T acts distally on
${\rm Sub}^a_G$
, then T acts distally on
 $G/C$
.
$G/C$
.
Proof. As
![]() $G/G^0$
is discrete and C as above is characteristic in G, T acts distally on G (resp.
$G/G^0$
is discrete and C as above is characteristic in G, T acts distally on G (resp.
![]() $G/C$
) if and only if T acts distally on
$G/C$
) if and only if T acts distally on
![]() $G^0$
(resp.
$G^0$
(resp.
![]() $G^0/C$
). Moreover,
$G^0/C$
). Moreover,
![]() ${\rm Sub}^a_{G^0}$
is closed in
${\rm Sub}^a_{G^0}$
is closed in
![]() ${\rm Sub}^a_G$
and, if
${\rm Sub}^a_G$
and, if
![]() $T\in{\rm (NC)}$
(resp. T acts distally on
$T\in{\rm (NC)}$
(resp. T acts distally on
![]() ${\rm Sub}^a_G$
), then
${\rm Sub}^a_G$
), then
![]() $T|_{G^0}\in{\rm (NC)}$
(resp.
$T|_{G^0}\in{\rm (NC)}$
(resp.
![]() $T|_{G^0}$
acts distally on
$T|_{G^0}$
acts distally on
![]() ${\rm Sub}^a_{G^0}$
). Thus, to prove (a) and (b), we may assume that G is connected and C is central in G. Now (a) follows from the general statement in step 3 of the proof of Theorem 3·6. To prove (b), suppose T acts distally on
${\rm Sub}^a_{G^0}$
). Thus, to prove (a) and (b), we may assume that G is connected and C is central in G. Now (a) follows from the general statement in step 3 of the proof of Theorem 3·6. To prove (b), suppose T acts distally on
![]() ${\rm Sub}^a_G$
, where G is connected as assumed above. As C is central in G, by Lemma 3·3 we get that the automorphism of
${\rm Sub}^a_G$
, where G is connected as assumed above. As C is central in G, by Lemma 3·3 we get that the automorphism of
![]() $G/C$
corresponding to T belongs to
$G/C$
corresponding to T belongs to
![]() ${\rm (NC)}$
. As
${\rm (NC)}$
. As
![]() $G/C$
does not have a compact central subgroup of positive dimension, (a) implies that T acts distally on
$G/C$
does not have a compact central subgroup of positive dimension, (a) implies that T acts distally on
![]() $G/C$
.
$G/C$
.
Remark 3·8. Note that the first condition in (a) of Corollary 3·7 is necessary as every automorphism of the compact connected abelian Lie group
![]() $G={\mathbb T}^n$
, (
$G={\mathbb T}^n$
, (
![]() $n\geq 2$
), belongs to
$n\geq 2$
), belongs to
![]() ${\rm (NC)}$
, but G admits automorphisms which are not distal. Here,
${\rm (NC)}$
, but G admits automorphisms which are not distal. Here,
![]() ${\rm Aut}(G)$
is isomorphic to
${\rm Aut}(G)$
is isomorphic to
![]() ${\rm GL}(n,{\mathbb Z})$
. Any closed cyclic group A of G is finite and it is contained in a finite characteristic subgroup
${\rm GL}(n,{\mathbb Z})$
. Any closed cyclic group A of G is finite and it is contained in a finite characteristic subgroup
![]() $A_m$
, the set of all m-th roots of unity, for some
$A_m$
, the set of all m-th roots of unity, for some
![]() $m\in{\mathbb N}$
which depends on A. Now for any
$m\in{\mathbb N}$
which depends on A. Now for any
![]() $T\in{\rm Aut}(G)$
,
$T\in{\rm Aut}(G)$
,
![]() $T|_{A_m}$
has finite order, and hence
$T|_{A_m}$
has finite order, and hence
![]() $T\in{\rm (NC)}$
. However, if we take any hyperbolic map in
$T\in{\rm (NC)}$
. However, if we take any hyperbolic map in
![]() ${\rm GL}(2,{\mathbb Z})$
, its eigenvalues are of absolute value other than 1, and hence it is not distal on
${\rm GL}(2,{\mathbb Z})$
, its eigenvalues are of absolute value other than 1, and hence it is not distal on
![]() ${\mathbb T}^2$
. For
${\mathbb T}^2$
. For
![]() $n\geq 3$
, we can take a hyperbolic map on
$n\geq 3$
, we can take a hyperbolic map on
![]() ${\mathbb T}^2$
and extend it to
${\mathbb T}^2$
and extend it to
![]() ${\mathbb T}^n\cong{\mathbb T}^2\times {\mathbb T}^{n-2}$
naturally by putting the identity map on
${\mathbb T}^n\cong{\mathbb T}^2\times {\mathbb T}^{n-2}$
naturally by putting the identity map on
![]() ${\mathbb T}^{n-2}$
.
${\mathbb T}^{n-2}$
.
A locally compact group G is said to be pointwise distal if every inner automorphism is distal on G. The group G is said to be distal if the conjugacy action of G on G is distal, i.e. for
![]() $x\in G$
, the closure of
$x\in G$
, the closure of
![]() $\{gxg^{-1}\mid g\in G\}$
does not contain the identity e unless
$\{gxg^{-1}\mid g\in G\}$
does not contain the identity e unless
![]() $x=e$
. We get the following for inner automorphisms of almost connected groups.
$x=e$
. We get the following for inner automorphisms of almost connected groups.
Corollary 3·9. Let G be an almost connected locally compact Hausdorff group. If every inner automorphism of G belongs to
![]() ${\rm (NC)}$
, then G is distal. In particular, if every inner automorphism of G acts distally on
${\rm (NC)}$
, then G is distal. In particular, if every inner automorphism of G acts distally on
![]() ${\rm Sub}^a_G$
, then G is distal.
${\rm Sub}^a_G$
, then G is distal.
Proof. Let K be the largest compact normal subgroup of G. Let T be an inner automorphism of G. It is easy to see that T acts distally on K (see the last part of the proof of [Reference Raja and SHAH26, theorem 5·2]). Hence C(T) is closed and a simply connected nilpotent Lie group [Reference Raja and SHAH26, proposition 4·3]. In particular, it has no nontrivial compact subgroups. Moreover, if
![]() $T\in{\rm (NC)}$
, then
$T\in{\rm (NC)}$
, then
![]() $T|_{C(T)}$
also belongs to
$T|_{C(T)}$
also belongs to
![]() ${\rm (NC)}$
, and from Corollary 3·7 (a), it follows that
${\rm (NC)}$
, and from Corollary 3·7 (a), it follows that
![]() $T|_{C(T)}$
is distal i.e.
$T|_{C(T)}$
is distal i.e.
![]() $C(T)=\{e\}$
. Since this is true for all inner automorphisms of G, by [Reference Raja and SHAH26, theorem 4·1], we have that G is pointwise distal, and hence it is distal [Reference Rosenblatt27, theorem 9]. The second assertion follows from the first.
$C(T)=\{e\}$
. Since this is true for all inner automorphisms of G, by [Reference Raja and SHAH26, theorem 4·1], we have that G is pointwise distal, and hence it is distal [Reference Rosenblatt27, theorem 9]. The second assertion follows from the first.
Recall that an automorphism T of a connected Lie group is unipotent if the corresponding map
![]() ${\rm d}\, T$
on the Lie algebra is a unipotent linear transformation, i.e. all the eigenvalues of
${\rm d}\, T$
on the Lie algebra is a unipotent linear transformation, i.e. all the eigenvalues of
![]() ${\rm d}\, T$
are equal to 1. The following proposition will be very useful. In the special case of vector spaces, it is well known as Kolchin’s Theorem. It is also easy to deduce for compact connected abelian Lie groups by considering the corresponding map on the Lie algebra (see also [Reference Abels2, lemma 2·5]).
${\rm d}\, T$
are equal to 1. The following proposition will be very useful. In the special case of vector spaces, it is well known as Kolchin’s Theorem. It is also easy to deduce for compact connected abelian Lie groups by considering the corresponding map on the Lie algebra (see also [Reference Abels2, lemma 2·5]).
Proposition 3·10. Let G be a connected nilpotent Lie group and let
![]() $T\in{\rm Aut}(G)$
be unipotent. Then either
$T\in{\rm Aut}(G)$
be unipotent. Then either
![]() $T={\rm Id}$
or G has an increasing sequence of closed connected normal T-invariant subgroups
$T={\rm Id}$
or G has an increasing sequence of closed connected normal T-invariant subgroups
![]() $\{e\}= G_0 \subset G_1\subset \cdots \subset G_n=G$
,
$\{e\}= G_0 \subset G_1\subset \cdots \subset G_n=G$
,
![]() $n\geq 2$
, such that T acts trivially on
$n\geq 2$
, such that T acts trivially on
![]() $G_i/G_{i-1}$
,
$G_i/G_{i-1}$
,
![]() $1\leq i\leq n$
, and T does not act trivially on
$1\leq i\leq n$
, and T does not act trivially on
![]() $G_{i+1}/G_{i-1}$
,
$G_{i+1}/G_{i-1}$
,
![]() $1\leq i\leq n-1$
.
$1\leq i\leq n-1$
.
Proof. Suppose
![]() $T\ne{\rm Id}$
. As G is nilpotent,
$T\ne{\rm Id}$
. As G is nilpotent,
![]() $G/K$
is simply connected, where K is the largest compact connected central subgroup in G. Then G has a sequence of closed connected normal T-invariant subgroups
$G/K$
is simply connected, where K is the largest compact connected central subgroup in G. Then G has a sequence of closed connected normal T-invariant subgroups
![]() $\{e\}=Z_0\subset Z_1=K\subset \cdots \subset Z_m=G$
, such that
$\{e\}=Z_0\subset Z_1=K\subset \cdots \subset Z_m=G$
, such that
![]() $Z_1/Z_0=K$
and if G is not compact,
$Z_1/Z_0=K$
and if G is not compact,
![]() $Z_i/Z_{i-1}$
is a vector group and it is the center of
$Z_i/Z_{i-1}$
is a vector group and it is the center of
![]() $G/Z_{i-1}$
, for all
$G/Z_{i-1}$
, for all
![]() $i=2,\ldots, m$
. The automorphism on each
$i=2,\ldots, m$
. The automorphism on each
![]() $Z_i/Z_{i-1}$
corresponding to T is unipotent. From Kolchin’s Theorem for vector spaces and [Reference Abels2, lemma 2·5] for compact connected abelian Lie groups, it follows that there exists a sequence of closed connected normal subgroups in each
$Z_i/Z_{i-1}$
corresponding to T is unipotent. From Kolchin’s Theorem for vector spaces and [Reference Abels2, lemma 2·5] for compact connected abelian Lie groups, it follows that there exists a sequence of closed connected normal subgroups in each
![]() $Z_i/Z_{i-1}$
such that T-acts trivially on each successive quotient. Taking the pre-images of these subgroups in
$Z_i/Z_{i-1}$
such that T-acts trivially on each successive quotient. Taking the pre-images of these subgroups in
![]() $Z_i$
, we see that they are closed and T-invariant. Also since
$Z_i$
, we see that they are closed and T-invariant. Also since
![]() $Z_i/Z_{i-1}$
is central in
$Z_i/Z_{i-1}$
is central in
![]() $G/Z_{i-1}$
, any subgroup of
$G/Z_{i-1}$
, any subgroup of
![]() $Z_i$
which contains
$Z_i$
which contains
![]() $Z_{i-1}$
is normal in G. Now we have a finite sequence of closed connected normal T-invariant subgroups
$Z_{i-1}$
is normal in G. Now we have a finite sequence of closed connected normal T-invariant subgroups
![]() $\{e\}=H_0\subset \cdots\subset H_l=G$
, such that T acts trivially on
$\{e\}=H_0\subset \cdots\subset H_l=G$
, such that T acts trivially on
![]() $H_i/H_{i-1}$
,
$H_i/H_{i-1}$
,
![]() $i=1,\ldots l$
. As
$i=1,\ldots l$
. As
![]() $T\ne{\rm Id}$
and T acts trivially on
$T\ne{\rm Id}$
and T acts trivially on
![]() $H_1$
, there exists
$H_1$
, there exists
![]() $i_1$
such that
$i_1$
such that
![]() $1\leq i_1< l$
, T acts trivially on
$1\leq i_1< l$
, T acts trivially on
![]() $H_{i_1}$
and T does not act trivially on
$H_{i_1}$
and T does not act trivially on
![]() $H_{i_1+1}$
. Let
$H_{i_1+1}$
. Let
![]() $G_1=H_{i_1}$
. Having chosen
$G_1=H_{i_1}$
. Having chosen
![]() $G_k=H_{i_k}$
for
$G_k=H_{i_k}$
for
![]() $k\geq 1$
, if
$k\geq 1$
, if
![]() $G_k\ne G$
(equivalently,
$G_k\ne G$
(equivalently,
![]() $i_k\ne l$
), we choose
$i_k\ne l$
), we choose
![]() $G_{k+1}=H_j$
, where
$G_{k+1}=H_j$
, where
![]() $i_k<j\leq l$
and j is the largest such natural number such that T acts trivially on
$i_k<j\leq l$
and j is the largest such natural number such that T acts trivially on
![]() $H_j/G_k$
. As l is finite, there exists n such that
$H_j/G_k$
. As l is finite, there exists n such that
![]() $G_n=H_l=G$
.
$G_n=H_l=G$
.
The following is known but we give a proof for the sake of completeness. It does not hold for general compact abelian groups as there are some compact totally disconnected abelian groups which are torsion-free, e.g.
![]() ${\mathbb Z}_p$
, the ring of p-adic integers in
${\mathbb Z}_p$
, the ring of p-adic integers in
![]() ${\mathbb Q}_p$
, p a prime.
${\mathbb Q}_p$
, p a prime.
Lemma 3·11. Let G be a nontrivial connected compact abelian Lie group. Let
![]() $B_n=\{x\in G\mid x^n=e\}$
,
$B_n=\{x\in G\mid x^n=e\}$
,
![]() $n\in{\mathbb N}$
. Then the following holds: if
$n\in{\mathbb N}$
. Then the following holds: if
![]() $\{a_n\}\subset{\mathbb N}$
is an unbounded sequence, then
$\{a_n\}\subset{\mathbb N}$
is an unbounded sequence, then
![]() $\cup_n B_{a_n}$
is dense in G. In particular, the torsion group
$\cup_n B_{a_n}$
is dense in G. In particular, the torsion group
![]() $B=\cup_nB_n$
is a dense subgroup in G.
$B=\cup_nB_n$
is a dense subgroup in G.
Proof. Note that each
![]() $B_n$
is a finite subgroup and as G is abelian,
$B_n$
is a finite subgroup and as G is abelian,
![]() $B_mB_n\subset B_{mn}$
,
$B_mB_n\subset B_{mn}$
,
![]() $m,n\in{\mathbb N}$
. Hence B is a group. It follows from the first statement that B is dense in G.
$m,n\in{\mathbb N}$
. Hence B is a group. It follows from the first statement that B is dense in G.
Let
![]() $B'=\cup_n B_{a_n}$
. We may assume that
$B'=\cup_n B_{a_n}$
. We may assume that
![]() $\{a_n\}$
is strictly increasing and that
$\{a_n\}$
is strictly increasing and that
![]() $a_n\to \infty$
. As
$a_n\to \infty$
. As
![]() $G={\mathbb T}^k=({\mathbb S}^1)^k$
, where
$G={\mathbb T}^k=({\mathbb S}^1)^k$
, where
![]() ${\mathbb S}^1$
is the unit circle and
${\mathbb S}^1$
is the unit circle and
![]() $k=\dim G$
, it is enough to prove the statement for
$k=\dim G$
, it is enough to prove the statement for
![]() $G={\mathbb S}^1$
. There exists a continuous real one-parameter subgroup
$G={\mathbb S}^1$
. There exists a continuous real one-parameter subgroup
![]() $\{x(t)\}_{t\in{\mathbb R}}$
such that
$\{x(t)\}_{t\in{\mathbb R}}$
such that
![]() $x(0)=x(1)=e$
,
$x(0)=x(1)=e$
,
![]() $x(t)\ne e$
for all
$x(t)\ne e$
for all
![]() $t\in ]0,1[$
and
$t\in ]0,1[$
and
![]() $G=\{x(t)\mid t\in[0,1[\}$
. Now
$G=\{x(t)\mid t\in[0,1[\}$
. Now
![]() $x(1/a_n)\in B_{a_n}$
and
$x(1/a_n)\in B_{a_n}$
and
![]() $x(1/a_n)\to x(0)=e$
. Let
$x(1/a_n)\to x(0)=e$
. Let
![]() $t\in ]0,1[$
. As
$t\in ]0,1[$
. As
![]() $1/a_n\to 0$
, there exist
$1/a_n\to 0$
, there exist
![]() $m_n\in{\mathbb N}$
,
$m_n\in{\mathbb N}$
,
![]() $n\in{\mathbb N}$
, such that
$n\in{\mathbb N}$
, such that
![]() $m_n<a_n$
for all large n, and
$m_n<a_n$
for all large n, and
![]() $m_n/a_n\to t$
. Therefore,
$m_n/a_n\to t$
. Therefore,
![]() $x(m_n/a_n)\to x(t)$
. As
$x(m_n/a_n)\to x(t)$
. As
![]() $x(m_n/a_n)\in B_{a_n}$
, we get that B
′ is dense in G.
$x(m_n/a_n)\in B_{a_n}$
, we get that B
′ is dense in G.
Note that in a locally compact group G, the subgroup
![]() $G_x$
generated by an element x is either closed and hence a discrete cyclic group, or its closure
$G_x$
generated by an element x is either closed and hence a discrete cyclic group, or its closure
![]() $\overline{G}_x$
, being a compactly generated (locally compact) abelian group, is compact. If G is a Lie group, then either
$\overline{G}_x$
, being a compactly generated (locally compact) abelian group, is compact. If G is a Lie group, then either
![]() $G_x$
is discrete or
$G_x$
is discrete or
![]() $\overline{G}_x$
is a compact Lie group with finitely many connected components.
$\overline{G}_x$
is a compact Lie group with finitely many connected components.
We now state and prove a lemma which will play a crucial role in the proofs of main results in Section 4. Since we need to use Lemma 3·11 for the proof, we state it only for Lie groups even though it may hold for some locally compact (non-discrete) groups.
For
![]() $T\in{\rm Aut}(G)$
, let
$T\in{\rm Aut}(G)$
, let
![]() $S_T=\{x\in G\mid T(x)=x\}$
be the stabiliser of T. It is a closed subgroup of G.
$S_T=\{x\in G\mid T(x)=x\}$
be the stabiliser of T. It is a closed subgroup of G.
Lemma 3·12. Let G be a Lie group with not necessarily finitely many connected components and let
![]() $T\in{\rm Aut}(G)$
. Let H be a closed normal T-invariant subgroup of G such that H does not contain any nontrivial compact subgroup and
$T\in{\rm Aut}(G)$
. Let H be a closed normal T-invariant subgroup of G such that H does not contain any nontrivial compact subgroup and
![]() $T|_H={\rm Id}$
. Suppose there exists
$T|_H={\rm Id}$
. Suppose there exists
![]() $x\in G$
such that
$x\in G$
such that
![]() $T(x)=xy$
for some
$T(x)=xy$
for some
![]() $y\in H$
,
$y\in H$
,
![]() $y\ne e$
. Let
$y\ne e$
. Let
![]() $G_x$
be the cyclic subgroup generated by x. If
$G_x$
be the cyclic subgroup generated by x. If
![]() $G_x\cap S_T=\{e\}$
, then
$G_x\cap S_T=\{e\}$
, then
![]() $T\not\in{\rm (NC)}$
.
$T\not\in{\rm (NC)}$
.
Proof. Let G, T, H, x and y be as above. Suppose
![]() $G_x\cap S_T=\{e\}$
. Let G(x,y) be the subgroup of G generated by x and y. Then G(x,y) is countable and T-invariant, and its closure
$G_x\cap S_T=\{e\}$
. Let G(x,y) be the subgroup of G generated by x and y. Then G(x,y) is countable and T-invariant, and its closure
![]() $\overline{G(x,y)}$
is a T-invariant Lie subgroup, which is separable, and hence second countable. In particular,
$\overline{G(x,y)}$
is a T-invariant Lie subgroup, which is separable, and hence second countable. In particular,
![]() $\overline{G(x,y)}$
has countably many connected components. Replacing G by
$\overline{G(x,y)}$
has countably many connected components. Replacing G by
![]() $\overline{G(x,y)}$
, T by its restriction to
$\overline{G(x,y)}$
, T by its restriction to
![]() ${\overline{G(x,y)}}$
, and H by
${\overline{G(x,y)}}$
, and H by
![]() $\overline{G(x,y)}\cap H$
, we may assume that G is second countable and
$\overline{G(x,y)}\cap H$
, we may assume that G is second countable and
![]() $G/H$
is an abelian Lie group which is either discrete or compact. Now
$G/H$
is an abelian Lie group which is either discrete or compact. Now
![]() ${\rm Sub}_G$
is metrisable. We show that
${\rm Sub}_G$
is metrisable. We show that
![]() $T\not\in{\rm (NC)}$
. Since H is T-invariant and normal in G, we get for every
$T\not\in{\rm (NC)}$
. Since H is T-invariant and normal in G, we get for every
![]() $n\in{\mathbb Z}$
that
$n\in{\mathbb Z}$
that
![]() $T(x^n)=x^ny_n$
for some
$T(x^n)=x^ny_n$
for some
![]() $y_n\in H$
, where
$y_n\in H$
, where
![]() $y_n\ne e$
unless
$y_n\ne e$
unless
![]() $x^n=e$
, as
$x^n=e$
, as
![]() $G_x\cap S_T=\{e\}$
.
$G_x\cap S_T=\{e\}$
.
Step 1.
Suppose
![]() $G/H$
is discrete, i.e.
$G/H$
is discrete, i.e.
![]() $G=G_xH$
. We first show that
$G=G_xH$
. We first show that
![]() $G_x$
is discrete. Observe that if
$G_x$
is discrete. Observe that if
![]() $G_xH/H$
is finite, then for some
$G_xH/H$
is finite, then for some
![]() $n\in{\mathbb N}$
,
$n\in{\mathbb N}$
,
![]() $x^n\in G_x\cap H\subset G_x\cap S_T=\{e\}$
, and hence
$x^n\in G_x\cap H\subset G_x\cap S_T=\{e\}$
, and hence
![]() $G_x$
is finite. If possible, suppose
$G_x$
is finite. If possible, suppose
![]() $G_x$
is not discrete. Then
$G_x$
is not discrete. Then
![]() $G_x$
is infinite and relatively compact. This implies that
$G_x$
is infinite and relatively compact. This implies that
![]() $G/H=G_xH/H$
is compact, and hence it is finite. Then we get as above that
$G/H=G_xH/H$
is compact, and hence it is finite. Then we get as above that
![]() $G_x$
is finite, and it leads to a contradiction. Therefore,
$G_x$
is finite, and it leads to a contradiction. Therefore,
![]() $G_x$
is discrete, and hence, closed.
$G_x$
is discrete, and hence, closed.
There exists an unbounded sequence
![]() $\{n_k\}\subset{\mathbb N}$
such that
$\{n_k\}\subset{\mathbb N}$
such that
![]() $T^{n_k}(G_x)\to L$
(say). We show that
$T^{n_k}(G_x)\to L$
(say). We show that
![]() $L=\{e\}$
. If possible, suppose
$L=\{e\}$
. If possible, suppose
![]() $a\in L$
is such that
$a\in L$
is such that
![]() $a\ne e$
. Replacing a by
$a\ne e$
. Replacing a by
![]() $a^{-1}$
if necessary, we get that there exists
$a^{-1}$
if necessary, we get that there exists
![]() $\{m_k\}\subset{\mathbb N}$
such that
$\{m_k\}\subset{\mathbb N}$
such that
![]() $T^{n_k}(x^{m_k})\to a$
. If
$T^{n_k}(x^{m_k})\to a$
. If
![]() $G_x$
is finite, then passing to a subsequence if necessary, we can choose
$G_x$
is finite, then passing to a subsequence if necessary, we can choose
![]() $m_k=m_1$
for all k. Suppose
$m_k=m_1$
for all k. Suppose
![]() $G_x$
is infinite. As observed above,
$G_x$
is infinite. As observed above,
![]() $G/H$
is also infinite. Let
$G/H$
is also infinite. Let
![]() $\pi:G\to G/H$
be the natural projection. Since
$\pi:G\to G/H$
be the natural projection. Since
![]() $T(x)\in xH$
, we have that
$T(x)\in xH$
, we have that
![]() $\pi(x^{m_k})\to \pi(a)$
. As
$\pi(x^{m_k})\to \pi(a)$
. As
![]() $G/H$
is infinite and discrete, we get that
$G/H$
is infinite and discrete, we get that
![]() $\{m_k\}$
is eventually constant. In either case, we have that
$\{m_k\}$
is eventually constant. In either case, we have that
![]() $T^{n_k}(x^m)\to a$
for some
$T^{n_k}(x^m)\to a$
for some
![]() $m\in{\mathbb N}$
. Then
$m\in{\mathbb N}$
. Then
![]() $T^{n_k}(x^m)=x^my_m^{n_k}\to a$
. Also, since
$T^{n_k}(x^m)=x^my_m^{n_k}\to a$
. Also, since
![]() $a\ne e$
, we get that
$a\ne e$
, we get that
![]() $x^m\ne e$
and hence
$x^m\ne e$
and hence
![]() $y_m\ne e$
. Therefore,
$y_m\ne e$
. Therefore,
![]() $\{y_m^{n_k}\}_{k\in{\mathbb N}}$
is convergent, and hence
$\{y_m^{n_k}\}_{k\in{\mathbb N}}$
is convergent, and hence
![]() $y_m$
is contained in a nontrivial compact subgroup in H. This leads to a contradiction. Therefore,
$y_m$
is contained in a nontrivial compact subgroup in H. This leads to a contradiction. Therefore,
![]() $L=\{e\}$
and
$L=\{e\}$
and
![]() $T\not\in{\rm (NC)}$
.
$T\not\in{\rm (NC)}$
.
Step 2.
Now suppose
![]() $G/H$
is not discrete. As
$G/H$
is not discrete. As
![]() $G_xH$
is dense in G, we have that
$G_xH$
is dense in G, we have that
![]() $G/H$
is compact and
$G/H$
is compact and
![]() $G_x$
is infinite. Since
$G_x$
is infinite. Since
![]() $G/H$
is abelian and
$G/H$
is abelian and
![]() $H\subset S_T$
, we have that
$H\subset S_T$
, we have that
![]() $S_T$
is normal in G. Moreover,
$S_T$
is normal in G. Moreover,
![]() $G/S_T$
is infinite, as
$G/S_T$
is infinite, as
![]() $G_x$
is infinite and
$G_x$
is infinite and
![]() $G_x\cap S_T=\{e\}$
. As G is a Lie group,
$G_x\cap S_T=\{e\}$
. As G is a Lie group,
![]() $G^0$
, and hence,
$G^0$
, and hence,
![]() $G^0H$
is an open subgroup in G. Therefore,
$G^0H$
is an open subgroup in G. Therefore,
![]() $G/G^0H$
, being compact, is finite. We may replace x by
$G/G^0H$
, being compact, is finite. We may replace x by
![]() $x^n$
for some
$x^n$
for some
![]() $n\in{\mathbb N}$
and assume that
$n\in{\mathbb N}$
and assume that
![]() $G=G^0H$
. Here,
$G=G^0H$
. Here,
![]() $G^0/(G^0\cap H)$
is connected, and it is also compact as it is isomorphic to
$G^0/(G^0\cap H)$
is connected, and it is also compact as it is isomorphic to
![]() $G/H$
. Since
$G/H$
. Since
![]() $G/S_T$
is infinite and
$G/S_T$
is infinite and
![]() $H\subset S_T$
, we get that
$H\subset S_T$
, we get that
![]() $G/S_T=(G^0H)/S_T$
, and hence
$G/S_T=(G^0H)/S_T$
, and hence
![]() $G^0/(G^0\cap S_T)$
is compact and infinite.
$G^0/(G^0\cap S_T)$
is compact and infinite.
Note that
![]() $G^0$
is T-invariant, T acts trivially on
$G^0$
is T-invariant, T acts trivially on
![]() $H\cap G^0$
and on
$H\cap G^0$
and on
![]() $G^0/(H\cap G^0)$
. Also,
$G^0/(H\cap G^0)$
. Also,
![]() $xh\in G^0$
for some
$xh\in G^0$
for some
![]() $h\in H$
,
$h\in H$
,
![]() $T(xh)\in xH\cap G^0=xh(H\cap G^0)$
and
$T(xh)\in xH\cap G^0=xh(H\cap G^0)$
and
![]() $G_{xh}\cap S_T=\{e\}$
. Moreover
$G_{xh}\cap S_T=\{e\}$
. Moreover
![]() $G_{xh}(H\cap G^0)$
is dense in
$G_{xh}(H\cap G^0)$
is dense in
![]() $G^0$
and
$G^0$
and
![]() $G_{xh}$
is infinite, as
$G_{xh}$
is infinite, as
![]() $G_{xh}H=G_xH$
. We may replace x by xh and assume that
$G_{xh}H=G_xH$
. We may replace x by xh and assume that
![]() $x\in G^0$
, and we may also replace G, H by
$x\in G^0$
, and we may also replace G, H by
![]() $G^0$
,
$G^0$
,
![]() $H\cap G^0$
respectively, and assume G is a connected Lie group,
$H\cap G^0$
respectively, and assume G is a connected Lie group,
![]() $G/H$
is a compact connected abelian Lie group and
$G/H$
is a compact connected abelian Lie group and
![]() $G/S_T$
is infinite and compact. Note that
$G/S_T$
is infinite and compact. Note that
![]() $T(g)\in gH$
for all
$T(g)\in gH$
for all
![]() $g\in G$
. Let
$g\in G$
. Let
![]() $Q=\{g^{-1}T(g)\mid g\in G\}$
. Then
$Q=\{g^{-1}T(g)\mid g\in G\}$
. Then
![]() $e\in Q\subset H$
and, Q is connected as G is so. Therefore,
$e\in Q\subset H$
and, Q is connected as G is so. Therefore,
![]() $Q\subset H^0$
, and hence
$Q\subset H^0$
, and hence
![]() $T(g)\in gH^0$
for all
$T(g)\in gH^0$
for all
![]() $g\in G$
. Here,
$g\in G$
. Here,
![]() $H/H^0$
, being a discrete normal subgroup of
$H/H^0$
, being a discrete normal subgroup of
![]() $G/H^0$
, is central in
$G/H^0$
, is central in
![]() $G/H^0$
. Hence,
$G/H^0$
. Hence,
![]() $G/H^0$
is a covering group of
$G/H^0$
is a covering group of
![]() $G/H$
, and the later is abelian. Therefore,
$G/H$
, and the later is abelian. Therefore,
![]() $G/H^0$
is abelian and, being connected, it is isomorphic to
$G/H^0$
is abelian and, being connected, it is isomorphic to
![]() ${\mathbb R}^n\times {\mathbb T}^m$
, for
${\mathbb R}^n\times {\mathbb T}^m$
, for
![]() $n,m\geq 0$
and
$n,m\geq 0$
and
![]() $m+n\in{\mathbb N}$
. Let
$m+n\in{\mathbb N}$
. Let
![]() $\pi_0: G\to G/H^0$
be the natural projection.
$\pi_0: G\to G/H^0$
be the natural projection.
Suppose
![]() $m\in{\mathbb N}$
. Let
$m\in{\mathbb N}$
. Let
![]() $M=\pi_0^{-1}({\mathbb T}^m)$
. Then M is a closed connected T-invariant Lie subgroup and
$M=\pi_0^{-1}({\mathbb T}^m)$
. Then M is a closed connected T-invariant Lie subgroup and
![]() $H^0\subset M$
. By Theorem 3·7 in Ch. XV of [Reference Hochschild17],
$H^0\subset M$
. By Theorem 3·7 in Ch. XV of [Reference Hochschild17],
![]() $M=CH^0$
, where C is a maximal compact connected subgroup of G. Now
$M=CH^0$
, where C is a maximal compact connected subgroup of G. Now
![]() $M=C\ltimes H^0$
, since
$M=C\ltimes H^0$
, since
![]() $H^0$
does not have any nontrivial compact subgroup. Observe that C is isomorphic to
$H^0$
does not have any nontrivial compact subgroup. Observe that C is isomorphic to
![]() $\pi_0(C)$
, and hence it is nontrivial and abelian. Suppose
$\pi_0(C)$
, and hence it is nontrivial and abelian. Suppose
![]() $M\not\subset S_T$
, i.e.
$M\not\subset S_T$
, i.e.
![]() $C\cap S_T\subsetneq C$
. Note that
$C\cap S_T\subsetneq C$
. Note that
![]() $C\cap S_T$
is a closed (abelian) subgroup of C.
$C\cap S_T$
is a closed (abelian) subgroup of C.
As C is a compact connected abelian Lie group and the set of primes is an unbounded set in
![]() ${\mathbb N}$
, by Lemma 3·11, the set of elements of prime orders in C is dense in C. As
${\mathbb N}$
, by Lemma 3·11, the set of elements of prime orders in C is dense in C. As
![]() $C\setminus (C\cap S_T)$
is open in C, there exists
$C\setminus (C\cap S_T)$
is open in C, there exists
![]() $b\in C\setminus (C\cap S_T)$
such that
$b\in C\setminus (C\cap S_T)$
such that
![]() $b^p=e$
for some prime p. Since
$b^p=e$
for some prime p. Since
![]() $C/(C\cap S_T)$
is also a compact connected abelian Lie group, we have that
$C/(C\cap S_T)$
is also a compact connected abelian Lie group, we have that
![]() $b^n\in C\setminus (C\cap S_T)$
for all
$b^n\in C\setminus (C\cap S_T)$
for all
![]() $n<p$
and
$n<p$
and
![]() $T(b^n)=b^nh_n$
for some
$T(b^n)=b^nh_n$
for some
![]() $h_n\in H$
and
$h_n\in H$
and
![]() $h_n\ne e$
,
$h_n\ne e$
,
![]() $1\leq n<p$
. Let
$1\leq n<p$
. Let
![]() $G_b$
be the cyclic subgroup generated by b. Then
$G_b$
be the cyclic subgroup generated by b. Then
![]() $G_b\cap S_T=\{e\}$
. Note that
$G_b\cap S_T=\{e\}$
. Note that
![]() $\pi_0(G_b)$
is finite and discrete in
$\pi_0(G_b)$
is finite and discrete in
![]() $M/H^0$
, and hence in
$M/H^0$
, and hence in
![]() $G/H^0$
. Now arguing as in Step 1 for b,
$G/H^0$
. Now arguing as in Step 1 for b,
![]() $H^0$
instead of x, H respectively, we get that
$H^0$
instead of x, H respectively, we get that
![]() $T\not\in{\rm (NC)}$
.
$T\not\in{\rm (NC)}$
.
Now suppose
![]() $m=0$
or
$m=0$
or
![]() $C\subset S_T$
. Then
$C\subset S_T$
. Then
![]() $G/(CH^0)={\mathbb R}^n$
, where
$G/(CH^0)={\mathbb R}^n$
, where
![]() $n\in{\mathbb N}$
and, either
$n\in{\mathbb N}$
and, either
![]() $C=\{e\}$
or
$C=\{e\}$
or
![]() $C\subset S_T$
. As
$C\subset S_T$
. As
![]() $H\subset S_T\subsetneq G$
and
$H\subset S_T\subsetneq G$
and
![]() $G/S_T$
, being a compact connected abelian Lie group, is monothetic, there exists
$G/S_T$
, being a compact connected abelian Lie group, is monothetic, there exists
![]() $x_1\in G\setminus S_T$
such that its image in
$x_1\in G\setminus S_T$
such that its image in
![]() $G/S_T$
generates a (dense) infinite group. Hence
$G/S_T$
generates a (dense) infinite group. Hence
![]() $G_{x_1}\cap S_T=\{e\}$
, where
$G_{x_1}\cap S_T=\{e\}$
, where
![]() $G_{x_1}$
is the group generated by
$G_{x_1}$
is the group generated by
![]() $x_1$
in G. Moreover
$x_1$
in G. Moreover
![]() $\pi_0(x_1)$
generates a discrete infinite group in
$\pi_0(x_1)$
generates a discrete infinite group in
![]() $G/CH^0$
, and hence in
$G/CH^0$
, and hence in
![]() $G/H^0$
. Arguing as in Step 1, for
$G/H^0$
. Arguing as in Step 1, for
![]() $x_1$
,
$x_1$
,
![]() $H^0$
instead of x, H respectively, we get that
$H^0$
instead of x, H respectively, we get that
![]() $T\not\in{\rm (NC)}$
.
$T\not\in{\rm (NC)}$
.
4. Characterisation of automorphisms of Lie groups G which act distally on
 ${\rm Sub}_G$
${\rm Sub}_G$
In this section, we state and prove some of the main results characterising the class of automorphisms which belong to (NC) or act distally on
![]() ${\rm Sub}^a_G$
(see Theorems 4·1, 4·3 and 4·4). We also prove Proposition 4·2 for connected solvable Lie groups which will be useful in proving these theorems. After proving Theorems 4·1, we prove Theorems 4·3 and 4·4 which show for all connected Lie groups G that if T is unipotent or if
${\rm Sub}^a_G$
(see Theorems 4·1, 4·3 and 4·4). We also prove Proposition 4·2 for connected solvable Lie groups which will be useful in proving these theorems. After proving Theorems 4·1, we prove Theorems 4·3 and 4·4 which show for all connected Lie groups G that if T is unipotent or if
![]() $T\in ({\rm Aut}(G))^0$
, then the following holds: T acts distally on
$T\in ({\rm Aut}(G))^0$
, then the following holds: T acts distally on
![]() ${\rm Sub}^a_G$
if and only if T is contained in a compact subgroup of
${\rm Sub}^a_G$
if and only if T is contained in a compact subgroup of
![]() ${\rm Aut}(G)$
. We also characterise connected Lie groups G which act distally on
${\rm Aut}(G)$
. We also characterise connected Lie groups G which act distally on
![]() ${\rm Sub}^a_G$
(see Corollary 4·5).
${\rm Sub}^a_G$
(see Corollary 4·5).
Theorem 4·1. Let G be a connected Lie group without any compact central subgroup of positive dimension and let
![]() $T\in{\rm Aut}(G)$
. Then the following statements are equivalent:
$T\in{\rm Aut}(G)$
. Then the following statements are equivalent:
-
(i)
 $T\in{\rm (NC)}$
.
$T\in{\rm (NC)}$
. -
(ii) T acts distally on
 ${\rm Sub}^a_G$
.
${\rm Sub}^a_G$
. -
(iii) T acts distally on
 ${\rm Sub}_G$
.
${\rm Sub}_G$
. -
(iv) T is contained in a compact subgroup of
 ${\rm Aut}(G)$
.
${\rm Aut}(G)$
.
Note that Theorem 4·1 does not hold for all connected Lie groups and the condition in the hypothesis is necessary as illustrated by the example in Remark 3·8 of the group
![]() $G={\mathbb T}^n$
,
$G={\mathbb T}^n$
,
![]() $n\geq 2$
, for which every
$n\geq 2$
, for which every
![]() $T\in{\rm Aut}(G)\cong{\rm GL}(n,{\mathbb Z})$
belongs to
$T\in{\rm Aut}(G)\cong{\rm GL}(n,{\mathbb Z})$
belongs to
![]() ${\rm (NC)}$
. However, it admits many distal (unipotent) and non-distal automorphisms, each of which generates a discrete infinite group in
${\rm (NC)}$
. However, it admits many distal (unipotent) and non-distal automorphisms, each of which generates a discrete infinite group in
![]() ${\rm Aut}(G)$
.
${\rm Aut}(G)$
.
Before proving the theorem, we prove a somewhat stronger result about distality for unipotent automorphisms on connected solvable Lie groups. Note that Proposition 4·2 (i) below will later be generalised to all connected Lie groups, see Theorem 4·3.
Proposition 4·2. Let G be a connected solvable Lie group and let
![]() $T\in{\rm Aut}(G)$
be unipotent. Then the following hold:
$T\in{\rm Aut}(G)$
be unipotent. Then the following hold:
-
(i) If T acts distally on
 ${\rm Sub}^a_G$
, then
${\rm Sub}^a_G$
, then
 $T={\rm Id}$
.
$T={\rm Id}$
. -
(ii) If G does not have a compact central subgroup of positive dimension and
 $T\in{\rm (NC)}$
, then
$T\in{\rm (NC)}$
, then
 $T={\rm Id}$
.
$T={\rm Id}$
.
Proof.
Step 1.
Let G be as in the hypothesis. Suppose
![]() $T\in{\rm Aut}(G)$
acts distally on
$T\in{\rm Aut}(G)$
acts distally on
![]() ${\rm Sub}^a_G$
. Let K be the largest compact connected central subgroup of G. Then K is characteristic, and in particular, it is T-invariant and normal in G. If possible, suppose
${\rm Sub}^a_G$
. Let K be the largest compact connected central subgroup of G. Then K is characteristic, and in particular, it is T-invariant and normal in G. If possible, suppose
![]() $T|_K\ne{\rm Id}$
. By Proposition 3·10, there exist T-invariant compact connected (normal) nontrivial subgroups
$T|_K\ne{\rm Id}$
. By Proposition 3·10, there exist T-invariant compact connected (normal) nontrivial subgroups
![]() $K_1\subset K_2$
such that T acts trivially on
$K_1\subset K_2$
such that T acts trivially on
![]() $K_1$
and on
$K_1$
and on
![]() $K_2/K_1$
but it does not act trivially on
$K_2/K_1$
but it does not act trivially on
![]() $K_2$
. We may, without loss of any generality, assume that
$K_2$
. We may, without loss of any generality, assume that
![]() $K_1$
is the largest connected subgroup in
$K_1$
is the largest connected subgroup in
![]() $K_2$
such that
$K_2$
such that
![]() $T|_{K_1}={\rm Id}$
. As
$T|_{K_1}={\rm Id}$
. As
![]() $K_1$
and
$K_1$
and
![]() $K_2$
are compact connected abelian Lie groups, and
$K_2$
are compact connected abelian Lie groups, and
![]() $\dim K_1<\dim K_2$
, we can get a nontrivial compact connected subgroup
$\dim K_1<\dim K_2$
, we can get a nontrivial compact connected subgroup
![]() $M\subset K_2$
such that
$M\subset K_2$
such that
![]() $M\cap K_1=\{e\}$
. As
$M\cap K_1=\{e\}$
. As
![]() $M\subset K_2$
, for every
$M\subset K_2$
, for every
![]() $x\in M$
,
$x\in M$
,
![]() $T(x)=xy$
, for some
$T(x)=xy$
, for some
![]() $y\in K_1$
which depends on x. As M is monothetic, we can choose
$y\in K_1$
which depends on x. As M is monothetic, we can choose
![]() $g\in M$
, such that g generates a dense subgroup in M. Let
$g\in M$
, such that g generates a dense subgroup in M. Let
![]() $h\in K_1$
be such that
$h\in K_1$
be such that
![]() $T(g)=gh$
.
$T(g)=gh$
.
We now show that h has infinite order. If possible, suppose h has finite order m (say). Then
![]() $T(g^{mn})=g^{mn}$
,
$T(g^{mn})=g^{mn}$
,
![]() $n\in{\mathbb N}$
, and as
$n\in{\mathbb N}$
, and as
![]() $\{g^{mn}\mid n\in{\mathbb N}\}$
is dense in M, we get that T acts trivially on M. This leads to a contradiction to our assumption on
$\{g^{mn}\mid n\in{\mathbb N}\}$
is dense in M, we get that T acts trivially on M. This leads to a contradiction to our assumption on
![]() $K_1$
as
$K_1$
as
![]() $K_1\ne MK_1\subset K_2$
. As
$K_1\ne MK_1\subset K_2$
. As
![]() $K_1$
is compact, there exists an unbounded sequence
$K_1$
is compact, there exists an unbounded sequence
![]() $\{n_k\}\subset{\mathbb N}$
such that
$\{n_k\}\subset{\mathbb N}$
such that
![]() $h^{n_k}\to h$
. Passing to a subsequence if necessary, we may assume that
$h^{n_k}\to h$
. Passing to a subsequence if necessary, we may assume that
![]() $T^{n_k}(M)\to L$
for some compact group
$T^{n_k}(M)\to L$
for some compact group
![]() $L\subset K_2$
. As
$L\subset K_2$
. As
![]() $\{g^n\}_{n\in{\mathbb N}}$
is dense in M and
$\{g^n\}_{n\in{\mathbb N}}$
is dense in M and
![]() $T(g)=gh$
, we have that
$T(g)=gh$
, we have that
![]() $T^{n_k}(M)\subset MK_h$
, where
$T^{n_k}(M)\subset MK_h$
, where
![]() $K_h$
is the closed subgroup generated by h in
$K_h$
is the closed subgroup generated by h in
![]() $K_1$
. As
$K_1$
. As
![]() $T^{n_k}(g)=gh^{n_k}\to gh$
, we get that
$T^{n_k}(g)=gh^{n_k}\to gh$
, we get that
![]() $gh\in L$
. As M is a connected abelian Lie group, there exists a continuous real one-parameter group
$gh\in L$
. As M is a connected abelian Lie group, there exists a continuous real one-parameter group
![]() $\{g(t)\}_{t\in{\mathbb R}}\subset M$
such that
$\{g(t)\}_{t\in{\mathbb R}}\subset M$
such that
![]() $g(0)=e$
and
$g(0)=e$
and
![]() $g(1)=g$
. Let
$g(1)=g$
. Let
![]() $x_k=g(1/n_k)\in M$
,
$x_k=g(1/n_k)\in M$
,
![]() $k\in{\mathbb N}$
. We have that
$k\in{\mathbb N}$
. We have that
![]() $x_k\to e$
and
$x_k\to e$
and
![]() $x_k^{n_k}=g$
. Now
$x_k^{n_k}=g$
. Now
In particular,
![]() $h=y_k^{n_k}$
for all k, and it implies that
$h=y_k^{n_k}$
for all k, and it implies that
![]() $T^{n_k}(gx_k^{-1})=gh^{n_k}h^{-1}x_k^{-1}\to g$
. Therefore,
$T^{n_k}(gx_k^{-1})=gh^{n_k}h^{-1}x_k^{-1}\to g$
. Therefore,
![]() $g\in L$
and hence
$g\in L$
and hence
![]() $h\in L$
. As L is a closed subgroup, we have that
$h\in L$
. As L is a closed subgroup, we have that
![]() $M\subset L$
and
$M\subset L$
and
![]() $K_h\subset L$
. Since
$K_h\subset L$
. Since
![]() $T^{n_k}(M)\subset MK_h$
for all k, we have that
$T^{n_k}(M)\subset MK_h$
for all k, we have that
![]() $L=MK_h$
. As
$L=MK_h$
. As
![]() $T(MK_h)=MK_h$
, this contradicts the hypothesis that T acts distally on
$T(MK_h)=MK_h$
, this contradicts the hypothesis that T acts distally on
![]() ${\rm Sub}^a_G$
. Therefore,
${\rm Sub}^a_G$
. Therefore,
![]() $T|_K={\rm Id}$
. If G is compact, then
$T|_K={\rm Id}$
. If G is compact, then
![]() $G=K$
and
$G=K$
and
![]() $T={\rm Id}$
.
$T={\rm Id}$
.
Step 2.
Suppose G is not compact. Let
![]() $\pi:G\to G/K$
be the natural projection and let
$\pi:G\to G/K$
be the natural projection and let
![]() $\overline{T}$
be the automorphism of
$\overline{T}$
be the automorphism of
![]() $G/K$
corresponding to T. Then
$G/K$
corresponding to T. Then
![]() $\overline{T}$
is also unipotent, and by Lemma 3·3,
$\overline{T}$
is also unipotent, and by Lemma 3·3,
![]() $\overline{T}\in{\rm (NC)}$
in
$\overline{T}\in{\rm (NC)}$
in
![]() ${\rm Aut}(G/K)$
. Suppose (ii) holds. Since
${\rm Aut}(G/K)$
. Suppose (ii) holds. Since
![]() $G/K$
does not have any compact central subgroup of positive dimension, the statement in (ii) implies that
$G/K$
does not have any compact central subgroup of positive dimension, the statement in (ii) implies that
![]() $\overline{T}={\rm Id}$
. Now we have that
$\overline{T}={\rm Id}$
. Now we have that
![]() $T|_K={\rm Id}$
and
$T|_K={\rm Id}$
and
![]() $T(xK)=xK$
for all
$T(xK)=xK$
for all
![]() $x\in G$
. Let N be the nilradical of G, then
$x\in G$
. Let N be the nilradical of G, then
![]() $K\subset N$
,
$K\subset N$
,
![]() $N/K$
is simply connected and
$N/K$
is simply connected and
![]() $G/N$
is abelian and isomorphic to
$G/N$
is abelian and isomorphic to
![]() ${\mathbb R}^n\times {\mathbb T}^m$
, where
${\mathbb R}^n\times {\mathbb T}^m$
, where
![]() $m,n\geq 0$
. Let R be the closed connected (solvable) normal subgroup containing N, such that
$m,n\geq 0$
. Let R be the closed connected (solvable) normal subgroup containing N, such that
![]() $R/N={\mathbb R}^n$
,
$R/N={\mathbb R}^n$
,
![]() $K\subset N\subset R$
and
$K\subset N\subset R$
and
![]() $R/K$
is a closed connected solvable normal subgroup of
$R/K$
is a closed connected solvable normal subgroup of
![]() $G/K$
without any nontrivial compact subgroup. As
$G/K$
without any nontrivial compact subgroup. As
![]() $G/R={\mathbb T}^m$
is compact, we get by [Reference Hochschild17, chapter XV, theorem 3·7], that
$G/R={\mathbb T}^m$
is compact, we get by [Reference Hochschild17, chapter XV, theorem 3·7], that
![]() $G=CR$
, where C is a maximal compact connected subgroup of G which is abelian. As
$G=CR$
, where C is a maximal compact connected subgroup of G which is abelian. As
![]() $K\subset C$
, we have
$K\subset C$
, we have
![]() $T(C)=C$
. Here,
$T(C)=C$
. Here,
![]() $T|_C$
is also unipotent and from step 1, we get that
$T|_C$
is also unipotent and from step 1, we get that
![]() $T|_C={\rm Id}$
.
$T|_C={\rm Id}$
.
Now it is enough to show that
![]() $T|_R={\rm Id}$
. For every
$T|_R={\rm Id}$
. For every
![]() $x\in R$
,
$x\in R$
,
![]() $T(x)\in xK$
. There exists a neighbourhood U of the identity e in G such that every
$T(x)\in xK$
. There exists a neighbourhood U of the identity e in G such that every
![]() $x\in U$
is exponential. If
$x\in U$
is exponential. If
![]() $T(x)=x$
for every
$T(x)=x$
for every
![]() $x\in U\cap R$
, then
$x\in U\cap R$
, then
![]() $T|_R={\rm Id}$
, since
$T|_R={\rm Id}$
, since
![]() $U\cap R$
generates R. If possible, suppose
$U\cap R$
generates R. If possible, suppose
![]() $x\in U\cap R$
is such that
$x\in U\cap R$
is such that
![]() $x\not\in K$
and
$x\not\in K$
and
![]() $T(x)\ne x$
. Since x is exponential, it can be embedded in a continuous real one-parameter subgroup
$T(x)\ne x$
. Since x is exponential, it can be embedded in a continuous real one-parameter subgroup
![]() $\{x(t)\}_{t\in{\mathbb R}}$
as
$\{x(t)\}_{t\in{\mathbb R}}$
as
![]() $x=x(1)$
. We know that
$x=x(1)$
. We know that
![]() $\{x(t)\}_{t\in{\mathbb R}}$
is unbounded (and closed) as
$\{x(t)\}_{t\in{\mathbb R}}$
is unbounded (and closed) as
![]() $R/K$
has no nontrivial compact subgroups. Note that
$R/K$
has no nontrivial compact subgroups. Note that
![]() $T(x(t))=x(t)k(t)$
,
$T(x(t))=x(t)k(t)$
,
![]() $k(t)\in K$
for all
$k(t)\in K$
for all
![]() $t\in{\mathbb R}$
and
$t\in{\mathbb R}$
and
![]() $k(1)=k\ne e$
. Let
$k(1)=k\ne e$
. Let
![]() $M'=\overline{\{k(t)\mid t\in{\mathbb R}\}}$
. It is a connected compact subgroup of K. Let
$M'=\overline{\{k(t)\mid t\in{\mathbb R}\}}$
. It is a connected compact subgroup of K. Let
![]() $C_x=\{x(t)\}_{t\in{\mathbb R}}$
. It is a closed connected abelian subgroup of R. For some
$C_x=\{x(t)\}_{t\in{\mathbb R}}$
. It is a closed connected abelian subgroup of R. For some
![]() $t_0\in{\mathbb R}$
,
$t_0\in{\mathbb R}$
,
![]() $k(t_0)$
has infinite order, and hence, there exists an unbounded sequence
$k(t_0)$
has infinite order, and hence, there exists an unbounded sequence
![]() $\{n_m\}\subset{\mathbb N}$
such that
$\{n_m\}\subset{\mathbb N}$
such that
![]() $k(t_0)^{n_m}\to k(t_0)$
. Passing to a subsequence, we get that
$k(t_0)^{n_m}\to k(t_0)$
. Passing to a subsequence, we get that
![]() $\{k(t_0/l!)^{n_m}\}$
converges for every
$\{k(t_0/l!)^{n_m}\}$
converges for every
![]() $l\in{\mathbb N}$
. As
$l\in{\mathbb N}$
. As
![]() ${\rm Sub}^a_G$
is compact, passing to a subsequence if necessary, we get that
${\rm Sub}^a_G$
is compact, passing to a subsequence if necessary, we get that
![]() $\{T^{n_m}(C_x)\}$
converges to a closed abelian subgroup H (say). Now
$\{T^{n_m}(C_x)\}$
converges to a closed abelian subgroup H (say). Now
![]() $T^{n_m}(x(t_0))=x(t_0)k(t_0)^{n_m}\to x(t_0)k(t_0)$
. Therefore,
$T^{n_m}(x(t_0))=x(t_0)k(t_0)^{n_m}\to x(t_0)k(t_0)$
. Therefore,
![]() $x(t_0)k(t_0)\in H$
. Also,
$x(t_0)k(t_0)\in H$
. Also,
![]() $T^n(x(t/n))=x(t/n)k(t)$
,
$T^n(x(t/n))=x(t/n)k(t)$
,
![]() $n\in{\mathbb N}$
. Therefore,
$n\in{\mathbb N}$
. Therefore,
![]() $T^{n_m}(x(t/n_m))=x(t/n_m)k(t)\to k(t)\in H$
for all t, i.e.
$T^{n_m}(x(t/n_m))=x(t/n_m)k(t)\to k(t)\in H$
for all t, i.e.
![]() $M'\subset H$
and hence
$M'\subset H$
and hence
![]() $x(t_0)\in H$
. Moreover,
$x(t_0)\in H$
. Moreover,
![]() $T^{n_m}(x(t_0/l!))=x(t_0/l!)k(t_0/l!)^{n_m}\to x(t_0/l!)h_l$
for some
$T^{n_m}(x(t_0/l!))=x(t_0/l!)k(t_0/l!)^{n_m}\to x(t_0/l!)h_l$
for some
![]() $h_l\in M'$
such that
$h_l\in M'$
such that
![]() $k(t_0/l!)^{n_m}\to h_l$
for all
$k(t_0/l!)^{n_m}\to h_l$
for all
![]() $l\in{\mathbb N}$
. Hence
$l\in{\mathbb N}$
. Hence
![]() $x(t_0/l!)\in H$
for all
$x(t_0/l!)\in H$
for all
![]() $l\in{\mathbb N}$
. As H is a closed subgroup, we get that
$l\in{\mathbb N}$
. As H is a closed subgroup, we get that
![]() $C_x\subset H$
, and hence that
$C_x\subset H$
, and hence that
![]() $C_xM'\subset H$
. Since
$C_xM'\subset H$
. Since
![]() $C_xM'$
is T-invariant, we get by Lemma 2·2 (iii) that
$C_xM'$
is T-invariant, we get by Lemma 2·2 (iii) that
![]() $H=C_xM'$
. As
$H=C_xM'$
. As
![]() $C_x\ne C_xM'$
, it contradicts the hypothesis that T acts distally on
$C_x\ne C_xM'$
, it contradicts the hypothesis that T acts distally on
![]() ${\rm Sub}^a_G$
. Therefore,
${\rm Sub}^a_G$
. Therefore,
![]() $T(x)=x$
for every
$T(x)=x$
for every
![]() $x\in U\cap R$
and hence,
$x\in U\cap R$
and hence,
![]() $T|_R={\rm Id}$
. This implies that
$T|_R={\rm Id}$
. This implies that
![]() $T={\rm Id}$
assuming that (ii) holds. Therefore, (i) holds if (ii) holds.
$T={\rm Id}$
assuming that (ii) holds. Therefore, (i) holds if (ii) holds.
We now prove (ii). Suppose G has no compact central subgroup of positive dimension. Then its nilradical N is simply connected. Moreover,
![]() ${\rm Aut}(G)$
is almost algebraic [Reference Dani10, theorem 1], i.e. a closed subgroup of a finite index in an algebraic subgroup of
${\rm Aut}(G)$
is almost algebraic [Reference Dani10, theorem 1], i.e. a closed subgroup of a finite index in an algebraic subgroup of
![]() ${\rm GL}(\mathcal G)$
, where
${\rm GL}(\mathcal G)$
, where
![]() $\mathcal G$
is the Lie algebra of G. There exists a continuous unipotent one-parameter subgroup
$\mathcal G$
is the Lie algebra of G. There exists a continuous unipotent one-parameter subgroup
![]() $\{T_t\}_{t\in{\mathbb R}}\subset{\rm Aut}(G)$
such that
$\{T_t\}_{t\in{\mathbb R}}\subset{\rm Aut}(G)$
such that
![]() $T=T_1$
. Let
$T=T_1$
. Let
![]() $G'=\{T_t\}_{t\in{\mathbb R}}\ltimes G$
. Then G
′ is a connected solvable Lie group. By [Reference Raghunathan24, proposition 3·11], the commutator subgroup of G
′ is nilpotent and, as it is contained in G, it is contained in N. This implies that each
$G'=\{T_t\}_{t\in{\mathbb R}}\ltimes G$
. Then G
′ is a connected solvable Lie group. By [Reference Raghunathan24, proposition 3·11], the commutator subgroup of G
′ is nilpotent and, as it is contained in G, it is contained in N. This implies that each
![]() $T_t$
acts trivially on
$T_t$
acts trivially on
![]() $G/N$
.
$G/N$
.
By Proposition 3·10, either
![]() $T|_N={\rm Id}$
or there exists a sequence of closed connected normal T-invariant subgroups of N;
$T|_N={\rm Id}$
or there exists a sequence of closed connected normal T-invariant subgroups of N;
![]() $\{e\}=G_0\subset\cdots \subset G_m=N$
,
$\{e\}=G_0\subset\cdots \subset G_m=N$
,
![]() $m\geq 2$
, such that T acts trivially on
$m\geq 2$
, such that T acts trivially on
![]() $G_k/G_{k-1}$
,
$G_k/G_{k-1}$
,
![]() $1\le k\le m$
, and T does not act trivially on
$1\le k\le m$
, and T does not act trivially on
![]() $G_{k+1}/G_{k-1}$
,
$G_{k+1}/G_{k-1}$
,
![]() $1\le k\le m-1$
.
$1\le k\le m-1$
.
Suppose
![]() $T\in{\rm (NC)}$
. If possible, suppose
$T\in{\rm (NC)}$
. If possible, suppose
![]() $T|_N\ne {\rm Id}$
. Note that
$T|_N\ne {\rm Id}$
. Note that
![]() $G_1\subset G_2\cap S_T\subsetneq G_2$
, where
$G_1\subset G_2\cap S_T\subsetneq G_2$
, where
![]() $S_T$
is the stabiliser of T. There exists
$S_T$
is the stabiliser of T. There exists
![]() $x\in G_2\setminus (G_2\cap S_T)$
such that the image of x in
$x\in G_2\setminus (G_2\cap S_T)$
such that the image of x in
![]() $G_2/(G_2\cap S_T)$
generates an infinite group; this is true since
$G_2/(G_2\cap S_T)$
generates an infinite group; this is true since
![]() $G_2/G_1$
is (simply) connected and nilpotent. Now
$G_2/G_1$
is (simply) connected and nilpotent. Now
![]() $G_x\cap S_T=\{e\}$
, where
$G_x\cap S_T=\{e\}$
, where
![]() $G_x$
is the cyclic subgroup generated by x. Moreover,
$G_x$
is the cyclic subgroup generated by x. Moreover,
![]() $T(x)=xy$
,
$T(x)=xy$
,
![]() $y\ne e$
and
$y\ne e$
and
![]() $y\in G_1$
. As N is simply connected and nilpotent,
$y\in G_1$
. As N is simply connected and nilpotent,
![]() $G_1$
does not contain any nontrivial compact subgroup. By Lemma 3·12, it follows that
$G_1$
does not contain any nontrivial compact subgroup. By Lemma 3·12, it follows that
![]() $T|_{G_2}\notin{\rm (NC)}$
, and hence
$T|_{G_2}\notin{\rm (NC)}$
, and hence
![]() $T|_N\not\in{\rm (NC)}$
, which contradicts the hypothesis. Hence
$T|_N\not\in{\rm (NC)}$
, which contradicts the hypothesis. Hence
![]() $T|_N={\rm Id}$
. If G is nilpotent, then
$T|_N={\rm Id}$
. If G is nilpotent, then
![]() $T={\rm Id}$
. Now suppose G is not nilpotent.
$T={\rm Id}$
. Now suppose G is not nilpotent.
As observed above, T acts trivially on
![]() $G/N$
. If possible, suppose
$G/N$
. If possible, suppose
![]() $T\ne{\rm Id}$
. Then
$T\ne{\rm Id}$
. Then
![]() $N\subset S_T\ne G$
and, as
$N\subset S_T\ne G$
and, as
![]() $[G,G]\subset N$
[Reference Raghunathan24, proposition 3·11], we get that
$[G,G]\subset N$
[Reference Raghunathan24, proposition 3·11], we get that
![]() $S_T$
is a proper closed normal subgroup of G and
$S_T$
is a proper closed normal subgroup of G and
![]() $G/S_T$
is a nontrivial connected abelian group. There exists
$G/S_T$
is a nontrivial connected abelian group. There exists
![]() $x\in G\setminus S_T$
such that the image of x in
$x\in G\setminus S_T$
such that the image of x in
![]() $G/S_T$
generates an infinite group. In particular,
$G/S_T$
generates an infinite group. In particular,
![]() $G_x\cap S_T=\{e\}$
, where
$G_x\cap S_T=\{e\}$
, where
![]() $G_x$
is the cyclic group generated by x. As T acts trivially on
$G_x$
is the cyclic group generated by x. As T acts trivially on
![]() $G/N$
,
$G/N$
,
![]() $T(x)=xg$
for some
$T(x)=xg$
for some
![]() $g\in N$
and
$g\in N$
and
![]() $g\ne e$
. Since N is simply connected and nilpotent, it has no nontrivial compact subgroup. Since
$g\ne e$
. Since N is simply connected and nilpotent, it has no nontrivial compact subgroup. Since
![]() $T|_N={\rm Id}$
, we get by Lemma 3·12 that
$T|_N={\rm Id}$
, we get by Lemma 3·12 that
![]() $T\not\in{\rm (NC)}$
. This contradicts the hypothesis, and hence
$T\not\in{\rm (NC)}$
. This contradicts the hypothesis, and hence
![]() $T={\rm Id}$
.
$T={\rm Id}$
.
Proof of Theorem 4·1. Let G be a connected Lie group such that it does not admit any nontrivial compact connected central subgroup and let
![]() $T\in {\rm Aut}(G)$
. It is easy to see that (iv)
$T\in {\rm Aut}(G)$
. It is easy to see that (iv)
![]() $\Rightarrow \textrm{(iii)}\Rightarrow \textrm{(ii)}\Rightarrow \textrm{(i)}$
. Now suppose (i) holds, i.e.
$\Rightarrow \textrm{(iii)}\Rightarrow \textrm{(ii)}\Rightarrow \textrm{(i)}$
. Now suppose (i) holds, i.e.
![]() $T\in{\rm (NC)}$
. To show the equivalence of
$T\in{\rm (NC)}$
. To show the equivalence of
![]() $\textrm{(i)}-\textrm{(iv)}$
, it is enough to show that (iv) holds; i.e. we need to show that T is contained in a compact subgroup of
$\textrm{(i)}-\textrm{(iv)}$
, it is enough to show that (iv) holds; i.e. we need to show that T is contained in a compact subgroup of
![]() ${\rm Aut}(G)$
.
${\rm Aut}(G)$
.
Step
1. Let
![]() $\mathcal G$
be the Lie algebra of G. For any
$\mathcal G$
be the Lie algebra of G. For any
![]() $\tau\in{\rm Aut}(G)$
, let
$\tau\in{\rm Aut}(G)$
, let
![]() ${\rm d}\, \tau$
be the corresponding Lie algebra automorphism of
${\rm d}\, \tau$
be the corresponding Lie algebra automorphism of
![]() $\mathcal G$
. Then we can view
$\mathcal G$
. Then we can view
![]() ${\rm Aut}(G)$
as a closed subgroup of
${\rm Aut}(G)$
as a closed subgroup of
![]() ${\rm GL}(\mathcal G)$
. By Corollary 3·7 (a), we have that T acts distally on G. By [Reference Abels2, theorem 1·1], the Lie algebra automorphism
${\rm GL}(\mathcal G)$
. By Corollary 3·7 (a), we have that T acts distally on G. By [Reference Abels2, theorem 1·1], the Lie algebra automorphism
![]() ${\rm d}\, T$
on the Lie algebra
${\rm d}\, T$
on the Lie algebra
![]() $\mathcal G$
of G corresponding to T is distal and hence, all the eigenvalues of
$\mathcal G$
of G corresponding to T is distal and hence, all the eigenvalues of
![]() ${\rm d}\, T$
have absolute value 1 [Reference Abels1, theorem 1′]. Since G has no compact central subgroup of positive dimension, by [Reference Dani10, theorem 1] (see also [Reference Previts and WU22])
${\rm d}\, T$
have absolute value 1 [Reference Abels1, theorem 1′]. Since G has no compact central subgroup of positive dimension, by [Reference Dani10, theorem 1] (see also [Reference Previts and WU22])
![]() ${\rm Aut}(G)$
is an almost algebraic subgroup of
${\rm Aut}(G)$
is an almost algebraic subgroup of
![]() ${\rm GL}(\mathcal G)$
, i.e. a closed subgroup of finite index in an algebraic group. Let H be the smallest almost algebraic subgroup containing T in
${\rm GL}(\mathcal G)$
, i.e. a closed subgroup of finite index in an algebraic group. Let H be the smallest almost algebraic subgroup containing T in
![]() ${\rm Aut}(G)$
. Then H is abelian and it acts distally on G [Reference Abels1, corollary 2·3], and
${\rm Aut}(G)$
. Then H is abelian and it acts distally on G [Reference Abels1, corollary 2·3], and
![]() $H=\mathcal K\times\mathcal U$
, where
$H=\mathcal K\times\mathcal U$
, where
![]() $\mathcal K$
is a compact abelian group and
$\mathcal K$
is a compact abelian group and
![]() $\mathcal U$
is unipotent and abelian, and in fact, a unipotent one-parameter group
$\mathcal U$
is unipotent and abelian, and in fact, a unipotent one-parameter group
![]() $\{T_t\}_{t\in{\mathbb R}}$
[Reference Abels1, corollary 2·5]. Note that all the eigenvalues of each
$\{T_t\}_{t\in{\mathbb R}}$
[Reference Abels1, corollary 2·5]. Note that all the eigenvalues of each
![]() $T_t$
are equal to 1. Then each
$T_t$
are equal to 1. Then each
![]() $T_t$
acts distally on G [Reference Abels1, theorem 1′]. Let
$T_t$
acts distally on G [Reference Abels1, theorem 1′]. Let
![]() $T=T_sT_u=T_uT_s$
, where
$T=T_sT_u=T_uT_s$
, where
![]() $T_s\in \mathcal K$
and
$T_s\in \mathcal K$
and
![]() $T_u=T_{t_0}\in\mathcal U$
, for some
$T_u=T_{t_0}\in\mathcal U$
, for some
![]() $t_0\in{\mathbb R}$
,
$t_0\in{\mathbb R}$
,
![]() $t_0\ne 0$
. By Lemma 3·4,
$t_0\ne 0$
. By Lemma 3·4,
![]() $T_u$
, and hence each
$T_u$
, and hence each
![]() $T_t$
,
$T_t$
,
![]() $t\in{\mathbb R}$
, belongs to
$t\in{\mathbb R}$
, belongs to
![]() ${\rm (NC)}$
. Now to show that T is contained in a compact subgroup of
${\rm (NC)}$
. Now to show that T is contained in a compact subgroup of
![]() ${\rm Aut}(G)$
, it enough to show that
${\rm Aut}(G)$
, it enough to show that
![]() $T_u={\rm Id}$
.
$T_u={\rm Id}$
.
Step
2. Let R be the solvable radical of G. Then each
![]() $T_t|_R$
is unipotent and it belongs to
$T_t|_R$
is unipotent and it belongs to
![]() ${\rm (NC)}$
. Since the largest compact connected central subgroup of R, being characteristic in G, is central in G by [Reference Iwasawa18, theorem 4], and hence it is trivial. Therefore, R does not have any compact central subgroup of positive dimension. By Proposition 4·2,
${\rm (NC)}$
. Since the largest compact connected central subgroup of R, being characteristic in G, is central in G by [Reference Iwasawa18, theorem 4], and hence it is trivial. Therefore, R does not have any compact central subgroup of positive dimension. By Proposition 4·2,
![]() $T_t|_R={\rm Id}$
. If G is solvable then
$T_t|_R={\rm Id}$
. If G is solvable then
![]() $T_t={\rm Id}$
for each t.
$T_t={\rm Id}$
for each t.
Suppose G is not solvable. We show that
![]() $T_t$
acts trivially on
$T_t$
acts trivially on
![]() $G/R$
. Let
$G/R$
. Let
![]() $G_s=G/R$
. Then
$G_s=G/R$
. Then
![]() $G_s$
is a connected semisimple Lie group. Moreover,
$G_s$
is a connected semisimple Lie group. Moreover,
![]() ${\rm Inn}(G_s)$
is the connected component of the identity in
${\rm Inn}(G_s)$
is the connected component of the identity in
![]() ${\rm Aut}(G_s)$
and it is a subgroup of finite index in
${\rm Aut}(G_s)$
and it is a subgroup of finite index in
![]() ${\rm Aut}(G_s)$
. Let
${\rm Aut}(G_s)$
. Let
![]() $\eta:G\to G_s$
be the natural projection and let
$\eta:G\to G_s$
be the natural projection and let
![]() $T^{\prime}_t$
be the automorphism of
$T^{\prime}_t$
be the automorphism of
![]() $G_s$
corresponding to
$G_s$
corresponding to
![]() $T_t$
for each t. We now show that each
$T_t$
for each t. We now show that each
![]() $T^{\prime}_t$
is trivial. Since
$T^{\prime}_t$
is trivial. Since
![]() $\{T^{\prime}_t\}$
is unipotent and connected, there exists a Ad-unipotent one-parameter subgroup
$\{T^{\prime}_t\}$
is unipotent and connected, there exists a Ad-unipotent one-parameter subgroup
![]() $\{u_t\}$
in
$\{u_t\}$
in
![]() $G_s$
such that
$G_s$
such that
![]() $T^{\prime}_t={\rm inn} (u_t)$
, the inner automorphism by
$T^{\prime}_t={\rm inn} (u_t)$
, the inner automorphism by
![]() $u_t$
in
$u_t$
in
![]() $G_s$
. Suppose
$G_s$
. Suppose
![]() $\{u_t\}$
is nontrivial.
$\{u_t\}$
is nontrivial.
Let U be a maximal connected Ad-unipotent subgroup of
![]() $G_s$
containing
$G_s$
containing
![]() $\{u_t\}$
, i.e. a maximal connected nilpotent subgroup containing
$\{u_t\}$
, i.e. a maximal connected nilpotent subgroup containing
![]() $\{u_t\}$
such that for all
$\{u_t\}$
such that for all
![]() $u\in U$
,
$u\in U$
,
![]() ${\rm Ad}(u)$
is a unipotent linear transformation of the Lie algebra of
${\rm Ad}(u)$
is a unipotent linear transformation of the Lie algebra of
![]() $G_s$
. Let
$G_s$
. Let
![]() $G_s=KAN$
be an Iwasawa decomposition, where A is a closed abelian subgroup, N is a maximal connected Ad-unipotent subgroup of
$G_s=KAN$
be an Iwasawa decomposition, where A is a closed abelian subgroup, N is a maximal connected Ad-unipotent subgroup of
![]() $G_s$
which is normalised by A, and AN is a closed solvable subgroup of
$G_s$
which is normalised by A, and AN is a closed solvable subgroup of
![]() $G_s$
(see [Reference Knapp20, proof of Theorem 6·46]). Since any two maximal connected Ad-unipotent subgroups are conjugate to each other, we get that N and U are conjugate by an element in a compact set contained in K (see [Reference Dani and SHAH11, Lemma 4·4]). If necessary, we may replace AN by its conjugate and assume that
$G_s$
(see [Reference Knapp20, proof of Theorem 6·46]). Since any two maximal connected Ad-unipotent subgroups are conjugate to each other, we get that N and U are conjugate by an element in a compact set contained in K (see [Reference Dani and SHAH11, Lemma 4·4]). If necessary, we may replace AN by its conjugate and assume that
![]() $U=N$
, i.e.
$U=N$
, i.e.
![]() $u_t\in N$
for all
$u_t\in N$
for all
![]() $t\in{\mathbb R}$
. Then AN is
$t\in{\mathbb R}$
. Then AN is
![]() $T^{\prime}_t$
-invariant.
$T^{\prime}_t$
-invariant.
Let
![]() $B=\eta^{-1}(AN)$
, where
$B=\eta^{-1}(AN)$
, where
![]() $\eta:G\to G/R$
is as above for the radical R of G. Then B is a closed connected solvable subgroup of G. Note that since AN is
$\eta:G\to G/R$
is as above for the radical R of G. Then B is a closed connected solvable subgroup of G. Note that since AN is
![]() $T^{\prime}_t$
-invariant, we have that B is
$T^{\prime}_t$
-invariant, we have that B is
![]() $T_t$
-invariant for each t. Since A and N are simply connected and R has no compact central subgroup of positive dimension, we get that B has no compact central subgroup of positive dimension. As each
$T_t$
-invariant for each t. Since A and N are simply connected and R has no compact central subgroup of positive dimension, we get that B has no compact central subgroup of positive dimension. As each
![]() $T_t|_{B}$
belongs to
$T_t|_{B}$
belongs to
![]() ${\rm (NC)}$
, by Proposition 4·2,
${\rm (NC)}$
, by Proposition 4·2,
![]() $T_t|_{B}={\rm Id}$
for each t. This implies that
$T_t|_{B}={\rm Id}$
for each t. This implies that
![]() $u_t$
centralises AN for all
$u_t$
centralises AN for all
![]() $t\in{\mathbb R}$
. Let
$t\in{\mathbb R}$
. Let
![]() ${\mathcal G}_s$
be the Lie algebra of
${\mathcal G}_s$
be the Lie algebra of
![]() $G_s$
and let
$G_s$
and let
![]() ${\mathcal A}$
and
${\mathcal A}$
and
![]() ${\mathcal N}$
be the Lie subalgebra of A and N respectively. If
${\mathcal N}$
be the Lie subalgebra of A and N respectively. If
![]() $X\in {\mathcal N}$
is such that
$X\in {\mathcal N}$
is such that
![]() $\exp tX=u_t$
,
$\exp tX=u_t$
,
![]() $t\in{\mathbb R}$
, then from above, X belongs to the center of
$t\in{\mathbb R}$
, then from above, X belongs to the center of
![]() ${\mathcal A}\oplus{\mathcal N}$
, the Lie algebra of AN. This leads to a contradiction as the centraliser of
${\mathcal A}\oplus{\mathcal N}$
, the Lie algebra of AN. This leads to a contradiction as the centraliser of
![]() ${\mathcal A}$
in
${\mathcal A}$
in
![]() ${\mathcal A}\oplus{\mathcal N}$
is
${\mathcal A}\oplus{\mathcal N}$
is
![]() ${\mathcal A}$
[Reference Knapp20, lemma 6·50]. Therefore,
${\mathcal A}$
[Reference Knapp20, lemma 6·50]. Therefore,
![]() $u_t=e$
, and hence
$u_t=e$
, and hence
![]() $T^{\prime}_t={\rm Id}$
, for each t.
$T^{\prime}_t={\rm Id}$
, for each t.
Step
3. Now we have from steps 1 and 2 that
![]() $T_t|_R={\rm Id}$
and
$T_t|_R={\rm Id}$
and
![]() $T_t$
acts trivially on
$T_t$
acts trivially on
![]() $G/R$
for each t, where R is the radical of G. If R is central in G, then the preceding assertions would imply that each
$G/R$
for each t, where R is the radical of G. If R is central in G, then the preceding assertions would imply that each
![]() $T_t$
acts trivially on
$T_t$
acts trivially on
![]() $\overline{[G,G]}$
, the closure of the commutator subgroup of G, and as
$\overline{[G,G]}$
, the closure of the commutator subgroup of G, and as
![]() $G=\overline{[G,G]}R$
, we get that
$G=\overline{[G,G]}R$
, we get that
![]() $T_t={\rm Id}$
in this case and, in particular, when G is semisimple. Now we want to prove that
$T_t={\rm Id}$
in this case and, in particular, when G is semisimple. Now we want to prove that
![]() $T_t={\rm Id}$
, for each t in the general case.
$T_t={\rm Id}$
, for each t in the general case.
For the natural projection
![]() $\eta:G\to G/R$
, the subgroup AN of
$\eta:G\to G/R$
, the subgroup AN of
![]() $G/R$
and the subgroup
$G/R$
and the subgroup
![]() $B=\eta^{-1}(AN)$
of G as in step 2, let
$B=\eta^{-1}(AN)$
of G as in step 2, let
![]() $B_x=xBx^{-1}$
, for a fixed
$B_x=xBx^{-1}$
, for a fixed
![]() $x\in G$
. Then
$x\in G$
. Then
![]() $B_x$
is a closed connected solvable subgroup of G,
$B_x$
is a closed connected solvable subgroup of G,
![]() $\eta(B_x)=\eta(x)AN\eta(x)^{-1}$
is also a closed connected solvable group of
$\eta(B_x)=\eta(x)AN\eta(x)^{-1}$
is also a closed connected solvable group of
![]() $G/R$
, and
$G/R$
, and
![]() $B_x$
is
$B_x$
is
![]() $T_t$
-invariant, as
$T_t$
-invariant, as
![]() $T_t$
acts trivially on
$T_t$
acts trivially on
![]() $G/R$
, for each t. Since
$G/R$
, for each t. Since
![]() $B_x$
is a conjugate of B, it does not have any compact central subgroup of positive dimension. Now by Proposition 4·2, we get that the restriction of each
$B_x$
is a conjugate of B, it does not have any compact central subgroup of positive dimension. Now by Proposition 4·2, we get that the restriction of each
![]() $T_t$
to
$T_t$
to
![]() $B_x$
is trivial. Since this is true for every
$B_x$
is trivial. Since this is true for every
![]() $x\in G$
and the closed subgroup generated by
$x\in G$
and the closed subgroup generated by
![]() $H=\cup_{x\in G}\eta(B_x)$
is a closed normal subgroup containing AN in
$H=\cup_{x\in G}\eta(B_x)$
is a closed normal subgroup containing AN in
![]() $G/R$
, we have that H contains all the non-compact simple factors of
$G/R$
, we have that H contains all the non-compact simple factors of
![]() $G/R$
. Therefore, each
$G/R$
. Therefore, each
![]() $T_t$
is trivial on a closed co-compact normal subgroup
$T_t$
is trivial on a closed co-compact normal subgroup
![]() $\eta^{-1}(H)$
in G which contains R. That is, if
$\eta^{-1}(H)$
in G which contains R. That is, if
![]() $G/R$
has no nontrivial compact simple factors, then
$G/R$
has no nontrivial compact simple factors, then
![]() $T_t={\rm Id}$
, for each t.
$T_t={\rm Id}$
, for each t.
Step
4. Let S
′ be the product of all compact simple factors of
![]() $G/R$
and let
$G/R$
and let
![]() $G'=\eta^{-1}(S')$
. Then G
′ is a closed characteristic (normal) subgroup in G. Let
$G'=\eta^{-1}(S')$
. Then G
′ is a closed characteristic (normal) subgroup in G. Let
![]() $G'=S_cR$
be the Levi decomposition of G
′. Then
$G'=S_cR$
be the Levi decomposition of G
′. Then
![]() $S_c$
is compact and it is the product of all simple compact factors of a Levi subgroup in G. As
$S_c$
is compact and it is the product of all simple compact factors of a Levi subgroup in G. As
![]() $G=G'\eta^{-1}(H)=S_c\eta^{-1}(H)$
, and
$G=G'\eta^{-1}(H)=S_c\eta^{-1}(H)$
, and
![]() $T_t$
acts trivially on
$T_t$
acts trivially on
![]() $\eta^{-1}(H)$
, it is enough to show that
$\eta^{-1}(H)$
, it is enough to show that
![]() $T_t|_{S_c}={\rm Id}$
.
$T_t|_{S_c}={\rm Id}$
.
Here,
![]() $G'=S_cR$
is a closed subgroup. As G
′ is characteristic, it is
$G'=S_cR$
is a closed subgroup. As G
′ is characteristic, it is
![]() $T_t$
-invariant for each t. Let
$T_t$
-invariant for each t. Let
![]() $[S_c,R]$
be the group generated by
$[S_c,R]$
be the group generated by
![]() $\{xyx^{-1}y^{-1}\mid x\in S_c, y\in R\}$
. By [Reference Hochschild17, chapter XI, theorem 3·2],
$\{xyx^{-1}y^{-1}\mid x\in S_c, y\in R\}$
. By [Reference Hochschild17, chapter XI, theorem 3·2],
![]() $\overline{[S_c,R]}\subset N$
; here N denotes the nilradical of R, which is the same as the nilradical of G. Note that
$\overline{[S_c,R]}\subset N$
; here N denotes the nilradical of R, which is the same as the nilradical of G. Note that
![]() $\overline{[R,R]}\subset N$
[Reference Raghunathan24, proposition 3·11]. Let
$\overline{[R,R]}\subset N$
[Reference Raghunathan24, proposition 3·11]. Let
![]() $G^{\prime}_1$
be the closure of the group [G
′, G
′]. Then
$G^{\prime}_1$
be the closure of the group [G
′, G
′]. Then
![]() $S_c\subset G^{\prime}_1\subset S_cN$
. As
$S_c\subset G^{\prime}_1\subset S_cN$
. As
![]() $G^{\prime}_1$
is
$G^{\prime}_1$
is
![]() $T_t$
-invariant, we have that
$T_t$
-invariant, we have that
![]() $T_t(S_c)\subset S_cN$
. Since each
$T_t(S_c)\subset S_cN$
. Since each
![]() $T_t$
acts trivially on
$T_t$
acts trivially on
![]() $G'/R$
, we have that for
$G'/R$
, we have that for
![]() $x\in S_c$
,
$x\in S_c$
,
![]() $x^{-1}T_t(x)\in (S_c\cap R)N$
. As
$x^{-1}T_t(x)\in (S_c\cap R)N$
. As
![]() $S_c\cap R$
is a finite subgroup and
$S_c\cap R$
is a finite subgroup and
![]() $S_c$
is connected,
$S_c$
is connected,
![]() $T_t(x)\in xN$
for all
$T_t(x)\in xN$
for all
![]() $x\in S_c$
and for all t. Note that the nilradical N of G is simply connected and has no nontrivial compact subgroups. Let K be a maximal compact connected abelian subgroup of
$x\in S_c$
and for all t. Note that the nilradical N of G is simply connected and has no nontrivial compact subgroups. Let K be a maximal compact connected abelian subgroup of
![]() $S_c$
. If possible, suppose for some t,
$S_c$
. If possible, suppose for some t,
![]() $T_t|_K\ne{\rm Id}$
. Let
$T_t|_K\ne{\rm Id}$
. Let
![]() $S_{T_t}$
be the stabiliser of
$S_{T_t}$
be the stabiliser of
![]() $T_t$
. Then
$T_t$
. Then
![]() $K\cap S_{T_t}$
is a proper closed subgroup of K. Now as
$K\cap S_{T_t}$
is a proper closed subgroup of K. Now as
![]() $K/(K\cap S_{T_t})$
is a nontrivial compact connected abelian group, it is monothetic and hence, there exists
$K/(K\cap S_{T_t})$
is a nontrivial compact connected abelian group, it is monothetic and hence, there exists
![]() $x\in K$
such that the image of x in
$x\in K$
such that the image of x in
![]() $K/(K\cap S_{T_t})$
generats a dense infinite group. In particular,
$K/(K\cap S_{T_t})$
generats a dense infinite group. In particular,
![]() $G_x\cap S_{T_t}=\{e\}$
. As
$G_x\cap S_{T_t}=\{e\}$
. As
![]() $T_t(x)\in xN$
,
$T_t(x)\in xN$
,
![]() $T_t|_N={\rm Id}$
and N has no nontrivial compact subgroups, by Lemma 3·12,
$T_t|_N={\rm Id}$
and N has no nontrivial compact subgroups, by Lemma 3·12,
![]() $T_t\not\in{\rm (NC)}$
, which leads to a contradiction. Therefore,
$T_t\not\in{\rm (NC)}$
, which leads to a contradiction. Therefore,
![]() $T_t|_K={\rm Id}$
for all t. Since the union of all maximal compact connected abelian subgroups of
$T_t|_K={\rm Id}$
for all t. Since the union of all maximal compact connected abelian subgroups of
![]() $S_c$
is dense in
$S_c$
is dense in
![]() $S_c$
, we have that
$S_c$
, we have that
![]() $T_t|_{S_c}={\rm Id}$
for all t. As observed above, this shows that
$T_t|_{S_c}={\rm Id}$
for all t. As observed above, this shows that
![]() $T_t={\rm Id}$
for all t. As observed at the end of step 1, this implies that T is contained in a compact subgroup of G. Therefore,
$T_t={\rm Id}$
for all t. As observed at the end of step 1, this implies that T is contained in a compact subgroup of G. Therefore,
![]() $\textrm{(i)}\Rightarrow \textrm{(iv)}$
and
$\textrm{(i)}\Rightarrow \textrm{(iv)}$
and
![]() $\textrm{(i)} - \textrm{(iv)}$
are equivalent.
$\textrm{(i)} - \textrm{(iv)}$
are equivalent.
We know from Remark 3·8 that all automorphisms of connected compact abelian Lie groups of dimension greater than or equal to 2 belong to class (NC) and, in particular, this hold for nontrivial unipotent automorphisms of such groups. The following theorem shows that a connected Lie group G does not admit any nontrivial unipotent automorphism which acts distally on
![]() ${\rm Sub}^a_G$
.
${\rm Sub}^a_G$
.
Theorem 4·3. Let G be a connected Lie group and let
![]() $T\in {\rm Aut}(G)$
be unipotent. Then T acts distally on
$T\in {\rm Aut}(G)$
be unipotent. Then T acts distally on
![]() ${\rm Sub}^a_G$
if and only if
${\rm Sub}^a_G$
if and only if
![]() $T={\rm Id}$
.
$T={\rm Id}$
.
Proof. Let G and T be as in the hypothesis. One way implication is obvious. Now suppose T acts distally on
![]() ${\rm Sub}^a_G$
. We show that
${\rm Sub}^a_G$
. We show that
![]() $T={\rm Id}$
.
$T={\rm Id}$
.
Let R be the solvable radical of G. Then R is T-invariant and by Proposition 4·2,
![]() $T|_R={\rm Id}$
. Let C be the largest compact connected central subgroup. If C is trivial, then the assertion follows from Theorem 4·1 as the only unipotent automorphism contained in a compact subgroup of
$T|_R={\rm Id}$
. Let C be the largest compact connected central subgroup. If C is trivial, then the assertion follows from Theorem 4·1 as the only unipotent automorphism contained in a compact subgroup of
![]() ${\rm Aut}(G)$
is the identity map. Suppose C is nontrivial. Let
${\rm Aut}(G)$
is the identity map. Suppose C is nontrivial. Let
![]() $\overline{T}$
be the automorphisms of
$\overline{T}$
be the automorphisms of
![]() $G/C$
corresponding to T. Then by Lemma 3·3,
$G/C$
corresponding to T. Then by Lemma 3·3,
![]() $\overline{T}\in{\rm (NC)}$
. Note that
$\overline{T}\in{\rm (NC)}$
. Note that
![]() $\overline{T}$
is also unipotent. Now by Theorem 4·1,
$\overline{T}$
is also unipotent. Now by Theorem 4·1,
![]() $\overline{T}$
is contained in a compact subgroup of
$\overline{T}$
is contained in a compact subgroup of
![]() ${\rm Aut}(G/C)$
, and being unipotent,
${\rm Aut}(G/C)$
, and being unipotent,
![]() $\overline{T}$
is trivial. As C is connected and central, it follows that T acts trivially on
$\overline{T}$
is trivial. As C is connected and central, it follows that T acts trivially on
![]() $\overline{[G,G]}$
. Now as
$\overline{[G,G]}$
. Now as
![]() $G=\overline{[G,G]}R$
, we get that
$G=\overline{[G,G]}R$
, we get that
![]() $T={\rm Id}$
.
$T={\rm Id}$
.
The following theorem shows that a part of Theorem 4·1 can be generalised to all connected Lie groups if we restrict the class of automorphisms to
![]() $({\rm Aut}(G))^0$
, the connected component of the identity in
$({\rm Aut}(G))^0$
, the connected component of the identity in
![]() ${\rm Aut}(G)$
. Example 4·7 illustrates that Theorem 4·1 can not be generalised fully even if we restrict to
${\rm Aut}(G)$
. Example 4·7 illustrates that Theorem 4·1 can not be generalised fully even if we restrict to
![]() $({\rm Aut}(G))^0$
.
$({\rm Aut}(G))^0$
.
Theorem 4·4. Let G be a connected Lie group and let
![]() $T\in{\rm Aut}(G)$
. Suppose T belongs to
$T\in{\rm Aut}(G)$
. Suppose T belongs to
![]() $({\rm Aut}(G))^0$
, the connected component of the identity in
$({\rm Aut}(G))^0$
, the connected component of the identity in
![]() ${\rm Aut}(G)$
. Then
${\rm Aut}(G)$
. Then
![]() $\textrm{(ii)}-\textrm{(iv)}$
in Theorem 4·1 are equivalent.
$\textrm{(ii)}-\textrm{(iv)}$
in Theorem 4·1 are equivalent.
Proof. Let G be a connected Lie group and let
![]() $T\in({\rm Aut}(G))^0$
. It is enough to show that
$T\in({\rm Aut}(G))^0$
. It is enough to show that
![]() $\textrm{(ii)}\Rightarrow \textrm{(iv)}$
in Theorem 4·1. Suppose (ii) holds, i.e. T acts distally on
$\textrm{(ii)}\Rightarrow \textrm{(iv)}$
in Theorem 4·1. Suppose (ii) holds, i.e. T acts distally on
![]() ${\rm Sub}^a_G$
. We want to prove that T is contained in a compact subgroup of
${\rm Sub}^a_G$
. We want to prove that T is contained in a compact subgroup of
![]() ${\rm Aut}(G)$
.
${\rm Aut}(G)$
.
Let C be the largest compact connected central subgroup of G. Then C is characteristic. As C is compact and abelian,
![]() ${\rm Aut}(C)$
is totally disconnected and hence every element of
${\rm Aut}(C)$
is totally disconnected and hence every element of
![]() $({\rm Aut}(G))^0$
acts trivially on C. In particular,
$({\rm Aut}(G))^0$
acts trivially on C. In particular,
![]() $T|_C={\rm Id}$
. Also, by Corollary 3·7 (a), T acts distally on G. Therefore, the eigenvalues of
$T|_C={\rm Id}$
. Also, by Corollary 3·7 (a), T acts distally on G. Therefore, the eigenvalues of
![]() ${\rm d}\, T$
on the Lie algebra
${\rm d}\, T$
on the Lie algebra
![]() $\mathcal G$
of G are of absolute value 1. Moreover,
$\mathcal G$
of G are of absolute value 1. Moreover,
![]() $({\rm Aut}(G))^0$
is almost algebraic as a closed subgroup of
$({\rm Aut}(G))^0$
is almost algebraic as a closed subgroup of
![]() ${\rm GL}(\mathcal G)$
[Reference Wigner33, Reference Wigner34]; see also [Reference Dani10, theorem 2]. Let
${\rm GL}(\mathcal G)$
[Reference Wigner33, Reference Wigner34]; see also [Reference Dani10, theorem 2]. Let
![]() $G_T$
be the smallest almost algebraic group in
$G_T$
be the smallest almost algebraic group in
![]() $({\rm Aut}(G))^0$
containing T. By [Reference Abels1, corollary 2·5],
$({\rm Aut}(G))^0$
containing T. By [Reference Abels1, corollary 2·5],
![]() $G_T=\mathcal K\times \mathcal U$
where
$G_T=\mathcal K\times \mathcal U$
where
![]() $\mathcal K$
is compact and abelian, and
$\mathcal K$
is compact and abelian, and
![]() $\mathcal U$
is unipotent and abelian. In fact,
$\mathcal U$
is unipotent and abelian. In fact,
![]() $\mathcal U$
is a unipotent one-parameter group
$\mathcal U$
is a unipotent one-parameter group
![]() $\{T_t\}$
in
$\{T_t\}$
in
![]() $({\rm Aut}(G))^0$
, such that
$({\rm Aut}(G))^0$
, such that
![]() $T=T_sT_u=T_uT_s$
,
$T=T_sT_u=T_uT_s$
,
![]() $T_s\in\mathcal K$
and
$T_s\in\mathcal K$
and
![]() $T_u=T_1$
is unipotent. By [Reference Shah and YADAV31, lemma 2·2],
$T_u=T_1$
is unipotent. By [Reference Shah and YADAV31, lemma 2·2],
![]() $T_u$
acts distally on
$T_u$
acts distally on
![]() ${\rm Sub}^a_G$
. By Theorem 4·3,
${\rm Sub}^a_G$
. By Theorem 4·3,
![]() $T_u={\rm Id}$
. Therefore,
$T_u={\rm Id}$
. Therefore,
![]() $T=T_s$
is contained in a compact subgroup of
$T=T_s$
is contained in a compact subgroup of
![]() $({\rm Aut}(G))^0$
, i.e. (iv) holds.
$({\rm Aut}(G))^0$
, i.e. (iv) holds.
The following corollary characterises the class of connected Lie groups G which act distally on
![]() ${\rm Sub}^a_G$
. Recall that the action of G on
${\rm Sub}^a_G$
. Recall that the action of G on
![]() ${\rm Sub}_G$
is the same as the action of
${\rm Sub}_G$
is the same as the action of
![]() ${\rm Inn}(G)$
on
${\rm Inn}(G)$
on
![]() ${\rm Sub}_G$
, where
${\rm Sub}_G$
, where
![]() ${\rm Inn}(G)$
is the group of inner automorphisms of G.
${\rm Inn}(G)$
is the group of inner automorphisms of G.
Corollary 4·5. Let G be a connected Lie group. Then the following are equivalent:
-
(i) Every inner automorphism acts distally on
 ${\rm Sub}^a_G$
.
${\rm Sub}^a_G$
. -
(ii) Every inner automorphism acts distally on
 ${\rm Sub}_G$
.
${\rm Sub}_G$
. -
(iii) G acts distally on
 ${\rm Sub}^a_G$
.
${\rm Sub}^a_G$
. -
(iv) G acts distally on
 ${\rm Sub}_G$
.
${\rm Sub}_G$
. -
(v) Either G is compact or
 $G={\mathbb R}^n\times K$
, for a compact group K and some
$G={\mathbb R}^n\times K$
, for a compact group K and some
 $n\in{\mathbb N}$
.
$n\in{\mathbb N}$
.
Moreover, if G has no compact central subgroup of positive dimension, then the above statements are also equivalent to the following:
-
(vi) Every inner automorphism of G belongs to
 ${\rm (NC)}$
.
${\rm (NC)}$
.
The condition on the center of G in the above corollary is necessary for the equivalence of the statement (vi) with (i)–(v) as illustrated by Example 4·7 below.
Proof of Corollary 4·5. Let G be a connected Lie group.
![]() $\textrm{(iv)}\Rightarrow \textrm{(iii)}\Rightarrow \textrm{(i)}$
and
$\textrm{(iv)}\Rightarrow \textrm{(iii)}\Rightarrow \textrm{(i)}$
and
![]() $\textrm{(iv)}\Rightarrow \textrm{(ii)}\Rightarrow \textrm{(i)}$
obviously hold. We also have that
$\textrm{(iv)}\Rightarrow \textrm{(ii)}\Rightarrow \textrm{(i)}$
obviously hold. We also have that
![]() $\textrm{(v)}\Rightarrow \textrm{(iv)}$
, as
$\textrm{(v)}\Rightarrow \textrm{(iv)}$
, as
![]() ${\rm Inn}(G)=\{{\rm inn}(k)\mid k\in K\}$
is compact. To show that
${\rm Inn}(G)=\{{\rm inn}(k)\mid k\in K\}$
is compact. To show that
![]() $\textrm{(i)}-\textrm{(v)}$
are equivalent, it is enough to show that
$\textrm{(i)}-\textrm{(v)}$
are equivalent, it is enough to show that
![]() $\textrm{(i)}\Rightarrow \textrm{(v)}$
. Suppose (i) holds, i.e. every inner automorphism of G acts distally on
$\textrm{(i)}\Rightarrow \textrm{(v)}$
. Suppose (i) holds, i.e. every inner automorphism of G acts distally on
![]() ${\rm Sub}^a_G$
. We want to show that (v) holds
${\rm Sub}^a_G$
. We want to show that (v) holds
Suppose G is not compact. We need to show that G is a product of
![]() ${\mathbb R}^n$
and a compact subgroup for some
${\mathbb R}^n$
and a compact subgroup for some
![]() $n\in{\mathbb N}$
. As every inner automorphism acts distally on
$n\in{\mathbb N}$
. As every inner automorphism acts distally on
![]() ${\rm Sub}^a_G$
, by Corollary 3·9, G is distal. By [Reference Rosenblatt27, theorem 9] and [Reference Jenkins19, corollary 2·1(ii)],
${\rm Sub}^a_G$
, by Corollary 3·9, G is distal. By [Reference Rosenblatt27, theorem 9] and [Reference Jenkins19, corollary 2·1(ii)],
![]() $G/R$
is compact where R is the solvable radical of G. Let N be the nilradical of G. Let C be the largest compact normal subgroup of N. Then C is connected and central in G and
$G/R$
is compact where R is the solvable radical of G. Let N be the nilradical of G. Let C be the largest compact normal subgroup of N. Then C is connected and central in G and
![]() $N/C$
is simply connected and nilpotent. Note that every inner automorphism of G by an element of N is unipotent, i.e.
$N/C$
is simply connected and nilpotent. Note that every inner automorphism of G by an element of N is unipotent, i.e.
![]() ${\rm Ad}(x)$
is unipotent for all
${\rm Ad}(x)$
is unipotent for all
![]() $x\in N$
. By Theorem 4·3,
$x\in N$
. By Theorem 4·3,
![]() ${\rm inn}(x)={\rm Id}$
for every
${\rm inn}(x)={\rm Id}$
for every
![]() $x\in N$
i.e. N is abelian and central in G. In particular, since
$x\in N$
i.e. N is abelian and central in G. In particular, since
![]() $R/N$
is abelian, R is nilpotent, and hence
$R/N$
is abelian, R is nilpotent, and hence
![]() $R=N$
. Therefore, R is central in G. Now G is a compact extension of
$R=N$
. Therefore, R is central in G. Now G is a compact extension of
![]() $Z^0$
, the connected component of the center Z of G. Let
$Z^0$
, the connected component of the center Z of G. Let
![]() $Z^0={\mathbb R}^n\times C$
, where C is compact and,
$Z^0={\mathbb R}^n\times C$
, where C is compact and,
![]() $n\in{\mathbb N}$
as G is non-compact. Then the subgroup
$n\in{\mathbb N}$
as G is non-compact. Then the subgroup
![]() $V={\mathbb R}^n$
is a (nontrivial) vector group which is central. Using [Reference Iwasawa18, lemma 3·7], we get that
$V={\mathbb R}^n$
is a (nontrivial) vector group which is central. Using [Reference Iwasawa18, lemma 3·7], we get that
![]() $G={\mathbb R}^n\times K$
, where K is the maximal compact subgroup of G, i.e. (v) holds.
$G={\mathbb R}^n\times K$
, where K is the maximal compact subgroup of G, i.e. (v) holds.
If G does not have any compact central subgroup of positive dimension, by Theorem 4·1, we get that
![]() $\textrm{(vi)} \Leftrightarrow \textrm{(i)}$
, and hence the last assertion follows.
$\textrm{(vi)} \Leftrightarrow \textrm{(i)}$
, and hence the last assertion follows.
An automorphism T of a locally compact group G is said to have bounded orbits if all its orbits are relatively compact, i.e. for every
![]() $x\in G$
,
$x\in G$
,
![]() $\{T^{n}(x)\}_{n\in{\mathbb Z}}$
is relatively compact. In particular, if T is contained in a compact subgroup of
$\{T^{n}(x)\}_{n\in{\mathbb Z}}$
is relatively compact. In particular, if T is contained in a compact subgroup of
![]() ${\rm Aut}(G)$
, then T has bounded orbits. The following result is for any automorphism on a general connected Lie group which acts distally on
${\rm Aut}(G)$
, then T has bounded orbits. The following result is for any automorphism on a general connected Lie group which acts distally on
![]() ${\rm Sub}^a_G$
.
${\rm Sub}^a_G$
.
Corollary 4·6. Let G be a connected Lie group and let
![]() $T\in{\rm Aut}(G)$
. If T acts distally on
$T\in{\rm Aut}(G)$
. If T acts distally on
![]() ${\rm Sub}^a_G$
, then T has bounded orbits.
${\rm Sub}^a_G$
, then T has bounded orbits.
Proof. Suppose T acts distally on
![]() ${\rm Sub}^a_G$
. Let C be the largest compact connected central subgroup of G. Then C is characteristic in G and
${\rm Sub}^a_G$
. Let C be the largest compact connected central subgroup of G. Then C is characteristic in G and
![]() $G/C$
does not have any compact central subgroup of positive dimension. Moreover, by Lemma 3·3, the automorphism
$G/C$
does not have any compact central subgroup of positive dimension. Moreover, by Lemma 3·3, the automorphism
![]() $\overline{T}$
of
$\overline{T}$
of
![]() $G/C$
corresponding to T belongs to
$G/C$
corresponding to T belongs to
![]() ${\rm (NC)}$
in
${\rm (NC)}$
in
![]() ${\rm Aut}(G/C)$
and by Theorem 4·1, we get that
${\rm Aut}(G/C)$
and by Theorem 4·1, we get that
![]() $\overline{T}$
has bounded orbits. Therefore, T itself has bounded orbits, since C is compact.
$\overline{T}$
has bounded orbits. Therefore, T itself has bounded orbits, since C is compact.
The converse of Corollary 4.6 does not hold as illustrated by the following example. The example also illustrates that in Theorem 4·3, the statement that a unipotent automorphism T of a connected Lie group G acts distally on
![]() ${\rm Sub}^a_G$
can not be replaced by the statement that T belongs to the class (NC). It also shows that Theorem 4·1 can not be completely generalised to any connected Lie group G even if we restrict the class of automorphisms to
${\rm Sub}^a_G$
can not be replaced by the statement that T belongs to the class (NC). It also shows that Theorem 4·1 can not be completely generalised to any connected Lie group G even if we restrict the class of automorphisms to
![]() $({\rm Aut}(G))^0$
, as in Theorem 4·4. Moreover, the example also illustrates that the condition on the center in Corollary 4·5 is necessary for the statement (vi) to be equivalent to
$({\rm Aut}(G))^0$
, as in Theorem 4·4. Moreover, the example also illustrates that the condition on the center in Corollary 4·5 is necessary for the statement (vi) to be equivalent to
![]() $\textrm{(i)}-\textrm{(v)}$
in the theorem.
$\textrm{(i)}-\textrm{(v)}$
in the theorem.
Example 4·7. Let
![]() $G={\mathbb H}/D$
, where
$G={\mathbb H}/D$
, where
![]() ${\mathbb H}$
is the 3-dimensional Heisenberg group (the group of strictly upper triangular - unipotent - matrices in
${\mathbb H}$
is the 3-dimensional Heisenberg group (the group of strictly upper triangular - unipotent - matrices in
![]() ${\rm SL}(3,{\mathbb R}))$
and D is a discrete central subgroup of
${\rm SL}(3,{\mathbb R}))$
and D is a discrete central subgroup of
![]() ${\mathbb H}$
isomorphic to
${\mathbb H}$
isomorphic to
![]() ${\mathbb Z}$
. Then G is a connected step-2 nilpotent Lie group, its center Z of G is compact and
${\mathbb Z}$
. Then G is a connected step-2 nilpotent Lie group, its center Z of G is compact and
![]() $G/Z\cong{\mathbb R}^2$
. Let T be any nontrivial inner automorphism of G, i.e.
$G/Z\cong{\mathbb R}^2$
. Let T be any nontrivial inner automorphism of G, i.e.
![]() $T={\rm inn}(x)$
for some
$T={\rm inn}(x)$
for some
![]() $x\not\in Z$
, Note that T has bounded orbits as
$x\not\in Z$
, Note that T has bounded orbits as
![]() $T^n(g)\in gZ$
,
$T^n(g)\in gZ$
,
![]() $n\in{\mathbb Z}$
, for every
$n\in{\mathbb Z}$
, for every
![]() $g\in G$
. As G is connected and nilpotent, T is nontrivial and unipotent and Theorem 4·3 implies that T does not act distally on
$g\in G$
. As G is connected and nilpotent, T is nontrivial and unipotent and Theorem 4·3 implies that T does not act distally on
![]() ${\rm Sub}^a_G$
. However, T belongs to (NC). For if A is a discrete cyclic subgroup of G, it is either finite and hence central in G, in which case it is T-invariant, or its image in
${\rm Sub}^a_G$
. However, T belongs to (NC). For if A is a discrete cyclic subgroup of G, it is either finite and hence central in G, in which case it is T-invariant, or its image in
![]() $G/Z$
is a discrete infinite cyclic group and as T acts trivially on
$G/Z$
is a discrete infinite cyclic group and as T acts trivially on
![]() $G/Z$
, it follows that
$G/Z$
, it follows that
![]() $T\in{\rm (NC)}$
. Also
$T\in{\rm (NC)}$
. Also
![]() $T\in ({\rm Aut}(G))^0$
and in fact, it generates a non-compact subgroup in
$T\in ({\rm Aut}(G))^0$
and in fact, it generates a non-compact subgroup in
![]() $({\rm Aut}(G))^0$
. Moreover, every inner automorphism of G belongs to
$({\rm Aut}(G))^0$
. Moreover, every inner automorphism of G belongs to
![]() ${\rm (NC)}$
.
${\rm (NC)}$
.
The map T in the above example acts trivially on the central torus and it also acts trivially on the quotient group modulo the central torus. Such maps on connected Lie groups are known as (isotropic) shear automorphisms (see [Reference Dani10]).
Remark 4·8. (1) For the unit circle
![]() ${\mathbb S}^1$
,
${\mathbb S}^1$
,
![]() ${\rm Aut}({\mathbb S}^1)$
is finite. Therefore, using [Reference Previts and WU22, corollary 2·5], Corollary 3·7 and Theorem 4·4, one can show that Theorem 4·1(ii)-(iv) are equivalent for a somewhat larger class of connected Lie groups whose maximal torus is central and it is of dimension at most 1. This class includes connected nilpotent Lie groups whose largest compact (connected) central subgroup is of dimension 1, e.g. G as in Example 4·7. It also includes the Lie group of the form
${\rm Aut}({\mathbb S}^1)$
is finite. Therefore, using [Reference Previts and WU22, corollary 2·5], Corollary 3·7 and Theorem 4·4, one can show that Theorem 4·1(ii)-(iv) are equivalent for a somewhat larger class of connected Lie groups whose maximal torus is central and it is of dimension at most 1. This class includes connected nilpotent Lie groups whose largest compact (connected) central subgroup is of dimension 1, e.g. G as in Example 4·7. It also includes the Lie group of the form
![]() ${\rm SL}(2,{\mathbb R})\ltimes G$
, where G is as in the above example. (2) It would be interesting to not only identify the spaces
${\rm SL}(2,{\mathbb R})\ltimes G$
, where G is as in the above example. (2) It would be interesting to not only identify the spaces
![]() ${\rm Sub}^a_G$
and
${\rm Sub}^a_G$
and
![]() ${\rm Sub}_G$
, but describe the action of
${\rm Sub}_G$
, but describe the action of
![]() ${\rm Aut}(G)$
on them, as it is done in [Reference Bridson, De La Harpe and Kleptsyn8] for some subspaces of
${\rm Aut}(G)$
on them, as it is done in [Reference Bridson, De La Harpe and Kleptsyn8] for some subspaces of
![]() ${\rm Sub}_{\mathbb H}$
, for the 3-dimensional Heisenberg group
${\rm Sub}_{\mathbb H}$
, for the 3-dimensional Heisenberg group
![]() ${\mathbb H}$
. (3) In case of compact abelian (Lie) groups G, we study the action of unipotent automorphisms. It would be interesting to study the action of a general T in
${\mathbb H}$
. (3) In case of compact abelian (Lie) groups G, we study the action of unipotent automorphisms. It would be interesting to study the action of a general T in
![]() ${\rm Aut}(G)$
on
${\rm Aut}(G)$
on
![]() ${\rm Sub}_G$
for such compact groups G, as it would give more insight for the action of
${\rm Sub}_G$
for such compact groups G, as it would give more insight for the action of
![]() ${\rm Aut}(G)$
on
${\rm Aut}(G)$
on
![]() ${\rm Sub}_G$
for a general connected Lie group G. (4) For general locally compact groups G, (especially for totally disconnected groups), a comprehensive study is needed for the action of
${\rm Sub}_G$
for a general connected Lie group G. (4) For general locally compact groups G, (especially for totally disconnected groups), a comprehensive study is needed for the action of
![]() ${\rm Aut}(G)$
on
${\rm Aut}(G)$
on
![]() ${\rm Sub}_G$
.
${\rm Sub}_G$
.
We conclude with a mention of the following: using many results in this paper, further study of class (NC) and the distality of actions of automorphisms of G on
![]() ${\rm Sub}_G$
have been carried out where G is a certain type of locally compact group or a lattice in a Lie group [Reference Palit and SHAH35, Reference Ppalit, PRAJAPATI and SHAH37]. Expansivity of the action of automorphisms of G on
${\rm Sub}_G$
have been carried out where G is a certain type of locally compact group or a lattice in a Lie group [Reference Palit and SHAH35, Reference Ppalit, PRAJAPATI and SHAH37]. Expansivity of the action of automorphisms of G on
![]() ${\rm Sub}_G$
has also been studied for locally compact groups and lattices in Lie groups recently [Reference Prajapati and SHAH36, Reference Ppalit, PRAJAPATI and SHAH37].
${\rm Sub}_G$
has also been studied for locally compact groups and lattices in Lie groups recently [Reference Prajapati and SHAH36, Reference Ppalit, PRAJAPATI and SHAH37].
Acknowledgments
R. Shah would like to thank: S. G. Dani for extensive discussions on the structure of semisimple Lie groups and I. Chatterji and Université Nice Sophia Antipolis, France, for hospitality during a visit in June 2019 while a part of work was carried out. R. Shah would also like to acknowledge the MATRICS research grant from DST-SERB, Govt. of India, which partially supported A. K. Yadav as a visiting scholar at JNU, New Delhi in 2018. A. K. Yadav would like to thank the Ambedkar University Delhi for an adjunct faculty position in 2018 and Krishnendu Gongopadhyay for a visiting position under a research grant from NBHM, DAE, Govt. of India, at IISER Mohali in early 2019. We thank the anonymous referee for suggestions which led to some improvements in the presentation of this paper.