Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-06T15:19:18.127Z Has data issue: false hasContentIssue false
  • English
  • Français

Classifying spaces for commutativity of low-dimensional Lie groups

Part of: Lie groups Fiber spaces and bundles

Published online by Cambridge University Press:  12 July 2019

OMAR ANTOLÍN–CAMARENA ,
SIMON PHILIPP GRITSCHACHER  and
BERNARDO VILLARREAL
OMAR ANTOLÍN–CAMARENA
Affiliation:
Instituto de Matemáticas, UNAM, Mexico City. e-mail: omar@matem.unam.mx
SIMON PHILIPP GRITSCHACHER
Affiliation:
Centre for Symmetry and Deformation, University of Copenhagen. e-mail: gritschacher@math.ku.dk
BERNARDO VILLARREAL
Affiliation:
Instituto de Matemáticas, UNAM, Mexico City. e-mail: villarreal@matem.unam.mx
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For each of the groups G = O(2), SU(2), U(2), we compute the integral and 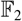$\mathbb{F}_2$-cohomology rings of BcomG (the classifying space for commutativity of G), the action of the Steenrod algebra on the mod 2 cohomology, the homotopy type of EcomG (the homotopy fiber of the inclusion BcomG → BG), and some low-dimensional homotopy groups of BcomG.

MSC classification

Primary: 55R40: Homology of classifying spaces, characteristic classes 22E99: None of the above, but in this section
Secondary: 55R20: Spectral sequences and homology of fiber spaces
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 169 , Issue 3 , November 2020 , pp. 433 - 478
Copyright
© Cambridge Philosophical Society 2019

Footnotes

†

This author gratefully acknowledges financial support from the London Mathematical Society through a Postdoctoral Mobility Grant (PMG 16-17 22), and would like to thank the Pacific Institute for the Mathematical Sciences at the University of British Columbia for their hospitality. The author is supported by the Danish National Research Foundation through the Centre for Symmetry and Deformation (DNRF92).

References

REFERENCES

Adem, A. and Cohen, F.. Commuting elements and spaces of homomorphisms. Math. Ann. 338 (2007), 587–626. (Erratum posted July 2009.)CrossRefGoogle Scholar
Adem, A. and GóMez, J. M.. A classifying space for commutativity in Lie groups. Algebr. Geom.Topol. 15 (2015), 493–535.CrossRefGoogle Scholar
Adem, A., F. , COHEN and Torres–Giese, E.. Commuting elements, simplicial spaces and filtrations of classifying spaces. Math. Proc. Camb. Phil. Soc. 152 (2012), 1, 91–114.CrossRefGoogle Scholar
Baird, T. J.. Cohomology of the space of commuting n-tuples in a compact Lie group. Algebr. Geom. Topol. 7 (2007), 737–754.CrossRefGoogle Scholar
Borel, A.. Sur la cohomologie des espaces fibre principaux et des espaces homogenes de groupes de Lie compacts. Ann. of Math. (2) 57 (1953), 115–207.CrossRefGoogle Scholar
Brown, E.. The cohomology of BSOn and BOn with integer coefficients. Proc. Amer. Math. Soc. 85 (1982), 283–288.Google Scholar
Decker, W., Greuel, G.–M., Pfister, G. and SchöNemann, H.. SINGULAR 4-1-0 — A computer algebra system for polynomial computations. http://www.singular.uni-kl.de (2016).Google Scholar
Gritschacher, S. P.. The spectrum for commutative complex K-theory. Algebr. Geom. Topol. 18 (2018), 1205–1249.CrossRefGoogle Scholar
Gritschacher, S. P.. Commutative K-theory. PhD thesis. University of Oxford (2017).Google Scholar
Pettet, A. and Souto, J.. Commuting tuples in reductive groups and their maximal compact subgroups. Geom. Topol. 17 (2013), 2513–2593CrossRefGoogle Scholar
Villarreal, B.. A simplicial approach to spaces of homomorphisms. PhD thesis. University of British Columbia (2017).Google Scholar
Villarreal, B.. Cosimplicial groups and spaces of homomorphisms. Algebr. Geom. Topol. 17 (2017), 3519–3545.CrossRefGoogle Scholar
Whitehead, G. W.. Elements of homotopy theory. Graduate Texts in Mathematics, no. 61 (Springer-Verlag, New York-Berlin, 1978).CrossRefGoogle Scholar
Wu, J.. Homotopy theory of the suspensions of the projective plane. Mem. Amer. Math. Soc. 769 (2003).CrossRefGoogle Scholar