Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-12T03:19:26.075Z Has data issue: false hasContentIssue false
  • English
  • Français

The majorisation principle for convex functions

Published online by Cambridge University Press:  24 February 2022

G. J. O. Jameson
G. J. O. Jameson*
Affiliation:
13 Sandown Road, LancasterLA1 4LN e-mail: pgjameson@talktalk.net
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

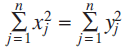Given positive numbers xj, yj such that $\sum\limits_{i = 1}^n {{x_j}} = \sum\limits_{j = 1}^n {{y_j}} $ , it can happen that $\sum\limits_{j = 1}^n {x_j^2} = \sum\limits_{j = 1}^n {y_j^2} $ : for example, 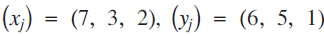$({x_j}) = (7,\,3,\,2),\,({y_j}) = (6,\,5,\,1)$ . However, such cases are exceptional.

Type
Articles
Information
The Mathematical Gazette , Volume 106 , Issue 565 , March 2022 , pp. 95 - 102
Check for updates
Copyright
© The Authors, 2022. Published by Cambridge University Press on behalf of The Mathematical Association

References

Hardy, G. H., J. Littlewood and G. Pólya, Some simple inequalities satisfied by convex functions, Messenger Math. 58 (1929) pp. 145–152.Google Scholar
Karamata, J., Sur une inégalité relative aux fonctions convexes, Publ. Math. Univ. Belgrade 1 (1932) pp. 145–148.Google Scholar
Jameson, G. J. O., Monotonicity of the midpoint and trapezium estimates for integrals, Math. Gaz. 105 (2021) pp. 433–441.10.1017/mag.2021.110CrossRefGoogle Scholar
Kadelburg, Z., Duhis, D., Luhis, M. and Matis, I., Inequalities of Karamata, Schur and Muirhead, and some applications, Teaching of Math. 8 (2005) pp. 31–45.Google Scholar
Hardy, G. H., Littlewood, J. and Pólya, G., Inequalities (2nd edn.), Cambridge University Press (1967).Google Scholar
Marshall, A. W. and Olkin, I., Inequalities: Theory of majorization and its applications, Academic Press (1979).Google Scholar
Bennett, Grahame, Some forms of majorization, Houston J. Math. 36 (2010) pp. 1037–1066.Google Scholar