INTRODUCTION
Increased uncertainty about the current growth rate of productivity, potential output, and the natural rate of unemployment has led to questions about how monetary policy should be altered in the face of this uncertainty. The question is extremely important from a practical point of view (What should the Federal Reserve do today?), as well as being of particular theoretical interest (What are the various types of uncertainty faced by policymakers, and what effects should each of these have on optimal policy?).
A natural place to begin the investigation of these difficult questions is within the framework of monetary policy rules, such as those put forward by Taylor (1993). The advantage of these rules is that they are explicit, well defined, and simple functions of variables within a completely specified economic model. Different types of uncertainty within the model can then be specified and their effects studied. The fact that Taylor-type rules have matched the historical behavior of the Federal Reserve for the past 15–20 years also lends support to their use as an analytical laboratory for the investigation of these issues.
A typical setup involves an economy that is linear in all of its variables, and policymakers who minimize an expected discounted sum of squared deviations of goal variables from their respective targets. The following backward-looking model serves as an example
1 I consider rational expectations models in the main body of the paper.
:
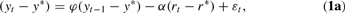
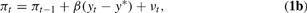
where yt, πt, and rt refer to output, inflation, and the real interest rate in period t; y* and r* denote the levels of potential output and the “natural” rate of interest consistent with long-run equilibrium, respectively; and rt is set by policymakers at the beginning of period t on the basis of information available through the end of period t−1. A typical specification of policymakers' preferences is
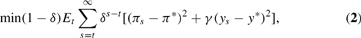
a simple discounted sum of expected squared deviations of output from potential and inflation from its target, π*, with weight γ placed on the output gap. The case γ = 0 corresponds to pure inflation targeting by policymakers, but does not necessarily prevent current or past values of the output gap from entering policymakers' optimal reaction function, since these variables may help forecast future values of inflation. Note that it is assumed in the model for simplicity that policymakers have control over the short-term real interest rate, rt.
This is a simple, discrete-time dynamic programming problem with quadratic objective and linear constraints, the solution of which is well known [Sargent (1987)]:
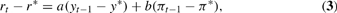
where a and b are constants, determined by the parameters of the model. The form of equation (3) and the values of a and b are the same no matter what the variances of ε and ν—policymakers behave in a certainty-equivalent fashion regardless of the variance associated with the laws of motion of the economy.
A major implication of this finding is that uncertainty about thelevel of potential output, y*, should have no effect on the monetary policy rule. If at time t we have y* = ŷ*+ η, where η is a mean-zero stochastic disturbance and ŷ* ≡ Et y*, then the form of equations (1a) and (1b) is essentially unchanged, with y* replaced by ŷ*, εt replaced by
, and νt replaced by
. Then, as before, the variances of
and
, and hence the variance of η, have no effect on the optimal policy rule—one simply replaces y* with ŷ* in equation (3) and acts as if this estimate ŷ* were known with certainty. This result is emphasized by Estrella and Mishkin (1999), and is standard in the literature on monetary policy rules.
To be sure, not all types of uncertainty are sterile when it comes to their effects on optimal policy. For example, if policymakers are unsure about the effects of their control variable rt on the economy, so that α is stochastic, the optimal choice of rt will depend on the degree of uncertainty underlying the parameter α [Brainard (1967), Sack (2000)]. Here, the uncertainty is multiplicative with respect to the control variable, rather than being simply additive.2
Uncertainty about r*, yt−1, and πt−1 is also additive with respect to the control variable rt, and thus also has no effect on the optimal policy in (3).
In this paper, however, I abstract away from multiplicative uncertainty for a number of reasons. First, it is well known that certainty-equivalence does not hold in the presence of multiplicative uncertainty. Second, the effects of multiplicative uncertainty on policymakers' optimal response function (3) are ambiguous in sign (when more than one coefficient is stochastic), and found by several authors to be quantitatively small in simulations [
Estrella and Mishkin (1999),
Rudebusch (2001)].
3 Sack (2000), however, finds larger effects of parameter uncertainty within a monthly VAR framework.
Finally, the uncertainty with which policymakers seem to have been the most concerned recently is primarily additive: Has there been a structural break in the growth rate of productivity, potential output, and the level of the natural rate of unemployment? These are questions about the state variables of the economy themselves, and not about the effects of choice variables
on the economic state.
The main point of this paper is that additive uncertainty can have important effects on optimal policy, even within a linear-quadratic framework. Suppose, for example, that the state of the economy is Xt, an unobserved, possibly large, vector.4
Some components of Xt can be observed without altering the results.
Suppose further that the output gap and inflation are functions of this unobserved state of the economy
Xt. Policymakers will behave in a certainty-equivalent fashion with respect to
Et Xt, the expected value of
Xt, but will use the output gap and inflation to help infer the value of
Et Xt. This inference stage of the problem, because it is one of signal extraction, is sensitive to the amount of uncertainty that is present in the indicator variables of the system. In particular, as the noise in the output gap,
yt −
y*
t, increases relative to the signal about
Xt, it is optimal to decrease the coefficient on
yt −
y*
t in the estimation of
Et Xt, and to increase the coefficient on inflation in that estimation. Thus, the optimal policy, when expressed as a reduced-form function of the output gap and inflation, rather than
Et Xt, is
not invariant to the degree of additive uncertainty in the former variables. Note that both the rule itself and policymakers' estimate
Et Xt are fully optimal in this framework—at every time
t, policymakers' interest-rate choice and estimate of state variables are globally optimal and cannot be improved upon in any way. Note also that the output gap need not be directly observable to be an indicator variable in this framework—an unbiased estimate of the output gap is all that is required.
Previous Literature
Previous studies of non-certainty-equivalence with additive uncertainty have followed either Smets (1998) or Orphanides (1998). Smets (1998) points out that certainty-equivalence fails to hold when policymakers are constrained to respond to only a limited subset of the state variables of the system, so that the policy rule is a constrained optimum, rather than a global optimum. [This restriction makes sense, in particular, when the size of the state space is large, as in Orphanides et al. (2000), who work with the Federal Reserve Board's macro model.] Uncertainty about any of the variables in the policymakers' simple rule will then lead the optimal coefficients of the simple rule to change.5
Uncertainty about any state variables not in the policymakers' simple rule will have no effect; this will be obvious from the discussion of the results in Section 2.
Orphanides (1998) focuses on the fact that the data, such as the output gap and inflation rate, are observed only imperfectly in real time. By the certainty-equivalence principle, policymakers' optimal response in this case is to formulate best estimates of the output gap, Et(yt − y*t), and inflation, Et πt, and act as if these estimates were known with certainty. Orphanides and others [Aoki (1999), Rudebusch (2001, 2002)] bring about non-certainty-equivalence in this framework by constraining policy to react to the actual real-time data, rather than to the best estimates above. This naturally raises the question as to why the actual real-time data are not (real-time) best estimates of the true values.
For example, if y*t denotes the level of potential output, and y*t|t the real-time estimate of the level of potential output, one would normally expect that
where ηt is a mean-zero random variable. In this case, y*t|t = Et y*t, and so, the real-time data are the real-time best estimates! The constraint that policymakers react only to the real-time data is then not really a constraint at all, and the certainty-equivalence principle holds.
It is only because Orphanides formulates the real-time data problem as one of signal extraction, with
where y*t (the true value underlying the data, or signal) and ηt (the noise) are orthogonal random variables, that the certainty-equivalence principle is circumvented. Note that in (4′), the real-time data y*t|t has the property that y*t|t ≠ Et y*t, so that it is no longer an unbiased estimate. When the problem is modified in this manner, an increase in the variance of ηt now does have an effect on the best estimate Et y*t—in particular, if y*t and ηt are normally distributed around zero, then Et y*t =
y*t|t in the univariate case. Although the optimal policy is still a certainty-equivalent function of policymakers' best estimate Ety*t, expressing the policy as a function of the real-time y*t|t now leads to effects of additive uncertainty ηt on the coefficients in the optimal rule. It is in this respect that Orphanides (1998) finds an exception to the certainty-equivalence principle.
It should be clear from the above analysis that the use of real-time data per se has nothing to do with the non-certainty-equivalence demonstrated in Orphanides (1998). Instead, it is the introduction of a signal extraction problem into the policymakers' inference step that drives the result. The general implications of formulating policymakers' inference problem in this way is the aim of the present paper. In addition, the policies that are emphasized by Orphanides (1998), Orphanides et al. (2000), and Rudebusch (2001, 2002) are not fully optimal, so that it is difficult in those papers to distinguish between the effects of uncertainty itself and the effects of uncertainty interacting with a substantially constrained policy response function. In the present paper, all policy rules and all estimation are fully optimal.
A recent paper by Svensson and Woodford (2000) also considers several of the same issues as the present paper. There are two main contributions of the present paper that differentiate it from theirs. First, I show how the results of this paper are applicable to indicator variables that are estimated (such as the output gap), rather than simply indicator variables that are directly observed (output, unemployment, inflation, money growth, etc.). Second, I consider the effects of a structural break in uncertainty about an indicator variable, rather than an increase in the level of uncertainty about an indicator that stretches back into the infinite past. The latter is merely a thought experiment, whereas the former corresponds to situations faced by actual policymakers in practice, such as the (possible) structural break in U.S. productivity growth in the late 1990's.
The remainder of the paper proceeds as follows. Section 2 develops the relationship between signal extraction and non-certainty-equivalence in a simple descriptive model of the economy, under both naive and rational expectations. Section 3 extends these results to the general linear-quadratic-Gaussian framework and proves the coefficient attenuation result for the general case. Section 4 extends the basic model forward in time to allow for the dynamic propagation of uncertainty, and proves that the results of Section 2 are robust to this extension. Section 5 discusses the results and concludes.
BASIC MODEL
Policymakers have preferences over inflation and output of the form
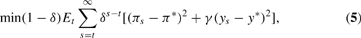
where π* denotes policymakers' long-run target for the inflation rate and y* denotes the level of “potential” output consistent with long-run equilibrium.
6 For simplicity, I assume from now on that y* is constant, rather than growing over time, but this assumption is not essential.
The case γ = 0 corresponds to pure inflation targeting, but does not necessarily preclude current or past values of the output gap from entering policymakers' optimal reaction function, since they may help forecast inflation.
For the purposes of this section, the unobserved “signal” variable Xt is taken to be a scalar. The interpretation in this case is that the true underlying state of the economy is scalar, or that Xt is an index of inflationary pressures or “excess demand.” Xt is assumed to evolve according to
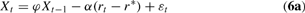
with the output gap and inflation being observable functions of this unobserved state:
Here, r* denotes the “natural” rate of interest, consistent with long-run equilibrium in the model; and α, β, and φ are known positive parameters with φ < 1. The stochastic disturbances εt, ηt, and νt are independent of each other, over time, and of current and prior values of X, y, and π; and are normally distributed with constant variances σε2, ση2, and σν2, respectively. The variable Xt (and its past values) are never observed by policymakers and must be inferred from previous observations of output and inflation. Equations (6b) and (6c) represent the signal extraction aspect of the problem, with ηt and νt denoting noise disturbances that are orthogonal to the underlying signal Xt.
One may assume that y* is observed with certainty or, alternatively, that it is stochastic.
7 I assume that π* and r* are known with certainty, although in principle these restrictions, too, could be dropped.
Letting
y* =
ŷ* + ζ, where ζ is a random variable, one can rewrite equation (6b) as
where
.
8 I assume here that the error ζ is orthogonal to current and past values of X and all other variables of the system. This is the case, for example, when the uncertainty surrounding y* is due to a regime change that has been known to occur in the previous period, so that y*, which was previously known with certainty, is suddenly uncertain. The more general case, where ζ is correlated with Xt, is not difficult, and is solved in Sections 3 and 4. The results there are essentially identical to those presented here.
From the point of view of policymakers' decision at time
t, this is equivalent to simply increasing the variance of η
t in equation (6b), and so, the analysis is simplified, without loss of generality, by restricting attention to that equation and studying the effects of an increase in σ
η2. In this way, policymakers' signal extraction problem when the indicator variables are uncertain or
estimated (as the output gap is here) is not fundamentally different from the signal extraction problem they would face when all the indicator variables are perfectly observed.
9 See note 8. The separation of estimation and control in this model [Bertsekas (1987, p. 292)] implies that the optimal policy [equation (8), below] is unaffected even as policymakers learn about y* and revise their estimates over time. (One should think of the state of the economy in this case as being [y*,Xt]′, with policymakers learning about y* as well as Xt.)
Economic agents' prior expectation of the inflation rate, πte, can be either a rational expectation (πte ≡ Et πt, where Et denotes the expectation at the beginning of period t, before shocks are realized), or a naive expectation (πte ≡πt−1), without altering the results below (see the solution in the Appendix).10
The special linear-quadratic structure of the problem is lost unless πte is either a rational expectation or a fixed linear combination of finitely many lags of observable variables, but the general results of this paper apply as long as one of these two conditions is met. Note also that the exact process by which agents' expectations are formed has no effect on policymakers' period t estimation problem regarding Xt. It is only because of the control aspects of policymakers' problem that assumptions about agents' expectations are required at all.
In either case, π
te is known to policymakers and fixed at the beginning of period
t.
The timing of policymakers' observations and actions is as follows. At the beginning of period t, policymakers update their beliefs about Xt−1 based on observations of yt−1, πt−1, and the earlier choice of rt−1. On the basis of these updated beliefs, policymakers then choose a value of rt that minimizes the expected loss function (5). Shocks to the economy (εt, ηt, and νt) are then realized and the values yt and πt are observed. Thus, policymakers' information set at time t is
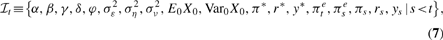
where E0X0 and Var0 X0 denote the mean and variance of policymakers' prior (time 0) distribution on X0, which is assumed to be Gaussian.
11 Meyer et al. (2001) and Swanson (2001) consider the case of optimal estimation and control when policymakers' priors are not normally distributed. We can also drop the assumption of normality within the framework of the present paper if we restrict policymakers to linear (as opposed to fully optimal) estimates of the unobserved state Xt, since Kalman filtering is the optimal linear inference procedure.
Policymakers update beliefs about Xt−1 via Kalman filtering. Because (εt, ηt, νt) is multivariate normally distributed, this is the optimal inference procedure (in the sense of minimizing the mean-squared error of the estimate), and is equivalent to Bayesian updating.
The optimal solution to policymakers' problem (5), given the structure of the economy (6) and information set (7), is
where a and b are positive constants determined by the parameters of the system, given in the Appendix. Note that a and b are completely invariant to σε2, ση2, σν2, and Vart Xt−1 (policymakers' time t prior variance on Xt−1, derived recursively from Var0 X0 by the Kalman filtering algorithm). In this respect, the linear-quadratic problem with signal extraction displays certainty-equivalence.
In forming the optimal estimate Et Xt−1, however, policymakers do respond to the amount of uncertainty in the problem. Their prior (time t − 1, i.e., before values of yt−1 and πt−1 are observed) distribution on (Xt−1, yt−1 − y*, πt−1 − πt−1e) is given by
where I have let σx2 denote Vart−1 Xt−1, policymakers' prior, time t − 1, variance on Xt−1. Their posterior distribution on Xt−1, after observing yt−1 and πt−1, then has mean
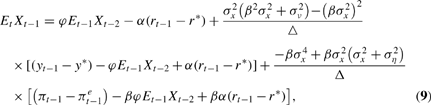
where Δ ≡(σx2+ση2) (β2σx2 + σν2) − (βσx2)2 = σx2 σν2 + β2σx2ση2 + ση2 σν2. Equation (9) is analogous to the simpler formula for signal extraction with one observable variable, Et Xt−1 = Et−1 Xt−1 + [σx2/(σx2+ση2)] [(yt−1−y*) − Et−1 (yt−1−y*)], with additional terms in the coefficients that take into account the covariance between output and inflation.
12 Given the normality assumption, the formula for the best predictor Et Xt−1 is the theoretical regression/projection
where
This yields
which is the expression given in (9).
Grouping terms in (9) yields
where the Et−1 Xt−2 term can be cascaded backward and expressed as a function of lagged observations of the output gap, the inflation surprise, and interest rates, to the point where the original distribution on X0 is negligible, as it is multiplied by a large power of φ.
Note that, even though policymakers' optimal reaction function (8) is certainty-equivalent in terms of the estimate Et Xt−1, when the optimal policy is expressed as a function of present and past indicator variables (the output gap, inflation surprise, and interest rates), certainty-equivalence in the reduced form no longer holds. The variances of the additive disturbance terms enter into the coefficients of (10).
For example, consider the effects of a sudden increase in uncertainty surrounding potential output y* on equation (10). As shown in note 8, this can be regarded as an increase in ση2, holding σν2 and σx2 constant. As ση2 increases, the quantity Δ increases, but less than proportionately. This implies that the coefficient on yt−1 − y* in (10) decreases in magnitude, so that policymakers place less weight on the noisy output gap in forming their inference about the underlying state of the economy. Thus, we have an example of coefficient attenuation on the noisy or uncertain variable. In addition, the coefficients on each of the other variables in equation (10) increase in absolute value: Policymakers place more weight on those variables about which they are relatively more certain. In this sense, policymakers become “less proactive and more reactive,” responding less forcefully to the current output gap, and more forcefully to the current inflation surprise, and past output gaps and inflation surprises, because these variables provide more reliable information about the current state of the economy.13
This “less proactive” result could be emphasized by setting up the model with an additional lag in equation (6c),
so that current output is more closely related to future than to current inflation. This is the timing used by Svensson (1997); however, it complicates the analysis by making the signal extraction problem a function of two lags of the variable Xt instead of only one, which is why this approach was not taken here.
These conclusions are not idiosyncratic to an increase in the variance of the additive disturbance ηt. For example, an increase in σν2, instead of ση2, leads to a decrease in the coefficient on (πt−1 − πt−1e) in equation (10), and an increase in the coefficients on the other variables in that equation. Exactly analogous results (lower coefficient on the noisy variable, higher coefficients on the others) obtain in response to an increase in σx2, the policymakers' prior variance on Xt−1. Thus, the result described above is robust, and derives not from any special assumptions surrounding the model, but rather from the general principle that in linear regression, or statistical projection, less weight is given to observations that have higher variance.
Obviously, as with linear regression and statistical projection, the covariances between the different variables matter for the coefficients in (10). So far, I have abstracted away from this problem by assuming that the disturbances are orthogonal to each other, and to policymakers' prior for the variable Xt−1, but I show below for the general case, with arbitrary covariances, that the coefficient attenuation result still holds: An increase in the uncertainty surrounding a given variable causes policymakers to assign less weight to that variable in forming their best estimate of the underlying state of the economy, Et Xt−1. Moreover, the amplification of the coefficients on inflation and its lags in (10) is also quite robust, and holds for models more general than that of the present section. For example, Section 4 proves this result for the case in which increased uncertainty about potential output extends backward any number of periods, is correlated across time, and is correlated with policymakers' priors about the unobserved state of the economy Xt−1, in a manner that is consistent with policymakers learning about potential output over time.
Signal Extraction vs. Imperfect Observation of State Variables
Note that the above results hinge crucially on setting up model (6) as one involving signal extraction, rather than one simply involving imperfect observation of state variables. For example, replacing (6b) with
or, with an uncertain potential output,
where y* ≡ ŷ* + ζ and
, the non-certainty-equivalence results described above are completely eliminated. In both (6b[dagger]) and (6b[Dagger]), the policymakers' optimal estimate of the underlying state of the economy, Et Xt−1, is simply (yt−1 − y*) in the first case, and (yt−1 − ŷ*) in the second. Plugged into the certainty-equivalent structural response in equation (8), the reduced-form policy response thus retains the certainty-equivalence property.
Note that this analysis implies that it is not real-time data per se that justify caution on the part of policymakers in Orphanides (1998) and Rudebusch (2001). If the real-time data are unbiased forecasts of the true values, analogous to (6b[dagger]) or (6b[Dagger]), then certainty-equivalence holds, and the amount of uncertainty surrounding these real-time estimates (ση2) is completely irrelevant for optimal policy. Certainty equivalence only fails to hold in their framework if the real-time data are realizations of true values plus noise (and thus are biased estimates of the true values), so that estimation of the true values involves a signal extraction problem, as in (6b).
This naturally raises the question as to whether the real-time data are better modeled as rational estimates or as noise-contaminated observations. Orphanides (1998, 2001) presents figures demonstrating that the output gap, in particular, has been badly mismeasured by policymakers in real time. However, both the size of these errors and their serial correlation were not evident until several years after the fact, and so, it is not clear that these real-time estimates of the output gap were not rational at the time. To take the position that policymakers were deliberately irrational in their real-time estimates seems unwarranted without a more rigorous analysis to support this point of view.
Rigorous analysis of the performance of real-time data and official forecasts has been undertaken by a number of authors, albeit with data that are more readily observable than the output gap, such as real GDP and inflation. Mankiw and Shapiro (1986) analyze whether the real-time real GNP data produced by the BEA are better modeled as a rational forecast or as a realization with noise of the “true” (i.e., “final release”) value. They find that the real-time data appear to be unbiased and efficient rational forecasts. McNees (1995) looks at the official forecasts of real GNP/GDP and inflation published by the CBO and Federal Reserve System (as presented in “Humphrey-Hawkins” reports) and finds that they perform at least as well, if not better, than private-sector forecasts in terms of mean-squared error. Romer and Romer (2000) find that not only are the Federal Reserve Board's internal “Greenbook” forecasts of output and inflation unbiased and efficient, they completely dominate private-sector forecasts, in the sense that the private-sector forecast should be thrown out entirely if the Board's forecasts were to be made public.
These results might at first seem to contradict Rudebusch's (2001) finding of a significant, irrational “noise” component in the real-time inflation data (as measured by either the GNP/GDP deflator or fixed-weight price index). However, as in Orphanides (1998, 2001), Rudebusch's “final” data are from the perspective of the late 1990's, and thus include definitional revisions to GNP and changes in base year. In contrast, all of the papers cited above take particular care to evaluate the performance of the forecasts with respect to a final measure of the statistic on a definitionally consistent basis. For example, it seems unfair to evaluate the rationality of policymakers' 1970 estimate of real GNP and inflation using today's estimates of 1970 GDP in chain-weighted 1996 dollars, yet this is exactly what Orphanides and Rudebusch do. Thus, it is likely that the “noise” found by Rudebusch (2001) reflects nothing other than definitional changes in the data rather than deviations from rationality in policymakers' estimates.14
The problem of definitional revisions to output and inflation does raise an interesting theoretical issue: Whereas it is fairly clear that the rationality of a forecast should be evaluated using definitionally consistent realizations of the statistic, it is not so obvious that this is the correct approach when we start to consider policymakers' welfare. For example, it is possible that the post-definitional-change statistic is a better measure of the loss that policymakers, and society, actually experienced.
I would, however, take the following view. Policymakers' losses are a function of the true underlying state of the economy. The various aggregate statistics are generally poor reflections of this state. A definitional change in one of the aggregate statistics changes the relationship between the true state of the economy and the given aggregate statistic, but does not change the true state of the economy itself. Thus, the optimal coefficients in policymakers' signal extraction problem should change in response to the definitional revision, but there is not any irrational “noise” in the real-time data or in policymakers' losses.
The case for biased real-time data is thus somewhat uncompelling from an empirical as well as a theoretical standpoint. This implies that models incorporating only real-time data uncertainty should be certainty-equivalent. However, framing policymakers' inference problem about the state of the economy as one of signal extraction more generally, as is done in this paper, is still quite plausible. The interpretation of policymakers' estimation process in this case is one of an unobserved state of the economy that must be inferred using (possibly a large number of) economic indicators. For example, Alan Greenspan of the Federal Reserve Board is renowned for looking at a vast array of economic indicators in an attempt to infer the current state of the economy and its future course. When policymakers face a signal extraction problem such as this, a strong case for caution in the face of uncertainty can still be made.
Coefficient Attenuation, Simple Rules, and Robust Control
The implications of this paper contrast in an interesting way with those from the literature on “simple rules” and “robust control.” In particular, the signal extraction framework of the preceding section found that an increase in uncertainty surrounding a given indicator variable should be met with an attenuation in policymakers' response coefficient to that variable, and an amplification of their response coefficients on all other indicators, about which uncertainty has not changed.
The literature on “simple rules,” in contrast, generally finds that policymakers should attenuate their response coefficients on all variables in their reaction function, even if the increase in uncertainty surrounds only a single variable.15
Drew and Hunt (2000) provide one exception to this rule, but their model and findings are idiosyncratic for a number of reasons. First, the Reserve Bank of New Zealand's macro model is significantly nonlinear, so that certainty-equivalence would fail to hold even with a fully optimal rule. Second, and more important, policymakers' estimate of potential output is irrational, using an HP filter that yields estimates that are significantly correlated with the business cycle. Policymakers thus have a strong incentive to react aggressively to the output gap estimated in this way, since it will generally be smaller than the true output gap that enters their loss function.
This literature, typified by
Smets (1998), considers optimal policy within a class of rules that react to only a limited subset of state variables in the model. Because these simple rules are not globally optimal, they typically do not possess the certainty-equivalence property. Thus, observation error on a variable, even of the type in (6b
[dagger]) and (6b
[Dagger]), will generally lead to non-certainty-equivalent behavior in these constrained-optimal rules.
For example, Smets (1998) restricts policymakers to rules involving only one lag of output, the four-quarter average inflation rate, and one lag of the interest rate as arguments, and finds that the optimal coefficients on all of these variables are attenuated by an increase in uncertainty surrounding the output gap. Orphanides et al. (2000), investigating a similarly constrained class of rules within the Federal Reserve Board's FRB/US model, also find that attenuating the coefficients on every variable in the rule is the best response to increased uncertainty surrounding the output gap.16
Orphanides et al. (2000) do find that under some circumstances an amplification in the coefficient on the inflation rate is optimal. However, this only occurs when they increase the relative weight on the output gap in policymakers' loss function to high levels (0.75 or above).
The reason that these findings differ from those of the present paper can be explained as follows. The optimal rule in all of these models is a function of multiple lags of the output gap, inflation, and interest rates (and, in the FRB/US model, many other variables as well). To the extent that these variables are omitted, those that enter the simple rule serve partially as proxies for the variables that have been excluded. If the four-quarter average inflation rate enters negatively into an estimation equation for some of these other terms (such as past values of the interest-rate), then the desired amplification in coefficients on current and past inflation that I find will be offset by the desired amplification in the coefficients on these additional lagged output, inflation, and interest-rate terms, making the overall effect on the inflation coefficient ambiguous.
17 There are some other minor differences at work as well. For example, Smets (1998) evaluates the effects of increases in the variance of the output gap that go back into the infinite past, whereas the experiment considered in this section has been one of a change in regime or structural break at a given point in time t. However, I show in Section 4 that the results of this paper continue to hold when uncertainty about the output gap extends backward any number of periods. Also, Smets (1998) and Orphanides et al. (2000) constrain their simple policy rules to be functions of inflation deviations from target [the four-quarter moving average of (πt−1 − π*)] rather than the inflation surprise (πt−1 − πt−1e), which would be closer to the optimal inference procedure that I derive in equation (10).
Finally, the emerging literature on robust control arrives at just the opposite conclusion: Policymakers ought to respond more aggressively to every variable in their reaction function when faced with model uncertainty. This literature, typified by Onatski and Stock (2000), chooses coefficients of a policy rule to minimize the maximum loss over all possible values for a given parameter within a given range; thus, the policymaker is guaranteed not to make mistakes that are extremely costly for parameters within this range. This approach is clearly very different from the maximization-of-expected-value approach that I have taken here, and so, it is not surprising that the results differ. Intuitively, their findings are driven by the fact that a bad draw on the effectiveness of the policy tool (the parameter α in my model) can result in very large losses if the rule's responsiveness is not sufficiently great. However, it is not clear that an increase in additive uncertainty about potential output would lead to the same conclusions.
SIGNAL EXTRACTION IN THE GENERAL LQG FRAMEWORK
The analysis of the preceding section can be generalized to a standard linear-quadratic-Gaussian framework [e.g., Bertsekas (1987)]. In this case, the underlying state of the economy Xt is permitted to be a vector, and Xt evolves according to a linear function of one lag of itself and a vector of policy instruments rt:
where A and B are known matrices of the appropriate dimensions. Any constants can be incorporated by defining one component of Xt to be a vector of ones. I denote the observable variables of the system by Zt. These may be a subset of the variables in Xt, noisy realizations of a linear function of variables in Xt, or some combination of the two. Thus,
where C is a known matrix of appropriate dimension, with every observable relationship among the elements of Xt corresponding to a row in (12). The noise vector ηt may have some components that are always zero, corresponding to elements of Xt that are actually observed. Other components of Xt, which are not directly observed, must be inferred from observations of Zt.
18 Note that equations in (12) that are redundant, or are not informative about Xt, in the sense that policymakers' prior variances on the corresponding elements of Zt are zero, should be dropped from (12). Intuitively, realizations of these components of Zt contain no new information, and thus are irrelevant for updating policymakers' beliefs about Xt. Mathematically, this ensures that the matrix C Σt−1|t−1 C′ + Ση is nonsingular in the updating equations that follow.
Note that (12) has been set up as a signal extraction problem rather than one of imperfect observation (in which case
Xt would be a function of the observable variables
Zt plus disturbance terms). The latter would exhibit certainty-equivalence; the former does not (with respect to the observable variables).
The stochastic disturbances εt and ηt are assumed to be independent of each other, over time, of current and past values of r, X, and Z, and are (multivariate) normally distributed with constant variance-covariance matrices Σε and Ση, respectively.19
No difficulties arise when one allows Σε and Ση to vary over time, as long as this variation is independent of the policy instrument.
In practice, these assumptions are not as restrictive as it might seem because serial correlation and cross correlation of η
t and ε
t can be introduced by including lags of these variables as elements of
Xt, and redefining the disturbances in (11) and (12) to be orthogonal innovations to these processes.
20 Aoki (1967, pp. 38–39), for example, makes this observation.
Correlation between η
t and
Xt can be introduced in a similar fashion.
Policymakers minimize a quadratic loss function:
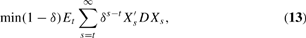
where D is a positive semidefinite matrix. Note that this specification does not preclude policymakers' preferences from depending on observables Z, since X can be expanded to include elements of Z as needed. Past values of r can also be incorporated into X and Z.
Policymakers choose a value for the vector of instruments rt at the beginning of each period t, conditional on all information available through the end of period t−1. After rt is chosen, the shocks εt and ηt are realized, and the value of the vector Zt is observed. Policymakers' information set at the beginning of period t is thus
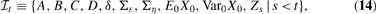
where E0X0 and Var0 X0 denote the mean and variance of policymakers' prior (time 0) distribution on X0, which is assumed to be normal.
Policymakers update beliefs about Xt via Kalman filtering, which is the optimal inference procedure, given the assumptions of normality above. Letting Σs|t denote Vart Xs, the variance of Xs conditional on information available at the beginning of period t, we have the recursive equations
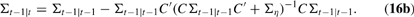
Note that the variance Σt|t evolves deterministically over time, as is typical in the LQG framework. In particular, the variances of policymakers' future estimates are unaffected by their choice of the current instrument rt.
21 The policymaker's choice of rt does not affect the signal extraction aspects of the problem—neither the variance of ηs nor the variance of Xs for any s ≥ t—because it is assumed that the coefficient matrices a and C are known with certainty. This is in marked contrast to the “experimentation” motive that is present in Wieland (1998), where policymakers' choice of rt helps to resolve the Brainard uncertainty about the multiplicative parameters of the model.
This leads to separability between the estimation and control stages of policymakers' problem, and hence to the certainty-equivalence result of the following proposition.
PROPOSITION 1
The optimal solution to policymakers' problem (13), subject to the law of motion (11), observation equation (12), and information set (14) is given by
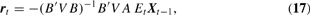
where V is the “value” matrix, defined to be the unique negative semidefinite solution to the Riccati equation
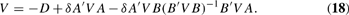
Proof. See Bertsekas (1987, pp. 292–293). █
Equation (17) is certainty-equivalent with respect to the state variable Xt−1. However, as should be clear from the preceding section, certainty-equivalence generally will not hold with respect to the observable variables Zt−1. The following proposition demonstrates this fact by proving the coefficient attenuation result from the preceding section for the general LQG framework. Note that by holding Σt−1|t−1 fixed in what follows, the model is consistent with the interpretation that a structural break in the degree of uncertainty surrounding the indicator variables has occurred in the previous period.
PROPOSITION 2
Suppose that the variance of the first component of ηt−1 in (12) is increased, in the sense that element (1,1) of Ση is increased while all other elements of Ση, and all elements of Σt−1|t−1 in (15) and (16), are held fixed. Then, policymakers' optimal response to observables, obtained by substituting (15) into (17), exhibits an attenuation in the response of all elements of policymakers' instrument rt to the first component of Zt−1.
Proof Recall that rt is a vector of instruments; hence the proposition states that the optimal setting of each of these is attenuated with respect to the first component ofZt−1. This is intuitive because the ordering of the elements of rt is arbitrary.
Let M denote the positive-definite matrix C Σt−1|t−1 C′ + Ση in equation (15), and partition M into
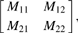
where M11 is a scalar, M21 a column vector, and M12 = M21′. Letting N denote M−1 and partitioning N in accordance with M, we have
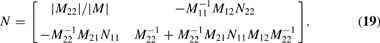
Let M11 be multiplied by a factor λ > 1, corresponding to the increase in Ση. Then, |M| increases in magnitude because, expanding along the first row or column, |M| = M11 |M22| + S, where S is a sum of element-cofactor products not involving M11, and M11, |M22|, and |M| are positive. Thus, N11 is attenuated, and it follows from (19) that N21 is attenuated in the same proportion, say, by the factor μ < 1. Thus, the first column of N is attenuated by the factor μ.
Inspection of (18) reveals that V is invariant to the change in Ση, and by the invariance of the other parameters in (15), (16), and (17), it follows that the first column of − (B′VB)−1 B′V A Σt−1|t−1 C′ (CΣt−1|t−1C′ + Ση)−1 is attenuated by the same factor μ. These are exactly the coefficients in question, completing the proof. █
One would like to be able to increase the covariances among the components of ηt as well, but unfortunately, completely general statements in this case cannot be made.
SIGNAL EXTRACTION DYNAMICS IN THE BASIC MODEL
The analysis of the preceding sections has been essentially static in nature, in that a structural break in uncertainty was known to have occurred in the previous period. It is not clear, then, that the results still apply if the increase in uncertainty occurs several periods earlier, particularly when we take into account the fact that uncertainty about potential output is typically serially correlated, and feeds through to increased uncertainty about subsequent estimates of X, the unobserved state of the economy.
The analysis of this section thus focuses on the dynamic effects of a structural break in uncertainty surrounding y*—that is, how optimal policy is affected as this uncertainty propagates forward through time. Again, this is in contrast to Svensson and Woodford (2000), who consider only counterfactual experiments in which uncertainty about an indicator is increased going back into the infinite past.
The model here is essentially the same as in Section 2. Policymakers' preferences have the form
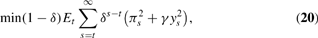
where, for ease of notation, πs now denotes the deviation of inflation from policymakers' target and ys denotes the output gap, both at time s. The economy follows:
where Xt denotes the unobserved state of the economy, rt the deviation of the real interest rate from its “natural” value, and πte agents' expectation of inflation, as before.
The error term η is now allowed to be persistent:
where [theta] can be regarded as the degree of persistence of shocks to potential output. The normally distributed disturbances εt, νt, and ξt are assumed to be orthogonal to each other, across time, and to all other variables in the system.
The timing of policymakers' observations and actions is the same as in Section 2, with information set
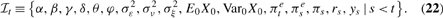
Policymakers' optimal solution to (20), subject to (21) and (22), is given by
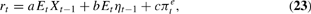
where a, b, and c are constants invariant to the uncertainty surrounding X and η (see the Appendix). In contrast to Section 2, policymakers now care about past values of η as well as X. Note that because yt−1 = Xt−1 + ηt−1, we can rewrite (23) as
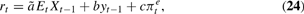
where
.
As values of y and π are observed, policymakers update their beliefs about X and η by Kalman filtering. Letting σXt2, σηt2, and σxηt denote Vart Xt, Vart ηt, and Covt (Xt,ηt), respectively, policymakers' best estimate of Xt−1 at time t is given by
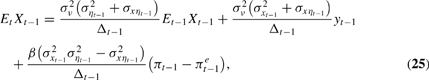
where Δt ≡β2 (σXt2 σηt2 − σxηt2) + σν2 (σXt2 + 2σxηt + σηt2) for all t. Equation (25) was derived exactly as was policymakers' estimation equation (10) in Section 2. The Et−1 Xt−1 term can be written as φ Et−1 Xt−2 − α rt−1 and cascaded backward, as before.
Given an exogenous increase in uncertainty about ηs at the beginning of period s < t, we must begin by tracing out its effects on subsequent values of ση2, σx2, and σxη. The interpretation of the exogeneity of the increase in σηs2 is that of a structural break in uncertainty surrounding potential output in period s. The case in which uncertainty about η increases exogenously in several periods s1, s2, …, sk, although perhaps more interesting, is simply a positive linear combination of the effects given below, and thus does not need to be considered separately.
A straightforward computation [using equations (16) from the preceding section] shows that policymakers' variances evolve according to
22 Note that Xt and ηt are correlated since ηt−1 = yt−1 − Xt−1. Hence, Covt (Xt−1, ηt−1) = − Vart Xt−1 and Covt (Xt,ηt) = − φ[theta] Vart Xt−1.
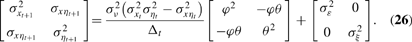
For notational convenience, define
which is the key term in (26). Totally differentiating Nt with respect to σηs2, using (26), yields
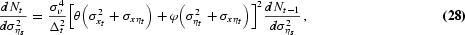
which is a recursive sequence terminating with
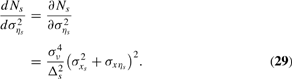
The first equality in (29) follows from the assumption that the increase in uncertainty about ηs in period s is exogenous, whereas the covariance σxηs and variance σxs2, which derive from uncertainty about η and X in prior periods, are held fixed.
Note that equations (28) and (29) imply d Nτ/ d σηs2 ≥ 0 for all τ ≥ s. This fact, together with the relations implied by (26), helps us assess the effects of the break in uncertainty about ηs on the coefficients in the period-t estimation equation (25).
For example, the coefficient on the most recent inflation surprise, (πt−1 − πt−1e), unambiguously increases in (25). This follows from the fact that
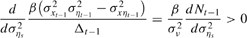
and the coefficient on the inflation surprise in (25) is positive. Thus, the finding of an amplification of the coefficient on inflation in Section 2 is robust to extending the increase in uncertainty about the output gap backward any number of periods.
Similarly, the coefficient on the most recent output gap, yt−1, is necessarily attenuated, under the assumption that [theta] > φ (which corresponds to assuming shocks to potential output are more persistent than movements in the output gap):
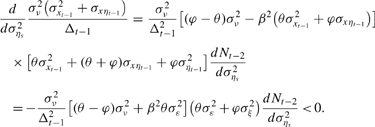
Thus, this finding from Section 2 is also robust, no matter when the structural break in uncertainty occurred.
23 Technically, this is only attenuation under the assumption that policymakers' total response to the output gap, b + σν2 (σXt−12+ σxηt−1) / Δt−1, is positive. This assumption seems warranted (it can be shown that b > 0, for instance).
The coefficient on the lagged estimate of the state variable, Et−1 Xt−1, may either increase or decrease in (25), according to
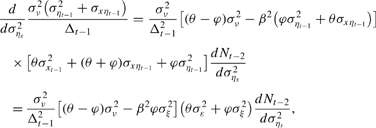
which is positive if and only if ([theta]−φ) > β2 φσξ2 / σν2.
24 The coefficient on Et−1 Xt−1 in (25) is necessarily positive, assuming again that [theta] > φ (and one can show that ã > 0 in any case).
Coefficients on lags of inflation and the output gap, obtained by cascading the expectational term backward in (25), may thus also go either way, depending on the sign of the derivative above. For example, if ([theta] − φ) > β
2 φ σ
ξ2/σ
ν2, then the coefficient on
Eτ Xτ increases for every τ ≥
s. It then follows that the coefficient on the lagged inflation surprise (π
τ − π
τe) also increases for every τ ≥
s (although the change in coefficient on lags of the output gap,
yτ, is not clear for
s ≤ τ ≤
t−2). If ([theta] − φ) < β
2φ σ
ξ2 / σ
ν2, then the coefficient on
Eτ Xτ decreases for every τ ≥
s, the coefficient on
yτ also decreases for every τ ≥
s, and the change in coefficient on (π
τ − π
τe) now becomes analytically unclear for
s ≤ τ ≤
t−2.
Note that I use the terminology “not clear,” rather than “ambiguous,” here because the change in coefficients may be theoretically unambiguous, but computation of the analytical derivatives and a further sign check of the result would be required to ascertain this fact, and these computations quickly become very burdensome. For example, it can be shown analytically that the coefficient on the second lag of the inflation surprise, (πt−2 − πt−2e), also necessarily increases for [theta]>φ (no matter what the value of β2 φ σξ2 / σν2), further corroborating the finding that policymakers should react more aggressively to inflation.
CONCLUSIONS
A standard result in the literature is that optimal monetary policy in a linear-quadratic framework is certainty-equivalent. It was emphasized in this paper that optimal policy is not certainty-equivalent with respect to indicator variables when policymakers face a signal extraction problem in their estimation of the economic state. For example, the state of the economy could be an unobserved aggregate concept such as “excess demand” or “inflationary pressure,” with policymakers using many measures of output, employment, capacity utilization, and inflation to help them infer the actual level of excess demand or inflationary pressure, as in Stock and Watson (1998, 2000) and Bernanke and Boivin (2002). It should be emphasized that the results of the present paper apply to indicator variables that are estimated (such as the output gap) as well as those that are directly observed (such as output, unemployment, and inflation).
This paper shows that increased uncertainty about an indicator variable causes policymakers' optimal responsiveness to that indicator to be attenuated. It also shows, fairly generally, that it is optimal for policymakers to amplify their responsiveness to all other economic indicators, about which uncertanity has not changed.
The signal extraction framework is crucial to the above results. If, instead, policymakers simply observe an unbiased estimate
of the state of the economy X, then certainty-equivalence holds, even when policy is expressed in terms of the observable estimate
.
This last observation has important implications for the real-time data literature of Orphanides (1998, 2001), Rudebusch (2001, 2002), and others. In those papers, if the real-time data were unbiased estimates of the true state of the economy X, then the optimal policy would still be certainty-equivalent, even when expressed as a function of the real-time data,
. Orphanides and Rudebusch only find coefficient attenuation because they assume, perhaps unrealistically, that the real-time data are noisy indicators (rather than rational expectations) of the underlying true values of the data. Policymakers thus face a signal extraction problem in their estimation of the true data X, leading to a non-certainty-equivalent policy in terms of the noisy indicators (the observable data). The results in Orphanides and Rudebusch are thus completely in line with those of the present paper, given their assumptions.
Whether one regards the insights of the present paper as valuable in practice depends on the extent to which one believes policymakers use the signal extraction framework. For example, models of the economy that have a large number of macroeconomic indicators but a relatively smaller number of fundamental, unobserved state variables fit this framework very well. Alternatively, economic models in which every single variable is important to the law of motion for the economy are generally not well represented by the signal extraction framework of this paper. It is not clear in practice which type of model provides the better representation of the actual economy, or which type of model is used by policymakers; thus, both frameworks should be of some interest.
ACKNOWLEDGEMENT
I thank Dave Small, Glenn Rudebusch, Volker Wieland, Brian Sack, Athanasios Orphanides, Ben McCallum, Frank Smets, Larry Meyer, John Taylor, two anonymous referees, and participants at the San Francisco Fed–Stanford SIEPR Conference and 2000 World Congress of the Econometric Society for helpful discussions, comments, and suggestions. The views expressed in this paper, and all errors and omissions, should be regarded as those solely of the author, and are not necessarily those of the individuals listed above, the Federal Reserve System, or its Board of Governors.
