DEMAND FOR MONETARY SERVICES

We assume a weakly separable monetary utility function, so that the representative money holder faces the following problem:

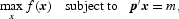
where x = (x₁, x₂, …, x₈) is the vector of monetary asset quantities described in Table 1; p = (p₁,p₂,…, p₈) is the corresponding vector of monetary asset user costs; and m is the expenditure on the services of monetary assets.

Because the economic agent involved in this study is the household, it is important to work with data that reflect this composite agent's selection of monetary services. In practice, the assets in the official M2 definition of money are appropriate, but we have excluded the rapidly growing retail money market mutual funds, as does much of the empirical literature, mainly because satisfactory monetary aggregates cannot be obtained using this asset most probably because the household employs this particular asset for its savings properties and not for its monetary services.

Moreover, because the flexible functional forms are parameter intensive we rationalize the estimation to a small set of monetary asset demand equations by imposing the following separable structure of preferences:

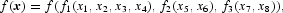
where the subaggregator functions f_i(i = 1, 2, 3) provide subaggregate measures of monetary services. Here the subaggregates will be thought of as Divisia quantity indexes that can allow for less than perfect substitutability among the relevant monetary components.

As already noted, the main reason for employing subaggregates, rather than studying all eight items, is that our models are very parameter intensive. We have separated the group of assets into three collections based on empirical pretesting. The pretesting, for which there is a large literature [see Barnett et al. (1992)] is based on the NONPAR GARP procedure of Varian (1982, 1983). The specific collection used here is very much like that reported in the literature.

THE DATA

The Federal Reserve Bank of St. Louis, in its Monetary Services Index project, provides monetary quantities as well as user costs, for the eight items listed in Table 1 (and many others, up through the L definition of money in the Federal Reserve's lexicon). For our empirical work, we require per capita real data, and to that end, we have divided each measure of monetary services by the U.S. CPI (for all items) and total U.S. population. Those data are quarterly from 1970:1 to 2003:2 (a total of 134 observations). The calculation of the user costs, which are the appropriate prices for monetary services, is explained in several online publications of the Federal Reserve Bank of St. Louis or in Barnett et al. (1992), Barnett and Serletis (2000), and Serletis (2001).

To provide the three subaggregates shown in Table 1, we employ a Divisia quantity index, defined (in discrete time) as

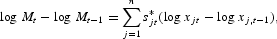
according to which the growth rate of the subaggregate is the weighted average of the growth rates of the component quantities, with the Divisia weights being defined as the expenditure shares averaged over the two periods of the change, s*_jt = (1/2)(s_jt + s_j,t−1) for j = 1, …, n, where s_jt = π_jtx_jt/[sum ]π_ktx_kt is the expenditure share of asset j during period t, and π_jt is the user cost of asset j. What this does, up to a third-order remainder term, is preserve the microeconomic characteristics of the underlying monetary assets.

The collection of assets, then, are as follows: Subaggregate A is composed of currency, travelers' checks, and other checkable deposits including Super NOW accounts issued by commercial banks and thrifts (series 1 to 4 in Table 1). Subaggregate B is composed of savings deposits issued by commercial banks and thrifts (series 5 and 6), and subaggregate C is composed of small time deposits issued by commercial banks and thrifts (series 7 and 8). Finally, Divisia user cost indexes are calculated by applying Fisher's (1922) weak factor reversal test.

FOURIER AND AIM MODELS

Our objective is to estimate a system of demand equations derived from an indirect utility function. The most important advantage of using the indirect utility approach is that prices enter as exogenous variables in the estimation process and the demand system is easily derived by applying Roy's identity.

In this section, we briefly present the basic properties of two models that we plan to use in our empirical work. As we have already indicated, the models are the Fourier and the AIM. Although there is some comparison implied in our presentation in this section, our purpose is basically to make clear the properties of the models with which we will work.

The Fourier

We follow the procedure explained by Gallant (1981) for expanding the indirect utility function using the Fourier series

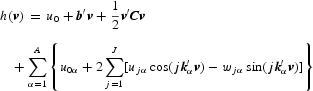
in which

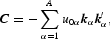
where v denotes income-normalized prices (=p/m), k_α is a multi-index—an n-vector with integer components—and u₀, {b}, {u}, and {w} are parameters to be estimated. As Gallant (1981) shows, the length of a multi-index, denoted as |k_α|* = [sum ]ⁿ_i=1|k_iα|, reduces the complexity of the notation required to denote high-order partial differentiation and multivariate Fourier series expansions.¹

For example, with n = 3 in (1), the multi-index λ′ = (5, 2, 7), generates the 14th-order partial derivative, as follows:

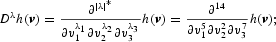
see Gallant (1981) for more details.

The parameters A (the number of terms) and J (the degree of the approximation) determine the degree of the Fourier polynomials.²

The Fourier flexible functional form has the ability to achieve close approximation in Sobolev norm, which confers nonparametric properties on the functional form. This is the reason the Fourier flexible form is considered to be a semi-nonparametric functional form.

By applying Roy's modified identity,

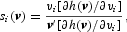
to (1), we obtain the Fourier demand system

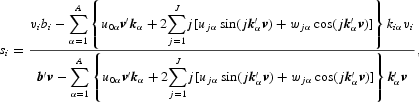
for i = 1, 2, 3 monetary assets; the time subscript t has been suppressed.

Eastwood and Gallant (1991) show that Fourier functions produce consistent and asymptotically normal parameter estimates when the number of parameters to be estimated equals the number of effective observations raised to the power of 2/3. This result follows from Huber (1981) and is similar to optimal bandwidth results in many nonparametric models. In our case, with n = 3 and T = 134, the number of effective observations is 268 (=2 ×134)—since we estimate (n − 1) share equations—and we should therefore estimate (approximately) 41 (=268^2/3) parameters. As we impose the normalization b_n = [sum ]ⁿ⁻¹_i=1b_i, the Fourier demand system has (n − 1) b, Au_0α, AJu_jα, and AJw_jα parameters to be estimated, for a total of (n − 1) + A(1 + 2J) free parameters. By setting (n − 1) + A(1 + 2J) equal to 41, in this application we choose the values of A and J to be 13 and 1, respectively. This also determines the elementary multi-indexes used in this paper, as shown in Table 2.

Because a Fourier series is a periodic function in its arguments but the indirect utility function is not, the scaling of the data is also important. In empirical applications, to avoid having the approximation diverge from the true indirect utility function, the data should be rescaled so that the income-normalized prices lie on 0 ≤ v_i ≤ 2π. The income-normalized prices v_i(i = 1, …, n) typically are rescaled as follows: v_i × [(2π − ε)/max{v_i:i = 1, …, n}], with (2π − ε) set equal to 6, as in Gallant (1982). In our case, however, the income-normalized prices v_i(i = 1, …, n) are already between 0 and 2π, so we performed no such rescaling.

The AIM

Following Barnett and Yue (1988), the reciprocal indirect utility function for the asymptotically ideal model of first-order approximation for n = 3 (our problem in hand) is

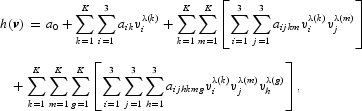
where λ(z) = 2^−z for z = {k, m, g} is the exponent set and a_ik, a_ijkm, and a_ijhkmg, for all i, j, h = 1, 2, 3, are the parameters to be estimated. The number of parameters is reduced by deleting the diagonal elements of the parameter arrays so that i ≠ j, j ≠ h, and i ≠ h. This does not alter the span of the model's approximation.

To avoid the extensive multiple subscripting in the coefficients a_ijhkmg, we follow Barnett and Yue (1988), and reparameterize by stacking the coefficients as they appear in (4) into a single vector of parameters, b = (b₀, …, b₂₆)′ containing the 27 coefficients in (4), as follows:

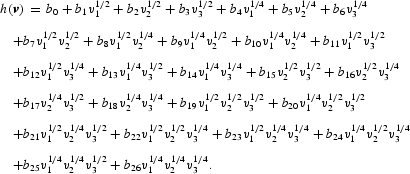
Applying the modified version of Roy's identity, (2), to (5), we obtain the AIM demand system

where D is the sum of the numerators in equations (6), (7), and (8).

COMPUTATIONAL CONSIDERATIONS

Demand systems (3) and (6)–(8) can be written as

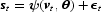
with an error term appended. In (9), s = (s₁, …, s_n)′, ψ(v,θ) = [ψ₁(v,θ),…, ψ_n(v, θ)]′, and ψ_i(v,θ) is given by the right-hand side of each of (3) and (6)–(8).

As Gallant and Golub (1984, p. 298) put it,

all statistical estimation procedures that are commonly used in econometric research can be formulated as an optimization problem of the following type [Burguete et al. (1982)]:

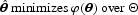
with φ(θ) twice continuously differentiable in θ.

In this paper, we follow Gallant and Golub (1984) and use Zellner's (1962) seemingly unrelated regression method to estimate θ. Hence, φ(θ) has the form

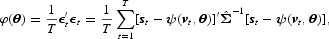
where T is the number of observations and

is an estimate of the variance-covariance matrix of (9). In minimizing (10), we use the TOMLAB/NPSOL tool box with MATLAB see http://tomlab.biz/products/npsol. NPSOL uses a sequential quadratic programming algorithm and is suitable for both unconstrained and constrained optimization of smooth (i.e., at least twice continuously differentiable) nonlinear functions.

Because results in nonlinear optimization are sensitive to the initial parameter values, to achieve global convergence, we randomly generated 500 sets of initial parameter values and chose the starting θ that led to the lowest value of the objective function. The parameter estimates that minimize the objective function are reported in the first column of Tables 3 and 4 for the Fourier and AIM, respectively. As in Gallant (1981) and Barnett and Yue (1988) we do not have access to asymptotic standard errors that can be supported by statistical theory. We also report the number of positivity, monotonicity, and curvature violations, since the usefulness of flexible functional forms depends on whether they satisfy these theoretical regularity conditions. The regularity conditions are checked as follows:

• Positivity is checked by direct computation of the values of the estimated budget shares,
  . It is satisfied if
  , for all t.
• Monotonicity is checked by choosing a normalization on the indirect utility function so as to make h(p, m) decreasing in its arguments and by direct computation of the values of the first gradient vector of the estimated indirect utility function. It is satisfied if
  and
  or, equivalently, if
  , where
  .
• Curvature requires that the Slutsky matrix be negative semidefinite and is checked by performing a Cholesky factorization of that matrix and checking whether the Cholesky values are nonpositive [since a matrix is negative semidefinite if its Cholesky factors are nonpositive—see Lau (1978, Theorem 3.2)]. Curvature can also be checked by examining the Allen elasticities of substitution matrix, provided that the monotonicity condition holds. It requires that this matrix be negative semidefinite.

The results of the regularity tests for each model are presented in the last three rows of each of Tables 3 and 4. The numbers in the tables represent the number of times the regularity conditions are violated. For both models, the positivity and monotonicity conditions are satisfied at every data point, whereas the curvature condition is violated at 108 data points with the Fourier and at every data point with the AIM. As Barnett (2002, p. 199) put it in his Journal of Econometrics Fellow's opinion article, without satisfaction of all three theoretical regularity conditions

IMPOSING CURVATURE RESTRICTIONS

The indirect utility function should be a quasi-convex function in income-normalized prices, v_i(i = 1, …, n)—as already noted, this is the curvature condition. Gallant and Golub (1984), following Diewert et al. (1977), argue that a necessary and sufficient condition for quasi-convexity of h(v, θ) is

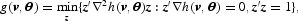
where ∇h(v,θ)=(∂/∂ v) h(v,θ) and ∇²h(v,θ)=(∂²/∂ v∂ v′)h(v,θ), and g(v, θ) is nonnegative (i.e., zero or positive) when the quasi-convexity (curvature) constraint is satisfied and negative when it is violated; g(v, θ) is referred to as the “constraint indicator.” Hence, as in Gallant and Golub (1984), we impose quasi convexity by modifying the optimization problem as follows:

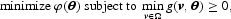
where Ω is a finite set with the finite number of elements v_i (i = 1, …, n). Curvature can be imposed at some representative point in the data (i.e., locally), over a region of data points, or at every data point in the sample (i.e., globally).

Let us briefly describe in more detail the Gallant and Golub (1984) method for imposing curvature restrictions on flexible functional forms. Define a real symmetric n × n matrix A = ∇²h(v, θ) [note that this is the Hessian matrix of the indirect utility function, h(v, θ)] and an n × 1 vector α = ∇h(v, θ) as the gradient vector of h(v, θ). The curvature condition (11) can be written as

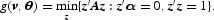
The next step is to partition α as α=(α₁, α₍₂₎′)′, where α₁ is the first element of α and α₍₂₎ is an (n − 1) × 1 vector of the remaining elements of α, and construct an n × 1 vector u,

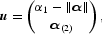
where ‖α‖ is the norm of α, defined as ‖α‖ = ([sum ]ⁿ_i=1α²_i)^1/2. With this notation, we define the following:

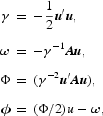
where γ is a scalar, Φ is an n × n matrix, and ω and ϕ are n × 1 vectors. The next and final step is to form an n × n matrix K as follows:

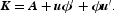
Let's delete the first row and column of K and rename the (n − 1) × (n − 1) thereby obtained matrix as K₂₂. A necessary and sufficient condition for curvature [or, equivalently, for the indicator function (11) to be nonnegative] is that K₂₂ should be a positive semidefinite matrix. In this paper, we use the ‘chol’ command in MATLAB to perform a Cholesky factorization of the K₂₂ matrix and construct an indicator of whether K₂₂ is positive semidefinite (this indicator is zero when K₂₂ is positive semidefinite and a positive integer otherwise). Hence, we run a constrained optimization subject to the constraint that K₂₂ is positive semidefinite (in which case curvature is satisfied). As already noted, we can evaluate K₂₂ at a single data point, over a region of data points, or at every data point in the sample.

Using NPSOL, we performed the computations and report the results in the second and third columns of Tables 3 and 4, where the second column shows the results when the quasi-convexity constraint is imposed locally (in 1970:3) and the third column shows the results when the constraint is imposed at every data point in the sample. Clearly, the effect of imposing the quasi-convexity constraint locally is negligible, as the number of curvature violations drops from 108 to 107 with the Fourier and from 134 to 109 with the AIM. Note also that the imposition of local curvature does not induce violations of monotonicity for both the Fourier and AIM that satisfy monotonicity (at all observations) when the local curvature condition is not imposed.

However, imposing the constraint at every data point (again using NPSOL), we obtain the results reported in the last column of each of Tables 3 and 4. Imposition of the quasi-convexity constraint globally has a significant impact on both models, as we obtain parameter estimates that are consistent with all three theoretical regularity restrictions (positivity, monotonicity, and curvature) at every data point in the sample. In this regard, Barnett and Pasupathy (2003, p. 151) argue that

In our case, the imposition of curvature globally does not produce spurious violations of monotonicity, thereby assuring true theoretical regularity. Hence, in what follows we discuss the income and price elasticities as well as the elasticities of substitution based on the Fourier and AIM models that (with our data set) satisfy both the neoclassical monotonicity and curvature conditions. We believe that much of the older literature in this area does not impose full regularity—that is, both monotonicity and curvature—and hence has to be disregarded.

INCOME AND PRICE ELASTICITIES

In the demand systems approach to estimation of economic relationships, the primary interest, especially in policy analysis, is in how the arguments of the underlying functions affect the quantities demanded. This is conventionally and completely expressed in terms of income and price elasticities and in elasticities of substitution. These elasticities can be calculated directly from the estimated budget share equations by writing the left-hand side as

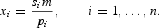
In particular, the income elasticities, η_im, can be calculated as

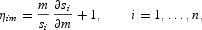
and the uncompensated (Cournot) price elasticities, η_ij, as

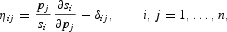
where δ_ij = 0 for i ≠ j and 1 otherwise. If η_ij>0, the assets are gross substitutes; if η_ij < 0, they are gross complements; and if η_ij = 0, they are independent.

We begin by presenting the income elasticities in Part A of Table 5, evaluated at the mean of the data, for the three subaggregates and the two models.³

ELASTICITIES OF SUBSTITUTION

From the point of view of monetary policy, the measurement of the elasticities of substitution among the three monetary assets is of prime importance. As we have already pointed out, the currently popular simple-sum approach to monetary aggregation requires, in effect, that the elasticities of substitution be very high especially among the components of the aggregate M2. By “very high” we mean infinite, of course, but since the policy literature has not addressed the question of how high such an estimate should be to warrant a simple-sum calculation from a practical standpoint, all we can do is report our results.

There are currently two methods employed for calculating the partial elasticity of substitution between two variables, the Allen and the Morishima. Following Serletis (2001), the Allen partial elasticity of substitution between two liquid assets i and j, σ^a_ij, can be calculated as

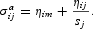
The Allen elasticity of substitution is the traditional measure and has been employed to measure substitution behavior and structural instability in a variety of contexts. However, when there are more than two goods, the Allen elasticity may be uninformative. For two assets the relationship is unambiguous: The assets must be substitutes. When there are more than two assets, the relationship becomes complex and depends on things such as the direction taken toward the point of approximation. In that case the Morishima elasticity of substitution is the correct measure of substitution elasticity:

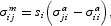
where s_i is the share of asset i in the consumer's budget. Notice that the Morishima elasticity looks at the impact on the ratio of two goods (x_i/x_j). Assets will be Morishima complements (substitutes) if an increase in the price of j causes x_i/x_j to decrease (increase).

Table 6 shows estimates of both the Allen and Morishima elasticities, evaluated at the means of the data. For Part A, we expect the three diagonal terms, representing the Allen own-elasticities of substitution for the three assets to be negative. This expectation is clearly achieved. However, because the Allen elasticity of substitution produces ambiguous results off-diagonal, we use the Morishima elasticity of substitution to investigate the substitutability/complementarity relation between assets. Based on the asymmetrical Morishima elasticities of substitution—the correct measures of substitution—as documented in Part B of Table 6, the assets are Morishima substitutes with only one of these elasticities being negative. Moreover, all Morishima elasticities of substitution are less than unity, irrespective of the model used.

This clearly indicates difficulties for a simple-sum-based monetary policy and helps explain why recent attempts to target and control the money supply (simple sum M2) have been abandoned in favor of interest-rate procedures.

CONFIDENCE INTERVALS FOR THE ELASTICITY ESTIMATORS

The elasticities are parametric functions, σ(θ), and a parametric bootstrap could be used, as in Gallant and Golub (1984), to compute standard errors or confidence intervals for the estimates reported in Tables 5 and 6. This involves the use of Monte Carlo methods to obtain a reliable estimate of the sampling distribution of σ(θ) by generating a large enough sample from the distribution of the constrained estimator; see also Anderson and Thursby (1986) for similar Monte Carlo experiments in the case of translog demand models. At each Monte Carlo trial, however, we need to search over a wide range of starting values of θ, using TOMLAB/NPSOL (as discussed in Section 5), to achieve global convergence.

In particular, as already mentioned in Section 5, for each Monte Carlo trial we need to randomly generate 500 sets of initial parameter values and choose the starting θ that leads to the lowest value of the objective function. In terms of cost, with 134 observations and the models used in this paper, it takes on average 2.5 minutes of CPU time on a Pentium-4 PC per random draw of initial parameter values. This amounts to over 20 hours of CPU time for each Monte Carlo trial. If we were to use 250 Monte Carlo trials, as in Gallant and Golub (1984), it will take over 5,000 hours of CPU time to obtain bootstrap standard errors! This is not affordable at present, unless we use a smaller number of sets of initial parameter values at each Monte Carlo trial. We are against such an approach, however, because it will likely lead to the non-optimization of the objective function in some (if not all) of the Monte Carlo trials and consequently to extremely wide confidence intervals.