INTRODUCTION
It has become widely accepted that, for most purposes, changes in monetary aggregates are of little interest for the U.S. monetary policy process. This viewpoint is summarized nicely by the title of the paper by Leeper and Roush (2003): “Putting ‘M’ Back into Monetary Policy.” Numerous recent papers have presented evidence that money growth has no predictive power for inflation, and this finding is robust to changes in the sample period and econometric methodology.1
See, for example, Leeper and Roush (2002, 2003), Stock and Watson (1999a), and the references contained therein. Recent empirical papers on inflation forecasting include, among many others, Clark and McCracken (in press), Gerlach and Svensson (2003), and Stock and Watson (2003). See these papers for an extensive list of references.
This paper asks whether such a conclusion is warranted. Specifically, the papers cited earlier have focused on forecasts from linear vector autoregressive (VAR) models:
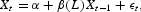
where Xt=(πt, Δmt)′, πt is the inflation rate at time t, and Δmt is the growth rate of a monetary aggregate. The popularity of VAR modeling arises from the fact that it is an atheoretical approach, and as such requires very few assumptions. The Wold Decomposition Theorem suggests that linear models are a good starting point [see Diebold (1998, pp. 179–180) for a related discussion]. If the system of interest is nonlinear, it may be better to directly estimate a nonlinear model rather than a linear approximation.
Aside from the obvious importance of correct specification in practical forecasting situations, the finding of a nonlinear relationship between inflation and fundamentals would have implications for VAR models of monetary policy. The price puzzle, a finding that tighter monetary policy is initially followed by a rise in the price level, is argued to be the result of information omitted from the Federal Reserve's reaction function. “Solutions” to the price puzzle consist of adding variables to the model, such as commodity prices [see, e.g., Hanson (2004)]. Yet the omitted information also might take the form of a more complicated functional form. Predictable movements in the variables are interpreted as shocks, which can lead to a price puzzle in the same way that omitting relevant variables from the model leads to a price puzzle. A different literature has studied changes in the parameters of the Federal Reserve's reaction function. It is common to include a measure of money growth in the reaction function, based on the argument that money growth has played an important role in monetary policy decisions. When the relationship between inflation and money growth is nonlinear, the reaction function will in general also be nonlinear. Boivin (2001) accounts for nonlinearities with a time-varying parameter VAR model, using an estimation strategy that accommodates the many estimated parameters in a VAR model.
Our baseline model is a fully nonparametric model that allows for any kind of nonlinearity in the relationship between money growth and inflation. We compare the linear univariate and bivariate VAR inflation forecasts that have been used in previous studies to their nonparametric counterparts. We then compare the forecast performance of the nonparametric models that include either money growth or velocity to autoregressive models, which provides a measure of the out-of-sample information content of these variables for inflation. Finally, we present evidence that a threshold model captures the nonlinearity in inflation well, although a threshold model does not always forecast well out-of-sample. The idea that a parametric nonlinear model can fit the data well without providing large improvements in forecast performance is not new [see, e.g., Kilian and Taylor (2003) and Clements et al. (2004)].
A nonparametric approach should in principal be preferred to parametric approaches, because it is more general (the linear model is nested by the nonparametric model). As few other macroeconomic papers have attempted to exploit the gains from nonparametric modeling,2
See, for example, Diebold and Nason (1990). This is one of the few papers to have analyzed nonparametric forecasts of macroeconomic variables, and the conclusion of the paper was actually that nonparametric models are not useful. Note that we are referring specifically to nonparametric forecasts here (as opposed to other types of nonlinear models).
For examples of in-sample nonlinearity tests, see, for example, Michael, Nobay, and Peel (1997), Taylor (2001), and Hamilton (2003). Granger (2001) concludes that the evidence for nonlinearity in macroeconomic data is weak, and finds it troubling that few of the papers he reviews look at forecast performance. Diebold (1998) takes a more pessimistic view, arguing that nonlinearities “require large amounts of high quality data” and that many nonlinearities “simply don't appear to be important in macroeconomics.” See Clements et al. (2004) for additional discussion. Chen, Racine, and Swanson (2001) find some evidence of nonlinearity in U.S. inflation using a neural network-based semiparametric model with 1948 to 1995 quarterly data.
The paper proceeds as follows. Section 2 describes the data. Section 3 presents evidence on the importance of allowing for a flexible functional form, and discusses our findings on the information content of monetary aggregates for inflation. Section 4 summarizes our findings and suggests directions for future research.
DATA
All of the data series were downloaded from the St. Louis Federal Reserve bank Web site, and cover the period from January 1959 to May 2002. The monetary aggregate data we analyze are simple sum M1, M2, and M3, and the corresponding M1, M2, and M3 Divisia monetary services index data [see, e.g., Belongia and Chalfant (1989), Belongia (1996), and the collection of papers in Barnett and Serletis (2000) for discussion and empirical evidence on the advantages and disadvantages of using Divisia monetary aggregates]. The consumer price index series is used in place of other possible measures of the price level, because it is available at a monthly frequency, and has been studied widely in the literature. Use of data available at a quarterly frequency, such as the GDP deflator, would prohibit the use of nonparametric methods, because the sample size would be too small to allow for an informative out-of-sample forecast comparison. The velocity series is calculated as V=PQ/M, where PQ is the index of industrial production (nominal) and M is one of the six monetary aggregates.
EMPIRICAL RESULTS
As a benchmark, we first replicate for our updated data the well-known result that money growth is useless as an inflation indicator. Then we show how the results change when relaxing assumptions on functional form, and expand the models to include velocity. We finish by evaluating the in-sample fit and out-of-sample forecasts of threshold models. The advantage of these parametric nonlinear models is that they are easy to interpret.
Linear Models
Forecasts here and throughout this paper are made using a recursive estimation procedure with an increasing window of data, so that each forecast is based on a model estimated using only data available through the date that forecast would have been made. Because our first forecasted inflation rate is January 1994, the corresponding one-step ahead model was estimated using data available through December 1993. Observations for January 1994 were then added to the dataset, all models were reestimated, and one-step ahead forecasts were produced for the inflation rate in February 1994. The procedure was repeated to make a series of 100 forecasts for each model and forecast horizon, covering the period January 1994 through April 2002. Given the different forecast series and the observed historical inflation series, the mean squared prediction error (MSPE) was calculated for each model as
. The out-of-sample period was chosen for two reasons. First, the nonparametric models we look at below require a sufficiently large estimation sample. Second, this time period is more interesting than previous time periods. It has been argued that there may have been stable money demand relationships in earlier years but that they had broken down by the early 1990s. Good forecast performance in this time period would be an important finding.
Table 1 reports the MSPE of a linear model including money growth as a regressor:
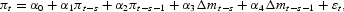
relative to the autoregressive model:
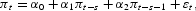
where the forecast horizon is given by s=1, 6, 12, and 24. To choose the lag length, the Schwarz information criterion (SIC) selected a VAR model with two lags of inflation and money growth.4
An alternative would be to select the lag length each time a forecast is made [see, e.g., Stock and Watson (2003)]. Given that we use an increasing window of data for estimation, and that the number of observations ranges from approximately 400 for the initial forecasts to 500 for the final forecast, the optimal lag length choice will not change much through time.

At one-month and six-month forecast horizons, consistent with our prior expectations, any gains from including money are unimportant. In fact, the inefficiency associated with including money growth variables actually leads to as much as a 13% increase in MSPE! Interestingly, at the longer horizons (12 and 24 months) money growth does have value in some cases, contrary to the conclusions in recent studies, with an MSPE reduction in one case of 23%. Outside of three cases, however, any gains are small, with the VAR model offering little or no improvement over the AR model. Overall, the case for using money growth as an indicator variable for inflation is weak.
Relaxing Assumptions about Functional Form
We have confirmed the well-known result that inflation forecasts from linear VAR models are usually not more accurate than an autoregressive model. This section compares the linear inflation forecasting models earlier, used by previous authors (see the papers cited in the Introduction) to their nonparametric counterparts. The benchmark in each case is the s-step ahead linear model
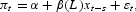
with xt−s=πt−s for an AR model, and xt−s=(πt−s, Δmt−s) for a VAR model, where mt can be any one of the six monetary aggregates: M1t, M2t, M3t, M1Dt, M2Dt, and M3Dt. Forecasts for each linear model are compared to those of a general nonparametric model
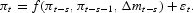
The nonparametric model relaxes any assumptions about functional form, so that the only restrictions in equation (3) are the variables included in x and the lag length. This model encompasses all nonlinear models that have been proposed, including threshold, smooth transition, and Markov switching models [see, e.g., Granger and Teräsvirta (1993) or Hamilton (1994)]. By contrast, even if equation (2) is not correctly specified, as is almost certainly the case, it might still provide a better approximation than equation (3) in practice. The nonparametric model converges more slowly than the linear model, so that there is no a priori reason to expect one model to forecast better out-of-sample. In fact, for a nonparametric model to be of use with a sample of several hundred observations, which is true for this paper, it is necessary that the linear model be severely misspecified.
We estimate the nonparametric models using the Nadaraya-Watson kernel estimator [Nadaraya (1965), Watson (1964)]. The forecast of inflation at time T + s is given by
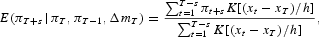
where xt=(πt, πt−1, Δmt) and K(·) is the product normal kernel function. A practical difficulty associated with any nonparametric estimation is the choice of bandwidth h, and the recursive nature of our analysis makes matters more difficult, as we need to choose the bandwidth thousands of times. Each time a forecast was made, out-of-sample inflation forecasts were calculated for the previous 50 observations using many different bandwidth choices, and we set h equal to the value that yielded the lowest MSPE for those 50 forecasts. For example, to make a one-step ahead forecast of inflation for January 1995, we use the value of h that produced the best forecasts over the period November 1990 to December 1994. There is little theoretical guidance as to the selection of bandwidth for out-of-sample forecasts. The intuition behind our procedure is that we are interested in producing out-of-sample forecasts, so we should use the bandwidth that has produced the best forecasts in the past. To the extent that this procedure is not optimal, our nonparametric forecasts can be improved further.
Table 2 offers a comparison of the linear and nonlinear models. DM test statistics are reported in parenthesis.5
It is known that the DM statistic does not have an asymptotic normal distribution when the models are nested [see, e.g., Clark and McCracken (2001)]. We nevertheless view it to be both a useful available alternative and better than not reporting any significance tests.
Corradi and Swanson (2002, 2004) have developed a formal test for out-of-sample nonlinear predictive accuracy, but their test does not allow for comparison of nonparametric models. Fan and Li's tests (1996) allow for comparison of nonparametric models, but they only consider the case of in-sample tests.

Table 3 reports the MSPE of each nonparametric model with money growth relative to the nonparametric AR(2) model at each horizon. There are two things to note here. First, the VAR model usually does better than the AR model, with the MSPE ratio in most cases less than one. This is quite different from Table 1, where the MSPE ratio was greater than 1 in 12 cases, especially in light of the fact that the nonparametric AR model is already outperforming the linear AR model. Second, most of the gains appear to be a result of allowing for a nonlinear functional form, rather than from the inclusion of money growth.

For the nonparametric AR model, we use the same number of lags (two lags) as that used in the linear AR model. Using the same set of explanatory variables enables us to determine whether relaxing the linear functional form is responsible for the improved forecasts. Gao and Tong (2004) have recently proposed a procedure for selecting the number of lags in a nonparametric AR model framework. For the data we used, Gao and Tong's procedure for selecting the number of lags in the nonparametric model led to a slight improvement in the forecasting accuracy. In the remaining part of the paper, we continue to consider the cases of using two lags in the nonparametric AR model, and adding one lag of money growth (in Section 3.5, a lag of velocity) for the nonparametric VAR model to better focus on the effects of functional form.
Specification Tests
These forecasting results suggest that the linear AR and VAR models are misspecified. In this section we formally test the correctness of linear AR and VAR models. We test the null hypothesis of a linear specification against a general nonparametric (nonlinear) model. The consistent model specification test proposed by Fan and Li (1996), Li (1999), and Zheng (1996) will be used to test the following null hypotheses for the inflation model: (i) a linear AR model: πt = β0 + β1πt−s +β2πt−s−1 + ut against a nonparametric AR model: πt=g(πt−s, πt−s−1)+ut; (ii) a linear VAR model, πt=β0+β1πt−s+β2πt−s−1+β3Δmt−s+ut against a nonparametric VAR model: πt=g(πt−s, πt−s−1, Δmt−s)+ut; and (iii) a nonparametric AR model: πt=g(πt−s, πt−s−1)+ut against a nonparametric VAR model: πt=g(πt−s, πt−s−1, Δmt−s)+ut.
Briefly, the testing procedure is implemented in the following manner. Start by introducing some notation: wt=(πt−s, πt−s−1), zt=Δmt−s. Then the above hypotheses can be tested based on E(ut[mid ]xt)=0, where ut=πt−β0−wtβ and xt=wt for (i); ut=πt−β0−wtβ−ztγ and xt=(wt, zt) for (ii); ut=πt−g(wt) and xt=(wt, zt) for (iii). The test statistic proposed by Fan and Li (1996), and Zheng (1996) is a kernel estimate of I=E[utE(ut[mid ]xt)f(xt)]. This is because I=E{[E(ut[mid ]xt)]2f(xt)}≥0, and I=0 if and only if the null hypothesis is true. Therefore, I serves as a proper candidate for testing the null hypothesis of E(ut[mid ]xt)=0. A feasible test statistic is given by
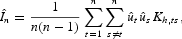
where
is the residual (estimated error) from the null model,
is the product kernel function, and hj is the smoothing parameter associated with xj (j=1, …, d), d is the dimension of xt (d=2 for (i), and d=3 for (ii) and (iii)). A standardized test is given by
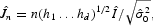
where
. Under the null hypothesis and some regularity conditioins,
has an asymptotic standard normal distribution.
Li and Wang (1998), and Hsiao and Li (2001) show that in finite sample applications, the
test is significantly undersized (there is finite sample negative bias under the null hypothesis). They recommend using bootstrap procedures to better approximate the finite sample null distribution of the test statistic
. Hsiao and Li (2001) proposed a bootstrap procedure for time series data. We adopt the bootstrap procedure suggested by Hsiao and Li (2001) to obtain the critical values for the test statistic
. The number of bootstrap replications is 1,000. The bootstrap critical values differ for each case, so rather than reporting all of the test statistics and bootstrap critical values, we summarize the testing results.
For case (i) of testing a linear AR model, we reject the null of a linear AR model for all t=1, 6, 12, 24 at the 5% level based on bootstrap critical values.
For case (ii) of testing a linear VAR model, we reject the null of a linear VAR model for all money growth models, and for s=1, 6, 12, 24 at the 5% level based on bootstrap critical values.
For case (iii) of testing a nonparametric AR model, the results are mixed. For s=1, we do not reject the null hypothesis of a nonparametric AR model at the 5% level for all money growth models. For s=6, we reject the null hypothesis of a nonparametric AR model at the 5% level for m=M1 and M3, but we do not reject the null hypothesis at the 5% level for m=M2, M1D, M2D and M3D. For s=12, we reject the null hypothesis of a nonparametric AR model at the 5% level for m=M2 and M3, but we do not reject the null hypothesis at the 5% level for m=M1, M1D, M2D and M3D. For s=24, we reject the null hypothesis of a nonparametric AR model at the 5% level for m=M1, M2, M2D, and M3D, but we do not reject the null hypothesis at the 5% level for m=M3 and M1D.
These in-sample testing results are largely consistent with the out-of-sample prediction results. The linear AR and linear VAR models are strongly rejected, and we conclude that there is significant nonlinearity in the relationship between inflation and its lagged values, and between inflation and money growth. Also, there is some weak evidence that a nonparametric VAR model fits better than a nonparametric AR model in in-sample fit. Our primary interest is in producing out-of-sample forecasts, so in the next section we compare forecast performance of a nonparametric model with velocity replacing the money growth variable.
Forecasting Inflation with Velocity
These results suggest the importance of functional form, but with a few exceptions, out-of-sample causality from money growth to inflation is still hard to find. There are, however, alternative ways to incorporate information on the behavior of monetary aggregates into the model. We now evaluate the information content of velocity, motivated by the P* inflation forecasting model that has been studied by many authors [see, e.g., Gerlach and Svensson (2003) and the references contained therein]. Despite the lack of a formal theoretical basis for the P* model [Gerlach and Svensson (2003)], it is nevertheless popular as a tool for forecasting inflation. In keeping with our use of monthly data, the measure of output is industrial production.
Table 4 shows that the forecast improvements from using nonparametric VAR models versus linear VAR models are more pronounced than for money growth. With only one exception, the nonparametric (nonlinear) VAR model always outperforms its linear counterpart, and in many cases the differences are substantial. The only difference between the models is that the linear model imposes restrictions on functional form, suggesting that it is crucial to allow for nonlinearity when estimating P*-type models. To the best of our knowledge, this is the first paper to demonstrate important nonlinearities in the (out-of-sample) P* inflation forecasting model. Table 5 is particularly interesting. Our earlier results suggested only modest improvements in the forecast performance of a nonparametric VAR model over the autoregressive benchmark when money growth is included. When money growth is replaced by velocity, we find strong evidence of causality. Even at a one-month forecast horizon, the velocity of three of the aggregates reduces the MSPE by 10% or more. The forecast improvement grows with the forecast horizon, and at a 24-month horizon including velocity of Divisia M2 or Divisia M3 reduces the MSPE by 40%.


Note that the relative MSPE comparison between the nonparametric VAR model with velocity and the nonparametric VAR model with money growth can be obtained as a ratio of the results of Table 5 to that of Table 3 (as they both have the MSPE of the nonparametric AR model in the denominator). We observe that the nonparametric VAR models with velocity generally perform much better (have a smaller MSPE) than the nonparametric VAR models with money growth.
To sum up our results, we have shown that the relationship between money growth and inflation is nonlinear, with a linear VAR model forecasting no better (and usually worse) than an autoregressive benchmark, and the nonparametric model producing small forecasting gains. Tables 4 and 5 show that the relationship between inflation and velocity is also nonlinear, and when we relax the strict assumptions of the linear model, velocity serves as a very important source of information about inflation. This suggests that the P* model is still useful for predicting U.S. inflation.
We also have carried out in-sample specification tests for testing (i) a parametric VAR model (with velocity) versus a nonparametric VAR model, and (ii) a nonparametric AR model versus a nonparametric VAR model (with velocity). The test statistic is the same as discussed in Section 3.3 with
being the estimated error from the null model, xt=(πt−s, πt−s−1, vt−s), where v=V1, V2, V3, V1D, V2D, V3D. The testing results are as follows.
For case (i) of testing a linear VAR, we reject the null hypothesis of a linear VAR model for all s=1, 6, 12, and 24 at the 5% level based on bootstrap critical values (for all measures of velocity). For case (ii) of testing a nonparametric AR model versus a nonparametric VAR model, the results are mixed. For s=1, we reject the null for all measures of velocity. For s=6, we reject the null for V1, V2, V3, V2D, and V3D, but we do not reject the null with V1D. For s=12 and s=24, we reject the null for all measures of velocity. Thus, the in-sample testing results suggest that there is significant nonlinear interaction between inflation and money growth.
One difficulty with using a nonparametric estimation approach is that the interpretation of the model is more difficult. We therefore consider next the forecasts from a parametric nonlinear model, the threshold model.
Threshold autoregressive (TAR) models [see, e.g, Hansen (1996, 2000)] are similar to the linear AR but allow for multiple regimes. In the leading case of two regimes, the TAR model can be written
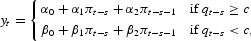
where qt−s is a “switching variable” observable at the time a forecast is made, equal to money growth or velocity, and c is the “threshold.” It is straightforward to compute multivariate threshold forecasts by simply adding additional variables to each equation. When q represents money growth, there is an intuitive interpretation of the TAR model. During periods of high money growth (such as during the 1970s) the money supply might be a dominant factor in the determination of the price level, whereas in other periods money growth is only a minor factor in the determination of the price level. There is no reason to believe that inflation will behave in the same way across the two regimes. When q represents velocity, a threshold model can be motivated by observing that changes in velocity may be reflecting changes in the inflation generating process itself, possibly due to differences in the predictability of inflation in different regimes.
We have examined both full sample tests for threshold nonlinearity as well as the out-of-sample forecast gains from using a threshold model. A number of published papers have addressed the choice between in-sample testing and out-of-sample forecast comparison when the goal is to evaluate theories (i.e., to explain the data rather than just produce forecasts). Authors such as West (1996) begin with the assumption that out-of-sample forecast evaluation is of interest, without providing any underlying motivation for evaluating the forecasts, whereas authors such as Kilian and Taylor (2003) and Clements et al. (2004) have provided reasons why an estimated nonlinear model may not forecast as well as simple benchmark models, even when the true data generating process is the nonlinear model being used to compute forecasts. Potter (1999) gives reasons why it is difficult to forecast using threshold models, because small errors in classification of observations into regimes can dramatically increase the mean squared error of the forecasts.
We do not take sides in this debate. Instead, we consider both approaches to model evaluation. If in-sample tests uncover evidence favoring a nonlinear specification, or if the out-of-sample forecasts of that specification are better than those of a linear model, the nonlinear model deserves further consideration. The main difficulty with tests for threshold nonlinearity is that the value of the threshold is not identified under the null hypothesis. Hansen (1996, 2000) has provided a simulation procedure for inference that controls the size of the test.
Our findings for the threshold model can be summarized as follows. In-sample tests, following the strategy outlined by Hansen (1996), do not reject linearity for any of the monetary aggregates, but do reject in all cases for each of the six velocity variables. This is strong evidence that the large improvements in forecast performance from including velocity in the nonparametric model (Tables 4 and 5) is a result of a simple type of nonlinearity. In contrast, the threshold model seldom yields better out-of-sample forecast performance than the linear AR model, even when velocity is used as the switching variable. This might be explained by problems with classifying observations into different regimes as described by Potter (1999). Tables with detailed results can be obtained from the authors on request.
CONCLUSION
This paper has evaluated the performance of nonparametric forecasting models of inflation. When relaxing assumptions about functional form, money growth and velocity contain information about inflation for horizons as short as one month. It is particularly interesting that the forecast improvement from including velocity is so large—over 40% in some cases. We have found these results in spite of the fact that we focus on the period from 1994 to 2002, a time period for which it is widely believed that the demand for money was unstable. Our results also suggest that the nonlinearity may be captured by a threshold model, even though the threshold model often does not provide good forecasts, possibly because of difficulties in assigning observations to one of the regimes. We conclude that arguments that the Federal Reserve can learn nothing by monitoring the behavior of monetary aggregates may be premature, as they are based on analysis of an overly restrictive set of models.
As suggested in the Introduction, our findings of nonlinearity have important implications for VAR models of monetary policy. More generally, our results indicate that nonparametric methods are sometimes a useful tool for macroeconomic forecasting, with the benefits of relaxing assumptions on functional form substantially outweighing any efficiency losses. It would be worthwhile to see whether our findings for inflation carry over to forecasts of other macroeconomic variables. The univariate results of Stock and Watson (1999b) may provide a useful starting point.
Li's research is partially supported by the Private Enterprise Research Center, Texas A&M University. We are grateful to two anonymous referees, an associate editor, and the editor, W.A. Barnett, for many insightful comments that have led to a much improved paper. We would also like to thank Ben Keen, Jeff Racine, and participants at the Southern Economic Association meetings for useful comments and discussions.







