FIRST CASH-IN-ADVANCE MODEL²

The basic model is a continuous-time formulation of one in Roldos (1992), which can be traced to Roldos (1991) and Jones (1971).

Consider a small open economy in which there is a representative infinitely lived household that maximizes an intertemporal utility function:

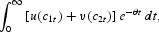
where θ>0 is the rate of time discount, c_it is the consumption of good i at time t. The momentary utility functions

and

are strictly increasing, strictly concave, continuously differentiable, and satisfies Inada conditions, respectively.

The production side of the economy is described by two representative firms. One of them produces good 1 (the industrial goods), using labor l and capital k, according to a constant-returns-to-scale production function

. The industrial goods can be either consumed or added to the existing capital stock. The capital does not depreciate. The other firm produces good 2 (the agricultural goods), using (fixed-quantity) land

and labor 1−l, according to the constant-returns-to-scale production function

. The agricultural goods can only be consumed. The production functions F and G satisfy

and the Inada conditions, respectively.

In the setup, we assume that labor is mobile across firms. The household supplies its unit labor endowment inelastically, so that if l is the fraction of labor used in producing the industrial goods, 1−l is the fraction of labor used in producing the agricultural goods. The economy faces given international prices of those goods, and units are chosen in such a way that allows normalization of both prices at unity. The exchange rate e_t converts them to domestic monetary units.

The cash is injected into the system through lump-sum transfers T_t (withdrawn by lump-sum taxes). The budget constraint of the household and the investment constraint can be written as follows:

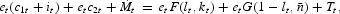
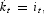
with k₀, M₀ given. In the expressions, since

can be converted to i_t on a one-to-one basis, they have the same nominal price at t. In this section, it is assumed that cash is needed to purchase the industrial goods; that is, a cash-in-advance constraint is imposed as follows:

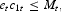
where M_t is the cash balance at time t.

Denoting by H the Hamiltonian of the problem, α, β, and γ the multipliers for (1)–(3), one can write H as³

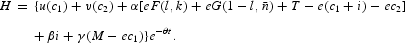
The first-order conditions for an interior optimal path are given by (1)–(3) and

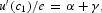
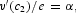
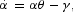
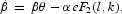
and two transversality conditions:

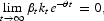
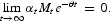
Equation (4) equates the marginal utility of the industrial goods per dollar spent to the sum of the marginal utility of income and the marginal utility of cash; equation (5) equates the marginal utility of the agricultural goods per dollar spent to the marginal utility of income; equation (6) equates the value of marginal product of labor in each sector; equation (7) equates the marginal utility of investment per dollar spent to the marginal utility of income. Equation (8) describes the dynamic motion of the marginal utility of income, while equation (9) describes the dynamic motion of investment. Equation (10) is used to rule out Ponzi-game behavior in trading physical capital, while equation (11) is used to rule out similar behavior in trading cash.

To simplify the system of (4)–(9), we first substitute (4) and (5) into (8) to obtain

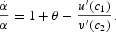
Next, substitute (7) into (5) and (9) to obtain

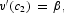
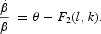
Combining (13) and (14), we obtain

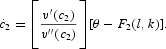
The equilibrium conditions for the economy require that the money market clears and the trade is balanced. By Walras's law, we only need to impose the latter equilibrium condition:

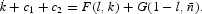
Following Stockman and Roldos, we will conduct the analysis under the assumption that the cash-in-advance constraint is binding. Multiply (3) by α and substitute (7) into it to obtain

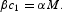
Taking logarithm of both sides of (17) and differentiating with respect to time,

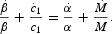
Money supply is assumed to follow a constant growth rate, μ,

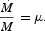
Substituting (12), (14), and (19) into (18), we have

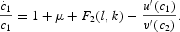
The equilibrium motions of

are thus completely characterized by (6), (15), (16), and (20).

In a steady state,

. This implies

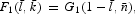
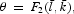
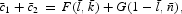
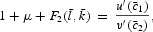
where a bar over the variable denotes its steady-state value.

It is straightforward to verify that the system of (21)–(24) has a unique steady state. Equation (22) implies that the steady-state marginal productivity of capital is tied to the rate of time preference. The intuition underlying this result can be explained as follows. Since the cash-in-advance constraint (3) does not apply to either c₂ or

, the household can reduce c₂ and, through (16), add to the investment at t directly. The increase in the production of the industrial goods can be used to increase

for all s>t.⁴

by one unit incurs a loss of utility by

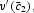
whereas augmenting the capital stock by one unit forever incurs a gain of utility by

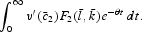
Equating these two expression, one obtains the result that the steady-state real rate of return of capital is determined by (22).

We now study the effects of a perfectly anticipated inflation on the steady-state capital, the consumption goods and the trade pattern. Totally differentiate (21)–(24),

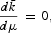
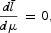
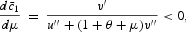
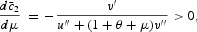
where all derivatives are evaluated at the steady state.

The reasoning for the results in (25)–(28) can be explained as follows. Because cash is used to purchase c₁, but not to purchase c₂, an increase in the opportunity cost of holding money raises the price of c₁ relative to c₂, this induces a substitution of c₂ for c₁. If the economy is originally at the steady state, the domestic production is not affected by the increase in μ; yet, this will cause a once-and-for-all increase (decrease) in c₂ (c₁).⁵

The effect of an increase in the rate of monetary growth on the pattern of trade demonstrated above is thus an example of commodity substitution, which is different from the factor-supply effect emphasized by Stockman and Roldos. In the next section, we study another specification of the cash-in-advance constraint, which serves to illustrate both commodity-substitution and factor-supply effects.

SECOND CASH-IN-ADVANCE MODEL

In this section, the basic structure of the model in the preceding section is retained. However, instead of assuming (3), it is assumed that cash is needed to purchase the industrial and the investment goods:

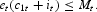
The first-order conditions for an interior optimal path are given by (1), (2), and (29), and are the same as (4)–(9), except that (7) becomes

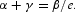
Follow the same procedure as in Section 2 to simplify the system of the first-order conditions; we still have (12). Then, substitute (7a) into (4) and (5) into (9) to obtain

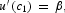
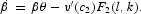
Combining (30) and (31), we obtain

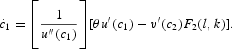
For the equilibrium conditions, condition (16) must hold to keep trade balanced. When the cash-in-advance constraint is binding, we multiply (29) by α and substitute (5) and (16) into it to obtain

Taking logarithm of both sides of (33) and differentiating with respect to time, and taking (6) into account,

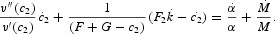
As before, let the money supply follow a constant growth rate, μ. Substituting (12) and (16) into (34), we have

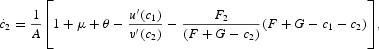
where

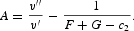
The equilibrium motions of

are thus completely characterized by (6), (16), (32), and (35).

In the steady state,

, which implies (21) and (23) and that

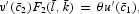
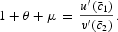
Given the conditions imposed, it is straightforward to verify that a unique steady state exists. Before the formal comparative analysis, we note that equations (36) and (37) imply

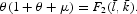
To understand the intuition underlying (38), one can start from (36) and (37). Condition (36) describes the opportunity cost of purchasing c₁ in terms of c₂: μ represents the inflation tax, and θ represents the cost of converting current income into cash momentarily later in order to purchase c₁. Condition (37) can be understood as another expression of the opportunity cost of c₁ in terms of c₂. Since the cash-in-advance constraint (29) applies to both c₁ and

equally, the household can reduce c₁ and add to the investment at t directly. The increase in the production of the industrial goods can be used to increase

for all s>t.⁶

, whereas augmenting the capital stock by one unit forever incurs a gain of utility by

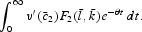
Equating these two expression, we obtain (36).

To study the effects of a perfectly anticipated inflation on the steady-state capital and the consumption goods, we have

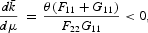
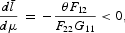
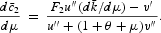
The reasoning for the above results can be explained as follows. Because purchasing the investment goods requires cash, the inflation tax reduces the rate of return on investment and lowers the steady-state capital stock. Also, because l and k are substitutes (F₁₂>0), the supply of labor in the first sector is reduced. Thus,

and

are both negative. These are the changes in the factor supplies due to inflation. The effects of inflation on c₁ and c₂ can be decomposed into the factor-supply effect and the commodity-substitution effect. In (41), the factor-supply effect of inflation on c₁ is

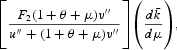
and the commodity-substitution effect is

Since both effects are negative, higher inflation reduces c₁ unambiguously. The total effect of inflation on c₂ is uncertain though. This is because the positive commodity-substitution effect,

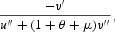
and the negative factor-supply effect,

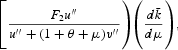
offset each other.

The effect of inflation on the volume and pattern of trade is uncertain in this case. Higher inflation induces the economy to produce less of the industrial goods, but its (domestic) consumption is also less. Higher inflation induces the economy to produce more of the agricultural goods, but its effect on the domestic consumption is ambiguous. Hence, the trade volume, measured in terms of

or

, may either increase or decrease as the factor-supply effect works against the commodity-substitution effect. This ambiguity will not be present when the cash-in-advance constraint (29) is revised to include c₂. In the next section, we set out such a model and examine the equilibrium properties.⁷

To study the dynamic behavior of the system in the neighborhood of the steady state, we can first solve for l(k) from (6). Substitute l(k) into (16), (32), and (35), and linearize around the steady state to obtain

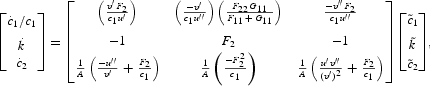
and

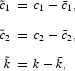
where all derivatives are evaluated at the steady state.

For the steady state to be a saddle point, it is necessary that the matrix in (43) have a unique negative characteristic root. The product of the characteristic roots of the system is given by the determinant

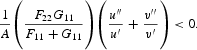
This establishes that there are either three negative roots or one. To establish that there is only one negative root, we proceed to examine the trace of the matrix, which is given by

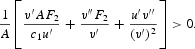
Since the trace is positive, this implies that there is at least one positive root. However, since we know it has either zero or two positive roots, it has two. There is therefore a unique negative characteristic root, and a unique perfect-foresight path satisfying (16), (32), and (35) that converges to the steady state.

THIRD CASH-IN-ADVANCE MODEL

In this section, we assume that the cash-in-advance constraint is imposed as follows:

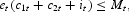
where M_t is the cash balance at time t.

The first-order conditions for an interior optimal path are given by (1), (2), and (44), and are the same as (4)–(9) except here, (5) becomes

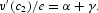
To simplify the system, we first rewrite (8) as

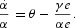
Define

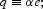
then, (7) implies that

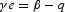
and (45) and (9) can be rewritten as

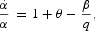
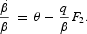
Again, trade must be balanced; that is, condition (16) holds. When the cash-in-advance constraint is binding, we multiply (44) by α and substitute (46) and (16) into it to obtain

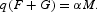
Taking the logarithm of both sides of (50) and differentiating with respect to time, after taking (6) into account, we obtain

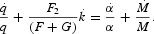
Substituting (16) and (48) into (51), we have

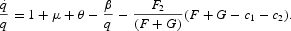
From (4), (5b), and (7),

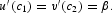
we substituting (53) into (52) and (49) to obtain

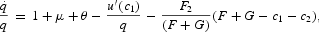
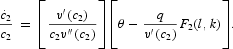
The equilibrium motions of

are thus completely characterized by (6), (16), (53), (54), and (55).

In the steady state,

. This implies (21) and (23) and that

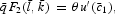
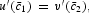
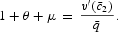
Note that equations (56) and (58) imply that

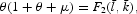
which is identical to (38). To understand this result, one can start from (56) and (58). By definition, q is the marginal utility of income at t. Since current income cannot be used to purchase contemporary consumption goods, and it must be transformed into cash momentarily later to do the purchase, (58) expresses the opportunity cost of c₁ in terms of the current income: μ represents the inflation tax, and θ represents the time discount of income. Condition (56) can be understood as another expression of the opportunity cost of c₁ in terms of current income. Since the cash-in-advance constraint (44) applies to c₁ and

simultaneously, the household can reduce c₁ and add to the investment at t directly. The increase in the production of the industrial goods can be used to increase future income. In the steady state, reducing c₁ by one unit incurs a loss of utility by

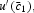
whereas augmenting the capital stock by one unit forever incurs a gain of utility by

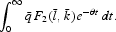
Equating these two expression, one obtains (56).

To study the effects of a perfectly anticipated inflation on the steady-state capital and the consumption goods, totally differentiate (21), (23), and (56)–(58), and we have

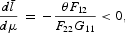
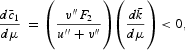
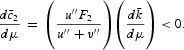
The reasoning for the results in (60)–(63) can be explained as follows. First, (60) and (61) are identical to (39) and (40). This implies that the inflation has the same effects on factor supplies, provided that the investment is cash constrained. Comparing (62) and (63) with (41) and (42), we see that only the factor-supply effect is present. This is because both c₁ and c₂ are cash constrained, the inflation does not change their relative prices, and hence the commodity substitution effect appeared in the preceding sections, but not here.

The effect of inflation on the volume and pattern of trade can be seen as follows. Higher inflation induces the economy to produce fewer industrial goods and more agricultural goods. The economy will consume fewer agricultural goods. Hence, if the economy is originally importing the industrial goods and exporting the agricultural goods, it will import and export more of both goods as the inflation rate increases; that is, trade volume will increase.

To study the dynamic behavior of the system in the neighborhood of the steady state, we first solve for l(k) from (6) and c₁(c₂) from (57), substitute l(k) and c(c₂) into (16), (54), and (55), and linearize around the steady state to obtain

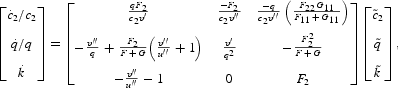
and

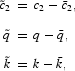
where all derivatives are evaluated at the steady state.

Again, for the steady state to be a saddle point, it is necessary that the matrix in (64) have a unique negative characteristic root. The product of the characteristic roots of the system is given by the determinant

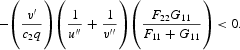
This establishes that there are either three negative roots or one. To establish that there is only one negative root, we proceed to examine the trace of the matrix, which is given by

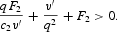
Since the trace is positive, this implies that there is at least one positive root. And since we know it has either zero or two positive roots, it should have two. There is therefore a unique negative characteristic root, and a unique perfect-foresight path satisfying (16), (54), and (55) that converges to the steady state.