INTRODUCTION
A fundamental characteristic of banks is that their assets and liabilities have different maturity structures. A bank's liabilities are largely short-term deposits, whereas a substantial part of its assets are typically held in long-term, less liquid investments. This maturity transformation activity produces substantial social benefits, but it also exposes banks to the possibility of a liquidity shortage. If total withdrawal demand exceeds the value of the liquid assets in the banking system, a “crisis” will occur in which some withdrawal demand cannot be met.1
We use the term “banking crisis” to indicate a situation where withdrawal demand is larger than total cash reserves and depositors in need of liquidity suffer consumption losses. Champ, Smith, and Williamson (1996) argued that this definition describes the crises of the nineteenth-century U.S. banking system very well. A comprehensive discussion of the features of modern banking crises around the world is provided by Boyd, Kwak, and Smith (in press).
A number of previous papers have shown, in general equilibrium settings, how discount window lending can facilitate the smooth functioning of the banking system and lead to better equilibrium allocations. In Sargent and Wallace (1982), for example, the demand for credit fluctuates deterministically and there is a legal restriction on the issue of private credit instruments. Having a discount window offer loans at a zero nominal interest rate leads to the existence of a Pareto optimal equilibrium, whereas closing the discount window does not. A zero nominal interest rate on discount window loans is optimal in this setting for two reasons. First, because the central bank can costlessly print and lend fiat currency, this rate equates the private cost of liquidity to the social cost of creating it. Second, the market nominal interest rate that supports the Pareto optimal allocation in this environment is also zero. The discount window loans are therefore being made at the market rate of interest and, thus, do not distort savings decisions away from the optimal level. The benefits of providing discount window loans at a zero nominal interest rate have since been established in a variety of environments; examples include Freeman (1996), which focuses on the role of liquidity in the payments system, and Williamson (1998), which examines a model with moral hazard.2
In a later paper, Freeman (1999) studied an environment with aggregate financial shocks and compared zero-nominal-rate discount window lending with other ways of providing an elastic currency. See also Schreft and Smith (2002), which showed how discount window lending can be superior to open market operations as a policy tool, and Williamson (2003), which focused on the role of overnight lending in the payments system.
Several recent papers study monetary policy in environments where the social return on real investment is always higher than the social return on money, and hence a market nominal interest rate of zero cannot lead to an optimal allocation. [See, for example, Bhattacharya, Haslag, and Russell (in press), Haslag and Martin (2003), and Schreft and Smith (2002).] The proper operation—and even the desirability—of a discount window in such settings is not well understood. Smith (2002) presented one such environment. When there is no discount window, a fundamental tension arises between the stability of the banking system and the efficiency of equilibrium allocations. If monetary policy generates a positive nominal interest rate, banks perceive an opportunity cost of holding cash reserves and therefore economize on such holdings. As a result, the banking system is relatively illiquid, and there are recurrent crises in which bank reserves are exhausted and agents in need of liquidity suffer losses in consumption. These crises can be avoided entirely if monetary policy instead conforms to the Friedman rule and generates a zero nominal interest rate. In this case, there is no opportunity cost of holding cash and banks therefore hold sufficient reserves to meet any possible level of liquidity demand. However, banks are then no longer performing their maturity-transformation function and the level of investment is far below optimal.
This environment seems to represent precisely the type of situation where discount window lending would be a useful policy tool. If after observing withdrawal demand banks could obtain loans of currency (“discounting” their real investments to the central bank), they could continue to serve their intermediary function and at the same time crises caused by a shortage of liquidity might be averted. Smith (2002) showed that this intuition is correct: Granting banks access to discount window loans at a zero nominal interest rate eliminates liquidity-induced banking crises. In this respect, his results are in line with the previous literature. However, he also showed that this policy leads to a “massive” indeterminacy of equilibrium, which he interprets as a form of macroeconomic instability.3
Smith and Weber (1999) studied a related environment and showed how having an elastic currency generated by private banknote issue can lead to a similar indeterminacy of equilibrium.
We show, in this same environment, how opening a discount window can be unambiguously beneficial. We do so by broadening the set of policies under consideration. When the nominal interest rate charged on discount window loans is positive and higher than the market interest rate, there is a unique stationary equilibrium in which money has value. In other words, free access can be granted to discount window loans without generating indeterminacy as long as borrowing from the discount window is more expensive than holding cash reserves. In addition, charging a positive interest rate at the discount window allows monetary policy to generate a positive market interest rate and thereby encourage real investment. There are downsides to this approach, however: Banking crises will occur in equilibrium and real investment will remain below the efficient level. Nevertheless, we show that a proper combination of monetary and discount window policies can make the welfare cost of these inefficiencies arbitrarily small. The near-optimal policies entail having low (but positive) market nominal interest rates and nearly costless liquidity at the discount window, and thus approximately implement the Friedman rule.
The remainder of the paper is organized as follows: In the next section, we present the basic model and describe in detail the optimal behavior of banks. In Section 3 we describe the equilibria of the model under different policy regimes. In Section 4 we present the corresponding welfare and optimal policy analysis, and in Section 5 we offer some concluding remarks.
THE MODEL
We begin by presenting the environment of Smith (2002) and then introduce a discount window that offers loans at a positive nominal interest rate. The majority of the section is devoted to deriving the optimal behavior of competitive banks as a function of the monetary and discount window policies.
The Environment
The economy consists of an infinite sequence of two-period lived, overlapping generations of agents, plus an initial old generation. In each period t=0, 1, 2, …, a continuum of identical agents with unit mass is born in each of two locations. There is a single consumption good; each agent is endowed with w>0 units of this good when young and none when old. Agents only care about consumption in the second period of life and have the utility function u(c)=ln(c).4
As in Champ, Smith, and Williamson (1996) and others, the assumption of logarithmic utility here permits the solution to the bank's problem to be characterized analytically.
At the beginning of a period, young agents receive their endowment and, possibly, a transfer of currency. At this point, neither agents nor banks can move between or communicate across locations, and therefore trade can only occur within each location. Young agents can trade with old agents and can deposit resources in a bank. Banks can also trade with old agents in this market. After trade takes place and deposits have been made, there is an opportunity to invest goods in a storage technology. This technology transforms one unit of the period t good into R>1 units of the period t+1 good, and it is the only form of real investment available. Goods that are neither consumed nor placed into this technology will perish once the investment opportunity has passed. With the deposits it receives, a bank first engages in trade to achieve the desired allocation of its portfolio between money and goods and then invests the goods in the storage technology.
After the investment opportunity has passed, a fraction πt of young agents in each location discover that they will be moved to the other location.5
The stochastic relocations in this model play a role similar to that of the portfolio-preference shocks commonly used in the literature on bank runs. Diamond and Dybvig (1983) is the classic reference; see also the recent papers by Peck and Shell (2003) and Ennis and Keister (2003) and the references therein. However, we should emphasize that a crisis in our model is caused by a high realization of liquidity demand, not a self-fulfilling bank run.
The relocation probability πt is a random variable in each period. Because there is a continuum of young agents, it represents both the probability of relocation for each agent and the fraction of all agents who move. That is, πt gives the size of the aggregate liquidity shock in period t; higher realizations of πt correspond to higher demand for liquid assets. It is publicly observable and is independently and identically distributed over time. Let G represent the distribution function, which is assumed to be smooth and strictly increasing on [0,1], and g the associated density function. We should emphasize that the market where goods are exchanged for money in period t meets before the realization of πt. After πt is realized, no trade occurs until the following period. As a result, the general price level in period t will not depend on the realization of liquidity demand in that period.
Monetary and Discount Window Policies
The central bank has two policy variables, both of which are chosen once and for all in the initial period. First, it sets a (gross) growth rate σ for the money supply, that is,
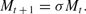
Monetary injections/withdrawals take place through lump-sum transfers to young agents. Let τt denote the real value of the transfer given to young agents at time t; a negative value of τt denotes a tax that must be paid in currency. These transfers take place at the beginning of each period, and hence a state-contingent policy where σ depends on the realization of πt is infeasible. We assume that σR≥1 holds. In a stationary equilibrium, σR will be the market nominal interest rate, and we are therefore ruling out policies that would lead money to have a strictly higher return than investment. The qualitative properties of equilibrium under such a policy would be very similar to the case where σR=1 holds. Excluding these policies simplifies the presentation without any loss of economic insight.
Second, the central bank sets a (gross) nominal interest rate ϕ≥1 on discount window loans.6
In principle, the interest rate ϕ could be made contingent on the realization of πt. However, we show below that policies where ϕ is fixed can achieve allocations arbitrarily close to the first-best, and hence there is no gain in looking at more general policy rules.
If, in period t, a bank demands a loan of λt (measured in real terms, per unit of deposits), it receives λtpt dollars from the discount window, where pt is the general price level in period t.7
By symmetry, pt will be the same in both locations. Throughout the analysis, we only consider equilibria where money has value and hence pt is finite for all t.
Banks
A bank offers to pay a return
to a depositor if she is relocated and a return dt(πt) if she is not. As the notation indicates, both of these returns can depend on the size of the (observable) aggregate liquidity shock. It is assumed that banks behave competitively in the sense that they (i) take the real return on assets as given and (ii) choose the deposit return schedules
and dt to maximize the expected utility of young lenders. A young lender will therefore deposit her entire income w+τt in a bank; there is no incentive to hold assets directly in this environment. Without any loss of generality, we consider a representative bank that holds all deposits in the economy.
Per unit of deposits, the bank acquires an amount γt of real money balances and invests the remaining 1−γt. Let δt denote the fraction of this investment that is liquidated early and given to movers, and (1−δt) the fraction held until maturity and given to nonmovers. Let λt≥0 denote the real value of the bank's borrowing from the discount window. The bank faces two constraints on the return schedules it can offer. First, relocated agents must be given currency or liquidated investment. Let αt(πt) denote the fraction of the bank's cash reserves given to movers. Because the real return to holding money between periods t and t+1 is given by (pt/pt + 1), the return offered to movers must satisfy
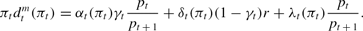
The second constraint is that payments to nonmovers cannot exceed the value of the bank's residual portfolio—remaining cash reserves plus matured investment minus the repayment of the discount window loan. This constraint can be written as
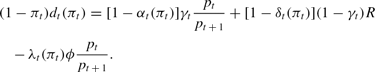
The bank will therefore choose the functions
and dt to maximize
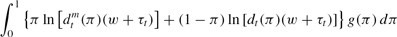
subject to (2), (3), and non-negativity constraints. Let It≡R(pt + 1/pt) denote the (gross) market nominal interest rate. That is, It reflects the additional return that investment offers over currency and hence represents the opportunity cost of holding cash reserves. Substituting in the two constraints and performing some manipulations, the bank's problem can be written as maximizing
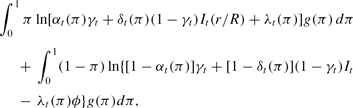
subject to
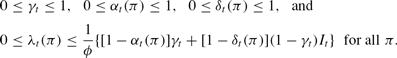
The final inequality represents the constraint that borrowing at the discount window in period t cannot exceed the bank's ability to repay the loan in period t+1.
The fractions of currency reserves and investment paid out to movers, as well as the amount of discount window borrowing, are chosen after the realization of πt, whereas the fraction of currency in the bank's asset portfolio is chosen before the realization of πt. Hence, we can solve the problem backwards, by first finding the optimal values of αt, δt, and λt as functions of γt and πt. That is, we can first choose (αt, δt, λt) to
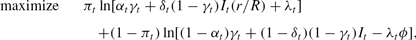
subject to the constraints above. We begin the process of solving this problem by showing that, outside of one knife-edge case, the bank may respond to high liquidity demand by either liquidating investment or borrowing from the discount window, but not both.
PROPOSITION 1. If ϕ<R/r holds, the solution to (5) has δt=0 for all values of γt and πt. If ϕ>R/r holds, the solution to (5) has λt=0 for all values of γt and πt.
The proof of this proposition is contained in the Appendix, but the intuition is straightforward. Borrowing from the discount window and liquidating investment are both ways of generating additional consumption for movers as a group (at the expense of nonmovers). The bank will only use the less costly of the two methods. If the interest rate at the discount window is low, borrowing is less costly and the bank will never liquidate investment. If the interest rate at the discount window is high enough, however, liquidation is less costly and the discount window will be inactive. In the latter case, our model reduces to that presented in Smith (2002). Because we are interested in optimal discount window policies, we focus on the case where ϕ<R/r holds. In Section 4, we show how such policies can always increase welfare relative to having an inactive discount window.8
There is one borderline case that the proposition does not cover, when ϕ is exactly equal to R/r. In this case the solution to (5) is not unique, because the bank is indifferent between liquidating investment and borrowing from the discount window. In what follows, we ignore this knife-edge case in order to simplify the presentation. The results in Section 4 show that setting ϕ=R/r cannot be part of an optimal policy.
In this case, the solution to (5) sets δt to zero for all values of πt and sets
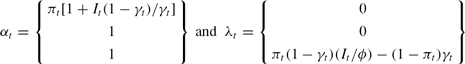
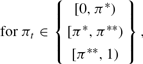
where we have
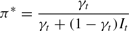
and
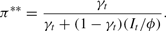
When demand for liquidity is fairly low (i.e., the relocation shock is below a critical value π*), the bank is able to give movers and nonmovers the same return by paying out only a fraction of its reserves to movers. When the realization of the relocation shock is greater than π*, however, this approach is no longer feasible. In this case, there are so many movers that even if all of the bank's cash reserves are given to them, they will receive a lower return than the (relatively few) nonmovers. The bank then has an incentive to borrow currency from the discount window so that it can transfer resources from nonmovers to movers. However, such borrowing is costly and, as a result, the bank only undertakes it if the number of movers is above a second critical level π**. For values of πt above π*, a banking crisis occurs:
holds and depositors who need liquidity suffer losses in consumption.
Some intuition for the range of inaction [π*, π**] can be gained by thinking about the set of feasible ways for the bank to divide resources between movers (as a group) and nonmovers (as a group), given that γt is already fixed. One action that is always feasible is to give all cash reserves to movers and the return from all investment to nonmovers. If instead the bank wants to give fewer total resources to movers and more to nonmovers, perhaps because there are very few movers this period, it can do so on a one-for-one basis. That is, for every unit of future consumption (in the form of currency) that is taken away from movers as a group, exactly one unit is given to nonmovers as a group. Now suppose that instead the bank wants to give more resources to movers and fewer to nonmovers, perhaps because there is a large number of movers. In this case the bank must either liquidate investment or obtain a loan from the discount window, so that for every unit of additional consumption given to movers, nonmovers must give up either R/r or ϕ units. This difference in the rates of transformation is what leads to the range of inaction [π*, π**] in the optimal levels of αt and λt. When there are very few movers, the optimal action is to give almost all of the resources to nonmovers, and hence we are in the region where the rate of transformation is unity. As we examine larger and larger realizations of πt, the solution gives more and more of the bank's currency reserves to movers. At πt=π*, the optimal action reaches the kink in the constraint set where all currency reserves are given to movers. This point remains the optimal choice for a range of values of πt; only when the realization is greater than π** is it optimal to move to the steeper-sloped part of the boundary. In conjunction with (8), this reasoning also demonstrates how the interest rate on discount window loans determines the potential severity of banking crises. The more costly it is to borrow, the larger πt must be (and therefore the larger the gap between the returns of movers and nonmovers must be) for a bank to be willing to borrow to ease the crisis.
We now proceed to solve for the optimal value of γt. To do so, we substitute the optimal values of αt and λt into the bank's objective function in (4) so that the only remaining variable to be determined is γt. The problem can then be written as
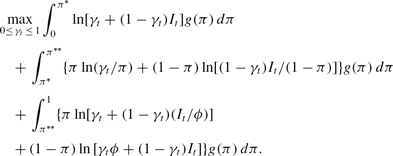
Because borrowing is costly, the solution to this problem will be interior as long as 1<It<ϕ holds. The first-order condition is given by

which can be reduced to
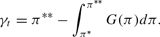
This equation implicitly defines (recall that γt appears in the expressions for π* and π** above) the solution to the bank's portfolio allocation problem as a function of the variable It∈(1, ϕ). Let γϕ(It) denote this solution, where the ϕ subscript indicates that the solution (i) applies in the region of the parameter space where the discount window is active and (ii) depends on the interest rate charged on discount window loans. The next proposition establishes some properties of this solution.
PROPOSITION 2. For any given ϕ∈(1, R/r) and any It>0, the bank's problem has a unique solution. The reserve–deposit ratio γϕ in this solution is a continuous function of It and satisfies:
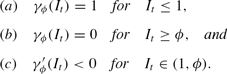
To see the intuition for this result, suppose that It≤1 holds. Then the return on currency is at least as high as the return on investment. Because currency offers the additional advantage of being liquid, the bank will hold only currency. If It≥ϕ holds, on the other hand, then borrowing from the discount window costs no more than holding cash reserves. Because the quantity of borrowing can be tailored to the realization of liquidity demand, the bank will hold no cash reserves. For intermediate values of It, the bank will hold both types of assets, with the fraction of resources placed in currency being a decreasing function of It. A formal proof of the proposition is given in the Appendix. Having solved the optimization problem of the bank, we now turn to an analysis of general equilibrium.
EQUILIBRIUM
An equilibrium consists of sequences for the price level {pt} and for bank decision rules {γt, αt, δt, λt} such that (i) given {pt}, the decision rules solve the bank's problem (4) in each period; (ii) the market where money is traded for goods at the beginning of each period clears; and (iii) the government's budget constraint

holds in each period. Because young agents deposit all of their income in the bank, the market-clearing condition for period t can be written as
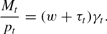
Define zt≡Mt/pt to be the (per-capita) level of real balances in the economy. Then we have
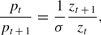
and hence the market nominal interest rate is given by
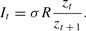
We can then rewrite
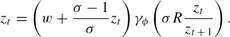
As this expression shows, the behavior of real money balances is governed by a deterministic difference equation. Because markets meet before the realization of the liquidity shock, ex post liquidity demand cannot affect the current-period price level. In addition, currency borrowed from the discount window is removed from circulation when these loans are repaid at the beginning of the following period and hence has no effect on future price levels. For these reasons, the price level and the level of real money balances both follow deterministic paths. It is important to keep in mind, however, that equilibrium consumption is potentially stochastic. Depending on the bank's level of cash reserves and the discount window policy, the returns received by depositors may depend on the realization of πt.
Following Smith (2002), we focus on stationary equilibria, where zt=z for all t. In such equilibria, the nominal interest rate is given by It=σR and the level of real balances by
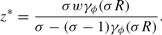
This expression demonstrates that a stationary equilibrium with valued fiat currency exists if and only if γϕ(σR) > 0 holds. In other words, the central bank must set its two policies in such a way that banks demand a positive amount of reserves. Using Proposition 2, a necessary and sufficient condition for this to be the case is that
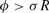
holds. If this inequality were reversed, borrowing from the discount window would be a strictly better source of liquidity than holding cash reserves. The demand for cash reserves would then be zero and money would have no value. The expression for z* in (11) also demonstrates that, when (12) holds, there is a unique positive level of real money balances consistent with stationary equilibrium. We summarize these results in the following proposition:
PROPOSITION 3. If (12) holds, there exists a unique stationary monetary equilibrium.
In other words, discount window lending does not lead to indeterminacy of stationary equilibrium in this environment if the loans carry a “penalty” rate of interest.9
Interestingly, this type of policy was advocated by Bagehot (1873), who stated that in times of crisis the monetary authority should act as a lender of last resort and lend freely to the banking system, but “at a penalty rate.” Martin (2002) argued that Bagehot's prescription applies in a commodity money regime where total reserves are scarce, but not in a fiat money regime where currency can be freely printed. Proposition 3 gives an example of how a penalty-rate policy can be useful in a fiat money system.
BANKING CRISES AND WELFARE
We now examine the welfare properties of the equilibrium described above, continuing to assume that (12) holds. Recall that a banking crisis occurs whenever movers receive a lower return on their deposits than do nonmovers. We begin by establishing that, for all but one choice of monetary policy, banking crises will occur in equilibrium.
PROPOSITION 4. If σR=1 holds, banking crises never occur in equilibrium. If σR>1 holds, however, banking crises occur with positive probability in each period.
This result follows directly from Proposition 2, using the fact that It=σR holds in a stationary equilibrium. With It=1, the bank will set γt to unity and therefore will have sufficient cash reserves to meet any level of liquidity demand. With It>1, on the other hand, the bank will set γt less than unity, and therefore with positive probability the realized value of πt will be greater than π*. Because ϕ>1 holds, it follows from (7) and (8) that such a value of πt will necessarily lead to a crisis.
The welfare cost of a banking crisis depends on two factors: the size of the wedge between the returns given to the two types of depositors and the amount of revenue the discount window collects and removes from the economy. Both of these distortions clearly depend on the realized value of πt as well as on the interest rate at the discount window. We can calculate the largest possible wedge between the two returns using (6). For values of πt greater than π**, we have
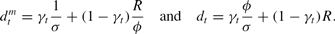
The difference between these two expressions is strictly increasing in ϕ. In other words, a lower interest rate on discount window loans implies a better “worst-case scenario” in terms of the gap between
and dt. Using (6) again, we can write the revenue collected by the discount window when πt is greater than π** as
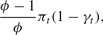
which is also strictly increasing in ϕ. Thus, lowering the interest rate increases the total resources available to the bank—and hence the average return given to depositors—during times of crisis. Minimizing the welfare loss due to banking crises therefore clearly requires charging a low interest rate at the discount window.
The analysis of the previous sections, however, has shown how the choice of discount window policy restricts the set of monetary policies that can be followed. Together, these two policies determine the level of real investment and hence the total wealth of the economy in the following period. How should a benevolent central bank set the policy pair (σ, ϕ)? Following Smith (2002), we take the objective to be the steady-state utility of a young agent.10
That is, we ignore the initial old generation in our welfare calculations. See footnote 9 in Smith (2002) on this issue.
PROPOSITION 5.For any ε>0, there exists a policy (σ, ϕ) such that steady-state welfare in the unique stationary equilibrium generated by (σ, ϕ) is within ε of the first-best value ln(Rw).
Getting very close to the first-best allocation requires having nearly all of the economy's total endowment placed into storage (and very little held as cash reserves). The bank will be willing to hold very little currency only if borrowing from the discount window is relatively inexpensive, that is, if ϕ is very close to unity. In order for a stationary monetary equilibrium to exist and be unique, we need 1<σR<ϕ to hold, and hence for σR to be very close to unity as well. In the proof in the appendix, we show that a sequence of policies can be constructed so that, along this sequence, the allocation in the unique stationary monetary equilibrium converges uniformly to the first-best allocation described above. This policy sequence converges to σ=1/R and ϕ=1, so that in the limit the nominal interest rate would be zero both in the market and at the discount window. The near-optimal policies can therefore be viewed as approximating the Friedman rule. We should emphasize that this result is not driven by our assumption that agents derive no utility from the revenue made by the central bank on discount window loans. Because a low interest rate policy can bring the economy very close to the first-best allocation, it is better than a high interest rate policy regardless of how this revenue is used.
Note that the first-best allocation itself cannot be implemented. Achieving the first-best allocation requires that all of the economy's resources be placed into storage, which implies that there must be zero demand for cash reserves and hence money cannot have value. When money has no value, discount window lending is clearly ineffective. This fact points to an important distinction between money and liquidity. Money is an asset that is inherently liquid, but a demand for liquidity does not necessarily imply a demand for money. Indeed, the benefit of having a discount window in this environment derives precisely from the fact that it helps meet the liquidity needs of relocated agents in a way that does not prevent socially productive investments from being undertaken.11
In this way, our Proposition 5 is closely related to Proposition 5 in Haslag and Martin (2003). They studied a model where the fraction of agents relocated is the same in every period and showed how discount window lending can allow banks to hold fewer reserves and make more productive investment.
CONCLUDING REMARKS
Studying environments where the social return on investment is always higher than the social return on money is important for understanding the aggregate tradeoff between liquidity and real investment. Previous work has indicated that opening a discount window in such an environment may lead to macroeconomic instability. We show that this need not be the case. By charging a positive interest rate on discount window loans, a central bank can open a discount window without generating indeterminacy of equilibrium. Furthermore, by carefully coordinating this interest rate with the growth rate of the money supply, allocations arbitrarily close to the first-best can be implemented.
The specific policy prescriptions of our analysis obviously depend on the specific features of the environment we consider. In particular, the nonexistence of an exact optimal policy stems from the fact that discount window loans are a perfect substitute for cash reserves. This feature would most likely change if money played another role in the model, such as facilitating investment or market transactions. The demand for currency would then not be completely undermined by a costless-liquidity policy at the discount window, and an exact optimal policy would likely exist. It would be interesting to know under what conditions this policy would or would not correspond to the Friedman rule. Similarly, the only uncertainty in our model is about liquidity demand. There is no uncertainty about the real value of a bank's assets or a bank's ability to repay a discount window loan. It would be interesting to know how the optimal discount window policy would change in the presence of solvency shocks12
In a different environment, Freeman (1999) studied this problem and found that a zero-nominal-rate lending policy should be combined with quantity restrictions at the discount window. See also Antinolfi, Huybens, and Keister (2001) on the role of quantity restrictions.
Williamson (1998) studied a model in which there is moral hazard and showed that in this setting, discount window lending at a zero nominal interest rate is welfare improving.
APPENDIX
Proof of Proposition 1
The derivatives of the objective function (5) with respect to the three choice variables are
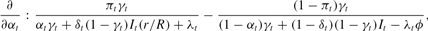


Suppose that ϕ < R/r holds. For the solution to have δt > 0, we need (14) to be non-negative. However, this would imply that both (13) and (15) are strictly positive, and therefore that the solution must have αt and λt at their maximum possible values. In other words, it must be the case that no resources are kept for nonmovers, so that dt = 0 holds. Given this, it is straightforward to show that
is strictly decreasing in δt (because an increase in liquidation implies a corresponding decrease in discount window borrowing and liquidation is more costly). Therefore, the solution cannot have δt>0.
Now, suppose that ϕ>R/r holds. For the solution to have λt>0, we need (15) to be non-negative. This would imply that both (13) and (14) are strictly positive, and therefore that the solution must have αt=1 and δt=1. However, the bank would then have no resources left at time t+1 with which to repay the loan, and therefore the upper bound on λt would be zero. Hence, the solution cannot have
Proof of Proposition 2
Let M(γt, It) denote the objective function in (9). Because this function is strictly concave and the constraint set is compact, we know that there is a unique solution to the bank's problem for any It>0. The first derivative of the objective can be written as
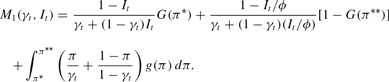
Using L'Hôpital's rule, one can show
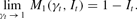
If It≤1 holds, then this limit is non-negative and the concavity of the objective function implies that the solution must be at the boundary point γt=1. This establishes part (a) of the proposition. Part (b) is established in a similar manner. Again using L'Hôpital's rule, we have
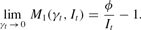
If It≥ϕ holds, this limit is non-positive and, thus, the solution must be γt=0.
For values of It strictly between unity and ϕ, the solution to the problem is defined by the first-order condition M1(γt, It)=0. The effect of a change in It on the optimal value of γt is then determined by implicit differentiation of the identity
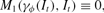
which yields
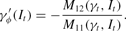
Differentiating (16) with respect to It yields

By strict concavity we know that M11 is also negative and, therefore, we have
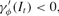
which establishes part (c) of the proposition. Finally, the limits displayed above show that the function γϕ(It) is continuous at the points It=1 and It=ϕ, and hence is continuous over the whole domain. This completes the proof of the proposition.[squf ]
Proof of Proposition 5
Fix any sequence
of discount window interest rates such that 1<ϕj<R/r holds for all j and
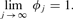
Next, fix a sequence
of reserve-deposit ratios such that
holds for all j and

For each j, find the money growth rate σj that would lead the bank to choose
as the reserve-deposit ratio. That is, choose σj to satisfy
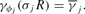
From Proposition 2, we know that such a value of σj always exists. Furthermore, because
is strictly between zero and unity, we must have
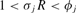
for all j, and therefore the sequence {σj} must converge to 1/R.
Proposition 3 implies that each policy (σj, ϕj) generates a unique stationary monetary equilibrium. From (6) it is straightforward to show that in such an equilibrium, both
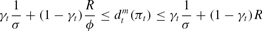
and
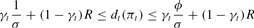
hold for all πt∈[0, 1]. These two expressions show that as
converges to zero and ϕ to unity, the functions
and dt both converge uniformly to the constant function R. The expected utility level of a young agent along the sequence of policies (σj, ϕj) must therefore converge to ln(Rw), which establishes the result. [squf ]
We thank the associate editor, two anonymous referees, Huberto Ennis, and seminar participants at the Federal Reserve Bank of New York, the 7th SAET Conference in Vigo, the Third Missouri Economics Conference at the University of Missouri-Columbia, and the Clarence Tow Conference on Money and Banking at the University of Iowa for valuable comments. We are deeply indebted to Bruce Smith for his useful comments and for many years of encouragement and support. We gratefully acknowledge financial support from the Weidenbaum Center on the Economy, Government, and Public Policy at Washington University. Part of this work was completed while Keister was visiting the University of Texas at Austin, whose hospitality and support are also gratefully acknowledged.


