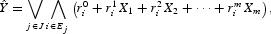RIESZ SPACES AND BANACH LATTICES

The objective of this section is to present a brief discussion of the basic mathematical background in Riesz space theory needed for the present work and to study the Riesz estimators in Aliprantis, Harris, and Tourky (2006). The mathematics behind the theory of Riesz estimators are those of Riesz spaces and Banach lattices. We recall here some basic properties of Riesz spaces, and for details and terminology we refer to Abramovich and Aliprantis (2002a), Aliprantis and Border (1999), Aliprantis and Burkinshaw (2003), Luxemburg and Zaanen (1971), and Schaefer (1974).

An ordered vector space is a real vector space L equipped with an order relation ≥ that is compatible with the algebraic structure of L in the sense that if x≥y, then:

An ordered vector space L is said to be a Riesz space (or a vector lattice) if L is also a lattice in the sense that every nonempty finite subset of L has a supremum (least upper bound) and an infimum (greatest lower bound). Following the standard terminology from lattice theory, we shall denote the supremum and infimum of a set {x₁, …, x_n} by

respectively. In particular, the supremum and infimum of any pair of vectors x and y are denoted by x∨y and x∧y, respectively. The simplest example of a Riesz space is R with the usual order. Here x∨y and x∧y are the largest and smallest numbers of the set {x, y}; for instance, 2∨3=3, 1∧0=0, and 3∧3=3.

For an element x of a Riesz space L, the positive part of x is defined by x⁺=x∨0, the negative part by x⁻=(−x)∨0, and the absolute value by |x|=x∨(−x).

The following is a simple but very useful result.

LEMMA 2.1. An ordered vector space is a Riesz space if and only if x⁺ exists for each vector x.

For an illustration of the above notions, let L=C[0, 1], the vector space of all continuous real valued functions defined on ]0, 1]. With the pointwise ordering and algebraic operations C[0, 1] is a Riesz space such that for each x∈L and each t∈[0, 1] we have

Similarly, if x∈L and r∈R, then for each t∈[0, 1] we have

Also, notice that if {x₁, …, x_n}∈C[0, 1], then for each t∈[0, 1] we have

Since C(Rⁿ) with the pointwise ordering is a Riesz space, the above formulas are also true for functions of C(Rⁿ).

Our interest here is in the structure of the Riesz subspaces of a Riesz space. A vector subspace M of a Riesz space L is said to be a Riesz subspace (or a vector sublattice) if x, y∈M imply that both x∨y and x∧y belong to M. If we consider the product vector space R^Ω (where Ω is any nonempty set) and order it pointwise, then (with the above lattice operations) R^Ω is a Riesz space. Moreover, if Ω is a topological space, then C(Ω) (the vector space of all continuous real-valued functions on Ω) and C_b(Ω) (the vector space of all uniformly bounded continuous real-valued functions on Ω) are both Riesz subspaces of R^Ω.

It should be clear that arbitrary intersections of Riesz subspaces are Riesz subspaces. This implies that every nonempty subset A of a Riesz space L is included in a smallest Riesz subspace, called the Riesz subspace (or the vector sublattice) generated by A and denoted

.

Next, we shall briefly describe the Riesz subspace

, an important subspace for our work. For every nonempty subset A of a Riesz space L, the symbol A^∧ will denote the collection of all vectors that can be written as infima of finite subsets of A. That is, a vector a∈L belongs to A^∧ if there exist vectors a₁, a₂, …, a_k∈A such that

. Similarly, A^∨ is the set consisting of all suprema of finite subsets of A. We write A^∨∧ for (A^∨)^∧ and A^∧∨ for (A^∧)^∨. So, a vector a belongs to A^∨∧ if and only if there exists a finite family {E_j}_j∈J of nonempty finite subsets of L such that

. It turns out that A^∨∧=A^∧∨ is always true.

Now we can describe the Riesz subspace generated by a set as follows. For proofs and more discussion, see Section 5 of Abramovich and Aliprantis (2002a,b).

LEMMA 2.2. The Riesz subspace

generated by a vector subspace A of a Riesz space coincides with A^∧∨ and also with A^∨∧. That is,

.

COROLLARY 2.3. The Riesz subspace generated by a nonempty subset A of a vector lattice is precisely the vector space

where [A] is the linear span of A.

When a Riesz space L is equipped with a norm that is compatible with the order structure of the space in the sense that |x|≤|y| implies ‖x‖≤‖y‖, then L is called a normed Riesz space.¹

The two classical examples of Banach lattices are the

-spaces, where

is a compact topological space and the norm is the sup norm ‖ · ‖_∞, that is,

and the L_p(μ)-spaces, where 1≤p≤∞, and the norm is given by

ONE-DIMENSIONAL PIECEWISE LINEAR FUNCTIONS

We present here a few properties and formulas dealing with continuous piecewise linear functions defined on R or on a closed interval of R.

DEFINITION 3.1. A function

is called piecewise linear (affine) if there exist real numbers −∞<a₀<a₁<[sdot ][sdot ][sdot ]<a_k<∞ and pairs of real numbers (m_i, b_i), i=0, 1, …, k, k+1, such that

The parameters {a₀, a₁, …, a_k} and the pairs (m_i, b_i), i=0, 1, …, k, k+1, are referred to as a representation of f and the functions f_i(t)=m_it+b_i as the components of the representation.

Similarly, a function

where [a, b] is a closed interval of R, is piecewise linear if there exist a partition a=a₀<a₁<[sdot ][sdot ][sdot ]<a_k=b of the interval [a, b[ and pairs of real numbers (m_i, b_i), i=1, …, k, such that f(t)=m_it+b_i for all a_i−1≤t≤a_i.

Notice that, according to these definitions, piecewise linear functions are automatically continuous. The following result should be obvious.

LEMMA 3.2. If

is piecewise linear, then its restriction to any closed interval of R is likewise piecewise linear. Moreover, if [a, b[ is any closed subinterval of R, then the components of the piecewise linear function

are among the components of

.

In addition, every piecewise linear function on a closed interval of R can be extended to a piecewise linear function to all of R.

The piecewise linear functions on a closed interval are characterized as follows. The idea is depicted in Figure 1.

Notice that f(t)=b1+t+−2(t−a1)++2(t−a2)+.

LEMMA 3.3. Let

be a piecewise linear function. If {a₀, a₁, …, a_k} and (m_i, b_i), i=1, …, k, is any representation of f, then for each t∈R we have

In particular, a function

is piecewise linear if and only if there exist a partition a=a₀<a₁<[sdot ][sdot ][sdot ]<a_k=b of [a, b] and constants c, c₀, c₁, …, c_k such that for each t∈[a, b] we have

.

Proof. Let a≤t≤b. If a₀≤t≤a₁, then note that

So, we can assume that a_j−1≤t≤a_j for some 1<j≤k. Notice that for each 1<i≤k−1 we have m_ia_i + b_i=m_{i + 1}a_i + b_{i + 1} or (m_{i + 1}−m_i)a_i=−(b_{i + 1}−b_i). Consequently, we have

and the proof is finished.

COROLLARY 3.4 [Brown, Huijsmans, and de Pagter (1991)]. The vector subspace generated in C[0, 1] by the collection {1, t}∪{(α−t)⁺:, α ∈ R} coincides with the Riesz subspace of all piecewise linear functions on [0, 1].

COROLLARY 3.5. Let

be a piecewise linear function. If {a₀, a₁, …, a_k} and (m_i, b_i), i=0, 1, …, k, k + 1, is an arbitrary representation of g, then for each t∈R we have

In particular, a function

is piecewise linear if and only if there exist real constants m₀, b₀, a₀, a₁, …, a_k and c₀, c₁, …, c_k such that for each t∈R we have

Proof. Consider the function

defined by

As in the proof of Lemma 3.3, it is easy to see that h(t)=f(t) for all a₀≤t≤a_k. Moreover, h(t)=m₁t+b₁ for all t≤a₀ and h(t)=m_kt+b_k for all t≥a_k. Since

it follows that

as desired.

We close the section with two results that will be useful for our study later.

LEMMA 3.6. Let

be a piecewise linear function and let {a₀, a₁, …, a_k} and (m_i, b_i), i=1, …, k, be a representation of f. Also let

the slope of the line segment joining the points (a, f(a)) and (b, f(b)).

Then there exist some 1≤i≤k with m_i≥m and some a_i−1≤ξ≤a_i satisfying f(ξ)=m(ξ−a)+f(a).

Proof. Assume by way of contradiction that if m_i≥m, then we have f(t)≠m(t−a)+f(a) for all a_i−1≤t≤a_i. In particular, we have m₁<m. Given that for a≤t≤a₁ we have f(t)=m₁t+b₁=m₁(t−a)+f(a), the latter implies f(t)<m(t−a)+f(a) for all a<t≤a₁. Notice that for each a₁≤t≤a₂ we have

So, if m₂<m, then for each a₁≤t≤a₂ we have f(t)<m(t−a)+f(a). On the other hand, if m₂≥m, then for each a₁≤t≤a₂ we must have f(t)<m(t−a)+f(a); otherwise (by the intermediate value theorem) there should exist some a₁≤ξ≤a₂ with f(ξ)=m(t−a)+f(a), which contradicts our assumption. The same argument yields f(t)<m(t−a)+f(a) for all a₂≤t≤a₃. Continuing this way we see that f(a_k)=f(b)<m(b−a)+f(a)=f(b), which is impossible.

As an immediate consequence we get the following result.

COROLLARY 3.7 [Ovchinnikov (2002)]. Let

be a piecewise linear function and let {a₀, a₁, …, a_k} and (m_i, b_i), i=1, …, k, be the parameters of a representation of f. Then there exists some 1≤i≤k such that f(a)≥m_ia+b_i and f(b)≤m_ib+b_i.

Proof. According to Lemma 3.6 there exist some 1≤i≤k and some a_i−1≤ξ≤a_i satisfying

and f(ξ)=m(t−a)+f(a). Note that for each a_i−1≤t≤a_i we have m_it+b_i=m_i(t−ξ)+f(ξ) and that for all a≤t≤b we have m(t−a)+f(a)=m(t−ξ)+f(ξ). This implies m_it+b_i≤m(t−a)+f(a) for all a≤t≤ξ and m_it+b_i≥m(t−a)+f(a) for all ξ≤t≤b, and our conclusion follows.

MULTIVARIATE PIECEWISE LINEAR FUNCTIONS

Recall that any function

of the form f(x)=α+a·x, where α∈R is a constant and a∈R^m is a fixed vector, is called an affine function. As usual, an affine function f is linear if α=0, i.e., f(x)=a·x. A function

, where S is a subset of R^m, is said to be an affine function if it is the restriction of an affine function defined on R^m. Let Aff denote the collection of all affine functions on R^m and note that Aff is a vector subspace of C(R^m).

LEMMA 4.1. Regarding affine functions we have the following:

1. The vector space Aff of all affine functions is the linear span in C(R^m) of the functions {1, e₁, e₂, …, e_m}, where 1(x)=1 and e_i(x)=x_i for all x∈R^m. That is, we have
   and so Aff is an (m+1)-dimensional vector space.²

   As a matter of fact, if we identify every vector

   with the affine function on R^m defined by

   , then it is not difficult to see that we can identify Aff with the vector space R^m+1.

2. Two affine functions
   coincide if and only if f(x)=g(x) for all x in a nonempty open subset of R^m. In particular, if a subset S of R^m has an interior point, then any affine function on S is the restriction of a unique affine function defined on R^m.

Proof. The proof of part (1) is obvious. The proof of part (2) follows easily from the following simple property: If a nonzero linear functional f satisfies f(x)≥α for all x in a nonempty open set

, then f(x)>α must be the case for all

.

To see this, fix

and assume that f(x)=α. Since

is an open set, there exists some ε>0 such that

. So, for each y∈B(0, ε) we have α+f(y)=f(x+y)≥α or f(y)≥0. This implies f(y)=0 for all y∈B(0, ε) and so f=0, which is impossible.

We are now ready to introduce the general concept of piecewise linear function.

DEFINITION 4.2. A function

is called piecewise linear (or piecewise affine) if there exist distinct affine functions f₁, f₂, …, f_p and subsets S₁, S₂, …, S_p of R^m such that:

1. Each S_i is closed with nonempty interior and
   .³

   If A is any subset of R^m, then Int(A) denotes its interior and

   its closure. We remark that the sets S_i are not assumed to be connected.

2. If i≠j, then Int(S_i)∩Int(S_j)=[empty ].
3. .
4. If x∈S_i, then f(x)=f_i(x).

We also introduce the following terminology and notation.

1. The sets S_i are called the regions of f and the functions f_i will be referred to as the components of f.
2. The pairs (S₁, f₁), …, (S_p, f_p) are the characteristic pairs of f.
3. The set of all piecewise linear functions will be denoted by PL.

A remark is in order here. The same definition of a piecewise linear function can be given for solid domains, that is, for closed convex subsets of R^m with nonempty interior. All results in this section hold true for piecewise linear functions with solid domains. We assume that our functions have domain R^m for the sole purpose of simplifying the exposition. The reader can verify directly that when m=1 the definitions for piecewise linear functions given in Definitions 3.1 and 4.2 are equivalent; see also Corollary 4.10

Here is an example of an piecewise linear function with a solid domain in R².

Example 4.3. Let Q=[0, 12]×[0, 12]={(x, y)∈R²: 0≤x≤12; 0≤y≤12}. Consider the piecewise linear function

defined by

The regions of this function are shown in Figure 2 and its graph is depicted in Figure 3.

The regions of the function $f\colon {\bf R}^2\to {\bf R}$.

The graph of $f\colon {\bf R}^2\to{\bf R}$.

Notice that the regions cannot be specified by separate thresholds on the variables x₁ and x₂. This would be the case only when the function f is itself separable.

The rest of the discussion in this section is devoted to the properties of piecewise linear functions. The fundamental result for our work will be obtained in the sequel (see Theorem 4.15) and it states that the collection of all piecewise linear functions is precisely the Riesz subspace generated in C(R^m) by the affine functions.

LEMMA 4.4. Every piecewise linear function is continuous.

Proof. Let

be piecewise linear and let

. If

, then (by passing to a subsequence) we can assume without loss of generality that there exists some ε>0 such that |f(x_n)−f(x)|≥ε for each n. Now notice that there exist some i and a subsequence {y_n} of {x_n} satisfying y_n∈S_i for each n. But then we have

, which is impossible. This shows that f is continuous.

The following result presents an extremely simple characterization of piecewise linear functions.

THEOREM 4.5. A continuous function

is piecewise linear if and only if there exist affine functions f₁, …, f_k such that for each x∈R^m there exists some 1≤i≤k satisfying f(x)=f_i(x).

Moreover, the set of components of f is a subcollection of the collection of affine functions {f₁, …, f_k}.

Proof. If f is piecewise linear, then the condition is trivially true. So, for the converse, assume that there exist affine functions f₁, …, f_k such that for each x∈R^m there exists some 1≤i≤k such that f(x)=f_i(x). We can assume that the affine functions f₁, …, f_k are distinct. We claim the following:

• For each nonempty open subset V of R^m there exists a nonempty open subset W of V and some 1≤i≤k such that f=f_i on W.

To see this, assume by way of contradiction that the claim is false. This implies that f≠f₁ on V, that is, f₁(v)≠f(v) for some v∈V. Since f and f₁ are continuous, there exists some nonempty open subset V₁ of V such that f₁(x) ≠f(x) for all x∈V₁. Similarly, since (by our hypothesis) f≠f₂ on V₁ there exists some nonempty open subset V₂ of V₁ such that f₂(x)≠f(x) for all x∈V₂. Continuing this way, we see that there exist nonempty open sets V_k⊆V_k−1⊆[sdot ][sdot ][sdot ]⊆V₁⊆V such that for each 1≤i≤k we have f_i(x)≠f(x) for all x∈V_i. But then for each x∈V_k we have f(x)≠f_i(x) for all 1≤i≤k, which is impossible, and our claim has been established.

Now for each 1≤i≤k let

. That is,

is the largest open set on which f=f_i. By the preceding discussion

for at least one i. (To see this take V=R^m and apply ([bull ]).) Deleting the

with

, we can assume that

for each i. Put

, and note that f=f_i on S_i. We shall verify that the closed sets S₁, …, S_k satisfy the conditions of Definition 4.2. Start by observing that condition (4) is obvious.

For (1) note that from

, we get that Int(S_i)≠[empty ] and that

. Moreover,

must be the case, since otherwise the maximality property of

will be violated. The condition

for i≠j should be obvious and the validity of (2) follows. If

, then by the above discussion there exists some nonempty open subset Q of

and some 1≤[ell ]≤k such that f=f_{[ell ]} on Q. But then the open set

violates the maximality property of

. Hence,

.

That the components of f are among the affine functions f₁, …, f_k should be obvious from the above discussion.

An immediate consequence of the preceding result is that PL is a Riesz subspace.

COROLLARY 4.6. The collection of all piecewise linear functions on R^m is a Riesz subspace of C(R^m). In particular,

.

Recall that an affine transformation from R^k to R^m is any function

of the form T(t)=At+b, where A is an m×k real matrix and b∈R^m is a fixed vector. Now if T is an affine transformation and

is an affine function, then the function

is also an affine function. To see this, assume that f is defined as f(x)=α+u·x and note that for each t∈R^k we have

This conclusion in connection with Theorem 4.5 yields the following result.

COROLLARY 4.7. If

is an arbitrary piecewise linear function and

is an affine transformation, then the function

is piecewise linear. Moreover, if f has the components f₁, …, f_p, then the components of f○T are among the affine functions f₁○T, …, f_p○T.

In particular, for any two fixed vectors a, b∈R^m the function

defined via the formula θ(t)=f(ta+(1−t)b), is (one-dimensional) piecewise linear.

A hyperplane of R^m is any subset of the form H={x∈R^m: a·x=α}, where a∈R^m is a nonzero vector and α∈R is a constant. Clearly, every hyperplane is a closed set and has Lebesgue measure zero. Notice that two affine functions

either do not agree at any point or the set that they agree is a hyperplane, that is, the set [f=g]={x∈R^m: f(x)=g(x)} is either empty or a hyperplane.

The boundaries of the regions of a piecewise linear function are parts of hyperplanes.

LEMMA 4.8. Let (S₁, f₁), …, (S_p, f_p) be the characteristic pairs of a piecewise linear function

. For each i let

and S_i∩S_j≠[empty ]}. Then the boundary of the region S_i has the following property:

In particular,

1. each boundary ∂S_i has Lebesgue measure zero and consists of, “parts” of hyperplanes, and
2. if x∈Int(S_i) for some i, then x∉S_j for all j≠i.

Proof. Let x∈∂S_i. Since

, there exists for each n some

such that

. It follows that for some j≠i we have x_n∈S_j for infinitely many n. This implies

and so x∈S_i∩S_j.

Now assume that x∈S_i∩S_j for some j≠i. If x∉∂S_i, then x∈Int(S_i) and so there exists some δ>0 such that B(x, δ)⊆Int(S_i). Since Int(S_i)∩Int(S_j)=[empty ], we infer that x∈∂S_j. From

, it follows that there exists some y∈Int(S_j) such that y∈B(x, δ). This implies y∈Int(S_i)∩Int(S_j), which is impossible. Consequently, x∈∂S_i, and the proof is finished.

The characteristic pairs of a piecewise linear function are uniquely determined.

LEMMA 4.9. The regions and the components of an arbitrary piecewise linear function

are uniquely determined in the following sense: If another collection of pairs {(S₁′, g₁), …, (S_q′, g_q)} satisfies properties (1)–(4) of Definition 4.2., then q=p and {(S₁′, g₁), (S₂′, g₂), …, (S_q′, g_q)} is a permutation of the collection of pairs {(S₁, f₁), (S₂, f₂), …, (S_p, f_p)}.

Proof. Fix some 1≤i≤p. Because Int(S_i) is nonempty (and hence it has positive Lebesgue measure), it follows from Lemma 4.8 that there exists some 1≤j≤q such that the open set V=Int(S_i) ∩ Int(S_j′) is nonempty. In particular, as f_i(x)=g_j(x)=f(x) holds true for each x∈V, it follows from part (2) of Lemma 4.1 that f_i=g_j.

Now let x∈Int(S_i). Fix δ>0 such that B(x, δ)⊆Int(S_i) and let 0<ε<δ. As above, B(x, ε)∩Int(S_r′)≠[empty ] must hold true for some index 1≤r≤q. But then (as above again) g_j=f_i=g_r must be the case. Because the affine functions g₁, …, g_q are all distinct, we infer that r=j. Therefore, B(x, ε)∩Int(S_j′)≠[empty ] for all 0<ε<δ. This implies

, and so Int(S_i)⊆S_j′. Consequently,

.

By the symmetry of the situation, there exists some 1≤m≤p such that S_j′⊆S_m. This implies Int(S_i)∩Int(S_m)=Int(S_i)≠[empty ], from which it follows that m=i. Therefore, S_i=S_j′ and so (S_i, f_i)=(S_j′, g_j). From the last result, the desired conclusion now easily follows.

Another consequence of Theorem 4.5 is that for real functions defined on R the definitions for piecewise linear functions given in Definitions 3.1 and 4.2 are equivalent.

COROLLARY 4.10. A function

is piecewise linear according to Definition 3.1 if and only if it is piecewise linear according to Definition 4.2.

Proof. Let

be a function. If f is piecewise linear according to Definition 3.1, then f is clearly piecewise linear according to Definition 4.2.

For the converse, assume that f is piecewise linear according to Definition 4.2. Let {(S₁, f₁), (S₂, f₂), …, (S_p, f_p)} be the collection of characteristic pairs of f. Notice that every f_i is of the form f_i(t)=m_it+b_i. So, every nonempty set of the form [f_i=f_j] is simply a point of R. This is connection with Lemma 4.8 shows that the boundary of each S_i is a finite set. Now each Int(S_i) is the union of an at most countable collection of pairwise disjoint open intervals. Because ∂S_i is a finite set, a moment's thought reveals that Int(S_i) is a union of a finite number of pairwise disjoint open intervals. From this it follows that S_i is the union of the closures of these intervals. Now it is easy to see that f is a piecewise linear function according to Definition 3.1.

In order to further study piecewise linear functions, we shall need the theory of arrangements of hyperplanes, which are well-studied combinatorial constructions that are closely related to vector lattices and the simplex methods in linear programming; see Chapter 4 of Björner, Las Vergnas, Sturmfels, White, and Ziegler (1999).

Recall once more that any subset of R^m of the form H={x∈R^m: a·x=α}, where a∈R^m is a nonzero fixed vector and α∈R is a constant, is called a hyperplane of R^m. We can assume without loss of generality that ‖a‖=1 and refer to a as a (unit) vector normal to H. Since H={x∈R^m:(−a)·x=−α}, we see that −a is also another (unit) normal vector to H. In other words, H has essentially two unit normal vectors, each of which defines an orientation in the sense that it divides R^m into three parts: a “positive” part {x∈R^m: a·x>α}, a “zero” part {x∈R^m: a·x=α}, and a “negative” part {x∈R^m: a·x<α}. Of course, if we let H={x∈R^m:(−a)·x=−α}, then the orientation changes: the positive part is now negative and the negative part is positive. Thus, writing H in the form H={x∈R^m: a·x=α}, the vector a defines automatically an orientation, and H is called an oriented hyperplane.

Now let E be a finite index set and let (H_e)_e∈E, where H_e={x∈R^m: a_e·x=α_e}, be a family of (oriented) hyperplanes in R^m. The family (H_e)_e∈E, is called an oriented arrangement of hyperplanes (or simply an arrangement). Every arrangement of hyperplanes (H_e)_e∈E “almost” subdivides R^m into a finite number of nonempty convex regions. The subdivisions are obtained by means of the “sign” mapping x[map ]σ_x, from R^m to {+, −, 0}^E, that is defined by

that is, σ_x=(Sign(a_e·x−α_e))_e∈E. Let

denote the range of the function σ, that is,

.

A vector

satisfying T(e)≠0 for all e∈E is called a tope of

. Note that σ_x is a tope if and only if

. Let T₁, T₂…, T_J be an enumeration of the topes of

. For each 1≤h≤J let

Obviously, each K_h is a nonempty, open, and convex set. Moreover, from the identity

, we see that

. The sets K₁, K₂, …, K_J are called the cells induced by the arrangement of the hyperplanes (H_e)_e∈E. It should not be difficult to see that the collection of cells {K₁, K₂, …, K_J} is independent of the orientation of the planes H_e, and so we can refer to {K₁, K₂, …, K_J} as the collection of cells generated (or induced) by the family of hyperplanes (H_e)_e∈E. For an example of an arrangement of hyperplanes, see Figure 4.

An arrangement of four oriented hyperplanes in R2.

Now let {f₁, …, f_p}, where p≥2, be a collection of distinct affine functions on R^m. If for each 1≤i<j≤p we let H_i,j=[f_i=f_j], then the set

is a finite set. Letting H_e=[f_i=f_j]={x∈R^m: a_e·x=α_e} for each e=(i, j)∈E, we see that the family (H_e)_e∈E is an arrangement of hyperplanes, called an arrangement generated by {f₁, …, f_p}. The collection of cells generated by (H_e)_e∈E is called the collection of cells generated (or induced) by {f₁, …, f_p}.

With this terminology at hand, we are now ready to state several extra properties of piecewise linear functions.

LEMMA 4.11. Let F={f₁, …, f_k} be a finite collection of distinct affine functions of R^m and let {K₁, K₂, …, K_J} be the collection of cells induced by F. Assume also that

is a continuous function such that for each x∈R^m there exists some 1≤i≤k satisfying f(x)=f_i(x).⁴

1. If f(x)=f_i(x), then f(y)=f_i(y) for all y∈K_h.
2. If f(x)>f_i(x), then f(y)>f_i(y) for all y∈K_h.
3. If f(x)<f_i(x), then f(y)<f_i(y) for all y∈K_h.

Moreover, for each 1≤h≤J there is a unique 1≤i_h≤k with

on K_h.

Proof. We shall prove (1) first. To this end, suppose that some x∈K_h satisfies f(x)=f_i(x).

Let

and note that X is an open dense subset of R^m. Notice that for each z∈X any pair of distinct functions f_i, f_j∈F we have

. So for each z∈X there exists a unique 1≤i_z≤k such that

. Because f and the f_i are continuous functions and

for each j≠i_z, there exists an open neighborhood N_z⊆X of z such that for each y∈N_z and all j≠i_z we have f(y)≠f_j(y) and

. This implies that for each y∈N_z we have

, that is, i_y=i_z.

Now fix y∈K_h. Let L(x, y) be the line segment joining x and y and notice that L(x, y)⊆K_h as K_h is convex. Because L(x, y) is compact, there exists a finite set Z={z₁, …, z_r}⊆L(x, y) such that

. We can assume that the neighborhoods {N_z: z∈Z} form a chain, that is,

for each t=1, …, r−1; see (Abramovich and Aliprantis, 2002b, Problem {1.5.7}, p. {50}). This easily implies that for each z∈L(x, y) we have

. In particular, i_x=i_y.

Therefore, we have shown that for each K_h there exists a unique index 1≤i_h≤k such that y∈K_h implies

. This proves (1) and the last part of the lemma.

To establish (2), assume that f(x)>f_i(x) holds true for some x∈K_h and that some other y∈K_h satisfies f(y)≤f_i(y). If f(y)=f_i(y), then according to (1) we must have f(x)=f_i(x), which is impossible. If f(y)<f_i(y), then there exists some z in the line segment joining x and y (and hence z∈K_h) satisfying f(z)=f_i(z). But then (according to (1) again) we get f(x)=f_i(x), a contradiction. This establishes (2) and the validity of (3) can be proven in a similar fashion.

From Theorem 4.5 we know that if for a continuous function

and affine functions f₁, …, f_k for each x∈R^m there exists some 1≤i≤k satisfying f(x)=f_i(x), then f is piecewise linear. The next result constructs the characteristic pairs of such a piecewise linear function from a given collection of affine functions.

THEOREM 4.12. Assume that a continuous function

and a finite set of distinct affine functions F={f₁, …, f_k} are such that for each x∈R^m there exists some 1≤i≤k satisfying f(x)=f_i(x). Let {K₁, K₂, …, K_J} be the cells generated by F. For each 1≤i≤k let

and then define

. We have the following.

1. If
   is the family of nonempty E_i, then the family
   is precisely the family of characteristic pairs of the piecewise linear function f.
2. For each 1≤h≤J there exists exactly one
   such that K_h⊆Int(S_i).
3. For each
   the nonempty set Int(S_i) is a union of a finite collection of pairwise disjoint nonempty open and connected subsets of R^m.

Proof. (a) We know from Theorem 4.5 that the function f is piecewise linear whose components are among the f₁, …, f_k. The proof here will present also an alternate constructive proof of Theorem 4.5. Let {K₁, …, K_J} be the collection of cells generated by F and for each 1≤i≤k define E_i and S_i as in the statement of the lemma.

According to Lemma 4.11 at least one of the E_i is nonempty; relabeling, we can assume that E₁, …, E_p are the nonempty E_i, that is,

. Clearly, f=f_i on S_i. Because the affine functions f₁, …, f_k are distinct, it follows from part (2) of Lemma 4.1 that E_r∩E_s=[empty ] for r≠s and from Lemma 4.11 we see that

. The latter yields

Next notice that because for each 1≤i≤p we have

, it follows, on one hand, that Int(S_i)≠[empty ] and, on the other hand, that

. Moreover, using part (2) of Lemma 4.1, it is easy to see that Int(S_r)∩Int(S_s)=[empty ] for r≠s. Because f=f_i holds true for each 1≤i≤p, it follows from Definition 4.2 that f is a piecewise linear function with characteristic pairs (S₁, f₁), …, (S_p, f_p).

(b) Now let 1≤h≤J. According to Lemma 4.11 there exists a unique 1≤i_h≤k such that

on K_h. This implies that

and

.

(c) Observe that for each

every component of Int(S_i), that is, every maximal (with respect to ⊇) nonempty and connected subset of Int(S_i), is open. Now notice that every K_h⊆Int(S_i) is open and connected (as being a convex set) and so is included in some component of Int(S_i). Moreover, from the definition of S_i, it is not difficult to see that every component of Int(S_i) includes some K_h. Thus, the number of components of Int(S_i) is at most J, and the proof is finished.

To continue our study, we need one more property of piecewise linear functions.

LEMMA 4.13 [Ovchinnikov (2002)]. If

is a piecewise linear function with components f₁, …, f_p, then for any pair a, b∈R^m there exists a component f_i of f satisfying f_i(a)≤f(a) and f_i(b)≥f(b).

Proof. Fix a, b∈R^m and consider the continuous function

defined via the formula by g(t)=f[tb+(1−t)a[. By Corollary 4.7, g is a one-dimensional piecewise linear function whose components are among the affine functions g₁, g₂, …, g_p, where g_i(t)=f_i(tb+(1−t)a). Consider g restricted to [0, 1] and then use Lemma 3.2 in conjunction with Corollary 3.7 to see that there exists a component g_i satisfying f(a)=g(0)≥g_i(0)=f_i(a) and f(b)=g(1)≤g_i(1)=f_i(b).

The next result presents the basic structural properties of piecewise linear functions. Its proof is based on the discussion by Ovchinnikov on the referees' comments concerning his paper Ovchinnikov (2002).

THEOREM 4.14. Assume that

is a piecewise linear function with characteristic pairs {(S₁, f₁), …, (S_p, f_p)} and let {K₁, K₂, …, K_J} be the set of cells induced by {f₁, …, f_p}.

1. If for each h we pick x_h∈K_h and let E_h={i∈{1, …, p}: f_i(x_h)≥f(x_h)}, then E_h is nonempty and
   
   In particular, f∈{f₁, f₂, …, f_p}^∨∧.
2. If J* is the subset of {1, …, J} having the property that for each 1≤h≤J there exists a j∈J* such that E_j⊆E_h, then we have
   

Proof. (1) For each 1≤h≤J fix some x_h∈K_h and then use Theorem 4.12 to choose some 1≤j≤p such that K_h⊆Int(S_j). Clearly, f_j(x_h)=f(x_h). This implies that if for each 1≤h≤J we let

then, on the one hand, E_h≠[empty ] and, on the other hand, a glance at Lemma 4.11 guarantees that for each i∈E_h and each y∈K_h we have f_i(y)≥f(y). Now for each 1≤h≤J consider the function

and note that F_h(y)≥f(y) for each y∈K_h. Because for some j∈E_h we have f_j(x_h)=f(x_h), it follows from Lemma 4.11 that f_j(y)=f(y) for all y∈K_h. Thus, F_h(y)=f(y) for all y∈K_h.

Next, fix y∈R^m. For each 1≤h≤J there exists (according to Lemma 4.13) some f_j satisfying f_j(y)≤f(y) and f_j(x_h)≥f(x_h). In particular, it follows that we have j∈E_h and consequently

for all 1≤h≤J. This implies

for all y∈R^m.

On the other hand, because for each x∈K_h we have F_h(x)=f(x), it must be the case that

on

. Because

is dense in R^m and

and f are both continuous functions, it follows that

holds true on R^m.

(2) To establish this identity, note first that if E_j⊆E_h, then

. This implies

for each 1≤h≤J, and consequently we have

, and the proof is finished.

Combining Corollary 4.6 and Theorem 4.14 we are now ready to state the fundamental result for this work.

THEOREM 4.15. The vector space PL of all piecewise linear functions is a vector sublattice of the Riesz space C(R^m) and coincides with

that is,

.

In other words, PL is precisely the Riesz subspace of C(R^m) generated by the (m+1)-dimensional vector subspace Aff of all affine functions.

The next example reported in Ovchinnikov (2002) shows that piecewise polynomial functions need not admit a sup-inf representation.

Example 4.16. Define the piecewise quadratic function

as follows:

Notice that x²∨0=x² and x²∧0=0.

Noting that the set {f₁, f₂, …, f_p}^∨∧ is finite, Theorem 4.15 yields also the following.

COROLLARY 4.17. If F={f₁, f₂, …, f_p} is a finite set of affine functions on R^m, then a function f∈C(R^m) is piecewise linear with components in F if and only if f belongs to the finite set F^∨∧.

Theorem 4.14 also provides an algorithm for constructing the sup-inf representation of a piecewise linear function with components f₁, f₂, …, f_p and unknown regions. The next example is a rudimentary algorithm illustrating this.

Example 4.18 (From f, f₁, f₂, …, f_p to

).}\,\, Take

with components f₁, f₂, …, f_p. Following Theorem 4.14 the function f can be reconstructed using the following step:

Step I: Determine E={(i, j): 1≤i<j≤p and [f_i=f_j]≠[empty ]} and then for each e=(i, j)∈E pick α_e∈R and a_e∈R^m such that

Step II: Using the hyperplane arrangement (H_e)_e∈E determine the cells K₁, …, K_J.

Step III: For each h=1, 2, …, J choose some x_h from the cell K_h.

Step IV: For each

determine E_h={i∈{1, …, p}f_i(x_h)≥f(x_h)}.

Step V: Select a “minimal” set J*⊆{1, 2, …, J} so that it satisfies property (2) of Theorem 4.14. Then we have

This procedure gives a desired sup-inf representation of f.

The next example illustrates the preceding algorithm. It also shows how in applying this algorithm, we can restrict our attention to a closed convex domain with nonempty interior.

Example 4.19. Consider once again Example 4.3 but with the restricted domain shown in Figure 5. Take the four affine components of the function f:

These four affine functions induce eight cells. They are the eight regions of the oriented arrangement in Step I of the algorithm of Example 4.18 and they are depicted in Figure 5.

The eight regions of the oriented arrangement.

Notice that E₁={1, 2, 3}, E₂={1, 2, 3}, E₃=E₄=E₅=E₆=E₇=E₈={3, 4}. Therefore, if we take J*={1, 3}, then we can write

Because we have restricted the domain, we can now write f=(f₃∧f₄)∨(f₁∧f₂); compare Figures 3 and 6.

The graphs of f1∧f2 andf3∧f4.

A rudimentary algorithm for computing the regions of the functions in

by means of Theorem 4.12 is presented next.

Example 4.20 (From

to PL). Take f∈{f₁, f₂, …, f_p}^∨∧, where as usual f₁, f₂, …, f_p are affine functions on

. Following Theorem 4.12 the regions of the function f can be obtained using the following steps:

1. Step I: Determine E={(i, j): 1≤i<j≤p and [f_i=f_j]≠[empty ]} and for each e=(i, j)∈E and then pick α_e∈R and a_e∈R^m such that H_e={x∈R^m: a_e·x=α_e}=[f_i=f_j].
2. Step II: Use the hyperplane arrangement (H_e)_e∈E to determine the cells K₁, …, K_J.
3. Step III: For each h=1, 2, …, J choose some x_h∈K_h and then let
   
4. Step IV: For each h=1, 2, …, J determine the set I_h={j∈{1, …, J}: i_j=i_h}.
5. Step V: For each h=1, 2, …, J let
   .

The characteristic pairs of the piecewise linear function f are distinct members of the family

.