Published online by Cambridge University Press: 01 September 2004
This paper uses daily observations for the Canadian dollar–U.S. dollar exchange rate over the recent flexible exchange-rate period (from January 2, 1974, to October 28, 2002), and various tests from dynamical systems theory, such as a chaos test, a self-organized criticality test, and a threshold effects test, to support a stochastic nonlinear origin for the series.
Interest in nonlinear processes has, in the recent past, experienced a tremendous rate of development, and the literature is still growing. One type of nonlinear process is chaos. Chaos is interesting because of its ability to generate output that mimics the output of stochastic systems, thereby offering an alternative explanation for the behavior of economic variables. In addition, chaos offers the potential for management and control, although doing so might require considerable expansion in regulatory policy instruments. Another type of nonlinear process is self-organized criticality, recently discovered in physics. Self-organized criticality is a probabilistic process. It incorporates a dominant long-run trend toward greater sensitivity and a short-run catastrophic element, which is triggered by random shocks within the system. Unlike a chaotic system, however, prediction and control in a self-organized critical system is almost impossible, and the best way to control the system is by manipulating its rules, rather than by managing its outcomes.
The subject of this paper is to contrast the apparent random-walk behavior of the nominal exchange rate between Canada and the United States with nonlinear dynamics, and to identify the nonlinear process that most affects the exchange rate. The paper is organized as follows. In the next section, we investigate the univariate time-series properties of the Can$US$ nominal exchange-rate series. Section 3 tests for deterministic chaos using the Nychka et al. (1992) Lyapunov exponent estimator and its limit distribution. In Section 4, we test for self-organized criticality, and in Section 5, for threshold effects. The final section provides a brief summary and conclusion.
We test for stochastic trends (unit roots) in the autoregressive representation of the logged Canadian dollar per U.S. dollar nominal exchange rate, over the period from January 2, 1974, to October 28, 2002, using four alternative testing procedures, to deal with anomalies that arise when the data are not very informative about whether or not there is a unit root. In particular, in the first three columns of panel A of Table 1, we report p-values [based on the response surface estimates given by MacKinnon (1994)] for the augmented weighted symmetric (WS) unit root test [see Pantula et al. (1994)], the augmented Dickey–Fuller (ADF) test [see Dickey and Fuller (1981)], and the nonparametric
test of Phillips (1987) and Phillips and Perron (1988). Moreover, given that unit root tests have low power against relevant alternatives, in the last two columns of panel A of Table 1, we present Kwiatkowski et al. (1992) tests, known as KPSS tests, for level and trend stationarity.

As can be seen, the null hypothesis of a unit root can be rejected. Moreover, the t-statistic
that tests the null hypothesis of level stationarity is large relative to the 5% critical value of 0.463 given by Kwiatkowski et al. (1992) and the t-statistic
that tests whether the null hypothesis of trend stationarity exceeds the 5% critical value of 0.146 (also given by Kwiatkowski et al.). Combining the results of our tests of the stationarity hypothesis with the results of our tests of the unit root hypothesis, we conclude that the (logged) nominal exchange-rate series has at least one unit root.
The null hypothesis of a second unit root is also tested in panel B of Table 1, using the same four testing procedures. Clearly, the nominal exchange-rate series appears to be stationary in the logarithmic first differences, since the null hypothesis of a unit root is rejected and the null hypotheses of level and trend stationarity cannot be rejected. Hence, in what follows, we use the the logarithmic first difference of the nominal exchange rate.
In this section, we contrast the apparent random-walk behavior of the nominal exchange rate with nonlinear chaotic dynamics. In doing so, we follow the recent contributions by Whang and Linton (1999) and Linton and Shintani (2003) and construct the standard error for the Nychka et al. (1992) dominant Lyapunov exponent for the logged first difference of the Canadian dollar exchange-rate series, thereby providing a statistical test for chaos. We also follow Shintani and Linton (2003) and Serletis and Shintani (2003) and report both global and local Lyapunov exponents. As argued by Bailey (1996), local Lyapunov exponents provide a more detailed description of the system's dynamics, in the sense that they can identify differences in short-term predictability among regions in the state space.
Let {Xt}Tt=1 be a random scalar sequence generated by the following nonlinear autoregressive model:

where θ:Rm→R is a nonlinear dynamic map and {ut}Tt=1 is a random sequence of i.i.d. disturbances with E(ut)=0 and E(u2t)=σ2<∞. We also assume θ to satisfy a smoothness condition, and Zt=(Xt, …, Xt−m+1)′∈Rm to be strictly stationary and to satisfy a class of mixing conditions; see Whang and Linton (1999) and Shintani and Linton (2003) for details regarding these conditions.
Let us express the model (1) in terms of a map,
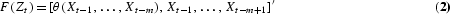
with Ut=(ut, 0, …, 0)′ such that
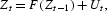
and let Jt be the Jacobian of the map F in (2) evaluated at Zt. Then, the dominant Lyapunov exponent of system (1) is defined by

where
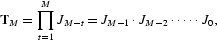
and νi(A) is the ith largest eigenvalue of a matrix A. Necessary conditions for the existence of the Lyapunov exponent are available in the literature. Usually, if max{ln ν1(J′tJt), 0} has a finite first moment with respect to the distribution of Zt, then the limit in (3) almost surely exists and will be a constant, irrespective of the initial condition.
To obtain the Lyapunov exponent from observational data, Eckmann and Ruelle (1985) and Eckmann et al. (1986) proposed a method based on nonparametric regression, which is known as the Jacobian method. The basic idea of the Jacobian method is to substitute θ in the Jacobian formula by its nonparametric estimator
. In other words, it is the sample analogue estimator of (3). Note that we distinguish between the “sample size” t used for estimating the Jacobian
and the “block length” M, which is the number of evaluation points used for estimating the Lyapunov exponent. Formally, the Lyapunov exponent estimator of λ can be obtained by
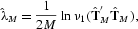
where
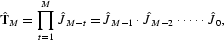
and
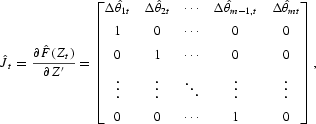
for t=0, 1, …, M−1, and
for j=1, …, m in which ej=(0, …, 1, …, 0)′∈Rm denotes the jth elementary vector.
Using the argument of Whang and Linton (1999), Shintani and Linton (2003) showed that under some reasonable condition, the neural network estimator
is asymptotically normal and its standard error can be obtained using
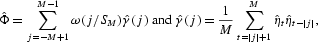
where
, with
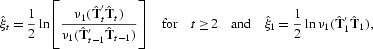
where ω(·) and SM denote a kernel function and a lag truncation parameter, respectively. Note that the standard error is essentially the heteroskedasticity and autocorrelation covariance estimator of Andrews (1991) applied to
. We employ the QS kernel for ω(·) with SM selected by the optimal bandwidth selection method recommended by Andrews.
Lyapunov exponent point estimates along with their t-statistics (in parentheses) are displayed in Table 2. The results are presented for dimensions 1 through 6, with the optimal value of the number of hidden units (k) in the neural net being chosen by minimizing the BIC criterion. The p-values for the null hypothesis H0:λ[ges ]0 are reported in brackets. The Full column under each value of k shows the estimated largest Lyapunov exponent using the full sample. The Block column shows median values for the block estimation, with the number of blocks (B) being set equal to 8.

In general, the reported Lyapunov exponent point estimates are negative and in every case we reject the null hypothesis of chaotic behavior. Of course, the estimates depend on the choice of the dimension parameter, m. As m increases, the Lyapunov exponent point estimates increase in value. However, the presence of dynamic noise makes it difficult and perhaps impossible to distinguish between (noisy) high-dimensional chaos and pure randomness. For this reason, as in Serletis and Shintani (2003), we do not pursue the investigation of high-dimensional chaos in the present paper.
As already noted in the introduction, another type of nonlinear process is self-organized criticality, recently discovered in physics by Bak et al. (1987). As Bak et al. (1988, p. 364) put it “[t]he temporal ‘fingerprint’ of the self-organized critical state is the presence of flicker noise or 1/f noise.”
Since noise can be classified according to its power spectrum (a decomposition of the series into components with different frequencies by their contribution to the variance), in this section we calculate the power spectrum of the logged nominal exchange-rate series. We follow Li (1991) and calculate the power spectrum P(f), using the following discrete Fourier transform:
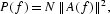
where ||A(f)|| is the module of the complex number
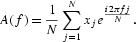
The power spectrum P(f) can be modeled as a power-law function, P(f)=1/fα, where f is the frequency and α is a characteristic exponent. When plotted on a log-log scale, power laws appear as straight lines, since log [P(f)]=−αlog(f) where −α is the slope. The power law indicates that there is “scale invariance,” in the sense that no particular frequency is singled out and that the properties of any given frequency stand for all frequencies. If α=0, the series is white noise and the power spectrum is flat. If α=2, the time series is called 1/f2 noise. A random-walk series (the best-known nonstationary series) is exactly 1/f2 noise—see Li (1991). If α=1, the series is called 1/f noise or flicker noise.
We present the power spectrum of the logarithmic first difference of the nominal exchange rate in Figure 1. A least-squares, best-fit line to all spectral components indicates behavior of the type 1/fα, where α=0.36. This behavior is consistent with the evidence reported in the preceding two sections.

Power spectrum.
A synthesis of the linear econometric approach with the nonlinear disequilibrium approach to economic fluctuations has recently been provided by a class of nonlinear time-series models known as switching regression or threshold autoregressive (TAR) models; see Tong (1990) for a review of such models. These models involve interesting nonlinearities, with switches in parameter values according to the region in which the recent past of the series lies. Moreover, the fact that the switching (transition) variable is a lag of the dependent variable makes these models capable of characterizing different forms of asymmetric behavior.
In this section, we explore the presence of such nonlinearities in the exchange rate using the most popular TAR model, the self-exciting threshold autoregressive (SETAR) model. A two-regime version of this model for the logarithmic first difference of the nominal exchange rate can be written as

where p≥1 is the autoregressive order (or delay parameter) and κ is the threshold parameter. According to (4), xt is generated by one of two distinct autoregressive models, depending on the level of one lagged variable, xt–d; the model could be generalized to depend on the levels of more than one lagged variable and/or to have more than two distinct regimes.
Following Potter (1995) and Hansen (1996), we estimated the model using least squares, allowing the threshold parameter to vary from the 15th to the 85th percentile of the empirical distribution of xt and the delay parameter from 1 to 5. Our estimates are
,
, and (with heteroskedastic-consistent standard errors in parentheses):
Regime A. xt−4[les ]−0.20474:
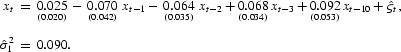
Regime B. xt−4>−0.20474:
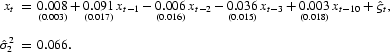
We test the null hypothesis of no threshold effect (single regime), using the LM-based test statistics used by Hansen (1996), and report the results in Table 3 (with p-values in parentheses).

Clearly, the null hypothesis of no threshold effect (single regime) is rejected, at conventional significance levels, providing evidence in favor of SETAR nonlinearity in the Can$/US$ nominal exchange rate.
We have used daily observations for the Canadian dollar–U.S. dollar nominal exchange rate, over the recent flexible exchange-rate period, and applied tests from dynamical systems theory to distinguish between deterministic and stochastic origin for the series. We have found evidence consistent with a threshold autoregressive-type nonlinearity in the exchange rate, suggesting that successful stochastic nonlinear modeling of the exchange rate would produce a richer notion of exchange-rate fluctuations than linear time-series models allow. We leave this for further research.
We would like to thank Mototsugu Shintani and Doug Nychka for help with the computer programs. Serletis also gratefully acknowledges financial support from the Social Sciences and Humanities Research Council of Canada.

Unit root and stationarity testsa

Lyapunov exponent estimatesa
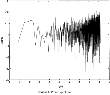
Power spectrum.

Tests for threshold effects