A prime sieve is an algorithm that finds the primes up to a bound  $n$. We say that a prime sieve is incremental, if it can quickly determine if
$n$. We say that a prime sieve is incremental, if it can quickly determine if 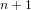 $n+1$ is prime after having found all primes up to
$n+1$ is prime after having found all primes up to  $n$. We say a sieve is compact if it uses roughly
$n$. We say a sieve is compact if it uses roughly 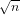 $\sqrt{n}$ space or less. In this paper, we present two new results.
$\sqrt{n}$ space or less. In this paper, we present two new results.
–We describe the rolling sieve, a practical, incremental prime sieve that takes 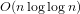 $O(n\log \log n)$ time and
$O(n\log \log n)$ time and 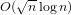 $O(\sqrt{n}\log n)$ bits of space.
$O(\sqrt{n}\log n)$ bits of space.
–We also show how to modify the sieve of Atkin and Bernstein from 2004 to obtain a sieve that is simultaneously sublinear, compact, and incremental.
The second result solves an open problem given by Paul Pritchard in 1994.
 $X_{0}(n)$ and isogenies of elliptic curves over quadratic fields
$X_{0}(n)$ and isogenies of elliptic curves over quadratic fields
 $\text{PSL}_{2}(13)$ in the Monster contains
$\text{PSL}_{2}(13)$ in the Monster contains  $13A$-elements
$13A$-elements
 ${\it\lambda}$-invariants attached to cyclic cubic number fields
${\it\lambda}$-invariants attached to cyclic cubic number fields