1. INTRODUCTION
Plasma diagnostics using electromagnetic probes (Hutchinson, Reference Hutchinson1987) has been successful to characterize a great variety of states of matter relevant for, e.g., fusion research or technical applications. Recent developements of spatially and or temporally coherent sources of intense short wavelength radiation in the X-ray-ultraviolet (XUV) and soft X-ray regime (Ackermann et al., Reference Ackermann, Asova, Ayvazyan, Azima, Baboi, Bähr, Balandin, Beutner, Brandt, Bolzmann, Brinkmann, Brovko, Castellano, Castro, Catani, Chiadroni, Choroba, Cianchi, Costello, Cubaynes, Dardis, Decking, Delsim-Hashemi, Delserieys, Pirro, Dohlus, Düsterer, Eckhardt, Edwards, Faatz, Feldhaus, Flöttmann, Frisch, Fröhlich, Garvey, Gensch, Gerth, Görler, Golubeva, Grabosch, Grecki, Grimm, Hahn, Han, Honkavaara, Hott, Hüning, Ivanisenko, Jaeschke, Jalmuzna, Jezynski, Kammering, Katalev, Kavanagh, Kennedy, Khodyachykh, Klose, Kocharyan, Körfer, Kollewe, Koprek, Korepanov, Kostin, Krassilnikov, Kube, Kuhlmann, Lewis, Lilje, Limberg, Lipka, Löhl, Luna, Luong, Martins, Meyer, Michelato, Miltchev, Möller, Monaco, Müller, Napieralski, Napoly, Nicolosi, Nölle, Nuñez, Oppelt, Pagani, Paparella, Pchalek, Pedregosa-Gutierrez, Petersen, Petrosyan, Petrosyan, Petrosyan, Pflüger, Plönjes, Poletto, Pozniak, Prat, Proch, Pucyk, Radcliffe, Redlin, Rehlich, Richter, Roehrs, Roensch, Romaniuk, Ross, Rossbach, Rybnikov, Sachwitz, Saldin, Sandner, Schlarb, Schmidt, Schmitz, Schmüser, Schneider, Schneidmiller, Schnepp, Schreiber, Seidel, Sertore, Shabunov, Simon, Simrock, Sombrowski, Sorokin, Spanknebel, Spesyvtsev, Staykov, Steffen, Stephan, Stulle, Thom, Tiedtke, Tischer, Toleikis, Treusch, Trines, Tsakov, Vogel, Weiland, Weise, Wellhöfer, Wendt, Will, Winter, Wittenburg, Wurth, Yeates, Yurkov, Zagorodnov and Zapfe2007; Landen et al., Reference Landen, Glenzer, Edwards, Lee, Collins, Cauble, Hsing and Hammel2001; Lee et al., Reference Lee, Baldis, Cauble, Landen, Wark, Ng, Rose, Lewis, Riley, Gauthier and Audebert2003a) allow for the application of spectroscopy (Zastrau et al., Reference Zastrau, Fortmann, Fäustlin, Cao, Döppner, Glenzer, Gregori, Laarmann, Lee, Przystawik, Radcliffe, Reinholz, Röpke, Thiele, Tiggesbäumker, Truong, Toleikis, Uschmann, Wierling, Tschentscher, Förster and Redmer2008) and scattering techniques (Glenzer et al., Reference Glenzer, Gregori, Lee, Rogers, Pollaine and Landen2003; Riley et al., Reference Riley, Khattak, Garcia Saiz, Gregori, Bandyopadhyay, Notley, Neely, Chambers, Moore and Comley2007) also in the field of warm dense matter (WDM) (Riley et al., Reference Riley, Weaver, McSherry, Dunne, Neely, Notley and Nardi2002; Lee et al., Reference Lee, Moon, Chung, Rozmus, Baldis, Gregori, Cauble, Landen, Wark, Ng, Rose, Lewis, Riley, Gauthier and Audebert2003b). Thereby we refer to states of matter at densities ranging from slightly below condensed matter to electron densities n e corresponding to several times the solid densities, i.e., compressed matter, and temperatures T of several eV.
At those conditions, optical lasers, the traditional “working-horse” of plasma spectroscopy and plasma scattering, cannot be used in WDM related experiments due to the short critical wavelength 
, where 
is the electronic plasma frequency. For instance, at electron densities of n e = 1023 cm−3, the critical wavelength is λcrit ≃ 100 nm, i.e., radiation of longer wavelength is reflected at the surface, only photons of shorter wavelength can penetrate the medium and probe the inner layers of the plasma. Recently, collective Thomson scattering on solid density targets using few keV X-ray sources has been demonstrated (Glenzer et al., Reference Glenzer, Landen, Neumayer, Lee, Widmann, Pollaine, Wallace, Gregori, Höll, Bornath, Thiele, Schwarz, Kraeft and Redmer2007; Kritcher et al., Reference Kritcher, Neumayer, Castor, Döppner, Falcone, Landen, Lee, Lee, Morse, Ng, Pollaine, Price and Glenzer2008; Garcia Saiz et al., Reference Garcia Saiz, Gregori, Gericke, Vorberger, Barbrel, Clarke, Freeman, Glenzer, Khattak, Koenig, Landen, Neely, Neumayer, Notley, Pelka, Price, Roth, Schollmeier, Spindloe, Weber, van Woerkom, Wunsch and Riley2008). A similar experiment, using the free electron laser facility FLASH at DESY, Hamburg, to scatter from solid density kryogenic hydrogen, was designed by Höll et al. (Reference Höll, Bornath, Cao, Döppner, Düsterer, Förster, Fortmann, Glenzer, Gregori, Laarmann, Meiwes-Broer, Przystawik, Radcliffe, Redmer, Reinholz, Röpke, Thiele, Tiggesbumker, Toleikis, Truong, Tschentscher, Uschmann and Zastrau2007), see also Cao et al. (Reference Cao, Uschmann, Zamponi, Kämmpfer, Fuhrmann, Förster, Höll, Redmer, Toleikis, Tschentscher and Glenzer2007) for the same setup using a PMMA target.
Under WDM conditions, the plasma coupling parameter
i.e., the ratio of correlation (Coulomb) energy to kinetic energy, as well as the degeneracy parameter
are close to unity; 
is the electronic Fermi energy. This means that the system can neither be described as an ideal, classical plasma, neglecting the interaction among particles, nor as an ideal quantum gas at zero temperature. Both particle interactions and strong correlations as well as partial quantum degeneracy have to be accounted for in theoretical models for WDM.
Besides state-of-the-art computer simulation methods based on, e.g., finite-temperature density functional theory (Holst et al., Reference Holst, Redmer and Desjarlais2008) or Quantum Monte Carlo techniques (Militzer & Pollock, Reference Militzer and Pollock2005), analytical approaches to WDM are indispensable. They provide benchmark calculations for the purely numerical methods and allow to treat also regions of the parameter space not accessible by numerical methods, such as lower densities or high temperatures (classical, weakly coupled plasmas), or very high densities and low temperatures (completely degenerate systems).
In this article, we elaborate an analytical approach to the dynamical structure factor, which is the central quantity in determining the Thomson scattering spectrum from a correlated plasma. By using the Born-Mermin ansatz for the contributions from free electrons to the scattering spectrum, we go beyond the widely used random phase approximation (see Gregori et al., Reference Gregori, Glenzer, Rozmus, Lee and Landen2003). The aim is to present a closed set of formulae that allow the quick and reliable calculation of Thomson scattering spectra as a function of the transfer wavenumber k and the transfer energy 
which depend on the plasma parameters density, temperature, and ionization stage as well as the photon energy of the probe and the scattering angle. The approach is valid for classical, non-degenerate plasmas as well as for moderately degenerate plasmas, where 0.1 < θ < 1. Thus, it can be applied to scattering from classical, weakly coupled plasmas, WDM, as well as from cold targets (metals). For example, a system being transferred from a condensed matter state at low temperatures and high densities to WDM conditions by, e.g., interaction with intense, short pulse laser radiation, and being probed by Thomson scattering at various times of its evolution (Kritcher et al., Reference Kritcher, Neumayer, Castor, Döppner, Falcone, Landen, Lee, Lee, Morse, Ng, Pollaine, Price and Glenzer2008) can be described within a common, unified approach.
A central issue is in this context how collisions among the different particles and their impact on the scattering spectrum can be described in a consistent way. This will be achieved via the Born-Mermin ansatz, which will be discussed in detail. It will be shown that collisions are most important in the regime of WDM. At much higher temperatures or lower densities (weakly coupled plasmas) as well as in the case of strongly degenerate systems near T = 0 K and at high densities, the collisionless theory is sufficient to describe the scattering spectrum (Thiele et al., Reference Thiele, Redmer, Reinholz and Röpke2006; Thiele, Reference Thiele2007).
For the sake of completeness, we should mention that inverse Thomson scattering has recently known increasing interest as a mechanism to generate short-wavelength coherent radiation by scattering optical laser radiation on a counterpropagating relativistic electron beam (Bessonov et al., Reference Bessonov, Gorbunkov, Ishkhanov, Kostryukov, Maslova, Shvedunov, Tunkin and Vinogradov2008; Kulagin et al., Reference Kulagin, Cherepenin, Hur, Lee and Suk2008). Pulses of X-ray radiation with 9 × 106 photons per pulse have been predicted, e.g., by Priebe et al. (Reference Priebe, Laundy, Macdonald, Diakun, Jamison, Jones, Holder, Smith, Phillips, Fell, Sheehy, Naumova, Sokolov, Ter-Avetisyan, Spohr, Krafft, Rosenzweig, Schramm, Grüner, Hirst, Collier, Chattopadhyay and Seddon2008), using this technique.
The work is organized as follows: After this introduction, the theory of Thomson scattering will be outlined. A thorough analysis of the scattering geometry is followed by the introduction of the dynamical structure factor, i.e., the density autocorrelation function that gives the scattering intensity in a many-particle system. Its high-frequency part, containing the scattering on collective plasma waves (plasmons), is tightly connected to the electronic density response function or dielectric function. In Section 3, the Born-Mermin approach for the dielectric function will be introduced, which allows to include collisions into the high-frequency part of the dynamic structure factor via the collision frequency. The collision frequency determines the width of the plasmon resonance in addition to Landau damping, which is described by the random phase approximation (RPA), i.e., the mean-field approximation, where collisions are neglected. Section 4 contains synthetic spectra for various experimental conditions. In particular, scattering of X-rays on solid density and compressed beryllium will be calculated as well as scattering of XUV free electron laser radiation on near solid density hydrogen. Section 5 contains a summary and the conclusions.
2. THEORY OF THOMSON SCATTERING AND DYNAMICAL STRUCTURE FACTOR
Consider the scattering of a plane electromagnetic wave moving along the z-axis of the reference frame with wavevector ki = k iez and frequency ωi and with its electric field vector oriented parallel to the x-axis (cf. Fig. 1), scattering on an electron. Classical eletrodynamics tells us that the electron will rescatter the incoming light into a solid angle dΩ with a differential scattering cross-section defined by the scattering angle ϑ and the azimuthal angle ϕ through
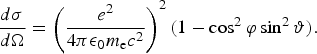
Note that the accurate treatment of this problem within the framework of quantum electrodynamics leads to the same result in the limit of small photon energies, i.e., 
. The total scattering cross-section, obtained after integration over the solid angle dΩ = sinϑdϑdϕ, yields the well-known Thomson cross-section
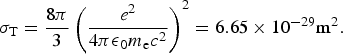
Besides the shift in the wavevector k, determined by the scattering geometry, also the frequency of the scattering wave is shifted due to the Doppler effect,
with the velocity of the electron v.
Fig. 1. Schematic view of the scattering geometry. The incoming wave, characterized by the wavevector ki and polarization plane (plane of the electric field vector Ei) is scattered into the direction of the detector, which fixes the direction of the final wavevector kf, k = kf − ki is the transfer wavevector, ϑ is the scattering angle, ϕ is the angle between the plane of polarization of the initial wave and the plane spanned by ki and kf.
The scattering from a many-particle system takes place on the density fluctuations. Thus, one needs to know the total electron density autocorrelation function 
to determine the scattering cross-section. By 〈…〉t, we denote the averaging over the equilibrium ensemble, i.e., the correlation function is independent of the time argument t. Its Fourier transform, the dynamical structure factor (DSF)
yields the scattering spectrum as function of the frequency shift and the transfer wavevector,
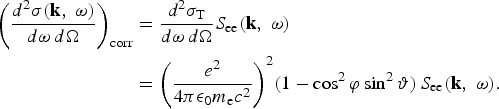
Due to the cos ϕ term in the scattering cross-section, the scattering most efficiently takes place into a plane that is perpendicular to the polarization plane of the incoming wave, i.e., for ϕ = 90°. For unpolarized light, the cross-section should be averaged over all initial polarizations, yielding
The DSF is a key quantity in many-particle theory, measuring the degree of correlation in the system. Besides the Doppler broadened single-particle spectrum, it also contains the collective excitations in the plasma, such as ion acoustic waves and longitudinal plasma oscillations (plasmons). The latter are visible in the scattering spectrum as inelastic contributions, shifted from the frequency of the incoming photon by roughly the plasma frequency ωpl,e. Ion acoustic waves, on the other hand, are not detectable in X-ray scattering spectra due to the finite probe and detector bandwidth and, thus, merge with the elastically scattered part of the spectrum.
In general, the scattering parameter
separates between collective and non-collective scattering. Here, the inverse Debye screening length 
was introduced. In the collective scattering regime, i.e., α > 1, the collective motion is detected, whereas in the non-collective scattering regime, small length scales are resolved, i.e., the scattering is sensitve to the individual particles.
Due to Eq. (8), Thomson scattering provides a mean to perform a direct measurement of the DSF; and thus to check concepts of many-particle theory in this strongly correlated regime. After integrating the DSF over its frequency argument, the static structure factor is obtained,
The latter is related to the well-known pair correlation function g ee(r), i.e.,
This relation allows for the comparison between analytical approaches to the DSF and molecular dynamics (MD) or quantum molecular dynamics (QMD) simulations of strongly correlated systems, which usually provide particle trajectories (orbitals) and thereby allow the determination of the pair correlation functions. Furthermore, the static structure factor is directly related to equation-of-state properties and thermodynamic functions. For instance, the isothermal compressibility of the electron subsystem 
is given by the value of the static structure factor at vanishing wavenumber, i.e. 
, where 
is the isothermal compressibility of the ideal gas.
Various approaches exist to determine the DSF in correlated systems. Among these are analytical techniques, based on many-body perturbation theory (Mahan, Reference Mahan1981) and linear response theory (Zubarev et al., Reference Zubarev, Morozov and Röpke1996). In this article, we apply the Born-Mermin approach (Redmer et al., Reference Redmer, Reinholz, Röpke, Thiele and Höll2005; Höll et al., Reference Höll, Bornath, Cao, Döppner, Düsterer, Förster, Fortmann, Glenzer, Gregori, Laarmann, Meiwes-Broer, Przystawik, Radcliffe, Redmer, Reinholz, Röpke, Thiele, Tiggesbumker, Toleikis, Truong, Tschentscher, Uschmann and Zastrau2007; Thiele et al., Reference Thiele, Bornath, Fortmann, Höll, Redmer, Reinholz, Röpke, Wierling, Glenzer and Gregori2008) to the DSF.
In the chemical picture, i.e., treating electrons, ions of different charge states, and neutrals as separate species and neglecting transitions between these species (i.e., recombination or ionization), one can decompose the DSF into various contributions, as was shown by Chihara (Reference Chihara2000),
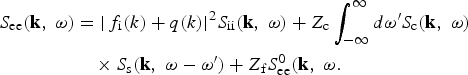
The first part gives the correlation of electrons that are weakly and tightly bound to the ions and follow the ion's movement adiabatically. The amplitude is determined by the atomic form factor f i(k), i.e., the charge distribution of the electrons in the valence shell orbitals and the screening cloud q(k), which gives the distribution of quasi-free electrons screening the ion's charge (Gregori et al., Reference Gregori, Ravasio, Höll, Glenzer and Rose2007). Due to the ion's comparatively large mass, they carry only a very small recoil energy and hence, the ion contribution forms a narrow resonance around ω = 0, i.e., at the initial frequency of the scattering photon. For the present conditions (photon energies between 0.1 and 10 keV), the ion feature cannot be resolved. Therefore, the frequency dependence of the ion feature is usually condensed into a delta function, i.e., S ii(k, ω) = S ii(k) δ (ω). Note however, that the ion feature can be measured with high resolution in optical Thomson scattering on dilute plasmas (e.g., magnetic fusion plasmas), see Snyder et al. (Reference Snyder, Reynolds, Fincke, Lassahn, Grandy and Repetti1994).
The second term contains the contribution of core electrons, S c(k, ω) and describes Raman type transitions of inner shell electrons to the continuum, modulated by the ion's movement that is contained in S s(k, ω) (Sahoo et al., Reference Sahoo, Gribakin, Naz, Kohanoff and Riley2008). Since the energy transferred from the photon to the electron has to overcome the binding energy E B, the core-electron contribution forms a continuous spectrum from ω = −∞ up to ω = −E B/ħ.
Finally, S ee0(k, ω) is the free electron contribution. It determines the behavior of the total electron structure factor at frequencies close to the plasma frequency. It is often referred to as the high-frequency part of S ee(k, ω).
In Eq. (13), the effective charge numbers are used. Z f is the mean ionization of ions. The remaining charge Z − Z f is subdivided into the number of valence electrons Z v and the number of core electrons Z c, such that Z − Z f = Z v + Z c.
We will focus here on the free electron contribution to the DSF, i.e., the last term in the Chihara separation (13). The treatment of the ion-feature, which is predominantly determined by the static ion-ion structure factor can be found in, e.g., Gregori et al. (Reference Gregori, Ravasio, Höll, Glenzer and Rose2007).
We use the fluctuation-dissipation theorem to calculate the DSF
with the number density of free electrons n e, the electron temperature T e, and the electronic dielectric function εe(k, ω).
3. CALCULATION OF THE DSF
3.1. Random Phase Approximation
The simplest approach to the dielectric function is the random phase approximation, i.e., the mean-field theory, also known as Lindhard-formula (Mahan, Reference Mahan1981). We adopt the notation of Arista and Brandt (Reference Arista and Brandt1984) in which the RPA dielectric function is given by
with the dispersion function
The Fermi momentum p F, velocity v F, and energy ɛF are given, respectively, by
The electron feature using the RPA has been analyzed in detail by Gregori et al. (Reference Gregori, Glenzer, Rozmus, Lee and Landen2003). Here, we go beyond the RPA and include electron-ion collisions.
3.2. Inclusion of collisions: Mermin approach
In X-ray Thomson scattering experiments on solid-density Be plasmas (Glenzer et al., Reference Glenzer, Landen, Neumayer, Lee, Widmann, Pollaine, Wallace, Gregori, Höll, Bornath, Thiele, Schwarz, Kraeft and Redmer2007), it was observed that collisionless theories of the DSF do not reproduce the correct width of collective plasmon excitations in the scattering spectrum. The additional width stems from collisions among the plasma constituents. Since at small wavenumbers, where the plasmons are found, electron-electron collisions can be neglected (the corresponding cross-section behaves like k 2) (Röpke et al., Reference Röpke, Redmer, Wierling and Reinholz1999), we consider only electron-ion collisions. The Born-Mermin approximation (Höll et al., Reference Höll, Bornath, Cao, Döppner, Düsterer, Förster, Fortmann, Glenzer, Gregori, Laarmann, Meiwes-Broer, Przystawik, Radcliffe, Redmer, Reinholz, Röpke, Thiele, Tiggesbumker, Toleikis, Truong, Tschentscher, Uschmann and Zastrau2007; Redmer et al., Reference Redmer, Reinholz, Röpke, Thiele and Höll2005) combines the Mermin approach for the dielectric function (Selchow et al., Reference Selchow, Röpke, Wierling, Reinholz, Pschiwul and Zwicknagel2001) with the energy-dependent collision frequency (or inverse relaxation time) (Röpke et al., Reference Röpke, Redmer, Wierling and Reinholz1999; Reinholz et al., Reference Reinholz, Redmer, Röpke and Wierling2000) that is calculated in second-order perturbation theory with respect to the statically screened electron-ion potential.
The Mermin formula for the dielectric function reads (Mermin, Reference Mermin1970)
with the dynamic collision frequency ν(ω) and the collisionless dielectric function εeRPA(k, ω). The RPA dielectric function is computed without any further approximation, i.e., it is valid for any degeneracy parameter θ.
3.3. Collision frequency
The collision frequency is taken in Born approximation (Reinholz et al., Reference Reinholz, Redmer, Röpke and Wierling2000),
![\eqalignno{{\rm \nu}^{\rm B}\lpar {\rm \omega}\rpar &= - i {{\rm \epsilon}_0 n_{\rm i} \over 6{\rm \pi}^2 e^2m_{\rm e} n_{\rm e}}\vint_0^{\infty}dq \ q^6 \left[V_{\rm ei}^{\rm S}\lpar q\rpar \right]^2 \cr &\quad \times S_{\rm ii}\lpar q\rpar {1 \over {\rm \omega}}\left[{\rm \epsilon}^{\rm RPA}_{\rm e}\lpar q\comma \; {\rm \omega}\rpar - {\rm \epsilon}^{\rm RPA}_{\rm e}\lpar q\comma \; 0\rpar \right].}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022040400858-0452:S026303460900041X_eqn22.gif?pub-status=live)
is the statically screened potential with the inverse screening length κsc. S ii(q) is the aforementioned static ion-ion structure factor.
Special care has to be taken that correlations are not counted twice. In particular, correlations that are accounted for in the screened potential V eiS (q) must not be considered in the static structure factor S ii (q) again. Therefore, two variants of the collision frequency are possible. On the one hand, all correlations are condensed into the screened potential via the screening parameter κsc, which in this case is the sum of ionic and electronic contributions:
Note that quantum degeneracy of electrons is fully accounted for via the Fermi integrals 
. Γ(ν) is the well-known Gamma function, (see Abramowitz & Stegun, Reference Abramowitz and Stegun1970). Ions can be treated as classical particles, i.e., the Debye expression is valid. In this case, the ion-ion structure factor in Eq. (22) is S ii (q) = 1. This variant of the collision frequency is referred to as the two-component screening variant (TCS) in the remaining part of this article.
On the other hand, considering only electrons as contributing to the screening of the electron-ion potential, the non-ideal ionic structure factor has to be taken into account. We note that in the Debye-Hückel approximation for the ion-ion structure factor, this procedure is equivalent to the TCS-method, since the product of the screened potential with only electronic screening and the Debye-Hückel structure factor yields
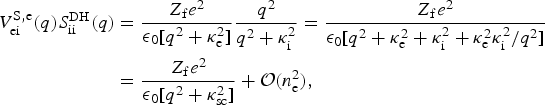
i.e., the TCS-approximation is restored when terms on the order of n 2 are neglected. This applies to weakly coupled plasmas where the Debye-Hückel approximation is sufficient.
Nevertheless, the use of the second variant (OCS, one-component screening), allows the use of more sophisticated models for the ion-ion structure factor in the collision integral, such as HNC calculations (Schwarz et al., Reference Schwarz, Bornath, Kraeft, Glenzer, Höll and Redmer2007) or (Q)MD simulations (Holst et al., Reference Holst, Redmer and Desjarlais2008).
A refinement with respect to the electronic screening of the electron-ion potential can be achieved by replacing the denominator q 2 + κe2 in the screened potential by the q-dependent screening factor q 2Re εeRPA (q, 0), i.e., taking into account the wavenumber dependence of the screening length. This ensures the convergence of the Born approximation with the Lenard-Balescu type collision integral in the case of vanishing frequency (Thiele et al., Reference Thiele, Redmer, Reinholz and Röpke2006). Table 1 gives a summary of the variants of the collision frequency, i.e., the possible approximations regarding the screened potential and the ion-ion structure factor. Figure 2 shows the real part of the dynamical collision frequency in Born approximation, Eq. (22) treating electronic and ionic correlations in the collision integral in various approximations, cf. Table 1, i.e., in TCS approximation and in OCS approximation. In the latter case, the ion-ion structure factor is taken in the Debye-Hückel approximation (OCS-DH) and from HNC calculations (OCS-HNC). All nine curves show a similar behavior as a function of the frequency argument. Below the plasma frequency, ω = ωpl,e, the real part of the collision frequency evolves independently of the frequency. In the vicinity of the plasma frequency, the collision frequency bends downward and quickly decreases at frequencies large against the plasma frequency. In this case, the power-law behavior Re ν(ω) ∝ ω−7/2 is found (Reinholz et al., Reference Reinholz, Morozov, Röpke and Millat2004). The imaginary part of the collision frequency can easily be obtained by using the Kramers-Kronig relation.
Fig. 2. Real part of the collision frequency in Born approximation using various approximations for electronic and ionic correlations in the collision integral, see Tab. 1. Results are shown for three different electron densities n e, i.e. 1022; 1023; and 1024 cm−3. The mean ion charge is Z f = 2.0 and the plasma temperature is T i = T e = 10 eV, θ is the degeneracy parameter, see Eq. 2.
Table 1. Summary of different approximations for electronic and ionic correlation in the collision integral. TCS denotes the two-component screening approximation, OCS-DH stands for one-component screening with Debye-H”uckel static ion-ion structure factor, and OCS-HNC is the one-component screening approximation with the static ion-ion structure factor taken from twocomponent HNC calculations
Comparing the collision frequency at various densities, the following interesting observations are made: The increase in density from 1022 cm−3 (green curves) to 1023 cm−3 (red curves) gives also an increase in the collision frequency. This is due to the increased coupling parameter, the electrons scatter more likely on ions in the case of higher density. However, comparing the case n e = 1023 cm−3 to the highest density, n e = 1024 cm−3 (black curves), this argument does not hold any longer in the case of the TCS model (solid curves), where a decrease in the collision frequency is observed. This can be understood by inspecting the degeneracy parameter θ for the three different densities. While the lowest density case is non-degenerate (θ = 5.9), the plasma at n e = 1023 cm−3 is weakly degenerate (θ = 1.3), and in the highest density case θ is decreased down to 0.27. In this case, scattering processes that involve transfer energies smaller than the Fermi energy are largely suppressed due to the Pauli exclusion principle, i.e., scatterings inside the Fermi sphere are forbidden since the final state is already occupied. This leads to the observed lowering of the collision frequency when increasing the density from 1023 cm−3 to 1024 cm−3. In the OCS models, this effect is not observed, since in the collision integral (22), contributions from small transfer momenta are suppressed due to the ionic structure factor S ii(q), such that the effect of Pauli blocking is reduced.
Finally, we compare the different models, i.e., the TCS (solid curves), OCS-DH (dashed curves), and the OCS-HNC calculations (dash-dotted curves). In the lowest density case, the TCS results and the OCS calculation with the Debye-Hückel type ion-ion structure factor (OCS-DH) are close together. This stems from the aforementioned equivalence of both models in the case of classical, weakly coupled plasmas, cf. Section 3. At higher densities the difference between TCS and OCS-DH increases. The reason for this behavior is that, on the one hand, the terms on the order of n e2, which are neglected in the TCS approximation as compared to the OCS-DH approximation become important. On the other hand, the electronic screening parameter κe starts to deviate from the classical Debye expression 
.
In all three cases of density, the HNC calculation yields the largest collision frequency. This is due to the finite compressibility obtained in the the two-component HNC calculation, i.e., the finite value for the ion-ion structure factor at vanishing wavenumber S ii(k = 0). Therefore, the integrand in Eq. (22) becomes large compared to the OCS-DH case, where the behavior S iiDH (k) ∝ k 2 at small k leads to a much smaller collision frequency. On the other hand, the screening parameter κsc is purely electronic in the OCS calculations, leading to a larger collision frequency compared to the TCS approximation.
4. SYNTHETIC SPECTRA
In order to generate synthetic scattering spectra comparable to experimental data from Thomson scattering experiments, the Thomson scattering cross-section needs to be convoluted with an appropriate weighting function that models the finite bandwidth of the probe radiation source and the finite detector's spectral resolution. Here, we use a normalized Gaussian function
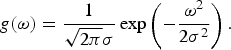
The variance σ2 is fixed by the full width at half maximum (FWHM) of the probe and the detector bandwidth as
with
Summarizing, we have to compute the following expression for the synthetic spectrum
![\eqalignno{{\cal S}\lpar k\comma \; {\rm \omega}\rpar &= {1 \over \sqrt{2{\rm \pi}}{\rm \sigma}}\left[Z_{\rm f}\vint_{-\infty}^\infty S_{\rm ee}^0\lpar k\comma \; {\rm \omega}^\prime\rpar \exp\left(-{{\rm \omega}-{\rm \omega}_{\rm i}-{\rm \omega}^\prime \over 2{\rm \sigma}^2}\right)d{\rm \omega}^\prime \right. \cr & \quad \left. + \; \lpar\, f_{\rm i}\lpar k\rpar + q\lpar k\rpar \rpar ^{2} S_{\rm ii}\lpar k\rpar \exp\left(-{\lpar {\rm \omega}-{\rm \omega}_{\rm i}\rpar ^2 \over 2{\rm \sigma}^2}\right)\right].}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022040400858-0452:S026303460900041X_eqn28.gif?pub-status=live)
4.1. X-ray scattering on beryllium targets
Figure 3 shows the electronic contribution to the DSF, Z fS ee0 (k, ω), assuming scattering of X-ray photons with photon energy 
(Cl-Lyman α) under ϑ = 40° scattering angle on a Be plasma at a temperature of k BT = 10 eV and at densities n e = 1·1023 cm−3 (right curves) and n e = 1.0·1024 cm−3 (left curves). The results are shown as a function of the energy shift from the photon energy, i.e., 
corresponds to the photon energy of the probe. The collisionless (RPA) calculation is shown as thin dotted line, while the thicker curves show the results obtained by using the Born-Mermin scheme as outlined in Section 2. The different collisional calculations correspond to different models for the electronic and ionic correlations in the collision integral, cf. Section 3.3.
Fig. 3. (Color online) Electron feature of the DSF for compressed Be (left curves, n e = 1024 cm−3) and near solid density Be (right curves, n e = 1023 cm−3). The dashed curve shows the RPA result, i.e the collisionless plasma. The other curves have been obtained taking into account the collision frequency. The curves differ with respect to the model for the ionic structure factor and the inverse screening length used in the collision integral. Parameters: Z f = 2.0, T e = T i = 10 eV, photon energy ħωi = 2.96 keV (Cl-Lyman α), scattering angle ϑ = 40°.
The differences in the collision frequency (cf. Fig. 2), directly translate into differences in the plasmon resonance in the dynamic structure factor. Larger values for Re ν(ω) in the vicinity of the plasma frequency lead to broader plasmon resonances. Since the dynamic structure factor is normalized to the density of the system, the peak of the plasmon resonance decreases when the width increases, such that the integral over all energies is a conserved quantity.
Comparing the spectra for both densities, one finds that in the case of compressed Be (n e = 1024 cm−3), the account for collisions leads to a smaller change in the overall behavior than in the case of near solid density Be (n e = 1023 cm−3). This is again due to suppression of collisions (Pauli blocking) that was already observed in the behavior of the collision frequency itself, (cf. Section 3).
4.2. Scattering of XUV photons on hydrogen at near solid density
As a further application of the presented formalism, we show in Figure 4 calculations for the fraction of scattered photons during scattering of XUV photons on a hydrogen target at three different near-solid densities (solid curves: n e = 1021 cm−3, dashed curves: n e = 5 × 1021 cm−3, dotted curves: n e = 1022 cm−3. Three different photon energies of the probe beam have been adopted, 
(upper graph), 
(middle), and 
(lower graph). The scattering angle is fixed at 90°. In all calculations, convolution with a Gaussian has been performed to model the finite spectral bandwidth of the detector and the beam. The relative bandwidth was assumed as Δω/ωi = 1%, and the plasma length was fixed at 10 µm.
Fig. 4. Scattered fraction of photons as a function of the energy shift for three different initial photon wavelengths (25 nm (top), 13.5 nm (middle), and 6 nm (bottom)). Results are shown for n e = 1 × 1021 cm−3 (solid curve), n e = 5 × 1021 cm−3 (dashed curve), and n e = 10 × 1021 cm−3 (dotted curve). L = 10 µm is the plasma length.
At higher densities, one observes a larger separation between the elastic scattering feature and the inelastic plasmon feature. The same effect is obtained by increasing the photon energy and thereby the scattering wavevector. On the other hand, a larger photon energy leads to a larger absolute spectral bandwidth (the relative bandwidth being kept constant in all three cases). Thus, in the case of 
, the plasmon resonance at n e = 5 × 1021 cm−3 (green curve) merges with the Rayleigh peak and only the n e = 1022 cm−3 curve (magenta) yields a measurable plasmon feature. The black curve (n e = 1021 cm−3) does not show any plasmon feature at all. This is due to the scattering parameter α = κD/k being already smaller than one in this case.
From these results, we conclude, that a Thomson scattering experiment at near solid density hydrogen should favourably be performed at photon energies of around 90 eV which are available at the Free Electron Laser Hamburg (FLASH). This setting assures a nicely separated plasmon feature.
5. CONCLUSIONS
In this article, we have presented a systematic approach to the calculation of the Thomson scattering cross-section in a strongly correlated plasma. The focus was on the free electron feature of the dynamical structure factor which contains the plasmon resonances in the case of collective scattering, i.e., at transfer wavenumbers small compared to the inverse Debye screening length. Special emphasis was paid on the consistent treatment of electron-ion collisions. This is crucial in the case of plasmas under warm dense matter conditions, since the plasma is both moderately coupled (Γ ≃ 1) and weakly degenerate (θ ≲ 1). To achieve this, the Born-Mermin approximation for the dynamical structure factor was introduced. The DSF is related to the dielectric function via the fluctuation-dissipation theorem, which itself is calculated using the generalized Mermin ansatz (cf. Eq. (21)), with the frequency-dependent collision frequency ν(ω). The latter is calculated in Born approximation.
Results have been presented for the dynamical collision frequency at various densities using different approximations for the ion-ion structure factor that enters the collision frequency. It was shown, that the collision frequency increases with rising density as long as the degeneracy parameter is larger than one, but decreases when degeneracy becomes important, i.e., θ < 1. This behaviour is expected since in degenerate systems Pauli blocking suppresses scattering inside the Fermi sphere. The restoration of the collisionless approximation (RPA) for high densities is well known.
Scattering spectra were calculated for two different experimental scenarios: First, scattering of keV-photons on uncompressed and compressed Be targets was studied. Here again, collisions are most significant as long as the plasma is not degenerate, i.e., in the uncompressed material. Second, scattering of XUV photons (photon energies between 50 and 200 eV) on hydrogen at near solid density was investigated to infer optimal experimental parameters. Under 90° scattering angle, one obtains a well-defined plasmon resonance which is satisfyingly separated from the central Rayleigh peak at a photon energy of 92 eV, i.e., at 13.5 nm wavelength.
Acknowledgements
This work was supported by the Collaborative Research Center (SFB) 652 of the German Research Society (DFG) “Strong Correlations and Coherent Phenomena in Radiation Fields: Coulomb Systems, Cluster, and Particles”, by the Virtual Institute VH-VI-104 of the Helmholz Association “Plasma Physics Research using FEL radiation” and the Federal Ministry for Education and Science (BMBF) under grant FSP 301-FLASH, project No. 05 KS7HRA.
