Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-06T17:03:42.982Z Has data issue: false hasContentIssue false
  • English
  • Français

Trapping of electromagnetic radiation in self-generated and preformed cavities

Published online by Cambridge University Press:  22 August 2013

Shixia Luan ,
Wei Yu ,
Jingwei Wang ,
Mingyang Yu ,
Suming Weng ,
Masakatsu Murakami ,
Jingwei Wang ,
Han Xu  and
Hongbin Zhuo
Shixia Luan*
Affiliation:
Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai, China
Wei Yu
Affiliation:
Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai, China
Jingwei Wang
Affiliation:
Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai, China
Mingyang Yu
Affiliation:
Institute for Fusion Theory and Simulation, Zhejiang University, Hangzhou, China; Institute for Theoretical Physics I, Ruhr University, Bochum, Germany
Suming Weng
Affiliation:
Institute of Laser Engineering, Osaka University, Osaka, Japan
Masakatsu Murakami
Affiliation:
Institute of Laser Engineering, Osaka University, Osaka, Japan
Jingwei Wang
Affiliation:
Institute of Laser Engineering, Osaka University, Osaka, Japan
Han Xu
Affiliation:
College of Science, National University of Defense Technology, Changsha, China
Hongbin Zhuo
Affiliation:
College of Science, National University of Defense Technology, Changsha, China
*
Address correspondence and reprint requests to: Shixia Luan, No.390, Qinghe Road, Jiading, Shanghai, 201800, China. E-mail: sxluan@siom.ac.cn
Rights & Permissions [Opens in a new window]

Abstract

Laser light trapping in cavities in near-critical density plasmas is studied by two-dimensional particle-in-cell simulation. The laser ponderomotive force can create in the plasma a vacuum cavity bounded by a thin overcritical-density wall. The laser light is self-consistently trapped as a half-cycle electromagnetic wave in the form of an oscillon-caviton structure until it is slowly depleted through interaction with the cavity wall. When the near-critical density plasma contains a preformed cavity, laser light can become a standing wave in the latter. The trapped light is characterized as multi-peak structure. The overdense plasma wall around the self-generated and preformed cavities induced by the laser ponderomotive force is found to be crucial for pulse trapping. Once this wall forms, the trapped pulse can hardly penetrate.

Keywords

Laser light trapping in cavitiesNear-critical density plasmasOscillon-caviton structureOverdense plasma wallPreformed cavity
Type
Research Article
Information
Laser and Particle Beams , Volume 31 , Issue 4 , December 2013 , pp. 589 - 595
Copyright
Copyright © Cambridge University Press 2013 

1. INTRODUCTION

Laser propagation in plasma depends on the laser properties as well as the plasma density. In low-density plasmas (n 0 ≪ n c, where n c is the critical density), the laser pulse can propagate a considerable distance. In solid-density plasmas (n 0 ≫ n c), on the other hand, it can penetrate only about a skin length and is reflected. In the recent years, the interaction of short and intense laser pulses (Perry & Mourou, Reference Perry and Mourou1994; Umstadter, Reference Umstadter2003) with gaseous (Tajima & Dawson, Reference Tajima and Dawson1979; Wang et al., Reference Wang, Yu, Yu, Xu, Wang and Yuan2009; Reference Wang, Yu, Yu, Lei, Wang, Senecha, Wang, Murakami and Mima2010; Reference Wang, Sheng, Li, Chen, Dong, Lu, Ma and Zhang2011; Sun et al., Reference Sun, Ott, Lee and Guzdar1987; Borghesi et al., Reference Borghesi, Mackinnon, Barringer, Gaillard, Gizzi, Meyer, Willi, Pukhov and Meyer-Ter-Vehn1997), solid-density (Kruer & Estabrook, Reference Kruer and Estabrook1985; Luan et al., Reference Luan, Yu, Yu, Ma, Zhang, Sheng and Murakami2011; Reference Luan, Yu, Murakami, Zhuo, Yu, Ma and Mima2012a; Brunel et al., Reference Brunel1987), as well as near-critical density (Willingale et al., Reference Willingale, Nilson, Thomas, Bulanov, Maksimchuk, Nazarov, Sangster, Stoeckl and Krushelnick2011; Reference Willingale, Nagel, Thomas, Bellei, Clarke, Dangor, Heathcote, Kaluza, Kamperidis, Kneip, Krushelnick, Lopes, Mangles, Nazarov, Nilson and Najmudin1997; Kuznetsov et al., Reference Kuznetsov, Esirkepov, Kamenets and Bulanov2001; Mourou et al., Reference Mourou, Chang, Maksimchuk, Nees, Bulanov, Yu, Bychenkov, Esirkepov, Naumova, Pegoraro and Ruhl2002; Nakamura et al., Reference Nakamura and Mima2008) plasmas has been widely investigated. However, creating near-critical density plasma with steep density gradient and optically probing the laser-plasma interaction region is experimentally challenging (Willingale et al., Reference Willingale, Nilson, Thomas, Bulanov, Maksimchuk, Nazarov, Sangster, Stoeckl and Krushelnick2011; Reference Willingale, Nagel, Thomas, Bellei, Clarke, Dangor, Heathcote, Kaluza, Kamperidis, Kneip, Krushelnick, Lopes, Mangles, Nazarov, Nilson and Najmudin1997). Recently, low-density foam targets have been fabricated using supersonic gas jets and in situ polymerization (Willingale et al., Reference Willingale, Nagel, Thomas, Bellei, Clarke, Dangor, Heathcote, Kaluza, Kamperidis, Kneip, Krushelnick, Lopes, Mangles, Nazarov, Nilson and Najmudin1997), thus making available near-critical density plasmas suitable for experiments.

Electromagnetic (EM) solitary waves (Yu et al., Reference Yu, Shukla and Spatschek1978; Luan et al., Reference Luan, Zhang and Sheng2008; Reference Luan, Yu, Xu, Murakami, Zhuo, Wang, Wang and Wu2012b; Bulanov et al., Reference Bulanov, Esirkepov, Naumova, Pegoraro and Vshivkov1999; Esirkepov et al., Reference Esirkepov, Kamenets, Bulanov and Naumova1998; Reference Esirkepov, Nishihara, Bulanov and Pegoraro2002; Sentoku et al., Reference Sentoku, Esirkepov, Mima, Nishihara, Califano, Pegoraro, Sakagami, Kitagawa, Naumova and Bulanov1999; Weber et al., Reference Weber, Lontano, Passoni, Riconda and Tikhonchuk2005; Farina et al., Reference Farina, Lontano and Bulanov2000; Sanchez-Arriaga et al., Reference Sanchez-Arriaga and Lefebvre2011a; Sanchez-Arriaga et al., Reference Sanchez-Arriaga and Lefebvre2011b) can self-consistently appear when a laser pulse propagates in a near-critical density plasma (Yu et al., Reference Yu, Shukla and Spatschek1978; Luan et al., Reference Luan, Yu, Xu, Murakami, Zhuo, Wang, Wang and Wu2012b). On the ion time scale, they can appear as post-solitons (Yu et al., Reference Yu, Shukla and Spatschek1978; Luan et al., Reference Luan, Yu, Xu, Murakami, Zhuo, Wang, Wang and Wu2012b; Naumova et al., Reference Naumova, Bulanov, Esirkepov, Farina, Nishihara, Pegoraro, Ruhl and Sakharov2001; Bulanov et al., Reference Bulanov and Pegoraro2002; Borghesi et al., Reference Borghesi, Bulanov, Campbell, Clarke, Esirkepov, Galimberti, Gizzi, Mackinnon, Naumova, Pegoraro, Ruhl, Schiavi and Willi2002), in which the EM radiation sits inside a self-generated plasma cavity. Depending on the laser and plasma conditions, the latter can co-move with the laser pulse or be stationary (Yu et al., Reference Yu, Shukla and Spatschek1978; Luan et al., Reference Luan, Yu, Xu, Murakami, Zhuo, Wang, Wang and Wu2012b; Naumova et al., Reference Naumova, Bulanov, Esirkepov, Farina, Nishihara, Pegoraro, Ruhl and Sakharov2001; Bulanov et al., Reference Bulanov and Pegoraro2002; Borghesi et al., Reference Borghesi, Bulanov, Campbell, Clarke, Esirkepov, Galimberti, Gizzi, Mackinnon, Naumova, Pegoraro, Ruhl, Schiavi and Willi2002; Sarri et al., Reference Sarri, Singh, Davies, Fiuza, Lancaster, Clark, Hassan, Jiang, Kageiwa, Lopes, Rehman, Russo, Scott, Tanimoto, Najmudin, Tanaka, Tatarakis, Borghesi and Norreys2010; Zhu et al., Reference Zhu, Wu, Dong, Hong, Teng, Zhou, Cao and Gu2012). Experiments with near-critical density plasmas have demonstrated the existence of well-isolated solitons and post-solitons (Borghesi et al., Reference Borghesi, Bulanov, Campbell, Clarke, Esirkepov, Galimberti, Gizzi, Mackinnon, Naumova, Pegoraro, Ruhl, Schiavi and Willi2002; Sarri et al., Reference Sarri, Singh, Davies, Fiuza, Lancaster, Clark, Hassan, Jiang, Kageiwa, Lopes, Rehman, Russo, Scott, Tanimoto, Najmudin, Tanaka, Tatarakis, Borghesi and Norreys2010; Zhu et al., Reference Zhu, Wu, Dong, Hong, Teng, Zhou, Cao and Gu2012).

This paper investigates EM radiation trapping in self-generated as well as preformed cavities using two-dimensional (2D) particle-in-cell (PIC) simulation. In Section 2, simulations are performed to detect laser trapping in the self-generated cavity when the laser enters near-critical density plasma. The laser pulse is partially reflected and partially transmitted into the plasma. The ponderomotive force of the light pulse modifies the local plasma density and self-consistently creates in the cavity an oscillon (Stenflo & Yu, Reference Stenflo and Yu1989; Reference Stenflo and Yu1996), or a half-cycle EM standing wave. Section 3 considers laser-light trapping in a preformed cavity in near-critical density plasma. In this case, a multi-peaked EM wave is formed in the cavity. A discussion is given in Section 4.

2. LIGHT TRAPPING IN SELF-GENERATED CAVITY

We performed two-dimensional in space and three dimensional in velocity (2D3V) PIC simulations for laser light trapping in near-critical density plasma. A Gaussian laser pulse is incident along the z axis from the left vacuum region into a homogeneous plasma located at 10 < z/λ0 < 50. The computation box is 60λ0 × 30λ0 in size. The spatial mesh contains 1500 × 750 cells, and each cell contains 16 ions and 16 electrons. The ion-electron mass ratio is 1836, and the initial electron density is n = n(0) = Zn i (0) = 0.7, where n i is the ion density. The incident laser strength, pulse duration, and spot size are a L = 0.4, τ = 10T 0, and b = 5λ, respectively.

When the laser pulse is incident on the left vacuum-plasma boundary, it is partially reflected back to the left vacuum and partially transmitted into the near-critical density plasma. As the transmitted light propagates, the laser ponderomotive force, proportional to the gradient of EM energy density, pushes the plasma away from the region where the EM field is strong. Figure 1 is for the EM energy density E 2 + B 2, the electron and ion densities at t = 77T 0, which is well into the ion time scale. We can see in Figures 1a and 1b that the electrons pushed away by the laser light pile up to form an overcritical-density plasma wall around a cavity, which traps the light. The maximum EM energy density occurs at the cavity center, and the EM field vanishes a short distance (of the order of the effective skin depth) into the high-density plasma wall. Figure 1c is for the densities of the EM energy, electrons, and ions along the laser axis. As expected, the electrons and ions behave almost as a quasi-neutral plasma, with only very little charge separation. The density of plasma wall is more than twice the critical density, thereby preventing the EM radiation from leaving the cavity. Clearly, the near-critical density background plasma plays a crucial role in the existence of the localized structure: the laser light is effectively trapped and stopped by the overdense cavity wall induced by its ponderomotive pressure. Otherwise, a laser can propagate through underdense plasma and be reflected by overdense plasma.

Fig. 1. (Color online) Normalized EM energy density E 2 + B 2 (a) and the electron density (b), as well as the EM energy density (blue dashed-dotted line), electron (red solid line), and ion (green dashed line) densities along the laser axis (c) at t = 77T 0, for a L = 0.4, τ = 10T 0, b = 5λ0, and n 0 = 0.7n c. One can see a standing half-cycle EM wave trapped in a self-generated plasma cavity.

The EM pulse trapped inside the self-generated cavity oscillates in time. Figure 2 is for the normalized electric field component E x at t = 102T 0 (1) and t = 103T 0 (2), about half an oscillation period (~2T 0) apart. The trapped half-cycle standing EM wave can be identified as an oscillon (Stenflo & Yu, Reference Stenflo and Yu1996), and the self-generated cavity a caviton (Wong et al., Reference Wong, Leung and Eggleston1977; Cheung et al., Reference Cheung, Wong, Darrow and Qian1982) with overdense plasma wall.

Fig. 2. (Color online) The normalized electric field E x at t = 102T 0 (a) and t = 103T 0 (b), about half an oscillation cycle apart.

EM radiation can be trapped in an empty cavity surrounded by an overdense plasma wall. Furthermore, the trapped EM radiation should satisfy the vacuum wave equation

(1)$$\nabla ^2 {\bf E} - \partial _{tt} {\bf E} = 0\comma$$

where time and space coordinates are normalized by ω0−1k 0−1, respectively. A simple cylindrically symmetric solution of the vacuum wave equation is

(2)$$E\lpar r\comma \; t\rpar = C\, \cos \lpar t\rpar \sin \lpar r\rpar /r\comma$$

where E(r, t) is the radial electric field, the constant C = 0.2 is determined by best-fit of this solution to that of the simulation. Figure 3 shows E(r, t) at t = cos−1 (−1) and cos−1 (1), namely half an oscillation period apart. We see that the behavior of E(r, t) is consistent with that from the simulation, even though the boundary and initial conditions have not been applied.

Fig. 3. (Color online) The normalized electric field E x at t = cos−1 (−1) (a) and cos−1 (1) (b), from Eq. (2) for C = 0.2.

3. LIGHT TRAPPING IN PREFORMED CAVITY

We now consider propagating a laser pulse in plasma containing a preformed cavity. As illustrated in Figure 4, a laser pulse enters near-critical-density plasma with a preformed vacuum cavity. The cavity radius is R = 2λ0, and its center is at (y, z) = (0, 16λ0).

Fig. 4. (Color online) Schematic of laser-pulse entering a near-critical density plasma containing a preformed cavity. The plasma density and the laser parameters are the same as that in the preceding case.

Laser propagation in plasma depends on the plasma density, or the dielectric coefficient ɛ = 1 − n e/n c, such that ɛ ~ 0 in near-critical density plasma and ɛ ~ 1 inside the preformed vacuum cavity. Figure 5 shows the electric field component E x, and the electron density n e along the laser axis, at t = 21T 0 and 27T 0. The plasma density and the laser parameters are the same as that in the preceding case. As the laser pulse reaches the preformed cavity at t = 21T 0, its EM field is strongly modified because of the abrupt change in the plasma density: at the plasma-vacuum boundary a part of the laser light is back-scattered, enhancing its tail and exciting electron density oscillations with amplitude remaining less than n c. The rest of the laser pulse enters the cavity and interacts with the plasma at its front. A thin enhanced electron layer of maximum density n e ~ 1.2n c is formed in front of the cavity by the compressed electrons, as can be seen in Figure 5d for t = 27T 0. The laser light is reflected, forming a standing EM wave in the slightly modified cavity. However, a part of the laser energy can tunnel through the narrow above-critical-density electron layer, forming in its front an oscillon-caviton structure, similar to that in a plasma without preformed cavity, but much smaller.

Fig. 5. (Color online) The normalized electric field component E x at t = 21T 0 (a) and t = 27T 0 (c), and the electron density n e (blue solid curve) along the laser axis at t = 21T 0 (b) and t = 27T 0 (d), for a L = 0.4, τ = 10T 0, n 0 = 0.7n c, and b = 5λ0. One can see that at t = 27T 0 the electrons in a thin layer at the leading edge of the preformed cavity has become overdense.

Figure 6 shows the electric field component E x and the electron density n e at t = 81T 0, as well as the electron density along the laser axis direction. EM fields are trapped in the two cavities bounded by ponderomotive-force driven overdense plasma walls that prevent the light from leaving. As a result, the radiation can be trapped for rather long times. As aforementioned, the self-generated small cavity is attributed to radiation tunneling from the preformed cavity. The trapped radiation in this self-generated small cavity again undergoes single-peak oscillation. However, in the preformed cavity with radius larger than laser wavelength, EM radiation becomes a multi-peak structure, as shown in Figure 7a. Our simulation shows that at t = 81T 0 about 7% of the incident laser energy is still in the cavities.

Fig. 6. (Color online) The electric field E x (a) and the electron density n e (b) at t = 81T 0, and the electron density (c) along the laser axis direction. A caviton containing an EM oscillon appears in front of the preformed cavity.

Fig. 7. (Color online) The normalized laser electric field E x (a) trapped in a preformed cavity of radius R = 4λ0, and the electron density (b), at t = 151T 0.

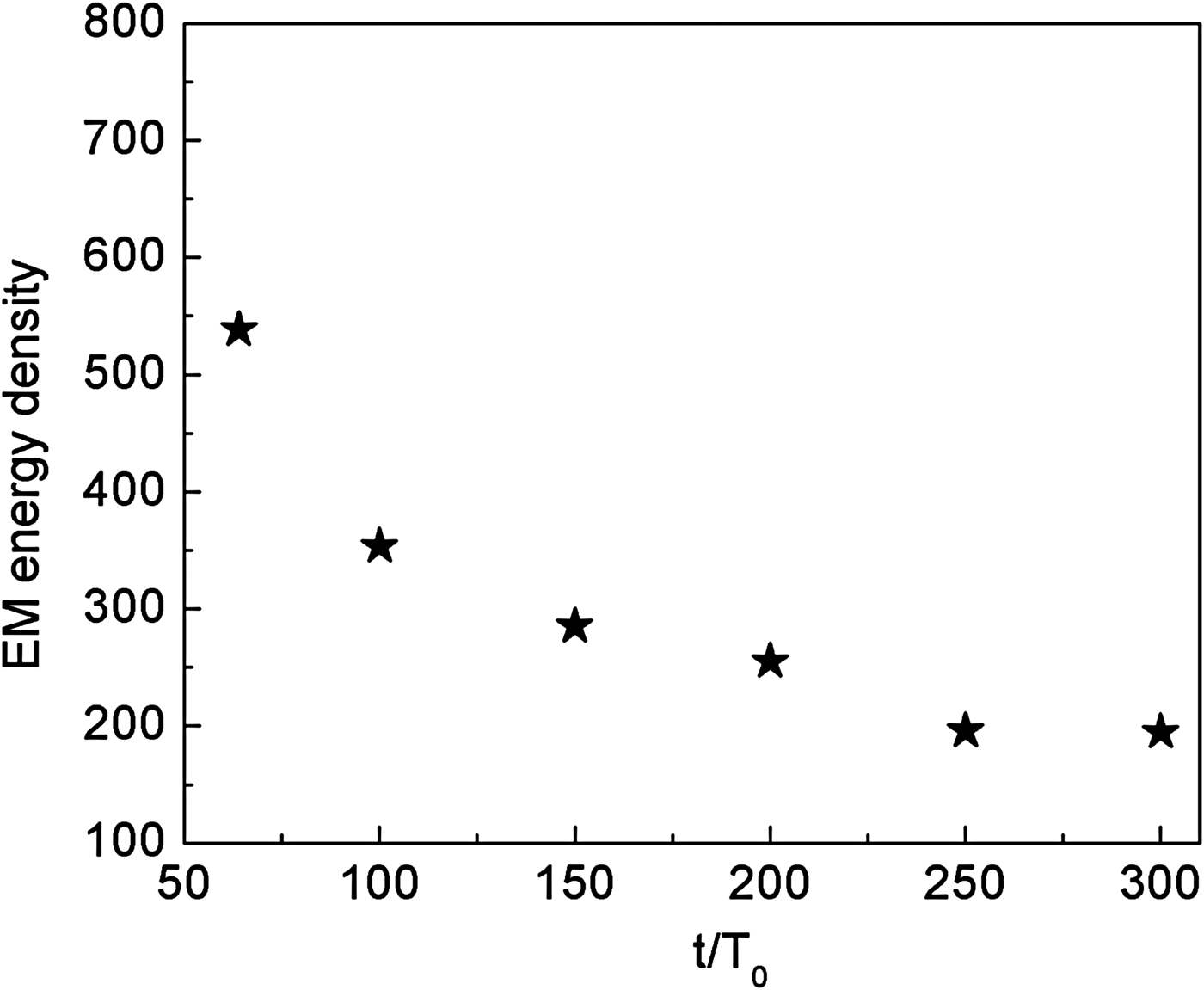
Figure 7 shows the normalized laser electric field E x (1) and electron density (2) at t = 151T 0 for a larger preformed cavity of radius R = 4λ0. The other parameters are the same as that in Figure 6. We can see in Figure 8 for the evolution of the EM energy in the preformed cavity that about 4% of incident laser energy is still trapped there at such long times. This is because in the larger cavity EM energy depletion, which takes place only at the cavity boundary, occurs very slowly since there the EM wave intensity is very low. In fact, the laser light can be stably trapped in the preformed cavity for more than 300T 0.

Fig. 8. Evolution of the energy of the EM wave trapped in the preformed cavity of radius R = 4λ0.

4. DISCUSSION

In this paper, we have investigated light trapping in self-generated and pre-formed cavities during the propagation of a laser pulse in near-critical density plasmas using 2D PIC simulation. A considerable part of the laser light is trapped as an EM oscillon in the self-generated caviton bounded by an overdense plasma wall. In near-critical density plasma with a preformed cavity, however, the laser ponderomotive force only slightly increases the density of the bounding plasma, but sufficient to reflect and trap the light, forming a standing wave structure. However, a part of the laser light can tunnel through the thin overdense plasma layer at the boundary, and self-consistently form an oscillon-in-caviton structure in front of the preformed cavity. Clearly, the self-consistent overdense plasma boundary layer induced by the ponderomotive force plays an important role for the long-term trapping of the EM oscillon as well as the standing EM wave.

ACKNOWLEDGEMENTS

This work was supported by the National Natural Science Foundation of China (Nos. 11174303, 11204329, 11127901), and the National Basic Research Program of China (Nos. 2013CBA01500, 2011CB808100).

References

REFERENCES

Borghesi, M., Bulanov, S., Campbell, D.H., Clarke, R.J., Esirkepov, T.Zh., Galimberti, M., Gizzi, L.A., Mackinnon, A.J., Naumova, N.M., Pegoraro, F., Ruhl, H., Schiavi, A. & Willi, O. (2002). Macroscopic evidence of soliton formation in multiterawatt laser-plasma interaction. Phys. Rev. Lett. 88, 135002.CrossRefGoogle ScholarPubMed
Borghesi, M., Mackinnon, A.J., Barringer, L., Gaillard, R., Gizzi, L.A., Meyer, C., Willi, O., Pukhov, A. & Meyer-Ter-Vehn, J. (1997). Relativistic channeling of a picosecond laser pulse in a near-critical preformed plasma. Phys. Rev. Lett. 78, 879–882.CrossRefGoogle Scholar
Brunel, F. (1987). Not-so-resonant, resonant absorption. Phys. Rev. Lett. 59, 52–55.CrossRefGoogle ScholarPubMed
Bulanov, S.V. & Pegoraro, F. (2002). Stability of a mass accreting shell expanding in a plasma. Phys. Rev. E 65, 066405.CrossRefGoogle ScholarPubMed
Bulanov, S.V., Esirkepov, T.Zh., Naumova, N.M., Pegoraro, F. & Vshivkov, V.A. (1999). Solitonlike electromagnetic waves behind a superintense laser pulse in a plasma. Phys. Rev. Lett. 82, 3440–3443.CrossRefGoogle Scholar
Cheung, P.Y., Wong, A.Y., Darrow, C.B. & Qian, S.J. (1982). Simultaneous observation of caviton formation, spiky turbulence, and electromagnetic radiation. Phys. Rev. Lett. 48, 1348–1351.CrossRefGoogle Scholar
Esirkepov, T.Zh., Kamenets, F.F., Bulanov, S.V. & Naumova, N.M. (1998). Low-frequency relativistic electromagnetic solitons in collisionless plasmas. JETP Lett. 68, 36–41.CrossRefGoogle Scholar
Esirkepov, T., Nishihara, K., Bulanov, S.V. & Pegoraro, F. (2002). Three-dimensional relativistic electromagnetic subcycle solitons. Phys. Rev. Lett. 89, 275002.CrossRefGoogle ScholarPubMed
Farina, D., Lontano, M. & Bulanov, S.V. (2000). Relativistic solitons in magnetized plasmas. Phys. Rev. E 62, 4146–4151.CrossRefGoogle ScholarPubMed
Kruer, W.L. & Estabrook, K. (1985). J × B heating by very intense laser light. Phys. Fluids 28, 430–432.CrossRefGoogle Scholar
Kuznetsov, A.V., Esirkepov, T.Zh., Kamenets, F.F. & Bulanov, S.V. (2001). Efficiency of ion acceleration by a relativistically strong laser pulse in an underdense plasma. Plasma Phys. Rep. 27, 211–220.CrossRefGoogle Scholar
Luan, S.X., Yu, W., Murakami, M., Zhuo, H.B., Yu, M.Y., Ma, G.J. & Mima, K. (2012 a). Time evolution of solid-density plasma during and after irradiation by a short, intense laser pulse. Laser Part. Beams 30, 407–414.CrossRefGoogle Scholar
Luan, S.X., Yu, W., Xu, W.W., Murakami, M., Zhuo, H.B., Wang, J.W., Wang, X. & Wu, H.C. (2012 b). Model study on laser interaction with near-critical density plasma. Appl. Phys. B 108, 875–882.CrossRefGoogle Scholar
Luan, S.X., Yu, W., Yu, M.Y., Ma, G.J., Zhang, Q.J., Sheng, Z.M. & Murakami, M. (2011). Analytical model for interaction of short intense laser pulse with solid target. Phys. Plasmas 18, 042701.CrossRefGoogle Scholar
Luan, S.X., Zhang, Q.J. & Sheng, Z.M. (2008). The formation of relativistic electromagnetic solitons in plasma Bragg gratings induced by two counter-propagating laser pulses. Appl. Phys. B 93, 793–799.CrossRefGoogle Scholar
Mourou, G., Chang, Z., Maksimchuk, A., Nees, J., Bulanov, S.V., Yu, V., Bychenkov, T., Esirkepov, Zh., Naumova, N.M., Pegoraro, F. & Ruhl, H. (2002). On the design of experiments for the study of relativistic nonlinear optics in the limit of single-cycle pulse duration and single-wavelength spot size. Plasma Phys. Rep. 28, 12–27.CrossRefGoogle Scholar
Nakamura, T. & Mima, K. (2008). Magnetic-Dipole Vortex Generation by Propagation of ultraintense and ultrashort laser pulses in moderate-density plasmas. Phys. Rev. Lett. 100, 205006.CrossRefGoogle ScholarPubMed
Naumova, N.M., Bulanov, S.V., Esirkepov, T.Zh., Farina, D., Nishihara, K., Pegoraro, F., Ruhl, H. & Sakharov, A.S. (2001). Formation of electromagnetic postsolitons in plasmas. Phys. Rev. Lett. 87, 185004.CrossRefGoogle Scholar
Perry, M.D. & Mourou, G. (1994). Terawatt to petawatt subpicosecond Lasers. Science 264, 917–924.CrossRefGoogle ScholarPubMed
Sanchez-Arriaga, G. & Lefebvre, E. (2011 a). Two-dimensional s-polarized solitary waves in relativistic plasmas. I. The fluid plasma model. Phys. Rev. E 84, 036403.CrossRefGoogle ScholarPubMed
Sanchez-Arriaga, G. & Lefebvre, E. (2011 b). Two-dimensional s-polarized solitary waves in plasmas. II. Stability, collisions, electromagnetic bursts, and post-soliton evolution. Phys. Rev. E 84, 036404.CrossRefGoogle ScholarPubMed
Sarri, G., Singh, D.K., Davies, J.R., Fiuza, F., Lancaster, K.L., Clark, E.L., Hassan, S., Jiang, J., Kageiwa, N., Lopes, N., Rehman, A., Russo, C., Scott, R.H.H., Tanimoto, T., Najmudin, Z., Tanaka, K.A., Tatarakis, M., Borghesi, M. & Norreys, P.A. (2010). Observation of postsoliton expansion following laser propagation through an underdense plasma. Phys. Rev. Lett. 105, 175007.CrossRefGoogle ScholarPubMed
Sentoku, Y., Esirkepov, T.Zh., Mima, K., Nishihara, K., Califano, F., Pegoraro, F., Sakagami, H., Kitagawa, Y., Naumova, N.M. & Bulanov, S.V. (1999). Bursts of superreflected laser light from inhomogeneous plasmas due to the generation of relativistic solitary waves. Phys. Rev. Lett. 83, 3434–3437.CrossRefGoogle Scholar
Stenflo, L. & Yu, M.Y. (1989). An exact nonlinear cylindrical surface wave solution. Phys. Fluids B 1, 1543–1544CrossRefGoogle Scholar
Stenflo, L. & Yu, M.Y. (1996). Origin of oscillons. Nature 384, 224.CrossRefGoogle Scholar
Sun, G.Z., Ott, E., Lee, Y.C. & Guzdar, P. (1987). Self-focusing of short intense pulses in plasmas. Phys. Fluids 30, 526–532.CrossRefGoogle Scholar
Tajima, T. & Dawson, J.M. (1979). Laser electron accelerator. Phys. Rev. Lett. 43, 267–270.CrossRefGoogle Scholar
Umstadter, D. (2003). Relativistic laser–plasma interactions. J. Phys. D 36, 151–165.CrossRefGoogle Scholar
Wang, J.W., Yu, W., Yu, M.Y., Lei, A.L., Wang, X., Senecha, V.K., Wang, X.G., Murakami, M. & Mima, K. (2010). Guiding of intense laser pulse in uniform plasmas and preformed plasma channels. Phys. Plasmas 17, 103109.CrossRefGoogle Scholar
Wang, W.M., Sheng, Z.M., Li, Y.T., Chen, L.M., Dong, Q.L., Lu, X., Ma, J.L. & Zhang, J. (2011). Studies on the mechanisms of powerful terahertz radiations from laser plasmas. Chin. Opt. Lett. 9, 110002.Google Scholar
Wang, X., Yu, W., Yu, M.Y., Xu, H., Wang, J.W. & Yuan, X. (2009). Simple model for wakefield excitation by intense short-pulse laser in underdense plasma. Phys. Plasmas. 16, 053107.CrossRefGoogle Scholar
Weber, S., Lontano, M., Passoni, M., Riconda, C. & Tikhonchuk, V.T. (2005). Electromagnetic solitons produced by stimulated Brillouin pulsations in plasmas. Phys. Plasmas 12, 112107.CrossRefGoogle Scholar
Willingale, L., Nagel, S.R., Thomas, A.G.R., Bellei, C., Clarke, R.J., Dangor, A.E., Heathcote, R., Kaluza, M.C., Kamperidis, C., Kneip, S., Krushelnick, K., Lopes, N., Mangles, S.P. D., Nazarov, W., Nilson, P.M. & Najmudin, Z. (1997). Characterization of high-intensity laser propagation in the relativistic transparent regime through measurements of energetic proton beams. Phys. Rev. Lett. 102, 125002.Google Scholar
Willingale, L., Nilson, P.M., Thomas, A.G.R., Bulanov, S.S., Maksimchuk, A., Nazarov, W., Sangster, T.C., Stoeckl, C. & Krushelnick, K. (2011). High-power, kilojoule laser interactions with near-critical density plasma. Phys. Plasmas 18, 056706.CrossRefGoogle Scholar
Wong, A.Y., Leung, P. & Eggleston, D. (1977). Particle-cavition interactions. Phys. Rev. Lett. 39, 1407–1411.CrossRefGoogle Scholar
Yu, M.Y., Shukla, P.K. & Spatschek, K.H. (1978). Localization of high-power laser pulses in plasmas. Phys. Rev. A 18, 1591–1596.CrossRefGoogle Scholar
Zhu, B., Wu, Y.C., Dong, K.G., Hong, W., Teng, J., Zhou, W.M., Cao, L.F. & Gu, Y.Q. (2012). Observation of a strong correlation between electromagnetic soliton formation and relativistic self-focusing for ultra-short laser pulses propagating through an under-dense plasma. Phys. Plasmas 19, 102304.CrossRefGoogle Scholar
Figure 0

Fig. 1. (Color online) Normalized EM energy density E2 + B2 (a) and the electron density (b), as well as the EM energy density (blue dashed-dotted line), electron (red solid line), and ion (green dashed line) densities along the laser axis (c) at t = 77T0, for aL = 0.4, τ = 10T0, b = 5λ0, and n0 = 0.7nc. One can see a standing half-cycle EM wave trapped in a self-generated plasma cavity.

Figure 1

Fig. 2. (Color online) The normalized electric field Ex at t = 102T0 (a) and t = 103T0 (b), about half an oscillation cycle apart.

Figure 2

Fig. 3. (Color online) The normalized electric field Ex at t = cos−1 (−1) (a) and cos−1 (1) (b), from Eq. (2) for C = 0.2.

Figure 3

Fig. 4. (Color online) Schematic of laser-pulse entering a near-critical density plasma containing a preformed cavity. The plasma density and the laser parameters are the same as that in the preceding case.

Figure 4

Fig. 5. (Color online) The normalized electric field component Ex at t = 21T0 (a) and t = 27T0 (c), and the electron density ne (blue solid curve) along the laser axis at t = 21T0 (b) and t = 27T0 (d), for aL = 0.4, τ = 10T0, n0 = 0.7nc, and b = 5λ0. One can see that at t = 27T0 the electrons in a thin layer at the leading edge of the preformed cavity has become overdense.

Figure 5

Fig. 6. (Color online) The electric field Ex (a) and the electron density ne (b) at t = 81T0, and the electron density (c) along the laser axis direction. A caviton containing an EM oscillon appears in front of the preformed cavity.

Figure 6

Fig. 7. (Color online) The normalized laser electric field Ex (a) trapped in a preformed cavity of radius R = 4λ0, and the electron density (b), at t = 151T0.

Figure 7

Fig. 8. Evolution of the energy of the EM wave trapped in the preformed cavity of radius R = 4λ0.