1. INTRODUCTION
The optical manipulation of atoms and ions has been a subject of increasing relevance in many fields of physics in recent years. In particular, the dynamics of charged particles in electromagnetic (EM) fields is of great importance in plasma physics. The fully relativistic motion of particles in the field of an EM plane wave has been the subject of interesting investigations (Roberts & Buchsbaum, 1964; Bourdier & Gond, 2000), including recent studies of stochastic heating effects (Patin et al., 2005, 2006). The interest of these studies is enhanced by the fact that it is nowadays possible to operate lasers with an effective power on the order of 1019 W/cm2 during time intervals of a few femptoseconds (Malka et al., 1997; Schnürer et al., 2005). Thus, it could be possible to use such ultrashort and energetic pulses for either trapping subatomic particles or accelerating them up to relativistic speeds (Malka & Fritzler, 2004; Glinec et al., 2005; Mangles et al., 2006; Schnürer et al., 2005).
Given the importance of the process, it is worth exploring other possible EM field configurations. In this paper, we consider Bessel modes; these, in ideal conditions, propagate with a constant intensity pattern (Durnin, 1987), have the property of self-reconstruction (Bouchal & Olivik, 1995; Bouchal et al., 1996; Horák et al., 1997), and posses an angular momentum additional to that provided by their polarization state (Allen et al., 1992; Jáuregui & Hacyan, 2005). Experimental realizations of such beams (Durnin et al., 1987; Turunen et al., 1988; McGloin & Dholakia, 2005) and their mechanical effects on atoms and microparticles (Arlt et al., 2001; Garcés-Chávez et al., 2002) are the subject of many current investigations. The possibility of accelerating particles or plasmas using a Bessel laser beam has been discussed by previous authors. For instance, an axial acceleration can be produced by the corresponding component of the EM field (Hafizi et al., 1997), and there are stable orbits that could be used for the trapping of charged particles (Bialynicki-Birula et al., 2005).
In the present paper, we study in depth the effects of ideal Bessel modes, both for the transverse and axial motion of a charged particle. Previous studies did not consider the most general form of a Bessel beam; here, we take into account the combinations of transverse electric and magnetic modes that give different polarization states, thus identifying the relevant features of the particle dynamics. In Section 2 of the present paper, we present a brief summary of the main properties of a Bessel beam based on a previous work (Jáuregui & Hacyan, 2005). In Section 3, the equations of motion are written down and the constants of motion are identified; it is shown that these equations are considerably simplified in a particular reference frame that we defined as antiparaxial (Hacyan & Jáuregui, 2006). In Section 4, a numerical analysis of some particular configurations is presented; we found that there are alternating regions in phase space where the particle gets trapped in the transverse plane of the wave, together with other regions in which they are radially accelerated. Some conclusions are presented at the end.
2. EM BESSEL MODES
An EM field with cylindrical symmetry can be conveniently described in terms of Hertz potentials Π1 and Π2 (Nisbet, 1955, 1957). In cylindrical coordinates {ρ,φ,z}, these potentials give rise to transverse magnetic (TM) and electric (TE) modes, respectively, and their explicit expressions are

where Jm is the Bessel function of integer order m, ω is the frequency,

are the wavenumbers, and

determine the amplitude of the fields; unless otherwise stated, we use units in which c = 1. The EM four-vector potential is

and satisfies the Lorentz gauge condition (Jáuregui & Hacyan, 2005). The corresponding electric field is

where

The magnetic field is found via the duality transformation

.
By superpositions of TE and TM different polarizations of Bessel modes are obtained. In the literature (Barnett & Allen, 1994) the following modes are taken as analogous to right

and left

polarized plane wave modes:

Their superpositions

define linearly polarized modes. In terms of TE and TM modes,

The mechanical properties of the photons associated with Bessel modes are directly related to the numbers ω,kz,m that characterize them, along with the polarization (Jáuregui & Hacyan, 2005). In fact, ħω,ħkz,mħ correspond to the energy, linear momentum, and orbital angular momentum along the z direction, respectively. A superposition of TE and TM with equal weights
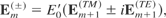
corresponds to photons with a projection of the spin angular momentum along the z axis, i.e., an helicity ±ħkz /ω. In the paraxial limit, the definition of circular polarized beams through Eq. (6) coincides with that given by Eq. (7).
3. MOTION OF CHARGED PARTICLES
Consider a particle of charge e and mass M (for instance, an electron) moving in an EM field. The standard Lagrangian is

where

. Here the dot represents a derivative with respect to time t in the laboratory system. Let us consider the particular case of a Bessel beam. Using the fact that

the equations of motion take the form:



From the above equations, one can also obtain the formula for the change in kinetic energy, d(Mγ)/dt = eE·v, which takes the explicit form:

Combining the above equations, one finds the following two constants of motion:

and

the first is related to the angular momentum Lz and the second to the linear momentum along the z axis, Pz. The existence of such conserved quantities is due to the fact that Bessel travelling waves depend on z, φ, and t only through the combination kz z + mφ − ωt.
Notice that the conserved linear momentum Pz is the sum of three terms whose origin can be directly identified. The first is the particle mechanical linear momentum; the second is the product of kz /ω (proportional to the beam z-linear momentum) and the particle rest energy M; the third term arises from the axial electric field of TM modes. Similarly, the angular momentum Lz is the sum of the particle angular momentum, the product of m/ω (proportional to the beam z-orbital angular momentum) with the particle rest energy M, and the angular momentum related to the polarization state of the wave that can be transmitted to the charge.
As a direct consequence of Eq. (15),

with φ(t) = mφ(t) + kz z(t) + ωt + φTM and φTM the phase associated with the complex amplitude E0TM. A similar equation can be written for

. The identification of conserved quantities reduces effectively the number of equations to be solved. It also follows that there are natural bounds to the momentum and angular momentum the particle may acquire via its interaction with the EM field.
The equations of motion can be further simplified if the description of the system is made in a particular reference frame, in which each mode takes a simpler form (Hacyan & Jáuregui, 2006), namely the frame moving along the z axis with velocity kz /ω (and Lorentz factor γ = ω/k⊥). The standard Lorentz transformations has the form:

with the same transformations for the t and z components of the potential Aμ. Thus, there is a particular reference frame in which kz′ = 0 and, therefore, the EM field does not depend on the coordinate z′. Changing to this particular frame is equivalent to taking an antiparaxial limit (Hacyan & Jáuregui, 2006).
4. SOME ILLUSTRATIVE NUMERICAL EXAMPLES
Before proceeding to solve numerically the above equations, it is necessary to make some precisions about the orders of magnitude of the different parameters involved and the units to be used. First, we set k⊥ = 1, which implies that 1/k⊥ and 1/(k⊥ c) are taken as units of length and time, respectively; M establishes the unit of mass. There remains the laser-strength parameter defined in the literature as e0 = eE0 /Mc, that appears frequently in the equations; it is a measure of the coupling of the EM field as compared with the inertia of the charged particle and has units of frequency. In recent experiments involving electrons and femptosecond lasers, the similar dimensionless parameter e0 /ω takes values as high as ∼3, which requires intensities as high as 1021 W/cm2 (Malka et al., 1997). Since we are interested in exploring the possibility of using lasers that alter significantly the motion of charged particles, we will take e0 /ck⊥ = 0.2 in all our numerical calculations; this can be realized for an electron in the field of a moderately high intensity laser.
There are three particularly interesting beam configurations. The first two correspond to purely TE modes, Π1 = 0, and purely TM modes, Π2 = 0. The other case corresponds to right (or left) circularly polarized waves, which we take as the superpositions defined by Eq. (5). In the following sections, we examine these cases.
4.1. TE modes
In this subsection, all calculations are performed in the antiparaxial frame for which kz′ = 0, since the equations of motion are considerably simpler. The transformation back to the laboratory frame is given by a Lorentz transformation along the z-axis with a velocity −kz /ω; accordingly, the transverse trajectories of the charged particles are essentially the same in both frames. In this frame, the TE electromagnetic field is given by

and

Thus, the electric field is confined to the transverse plane and the magnetic field wave is aligned in the z direction. Notice that here and in the following section, the dot represent a derivative with respect to the time t′ in the inertial frame moving with velocity kz /ω along the z axis. The proper time of the particle will be denoted by τ, and therefore γdτ = dt′. The equations of motion take form:


and

The particle moves with constant speed in the z direction with respect to its proper time. Finally, the following integral of motion follows:

The above equations have been numerically solved to show some typical trajectories. All computations were performed using the program DE developed at the University of Florida (Shampine & Gordon, 1975). In the following examples we took the initial conditions

, and we analyzed various possibilities with different values of

. The general result is that for certain almost periodic values of the initial condition, ρ(0), the particle is trapped in the transverse direction with a projected trajectory in the XY plane forming concentric rings around the axis. The values of ρ(0) for bound and unbound radial motions are given in Table 1 for m = 0,1,2,3,4. Some typical trajectories are shown in Figure 1.
Values of the radial initial condition k⊥ ρ(0) that lead to confined (first three columns) and unconfined (last three columns) transverse motion when the particle interacts with a TE mode (e0 /ck⊥ = 0.2). The other initial conditions are taken as in the antiparaxial system. Distances are measured in units of k⊥−1.


Projections on the XY plane of two typical trajectories of a charged particle immersed in a TE beam of zeroth order. In both cases, the initial conditions are . In the first figure, k⊥ ρ(0) = 0.774 and the motion is radially bound. Similar trajectories are obtained for 0 ≤ k⊥ ρ(0) ≤ 0.774. In the second figure, k⊥ ρ(0) = 0.775 and the particle moves away from the symmetry axis. The axes in the plot refer to the dimensionless variables k⊥ x, k⊥ y; the description is made in the antiparaxial system with kz = 0.
Notice that the trapping conditions have been obtained for values of ρ(0) near zero in almost all cases. The exception is m = 1; from the corresponding equations of motion, it can be seen directly that, in this particular case, there is a centrifugal force near the axis due to a term proportional to the Bessel function J0, the only one that is different from zero at the axis of symmetry (recall that J1′ = (J0 − J2)/2, and J1 /x = (J0 + J1)/2). Notice also that the separation between border boundary conditions ρ(0) leading to bound and unbound trajectories is of the same order of magnitude as the separation between zeros in the corresponding Bessel function.
4.2. TM modes
For TM modes, the equations of motion in the antiparaxial frame are
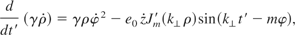

together with the integrals of motion:


From Eqs. (25) and (26) we notice that the speed in the z-direction of the particle is conditioned by its radial trajectory.
Numerical calculations were performed with the same initial conditions as for TE modes:

. We also explored several values of ρ(0) and m. Contrary to the corresponding results for TE modes, a confined motion in the XY plane is obtained for small values of ρ(0) and m = 1; this is also the case for m = 2,3. However, for m ≥ 4, small values of ρ(0) lead to unbound motion in the XY plane. It can also be shown that for

is a solution of the equations of motion regardless of the value for ρ(0) whenever

. The bound trajectories of a charged particle in a TM mode are also qualitatively different from those in a TE modes, as can be seen in Figure 2. The basic reason is that for TM modes in the antiparaxial system, the electric field of the beam is directed along the z-axis while the magnetic field is constrained to the transverse plane, namely:

and

In Figure 2, the evolution of the velocity

in the antiparaxial frame is illustrated. Notice that, as expected, particles that have a bounded radial motion in a region of greater values for the corresponding Bessel function Jm(k⊥ ρ), can be accelerated to higher velocities

by the EM wave.

Radial and z components of the velocities for two typical trajectories of a charged particle in a first order TM beam (first column) and a second order TM beam (second column). The description is made in the antiparaxial frame. The initial conditions are .
4.3. Circular polarization
In this subsection, we use the standard definition of circular polarization as given by Eq. (5) and, in order to avoid any confusion, we describe the motion of the charged particle in the laboratory frame. The constants of motion Lz and Pz are now


Thus the polarization of the beam leads to an additional term in the expression for angular momentum Lz.
For the numerical calculations, we considered initial conditions similar to those for TE and TM modes:

, with different values for

. We found that, as in previous cases, there are bound and unbound transverse trajectories according to the values of

. The intervals of ρ(0) that lead to unbound motions get shorter with respect to those of bound motions as ρ(0) increases. For this field configuration, we have also studied whether the given values of Lz or Pz are sufficient to characterize bound and unbound motions in the transverse direction; the answer turned out to be negative, since for fixed values of all initial conditions (with the exception of ρ(0)), the constants of motion Lz and Pz can be evaluated as functions of ρ(0), but this function is not injective and therefore two values of ρ(0) yielding bound and unbound transverse trajectories can lead to the same value of Lz. An illustrative example of this fact is given in Table 2.
Values of the radial initial condition k⊥ ρ(0) that lead to confined (first three columns) and unconfined (last three columns) transverse motion when the charge interacts with a left (L) circularly polarized Bessel beam (e0 /ck⊥ = 0.2) with m = 0. The other initial conditions are taken as in the laboratory system. Varying k⊥ ρ(0) for a given Pz is equivalent to changing . In the lower half of the Table, the corresponding trapping conditions are given in terms of the constant of motion Lz.

In Figure 3, typical projections of the trajectories on the XY plane and the evolution of the z component of the velocity are illustrated for a charged particle immersed in a first order left polarized Bessel beam with kz = k⊥. In the two examples, the initial conditions are φ(0) = z(0) = 0, Pz = −0.625175M (so that

),

. This latter condition implies that the angular momentum Lz arises just from the electromagnetic interaction (see Eq. (30)). In the first column k⊥ ρ(0) = 1.85 and thus Lz = −0.788447M/k⊥; and the particle has an bounded trajectory in the XY plane, and its velocity oscillates starting from

up to

. In the second column k⊥ ρ(0) = 1.84, the particle has an unbounded trajectory in the XY plane and acquires an asymptotic velocity

. The latter behavior is due to the fact that the interaction with the Bessel beam vanishes as the particle moves far away from the symmetry axis.

Radial and z components of the velocities for two typical trajectories of a charged particle in a first order polarized Bessel beam, in the laboratory frame. See Section 4.3 for details.
5. CONCLUSIONS
Our results show that Bessel modes can be useful in manipulating the motion of charged particles, either to trap them or accelerate them to relativistic speeds, provided that the power of the laser is sufficiently high and can be sustained for a long enough time interval. From a theoretical point of view, we have identified some relevant features of the dynamics of the particles under ideal conditions. In particular, the constants of motion have been identified, showing through their explicit expressions the role of different polarizations in the interchange of linear and angular momentum between the particle and light. These constants of motion are also relevant for understanding the influence of the transverse motion in the axial velocity.
Summing up, radially bound and unbound trajectories, and also substantial axial accelerations, can be obtained depending on the initial conditions and the beam polarization. More general configurations that permit to better control the motion of charged particles will be studied in forthcoming publications.







