1. INTRODUCTION
The interaction of an intense short-pulse laser with plasmas is a major area due to its relevance to laser-driven fusion, laser-driven particle accelerator, X-ray laser, and other related areas (Modena et al., Reference Modena, Najmudin, Dangor, Clayton, Marsh, Joshi, Malka, Darrow, Danson, Neely and Walsh1995; Esarey et al., Reference Esarey, Sprangle, Krall and Ting1996; Shukla, Reference Shukla1999; Reference Shukla, Rao, Yu and Tsintsadze1986; Suk et al., Reference Suk, Barov, Rosenzweig and Esarey2001; Umstadter, Reference Umstadter2001; Bingham et al., Reference Bingham, Mendonca and Shukla2004; Fuerbach et al., Reference Fuerbach, Fernandez, Apolonski, Fuji and Krausz2005; Gibbon, Reference Gibbon2005; Hoffmann et al., Reference Hoffmann, Blazevic, Rosmej, Spiller, Tahir, Weyrich, Dafni, Kuster, Ni, Roth, Udrea and Varentsov2007; Gupta et al., Reference Gupta, Hur, Hwang, Suk and Sharma2007; Sandhu et al., Reference Sandhu, Kumar, Sengupta, Das and Kaw2005; Hora, Reference Hora2007; Flippo et al., Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007; Chen et al., Reference Chen, Unick, Vafaei-Najafabadi, Tsui, Fedosejevs, Naseri, Masson-Laborde and Rozmus2008). In these applications, it is required to propagate the laser pulse up to several Rayleigh lengths while preserving an efficient interaction with the plasma. In the last decades, significant progress in this direction has been made and continues to be a subject of great fascination among researchers (Chen & Sudan, Reference Chen and Sudan1993; Chessa et al., Reference Chessa, Mora and Atonsen1998; Ren et al., Reference Ren, Duda, Hemker, Mori, Katsouleas, Antonsen and Mora2001; Leemans et al., Reference Leemans, Volfbeyn, Guo, Chattopadhyay, Schroeder, Shadwick, Lee and Wurtele1998). It occurs when the refractive index of the plasma is an increasing function of intensity. This dependence may be through local electron density depression, caused by ponderomotive force and subsequent plasma diffusion. Durfee and Milchberg (Reference Durfee Iii and Milchberg1993) experimentally observed plasma-channeling of a short-pulse laser to long distances. These studies, conducted with long pulses, have observed the phenomena of self-focusing of laser beams in plasma under a wide variety of conditions. It is caused by the intensity dependent refractive index that may arise due to a relativistic mass effect, ponderomotive force induced plasma diffusion or non-uniform Ohmic heating and subsequent plasma diffusion. The relativistic mass non-linearity arises instantly, however, it requires very high laser intensity such as that observed when the electron quiver-velocity is comparable to the velocity of light in vacuum. The two non-linearity's require a relaxation time to settle down, as they involve physical displacement of the plasma from the region of high-intensity to outside the domain of the beam. Ponderomotive non-relativistic self-focusing at higher laser intensities becomes dominant (Sodha et al., Reference Sodha, Ghatak and Tripathi1976; Hauser et al., Reference Hauser, Scheid and Hora1988).
During particle-in-cell simulations of laser produced plasmas, researchers have observed the strong flows of relativistic electrons axially co-moving with the laser pulse and showing the existence of strong direct current magnetic fields that can influence non-linear phenomena (Pukhov & Meyer-ter-Vehn, Reference Pukhov and Meyer-Ter-Vehn1996; Gahn et al., Reference Gahn, Tsakiris, Pukhov, Meyer-Ter-Vehn, Pretzler, Thirolf, Habs and Witte1999). Borghesi et al. (Reference Borghesi, Mackinnon, Gaillard, Willi, Pukhov and Meyer-Ter-Vehn1998) have also observed multi-mega-gauss azimuthal magnetic-field generation with picosecond and sub-picosecond laser pulses. For direct electron acceleration, Tsakiris et al. (Reference Tsakiris, Gahn and Tripathi2000) used the laser created plasma channel with the radial electric field and the self-generated magnetic field. The magnetic field is very important in electron acceleration by a high power laser (Gupta & Suk, Reference Gupta and Suk2006; Liu et al., Reference Liu, He and Hora2006). It enhances the electron energy and collimates the accelerated electron beam. Wagner et al. (Reference Wagner, Tatarakis, Gopal, Beg, Clark, Dangor, Evans, Haines, Mangles, Norreys, Wei, Zepf and Krushelnick2004) proposed an experimental scheme to accelerate the electrons in the presence of a static magnetic field parallel to the laser's magnetic field. The magnetic field changes the dispersion relation of the laser beam and modifies the plasma electron density. It is very important in the context of laser self-focusing.
Under paraxial approximations, several analyses relevant to this study have been performed (Chen et al., Reference Chen and Sudan1993; Chess et al., Reference Chessa, Mora and Atonsen1998; Ren et al., Reference Ren, Duda, Hemker, Mori, Katsouleas, Antonsen and Mora2001; Sun et al., Reference Sun, Ott, Lee and Guzdar1987; Gupta et al., Reference Gupta, Suk and Hur2007; Esarey et al., Reference Esarey, Sprangle and Krall1997). In these analyses, the main assumption was the consideration of paraxial approximations. When the scale of transverse variation is much larger than the scale length in the propagation direction, the variation of the transverse intensity distribution is negligible (transverse dynamic is neglected) and may be ignored under the paraxial approximation theory. If the self-focusing is a dominant process, this approximation would not be valid. To calculate the total energy of the laser pulse, one needs to consider the transverse distribution of intensity since this can influence the laser-plasma interactions. Johnson and Chu (Reference Johnson and Chu1974) conducted experiments to find out the electron density evaluation and pulse self-focusing in laser-produced plasmas through hydrodynamics expansion of the radial plasma profile. Liu and Tripathi (Reference Liu and Tripathi2001) have studied the steady state self-focusing of a laser beam in plasma in the presence of an azimuthal magnetic field. They find that due to uneven focusing in two transverse directions, laser spot acquires an elliptic cross-section. Recently, Gupta et al. (Reference Gupta, Hur and Suk2007) proposed the introduction of a localized plasma density ramp for the relativistic self-focusing of an intense laser. Moreover, a theory of steady static self-focusing in plasma, perpendicular to the direction of electromagnetic wave propagation, immersed in a uniform magnetic field, has been developed by Gupta et al. (Reference Gupta, Hur and Suk2007). The non-linearity arises through the ponderomotive force and subsequent redistribution of plasma along the magnetic field.
In order to understand these non-linear phenomena, we propose a study of self-focusing of a laser beam under the non-paraxial approximations, where features a magnetic field to guide the laser beam. The results of the present study demonstrate that it is possible to under the actual non-linear focusing of the laser beam if the non-paraxial approximation is considered with the guiding magnetic field. In this research, we report a theoretical model of transient self-focusing of a short laser pulse, with Gaussian radial intensity distribution, in magnetized plasma, under non-paraxial ray approximation. Non-linearity arises due to the ponderomotive force and subsequent ambi-polar diffusion of the plasma. The magnetic field also affects the subsequent plasma diffusion, consequently the laser self-focusing. In Section 2, we deduce the equations governing non-linear high-order electron velocities (or radial electron flow) and subsequent evolution of plasma density via ambi-polar diffusion. The effect of this has been calculated by using effective plasma permittivity. In Section 3, we solve the wave equation to obtain an equation for beam width parameter. This equation is solved numerically to study the variation of the beam width parameter (which is the function of laser spot size) as a function of axial distance at different times. The results are discussed in Section 4.
2. NON-LINEAR EFFECT
Consider plasma of uniform equilibrium electron density n 0 immersed in a static magnetic field B sŷ. An intense short-pulse laser, propagates through the plasma along z-direction, 
$\vec E=\hat yA\lpar x\comma \; z\comma \; t\rpar \exp \lsqb \!-i\lpar {\rm \omega} t - kz\rpar \rsqb $, where A 2 = A 002g(t)exp (−x 2/r 02) at z = 0, g(t) characterizes the temporal shape of the pulse, step function g(t) = 0 for t < 0, and g(t) = 1 for t > 0. For z > 0, we may write, ∣A∣2 = (A 002/f 2)g(t − z/υg)exp(−x 2/r 02f 2), where k = (ω/c)(1 − ωp2/ω2)1/2, υg = c(1 − ωp2/ω2)1/2, ωp = (4πn 0e 2/m)1/2 is the plasma frequency, r 0 is transverse half width of the laser, f(z)is the beam width parameter, and −e and m are the charge and mass of an electron. Here we have assumed that ω≫ωc where ωc is the electron cyclotron frequency. Further, we assume that the length of the plasma channel L < r 0 υg/c s, where c s is the sound speed so that the plasma channel evolves almost simultaneously in the entire axial length of the plasma. As the channel evolves, the laser self-focuses with the distance of propagation. However, we address the issue of self-focusing later. The oscillatory velocity of the electrons induced by the laser can be given by 
$\vec {\rm \upsilon}=e\vec E/mi{\rm \omega}. $ The laser also exerts a ponderomotive force on the electrons,
$\vec F_p=e\nabla \phi _p \vert \vert \hat x$, where 
$ \phi_p=- \lpar m/2e\rpar \vec {\rm \upsilon} .\vec {\rm \upsilon} ^\ast =- \lpar e/m{\rm \omega} ^2\rpar \vec E.\vec E^{\ast} .$ The quasi-static motion of electrons and ions is governed by the equations of motion
$$\displaystyle{{\partial {\rm \vec \upsilon} } \over {\partial t}}=- \displaystyle{e \over m}\vec E_s - \displaystyle{e \over {mc}}\lpar \vec {\rm \upsilon} \times \vec B_s\rpar +\displaystyle{e \over m}\nabla \phi _p\comma$$
$$m_i \displaystyle{{\partial \vec {\rm \upsilon} _i } \over {\partial t}}=e\vec E_s\comma$$where magnetic force on the ions has been neglected owing to their large mass. Non-linearity arises due to the ponderomotive force and subsequent ambi-polar diffusion of the plasma. Taking the z-components of Eqs. (1) and (2) in the ambi-polar diffusion process (υiz ≈ υz), we get ∂υz/∂t = −ωcυx. Now, using the continuity equation, ∂n/∂t + (∂/∂x)nυx) = 0, we can get the perturbed plasma density Δn = (n 0/ωc)∂υz/∂x, where we have used n = n 0 + Δn and the expression of υx obtained in above calculation. Now, we expand the z-component of the velocity in the non-paraxial region as υz = υ1x + υ3x 3 + υ5x 5, where even power of x turn out to be zero, hence it has been dropped. Using this expansion of υz and expanding ϕp in power of x, we get, on equating coefficients of equal powers of x on both sides,
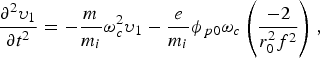$$\displaystyle{{\partial ^2 {\rm \upsilon} _1 } \over {\partial t^2 }}=- \displaystyle{m \over {m_i }}{\rm \omega} _c^2 {\rm \upsilon} _1 - \displaystyle{e \over {m_i }}\phi _{\,p0} {\rm \omega} _c \left({\displaystyle{{ - 2} \over {r_0^2 f^2 }}} \right)\comma$$
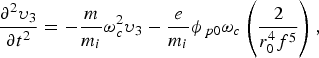$$\displaystyle{{\partial ^2 {\rm \upsilon} _3 } \over {\partial t^2 }}=- \displaystyle{m \over {m_i }}{\rm \omega} _c^2 {\rm \upsilon} _3 - \displaystyle{e \over {m_i }}\phi _{\,p0} {\rm \omega} _c \left({\displaystyle{2 \over {r_0^4 f^5 }}} \right)\comma$$
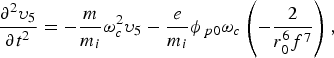$$\displaystyle{{\partial ^2 {\rm \upsilon} _5 } \over {\partial t^2 }}=- \displaystyle{m \over {m_i }}{\rm \omega} _c^2 {\rm \upsilon} _5 - \displaystyle{e \over {m_i }}\phi _{\,p0} {\rm \omega} _c \left({ - \displaystyle{2 \over {r_0^6 f^7 }}} \right)\comma$$where ϕp0 = eA 002/mω2 and ωc = eB s/mc. Using the expansion of υz in the expression of Δn, we obtain Δn = (Δn)0 + (Δn)2x 2 + (Δn)4x 4, where (Δn)0 = (n 0/ωc)υ1, (Δn)2 = (3n 0/ωc)υ3, and (Δn)4 = (5n 0/ωc)υ5. Using n = n 0 + Δn in the expression of non-linear dielectric constant of plasma, the modified dielectric constant of the plasma can be written as ɛ = ɛ0 + ɛ2x 2 + ɛ4x 4, where ɛ0 = 1 − (ωp2/ω2), ɛ2 = (3ωp2υ3/ω2 ωc), and ɛ4 = (5ωp2υ5/ω2ωc). It is noted that the quantity ɛ4 arises due to the non-paraxial approximation. In paraxial region, where the higher order terms can be neglected, the quantity ɛ4 turns out to be zero.
3. SELF-FOCUSING
The wave equation governing by the propagation of the laser is
$$\nabla ^2 \vec E = \displaystyle{{4{\rm \pi} } \over {c^2 }}\displaystyle{{\partial \vec J} \over {\partial t}} + \displaystyle{1 \over {c^2 }}\displaystyle{{\partial \vec E} \over {\partial t}}$$
where 
$\vec J=- ne{\rm \vec \upsilon} $ is the current density. Using the expression of laser electric field in Eq. (6), in the quasi-static approximation, one obtains,
$\nabla _ \bot ^2 A+2ik\lpar \partial A/\partial z^{\prime}\rpar +{\rm \varepsilon} _2 \lpar {\rm \omega} ^2 /c^2\rpar x^2 A+$
${\rm \varepsilon} _4 \lpar {\rm \omega} ^2 /c^2\rpar x^4 A=0$, where 
$z^{\prime}=z - {\rm \upsilon} _g t$, We introduce an Eikonal, A as A = A 0(x, z′)e iS(x,z′), where A 0(x, z′) and S(x, z′) are the real function of z, and z′. By substitute the value of A and separating the real and imaginary part of in above expression, the following set of equations is obtained.
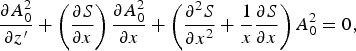$$\displaystyle{{\partial A_0^2 } \over {\partial z^{\prime}}}+\left({\displaystyle{{\partial S} \over {\partial x}}} \right)\displaystyle{{\partial A_0^2 } \over {\partial x}}+\left({\displaystyle{{\partial ^2 S} \over {\partial x^2 }}+\displaystyle{1 \over x}\displaystyle{{\partial S} \over {\partial x}}} \right)A_0^2=0\comma$$
$$2\displaystyle{{\partial S} \over {\partial z}}+\left({\displaystyle{{\partial S} \over {\partial x}}} \right)^2 - \displaystyle{{{\rm \varepsilon} _2 } \over {{\rm \varepsilon} _0 }}x^2 - \displaystyle{{{\rm \varepsilon} _4 } \over {{\rm \varepsilon} _0 }}x^4=\displaystyle{1 \over {kA_0 }}\left({\displaystyle{{\partial ^2 A_0 } \over {\partial x^2 }}+\displaystyle{1 \over x}\displaystyle{{\partial A_0 } \over {\partial x}}} \right).$$In non-paraxial approximation (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968) we express the A 02 as given earlier and the Eikonal S up to the second power of x 2. Equating the coefficients of various powers of x on both sides, we obtain the equation governing the beam width parameter as
$$\displaystyle{{\partial ^2 f} \over {\partial z^{\prime2}}}=\displaystyle{1 \over {R_d^2 f^3 }} - \displaystyle{{{\rm \varepsilon} _2 } \over {{\rm \varepsilon} _0 }}f - \displaystyle{{r_0^2 {\rm \varepsilon} _4 } \over {{\rm \varepsilon} _0 }}f\comma$$where R d = kr 02 is the diffraction length. The first term on the right side is due to diffraction divergence. The second is due to non-linear refraction in paraxial region, and the last one shows self-focusing beyond the axial region. Now, we introduce the dimensionless variables, ξ = z′/R d, τ = tω, V 3 = (υ3r 02/ω), and V 5 = (υ5r 04/ω), then Eqs. (4), (5), and (9) can be written as
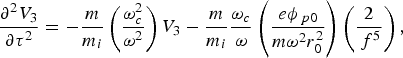$$\displaystyle{{\partial ^2 V_3 } \over {\partial {\rm \tau} ^2 }}=- \displaystyle{m \over {m_i }}\left({\displaystyle{{{\rm \omega} _c^2 } \over {{\rm \omega} ^2 }}} \right)V_3 - \displaystyle{m \over {m_i }}\displaystyle{{{\rm \omega} _c } \over {\rm \omega} }\left({\displaystyle{{e\phi _{\,p0} } \over {m{\rm \omega} ^2 r_0^2 }}} \right)\left({\displaystyle{2 \over {\,f^5 }}} \right)\comma$$
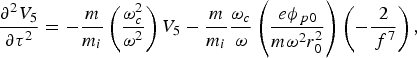$$\displaystyle{{\partial ^2 V_5 } \over {\partial {\rm \tau} ^2 }}=- \displaystyle{m \over {m_i }}\left({\displaystyle{{{\rm \omega} _c^2 } \over {{\rm \omega} ^2 }}} \right)V_5 - \displaystyle{m \over {m_i }}\displaystyle{{{\rm \omega} _c } \over {\rm \omega} }\left({\displaystyle{{e\phi _{\,p0} } \over {m{\rm \omega} ^2 r_0^2 }}} \right)\left({ - \displaystyle{2 \over {\,f^7 }}} \right)\comma$$
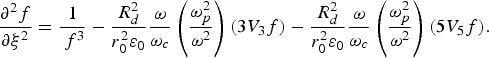$$\displaystyle{{\partial ^2 f} \over {\partial {\rm \xi} ^2 }}=\displaystyle{1 \over {\,f^3 }} - \displaystyle{{R_d^2 } \over {r_0^2 {\rm \varepsilon} _0 }}\displaystyle{{\rm \omega} \over {{\rm \omega} _c }}\left({\displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} ^2 }}} \right)\lpar 3V_3 f\rpar - \displaystyle{{R_d^2 } \over {r_0^2 {\rm \varepsilon} _0 }}\displaystyle{{\rm \omega} \over {{\rm \omega} _c }}\left({\displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} ^2 }}} \right)\lpar 5V_5 f\rpar .$$Eq. (11) and the last term on the right-hand side in Eq. (12) do not appear in the case of the paraxial approximation study; these equations arise due to the off-axis approximations. The results change significantly by using the latest approximation. Using the boundary conditions f(ξ = 0, τ) = 1, (∂f/∂ξ) = 0 at ξ = 0 for all times (corresponding to an initially plane wave front) and V 3(ξ, 0) = 0, (∂V 3/∂τ) = 1, V 5(ξ, 0) = 0, (∂V 5/∂τ) = 1 at τ = 0, we solved Eqs. (10)–(12) by using the Runga-Kutta technique. For this calculation, we use the typical parameters, laser wavelength λ0 = 1.053 μm (ω = 2 × 1015rad/sec.), and n 0 = 0.2n cr = 2.2 × 1020/λ02(μ).cm −3 with a magnetic field of about B s = 12 × 106Gauss. The laser intensity is I 0 = 5 × 1014W/cm 2 with the laser spot size of r 0 = 10 μm. For an incident laser power exceeding a particular value known as the threshold power a self-focusing of the laser beam should occur. This threshold power can be estimated by balancing the diffraction and non-linear effects. For MW power of laser, the threshold power (P cr(W) = 1.15 × 104T e, where T e is the plasma electron temperature) depends on the temperature. However, for high-intensity lasers, the critical power [P cr(W) = 2.16 × 1030/n 0(cm −3)] depends mainly on the density of the plasma electron. In our calculation, the critical power can be calculated by equating both terms on the right-hand side of Eq. (12). From our theory, for the given experimental parameters, the threshold power of self-focusing turns out to be about P cr(W) = 1.05 × 1010W.
In Figure 1, we have depicted three-dimensional surface plot for the variation of the beam width parameter (f) with the normalized distance (ξ) at different values of time (τ) for (R d2/r 02) = 50, (ωp2/ω2) = 0.1, and (eϕp0/r 02ω2m) = 0.05, where the magnetic field has been considered zero in order to compare it with the next case. It is shown that the beam width parameter decreases with the propagation distance and reaches a minimum value, after which it increases with the propagation distance due to the saturation of non-linearity. It is also observed that the pulse diverges early in time. As time passes the non-linearity induced self-convergence takes over the diffraction-divergence and the pulse starts focusing gradually up to 2R d. At τ = 2000 the pulse focuses over a length of 1.8R d. At τ ≥ 3000 the beam has dug a significant cavity in the plasma and it focuses over a length of ~1.2R d.
Fig. 1. Surface-diagram for beam width (f) with the propagation distance (ξ) and the time (τ) for I 0 = 5 × 1014, W/cm 2 (with λ0 = 1.053 μm), (R d2/r 02) = 50, (ωp2/ω2) = 0.1, and (eϕp0/r 02 ω2m) = 0.05 (here the magnetic field has been considered zero).
In Figure 2, we have seen the effect of the magnetic field on laser self-focusing. The three-dimensional surface plot shows the beam width parameter with the propagation distance at different times for ωc/ω= 0.105(corresponding to the magnetic field strength of B s = 12 MG with the given laser wavelength of λ0 = 1.053 μm). In the presence of a transverse magnetic field, the beam width parameter decreases rapidly and does not increase much. The plasma density soon minimizes on the axis corresponding to the radial direction due to the effect of a magnetic field. Hence, the laser receives the condition for self-focusing and becomes focused. From our simulations, it is also observed that the magnetic field not only strengthens, but also increases the rate of self-focusing of the laser pulse. From Figure 2, one may see that the beam width parameter acquires a minimum value in very short propagation distance compared to the former case. For example, the beam width parameter reaches the value of 0.3 in a distance of ~0.6R d at time τ = 5000. Hence, it is concluded that as the magnetic field enhances the rate of self-focusing of a laser in plasma. Furthermore, under non-paraxial approximation, we need to consider the off-axis effects of the laser pulse on plasma dynamics. The calculation shows that due to the off-axis plasma behavior this approximation significantly affects self-focusing.
Fig. 2. Surface-diagram for beam width (f) with the propagation distance (ξ) and the time (τ) for I 0 = 5 × 1014W/cm 2 (with λ0 = 1.053 μm), (R d2/r 02) = 50, (ωp2/ω2) = 0.1, (eϕp0/r 02 ω2m) = 0.05, and ωc/ω = 0.105 (B s = 12 MG).
Figure 3 shows the same for higher magnetic field strength ωc/ω = 0.21 (corresponding to the magnetic field strength of B s = 24 MG with the given laser wavelength of λ0 = 1.053 μm). However, in the presence of a strong magnetic field, the plasma density soon reaches its minimum on the axis. Hence, the external magnetic field enhances the rate of plasma diffusion. Due to the ambi-polar motion, plasma diffusion sets in early, and the electron's velocity increases with the normalized radial distance. With time the density of plasma decreases more on the axis, and the corresponding electron velocity increases due to the effect of the ponderomotive force. Due to the effect of a strong magnetic field, the non-linear velocity increases which contributes to the non-linearity responsible for the self-focusing of the laser. By comparing the results of Figures 2 and 3, strong self-focusing can be observed. What results is an increased rate of the self-focusing of a laser if a magnetic field of sufficient strength is applied.
Fig. 3. Surface-diagram for beam width (f) with the propagation distance (ξ) and the time (τ) for I 0 = 5 × 1014W/cm 2 (with λ0= 1.053 μm), (R d2/r 02) = 50, (ωp 2/ω2) = 0.1, (eϕp0/r 02 ω2m) = 0.05, and ωc/ω = 0.21(B s = 24 MG).
4. CONCLUSION
An intense Gaussian laser pulse propagating through plasma exerts a ponderomotive force on plasma electrons. During early stages of the process, the plasma density is maximized on the axis. With the passes of time, the plasma electrons experience a ponderomotive force in the radial direction due to the Gaussian radial distribution of the intensity of the laser, causing an ambi-polar diffusion of the plasma. This leads to decreases in the plasma density on the axis, and the occurrence of a density-depleted channel on the axis. This density depleted channel is very useful for laser guiding in plasmas. As the channel evolves, self-focusing of the laser becomes stronger since low density acts as a duct to guide and self-focus the laser beam, which further intensifies the wave maximum. The higher value of the magnetic field shows a strong self-focusing of a laser in plasma. Due to the higher-order plasma particle velocity consideration in non-paraxial approximation, the off-axis plasma distribution is affected by the laser pulse. In this calculation, the higher-order non-linearity terms have been included under non-paraxial approximations. Consequently their effects become important for the self-focusing of a laser in magnetized plasma.
ACKNOWLEDGMENTS
This work was partially supported by the University of Delhi (India) under the R&D program 2012 and the Department of Science and Technology, Govt. of India under the SERC Fast Track Scheme for Young Scientists. This research was also financially supported by the National Research Foundation of Korea (grant numbers: 2012-0000165, R15-2008-006-01001-0, 2012-005900).
