2. BUBBLE MERGER MODELS

Bubble merger models predict the penetration rate of fingers of light fluid (bubbles) into the heavy fluid. For acceleration-driven mixing, it is observed that the bubbles increase in size, through a process of bubble competition and merger.

In this process, advanced bubbles are accelerated relative to the mean bubble motion, whereas retarded ones are held back. Thus the smaller bubbles (also generally the retarded ones) become removed from the interface of advancing bubbles, whereas the larger, advanced ones expand to fill the resulting space. Sharp and Wheeler (1961) proposed a model to describe this process. The model was corrected by Glimm and Sharp (1990, 1997) to include the hydrodynamical accelerations (positive and negative) given to advanced and retarded bubbles due to their positions relative to the mean bubble penetration height. Such models were extended to three dimensions by Oron et al. (2001) and independently by Cheng et al. (2002a), with improved predictions. The three-dimensional (3D) models predict not only the growth rates for the bubble interface (both agree with experiment; Cheng et al. is slightly higher), they also predict the bubble height-to-width ratio. For this quantity, the two models are distinctly different in their predictions (see Table 1). Agreement of the Cheng et al. model with experimental data is very satisfactory.

Bubble height-to-width ratios in experiments and models

The bubble dynamic equations are formulated in scaled variables, from which the Agt² dynamic growth has been removed. This being the case, the self-similar, late time solution appears as a fixed point. In fact, it is a renormalization group (RNG) fixed point.

For steady acceleration, that is, Rayleigh–Taylor (RT) mixing, the bubble penetration height h_b satisfies the scaling law h_b = α_b Agt². Four directly measurable quantities determine the growth rate constant α_b in this formula. The measurements, the relation of these quantities to α_b, and the experimental validation of this relation are contained in Cheng et al. (2002a). We list the four quantities: (1) Let t_m′ be the time to merger for a pair of interacting bubbles. Then ω = 〈1/t_m′〉_* is the mean inverse time to merger, and thus the mean merger rate. It is evaluated at the fixed point, (2) h_m′ is the maximum height separation, that is, the height for instantaneous merger, (3) c_b is the speed of a single bubble in a periodic array, and (4) k is a geometrical factor giving the increase in radius for a single merger event, slightly less than ½. Each of the proceeding is expressed in scaled units. Then the fixed point formula for α_b is

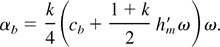
As written, the equation has been verified by direct comparison to experimental data (Cheng et al., 2002a). To obtain a closed expression for α_b, the above quantities are evaluated directly within a statistical model for the bubble dynamics. Two quantities define this model: the bubble velocity and the bubble merger criteria. The bubble velocity is defined as the sum of a single (periodic array) bubble velocity and a bubble interaction term, the “envelope velocity.” The bubble velocity as a sum of these two terms has been tested against simulation data. The criteria for bubble merger is defined to be the time at which the retarded bubble starts to move backwards, using this two-term formula for the bubble velocity. Note that the bubble interaction term can have either sign, so that a zero total velocity is possible. The bubble merger criteria was shown to be an insensitive parameter in the model.

From these two inputs, ω and h_m′ are determined. The result is the determination α_b ≈ 0.5–0.6, in agreement with experimental results. The same formulas yield the bubble height-to-width ratio, cited in Table 1. Since (1) depends on two parameters, it is important to check it (as we do) on two independent sets of data. Specifically, ω is very sensitive to the bubble width whereas α_b can mask canceling errors between ω and h_m′.

3. COMPRESSIBLE MIXING ZONE DYNAMICS

The bubble merger model is readily extended to compressible flow. The single bubble velocity, c_b in scaled variables, must be determined for compressible flow. This quantity affects the envelope velocity and thus the total bubble velocity. The remainder of the analysis is unchanged. See Chen et al. (1993). This same reference shows that α_b increases with increasing values of the dimensionless compressibility λg/c_h². It was also shown that the bubble merger model predictions for α_b, as corrected in this manner for compressibility, were in good to moderate agreement with simulation results.

4. CENTER OF MASS MOTION

For steady acceleration (Rayleigh–Taylor) incompressible mixing, the center of mass Z_COM of the mixing zone satisfies Z_COM = α_COM Agt², in accordance with the self-similar scaling of the flow. Z_COM ≈ 0 for Atwood numbers A < 0.8. For general values of A, the scaling law α_COM = const.A^γ fits the data. Here the constant is determined by the known value α_s = 1/2 for A = 1 (free fall) and an assumed value for α_b, whereas γ ≈ 10 is insensitive to the data. Thus Z_COM and α_COM very efficiently constrain the self-similar flow. The COM relation introduces a new equation that establishes a link between the bubble and spike mixing growth rates. Given a value for α_COM, we have determined that the ratio α_s /α_b is a solution of a quadratic equation. Thus spike data can be predicted from a knowledge of bubble data. See Glimm et al. (1999) and Cheng et al. (1999, 2000). See Figure 1.

The ratio αs /αb is determined by a COM assumption and compared to the experimental data of Dimonte and Schneider (2000) and to a power law fit. The power law is unphysical for A = 1, and thus this fit fails to reproduce the experimental data for large A. Our values for αs /αb agree with the experimental data for all values of A.

5. BUOYANCY DRAG EQUATIONS

A number of authors have considered buoyancy drag equations to describe the dynamics of the edge of the mixing zone. These equations are fundamental for all models of mix, as the data they supply is of such basic importance. Our version of these equations has fewer parameters and greater predictive power than similar equations introduced by others. See Cheng et al. (2000). In addition, we have a finite drag coefficient in the limit A = 1, as is required on intuitive grounds. The equations have the form

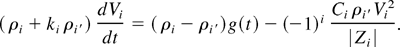
Note that the density ρ_i′ in the drag term in (2) is the density of the fluid being displaced. This form of drag is taken by classical text books in fluid dynamics, but has been incorrectly replaced by ρ_i, the density of the displacing fluid, by a number of workers, leading to a divergent drag coefficient in the limit A → 1.

Here k_i = 1 is an added mass coefficient, Z_i is the penetration distance of the mixing zone on side i = 1 (bubble) and i = 1 (spike), V_i is the edge velocity, and C_i is the drag coefficient. Also g(t) is the acceleration.

There is only one undetermined parameter in (2), namely, C₁ (as C₂ is determined from C₁ by the COM theory). C_i itself is determined from our bubble merger model, or simulations, or from experiment. Substituting the h_i = α_i Agt² late time asymptotic solution for RT mixing, we can determine α_i uniquely in terms of C_i and conversely. Thus the equation is completely determined by the RT data, and in view of Section 4, it is uniquely determined in terms of the RT bubble data alone (with exceptions noted above for large A).

Thus (2) can be used to predict Richtmyer–Meshkov (RM) mixing rate exponents θ_i. The late time RM asymptotics are predicted for the first time from the α_i and usually from α_b alone. We obtain a zero parameter agreement with experiment and with known A = 1 spike limits. See Cheng et al. (2000) and Figure 2.

The exponent θs for RM mixing. The solid and dotted lines are the predictions of Cheng et al. (2000) for αb = 0.05 and for αb = 0.06, respectively. The solid dots are LEM experiments of Dimonte and Schneider (1996).

For g(t) = g, a constant (steady RT mixing), the large time asymptotic solution of the buoyancy drag equation (2) is |Z_i| = α_i Agt². The equation cannot be integrated in closed form for general t, but a closed form approximate evaluation of the next two lower orders (the term proportional to t and the constant term) was obtained. The result exhibited an explicit dependence of these lower order terms on the initial conditions, in contrast to the leading order asymptotics, which is independent of initial conditions. The result is

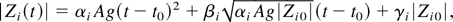
where Z_i0 is an initial amplitude, and V_i0 is an initial velocity. We also define

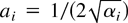
and f_i0 = (1 − a_i|V_i0′|)/ (1 + a_i|V_i0′) as a transform of the scaled initial velocity

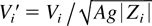
. Then with

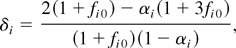
a computation shows that β_i = 2δ_i and γ_i = δ_i². Note the explicit dependence on initial conditions in the lower rather than leading order terms.

This analysis allows an improved fit and interpretation of experimental data. For example, the data of Smeeton and Youngs (1987) and of Read (1984) can be reliably distinguished from the leading order asymptotics and the dependence of this data on Z(t = 0) or V(t = 0) can be observed. See Figure 3.

Dependence of the exact solution of Eq. (1) on variation of the initial data Zb0. The best fitting value for the data of Smeeton and Youngs (1987) is Zb0 = 0.75 for their experiment number 101.

Speculations concerning the cause of discrepancy between simulation and experiment have focused on three possible explanations: (a) numerical diffusion in the untracked simulations, (b) preasymptotic behavior in the simulations, and (c) noise in the experiments of a specific spectral power that generates t² modification to the t² experimental data. Issue (a) is in fact a sufficient explanation (see George et al., 2002). It is possible that (b) may be a contributing explanation. To explore this possibility, the preasymptotic solutions (3) of (2) will be helpful. Issue (c) is discussed in Glimm et al. (2001).

6. MIX MODEL EQUATIONS

Two phase flow equations appropriate to a chunk mix regime have been proposed and studied in detail (see Glimm et al., 1998, 1999, and related papers). The model has several attractive features: it is mathematically stable, that is, totally hyperbolic with real characteristics for time propagation. The equations are thermodynamically determinate, using equation of state models for each constituent in an unmixed mode. Commonly used mix models fail one or both of these properties. In fact, a thermodynamically determinate set of equations is often achieved by assumption of molecular mix, leading to models that possess a single temperature.

The chunk mix equations have been analyzed in great detail, with closed form solutions obtained for the incompressible limit (Glimm et al., 1998, 1999). Perturbation terms in the weakly compressible limit have been computed in closed form through second order in the Mach number (Glimm & Jin, 2001; Jin, 2001). This is the order for which the incompressible pressure first appears. Results for the volume fraction in this limit are displayed in Figure 4.

Volume fraction of the light fluid, showing the incompressible solution, a perturbation term, and the compressible solution computed perturbatively through first order.

Here we discuss new insight regarding closure that have emerged from a study of the weakly compressible theory. The equations resemble the Euler equations for each fluid considered separately. They are coupled through three interface terms. Two of these are a term p*∂β_k /∂z added to the momentum equation for species k and a term (pv)*∂β_k /∂z is added to the energy equation, also for species k. Here β_k is the volume fraction of species k. We use the notation X* to denote the quantity X averaged over the interface, and X_k to denote a volume average of X over the phase volume occupied by species k. Closure assumptions, such as neglect of Reynolds stress terms within a single species phase average, and an assumed identity of volume and mass weighted averages within a single phase average are discussed in Glimm et al. (1998) and earlier papers. The third interface term occurs in the (new) interface equation

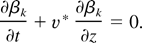
The important closure relations are those for the interface quantities p* and (pv)* and v*. The closure for (pv)* is highly constrained in terms of the v* and p* closures. These two are also constrained to be convex combinations of the corresponding phase quantities, v_k and p_k, with convex coefficients μ_k′^x, x = v, p. We make the hypotheses (appropriate for a chunk mix regime) that there are no internal length scales within the mixing layer, so that the μs must be functions of dimensionless variables, such as β_k. Taking the functional dependence to be fractional linear in β_k, all but one of the four parameters in the fractional linear dependence is determined in an obvious manner by the boundary conditions at z = Z_k, the edges of the mixing zone. In this way the closure is mainly driven by directly observable data, a feature that the authors regard as highly desirable. In fact the edges Z_k are determined by the buoyancy equation (2). The closure relation for p* is set in terms of the ratio of densities (Glimm et al., 1998; Glimm & Jin, 2001). We now discuss the v* closure relation, that is, the equation for the fractional linear definition of μ_k^v in

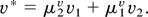
After inserting obvious mixing zone boundary constraints, and our assumed form μ_k^v, we have

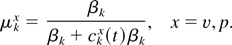
c_k^v was interpreted as a ratio of the volumetric growth rates for the mixing zone for the two phases, c_k^v = |V_k′ /V_k|, in the incompressible case (Glimm et al., 1998, 1999). Here V_k = ∂Z_k /∂t. As is observed below, both the convex sum property (6) and the fractional linear form (7) for the convex coefficients can be derived from the primitive equations, and are thus independent of closure assumptions. Closure thus is a specification of c_k^v.

The volumetric mixing rate constraint determining the v* closure has been extended to the fully compressible case (Glimm & Jin, 2001). Because of compressibility, new terms enter into the phase volume growth rates, including the compressibility of the two phases. In dimensionless terms, this influence enters as a ratio of the sound speeds for the two fluids in the weakly compressible limit. We start with an exact identity for c_k^v, valid for the fully compressible two-fluid equations, derived in the absence of any closure assumptions at all. Note that the interface equation, the convex sum property for v*, and the fractional linear form for μ_k^v are all derived in this equation independently of closure assumptions. We have

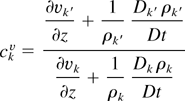
is the ratio of logarithmic rates of volume creation for the two species, where D_k /Dt = ∂/∂t + v_k∂/∂t is the convective derivative defined by the velocity v_k. Then the closure (absence of internal length scales) can be interpreted as an equation for c_k^v, namely,

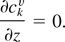
It is of interest to analyze the v* closure in the weakly compressible perturbative analysis. There we find that the incompressible pressures, the ratios of the compressible sound speeds, the second order contribution to the phase volume expansion ratio |V_k /V_k′|, and the second order perturbation term in the expansion of c_k^v are linked by a newly derived equation (Glimm & Jin, 2001; Jin, 2001). This equation removes an indeterminancy in the incompressible equations, previously not understood, and shows that the two phase incompressible equations, in contrast to the single phase case, remember the compressible fluids from which they are derived. We first reformulate (9) as

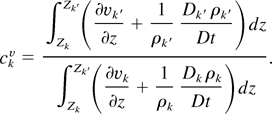
The formula (10) can now be expanded perturbatively in powers of the Mach number, and the second-order term in this expansion includes the incompressible pressure. The resulting equation is the desired new equation for the incompressible pressure. See Jin (2001) and Glimm & Jin (2001).

On the basis of the above analysis, we are able to link the phenomenological drag coefficients in the buoyancy drag equation for the edge motion with fundamental laws of physics. Newton's law of acceleration, applied at the edge of the mixing zone is equivalent to the momentum equation, evaluated at this location. The equations can be highly simplified in this evaluation (Glimm et al., 1999) and resemble buoyancy drag equations (2). In fact, they are different, due to the absence of phenomenological quantities. Thus the added mass and the drag are replaced by exact quantities, which, however, are not convenient to evaluate. Specifically they relate to the pressure difference between the phases and the gradient of the pressure difference. A closed form solution for the pressure equation in the incompressible limit, to be published, reveals terms that can be readily identified as inertial terms (added mass), fundamentally exact drag terms (depending on velocity differences), and pressure difference terms (interpreted as phenomenological corrections to the drag terms). Thus we see that the buoyancy drag equations can be obtained via a closure relation that expresses the added mass and drag as pressure difference terms in the exact momentum equation and relates these to quantities known in the buoyancy drag equation, namely, lengths, velocities, and accelerations.

7. EFFECTIVE DIFFUSION AND REYNOLDS STRESS

Reduced multiphase mixture models have fewer equations and fewer variables. They are logically derived from more complete models. Here we derive a single-velocity, single-temperature model from the chunk mix model of Section 6, following Cheng et al. (2002b). For models with a single velocity, this velocity will express mean fluid flow, and cannot drive the mixture process, which is then modeled as a diffusion process. The point is to determine the (time and spatially dependent) interspecies diffusivity, which governs the mixing rates diffusivity. Assuming this to be a function of the volume fraction β_k, Alon and Shvarts (1996) propose diffusion proportional to β_k(1 − β_k) = β₁ β₂. We find corrections to this form that reflect the deviation of the volume fraction from being a linear function of z.

The key to the computation of the diffusivity is a determination of entrainment time. For a given parcel of fluid k at a given space time location within the mixing zone, the entrainment time is defined to be (the earlier) time at which that parcel entered the mixing zone. Given the velocity history of the two phases, available in closed form (in terms of the edge positions Z_k), one integrates backward in time until the moving edge Z_k′(s) is encountered. This motion is then interpreted as a diffusion process, and the exact value of diffusion that duplicates this motion is determined. For RT mixing, the diffusivity can be determined in closed form, whereas for RM mixing, the diffusivity is solved via an approximate closed-form expression, and also by integration of an ordinary differential equation. For the general case, the solution is given up to a quadrature. For the RT case, the closed-form expression for the diffusivity D is

where

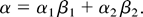
Note that the formula is not symmetric between β₁ and β₂ because α₁ ≠ α₂ for A > 0. The factor in the square brackets is the correction to the formula of Alon and Shvarts (1996). This factor reflects the lack of symmetry between the two phases and is especially significant for Richtmyer–Meshkov mixing (see Fig. 5).

The diffusion coefficient D across the mixing layer in RT mixing. The dash-dotted line is for A = 0.5, α2 = 0.07 and the solid line is for A = 0.96, α2 = 0.18.

The dominant component R_zz of the Reynolds stress tensor is also determined in Cheng et al. (2002b).