1. INTRODUCTION
The problem of efficient generation of terahertz (THz) radiation, frequency range 0.1–10 THz, has attracted considerable interest over the past 10 years due to a lot of important promising applications. Numerous applications can be found in a wide range of fields such as physics, chemistry, biology, information, and security (Cooke & Jespen, Reference Cooke and Jespen2009; Bartman et al., Reference Bartman, Litvak and Suvorov2011; Tao et al., Reference Tao, Padilla, Zhang and Averitt2011; Kim et al., Reference Kim, Kim, Park, Han and Son2012). Various techniques have been employed for THz generation using high-power lasers. Many laser-based THz emitters have been proposed to generate THz wave, using electro-optic crystals (ZnTe, GaAs, LiNbo3, etc.), semiconductors and photoconductive antennas (Jepsen et al., Reference Jepsen, Jacobsen and Keiding1996; Hashimshony et al., Reference Hashimshony, Zigler and Papadopoulos1999; Lee et al., Reference Lee, Meade, Perlin, Winful, Norris and Galvanauskas2000; Faure et al., Reference Faure, Tilborg, Kanidal and Leemans2004; Vodopyanov, Reference Vodopyanov2008; Chen et al., Reference Chen, Zhou, Werley and Nelson2011). When the energy or focusing intensity of the pump laser is high, the materials may be damaged (Li et al., Reference Li, Wang, Chun and Sheng2012b ). In contrast, plasmas can overcome the damage problem of neutral materials. Recent studies have shown that plasmas are promising media to generate strong THz radiation (Sheng et al., Reference Sheng, Mima, Zhang and Sanuki2005). In principle, the laser intensity can be arbitrarily high for plasmas. The typical intensity of a multi-terawatt (TW) laser system is higher than 1018 w/cm2 (up to 1021 w/cm2 with a Petawatt laser) (Li et al., Reference Li, Wang, Chun and Sheng2012b ). Hamster et al. (Reference Hamster, Sullivan, Gordon, White and Falcone1993) observed a high-power THz radiation from a plasma short pulse produced by laser, employing 1 TW, 100 fs laser beam focused on gas and solid targets. They also observed THz radiation in a laser-induced plasma channel where ponderomotive force drives radiation. Antonsen et al. (Reference Antonsen, Palastro and Michberg2007) examined the ponderomotive force-driven THz radiation generation in a plasma with space periodic axial density variation. Wu et al. (Reference Wu, Sheng, Dong, Xu and Zhang2007) have studied the effect of transverse magnetic field on the wakefield process and found a significant enhancement in the efficiency of THz generation. Fedele et al. (Reference Fedele, Angelis and Katsouleas1986) have reported radial electric field components generated by the propagation of two electromagnetic waves resonantly beating in a plasma. Malik et al. (Reference Malik, Malik and Kawata2010) investigated the THz generation by tunnel ionization of a gas jet with the help of superposed femtosecond laser pulses and by laser beating in periodically modulated plasma. They also reported the generation of tunable THz radiation under the application of 2 fs laser pulses with an external magnetic field (Malik & Malik, Reference Malik and Malik2011). The resonant excitation of THz radiation by beating of two spatial-Gaussian laser beams has been proposed by Malik et al. (Reference Malik, Malik and Stroth2012). Bakhtiari et al. (Reference Bakhtiari, Golmohamady, Yosefi, Kashani and Ghafary2015a ) have studied the THz generation by beating of two dark hollow laser beams and two circular flat-topped laser beams. Bakhtiari et al. (Reference Bakhtiari, Yosefi, Golmohamady, Jazaayeri and Ghafary2015b ) have showed strongly THz radiation generation through shape control of emitted THz radiation in collisional plasmas. Chauhan and Parashar (Reference Chauhan and Parashar2014) have considered two laser beams, which obliquely incident on a plasma slab for two different electron density profiles. Parashar (Reference Parashar2014) has reported THz radiation by beating of two laser beams, which obliquely incident on the plasma. Kumar et al. (Reference Kumar, Tripathi and Jeong2015) investigated THz generation in hot plasma with step density profile by two obliquely incident of lasers on the plasma. Compared with low-density gases, overdense plasmas of solids have higher electron density thus holding the promise of producing higher-power THz pulses (Li et al. Reference Li, Wang, Chun and Sheng2012b ). Interaction of laser with an overdense plasma also results in generation of electromagnetic radiation at harmonics of incident wave in the reflected component. Gopal et al. (Reference Gopal, May, Herzer, Reinhard, Minardi, Schubert, Dillner, Pradarutti, Polz, Gaumnitz, Kaluza, Jäckel, Riehemann, Ziegler, Gemuend, Meyer and Paulus2012) have reported experimental observation of THz radiation from the rear surface of a solid target with an intense laser pulse and showed THz radiation is mostly emitted at large angles to the target normal. Adak et al. (Reference Adak, Robinson, Singh, Chatterjee, Lad, Pasley and Kumar2015) have observed experimentally THz radiation by a pump pulse at an angle of 45° and a probe pulse at near normal incident, which are focused on a polished BK-7 glass target. Weiss et al. (Reference Weiss, Wallenstein and Beigang2000) have showed experimentally by applying an external magnetic field, the power of the generated THz radiation is increased for all examined semiconductor materials. Hangyo et al. (Reference Hangyo, Migita and Nakayama2001) have studied experimentally THz radiation from indium arsenide (InAs) surfaces in the presence of the magnetic field, which excited by femtosecond laser pulses. McLaughlin et al. (Reference McLaughlin, Corchia, Johnston, Chen, Ciesla, Arnone, Jones, Linfield, Davies and Pepper2000) have demonstrated experimentally enhancement of THz emission from InAs in the presence of magnetic fields up to 8 T. Migita and Hangyo (Reference Migita and Hangyo2001) have reported experimentally enhancement of THz radiation from InAs surfaces under magnetic fields excited by ultrashort laser pulses for low and high pump power densities. Li et al. (Reference Li, Li, Zhou, Wang, Du, Ding, Lin, Liu, Sheng, Peng, Chen, Ma, Lu, Wang, Wei and Zhang2012a ) have reported a plasma-based strong THz source generated in intense laser–solid interactions at relativistic intensities when the laser pulses are incident onto a copper foil at 67.5° Li et al. (Reference Li, Zhou, Ding, Du, Liu, Li, Wang, Sheng, Ma, Chen, Lu, Dong, Wang, Lou, Shi, Wei and Zhang2011) have studied interactions of 100 fs laser pulses with solid targets. Shvartsburg and Stenflo (Reference Shvartsburg and Stenflo1994) have formulated a new method to study reflection of wideband electromagnetic pulses at a plasma boundary. Aliev et al. (Reference Aliev, Frolov, Brodin and Stenflo1993) have studied total backward reflection of electromagnetic radiation due to resonant excitation of surface wave over plasma. Parashar et al. (Reference Parashar, Mishra and Mahajan2013) have studied THz radiation in the overdense plasma. Chen et al. (Reference Chen, Li and Yu2013) have studied THz radiation by interaction of a relativistic circularly polarized laser pulse with an overdense plasma and have showed remarkably intense THz pulses.
In this work, we study THz radiation generation via nonlinear mixing of two obliquely incident laser beams over an overdense plasma in the presence of magnetic field. Overdense plasmas have been considered since it can be easily realized by employing a metallic sheet or a semiconductor. Also contrary to neutral materials and plasma filaments, almost arbitrarily high laser energies and intensities can be used in laser–solid interactions (Li et al., Reference Li, Wang, Chun and Sheng2012b ).
This paper is organized as follows: In Section 2, we study nonlinear oscillatory current density due to the ponderomotive force developed during photo mixing of two laser beams in the presence of static magnetic field. In Sections 3 and 4, we evaluate the THz radiation field and efficiency. In Section 5, we present the results of analytical investigations. Conclusions are presented in Section 6.
2. CALCULATION OF NONLINEAR CURRENT DENSITY
We consider two p-polarized lasers with frequencies ω1, ω2 and wave vector
$\vec k_1$
,
$\vec k_2$
, propagating and polarized in the xy-plane that obliquely incident on an overdense plasma in the presence of a static magnetic field B
0 along the z-direction (Fig. 1).
Fig. 1. Schematic diagram of THz radiation generation from overdense plasma.
We consider the electric field of incident lasers as
$$\vec E_j = \vec E_{\,j0}\exp \left( { - i\left( {{\rm \omega} _jt - \displaystyle{{{\rm \omega} _j} \over c}\cos {\rm \theta} _ix - \displaystyle{{{\rm \omega} _j} \over c}\sin {\rm \theta} _iy} \right)} \right),$$
where
$\vec E_{\,j0} = A_{\,j{\rm 0}}( - \tan {\rm \theta} _i\hat x + \hat y)$
, j = 1,2.
In an overdense plasma, where the frequency of incident laser beam smaller than plasma frequency, the electromagnetic radiation cannot penetrate deeply into the plasma. It penetrates into the plasma as far as the evanescence length, which is of the order of ~c/ωp (Bulanov et al., Reference Bulanov, Califano, Dudnikova, Zh. Esirkepov, Inovenkov, Kamenets, Liseikina, Lontano, Mima, Naumova, Nishihara, Pegoraro, Ruhl, Sakharov, Sentoku, Vshivkov, Zhakhovskii and Shafranov2001), where, c is the speed of light in the vacuum and ωp is the plasma frequency. Therefore the transmitted fields of laser in the plasma, can be written as (Parashar et al., Reference Parashar, Mishra and Mahajan2013).
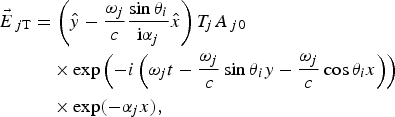$$\eqalign{{\vec E}_{\,j{\rm T}} & = \left( {\hat y - \displaystyle{{{\rm \omega} _j} \over c}\displaystyle{{\sin {\rm \theta} _i} \over {{\rm i}{\rm \alpha} _j}}\hat x} \right)T_jA_{\,j0} \cr & \quad \times \exp \left( { - i\left( {{\rm \omega} _jt - \displaystyle{{{\rm \omega} _j} \over c}\sin {\rm \theta} _iy - \displaystyle{{{\rm \omega} _j} \over c}\cos {\rm \theta} _ix} \right)} \right) \cr & \quad \times\exp ( - {\rm \alpha} _jx),} $$
where
${\rm \alpha} _j = ({\rm \omega} _{\rm p}^2 /c^2 - {\rm \omega} _j^2 \cos ^2{\rm \theta} _i/c^2)^{1/2}$
, ωp = (4πn
0
e
2/m)1/2, T
j
= 2/(1 + (iω
j
/α
j
c)cosθ
i
), n
0 is equilibrium electron density, m and e are the electron mass and charge. Since the plasma is overdense, the plasma frequency ωp must be larger than ω1 and ω2. It is supposed that ω1 > ω2, therefore n
0 > n
c. n
c is the critical density and given by
$n_{\rm c} = m{\rm \omega} _1^2 /4{\rm \pi} e^2$
. Lasers impart oscillatory velocity to the electrons of plasma
$\vec v_j = {{e{\vec E}_j} / {mi{\rm \omega} _j}}$
and exert beat frequency ponderomotive force on them.
$$\vec F_{\rm p}^{{\rm NL}} = - \displaystyle{m \over 2}\vec \nabla (\vec v_1 \bullet \vec v_2^{\, *} ).$$
The nonlinear perturbations in the electron density
$n_{\rm e}^{{\rm NL}} $
due to nonlinear ponderomotive force
$\vec F_{\rm p}^{{\rm NL}} $
are obtained by solving of continuity equation
$$n_{\rm e}^{{\rm NL}} = \displaystyle{{n_0} \over {m({\rm \omega} ^2 - {\rm \omega} _{\rm c}^2 )}}\vec \nabla. \left( {\vec F_{\rm p}^{\,{\rm NL}} + \vec F_{\rm p}^{{\rm NL}} \times \displaystyle{{{\rm \omega} _{\rm c}\hat z} \over {i{\rm \omega}}}} \right),$$
where ωc = eB0/mc, ω = ω1 − ω2 are the electron cyclotron frequency and beating frequency. The density perturbation produces a self-consistent space charge field
$\vec E = - \vec \nabla {\phi} $
that also produces a density perturbation
$n_{\rm e}^{\rm L} = - ({\rm \chi} _{\rm e}/4{\rm \pi} e)\vec \nabla. (\vec \nabla {\phi} )$
, where
${\rm \chi} _{\rm e} = - {\rm \omega} _{\rm p}^2 /({\rm \omega} ^2 - {\rm \omega} _{\rm c}^2 )$
. Linear ponderomotive force is given by
$\vec F^{\,\rm L} = e\vec \nabla {\phi} $
. Using Poisson's equation
$\vec \nabla. (\vec \nabla {\rm \phi} ) = $
$4{\rm \pi} e(n_{\rm e}^{\rm L} + n_{\rm e}^{{\rm NL}} )$
and equation of motion
$m(d\vec v_{\rm \omega} ^{\,{\rm NL}} /dt) = \vec F^{\,\rm L} + $
$\vec F^{{\,\rm NL}} - \vec v_{\rm \omega} ^{{\,\rm NL}} \times (e{\rm B}_0/c)\hat z$
the nonlinear electron velocity obtained as follows:
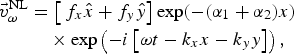$$\eqalign{\vec v_{\rm \omega} ^{{\rm NL}} & = \left[ {\,f_x\hat x + f_y\hat y} \right]\exp ( - ({\rm \alpha} _1 + {\rm \alpha} _2)x) \cr & \quad \times \exp \left( { - i\left[ {{\rm \omega} t - k_xx - k_yy} \right]} \right),} $$
where f x , fy, f 0, k y , and k x are defined as
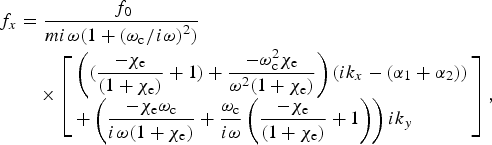$$\eqalign{\,f_x & = \displaystyle{{\,f_0} \over {mi{\rm \omega} (1 + {({\rm \omega} _{\rm c}/i{\rm \omega} )}^2{\rm )}}} \cr & \quad \times \left[ \matrix{\left( {(\displaystyle{{ - {\rm \chi} _{\rm e}} \over {(1 + {\rm \chi} _{\rm e})}} + 1) + \displaystyle{{ - {\rm \omega} _{\rm c}^2 {\rm \chi} _{\rm e}} \over {{\rm \omega} ^2(1 + {\rm \chi} _{\rm e})}}} \right)(ik_x - ({\rm \alpha} _1 + {\rm \alpha} _2)) \hfill \cr + \left( {\displaystyle{{ - {\rm \chi} _{\rm e}{\rm \omega} _{\rm c}} \over {i{\rm \omega} (1 + {\rm \chi} _{\rm e})}} + \displaystyle{{{\rm \omega} _{\rm c}} \over {i{\rm \omega}}} \left( {\displaystyle{{ - {\rm \chi} _{\rm e}} \over {(1 + {\rm \chi} _{\rm e})}} + 1} \right)} \right)ik_y \hfill} \right],} $$
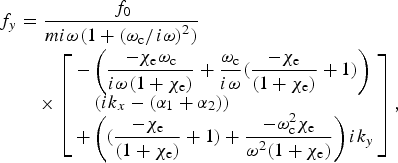$$\eqalign{\,f_y & = \displaystyle{{\,f_0} \over {mi{\rm \omega} (1 + {({\rm \omega} _{\rm c}/i{\rm \omega} )}^2{\rm )}}} \cr & \quad \times \left[ \matrix{ - \left( {\displaystyle{{ - {\rm \chi} _{\rm e}{\rm \omega} _{\rm c}} \over {i{\rm \omega} (1 + {\rm \chi} _{\rm e})}} + \displaystyle{{{\rm \omega} _{\rm c}} \over {i{\rm \omega}}} (\displaystyle{{ - {\rm \chi} _{\rm e}} \over {(1 + {\rm \chi} _{\rm e})}} + 1)} \right) \hfill \cr \quad (ik_x - ({\rm \alpha} _1 + {\rm \alpha} _2)) \hfill \cr + \left( {(\displaystyle{{ - {\rm \chi} _{\rm e}} \over {(1 + {\rm \chi} _{\rm e})}} + 1) + \displaystyle{{ - {\rm \omega} _{\rm c}^2 {\rm \chi} _{\rm e}} \over {{\rm \omega} ^2(1 + {\rm \chi} _{\rm e})}}} \right)ik_y \hfill} \right],} $$
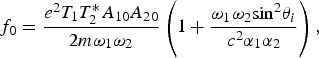$$f_0 = \displaystyle{{e^2T_1T_2^* A_{10}A_{20}} \over {2m{\rm \omega} _1{\rm \omega} _2}}\left( {1 + \displaystyle{{{\rm \omega} _1{\rm \omega} _2{\sin} ^2{\rm \theta} _i} \over {c^2{\rm \alpha} _1{\rm \alpha} _2}}} \right),$$
$$k_y = \displaystyle{{{\rm \omega} \sin {\rm \theta} _i} \over c},\quad k_x = \displaystyle{{{\rm \omega} \cos {\rm \theta} _i} \over c}.$$
From Eq. (5) we can calculate the nonlinear current density
$\vec J_{\rm \omega} ^{\,{\rm NL}} $
as
$$\vec J_{\rm \omega} ^{{\rm NL}} = - n_0e\vec v_{\rm \omega} ^{{\rm NL}}, $$
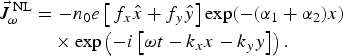$$\eqalign{\vec J_{\rm \omega} ^{\,{\rm NL}} & = - n_0e\left[ {\,f_x\hat x + f_y\hat y} \right]\exp ( - ({\rm \alpha} _1 + {\rm \alpha} _2)x) \cr & \quad \times \exp \left( { - i\left[ {{\rm \omega} t - k_xx - k_yy} \right]} \right).} $$
3. THz RADIATION GENERATION
The wave equation governing the THz wave is derived from the third and fourth Maxwell's equations
$$\nabla ^2\vec E_{\rm \omega} - \vec \nabla (\vec \nabla .\vec E_\omega ) + \displaystyle{{\omega ^2} \over {c^2}}\overline {\overline {\rm \varepsilon} } \vec E_\omega = \displaystyle{{ - 4\pi i\omega } \over {c^2}}\vec J_\omega ^{\,{\rm NL}}, $$
where
$\overline {\overline {\rm \varepsilon} }$
is the electric permittivity tensor with components
${\rm \varepsilon} _{xx} = {\rm \varepsilon} _{yy} = 1 - ({\rm \omega} _{\rm p}^2 /({\rm \omega} ^2 - {\rm \omega} _{\rm c}^2 ))$
,
${\rm \varepsilon} _{xy} = - {\rm \varepsilon} _{yx} = (i{\rm \omega} _{\rm p}^2 {\rm \omega} _{\rm c}/$
${\rm \omega} ({\rm \omega} ^2 - {\rm \omega} _{\rm c}^2 )), {\rm \varepsilon} _{zz} = 1 - ({\rm \omega} _{\rm p}^2 /{\rm \omega} ^2),$
and ε
xz
= ε
yz
= ε
zx
= ε
zy
= 0 (Bittencourt, Reference Bittencourt2004). The solution of wave equation in the vacuum x < 0 is given by plane wave as
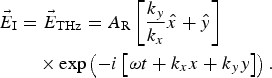$$\eqalign{{\vec E}_{\rm I} & = {\vec E}_{{\rm THz}} = A_{\rm R}\left[ {\displaystyle{{k_y} \over {k_x}}\hat x + \hat y} \right] \cr & \quad \times \exp \left( { - i\left[ {{\rm \omega} t + k_xx + k_yy} \right]} \right).} $$
Equation (7) is nonhomogeneous second-order partial differential equation. The general solution of this equation comprises from its particular solution and solution of homogeneous part. Homogeneous part of Eq. (7) is
$\nabla ^2\vec E_{\rm \omega} - \vec \nabla (\vec \nabla. {\rm } \vec E_{\rm \omega} ) +({\rm \omega} ^2/c^2) $
$\overline {\overline {\rm \varepsilon} } \vec E_{\rm \omega} = 0,$
which its solution is as
$$A_{\rm T}[{\rm \delta} \hat x + \hat y]\exp ( - i[{\rm \omega} t - k_xx - k_yy]),$$
where
$${\rm \delta} = \displaystyle{{( - k_y{\rm \beta} + ({\rm \omega} ^2/c^2){\rm \varepsilon} _{yx})} \over {( - k_y^2 + ({\rm \omega} ^2/c^2){\rm \varepsilon} _{xx}){\rm}}}, \quad {\rm \beta} = \sqrt {\displaystyle{{{\rm \omega} ^2} \over {c^2}}\left( {{\rm \varepsilon} _{xx} + \displaystyle{{{\rm \varepsilon} _{yx}^2} \over {{\rm \varepsilon} _{xx}}}} \right) - k_y^2}.$$
Particular solution of Eq. (7) is given by
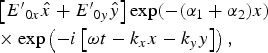$$\eqalign{& \left[ {{{E}^{\prime}}_{0x}\hat x + {\rm} {{E}^{\prime}}_{0y}\hat y} \right]\exp ( - ({\rm \alpha} _1 + {\rm \alpha} _2)x) \cr & \times \exp \left( { - i\left[ {{\rm \omega} t - k_xx - k_yy} \right]} \right),} $$
where
$$\eqalign{{\rm} {{E}^{\prime}}_{0x} = \displaystyle{{\left( {4{\rm \pi} i{\rm \omega} n_0e/c^2} \right)} \over \matrix{( - k_y^2 + (ik_x - ({\rm \alpha} _1 + {\rm \alpha} _2))^2)({\rm \omega} ^2/c^2){\rm \varepsilon} _{xx} \hfill \cr \quad + (({\rm \omega} ^2/c^2){\rm \varepsilon} _{xx})^2 + (({\rm \omega} ^2/c^2){\rm \varepsilon} _{yx})^2 \hfill}} \cr \quad \times \left( \matrix{\,f_y((ik_x - ({\rm \alpha} _1 + {\rm \alpha} _2))ik_y + \displaystyle{{{\rm \omega} ^2} \over {c^2}}{\rm \varepsilon} _{yx}) \hfill \cr + f_x((ik_x - ({\rm \alpha} _1 + {\rm \alpha} _2))^2 + \displaystyle{{{\rm \omega} ^2} \over {c^2}}{\rm \varepsilon} _{xx}) \hfill} \right),} $$
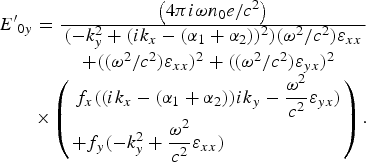$$\eqalign{{\rm} {{E}^{\prime}}_{0y} = \displaystyle{{\left( {4{\rm \pi} i{\rm \omega} n_0e/c^2} \right)} \over \matrix{( - k_y^2 + (ik_x - ({\rm \alpha} _1 + {\rm \alpha} _2))^2)({\rm \omega} ^2/c^2){\rm \varepsilon} _{xx} \hfill \cr \quad + (({\rm \omega} ^2/c^2{\rm )}{\rm \varepsilon} _{xx})^2 + (({\rm \omega} ^2/c^2){\rm \varepsilon} _{yx})^2 \hfill}} \cr \quad \times \left( \matrix{\,f_x((ik_x - ({\rm \alpha} _1 + {\rm \alpha} _2))ik_y - \displaystyle{{{\rm \omega} ^2} \over {c^2}}{\rm \varepsilon} _{yx}) \hfill \cr + f_y( - k_y^2 + \displaystyle{{{\rm \omega} ^2} \over {c^2}}{\rm \varepsilon} _{xx}) \hfill} \right).}$$
Therefore, general solution of Eq. (7) in the plasma x ≥ 0 is
$$\eqalign{{\vec E}_{{\rm II}} & = \left( \matrix{A_{\rm T}\left[ {{\rm \delta} \hat x + \hat y} \right] \hfill \cr + \left[ {{\rm} {{E}^{\prime}}_{{\rm 0}x}\hat x + {\rm} {{E}^{\prime}}_{0y}\hat y} \right]\exp ( - ({\rm \alpha} _1 + {\rm \alpha} _2)x){\rm} \hfill} \right) \cr & \quad \times \exp \left( { - i\left[ {{\rm \omega} t - k_xx - k_yy} \right]} \right).} $$
A R and A T are the constant coefficients. On applying the boundary conditions at x = 0, (E I) y = (E II) y and (εIE_I)x = (εII E II) x .We obtain from Eqs (8) and (9)
$$A_{\rm R} = A_{\rm T} + {E}^{\prime}_{0y}$$
and
$$A_{\rm R}\displaystyle{{k_y} \over {k_x}} = {\rm \varepsilon} _{xx}\left[ {A_{\rm T}{\rm \delta} + {{E}^{\prime}}_{0x}} \right] - {\rm \varepsilon} _{yx}\left[ {A_{\rm T} + {{E}^{\prime}}_{0y}} \right].$$
From Eqs (10) and (11), the amplitude of generated THz wave in the reflected component is obtained as follows:
$$\left \vert {A_{\rm R}} \right \vert = \left \vert {\displaystyle{{ - {\rm \varepsilon} _{xx}{\rm \delta} {{E}^{\prime}}_{0y} + {\rm \varepsilon} _{xx}{{E}^{\prime}}_{0x}} \over {k_y/k_x - {\rm \varepsilon} _{xx}{\rm \delta} + {\rm \varepsilon} _{yx}}}} \right \vert. $$
4. THZ RADIATION EFFICIENCY
The efficiency of the emitted radiation is the ratio of the energy of THz radiation and the energy of the incident lasers. According to Rothwell and Cloud (Reference Rothwell and Cloud2009) in general, the average electromagnetic energy stored per unit volume is given by the formula:
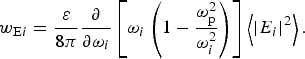$$w_{{\rm E}i} = \displaystyle{{\rm \varepsilon} \over {8{\rm \pi}}} \displaystyle{\partial \over {\partial {\rm \omega} _i}}\left[ {{\rm \omega} _i\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _i^2}}} \right)} \right]\left\langle {{\left\vert {E_i} \right\vert} ^2} \right\rangle. $$
The energy densities of the incident lasers and THz radiation are evaluated as
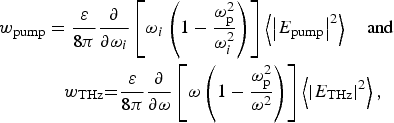$$\eqalign{w_{{\rm pump}}& = \displaystyle{{\rm \varepsilon} \over {{\rm 8{\rm \pi}}}} \displaystyle{\partial \over {\partial {\rm \omega} _i}}\left[ {{\rm \omega} _i\left( {{\rm 1} - \displaystyle{{{\rm \omega} _{\rm p}^{\rm 2}} \over {{\rm \omega} _i^{\rm 2}}}} \right)} \right]\left\langle {{\left \vert {E_{{\rm pump}}} \right \vert} ^{\rm 2}} \right\rangle \quad {\rm and}\quad \cr & \quad w_{{\rm THz}}{\rm =} \displaystyle{{\rm \varepsilon} \over {{\rm 8{\rm \pi}}}} \displaystyle{\partial \over {\partial {\rm \omega}}} \left[ {{\rm \omega} \left( {{\rm 1} - \displaystyle{{{\rm \omega} _{\rm p}^{\rm 2}} \over {{\rm \omega} ^2}}} \right)} \right]\left\langle {{\left\vert {E_{{\rm THz}}} \right \vert} ^{\rm 2}} \right\rangle,}$$
respectively. Based on this and following the method used by Malik et al. (Reference Malik, Singh and Sajal2014), the efficiency of the THz radiation (η) is calculated as
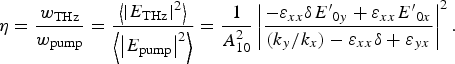$${\rm \eta} = \displaystyle{{w_{{\rm THz}}} \over {w_{{\rm pump}}}} = \displaystyle{{\left\langle {{\left \vert {E_{{\rm THz}}} \right \vert} ^2} \right\rangle} \over {\left\langle {{\left \vert {E_{{\rm pump}}} \right \vert} ^2} \right\rangle}} = \displaystyle{1 \over {A_{10}^2}} \left \vert {\displaystyle{{ - {\rm \varepsilon} _{xx}{\rm \delta} {{E}^{\prime}}_{0y} + {\rm \varepsilon} _{xx}{{E}^{\prime}}_{0x}} \over {(k_y/k_x) - {\rm \varepsilon} _{xx}{\rm \delta} + {\rm \varepsilon} _{yx}}}} \right \vert ^2.$$
5. RESULTS AND DISCUSSION
We have used the following set of parameters λ1 = 9.6, λ2 = 9.75 µm, and eA 20/ω1 mc = 0.003. The typical parameters can be belonged to a CO2 laser. Plasma frequency supposed as ωp = 2.25 × 1014 rad/s, which is corresponding to the electron density n 0 = 1.6 × 1019 cm−3. Critical density supposed as n c = 1.2 × 1019 cm−3. In Figure 2, the normalized THz wave amplitude |A R/A 10| versus angle of incident lasers θ i is plotted. As the figure shows, in the absence of magnetic field the normalized THz amplitude has a minimum about θ i = 20° and a maximum about θ i = 70°. In the presence of a magnetic field, the form of curve roughly does not change, but the magnetic field increases generated THz amplitude for all angles of incident.
Fig. 2. Normalized THz amplitude |A R/A 10| versus angle of incident θ i for different values of magnetic field strength.
Figure 3 shows the variation of efficiency of THz radiation with normalized beating frequency for different values of magnetic field strength. From this figure it is clear that the effect of magnetic field gradually disappears in large beating frequency. Also by increasing of beating frequency the efficiency is decreasing, the similar behavior occurs in the underdense plasma (Malik et al., Reference Malik, Singh and Sajal2014). This figure and Figure 4 illustrate that the present scheme of frequency-mixing of two laser beams in an overdense magnetized plasma is very effective. High efficiency can be obtained if large angle of incident lasers and strong magnetic field are used. Figure 3 also shows that the efficiency of THz radiation from an overdense magnetized plasma is greater than the underdense plasma (Malik et al. Reference Malik, Malik and Kawata2010, Reference Malik, Malik and Stroth2012, Reference Malik, Singh and Sajal2014; Malik & Malik, Reference Malik and Malik2011; Bakhtiari et al. Reference Bakhtiari, Golmohamady, Yosefi, Kashani and Ghafary2015a , Reference Bakhtiari, Yosefi, Golmohamady, Jazaayeri and Ghafary b ). Malik and Singh (Reference Malik and Singh2015) have proposed THz radiation generation by beating of two super-Gaussian lasers in rippled density plasma and realized the efficiency about 0.25 for an applied magnetic field about 60 kG, where the present scheme can be realized efficiency about 0.27 for the applied magnetic field about 50 kG.
Fig. 3. Variation of efficiency of THz radiation versus normalized beating frequency for different values of strength of magnetic field.
Fig. 4. Efficiency of THz radiation versus angle of incident θ i for different values of strength of magnetic field, when ω/ωp = 0.01338.
6. CONCLUSION
We have presented a scheme for THz generation based on nonlinear mixing of two obliquely incident laser beams on an overdense magnetized plasma. It is investigated that the amplitude and efficiency of the THz wave increases with increasing of magnetic field also THz wave amplitude can be optimized at a particular angle which occurred in large incident angle of lasers. Our analytical investigations show that this scheme is quite effective for getting the strong THz radiation and the efficiency of THz radiation from an overdense magnetized plasma is greater than the underdense plasma. A natural extension for future works is to include collision into this scheme.
ACKNOWLEDGMENT
Authors thank members of Department of Physics, Iran University of Science & Technology for their helpful discussion.
